应用光学2018(第二章)2
应用光学习题(第二章)

个面对不晕像点。
n2 n2 n 1 l2 r2 r2 n2 n n2 n2 l2 r2 n 1r2 n2
1 n n 1 n 1 r1 - r2 r1 r2 n n n 由于 d始终都是大于零的,所 以r1 r2 (由于 r1 0,r2 0,且 r1 r2,该透镜为负弯月型透 镜)
1 n2
S1
S1与S2重合,所以 r2 l2 l2
d l1 l2
n
r1
C1 l2 l2 l1 r2 l1
C2
n1 n1 1 n 而 l1 r1 r1 n1 n 1 n d r1 r2 n
b. 同心球面透镜 物像点重合且位于两个 球面的共同曲率中心 C1,C 2点上Leabharlann 所以编号出处
2_004
P193_7
什么是不晕透镜?当透 镜成无球差点实像点时 ,应采用 什么样的结构形式 ?
答: ( 1)所谓不晕透镜,是轴 上物点单色光成像时, 不产生球差的透镜
(2) 由于不晕条件,物象点 在透镜的同一侧,所以 不晕透镜 分为两种情况:一种是 实物成虚像,而另一种 是虚物成实像。 该题中得到实像点时, 采用的就是虚物成实像 的形式(会聚光入射) r1 0,r2 0 a. 正弯月单透镜 r1 r2 r1 r2,所以第一个面对球心 C 1点在 C2点的左边
,S2,S 同心球面透镜构成不晕 透镜C ( ,S1,S1 2 C1 2)
n1 1
1 n2
C1 C2
n
r1 l1 l1 r2 l2 l2
,S2与S2重合 S1,S1 d r1 r2
编号
出处
2_005
应用光学作业题答案

第二题: (1)光线由水中射向空气,求在界面处发生全反射的临界角。
解: 全反射的临界角Im arcsin(n '/ n)
光线由水中射向空气,n’=1,n=1.333
则 Im arc sin(n '/ n)=arc sin(1/1.333)=48.61
(2)光线由玻璃内部射向空气,求发生全反射的临界角。
1 l2
'
-
1 130
=
1 120
l2'=-62.4mm
A”成象于透镜2左侧62.4mm处。
(2)等效光组成象的方法:
解: H’
A
F1
F2’
F1’
F2
f1’=120mm f2’=-120mm d=70mm △= d-f1’- f2’=70mm
f ' f1 ' f2 ' 120 (120) 205.714mm
n0sini1=nsini1’ sini1=0.6552 i1=40.93° 由三角形内角和可求出太阳和幻
日之间的夹角
α=180 °-2×(i1-i1’) =158.14 °
第七题:
为了从坦克内部观察外界目标,需要在坦克上开一个孔,假 定坦克壁厚250mm,孔宽150mm,在孔内装一块折射率 n=1.52的玻璃,厚度与装甲厚度相同,问能看到外界多大的 角度范围?
O’
A’
解:(1)对于在球心的气泡,以O作为 球面顶点,根据符号规则,
O L’A=-200mm,n’=1,n=1.52
由 n ' n n ' n l' l r
1 -1.52 = 1-1.52 l=-200mm -200 l -200
最新应用光学课件第二章幻灯片课件

靠近光轴的区域叫近轴区,近轴区域内的光 线叫近轴光线
• 近轴光路计算公式有误差 • 相对误差范围
s
in sin
0.100
5
应用光学§讲2稿-3 球面近轴范围内成像性质和近轴光路计算公式
1. 轴上点
近轴光线的成像性质
ilru kilrku
r
r
i'ni n'
k'inki n'
u ' u i i ' k ' u k u k k i' i
应用光学课件第二章
应用光学讲稿
§ 2-1 共轴球面系统中的光路计算公式
求一物点的像,即求所有出射光线位置,交点就是 该物点的像点。
因为所有出射光线位置的求法是相同的,只须找出 求一条出射光线的方法即可。
因为所有的球面的特性是一样的,只须导出光线经 过一个球面折射时由入射光线位置计算出射光线位置 的公式, 即球面折射的光路计算公式。
sinU=u sinU'=u' sinI=i sinI'=i’
得到新的公式组
应用光学§讲2稿-3 球面近轴范围内成像性质和近轴光路计算公式
sin I L r sin U r
sin I ' n sin I n'
i lru r
i' n i n'
U'U I I'
u' u i i'
L' r sin I ' r sin U '
-1°
- 100 10
0.1920 0.1932弧度
0.1266 0.1269弧度 0.0488弧度
u1 l1 r1 i1=(l1-r1)÷ r1×u1
应用光学第二版胡玉禧课件第二章

−l
β =
y' y
y' nl ' = β = y n ' l (2.15) -------垂轴放大率仅取决于共轭面的位置。
l'
第二章
高斯光学
四、近轴光学公式的实际意义 1、作为衡量光学系统成像质量的标准; 2、近似确定光学系统的成像尺寸。 例1.(习题1)一根长500mm, n =1.5的玻璃棒,两端面为凸 球面,半径分别为50mm和100mm,高1mm的物体位于左端 球面顶点之前200mm处,
图2.11 过节点的光线
第二章
高斯光学
B A′ A F H H′ F′ B′
§2-5 由基面、基点求理想像
一、作图法求像 1、典型光线及性质 2、用作图法求光学系统的理想像 1) 轴外 点B或 一垂 轴线 段AB 的像 (图2.14-5)
B′ B A′ F A N H M M ′ N′ H′ F′
M 2 ' A2 ' // N 2 ' F2 '
图(d):为(a)、(b)、(c)的总结果图。
B′ A2 F2 H2 H F1′ 2′ A2′ F2′ A1′ A1 F1 M1′
M1 H1 F2
M2
M2′ A2′ F ′ 2
H1′ H2 F1′ 2′ H
图 (c)
图 (d )
第二章
二、解析法求像
高斯光学
3、作图注意几点(P.37)
图2. 16
作图法求轴上点的像
第二章
高斯光学
图(b):同2)中法一;
轴上点经两个光组的像 图(a):作A1M1 ;
M1
A F1 F2 H1 H1′H2 F ′H2′ 1 F2′ A1
应用光学【第二章】第二部分

得
y ' nl ' y n' l
l'
l
这就是物像大小的关系式。 利用公式就可以由任意位置和大小的物体,求得单 个折射球面所成的近轴像的大小和位置。
对由若干个透镜组成的共轴球面系统,逐面应用公 式就可以求得任意共轴系统所成的近轴像的位置和大小。
应用光学讲稿
三.近轴光学基本公式的作用 近轴光学公式只适于近轴区域,有什么用? 第一,作为衡量实际光学系统成像质量的标准。 用近轴光学公式计算的像,称为实际光学系统的理 想像。
U1 -1 ; L'1 35.969 U1 -2 ; L'1 34.591 U1 -3 ; L'1 32.227
应用光学讲稿
这说明,由同一物点A发出的光线,经球面折射 后,不交于一点。球面成像不理想。 U1越小,L1’变化越慢。当U1相当小时,L1 ’几乎 不变。靠近光轴的光线聚交得较好。 光线离光轴很近则,U、U'、I、I'都很小。
Lr sin I sin U r n sin I ' sin I n' U'U I I' sin I ' L' r r sin U ' 转面公式:
应用光学讲稿
lr i u r n i' i n' u' u i i ' i' l' r r u
L2 L2 'd U2 U '
l ' f (n, n' , r, l )
应用光学讲稿
一. 物像位置关系式 把公式(2-11)两侧同除以h,得:
n' u ' nu n'n h h r
应用光学 第二章

在光的传播方向上,各点的光矢量在确定的平面 内,这种光称为平面偏振光。也由于在垂直于传 播方向的平面内,平面偏振的光矢量端点的轨迹 为一直线,又称为线偏振光。
120:1415-9-14
2-1A
31 / 135
圆偏振光和椭圆偏振光
传播方向相同、振动方向相互垂直、相位差恒 定的两平面偏振光叠加(或组合)可合成光矢 量有规则变化的圆偏振光和椭圆偏振光。
假设:平面波波矢量k平行于xz平面。
x
x
考察:z=0平面的复振幅分步。
波矢量k平行于xz平面——k的方向 余弦cosα,0,cosγ
o
z
E~ = Aexp(ik ⋅ r) = Aexp(ikx cosα )
o
y
等位相点的轨迹为:x=const的直线
120:1415-9-14
2-1
光强度也可以由复振幅表示:
圆偏振光和椭圆偏振光:光矢量端点的轨迹为一圆或椭圆,
即光矢量不断旋转,其大小、方向随时间有规律的变化。
Ey
Ey
Ex
Ex
120:1415-9-14
2-1A
32 / 135
3. 非偏振(自然光) P=0
由普通光源发出的光波都不是单一的平面偏振光, 而是许多光波的总和:它们具有一切可能的振动方 向,在各个振动方向上振幅在观察时间内的平均值 相等,初相位完全无关,这种光称为非偏振光,或 称自然光。
取余ቤተ መጻሕፍቲ ባይዱ函数为特解:
E = Acos[2π (z − vt)] λ
B
=
A'
cos[
2π λ
(z
−
vt)]
120:1415-9-14
2-1
《应用光学》第2章课后答案解析

l = 2f′
B F′ B′ A A′ H H′
F
像平面为 A’B’所在平 面,如图示.
5 试用作图法对位于空气中的负透镜组( f 0 )分别求 下列不同物距的像平A′ H
H′
F
像平面为 A’B’所在平 面,如图示.
5 试用作图法对位于空气中的负透镜组( f 0 )分别求 下列不同物距的像平面位置.
第二章 部分习题答案
牛顿公式 一、物像位置关系 二、物像大小关系 1、垂轴放大率 2、轴向放大率 3、角放大率 三、物方像方焦距关系 四、物像空间不变式
f' n' f n
y nl y nl
高斯公式
f' f 1 l' l
nuy n' u' y'
2. 有一放映机,使用一个凹面反光镜进行聚光照明,光源经过反
f' l 2
B
B′ A F′ A′ H H′
F
像平面为 A’B’所在平 面,如图示.
5 试用作图法对位于空气中的负透镜组( f 0 )分别求 下列不同物距的像平面位置.
l=0
B
B′
F′ H A
A′ H′
F
像平面为: 像方主平面
5 试用作图法对位于空气中的负透镜组( f 0 )分别求 下列不同物距的像平面位置.
考虑物镜组二主面之间的距离)。 解:
9. 已知航空照相机物镜的焦距f′=500mm,飞机飞行高度为
6000m,相机的幅面为300×300mm2,问每幅照片拍摄的地
面面积。 解:
10. 由一个正透镜组和一个负透镜组构成的摄远系统,前组
正透镜的焦距f1′=100,后组负透镜的焦距f2 ′=-50,要 求由第一组透镜到组合系统像方焦点的距离D与系统的组合 焦距之比为1∶1.5,求二透镜组之间的间隔d应为多少?组 合焦距等于多少?
物理光学与应用光学习题解第二章
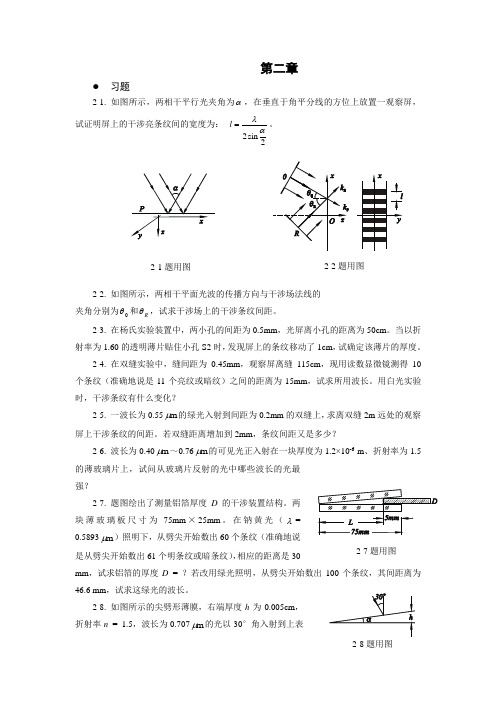
第二章习题2-1. 如图所示,两相干平行光夹角为α,在垂直于角平分线的方位上放置一观察屏,试证明屏上的干涉亮条纹间的宽度为: 2sin2αλ=l 。
2-2. 如图所示,两相干平面光波的传播方向与干涉场法线的 夹角分别为0θ和R θ,试求干涉场上的干涉条纹间距。
2-3. 在杨氏实验装置中,两小孔的间距为0.5mm ,光屏离小孔的距离为50cm 。
当以折射率为1.60的透明薄片贴住小孔S2时,发现屏上的条纹移动了1cm ,试确定该薄片的厚度。
2-4. 在双缝实验中,缝间距为0.45mm ,观察屏离缝115cm ,现用读数显微镜测得10个条纹(准确地说是11个亮纹或暗纹)之间的距离为15mm ,试求所用波长。
用白光实验时,干涉条纹有什么变化?2-5. 一波长为0.55m μ的绿光入射到间距为0.2mm 的双缝上,求离双缝2m 远处的观察屏上干涉条纹的间距。
若双缝距离增加到2mm ,条纹间距又是多少?2-6. 波长为0.40m μ~0.76m μ的可见光正入射在一块厚度为1.2×10-6 m 、折射率为1.5的薄玻璃片上,试问从玻璃片反射的光中哪些波长的光最强?2-7. 题图绘出了测量铝箔厚度D 的干涉装置结构。
两块薄玻璃板尺寸为75mm ×25mm 。
在钠黄光(λ=0.5893m μ)照明下,从劈尖开始数出60个条纹(准确地说是从劈尖开始数出61个明条纹或暗条纹),相应的距离是30mm ,试求铝箔的厚度D = ?若改用绿光照明,从劈尖开始数出100个条纹,其间距离为46.6 mm ,试求这绿光的波长。
2-8. 如图所示的尖劈形薄膜,右端厚度h 为0.005cm ,折射率n = 1.5,波长为0.707m μ的光以30°角入射到上表2-1题用图2-2题用图2-7题用图2-8题用图面,求在这个面上产生的条纹数。
若以两块玻璃片形成的空气尖劈代替,产生多少条条纹?2-9. 利用牛顿环干涉条纹可以测定凹曲面的曲率半径,结构如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上式为角放大率与横向放大率之间的关系式。
角放大率表明了折射球面将光束变宽或变细的能 力,只与共轭点的位置有关,与光线的孔径角无关
2018/7/4 25
将轴向放大率与角放大率公式相乘,有:
上式为三种放大率的关系。
将 代入 可得:
y' n u y n' u'
即:
y n u y' n' u' J
这时U,U’,I,I’ 都很小,我们用弧 度值来代替它的正弦值,并用小写字母表示。
sin I i sin I' i' sin U u sin U ' u'
同时L,L’也用小写表示。
2018/7/4 4
则大L公式可写成:
Lr sin I sin U r n sin I ' sin I n'
y' nl' y n' l
还可发现,当物体由远而近时,即 l 变小, 则β增大
! !
2018/7/4
成像的位置、大小、虚实、倒正极为 重要!!!
20
(二)轴向放大率
轴向放大率表示光轴上一对共轭点沿轴向移动量之间的 关系。它定义为物点沿光轴作微小移动 dl 时,所引起的像 点移动量 dl’ 与 dl 之比,用α表示。
dl' dl
对公式
n' n n' n l' l r
n' dl ' ndl 2 0 2 l' l
微分,有
2018/7/4
21
整理后
dl' nl' 2 dl n' l
nl ' n' l
2
由于
所以
n' 2 n
22
2018/7/4
讨论:
由
n' 2 n
2018/7/4
18
(2)若β>0, 即 l 与 l’ 同号,表示物象在折射球面 同侧,物像虚实相反。反之l 与 l’ 异号,物像虚 实相同。
l l’
可归结为: β> 0, 成正立像且物像虚实相反。 β< 0, 成倒立像且物像虚实相同。
2018/7/4 19
(3)若|β| >1, 则| y’ | > | y |,成放大 像, 反之 |y’ | < | y |,成缩小 像
n’
u’ A’
O
r
l’
-y’
B’
在近轴区内,角放大率定义为一对共轭光线 与光轴夹角u’ 与 u 的比值,用γ表示
u' u
2018/7/4 24
将式
可得
l u = l ’ u’ = h
代入上式
u' l u l'
n 1 n'
上式两边乘以n’/n,并利用垂轴放大率公式,可得
n 1 i' i 0.1288 0.085 n' 1.5163
u' u i i' 0.017 0.12886 0.085 0.02686
i' 0.085 l' r( 1 ) 36.48 ( 1 ) 151.923mm u' 0.02686
n h
E
n’ C u’ A’ -y’ B’
O
r
l’
(一)垂轴放大率
垂直于光轴,大小为 y 的物体经折射球面后成的像大小为 y’ ,则
y' y
β 称为垂轴放大率或横向放大率
2018/7/4 16
B y -u A -l
n h
E
n’ C u’ A’ -y’ B’
O
r
l’
△ABC∽ △A’B’C 有:
光路的计算
2018/7/4
1
※ 这种通过公式来计算光线实际光路 的过程称:光路追迹。
光学计算位数较多,较繁复,为了 避免计算错误,在求出U’ 后,还可 以用下面校对公式进行验算
I ' U ' L sinU cos 2 L' I U sinU ' cos 2 此公式不再推导。
2018/7/4 2
与大L公式计算的结果比较:L’=150.7065mm.(1°)
2018/7/4 7
§2-5 近轴光学的基本公式和它的 实际意义(§2-4)
一、物像位置关系式
i' lr 如将 i u 和 l' r( 1 ) u' r n i 中的 i, i’ 代入 i' n'
可得:
nu( l r ) n' u'( l' r )
h( n' n ) n' u' nu r
2018/7/4 9
将
l u = l’ u’ = h
代入,消去u和u’ , 可得
1 1 1 1 n( ) n'( ) Q r l r l'
也可表示为
n' n n' n l' l r
上式称为单个折射球面物像位置公式
2018/7/4
sin
的大小来确定。
sin
例: sin sin 0.001 θ<5o
2018/7/4 14
二、物像大小关系式
轴上点成像只需知道位置即可,但
如果是有一定大小物体经球面成像后, 只知道位置就不够了,还需知道成像的
大小、虚实、倒正。
2018/7/4
15
B y -u A -l
2018/7/4 11
其中:
h( n' n ) n' u' nu r
给出了u 和 u’ 的关系
n' n n' n l' l r
给出了l 和 l’ 的关系
2018/7/4 12
由阿贝不变量公式和物像位置关系公式可 知,l’ 与 u 无关。 这说明轴上点发出的靠近光轴的细小同心 光束经球面折射后仍是同心光束,可以会聚到 一点,也就是所成的像是完善的。
h i r
小 l 公式也称为近轴光线的光路追迹公式
2018/7/4 6
例2:仍用上例的参数,r = 36.48mm, n=1, n’=1.5163
l = - 240mm, sinU= u = - 0.017, 求:l ’, u’
lr 240 36.48 i u ( 0.017 ) 0.1288 r 36.48
U' U I I'
(2-1)
lr i u r
n i' i n'
(2-2)
u' u i i'
(2-4)
sin I ' L' r( 1 ) sinU '
i' l' r( 1 ) u'
称为小 l 公式
5
2018/7/4
n
i h O
E φ r
n’ C
当无限远物点发出的平行光入射时,有 继续用其余三个公式。
由阿贝不变量公式可得: 可得:
2018/7/4
y' l' r y l r
l' r nl' l r n' l
代入上式
y' nl' y n' l
17
可见β只取决于介质折射率和物体位置。
对横向放大率的讨论 根据β的定义和公式,可以确定物体的成像特性: (1)若β>0, 即 y 与 y’ 同号,表示成正立像。 反之成倒立像。
2018/7/4 27
例2-3:已知一个光学系统的结构参数,r = 36.48mm, n=1, n’=1.5163 l = - 240mm, y=20mm 已求出:l’=151.838 mm,现求β, y’ (横向放大率与像的大小)
解:
nl' 1151.838 0.4172 n' l 1.5163 ( 240 ) y' y 0.4172 20 8.3448mm
β<0: 倒立、实像、两侧
|β|<1:缩小
2018/7/4 28
上例中,若l1= - 100mm, l2= -30mm, 求像的位置大小。
利用公式
n' n n' n l' l r
当 l1= - 100mm 时: l1’=365.113mm β1= - 2.4079 y1’= - 48.1584mm
左边是物方参量,右边是像方参量
8
2018/7/4
对于近轴光而言,AE= - l ,EA’= l ’, tgu = u, tgu’ = u’
n i h -u A -l O E i’ φ r C u’ n’
A’
l’
有: l u = l’ u’ = h
将上式代入 nu( l r ) n' u'( l' r ),消去 l , l’ ,整理后得:
※ 由近轴细光束成的完善像称为高斯像
※ 光学系统在近轴区成像性质和规律 的光学称为高斯光学或近轴光学。
2018/7/4 13
在近轴区,我们用弧度代替了正弦,实际上,把正 弦展开成级数,可得:
1 3 1 5 1 7 sin ...... 3! 5! 7!
用θ代替了sinθ,误差是后面各项的和。 θ愈大,误差 愈大,θ很小时才有足够的精度。 误差所允许的范围就是近轴区的范围,它由相对误差
