齿轮受力分析例题
机械原理典型例题齿轮

⑵画出啮合图,标出啮合线,啮合角,极
限啮合点N1,N2;
⑶从啮合图中标出实际啮合线B1B2,量出 其长短,并计算该对齿轮传动的重合度ε,
说明这对齿轮能否连续传动。(取长度比
例尺
l 1mm /)mm
例4:一对标准直齿圆柱齿轮外啮合传动,其齿数为
Z1=20,Z2=30,模数m=3,分度圆压力角a=20º, ha*=1,安装中心距aˊ=75.5mm。求:
r2I’=30.6mm
2-3啮合: r2Ⅱ’ a23’=r2Ⅱ’+ r3’=70.5 i23= r3’/r2Ⅱ’=Z3/Z2=40/30
r2Ⅱ’=30.21mm
例2:有3个正常齿制且压力角α=20°标准齿轮,
m1=2mm,Z1=20,m2=2,Z2=50,m3=5, Z3=20。这3个齿轮的齿形有何不同?可以用同一把 成形铣刀加工吗?可以用同一把滚刀加工吗?
0 0 0 - + 0 0 - +0 0 - -
习题评讲
6-22:有一对渐开线标准直齿圆柱齿轮, Z1=21,Z2=61,m=2.5mm,α=20°, 求两齿轮的以下参数:
1)分度圆齿距P1,P2;
p1 p2 m 3.14 2.5 7.85mm
2)基园齿距Pb1,Pb2;
rp α rb
,
和 对于在恒定转矩。的传动中,轮齿间正压力的大小和方向始终不变 2)渐开线齿廓上K点的压力角应是 k点的速度方向线与过K点的法线 所夹
的锐角,齿廓上各点的压力角都不相等,在基圆上的压力角等于 0 。
3)一对渐开线直齿圆柱齿轮无齿侧间隙的条件是 s1=e2, 。s2=e1 4)渐开线直齿圆柱齿轮的正确啮合条件是 m1=m2, a1。=a2 5)为了使一对渐开线直齿圆柱齿轮能连续定传动比工作,应使实际啮合线段
齿轮受力分析专题

练习:
从 动
主 动
三、锥齿轮的受力分析
从动
主 动
练习:
四、蜗杆传动受力分析:
在分析蜗杆和蜗轮受力方向时,必须先指明主动轮和从动轮(一般蜗杆为主动轮); 蜗杆或蜗轮的旋向:左旋或右旋;蜗杆的转向和位置
二、斜齿轮的受力分析
受力情况分析:直齿齿轮受力情况只在两个齿轮啮合的时候会产生力的作用, 啮合齿的受力情况如图所示:力(Fn)的方向为啮合点的法线方向。
径向力Fr Fn可以分解为 圆周力Ft 方向的判定:外啮合的径向力有啮合点指向各自的轮心。 方向的判定:同直齿圆柱齿轮传动一致,主反从同。
轴向力Fx 方向的判定:主动轮的左右手定则来判定。
1
Ⅰ
4
5
6 位置1
Ⅲ
位置2
Ⅱ
3 2
Ⅳ
1
Ⅰ
4
Ⅱ
Fr1 Fa1 ⊙ Fa2 Ft1 F × ○ × t4 ○ Ft2 F Fa3 r2 Fa4 ⊙ Ft3
位置2
Fa5
五 两级圆柱齿轮传动的情况
n1
输入轴 中间轴
n2
n3
3
Fa2
1
Fa3
2
4
Fa1 n3
外 啮 合 平 面 图 画 法
外 啮 合
外 啮 合 平 面 图 画 法
内 啮 合
Fr2
Ft1
主 动 轮 Ft2 Fr1 n2
Fr2
Ft1
n1
内 啮 合 平 面 图 画 法
(完整版)机械设计受力分析题

1.(10分) 如图4-1传动系统,要求轴Ⅱ、Ⅲ上的轴向力抵消一部分,试确定:1)蜗轮6的转向;2)斜齿轮3、4和蜗杆5、蜗轮6的旋向;3)分别画出蜗杆5,蜗轮6啮合点的受力方向。
1.(12分)(1) 蜗轮6的转向为逆时针方向;(2分)(2)齿轮3左旋,齿轮4右旋,蜗杆5右旋,蜗轮6右旋;(4分)(3)蜗杆5啮合点受力方向如图(a);蜗轮6啮合点受力方向如图(b)。
(6分)图4-12、传动力分析如图所示为一蜗杆-圆柱斜齿轮-直齿圆锥齿轮三级传动。
已知蜗杆为主动,且按图示方向转动。
试在图中绘出:(1)各轮传向。
(2.5分)(2)使II 、III 轴轴承所受轴向力较小时的斜齿轮轮齿的旋向。
(2分)(3)各啮合点处所受诸分力t F 、r F 、a F 的方向。
(5.5分)3.(10分)如图4-1为圆柱齿轮—蜗杆传动。
已知斜齿轮1的转动方向和斜齿轮2的轮齿旋向。
(1)在图中啮合处标出齿轮1和齿轮2所受轴向力F a1和F a2的方向。
(2)为使蜗杆轴上的齿轮2与蜗杆3所产生的轴向力相互抵消一部分,试确定并标出蜗杆3轮齿的螺旋线方向,并指出蜗轮4轮齿的螺旋线方向及其转动方向。
(3)在图中啮合处标出蜗杆和蜗轮所受各分力的方向。
(1)在图中啮合处齿轮1和齿轮2所受轴向力F a1和F a2的方向如图(2分)。
(2)蜗杆3轮齿的螺旋线方向,蜗轮4轮齿的螺旋线方向及其转动方向如图(2分)。
(3)蜗杆和蜗轮所受各分力的方向。
(6分)4.(15分) 解:本题求解步骤为;(1.)由I轴给定转向判定各轴转向;(2.)由锥齿轮4.5轴向力方向及Ⅲ、Ⅳ轴转向可定出3、6的螺旋方向;(3.)继而定1、2的螺旋方向;(4.)由蜗杆轴力Fa6判定Ft7,从而确定蜗杆转动方向;(5.)判别各力的方向。
5. 如图所示为一蜗杆-圆柱斜齿轮-直齿圆锥齿轮三级传动。
已知蜗杆为主动,且按图示方向转动。
试在图中绘出:(1)各轴转向。
(2)使II、III轴轴承所受轴向力较小时的斜齿轮轮齿的旋向。
齿轮传动受力分析
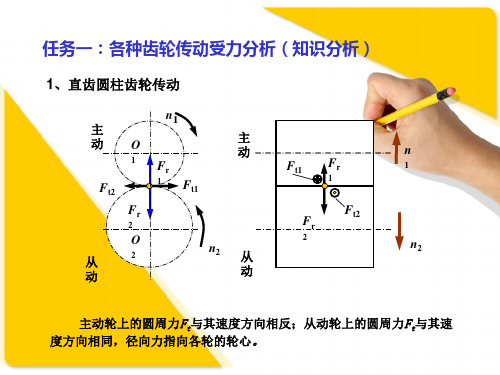
任务三:综合分析(知识应用)
1、斜—斜齿轮传动的受力分析
n1
输入轴
中间轴 n2
n3
3
Fx2
3 Fx3
4
1
2
2
Fx1
输出轴
n3
中间轴上两个齿轮的轴向力方向相反,减轻中间轴和轴承的受力。
2、锥—斜齿轮传动的受力分析
输入轴
n1
中间轴
Fx2
n2
2
1 3
3
Fx3
n3
4
中间轴上两个齿轮的轴向力方向相反,减轻中间轴和轴承的受力。
(5)为了使Ⅱ轴上的轴向力尽可能小,齿轮Z6的旋向为
轴向力方向为
。
,Z6产生的
(6)若该传动系统在结构上要求Ⅲ轴和Ⅳ轴的中心距为102 mm,齿轮Z5的
模数为2mm。则Z5和Z7这对齿轮传动应为
(高度变位、正角度变位、
负角度变位)齿轮传动。此时的啮合角
(大于、小于、等于)分度
圆上齿形角,Z7的齿廓形状为
各力的计算Fx1 Ft2
Ft 2
2T2 d2
Fr1 Fr2
Fr2 Ft 2 t a n
2
2
n2
Fr1
Fx1
Ft2
n1
Fr1
1
n2 Fr1
Fx2
Ft1
n1 1 Fr1
在分析蜗杆和蜗轮受力方向时,必须先指明主动轮和从动轮(一般蜗 杆为主动轮);蜗杆或蜗轮的螺旋方向:左旋或右旋;蜗杆的转向和位置。
蜗杆与蜗轮轮齿上各方向判断如下:
① 圆周力的方向:主动轮圆周力与其节点速度方向相反,从 动轮圆周力与其节点速度方向相同;
② 径向力的方向:由啮合点分别指向各自轴心; ③ 轴向力的方向 :蜗杆主动时,蜗杆轴向力的方向由“主 动轮左、右手定则”判断,即右旋蜗杆用右手(左旋用左手),四 指顺着蜗杆转动方向弯曲,大拇指指向即蜗杆轴向力的方向。 蜗轮轴向力的方向与蜗杆圆周力方向相反。
齿轮受力分析例题
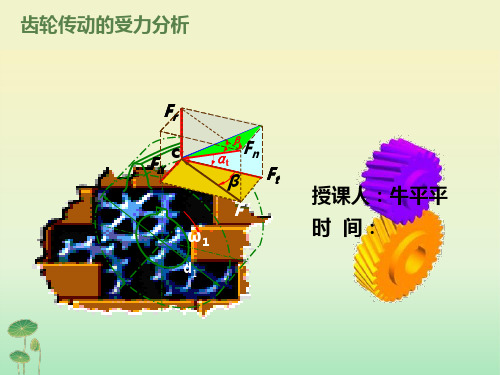
Ft1
Fr1
Fr2
Ft2
从动
主反从同
n1 n2
2、斜齿圆柱齿轮
主动
O Fx1
Ft2 1 Fr2
O
从动
2
n
1
Fr1 Ft1
Fx
n2
2
主动
n1
Ft1
Fr1
Fx
1
Fx
Fr2 Ft2 2
n2
从动
Ft 、Fr的判定与直齿轮相同。 Ft 主反从同
主动轮 轴向力Fx1左旋用左手;右旋用右手判断。从动轮Fx2与其相反。
5、各种齿轮传动受力分析比较
受力名称齿轮类型
圆周力 Ft
径向力 Fr
轴向力 Fx
对主动轮来说 直 齿 圆 柱 齿 轮 传是动阻力,其方
向与主动轮在 啮合点处的运 斜 齿 圆 柱 齿 轮 传动动方向相反; 对从动轮来说 是动力,其方 直 齿 圆 锥 齿 轮 传向动与从动轮在 啮合点处的运
(主动方反向从一同致)
6
Fr6 Ft6 Ⅲ
位置1 位置2
3 2
例题2
如图所示为一机械传动方案,Ⅰ轴为输入轴,按图中箭头所示方向 转动。已知: Z1、Z2和Z3为直齿圆锥齿轮,Z4,Z6为斜齿轮,Z12为 标准直齿圆柱齿轮。分析该传动方案,回答下列问题:
(1)Z2所受的圆周垂力直纸(面垂向直外 纸面向里、 。
(2)为了使Ⅱ轴上的轴向力尽
可能小,齿轮Z6的旋向为
,Z6产右生旋的轴向力方向为
。
向上
(3)如图所示状态下,螺母的
移动方向为
向为 。
,齿条向的下运动方
(4)齿轮Z1和Z2的啮向合条右件为
和。
课堂小结
齿轮受力分析例题PPT课件

个人观点供参考,欢迎讨论!
齿轮受力分析习题课
例题1
传动中,蜗杆(左旋)主动,转向如图所示。圆柱齿 轮为斜齿轮,为使Ⅱ、Ⅲ轴的轴向力平衡,试确定: (1)蜗轮2的螺旋线方向; (2)齿轮3、4螺旋线方向; (3)蜗轮2和齿轮3所受轴向力方向; (4) Ⅲ轴上圆锥齿轮6应放置在左边的位置1或是右边 的位置2? (5)在图上画出5轮所受力的方向;
1
Ⅱ
2
Ⅰ
Ⅳ
4
5
6 位置a1 Fa2 ○× Ft1
Ft2 Fr2
Ⅱ
Ⅰ
4
Ft4 Fa4
○×
⊙Ft3
Fa3
6 位置1
Fa5 5 ○⊙×FtF5 a6
Ft6 Ⅲ
位置2
3 2
1 F a2
Ⅱ
2
Ⅰ
Ⅳ
F a5
4
5
·
F r5 F t6
Ⅲ
6 F a3 位 置 1
位置2
3
解:(1)蜗轮的螺旋线方向为左旋; (2)齿轮3为左旋,齿轮4为右旋; (3)蜗轮2和齿轮3的轴向力如图所示;
齿轮受力分析例题

1
Ⅱ
2
Ⅰ
Ⅳ
4
5
6 位置1
Ⅲ
位置2
3
Ⅳ
1
Fr1 ⊙Fa1 Fa2 ○× Ft1
Ft2 Fr2
Ⅱ
Ⅰ
4
Ft4 Fa4
○×
⊙Ft3
Fa3
6 位置1
Fa5 5 ○⊙×FtF5 a6
Ft6 Ⅲ
位置2
3 2
1 Fa2
Ⅱ
2
Ⅰ
Ⅳ
Fa5
4
5
·
Fr5 Ft6
Ⅲ
6 Fa3 位置1 位置2
3
解:(1)蜗轮的螺旋线方向为左旋; (2)齿轮3为左旋,齿轮4为右旋; (3)蜗轮2和齿轮3的轴向力如图所示;
(4)Ⅲ轴上圆锥齿轮5应放置在右边的位置2; (5)5轮所受力的方向如图所示。
Fr1 Fn1
Fr2 Ft2 tan
Fa1
cos n cos1
Ft 2
cos n cos1
2T2
d 2cos n cos1
Fnc KFn
蜗轮的材料相对较弱, 仅计算蜗轮的σH 与σF,将蜗 轮视为斜齿轮,将式 (11.8)、将式(11.10)作 为计算σH 与σF 的基础。
作用力的方向(示意图)
右
蜗轮的转向→ 与Fa 1 反向
FaF1r1
Ft1
Fa2
Ft2
Fr2
Fr1 Fa1 Ft1
Fa2 Ft2 Fr2
右
例题1
传动中,蜗杆(左旋)主动,转向如图所示。圆柱齿 轮为斜齿轮,为使Ⅱ、Ⅲ轴的轴向力平衡,试确定: (1)蜗轮2的螺旋线方向; (2)齿轮3、4螺旋线方向; (3)蜗轮2和齿轮3所受轴向力方向; (4) Ⅲ轴上圆锥齿轮6应放置在左边的位置1或是右边 的位置2? (5)在图上画出5轮所受力的方向;
机械力学中的受力分析案例研究

机械力学中的受力分析案例研究机械力学是研究力学平衡与运动规律的基本学科,它对于解决实际工程问题具有重要的指导作用。
在机械力学中,受力分析是解决力学问题的关键步骤之一。
本文将通过几个案例研究,展示机械力学中受力分析的应用。
案例一:简支梁上的荷载分析在结构力学中,简支梁是一种常见的结构形式。
假设有一根长度为L的简支梁,两端固定在支座上,中间受到集中力P的作用。
我们需要分析梁的受力情况。
首先,我们需要确定梁的受力方式。
根据力学平衡原理,我们可以得到以下等式:ΣFx = 0:该方程表示梁在水平方向上的受力平衡,由于梁的两端固定,横向支配力为零。
ΣFy = 0:该方程表示梁在垂直方向上的受力平衡,支点对其产生的反作用力和荷载P构成一个力的平衡。
根据以上原理,我们可以得到简支梁上的受力分析结果:支座对梁产生一个大小为P的垂直向上的支持力,该支持力通过梁向上传递,直到达到另一个支座。
案例二:斜面上的物体分析斜面是力学中常见的几何形状,它对于解决坡道、斜坡等问题具有重要的应用价值。
假设有一个物体放置在倾角为θ的光滑斜面上,我们需要分析物体的受力情况。
根据受力分析的原理,我们可以得到以下结论:物体受到重力的作用,该重力可以分解为垂直于斜面和平行于斜面的两个分力,其中平行于斜面的分力会使物体下滑,垂直于斜面的分力受到斜面支持。
通过计算,我们可以得到物体在斜面上受力的大小和方向。
根据受力平衡条件,我们可以分析物体在斜面上的平衡状态,进而判断物体是否会滑动。
案例三:齿轮传动系统的力学分析齿轮传动广泛应用于各种机械设备中,它可以将动力传递给其他部件。
在齿轮传动中,我们需要进行力学分析,以确定齿轮的受力情况。
对于齿轮传动系统,我们需要分析各个齿轮之间的受力关系。
通过力学平衡原理,我们可以计算齿轮之间的各种受力,如法向力、切向力等。
在齿轮传动系统中,我们还需要考虑齿轮的强度分析。
齿轮在传递动力的过程中会承受很大的载荷,我们需要通过受力分析来确定齿轮的强度是否满足工程要求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例题1 传动中,蜗杆(左旋)主动,转向如图所示。圆柱齿 轮为斜齿轮,为使Ⅱ、Ⅲ轴的轴向力平衡,试确定: (1)蜗轮2的螺旋线方向; (2)齿轮3、4螺旋线方向; (3)蜗轮2和齿轮3所受轴向力方向; (4) Ⅲ轴上圆锥齿轮6应放置在左边的位置1或是右边 的位置2? (5)在图上画出5轮所受力的方向;
Ⅳ
1
Ⅰ
4
5
6 位置1
Ⅲ
位置2
Ⅱ
3 2
Ⅳ
1
Ⅰ
Fa5 Ft5 5 ⊙ Fa6 × ○ Ft6 Ⅲ
位置2
4
Ⅱ
Fr1 Fa1 ⊙ Fa2 Ft1 F × ○ × t4 ○ Ft2 F Fa3 r2 Fa4 ⊙ t3 F
3 2
6 位置1
Ⅳ
1
Ⅰ
Fa5
·பைடு நூலகம்
4
5 Fr5 Ft6 6 位置1
Ⅲ
Fa2 Fa3
位置2
Ⅱ
3 2
解:(1)蜗轮的螺旋线方向为左旋; (2)齿轮3为左旋,齿轮4为右旋; (3)蜗轮2和齿轮3的轴向力如图所示; (4)Ⅲ轴上圆锥齿轮5应放置在右边的位置2; (5)5轮所受力的方向如图所示。
齿轮受力分析习题课
斜齿圆柱齿轮轮齿的受力分析
斜齿圆柱齿轮轮齿所受总法向力 斜齿圆柱齿轮轮齿所受总法向力Fn可分解为三个分力 : 轮齿所受总法向力
2T1 径向力: 轴向力: 轴向力: Fa = Ft tg β 径向力: 圆周力: 圆周力: Ft = d1
长方体对角面即轮齿法面
Fr =
Ft tgαn cosβ
d1 2
F’
β
F’ n1
圆周力F 的方向在主动轮上与运动方向相反, 圆周力 t的方向在主动轮上与运动方向相反,在 从动轮上与运动 方向相同; 方向相同; 轴向力F 的方向按主动轮的螺旋线方向和转向,用左、 轴向力 a的方向按主动轮的螺旋线方向和转向,用左、右手螺旋 定则来确定。 定则来确定。 主动轮右旋,用右手;左旋,用左手: 主动轮右旋,用右手;左旋,用左手:四指弯曲方向 表示主动轮的回转方向, 表示主动轮的回转方向,其拇指所指方向即为主动轮上轴向力 Fa1的方向;从动轮的轴向力 a2与主动轮上轴向力 a1的方向相反。 的方向;从动轮的轴向力F 与主动轮上轴向力F 的方向相反。
Fr
Fa
Fr Fn αn Ft
c
β
Ft Fa
Fn αn F’
Fr = F’ tgαn
长方体底面
β
T1 ω1
d1 2
F’
β
F’ αn :法向压力角 法向压力角
β : 节圆螺旋角
F’=Ft /cosβ
Fr
Fa1
Fr Fn αn Ft1
c
β
Ft1 Fa1
Fn αn F’ 径向力指 向各自的 轴心
β
T1 ω1
