【管理资料】机械臂正运动学方程的DH表示法及逆运动学汇编
机械臂运动学与逆运动学分析

机械臂运动学与逆运动学分析机械臂作为一种广泛应用于工业生产中的自动化设备,其运动学和逆运动学分析是研究和设计机械臂的重要基础。
本文将围绕机械臂的运动学和逆运动学两个方面展开论述,具体介绍其原理和应用。
一、机械臂运动学分析机械臂的运动学分析主要涉及到机械臂的位置、速度和加速度等方面的研究。
在机械臂的运动学分析中,我们首先要研究机械臂的正运动学问题,即确定机械臂末端执行器的位置、速度和加速度如何随着关节角度的变化而变化。
其次,我们还要研究机械臂的逆运动学问题,即如何根据末端执行器的位置、速度和加速度,求解关节角度的解。
在机械臂运动学分析中,我们通常采用的是解析方法和数值计算方法相结合的方式。
在解析方法中,我们利用几何和向量的知识推导出机械臂末端执行器的位置、速度和加速度表达式,从而快速得到解析解。
而在数值计算方法中,我们通过数值逼近和迭代计算等方法,求解非线性运动学方程,从而得到逆运动学解。
二、机械臂逆运动学分析机械臂逆运动学分析是指在已知机械臂末端执行器的位置、速度和加速度的情况下,求解关节角度的解。
逆运动学问题在机械臂的轨迹规划、路径规划和运动控制等方面起着至关重要的作用。
机械臂的逆运动学分析存在多解性和奇异性的问题。
多解性是指对于给定的末端执行器的位置、速度和加速度,存在多组关节角度解。
奇异性则是指在某些特殊位置附近,机械臂出现无法运动的情况。
解决这些问题是机械臂逆运动学分析的重要挑战。
为了求解机械臂的逆运动学问题,我们通常采用迭代法和优化算法等方法。
在迭代法中,我们从初始猜测的关节角度出发,通过迭代计算的方式,逐步调整关节角度,使末端执行器的位置、速度和加速度与给定值尽量接近。
而在优化算法中,我们将逆运动学问题转化为求解最优化问题,通过优化算法求解关节角度的解。
三、机械臂运动学与逆运动学的应用机械臂的运动学和逆运动学分析在工业自动化中有着广泛的应用。
首先,它可以用于机械臂的轨迹规划和路径规划。
机械臂的运动学与逆运动学分析

机械臂的运动学与逆运动学分析机械臂是一种能够模拟人类手臂运动的自动化机器人。
它广泛应用于工业领域,用于完成各种复杂的操作任务。
机械臂的运动控制是实现其功能的关键,其中运动学和逆运动学分析是研究机械臂运动的基础。
一、机械臂的运动学分析运动学分析主要关注机械臂的位置、速度和加速度等运动参数的计算。
机械臂主要由关节连接的刚性杆件组成,每个关节可以沿特定方向进行旋转或平移运动。
在机械臂运动学中,我们关注的是机械臂末端执行器的位置和姿态。
1. 正运动学分析正运动学分析指的是根据机械臂各关节的运动参数,计算机械臂末端执行器的位置和姿态。
通常,我们采用坐标变换矩阵的方法来进行计算。
通过将各个关节的运动连续相乘,可以得到机械臂末端执行器相对于机械臂基座标系的位姿矩阵。
以一个3自由度的机械臂为例,设第一关节绕Z轴旋转角度为θ1,第二关节绕Y轴旋转角度为θ2,第三关节绕X轴旋转角度为θ3。
则机械臂末端执行器相对于基座标系的位姿矩阵可以表示为:[cos(θ2+θ3) -sin(θ2+θ3) 0 a1*cos(θ1)+a2*cos(θ1+θ2)+a3*cos(θ1+θ2+θ3)][sin(θ2+θ3) cos(θ2+θ3) 0 a1*sin(θ1)+a2*sin(θ1+θ2)+a3*sin(θ1+θ2+θ3)][0 0 1 d1+d2+d3][0 0 0 1]其中,a1、a2、a3和d1、d2、d3分别为机械臂的长度和位移参数。
通过这个矩阵,我们可以得到机械臂末端执行器的位置和姿态。
2. 速度和加速度分析除了机械臂末端执行器的位置和姿态,机械臂的速度和加速度也是非常重要的运动参数。
通过对机械臂运动学模型的导数运算,我们可以得到机械臂的速度和加速度表达式。
机械臂的速度可以表示为:v = J(q) * q_dot其中,v为机械臂末端执行器的速度向量,J(q)为机械臂的雅可比矩阵,q为机械臂各关节的角度向量,q_dot为各关节的角速度向量。
机械臂运动学逆解

机械臂运动学逆解一、前言机械臂是一种多自由度的机器人,具有广泛的应用领域,如工业生产线、医疗手术、军事等。
机械臂的运动学逆解是机械臂控制中非常重要的一部分,本文将详细讲解机械臂运动学逆解的相关知识。
二、机械臂运动学基础1. 坐标系在机械臂中,通常采用笛卡尔坐标系和关节坐标系描述位置和姿态。
笛卡尔坐标系是一个三维直角坐标系,由三个互相垂直的轴组成。
关节坐标系则是由每个关节的旋转轴所确定的坐标系。
2. 运动学模型在运动学模型中,我们通常采用DH(Denavit-Hartenberg)参数来描述机械臂各个关节之间的相对位置和姿态。
DH参数包括四个量:a、α、d和θ。
其中a表示前一个关节沿着x轴方向移动到达当前关节时x轴方向上的位移;α表示前一个关节绕z轴旋转到达当前关节时z轴方向上与x轴正方向之间夹角的大小;d表示当前关节沿着z轴方向上的位移;θ表示当前关节绕z轴旋转的角度。
3. 正运动学正运动学是机械臂控制中最基本的问题,其目的是通过给定各个关节的角度,计算出机械臂末端执行器的位置和姿态。
正运动学可以通过矩阵变换来实现。
4. 逆运动学逆运动学是机械臂控制中比较困难的问题,其目的是通过给定机械臂末端执行器的位置和姿态,计算出各个关节应该具有的角度。
逆运动学通常采用解析法或数值法来解决。
三、机械臂运动学逆解方法1. 解析法解析法是指通过数学公式求解机械臂逆运动学问题。
对于一些简单的机械臂模型,可以采用此方法求解。
例如对于一个二自由度平面机械臂,可以通过三角函数公式求解出各个关节应该具有的角度。
2. 数值法数值法是指通过迭代计算来求解机械臂逆运动学问题。
数值法通常包括牛顿-拉夫森方法、雅可比方法等。
其中,牛顿-拉夫森方法是通过不断迭代来逼近解的方法,而雅可比方法则是通过求解雅可比矩阵来实现。
3. 混合法混合法是指将解析法和数值法相结合来求解机械臂逆运动学问题。
该方法通常采用解析法求得初始值,然后通过数值法进行迭代计算,以提高计算精度。
机器人运动学正问题与机器人运动学逆问题

机器⼈运动学正问题与机器⼈运动学逆问题机器⼈运动学正问题与机器⼈运动学逆问题2014-11-12 11:26 作者:管理员11 来源:未知浏览: 77 次字号: ⼤中⼩摘要:机器⼈运动学正问题机器⼈运动学正问题指已知机器⼈杆件的⼏何参数和关节变量,求末端执⾏器相对于机座坐标系的位置和姿态。
机器⼈运动学⽅程的建⽴步骤如下: 1)根据D-H法建⽴机器⼈的机座坐标系和各杆件坐标系。
2)确定D-H参数和关节变最。
3)从机座坐机器⼈运动学正问题机器⼈运动学正问题指已知机器⼈杆件的⼏何参数和关节变量,求末端执⾏器相对于机座坐标系的位置和姿态。
机器⼈运动学⽅程的建⽴步骤如下:1)根据D-H法建⽴机器⼈的机座坐标系和各杆件坐标系。
2)确定D-H参数和关节变最。
3)从机座坐标系出发,根据各杆件尺⼨及相互位置参数,逐⼀确定A矩阵。
4)根据需要将若⼲个A矩阵连乘起来,即得到不同的运动⽅程。
对6⾃由度机器⼈,⼿部相对于机座坐标系的位姿变化为T6=A1·A2·A3·A4·A5·A6 (27.2-1)此即⼿部的运动⽅程。
机器⼈运动学逆问题机器⼈运动学逆间题指已知机器⼈杆件的⼏何参数和末端执⾏器相对于机座坐标系的位姿.求机器⼈各关节变量。
求解机器⼈运动学逆问题的解析法⼜称为代数法和变量分离法。
在运动⽅程两边乘以若千个A矩阵的逆阵,如将得到的新⽅程展开,每个⽅程可有12个⼦⽅程,选择等式左端仅含有所求关节变童的⼦⽅程进⾏求解,可求出相应的关节变盒。
除解析法外,还有⼏何法、迭代法等。
(责任编辑:laugh521521)。
机器人技术大作业(puma机器人的关节坐标建立、dh参数表给出、正逆运动学推导、matlab工作空间
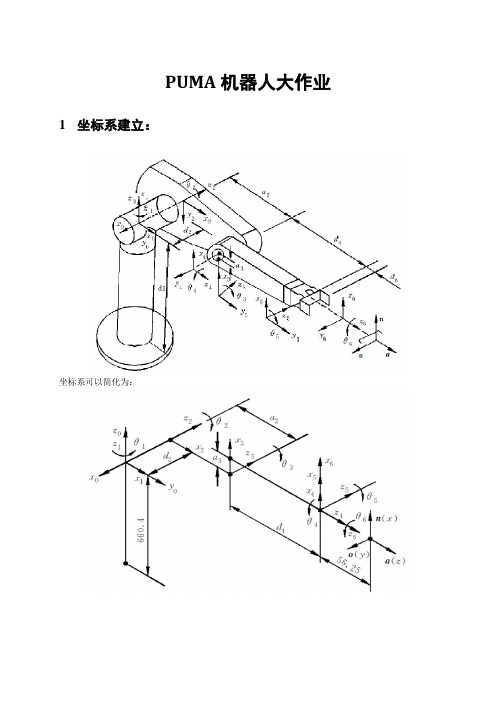
PUMA机器人大作业1坐标系建立:坐标系可以简化为:2 D-H 参数表:PUMA 机器人的杆件参数:1d 0.6604m =,2d 0.14909m =,4d 0.43307m =,6d 0.05625m =,2a 0.4318m =,3a 0.02032m =3 正运动学推导由式111111111100001ii i i i i i i i i i i i i i i i i i c s a s c c c s d s T s s c s c d c θθθαθαααθαθααα-----------⎡⎤⎢⎥--⎢⎥=⎢⎥⎢⎥⎣⎦可得: 111101000000100001c s s c T -⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,222122200001000001c s d T s c -⎡⎤⎢⎥⎢⎥=⎢⎥--⎢⎥⎣⎦,332332300000100001c s a s c T -⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦44343444000100001c s a d T s c -⎡⎤⎢⎥⎢⎥=⎢⎥--⎢⎥⎣⎦,554555000010000001c s T s c -⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦,665666000010000001c s T s c -⎡⎤⎢⎥⎢⎥=⎢⎥--⎢⎥⎣⎦0123456123456T T T T T T T =机械手变换矩阵601x x x x yy y y z z z z n o a p n o a p T n o a p ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦23654164123651654164123654164123651654164123654642365()()()x y z n c c c c c s s c s c s c c c s s s c s n c c c c s s s s s c s s c c s c s c c n s c c c s s c c s =--++=----=--- 23654164123651654164123654164123651645164123654642365()()()x y z o c s c c c c s c s s s c s c s s c c s o c s c c s c s s s s s s s s c c c c c o s s c c s s c c s =-++-+=-+++-=++ 2354123515412354123515412352354x y z a c s c c s c c s s s a c s c s s c s s s c a c c s s c =---=--+=-+ 3231221423121323122142312142332322x y z p a c c a c c d s c d s p a c s a c s d s s d c p d c a s a s =+--=+-+=---4 逆运动学推导1.求1θ用逆变换011T -左乘方程00123456123456T T T T T T T =两边: 010123451623456T T T T T T T -=11111600000010000101xx x x yy y y zz z z c s n o a p s c n o a p T n o a p ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦得112x y s p c p d -+=三角代换 cos x p ρφ=,sin y p ρφ=式中,ρ=tan 2(,)x y a p p φ=得到1θ的解12a tan 2(,)a tan 2(,y x p p d θ=-2.求3θ矩阵方程两端的元素(1,4)和(2,4)分别对应相等113232242342332322x y z c p s p a c a c d s p d c a s a s +=+-⎧⎨-=++⎩平方和为:4333d s a c k +=其中 2222222242322x y z p p p d d a a k a ++----=解得:334a tan 2(,)a tan 2(,a d k θ=- 3.求2θ在矩阵方程00123456123456T T T T T T T =两边左乘逆变换013T -。
浅析机器人(正)运动学D-H变换原理及算法

浅析机器人(正)运动学D-H变换原理及算法经常给客户培训,期间会有善于思考的朋友们提出一些很有价值的问题!比如,有人会问,机器人是怎么运动的?这种问题往往让我不知从何下手!多数情况下我都是讲一下机器人的各种坐标系用法,大家也都把这些坐标系的用法当成机器人最基础的知识来使用了!买来的机器人简单应用这也足够用了!对于复杂的非标应用,就很难搞定了,有些复杂功能,你得了解机器人最底层的逻辑,才能写出客户想要的功能!例如和多个外部轴同步运动共用坐标系;例如开发自动校准机器人零点的非标功能;或者你们自己设计一个三轴或更多轴的运动平台,需要坐标系的运用;等等!今天我用最简单的语言给大家浅析下机器人最底层的算法,运动学正解;意在让大家了解其原理,懂其原理,大家遇到问题可以有个思路,思路对了,具体的程序就容易了!什么是运动学正解?本文都用如下图六轴机械手举例!有实体图和简化成只有六个电机的连杆结构,主要用连杆电机图做计算逻辑的解析!机器人实体图机器人电机轴位置图什么是运动学(正)解;机器人得有坐标数据,大家才能知道机器人现在在哪里,然后写出它去哪里的程序!机器人的坐标怎么理解呢?比如六轴焊接机器人,我使用它就是为了焊接,我只需要它的焊枪头的位置数据!焊枪头在哪里,就可以说机器人在哪里!那么机器人焊枪头的坐标数据是怎么来的呢?说到坐标,就得有一个原点或者基准,这个原点和基准是不会变化的!这个基准就是在机器人的底座上,永远不会变化;正运动学就是求这个焊枪头在基准坐标里的位置;焊接机器人怎么求焊枪头位置数据(TCP)呢?以下面两幅图为例讲解,分别是机器人正视图和其连杆机构,机器人右视图和其连杆机构!机器人正视图和其连杆机构机器人右视图和其连杆机构假定机器人这个姿势六个电机都在零点,如下两图所示,首先我们要给连杆简图建立坐标系,坐标系怎么建立呢?分六步完成:第一步:找电机轴,标出轴线,如图Z1-Z6为轴线,对应六个关节轴,正视图和右视图配合看着比较清晰;正视图轴线右视图轴线第二步:找出关节轴i和i+1之间的公垂线(就是和两条相邻的轴线都垂直的线),如果两条轴线相交则没有公垂线,那么就取其交点;以公垂线与关节轴i的交点或相交轴线的交点为坐标系{i}的原点(例如Z1和Z2的公垂线为L1,L1与Z1的交点就是坐标原点O1);如下图红点和红圈都是坐标系原点:坐标系原点正视图坐标系原点右视图第三步:确定Z轴(图中已经标出),和轴线是同一条线;(没有规定Z轴方向,所以可以有两个方向,我们就使用图示的方向,所以每家机器人规定的方向可能会不同!)第四步:规定X轴沿着公垂线的指向,或者轴线相交的情况下规定X垂直于相交直线的平面;(垂直于相交平面的直线又有两个方向,我们只用图示的方向,所以每家机器人的X方向也可能有所不同!)如下图,红色箭头代表X轴:确定X轴,正视图确定X轴,右视图第五步:右手定则确定Y轴方向;如上图,绿色箭头为Y轴方向;第六步:尽量使基坐标O0和坐标系O1重合,图中就是重合状态,也有的机器人基坐标在O1下方或者角度有偏移,都无所谓,就是参数有点变化,下面讲到参数!坐标系定义好了,要转换坐标系了(例如坐标系O1转换到坐标系O2),正常情况下,把一个坐标系转换到另一个坐标系需要6个参数,(X/Y/Z/A/B/C),三个坐标值和三个坐标旋转数据,每个电机定义好坐标系用这六个参数一样可以完成坐标系转换;但是国外有两个真专家(Denavit-Hartenberg),研究出来用四个参数就可以求解的方法,后人就一直用他们的方法简化运算,我也就讲他们的方法D-H变换了,上面规定设定坐标系的步奏也是为了找到这四个参数。
FANUC 机械手资料相关 机器人正运动学方程的D-H表示法

2.8机器人正运动学方程的D-H表示法在1955年,Denavit和Hartenberg在“ASME Journal of Applied Mechanics”发表了一篇论文,后来利用这篇论文来对机器人进行表示和建模,并导出了它们的运动方程,这已成为表示机器人和对机器人运动进行建模的标准方法,所以必须学习这部分内容。
Denavit-Hartenberg(D-H)模型表示了对机器人连杆和关节进行建模的一种非常简单的方法,可用于任何机器人构型,而不管机器人的结构顺序和复杂程度如何。
它也可用于表示已经讨论过的在任何坐标中的变换,例如直角坐标、圆柱坐标、球坐标、欧拉角坐标及RPY坐标等。
另外,它也可以用于表示全旋转的链式机器人、SCARA机器人或任何可能的关节和连杆组合。
尽管采用前面的方法对机器人直接建模会更快、更直接,但D-H表示法有其附加的好处,使用它已经开发了许多技术,例如,雅克比矩阵的计算和力分析等。
假设机器人由一系列关节和连杆组成。
这些关节可能是滑动(线性)的或旋转(转动)的,它们可以按任意的顺序放置并处于任意的平面。
连杆也可以是任意的长度(包括零),它可能被弯曲或扭曲,也可能位于任意平面上。
所以任何一组关节和连杆都可以构成一个我们想要建模和表示的机器人。
为此,需要给每个关节指定一个参考坐标系,然后,确定从一个关节到下一个关节(一个坐标系到下一个坐标系)来进行变换的步骤。
如果将从基座到第一个关节,再从第一个关节到第二个关节直至到最后一个关节的所有变换结合起来,就得到了机器人的总变换矩阵。
在下一节,将根据D-H表示法确定一个一般步骤来为每个关节指定参考坐标系,然后确定如何实现任意两个相邻坐标系之间的变换,最后写出机器人的总变换矩阵。
图2.25 通用关节—连杆组合的D-H表示假设一个机器人由任意多的连杆和关节以任意形式构成。
图2.25表示了三个顺序的关节和两个连杆。
虽然这些关节和连杆并不一定与任何实际机器人的关节或连杆相似,但是他们非常常见,且能很容易地表示实际机器人的任何关节。
机械臂d-h法 正运动学

机械臂D-H法正运动学研究一、D-H参数定义Denavit-Hartenberg (D-H) 方法是一种广泛用于描述机器人臂杆的参数化方法。
在D-H参数中,每一个关节都有一个与之对应的连杆,其中包含了四个参数:关节角度、连杆长度、连杆偏移量和关节旋转轴。
这些参数提供了机械臂的位置和姿态信息,使得我们能够全面描述机械臂的状态。
二、连杆变换矩阵连杆变换矩阵是D-H参数的核心部分,它描述了从一个连杆到下一个连杆的坐标变换。
通过连续应用这些变换矩阵,我们可以得到机械臂末端执行器的全局位置和姿态。
这些变换矩阵是仿射变换的一种,包括了平移和旋转。
三、关节角度计算关节角度是描述机械臂运动状态的重要参数。
通过测量或计算每个关节的角度,我们可以确定机械臂的位置和姿态。
关节角度的计算是机械臂控制的关键步骤,通常需要通过传感器或编码器进行测量。
四、正运动学方程建立正运动学方程是描述机械臂末端执行器位置和姿态的数学模型。
通过已知的关节角度和D-H参数,我们可以计算出末端执行器的位置和姿态。
正运动学方程是非线性方程,通常需要通过数值方法进行求解。
五、运动学逆解在某些情况下,我们已知末端执行器的位置和姿态,需要求解关节角度。
这就是运动学逆解问题。
解决逆解问题需要用到正运动学方程的反向求解,需要找到使得末端执行器达到特定位置和姿态的关节角度。
六、工作空间分析工作空间是指机械臂末端执行器能够达到的所有位置和姿态的集合。
工作空间分析是评估机械臂性能的重要步骤,包括工作空间的形状、大小以及可达性等。
通过优化D-H参数和工作空间设计,可以提高机械臂的灵活性和工作效率。
七、碰撞检测与避障在机器人操作中,碰撞检测和避障是非常重要的安全措施。
通过实时监测机械臂与环境或其他物体之间的距离和角度关系,我们可以避免发生碰撞事故。
同时,为了确保机器人能够自主适应不同的环境,需要进行实时的路径规划和避障策略设计。
这些技术依赖于对工作空间的精确理解以及对运动学方程的实时求解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本思路
• 首先给每个关节指定一个参考坐标系,然 后,确定从一个关节到下一个关节(一个 坐标到下一个坐标)来进行变换的步骤。
• 如果从基座到第一个关节,再从第一个关 节到第二个关节直至到最后一个关节的所 有变换结合起来,就得到了机器人的总变 换矩阵。
2
3
给每个关节指定本地参考坐标系
——确定z轴
• 如果关节是旋转的,Z轴位于按右手规则旋转的
方向。绕Z轴的旋转角 是关节变量;
• 如果关节是滑动的,Z轴为沿直线运动的方向。 沿Z轴的连杆长度d是关节变量;
注意:在每一种情况下,关节n处的Z轴下标为n-1。 例如,表示关节n+1的Z轴是Zn
4
给每个关节指定本地参考坐标系
An1S0n1
No
0
Cn1Cn1 Sn1
0
Cn1Sn1 an1Sn1
Cn1
0
dn1 1
Imag • 上式中:C n 1=cos n 1
S n 1 =sin n 1
15
• 比如,一般机器人的关节2与关节3之间的 变换可以简化为:
C3 S3C3 S3S3 a3C3
2T3A3S03
0
C3C3 S3
• 从参考坐标系开始,我们可以将其转换到 机器人的基座,然后到第一个关节,第二 个关节… …,直至末端执行器。
13
• 从而得到结果如下:
n T n 1 A n 1 R z , n 1 o T 0 , 0 , d t n r 1 T a a n 1 , 0 r , 0 n R a x , a n 1 o n
0
C3S3 C3
0
a3S3
d3 1
16
推广到n个自由度
• 在机器人的基座上,可以从第一个关节开始变换 到第二个关节,然后到第三个关节……,再到机 器人的末端执行器。
• 若表把示每变个 换变 的换 矩定 阵义。为在机i 器1T人i 的,基则座可与以手得之到间许的多总
变换则为:
R T H R T 1 1 T 2 2 T 3 n 1 T n A 1 A 2 A 3 A n
cos(a) sin(a) 0 cos(b) 0 sin(b) 1
sin(a) cos(a) 0• 0
1
0
•
0
0
0 1 sin(b) 0 cos(b) 0
0 cos(g) sin(g)
0 sin(g) cos(g)
=
24
25
此课件下载可自行编辑修改,仅供参考! 感谢您的支持,我们努力做得更好!谢谢
• 两关节Z轴相交,它们之间没有公垂线(或 者说公垂线距离为零)。这时可将垂直于 两条轴线构成的平面的直线定义为X轴(相 当于选取两条Z轴的叉积方向作为X轴), 可简化模型;
6
关节变量
• 在图(a)中, 角表示绕Z轴的旋转角,d表示在
Z轴上两条相邻的公垂线之间的距离,a表示每一
条公垂线的长度(也叫关节偏移量),角 表示
Cn1 Sn1 0 0 1 0 0 0 1 0 0 an1 1 0
0 0
Sn1
0
0
Cቤተ መጻሕፍቲ ባይዱ1
0 0
0 1 0
00 0 0 1 0
1 0 0
0 1 0
0 0
d1n1
0 0
1 0 0
0 1 0
0 0 Cn1 Sn1 0
0
1
0 0
Sn1
0
Cn1
0
0 1
14
Cn1 Sn1Cn1 Sn1Sn1 an1Cn1
——确定x轴 • 当关节不平行或相交时,z轴通常是斜线,
但总有一条距离最短的公垂线,它正交于 任意两条斜线。在公垂线方向上定义本地 参考坐标系的x轴。 • 如果an表示Zn-1与Zn之间的公垂线,则xn的 方向将沿an
5
给每个关节指定本地参考坐标系
——特殊情形
• 两关节Z轴平行,就会有无数条公垂线,此 时可挑选与前一关节的公垂线共线的一条, 可简化模型;
两个相邻的Z轴之间的角度(也叫关节扭转)
7
坐标变换
• 假设现在位于本地坐标系 xn zn ,那么通
过四步标准运动即可到达下一个本地坐标 系 xn1 zn1
旋转平移平移旋转
8
1.旋转
9
2.平移
10
3.平移
11
4旋转
12
• 在n+1和n+2坐标系间严格地按照同样的四 个运动顺序可以将一个坐标变换到下一个 坐标系。
其中n是关节数
17
18
19
lad 32 124iii
20
21
• 在机器人的基座和手之间的总变换为:
RTHA 1A2A 3A4A 5A 6
C12C46 C12S46 S12 l4S12l3S12l6S12l5C4C12
S12C46
S12S46
C12
l3S12l4C12l6C12l5C4S12
S46 C46 00
0 l2l5S4 01
22
机械臂的逆运动学
• 当机器人的末端姿态以 RPY 角( a , b, g)给
定后,可得与之相对应的旋转矩阵,再结
合末端位置输入,即给定了机器人末端相
对于基础坐标系的相对变换矩阵 为:
0T
6
23
RPY角(a,b,g)
R x y z ( a ,b ,g ) R ( z ,a )• R (y ,b )• R ( x ,g )
