5天线测量第五章解析
05导航雷达第五章雷达观测

3.操作技术因素
为了提高所使用雷达的距离分辨力,应注意:
1)尽量使用小量程,使用窄脉冲发射,
2)将雷达调整在最佳工作状态, 3)并适当减小增益和屏幕亮度,不使用回波扩展。 4)适当使用FTC,可以显著提高距离分辨力。
4.结论和IMO性能标准(距离分辨力)
IMO最新雷达性能标准规定,在平静的海面使用1.5 n mile 或更小的量程,在量程的50%~100%范围内,两个点目标的 距离分辨力应不低于40 m(此前的标准为50 m)。
2、若在8.8n mile之外,其岸线前沿在雷达探测地平之下,雷 达不能探测到岛屿的前沿,只能通过测量目标的后沿定位。
2.目标雷达最大作用距离
在自由空间中,雷达能够探测到目标的最远距离称为目标的 雷达最大作用距离。
Rmax 2 = 4
2 2 PG 0 64 3 Pr min
式中, PT ——雷达峰值功率(W) GA ——天线增益 ——工作波长(m) Prmin ——接收系统门限功率(W) 0 ——目标的有效散射面积(m2)
1.目标雷达探测地平 R max = 2.2( hA + h T ) (n mile)
hA为雷达天线高度,hT为目标高度。
2.2 hA
称为海面雷达地平;
对于海拔为0的岸线,必须距其小于该距离才能被发现。 例如,假设雷达天线高度为hA =16 m,则海面雷达地平约为 8.8n mile。如果利用海中小岛定位, 1、当岛屿在8.8 n mile之内时,其岸线前沿在雷达探测地平 之上,可以测量目标的前沿定位;
按照最新性能标准,2008年7月1日之后安装的雷达,在晴好天气,天线 高于水面15 m且本船静止时,雷达在不做任何其他调整仅改变量程时,能够 在40 m~1 n mile的水平距离中连续观测到表陡山,河口宽度为300米, 雷达天线水平波束宽度为1度,本船离河口_海里以 外时,雷达荧光屏上河口将被两侧陡山回波堵满。 A.7.5 B.9.3 C. 10.4 D.6
5G测量(完整版)

• 内置的GPS接收机可为测量提供相对于的当前地理信息且该信息更被 保存至测量文档中
• 除地理信息定位功能之外,还提供外部参考来提高FieldFox的频率精 度
Keysight Confidential
2/10/2020 Page 26
附件选择 针对于32/44/50GHz型号
Description
8. DC可偏置电压源
9. 具备瀑布图功能的干扰分析仪
10. 矢量电压表功能
11. 脉冲测量功能
12. 频率计数器
13. 长线缆测量功能
14. RTSA 实时频谱
• 该应用程序可以仿真 FieldFox 的前面板,支持用户在 iPad 或 iPhone 上按下 FieldFox 硬键或功能键,远程进行测量。
内置直流偏置可变电压源
• FieldFox内置1-32V可调的电压源,提供650mA最大电流和 8W最大 功率
• 该直流偏置电源可为被测放大器提供直流电源,例如(TMA)塔顶 放大器等
媲美实验室级的外场测量性能(续)
But PXA has better phase noise
Amplitude accuracy correlates within 0.2 dB
FieldFox
PXA
40 GHz Multitone Measurement Comparison
HIT 2015 Handheld 2/10/2020
uW FieldFox (w/DUT)
Laptop LAN-based Display Controller
67 GHz PSG
DC Power Supply
N1914A Power Meter & 26.5 GHz Sensor 50 GHz PXA 67 GHz PNA-X
《地籍与房产测绘》课件——第五章 GNSS与地籍测量

知识点二 GPS定位技术
GPS全球定位系统由空间星座部分、地面监 控部分以及用户接收机三部分组成。
一、 GPS概述
GPS(Global Positioning System)
是一种可以授时和测距的空间 交会定点的导航系统
可向全球用户提供连续、实时、高精度的三维位 置,三维速度和时间信息。
GPS的组成
地面监控部分
1 3
Colorado springs
5 5
Hawaii
Ascencion Diego Garcia
5
kwajalei n
GPS卫星星座
24 3
用户设备部分
按用途分:导航型、测地型、授时型
GPS接收 机硬件
用户设备
按载波频率分: 单频接收机、双频接收机
微处理机
终端设备
数据处理 软件
≤10 ≤10 ≤10 ≤10 ≤15
b(ppm)
≤2 ≤5 ≤10 ≤10 ≤20
最弱边相对 中误差
➢GPS 外业观测
① 天线安置---对中、整平、定向并量取天线高; ② 接收机操作; ③ 观测记录
任务一 GPS在地籍测量中的应用
一、GPS在地籍图测绘中的应用
➢ 它不要求通视,这样避免了常规地籍控制测量点
GPS测量的实施
工作程序:技术设计、选点与建立标志、外业观测、 成果检核与处理等阶段
➢ 踏勘选点及建立标志
① 在交通方便,易于安置接收设备的地方;
② 视野开阔,以便于同常规测量控制网的联测;
③ 在 15º 截止高度角以上应不存在障碍物;
④ GPS点应避开对电磁波接收有强烈吸收、反射等干扰影响的金 属和其它障碍物体。
GPS定位的关键是测定用户接受机天线至GPS卫星之间的距离
rs05

12
光学遥感器的组成
包括采光单元、分光单元、探测单元
采光单元 采用反射光学系统
KH-12卫星高分辨率成像 光学系统
13
光学遥感器的组成
分光单元 把光分解为光谱的过程叫分光,用于分光的元件有棱镜、衍 射光栅和分光滤光片 ▲棱镜: 利用物质的折射率随波长而不同
(,+)
+
14
31
光机扫描仪的构造
18
光机扫描仪的成像原理
19
Landsat的MSS MultiSpectral Scanner
MSS有4个波段: MSS4——0.5~0.6m 绿 MSS5——0.6~0.7m 橙 MSS6——0.7~0.8m 红 MSS7——0.8~1.18m 近红外
20
Landsat的TM Thematic Mapper TM有7个波段: TM1——0.45~0.52m 蓝 TM2——0.52~0.60m 绿 TM3——0.63~0.69m 红 TM4——0.76~0.90m 近红外 TM5——1.55~1.75m 短波红外 TM6——10.4~12.5m 热红外 TM7——2.08~2.35m 短波红外
24
5.成像光谱仪(Imaging Spectroscopy)
光谱分辨率的提高是遥感技术的一个重要发展趋势。 •光谱分辨率0.1m量级——多光谱(multispectral) •光谱分辨率0.01m量级——高光谱(hyperspectral) •光谱分辨率0.001m量级——超光谱(ultraspectral)
28
线列探测器加红外 S/N:较低
29
面阵探测器加推帚扫描型
扫描宽度窄 成像波段:可见光~短波红外 S/N:较高
30
第五章 GPS定位基本原理

第五章 GPS定位基本原理
8
2)、相对定位
• 确定同步跟踪相同的GPS信号的若干台接收机之间的相对 位臵的方法。可以消除许多相同或相近的误差(如卫星钟、 卫星星历、卫星信号传播误差等),定位精度较高。但其 缺点是外业组织实施较为困难,数据处理更为烦琐。
• 在大地测量、工程测量、地壳形变监测等精密定位领域内 得到广泛的应用。
j为卫星数,j=1,2,3,…
第五章 GPS定位基本原理
27
三、用测距码来测定伪距的特点
• 利用测距码测距的必要条件
– 必须了解测距码的结构
(1)易于将微弱的卫星信号提取出来。
卫星信号的强度一般只有噪声强度的万分之一或更低。 只有依据测距码的独特结构,才能将它从噪声的汪洋大海中 提取出来;
第五章 GPS定位基本原理
接收机钟差
t tk t tk (G) t (G) tk t
j j
j
信号真正传播时 间
第五章 GPS定位基本原理 22
如果不考虑大气折射的影响,则有:
' ct c[tk t ]
j
c tk (G ) t (G ) c(tk t )
j j
ρ = τ*C= △t*C 上式求得的距离ρ并不等于卫星至地面测站的真正距 离,称之为伪距。
第五章 GPS定位基本原理 19
二、伪距测量的观测方程
• 码相关法测量伪距时,有一个基本假设,即卫星钟和接 收机钟是完全同步的。
• 但实际上这两台钟之间总是有差异的。因而在R(t) =max 的情况下求得的时延τ就不严格等于卫星信号的传播时间 Δt,它还包含了两台钟不同步的影响在内。
第五章 GPS定位基本原理 17
第五章GPS卫星定位基本原理

测角交会法
B
P
P
A
C
A
B
前方交会
A
B
侧方交会
P
后方交会
A、B和C点坐标已知,P点坐标未知
精品文档
测边(距)交会法
3. 无线电接收机或卫星
▪ 无线电导航定位 ▪ 卫星激光测距定位
P
1)ABC为三个无线电信号发射台,坐标已
知
d1
d3
2)P为用户接收机
d2 A
C 3)采用无线电测距方法测得PA PB PC
3.由于伪距测量的精度较低,所以要有较多的
λ·No取平均值后才能获得正确的整波段数。
精品文档
5.3.3.1静态方法
二 经典方法
❖ 将整周未知数当做平差中的待定参数
一) 整数解 二) 实数解
精品文档
5.3.3.1静态方法
二 经典方法—整数解
1. 短基线定位时一般采用这种方法。
2 具体步骤:
1)首先根据卫星位置和修复了周跳后的相位观测 值进行平差计算,求得基线向量和整周未知数。
五
Fast ambiguity resolution approach
精品文档
5.3.3.1静态方法 一 伪距法
1.
k j ( N k j) ( N 0 j I( n ) ) P t
所以,得 N0j PInt)(
2.将载波相位测量的观测值(化为以距离为单位)
减去伪距实际观测值后即可得到λ·No。
4.特点 1)适用于导航和低精度测量
2) 定位速度快;
3)可作为载波相位测量中解决整波数不确定问题(模 糊度)的辅助资料。
精品文档
5.2 伪距测量 5.2.1伪距测量
第五章GPS测量的误差来源及其影响 第五节整周跳变分析与整周未知数的确定

GPS测量定位技术
一、整周跳变分析
2.整周跳变的检验和修正
卫星和接收机之间的距离在随时间而不断变化,其径向速度最
大可达0.9km/s,相应的载波相位观测值 亦 应随之变化,不过
该方法不考虑整周未知数的整数性质,通过平差计算求得 的整周未知数不再进行凑整和重新解算。这种方法一般用于基 线较长的相对定位中。
GPS测量定位技术
二、整周未知数的确定
2.“动态”测量法
在上述经典相对定位法中,是在基线向量未知的情况下, 通过静态相对定位解算整周未知数的。可是当观测站之间的基 线向量已知时,便可以根据基线端点两接收机的同步观测结果, 应用静态相对定位的双差模型直接求解相应的整周未知数,这 时观测时间可大为缩短,一般只需几分钟。
学习目标
•了解卫星星历误差,卫星钟误差,相对论效应的产生与 消减方法。 •理解接收机钟误差,相位中心位置误差的产生与消减方 法。 •掌握电离层折射误差、对流层折射误差、多路径误差的 产生与消减方法。整周未知数的确定。
GPS测量定位技术
第五节 整周跳变分析与整周未知数的确定
一、整周跳变分析
1.整周跳变及其发生
4次差
-0.5795 0.9639 -0.2721 -0.4219
GPS测量定位技术
2.整周跳变的检验和修正 但是,如果在过程中出现了整周跳变,势必要破坏上述 相位观测量的正常变化,高次差的随机特性也将受到破坏。 例如表5-4中在时刻的观测值中含有100周的周跳(表中有 *号的数据),四次差中将出现数十周的异常现象。这表明 通过求差有利于发现周跳。不过这种求高次差的方法难以 检验只有几周的小周跳,因为震荡器本身就有可能造成2周 左右的随机误差。
(整理)天线测量与微波测量实验讲义1
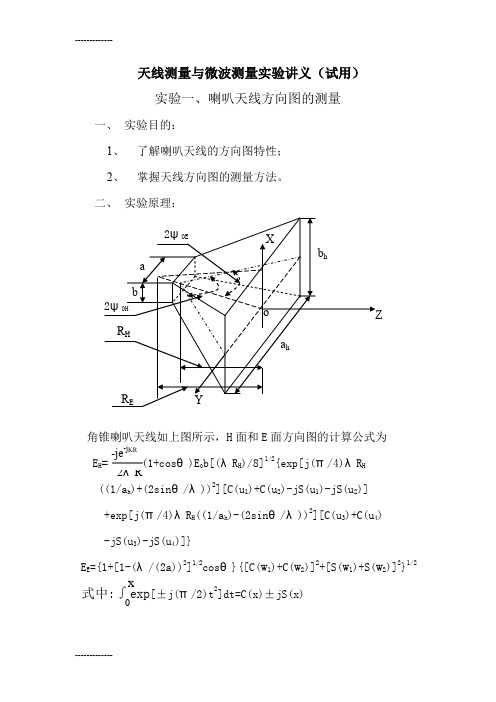
天线测量与微波测量实验讲义(试用)实验一、喇叭天线方向图的测量一、 实验目的:1、 了解喇叭天线的方向图特性;2、 掌握天线方向图的测量方法。
二、 实验原理:H 面和E 面方向图的计算公式为E H θ)E 0b[(λR H )/8]1/2{exp[j(π/4)λR Hθ/λ))2][C(u 1)+C(u 2)-jS(u 1)-jS(u 2)]+exp[j(π/4)λR H ((1/a h )-(2sin θ/λ))2][C(u 3)+C(u 4) -jS(u 3)-jS(u 4)]}E E 2]1/2cos θ}{[C(w 1)+C(w 2)]2+[S(w 1)+S(w 2)]2}1/2±j(π/2)t 2]dt=C(x)±jS(x)u1=(1/2)1/2{[a h/(λR H)1/2]+(λR H)1/2[(1/a h)+(2sinθ/λ)]}u2=(1/2)1/2{[a h/(λR H)1/2]-(λR H)1/2[(1/a h)+(2sinθ/λ)]}u3=(1/2)1/2{[a h/(λR H)1/2]+(λR H)1/2[(1/a h)-(2sinθ/λ)]}u4=(1/2)1/2{[a h/(λR H)1/2]-(λR H)1/2[(1/a h)-(2sinθ/λ)]} w1=[b h/(2λg R E)1/2]+{[(2λg R E)1/2/λ]sinθ}w2=[b h/(2λg R E)1/2]-{[(2λg R E)1/2/λ]sinθ}w1=[b h/(2λg R E)1/2]+{[(2λg R E)1/2/λ]sinθ}w1=[b h/(2λg R E)1/2]+{[(2λg R E)1/2/λ]sinθ}w1=[b h/(2λg R E)1/2]+{[(2λg R E)1/2/λ]sinθ}三、实验装置:测量方向图所需的基本设备可分为发射系统和接收系统两大部分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 2
n (n , 1, 2, 3, …… )
Ey E2
2 2
2E x E y E1 E 2
0
Ex E y E E 0 2 1
m E2 E1
2
直线方程
E y mEx
结论:当两个线极化波同相或反相时,其合成波是一个线极化波
E1=0,m=+1
平方项展开,并利用倍角公式
E ( E1 cos E2 sin cos ) 2 ( E2 sin sin ) 2
2
t g 1
E2 sin sin E1 cos E2 sin cos
E
2
1 2 2 2 2 E1 E 2 ( E1 E 2 ) cos 2 2 E1 E 2 cos sin 2 2
线极化波
椭圆极化波 极化测量主要是椭圆极化波各参数的测量
圆极化波
椭圆极化波的合成与其参数
两个线极化波合成椭圆极化t kz )
z=0的平面
sin t
E x E1 sin t E y E2 sin(t )
圆极化的利用 雷达利用圆极化天线来实现反云层、雨雪的干扰,气象雷达利用雨、雹等 的散射极化响应不同来识别目标性质; 飞行体上常用圆极化天线来提高通讯的可靠性,在剧烈摆动或滚动的飞行 器上装置圆极化天线,可以在任何状态下都能收到信息;[双方为圆极化,或 一方为圆极化] 在卫星通讯中,为了增加分配的无线电领带中信道的数目,对邻近通道, 使用高纯度的正交线极化天线来达到极化鉴别,缩短所需的频率间隔;[极化 隔离频率复用] 在电视广播中采用圆极化天线,可望克服重影; 在天文、航天通信及遥感遥测设备中采用圆极化天线,除可减小信号漏失 外,还可能消除由电离层法拉第旋转效应引起的极化畸变影响。
圆方程
E x E y E1
2
2
2
E1=E2
椭圆极化天线的主要参量
天线的极化特性,目前大多数都采用轴比AR、倾角τ 和旋向三个参数来评定,因此测量天线极化参数的任务 就是用直接或间接的方法来确定这三个参数 由于天线辐射场是有方向性的,因此其极化特性也具 有方向性,r=r(θ,φ),τ=τ(θ,φ) 多数情况下,天线极化参数的测量主要是针对天线特 定方向(θ,φ)来进行,比如天线主波束最大辐射方向,或 主波束半功率点方向等等,但有时也希望了解一定立体 角范围内的天线极化特性,即极化方向图。
sin 2
aEx bEx E y cE y 1
2
2
2 cos E1 E 2 sin 2 1 E 2 sin 2
2
椭圆极化波的合成与其参数
Ex E1
2 2
2 E x E y cos E1 E 2
Ey E2
2 2
sin 2
一般化椭圆方程
1.Ex与Ey同相或反相
Eφ与φ的关系即为极化图
倾角
椭圆极化波的倾角是指极化椭圆的长 轴OA与x坐标轴之间的夹角τ
x x cos y sin y x sin y cos
Ex Ex cos E y sin E y Ex sin E y cos
Ex E1
2 2
2 E x E y cos E1 E 2
Ey E2
2 2
sin
2
sin 2 2 cos2 cos sin 2 0 2 2 2 2 2 椭圆极化波的极化椭圆之 E E sin E2 sin E2 sin 1 2 长轴和短轴分别与新坐标 系x’y’重合,此项为零
极化图函数
E (t ) Ex cos E y sin
E x E1 sin t
E y E2 sin(t ) E (t ) E1 cos sin t E2 sin sin(t )
sin(t ) 展开整理
E (t ) E sin(t )
极化
天线的极化特性就成了某些天线设计和检验的一个重要方面。掌握极化的 基本理论和测量天线极化特性的方法是从事天线工作必备的知识和技能。 线极化、圆极化、椭圆极化,前两种为后一种的特殊形式。 椭圆极化波可以分解为两个同频线极化波,可以分解为两个同频反旋向的 圆极化波;反之,也可以合成椭圆极化波。
E1=E2,σ=π,m=-1
椭圆极化波的合成与其参数
2.Ex与Ey相位差±90°
1 2n 2
2 2
Ex E1
2 2
2 E x E y cos E1 E 2
Ey E2
sin 2
椭圆方程
Ex E1
2 2
Ey E1
2 2
E2 E1 2
1
3.Ex与Ey相位差±90°,且E1=E2
极化测量
椭圆极化 波的合成 与其参数 测量误差 椭圆极化 天线参数 的测量
极化传输 损失的确 定
极化 测量
椭圆极化 天线增益 的测量
图解法测 量技术
复极化比 的测量
极化
极化和场的振幅、相位一样也是表征电磁场基本特征的物理量。在电磁波的传 播过程中,无论场的振幅、相位或极化都可以包含有信息量,因而可以用来传 递信息。
Ex cost 1 sin t 1 E 1
2
Ex E1
E y E2 (sin t cos cost sin )
2
a b c
1 E1 sin 2
2
Ex E1
2 2
2 E x E y cos E1 E 2
Ey E2
2 2
2 2 sin sin 2 cos cos 2 Ex 2 2 2 2 EE E1 sin 2 sin E 2 sin E1 2 E cos tg 2 12 2 2 E1 2 E2 2 cos sin 2 cos sin 2 Ex E y 2 2 2 E 2 sin 2 E1 E 2 sin E1 sin 2 1 1 2E1 E2 cos tg 2 2 2 2 cos sin 2 cos sin 2 2 E E 1 2 1 Ey 2 2 2 2 E 2 sin E1 E 2 sin E1 sin
