非参数统计部分课后习题参考答案
非参数统计部分课后习题参考答案
课后习题参考答案第一章p23-252、（2）有两组学生，第一组八名学生的成绩分别为x 1：100，99，99，100，99，100，99，99；第二组三名学生的成绩分别为x 2：75,87,60。
我们对这两组数据作同样水平a=0.05的ｔ检验（假设总体均值为u ）：H 0：u=100 H 1：u<100。
第一组数据的检验结果为：df=7，t 值为3.4157，单边p 值为0.0056，结论为“拒绝H 0：u=100。
”（注意：该组均值为99.3750）；第二组数据的检验结果为：df=2，t 值为3.3290，单边ｐ值为0.0398;结论为“接受H 0：u=100。
”（注意：该组均值为74.000）。
你认为该问题的结论合理吗？说出你的理由，并提出该如何解决这一类问题。
答：这个结论不合理（6分）。
因为，第一组数据的结论是由于ｐ－值太小拒绝零假设，这时可能犯第一类错误的概率较小，且我们容易把握；而第二组数据虽不能拒绝零假设，但要做出“在水平ａ时，接受零假设”的说法时，还必须涉及到犯第二类错误的概率。
（4分）然而，在实践中，犯第二类错误的概率多不易得到，这时说接受零假设就容易产生误导。
实际上不能拒绝零假设的原因很多，可能是证据不足（样本数据太少），也可能是检验效率低，换一个更有效的检验之后就可以拒绝了，当然也可能是零假设本身就是对的。
本题第二组数据明显是由于证据不足，所以解决的方法只有增大样本容量。
（4分）第三章p68-713、在某保险种类中，一次关于1998年的索赔数额（单位：元）的随机抽样为（按升幂排列）： 4632，4728，5052，5064，5484，6972，7596，9480，14760，15012，18720，21240，22836，52788，67200。
已知1997年的索赔数额的中位数为5064元。
（1）是否1998年索赔的中位数比前一年有所变化？能否用单边检验来回答这个问题？（4分） （2）利用符号检验来回答（1）的问题（利用精确的和正态近似两种方法）。
非参数统计王星版第一章课后答案
非参数统计第一章课后答案#1.1AG E=c(18,23,22,21,20,19,20,20,20)fi rst3=sort(AGE)[(leng th(AG E)-2):leng th(AG E)]delet e.1=o rder(AGE)[(leng th(AG E)-2):leng th(AG E)]e xcept=AGE[-dele te.1]c(e xcept[1:2],19,e xcept[3:le ngth(excep t)])exce pt[2]=22#1.2a1=re p(1:3,rep(2,3))a2=c(1,8,10,11)a3=seq(1,30,l ength(a2))a4=s eq(1,5,2)a4=c(a1,a4,rep(0,2))a5=2:10a6=c(a2,a3[-(1:3)],a4)a7=c(rep(1,10),rep(0,8))#1.3lib rary(MASS)data(geys er)a=geys era1=subs et(a,waiti ng<70)a1=geyse r[gey ser$w aitin g<70,]#两个a1等价a2=sub set(a,wait ing<70&wai ting!=57)a2=ge yser[geyse r$wai ting<70&ge yser$waiti ng!=57,]#两个a2等价a3=s ubset(a,wa iting<70,c(dura tion))a4=subse t(a,d urati on>70,c(wa iting))#1.3li brary(MASS)a=g eyseratta ch(a)b1=w aitin g[wai ting<70]b2=wai ting[waiti ng<70&wait ing!=57]b3=dur ation[wait ing<70]b4=wait ing[d urati on>70]#1.4x=c(0,1,1,2,3,4)n um=fu nctio n(x){r=0p=c(r ep(0,lengt h(x)-1))q=c(re p(0,l ength(x)-1))fo r(i i n 1:(lengt h(x)-1)){f or(jin (i+1):l ength(x)){p[i]=p[i]+I(x[i]<x[j]) q[i]=q[i]+I(x[i]>x[j])} r=r+p[i]-q[i]}r}h=rep(0,1000)for(i in 1:le ngth(h)){x=r unif(5,-5,5)h[i]=num(x)}y=as.f actor(h)y y=lev els(y)a=rep(0,11)#记数记录-10:10:2各种结果出现的次数p=rep(0,11)for(i in 1:11){a[i]=su m(h==(-12+2*i))p[i]=a[i]/le ngth(h)}aph ist(h)h=rep(0,10000)f or(iin 1:lengt h(h)){x=samp le(1:5,5,r eplac e=T)#-5到5中间的整数随机抽样 h[i]=num(x)}y=as.facto r(h)yy=le vels(y)a=rep(0,len gth(y y))#记数记录-10:10各种结果出现的次数p=rep(0,le ngth(yy))for(i in 1:leng th(yy)){ a[i]=sum(h==(-11+i))p[i]=a[i]/l ength(h)}aphist(h)#当随机取10000次的一个结果 a=[71 321 774 1255 1637 1825 1684 1256 743 33896] # p=[0.0071 0.0321 0.07740.1255 0.1637 0.1825 0.1684 0.12560.0743 0.0338 0.0096] #当随机取十万次数据的一个结果#a=[795 3421 7553 12521 1677118180 16538 12553 7418 3400 850]#p=[0.00795 0.03421 0.075530.12521 0.16771 0.18180 0.16538 0.125530.074180.03400 0.00850]#1.5un iroot(f=fu nctio n(x)2*x^3-4*x^2+3*x-6, i nterv al=c(-10,10))f=func tion(x){2*x^3-4*x^2+3*x-6}f(0)a=-10b=10ro ot=fu nctio n(a,b){ c=(a+b)/2;w hile(abs(f(c))>0.00001){ if(f(c)*f(a)<0){b=c; c=(a+b)/2;}e lse {a=c;c=(a+b)/2;}} c#1.6x=seq(0,2*pi,0.2)y=sin(x)/(co s(x)+x)#1.7c harto num=f uncti on(x){a=c("a bcdef ghijk lmnop qrstu vwxyz ABCDE FGHIJ KLMNO PQRST UVWXY Z");b=s trspl it(a,"");for(i in 1:52){ if(b[[1]][i]==x){t=i;i=i+1}e lse{i=i+1}}t}#将字符转化为数字，小写为前26位，大写为后26位，输入为单个字符f7=fun ction(x){y=s trspl it(x,"");#将输入分为单个字符f or(iin 1:lengt h(y[[1]])){ t=chart onum(y[[1]][i]) if(t<14){t=t+13;y[[1]][i]=LE TTERS[t];} els e if(t>=14&t<=26){t=t-13;y[[1]][i]=LETTE RS[t];}e lse i f(t>=27&t<=39){t=t+13-26;y[[1]][i]=lette rs[t];}e lse{t=t-13-26;y[[1]][i]=l etter s[t];} }mima=y;mima}#1.8f1.81=f uncti on(a){ for(i in1:len gth(a)) {c[i]=a[lengt h(a)-i+1]}c}f1.82=fun ction(a,b){f or(iin 1:(leng th(a)+leng th(b))){ if(i%%2==1){c[i]=a[(i+1)/2];} els e{c[i]=b[i/2];}}c}#%%为求余符号#1.9f1.9=f uncti on(n,m){ a=re p(1,n);i=1;k=0;t=1; whil e(sum(a)>1|a[t]==0){t=i%%n; if(t==0){t=n;} else{t=i%%n} if(a[t]!=0){ k=k+1;i=i+1;}else{i=i+1} if(k%%m==0){k=0;a[t]=0;}}t}#1.10s tuden t<-re ad.ta ble("C:\\D ocume nts a nd Se tting s\\Ad minis trato r\\桌面\\非参数统计配套数据\\各章数据\\第一章\\s tuden t.txt",hea der = T)st udent1=as.data.frame(stud ent)mean s=app ly(st udent1[,2:6],1,mean)b1=d ata.f rame(stude nt1,m eans)b2=stude nt1[w hich(b==ma x(b)),]b3=I(s tuden t1[,2:6]<60)#判断每个学生每门课程是否及格b4=appl y(b3,1,sum)#找出每个学生有几门课程不及格b5=b1[wh ich(b4>1),]b6=b1[-w hich(b4>1),]t.tes t(b5$means,b6$m eans)#不说明情况下认为两总体方差不同，特殊说明var.equa l=TRU E 置信区间为均值差的置信区间wilc ox.te st(b5$mean s,b6$means)wil cox.t est(b5$mea ns,b6$mean s,pai res=F ALSE)#1.11bas ket<-read.table("C:\\Docu ments andSetti ngs\\Admin istra tor\\桌面\\非参数统计配套数据\\各章数据\\第一章\\bask et.tx t",he ader = T)A=I(bask et[,2:6]=='A')A=bas ket[,2:6]=='A'Asum=apply(A,1,sum)B=bas ket[,2:6]=='B'Bsum=apply(B,1,sum)a1=ba sket[which(Asum>0&Bs um>0),1]l ength(a1)#求个数a2=bas ket[w hich(Asum>0&Bsu m>=3),]le ngth(a2$ID)#求个数#1.12x=s eq(-10,10,0.05)y1=s in(x)y2=c os(x)y3=y1+y2plot(x,y1,col=1,lty=1,axe s=T,m ain="习题1.12",su b="si n（）,c os（）,sin()+cos()对比图")poi nts(x,y2,c ol=2,lty=3)poi nts(x,y3,c ol=3,lty=4)pl ot(x,y1,co l=1,l ty=1,main="习题1.12",s ub="s in（）,cos（）,sin()+cos()对比图")li nes(x,y1,c ol=1,lty=1)lin es(x,y2,co l=2,l ty=3)line s(x,y3,col=3,lt y=4)curv e(sin(x),-10,10,col=1,lty=1,ma in="习题1.12",sub="sin（）,co s（）,s in()+cos()对比图")curv e(cos(x),a dd=TR UE,co l=2,l ty=3)curv e(sin(x)+c os(x),add=TRUE,col=3,lty=4)#1.13x=seq(-5,5,lengt h=50)a=ru nif(500,-5,5)y=0.1*a*sin(2*a)f1=f uncti on(x,y){1-exp(-1/x^2+y^2)}z1=outer(x/2,x/2,f1)pe rsp(z1)f2=fun ction(x,y){0.1*x*sin(2*y)}z2=outer(x,x,f2)p ersp(z2)f3=fu nctio n(x,y){sin(x)+c os(x)}z3=outer(x,x,f3)p ersp(z3)plot(sin(3*x),s in(6*x),ty pe="l")#1.14a=rno rm(100,3,s qrt(5))b=rnorm(20,5,sqrt(3))c=c(a,b)h ist(c)box plot(c)qq norm(c)#1.15x=rnor m(100,0,1)y1=l og(ab s(x))#lamd a=0h ist(y1)qq norm(y1)q qline(y1,col = 2)y2=(x-1)#la mda=1hist(y2)qqnor m(y2)qqli ne(y2, col = 3)y3=1-1/x#lamda=-1h ist(y3)qq norm(y3)q qline(y2,col = 4)。
非参数统计部分课后习题参考答案
课后习题参考答案第一章p23-252、（2）有两组学生，第一组八名学生的成绩分别为x 1：100，99，99，100，99，100，99，99；第二组三名学生的成绩分别为x 2：75,87,60。
我们对这两组数据作同样水平a=0.05的ｔ检验（假设总体均值为u ）：H 0：u=100 H 1：u<100。
第一组数据的检验结果为：df=7，t 值为3.4157，单边p 值为0.0056，结论为“拒绝H 0：u=100。
”（注意：该组均值为99.3750）；第二组数据的检验结果为：df=2，t 值为3.3290，单边ｐ值为0.0398;结论为“接受H 0：u=100。
”（注意：该组均值为74.000）。
你认为该问题的结论合理吗？说出你的理由，并提出该如何解决这一类问题。
答：这个结论不合理（6分）。
因为，第一组数据的结论是由于ｐ－值太小拒绝零假设，这时可能犯第一类错误的概率较小，且我们容易把握；而第二组数据虽不能拒绝零假设，但要做出“在水平ａ时，接受零假设”的说法时，还必须涉及到犯第二类错误的概率。
（4分）然而，在实践中，犯第二类错误的概率多不易得到，这时说接受零假设就容易产生误导。
实际上不能拒绝零假设的原因很多，可能是证据不足（样本数据太少），也可能是检验效率低，换一个更有效的检验之后就可以拒绝了，当然也可能是零假设本身就是对的。
本题第二组数据明显是由于证据不足，所以解决的方法只有增大样本容量。
（4分）第三章p68-713、在某保险种类中，一次关于1998年的索赔数额（单位：元）的随机抽样为（按升幂排列）： 4632，4728，5052，5064，5484，6972，7596，9480，14760，15012，18720，21240，22836，52788，67200。
已知1997年的索赔数额的中位数为5064元。
（1）是否1998年索赔的中位数比前一年有所变化？能否用单边检验来回答这个问题？（4分） （2）利用符号检验来回答（1）的问题（利用精确的和正态近似两种方法）。
非参数统计答案范文
非参数统计答案范文1. 考察Mann-Whitney U检验：问题：对两组数据进行比较，数据不符合正态分布，要判断两组数据是否有显著差异。
如何选择合适的非参数检验方法？答案：Mann-Whitney U检验是一种适用于比较两组独立样本的非参数检验方法，适用于数据不符合正态分布的情况。
2. 考察Wilcoxon符号秩和检验：问题：对同一组数据进行配对比较，数据不符合正态分布，如何选择合适的非参数检验方法？答案：Wilcoxon符号秩和检验是一种适用于配对样本的非参数检验方法，适用于数据不符合正态分布的情况。
3. 考察Kruskal-Wallis检验：问题：有三组数据需要比较，但数据不符合正态分布，如何选择合适的非参数检验方法？答案：Kruskal-Wallis检验是一种适用于比较多组独立样本的非参数检验方法，适用于数据不符合正态分布的情况。
4. 考察Friedman检验：问题：有三组配对数据需要比较，但数据不符合正态分布，如何选择合适的非参数检验方法？答案：Friedman检验是一种适用于比较多组配对样本的非参数检验方法，适用于数据不符合正态分布的情况。
5. 考察Mood's中位数差异检验：问题：有两组独立样本数据需要比较，数据不符合正态分布，如何选择合适的非参数检验方法？答案：Mood's中位数差异检验是一种适用于比较两组独立样本的非参数检验方法，适用于数据不符合正态分布的情况。
6.考察符号检验：问题：对一组配对数据进行比较，但数据不符合正态分布，如何选择合适的非参数检验方法？答案：符号检验是一种适用于配对样本的非参数检验方法，适用于数据不符合正态分布的情况。
7.考察秩和检验：问题：有两组独立样本数据需要比较，如何选择合适的非参数检验方法？答案：秩和检验是一种适用于比较两组独立样本的非参数检验方法。
8. 考察Kolmogorov-Smirnov检验：问题：有一组数据需要验证其服从一些特定分布，如何进行检验？答案：Kolmogorov-Smirnov检验是一种非参数检验方法，可以用于验证数据是否符合一些特定分布。
王静龙《非参数统计分析》课后计算题参考答案汇编
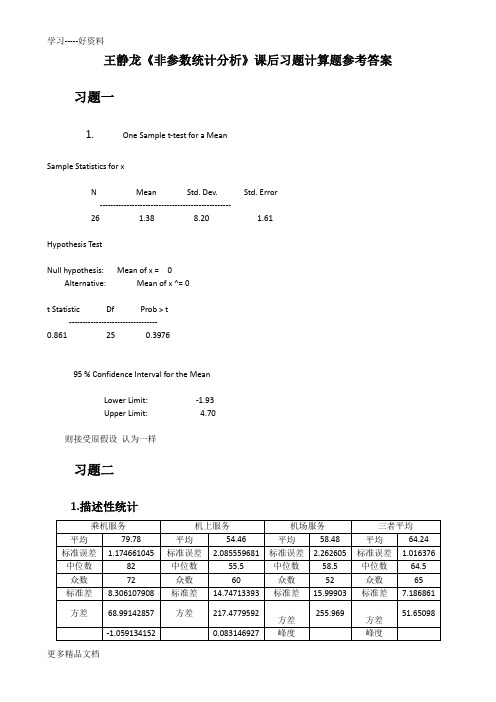
学习-----好资料更多精品文档王静龙《非参数统计分析》课后习题计算题参考答案习题一1.One Sample t-test for a MeanSample Statistics for xN Mean Std. Dev. Std. Error-------------------------------------------------26 1.38 8.20 1.61 Hypothesis TestNull hypothesis: Mean of x = 0Alternative: Mean of x ^= 0t Statistic Df Prob > t---------------------------------0.861 25 0.397695 % Confidence Interval for the MeanLower Limit: -1.93Upper Limit: 4.70则接受原假设认为一样习题二1.描述性统计更多精品文档习题三1.1{}+01=1339:6500:650013=BINOMDIST(13,39,0.5,1)=0.026625957S n H me H me P S +==<≤另外：在excel2010中有公式 BINOM.INV(n,p,a) 返回一个数值，它使得累计二项式分布的函数值大于或等于临界值a 的最小整数***0*0+1inf :2BINOM.INV(39,0.5,0.05)=141sup :1132S 1313n m i n d i n m m i n d d m i d αα==⎧⎫⎛⎫⎪⎪⎛⎫=≥⎨⎬⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭⎧⎫⎛⎫⎪⎪⎛⎫≤=-=⎨⎬ ⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭=≤=∑∑= 以上两种都拒绝原假设，即中位数低于65001.2学习-----好资料更多精品文档****01426201inf :221inf :122BINOM.INV(40,0.5,1-0.025)=26d=n-c=40-26=14580064006200nn i c n m i n c c i n m m i x x me x αα==⎧⎫⎛⎫⎪⎪⎛⎫=≤⎨⎬⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭⎧⎫⎛⎫⎪⎪⎛⎫=≥-⎨⎬⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭====∑∑2.{}+01=4070:6500:65002402*(1-BINOMDIST(39,70,0.5,1))=0.281978922S n H me H me P S +==≠≥=则接受原假设，即房价中位数是65003.1{}+01=15521552527207911::22n 1552=5.33E-112S n H p H p P S φ+=+==>≥≈比较大，则用正态分布近似**+**0:=1552155252720791inf :221inf :122m=BINOM.INV(2079,0.5,0.975)=1084nn i c n m i S n n c c i n m m i αα===+=⎧⎫⎛⎫⎪⎪⎛⎫=≤⎨⎬⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭⎧⎫⎛⎫⎪⎪⎛⎫=≥-⎨⎬⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭∑∑另外则拒绝原假设，即相信孩子会过得更好的人多3.2P 为认为生活更好的成年人的比例，则学习-----好资料更多精品文档1522=0.7465132079p 的比估计是：4.{}00.90610.90618154157860:65:6510.9060.094~(,)181541BINOMDIST(18153,157860,0.094,1)=0S n H P H P p S b n p P S +++===>=-=≥=-因为0〈0.05则拒绝原假设习题四1.()()++0.025+W =6+8+10+1+4+12+9+11+2+7=70p 2P W 70n=12c =65p 2P W 65=0.05≥≥符号秩和检验统计量：值为，当得所以值小于即拒绝原假设2．学习-----好资料更多精品文档()()++0.025+W =2.5+2.5+7+7+7+7+10.5+14+14+14+14+14+17.5+17.5+19+20+23+24=234.5p 2P W 234.5n=25 c =236p 2P W 236=0.05≥≥符号秩和检验统计量：值为，当得所以值小于即接受原假设{}011826:0:02182*(1-BINOMDIST(17,25,0.5,1))=0.043285251S n H me H me P S +===≠≥=+符号检验：则拒绝原假设学习-----好资料更多精品文档t t =0.861df=25 p=0.3976检验：统计量接受原假设3．（1）+0.0250.0250.025++=5+2+2=9833(1)322(3)0.052(9)0.05W n c n n d c P W P W ==+=-=≤=≤>查表可得：则 接受原假设Walsh 平均由小到大排列：50 55 60 65 65 70 70 70 75 75 75 80 80 80 80 80 80 80 85 85 85 8585 90 90 90 90 90 90 95 95 95 95 95 95 100 100 100 100 100 100 100 105 105学习-----好资料 更多精品文档105 105 105 110 110 110 110 110 115 115 120N=55 则对称中心为()()^281/290N W W θ+===()()1/1/1/40.527.50.5 1.967.771011461/40.527.50.5 1.9647.22898853d n n U c n n U αα--=+--=--==+++=++=因为c 不是整数，则^+1k d L k k w w θ（）（）介于与之间，其中表示比大的最小整数即为8 ^L θ为70与75之间，即为72.5 []-%72.5,105H L 则的点估计为90 95的区间估计为习题五1.171(,24,25,50)0.005060988i p P i p ===∑值很小，则拒绝原假设即认为女职工的收入比男职工的低。
非参数统计题目及答案
1．人们在研究肺病患者的生理性质时发现，患者的肺活量与他早在儿童时期是否接受过某种治疗有关，观察3组病人，第一组早在儿童时期接受过肺部辐射，第二组接受过胸外科手术，第三组没有治疗过，现观察到其肺活量占其正常值的百分比如下：这一经验是否可靠。
解：H 0：θ2≤θ1≤θ3 H 1:至少有一个不等式成立可得到 N=15由统计量H=)112+N N （∑=Ki i N R 1i 2-3(N+1)=）（1151512+(32×6.4+29×5.8+59×11.8)-3×(15+1)=5.46查表（5,5,5）在P(H ≥4.56)=0.100 P(H ≥5.66)=0.0509 即P （H ≥5.46）﹥0.05 故取α=0.05， P ﹥α ，故接受零假设即这一检验可靠。
2.关于生产计算机公司在一年中的生产力的改进（度量为从0到100）与它们在过去三年中在智力投资（度量为：低，中等，高）之间的关系的研究结果列在下表中：值等等及你的结果。
（利用Jonkheere-Terpstra 检验） 解：H 0：M 低=M 中=M 高 H 1：M 低﹤M 中﹤M 高U 12=0+9+2+8+10+9+10+2+10+10+8+0.5+3=82.5 U 13=10×8=80U 23=12+9+12+12+12+11+12+11=89 J=∑≤jijUi =82.5+80+89=251.5大样本近似 Z=[]72)32()324121i 222∑∑==+-+--ki i i ki n n N N n N J （）（～N （0,1）求得 Z=3.956 Ф(3.956)=0.9451取α=0.05 ， P >α，故接受原假设，认为智力投资对改进生产力有帮助。
非参数统计·王星_第二章课后习题答案
非参数统计 第 次作业第二章习题 2.1 解：（1）0110001000H :h H :h μ≥↔μ<建立的猜想应该与样本表现一致。
换句话说，正是样本表现使我们对总体的均值产生怀疑，进而才有了假设检验。
因此，0H 是我们就与样本想要推翻的假设，所以才要检验。
（2）由上一问，这样的假设脱离样本，样本呈现出落后于旧过程的情形，而非要用一种优于旧过程的假设，这样的假设是毫无意义的，也并不会带来好的结果。
2.2 解：（1）有问题。
假设检验在原假设条件成立下，得到拒绝域1645x .>，意思是拒绝0θ=，接受0θ≠。
而1000θ=只是其中的一种情况，故不能接受1000θ=。
改进方法：可直接提出假设对均值为1000进行检验。
即0110001000H :H :θ=↔θ≠（2）不合理。
样本2的样本量太小，不具备代表性，用其进行假设检验风险太大。
改进方法：若样本来自同一总体，独立观察，且需要对总体样本均值做出判断，可将两样本合并后再进行假设检验；若样本来自两个总体，需对两总体的均值做出比较，可取（12x x ---）作为检验统计量进行检验。
（3）t -=x -为样本均值，μ为总体均值，s 为样本标准差 01p Pr(t(n )t )=-≤，其中0t -=p 值是拒绝原假设0H 的最小显著水平。
若p α≥，则拒绝0H ；反之，接受0H（4）对总体均值进行双侧检验：00012112211111-H :|t(n )t (n )|(x t (n t (n α---αα--μ=μ↔μ≠μ⎧⎫->-⎨⎬⎩⎭α--+-拒绝域：故，置信区间为：（5）双侧检验：00101211221122''H :H :|u |u u u [x u ,x u α--αα----αα--μ=μ↔μ≠μ⎧⎫≥⎨⎬⎩⎭≤≤-+拒绝域：故置信区间为：- 当样本量很大时，依然可以用上法：222212211111_n i i _s (x x )[n(x (x ))]n n n [(x (x ))]n --=-=-=---=--∑由矩估计的相合性可知，2_x 是2E(x )的相合估计，2(x )-是2E(x )的相合估计 故2s 是2δ的相合估计。
非参数统计分析第六章课后答案
非参数统计分析第六章课后答案问题1：设有10个教师分别在两个学校中进行教学，分别记录了每位教师每日的教学小时数。
假设这两个学校的教学小时数分布不符合正态分布。
现在我们想要比较这两个学校的教学小时数平均值是否相等。
解答：对于这个问题，我们可以使用非参数统计方法-秩和检验。
首先将每个教师的教学小时数按照从小到大的顺序排列，并为每个小时数分配一个序号，即用秩来代替实际的数值。
然后根据两个学校的秩之和来进行比较。
步骤如下：1.将每个学校的教学小时数按照从小到大的顺序排列，并为每个小时数分配一个序号（秩）。
2.计算两个学校的秩和，并求出差值。
3.利用秩和差值来估计两个学校教学小时数平均值的差异性。
4.根据差异性的大小，进行假设检验，判断两个学校的教学小时数平均值是否相等。
问题2：某农场试验了两种肥料对苹果树生长的影响。
为此，从两个农场中随机选择了64棵苹果树，并给予不同的肥料进行处理。
试比较两种处理的效果是否相同。
解答：对于这个问题，我们可以使用非参数统计方法-符号检验。
符号检验是一种用于比较两个相关样本的方法，适用于样本量较小或者数据不符合正态分布的情况。
步骤如下：1.对于每棵苹果树，比较两种处理对树的生长效果，根据生长情况给予正或负的符号。
2.统计正负符号的个数，得到两种处理的得分。
3.根据得分判断两种处理的效果是否相同：如果得分大致相等，则说明两种处理的效果相同；如果得分明显偏向一种处理，则说明两种处理的效果不同。
问题3：某个城市公交车站每小时通过的乘客数量分别为：20、18、14、26、22、24、16、12、16、20。
我们想要推断乘客数量的中位数。
解答：对于这个问题，我们可以使用非参数统计方法-中位数检验。
中位数是一种非参数的统计量，它不受极端值的影响，适用于数据分布不符合正态分布的情况。
步骤如下：1.将数据按照从小到大的顺序排列。
2.根据数据的个数，找出中间位置的数值，即中位数的位置。
3.如果数据个数为奇数，则中位数即为中间位置的数值；如果数据个数为偶数，则计算中间位置两个数值的平均值作为中位数。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
课后习题参考答案第一章p23-252、（2）有两组学生，第一组八名学生的成绩分别为x 1：100，99，99，100，99，100，99，99；第二组三名学生的成绩分别为x 2：75,87,60。
我们对这两组数据作同样水平a=的ｔ检验（假设总体均值为u ）：H 0：u=100 H 1：u<100。
第一组数据的检验结果为：df=7，t 值为，单边p 值为，结论为“拒绝H 0：u=100。
”（注意：该组均值为）；第二组数据的检验结果为：df=2，t 值为，单边ｐ值为;结论为“接受H 0：u=100。
”（注意：该组均值为）。
你认为该问题的结论合理吗说出你的理由，并提出该如何解决这一类问题。
答：这个结论不合理（6分）。
因为，第一组数据的结论是由于ｐ－值太小拒绝零假设，这时可能犯第一类错误的概率较小，且我们容易把握；而第二组数据虽不能拒绝零假设，但要做出“在水平ａ时，接受零假设”的说法时，还必须涉及到犯第二类错误的概率。
（4分）然而，在实践中，犯第二类错误的概率多不易得到，这时说接受零假设就容易产生误导。
实际上不能拒绝零假设的原因很多，可能是证据不足（样本数据太少），也可能是检验效率低，换一个更有效的检验之后就可以拒绝了，当然也可能是零假设本身就是对的。
本题第二组数据明显是由于证据不足，所以解决的方法只有增大样本容量。
（4分）第三章p68-713、在某保险种类中，一次关于1998年的索赔数额（单位：元）的随机抽样为（按升幂排列）： 4632，4728，5052，5064，5484，6972，7596，9480，14760，15012，18720，21240，22836，52788，67200。
已知1997年的索赔数额的中位数为5064元。
（1）是否1998年索赔的中位数比前一年有所变化能否用单边检验来回答这个问题（4分） （2）利用符号检验来回答（1）的问题（利用精确的和正态近似两种方法）。
（10分） 》（3）找出基于符号检验的95％的中位数的置信区间。
（8分）解：（1）1998年的索赔数额的中位数为9480元比1997年索赔数额的中位数5064元是有变化，但这只是从中位数的点估计值看。
如果要从普遍意义上比较1998年与1997年的索赔数额是否有显著变化，还得进行假设检验，而且这个问题不能用单边检验来回答。
（4分）（2）符号检验（5分）设假设组：H ０：M ＝M ０＝5064H １：M ≠M ０＝5064符号检验：因为n +=11，n-=3，所以k=min(n+,n-)=3精确检验：二项分布b(14,，∑=-=30287.0)2/1,14(n b ，双边ｐ－值为,大于ａ＝，所以在ａ水平下，样本数据还不足以拒绝零假设；但假若ａ＝，则样本数据可拒绝零假设。
查二项分布表得ａ＝的临界值为（3，11），同样不足以拒绝零假设。
正态近似：（5分） np=14/2=7,npq=14/4=z=(3+/5.3≈>Z a/2=—仍是在ａ＝的水平上无法拒绝零假设。
说明两年的中位数变化不大。
（3）中位数95％的置信区间：（5064，21240）（8分）7、一个监听装置收到如下的信号：0，1，0，1，1，1，0，0，1，1，0，0，0，0，1，1，1，1，1，1，1，1，1，0，1，0，0，1，1，1，0，1，0，1，0，1，0，0，0，0，0，0，0，0，1，0，1，1，0，0，1，1，1，0，1，0，1，0，0，0，1，0，0，1，0，1，0，1，0，0，0，0，0，0，0，0。
能否说该信号是纯粹随机干扰（10分）解：建立假设组： H 0：信号是纯粹的随机干扰H 1：信号不是纯粹的随机干扰（2分）游程检验：因为n １=42，n ２=34，r=37。
（2分）根据正态近似公式得：Ｕ＝33.18)13442()3442()344234422(3442258.3813442344222≈-++--⨯⨯⨯⨯=≈++⨯⨯σ （2分）086.033.1858.3837-≈-=Z （2分）取显著性水平ａ＝，则Ｚａ/２＝,故接受零假设，可以认为信号是纯粹的随机干扰的。
（2分） {第四章p91-941、在研究计算器是否影响学生手算能力的实验中，13个没有计算器的学生（Ａ组）和10个拥有计算器的学生（Ｂ组）对一些计算题进行了手算测试．这两组学生得到正确答案的时间（分钟）分别如下：Ａ组：28， 20，20，27，3，29，25，19，16，24，29，16，29 Ｂ组：40，31， 25，29，30，25，16，30，39，25能否说Ａ组学生比Ｂ组学生算得更快利用所学的检验来得出你的结论．（12分）解、利用Wilcoxon 两个独立样本的秩和检验或Mann-Whitney U 检验法进行检验。
建立假设组：H 0：两组学生的快慢一致；H 1：A 组学生比B 组学生算得快。
（2分） 两组数据混合排序（在B 组数据下划线）：3，16，16，16，19，20，20，24，25，25，25，25，27，28，29， 29， 29， 29，30， 30，31，39，40（2分）A 组秩和R A ＝1+3*2+5+*2+8++13+14+*3=120; 】B 组秩和R B ＝3+*3++*2+21+22+23=156（2分） A 组逆转数和U A =120-(13*14)/2=29B 组逆转数和U B =156-(10*11)/2=101（2分）当n A =13，n B =10时，样本量较大，超出了附表的范围，不能查表得Mann-Whitney 秩和检验的临界值，所以用正态近似。
计算2326.21245.16362603612/)11013(*10*132/10*132912/)1(2/-≈-≈-=++-=++-=B A B A B A A n n n n n n U Z （2分）当显著性水平a 取时，正态分布的临界值Z a/2＝（1分）由于Z<Z a/2，所以拒绝H 0，说明A 组学生比B 组学生算得快。
（1分）4、在比较两种工艺（Ａ和Ｂ）所生产的产品性能时，利用超负荷破坏性实验。
记下损坏前延迟的时间名次（数目越大越耐久）如下：方法：A B B A B A B A A B A A A B A B A A A A ：序： 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20用Mann-Whitney 秩和检验判断Ａ工艺是否比Ｂ工艺在提高耐用性方面更优良（10分）解、设假设组：H 0：两种工艺在提高耐用性方面的优良性一致；H 1：A 工艺比B 工艺更优良（1分，假设也可用符号表达式） 根据样本数据知n A =13；n B =7（1分），计算A 工艺的秩和R A ＝1+4+6+8+9+11+12+13+15+17+18+19+20=153；（1分）B 工艺的秩和R B ＝2+3+5+7+10+14+16=57（1分）A 工艺的Mann-Whitney 秩和U A =R A -n A (n A +1)/2=153-(13*14)/2=62（1分）B 工艺的Mann-Whitney 秩和U B =R B -n B (n B +1)/2=57-(7*8)/2=29（1分）当n A =13，n B =7时，样本量较大，超出了附表的范围，不能查表得Mann-Whitney 秩和检验的临界值，所以用正态近似。
计算 …3075.16194.125.1625.1595.1612/)1713(*7*132/7*136212/)1(2/≈≈=++-=++-=B A B A B A A n n n n n n U Z （2分）当显著性水平a 取时，正态分布的临界值Z a/2＝（1分）由于Z<Z a/2，所以样本数据提供的信息不足以拒绝H 0，可以说A 、B 两种工艺在提高耐用性方面的优良性一致，A 工艺并不比B 工艺更优良。
（1分）第五章p118-1211、对5种含有不同百分比棉花的纤维分别做8次抗拉强度试验，试验结果如表4所示（单位：g/cm 2）：试问不同百分比纤维的棉花其平均抗拉强度是否一样，利用Kruskall —Wallis 检验法。
(14分) 解：建立假设组：H 0：不同百分比纤维的棉花其平均抗拉强度一样； H 1：不同百分比纤维的棉花其平均抗拉强度不一样。
（2分） 已知，k=5，n 1= n 2= n 3= n 4= n 5=8（2分）。
混合排序后各观察值的秩如表4所示：表4根据表4计算得：（6由于自由度k-1=5-1=4，n j ＝8>5，是大样本，所以根据水平a=，查Ｘ2分布表得临界值C=，（2分） 因为Q>C ，故以5%的显著水平拒绝H 0假设，不同百分比纤维的棉花其平均抗拉强度不一样。
（2分）…70H 1：顾客对3种服务的态度有显著性差异。
（2分）本例中，k=3，n=15。
（2分）又因6857.2841385.715.2535.2501665.78414012)1(3)1(122222212≈⨯-++++⨯⨯=+-+=∴∑=N n R N N H k j jj（5分）自由度k-1=3-1=2，（2分）取显著性水平a=，查Ｘ2分布表得临界值c=，（2分）因为Q>C ，故以5%的显著水平拒绝H 0假设，即顾客对3种服务的态度有显著性差异。
（2分）8、调查20个村民对3个候选人的评价，答案只有“同意”或“不同意”两种，结果见表1：解：建立假设组： H 0：三个候选人在村民眼中没有区别H 1：三个候选人在村民眼中有差别（2分）数据适合用Cochran Q 检验（2分）。
而且已知n=20，k=3，∑x i =∑y j ＝28。
（2分） &计算结果见表3：根据表2计算得：48221266118922222222=+++==++=∑∑ j i y x （2分）6154.1843233323257)13(3431414257464169281323222222=-⨯⎭⎬⎫⎩⎨⎧--=∴=++++==++=++===∑∑∑∑θ j i j i y X y x则7778.048283)328266)(13(3)()[1(2222≈-⨯--=---=∑∑∑∑jj i i y y k kx x k k Q （2分） 取显著性水平ａ＝，查卡方分布表得卡方临界值C ＝，由于Q<C ，故无法拒绝零假设，可以认为三个候选人在村民眼中没有区别。
（2分）第八章P170-1712.下面是某车间生产的一批轴的实际直径（单位：mm ）：；能否表明该尺寸服从均值为10，标准差为的正态分布(分别用K-S 拟合检验和卡方拟合检验)。
当n=10，a=时查表得K-S 拟合检验的临界值为。