典型习题解析
欧姆定律知识练习题及详细解析

欧姆定律知识练习题及详细解析【典型例题】类型一、探究电流与电压、电阻的关系1.某小组在探究电流与电压关系时,得到的实验数据如下表:R=10Ω电压U/V 2 4 6电流I/A 0.2 0.4 0.6(1) 分析数据发现:在______时,______跟______成______(填“正”或“反”)比。
(2)在坐标纸上画出U-I关系图。
(3) 在本实验中,滑动变阻器的作用除了保护电路外,主要是__________________。
【思路点拨】本题是物理课上常用的控制变量法,注意不变量,也就是在一定的前提下,还要注意电压和电流的因果关系,所以在表达时需注意。
【答案】(1)电阻一定;导体中的电流;导体两端的电压;正;(2) 如图所示;(3)改变定值电阻两端的电压【解析】(1)注意:在回答结论时一定要说上前提条件即电阻不变。
由表格可知电流改变的倍数与电压改变的倍数相等,即正比例关系。
在结论中一定要说电流与电压成正比,而不能说反。
这是因为有电压才有电流,电压是因,电流是果,因此结论一定要说电阻一定时,电流和电压成正比。
(2)做图时,在坐标上描出对应的点连线即可以。
因为电压若为0,电流也为0,所以该图象过原点。
【总结升华】本题的主要意图是考查描点作图法、分析实验结论的能力以及滑动变阻器在电路中的作用.举一反三:【变式】(2014•大港区二模)某同学在探究“电阻上的电流跟两端电压的关系”时,利用如图所示电路,在a、b两点间分别接入定值电阻R1、R2,R1>R2,通过调节滑动变阻器测得了多组数据,并根据数据绘制了两个电阻的U-I 关系图象,图中能正确反映两个电阻大小关系的是()【答案】B2. 小明同学,探究保持电压不变时,电流跟电阻的关系,得到的数据如下表。
电阻 5 6 1120 3(1)分析表中的数据,可以得出的结论【答案】(1)电压一定时,通过导体的电流与导体的电阻成反比(2)调节R′的阻值,保持电阻R两端电压不变【解析】(1)从表中的数据知在电压不变时,电阻增大到原来的几倍,电流就减小到原来的几分之一。
化学平衡典型习题和答案解析

化学平衡1.某温度下,在固定容积的密闭容器中,可逆反应A(g)+3B(g)→2C(g)达到平衡,测得平衡时A、B、C物质的量之比为n(A):n(B):n(C)=1:1:2,若保持温度不变,以1:1:2的物质的量之比再充入A、B和C,下列判断中正确的是()A.平衡不移动 B.平衡向逆反应方向移动C.新平衡时各物质的浓度都比原平衡时增大 D.C的质量分数减小2. 在一固定容积的密闭容器中充入2molA和1molB发生反应2A(g)+B(g) xC(g),达到平衡后 C体积分数为w% 若维持容器体积和温度不变按0.6mol A 0.3molB 1.4mol C为起始物质,达到平衡后 C体积分数仍为W% 则X的值为() A 1 B 2 C 3 D 43.对于密闭容器中的反应:N2(g) +3H2(g) 2NH3(g)△H<0,673K、30MPa下n(NH3)和n(H2)随时间变化的关系如下图所示。
下列叙述不正确的是A.点a的正反应速率比点b的大B.点c处的正反应速率比逆反应的大C.点d(t1时刻) 和点e(t2时刻) 处n(N2)一样多D.其他条件不变,773K下反应至t1时刻,n(H2)比上图中d点的值小4. 在4L密闭容器中充入6mol A气体和5mol B气体,在一定条件下发生反应:3A(g)+B(g)2C(g)+xD(g),10min达到化学平衡,生成了2mol C,经测定D的平均反应速率为0.05mol•L-1•min-1.下列判断正确的是()A.平衡时A的浓度为1.50mol•L- 1 B.x=1C.达到平衡时,在相同温度下容器内混合气体的压强是反应前的0.8倍 D.B的转化率为20%5. 体积相同的甲.乙两个容器中,分别都充有等物质的量的SO2和O2,在相同温度下发生反应:2SO2+O2⇌2SO3,并达到平衡.在这过程中,甲容器保持体积不变,乙容器保持压强不变,若甲容器中SO2的转化率为p%,则乙容器中SO2的转化率()A.等于p% B.大于p% C.小于p% D.无法6. 在相同温度下,有相同体积的甲、乙两容器,甲容器中充入1g N2和1g H2,乙容器中充入2g N2和2g H2。
值域的求法典型习题及解析

值域的求法习题一.解答题(共10小题)1.已知函数的定义域为集合A,函数的值域为集合B,求A∩B和(C R A)∩(C R B).2.已知函数f(x)=x2﹣bx+3,且f(0)=f(4).(1)求函数y=f(x)的零点,写出满足条件f(x)<0的x的集合;(2)求函数y=f(x)在区间(0,3]上的值域.3.求函数的值域:.4.求下列函数的值域:(1)y=3x2﹣x+2;(2);(3);(4);(5)(6);5.求下列函数的值域(1);(2);(3)x∈[0,3]且x≠1;(4).6.求函数的值域:y=|x﹣1|+|x+4|.7.求下列函数的值域.(1)y=﹣x2+x+2;(2)y=3﹣2x,x∈[﹣2,9];(3)y=x2﹣2x﹣3,x∈(﹣1,2];(4)y=.8.已知函数f(x)=22x+2x+1+3,求f(x)的值域.9.已知f(x)的值域为,求y=的值域.10.设的值域为[﹣1,4],求a、b的值.参考答案与试题解析一.解答题(共10小题)1.已知函数的定义域为集合A,函数的值域为集合B,求A∩B和(C R A)∩(C R B).可求可求2.已知函数f(x)=x2﹣bx+3,且f(0)=f(4).(1)求函数y=f(x)的零点,写出满足条件f(x)<0的x的集合;(2)求函数y=f(x)在区间(0,3]上的值域.x==23.求函数的值域:.得:34.求下列函数的值域:(1)y=3x 2﹣x+2;(2);(3);(4);(5)(6) ﹣+y=的范围,可得==3+,再利用反比例函数求解.t==+)≥,∴,y=y=y===3+,∵≠3+≠的值域为t=型值域,或+b+sin)+∈[,]+﹣,sin)∈,]得:5.求下列函数的值域(1);(2);(3)x∈[0,3]且x≠1;(4).2+t=y=的值域.=1+=5++5,=sin=sin)﹣,]﹣﹣,])∈,的值域为﹣y==2+,则其函数图象如下的值域为(﹣∝,﹣﹣+2||≥y=的值域为56.求函数的值域:y=|x﹣1|+|x+4|.1|+|x+4|=7.求下列函数的值域.(1)y=﹣x2+x+2;(2)y=3﹣2x,x∈[﹣2,9];(3)y=x2﹣2x﹣3,x∈(﹣1,2];(4)y=.,当x=时,7y=; 8.已知函数f (x )=22x +2x+1+3,求f (x )的值域.9.已知f (x )的值域为,求y=的值域.≤,﹣≤≤≤≤,]10.设的值域为[﹣1,4],求a 、b 的值.∈,4。
值域的求法典型习题及解析

值域的求法习题一.解答题(共10小题)1.已知函数的定义域为集合A,函数的值域为集合B,求A∩B和(C R A)∩(C R B).2.已知函数f(x)=x2﹣bx+3,且f(0)=f(4).(1)求函数y=f(x)的零点,写出满足条件f(x)<0的x的集合;(2)求函数y=f(x)在区间(0,3]上的值域.3.求函数的值域:.4.求下列函数的值域:(1)y=3x2﹣x+2;(2);(3);(4);(5)(6);5.求下列函数的值域(1);(2);(3)x∈[0,3]且x≠1;(4).6.求函数的值域:y=|x﹣1|+|x+4|.7.求下列函数的值域.(1)y=﹣x2+x+2;(2)y=3﹣2x,x∈[﹣2,9];(3)y=x2﹣2x﹣3,x∈(﹣1,2];(4)y=.8.已知函数f(x)=22x+2x+1+3,求f(x)的值域.9.已知f(x)的值域为,求y=的值域.10.设的值域为[﹣1,4],求a、b的值.参考答案与试题解析一.解答题(共10小题)1.已知函数的定义域为集合A,函数的值域为集合B,求A∩B和(C R A)∩(C R B).考点:函数的值域;交、并、补集的混合运算;函数的定义域及其求法。
1457182专题:计算题。
分析:由可求A,由可求B可求解答:解:由题意可得∴A=[2,+∞),∵∴B=(1,+∞),C R A=(﹣∞,2),C R B=(﹣∞,1]﹣﹣﹣(4分)∴A∩B=[2,+∞)∴(C R A)∩(C R B)=(﹣∞,1]﹣﹣﹣﹣﹣(6分)点评:本题主要考查了函数的定义域及指数函数的值域的求解,集合的交集、补集的基本运算,属于基础试题2.已知函数f(x)=x2﹣bx+3,且f(0)=f(4).(1)求函数y=f(x)的零点,写出满足条件f(x)<0的x的集合;(2)求函数y=f(x)在区间(0,3]上的值域.考点:函数的值域;二次函数的性质;一元二次不等式的解法。
1457182专题:计算题。
材料力学典型例题与详解(经典题目)
所以石柱体积为
V3
=
G ρ
=
[σ ]A(l) − ρ
F
= 1×106 Pa ×1.45 m 2 −1000 ×103 N = 18 m3 25 ×103 N/m3
三种情况下所需石料的体积比值为 24∶19.7∶18,或 1.33∶1.09∶1。 讨论:计算结果表明,采用等强度石柱时最节省材料,这是因为这种设计使得各截面的正应 力均达到许用应力,使材料得到充分利用。 3 滑轮结构如图,AB 杆为钢材,截面为圆形,直径 d = 20 mm ,许用应力 [σ ] = 160 MPa ,BC 杆为木材,截面为方形,边长 a = 60 mm ,许用应力 [σ c ] = 12 MPa 。试计算此结构的许用载
= 1.14 m 2
A
2=
F+ρ [σ ] −
A1 l1 ρ l2
=
1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m 1×106 N/m 2 − 25×103 N/m3 × 5 m
= 1.31 m 2
A
3=
F
+ ρA1l1 + ρA2l2 [σ ] − ρ l3
= 1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m + 25×103 N/m3 ×1.31 m 2 × 5 m = 1.49m 2 1×106 N/m 2 − 25 ×103 N/m3 × 5 m
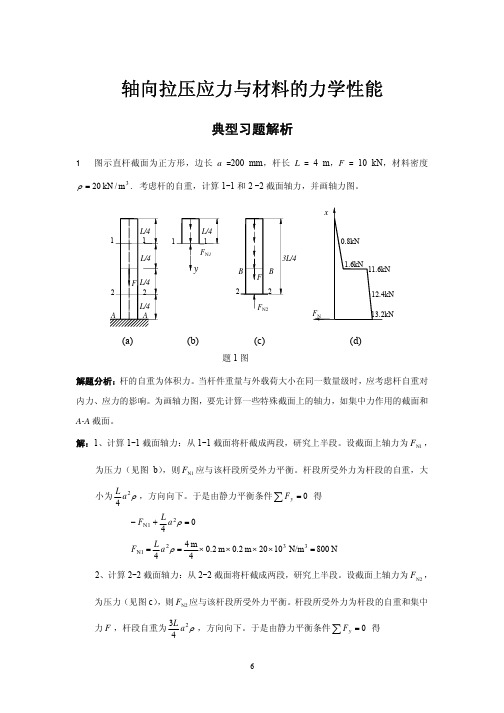
解:1、计算 1-1 截面轴力:从 1-1 截面将杆截成两段,研究上半段。设截面上轴力为 FN1 ,
为压力(见图 b),则 FN1 应与该杆段所受外力平衡。杆段所受外力为杆段的自重,大
(完整版)溶液配制与稀释典型习题+详解

(完整版)溶液配制与稀释典型习题+详解溶液配制练习一、固—水例1:配制50 g质量分数为5%的氯化钠钠溶液,需要氯化钠多少克?水多少亳升?解析:这是溶液配制最基本、最典型的类型。
可由公式:溶质质量=溶液质量×溶质质量分数;溶剂质量=溶液质量—溶质质量和体积=质量/密度直接计算。
氯化钠质量=50 g×5%=2.5 g 水的质量=50 g—2.5 g =47.5 g水的体积=47.5 g/1 g/ ml=47.5 ml例2:配制500 ml质量分数为10%的氢氧化钠溶液(密度为1.1 g/cm3)需要氢氧化钠和水的质量各多少?解析:此题涉及溶液密度,要注意转化成质量来计算。
溶液中只有质量有加和关系,体积不能直接进行和差计算。
氢氧化钠溶质质=500 ml1.1 g/cm310%=55 g水的质量=500 ml1.1 g/cm3-55 g=495 g(不要计算成500—55=445)二、液—水例3:用25%的氯化钠溶液和水配制30kg10%的食盐溶液。
需要25%的氯化钠溶液和水各多少kg?解析:紧紧抓住配制前后的等量关系是关键。
可以利用配制前后溶质、溶剂的相对应相等来列方程解决。
设需要25%的氯化钠溶液和水质量为x和y25%x=30k g10%,解得x=12k g;Y=30k g—12k g=18k g例4:某工厂化验室配制5000 g20%的盐酸,需要38%的盐酸(密度为1.19 g/cm3)和水各多少毫升?解析:可以直接利用质量列方程计算。
设需要30%的盐酸体积为x,水的体积为y,5000 g×20%=x×1。
19 g/cm338% 解得x=2212 mlY=5000 g—2212 ml×1.19 g/cm338% =2453 ml三、液—液例5:要配制20%的食盐溶液100 g,需要10%和50%的食盐溶液各多少亳升?解析:此题可根据溶液配制前后的溶质、溶剂、溶液相等来列出议程组解决。
三视图习题加解析

三视图典型例题加解析一、选择题1如图,在下列四个几何体中,其三视图(正视图、侧视图、俯视图)中有且仅有两个相同的是( )A .②③④B .①②③C .①③④D .①②④解析:①的三个视图都是边长为1的正方形;②的俯视图是圆,正视图、侧视图都是边长为1的正方形;③的俯视图是一个圆及其圆心,正视图、侧视图是相同的等腰三角形;④的俯视图是边长为1的正方形,正视图、侧视图是相同的矩形.A2、平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为( )A.6π B .43π C .46πD .63π解析:利用截面圆的性质先求得球的半径长. 如图,设截面圆的圆心为O ′,M 为截面圆上任一点, 则OO ′=2,O ′M =1,∴OM =(2)2+1=3,即球的半径为3, ∴V =43π(3)3=43π.3.若一个几何体的三视图如图所示,则此几何体的体积为( )A.112 B .5 C.92D .4解析:三视图还原为实物图,利用六棱柱体积公式求解.由三视图可知,此几何体为直六棱柱,且底面的面积为4,高为1,则体积V =Sh =4.D4.一个几何体的三视图如图所示,则这个几何体的表面积为( )A .6+ 5B .6+2 5C .8+ 5D .8+2 5解析:由三视图知,该几何体是一个底面为直角三角形的直棱柱,其表面积等于2×(12×1×2)+(2×12+22+1×2+2×2)=8+25,选D.5.如图,正方体ABCD -A ′B ′C ′D ′的棱长为4,动点E 、F 在棱AB 上,且EF =2,动点Q 在棱D ′C ′上,则三棱锥A ′EFQ 的体积( )A .与点E 、F 位置有关B .与点Q 位置有关C .与点E 、F 、Q 位置都有关D .与点E 、F 、Q 位置均无关,是定值解析:因为V A ′-EFQ =V Q -A ′EF =13×(12×2×4)×4=163,故三棱锥A ′-EFQ 的体积与点E 、F 、Q 的位置均无关,是定值.6.一个几何体的三视图如图所示,则该几何体的表面积为________.解析:将三视图还原为直观图后求解.根据三视图可知几何体是一个长方体挖去一个圆柱,所以S =2×(4+3+12)+2π-2π=38.7.某商店门口标识墩的直观图以及正视图和俯视图如图所示,墩的上半部分是正四棱锥P -EFGH ,下半部分是长方体ABCD -EFGH .(1)请画出该标识墩的侧视图; (2)求该标识墩的体积.解析:(1)由于墩的上半部分是正四棱锥P -EFGH ,下半部分是长方形ABCD -EFGH ,故其侧视图与正视图全等.该标识墩的侧视图如图所示.(2)由三视图易得,长方体与正四棱锥的底面均是边长为40 cm 的正方形,长方体的高为20 cm ,正四棱锥的高为60 cm.故该标识墩的体积V =V P -EFGH +V ABCD -EFGH =13×40×40×60+40×40×20=64 000(cm 3).8.已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.(1)若M 为CB 的中点,证明:MA ∥平面CNB 1; (2)求这个几何体的体积.解析:(1)证明:取CB 1的中点P ,连接MP ,NP .因为M 为CB 的中点,所以MP ∥BB 1,且MP =12BB 1.由三视图可知,四边形ABB 1N 为直角梯形,AN ∥BB 1且AN =12BB 1,则MP ∥AN 且MP =AN ,所以四边形ANPM 为平行四边形,所以AM ∥NP .又因为AM ⊄平面 CNB 1,NP ⊂平面CNB 1,所以AM ∥平面CNB 1. (2)因为该几何体的正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,所以BC ⊥BA ,BC ⊥B 1B .又BB 1与BA 相交于点B ,连接BN ,所以BC ⊥平面ABB 1N ,所以BC 为三棱锥C -ABN 的高.取BB 1的中点Q ,连接QN ,因为四边形ABB 1N 是直角梯形且AN =12BB 1=4,所以四边形ABQN 为正方形,所以NQ ⊥BB 1,又BC ⊥平面ABB 1N ,NQ ⊂平面ABB 1N ,所以BC ⊥NQ ,又BC 与BB 1相交于点B ,所以NQ ⊥平面C 1B 1BC ,所以NQ 为四棱锥N -CBB 1C 1的高.所以该几何体的体积V =V C -ABN +VN -CBB 1C 1 =13CB ·S △ABN +13NQ ·S 四边形BCC 1B 1 =13×4×12×4×4+13×4×4×8=1603.9.给出如下四个命题:①棱柱的侧面都是平行四边形;②棱锥的侧面为三角形,且所有侧面都有一个共同的公共点;③多面体至少有四个面;④棱台的侧棱所在直线均相交于同一点.其中正确的命题个数有( ) A .1个 B .2个 C .3个 D .4个【解】D .10.圆锥底面半径为1cm,其中有一个内接正方体,求这个内接正方体的棱长.【解】分析:画出轴截面图,设正方体的棱长为x ,利用相似列关系求解. 过圆锥的顶点S 和正方体底面的一条对角线CD 作圆锥的截面,得圆锥的轴截面SEF ,正方体对角面CDD 1C 1,如图所示. 设正方体棱长为x ,则CC 1=x ,C 1D1=. 作SO ⊥EF 于O ,则SO =OE =1,1~ECC EOS ∆∆, ∴11CC EC SO EO ==.11∴ x =, cm 11.如图,正四棱锥P ABCD -底面的四个顶点,,,A B C D 在球O 的同一个大圆上,点P 在球面上,如果163P ABCD V -=,则球O 的表面积是A. 4πB. 8πC. 12π D. 16π【解】如图,正四棱锥P ABCD -底面的四个顶点,,,A B C D在球O 的同一个大圆上,点P在球面上,PO 与平面ABCD 垂直,是棱锥的高,PO =R ,22ABCD S R =,163P ABCD V -=,所以2116233R R ⋅⋅=,解得R =2,则球O 的表面积是16π,选D. 12求球的表面积和体积.【解】分析:作出轴截面,利用勾股定理求解.作轴截面如图所示,CC '=AC == 设球半径为R ,则222R OC CC '=+229=+= ∴3R =,∴2436S R ππ==球,34363V R ππ==球.。
[全]管道工程--典型习题+解析[全考点]
![[全]管道工程--典型习题+解析[全考点]](https://img.taocdn.com/s3/m/84f777853c1ec5da51e270d5.png)
管道工程典型习题+解析一、单项选择题1、下列管道开槽的施工要求错误的是()。
A、在沟槽边坡稳固后设置供施工人员上下沟槽的安全梯B、采用机械挖槽时,沟槽分层的深度应按机械性能确定C、人工开挖沟槽的槽深超过2m时应分层开挖,每层的深度不超过2mD、槽底原状地基不得扰动,机械开挖时槽底预留200~300mm土层,由人工开挖、整平【本题1 分,建议1 分钟内完成本题】【正确答案】C【答案解析】本题考查的是开槽管道的地基处理与安管。
人工开挖沟槽的槽深超过3m时应分层开挖,每层的深度不超过2m。
2、下面关于顶管工作井设备施工安全表述错误的是()。
A、施工供电应设置双路电源,自动切换B、动力、照明应分路供电,作业面移动照明应采用低压供电C、起重作业前应试吊,吊离地面100mm左右时,检查重物捆扎情况和制动性能D、起吊时工作井内可以站人,但必须采取防护罩等保护措施【本题1 分,建议1 分钟内完成本题】【正确答案】D【答案解析】本题考查的是不开槽管道施工方法与设备施工安全的有关规定。
起吊时工作井内严禁站人,当吊运重物下井距作业面底部小于500mm时,操作人员方可近前工作。
3、给水管道水压试验中,管道内注水与浸泡的做法错误的是()。
A、应从上游缓慢注入B、球墨铸铁管、钢管、化学建材管不少于24hC、内径小于1000mm的现浇钢筋混凝土管渠不少于48hD、内径大于1000mm的预应力钢筒混凝土管不少于72h【本题1 分,建议1 分钟内完成本题】【正确答案】A【答案解析】本题考查的是压力管道的水压试验。
管道内注水应从下游缓慢注入,注入时在试验管段上游的管顶及管段中的高点应设置排气阀,将管道内的气体排除。
4、下列属于管道的更新方法是()。
A、破管外挤B、内衬法C、缠绕法D、喷涂法【本题1 分,建议1 分钟内完成本题】【正确答案】A【答案解析】本题考查的是管道修复与更新。
常见的管道更新方法有破管外挤和破管顶进两种,其余三项为修复管道的方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第7章典型习题解析1.如图为镗刀在工件上镗孔的简化图保障镗孔精度,镗刀杆的弯曲变形不能过大 设径向切削力F=200N ,镗刀杆直径 d=10mm ,外伸长度为l=50mm 。
材料的 弹性模量为E=210Gpa 。
求镗刀头的截面 B 的转角和挠度 解:(1)列弯矩方程 M (x )=()()F l x F x l --=-(2)列挠曲线近似微分方程并积分:()()z EI v M x F x l ''==-积分得:22Z F EI X Flx c θ=-+ 2362Z F Flx EI v X Cx D =-++(3)确定积分常数固定端处的边界条件为:00x θ== 00x θ==00x θ==00x θ==得:C=0,D=0(4)确定转角方程和挠曲线方程将C=0,D=0带入式得梁的转角方程与挠曲线方程2()2Z F X lx EI θ=-32()62Z F X lx v EI =-(5)求B 截面的转角和挠度 以x=l 带入式得22B X LZ Fl EI θθ===-33B x lZFl f vEI ===-以上两式中令F=200N ,E=210Gpa ,l=50mm ,得出:0.0024B rad θ=- 0.0805B f mm =-2.图示等截面悬臂梁AB ,在自由端作用一集中力F ,梁的弯曲刚度为EI ,试求梁的挠曲线方程和转角方程,并确定其最大挠度y max 和最大转角θmax 。
解:(1)列出梁的弯矩方程建立坐标系如图a 所示,取x 处横截面右边一段梁作为脱离体(图b ),弯矩方程为:)()(x l F x M --= (a )(2)建立梁的挠曲线近似微分方程 由式(7−4)得:EI x l F EI x M xy )()(d d 22-=-= (b ) (3)对微分方程二次积分积分一次,得:⎪⎭⎫ ⎝⎛+-==C Fx Flx EI x y 2211d d θ (c )再积分一次,得:⎪⎭⎫ ⎝⎛++-=D Cx Fx Flx EI y 3261211 (d ) (4)利用梁的边界条件确定积分常数在梁的固定端,横截面的转角和挠度都等于零,即:0=x 时,0=y ,0=θ代入式(c )、(d ),求得C =0,D =0。
(5)给出转角方程和挠曲线方程⎪⎭⎫ ⎝⎛-==2211d d Fx Flx EI x y θ (e ) ⎪⎭⎫ ⎝⎛-=3261211Fx Flx EI y (f )(6)求最大挠度和最大转角根据梁的受力情况和边界条件,可知此梁的最大挠度和最大转角都在自由端即x =l 处。
将x =l 代入(e )、(f )两式,则可求得最大转角及最大挠度分别为:EI Fl EI Fl EI Fl 22222max =-=θ EI Fl EI Fl EI Fl y 362333max =-=挠度为正,说明梁变形时B 点向下移动,转角为正,说明横截面B 沿顺时针方向转动3.图示简支梁AB ,受均布荷载和集中力偶作用,梁的弯曲刚度为EI ,试用叠加法求梁跨中点C 的挠度值和A 、B 截面的转角。
解:此梁上的荷载可以分为两项简单荷载,如图(b )、(c )所示。
均布荷载单独作用时,从表格11−1可以查得: EI ql y Cq38454=,EI ql θAq 243=,EI ql θBq243-=集中力偶单独作用时,从表格7−1可以查得:EI l M y CM162e =,EI l M AM 3e =θ,EI lM BM 6e-=θ将以上两个结果叠加,得:EI l M EI ql y y y CMCq C 1638452e 4+=+=EI l M EI ql A 324e3+=θ4.图示悬臂梁AB ,承受均布荷载q 的作用。
已知:l =3m ,q =3kN/m ,4001=⎥⎦⎤⎢⎣⎡l f ,梁采用20a 号工字钢,其弹性模量E =200GPa ,试校核梁的刚度。
解:查得工字钢的惯性矩为:44m 100.237-⨯=I梁的最大挠度为:m104.610237.010200831038349434max --⨯=⨯⨯⨯⨯⨯⨯==EI ql y(a ) (b )(c )400146813106.43max <≈⨯=-l y满足刚度要求5.如图(a )所示的外伸梁,在某外伸端受集中力F 作用,已知梁的抗弯刚度EI Z 为常数。
试求外伸端C 的挠度与转角解:欲求C 处的挠度与转角,可先分别求出这两段梁的变形在C 点引起的转角和挠度,然后将其叠加,求其代数和(1):先只考虑BC 段变形令AB 段不变,在这种情况下,由于挠曲线的光滑连接,B 截面即不允许产生挠度,也不允许出现转角。
于是,此时BC 段可视为悬臂梁,如图(b )所示。
在集中力F 的作用下,C 点的挠度与转角可查得:212c Z Fa EI θ=-313c ZFa f EI =-(2)再只考虑bc 段变形,由于C 点的集中力F 作用,使AB 段引起变形,与将F 向B 点简化为一个集中力F 和一个集中力偶Fa ,使AB 段引起的变形使完全相同的。
这样只需讨论集中力偶Fa 对AB 梁的作用3B ZFalEI θ=-该转角在C 点引起的转角和挠度,其值分别为C23C B ZFalEI θθ==-22tan 3c B B ZFa lf a a EI θθ=≈=-(3)梁在C 点处的挠度和转角 由叠加法得22122(1)2323C C C Z Z Z Fa Fal Fa l EI EI EI aθθθ=+=--=-+32212()333c c c Z Z ZFa Fa l Fa f f f a l EI EI EI =+=--=-+6.使用积分法计算图所示梁的挠曲线方程,最大挠度和两端转角的表达式。
[解] 取坐标原点在固定端,梁的弯矩方程为()e M x M =-可得挠曲线近似微分方程为()e EI ''M x M ν=-=积分一次得转角方程为e 1EI 'M x C ν=+再积分一次得挠曲线方程为2e 121EI M x C x C 2ν=++ 在悬臂梁中,边界条件是固定端的挠度和转角都为零,即x 0,'0=ν= x 0,0=ν=由此边界条件即可确定两积分常数 1C 0= 2C 0= 显然最大转角和最大挠度都发生在x=L 处e maxM LEIθ=2e max M L 2EI ν=8.试用积分法求图所示梁的挠曲线方程及中间截面的挠度,EI 已知。
[解] 1、支座反力 0063,==A B q l q lR R 取坐标原点在A 端,弯矩方程为30011(0)66(x )=-≤≤M q lx q x x l l挠曲线方程 30011''(0)66=-+≤≤EI q lx q x x l lν积分得24'0011224=-++q lx q x EI C lυ35001236120=-+++q lx q x EI C x C lυ边界条件0,0,0==⎧⎨==⎩x x l υυ 解得 30173602C =0,C =q l所以 533000712036360=-+q x q l q l EI x x l υ 当2=l x 时, 44.8720=ql EIνl9.外伸梁承如图所示,试按叠加原理求D A B f f A ,及,θθ。
[解] 将结构分解如下A B 1(a)B 2l将(b )进一步分解如下l FM =利用附录查得各端的转角和挠度A θ为3B θ、1A θ和4B θ的叠加 EI ql A 483-=θB θ为3B θ和4B θ的叠加 EIql B 243-=θA f 为B A lf θ21+ EI ql f A 244=D f 为2D f 和3D f 的叠加 EIql f D 3844-=10.图所示的梁具有中间铰B 和C, EI 为已知, 按叠加原理求P 力作用处的挠度.[解] 将结构分解如下, 铰链处两段梁有互作用力,利用附录查得,各端的挠度()zz C EI FL EI L F f 63233== ()z z B EI FL EI L F f 2933233==()zz E EI FL EI L F f 6482331==AAC。
