二元一次方程组易错难题集
八年级数学专题 二元一次方程组重难点(参数问题、实际应用问题)(北师大版)
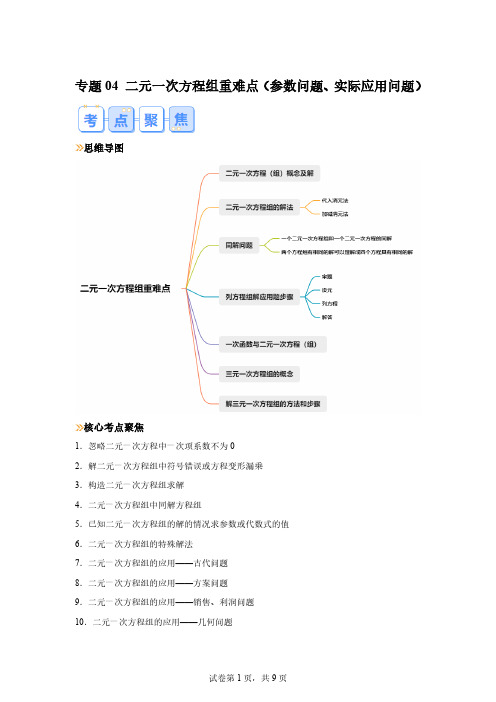
ì3x - 2 y = -1
ìx =1 ìm + 5 =1
ìm = -4
íî3x + 2 y = 7
,解得
í î
y
=
2
,即
íîn
+
3
=
2
,解得
íîn
=
-1
.
(1)学以致用,模仿乐乐同学的“整体换元”的方法,解方程组
ì ïï í ï ïî
x x
+ 3 + 3
y y
+ -
x x
5 5
y y
= =
4 .
-2
试卷第 2 页,共 9 页
义,否则,若把 y=ax+b 代入变形的原方程,必然得到一个恒等式; ③用代入法求出一个未知数的值后,再求另一个未知数时,一般代入变形后得到的方
程比较简单.
2.加减消元法
把方程组的两个方程(或先作适当变形)相加或相减,消去其中一个未知数,从而把
解二元一次方程组转化为解一元一次方程.这种解方程组的方法叫做加减消元法,简
联立成方程组,求出未知数的值,然后代入含有参数的方程即可求出参数的值.
四、列方程组解应用题步骤
1.列方程组解应用题是把“未知”转化为“已知”的重要方法,它的关键是把已知量和未 知量联系起来,找出题目中的相等关系.一般来说,有几个未知量就必须列出几个方
程,所列方程必须满足:
①方程两边表示的是同类量;②同类量的单位要统一;③方程两边的数值要相等.
y
=
与 41
íî2
x
+
3
y
=
-7
有相同的解,求
a,b
的值.
(易错题精选)初中数学方程与不等式之二元一次方程组难题汇编含答案

所以9-m<0
解得m>9
故选:A.
点睛:此题主要考查了非负数的应用,关键是根据平方数和绝对值的非负性构造二元一次方程组.
2.二元一次方程 的正整数解有()
A.1组B.2组C.3组D.4组
【答案】A
【解析】
【分析】
通过将方程变形,得到以 的代数式,利用倍数逻辑关系,枚举法可得.
【详解】
∵由 可得, , 是正整数.
16.小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把100个纸杯整齐叠放在一起时,它的高度约是( )
A.106cmB.110cmC.114cmD.116cm
【答案】A
【解析】
【分析】
通过观察图形,可知题中有两个等量关系:单独一个纸杯的高度加上3个纸杯叠放在一起高出单独一个纸杯的高度等于9,单独一个纸杯的高度加上8个纸杯叠放在一起高出单独一个纸杯的高度等于14.根据这两个等量关系,可列出方程组,再求解.
x-y=-1.
故选A.
【点睛】
本题考查了二元一次方程的解法,利用整体思想可以是本题解决过程变得简单.
12.《九章算术》是中国古代的数学专著,下面这道题是《九章算术》中第七章的一道题:“今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?”译文:“几个人一起去购买某物品,若每人出8钱,则多了3钱;若每人出7钱,则少了4钱.问有多少人,物品的价格是多少?”设有x人,物品价格为y钱,可列方程组为()
A. B. C. D.
【答案】A
【解析】
【分析】
设有x人,物品价值y钱,根据题意相等关系:①8×人数﹣3=物品价值,②7×人数+4=物品价值,可列方程组.
七年级数学试卷二元一次方程组易错压轴解答题精选及答案100

七年级数学试卷二元一次方程组易错压轴解答题精选及答案100一、二元一次方程组易错压轴解答题1.已知关于、的方程组(1)若是方程组的解时,求的值;(2)当时,若方程组的解满足为非正数,为负数,化简:.2.已知关于x,y的方程满足方程组.(1)若x﹣y=2,求m的值;(2)若x,y,m均为非负数,求m的取值范围,并化简式子|m﹣3|+|m﹣4|;(3)在(2)的条件下求s=2x﹣3y+m的最小值及最大值.3.某集团购买了150吨物资打算运往某地支援,现有甲、乙、丙三种车型供选择,每辆汽车的运载能力和运费如下表所示:(假设每辆车均满载)车型甲乙丙汽车运载量(吨/辆)5810汽车运费(元/辆)10001200150024000元,问分别需甲、乙两种车型各多少辆?(2)若该集团决定用甲、乙、丙三种汽车共18辆同时参与运送,请你写出可能的运送方案,并帮助该集团找出运费最省的方案(甲、乙、丙三种车辆均要参与运送).4.某学校准备购买若干台A型电脑和B型打印机.如果购买1台A型电脑,2台B型打印机,一共需要花费6200元;如果购买2台A型电脑,1台B型打印机,一共需要花费7900元。
(1)求每台A型电脑和每台B型打印机的价格分别是多少元?(2)如果学校购买A型电脑和B型打印机的预算费用不超过20000元,并且购买B型打印机的台数要比购买A型电脑的台数多1台,那么该学校至多能购买多少台B型打印机?5.在平面直角坐标系中,已知点A(a,0),B (b,0),a、b满足方程组,C 为y轴正半轴上一点,且 .(1)求A、B、C三点的坐标;(2)是否存在点D(t,-t)使?若存在,请求出D点坐标;若不存在,请说明理由.(3)已知E(-2,-4),若坐标轴上存在一点P,使,请求出P的坐标.6.学校组织植树活动,已知在甲处植树的有220人,在乙处植树的有96人.(1)若要使甲处植树的人数是乙处植树人数的3倍,应从乙处调多少人去甲处?(2)为了尽快完成植树任务,现调m人去两处支援,其中,若要使甲处植树的人数仍然是乙处植树人数的3倍,则应调往甲,乙两处各多少人?7.某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇,如表是近两周的销售情况:销售时段销售数量销售收入A种型号B种型号第一周3台4台1200元第二周5台6台1900元-进货成本)(1)求A、B两种型号的电风扇的销售单价;(2)若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?(3)在(2)的条件下,超市销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由。
二元一次方程组的解法易错点剖析

解二元一次方程组常见错解示例一、概念不清例1.下面不是二元一次方程组的是( ) .(A)1,2;xy=-⎧⎨=⎩(B) x+ 2y= 4y-3x= 8;(C)6,113;4x yx y+=⎧⎪⎨+=⎪⎩(D)3416,5633.x yx y+=⎧⎨-=⎩错解:选B .错解分析:错选B 原因是对二元一次方程组的概念理解不透彻. 事实上,二元一次方程组有两个特点:1.方程组中的每一个方程都是一次方程;2.方程组中含有两个且只含有两个未知数. C 中虽然含有两个未知数,但1134x y+=不是一次方程,所以C 就不是二元一次方程组. 要特别注意B这种形式的等式. 实际上它可以写成x + 2y = 8 和4y - 3x = 8 这两个方程,它们可以组成一个二元一次方程组. A、B、D都是二元一次方程组.正确答案:选 C.二、张冠李戴例2.若一个二元一次方程的一组解是1,2,xy=⎧⎨=⎩则这个方程可以是( 只要求写出一个) .错解:3, 3 1. x yx y+=⎧⎨-=⎩错解分析:题目要求写出一组解是12xy=⎧⎨=⎩的二元一次方程,而不是二元一次方程组,错误的原因是把二元一次方程的“冠”戴在了二元一次方程组的头上.正解:x+ y= 3(符合题意即可,答案不唯一) .三、循环代入 例3.解方程组398510-=⎧⎨-=⎩x y x y ①,②.错解:由①,得 y = 3x - 9 ③ 将③代入①,得3x - ( 3x - 9) = 9, 即9= 9.因此,原方程组的解是一切实数.错解分析:本题错在对代入法的主要步骤掌握不牢,理解不够深刻. 错解中出现了“9= 9”这个恒等式的原因是方程③是由方程①变形得到的,接着又代入方程①,犯下了循环代入的错误.正解:由①, 得 y = 3x - 9 ③ 将③代入②, 得8x - 5( 3x - 9) = 10. 解之,得x = 5.将x = 5 代入③,得y = 6. 所以原方程组的解是5,6.x y =⎧⎨=⎩四、换元后未还原 例4.解方程组3()4()1,1.26x y x y x y x y +--=⎧⎪+-⎨+=⎪⎩错解:设x + y = a ,x - y = b , 则原方程组可化为341,1.26a b a b -=⎧⎪⎨+=⎪⎩解之,得5,31.a b ⎧=⎪⎨⎪=⎩所以原方程组的解是5,31.x y ⎧=⎪⎨⎪=⎩错解分析:整体换元的解题策略是正确的,但没有把元换回来, 因而致错. 正解:设x+ y= a,x- y= b,则原方程组可化为341,1. 26a ba b-=⎧⎪⎨+=⎪⎩解之,得5,31. ab⎧=⎪⎨⎪=⎩所以5,31. x yx y⎧+=⎪⎨⎪-=⎩解之,得4,31.3 xy⎧=⎪⎪⎨⎪=⎪⎩这就是原方程组的解.二元一次方程(组)错解示例一、例1.有下列各式:①2x+y-1;②ab-2b=7;③x-5=6;④1x-2y =1;⑤x=y;⑥2x-3y=5-x;⑦2x2+2x-6=2x2-(x+y).其中是二元一次方程的有。
七年级数学试卷二元一次方程组易错压轴解答题训练经典题目(含答案)

七年级数学试卷二元一次方程组易错压轴解答题训练经典题目(含答案)一、二元一次方程组易错压轴解答题1.关于x,y的二元一次方程ax+by=c(a,b,c是常数),b=a+1,c=b+1.(1)当时,求c的值.(2)当a=时,求满足|x|<5,|y|<5的方程的整数解.(3)若a是正整数,求证:仅当a=1时,该方程有正整数解.2.某地新建了一个企业,每月将生产1 960 t污水,为保护环境,该企业计划购置污水处理器,并在如下两个型号中选择:污水处理器型号 A型 B型处理污水能力(t/月) 240 180B型污水处理器的总价为44万元,售出的1台A型、4台B型污水处理器的总价为42万元.(1)求每台A型、B型污水处理器的价格;(2)为确保将每月产生的污水全部处理完,该企业决定购买上述的污水处理器,那么至少要支付多少钱?3.第19届亚运会将于2022年在杭州举行,“丝绸细节”助力杭州打动世界.杭州丝绸公司为亚运会设计手工礼品,投入元钱,若以2条领带和1条丝巾为一份礼品,则刚好可制作600份礼品;若以1条领带和3条丝巾为一份礼品,则刚好可制作400份礼品.(1)若万元,求领带及丝巾的制作成本是多少?(2)若用元钱全部用于制作领带,总共可以制作几条?(3)若用元钱恰好能制作300份其他的礼品,可以选择条领带和条丝巾作为一份礼品(两种都要有),请求出所有可能的、的值.4.为了防治“新型冠状病毒”,我市某小区准备用5400元购买医用口罩和洗手液发放给本小区住户.若医用口罩买800个,洗手液买120瓶,则钱还缺200元;若医用口罩买1200个,洗手液买80瓶,则钱恰好用完.(1)求医用口罩和洗手液的单价;(2)由于实际需要,除购买医用口罩和洗手液外,还需增加购买单价为6元的N95口罩.若需购买医用口罩,N95口罩共1200个,其中N95口罩不超过200个,钱恰好全部用完,则有几种购买方案,请列方程计算.5.文雅书店出售A,B两种书籍,已知A书籍单售为每本50元,B书籍单售为每本30元,整套(A,B各一本)出售为每套70元。
七年级初一数学下学期第八章 二元一次方程组单元 易错题难题质量专项训练

20.某“欣欣”奶茶店开业大酬宾推出 四款饮料. 千克 饮料的原料是 千克苹果, 千克梨, 千克西瓜;1千克 饮料的原料是 千克苹果, 千克梨, 千克西瓜; 千克 饮料的原料是 千克苹果, 千克梨, 千克西瓜; 千克 饮料的原料是 千克苹果, 千克梨, 千克西瓜;如果每千克苹果的成本价为 元,每千克梨的成本价为 元,每千克西瓜的成本价为 元.开业当天全部售罄,销售后,共计苹果的总成本为 元,并且梨的总成本为 元,那么西瓜的总成本为_____元
22.阅读以下内容:
已知有理数m,n满足m+n=3,且 求k的值.
三位同学分别提出了以下三种不同的解题思路:
甲同学:先解关于m,n的方程组 ,再求k的值;
乙同学:将原方程组中的两个方程相加,再求k的值;
丙同学:先解方程组 ,再求k的值.
(1)试选择其中一名同学的思路,解答此题;
(2)在解关于x,y的方程组 时,可以用①×7﹣②×3消去未知数x,也可以用①×2+②×5消去未知数y.求a和b的值.
A. B. C. D.
3.若 ,则x+y的值是( )
A.﹣5B.5C.﹣4D.4
4.若方程6kx﹣2y=8有一组解 ,则k的值等于(( )
A. B. C. D.
5.小明、小颖、小亮玩飞镖游戏,他们每人投靶 次,中靶情况如图所示.规定投中同一圆环得分相同,若小明得分 分,小亮得分 分,则小颖得分为()
《二元一次方程组》-二元一次方程组易错题解析

选择题1、下列方程①3x+6=2x,②xy=3,③,④中,二元一次方程有几个()A、1个B、2个C、3个D、4个2、如果是方程2x+y=0的一个解(m≠0),那么()A、m≠0,n=0B、m,n异号C、m,n同号D、m,n可能同号,也可能异号3、二元一次方程x+3y=10的非负整数解共有()对.A、1B、2C、3D、44、方程(|x|+1)(|y|﹣3)=7的整数解有()A、3对B、4对C、5对D、6对5、(2007•枣庄)已知方程组:的解是:,则方程组:的解是()A 、B 、C 、D 、6、解方程组时,一学生把c 看错得,已知方程组的正确解是,则a,b,c的值是()A、a,b不能确定,c=﹣2B、a=4,b=5,c=﹣2C、a=4,b=7,c=﹣2D、a,b,c都不能确定7、若关于x、y 的方程组只有一个解,则a的值不等于()A 、B 、﹣C 、D 、﹣8、若方程组的解是,则方程组的解是()《二元一次方程组》二元一次方程组易错题解析A、B、C、D、9、若方程组的解是,则方程组的解是()A、B、C、D、10、若方程组有无穷多组解,(x,y为未知数),则()A、k≠2B、k=﹣2C、k<﹣2D、k>﹣2填空题11、若是方程2x+y=0的解,则6a+3b+2=_________.12、已知二元一次方程3x+y=0的一个解是,其中a≠0,那么9a+3b﹣2的值为_________.13、若是方程3x+y=1的一个解,则9a+3b+4=_________.14、若4x﹣3y=0且x≠0,则=_________.15、已知方程组的解适合x+y=2,则m的值为_________.16、当a=_________时,方程组无解.17、关于x、y的方程组的解x,y的和为12,则k的值为_________.答案与评分标准选择题1、下列方程①3x+6=2x,②xy=3,③,④中,二元一次方程有几个()A、1个B、2个C、3个D、4个考点:二元一次方程的定义。
二元一次方程组易错难题集

试题(一)1.把103.02.017.07.0=--x x 中的分母化为整数2.甲每秒跑7m,乙每秒跑6.5m,甲让乙先跑5m,设x秒后甲可追上乙,列方程是3.连续两次降价10%,降价后为a 元,则原价为4.试卷有25道题,做对一题得4分,做错(或不做)1题倒扣1分,某人共得70分,他做对道题。
5.一辆长4米,速度为110千米/时的轿车超一辆长12米,速度为100千米/时的卡车,则要花费的时间是6.甲单独做需x 天完成,乙单独做需y 天完成,两人合作需天7.当m =_____时,(m -3)x |m|-2+m -3=0是一元一次方程。
8.如果2、2、5和x 的平均数为5,而3、4、5、x 和y 的平均数也是5,那么x =_____,y =____.9.一船在相距80千米的码头间航行,顺水需4小时,逆水需5小时,则水流速度为10、若()()k x k m x m -=-有唯一解,则k ____m _____。
11、已知524x m mx x -=--的解在2与10之间(不包括2和10),则m 的取值为_____。
12、当m=时,()0332=-+--m xm m 是一元一次方程,方程的解是。
13、若012=--x bx 的解是非负数,则b 的取值范围是。
14.若x a x x 4)]3(2[3=--和185143=--+xa x 有相同的解,这个相同解是。
15.一个三位数满足:①三个数位上的数字和为20;②百位上的数字比十位上的数字大5;③个位上的数字是十位上的数字的3倍。
这个三位数是?16.将彩电按成本价提高50%,然后“大酬宾,八折优惠”,结果每台仍获利270元,每台彩电成本价是?17.一队学生去郊游,以每小时5千米的速度行进,经过一段时间后。
通讯员骑自行车从学校出发,以每小时14千米的速度按原路追上去,用去10分钟追上学生队伍,通讯员出发前,试题(二)1.若1312a x y -与23b a b x y -+-是同类项,那么a= 、b=2. 如果()43713x y kx k y +=⎧⎪⎨+-=⎪⎩的解x y 、的值相等,则k =3..如果21x y =⎧⎨=⎩是方程组75ax by bx cy +=⎧⎨+=⎩的解,则a c 与的关系是( )A.49a c +=B.29a c += C. 49a c -= D. 29a c -=4..方程组59x y kx y k+=⎧⎨-=⎩的解也是方程236x y +=的解,则k 的值是 . 5.方程组()1602111x y x y +-=⎧⎪⎨+-=⎪⎩的解是 .6. 已知231x y =-⎧⎨=⎩是方程组11ax by bx ay +=⎧⎨+=⎩的解,则()()a b a b +-= .7、用16元钱买面值为20分、60分、1元的三种邮票共18枚,每枚邮票至少买1枚,共有 种不同的买法. 8.方程72=+yx 写出正整数解9、求方程12511=+y x 的正整数解 .10、用正三角形和正六边形来进行镶嵌,则需________个正三角形和________个正六边形或________个正三角形和_________个正六边形.11. m 取整数值 时,方程组⎩⎨⎧=+=+1442y x my x 的解是整数12.方程组210320mx y x y +=⎧⎨-=⎩有整数解,则正整数m=______. 13.解方程组.⎩⎨⎧=+=+887.53.41127.43.5y x y x14、已知⎩⎨⎧=-+=--0720634z y x z y x ,求22222275632z y x z y x ++-+=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
试题(一)1.把103.02.017.07.0=--x x 中的分母化为整数2.甲每秒跑7m,乙每秒跑6.5m,甲让乙先跑5m,设x秒后甲可追上乙,列方程是3.连续两次降价10%,降价后为a 元,则原价为4.试卷有25道题,做对一题得4分,做错(或不做)1题倒扣1分,某人共得70分,他做对道题。
5.一辆长4米,速度为110千米/时的轿车超一辆长12米,速度为100千米/时的卡车,则要花费的时间是6.甲单独做需x 天完成,乙单独做需y 天完成,两人合作需天7.当m =_____时,(m -3)x |m|-2+m -3=0是一元一次方程。
8.如果2、2、5和x 的平均数为5,而3、4、5、x 和y 的平均数也是5,那么x =_____,y =____.9.一船在相距80千米的码头间航行,顺水需4小时,逆水需5小时,则水流速度为10、若()()k x k m x m -=-有唯一解,则k ____m _____。
11、已知524x m mx x -=--的解在2与10之间(不包括2和10),则m 的取值为_____。
12、当m=时,()0332=-+--m xm m 是一元一次方程,方程的解是。
13、若012=--x bx 的解是非负数,则b 的取值范围是。
14.若x a x x 4)]3(2[3=--和185143=--+xa x 有相同的解,这个相同解是。
15.一个三位数满足:①三个数位上的数字和为20;②百位上的数字比十位上的数字大5;③个位上的数字是十位上的数字的3倍。
这个三位数是?16.将彩电按成本价提高50%,然后“大酬宾,八折优惠”,结果每台仍获利270元,每台彩电成本价是?17.一队学生去郊游,以每小时5千米的速度行进,经过一段时间后。
通讯员骑自行车从学校出发,以每小时14千米的速度按原路追上去,用去10分钟追上学生队伍,通讯员出发前,试题(二)1.若1312a x y -与23b a b x y -+-是同类项,那么a= 、b=2. 如果()43713x y kx k y +=⎧⎪⎨+-=⎪⎩的解x y 、的值相等,则k =3..如果21x y =⎧⎨=⎩是方程组75ax by bx cy +=⎧⎨+=⎩的解,则a c 与的关系是( )A.49a c +=B.29a c += C. 49a c -= D. 29a c -=4..方程组59x y kx y k+=⎧⎨-=⎩的解也是方程236x y +=的解,则k 的值是 . 5.方程组()1602111x y x y +-=⎧⎪⎨+-=⎪⎩的解是 .6. 已知231x y =-⎧⎨=⎩是方程组11ax by bx ay +=⎧⎨+=⎩的解,则()()a b a b +-= .7、用16元钱买面值为20分、60分、1元的三种邮票共18枚,每枚邮票至少买1枚,共有 种不同的买法. 8.方程72=+yx 写出正整数解9、求方程12511=+y x 的正整数解 .10、用正三角形和正六边形来进行镶嵌,则需________个正三角形和________个正六边形或________个正三角形和_________个正六边形.11. m 取整数值 时,方程组⎩⎨⎧=+=+1442y x my x 的解是整数12.方程组210320mx y x y +=⎧⎨-=⎩有整数解,则正整数m=______. 13.解方程组.⎩⎨⎧=+=+887.53.41127.43.5y x y x14、已知⎩⎨⎧=-+=--0720634z y x z y x ,求22222275632z y x z y x ++-+=。
15、现有A 、B 、C 三种型号的产品出售,若售A3件,B7件,C1件,共得315元;若售A4件,B10件,C1件,共得42元。
问售出A 、B 、C 各一件共得多少元?16、解方程组()()5151422ax y x by +=⎧⎪⎨=-⎪⎩时,甲看错了方程()1解得21x y =⎧⎨=⎩,乙看错()2,解得54x y =⎧⎨=⎩,试求2002200610b a⎛⎫+- ⎪⎝⎭的值。
17、某中学一栋4层的教学大楼,每层楼有8间教室,共有4道门,其中两道正门大小相同,两道侧门大小也相同.安全检查中,对4道门进行了训练:当同时开启一道正门和两道侧门时,2分钟内可以通过560名学生;当同时开启一道正门和一道侧门时,4分钟可以通过800名学生. (1) 求平均每分钟一道正门和一道侧门各可以通过多少名学生?(2)紧急情况时因学生拥挤,出门的效率将降低20%.在紧急情况下全大楼的学生应在5分钟内通过这4道门安全撤离.假设这栋教学大楼每间教室最多有45名学生,问:建造的这4道门是否符合安全规定?请说明理由.试题(三)1.如果⎪⎩⎪⎨⎧=+=+=+468x z z y y x 的解使kx+2y-z 的值为10,那么k=2.方程:4x+3y=20的非负整数解为3.若623)1225(2=-++--y x y x ,则2x+4y=4、已知2647x ay x y -=⎧⎨+=⎩有整数解, 则正整数a= ,5.已知:6152423+-=+=+y x y x y x ,x= 、y= 。
6、若⎩⎨⎧=++=+k y x k y x 32253的解x 、y 的值的和为2,求x = 、y = 、k= 。
7.若方程组⎩⎨⎧-=+=-154by ax y x 与⎩⎨⎧=-=+184393by ax y x 有公共的解,a= 、b= 。
8.当k= 时,方程组⎪⎩⎪⎨⎧=+=-13621y x y kx 没有解;当k= 时,有唯一解。
9.如果⎩⎨⎧=+=-152163by x ay x 的解是⎩⎨⎧==17y x ,那么⎩⎨⎧=-++=--+15)()(216)()(3y x b y x y x a y x 的解是10.若甲、乙两组同时施工,8天可以完成,需付两组费用共3520元;若先请甲组单独做6天,再请乙组单独做12天可以完成,需付两组费用共3480元.若只选一个组单独完成,从节约开支角度考虑,这家商店应选择哪个组?11.师傅对徒弟说“我像你这样大时,你才4岁,当你像我这样大时,我已经52岁了”.问师傅与徒弟现在的年龄各是多少岁?12、甲、乙两列火车均长180米,如果相对行驶,从车头相遇到车尾相离共需12秒;如果同向行驶,那么从甲的车头遇到乙的车尾,直到甲的车尾超过乙的车头共需60秒,求甲、乙两列车的速度。
13、有62名工人,生产甲、乙两种零件,每人每天平均能生产甲零件12个或乙零件23个,应分配多少人生产甲零件,多少人生产乙零件,才能使每天生产的甲零件和乙零件刚好配套?(每3个甲零件和2个乙零件配成一套)14、一个三位数和一个两位数的差为225,在三位数的左边写这个两位数,得到一个五位数,在三位数的右边写上这个两位数,也得到一个五位数。
已知前面的五位数比后面的五位数大225,求这个三位数和两位数。
试题(四)1.已知(3x -2y+1)²与|4x -3y -3|互为相反数,则x=__________,y=__________。
2.已知y=kx+b,当x=1时,y=-1,当x=3时,y=-5,则k=__________,b=__________。
3.若方程组⎩⎨⎧=+=+54ay bx by ax 的解是⎩⎨⎧==12y x ,则a+b=__________。
4.已知⎩⎨⎧=-+=--082043z y x z y x 则zx yz xy z y x 2222++++的值是______。
5.已知关于x 、y 的方程组⎩⎨⎧=+=+.3,0ny x y mx ,解是⎩⎨⎧-==,21y x 则n m+2的值为 ______6.如果5x3m -2n -2yn -m+11=0是二元一次方程,则m= ______n=______7.已知3-x+2y=0,则3x-6y+9的值是______8.6年前,A 的年龄是B 的3倍,现在A 的年龄是B 的2倍,则A 现在的年龄为______9、解方程组⎪⎩⎪⎨⎧=-+=-+=-+635333z y x y x z x z y10、解关于x 、y的方程组⎩⎨⎧-=+=-1m my x m y mx11、甲、乙两人同时解方程组⎩⎨⎧=--=+)2(5)1(8ny mx ny mx 甲看错了方程⑴得42x y =⎧⎨=⎩,乙看错了方程中得25x y =⎧⎨=⎩,试求正确,m n 的值及方程组的解。
13、定义“*”:)1)(1(++++=*B A Y B A X B A ,已知321=*,432=*,求43*的值.14.某人买13个鸡蛋,5个鸭蛋、9个鹅蛋共用去了9.25元;买2个鸡蛋,4个鸭蛋、3个鹅蛋共用去了3.20元.试问只买鸡蛋、鸭蛋、鹅蛋各一个共需 元.15、西北某地区为改造沙漠,决定从2002年起进行“治沙种草”,把沙漠地变为草地,并出台了一项激励措施:在“治沙种草”的过程中,每一年新增草地面积达到10亩的农户,当年都可得到生活补贴费1500元,且每超出一亩,政府还给予每亩a 元的奖励.另外,经治沙种草后的土地从下一年起,平均每亩每年可有b 元的种草收入.下表是某农户在头两年通过“治沙种草”每年获得的总收入情况:年份新增草地的亩数年总收入2002年20亩2600元2003年26亩5060元(注:年总收入=生活补贴费+政府奖励费+种草收入)试根据以上提供的资料确定a、b的值;16、某校初一年级一班、二班共104人到博物馆参观,一班人数不足50人,二班人数超过50人,已知博物馆门票规定如下:1~50人购票,票价为每人13元;51~100人购票为每人11元,100人以上购票为每人9元(1)若分班购票,则共应付1240元,求两班各有多少名学生?(2)请您计算一下,若两班合起来购票,能节省多少元钱?(3)若两班人数均等,您认为是分班购票合算还是集体购票合算?17、一种绿色蔬菜,若直接销售,每吨利润为1000元;经粗加工后,每吨利润可达4500元;经精加工后,每吨利润7500元,一家公司收获这种蔬菜140吨,该公司加工能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,该公司必须在15天内将这批蔬菜全部销售或加工完毕,该公司研制了三种可行方案:方案一:将蔬菜全部进行粗加工;方案二:尽可能多地对蔬菜进行精加工,没有来得及加工的蔬菜,直接销售;方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好15天完成。
你认为哪种方案获利最多?为什么?。
