第三章立体的投影习题课
第3章 基本几何体的投影——答案
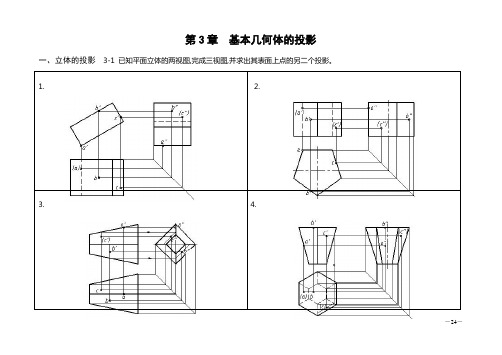
4.求作斜二测图
班级:姓名:学号:Fra bibliotek3-12作业截交线、相贯线作业
作业指导
一、目的
初步掌握切口平面体、回转体和相贯体的三视图画法。
二、内容和要求
1.根据3-13中的切口平面体、回转体和相贯体轴测图画三视图。
2.用A3图纸,比例自定,横放,按老师选定的题目作图。
三、作图步骤
1.形体分析:分析未切割前完整立体形状,截切平面位置,截交线与截断面的形状、空间位置、投影特点;参与相贯两形体的形状,相
1.
2.用近似画法求作相贯线的投影
3.用近似画法求作相贯线的投影
4.补画主视图
班级:姓名:学号:
3-8利用辅助平面法求相贯线的投影。
1.补画主、俯视图上的投影
2.补全俯视图上的投影
3.
班级:姓名:学号:
3-9求作特殊情况相贯线及综合相交立体的相贯线的投影。
1.
2.
3.补全主视图中的缺线
4.补全主、俯视图中的缺线
班级:姓名:学号:
四、轴测投影3-10求作平面体的正等测图。
1.已知柱体特征面的轴测投影与柱体厚度,完成柱体正等测图
(1)
(2)
(3)
2.用上图的方法,根据平面体的两面视图,画出其轴测图(尺寸数字按1∶1由图中量取)
(1)
(2)
(3)
班级:姓名:学号:
3-11求作回转体的正等测图及斜二测图。
1.
2.
对位置及相贯线形状、投影特点。
2.选择主视图的投影方向后,确定完整体的特征形方向和切口、切槽的特征方向,相贯体上相贯线哪个投影与圆柱面投影相重合,需要
求作的投影及求作的方法。
3.画完整体三视图(先画特征视图)。
9基本体的投影(习题10)

3.2 曲面立体的投影
1. 圆柱
1) 圆柱的投影
上下底圆的水平投影反 映实形,其正面和侧面 投影重影为一直线;而 圆柱面则用曲面投影的 转向轮廓线表示。
绘图步骤: (1) 先绘出圆柱的对称线、 回转轴线。 —细点划线 (2)绘出圆柱的顶面和底 面。—粗实线 (3)画出正面转向轮廓线和 侧面转向轮廓线。—粗实线
3)检查三视图确认无误。
(2)若已知三视图中的两幅图,补画第三幅图。 1)对照已知三视图中的两幅图,找全平面立体的交点并进行
编号。
2)根据投影规律,找出交点在第三幅图中的具体投影位置, 对相应点进行连线。 3)检查三视图确认无误。
3.1 平面立体的投影 1、棱柱
1)棱柱的投影
一个投影为多 边形,另外两个 投影轮廓线为矩 形。
回转体:母线绕轴旋转,形成回转面。 由回转面或回转面与平面所围成的立体 为回转体。
投影绘制的方法: (1)若已知轴测图,绘制三视图 1)找出曲面立体的特殊点。 2)根据投影规律绘制曲面立体特殊点的三面投影。 3)检查三视图确认无误。 (2)若已知三视图中的两幅图,补画第三幅图。 1)对照已知三视图中的两幅图,找全曲面立体的特殊点。 2)根据投影规律,绘制曲面立体特殊点的三面投影。 3)检查三视图确认无误。
以五棱柱的投影为例:
水平投影 正面投影 侧面投影
H
Y1
Y2
Y2 Y1 W
棱柱类立体的投影特征:
棱柱类立体的棱面在某一投影面上有积聚性。
2) 棱柱表面上的点
1’ 2’(6’) 3’(5’) 4’
(a)
7’
8’(12’) 6(12)
9’(11’) 5(11)
10’
4(10) 1(7)
第三章立体的投影4习题课

台湾 架设第一条电报线,成为中国自
出行 (1)新式交通促进了经济发展,改变了人们的通讯手段和 , 方式 转变了人们的思想观念。
(2)交通近代化使中国同世界的联系大大增强,使异地传输更为便 捷。 (3)促进了中国的经济与社会发展,也使人们的生活
多姿多彩 。
[合作探究· 提认知]
电视剧《闯关东》讲述了济南章丘朱家峪人朱开山一家, 从清末到九一八事变爆发闯关东的前尘往事。下图是朱开山 一家从山东辗转逃亡到东北途中可能用到的四种交通工具。
平行于轴线 θ = 0°
双曲线
平行于一条素线 过锥顶 θ =α 直线(三角形)
抛物线 直线
历史ⅱ岳麓版第13课交通与通讯 的变化资料
精品课件欢迎使用
[自读教材· 填要点] 一、铁路,更多的铁路 1.地位
铁路是
交通运输 建设的重点,便于国计民生,成为国民经济
发展的动脉。 2.出现 1881年,中国自建的第一条铁路——唐山 路建成通车。 1888年,宫廷专用铁路落成。 至胥各庄铁 开平
一、近代交通业发展的原因、特点及影响 1.原因 (1)先进的中国人为救国救民,积极兴办近代交通业,促
进中国社会发展。
(2)列强侵华的需要。为扩大在华利益,加强控制、镇压
中国人民的反抗,控制和操纵中国交通建设。
(3)工业革命的成果传入中国,为近代交通业的发展提供 了物质条件。
2.特点 (1)近代中国交通业逐渐开始近代化的进程,铁路、水运和
报先后发明。
(3)近代以来,交通、通讯工具的进步,推 动了经济与社会的发展。
关键词——交通和通讯不断进步、辛亥革命和国民大革命顺应 时 代潮流 图说历史 主旨句归纳 (1)1911年,革命党人发动武昌起义,辛亥
近年届九年级数学下册第三章3.1投影练习湘教版(2021年整理)

2019届九年级数学下册第三章3.1 投影练习(新版)湘教版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2019届九年级数学下册第三章3.1 投影练习(新版)湘教版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2019届九年级数学下册第三章3.1 投影练习(新版)湘教版的全部内容。
第3章投影与视图3.1 投影知识点1 平行投影1.平行投影中的光线是(A)A.平行的B.不平行的C.聚成一点的D.向四周发散的2.下列投影是平行投影的是(A)A.太阳光下窗户的影子B.台灯下书本的影子C.在手电筒照射下纸片的影子D.路灯下行人的影子3.下列图中是太阳光下形成的影子的是(A)4.一木杆按如图所示的方式直立在地面上,请在图中画出它在阳光下的影子.(用线段AB表示)解:如图.知识点2 中心投影5.下列哪种影子不是中心投影(D)A.皮影戏中的影子B.晚上在墙上的手影C.舞厅中霓虹灯形成的影子D.林荫道上的树影6.如图,晚上小亮在路灯下散步,他从A处向着路灯灯柱方向径直走到B处,这一过程中他在该路灯灯光下的影子(A)A.逐渐变短B.逐渐变长C.先变短后变长D.先变长后变短7.画出如图中各木杆在灯光下的影子.解:如图.线段AB,A′B′是两根木杆的影子.知识点3 正投影8.如图,按照箭头所指的投影方向,图中圆柱的正投影是(B)A.圆B.矩形C.梯形D.圆柱9.(教材P99习题T4变式)画出如图物体(正三棱柱)的正投影:(1)投影线由物体前方射到后方;(2)投影线由物体左方射到右方;(3)投影线由物体上方射到下方.解:中档题10.正方形的正投影不可能是(D)A.正方形B.长方形C.线段D.梯形11.下图表示一块三角尺在光线照射下形成的投影,其中(2)是平行投影;(1)是中心投影;(3)是正投影.(1)(2) (3)12.如图分别是两棵树及其影子的情形.图甲图乙(1)哪个图反映了阳光下的情形?哪个图反映了路灯下的情形?(2)请画出图中表示小丽影长的线段;(3)阳光下小丽影子长为1。
九年级数学下册习题课件-3.1 投影1-湘教版

然后他将速度提高到原来的 1.5 倍,再行走 2 s 到达点 H,此 时他(GH)在同一灯光下的影长为 BH.(点 C,E,G 在一条直 线上) (1)请在图中画出光源 O 点的位置,并画出小明位于点 F 时在这 个灯光下的影长 FM(不写画法);
解:如图所示.
(2)求小明原来的速度.
解:设小明原来的速度为 x m/s, 则 CE=2x m,AM=AF-MF=(4x-1.2)m,EG=3x m, ∴BM=AB-AM=(13.2-4x)m. ∵点 C,E,G 在一条直线上,CG∥AB, ∴△OCE∽△OAM,△OEG∽△OMB.
【点拨】∵立体图形是长方体, ∴底面 ABCD∥底面 EFGH,即 S1=S, ∵EM>EF,EH=EH, ∴S1<S2,∴S=S1<S2.
【答案】 S=S1<S2
13.如图,小强和小华同时站在路灯下,小强的身高 EF=1.8 m, 小华的身高 MN=1.5 m,他们的影子恰巧等于自己的身高, 即 BF=1.8 m,CN=1.5 m,且两人相距 4.7 m,则路灯 AD 的高度是________.
第3章 投影与视图
3.1 投 影
提示:点击 进入习题
答案显示
新知笔记 1 光线;像 2 平行 3 一点 4 垂直
1A 6B
2D 7D
3B
4 14
8 8 13 9 D
5 10 3 3
10
11 C 12 S=S1<S2 13 4 m 14 见习题 15 见习题
16 见习题 17 见习题
1.光线照射物体,会在平面上(如地面、墙壁)留下它的影子, 把 物体映成它的影子叫作投影. 照射的___光__线___叫投影线, 投 影所在的平面叫投影面. 物体在投影下的___像_____简称为物 体的投影.
完整版湘教版九年级下册数学第3章 投影与视图含答案

湘教版九年级下册数学第3章投影与视图含答案一、单选题(共15题,共计45分)1、如图所示的几何体的俯视图是()A. B. C. D.2、用6个完全相同的小正方体组合成如图所示的立体图形,它的左视图为()A. B. C. D.3、图①是由一个完全相同的小正方体组成的立体图形,将图①中的一个小正方体改变位置后如图②,则三视图发生改变的是()A.主视图,俯视较和左视图都改变B.左视图C.俯视图D.主视图4、如图,共有12个大不相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分.现从其余的小正方形中任取一个涂上阴影,则能构成这个正方体的表面展开图的概率是()A. B. C. D.5、如图是一无盖的正方体盒子,其展开图不能是()A. B. C. D.6、如图,墨水瓶的瓶盖和瓶身都是圆柱形,则它的俯视图是A. B. C. D.7、由大小相同的正方体木块堆成的几何体的三视图如右图所示,则该几何体中正方体木块的个数是( )A.6个B.5个C.4个D.3个8、如图所示的正方体展开后的平面图形是( )A. B. C. D.9、如图,一个放置在水平实验台上的锥形瓶,它的俯视图为()A. B. C. D.10、如图,这是由5个大小相同的小正方体摆成的立体图形,它的俯视图是()A. B. C. D.11、下列几何体的主视图是三角形的是()A. B. C. D.12、一个几何体由大小相同的小正方体搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在这个位置小正方体的个数.从左面看到的这个几何体的形状图的是()A. B. C. D.13、如图所示的几何体的左视图是()A. B. C. D.14、由5个完全相同的正方体组成的几何体的主视图是()A. B. C. D.15、下列几何体中,侧面展开图可能是正方形的是()A.正方体B.圆柱C.圆锥D.球体二、填空题(共10题,共计30分)16、在数学活动课上,老师带领数学小组测量大树的高度.如图,数学小组发现大树离教学楼有5m,高1.4m的竹竿在水平地面的影子长1m,此时大树的影子有一部分映在地面上,还有一部分映在教学楼的墙上,墙上的影子离为2m,那么这棵大树高________m.17、如图,长方形 ABCD 的长 AB=4,宽 BC=3,以 AB 所在的直线为轴,将长方形旋转一周后所得几何体的主视图的面积是________.18、如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在图的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,则小桥所在圆的半径为________ m19、一个几何体是由许多规格相同的小正方体堆积而成的,其主视图、左视图如图所示,要摆成这样的几何体,至少需用________个正方体,最多需用________个正方体;20、如图是一个几何体的三视图,根据图示的数据可计算出该几何体的表面积为________.21、如图,一个正方体,6个面上分别写着6个连续的整数,且每个相对面上的两个数之和相等,如图所示,你能看到的数为9、12、13,则六个整数之和为________.22、某数学兴趣小组利用太阳光测量一棵树的高度(如图),在同一时刻,测得树的影长为4.8米,小明的影长为1.2米,已知小明的身高为1.5米,则树高为________ 米.23、一张桌子摆放若干碟子,从三个方向上看,三种视图如图所示,则这张桌子上共有________个碟子.24、如图是由一些相同的小正方体构成的立体图形的三种视图,那么构成这个立体图形的小正方体有________ 个.25、某几何体的三视图如图所示,则组成该几何体的小正方体的个数是________三、解答题(共5题,共计25分)</span>26、由大小相同的5个小立方块搭成的几何体如图所示,请在方格中画出该几何体从上面和左面看到的形状图(用黑色笔将虚线画为实线).27、已知一个几何体的三视图和有关的尺寸如图所示,请写出该几何体的名称,并根据图中所给的数据求出它的表面积和体积.28、一个几何体的三视图如图所示,已知主视图、左视图和俯视图如图所示.(1)请说出这个几何体的名称;(2)根据图中给出的数据(单位:分米),求这个几何体的侧面积.29、小刚的桌上放着两个物品,它的三视图如图所示,你知道这两个物品是什么吗?30、如图所示的平面图形折叠成正方体后,相对面上的两个数之和为10,求的值.参考答案一、单选题(共15题,共计45分)1、D3、D4、D5、C6、A7、C8、D9、B10、A11、B12、B13、D14、A15、B二、填空题(共10题,共计30分)16、17、18、19、20、21、22、24、25、三、解答题(共5题,共计25分)26、27、28、29、30、。
第三章立体的投影习题8月
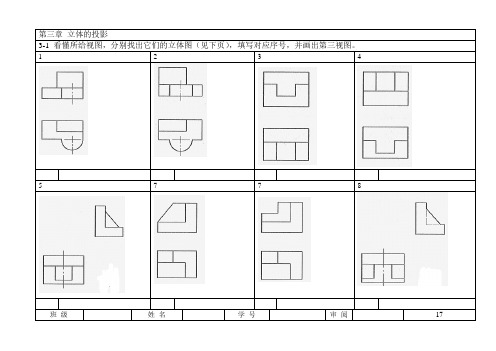
3-1 看懂所给视图,分别找出它们的立体图(见下页),填写对应序号,并画出第三视图。
1 2 3 45 7 7 8班级姓名学号审阅171 2 3 46 7 89 10 11 12 班级姓名学号审阅18第三章立体的投影3-2 求作体的第三视图,并补全立体表面上点的其余两投影。
1 2 34 5 6班级\ 姓名学号审阅193-3 求作第三视图1 2 34 5 6班级姓名学号审阅203-4 求作左视图,并用彩色笔勾画平面P的三面投影。
3-5 求作俯视图,并用彩色笔勾画出Q面的三面投影。
班级姓名学号审阅213-6 补全下列切割体的投影。
1 23 41 2班级姓名学号审阅223-7补全下各组视图中所缺的漏线或第三视图。
1 23 4班级姓名学号审阅233-8 已知主视图和俯视图,选择正确的左视图。
1 2 3 43-9 已知主视图和俯视图,选择正确的左视图。
1 2 3 4班级姓名学号审阅243-10 完成复合回转体截交线的三面投影。
1 2班级姓名学号审阅253-11 求出立体图表面的相贯线。
1 23 4班级姓名学号审阅263-12 求作主视图。
3-13 求作俯视图。
3-14 求作主视图。
3-15 求作俯视图。
班级姓名学号审阅273-16 求出立体表面的相贯线。
1 23 4班级姓名学号审阅283-17 已知主视图和俯视图,选择正确的左视图。
1 2 3 43-18 已知主视图和俯视图,选择正确的主视图。
1 2 3 4班级姓名学号审阅293-19 用辅助平面法补全主视图和俯视图上所缺的线。
班级姓名学号审阅303-20 根据已知图画正等轴测图。
3-21 根据已知视图画正等轴测图及斜二轴测图。
班级姓名学号审阅31。
第三章-立体的投影PPT课件

1″ 7″
9″
4(2)
6(8)
3(1) 5(7)
10(9)
可编辑课件PPT
35
可编辑课件PPT
36
可编辑课件PPT
37
可编辑课件PPT
38
3.3 曲面立体
曲面立体:所有表面都是由曲面或曲面和平面 所围成的立体称为曲面立体。它们通常被称为 回转体。
一动线绕一定线回转一周后形成的曲面称为回 转面。不动线称为回转轴,动线称为母线,母 线在回转面上的任意位置称为素线。
4(8) 3(7) 2(6)
1(5)
可编辑课件PPT
68
二、 平面与圆锥相交
1. 平面与圆锥相交所得截交线形状 2. 例题
可编辑课件PPT
69
1. 平面与圆锥相交所得截交线形状
圆
过锥顶的两直线
小小规定
可编辑课件PPT
5
一、 棱柱
1. 棱柱的组成
正面投影
由两个底面和几个侧 面组成。侧面与侧面 的交线叫侧棱,侧棱 相互平行。
2. 棱柱的投影
侧面投影
水平投影
可编辑课件PPT
在图示位置时,六棱 柱的两底面为水平面, 在水平投影中反映实 形。前后两侧面是正 平面,其余四个侧面 是铅垂面,它们的水 平投影都积聚成直线, 与六边形的边重合。
s
1
4 2 ●
●
●
解题步骤
1.空间分析:截平面与 四条侧棱均相交,因此 截交线是一个四边形。
3
● 3
2.投影分析:截平面为
正垂面,截交线的正面
投影已知,水平投影和
侧面投影未知;
4 ●
3
1
●
s●
2●
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2) k
(m) 1
1
例3 已知圆锥表面上点的投影1、2,求其它两面投影。
辅助素线法
如何在圆锥面上作直线?
过锥顶作一条素线。 s
● ●
s
辅助圆法
S
●
1
(2)
●
(2)
m
1
2 s
m
●
M
1
例4 求立体截切后的投影
6
6 5
3
(5 )
1 2
4(8) 3 (7)
2(6) 1(5)
求空心圆筒开槽的H、W面投影图
例 10求空心圆筒截切的H、W面投影图
求空心圆筒截切的H、W面投影图
例11:求圆锥被截切后的水平及侧面投影
1’(2’)
2’’
1’’
2
1
例11: 求圆锥被截切后的水平及侧面投影
例12:求圆锥被截切后的侧面投影
3' 2‘(4‘) 4" 5"
2(3)(6)(7) 1(8) 8
7
3 1 2
截交线的形状?
4
例 7: 求八棱柱被平面P截切后的水平投影。
例 8求截切实心圆柱后的侧面投影 1‘(2’)
2" 3‘(4’) 5‘(6‘)
6" 4"
1"
3" 5"
2,4
6
1,3
5
例 9求空心圆筒开槽的H、W面投影图
1‘(2‘)(3‘)(4‘) 4" 3" 2" 1" 8" 5‘(6‘)(7‘)(8‘) 7" 6"
⒉ 作图
当相贯线的投影为非圆曲线时,其作图步骤为: ⑴ 找点 ☆ 先找特殊点 特殊点包括:最上点、最下点、最左点、 最右点、最前点、最后点、 轮廓线上的点等。
☆ 补充若干中间点 ⑵连线 ⑶检查、加深 尤其注意检查回转体轮廓素线的投影。
三、平面体与圆柱体相贯
⒈ 相贯线的产生:
外表面与外表面相交, 外表面与内表面相交, 内表面与内表面相交。
圆柱与圆柱孔、圆柱孔与圆柱孔相贯形式
(a) 圆柱上穿孔
(b) 孔孔相贯
(c) 半圆柱孔上穿孔
圆柱与棱柱相贯
五、多体相贯
每个局部都是两体相贯,首先分析它是由 哪些基本体组成的,然后两两进行相贯线的 分析与作图。
例1 圆球表面上取点
例2
★辅助圆法
k
圆的半径?
1
1
(2)
m
(2 )
⒉ 求相贯线的方法: 求平面体的棱面与圆柱面的截交线,依次连接起 来。 ⒊ 相贯线的形状及投影: 相贯线为封闭的空间折线。相贯线在非积聚性投 影上总是向被穿的圆柱体里面弯折,而且在两体相 交区域内不应有圆柱体轮廓线的投影。
四、两圆柱体相贯 ⒈ 相贯线的产生:
外表面与外表面相交, 外表面与内表面相交, 内表面与内表面相交。 ⒉ 求相贯线的方法: 常用的方法是利用积聚性表面 取点,也可用辅助平面法。 ⒊ 相贯线的形状及投影: 相贯线为光滑封闭的空间曲线。当两圆柱正交,小 圆柱穿大圆柱时,相贯线在非积聚性投影上总是向大 圆柱里弯曲,当两圆柱直径相等时,相贯线在空间为 两个椭圆,其投影变为直线。
3" 2"
1‘(5‘)
5 4
1"
3
2 1
例13 求吊环的截交线 。
例14
两圆锥共锥顶相贯线 为相交两直线
4
4
1 2
(3 )
Ⅵ Ⅴ
3 5 1 2 4 6
Ⅳ Ⅲ Ⅰ Ⅱ
例5
求带缺口圆锥的水平投影和侧面投影。
1’ 2’(3’) 6’
1”
3”
4’(5’) 5” 6” 4”
2”
5
3
6 1 2 4
例6
求带凹槽半球的水平投影和侧面投影。
例 7: 求八棱柱被平面P截切后的水平投影。
P
4 ( 5 ) 7 5 6 3 4 2 1 Ⅷ Ⅰ 5 6 Ⅶ Ⅵ Ⅲ 8 Ⅱ Ⅴ Ⅳ
工程制图(B)
一、基本内容 ⒈ 立体表面相贯线的概念
相贯线的性质:表面性 共有性 封闭性
回 顾
⒉ 求相贯线的基本方法
面上找点பைடு நூலகம் 辅助平面法
二、解题过程 ⒈ 交线分析
⑴ 空间分析: 分析相交两立体的表面形状, 形体大小及相 对位置,预见交线的形状。 ⑵ 投影分析: 是否有积聚性投影?找出相贯线的已知投影, 预见未知投影,从而选择解题方法。
