函数的凹凸性与作图
合集下载
高数上凹向、拐点、作图

解
2 y 36 x 24 x 36 x x 3 2 2 0 3 得 x 0 , x 令y 0 1 2 · · 3 x 0时, y 0; 在区间(-∞,0]内曲线是凹的。 2 2 0 x 时, y 0 ; 在区间[0, ]上曲线是凸的。 3 3 2 x 时, y 0. 在区间[ 2 ,+∞)内曲线是凹的。 3 3 2 11 0 , 1、 , 是拐点. 3 27
x2 2
得到曲线上的两个点 (0 ,
1 2
)、( 1,
1
另外f 2
1 , 2 2 e
1
加辅助点 ( 2 ,
2e 1 ). 2 2 e
)
1
2
注:本例特点 (1)利用函数的奇偶性; (2)补充点(0 ,y ( 0 ) ),(2 ,y ( 2 ) ); (3)有水平渐近线。
f ' ( x1 ) f ' ( x2 ) f ' ( x3 ),
f x 递减
f x 0
f x 0
在有些教材中,凹的(曲线)又叫“上凹”,凸的又叫“下凹”。
连续曲线上,不同凹向曲线段的分界点,称为曲线的拐点。 注意:拐点是曲线上的点,应由两个坐标表示:( x0 , f ( x0 ) ). 前面讲过的极值点,是取得极值时自变量的值,记 为 x = xi。 两者不同。 2、曲线凹向的判定 P106定理3.8 函数y = f ( x ) 在闭区间 [ a , b ] 上连续,在开区间内二阶可导, 则当 仍可用“雨水法则” f ”( x ) > 0 时,曲线上凹(凹); 帮助记忆 f ”( x ) < 0 时,曲线下凹(凸)。
2 y 36 x 24 x 36 x x 3 2 2 0 3 得 x 0 , x 令y 0 1 2 · · 3 x 0时, y 0; 在区间(-∞,0]内曲线是凹的。 2 2 0 x 时, y 0 ; 在区间[0, ]上曲线是凸的。 3 3 2 x 时, y 0. 在区间[ 2 ,+∞)内曲线是凹的。 3 3 2 11 0 , 1、 , 是拐点. 3 27
x2 2
得到曲线上的两个点 (0 ,
1 2
)、( 1,
1
另外f 2
1 , 2 2 e
1
加辅助点 ( 2 ,
2e 1 ). 2 2 e
)
1
2
注:本例特点 (1)利用函数的奇偶性; (2)补充点(0 ,y ( 0 ) ),(2 ,y ( 2 ) ); (3)有水平渐近线。
f ' ( x1 ) f ' ( x2 ) f ' ( x3 ),
f x 递减
f x 0
f x 0
在有些教材中,凹的(曲线)又叫“上凹”,凸的又叫“下凹”。
连续曲线上,不同凹向曲线段的分界点,称为曲线的拐点。 注意:拐点是曲线上的点,应由两个坐标表示:( x0 , f ( x0 ) ). 前面讲过的极值点,是取得极值时自变量的值,记 为 x = xi。 两者不同。 2、曲线凹向的判定 P106定理3.8 函数y = f ( x ) 在闭区间 [ a , b ] 上连续,在开区间内二阶可导, 则当 仍可用“雨水法则” f ”( x ) > 0 时,曲线上凹(凹); 帮助记忆 f ”( x ) < 0 时,曲线下凹(凸)。
《函数曲线的凹凸性》课件

《函数曲线的凹凸性》 ppt课件
CONTENTS 目录
• 引言 • 函数曲线的凹凸性判定 • 函数曲线的凹凸性性质 • 函数曲线的凹凸性与导数的关系 • 函数曲线的凹凸性与几何意义 • 总结与展望
CHAPTER 01
引言
凹凸性的定义
凹函数
对于函数$f(x)$,如果在区间$I$上,对于任意$x_1 < x_2$,都有$f(frac{x_1+x_2}{2}) geq frac{f(x_1) + f(x_2)}{2}$,则称$f(x)$在区间$I$上是凹函数。
函数曲线的凹凸性可能会随着自变量x 的变化而发生变化。
凸函数曲线
表示函数图像呈上凸的几何形状,即 任意两点之间的连线位于曲线上方。
几何形状的凹凸性实例
下凹函数曲线
$f(x) = x^2$,$f(x) = sin x$
上凸函数曲线
$f(x) = log x$,$f(x) = e^x$
几何形状的凹凸性与生活中的应用
02
二次函数是典型的凹函数和凸函数,其图像为抛物 线。
03
指数函数和幂函数在其定义域内是凹函数,对数函 数在其定义域内是凸函数。
CHAPTER 04
函数曲线的凹凸性与导数的关系
导数与凹凸性的关系
01
导数大于0的区间内,函数曲线为 凹;
02
导数小于0的区间内,函数曲线为 凸。
导数在判断凹凸性中的应用
凸函数
对于函数$f(x)$,如果在区间$I$上,对于任意$x_1 < x_2$,都有$f(frac{x_1+x_2}{2}) leq frac{f(x_1) + f(x_2)}{2}$,则称$f(x)$在区间$I$上是凸函数。
CONTENTS 目录
• 引言 • 函数曲线的凹凸性判定 • 函数曲线的凹凸性性质 • 函数曲线的凹凸性与导数的关系 • 函数曲线的凹凸性与几何意义 • 总结与展望
CHAPTER 01
引言
凹凸性的定义
凹函数
对于函数$f(x)$,如果在区间$I$上,对于任意$x_1 < x_2$,都有$f(frac{x_1+x_2}{2}) geq frac{f(x_1) + f(x_2)}{2}$,则称$f(x)$在区间$I$上是凹函数。
函数曲线的凹凸性可能会随着自变量x 的变化而发生变化。
凸函数曲线
表示函数图像呈上凸的几何形状,即 任意两点之间的连线位于曲线上方。
几何形状的凹凸性实例
下凹函数曲线
$f(x) = x^2$,$f(x) = sin x$
上凸函数曲线
$f(x) = log x$,$f(x) = e^x$
几何形状的凹凸性与生活中的应用
02
二次函数是典型的凹函数和凸函数,其图像为抛物 线。
03
指数函数和幂函数在其定义域内是凹函数,对数函 数在其定义域内是凸函数。
CHAPTER 04
函数曲线的凹凸性与导数的关系
导数与凹凸性的关系
01
导数大于0的区间内,函数曲线为 凹;
02
导数小于0的区间内,函数曲线为 凸。
导数在判断凹凸性中的应用
凸函数
对于函数$f(x)$,如果在区间$I$上,对于任意$x_1 < x_2$,都有$f(frac{x_1+x_2}{2}) leq frac{f(x_1) + f(x_2)}{2}$,则称$f(x)$在区间$I$上是凸函数。
高等数学课件3-7凹凸性

凹凸性研究的重要成果和突破
添加项标题
19世纪初,法国数学家拉格朗日提出了函数的凹凸性概念,为 研究函数的性质提供了新的工具。
添加项标题
19世纪末,德国数学家魏尔斯特拉斯提出了函数的极值定理, 为研究函数的凹凸性提供了理论基础。
添加项标题
20世纪初,英国数学家哈代和波兰数学家莱维提出了函数的凹 凸性判别法,为研究函数的凹凸性提供了新的方法。
化证明过程
举例:利用凸 函数的性质, 可以证明不等 式f(x) > g(x)
凹凸性在优化问题中的应用
凸优化问题:求解凸函数最小值 凹优化问题:求解凹函数最大值 凸优化算法:梯度下降法、牛顿法等
凹优化算法:梯度上升法、牛顿法等
凸优化与凹优化的区别:凸优化问题有 唯一解,凹优化问题可能有多个解
凸优化与凹优化的应用:在机器学习、 图像处理、信号处理等领域有广泛应用
,
汇报人:
目录
凹函数和凸函数的定义
凹函数:对于任意x1,x2∈D, f(x1)+f(x2)≥2f((x1+x2)/2)
凹函数和凸函数的区别在于不等号 的方向不同
添加标题
添加标题
凸函数:对于任意x1,x2∈D, f(x1)+f(x2)≤2f((x1+x2)/2)
添加标题Βιβλιοθήκη 添加标题凹函数和凸函数的定义是判断函数 凹凸性的基础
研究前景:凹凸性研究在许多领域都有广泛的应用前景,如优化问题、图像处理、机 器人控制等
汇报人:
凹凸性的几何意义
凸性:函数在某点处的切线斜 率大于等于该点处的函数值
凹性:函数在某点处的切线斜 率小于等于该点处的函数值
凸性函数:函数图像在定义域 内任意两点之间是凸的
3.5凹凸性与函数图形描绘PPT课件

3.5 曲线的凹凸性与函数作图
• 一.曲线的凹凸性及拐点 • 二.函数图形的描绘
一、凹凸性及拐点
y
y f (x) B
凹
A
oa
bx
y f (x)
y
B
凸
A oa
bx
1.定义 设函数f(x)在区间I上除端点外都可导,
x0为I的任一内点,若对 x I( x x0 ),恒有
f (x) f (x0 )(x x0 ) f (x0 ) ( f (x) f (x0)(x x0) f (x0)) 则称函数曲线 y 在f (区x)间I上是(向上)凹 的. (凸)
5 补充点,如与坐标轴的 交点、间断点、始点、 终点.
6 光滑连接各点,绘出函 数图形。
例5
作函数 ( x)
1
x2
e2
的图形.
2
解 1 [0,), (偶函数, 图形关于y轴对称)
2 ( x)
令 ( x) 0,
x
x2
e 2,
2
(
x)
(
x
1)(
x
1)
e
x2 2
.
2
得驻点 x 0,
令 ( x) 0,
得 x 1, x 1.
3°列表确定函数增减区间,凹凸区间及极值点 与拐点:
x
( x) ( x) ( x)
0 (0,1) 1 (1,)
0
0
1 2
拐点
(1, 1 ) 2e
4 lim ( x) lim
1
x2
e 2 0,
得水平渐近线
y 0.
x
x 2
( x)
1
x2
e2
2
写在最后
• 一.曲线的凹凸性及拐点 • 二.函数图形的描绘
一、凹凸性及拐点
y
y f (x) B
凹
A
oa
bx
y f (x)
y
B
凸
A oa
bx
1.定义 设函数f(x)在区间I上除端点外都可导,
x0为I的任一内点,若对 x I( x x0 ),恒有
f (x) f (x0 )(x x0 ) f (x0 ) ( f (x) f (x0)(x x0) f (x0)) 则称函数曲线 y 在f (区x)间I上是(向上)凹 的. (凸)
5 补充点,如与坐标轴的 交点、间断点、始点、 终点.
6 光滑连接各点,绘出函 数图形。
例5
作函数 ( x)
1
x2
e2
的图形.
2
解 1 [0,), (偶函数, 图形关于y轴对称)
2 ( x)
令 ( x) 0,
x
x2
e 2,
2
(
x)
(
x
1)(
x
1)
e
x2 2
.
2
得驻点 x 0,
令 ( x) 0,
得 x 1, x 1.
3°列表确定函数增减区间,凹凸区间及极值点 与拐点:
x
( x) ( x) ( x)
0 (0,1) 1 (1,)
0
0
1 2
拐点
(1, 1 ) 2e
4 lim ( x) lim
1
x2
e 2 0,
得水平渐近线
y 0.
x
x 2
( x)
1
x2
e2
2
写在最后
函数的凹凸与曲线的凸向、拐点和渐近线、函数作图

x y x ln x y ln y 。 从而 ( x y )ln 2
10
2.8.3-5 函数的凹凸与曲线的凸向、拐点和渐近线及函数作图
二、曲线的拐点
1. 定义:连续曲线上曲线向上凸与向下凸的分界点 称为曲线的拐点。
2£ Õ ã Ä Ð ¨· ® ¹ µ µ Ŷ¨
与极值点判断类似 , f ( x ) 0 的点和 f ( x ) 不存在 的点,是拐点横坐标 的可疑点。
2(1 x 2 ) 2x (2) y 2 , y 2 , 2 ( x 1) x 1
(3)令 y 0 ,得 x 1 , x 1 。
x y
曲线 y
Hale Waihona Puke (, 1)-1 0拐点 (-1,ln2)
(-1, 1) +
1 0
拐点 (1,ln2)
(1, )
例如: f ( x ) x 4 , f ( x ) 12 x 2 ,有 f (0) 0 ,但 (0,0)不是拐点。
12
2.8.3-5 函数的凹凸与曲线的凸向、拐点和渐近线及函数作图
例 2.求曲线 y ln( x 1) 的凸向和拐点。
2
解: (1)函数的定义域为 (,) ;
则称函数 f 为区间 I 上的凸函数; 若总有 f ( p1 x1 p2 x2 ) p1 f ( x1 ) p1 f ( x2 ) ,则称函数 f 为区间 I 上的凹函数。
3
2.8.3-5 函数的凹凸与曲线的凸向、拐点和渐近线及函数作图
y
y f ( x)
y
A
o a x1
D B
C
x
x2 b x
2
x2 x x x1 令 p1 , p2 , 则 p1 0 , p2 0 且 p1 p2 1 , x2 x1 x2 x1
10
2.8.3-5 函数的凹凸与曲线的凸向、拐点和渐近线及函数作图
二、曲线的拐点
1. 定义:连续曲线上曲线向上凸与向下凸的分界点 称为曲线的拐点。
2£ Õ ã Ä Ð ¨· ® ¹ µ µ Ŷ¨
与极值点判断类似 , f ( x ) 0 的点和 f ( x ) 不存在 的点,是拐点横坐标 的可疑点。
2(1 x 2 ) 2x (2) y 2 , y 2 , 2 ( x 1) x 1
(3)令 y 0 ,得 x 1 , x 1 。
x y
曲线 y
Hale Waihona Puke (, 1)-1 0拐点 (-1,ln2)
(-1, 1) +
1 0
拐点 (1,ln2)
(1, )
例如: f ( x ) x 4 , f ( x ) 12 x 2 ,有 f (0) 0 ,但 (0,0)不是拐点。
12
2.8.3-5 函数的凹凸与曲线的凸向、拐点和渐近线及函数作图
例 2.求曲线 y ln( x 1) 的凸向和拐点。
2
解: (1)函数的定义域为 (,) ;
则称函数 f 为区间 I 上的凸函数; 若总有 f ( p1 x1 p2 x2 ) p1 f ( x1 ) p1 f ( x2 ) ,则称函数 f 为区间 I 上的凹函数。
3
2.8.3-5 函数的凹凸与曲线的凸向、拐点和渐近线及函数作图
y
y f ( x)
y
A
o a x1
D B
C
x
x2 b x
2
x2 x x x1 令 p1 , p2 , 则 p1 0 , p2 0 且 p1 p2 1 , x2 x1 x2 x1
高等数学第七节 曲线的凹凸及拐点 函数作图

的凹凸与拐点,了解函数作图的基本方法.
2、本节重点、难点 重点:曲线凹凸的判定. 难点:曲线凹凸的判定.
3、本节知识结构
曲 线 的函 凹数 凸作 及图 拐 点
曲线的凹凸 及拐点
函数作图
凹凸、拐点的定义 定理(凹凸性定理)
水平渐近线、 垂直渐近线 作图步骤
当 x0时 ,y0,曲线是 ; 凸的
当 x0时 ,y0,曲线是 , 凹的
所( 以 ,0 )为凸 ,(0, 区 )为 间 凹 . 区间
因x为 0时不在,所 定以 义曲 域.线 内无
二、函数作图 作函数的,图 大形 致应遵循以:下步骤 (1)初步 :如 研 讨 究 论 ,对定 称 ,周 义 性 期 ,等 域 ;性 等
地掌握其形状.
图321,函 y f ( x 数 ) 的 A 段 B y g ( x 与 ) 的 C 段 ,它 D
都是,但 递 A段 B 增是 的凸 ,C段 D 的是 递凹 ,增的
因此还需要判断曲的线凹的凸 .
y
B
D
图321
yf(x)
A
C
o
yg(x)
x
从图 322中可以,看到 当x增大,曲 时线上对应点 斜处 率的 递 (左 切 减 图 )线 , 则曲线是凸的;
f ( x) s i nx 的渐近线? x
思考题解答
limsinx0 x x
y 0 是 其 图 象 的 渐 近 线 .
y sin x x
limsinx1 x0 x
x 0 不 是 其 图 象 的 渐 近 线 .
三、小结
1、本节基本要求 理解曲线凹凸与拐点的概念,会求较简单曲线
当x增大,曲 时线上对应点 斜处 率的 递 (右 切 增 图 )线 ,
2、本节重点、难点 重点:曲线凹凸的判定. 难点:曲线凹凸的判定.
3、本节知识结构
曲 线 的函 凹数 凸作 及图 拐 点
曲线的凹凸 及拐点
函数作图
凹凸、拐点的定义 定理(凹凸性定理)
水平渐近线、 垂直渐近线 作图步骤
当 x0时 ,y0,曲线是 ; 凸的
当 x0时 ,y0,曲线是 , 凹的
所( 以 ,0 )为凸 ,(0, 区 )为 间 凹 . 区间
因x为 0时不在,所 定以 义曲 域.线 内无
二、函数作图 作函数的,图 大形 致应遵循以:下步骤 (1)初步 :如 研 讨 究 论 ,对定 称 ,周 义 性 期 ,等 域 ;性 等
地掌握其形状.
图321,函 y f ( x 数 ) 的 A 段 B y g ( x 与 ) 的 C 段 ,它 D
都是,但 递 A段 B 增是 的凸 ,C段 D 的是 递凹 ,增的
因此还需要判断曲的线凹的凸 .
y
B
D
图321
yf(x)
A
C
o
yg(x)
x
从图 322中可以,看到 当x增大,曲 时线上对应点 斜处 率的 递 (左 切 减 图 )线 , 则曲线是凸的;
f ( x) s i nx 的渐近线? x
思考题解答
limsinx0 x x
y 0 是 其 图 象 的 渐 近 线 .
y sin x x
limsinx1 x0 x
x 0 不 是 其 图 象 的 渐 近 线 .
三、小结
1、本节基本要求 理解曲线凹凸与拐点的概念,会求较简单曲线
当x增大,曲 时线上对应点 斜处 率的 递 (右 切 增 图 )线 ,
4.4 函数的凹凸性与函数的作图

称 设曲线 y f ( x) ,如果 lim f ( x) c ,则 x y f ( x) yc 直线 为曲线 的水平渐近线.
2.铅垂渐近线
如果曲线 y f ( x) 在点 x0 间断,且
lim f ( x) ,则称直线 x x0 为曲线 x y f ( x) 的铅垂渐近线.
y 6 6 x 6(1 x)
y
x 0
6 0 ,所以 x 0 为极小值点,
f (0) 0 为极小值;y Nhomakorabeax2
6 0 ,所以 x 2为极大值点,
f (2) 4 为极大值.
(5)令 y 0 ,得 x 1.在 x 1 的左 侧有 y 0 ,在 x 1的右侧有 y 0 , 而 f (1) 2 ,所以 (1,2)是拐点.
例 解
证明函数 y ln x 的图像是处处下凹(凹)的
函数y ln x的定义域为(0, )
1 y x 1 y 2 0 x
x (0, )
故曲线在整个定义域内是下凹(凸)的
定义4.3 曲线上凹与下凹的分界点称为 曲线的拐点. 求拐点的一般步骤: ①求函数的二阶导数 f ( x) ; ②令 f ( x) 0,解出全部根,并求出所 有二阶导数不存在的点; ③对步骤②求出的每一个点,检查其左、 右邻近的 f ( x) 的符号,如果异号则该点为曲 线的拐点;如果同号则该点不是曲线的拐点.
y
y f ( x)
A
B
y
y f ( x)
B
A
o
a
b
x
o
a
f ( x ) 递增
y 0
f ( x ) 递减
b x y 0
2.铅垂渐近线
如果曲线 y f ( x) 在点 x0 间断,且
lim f ( x) ,则称直线 x x0 为曲线 x y f ( x) 的铅垂渐近线.
y 6 6 x 6(1 x)
y
x 0
6 0 ,所以 x 0 为极小值点,
f (0) 0 为极小值;y Nhomakorabeax2
6 0 ,所以 x 2为极大值点,
f (2) 4 为极大值.
(5)令 y 0 ,得 x 1.在 x 1 的左 侧有 y 0 ,在 x 1的右侧有 y 0 , 而 f (1) 2 ,所以 (1,2)是拐点.
例 解
证明函数 y ln x 的图像是处处下凹(凹)的
函数y ln x的定义域为(0, )
1 y x 1 y 2 0 x
x (0, )
故曲线在整个定义域内是下凹(凸)的
定义4.3 曲线上凹与下凹的分界点称为 曲线的拐点. 求拐点的一般步骤: ①求函数的二阶导数 f ( x) ; ②令 f ( x) 0,解出全部根,并求出所 有二阶导数不存在的点; ③对步骤②求出的每一个点,检查其左、 右邻近的 f ( x) 的符号,如果异号则该点为曲 线的拐点;如果同号则该点不是曲线的拐点.
y
y f ( x)
A
B
y
y f ( x)
B
A
o
a
b
x
o
a
f ( x ) 递增
y 0
f ( x ) 递减
b x y 0
4-6函数的凸凹性与函数作图 (2)
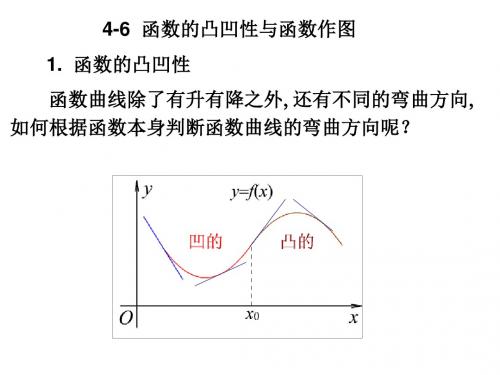
4-6 函数的凸凹性与函数作图 1. 函数的凸凹性 函数曲线除了有升有降之外, 还有不同的弯曲方向, 如何根据函数本身判断函数曲线的弯曲方向呢?
函数的凸(向上凸)凹(向下凸)性定义
设 y f x在 a,b 上可导, 若对于每一点 x0 a,b ,都有
f x f x0 f x0 x x0 , xa,b x x0;
曲线的拐点
上例中点x b 就是一个拐点. 3a
定理2 设 y f x 在 a,b内有连续的二阶导数, 若点
c a,b是 y f x 的拐点,则 f c 0.
证 用反证法 . 设f (c) 0,不妨设f (c) 0.由f (x)的连续性,
是曲线y f (x)的过点( x0, f (x0 ))的切线方程, f (x)在(a,b)上
向上凸, 曲线弧总是在它的切线的下方, f (x)在(a,b)上 向下凸, 曲线弧总是在它的切线的上方.
定理1 (曲线凹凸性的判定法)
设f(x)在(a, b)内具有二阶导数, 对于每一点 x a,b
必存在c的一个邻域 U( c), 使
f (x) 0, x U (c). 由定理1,f (x)在整个U (c)内都是向下凸的 , 不论x是在c的左 侧附近还是在 c的右侧附近 , 这与c是拐点矛盾. 证毕.
二阶导数为零仅是拐点的必要条件,但不是充分条件.
补例 判断曲线
的凹凸性.
y
解 y 4x3,
f x0 0或不存在.
如果在 x0的左右两侧
f x异号, 则 x0, f x0
拐点
是拐点.
补例 求曲线
的拐点.
2
5
解
y
1 3
x
函数的凸(向上凸)凹(向下凸)性定义
设 y f x在 a,b 上可导, 若对于每一点 x0 a,b ,都有
f x f x0 f x0 x x0 , xa,b x x0;
曲线的拐点
上例中点x b 就是一个拐点. 3a
定理2 设 y f x 在 a,b内有连续的二阶导数, 若点
c a,b是 y f x 的拐点,则 f c 0.
证 用反证法 . 设f (c) 0,不妨设f (c) 0.由f (x)的连续性,
是曲线y f (x)的过点( x0, f (x0 ))的切线方程, f (x)在(a,b)上
向上凸, 曲线弧总是在它的切线的下方, f (x)在(a,b)上 向下凸, 曲线弧总是在它的切线的上方.
定理1 (曲线凹凸性的判定法)
设f(x)在(a, b)内具有二阶导数, 对于每一点 x a,b
必存在c的一个邻域 U( c), 使
f (x) 0, x U (c). 由定理1,f (x)在整个U (c)内都是向下凸的 , 不论x是在c的左 侧附近还是在 c的右侧附近 , 这与c是拐点矛盾. 证毕.
二阶导数为零仅是拐点的必要条件,但不是充分条件.
补例 判断曲线
的凹凸性.
y
解 y 4x3,
f x0 0或不存在.
如果在 x0的左右两侧
f x异号, 则 x0, f x0
拐点
是拐点.
补例 求曲线
的拐点.
2
5
解
y
1 3
x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机动 目录 上页 下页 返回 结束
6)绘图
x ( , 1) 1 (1,1)
y
1
无 定 义
(1, 3) 3
(3 , )
2
(极大)
0
(极小)
铅直渐近线 斜渐近线 特殊点
x 1 1 5 y x 4 4
( x 3) 2 y 4( x 1)
x
y
0 9 4
2 1 4
3) 判别曲线形态
x y y y
0 0
1 2
(0 , 1)
1
0
1 2 e
(1, )
(极大)
机动
(拐点)
目录 上页 下页 返回 结束
x y y y
0 0
1 2
(0 , 1)
1
0
1 2 e
(1, )
(极大)
(拐点)
4) 求渐近线
y
A
1 2
lim y 0
( k x b)
f ( x) b k lim [ ] x x x f ( x) k lim x x
(或 x )
f ( x) b lim x[ k ]0 x x x f ( x) b lim [ k ]0 x x x
b lim [ f ( x) k x]
y
C M
y f ( x)
y kxb
L
PN
有渐近线
但抛物线
x y 0 a b
无渐近线 .
o
y
x
x
o
机动
目录
上页
下页
返回
结束
1. 水平与铅直渐近线 若 则曲线
(或 x )
有水平渐近线 y b . 有垂直渐近线 x x0 .
若
(或 x x0 )
则曲线
例1. 求曲线
的渐近线 .
2 1
1 解: lim ( 2) 2 x x 1
y 2 为水平渐近线; 1 lim ( 2) , x 1为垂直渐近线. x1 x 1
机动 目录 上页 下页 返回 结束
2. 斜渐近线 若
(或 x )
( k x b)
斜渐近线 y k x b .
2 4 y 8 y 4 x y 0 1 4 y y 2( x 1)
令 y 0 得 x 1, 3 ;
机动 目录 上页 下页 返回 结束
3) 判别曲线形态
x ( , 1) 1 (1,1) y 0 y y 2
1
0 12 3
机动
目录
上页
下页
返回
结束
例5. 描绘函数
解: 1) 定义域为 2) 求关键点 2 x 1 xe 2 , y 2
的图形. 图形对称于 y 轴.
1 y e 2
2 x 2
(1 x 2 )
令 y 0 得 x 0 ; 令 y 0 得 x 1
f (1) f (0) f ( ) (0 1)
机动 目录 上页 下页 返回 结束
3)
1
1 2 3
x ( , 0) y y y x 1 3 y 2 2 3
0 0
(0 ,1)
1
0
4 3
(1, 2)
2 ( 2 , ) 0
2 3
2
(极大)
(拐点)
(极小)
4)
机动
目录
上页
下页
返回
结束
例4. 描绘方程
的图形.
( x 3) 2 , 定义域为 解: 1) y 4( x 1) 2) 求关键点 2( x 3) 4 y 4 y 4 x y 0 x 3 2y y 2( x 1)
机动
目录上页ຫໍສະໝຸດ 下页返回结束
令
得:
机动
目录
上页
下页
返回
结束
充分性: 设
单调增加, 对函数
分别在区间
上用拉格朗日中值定理得:存在
机动
目录
上页
下页
返回
结束
定理2.(凹凸判定法) 设函数 (1) 在 I 内 (2) 在 I 内 证: 则
在区间I 上有二阶导数 在 I 内图形是下凸的 ;
则 在 I 内图形是上凸的 . 利用一阶泰勒公式可得
x
y
1 2
e
x2 2
y 0 为水平渐近线
5) 作图
B
o
x
机动
目录
上页
下页
返回
结束
思考与练习
1. 曲线 y
1 e
x2
2
1 e x
(D )
(B) 仅有水平渐近线;
(A) 没有渐近线;
(C) 仅有铅直渐近线;
(D) 既有水平渐近线又有铅直渐近线. 提示: lim
1 e
f (1 ) x1 x2 x1 x2 x1 x2 2 x1 x2 f ( x1 ) f ( ) f ( ) ) ( x1 ) 2 ! ( x1 2 2 2 2 x1 x2 x1 x2 f ( 2 ) x1 x2 x1 x2 2 )( x2 f ( x2 ) f ( ) f ( ) ) 2 ! ( x2 2 2 2 2 两式相加
(0 , )
上凸
的拐点 .
机动
目录
上页
下页
返回
结束
说明:
1) 若在某点二阶导数为 0 , 在其两侧二阶导数不变号, 则曲线的凸性不变 . 2) 根据拐点的定义, 可得拐点的判别法如下: 若曲线 的一个拐点. 或不存在, 但 f ( x) 在 x0 两侧异号, 则点( x0 , f ( x0 )) 是曲线
x1 x2 f ( x1) f ( x2 ) 2 f ( ) 2
f ( x1 ) f ( x2 ) 2
(
1 2!
x2 x1 2 [f 2
)
(1 ) f ( 2 )]
当 f ( x) 0时,
x1 x2 f( ), 2
说明 (1) 成立; (2) 证毕
x2 x
返回 结束
(2) 若恒有
则称 图形是上凸的; 或称f (x)为I上的上凸函数。
弦在弧的下方;切线在曲线的上方。
下凸也称为凸,上凸也称为凹。 y
o
x1
x1 x2 2
x2 x
机动
目录
上页
下页
返回
结束
等价定义: 定义1´:设函数 在区间 I 上连续 ,
(1) 若恒有
则称
图形是下凸的; (弦在弧的上方,或切线在曲线下方) (2) 若恒有 则称
(极大)
(1, 3) 3 0 无 定
1
(3 , )
义
0
(极小)
4) 求渐近线
lim y , x 1 为铅直渐近线
x1
( x 3)( x 1) 2 ( x 3) , y y , y 2 4( x 1) 4( x 1) ( x 1)3
机动 目录 上页 下页 返回 结束
例5:证明不等式
例5.4 例5.5
1 n x y n n (x y ) ( ) ( x 0, y 0, x y, n 1) 2 2
证明:设 f (t ) t n (t 0, n 1)
则
f (t ) nt n1, f (t ) n(n 1)t n2 ,
3
1
2 x 2 3x b lim [ f ( x) x] lim 2 x x x 2 x 3
y x 2 为曲线的斜渐近线 .
机动 目录 上页 下页 返回 结束
三、函数的作图
步骤 : 1. 确定函数 期性 ; 的定义域 , 并考察其对称性及周 并求出 及 为 0 和不存在
第五节
第三章
曲线的凸性与函数作图
一、曲线的凸性
二、渐近线 三、函数的作图
机动
目录
上页
下页
返回
结束
一、曲线的凸性
定义1 . 设函数 在区间 I 上连续 ,
(1) 若恒有
则称
图形是下凸的; 或称f (x)为I上的下凸函数。
B
弦在弧的上方;切线在曲线的下方。
A
y
o
机动
x1
目录
x1 x2 2
上页 下页
机动 目录 上页 下页 返回 结束
2
y 1 1 又因 lim , 即 k x x 4 4 2 ( x 3 ) 1 1 x] b lim ( y x) lim [ x 4( x 1) 4 x 4 5x 9 5 lim 2 ( x 3 ) x 4( x 1) 4 y 4( x 1) 1 5 y x 为斜渐近线 ( x 3)( x 1) 4 4 y 4( x 1) 2 0 2 5) 求特殊点 x 2 1 y y 9 3 ( x 1 ) 4 4
( A) ( B) (C ) ( D)
f (1) f (0) f (1) f (0) f (1) f (1) f (0) f (0) f (1) f (0) f (1) f (0) f (1) f (0) f (1) f (0)
提示: 利用 f ( x) 单调增加 , 及
x (或 x )
机动 目录
上页
下页
返回
结束
例2. 求曲线
的渐近线 .
x3 解: y , lim y , ( x 3)(x 1) x3
6)绘图
x ( , 1) 1 (1,1)
y
1
无 定 义
(1, 3) 3
(3 , )
2
(极大)
0
(极小)
铅直渐近线 斜渐近线 特殊点
x 1 1 5 y x 4 4
( x 3) 2 y 4( x 1)
x
y
0 9 4
2 1 4
3) 判别曲线形态
x y y y
0 0
1 2
(0 , 1)
1
0
1 2 e
(1, )
(极大)
机动
(拐点)
目录 上页 下页 返回 结束
x y y y
0 0
1 2
(0 , 1)
1
0
1 2 e
(1, )
(极大)
(拐点)
4) 求渐近线
y
A
1 2
lim y 0
( k x b)
f ( x) b k lim [ ] x x x f ( x) k lim x x
(或 x )
f ( x) b lim x[ k ]0 x x x f ( x) b lim [ k ]0 x x x
b lim [ f ( x) k x]
y
C M
y f ( x)
y kxb
L
PN
有渐近线
但抛物线
x y 0 a b
无渐近线 .
o
y
x
x
o
机动
目录
上页
下页
返回
结束
1. 水平与铅直渐近线 若 则曲线
(或 x )
有水平渐近线 y b . 有垂直渐近线 x x0 .
若
(或 x x0 )
则曲线
例1. 求曲线
的渐近线 .
2 1
1 解: lim ( 2) 2 x x 1
y 2 为水平渐近线; 1 lim ( 2) , x 1为垂直渐近线. x1 x 1
机动 目录 上页 下页 返回 结束
2. 斜渐近线 若
(或 x )
( k x b)
斜渐近线 y k x b .
2 4 y 8 y 4 x y 0 1 4 y y 2( x 1)
令 y 0 得 x 1, 3 ;
机动 目录 上页 下页 返回 结束
3) 判别曲线形态
x ( , 1) 1 (1,1) y 0 y y 2
1
0 12 3
机动
目录
上页
下页
返回
结束
例5. 描绘函数
解: 1) 定义域为 2) 求关键点 2 x 1 xe 2 , y 2
的图形. 图形对称于 y 轴.
1 y e 2
2 x 2
(1 x 2 )
令 y 0 得 x 0 ; 令 y 0 得 x 1
f (1) f (0) f ( ) (0 1)
机动 目录 上页 下页 返回 结束
3)
1
1 2 3
x ( , 0) y y y x 1 3 y 2 2 3
0 0
(0 ,1)
1
0
4 3
(1, 2)
2 ( 2 , ) 0
2 3
2
(极大)
(拐点)
(极小)
4)
机动
目录
上页
下页
返回
结束
例4. 描绘方程
的图形.
( x 3) 2 , 定义域为 解: 1) y 4( x 1) 2) 求关键点 2( x 3) 4 y 4 y 4 x y 0 x 3 2y y 2( x 1)
机动
目录上页ຫໍສະໝຸດ 下页返回结束
令
得:
机动
目录
上页
下页
返回
结束
充分性: 设
单调增加, 对函数
分别在区间
上用拉格朗日中值定理得:存在
机动
目录
上页
下页
返回
结束
定理2.(凹凸判定法) 设函数 (1) 在 I 内 (2) 在 I 内 证: 则
在区间I 上有二阶导数 在 I 内图形是下凸的 ;
则 在 I 内图形是上凸的 . 利用一阶泰勒公式可得
x
y
1 2
e
x2 2
y 0 为水平渐近线
5) 作图
B
o
x
机动
目录
上页
下页
返回
结束
思考与练习
1. 曲线 y
1 e
x2
2
1 e x
(D )
(B) 仅有水平渐近线;
(A) 没有渐近线;
(C) 仅有铅直渐近线;
(D) 既有水平渐近线又有铅直渐近线. 提示: lim
1 e
f (1 ) x1 x2 x1 x2 x1 x2 2 x1 x2 f ( x1 ) f ( ) f ( ) ) ( x1 ) 2 ! ( x1 2 2 2 2 x1 x2 x1 x2 f ( 2 ) x1 x2 x1 x2 2 )( x2 f ( x2 ) f ( ) f ( ) ) 2 ! ( x2 2 2 2 2 两式相加
(0 , )
上凸
的拐点 .
机动
目录
上页
下页
返回
结束
说明:
1) 若在某点二阶导数为 0 , 在其两侧二阶导数不变号, 则曲线的凸性不变 . 2) 根据拐点的定义, 可得拐点的判别法如下: 若曲线 的一个拐点. 或不存在, 但 f ( x) 在 x0 两侧异号, 则点( x0 , f ( x0 )) 是曲线
x1 x2 f ( x1) f ( x2 ) 2 f ( ) 2
f ( x1 ) f ( x2 ) 2
(
1 2!
x2 x1 2 [f 2
)
(1 ) f ( 2 )]
当 f ( x) 0时,
x1 x2 f( ), 2
说明 (1) 成立; (2) 证毕
x2 x
返回 结束
(2) 若恒有
则称 图形是上凸的; 或称f (x)为I上的上凸函数。
弦在弧的下方;切线在曲线的上方。
下凸也称为凸,上凸也称为凹。 y
o
x1
x1 x2 2
x2 x
机动
目录
上页
下页
返回
结束
等价定义: 定义1´:设函数 在区间 I 上连续 ,
(1) 若恒有
则称
图形是下凸的; (弦在弧的上方,或切线在曲线下方) (2) 若恒有 则称
(极大)
(1, 3) 3 0 无 定
1
(3 , )
义
0
(极小)
4) 求渐近线
lim y , x 1 为铅直渐近线
x1
( x 3)( x 1) 2 ( x 3) , y y , y 2 4( x 1) 4( x 1) ( x 1)3
机动 目录 上页 下页 返回 结束
例5:证明不等式
例5.4 例5.5
1 n x y n n (x y ) ( ) ( x 0, y 0, x y, n 1) 2 2
证明:设 f (t ) t n (t 0, n 1)
则
f (t ) nt n1, f (t ) n(n 1)t n2 ,
3
1
2 x 2 3x b lim [ f ( x) x] lim 2 x x x 2 x 3
y x 2 为曲线的斜渐近线 .
机动 目录 上页 下页 返回 结束
三、函数的作图
步骤 : 1. 确定函数 期性 ; 的定义域 , 并考察其对称性及周 并求出 及 为 0 和不存在
第五节
第三章
曲线的凸性与函数作图
一、曲线的凸性
二、渐近线 三、函数的作图
机动
目录
上页
下页
返回
结束
一、曲线的凸性
定义1 . 设函数 在区间 I 上连续 ,
(1) 若恒有
则称
图形是下凸的; 或称f (x)为I上的下凸函数。
B
弦在弧的上方;切线在曲线的下方。
A
y
o
机动
x1
目录
x1 x2 2
上页 下页
机动 目录 上页 下页 返回 结束
2
y 1 1 又因 lim , 即 k x x 4 4 2 ( x 3 ) 1 1 x] b lim ( y x) lim [ x 4( x 1) 4 x 4 5x 9 5 lim 2 ( x 3 ) x 4( x 1) 4 y 4( x 1) 1 5 y x 为斜渐近线 ( x 3)( x 1) 4 4 y 4( x 1) 2 0 2 5) 求特殊点 x 2 1 y y 9 3 ( x 1 ) 4 4
( A) ( B) (C ) ( D)
f (1) f (0) f (1) f (0) f (1) f (1) f (0) f (0) f (1) f (0) f (1) f (0) f (1) f (0) f (1) f (0)
提示: 利用 f ( x) 单调增加 , 及
x (或 x )
机动 目录
上页
下页
返回
结束
例2. 求曲线
的渐近线 .
x3 解: y , lim y , ( x 3)(x 1) x3
