您的位置：360文档中心› 初中数学旋转解题几何之令狐文艳创作

初中数学旋转解题几何之令狐文艳创作

合集下载

中学数学全套课件制作实例(几何画板)之令狐文艳创作

中学数学全套课件制作实例(几何画板)之令狐文艳创作

中学数学全套课件制作实例（几何画板）令狐文艳1、《几何画板》：绘制三角形内接矩形的面积函数图像2、《几何画板》：求过两点的直线方程3、《几何画板》：验证两点间距离公式4、《几何画板》：绘制分段函数的图像5、《几何画板》：绘制某区间内的函数图像6、《几何画板》：运用椭圆工具制作圆柱7、《几何画板》：绘制四棱台8、《几何画板》：绘制三棱柱9、《几何画板》：绘制正方体10、《几何画板》：绘制三角形的内切圆11、《几何画板》：通过不在一条直线上的3点绘制圆12、《几何画板》：给定半径和圆心绘制圆13、《几何画板》：绘制棱形14、《几何画板》：绘制平行四边形15、《几何画板》：绘制等腰直角三角形16、《几何画板》：旋转体教学17、《几何画板》：画角度的箭头18、《几何画板》：“派生”关系进行轨迹教学板19、《几何画板》：制作“椭圆”工具20、《几何画板》：显示圆和直线的位置关系21、《几何画板》：研究圆切线的性质22、《几何画板》：“垂径定理”的教学23、《几何画板》：证明三角形的中线交于一点24、《几何画板》：验证分割高线长定理25、《几何画板》：证明三角形外心和重心的距离等于垂心与重心的距离的一半26、《几何画板》：证明三角形内角和等于180度27、《几何画板》：验证三角形面积公式28、《几何画板》：验证勾股定理29、《几何画板》：验证正弦定理30、《几何画板》：验证圆弧的三项比值相等31、《几何画板》：巧用Excel制作函数图像32、《几何画板》：绘制极坐标系中的曲线函数图像33、《几何画板》：绘制带参数的幂函数图像34、《几何画板》：绘制带参数的正弦函数图像35、《几何画板》：绘制带参数的抛物线函数图像36、《几何画板》：绘制带参数的圆函数图像37、《几何画板》绘制带参数直线函数图像《几何画板》：绘制三角形内接矩形的面积函数图像第1步，启动几何画板，依次单击“图表”→“定义坐标系”菜单命令，在操作区建立直角坐标系。

中考数学压轴题之初中数学专题之令狐文艳创作

中考数学压轴题之初中数学专题之令狐文艳创作

中考数学压轴题专题复习令狐文艳1.（2008年四川省宜宾市）已知:如图,抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点A （-1，0）、B （0，3）两点，其顶点为 D.求该抛物线的解析式；（1） 若该抛物线与x 轴的另一个交点为E. 求四边形ABDE 的面积；（2） △AOB 与△BDE 是否相似？如果相似，请予以证明；如果不相似，请说明理由.（注：抛物线y=ax 2+bx+c(a ≠0)的顶点坐标为⎪⎪⎭⎫ ⎝⎛--a b ac a b 44,22）2. （08浙江衢州）已知直角梯形纸片OABC 在平面直角坐标系中的位置如图所示，四个顶点的坐标分别为O(0，0)，A(10，0)，B(8，32)，C(0，32)，点T 在线段OA 上(不与线段端点重合)，将纸片折叠，使点A 落在射线AB 上(记为点A ′)，折痕经过点T ，折痕TP 与射线AB 交于点P ，设点T 的横坐标为t ，折叠后纸片重叠部分(图中的阴影部分)的面积为S ；(1)求∠OAB 的度数，并求当点A ′在线段AB 上时，S 关于t 的函数关系式；(2)当纸片重叠部分的图形是四边形时，求t 的取值范围；(3)S 存在最大值吗？若存在，求出这个最大值，并求此时t的值；若不存在，请说明理由.3. （088AC =，D E ，分别是边AB AC ，的中点，点P 从点D 出发沿DE 方向运动，过点P 作PQ BC ⊥于Q ，过点Q 作QR BA ∥交AC 于 R ，当点Q 与点C 重合时，点P 停止运动．设BQ x =，QR y =．（1）求点D 到BC 的距离DH 的长；（2）求y 关于x 的函数关系式（不要求写出自变量的取值范围）；（3）是否存在点P ，使PQR △为等腰三角形？若存在，请求出所有满足要求的x 的值；若不存在，请说明理由．4.（08山东省日照市）在△ABC 中，∠A ＝90°，AB ＝4，AC ＝3，M 是AB 上的动点（不与A ，B 重合），过M 点作MN ∥BC 交AC 于点N ．以MN 为直径作⊙O ，并在⊙O 内作内接矩形AMPN ．令AM ＝x ．（1）用含x 的代数式表示△ＭNP 的面积S ；（2）当x 为何值时，⊙O 与直线BC 相切？AB C D E R PH Qy O B C A T y（3）在动点M 的运动过程中，记△ＭNP 与梯形BCNM 重合的面积为y ，试求y 关于x 的函数表达式，并求x 为何值时，y 的值最大，最大值是多少？5、（2007浙江金华）如图1，已知双曲线y=xk (k>0)与直线y=k ′x 交于A ，B 两点，点A 在第一象限.试解答下列问题：(1)若点A 的坐标为(4，2).则点B 的坐标为；若点A 的横坐标为m ，则点B 的坐标可表示为；（2）如图2，过原点O 作另一条直线l ，交双曲线y=xk (k>0)于P ，Q 两点，点P 在第一象限.①说明四边形APBQ 一定是平行四边形；②设点A.P 的横坐标分别为m ，n ，四边形APBQ 可能是矩形吗?可能是正方形吗?若可能，直接写出mn 应满足的条件；若不可能，请说明理由.6. （2008浙江金华）如图1，在平面直角坐标系中，己知ΔAOB 是等边三角形，点A 的坐标是(0，4)，点B 在第一象B图 1 B D 图 2 P图 3限，点P是x轴上的一个动点，连结AP，并把ΔAOP绕着点A按逆时针方向旋转.使边AO与AB重合.得到ΔABD.（1）求直线AB的解析式；（2）当点P运动到点（3，0）时，求此时DP的长及点D的坐标；（3）是否存在点P，使ΔOPD的面积等于43，若存在，请求出符合条件的点P的坐标；若不存在，请说明理由.7.(2008浙江义乌)如图1，四边形ABCD是正方形，G是CD边上的一个动点(点G与C、D不重合)，以CG为一边在正方形ABCD外作正方形CEFG，连结BG，DE．我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系：（1）①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系；②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α，得到如图2、如图3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断．（2）将原题中正方形改为矩形（如图4—6），且AB=a，BC=b，CE=ka， CG=kb (a≠b，k>0)，第(1)题①中得到的结论哪些成立，哪些不成立？若成立，以图5为例简要说明理由．（3）在第(2)题图5中，连结DG、BE，且a=3，b=2，k=12，求22BE DG+的值．8. (2008浙江义乌)如图1所示，直角梯形OABC 的顶点A 、C 分别在y 轴正半轴与x 轴负半轴上.过点B 、C 作直线l ．将直线l 平移，平移后的直线l 与x 轴交于点D ，与y 轴交于点E ．（1）将直线l 向右平移，设平移距离CD 为t (t ≥0)，直角梯形OABC 被直线l 扫过的面积（图中阴影部份）为s ，s 关于t 的函数图象如图2所示， OM 为线段，MN 为抛物线的一部分，NQ 为射线，N 点横坐标为4．①求梯形上底AB 的长及直角梯形OABC 的面积；②当42<<t 时，求S 关于t 的函数解析式；（2）在第（1）题的条件下，当直线l 向左或向右平移时（包括l 与直线BC 重合），在直线．．AB ．．上是否存在点P ，使PDE ∆为等腰直角三角形?若存在，请直接写出所有满足条件的点P 的坐标;若不存在，请说明理由．9.(2008山东烟台)如图，菱形ABCD 的边长为2，BD=2，E 、F 分别是边AD ，CD 上的两个动点，且满足AE+CF=2.（1）求证：△BDE ≌△BCF ； （2）判断△BEF 的形状，并说明理由；（3）设△BEF 的面积为S ，求S 的取值范围.10.(2008山东烟台)如图，抛物线21:23L y x x =--+交x 轴于A 、B 两点，交y 轴于M 点.抛物线1L 向右平移2个单位后得到抛物线2L ，2L 交x 轴于C 、D 两点.（1）求抛物线2L 对应的函数表达式；（2）抛物线1L 或2L 在x 轴上方的部分是否存在点N ，使以A ，C ，M ，N 为顶点的四边形是平行四边形.若存在，求出点N 的坐标；若不存在，请说明理由；（3）若点P是抛物线L上的一个动点（P不与点A、B重1合），那么点P关于原点的对称点Q是否在抛物线L上，请说2明理由.11.2008淅江宁波)2008年5月1日，目前世界上最长的跨海大桥——杭州湾跨海大桥通车了．通车后，苏南A地到宁波港的路程比原来缩短了120千米．已知运输车速度不变时，行驶时间将从原来的3时20分缩短到2时．（1）求A地经杭州湾跨海大桥到宁波港的路程．（2）若货物运输费用包括运输成本和时间成本，已知某车货物从A地到宁波港的运输成本是每千米1.8元，时间成本是每时28元，那么该车货物从A地经杭州湾跨海大桥到宁波港的运输费用是多少元？（3）A地准备开辟宁波方向的外运路线，即货物从A地经杭州湾跨海大桥到宁波港，再从宁波港运到B地．若有一批货物（不超过10车）从A地按外运路线运到B地的运费需8320元，其中从A地经杭州湾跨海大桥到宁波港的每车运输费用与（2）中相同，从宁波港到B地的海上运费对一批不超过10车的货物计费方式是：一车800元，当货物每增加1车时，每车的海上运费就减少20元，问这批货物有几车？12.(2008淅江宁波)如图1，把一张标准纸一次又一次对开，得到“2开”纸、“4开”纸、“8开”纸、“16开”纸…．已知标准纸．．．的短边长为a ． （1）如图2，把这张标准纸对开得到的“16开”张纸按如下步骤折叠：第一步 将矩形的短边AB 与长边AD 对齐折叠，点B 落在AD 上的点B '处，铺平后得折痕AE ；第二步 将长边AD 与折痕AE 对齐折叠，点D 正好与点E 重合，铺平后得折痕AF ．则:AD AB 的值是，AD AB ，的长分别是，．（2）“2开”纸、“4开”纸、“8开”纸的长与宽之比是否都相等？若相等，直接写出这个比值；若不相等，请分别计算它们的比值．（3）如图3，由8个大小相等的小正方形构成“L ”型图案，它的四个顶点E F G H ，，，分别在“16开”纸的边AB BC CD DA ，，，上，求DG 的长．（4）已知梯形MNPQ 中，MN PQ ∥，90M =∠，2MN MQ PQ ==，且四个顶点M N P Q ，，，都在“4开”纸的边上，请直接写出2个符合条件且大小不同的直角梯形的面积．13.（2008山东威海）如图，在梯形ABCD 中，AB ∥CD ，AB ＝7，CD ＝1，AD ＝BC ＝5．点M ，N 分别在边AD ，BC 上运动，并A B C D B C A D E G H F F E B ' 4开2开8开 16图1图2 图3 a保持MN ∥AB ，ME ⊥AB ，NF ⊥AB ，垂足分别为E ，F ．（1）求梯形ABCD 的面积；（2）求四边形MEFN 面积的最大值．（3）试判断四边形MEFN 能否为正方形，若能，求出正方形MEFN 的面积；若不能，请说明理由．14．（2008山东威海）如图，点A （m ，m ＋1），B （m ＋3，m －1）都在反比例函数xk y 的图象上． （1）求m ，k 的值； （2）如果M 为x 轴上一点，N 为y以点A ，B ，M ，N 试求直线MN 的函数表达式．（3）选做题：在平面直角坐标系中，点为（5，0），点Q 的坐标为（0，3移4个单位，然后再向上平移2则点P 1的坐标为，点Q 1的坐标为． 15．（2008湖南益阳）我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”，如果一条直线与“蛋圆”只有一个交点，那么这条直线叫做“蛋圆”的切线.如图12，点A 、B 、C 、D 分别是“蛋圆”与坐标轴的交点，已知点D 的坐标为(0，-3)，AB 为半圆的直径，半圆圆心MC DA B E F NM的坐标为(1,0)，半圆半径为2.(1) 请你求出“蛋圆”抛物线部分的解析式，并写出自变量的取值范围；(2)你能求出经过点C 的“蛋圆”切线的解析式吗？试试看；(3)开动脑筋想一想，相信你能求出经过点D 的“蛋圆”切线的解析式.16.(2008年浙江省绍兴市)标系中，(00)O ，，(60)A ，，(03)C ，单位长的速度沿OC 向终点C 出发以相等的速度沿AO 向终点时，另一点也停止运动．设点P （1）用含t 的代数式表示OP OQ ，（2）当1t 时，如图1，将△边上的点D 处，求点D 的坐标；（3） 连结AC ，将OPQ △沿PQ 翻折，得到EPQ △，如图2．问：PQ 与AC 能否平行？PE 与AC能否垂直？若能，求出相应的t 值；若不能，说明理由．17.(2008年辽宁省十二市)如图16，在平面直角坐标系中，直线y =-与x 轴交于点A ，与y 轴交于点C ，抛物线2(0)3y ax x c a =-+≠经过A B C ，，三点． （1）求过A B C ，，三点抛物线的解析式并求出顶点F 的坐标；（2）在抛物线上是否存在点P ，使ABP △为直角三角形，若存在，直接写出P 点坐标；若不存在，请说明理由；（3）试探究在直线AC 上是否存在一点M ，使得MBF △的周长最小，若存在，求出M 点的坐标；若不存在，请说明理由．18.(2008年沈阳市)如图所示，在平面直角坐标系中，矩形ABOC 的边BO 在x 轴的负半轴上，边OC 在y 轴的正半轴上，且1AB =，OB =ABOC 绕点O 按顺时针方向旋转60后得到矩形EFOD ．点A 的对应点为点E ，点B 的对应点为点F ，点C 的对应点为点D ，抛物线2y ax bx c =++过点A E D ，，．图1（1）判断点E 是否在y 轴上，并说明理由； （2）求抛物线的函数表达式；（3）在x 轴的上方是否存在点P ，点Q ，使以点O B P Q ，，，为顶点的平行四边形的面积是矩形ABOC 面积的2倍，且点P 在抛物线上，若存在，请求出点P ，点Q 的坐标；若不存在，请说明理由．19.(2008年四川省巴中市) 已知：如图14，抛物线2334y x =-+与x 轴交于点A ，点B ，与直线34y x b =-+相交于点B ，点C ，直线34y x b =-+与y 轴交于点E ． （1）写出直线BC 的解析式． （2）求ABC △的面积．（3）若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动（不与A B ，重合），同时，点N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动．设运动时间为t 秒，请写出MNB △的面积S 与t 的函数关系式，并求出点M运动多少时间时，MNB △的面积最大，最大面积是多少？20.(2008年成都市)如图，在平面直角坐标系xOy 中，△OAB 的顶点Ａ的坐标为（10，0），顶点B 在第一象限内，且ABsin ∠ （1）若点C 是点B 关于x 轴的对称点，求经过O 、C 、A 三点的抛物线的函数表达式；（2）在(1)中，抛物线上是否存在一点P ，使以P 、O 、C 、A 为顶点的四边形为梯形？若存在，求出点P 的坐标；若不存在，请说明理由；（3）若将点O 、点A 分别变换为点Q （ -2k ,0）、点R （5k ，0）（k>1的常数），设过Q 、R 两点，且以QR 的垂直平分线为对称轴的抛物线与y 轴的交点为N ，其顶点为M ，记△QNM 的面积为QMN S ∆，△QNR 的面积QNR S ∆，求QMN S ∆∶QNR S ∆的值. 21.(2008年乐山市)在平面直角坐标系中△ABC 的边AB 在x 轴上，且OA>OB,以AB 为直径的圆过点C 若C 的坐标为(0,2),AB=5, A,B 两点的横坐标X A ,X B 是关于X 的方程2(2)10x m x n -++-=的两根:(1) 求m ，n 的值(2) 若∠ACB的平分线所在的直线l 交x 轴于点D ，试求直线l 对应的一次函数的解析式(3) 过点D 任作一直线`l 分别交射线CA ，CB （点C 除外）于点M ，N ，则11CM CN+的值是否为定值，若是，求出定值，若不是，请说明理由22.(2008年四川省宜宾市)已知:如图,抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点A （-1，0）、B （0，3）两点，其顶点为D.(1)求该抛物线的解析式；(2)若该抛物线与x 轴的另一个交点为E. 求四边形ABDE 的面积；(3)△AOB 与△BDE 是否相似？如果相似，请予以证明；如果不相似，请说明理由. （注：抛物线y=ax2+bx+c(a ≠0)的顶点坐标为⎪⎪⎭⎫⎝⎛--a b ac a b 44,22）23.(天津市2008年)已知抛物线c bx ax y ++=232，（Ⅰ）若1==b a ，1-=c ，求该抛物线与x 轴公共点的坐标； （Ⅱ）若1==b a ，且当11<<-x 时，抛物线与x 轴有且只有一个公共点，求c 的取值范围；（Ⅲ）若0=++c b a ，且01=x 时，对应的01>y ；12=x 时，对应的02>y ，试判断当10<<x 时，抛物线与x 轴是否有公共点？若有，请证明你的结论；若没有，阐述理由．L`24.(2008年大庆市)如图①，四边形AEFG 和ABCD 都是正方形，它们的边长分别为a b ，（2b a ≥），且点F在AD 上（以下问题的结果均可用a b，的代数式表示）． （1）求DBF S △；（2）把正方形AEFG 绕点A 按逆时针方向旋转45°得图②，求图②中的DBF S △；（3）把正方形AEFG 绕点A 旋转一周，在旋转的过程中，DBF S △是否存在最大值、最小值？如果存在，直接写出最大值、最小值；如果不存在，请说明理由．.25.（2008年上海市）已知24AB AD ==，，90DAB ∠=，AD BC ∥（如图13）．E 是射线BC 上的动点（点E与点B 不重合），M 是线段DE 的中点．（1）设BE x =，ABM △的面积为y ，求y 关于x 的函数解析式，并写出函数的定义域；（2）如果以线段AB 为直径的圆与以线段DE 为直径的圆外切，求线段BE 的长；（3）联结BD ，交线段AM 于点N ，如果以A N D ，，为顶点的三角形与BME △相似，求线段BE 的长．26.（2008年陕西省）某县社会主义新农村建设办公室，为了解决该县甲、乙两村和一所中学长期存在的饮水困难问题，想D CBAEFGGFE ABCD ① ②ADMAD在这三个地方的其中一处建一所供水站．由供水站直接铺设管道到另外两处．如图，甲，乙两村坐落在夹角为30的两条公路的AB段和CD段（村子和公路的宽均不计），点M表示这所中学．点B在点M 的北偏西30的3km处，点A在点M的正西方向，点D在点M的南偏西60的处．为使供水站铺设到另两处的管道长度之和最短，现有如下三种方案：方案一：供水站建在点M处，请你求出铺设到甲村某处和乙村某处的管道长度之和的最小值；方案二：供水站建在乙村（线段CD某处），甲村要求管道建设到A处，请你在图①中，画出铺设到点A和点M处的管道长度之和最小的线路图，并求其最小值；方案三：供水站建在甲村（线段AB某处），请你在图②中，画出铺设到乙村某处和点M处的管道长度之和最小的线路图，并求其最小值．综上，你认为把供水站建在何处，所需铺设的管道最短？C C27.（2008年山东省青岛市）已知：如图①，在Rt△ACB中，∠C＝90°，AC＝4cm，BC＝3cm，点P由B出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm/s；连接PQ．若设运动的时间为t（s）（0＜t＜2），解答下列问题：（1）当t为何值时，PQ∥BC？（2）设△AQP的面积为y（2cm），求y与t之间的函数关系式；（3）是否存在某一时刻t，使线段PQ恰好把Rt△ACB的周长和面积同时平分？若存在，求出此时t的值；若不存在，说明理由；（4）如图②，连接PC，并把△PQC沿QC翻折，得到四边形PQP′C，那么是否存在某一时刻t，使四边形PQP′C为菱形？若存在，求出此时菱形的边长；若不存在，说明理由．28.（2008年江苏省南通市）已知双曲线k y x=与直线14y x =相交于A 、B 两点.第一象限上的点M （m ，n ）（在A 点左侧）是双曲线k y x=上的动点.过点B 作BD ∥y 轴于点D.过N （0，－n ）作NC ∥x 轴交双曲线k y x=于点E ，交BD 于点C.（1）若点D 坐标是（－8，0），求A 、B 两点坐标及k 的值. （2）若B 是CD 的中点，四边形OBCE 的面积为4，求直线CM 的解析式.（3）设直线AM 、BM 分别与y 轴相交于P 、Q 两点，且MA ＝pMP ，MB ＝qMQ ，求p －q 的值.29.（2008年江苏省无锡市）一种电讯信号转发装置的发射直径为31km ．现要求：在一边长为30km 的正方形城区选择若干个安装点，每个点安装一个这种转发装置，使这些装置转发的信号能完全覆盖这个城市．问：（1）能否找到这样的4个安装点，使得这些点安装了这种转发装置后能达到预设的要求？（2）至少需要选择多少个安装点，才能使这些点安装了这种转发装置后达到预设的要求？答题要求：请你在解答时，画出必要的示意图，并用必要的计P '图①算、推理和文字来说明你的理由．（下面给出了几个边长为30km 的正方形城区示意图，供解题时选用）压轴题答案1.解：（ 1）由已知得：310c b c =⎧⎨--+=⎩解得c=3,b=2∴抛物线的线的解析式为223y x x =-++(2)由顶点坐标公式得顶点坐标为（1，4）所以对称轴为x=1,A,E 关于x=1对称，所以E(3,0)设对称轴与x 轴的交点为F所以四边形ABDE 的面积=ABO S S ∆+=111()222AO BO BO DF OF EF DF ⋅++⋅+⋅=11113(34)124222⨯⨯++⨯+⨯⨯ =9（3）相似如图，BD=2222112BG DG +=+= BE=22223332BO OE +=+=图1 图2 图3 图4yxD EA BFOG==所以2220BD BE +=,220DE =即：222BD BE DE +=,所以BDE ∆是直角三角形所以90AOB DBE ∠=∠=︒,且2AO BO BD BE ==, 所以AOB DBE ∆∆.2.(1)∵A ，B 两点的坐标分别是A(10，0)和B(8，32)，∴381032OAB tan =-=∠，∴︒=∠60OAB当点A ´在线段AB 上时，∵︒=∠60OAB ，TA=TA ´， ∴△A ´TA 是等边三角形，且A T TP '⊥， ∴)t 10(2360sin )t 10(TP -=︒-=，)t 10(21AT 21AP P A -==='， ∴2TPA )t 10(83TP P A 21S S -=⋅'=='∆， 当A ´与B重合时，AT=AB=60sin 32︒所以此时10t 6<≤.(2)当点A ´在线段AB 的延长线，且点P 在线段AB(不与B 重合)上时，纸片重叠部分的图形是四边形(如图(1)，其中E 是TA ´与CB 的交点)，当点P 与B 重合时，AT=2AB=8，点 又由(1)中求得当A ´与B 重合时，T所以当纸片重叠部分的图形是四边形时，6t 2<<. (3)S 存在最大值 ○1当10t 6<≤时，2)t 10(83S -=， 在对称轴t=10的左边，S 的值随着t 的增大而减小，∴当t=6时，S 的值最大是32.○2当6t 2<≤时，由图○1，重叠部分的面积EB A TP A S S S '∆'∆-= ∵△A ´EB 的高是︒'60sin B A ， ∴23)4t 10(21)t 10(83S 22⨯----=当t=2时，S 的值最大是34；○3当2t 0<<，即当点A ´和点P 都在线段AB 的延长线是(如图○2，其中E 是TA ´与CB 的交点，F 是TP 与CB 的交点)， ∵ETF FTP EFT ∠=∠=∠，四边形ETAB 是等腰形，∴EF=ET=AB=4，∴3432421OC EF 21S =⨯⨯=⋅=综上所述，S 的最大值是34，此时t 的值是2t 0≤<.3.解：（1）Rt A ∠=∠，6AB =，8AC =，10BC ∴=． 点D 为AB 中点，132BD AB ∴==．90DHB A ∠=∠=，B B ∠=∠．BHD BAC ∴△∽△， DH BD AC BC ∴=，3128105BD DH AC BC ∴==⨯=． （2）QR AB ∥，90QRC A ∴∠=∠=．C C ∠=∠，RQC ABC ∴△∽△， ABT E COP FRQ QCAB BC∴=，10610y x -∴=，即y 关于x 的函数关系式为：365y x =-+． （3）存在，分三种情况：①当PQ PR =时，过点P 作PM QR ⊥于M ，则QM RM =．1290∠+∠=，290C ∠+∠=，1C ∴∠=∠．84cos 1cos 105C ∴∠===，45QM QP ∴=， 1364251255x ⎛⎫-+ ⎪⎝⎭∴=，185x ∴=． ②当PQ RQ =时，312655x -+=， 6x ∴=．③当PR QR =时，则R 为PQ 中垂线上的点， 于是点R 为EC 的中点，11224CR CE AC ∴===．tan QR BAC CR CA ==， 366528x -+∴=，152x ∴=．综上所述，当x 为185或6或152时，PQR △为等腰三角形． 4.解：（1）∵MN ∥BC ，∴∠AMN =∠B ，∠∴ △AMN ∽ △ABC ． ∴ AM AN ABAC=，即43x AN =．∴ AN ＝43x ． (2)分ABCD ERPH QM 2 1 HQA BCD E R PHQB图 1∴S=2133248MNP AMN S S x x x ∆∆==⋅⋅=．（0＜x＜4） ……………3分（2）如图2，设直线BC 与⊙O 相切于点D ，连结AO ，OD ，则AO =OD =21MN ．在Rt △ABC 中，BC由（1）知 △AMN ∽ △ABC ．∴ AM MN AB BC=，即45x MN =．∴ 54MN x =，∴ 58OD x =． (5)分过M 点作MQ ⊥BC 于Q ，则58MQ OD x ==． 在Rt△BMQ 与Rt△BCA 中，∠B 是公共角， ∴ △BMQ ∽△BCA ． ∴ BMQM BCAC=．∴ 55258324xBM x ⨯==，25424AB BM MA x x =+=+=．∴x ＝4996．∴ 当x ＝4996时，⊙O 与直线B C 相切． (7)分（3）随点M 的运动，当P AP ，则O 点为AP 的中点．∵MN ∥BC ，∴∠AMN =∠B ，∠AOM ∴ △AMO ∽ △ABP ． ∴12AMAO ABAP ==．AM ＝MB ＝2．故以下分两种情况讨论：BD 图 2QBP 图 3① 当0＜x ≤2时，2Δ83x S y PMN ==．∴当x＝2时，2332.82y =⨯=最大 (8)分② 当2＜x ＜4时，设PM ，PN 分别交BC 于E ，F ． ∵四边形AMPN 是矩形， ∴PN ∥AM ，PN ＝AM ＝x ． 又∵MN ∥BC ，∴ 四边形MBFN 是平行四边形． ∴FN ＝BM ＝4－x ． ∴ ()424PF x x x =--=-． 又△PEF ∽ △ACB ．∴ 2PEF ABC S PF AB S ∆∆⎛⎫= ⎪⎝⎭．∴()2322PEF S x ∆=-．……………………………………………… 9分 MNP PEFy S S ∆∆=-＝()222339266828x x x x --=-+-．……………………10分当2＜x ＜4时，29668y x x =-+-298283x ⎛⎫=--+ ⎪⎝⎭． ∴当83x =时，满足2＜x＜4，2y =最大． (11)分综上所述，当83x =时，y 值最大，最大值是2． …………………………12分P 图 45.解：（1）（-4，-2）；（-m,-k m）(2) ①由于双曲线是关于原点成中心对称的，所以OP=OQ,OA=OB,所以四边形APBQ 一定是平行四边形 ②可能是矩形，mn=k 即可不可能是正方形，因为Op 不能与OA 垂直.解：（1）作BE ⊥OA ， ∴ΔAOB 是等边三角形 ∴BE=OB ·sin60o=∴B(∵A(0,4),设AB 的解析式为4y kx =+,所以42+=,解得k =,的以直线AB 的解析式为（2）由旋转知，AP=AD,∠PAD=60o,∴ΔAPD 是等边三角形，PD=PA==6.解：（1）作BE ⊥OA ，∴ΔAOB 是等边三角形∴BE=OB ·sin60o=B(∵A(0,4),设AB 的解析式为4y kx =+,所以42+=,解得k =, 以直线AB的解析式为43y x =-+ （2）由旋转知，AP=AD,∠PAD=60o, ∴ΔAPD是等边三角形，PD=PA==如图，作BE ⊥AO,DH ⊥OA,GB ⊥DH,显然ΔGBD 中∠GBD=30°∴GD=12BD=2,DH=GH+GD=2+2,∴32,OH=OE+HE=OE+BG=37222+=∴,72)(3)设OP=x,则由（2）可得D(,22x x +)若ΔOPD 的面积为：13(2)224x x +=解得：3x -=所以P(3-,0)7.解:(1)①,BG DE BG DE =⊥………………………………………………………………2分②,BG DE BG DE=⊥仍然成立 ……………………………………………………1分在图（2）中证明如下∵四边形ABCD 、四边形ABCD 都是正方形 ∴BC CD =，CG CE =， 090BCD ECG ∠=∠= ∴BCG DCE ∠=∠…………………………………………………………………1分 ∴BCG DCE ∆≅∆（SAS ）………………………………………………………1分∴BG DE =CBG CDE ∠=∠又∵BHC DHO ∠=∠090CBG BHC ∠+∠= ∴090CDE DHO ∠+∠=∴090DOH ∠= ∴BG DE ⊥…………………………………………………………………………1分（2）BG DE⊥成立，BG DE=不成立 …………………………………………………2分简要说明如下∵四边形ABCD 、四边形CEFG 都是矩形，且AB a =，BC b =，CG kb =，CE ka =(a b ≠，0k >) ∴BC CG bDC CE a==，090BCD ECG ∠=∠= ∴BCG DCE ∠=∠∴BCG DCE ∆∆………………………………………………………………………1分∴CBG CDE ∠=∠又∵BHC DHO ∠=∠090CBG BHC ∠+∠= ∴090CDE DHO ∠+∠=∴090DOH ∠= ∴BG DE ⊥……………………………………………………………………………1分（3）∵BG DE ⊥∴22222222BE DG OB OE OG OD BD GE +=+++=+ 又∵3a =，2b =，k =12∴222222365231()24BD GE +=+++=………………………………………………1分 ∴22654BE DG +=………………………………………………………………………1分 8.解：（1）①2AB =……………………………………………………………………………2分842OA ==，4OC =，S梯形OABC=12 ……………………………………………2分②当42<<t 时，直角梯形OABC 被直线l 扫过的面积=直角梯形OABC 面积－直角三角开DOE 面积2112(4)2(4)842S t t t t =--⨯-=-+-…………………………………………4分（2）存在……………………………………………………………………………………1分123458(12,4),(4,4),(,4),(4,4),(8,4)3P P P P P ---…（每个点对各得1分）……5分对于第（2）题我们提供如下详细解答（评分无此要求）.下面提供参考解法二：①以点D 为直角顶点，作1PP x ⊥轴Rt ODE ∆在中，2OE OD =∴，设2OD b OE b==，.1Rt ODE Rt PPD ∆≈∆，（图示阴影）4b ∴=，28b =，在上面二图中分别可得到P 点的生标为P （－12，4）、P （－4，4）E 点在0点与A 点之间不可能；② 以点E 为直角顶点同理在②二图中分别可得P 点的生标为P （－83，4）、P （8，4）E 点在0点下方不可能. 以点P 为直角顶点同理在③二图中分别可得P 点的生标为P （－4，4）（与①情形二重合舍去）、P （4，4），E 点在A 点下方不可能.综上可得P 点的生标共5个解，分别为P （－12，4）、P （－4，4）、P （－83，4）、P （8，4）、P （4，4）．下面提供参考解法二：以直角进行分类进行讨论（分三类）： 第一类如上解法⑴中所示图22P DE y x b ∠=+为直角：设直线：，D 此时（-b,o)，E(O,2b)的中点坐标为b (-,b)2，直线DE 的中垂线方程：1()22by b x -=-+，令4y =得3(8,4)2bP -DE =即=2332640b b -+=解得121883b b P P ==∴=3b，将之代入（-8，4）（4，4)、22(4,4)P -； 第二类如上解法②中所示图22E DE y x b ∠=+为直角：设直线：，D 此时（-b,o)，E(O,2b)，直线PE 的方程：122y x b =-+，令4y =得(48,4)P b -．由已知可得PE DE ==22(28)b b =-解之得 ，123443b b P P ==∴=，将之代入（4b-8，4）（8，4)、48(,4)3P - 第三类如上解法③中所示图22D DE y x b ∠=+为直角：设直线：，D 此时（-b,o)，E(O,2b)，直线PD 的方程：1()2y x b =-+，令4y =得(8,4)P b --．由已知可得PD DE ==12544b b P P ==-∴=，将之代入（-b-8，4）（-12，4)、6(4,4)P -（6(4,4)P -与2P 重合舍去）．综上可得P 点的生标共5个解，分别为P （－12，4）、P （－4，4）、P （－83，4）、P （8，4）、P （4，4）．事实上，我们可以得到更一般的结论： 如果得出AB a OC b ==、、OA h =、设b ak -=，则P 点的情形如下9. 10.11.解：（1）设A 地经杭州湾跨海大桥到宁波港的路程为x 千米，由题意得1201023x x +=， ················ 2分解得180x =．A ∴地经杭州湾跨海大桥到宁波港的路程为180千米． ·· 4分（2）1.8180282380⨯+⨯=（元），∴该车货物从A 地经杭州湾跨海大桥到宁波港的运输费用为380元． ······················ 6分 （3）设这批货物有y 车，由题意得[80020(1)]3808320y y y -⨯-+=， ········· 8分 整理得2604160y y -+=，解得18y =，252y =（不合题意，舍去）， ········ 9分∴这批货物有8车． ················ 10分12.解：（1144a a ，，． ·············· 3分（2．5分（无“相等”不扣分有“相等”，比值错给1分（3）设DG x =，在矩形ABCD 中，90B C D ∠=∠=∠=，90HGF ∠=，90DHG CGF DGH ∴∠=∠=-∠，HDG GCF ∴△∽△， 12DG HG CF GF ∴==， 22CF DG x ∴==． ·················· 6分同理BEF CFG ∠=∠．EF FG =，FBE GCF ∴△≌△， 14BF CG a x ∴==-．················· 7分CF BF BC +=，1244x a x a ∴+-=， (8)分解得14x a =．即14DG a =． ·················· 9分（4）2316a ， ··················· 10分2278a -． 12分13.解：（1）分别过D ，C 两点作DG ⊥AB 于点G ，CH ⊥AB 于点H ．……………1分∵AB ∥CD ，∴DG ＝CH ，DG ∥CH ．∴ 四边形DGHC 为矩形，GH ＝CD ＝1．∵DG ＝CH ，AD ＝BC ，∠AGD ＝∠BHC ＝∴△AGD ≌△BHC （HL ）．∴AG ＝BH＝2172-=-GH AB ＝3．………2∵ 在Rt △AGD 中，AG ＝3，AD ＝5， ∴DG ＝4． ∴()174162ABCD S +⨯==梯形．………………………………………………3分（2）∵MN ∥AB ，ME ⊥AB ，NF ⊥AB ， ∴ME ＝NF ，ME ∥NF ． ∴ 四边形MEFN 为矩形． ∵AB ∥CD ，AD ＝BC ， ∴∠A ＝∠B ．∵ME ＝NF ，∠MEA ＝∠NFB ＝90°， ∴△MEA ≌△NFB （AAS ）．∴AE ＝BF ．……………………4分设AE ＝x ，则EF ＝7－2x ．……………5分 ∵∠A ＝∠A ，∠MEA ＝∠DGA ＝90°， ∴△MEA ∽△DGA ． ∴DGME AGAE =．∴ME ＝x 34．…………………………………………………………6分∴6494738)2(7342+⎪⎭⎫ ⎝⎛--=-=⋅=x x x EF ME S MEFN矩形． (8)分ABE F G H ABE FG H当x ＝47时，ME ＝37＜4，∴四边形MEFN 面积的最大值为649．……………9分（3）能． ……………………………………………………………………10分由（2）可知，设AE ＝x ，则EF ＝7－2x ，ME ＝x 34．若四边形MEFN 为正方形，则ME ＝EF ．即 =34x7－2x ．解，得1021=x ．……………………………………………11分∴EF ＝21147272105x -=-⨯=＜4．∴四边形MEFN 能为正方形，其面积为251965142=⎪⎭⎫⎝⎛=MEFNS 正方形．14.解：（1）由题意可知，()(1=+m m m 解，得 m ＝3∴A （3，4），B （6，2）；∴k ＝4×3=12（2）存在两种情况，如图：①当M 点在x 轴的正半轴上，N 点在y 轴的正半轴 上时，设M 1点坐标为（x 1，0），N 1点坐标为（0，y 1）．∵四边形AN 1M 1B 为平行四边形，∴ 线段N 1M 1可看作由线段AB 向左平移3个单位，再向下平移2个单位得到的（也可看作向下平移2个单位，再向左平移3个单位得到的）．由（1）知A 点坐标为（3，4），B 点坐标为（6，2）， ∴N 1点坐标为（0，4－2），即N 1（0，2）； ………………………………5分M 1点坐标为（6－3，0），即M 1（3，0）． ………………………………6分设直线M 1N 1的函数表达式为21+=x k y ，把x ＝3，y ＝0代入，解得321-=k ．∴直线M 1N 1的函数表达式为232+-=x y ． ……………………………………8分②当M 点在x 轴的负半轴上，N 点在y 轴的负半轴上时，设M 2点坐标为（x 2，0），N 2点坐标为（0，y 2）．∵AB ∥N 1M 1，AB ∥M 2N 2，AB ＝N 1M 1，AB ＝M 2N 2， ∴N 1M 1∥M 2N 2，N 1M 1＝M 2N 2．∴ 线段M 2N 2与线段N 1M 1关于原点O 成中心对称． ∴M 2点坐标为（-3，0），N 2点坐标为（0，-2）． ………………………9分设直线M 2N 2的函数表达式为22-=x k y ，把x ＝-3，y ＝0代入，解得322-=k ，∴直线M 2N 2的函数表达式为232--=x y ．所以，直线MN 的函数表达式为232+-=x y 或232--=x y ． (11)分（3）选做题：（9，2），（4，5）．………………………………………………2分 15.解：(1)解法1：根据题意可得：A (-1,0)，B (3,0)；则设抛物线的解析式为)3)(1(-+=x x a y (a ≠0)又点D (0，-3)在抛物线上，∴a (0+1)(0-3)=-3，解之得：a =1∴y =x 2-2x -3 ··············· 3分 自变量范围：-1≤x ≤3 ·········· 4分解法2：设抛物线的解析式为c bx ax y ++=2(a ≠0) 根据题意可知，A (-1,0)，B (3,0)，D (0，-3)三点都在抛物线上∴⎪⎩⎪⎨⎧-==++=+-30390c c b a c b a ，解之得：⎪⎩⎪⎨⎧-=-==321c b a∴y =x 2-2x -3 ········· 3分 自变量范围：-1≤x ≤3 ···· 4分(2)设经过点C “蛋圆”的切线CE 交x 轴于点E ，连结CM ，在Rt △MOC 中，∵OM =1，CM =2，∴∠CMO =60°,OC =3在Rt △MCE 中，∵OC =2，∠CMO =60°，∴ME =4∴点C 、E 的坐标分别为(0，3)，(-3,0) ··6分∴切线CE 的解析式为3x3y +=······· 8分(3)为：y =kx -3(k ≠即16.解：（1）6OP t =-，3OQ t =+．（2）当1t =时，过D 点作1DD OA ⊥，交OA 于1D ，如图1， 则53DQ QO ==，43QC =，1CD ∴=，(13)D ∴，． （3）①PQ 能与AC 平行． 若PQ AC ∥，如图2，则OP OAOQ OC=，即66233t t -=+，149t ∴=，而703t ≤≤， 149t ∴=．②PE 不能与AC 垂直．若PE AC ⊥，延长QE 交OA 于F ，如图3， 则23335t QF OQAC OC +==．23QF t⎫∴=+⎪⎭．21)1)3t =+．又Rt Rt EPF OCA △∽△，PE OCEF OA∴=， 63261)3t t -∴=⎛⎫+ ⎪⎝⎭，3.45t ∴≈，而703t ≤≤， 图1t ∴不存在．17.解：（1）直线y =x 轴交于点A ，与y 轴交于点C ．(10)A ∴-，，(0C ，················· 1分点A C ，都在抛物线上，∴抛物线的解析式为2y x =········· 3分 ∴顶点1F ⎛ ⎝⎭ (4)分（2）存在 ····················· 5分1(0P ······················ 7分2(2P······················ 9分（3）存在 ···················· 10分 理由： 解法一：延长BC 到点B '，使B C BC '=，连接B F '交直线AC 于点M ，则点M 就是所求的点．············· 11分 过点B '作B H AB '⊥于点H ．B点在抛物线233y x x =-(30)B ∴，在Rt BOC △中，tan 3OBC ∠=，30OBC ∴∠=，BC =x在Rt BB H'△中，12B H BB''==6BH H'==，3OH∴=，(3B'∴--，········12分设直线B F'的解析式为y kx b=+3k bk b⎧-=-+⎪∴⎨=+⎪⎩解得kb⎧=⎪⎪⎨⎪=⎪⎩62y x∴=-··················13分yy x⎧=-⎪∴⎨=-⎪⎩解得377xy⎧=⎪⎪⎨⎪=-⎪⎩37M⎛∴⎝⎭，∴在直线AC上存在点M，使得MBF△的周长最小，此时377M⎛-⎝⎭，．··················14分解法二：过点F作AC的垂线交y轴于点H，则点H为点F关于直线AC的对称点．连接BH交AC于点M，则点M过点F作FG y⊥轴于点G，则OB FG∥，BC FH∥90BOC FGH∴∠=∠=，BCO FHG∠=∠同方法一可求得(30)B，．在Rt BOC△中，tan3OBC∠=，30OBC∴∠=，可求得3GH GC==，GF∴为线段CH的垂直平分线，可证得CFH△为等边三角形，AC∴垂直平分FH．x图10即点H 为点F 关于AC的对称点．0H ⎛∴ ⎝⎭····· 12分设直线BH 的解析式为y kx b =+，由题意得03k b b =+⎧⎪⎨=⎪⎩解得k b ⎧=⎪⎪⎨⎪=⎪⎩y ∴=·················· 13分y y ⎧=⎪∴⎨⎪=⎩解得377x y ⎧=⎪⎪⎨⎪=-⎪⎩37M ⎛∴ ⎝⎭ ∴在直线AC上存在点M ，使得MBF △的周长最小，此时377M ⎛- ⎝⎭，． 118.解：（1）点E 在y 轴上 ·············· 1分 理由如下：连接AO ，如图所示，在Rt ABO △中，1AB =，BO =，2AO ∴= 1sin 2AOB ∴∠=，30AOB ∴∠= 由题意可知：60AOE ∠=点B 在x 轴上，∴点E 在y 轴上． ··········· 3分 （2）过点D 作DM x ⊥轴于点M1OD =，30DOM ∠=∴在Rt DOM △中，12DM =，2OM =点D 在第一象限，∴点D 的坐标为12⎫⎪⎪⎝⎭， ················ 5分由（1）知2EO AO ==，点E 在y 轴的正半轴上∴点E 的坐标为(02)，∴点A的坐标为( ················ 6分抛物线2y ax bx c =++经过点E ，由题意，将(A，122D ⎛⎫⎪ ⎪⎝⎭，代入22y ax bx =++中得32131242a a ⎧-+=⎪⎨++=⎪⎩解得899a b ⎧=-⎪⎪⎨⎪=-⎪⎩∴所求抛物线表达式为：28299y x x =--+ ······· 9分（3）存在符合条件的点P ，点Q ． ········· 10分 理由如下：矩形ABOC 的面积3ABBO ==∴以O B P Q ，，，为顶点的平行四边形面积为由题意可知OB 为此平行四边形一边， 又3OB =OB ∴边上的高为2 ················· 11分依题意设点P 的坐标为(2)m ， 点P在抛物线28299y x x =--+上 解得，10m =，28m =-1(02)P ∴，，22P ⎛⎫⎪ ⎪⎝⎭以O B P Q ，，，为顶点的四边形是平行四边形，PQ OB ∴∥，PQ OB == ∴当点1P 的坐标为(02)，时，点Q的坐标分别为1(Q，2Q ；当点2P的坐标为2⎛⎫ ⎪ ⎪⎝⎭时，点Q的坐标分别为328Q ⎛⎫- ⎪⎪⎝⎭，428Q ⎛⎫⎪ ⎪⎝⎭． ····· 14分（以上答案仅供参考，如有其它做法，可参照给分） 19.解：（1）在2334y x =-+中，令0y =12x ∴=，22x =-(20)A ∴-，，(20)B ， (1)又点B 在34y x b =-+上BC ∴的解析式为3342y x =-+ （2）由23343342y x y x ⎧=-+⎪⎪⎨⎪=-+⎪⎩，得11194x y =-⎧⎪⎨=⎪⎩2220x y =⎧⎨=⎩ ········· 4分914C ⎛⎫∴- ⎪⎝⎭，，(20)B ，4AB ∴=，94CD = ·················· 5分 1994242ABCS ∴=⨯⨯=△ ·················· 6分（3）过点N 作NP MB ⊥于点PBNP BEO ∴△∽△ ··················· 7分 BN NP BE EO∴= ····················· 8分由直线3342y x =-+可得：302E ⎛⎫ ⎪⎝⎭，∴在BEO △中，2BO =，32EO =，则52BE = 25322t NP∴=，65NP t ∴= ················· 9分 2312(04)55S t t t =-+<< (10)分 2312(2)55S t =--+·················· 11分此抛物线开口向下，∴当2t =时，125S =最大∴当点M 运动2秒时，MNB △的面积达到最大，最大为125．20.解：（1）如图，过点B 作BD ⊥OA 于点D. 在Rt △ABD 中， ∵∣AB ∣=∠∴∣BD ∣=∣AB ∣·sin ∠OAB=又由勾股定理，得∴∣OD ∣=∣OA ∣-∣AD ∣=10-6=4.∵点B 在第一象限，∴点B 的坐标为（4，3）.……3分 设经过O(0,0)、C （4，-3）、A(10,0)三点的抛物线的函数表达式为y=ax 2+bx(a ≠0).由1,164381001005.4a ab a b b ⎧=⎪+=-⎧⎪⇒⎨⎨+=⎩⎪=-⎪⎩。

经典竞赛几何题之令狐文艳创作

经典竞赛几何题之令狐文艳创作

绝密★启用前令狐文艳2018年05月17日张朋松的初中数学组卷试卷副标题考试范围：xxx；考试时间：100分钟；命题人：xxx题号一总分得分注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上第Ⅰ卷（选择题）请点击修改第I卷的文字说明评卷人得分一．解答题（共50小题）1．已知△ABC是等边三角形，D是BC边上的一个动点（点D 不与B，C重合）△ADF是以AD为边的等边三角形，过点F作BC的平行线交射线AC于点E，连接BF．（1）如图1，求证：△AFB≌△ADC；（2）请判断图1中四边形BCEF的形状，并说明理由；（3）若D点在BC 边的延长线上，如图2，其它条件不变，请问（2）中结论还成立吗？如果成立，请说明理由．2．在△ABC中，AH⊥BC于H，D，E，F分别是BC，CA，AB的中点（如图所示）．求证：∠DEF=∠HFE．3．在△ABC中，∠B=60°，∠A，∠C的角平分线AE，CF相交于点O，（1）如图1，若AB=BC，求证：OE=OF；（2）如图2，若AB≠BC，试判断线段OE与OF是否相等，并说明理由．4．如图，在△ABC中，BD是∠ABC的平分线，在△ABC外取一点E，使得∠EAB=∠ACB，AE=DC，并且线段ED与线段AB相交，交点记为K，问线段EK与DK有怎样的大小关系？并说明理由．5．已知如图，AC=BC，∠C=90°，∠A的平分线AD交BC于D，过B作BE垂直AD于E，求证：BE=AD．6．如图，已知AB=AC，∠BAC=60°，∠BDC=120°，求证：AD=BD+CD．7．如图△ABC，D是△ABC内的一点，延长BA至点E，延长DC 至点F，使得AE=CF，G，H，M分别为BD，AC，EF的中点，如果G，H，M三点共线，求证：AB=CD．8．如图，在正方形ABCD中，取AD，CD的边的中点E，F，连接CE，BF交于点G，连接AG，试判断AG与AB是否相等，并说明理由．9．如图，设点M是等腰Rt△ABC的直角边AC的中点，AD⊥BM 于E，AD交BC于D．求证：∠AMB=∠CMD（请用两种不同的方法证明）10．如图，在四边形ABCD中，AD=BC，E、F分别是DC及AB 的中点，射线FE与AD及BC的延长线分别交于点H及G．试猜想∠AHF与∠BGF的关系，并给出证明．提示：若猜想不出∠AHF与∠BGF的关系，可考虑使四边形ABCD为特殊情况．如果给不出证明，可考虑下面作法，连结AC，以F为中心，将△ABC旋转180°，得到△ABP．11．如图，D为△ABC中线AM的中点，过M作AB、AC边的垂线，垂足分别为P、Q，过P、Q分别作DP、DQ的垂线交于点N．（1）求证：PN=QN；（2）求证：MN⊥BC．12．在△ABC中，D为AB的中点，分别延长CA、CB到点E、F，使DE=DF，过E、F分别作CA、CB的垂线相交于P，设线段PA、PB的中点分别为M、N．求证：①△DEM≌△DFN；②∠PAE=∠PBF．13．如图：已知AB∥DC，∠BAD和∠ADC的平分线相交于点E，过点E的直线分别交AB、DC于B、C两点．猜想线段AD、AB、DC之间的数量关系，并证明．14．如图，已知△ABC中，AB=BC=CA，D、E、F分别是AB、BC、CA的中点，G是BC上一点，△DGH是等边三角形．求证：EG=FH．15．已知如图，CD是RT△ABC斜边上的高，∠A的平分线交CD于H，交∠BCD的平分线于G，求证：HF∥BC．16．已知：如图，在四边形ABCD中，AD∥BC，∠ABC=90°．点E是CD的中点，过点E作CD的垂线交AB于点P，交CB的延长线于点M．点F在线段ME上，且满足CF=AD，MF=MA．（1）若∠MFC=120°，求证：AM=2MB；（2）试猜想∠MPB与∠FCM数量关系并证明．17．如图，在△ABC中AC＞BC，E、D分别是AC、BC上的点，且∠BAD=∠ABE，AE=BD．求证：∠BAD=∠C．18．已知A，C，B在同一条直线上，△ACE，△BCF都是等边三角形，BE交CF于N，AF交CE于M，MG⊥CN，垂足为G．求证：CG=NG．19．如图所示，在△ABC中，∠ABC=2∠C，AD为BC边上的高，延长AB到E点，使BE=BD，过点D、E引直线交AC于点F，请判定AF与FC的数量关系，并证明之．20．如图，△ABC是边长为l的等边三角形，△BDC是顶角∠BDC=120°的等腰三角形，以D为顶点作一个60°角，角的两边分别交AB于M，交AC于N，连接MN，形成一个三角形，求证：△AMN的周长等于2．21．已知如图，在四边形ABCD中，AC平分∠BAD，CE⊥AB于E，且AE=（AB+AD），求证：∠B与∠D互补．22．如图，已知△ABC中，∠A=90°，AB=AC，∠1=∠2，CE⊥BD于E．求证：BD=2CE．23．AD是△ABC的角平分线，M是BC的中点，FM∥AD交AB的延长线于F，交AC于E．（1）求证：CE=BF；（2）探索线段CE与AB+AC之间的数量关系，并证明．24．如图，AD是△ABC的中线，AB=AE，AC=AF，∠BAE=∠FAC=90°．判断线段AD与EF数量和位置关系．25．如图，四边形ABCD中，BC=DC，对角线AC平分∠BAD，且AB=21，AD=9，BC=DC=10，求AC的长．26．如图，已知线段AB的同侧有两点C、D满足∠ACB=∠ADB=60°，∠ABD=90°﹣∠DBC．求证：AC=AD．27．如图，正方形ABDE和ACFG是以△ABC的AB、AC为边的正方形，P、Q为它们的中心，M是BC的中点，试判断MP、MQ 在数量和位置是有什么关系？并证明你的结论．28．如图，在△ABC中，AD为∠BAC的平分线，BP⊥AD，垂足为P．已知AB=5，BP=2，AC=9．试说明∠ABC=3∠ACB．29．如图，在△ABC中，∠B=90°，M为AB上一点，使得AM=BC，N为BC上一点，使得CN=BM，连接AN，CM相交于点P，试求∠APM的度数．30．已知如图，在△ABC中，∠B=60°，AD、CE是△ABC的角平分线，并且它们交于点O，（1）求：∠AOC的度数；（2）求证：AC=AE+CD．31．如图，已知△ABC中AB＞AC，P是角平分线AD上任一点，求证：AB﹣AC＞PB﹣PC．32．如图，在△ABC中，D为BC的中点，点E、F分别在边AC、AB上，并且∠ABE=∠ACF，BE、CF交于点O．过点O作OP ⊥AC，OQ⊥AB，P、Q为垂足．求证：DP=DQ．33．如图已知△ABC中，AB=AC，∠ABD=60°，且∠ADB=90°﹣∠BDC，求证：AB=BD+DC．34．如图，点C在线段AB上，DA⊥AB，EB⊥AB，FC⊥AB，且DA=BC，EB=AC，FC=AB，∠AFB=51°，求∠DFE度数．35．如图，已知△ABC是等腰直角三角形，∠C=90°，点M、N 分别是边AC和BC的中点，点D在射线BM上，且BD=2BM．点E在射线NA上，且NE=2NA，求证：BD⊥DE．36．如图，△ABC中，BD为∠ABC的平分线；（1）若∠A=100°，∠C=50°，求证：BC=BA+AD；（2）若∠BAC=100°，∠C=40°，求证：BC=BD+AD．37．如图，△ABC中，∠ACB=90°，∠CAD=30°，AC=BC=AD．求证：BD=CD．38．如图所示，在△ABF中，已知BC=CE=EF，∠BAC=∠CAD=∠DAE=45°，求的值．39．如图，已知过△ABC的顶点A，在∠BAC内部任意作一条射线，过B、C分别作此射线的垂线段BD、CE，M为BC边中点．求证：MD=ME．40．已知，如图，在正方形ABCD中，O是对角线的交点，AF 平分∠BAC，DH⊥AF于点H，交AC于点G，DH延长线交AB于点E求证：．41．已知：在△ABC中，∠A=90°，AB=AC，D为AC中点，AE ⊥BD于E，延长AE交BC于F，求证：∠ADB=∠CDF．42．如图，在△ABC中，AB=AC，延长AB到D，使BD=AB，E为AB中点，连接CE、CD，求证：CD=2EC．43．如图，在△ABC中，BD=CD，AG平分∠DAC，BF⊥AG，垂足为H，与AD交于E，与AC交于F，过点C的直线CM交AD的延长线于M，且∠EBD=∠MCD，AC=AM．求证：DE=CF．44．如图，BE、CF是△ABC的高，它们相交于点O，点P在BE 上，Q在CF的延长线上且BP=AC，CQ=AB，（1）求证：△ABP≌△QCA．（2）AP和AQ的位置关系如何，请给予证明．45．如图，在△ABC中，∠ACB=90°，CD⊥AB于D，AF平分∠BAC交CD于E，交BC于F，EG∥AB交BC于G，说明BG=CF的理由．46．在△ABC中，∠ACB=90°，D是AB上一点，M是CD的中点，若∠AMD=∠BMD，求证：∠CDA=2∠ACD．47．如图，已知：四边形ABCD中，AD=BC，E、F分别是DC、AB的中点，直线EF分别与BC、AD的延长线相交于G、H．求证：∠AHF=∠BGF．48．如图，在等腰直角△ABC中，AD=AE，AF⊥BE交BC于点F，过F作FG⊥CD交BE延长线于G，求证：BG=AF+FG．49．已知△ABC，∠C=90°，AC=BC．M为AC中点，延长BM到D，使MD=BM；N为BC中点，延长NA到E，使AE=NA，连接ED，求证：ED⊥BD．50．如图，在△ABC中，∠BAC=90°，AB=AC，D是△ABC内一点，且∠DAC=∠DCA=15°，求证：BD=BA．2018年05月17日张朋松的初中数学组卷参考答案与试题解析一．解答题（共50小题）1．已知△ABC是等边三角形，D是BC边上的一个动点（点D不与B，C重合）△ADF是以AD为边的等边三角形，过点F作BC的平行线交射线AC于点E，连接BF．（1）如图1，求证：△AFB≌△ADC；（2）请判断图1中四边形BCEF的形状，并说明理由；（3）若D点在BC 边的延长线上，如图2，其它条件不变，请问（2）中结论还成立吗？如果成立，请说明理由．【分析】（1）利用有两条边对应相等并且夹角相等的两个三角形全等即可证明△AFB≌△ADC；（2）四边形BCEF是平行四边形，因为△AFB≌△ADC，所以可得∠ABF=∠C=60°，进而证明∠ABF=∠BAC，则可得到FB∥AC，又BC∥EF，所以四边形BCEF是平行四边形；（3）易证AF=AD，AB=AC，∠FAD=∠BAC=60°，可得∠FAB=∠DAC，即可证明△AFB≌△ADC；根据△AFB≌△ADC可得∠ABF=∠ADC，进而求得∠AFB=∠EAF，求得BF∥AE，又BC∥EF，从而证得四边形BCEF是平行四边形．【解答】证明：（1）∵△ABC和△ADF都是等边三角形，∴AF=AD，AB=AC，∠FAD=∠BAC=60°，又∵∠FAB=∠FAD﹣∠BAD，∠DAC=∠BAC﹣∠BAD，∴∠FAB=∠DAC，在△AFB和△ADC中，，∴△AFB≌△ADC（SAS）；（2）由①得△AFB≌△ADC，∴∠ABF=∠C=60°．又∵∠BAC=∠C=60°，∴∠ABF=∠BAC，∴FB∥AC，又∵BC∥EF，∴四边形BCEF是平行四边形；（3）成立，理由如下：∵△ABC和△ADF都是等边三角形，∴AF=AD，AB=AC，∠FAD=∠BAC=60°，又∵∠FAB=∠BAC﹣∠FAE，∠DAC=∠FAD﹣∠FAE，∴∠FAB=∠DAC，在△AFB和△ADC中，，∴△AFB≌△ADC（SAS）；∴∠AFB=∠ADC．又∵∠ADC+∠DAC=60°，∠EAF+∠DAC=60°，∴∠ADC=∠EAF，∴∠AFB=∠EAF，∴BF∥AE，又∵BC∥EF，∴四边形BCEF是平行四边形．【点评】本题考查了等边三角形的性质、全等三角形的判定和性质以及平行四边形的判定，熟练掌握性质、定理是解题的关键．2．在△ABC中，AH⊥BC于H，D，E，F分别是BC，CA，AB的中点（如图所示）．求证：∠DEF=∠HFE．【分析】EF为中位线，所以EF∥BC，又因为∠HFE和∠FHB，∠DEF和∠CDE 分别为一组平行线的对角，所以相等；转化成求证∠FHB=∠CDE．【解答】证明：∵E，F分别为AC，AB的中点，∴EF∥BC，根据平行线定理，∠HFE=∠FHB，∠DEF=∠CDE；同理可证∠CDE=∠B，∴∠DEF=∠B．又∵AH⊥BC，且F为AB的中点，∴HF=BF，∴∠B=∠BHF，∴∠HFE=∠B=∠DEF．即∠HFE=∠DEF．【点评】本题考查了三角形的中位线定理，平行四边形的判定，直角三角形中斜边的中线为斜边边长的一半．3．在△ABC中，∠B=60°，∠A，∠C的角平分线AE，CF相交于点O，（1）如图1，若AB=BC，求证：OE=OF；（2）如图2，若AB≠BC，试判断线段OE与OF是否相等，并说明理由．【分析】（1）可证明△ACF≌△CAE，再由角平分线的性质得出∠OAC=∠OCA，从而得出OE=OF；（2）过点O作OH⊥AC，OM⊥BC，ON⊥AB，垂足分别为H，M，N，连接OB．根据角平分线的性质定理以及逆定理可推得点O在∠B的平分线上，从而得出∠OBN=∠OBM=30°，由已知得出∠OEM=∠OFN，能证明Rt△OFN≌Rt △OEM，则OE=OF成立．【解答】证明：（1）∵∠B=60°，AB=BC，∴∠A=∠C=60°，∵AECF分别平分∠A，∠C，∴∠OAC=∠OCA=30°，∴OA=OC，△ACF≌△CAE（ASA），∴AE=CF，∴OE=OF；（2）过点O作OH⊥AC，OM⊥BC，ON⊥AB，垂足分别为H，M，N，连接OB．∵点O在∠A，∠C的平分线上，∴ON=OH，OH=OM，从而OM=ON，∴点O在∠B的平分线上（1分）∴∠OBN=∠OBM=30°，ON=OM （2分）又∠OEM=∠B+∠A=60°+∠A∠OFN=∠A+∠C=（∠A+∠C）+∠A=（180°﹣60°）+∠A=60°+∠A．∴∠OEM=∠OFN．（2分）∴Rt△OFN≌Rt△OEM（AAS），（1分）∴OE=OF．（1分）【点评】本题考查了全等三角形的判定和性质以及角平分线的性质，注意一题多解以及方法的简单性．4．如图，在△ABC中，BD是∠ABC的平分线，在△ABC外取一点E，使得∠EAB=∠ACB，AE=DC，并且线段ED与线段AB相交，交点记为K，问线段EK与DK有怎样的大小关系？并说明理由．【分析】首先作出EI⊥AB，DH⊥AB，证明△EAI≌△DCF再得出DH=DF进而得出△EKI≌△DKH即可证出．【解答】解：结论：EK=DK．（2分）理由：过点E作EI⊥AB，过点D作DH⊥AB于H，DF⊥BC于F，在△EAI和△DCF中∵，∴△EAI≌△DCF（AAS），（2分）∴EI=DF，（2分）∵BD是∠ABC的平分线，∴DH=DF，（2分）∴DH=EI，在△EKI和△DKH中，∵，∴△EKI≌△DKH（AAS），（2分）∴EK=DK．（2分）【点评】此题主要考查了三角形全等证明方法，根据题意作出EI⊥AB，DH⊥AB，从而利于全等证明是解决问题的关键．5．已知如图，AC=BC，∠C=90°，∠A的平分线AD交BC于D，过B作BE垂直AD于E，求证：BE=AD．【分析】延长AC、BE交于点M，易证得△ACD≌△BCM，可得AD=BM①，可证得△AEM≌△AEB，可得EM=BE，即BM=2BE②，由①②即可得结论．【解答】解：如图，延长AC、BE交于点M，∵∠A的平分线AD，BE垂直AD于E，∴∠MAE=∠BAE，∠AEM=∠AEB=90°，∵AE=AE，∴△AEM≌△AEB（ASA），∴EM=BE，即BM=2BE①；∵∠A的平分线AD，AC=BC，∠C=90°，∴∠CAD=∠DAB=22.5°，∠ABC=45°，∵BE垂直AD于E，∴∠DAB+∠ABC+∠DBE=90°，即∠DBE=22.5°，∴∠CAD=∠DBE，又∵AC=BC，且∠ACB=∠BCM=90°，∴△ACD≌△BCM（ASA），∴AD=BM②；由①②得AD=2BE，即BE=AD．【点评】本题主要考查了全等三角形的判定和性质，涉及到等腰直角三角形的性质、三角形内角和定理等知识点，正确作出辅助线是解题的关键．6．如图，已知AB=AC，∠BAC=60°，∠BDC=120°，求证：AD=BD+CD．【分析】先延长DB，使BE=CD，连接AE，BC，根据已知条件得出A，B，D，C四点共圆，得出∠ACB=∠ADE，再根据等边三角形的性质得出△ABC是等边三角形，在△ABE和△ACD中，根据SAS得出△ABE≌△ACD，得出△ADE是等边三角形，得出AD=DE，再根据DE=BD+BE，即可证出AD=BD+CD．【解答】解：延长DB，使BE=CD，连接AE，BC，∵∠BAC+∠ACD+∠BDC+∠ABD=360°，∠BAC=60°，∠BDC=120°，∴∠ABD+∠ACD=180°，∴A，B，D，C四点共圆，∴∠ACB=∠ADE，∵∠ABD+∠ABE=180°，∴∠ABE=∠ACD，∵AB=AC，∴△ABC是等边三角形，∴∠ACB=60°，∴∠ADE=60°，在△ABE和△ACD中，，∴△ABE≌△ACD（SAS），∴AE=AD，∴△ADE是等边三角形，∴AD=DE，∵DE=BD+BE，∴AD=BD+CD．【点评】此题考查了全等三角形的判定与性质，用到的知识点是等边三角形的性质，全等三角形的判定与性质和三角形内角和定理，关键是根据题意作出辅助线．7．如图△ABC，D是△ABC内的一点，延长BA至点E，延长DC至点F，使得AE=CF，G，H，M分别为BD，AC，EF的中点，如果G，H，M三点共线，求证：AB=CD．【分析】由三角形的中位线得，MS∥AE，MS=AE，HS∥CF，HS=CF，由已知得HS=SM，从而得出∠SHM=∠SMH，则得出∠TGH=∠THG，GT=TH，最后不难看出AB=CD．【解答】证明：取BC中点T，AF的中点S，连接GT，HT，HS，SM，∵GHM分别为BD，AC，EF的中点，∴MS∥AE，MS=AE，HS∥CF，HS=CF，∵GT∥CD，HT∥AB，GT=CD，HT=AB，∴GT∥HS，HT∥SM，∴∠SHM=∠TGH，∠SMH=∠THG，∴∠TGH=∠THG，∴GT=TH，∴AB=CD．【点评】本题考查了三角形的中位线定理以及平行线的性质．8．如图，在正方形ABCD中，取AD，CD的边的中点E，F，连接CE，BF交于点G，连接AG，试判断AG与AB是否相等，并说明理由．【分析】延长CE、BA交于P，易证△CDE≌△BCF，可得∠CFB=∠DEC，即可求得CE⊥BF，进而可以求证△PAE∽△PBC，可得PA=AB，根据直角三角形斜边中线等于斜边一半性质即可解题．【解答】解：延长CE、BA交于P，∵在△CDE和△BCF中，，∴△CDE≌△BCF；（SAS）∴∠CFB=∠DEC，∵∠FCG+∠DEC=90°，∴CE⊥BF，∴△PAE∽△PBC，==，∴A是PB的中点，即AB=PB，∵RT△BPG中，AG=PB．∴AG=AB．【点评】本题考查了全等三角形的判定，考查了全等三角形对应角相等的性质，本题中求证△CDE≌△BCF是解题的关键．9．如图，设点M是等腰Rt△ABC的直角边AC的中点，AD⊥BM于E，AD交BC于D．求证：∠AMB=∠CMD（请用两种不同的方法证明）【分析】法（1）先延长AD至F，使得CF⊥AC，得出∠ABM=∠DAC，再根据AB=AC，CF⊥AC，得出△ABM≌△CAF，从而证出∠BMA=∠F，AM=CF，再根据所给的条件得出△FCD≌△MCD，即可得出∠AMB=∠F=∠CMD；法（2）先作∠BAC的平分线交BM于N，得出∠ABN=∠CAE，再根据∠BAN=∠C=45°，AB=AC，证出△BAN≌△ACD，得出AN=CD，证出△NAM≌△DCM，即可得出∠AMB=∠CMD．【解答】证明：法（1）如图，延长AD至F，使得CF⊥AC，∵AB⊥AC，AD⊥BM，∴∠ABM=∠DAC，又∵AB=AC，CF⊥AC，∴△ABM≌△CAF，∴∠BMA=∠F，AM=CF，∵∠BCA=∠BCF=45°，AM=CM=CF，DC=DC，∴△FCD≌△MCD，法（2）AD交BM于E，作∠BAC的平分线交BM于N，∵AE⊥BM，BA⊥AC，∴∠ABN=∠CAE，∵∠BAN=∠C=45°，AB=AC，∴△BAN≌△ACD．∴AN=CD，∵∠NAM=∠C=45°，AM=MC∴△NAM≌△DCM，∴∠AMB=∠CMD．【点评】此题考查了解等腰直角三角形；解题的关键是根据题意画出图形，再根据解等腰直角三角形的性质和相似三角形的判断与性质进行解答即可．10．如图，在四边形ABCD中，AD=BC，E、F分别是DC及AB的中点，射线FE与AD及BC的延长线分别交于点H及G．试猜想∠AHF与∠BGF的关系，并给出证明．提示：若猜想不出∠AHF与∠BGF的关系，可考虑使四边形ABCD为特殊情况．如果给不出证明，可考虑下面作法，连结AC，以F为中心，将△ABC旋转180°，得到△ABP．【分析】方法一：连AC，取其中点为M，连EM和FM，根据三角形的中位线平行于第三边并且等于第三边的一半可得EM∥AD，2EM=AD，同理FM∥BC，2FM=BC，再根据两直线平行，内错角相等可得∠AHF=∠MEF，两直线平行，内错角相等可得∠BGF=∠MFE，从而得证；方法二：作法，连结AC，以F为中心，将△ABC旋转180°，得到△ABP，根据独角戏互相平分的四边形的平行四边形可得APBC是平行四边形，根据平行四边形对边相等可得AP=BC=AD，连结AP，根据等边对等角可得∠APD=∠ADP，根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥DP根据两直线平行，同位角相等可得∠AHF=∠ADP，根据两边互相平行的两个角相等或互补可得∠BGF=∠APD，然后等量代换即可得证．【解答】答：∠AHF=∠BGF．证明：方法一：连AC，取其中点为M，连EM和FM，∵EM是△ACD的中位线，∴EM∥AD，2EM=AD，同理FM∥BC，2FM=BC，∴EM=FM，∴∠MEF=∠MFE，∵∠AHF=∠MEF，∠BGF=∠MFE，∴∠AHF=∠BGF；方法二：作法，连结AC，以F为中心，将△ABC旋转180°，得到△ABP，∵F是AB的中点，∴APBC是平行四边形，∴AP=BC=AD，连结AP，则∠APD=∠ADP，∵EF是△CDP的中位线，∴EF∥DP，∴∠AHF=∠ADP，∵GF∥DP，GB∥AP，∴∠BGF=∠APD，∴∠AHF=∠BGF．【点评】本题考查了三角形的中位线定理，等腰三角形的判定与性质，难点在于作辅助线构造出三角形的中位线．11．如图，D为△ABC中线AM的中点，过M作AB、AC边的垂线，垂足分别为P、Q，过P、Q分别作DP、DQ的垂线交于点N．（1）求证：PN=QN；（2）求证：MN⊥BC．【分析】（1）要证明PN=QN，只有证明这两条线段所在的三角形全等就可以了，连接DN，利用斜边直角边对应相等的两个三角形全等就可以了．（2）△BPM和△CQM是直角三角形，由条件知道MB=CM，取BM、CM的中点S、T，连接PS、QT可以得到PS=QT，利用角的关系证明∠SPN=∠TQN，再证明△SPN≌△TQN，从而得到NS=NT，利用等腰三角形的三线合一的性质证明MN⊥BC．【解答】证明：（1）方法一：连接DN∵D为△ABC中线AM的中点∴AD=MD，MB=CM∵MP⊥AB，MQ⊥AC∴∠APM=∠AQM=90°∴△APM、△AMQ是直角三角形∴PD=AM，QD=AM∴PD=QD∴Rt△DPN≌Rt△DQN（HL）∴NP=PQ；方法二：∵MP⊥AB，MQ⊥AC∴∠APM=∠AQM=90°，所以∠APM+∠AQM=180°，所以四边形APMQ为圆内接四边形．∵D为AM的中点，∴PD，DQ为以D为圆心的四边形APMQ内接圆的半径．∵PN⊥PD，QN⊥QD，∴PN，NQ为圆的两条切线，∴PN=NQ．（2）取BM、CM的中点S、T，连接SP、SN、TQ、TN∴SP=BM=MC=TQ∴∠SPN=90°﹣∠BPS﹣∠NPM=90°﹣∠B﹣∠DPA=90°﹣∠B﹣∠BAM=90°﹣∠AMC=90°﹣∠DMQ﹣∠QMT=90°﹣∠DQM﹣∠MQT=∠TQN∴△SPN≌△TQN∴SN=TN∵SM=TM∴NM⊥BC【点评】本题考查了全等三角形的判定与性质，直角三角形斜边上的中线等于斜边的一半，等腰三角形的判定与性质．12．在△ABC中，D为AB的中点，分别延长CA、CB到点E、F，使DE=DF，过E、F分别作CA、CB的垂线相交于P，设线段PA、PB的中点分别为M、N．求证：①△DEM≌△DFN；②∠PAE=∠PBF．【分析】①要证△DEM≌△DFN，由D、M、N分别是AB、AP、BP的中点，所以DM=BP，DN=AP，再有过E、F分别作CA、CB的垂线相交于P，所以EM=AP=DN，FN=BP=DM．又DE=DF所以△DEM≌△DFN．②由①得∠EMD=∠FND，由∠AMD=∠BND=∠APB所以∠AME=∠BNF，那么∠PAE=（180°﹣∠AME），∠PBF=（180°﹣∠BNF），即∠PAE=∠PBF．【解答】证明：①如图，在△ABP中，∵D、M、N分别是AB、AP、BP的中点，∴DM=BP，DN=AP，又∵PE⊥AE，BF⊥PF∴EM=AP=DN，FN=BP=DM，∵DE=DF∴△DEM≌△DFN（SSS）；②∵由①结论△DEM≌△DFN可知∠EMD=∠FND，∵DM∥BP，DN∥AP，∴∠AMD=∠BND=∠APB，∴∠AME=∠BNF又∵PE⊥AE，BF⊥PF，∴△AEP和△BFP都为直角三角形，又M，N分别为斜边PA与PB的中点，∴AM=EM=AP，BN=NF=BP，∴∠MAE=∠MEA，∠NBF=∠NFB，∴∠PAE=（180°﹣∠AME），∠PBF=（180°﹣∠BNF）．即∠PAE=∠PBF，【点评】此题考查了线段之间的关系，和全等三角形的判定和性质，同学们应该熟练掌握．13．如图：已知AB∥DC，∠BAD和∠ADC的平分线相交于点E，过点E的直线分别交AB、DC于B、C两点．猜想线段AD、AB、DC之间的数量关系，并证明．【分析】在AD上截取AF=AB，连接EF，根据SAS证△BAE≌△FAE，推出∠B=∠EFA，求出∠C=∠EFD，证△CDE≌△FDE，推出DC=DF，即可得出答案．【解答】答：AD=AB+DC，证明：在AD上截取AF=AB，连接EF，∵AE平分∠BAF，∴∠BAE=∠FAE，∵在△BAE和△FAE中∴△BAE≌△FAE（SAS），∴∠B=∠EFA，∵AB∥DC，∴∠B+∠C=180°，∵∠EFD+∠EFA=180°，∴∠C=∠EFD，∵DE平分∠CDA，∴∠CDE=∠FDE，∵在△CDE和△FDE中∴△CDE≌△FDE（AAS），∴DC=DF，∴AD=AF+DF=AB+DC．【点评】本题考查了全等三角形的性质和判定，平行线的性质，角平分线定义等知识点的应用，关键是能正确作辅助线．14．如图，已知△ABC中，AB=BC=CA，D、E、F分别是AB、BC、CA的中点，G是BC上一点，△DGH是等边三角形．求证：EG=FH．【分析】连接DE、DF，根据三角形中位线定理及等边三角形的性质，可证明△DEG≌△DFH，即可得结论．【解答】证明：连接DE、DF，（如图）∵D、E、F是各边中点，∴DE平行且等于AC，DF平行且等于BC，∵AB=BC=CA，∴∠A=∠B=∠C=60°，∴DE=DF，∠EDF=∠DFA=∠C=60°∵已知等边△DHG，∴DG=DH，∠HDG=60°=∠EDF，∴∠EDF﹣∠FDG=∠HDG﹣∠FDG，即∠1=∠2，∴△DEG≌△DFH（SAS），∴FH=EG．【点评】本题考查了三角形全等的判定及性质，涉及到三角形中位线定理、等边三角形的性质等知识点，熟练掌握三角形全等判定方法是解题的关键．15．已知如图，CD是RT△ABC斜边上的高，∠A的平分线交CD于H，交∠BCD的平分线于G，求证：HF∥BC．【分析】根据角平分线性质作辅助线连接FE，进而证得HCEF是菱形从而证得．【解答】证明：连接FE，∵CD是Rt△ABC斜边上的高，∴∠A=∠DCB，又∵AE平分∠A，CF平分∠BCD，∴∠DCF=∠DAE，又∵∠AHD=∠CHE，∠ADH=90度，∴∠CGE=90度，在三角形ACF中，AE是高，中线，角平分线，∴CF⊥HE，CG=FG，∴CH=FH，CE=EF，∴CF是△CHE的高，中线，角平分线，∴CH=CE，∴CH=HF=EF=CE，∴四边形HCEF是菱形，∴HF∥BC．【点评】本题考查了角平分线性质以及其应用，问题有一定难度．16．已知：如图，在四边形ABCD中，AD∥BC，∠ABC=90°．点E是CD的中点，过点E作CD的垂线交AB于点P，交CB的延长线于点M．点F在线段ME上，且满足CF=AD，MF=MA．（1）若∠MFC=120°，求证：AM=2MB；（2）试猜想∠MPB与∠FCM数量关系并证明．【分析】（1）连接MD，根据线段垂直平分线上的点到两端点的距离相等可得MD=MC，然后利用“边边边”证M明△MFC与△MAD全等，根据全等三角形对应角相等可得∠MAD=∠MFC，根据两直线平行，同旁内角互补求出∠BAD，然后求出∠BAM=30°，然后根据直角三角形30°角所对的直角边等于斜边的一半证明；（2）根据全等三角形对应角相等和轴对称的性质可得∠BMP=∠FMD=∠DMA，然后用∠BMP表示出∠FCM，再根据直角三角形两锐角互余列式整理即可得解．【解答】（1）证明：连接MD，∵点E是CD的中点，ME⊥D，∴MD=MC，在△MFC与△MAD中，，∴△MFC≌△MAD（SSS），∴∠MAD=∠MFC=120°，∵AD∥BC，∠ABC=90°，∴∠BAD=180°﹣∠ABC=180°﹣90°=90°，∴∠BAM=∠MAD﹣∠BAD=120°﹣90°=30°，∵∠ABM=90°，∴AM=2MB；（2）解：2∠MPB+∠FCM=180°．理由如下：由（1）可知∠BMP=∠FMD=∠DMA，∵∠FCM=∠ADM=∠DMC=2∠BMP，∴∠BMP=∠FCM，∵∠ABC=90°，∴∠MPB+∠BMP=90°，∴∠MPB+∠FCM=90°，∴2∠MPB+∠FCM=180°．【点评】本题考查了全等三角形的判定与性质，线段垂直平分线上的点到两端点的距离相等的性质，直角三角形两锐角互余，熟记各性质并作辅助线构造出全等三角形是解题的关键．17．如图，在△ABC中AC＞BC，E、D分别是AC、BC上的点，且∠BAD=∠ABE，AE=BD．求证：∠BAD=∠C．【分析】作∠OBF=∠OAE交AD于F，由已知条件用“ASA”可判定△AOE≌△BOF，所以AE=BF，再有条件AE=BD得BF=BD，所以∠BDF=∠BFD，再利用三角形的外角关系证得∠BOF=∠C，又因为∠BOF=∠BAD+∠ABE=2∠BAD，所以：∠BAD=∠C．【解答】证明：作∠OBF=∠OAE交AD于F，∵∠BAD=∠ABE，∴OA=OB．又∠AOE=∠BOF，∴△AOE≌△BOF（ASA）．∴AE=BF．∵AE=BD，∴BF=BD．∴∠BDF=∠BFD．∵∠BDF=∠C+∠OAE，∠BFD=∠BOF+∠OBF，∴∠BOF=∠C．∵∠BOF=∠BAD+∠ABE=2∠BAD，∴∠BAD=∠C，【点评】本题考查了全等三角形的判断和性质，常用的判断方法为：SAS，SSS，AAS，ASA．常用到的性质是：对应角相等，对应边相等．在证明中还要注意图形中隐藏条件的挖掘如：本题中的对顶角∠AOE=∠BOF．18．已知A，C，B在同一条直线上，△ACE，△BCF都是等边三角形，BE交CF于N，AF交CE于M，MG⊥CN，垂足为G．求证：CG=NG．【分析】先证△ACF与△ECB全等，得到∠AFC=∠ABE，再证△FMC≌△BNC 得到MC=MN，有条件MG垂直于NC而得到结论．【解答】证明：∵△ACE，△BCF都是等边三角形，∴AC=EC，FC=BC，∠ACE=∠BCF=60°，∴∠ECN=60°，∠BCE=∠ACF，∴△ACF≌△ECB，∴∠AFC=∠ABE，∵∠FCM=∠BCN=60°，CF=CB，∴△FMC≌△BNC，∴CM=CN，∵∠ECN=60°，∴△CNMN是等边三角形，∴CM=MN，∵MG⊥NC，∴GC=GN．【点评】本题考查了等边三角形的性质，通过两次全等得到MC=MN，通过MG垂直于NC得到结论．19．如图所示，在△ABC中，∠ABC=2∠C，AD为BC边上的高，延长AB到E 点，使BE=BD，过点D、E引直线交AC于点F，请判定AF与FC的数量关系，并证明之．【分析】根据等边对等角可得∠E=∠BDE，然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠ABC=2∠BDE，从而求出∠C=∠BDE，再求出∠C=∠CDF，然后根据等角对等边求出DF=FC，再根据等角的余角相等求出∠CAD=∠ADF，根据等角对等边求出DF=AF，即可得到AF=FC．【解答】解：AF=FC．理由如下：∵BE=BD，∴∠E=∠BDE，∵∠ABC=∠E+∠BDE=2∠BDE，∠ABC=2∠C，∴∠C=∠BDE，又∵∠BDE=∠CDF，∴∠C=∠CDF，∴DF=FC，∵AD为BC边上的高，∴∠CDF+∠ADF=∠ADC=90°，∠C+∠CAD=180°﹣90°=90°，∴∠CAD=∠ADF，∴DF=AF，∴AF=FC．【点评】本题考查了等腰三角形的判定与性质，等角的余角相等的性质，熟记性质与判定并准确识图是解题的关键．20．如图，△ABC是边长为l的等边三角形，△BDC是顶角∠BDC=120°的等腰三角形，以D为顶点作一个60°角，角的两边分别交AB于M，交AC于N，连接MN，形成一个三角形，求证：△AMN的周长等于2．【分析】可在AC延长线上截取CM1=BM，得Rt△BDM≌Rt△CDM1，得出边角关系，再求解△MDN≌△M1DN，得MN=NM1，再通过线段之间的转化即可得出结论．【解答】证明：如图，在AC延长线上截取CM1=BM，∵△ABC是等边三角形，△BDC是顶角∠BDC=120°的等腰三角形，∴∠ABC=∠ACB=60°，∠DBC=∠DCB=30°，∴∠ABD=∠ACD=90°，∴∠DCM1=90°，∵BD=CD，∵在△BDM和△CDM1中，，∴△BDM≌△CDM1（SAS），得MD=M1D，∠MDB=∠M1DC，∴∠MDM1=120°﹣∠MDB+∠M1DC=120°，∴∠NDM1=60°，在△MDN和△M1DN中，∵，∴△MDN≌△M1DN（SAS），∴MN=NM1，故△AMN的周长=AM+MN+AN=AM+AN+NM1=AM+AM1=AB+AC=2．【点评】本题主要考查了全等三角形的判定及性质问题，能够通过线段之间的转化进而求解一些简单的结论．21．已知如图，在四边形ABCD中，AC平分∠BAD，CE⊥AB于E，且AE=（AB+AD），求证：∠B与∠D互补．【分析】可在AB上截取AF=AD，可得△ACF≌△ACD，得出∠AFC=∠D，再由线段之间的关系AE=（AB+AD）得出BC=CF，进而通过角之间的转化即可得出结论．【解答】证明：在AB上截取AF=AD，连接CF，∵AC平分∠BAD，∴∠BAC=∠CAD，又AC=AC，∴△ACF≌△ACD（SAS），∴AF=AD，∠AFC=∠D，∵AE=（AB+AD），∴EF=BE，又∵CE⊥AB，∴BC=FC，∴∠CFB=∠B，∴∠B+D=∠CFB+∠AFC=180°，即∠B与∠D互补．【点评】本题主要考查了全等三角形的判定及性质以及等腰三角形的判定及性质问题，能够熟练运用三角形的性质求解一些简单的计算、证明问题．22．如图，已知△ABC中，∠A=90°，AB=AC，∠1=∠2，CE⊥BD于E．求证：BD=2CE．【分析】延长CE、BA交于F，根据角边角定理，证明△BEF≌△BEC，进而得到CF=2CE的关系．再证明∠ACF=∠1，根据角边角定理证明△ACF≌△ABD，得到BD=CF，至此问题得解．【解答】证明：如图，延长CE、BA交于F．∵CE⊥BD，∴∠BEF=∠BEC=90°，∴∠1=∠2，在△BEF和△BEC中，∴△BEF≌△BEC（ASA），∴EF=EC，∴CF=2CE，∵∠BAC=90°，∵CE⊥BD，∴∠ACF=∠1，在△ACF和△ABD中，∴△ACF≌△ABD（ASA），∴BD=CF，∴BD=2CE．【点评】本题考查全等三角形的判定与性质．解决本题主要是恰当添加辅助线，构造全等三角形，将所求问题转化为全等三角形内边间的关系来解决．23．AD是△ABC的角平分线，M是BC的中点，FM∥AD交AB的延长线于F，交AC于E．（1）求证：CE=BF；（2）探索线段CE与AB+AC之间的数量关系，并证明．【分析】（1）延长CA交FM的平行线BG于G点，利用平行线的性质得到BM=CM、CE=GE，从而证得CE=BF；（2）利用上题证得的EA=FA、CE=BF，进一步得到AB+AC=AB+AE+EC=AB+AF+EC=BF+EC=2EC．【解答】（1）证明：延长CA交FM的平行线BG于G点，∠G=∠CAD、∠GBA=∠BAD∵AD平分∠BAC，∴AG=AB，∵FM∥AD∴∠F=∠BAD、∠FEA=∠DAC∵∠BAD=∠DAC，∴∠F=∠FEA，∴EA=FA，∴GE=BF，∴M为BC边的中点，∴BM=CM，∵EM∥GB，∴CE=GE，∴CE=BF；（2）AB+AC=2EC．证明：∵EA=FA、CE=BF，∴AB+AC=AB+AE+EC=AB+AF+EC=BF+EC=2EC．【点评】本题考查了三角形的中位线定理，解题的关键是正确地构造辅助线，另外题目中还考查了平行线等分线段定理．24．如图，AD是△ABC的中线，AB=AE，AC=AF，∠BAE=∠FAC=90°．判断线段AD与EF数量和位置关系．【分析】猜想：EF=2AD，EF⊥AD．证明：延长AD到M，使得AD=DM，连接MC，延长DA交EF于N，易证BD=CD，即可证明△ABD≌△MCD，可得AB=MC，∠BAD=∠M，即可求得∠EAF=∠MCA，即可证明△AEF≌△CMA，可得EF=AM，∠CAM=∠F，即可解题．【解答】解：EF=2AD，EF⊥AD．证明：延长AD到M，使得AD=DM，连接MC，延长DA交EF于N，∴AD=DM，AM=2AD，∵AD是△ABC的中线，∴BD=CD，在△ABD和△MCD中，，∴△ABD≌△MCD，（SAS）∴AB=MC，∠BAD=∠M，∵AB=AE，∴AE=MC，∵AE⊥AB，AF⊥AC，∴∠EAB=∠FAC=90°，∵∠FAC+∠BAC+∠EAB+∠EAF=360°，∴∠BAC+∠EAF=180°，∵∠CAD+∠M+∠MCA=180°，∴∠CAD+∠BAD+∠MCA=180°，即∠BAC+∠MCA=180°，∴∠EAF=∠MCA．在△AEF和△CMA中，，∴△AEF≌△CMA，∴EF=AM，∠CAM=∠F，∴EF=2AD；∵∠CAF=90°，∴∠CAM+∠FAN=90°，∵∠CAM=∠F，∴∠F+∠FAN=90°，∴∠ANF=90°，∴EF⊥AD．【点评】本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，本题中求证△ABD≌△MCD和△AEF≌△CMA是解题的关键．25．如图，四边形ABCD中，BC=DC，对角线AC平分∠BAD，且AB=21，AD=9，BC=DC=10，求AC的长．【分析】作辅助线构建直角三角形，求证△CFD≌△CEB，即可得DF=EB，即可求得DF，根据DF求CF，根据CF、AF求AC．【解答】解：过C作CE⊥AB，CF⊥AD，∴∠CEA=90°，∠CFD=90°，∵AC平分∠BAD，∴CF=CE（角平分线上的点到角的两边的距离相等），又∵BC=DC，∴△CFD≌△CEB（HL），∴DF=EB，同理可得△ACF≌△ACE，∴AF=AE，∴AD+DF=AB﹣BE，即9+DF=21﹣BE，。

沪科版初中数学目录之令狐文艳创作

沪科版初中数学目录之令狐文艳创作

沪科版初中数学目录令狐文艳备注：七年级上册：1-5七年级下册：6-11八年级上册：12-17八年级下册：18-22九年级上册：23-25九年级下册：26-28第1章有理数1.1 正数和负数1.2 数轴1.3 有理数的大小1.4 有理数的加减1.5 有理数的乘除1.6 有理数的乘方1.7 近似数第2章整式加减2.1 用字母表示数2.2 代数式2.3 整式加减第3章一次方程与方程组3.1 一元一次方程及其解法3.2 二元一次方程组3.3 消元解决方程组3.4 用一次方程（组）解决问题第4章直线与角4.1 多彩的几何图形4.2 线段、射线、直线4.3 线段的长短比较4.4 角的表示与度量4.5 角的大小比较4.6 作线段与角第5章数据处理5.1 数据的收集5.2 数据的整理5.3 统计图的选择5.4 从图表中获取信息第6章实数6.1 平方根立方根6.2 实数第7章一一次不等与不等式组7.1 不等及其基本质7.2 一元次不等式7.3 一元次不等式组第8章整乘除与因分解8.1 幂的算8.2 整式法8.3平方差式与完全方公式8.4 整式法第12章平面直角坐标系12.1 平面上点的坐标12.2 图形在坐标系中的平移第13章一次函数13.1 函数13.2 一次函数-13.3 一次函数与一次方程、一次不等式13.4 二元一次方程组的图象解法第14章三角形中的边角关系14.1 三角形中的边角关系14.2 命题与证明第15章全等三角形15.1 全等三角形15.2 三角形全等的判定第16章轴对称图形与等腰三角形16.1 轴对称图形16.2 线段的垂直平分线16.3 等腰三角形16.4 角的平分线第17章勾股定理17.1 勾股定理17.2 勾股定理的逆定理第18章二次根式18.1 二次根式18.2 二次根式的运算――――（）第19章一元二次方程19.1 一元二次方程19.2一元二次方程的解法19.3一元二次方程的根的判别式19.4一元二次方程的根与系数的关系19.5 一元二次方程的应用第20章四边形20.1 多边形内角和20.2平行四边形20.3 矩形菱形正方形20.4 梯形第21章据的集中势21.1 平均21.2 中位与众数21.3从部看总体第22章数据的离程度22.1极差22.2 方差标准差第23章二次函数反比例函数23.1 二次数23.2 二次数y=ax^2图象和性质23.3二次第25章解直角三角形25.1 锐角三角函数25.2 锐角三角函数值25.3 解直角三角形及其应用第26章圆26.1 旋转26.2 圆的对称性26.3 圆的确定26.4 圆周角26.5 直线与圆的位置关系26.6 三角形的内切圆26.7 圆与圆的位置关系26.8 正多边形与圆26.9 弧长与扇形面积第27章投影与视图27.1 投影27.2 三视图第28章概率初步28.1 随机事件28.2 等可能情形下的概率计算28.3 用频数估计概率。

动点问题题型方法归纳之令狐文艳创作

动点问题题型方法归纳之令狐文艳创作

动点问题题型方法归纳令狐文艳动态几何特点----问题背景是特殊图形，考查问题也是特殊图形，所以要把握好一般与特殊的关系；分析过程中，特别要关注图形的特性（特殊角、特殊图形的性质、图形的特殊位置。

）动点问题一直是中考热点，近几年考查探究运动中的特殊性：等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。

下面就此问题的常见题型作简单介绍，解题方法、关键给以点拨。

一、三角形边上动点1、（2009年齐齐哈尔市）直线364y x =-+与坐标轴分别交于A B 、两点，动点P Q 、同时从O 点出发，同时到达A 点，运动停止．点Q 沿线段OA 运动，速度为每秒1个单位长度，点P 沿路线O →B →A 运动．（1）直接写出A B 、两点的坐标；（2）设点Q 的运动时间为t 秒，OPQ △的面积为S ，求出S 与t 之间的函数关系式；（3）当485S =时，求出点P 的坐标，并直接写出以点O P Q 、、为顶点的平行四边形的第四个顶点M 的坐标．图 B图 B 图 提2）问按点P 到拐点B 所有时间分段分类； 第（3）问是分类讨论：已知三定点O 、P 、Q ，探究第四点构成平行四边形时按已知线段身份不同分类-----①OP 为边、OQ 为边，②OP 为边、OQ 为对角线，③OP 为对角线、OQ 为边。

然后画出各类的图形，根据图形性质求顶点坐标。

2、（2009年衡阳市）如图，AB 是⊙O 的直径，弦BC=2cm ，∠ABC=60º．（1）求⊙O 的直径；（2）若D 是AB 延长线上一点，连结CD ，当BD 长为多少时，CD 与⊙O 相切；（3）若动点E 以2cm/s 的速度从A 点出发沿着AB 方向运动，同时动点F 以1cm/s 的速度从B 点出发沿BC 方向运动，设运动时间为)20)((<<t s t ，连结EF ，当t 为何值时，△BEF 为直角三角形．注意：第（3）问按直角位置分类讨论3、（2009重如图，已知抛物线(1)20)y a x a =-+≠经过点(2)A -，0，抛物线的顶点为D ，过O 作射线OM AD ∥．过顶点D 平行于x 轴的直线交射线OM 于点C ，B 在x 轴正半轴上，连结BC ．（1）求该抛物线的解析式；（2）若动点P 从点O 出发，以每秒1个长度单位的速度沿射线OM 运动，设点P 运动的时间为()t s ．问当t 为何值时，四边形DAOP 分别为平行四边形？直角梯形？等腰梯形？（3）若OC OB =，动点P 和动点Q 分别从点O 和点B 同时出发，分别以每秒1个长度单位和2个长度单位的速度沿OC 和BO 运动，当其中一个点停止运动时另一个点也随之停止运动．设它们的运动的时间为t ()s ，连接PQ ，当t 为何值时，四边形BCPQ 的面积最小？并求出最小值及此时PQ 的长．DAB=60° 当面积最大时，四边形BCPQ 的面积最小。

中考数学易错之令狐文艳创作

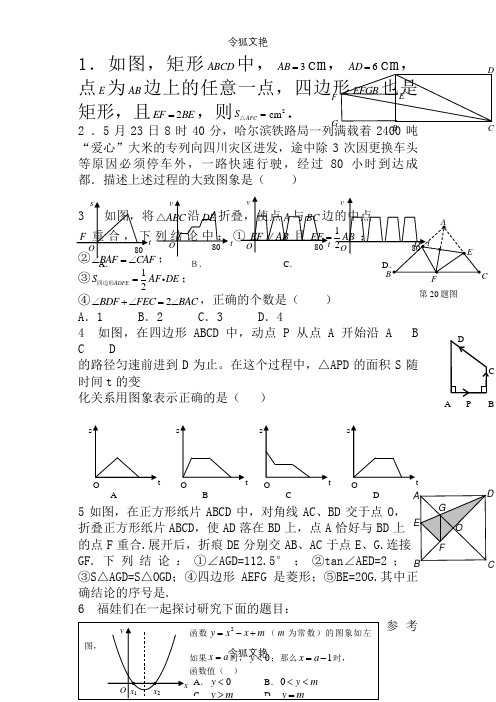
中考数学易错之令狐文艳创作

1．如图，矩形ABCD 中，3AB =cm ，6AD =cm ，点E 为AB 边上的任意一点，四边形EFGB 也是矩形，且2EF BE =，则AFCS =△2cm ． 2 ．5月23日8时40分，哈尔滨铁路局一列满载着2400吨“爱心”大米的专列向四川灾区进发，途中除3次因更换车头等原因必须停车外，一路快速行驶，经过80小时到达成都．描述上述过程的大致图象是（ ） ③12ADFE S AF DE =四边形； ④2BDF FEC BAC ∠+∠=∠，正确的个数是（ ）A ．1B ．2C ．3D ．44 如图，在四边形ABCD 中，动点P 从点A 开始沿C D的路径匀速前进到D 为止。

在这个过程中，△APD 的面积S 随时间t 的变化关系用图象表示正确的是（ ）5如图，在正方形纸片ABCD 中，对角线AC 、折叠正方形纸片ABCD ，使AD 落在BD 上，点A 的点F 重合.展开后，折痕DE 分别交AB 、AC GF.下列结论：①∠AGD=112.5°；③S△AGD=S△OGD；④四边形AEFG 是菱形；⑤BE=2OG.其中正确结论的序号是.6 福娃们在一起探讨研究下面的题目：参考 DCE F GBtA ． Ｂ．C ．F 第20题图令狐文艳下面福娃们的讨论，请你解该题，你选择的答案是（ ）贝贝：我注意到当 0x =时，0y m =>．晶晶：我发现图象的对称轴为12x =．欢欢：我判断出12x a x <<．迎迎：我认为关键要判断1a -的符号． 妮妮：m 可以取一个特殊的值．7 正方形ABCD 中，E 是BC 边上一点，以E 为圆心、EC 为半径的半圆与以A 为圆心，AB 为半径的圆弧外切，则sin EAB ∠的值为（ ） A ．43B ．34C ．45D ．358 一个函数的图象如图，给出以下结论： ①当0x =时，函数值最大；②当02x <<时，函数y 随x 的增大而减小； ③存在001x <<，当0x x =时，函数值为0． 其中正确的结论是（ ）A ．①② B ．①③ C ．②③ D ．①②③9．函数2y ax b y ax bx c =+=++和在同一直角坐标系内的图象大致是 （ ）10 如图，水平地面上有一面积为230cm π的扇形AOB ，半径OA=6cm ，且OA 与地面垂直.在没有滑动的情况下，将扇形向右滚动至OB 与地面垂直为止，则O 点移动的距离为（ ）A 、20cm B 、24cm C 、10cm π D 、30cm π11 在Rt △ABC 内有边长分别为,,a b c 的三个正方形，则,,a b c 满足的关系式是（ ）A 、b a c =+B 、b ac =C 、222b a c =+D 、22b a c ==12 古尔邦节，6位朋友均匀地围坐在圆桌旁共度佳节．圆桌半径为60cm ，每人离圆桌的距离均为10cm ，现又来了两名客人，每人向后挪动了相同的距离，再左右调整位置，使8人都坐下，并且8人之间的距离与原来6人之间的距离（即在圆周上两人之间的圆弧的长）相等．设每人向后挪动的距离为x ，令狐文艳根据题意，可列方程（ ）A ．2π(6010)2π(6010)68x +++=B ．2π(60)2π6086x +⨯=C ．2π(6010)62π(60)8x +⨯=+⨯D ．2π(60)82π(60)6x x -⨯=+⨯13 如图，两正方形彼此相邻且内接于半圆，若小正方形的面积为16cm 2，则该半圆的半径为（ ）．A ．(45)+cmB ．9 cmC ．45cmD ．62cm14如图，A B C D ，，，为O 的四等分点，动点P 从圆心O 出发，沿O C D O ---路线作匀速运动，设运动时间为t （s ）．()APB y =∠，则下列图象中表示y 与t 之间函数关系最恰当的是（ ）15 如图，边长为a 的正ABC △内有一边长为b 的内接正DEF △，则AEF △的内切圆半径为．16 如图，⊙O 的半径为2，点A 的坐标为（2，32），直线AB 为⊙O 的切线，B 为切点．则B 点的坐标为A ．⎪⎪⎭⎫ ⎝⎛-5823, B ．()13,- C ．⎪⎭⎫⎝⎛-5954, D ．()31,-17 如图，将边长为1的正三角形OAP 沿x 轴正方向连续翻转2008次，点P 依次落在点1232008P P P P ，，，的位置，则点2008P 的横坐标为．18 如图①，1O ，2O ，3O ，4O 为四个等圆的圆心，A ，B ，C ，D 为切点，请你在图中画出一条直线，将这四个圆分成面积相等的两部分，并说明这条直线经过的两个点A B C DOP Bty 045 90 Dt y 045 90 Aty45 90 Cy 045 90 （第12题）xy O1 1BA1P A O yx（第19题）P1o 2o 3o 4o C B D A第（18）题图①（第19令狐文艳是；如图②，1O ，2O ，3O ，4O ，5O 为五个等圆的圆心，A ，B ，C ，D ，E 为切点，请你在图中画出一条直线，将这五个．．圆．分成面积相等的两部分，并说明这条直线经过的两个点是．19 课题研究小组对附着在物体表面的三个微生物（课题小组成员把他们分别标号为1，2，3）的生长情况进行观察记录．这三个微生物第一天各自一分为二，产生新的微生物（分别被标号为4，5，6，7，8，9），接下去每天都按照这样的规律变化，即每个微生物一分为二，形成新的微生物（课题组成员用如图所示的图形进行形象的记录）．那么标号为100的微生物会出现在（ ） A ．第3天B ．第4天C ．第5天D ．第6天20如图所示，AB 是⊙O 的直径，AD ＝DE ，AE 与BD 交于点C ，则图中与∠BCE 相等的角有A ．2个B ．3个C ．4个D ．5个21.有一个附有进出水管的容器，每单位时间进、出的水量 都是一定的.设从某一时刻开始5分钟内只进水不出水，在接着的2分钟内只出水不进水，又在随后的15分钟内既进水又出水，刚好将该容器注满.已知容器中的水量y 升与时间x 分之间的函数关系如图所示.则在第7分钟时，容器内的水量为升.A.15 B.16 C.17 D.1821.如图，⊙O 1、⊙O 2内切于P 点，连心线和⊙O 1、⊙O 2分别交于A 、B 两点，过P 点的直线与⊙O 1、⊙O 2分别交于C 、D 两点，若∠BPC=60º，AB=2，则CD=.A.1B.2C.21D.41 22.已知:如图所示,抛物线y=ax 2+bx+c 的对称轴为x=-1，与x 轴交于A 、B 两点，交y 轴于点C ，且OB=OC ，则下列结论正确的个数是.①b=2a ②a-b+c>-1 ③0<b 2-4ac<4 ④ac+1=bA.1个B.2个C.3个D.4个E DA CO23.已知:如图,∠ACB=90º,以AC 为直径的⊙O 交AB 于D 点，过D 作⊙O 的切线交BC 于E 点，EF ⊥AB 于F 点，连OE 交DC 于P ，则下列结论:其中正确的有.①BC=2DE ； ②OE ∥AB; ③DE=2PD ；④AC•DF =DE•CD .A.①②③B.①③④C.①②④D.①②③④24 已知:如图，直线MN 切⊙O 于点C ，AB 为⊙O 的直径，延长BA 交直线MN 于M 点，AE ⊥MN ，BF ⊥MN ，E 、F 分别为垂足，BF 交⊙O 于G ，连结AC 、BC ，过点C 作CD ⊥AB ，D 为垂足,连结OC 、CG. 下列结论：其中正确的有.①CD=CF=CE ； ②EF 2=4AE •BF; ③AD •DB=FG •FB ； ④MC •CF=MA •BF. A.①②③ B.②③④ C.①③④ D.①②③④25 如图，M 为⊙O 上的一点,⊙M 与⊙O 相交于A 、 B 两点，P 为⊙O 上任意一点，直线PA 、PB 分别交 ⊙M 于C 、D 两点，直线CD 交⊙O 于E 、F 两点，连结PE 、PF 、BC ，下列结论：其中正确的有.①PE=PF ； ②PE 2=PA ·PC;③EA ·EB=EC ·ED ；④rRBC PB =（其中R 、r 分别为⊙O 、⊙M 的半径）.A.①②③B.①②④C.②④D.①②③④ 1 如图，菱形OABC 中，120A =∠，1OA =，将菱形OABC绕点O 按顺时针方向旋转90，则图中由BB '，B A ''，A C '，CB 围成的阴影部分的面积是．1 9 2D 3B 4B 5（1，4，5）6 C 7D 8 C9 C10 C11 A12 A13C14 C 15)a b - 16D17 2008 18 18．1O ，3O ，如图① （提示：答案不惟一，过31O O 与42O O 交点O 的任意直线都能将四个圆分成面积相等的两部分）；5O ，O ，如图② （提示：答案不惟一，如4AO ，3DO ，2EO ，1CO 等均可）．19 C第（18）题图②• M A BF O GC DE N'（第18题）20 D 25 2π3令狐文艳。

中考数学动点问题专题讲解之令狐文艳创作

中考数学动点问题专题讲解之令狐文艳创作

动点及动图形的专题复习教案令狐文艳所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想：分类思想函数思想方程思想数形结合思想转化思想注重对几何图形运动变化能力的考查从变换的角度和运动变化来研究三角形、四边形、函数图像等图形，通过“对称、动点的运动”等研究手段和方法，来探索与发现图形性质及图形变化，在解题过程中渗透空间观念和合情推理。

选择基本的几何图形，让学生经历探索的过程，以能力立意，考查学生的自主探究能力，促进培养学生解决问题的能力．图形在动点的运动过程中观察图形的变化情况，需要理解图形在不同位置的情况，才能做好计算推理的过程。

在变化中找到不变的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。

二期课改后数学卷中的数学压轴性题正逐步转向数形结合、动态几何、动手操作、实验探究等方向发展．这些压轴题题型繁多、题意创新，目的是考察学生的分析问题、解决问题的能力，内容包括空间观念、应用意识、推理能力等．从数学思想的层面上讲：（1）运动观点；（2）方程思想；（3）数形结合思想；（4）分类思想；（5）转化思想等．研究历年来各区的压轴性试题，就能找到今年中考数学试题的热点的形成和命题的动向，它有利于我们教师在教学中研究对策，把握方向．只的这样，才能更好的培养学生解题素养，在素质教育的背景下更明确地体现课程标准的导向．本文拟就压轴题的题型背景和区分度测量点的存在性和区分度小题处理手法提出自己的观点．函数揭示了运动变化过程中量与量之间的变化规律,是初中数学的重要内容.动点问题反映的是一种函数思想,由于某一个点或某图形的有条件地运动变化,引起未知量与已知量间的一种变化关系,这种变化关系就是动点问题中的函数关系.那么,我们怎样建立这种函数解析式呢?下面结合中考试题举例分析.一、应用勾股定理建立函数解析式)如图1,在半径为6,圆心角为90°的扇形OAB的弧AB上,有一个动点P,PH⊥OA,垂足为H,△OPH的重心为G.(1)当点P在弧AB上运动时,线段GO、GP、GH中,有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度.(2)设PH x=,求y关于x的函数解析式，并写出函数=,GP y的定义域(即自变量x的取值范围).(3)如果△PGH 是等腰三角形,试求出线段PH 的长.解:(1)当点P 在弧AB 上运动时,OP 保持不变,于是线段GO 、GP 、GH 中,有长度保持不变的线段，这条线段是GH=32NH=2132⋅OP=2. (2)在Rt △POH 中, 22236x PH OP OH -=-=, ∴2362121x OH MH -==. 在Rt △MPH 中,.∴y =GP=32MP=233631x + (0<x <6).(3)△PGH 是等腰三角形有三种可能情况:①GP=PH 时,x x =+233631,解得6=x . 经检验,6=x 是原方程的根,且符合题意.②GP=GH 时,2336312=+x ,解得0=x . 经检验,0=x 是原方程的根,但不符合题意.③PH=GH 时,2=x .综上所述,如果△PGH 是等腰三角形,那么线段PH 的长为6或2.二、应用比例式建立函数解析式例2如图2,在△ABC 中,AB=AC=1,点D,E 在直线BC 上运动.设BD=,x CE=y .(1)如果∠BAC=30°,∠DAE=105°,试确定y 与x 之间的函数解H M N G P O A B 图1 x y析式；(2)如果∠BAC 的度数为α,∠DAE 的度数为β,当α,β满足怎样的关系式时,(1)中y 与x 之间的函数解析式还成立?试说明理由.解:(1)在△ABC 中,∵AB=AC,∠BAC=30°,∴∠ABC=∠ACB=75°, ∴∠ABD=∠ACE=105°. ∵∠BAC=30°,∠DAE=105°, ∴∠DAB+∠CAE=75°,又∠DAB+∠ADB=∠ABC=75°,∴∠CAE=∠ADB,∴△ADB ∽△EAC, ∴ACBD CE AB =, ∴11x y =, ∴x y 1=.(2)由于∠DAB+∠CAE=αβ-,又∠DAB+∠ADB=∠ABC=290α-︒,且函数关系式成立,∴290α-︒=αβ-, 整理得=-2αβ︒90.当=-2αβ︒90时,函数解析式x y 1=成立.如 三、应用求图形面积的方法建立函数关系式例4（）如图,在△ABC 中,∠BAC=90°,AB=AC=22,⊙A 的半径为1.若点O 在BC 边上运动(与点B 、C 不重合),设BO=x ,△AOC 的面积为y .(1)求y 关于x 的函数解析式,(2)以点O 为圆心,BO 长为半径作圆O,求当⊙O与⊙A 相切时,A ED C B 图2 A CO 图8 H△AOC 的面积.解:(1)过点A 作AH ⊥BC,垂足为H.∵∠BAC=90°,AB=AC=22, ∴BC=4,AH=21BC=2. ∴OC=4-x . ∵AH OC S AOC ⋅=∆21, ∴4+-=x y (40<<x ).(2)①当⊙O 与⊙A 外切时,在Rt △AOH 中,OA=1+x ,OH=x -2, ∴222)2(2)1(x x -+=+. 解得67=x .此时,△AOC 的面积y =617674=-. ②当⊙O 与⊙A 内切时,在Rt △AOH 中,OA=1-x ,OH=2-x , ∴222)2(2)1(-+=-x x . 解得27=x .此时,△AOC 的面积y =21274=-.综上所述,当⊙O 与⊙A 相切时,△AOC 的面积为617或21.动态几何特点----问题背景是特殊图形，考查问题也是特殊图形，所以要把握好一般与特殊的关系；分析过程中，特别要关注图形的特性（特殊角、特殊图形的性质、图形的特殊位置。

初中数学经典难题(含答案)之令狐文艳创作

初中数学经典难题(含答案)之令狐文艳创作

经典难题（一）令狐文艳1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二）2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1C 2、D 2分别是AA 1、BB 1、CC 1、DD 1求证：四边形A 2B 2C 2D 24、已知：如图，在四边形ABCD 中，ADAB 、CD 的中点，AD 、BC 求证：∠DEN ＝∠F ．经典难题（二）1、已知：△ABC 中，H 外心，且OM ⊥BC 于M ． （1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO 2、设MN 是圆O 外一直线，过O 作OA ⊥MN 的两条直线，交圆于B 、C 及D 、E ，直线AGCEBMN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN DE ，设CD 、EB 分别交MN 于P 、Q 求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 侧作正方形ACDE 和正方形CBFG 求证：点P 到边AB 的距离等于经典难1、如图，四边形ABCD 为正方形，CD 相交于F ．求证：CE ＝CF 2、如图，四边形线EC 交DA 延长线于求证：AE ＝AF 3、设P 是正方形平分∠DCE ．求证：PA ＝PF 4、如图，PC 切圆O 线，AE 、AF 与直线＝AD ．（初三）经典难题（四）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．求：∠APB 的度数．（初二）2、设P 是平行四边形ABCDPDA ．求证：∠PAB ＝∠PCB ．（初二）3、Ptolemy （托勒密）定理：设ABCD 求证：AB ·CD ＋AD ·BC ＝AC ·BD ． （初三）4、平行四边形ABCD 中，设E 、F 分别是点，AE 与CF 相交于P ，且AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 内任一点，l PC ，求证：3≤L ＜2．2、已知：P 是边长为1的正方形ABCDPB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB 3a ，求正方形的边长．4、如图，△ABC中，∠ABC＝∠ACB＝800，D、E分别是AB、AC上的点，∠DCA＝300，∠EBA＝200，求∠BED的度数．经典难题（一）1、2、3、4、经典难题（二）1、2、3、4、E DC BA经典难题（三）1、2、3、 4、 经典难题（四）1、 2、 3、 4、证明：过D 作DQ ⊥AE ，DG ⊥CF,并连接DF 和DE ，如右图所示 则S △ADE =21S ABCD =S △DFC∴21 AE ﹒DQ = 21DG ﹒FC又∵AE=FC,∴DQ=DG,∴PD为∠APC的角平分线，∴∠DPA=∠DPC经典难题（五）1、2、3、3、4、。

河北中考数学题型分析之令狐文艳创作

河北中考数学题型分析之令狐文艳创作

—河北中考数学备考分析令狐文艳一、准确定向1、三部分内容第一部分：数与代数（60分）包括数与式、方程与不等式、函数（一次函数、二次函数、反比例函数）。

第二部分：图形与几何（48分）包括点线面三角形四边形圆等基本图形的性质、尺规作图、视图与投影、图形的变化（对称、平移、旋转）、图形的相似、证明等第三部分：统计与概率（12分）包括抽样与数据分析（三大数据代表、三种统计图）、事件的概率。

2、七大题型1.代数基本题：○1化简求值○2计算○3解方程（组）或小综合2.几何基本题：○1作图+计算○2全等+计算○3圆计算○4解直角三角形3.统计与概率：（1）数据分析：○1统计量○2统计图（2）概率：会画表和树状图（3）组合题（统计与概率组合、与函数等其它知识组合等）4.方程应用题：（加强考察）5.函数两道大题三类：(1)纯函数（2）实际应用（3）与几何知识结合6.几何两道大题两类：(1)几何证明（2）猜想结论+证明7.动态题（数形结合,一般以压轴题出现）(1)图形中的动态变化+函数性质考查(2)在图像中的动态变化（函数图像中动点、动线、动形）（注：后面大题根据难、易程度，题的位置可能发生变化）二、明确考点——近年河北中考试题分析1~18题（填空、选择题）1、题型特点：几乎所有的概念、性质、公式、法则、定理的基本辨别、运用等基础知识、核心与主干内容的基本用法等，以选择填空题的形式出现，与后八道大题相互照应、相互补充，以达突出主干、考查全面的目的。

2、攻克法宝：基础知识，不要死记，理解记忆，必须记死。

（1）实数运算 （2）代数式化简求值 19题特点分析重点：基本运算能力的考查1.解方程（一元一次，二元一次方程组）2.解不等式（组）3.代数式的化简及求值（包括分式）4.数的计算（加减乘除乘方的综合运算）12年（本小题满分8分）计算：|-5|-(2-3)0+6×(13- 12)+(-1)2．09年（本小题满分8• 已知a = 2，b= -1，求 ÷ 的值．2221a b a ab--+1a10年（本小题满分8分）• 解方程： 1211+=-x x 11年（本小题满分8分）20题特点分析属于数形结合题1.能分析简单的几何图形、直角坐标系2.会简单作图后进而基本图形计算。

中考数学压轴题(有答案)之令狐文艳创作

中考数学压轴题(有答案)之令狐文艳创作

中考初中数学压轴题精选（有答案）令狐文艳一．解答题（共30小题）1．（2014•攀枝花）如图，以点P（﹣1，0）为圆心的圆，交x轴于B、C两点（B在C的左侧），交y轴于A、D两点（A 在D的下方），AD=2，将△ABC绕点P旋转180°，得到△MCB．（1）求B、C两点的坐标；（2）请在图中画出线段MB、MC，并判断四边形ACMB的形状（不必证明），求出点M的坐标；（3）动直线l从与BM重合的位置开始绕点B顺时针旋转，到与BC重合时停止，设直线l与CM交点为E，点Q为BE的中点，过点E作EG⊥BC于G，连接MQ、QG．请问在旋转过程中∠MQG的大小是否变化？若不变，求出∠MQG的度数；若变化，请说明理由．2．（2014•苏州）如图，已知l1⊥l2，⊙O与l1，l2都相切，⊙O的半径为2cm，矩形ABCD的边AD、AB分别与l1，l2重合，AB=4cm，AD=4cm，若⊙O与矩形ABCD沿l 1同时向右移动，⊙O的移动速度为3cm/s，矩形ABCD的移动速度为4cm/s，设移动时间为t（s）（1）如图①，连接OA、AC，则∠OAC的度数为_________ °；（2）如图②，两个图形移动一段时间后，⊙O到达⊙O1的位置，矩形ABCD到达A1B1C1D1的位置，此时点O1，A1，C1恰好在同一直线上，求圆心O移动的距离（即OO1的长）；（3）在移动过程中，圆心O到矩形对角线AC所在直线的距离在不断变化，设该距离为d（cm），当d＜2时，求t的取值范围（解答时可以利用备用图画出相关示意图）．3．（2014•泰州）如图，平面直角坐标系xOy中，一次函数y=﹣x+b（b为常数，b＞0）的图象与x轴、y轴分别相交于点A、B，半径为4的⊙O与x轴正半轴相交于点C，与y轴相交于点D、E，点D在点E上方．（1）若直线AB与有两个交点F、G．①求∠CFE的度数；②用含b的代数式表示FG2，并直接写出b的取值范围；（2）设b≥5，在线段AB上是否存在点P，使∠CPE=45°？若存在，请求出P点坐标；若不存在，请说明理由．4．（2014•上海）如图1，已知在平行四边形ABCD中，AB=5，BC=8，cosB=，点P是边BC上的动点，以CP为半径的圆C与边AD交于点E、F（点F在点E的右侧），射线CE与射线BA交于点G．（1）当圆C经过点A时，求CP的长；（2）连接AP，当AP∥CG时，求弦EF的长；（3）当△AGE是等腰三角形时，求圆C的半径长．5．（2014•常州）在平面直角坐标系xOy中，点M（，），以点M为圆心，OM长为半径作⊙M．使⊙M与直线OM的另一交点为点B，与x轴，y轴的另一交点分别为点D，A（如图），连接AM．点P是上的动点．（1）写出∠AMB的度数；（2）点Q在射线OP上，且OP•OQ=20，过点Q作QC垂直于直线OM，垂足为C，直线QC交x轴于点E．①当动点P与点B重合时，求点E的坐标；②连接QD，设点Q的纵坐标为t，△QOD的面积为S．求S与t的函数关系式及S的取值范围．6．（2014•漳州）阅读材料：如图1，在△AOB中，∠O=90°，OA=OB，点P在AB边上，PE⊥OA于点E，PF⊥OB 于点F，则PE+PF=OA．（此结论不必证明，可直接应用）（1）【理解与应用】如图2，正方形ABCD的边长为2，对角线AC，BD相交于点O，点P在AB边上，PE⊥OA于点E，PF⊥OB于点F，则PE+PF 的值为_________ ．（2）【类比与推理】如图3，矩形ABCD的对角线AC，BD相交于点O，AB=4，AD=3，点P在AB边上，PE∥OB交AC于点E，PF∥OA交BD于点F，求PE+PF的值；（3）【拓展与延伸】如图4，⊙O的半径为4，A，B，C，D是⊙O上的四点，过点C，D的切线CH，DG相交于点M，点P在弦AB上，PE∥BC交AC于点E，PF∥AD于点F，当∠ADG=∠BCH=30°时，PE+PF是否为定值？若是，请求出这个定值；若不是，请说明理由．7．（2014•云南）已知如图平面直角坐标系中，点O是坐标原点，矩形ABCO是顶点坐标分别为A（3，0）、B（3，4）、C （0，4）．点D在y轴上，且点D的坐标为（0，﹣5），点P 是直线AC上的一动点．（1）当点P运动到线段AC的中点时，求直线DP的解析式（关系式）；（2）当点P沿直线AC移动时，过点D、P的直线与x轴交于点M．问在x轴的正半轴上是否存在使△DOM与△ABC相似的点M？若存在，请求出点M的坐标；若不存在，请说明理由；（3）当点P沿直线AC移动时，以点P为圆心、R（R＞0）为半径长画圆．得到的圆称为动圆P．若设动圆P的半径长为，过点D作动圆P的两条切线与动圆P分别相切于点E、F．请探求在动圆P中是否存在面积最小的四边形DEPF？若存在，请求出最小面积S的值；若不存在，请说明理由．8．（2014•湖州）已知在平面直角坐标系xOy中，O是坐标原点，以P（1，1）为圆心的⊙P与x轴，y轴分别相切于点M 和点N，点F从点M出发，沿x轴正方向以每秒1个单位长度的速度运动，连接PF，过点PE⊥PF交y轴于点E，设点F运动的时间是t秒（t＞0）．（1）若点E在y轴的负半轴上（如图所示），求证：PE=PF；（2）在点F运动过程中，设OE=a，OF=b，试用含a的代数式表示b；（3）作点F关于点M的对称点F′，经过M、E和F′三点的抛物线的对称轴交x轴于点Q，连接QE．在点F运动过程中，是否存在某一时刻，使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似？若存在，请直接写出t的值；若不存在，请说明理由．9．（2014•陕西）问题探究（1）如图①，在矩形ABCD中，AB=3，BC=4，如果BC边上存在点P，使△APD为等腰三角形，那么请画出满足条件的一个等腰三角形△APD，并求出此时BP的长；（2）如图②，在△ABC中，∠ABC=60°，BC=12，AD是BC边上的高，E、F分别为边AB、AC的中点，当AD=6时，BC边上存在一点Q，使∠EQF=90°，求此时BQ的长；问题解决（3）有一山庄，它的平面图为如图③的五边形ABCDE，山庄保卫人员想在线段CD上选一点M安装监控装置，用来监视边AB，现只要使∠AMB大约为60°，就可以让监控装置的效果达到最佳，已知∠A=∠E=∠D=90°，AB=270m，AE=400m，ED=285m，CD=340m，问在线段CD上是否存在点M，使∠AMB=60°？若存在，请求出符合条件的DM的长，若不存在，请说明理由．10．（2014•成都）如图，在⊙O的内接△ABC中，∠ACB=90°，AC=2BC，过C作AB的垂线l交⊙O于另一点D，垂足为E．设P是上异于A，C的一个动点，射线AP交l于点F，连接PC与PD，PD交AB于点G．（1）求证：△PAC∽△PDF；（2）若AB=5，=，求PD的长；（3）在点P运动过程中，设=x，tan∠AFD=y，求y与x之间的函数关系式．（不要求写出x的取值范围）11．（2014•宁波）木匠黄师傅用长AB=3，宽BC=2的矩形木板做一个尽可能大的圆形桌面，他设计了四种方案：方案一：直接锯一个半径最大的圆；方案二：圆心O1、O2分别在CD、AB上，半径分别是O1C、O2A，锯两个外切的半圆拼成一个圆；方案三：沿对角线AC将矩形锯成两个三角形，适当平移三角形并锯一个最大的圆；方案四：锯一块小矩形BCEF拼到矩形AFED下面，利用拼成的木板锯一个尽可能大的圆．（1）写出方案一中圆的半径；（2）通过计算说明方案二和方案三中，哪个圆的半径较大？（3）在方案四中，设CE=x（0＜x＜1），圆的半径为y．①求y关于x的函数解析式；②当x取何值时圆的半径最大，最大半径为多少？并说明四种方案中哪一个圆形桌面的半径最大．12．（2014•徐州）如图，矩形ABCD的边AB=3cm，AD=4cm，点E从点A出发，沿射线AD移动，以CE为直径作圆O，点F为圆O与射线BD的公共点，连接EF、CF，过点E作EG⊥EF，EG与圆O相交于点G，连接CG．（1）试说明四边形EFCG是矩形；（2）当圆O与射线BD相切时，点E停止移动，在点E移动的过程中，①矩形EFCG的面积是否存在最大值或最小值？若存在，求出这个最大值或最小值；若不存在，说明理由；②求点G移动路线的长．13．（2014•东昌府区三模）已知：如图，在△ABC中，AB=BC，D是AC中点，BE平分∠ABD交AC于点E，点O是AB 上一点，⊙O过B、E两点，交BD于点G，交AB于点F．（1）求证：AC与⊙O相切；（2）当BD=6，sinC=时，求⊙O的半径．14．（2014•安徽模拟）阅读材料：如图，△ABC中，AB=AC，P为底边BC上任意一点，点P到两腰的距离分别为r1，r2，腰上的高为h，连接AP，则S△ABP+S△ACP=S△ABC，即：AB•r1+AC•r2=AB•h，∴r1+r2=h（1）理解与应用如果把“等腰三角形”改成“等边三角形”，那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”，即：已知边长为2的等边△ABC内任意一点P到各边的距离分别为r 1，r2，r3，试证明：．（2）类比与推理边长为2的正方形内任意一点到各边的距离的和等于_________ ；（3）拓展与延伸若边长为2的正n边形A1A2…An内部任意一点P到各边的距离为r1，r2，…r n，请问r1+r2+…r n是否为定值（用含n的式子表示），如果是，请合理猜测出这个定值．15．（2014•安徽名校一模）如图△ABC中∠A=90°，以AB为直径的⊙O交BC于D，E为AC边中点，求证：DE是⊙O的切线．16．（2014•灌南县模拟）如图，AB是⊙O的直径，AC是弦，∠ACD=∠AOC，AD⊥CD于点D．（1）求证：CD是⊙O的切线；（2）若AB=10，AD=2，求AC的长．17．（2014•普陀区二模）如图，在等腰△ABC中，AB=AC=5，BC=6，点D为BC边上一动点（不与点B重合），过D作射线DE交AB边于E，使∠BDE=∠A，以D为圆心、DC的长为半径作⊙D．（1）设BD=x，AE=y，求y关于x的函数关系式，并写出定义域．（2）当⊙D与AB边相切时，求BD的长．（3）如果⊙E是以E为圆心，AE的长为半径的圆，那么当BD 的长为多少时，⊙D与⊙E相切？18．（2014•江西模拟）如图，矩形ABCD的边AB=4，BC=3．一简易量角器放置在矩形ABCD内，其零度线即半圆O 的直径与边AB重合，点A处是0刻度，点B处是180刻度．P 点是量角器的半圆弧上一动点，过P点的切线与边BC、CD （或其延长线）分别交于点E、F．设点P的刻度数为n，∠PAB=α．（1）当n=136时，α=_________ ，求出α与n的关系式；（2）在P点的运动过程中，线段EB与EP有怎样的数量关系，请予证明；（3）在P点的运动过程中，F点在直线CD上的位置随着α的变化而变化，当F点在线段CD上时、在CD的延长线上时、在DC的延长线上时，对应的α值分别是多少？（参考数据：tan56.3°≈1.5）（4）连接BP，在P点的运动过程中，是否存在△ABP与△CEF 相似的情况？若存在，求出此时n的值以及相应的EF的长；若不存在，请说明理由．19．（2014•广东一模）如图，正方形ABCD的边长是8cm，以正方形的中心O为圆心，EF为直径的半圆切AB于M、切BC于N，已知C为BG的中点，AG交CD于H．P，Q同时从A出发，P以1cm/s的速度沿折线ADCG运动，Q以cm/s的速速沿线段AG方向运动，P，Q中有一点到达终点时，整个运动停止．P，Q运动的时间记为t．（1）当t=4时，求证：△PEF≌△MEF；（2）当0≤t≤8时，试判断PQ与CD的位置关系；（3）当t＞8时，是否存在t使得=？若存在请求出所有t的值，若不存在，请说明理由．20．（2013•营口）如图，点C是以AB为直径的⊙O上的一点，AD与过点C的切线互相垂直，垂足为点D．（1）求证：AC平分∠BAD；（2）若CD=1，AC=，求⊙O的半径长．21．（2013•襄阳）如图，△ABC内接于⊙O，且AB为⊙O的直径．∠ACB的平分线交⊙O于点D，过点D作⊙O的切线PD交CA的延长线于点P，过点A作AE⊥CD于点E，过点B作BF⊥CD于点F．（1）求证：DP∥AB；（2）若AC=6，BC=8，求线段PD的长．22．（2013•曲靖）如图，⊙O的直径AB=10，C、D是圆上的两点，且．设过点D的切线ED交AC的延长线于点F．连接OC交AD于点G．（1）求证：DF⊥AF．（2）求OG的长．23．（2013•德阳）如图，已知AB是⊙O直径，BC是⊙O的弦，弦ED⊥AB于点F，交BC于点G，过点C作⊙O的切线与ED的延长线交于点P．（1）求证：PC=PG；（2）点C在劣弧AD上运动时，其他条件不变，若点G是BC 的中点，试探究CG、BF、BO三者之间的数量关系，并写出证明过程；（3）在满足（2）的条件下，已知⊙O的半径为5，若点O到BC的距离为时，求弦ED的长．24．（2013•贺州）已知：⊙O的直径为3，线段AC=4，直线AC和PM分别与⊙O相切于点A，M．（1）求证：点P是线段AC的中点；（2）求sin∠PMC的值．25．（2013•兰州）已知，如图，直线MN交⊙O于A，B两点，AC是直径，AD平分∠CAM交⊙O于D，过D作DE⊥MN于E．（1）求证：DE是⊙O的切线；（2）若DE=6cm，AE=3cm，求⊙O的半径．26．（2013•南宁）如图，在△ABC中，∠BAC=90°，AB=AC，AB是⊙O的直径，⊙O交BC于点D，DE⊥AC于点E，BE交⊙O 于点F，连接AF，AF的延长线交DE于点P．（1）求证：DE是⊙O的切线；（2）求tan∠ABE的值；（3）若OA=2，求线段AP的长．27．（2013•长沙）如图，△ABC中，以AB为直径的⊙O交AC 于点D，∠DBC=∠BAC．（1）求证：BC是⊙O的切线；（2）若⊙O的半径为2，∠BAC=30°，求图中阴影部分的面积．28．（2013•广安）如图，在△ABC中，AB=AC，以AB为直径作半圆⊙O，交BC于点D，连接AD，过点D作DE⊥AC，垂足为点E，交AB的延长线于点F．（1）求证：EF是⊙0的切线．（2）如果⊙0的半径为5，sin∠ADE=，求BF的长．29．（2013•沈阳）如图，OC平分∠MON，点A在射线OC上，以点A为圆心，半径为2的⊙A与OM相切于点B，连接BA并延长交⊙A于点D，交ON于点E．（1）求证：ON是⊙A的切线；（2）若∠MON=60°，求图中阴影部分的面积．（结果保留π）30．（2013•宜宾）如图，AB是⊙O的直径，∠B=∠CAD．（1）求证：AC是⊙O的切线；（2）若点E是的中点，连接AE交BC于点F，当BD=5，CD=4时，求AF的值．参考答案与试题解析一．解答题（共30小题）1．（2014•攀枝花）如图，以点P（﹣1，0）为圆心的圆，交x轴于B、C两点（B在C的左侧），交y轴于A、D两点（A在D的下方），AD=2，将△ABC绕点P旋转180°，得到△MCB．（1）求B、C两点的坐标；（2）请在图中画出线段MB、MC，并判断四边形ACMB的形状（不必证明），求出点M的坐标；（3）动直线l从与BM重合的位置开始绕点B顺时针旋转，到与BC重合时停止，设直线l与CM交点为E，点Q为BE的中点，过点E作EG⊥BC于G，连接MQ、QG．请问在旋转过程中∠MQG的大小是否变化？若不变，求出∠MQG的度数；若变化，请说明理由．考点：圆的综合题．专题：压轴题．分析：（1）连接PA，运用垂径定理及勾股定理即可求出圆的半径，从而可以求出B、C两点的坐标．（2）由于圆P是中心对称图形，显然射线AP与圆P的交点就是所需画的点M，连接MB、MC即可；证四边形ACMB是矩形；过点M作MH⊥BC，垂足为H，易证△MHP≌△AOP，从而求出MH、OH 长，进而得到点M的坐标．（3）易证点E、M、B、G在以点Q为圆心，QB为半径的圆上，从而得到∠MQG=2∠MBG．易得∠OCA=60°，从而得到∠MBG=60°，进而得到∠MQG=120°，所以∠MQG是定值．解答：解：（1）连接PA，如图1所示．∵PO⊥AD，∴AO=DO．∵AD=2，∴OA=．∵点P坐标为（﹣1，0），∴OP=1．∴PA==2．∴BP=CP=2．∴B（﹣3，0），C（1，0）．（2）连接AP，延长AP交⊙P于点M，连接MB、MC．如图2所示，线段MB、MC即为所求作．四边形ACMB是矩形．理由如下：∵△MCB由△ABC绕点P旋转180°所得，∴四边形ACMB是平行四边形．∵BC是⊙P的直径，∴∠CAB=90°．∴平行四边形ACMB是矩形．过点M作MH⊥BC，垂足为H，如图2所示．在△MHP和△AOP中，∵∠MHP=∠AOP，∠HPM=∠OPA，MP=AP，∴△MHP≌△AOP．∴MH=OA=，PH=PO=1．∴OH=2．∴点M的坐标为（﹣2，）．（3）在旋转过程中∠MQG的大小不变．∵四边形ACMB是矩形，∴∠BMC=90°．∵EG⊥BO，∴∠BGE=90°．∴∠BMC=∠BGE=90°．∵点Q是BE的中点，∴QM=QE=QB=QG．∴点E、M、B、G在以点Q为圆心，QB为半径的圆上，如图3所示．∴∠MQG=2∠MBG．∵∠COA=90°，OC=1，OA=，∴tan∠OCA==．∴∠OCA=60°．∴∠MBC=∠BCA=60°．∴∠MQG=120°．∴在旋转过程中∠MQG的大小不变，始终等于120°．点评：本题考查了垂径定理、勾股定理、全等三角形的判定与性质、矩形的判定与性质、圆周角定理、特殊角三角函数、图形的旋转等知识，综合性比较强．证明点E、M、B、G在以点Q为圆心，QB为半径的圆是解决第三小题的关键．2．（2014•苏州）如图，已知l1⊥l2，⊙O与l1，l2都相切，⊙O的半径为2cm，矩形ABCD的边AD、AB分别与l1，l2重合，AB=4cm，AD=4cm，若⊙O与矩形ABCD沿l 1同时向右移动，⊙O的移动速度为3cm/s，矩形ABCD的移动速度为4cm/s，设移动时间为t（s）（1）如图①，连接OA、AC，则∠OAC的度数为105 °；（2）如图②，两个图形移动一段时间后，⊙O到达⊙O1的位置，矩形ABCD到达A1B1C1D1的位置，此时点O1，A1，C1恰好在同一直线上，求圆心O移动的距离（即OO1的长）；（3）在移动过程中，圆心O到矩形对角线AC所在直线的距离在不断变化，设该距离为d（cm），当d＜2时，求t的取值范围（解答时可以利用备用图画出相关示意图）．考点：圆的综合题．专题：几何综合题；压轴题．分析：（1）利用切线的性质以及锐角三角函数关系分别求出∠OAD=45°，∠DAC=60°，进而得出答案；（2）首先得出，∠C1A1D1=60°，再利用A1E=AA1﹣OO1﹣2=t﹣2，求出t的值，进而得出OO1=3t得出案即可；（3）①当直线AC与⊙O第一次相切时，设移动时间为t1，②当直线AC与⊙O第二次相切时，设移时间为t2，分别求出即可．解答：解：（1）∵l1⊥l2，⊙O与l1，l2都相切，∴∠OAD=45°，∵AB=4cm，AD=4cm，∴CD=4cm，∴tan∠DAC===，∴∠DAC=60°，∴∠OAC的度数为：∠OAD+∠DAC=105°，故答案为：105；（2）如图位置二，当O1，A1，C1恰好在同一直线上时，设⊙O1与l1的切点为E，连接O1E，可得O1E=2，O1E⊥l1，在Rt△A1D1C1中，∵A1D1=4，C1D1=4，∴tan∠C1A1D1=，∴∠C1A1D1=60°，在Rt△A1O1E中，∠O1A1E=∠C1A1D1=60°，∴A1E==，∵A1E=AA1﹣OO1﹣2=t﹣2，∴t﹣2=，∴t=+2，∴OO1=3t=2+6；（3）①当直线AC与⊙O第一次相切时，设移动时间为t1，如图，此时⊙O移动到⊙O2的位置，矩形ABCD移动到A2B2C2D2的位置，设⊙O2与直线l1，A2C2分别相切于点F，G，连接O2F，O2G，O2A2，∴O2F⊥l1，O2G⊥A2C2，由（2）得，∠C2A2D2=60°，∴∠GA2F=120°，∴∠O2A2F=60°，在Rt△A2O2F中，O2F=2，∴A2F=，∵OO2=3t1，AF=AA2+A2F=4t1+，∴4t1+﹣3t1=2，∴t1=2﹣，②当直线AC与⊙O第二次相切时，设移动时间为t2，记第一次相切时为位置一，点O1，A1，C1共线时位置二，第二次相切时为位置三，由题意知，从位置一到位置二所用时间与位置二到位置三所用时间相等，∴+2﹣（2﹣）=t2﹣（+2），解得：t2=2+2，综上所述，当d＜2时，t的取值范围是：2﹣＜t＜2+2．点评：此题主要考查了切线的性质以及锐角三角函数关系等知识，利用分类讨论以及数形结合t的值是解题关键．3．（2014•泰州）如图，平面直角坐标系xOy中，一次函数y=﹣x+b（b为常数，b＞0）的图象与x轴、y轴分别相交于点A、B，半径为4的⊙O与x轴正半轴相交于点C，与y轴相交于点D、E，点D在点E上方．（1）若直线AB与有两个交点F、G．①求∠CFE的度数；②用含b的代数式表示FG2，并直接写出b的取值范围；（2）设b≥5，在线段AB上是否存在点P，使∠CPE=45°？若存在，请求出P点坐标；若不存在，请说明理由．考点：圆的综合题．专题：几何综合题；压轴题．分析：（1）连接CD，EA，利用同一条弦所对的圆周角相等求行∠CFE=45°，（2）作OM⊥AB点M，连接OF，利用两条直线垂直相交求出交点M的坐标，利用勾股定理求出FM 再求出FG2，再根据式子写出b的范围，（3）当b=5时，直线与圆相切，存在点P，使∠CPE=45°，再利用△APO∽△AOB和△AMP∽△AOB 似得出点P的坐标，再求出OP所在的直线解析式．解答：解：（1）①如图，∵∠COE=90°∴∠CFE=∠COE=45°，（圆周角定理）②方法一：如图，作OM⊥AB点M，连接OF，∵OM⊥AB，直线的函数式为：y=﹣x+b，∴OM所在的直线函数式为：y=x，∴交点M（b，b）∴OM2=（b）2+（b）2，∵OF=4，∴FM2=OF2﹣OM2=42﹣（b）2﹣（b）2，∵FM=FG，∴FG2=4FM2=4×[42﹣（b）2﹣（b）2]=64﹣b2=64×（1﹣b2），∵直线AB与有两个交点F、G．∴4≤b＜5，∴FG2=64×（1﹣b2）（4≤b＜5）方法二：①如图，作OM⊥AB点M，连接OF，∵直线的函数式为：y=﹣x+b，∴B的坐标为（0，b），A的坐标为（b，0），∴AB==b，∴sin∠BAO===，∴sin∠MAO===，∴OM=b，∴在RT△OMF中，FM==∵FG=2FM，∴FG2=4FM2=4（42﹣b2）=64﹣﹣b2=64×（1﹣b2），∵直线AB与有两个交点F、G．∴4≤b＜5，∴FG2=64×（1﹣b2）（4≤b＜5）（2）如图，当b=5时，直线与圆相切，∵在直角坐标系中，∠COE=90°，∴∠CPE=∠ODC=45°，∴存在点P，使∠CPE=45°，连接OP，∵P是切点，∴OP⊥AB，∴△APO∽△AOB，∴=，∵OP=r=4，OB=5，AO=，∴=即AP=，∵AB===，作PM⊥AO交AO于点M，设P的坐标为（x，y），∵△AMP∽△AOB，∴=∴=，∴y=，∴x=OM===∴点P的坐标为（，）．点评：本题主要考查了圆与一次函数的知识，解题的关键是作出辅助线，利用三角形相似求出点P的坐标．4．（2014•上海）如图1，已知在平行四边形ABCD中，AB=5，BC=8，cosB=，点P是边BC上的动点，以CP为半径的圆C与边AD交于点E、F（点F在点E的右侧），射线CE与射线BA交于点G．（1）当圆C经过点A时，求CP的长；（2）连接AP，当AP∥CG时，求弦EF的长；（3）当△AGE是等腰三角形时，求圆C的半径长．考点：圆的综合题．专题：压轴题．分析：（1）当点A在⊙C上时，点E和点A重合，过点A作AH⊥BC于H，直接利用勾股定理求出AC进而出答案；（2）首先得出四边形APCE是菱形，进而得出CM的长，进而利用锐角三角函数关系得出CP以及EF 长；（3）∠GAE≠∠BGC，只能∠AGE=∠AEG，利用AD∥BC，得出△GAE∽△GBC，进而求出即可．解答：解：（1）如图1，设⊙O的半径为r，当点A在⊙C上时，点E和点A重合，过点A作AH⊥BC于H，∴BH=AB•cosB=4，∴AH=3，CH=4，∴AC==5，∴此时CP=r=5；（2）如图2，若AP∥CE，APCE为平行四边形，∵CE=CP，∴四边形APCE是菱形，连接AC、EP，则AC⊥EP，∴AM=CM=，由（1）知，AB=AC，则∠ACB=∠B，∴CP=CE==，∴EF=2=；（3）如图3：过点C作CN⊥AD于点N，设AQ⊥BC，∵=cosB，AB=5，∴BQ=4，AN=QC=BC﹣BQ=4．∵cosB=，∴∠B＜45°，∵∠BCG＜90°，∴∠BGC＞45°，∴∠BGC＞∠B=∠GAE，即∠BGC≠∠GAE，又∠AEG=∠BCG≥∠ACB=∠B=∠GAE，∴当∠AEG=∠GAE时，A、E、G重合，则△AGE不存在．即∠AEG≠∠GAE∴只能∠AGE=∠AEG，∵AD∥BC，∴△GAE∽△GBC，∴=，即=，解得：AE=3，EN=AN﹣AE=1，∴CE===．点评：此题主要考查了相似三角形的判定与性质以及勾股定理以及锐角三角函数关系等知识，利用分类讨论得△AGE是等腰三角形时只能∠AGE=∠AEG进而求出是解题关键．5．（2014•常州）在平面直角坐标系xOy中，点M（，），以点M为圆心，OM长为半径作⊙M．使⊙M与直线OM的另一交点为点B，与x轴，y轴的另一交点分别为点D，A（如图），连接AM．点P是上的动点．（1）写出∠AMB的度数；（2）点Q在射线OP上，且OP•OQ=20，过点Q作QC垂直于直线OM，垂足为C，直线QC交x轴于点E．①当动点P与点B重合时，求点E的坐标；②连接QD，设点Q的纵坐标为t，△QOD的面积为S．求S与t的函数关系式及S的取值范围．考点：圆的综合题．专题：几何综合题；压轴题．分析：（1）首先过点M作MH⊥OD于点H，由点M（，），可得∠MOH=45°，OH=MH=，继而求∠AOM=45°，又由OM=AM，可得△AOM是等腰直角三角形，继而可求得∠AMB的度数；（2）①由OH=MH=，MH⊥OD，即可求得OD与OM的值，继而可得OB的长，又由动点P与点重合时，OP•OQ=20，可求得OQ的长，继而求得答案；②由OD=2，Q的纵坐标为t，即可得S=，然后分别从当动点P与B点重合时，过Q作QF⊥x轴，垂足为F点，与当动点P与A点重合时，Q点在y轴上，去分析求解即可求得答案．解答：解：（1）过点M作MH⊥OD于点H，∵点M（，），∴OH=MH=，∴∠MOD=45°，∵∠AOD=90°，∴∠AOM=45°，∵OM=AM，∴∠OAM=∠AOM=45°，∴∠AMO=90°，∴∠AMB=90°；（2）①∵OH=MH=，MH⊥OD，∴OM==2，OD=2OH=2，∴OB=4，∵动点P与点B重合时，OP•OQ=20，∴OQ=5，∵∠OQE=90°，∠POE=45°，∴OE=5，∴E点坐标为（5，0）②∵OD=2，Q的纵坐标为t，∴S=．如图2，当动点P与B点重合时，过点Q作QF⊥x轴，垂足为F点，∵OP=4，OP•OQ=20，∴OQ=5，∵∠OFC=90°，∠QOD=45°，∴t=QF=，此时S=；如图3，当动点P与A点重合时，Q点在y轴上，∴OP=2，∵OP•OQ=20，∴t=OQ=5，此时S=；∴S的取值范围为5≤S≤10．点评：此题考查了垂径定理、等腰直角三角形的性质以及勾股定理等知识．此题难度较大，注意掌握辅助线的法，注意掌握数形结合思想、分类讨论思想与方程思想的应用．6．（2014•漳州）阅读材料：如图1，在△AOB中，∠O=90°，OA=OB，点P在AB边上，PE⊥OA于点E，PF⊥OB于点F，则PE+PF=OA．（此结论不必证明，可直接应用）（1）【理解与应用】如图2，正方形ABCD的边长为2，对角线AC，BD相交于点O，点P在AB边上，PE⊥OA于点E，PF⊥OB于点F，则PE+PF的值为．（2）【类比与推理】如图3，矩形ABCD的对角线AC，BD相交于点O，AB=4，AD=3，点P在AB边上，PE∥OB交AC于点E，PF∥OA交BD于点F，求PE+PF的值；（3）【拓展与延伸】如图4，⊙O的半径为4，A，B，C，D是⊙O上的四点，过点C，D的切线CH，DG相交于点M，点P在弦AB上，PE∥BC交AC于点E，PF∥AD于点F，当∠ADG=∠BCH=30°时，PE+PF是否为定值？若是，请求出这个定值；若不是，请说明理由．考点：圆的综合题；等边三角形的判定与性质；矩形的性质；正方形的性质；弦切角定理；相似三角形的判定性质．专题：压轴题；探究型．分析：（1）易证：OA=OB，∠AOB=90°，直接运用阅读材料中的结论即可解决问题．（2）易证：OA=OB=OC=0D=，然后由条件PE∥OB，PF∥AO可证△AEP∽△AOB，△BFP∽△BOA，从而可得==1，进而求出EP+FP=．（3）易证：AD=BC=4．仿照（2）中的解法即可求出PE+PF=4，因而PE+PF是定值．解答：解：（1）如图2，∵四边形ABCD是正方形，∴OA=OB=OC=OD，∠ABC=∠AOB=90°．∵AB=BC=2，∴AC=2．∴OA=．∵OA=OB，∠AOB=90°，PE⊥OA，PF⊥OB，∴PE+PF=OA=．（2）如图3，∵四边形ABCD是矩形，∴OA=OB=OC=OD，∠DAB=90°．∵AB=4，AD=3，∴BD=5．∴OA=OB=OC=OD=．∵PE∥OB，PF∥AO，∴△AEP∽△AOB，△BFP∽△BOA．∴，．∴==1．∴+=1．∴EP+FP=．∴PE+PF的值为．（3）当∠ADG=∠BCH=30°时，PE+PF是定值．理由：连接OA、OB、OC、OD，如图4∵DG与⊙O相切，∴∠GDA=∠ABD．∵∠ADG=30°，∴∠ABD=30°．∴∠AOD=2∠ABD=60°．∵OA=OD，∴△AOD是等边三角形．∴AD=OA=4．同理可得：BC=4．∵PE∥BC，PF∥AD，∴△AEP∽△ACB，△BFP∽△BDA．∴，．∴==1．∴=1．∴PE+PF=4．∴当∠ADG=∠BCH=30°时，PE+PF=4．点评：本题考查了正方形的性质、矩形的性质、弦切角定理、相似三角形的判定与性质、等边三角形的判定与质等知识，考查了类比联想的能力，由一定的综合性．要求PE+PF的值，想到将相似所得的比式相加决本题的关键．7．（2014•云南）已知如图平面直角坐标系中，点O是坐标原点，矩形ABCO是顶点坐标分别为A（3，0）、B（3，4）、C（0，4）．点D在y轴上，且点D的坐标为（0，﹣5），点P是直线AC上的一动点．（1）当点P运动到线段AC的中点时，求直线DP的解析式（关系式）；（2）当点P沿直线AC移动时，过点D、P的直线与x轴交于点M．问在x轴的正半轴上是否存在使△DOM与△ABC相似的点M？若存在，请求出点M的坐标；若不存在，请说明理由；（3）当点P沿直线AC移动时，以点P为圆心、R（R＞0）为半径长画圆．得到的圆称为动圆P．若设动圆P的半径长为，过点D作动圆P的两条切线与动圆P分别相切于点E、F．请探求在动圆P中是否存在面积最小的四边形DEPF？若存在，请求出最小面积S的值；若不存在，请说明理由．考点：圆的综合题；待定系数法求一次函数解析式；垂线段最短；勾股定理；切线长定理；相似三角形的判定性质．专题：综合题；压轴题；存在型；分类讨论．分析：（1）只需先求出AC中点P的坐标，然后用待定系数法即可求出直线DP的解析式．（2）由于△DOM与△ABC相似，对应关系不确定，可分两种情况进行讨论，利用三角形相似求出OM 长，即可求出点M的坐标．（3）易证S△PED=S△PFD．从而有S四边形DEPF=2S△PED=DE．由∠DEP=90°得DE2=DP2﹣PE2=DP2﹣．根据“点到直线之间，垂线段最短”可得：当DP⊥AC时，DP最短，此时DE也最短，对应的四边DEPF的面积最小．借助于三角形相似，即可求出DP⊥AC时DP的值，就可求出四边形DEPF面积的小值．解答：解：（1）过点P作PH∥OA，交OC于点H，如图1所示．∵PH∥OA，∴△CHP∽△COA．∴==．∵点P是AC中点，∴CP=CA．∴HP=OA，CH=CO．∵A（3，0）、C（0，4），∴OA=3，OC=4．∴HP=，CH=2．∴OH=2．∵PH∥OA，∠COA=90°，∴∠CHP=∠COA=90°．∴点P的坐标为（，2）．设直线DP的解析式为y=kx+b，∵D（0，﹣5），P（，2）在直线DP上，∴∴∴直线DP的解析式为y=x﹣5．（2）①若△DOM∽△ABC，图2（1）所示，∵△DOM∽△ABC，∴=．∵点B坐标为（3，4），点D的坐标为（0．﹣5），∴BC=3，AB=4，OD=5．∴=．∴OM=．∵点M在x轴的正半轴上，∴点M的坐标为（，0）②若△DOM∽△CBA，如图2（2）所示，∵△DOM∽△CBA，∴=．∵BC=3，AB=4，OD=5，∴=．∴OM=．∵点M在x轴的正半轴上，∴点M的坐标为（，0）．综上所述：若△DOM与△CBA相似，则点M的坐标为（，0）或（，0）．（3）∵OA=3，OC=4，∠AOC=90°，∴AC=5．∴PE=PF=AC=．∵DE、DF都与⊙P相切，∴DE=DF，∠DEP=∠DFP=90°．∴S△PED=S△PFD．∴S四边形DEPF=2S△PED=2×PE•DE=PE•DE=DE．∵∠DEP=90°，∴DE2=DP2﹣PE2．=DP2﹣．根据“点到直线之间，垂线段最短”可得：当DP⊥AC时，DP最短，此时DE取到最小值，四边形DEPF的面积最小．∵DP⊥AC，∴∠DPC=90°．∴∠AOC=∠DPC．∵∠OCA=∠PCD，∠AOC=∠DPC，∴△AOC∽△DPC．∴=．∵AO=3，AC=5，DC=4﹣（﹣5）=9，∴=．∴DP=．∴DE2=DP2﹣=（）2﹣=．∴DE=，∴S四边形DEPF=DE=．∴四边形DEPF面积的最小值为．点评：本题考查了相似三角形的判定与性质、用待定系数法求直线的解析式、切线长定理、勾股定理、垂线段短等知识，考查了分类讨论的思想．将求DE的最小值转化为求DP的最小值是解决第3小题的关键．外，要注意“△DOM与△ABC相似”与“△DOM∽△ABC“之间的区别．8．（2014•湖州）已知在平面直角坐标系xOy中，O是坐标原点，以P（1，1）为圆心的⊙P与x轴，y轴分别相切于点M和点N，点F从点M出发，沿x轴正方向以每秒1个单位长度的速度运动，连接PF，过点PE⊥PF交y轴于点E，设点F运动的时间是t秒（t＞0）．（1）若点E在y轴的负半轴上（如图所示），求证：PE=PF；（2）在点F运动过程中，设OE=a，OF=b，试用含a的代数式表示b；（3）作点F关于点M的对称点F′，经过M、E和F′三点的抛物线的对称轴交x轴于点Q，连接QE．在点F运动过程中，是否存在某一时刻，使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似？若存在，请直接写出t的值；若不存在，请说明理由．考点：圆的综合题．专题：压轴题．分析：（1）连接PM，PN，运用△PMF≌△PNE证明；（2）分两种情况：①当t＞1时，点E在y轴的负半轴上；②当0＜t≤1时，点E在y轴的正半轴或原上，再根据（1）求解，（3）分两种情况，当1＜t＜2时，当t＞2时，三角形相似时还各有两种情况，根据比例式求出时间t．解答：证明：（1）如图，连接PM，PN，∵⊙P与x轴，y轴分别相切于点M和点N，∴PM⊥MF，PN⊥ON且PM=PN，∴∠PMF=∠PNE=90°且∠NPM=90°，∵PE⊥PF，∠NPE=∠MPF=90°﹣∠MPE，在△PMF和△PNE中，，∴△PMF≌△PNE（ASA），∴PE=PF；（2）解：分两种情况：①当t＞1时，点E在y轴的负半轴上，如图1，由（1）得△PMF≌△PNE，∴NE=MF=t，PM=PN=1，∴b=OF=OM+MF=1+t，a=NE﹣ON=t﹣1，∴b﹣a=1+t﹣（t﹣1）=2，∴b=2+a，②0＜t≤1时，如图2，点E在y轴的正半轴或原点上，。

几何五大模型一之令狐文艳创作

几何五大模型一之令狐文艳创作

几何五大模型令狐文艳一、等积变换模型1、等底等高的两个三角形面积相等。

2、两个三角形高相等，面积比等于它们的底之比。

3、两个三角形底相等，面积比等于它的的高之比。

二、共角定理模型两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形。

共角三角形的面积比等到于对应角（相等角或互补角）两夹边的乘积之比。

三、蝴蝶定理模型（说明：任意四边形与四边形、长方形、梯形，连接对角线所成四部的比例关系是一样的。

）四、相似三角形模型相似三角形：是形状相同，但大小不同的三角形叫相似三角形。

相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比。

相似三角形的面积比等于它们相似比的平方。

五、燕尾定理模等积变形: 等积变形是小学几何里面一个非常重要的思想，小学所以的几何题，或多或少的都会用到等积变形的思想，几何五大模型也都是依托等积变形思想变化而成的。

一半模型平行四边形、梯形、任意四边形中的一些一半模型。

一、 模型归纳总结1、等面积变换模型(1)直线AB 平行于CD ，可知BCD ACD S S ∆∆=；反之，如果BCD ACD S S ∆∆=，则可知直线AB 平行于CD ．如图A(2)两个三角形高相等，面积比等于它们的底之比；两个三角形底相等，面积比等于它们的高之比；::ABD ACD S S BD CD =△△如图B图A 图B(3)一半面积关系【例1】、如图，每一个正方形四边中点的连线构成另一内接小正方形，则阴影部分面积为原正方形面积的几分之几?【例2】、如右图，过平行四边形ABCD 内的一点P 作边的平行线EF 、GH ，若PBD ∆的面积为8平方分米，求平行四边形PHCF 的面积比平行四边形PGAE 的面积大多少平方分米？【例4】、如图1，一个长方形被切成8块，其中三块的面积分别为12，23，32，则图中阴影部分的面积为_____ 二、 不规则图形求面积的常用方法【例5】、右图中两个半径为1的14圆扇形'A O B ''与AOB 叠放在一起，POQO '是正方形，则整个阴影图形的面积是。

初中几何变换——翻折之令狐文艳创作

初中几何变换——翻折之令狐文艳创作

初中数学几何变换之令狐文艳轴对称一、知识梳理1、轴对称基本要素：对称轴。

2、基本性质：（1）对应线段、对应角相等（2）对应点所连线段被对称轴垂直平分（3）对称轴上的点到对应点的距离相等（4）对称轴两侧的几何图形全等3、应用 翻折问题、最值问题等二、常考题型类型一：轴对称性质1、如图，在平行四边形ABCD 中，13=AB ，4=AD ，将平行四边形ABCD 沿AE 翻折后，点B 恰好与点C 重合，则折痕AE 的长为__________.第1题 第2题第3题2、如图， 矩形中，AB =8，BC =6，P 为AD 上一点， 将△ABP 沿BP 翻折至△EBP ， PE 与CD 相交于点O ，且OE =OD ，则AP 的长为__________.3、如图，在△ABC中，AB=AC，BC=24，tanC=2，如果将△ABC沿直线l翻折后，点B落在边AC的中点E处，直线l与边BC交于点D，那么BD的长为。

4、如图，菱形纸片ABCD中，∠A=600，将纸片折叠，点A、D分别落在A’、D’处，且A’D’经过B，EF为折痕，当D’F CD时，CF的值为。

FD5、如图，在△ABC中，∠C＝90°，将△ABC沿直线MN翻折后，顶点C恰好落在AB边上的点D处，已知MN∥AB，MC＝6，NC＝23，则四边形MABN的面积是。

第4题第5题第6题6、如图，已知边长为5的等边三角形ABC纸片，点E在AC边上，点F在AB边上，沿着EF折叠，使点A落在BC 边上的点D的位置，且，则CE的长是。

7、如图1，在矩形纸片ABCD中，AB＝83，AD＝10，点E是CD的中点.将这张纸片依次折叠两次：第一次折叠纸片使点A与点E重合，如图2，折痕为MN，连接ME、NE；第二次折叠纸片使点N与点E重合，如图3，点B落在B′处，折痕为HG，连接HE，则tan∠EHG＝.图2图38、如图，在边长为6的正方形ABCD 中，E 是边CD 的中点，将△ADE 沿AE 对折至△AFE ，延长交BC 于点G ，连接AG .（1）求证：△ABG ≌△AFG ；（2）求BG 的长.类型二：轴对称应用1、菱形ABCD 在平面直角坐标系中的位置如图所示，顶点B （2，0），∠DOB =60°，点P 是对角线OC 上一个动点，E （0，﹣1），当EP +BP 最短时，点P 的坐标为．2、如图，∠AOB =30°，点M 、N 分别是射线OA 、OB 上的动点，OP 平分∠AOB ，且OP =6，当△PMN 的周长取最小值时，四边形PMON 的面积为．3、如图,在锐角△ABC 中,AB=6,∠BAC=60°,∠BAC 的平分线交BC 于点D,点M,N 分别是AD 和AB 上的动点,则BM+MN 的最小值为。

初二下学期数学压轴题之令狐文艳创作

初二下学期数学压轴题之令狐文艳创作

1在梯形ABCD中，AD∥BC，AB=CD=AD=5cm，BC=11cm，点P从点D开始沿DA边以每秒1cm的速度移动，点Q从点B开始沿BC边以每秒2cm的速度移动（当点P到达点A时，点P与点Q同时停止移动），假设点P移动的时间为x（秒），四边形ABQP的面积为y（cm2）．令狐文艳（1）求y关于x的函数解析式，并写出它的定义域；（2）在移动的过程中，求四边形ABQP的面积与四边形QCDP的面积相等时x的值；（3）在移动的过程中，是否存在x使得PQ=AB，若存在求出所有x的值，若不存在请说明理由．2. 如图，在正方形ABCD中，点E在边AB上（点E与点A、B不重合），过点E作FG⊥DE，FG与边BC相交于点F，与边DA的延长线相交于点G．（1）由几个不同的位置，分别测量BF、AG、AE的长，从中你能发现BF 、AG 、AE 的数量之间具有怎样的关系？并证明你所得到的结论；（2） 联结DF ，如果正方形的边长为2，设AE=x ，△DFG的面积为y ，求y 与x 之间的函数解析式，并写出函数的定义域；（3） 如果正方形的边长为2，FG的长为25，求点C 到直线DE 的距离．3O ，CE =AB OF4的图像与x 轴、y 轴分别相交于点A 、B．梯形AOBC 的边AC = 5．（1）求点C 的坐标；（2）如果点A 、C 在一次函数y=kx+b（k 、b 为常数，且k <0）的图像上，求这个一次函数的解析式．5．如图，直角坐标平面xoy 中，点A 在x 轴上，点C 与点E 在y 轴上，且E 为OC 中点，BC //x 轴，且BE ⊥AE （1）求证：AE 平分∠BAO ；（供操作实验用）（供证明计算用）（第2题图）D ABD ABAB CDO EF（第3（第4题图）（2）当OE =6， BC=4时，求直线AB 的解析式．6．如图，△ABC 中，点D 、E 分别是边BC 、AC 的中点，过点A 作AF//BC 交线段DE 的延长线相交于F 点，取AF 的中点G ，如果BC = 2 AB ．求证：（1）四边形ABDF 是菱形；（2）AC = 2DG ．7．边长为4的正方形ABCD 中，点O 是对角线AC 的中点，P 是对角线AC 上一动点，过点P作PF ⊥CD 于点F ，作PE ⊥PB 交直线CD 于点E ，设PA=x ，S ⊿PCE =y ，⑴ 求证：DF ＝EF ；（5分）⑵ 当点P 在线段AO 上时，求y 关于x 的函数关系式及自变量x 的取值范围；（3分）⑶ 在点P 的运动过程中，⊿PEC 能否为等腰三角形？如果能够，请直接写出PA 的长；如果不能，请简单说明理由。

初一下册数学压轴题精练答案之令狐文艳创作

初一下册数学压轴题精练答案之令狐文艳创作

初一下册数学压轴题精练答案令狐文艳参考答案与试题解析一．解答题（共9小题）1．如图1，在平面直角坐标系中，△AOB是直角三角形，∠AOB=90°，斜边AB与y轴交于点C．（1）若∠A=∠AOC，求证：∠B=∠BOC；（2）如图2，延长AB交x轴于点E，过O作OD⊥AB，若∠DOB=∠EOB，∠A=∠E，求∠A的度数；（3）如图3，OF平分∠AOM，∠BCO的平分线交FO的延长线于点P，∠A=40°，当△ABO绕O点旋转时（斜边AB与y轴正半轴始终相交于点C），问∠P的度数是否发生改变？若不变，求其度数；若改变，请说明理由．考点：三角形内角和定理；坐标与图形性质．专题：证明题．分析：（1）由直角三角形两锐角互余及等角的余角相等即可证明；（2）由直角三角形两锐角互余、等量代换求得∠DOB=∠EOB=∠OAE=∠E；然后根据外角定理知∠DOB+∠EOB+∠OEA=90°；从而求得∠DOB=30°，即∠A=30°；（3）由角平分线的性质知∠FOM=45°﹣∠AOC ①，∠PCO=∠A+∠AOC ②，根据①②解得∠PCO+∠FOM=45°+∠A，最后根据三角形内角和定理求得旋转后的∠P的度数．解答：（1）证明：∵△AOB是直角三角形，∴∠A+∠B=90°，∠AOC+∠BOC=90°，∵∠A=∠AOC，∴∠B=∠BOC；解：（2）∵∠A+∠ABO=90°，∠DOB+∠ABO=90°，∴∠A=∠DOB，又∵∠DOB=∠EOB，∠A=∠E，∴∠DOB=∠EOB=∠OAE=∠OEA，∵∠DOB+∠EOB+∠OEA=90°，∴∠A=30°；（3）∠P的度数不变，∠P=25°．理由如下：（只答不变不得分）∵∠AOM=90°﹣∠AOC，∠BCO=∠A+∠AOC，又∵OF平分∠AOM，CP平分∠BCO，∴∠FOM=45°﹣∠AOC ①，∠PCO=∠A+∠AOC ②，①+②得：∠PCO+∠FOM=45°+∠A，∴∠P=180°﹣（∠PCO+∠FOM+90°）=180°﹣（45°+∠A+90°）=180°﹣（45°+20°+90°）=25°．点评：本题综合考查了三角形内角和定理、坐标与图形的性质．解答时，需注意，△ABO 旋转后的形状与大小均无变化．2．在平面直角坐标系中，A（﹣1，0），B（0，2），点C 在x轴上．（1）如图（1），若△ABC的面积为3，则点C的坐标为（2，0）或（﹣4，0）．（2）如图（2），过点B点作y轴的垂线BM，点E是射线BM上的一动点，∠AOE的平分线交直线BM于F，OG⊥OF且交直线BM于G，当点E在射线BM上滑动时，的值是否变化？若不变，请求出其值；若变化，请说明理由．考点：三角形内角和定理；坐标与图形性质；垂线；平行线的性质；三角形的面积；三角形的外角性质．分析：（1）利用A，B点坐标，△ABC的面积为3，得出AC的长，进而得出C点坐标；（2）首先根据已知得出∠EOG=∠EOx，进而得出FM∥x轴，再利用已知得出∠BOF=∠EGO，即可得出∠BEO=2∠BOF，得出答案即可．解答：解：（1）∵A（﹣1，0），B（0，2），点C在x轴上．△ABC的面积为3，∴AC的长为3，则点C的坐标为（2，0）或（﹣4，0）；故答案为：（2，0）或（﹣4，0）；（2）∵∠AOE+∠EOx=180°，∴∠AOE+∠EOx=90°，即∠EOF+∠EOx=90°∵∠EOF+∠EOG=90°，∴∠EOG=∠EOx，∴FM∥x轴，∴∠GOx=∠EGO，∴∠EOG=∠EGO，∴∠BEO=2∠EGO，∵∠FOG=90°，∴∠EGO+∠OFG=90°，∵FM⊥y轴，∴∠BOF+∠OFG=90°，∴∠BOF=∠EGO，∴∠BEO=2∠BOF，∴=2．点评：此题主要考查了三角形内角和定理应用以及平行线的判定和三角形面积求法等知识，根据已知得出FM∥x轴以及∠BOF=∠EGO是解题关键．3．如图1，在平面直角坐标系中，A（a，0），B（b，0），C（﹣1，2），且|2a+b+1|+（a+2b﹣4）2=0．（1）求a，b的值；（2）①在x轴的正半轴上存在一点M，使△COM的面积=△ABC的面积，求出点M的坐标；②在坐标轴的其它位置是否存在点M，使△COM的面积=△ABC的面积仍然成立？若存在，请直接写出符合条件的点M 的坐标；（3）如图2，过点C作CD⊥y轴交y轴于点D，点P为线段CD延长线上一动点，连接OP，OE平分∠AOP，OF⊥OE．当点P运动时，的值是否会改变？若不变，求其值；若改变，说明理由．考点：三角形内角和定理；非负数的性质：绝对值；非负数的性质：偶次方；解二元一次方程组；三角形的面积；三角形的外角性质．分析：（1）根据非负数的性质即可列出关于a，b的方程组求得a，b的值；（2）①过点C做CT⊥x轴，CS⊥y轴，垂足分别为T、S，根据三角形的面积公式即可求得OM的长，则M的坐标即可求得；②根据三角形的面积公式，即可写出M的坐标；（3）利用∠BOF根据平行线的性质，以及角平分线的定义表示出∠OPD和∠DOE 即可求解．解答：解：（1）∵|2a+b+1|+（a+2b﹣4）2=0，又∵|2a+b+1|≥0，（a+2b﹣4）2≥0，∴|2a+b+1|=0且（a+2b﹣4）2=0．∴∴即a=﹣2，b=3．（2）①过点C做CT⊥x轴，CS⊥y轴，垂足分别为T、S．∵A（﹣2，0），B（3，0），∴AB=5，因为C（﹣1，2），∴CT=2，CS=1，△ABC的面积=AB•CT=5，要使△COM的面积=△ABC的面积，即△COM的面积=，所以OM•CT=，∴OM=2.5．所以M的坐标为（2.5，0）．②存在．点M的坐标为（0，5）或（﹣2.5，0）或（0，﹣5）．（3）的值不变，理由如下：∵CD⊥y轴，AB⊥y轴∴∠CDO=∠DOB=90°∴AB∥CD∴∠OPD=∠POB∵OF⊥OE∴∠POF+∠POE=90°，∠BOF+∠AOE=90°∵OE平分∠AOP∴∠POE=∠AOE∴∠POF=∠BOF∴∠OPD=∠POB=2∠BOF∵∠DOE+∠DOF=∠BOF+∠DOF=90°∴∠DOE=∠BOF∴∠OPD=2∠BOF=2∠DOE∴．点评：本题考查了非负数的性质，三角形的面积公式，以及角平分线的定义，平行线的性质，求点的坐标问题常用的方法就是转化成求线段的长的问题．4．长方形OABC，O为平面直角坐标系的原点，OA=5，OC=3，点B在第三象限．（1）求点B的坐标；（2）如图1，若过点B的直线BP与长方形OABC的边交于点P，且将长方形OABC的面积分为1：4两部分，求点P 的坐标；（3）如图2，M为x轴负半轴上一点，且∠CBM=∠CMB，N 是x轴正半轴上一动点，∠MCN的平分线CD交BM的延长线于点D，在点N运动的过程中，的值是否变化？若不变，求出其值；若变化，请说明理由．考点：平行线的判定与性质；坐标与图形性质；三角形的面积．分析：（1）根据第三象限点的坐标性质得出答案；（2）利用长方形OABC的面积分为1：4两部分，得出等式求出AP的长，即可得出P点坐标，再求出PC的长，即可得出OP的长，进而得出答案；（3）首先求出∠MCF=2∠CMB，即可得出∠CNM=∠NCF=∠MCF﹣∠NCM=2∠BMC﹣2∠DCM，得出答案．解答：解：（1）∵四边形OABC为长方形，OA=5，OB=3，且点B在第三象限，∴B（﹣5，﹣3）．（2）若过点B的直线BP与边OA交于点P，依题意可知：×AB×AP=×OA×OC，即×3×AP=×5×3，∴AP=2∵OA=5，∴OP=3，∴P（﹣3，0），若过点B的直线BP与边OC交于点P，依题意可知：×BC×PC=×OA×OC，即×5×PC=×5×3，∴PC=∵OC=3，∴OP=，∴P（0，﹣）．综上所述，点P的坐标为（﹣3，0）或（0，﹣）．（3）延长BC至点F，∵四边形OABC为长方形，∴OA∥BC．∴∠CBM=∠AMB，∠AMC=∠MCF．∵∠CBM=∠CMB，∴∠MCF=2∠CMB．过点M作ME∥CD交BC于点E，∴∠EMC=∠MCD．又∵CD平分∠MCN，∴∠NCM=2∠EMC．∴∠D=∠BME=∠CMB﹣∠EMC，∠CNM=∠NCF=∠MCF﹣∠NCM=2∠BMC﹣2∠DCM=2∠D，∴=．点评：此题主要考查了平行线的性质以及矩形的性质、图形面积求法等知识，利用数形结合得出的是解题关键．5．如图，直线AB∥CD．（1）在图1中，∠BME、∠E，∠END的数量关系为：∠E=∠BME+∠END；（不需证明）在图2中，∠BMF、∠F，∠FND的数量关系为：∠BMF=∠F+∠FND；（不需证明）（2）如图3，NE平分∠FND，MB平分∠FME，且2∠E与∠F互补，求∠FME的大小．（3）如图4中，∠BME=60°，EF平分∠MEN，NP平分∠END，EQ∥NP，则∠FEQ的大小是否发生变化？若变化，说明理由；若不变化，求∠FEQ的度数．考点：平行线的性质．分析：（1）过点E作EF∥AB，根据两直线平行，内错角相等可得∠BME=∠1，∠END=∠2，然后相加即可得解；先根据两直线平行，同位角相等求出∠3=∠FND，再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解；（2）设∠END=x°，∠BNE=y°，根据（1）的结论可得x+y=∠E，2x+∠F=y，然后消掉x并表示出y，再根据2∠E与∠F互补求出y，然后根据角平分线的定义求解即可；（3）根据（1）的结论表示出∠MEN，再根据角平分线的定义表示出∠FEN和∠ENP，再根据两直线平行，内错角相等可得∠NEQ=∠ENP，然后根据∠FEQ=∠FEN﹣∠NEQ整理即可得解．解答：解：（1）如图1，过点E作EF∥AB，∵AB∥CD，∴AB∥EF∥CD，∴∠BME=∠1，∠END=∠2，∴∠1+∠2=∠BME+∠END，即∠E=∠BME+∠END；如图2，∵AB∥CD，∴∠3=∠FND，∴∠BMF=∠F+∠3=∠F+∠FND，即∠BMF=∠F+∠FND；故答案为：∠E=∠BME+∠END；∠BMF=∠F+∠FND；（2）如图3，设∠END=x°，∠BNE=y°，由（1）的结论可得x+y=∠E，2x+∠F=y，消掉x得，3y=2∠E+∠F，∵2∠E与∠F互补，∴2∠E+∠F=180°，∴3y=180°，解得y=60°，∵MB平分∠FME，∴∠FME=2y=2×60°=120°；（3）由（1）的结论得，∠MEN=∠BME+∠END，∵EF平分∠MEN，NP平分∠END，∴∠FEN=∠MEN=（∠BME+∠END），∠ENP=∠END，∵EQ∥NP，∴∠NEQ=∠ENP，∴∠FEQ=∠FEN﹣∠NEQ=（∠BME+∠END）﹣∠END=∠BME，∵∠BME=60°，∴∠FEQ=×60°=30°．点评：本题考查了平行线的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，角平分线的定义，此类题目，过拐点作平行线是解题的关键，准确识图理清图中各角度之间的关系也很重要．6．在平面直角坐标系中，点B（0，4），C（﹣5，4），点A是x轴负半轴上一点，S四边形AOBC=24．（1）线段BC的长为5，点A的坐标为（﹣7，0）；（2）如图1，BM平分∠CBO，CM平分∠ACB，BM交CM于点M，试给出∠CMB与∠CAO之间满足的数量关系式，并说明理由；（3）若点P是在直线CB与直线AO之间的一点，连接BP、OP，BN平分∠CBP，ON平分∠AOP，BN交ON于N，请依题意画出图形，给出∠BPO与∠BNO之间满足的数量关系式，并说明理由．考点：三角形内角和定理；坐标与图形性质；三角形的面积；三角形的外角性质．专题：分类讨论．分析：（1）根据点B、C的横坐标求出BC的长度即可；再根据四边形的面积求出OA的长度，然后根据点A在y轴的负半轴写出点A的坐标；（2）根据两直线平行，同旁内角互补用∠CAO表示出∠ACB，再根据角平分线的定义表示出∠MAB和∠MBC，然后利用三角形的内角和定理列式整理即可得解；（3）分①点P在OB的左边时，根据三角形的内角和定理表示出∠PBO+∠POB，再根据两直线平行，同旁内角互补和角平分线的定义表示出∠NBP+∠NOP，然后在△NBO中，利用三角形的内角和定理列式整理即可得解；②点P在OB的右边时，求出∠CBP+∠AOP+∠BPO=360°，再根据角平分线的定义表示出∠PBN+∠PON，然后利用四边形的内角和定理列式整理即可得解．解答：解：（1）∵点B（0，4），C（﹣5，4），∴BC=5，S四边形AOBC=（BC+OA）•OB=（5+OA）•4=24，解得OA=7，所以，点A的坐标为（﹣7，0）；（2）∵点B、C的纵坐标相同，∴BC∥OA，∴∠ACB=180°﹣∠CAO，∠CBO=90°，∵BM平分∠CBO，CM平分∠ACB，∴∠MCB=（180°﹣∠CAO）=90°﹣∠CAO，∠MBC=∠CBO=×90°=45°，在△MBC中，∠CMB+∠MCB+∠MBC=180°，即∠CMB+90°﹣∠CAO+45°=180°，解得∠CMB=45°+∠CAO；（3）①如图1，当点P在OB左侧时，∠BPO=2∠BNO．理由如下：在△BPO中，∠PBO+∠POB=180°﹣∠BPO，∵BC∥OA，BN平分∠CBP，ON平分∠AOP，∴∠NBP+∠NOP=（180°﹣∠PBO﹣∠POB），在△NOB中，∠BNO=180°﹣（∠NBP+∠NOP+∠PBO+∠POB），=180°﹣[（180°﹣∠PBO﹣∠POB）+∠PBO+∠POB]，=90°﹣（∠PBO+∠POB），=90°﹣（180°﹣∠BPO），=∠BPO，∴∠BPO=2∠BNO；②如图2，当点P在OB右侧时，∠BNO+∠BPO=180°．理由如下：∵BC∥OA，∴∠CBP+∠AOP+∠BPO=360°，∵BN平分∠CBP，ON平分∠AOP，∴∠PBN+∠PON+∠BPO=×360°=180°，∴∠PBN+∠PON=180°﹣∠BPO，在四边形BNOP中，∠BNO=360°﹣∠PBN﹣∠PON﹣∠BPO=360°﹣（180°﹣∠BPO）﹣∠BPO=180°﹣∠BPO，∴∠BNO+∠BPO=180°．点评：本题考查了三角形的内角和定理，角平分线的定义，平行线的性质，以及坐标与图形性质，准确识图理清图中各角度之间的关系是解题关键，（3）要注意分情况讨论．7．如图1，在平面直角坐标系中，四边形OBCD各个顶点的坐标分别是O（0，0），B（2，6），C（8，9），D （10，0）；（1）三角形BCD的面积=30（2）将点C平移，平移后的坐标为C′（2，8+m）；①若S△BDC′=32，求m的值；②当C′在第四象限时，作∠C′OD的平分线OM，OM交于C′C于M，作∠C′CD的平分线CN，CN交OD于N，OM与CN相交于点P（如图2），求的值．考点：作图-平移变换；坐标与图形性质；三角形内角和定理．分析：（1）三角形BCD的面积=正方形的面积﹣3个小三角形的面积；（2）①分平移后的坐标为C′在B点的上方；在B点的下方两种情况讨论可求m 的值；②利用外角以及角平分线的性质得出∠ODC+∠CC′O=2∠P，即可得出答案．解答：解：（1）三角形BCD的面积为：×6×10=30；故答案为：30；（2）①当C在x轴上方，如图1所示：∵S△BDC′=32，D到BC″的距离为8，∴BC″=8，∵B（2，6），∴8+m=14，∴m=6，∵AB=6，BC′=8，∴C′在x轴下方，且AC′=2，∴8+m=﹣2，∴m=﹣10，即m=6或m=﹣10；②如图2，在△OC′M中，∵∠OMC是∠OMC′的外角，∴∠2+∠6=∠OMC，在△PMC中，∵∠OMC是∠CMP的外角，∴∠4+∠P=∠OMC，∴∠2+∠6=∠4+∠P，在△CND中，∵∠ONC是∠CND的外角，∴∠3+∠7=∠ONC，在△ONP中，∵∠ONC是∠ONP的外角，∴∠1+∠P=∠ONC，∴∠3+∠7=∠1+∠P，∴∠3+∠7+∠2+∠6=∠4+∠P+∠1+∠P，∵∠2=∠1，∠3=∠4，∴∠6+∠7=2∠P，∴∠ODC+∠CC′O=2∠P，∴=．点评：此题主要考查了外角的性质以及三角形面积求法和点坐标性质等知识，利用数形结合得出C′的不同位置是解题关键．8．如图，四边形ABCD中，AD∥BC，DE平分∠ADB，∠BDC=∠BCD．（1）求证：∠1+∠2=90°；（2）若∠ABD的平分线与CD的延长线交于F，且∠F=55°，求∠ABC；（3）若H是BC上一动点，F是BA延长线上一点，FH交BD于M，FG平分∠BFH，交DE于N，交BC于G．当H在BC上运动时（不与B点重合），的值是否变化？如果变化，说明理由；如果不变，试求出其值．考点：等腰三角形的性质；角平分线的定义；平行线的性质．专题：综合题．分析：本题考查了等腰三角形的性质、角平分线的性质以及平行线的性质，解决问题的关键在于熟悉掌握知识要点，并且善于运用角与角之间的联系进行传递．（1）由AD∥BC，DE平分∠ADB，得∠ADC+∠BCD=180，∠BDC=∠BCD，得出∠1+∠2=90°；（2）由DE平分∠ADB，CD平分∠ABD，四边形ABCD中，AD∥BC，∠F=55°，得出∠ABC=∠ABD+∠DBC=∠ABD+∠ADB，即∠ABC=70°；（3）在△BMF中，根据角之间的关系∠BMF=180°﹣∠ABD﹣∠BFH，得∠GND=180°﹣∠AED﹣∠BFG，再根据角之间的关系得∠BAD=﹣∠DBC，在综上得出答案．解答：（1）证明：AD∥BC，∠ADC+∠BCD=180，∵DE平分∠ADB，∠BDC=∠BCD，∴∠ADE=∠EDB，∠BDC=∠BCD，∵∠ADC+∠BCD=180°，∴∠EDB+∠BDC=90°，∠1+∠2=90°．解：（2）∠FBD+∠BDE=90°﹣∠F=35°，∵DE平分∠ADB，BF平分∠ABD，∴∠ADB+∠ABD=2（∠FBD+∠BDE）=70°，又∵四边形ABCD中，AD∥BC，∴∠DBC=∠ADB，∴∠ABC=∠ABD+∠DBC=∠ABD+∠ADB，即∠ABC=70°；（3）的值不变．证明：在△BMF中，∠BMF=∠DMH=180°﹣∠ABD﹣∠BFH，又∵∠BAD=180°﹣（∠ABD+∠ADB），∠DMH+∠BAD=（180°﹣∠ABD﹣∠BFH）+（180°﹣∠ABD﹣∠ADB），=360﹣∠BFH﹣2∠ABD﹣∠ADB，∠DNG=∠FNE=180°﹣∠BFH﹣∠AED，=180°﹣∠BFH﹣∠ABD﹣∠ADB，=（∠DMH+∠BAD），∴=2．点评：本题考查等腰三角形的性质及三角形内角和定理；此题为探索题，比较新颖，实际涉及的知识不多．9．如图（1）所示，一副三角板中，含45°角的一条直角边AC在y轴上，斜边AB交x轴于点G．含30°角的三角板的顶点与点A重合，直角边AE和斜边AD分别交x轴于点F、H．（1）若AB∥ED，求∠AHO的度数；（2）如图2，将三角板ADE绕点A旋转．在旋转过程中，∠AGH的平分线GM与∠AHF的平分线HM相交于点M，∠COF的平分线ON与∠OFE的平分线FN相交于点N．①当∠AHO=60°时，求∠M的度数；②试问∠N+∠M的度数是否发生变化？若改变，求出变化范围；若保持不变，请说明理由．考点：三角形内角和定理；角平分线的定义；平行线的性质；三角形的外角性质．专题：综合题．分析：（1）由AB∥ED可以得到∠BAD=∠D=60°，即∠BAC+∠CAD=60°，然后根据已知条件即可求出∠AHO；（2）①由∠AHO+∠AHF=180°，∠AHO=60°，可以求出∠AHF，而HM是∠AHF 的平分线，GM是∠AGH的平分线，∠MHF=∠MGH+∠M，由此即可求出∠M；②∠N+∠M的度数不变，当∠BAC与∠DAE没有重合部分时，∠GAH﹣∠OAF=（45°+∠OAH）﹣（30°+∠OAH）=15°；当AC与AD在一条直线上时，∠GAH﹣∠OAF=45°﹣30°=15°；当∠BAC与∠DAE有重合部分时，∠GAH﹣∠OAF=（45°﹣∠OAH）﹣（30°﹣∠OAH）=15°，即∠GAH﹣∠OAF=15°．而根据已知条件∠M=∠MHF﹣∠MGH=∠AHF﹣∠AGH=∠GAH，∠N=180°﹣（∠OFE+90°）=180°﹣（∠OAF+90°）﹣90°=90°﹣∠OAF，由此即可得到结论．解答：解：（1）∵AB∥ED∴∠BAD=∠D=60°（两直线平行，内错角相等），即∠BAC+∠CAD=60°．∵∠BAC=45°，∴∠CAD=60°﹣45°=15°，∠AHO=90°﹣∠CAD=75°；（2）①∵∠AHO+∠AHF=180°，∠AHO=60°，∴∠AHF=180°﹣60°=120°∵HM是∠AHF的平分线，∴∠MHF=∠AHF=60°（角平分线的定义）．∵GM是∠AGH的平分线，∠AGH=45°，∴∠MGH=∠AGH=22.5°，∵∠MHF=∠MGH+∠M，∴∠M=60°﹣22.5°=37.5°；②∠N+∠M的度数不变，理由是：当∠BAC与∠DAE没有重合部分时，∠GAH﹣∠OAF=（45°+∠OAH）﹣（30°+∠OAH）=15°；当AC与AD在一条直线上时，∠GAH﹣∠OAF=45°﹣30°=15°；当∠BAC与∠DAE有重合部分时，∠GAH﹣∠OAF=（45°﹣∠OAH）﹣（30°﹣∠OAH）=15°；∴∠GAH﹣∠OAF=15°．易得出∠M=∠MHF﹣∠MGH=∠AHF﹣∠AGH=∠GAH，∠N=180°﹣（∠OFE+90°）=180°﹣（∠OAF+90°）﹣90°=90°﹣∠OAF，∴∠M+∠N=∠GAH+90°﹣∠OAF=90°+×15°=97.5°（定值）．点评：此题比较复杂，考查了三角形的内角和、三角形的外角的性质、角平分线的性质、平行线的性质等多个知识，综合性比较强，难度比较大，学生首先心理上要相信自己，才能有信心解决问题．。

初中几何经典例题及解题技巧之令狐文艳创作

初中几何经典例题及解题技巧之令狐文艳创作

初中几何证明技巧及经典试题令狐文艳证明两线段相等1.两全等三角形中对应边相等。

2.同一三角形中等角对等边。

3.等腰三角形顶角的平分线或底边的高平分底边。

4.平行四边形的对边或对角线被交点分成的两段相等。

5.直角三角形斜边的中点到三顶点距离相等。

6.线段垂直平分线上任意一点到线段两段距离相等。

7.角平分线上任一点到角的两边距离相等。

8.过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等。

*9.同圆（或等圆）中等弧所对的弦或与圆心等距的两弦或等圆心角、圆周角所对的弦相等。

*10.圆外一点引圆的两条切线的切线长相等或圆内垂直于直径的弦被直径分成的两段相等。

11.两前项（或两后项）相等的比例式中的两后项（或两前项）相等。

*12.两圆的内（外）公切线的长相等。

13.等于同一线段的两条线段相等。

证明两个角相等1.两全等三角形的对应角相等。

2.同一三角形中等边对等角。

3.等腰三角形中，底边上的中线（或高）平分顶角。

4.两条平行线的同位角、内错角或平行四边形的对角相等。

5.同角（或等角）的余角（或补角）相等。

*6.同圆（或圆）中，等弦（或弧）所对的圆心角相等，圆周角相等，弦切角等于它所夹的弧对的圆周角。

*7.圆外一点引圆的两条切线，圆心和这一点的连线平分两条切线的夹角。

8.相似三角形的对应角相等。

*9.圆的内接四边形的外角等于内对角。

10.等于同一角的两个角相等。

证明两条直线互相垂直1.等腰三角形的顶角平分线或底边的中线垂直于底边。

2.三角形中一边的中线若等于这边一半，则这一边所对的角是直角。

3.在一个三角形中，若有两个角互余，则第三个角是直角。

4.邻补角的平分线互相垂直。

5.一条直线垂直于平行线中的一条，则必垂直于另一条。

6.两条直线相交成直角则两直线垂直。

7.利用到一线段两端的距离相等的点在线段的垂直平分线上。

8.利用勾股定理的逆定理。

9.利用菱形的对角线互相垂直。

*10.在圆中平分弦（或弧）的直径垂直于弦。

初高中数学几何衔接之令狐文艳创作

初高中数学几何衔接之令狐文艳创作

初高中衔接教材编排令狐文艳第一部分相交线1角的定义：具有公共端点的两条射线组成的图形叫做角。

这个公共端点叫做角的顶点，这两条射线叫做角的两条边。

表示方法符号：∠两条相交线出现四个角2余角和补角：两角之和为90°则两角互为余角，两角之和为180°则两角互为补角。

等角的余角相等，等角的补角相等3对顶角的定义如果一个角的两边分别是另一个角两边的反向延长线,且这两个角有公共顶点,那么这两个角是对顶角如图1，两条直线相交，构成两对对顶角。

∠1与∠3为一对对顶角，∠2与∠4为一对对顶角。

图1注意：1.对顶角一定相等，但是相等的角不一定是对顶角。

2.对顶角必须有共同顶点。

3.对顶角是成对出现的。

在证明过程中使用对顶角的性质时，以图1为例，∴∠1=∠3，∠2=∠4(对顶角相等)。

4同位角，内错角，同旁内角同位角：两条直线被第三条直线所截,在截线的同旁,被截两直线的同一方,我们把这种位置关系的角称为同位角.互为同位角的有：∠1与∠5,∠2与∠6,∠4与∠8,∠3与∠7；内错角：两条直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫做内错角.互为内错角的有：∠3与∠5,∠2与∠8同旁内角：两条直线被第三条直线所截,在两条直线之间,并在第三条直线同旁的两个角称为同旁内角 .互为同旁内角的有：∠3与∠8,∠2与∠5例题【基础题】请找出图中的同位角，内错角，同旁内角例题、【基础题】如图，O是直线AB一点，∠BOD=∠COE=90º，则（1）如果∠1=30º，那么∠2=，∠3= 。

（2）和∠1互为余角的有。

和∠1相等的角有。

例题【基础】32º的余角为，137º的补角是。

第二部分平行线1．定义在同一平面内，不相交的两条直线叫做平行线.2．特征在同一平面内【必须满足，这是一个难点】不相交说明强调在一个平面内，是因为高中的时候会出现一条线和一个面，那么这个时候存在着线和这个面内的有些直线不平行的问题，这个有点难理解。

初中数学内容提纲之令狐文艳创作

初中数学内容提纲之令狐文艳创作

初中数学内容提纲令狐文艳代数部分（一）有理数1．有理数的概念有理数。

数轴。

相反数。

数的绝对值。

有理数大小的比较。

（1）有理数的意义，用正数与负数表示相反意义的量，把给出的有理数归类。

（2）数轴、相反数、绝对值等概念和数轴的画法，用数轴上的点表示整数或分数（以刻度尺为工具），求有理数的相反数与绝对值（绝对值符号内不含字母）。

（3）有理数大小比较的法则，用不等号连接两个或两个以上不同的有理数。

2．有理数的运算有理数的加法与减法。

代数和。

加法运算律。

有理数的乘法与除法。

倒数。

乘法运算律。

有理数的乘方。

有理数的混的运算。

科学记数法。

近似数与有效数字。

（1）有理数的加、减、乘、除、乘方的意义，有理数的运算法则、运算律、运算顺序以及有理数的混合运算（不超过6个数），运用运算律简化运算。

（2）倒数概念，求有理数的倒数。

（3）大于10的有理数的科学记数法。

（4）近似数与有效数字的概念，根据指定的精确度或有效数字的个数，用四舍五入法求有理数的近似数；用计算器求一个数的平方与立方（尚无条件的学校可使用算表）。

（5）有理数的加法与减法、乘法与除法可以相互转化。

（二）整式的加减代数式。

代数式的值。

整式。

单项式。

多项式。

合并同类项。

去括号与添括号。

数与整式相乘。

整式的加减法。

（1）用字母表示有理数。

（2）代数式、代数式的值的概念，列出代数式表示简单的数量关系，求代数式的值。

（3）整式、单项式及其系数与次数、多项式次数、项与项数的概念，把一个多项式按某个字母降幂排列或升幂排列。

（4）合并同类项的方法，去括号、添括号的法则，数与整式相乘的运算以及整式的加减运算。

（5）用字母表示数、列代数式和求代数式的值、整式的加减，抽象概括的思维方法和特殊与一般的辩证关系。

（三）一元一次方程等式。

等式的基本性质。

方程和方程的解。

解方程。

一元一次方程及其解法。

一元一次方程的应用。

（1）等式和方程的有关概念，等式的基本性质，检验一个数是不是某个一元方程的解。

图形的平移翻折与旋转13之令狐文艳创作

图形的平移翻折与旋转13之令狐文艳创作

4.1图形的平移令狐文艳例1 2015年泰安市中考第15题如图1，在平面直角坐标系中，正三角形OAB的顶点B的坐标为（2, 0），点A在第一象限内，将△OAB沿直线OA的方向平移至△O′B′A′的位置，此时点A′的横坐标为3，则点B′的坐标为（）．） B．（3，）C．（4，D．（3，A．（4，图1 图2动感体验请打开几何画板文件名“15泰安15”，拖动点A'运动的过程中，可以体验到，△A′OC保持等边三角形的形状．答案A．思路如下：如图2，当点B的坐标为（2, 0），点A的横坐标为1．当点A'的横坐标为3时，等边三角形A′OC的边长为6．在Rt△B′CD中，B′C＝4，所以DC＝2，B′D＝时B′(4,．例2 2014年江西省中考第11题如图，在△ABC中，AB＝4，BC＝6，∠B＝60°，将△ABC 沿射线BC方向平移2个单位后，得到△A′B′C′，联结A′C，则△A′B′C的周长为_______．动感体验请打开几何画板文件名“14江西11”，拖动点B′运动，可以体验到，△A′B′C′向右移动2个单位后，△A′B′C是等边三角形．答案12．4.2图形的翻折例1 2015年上海市宝山区嘉定区中考模拟第18题如图1，在矩形ABCD中，AD＝15，点E在边DC上，联结AE，△ADE沿直线AE翻折后点D落到点F，过点F作FG⊥AD，垂足为G ．如果AD ＝3GD ，那么DE ＝_____．图1动感体验请打开几何画板文件名“15宝山嘉定18”，拖动点E 在DC 上运动，可以体验到，△ADE 与△AFE 保持全等，△AMF 与△FNE 保持相似（如图2所示）． 答案．思路如下：如图2，过点F 作AD 的平行线交AB 于M ，交DC 于N ． 因为AD ＝15，当AD ＝3GD 时，MF ＝AG ＝10，FN ＝GD ＝5． 在Rt △AMF 中，AF ＝AD ＝15，MF ＝10，所以AM ＝设DE ＝m ，那么NE ＝m ．由△AMF ∽△FNE ，得AM FNMF NE =，即10=．解得m ＝． 图2例2 2014年上海市中考第18题如图，已知在矩形ABCD 中，点E 在边BC 上，BE ＝2CE ，将矩形沿着过点E 的直线翻折后，点C 、D 分别落在边BC 下方的点C ′、D ′处，且点C ′、D ′、B 在同一条直线上，折痕与边AD 交于点F ，D ′F 与BE 交于点G ．设AB ＝t ，那么△EFG 的周长为______________（用含t 的代数式表示）．图1动感体验请打开几何画板文件名“14福州10”，拖动点F 在AD 上运动，可以体验到，当点C ′、D ′、B 在同一条直线上时，直角三角形BCE 的斜边BE 等于直角边C ′E 的2倍，△BCE 是30°角的直角三角形，此时△EFG 是等边三角形（如图2）． 答案．思路如下：如图2，等边三角形EFG 的高＝AB ＝t ，．图24.3图形的旋转例1 2015年扬州市中考第17题如图1，已知Rt△ABC中，∠ABC＝90°，AC＝6，BC＝4，将△ABC绕直角顶点C顺时针旋转90°得到△DEC，若点F是DE的中点，连接AF，则AF= ．图1 图2动感体验请打开几何画板文件名“15扬州17”，拖动点D绕着点C旋转，可以体验到，当旋转角为90°时，FH是△ECD的中位线，AF是直角三角形AHF的斜边．答案5．思路如下：如图2，作FH⊥AC于H．由于F是ED的中点，所以HF是△ECD的中位线，所以HF＝3．由于AE＝AC－EC＝6－4＝2，EH＝2，所以AH＝4．所以AF＝5．例2 2014年上海市黄浦区中考模拟第18题如图1，在△ABC中，AB＝AC＝5，BC＝4，D为边AC上一点，且AD＝3，如果△ABD绕点A逆时针旋转，使点B与点C重合，点D旋转至D'，那么线段DD'的长为．图1动感体验请打开几何画板文件名“14黄浦18”，拖动点B'绕点A逆时针旋转，可以体验到，两个等腰三角形ABB'与等腰三角形ADD'保持相似（如图2）．．思路如下：如图3，由△ABC∽△ADD'，可得．5∶4＝答案1253∶DD'．图 2 图34.4三角形例1 2015年上海市长宁区中考模拟第18题如图1，△ABC≌△DEF（点A、B分别与点D、E对应），AB＝AC＝5，BC＝6．△ABC固定不动，△DEF运动，并满足点E在BC边从B向C移动（点E不与B、C重合），DE始终经过点A，EF与AC边交于点M，当△AEM是等腰三角形时，BE＝_________．图1动感体验请打开几何画板文件名“15长宁18”，拖动点E 在BC 上运动，可以体验到，△AEM 有三个时刻成为等腰三角形，其中一个时刻点E 与点B 重合． 答案116或1．思路如下： 设BE ＝x ．由△ABE ∽△ECM ，得AB EA EC ME =，即56EA x ME=-． 等腰三角形AEM 分三种情况讨论：①如图2，如果AE ＝AM ，那么△AEM ∽△ABC ． 所以5566EA ME x ==-．解得x ＝0，此时E 、B 重合，舍去．②如图3，当EA ＝EM 时，516EA x ME ==-．解得x ＝1． ③如图4，当MA ＝ME 时，△MEA ∽△ABC ．所以6556EA ME x ==-．解得x ＝116． 图 2 图 3图4例2 2014年泰州市中考第16题如图1，正方形ABCD 的边长为3cm ，E 为CD 边上一点，∠DAE ＝30°，M 为AE 的中点，过点M 作直线分别与AD 、BC 相交于点P 、Q ．若PQ ＝AE ，则AP 的长等于__________cm ．图1动感体验请打开几何画板文件名“14泰州16”，拖动点P 在AD 上运动，观察度量值，可以体验到，存在两个时刻PQ ＝AE ． 答案 1或2．思路如下：如图2，当PQ ＝AE 时，可证PQ 与AE 互相垂直．在Rt △ADE 中，由∠DAE ＝30°，AD ＝3，可得AE ＝． 在Rt △APM 中，由∠PAM ＝30°，AMAP ＝2． 在图3中，∠ADF ＝30°，当PQ ＝DF 时，DP ＝2，所以AP ＝1．图2 图34.5四边形例1 2015年安徽省中考第9题如图1，矩形ABCD 中，AB ＝8，BC ＝4．点E 在边AB 上，点F 在边CD 上，点G 、H 在对角线AC 上．若四边形EGFH 是菱形，则AE 的长是（ ）．A ．．．5D ．6图1动感体验请打开几何画板文件名“15安徽09”，拖动点E 在AB 上运动，可以体验到，当EF 与AC 垂直时，四边形EGFH 是菱形（如图2）．答案C ．思路如下：如图3，在Rt △ABC 中，AB ＝8，BC ＝4，所以AC ＝由cos ∠BAC ＝AB AOAC AE =AE =．所以AE ＝5．图2 图3例2 2014年广州市中考第8题将四根长度相等的细木条首尾相接，用钉子钉成四边形ABCD ，转动这个四边形，使它形状改变．当∠B ＝90°时，如图1，测得AC ＝2．当∠B ＝60°时，如图2，AC 等于（ ）． (A)； (B)2； (C)； (D)．图 1图2动感体验请打开几何画板文件名“14广州08”，拖动点A 绕着点B 旋转，可以体验到，当∠B ＝90°时，△ABC 是等腰直角三角形；当∠B ＝60°时，△ABC 是等边三角形（如图3）． 答案(A)．思路如下：4.6圆例1 2015年兰州市中考第15题如图1，⊙O 的半径为2，AB ，CD 是互相垂直的两条直径，点P 是⊙O 上任意一点（P 与A ，B ，C ，D 不重合），过点P 作PM ⊥AB 于点M ，PN ⊥CD 于点N ，点Q 是MN 的中点，当点P 沿着圆周转过45°时，点Q 走过的路径长为__________． A. 4π B. 2π C. 6π D.3π 图1动感体验请打开几何画板文件名“15兰州15”，拖动点P 在圆周上运动一周，可以体验到，当点P 沿着圆周转过45°时，点Q 走过的路径是圆心角为45°半径为1的一段弧．答案A ．思路如下：如图2，四边形PMON 是矩形，对角线MN 与OP 互相平分且相等，因此点Q 是OP 的中点．如图3，当∠DOP ＝45°时，'D Q 的长为121=84ππ⨯⨯． 图2 图3例2 2014年温州市中考第16题如图1，在矩形ABCD 中，AD ＝8，E 是AB 边上一点，且AE ＝14AB ，⊙O 经过点E ，与边CD 所在直线相切于点G （∠GEB 为锐角），与边AB 所在直线相交于另一点F ，且EG ∶EF∶2．当边AD 或BC 所在的直线与⊙O 相切时，AB 的长是________．图1动感体验请打开几何画板文件名“14温州16”，拖动点B 运动，可以体验到，⊙O 的大小是确定的，⊙O 既可以与BC 相切（如图3），也可以与AD 相切（如图4）．答案12或4．思路如下：如图2，在Rt △GEH 中，由GH ＝8，EG ∶EF∶2，可以得到EH ＝4．在Rt △OEH 中，设⊙O 的半径为r ，由勾股定理，得r 2＝42＋(8－r )2．解得r ＝5．设AE ＝x ，那么AB ＝4x ．如图3，当⊙O 与BC 相切时，HB ＝r ＝5．由AB ＝AE ＋EH ＋HB ，得4x ＝x ＋4＋5．解得x ＝3．此时AB ＝12．如图4，当⊙O 与AD 相切时，HA ＝r ＝5．由AE ＝AH －EH ，得x ＝5－4＝1．此时AB ＝4．图 2 图 3图44.7函数图像的性质例1 2015年青岛市中考第8题如图1，正比例函数11y k x =的图像与反比例函数22k y x=的图像相交于A 、B 两点，其中点A 的横坐标为2，当y 1＞y 2时，x 的取值范围是（ ）．A ．x ＜－2或x ＞2B ． x ＜－2或0＜x ＜2C ．－2＜x ＜0或0＜x ＜2D ．－2＜x ＜0或x ＞2图1动感体验请打开几何画板文件名“15青岛08”，拖动点D 在x 轴上运动，观察线段EF 的两个端点E 、F 的位置关系，可以体验到，当－2＜x ＜0或x ＞2时，点E 在点F 的上方．答案D ．如图2所示．图2例2 2014年苏州市中考第18题如图1，直线l 与半径为4的⊙O 相切于点A ，P 是⊙O 上一个动点（不与点A 重合），过点P 作PB ⊥l ，垂足为B ，联结PA ．设PA ＝x ，PB ＝y ，则(x －y )的最大值是_____．图1动感体验请打开几何画板文件名“14苏州18”，拖动点P 在圆上运动一周，可以体验到，AF 的长可以表示x －y ，点F 的轨迹象两叶新树丫，当AF 最大时，OF 与AF 垂直（如图2）． 答案2．思路如下：如图3，AC 为⊙O 的直径，联结PC ．由△ACP ∽△PAB ，得AC PA AP PB =，即8x x y =．所以218y x =．因此2211(4)288x y x x x -=-=--+． 所以当x ＝4时，x －y 最大，最大值为2．图2 图3。

初中数学解题格式的规范之令狐文艳创作

初中数学解题格式的规范之令狐文艳创作

初中数学解题格式的规范令狐文艳一、填空题：解答填空题提出的要求是“正确、合理、迅速”，解答的基本策略是：快——运算要快，力戒小题大做；稳——变形要稳，防止操之过急；全——答案要全，避免对而不全；活——解题要活，不要生搬硬套；细——审题要细，不能粗心大意。

关于填空题,常见错误或不规范的答卷方式有:字迹不工整、不清晰、字符或字母的书写不规范或不正确等，等号与不等号没写就直接写数据；计算或化简没写最后结果；列代数式没化简；漏写单位；方程的解没写“ｘ＝”；函数表达式漏写“ｙ＝”，因式分解不彻底等。

二、关于解答题：解答题应答时，学生不仅要提供出最后的结论，还得写出或说出解答过程的主要步骤，提供合理、合法的说明，其次，解答题的考点相对较多，综合性强，难度较高，解答题成绩的评定不仅看最后的结论，还要看其推演和论证过程，分情况判定分数，答题过程要整洁美观、逻辑思路清晰、概念表达准确、答出关键语句和关键词。

比如要将你的解题过程转化为得分点,主要靠准确完整的数学语言表述,这一点往往被一些学生忽视,因此,卷面上大量出现“会而不对”“对而不全”的情况。

如简单几何证明题中的“跳步”,使很多人丢失得分, 尽管解题思路正确甚至很巧妙,但是由于不善于把“图形语言”准确地转移为“文字语言”,尽管学生“心中有数”却说不清楚,因此得分少。

只有重视解题过程的语言表述,“会做”的题才能“得分”。

对容易题要详写，过程复杂的试题要简写，答题时要会把握得分点。

三、常见的规范性问题1、在做计算题、化简求值、解方程、解应用题时，答题的开始必须写“解”字，然后再根据情况再写：“原式=”、“该式化简为=”、“将x= 代入化简式=”、“原方程=”、“由题意得”等解题提示语。

2、在做几何证明题时，答题的开始必须写“证明”、“由已知得”等文字语言，过程中每一证明步骤后都要用括号将理由写出，不容许跳跃步骤。

最后一定要写出结论来。

如：“因此”、“所以”3、方程（组）的结果一般用解（x1= x2= ）表示；不等式（组）的结果一般用解集( ＜undefinedx＜ )表示4、带单位的计算题或应用题，最后结果必须带单位，特别是应用题解题结束后一定要写符合题意的“答”。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

旋转基础练习一令狐文艳一、选择题1．在26个英文大写字母中，通过旋转180°后能与原字母重合的有（）A．6个B．7个C．8个D．9个2．从5点15分到5点20分，分针旋转的度数为（）A．20° B．26° C．30° D．36°3．如图1，在Rt△ABC中，∠ACB=90°，∠A=40°，以直角顶点C为旋转中心，将△ABC旋转到△A′B′C的位置，其中A′、B′分别是A、B的对应点，且点B在斜边A′B′上，直角边CA′交AB于D，则旋转角等于（）A．70° B．80° C．60°D．50°(图1) (图2) (图3)二、填空题．1．在平面内，将一个图形绕一个定点沿着某个方向转动一个角度，这样的图形运动称为________，这个定点称为________，转动的角为________．2．如图2，△ABC与△ADE都是等腰直角三角形，∠C和∠AED都是直角，点E在AB上，如果△ABC经旋转后能与△ADE重合，那么旋转中心是点_________；旋转的度数是__________．3．如图3，△ABC为等边三角形，D为△ABC内一点，△ABD经过旋转后到达△ACP的位置，则，（1）旋转中心是________；（2）旋转角度是________；（3）△ADP是________三角形．三、解答题．1．阅读下面材料：如图4，把△ABC沿直线BC平行移动线段BC的长度，可以变到△ECD的位置．如图5，以BC为轴把△ABC翻折180°，可以变到△DBC的位置．(图4) (图5) (图6) (图7)如图6，以A点为中心，把△ABC旋转90°，可以变到△AED的位置，像这样，其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的，这种只改变位置，不改变形状和大小的图形变换，叫做三角形的全等变换．回答下列问题如图7，在正方形ABCD中，E是AD的中AB．点，F是BA延长线上一点，AF=12（1）在如图7所示，可以通过平行移动、翻折、旋转中的哪一种方法，使△ABE移到△ADF的位置？（2）指出如图7所示中的线段BE与DF 之间的关系．2．一块等边三角形木块，边长为1，如图，现将木块沿水平线翻滚五个三角形，那么B点从开始至结束所走过的路径长是多少？旋转基础练习二一、选择题1．△ABC绕着A点旋转后得到△AB′C′，若∠BAC′=130°，∠BAC=80°，则旋转角等于（）A．50° B．210° C．50°或210° D．130°2．在图形旋转中，下列说法错误的是（） A．在图形上的每一点到旋转中心的距离相等B．图形上每一点转动的角度相同C．图形上可能存在不动的点D．图形上任意两点的连线与其对应两点的连线长度相等3．如图，下面的四个图案中，既包含图形的旋转，又包含图形的轴对称的是（）二、填空题1．在作旋转图形中，各对应点与旋转中心的距离________．2．如图，△ABC和△ADE均是顶角为42°的等腰三角形，BC、DE分别是底边，图中的△ABD绕A旋转42°后得到的图形是________，它们之间的关系是______，其中BDCE（填“>”,“<”或“=”）．3．如图，自正方形ABCD的顶点A引两条射线分别交BC、CD于E、F，∠EAF=45°，在保持∠EAF=45°的前提下，当点E、F分别在边BC、CD上移动时，BE+DF与EF的关系是________．三、解答题1．如图，正方形ABCD的中心为O，M为边上任意一点，过OM随意连一条曲线，将所画的曲线绕O点按同一方向连续旋转3次，每次旋转角度都是90°，这四个部分之间有何关系？2．如图，以△ABC的三顶点为圆心，半径为1，作两两不相交的扇形，则图中三个扇形面积之和是多少？旋转基础练习四一、选择题1．在英文字母VWXYZ中，是中心对称的英文字母的个数有（）A．1个 B．2个 C．3个D．4个2．下面的图案中，是中心对称图形的个数有（）A．1个 B．2个 C．3个D．4个3．如图，把一张长方形ABCD的纸片，沿EF折叠后，ED′与BC的交点为G，点D、C分别落在D′、C′的位置上，若∠EFG=55°，则∠1=（）A．55° B．125° C．70° D．110°二、填空题1．关于某一点成中心对称的两个图形，对称点连线必通过_________．2．把一个图形绕着某一个点旋转180°，如果它能够与另一个图形重合，那么就说这两个图形是_________图形．3．用两个全等的直角非等腰三角形可以拼成下面图形中的哪几种：_______（填序号）（1）长方形；（2）菱形；（3）正方形；（4）一般的平行四边形；（5）等腰三角形；（6）梯形．三、解答题1．仔细观察所列的26个英文字母，将相应的字母填入下表中适当的空格内．A B C D E F G H I J K L M N O P Q R S T U V W X Y Z2．如图，在正方形ABCD中，作出关于P 点的中心对称图形，并写出作法．3．如图，是由两个半圆组成的图形，已知点B是AC的中点，画出此图形关于点B成中心对称的图形．21085旋转基础练习六一、选择题1．下列图形中，既是轴对称图形，又是中心对称图形的是（）A ．等边三角形B ．等腰梯形C ．平行四边形D ．正六边形2．下列图形中，是中心对称图形，但不是轴对称图形的是（）A ．正方形B ．矩形C ．菱形D ．平行四边形3．如图所示，平放在正立镜子前的桌面上的数码“21085”在镜子中的像是（）A ．21085B ．28015C ．58012D ．51082二、填空题1．把一个图形绕着某一个点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做__________．2．请你写出你所熟悉的三个中心对称图形_________．3．中心对称图形具有什么特点（至少写出两个）_____________．三、解答题1．在平面内，如果一个图形绕一个定点旋转一定的角度后能与自身重合，那么就称这个图形是旋转对称图形，转动的这个角称为这个图形的一个旋转角，例如：正方形绕着它的对角线的交点旋转90°后能与自身重合，所以正方形是旋转对称图形，应有一个旋转角为90°．（1）判断下列命题的真假（在相应括号内填上“真”或“假”）①等腰梯形是旋转对称图形，它有一个旋转角为180°；（）②矩形是旋转对称图形，它有一个旋转角为180°；（）（2）填空：下列图形中是旋转对称图形，且有一个旋转角为120°是_____．（写出所有正确结论的序号）①正三角形；②正方形；③正六边形；④正八边形．（3）写出两个多边形，它们都是旋转对称图形，却有一个旋转角为72°，并且分别满足下列条件：①是轴对称图形，但不是中心对称图形；②既是轴对称图形，又是中心对称图形．2．如图，将矩形A1B1C1D1沿EF折叠，使B1点落在A1D1边上的B处；沿BG折叠，使D1点落在D处且BD过F点．（1）求证：四边形BEFG是平行四边形；（2）连接BB，判断△B1BG的形状，并写出判断过程．3．如图，直线y=2x+2与x轴、y轴分别交于A、B两点，将△AO B绕点O顺时针旋转90°得到△A1OB1．（1）在图中画出△A1OB1；（2）设过A、A1、B三点的函数解析式为y=ax2+bx+c，求这个解析式．答案：一、1．D 2．D 3．D二、1．中心对称图形2．答案不唯一3．答案不唯一三、1．（1）①假②真（2）①③（3）①例如正五边形正十五边形②例如正十边正二十边形2．（1）证明：∵A1D1∥B1C1，∴∠A1BD=∠C1FB又∵四边形ABEF是由四边形A1B1EF翻折的，∴∠B1FE=∠EFB，同理可得：∠FBG=∠D1BG，∠C1FB，∠FBG=90°-∴∠EFB=90°-1212∠A1BD，∴∠EFB=∠FBG∴EF∥BG，∵EB∥FG∴四边形BEFG是平行四边形．（2）直角三角形，理由：连结BB，∵BD1∥FC1，∴∠BGF=∠D1BG，∴∠FGB=∠FBG同理可得：∠B1BF=∠FB1B．∴∠B1BG=90°，∴△B1BG是直角三角形3．解：（1）如右图所示（2）由题意知A、A1、B1三点的坐标分别是（-1，0），（0，1），（2，0）∴1042a b cca b c=-+⎧⎪=⎨⎪=++⎩解这个方程组得12121abc⎧=-⎪⎪⎪=⎨⎪=⎪⎪⎩∴所求五数解析式为y=-12x2+12x+1．旋转基础练习七一、选择题1．下列函数中，图象一定关于原点对称的图象是（）A．y=1xB．y=2x+1 C．y=-2x+1 D．以上三种都不可能2．如图，已知矩形ABCD周长为56cm，O是对称线交点，点O到矩形两条邻边的距离之差等于8cm，则矩形边长中较长的一边等于（）A．8cm B．22cm C．24cm D．11cm二、填空题1．如果点P（-3，1），那么点P（-3，1）关于原点的对称点P′的坐标是P′_______．2．写出函数y=-3x 与y=3x具有的一个共同性质________（用对称的观点写）．三、解答题1．如图，在平面直角坐标系中，AOBACD（-3，1），B（-2，3），C（0，2），画出△ABC关于x轴对称的△A′B′C′，再画出△A′B′C′关于y轴对称的△A″B″C″，那么△A″B″C″与△ABC 有什么关系，请说明理由．2．如图，直线AB与x轴、y轴分别相交于A、B两点，且A（0，3），B（3，0），现将直线AB绕点O顺时针旋转90°得到直线A1B1．（1）在图中画出直线A1B1；（2）求出过线段A1B1中点的反比例函数解析式；（3）是否存在另一条与直线A1B1平行的直线y=kx+b（我们发现互相平行的两条直线斜率k相等）它与双曲线只有一个交点，若存在，求此直线的解析式；若不存在，请说明不存在的理由．答案:一、1．A 2．B二、1．（3，-1） 2．答案不唯一参考答案：关于原点的中心对称图形．三、1．画图略，△A″B″C″与△ABC 的关系是关于原点对称．2．（1）如右图所示，连结A 1B 1；（2）A 1B 1中点P （1.5，-1.5），设反比例函数解析式为y=k x ，则y=-2.25x． （3）A 1B 1：设y=k 1x+b 1113033b k =-⎧⎨=-⎩1113k b =⎧⎨=-⎩ ∴y=x+3 ∵与A 1B 1直线平行且与y=2.25x相切的直线是A 1B 1旋转而得到的．∴所求的直线是y=x+3，下面证明y=x+3与y=-2.25x⇒x 2+3x+2.25=0，4×1×2.25=0，∴y=x+3与y=-2.25x相切． 旋转基础练习八一、选择题1．在图所示的4个图案中既包含图形的旋转，还有图形轴对称是（）2．将三角形绕直线L旋转一周，可以得到如图所示的立体图形的是（）二、填空题1．基本图案在轴对称、平移、旋转变化的过程中，图形的______和______都保持不变．2．如上右图，是由________关系得到的图形．三、解答题1．（1）图案设计人员在进行图设计时，常常用一个模具板来设计一幅幅美丽漂亮的图案，你能说出用同一模具板设计出的两个图案之间是什么关系吗？（2）现利用同一模具板经过平移、旋转、轴对称设计一个图案，并说明你所表达的意义．2．如图，你能利用平移、旋转或轴对称这样的变化过程来分析它的形成过程吗？。

相关文档
最新文档