高斯定理及其适用范围
高斯定理(高斯定理是什么?高斯定理怎么用?)
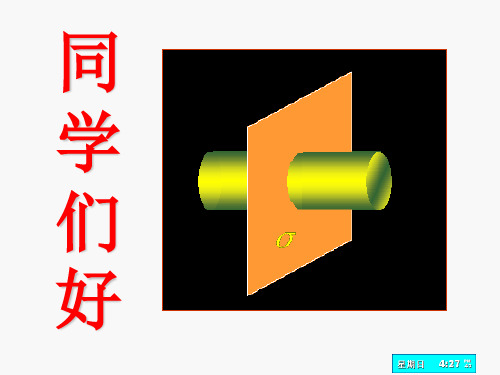
选取闭合的柱形高斯面
E dS S'
S
0 底面积
2S'E S'
E
S'
0
S' E
S'
E 20
E
EE
E
E 2 0
E
x
O
( 0)
讨论
无的 限电 大场 带叠 电加 平问 面题
0
0
高斯定理举例:
均匀带电球面(球体、球壳等)的 电场分布 均匀带电直线(圆柱面、圆柱体等)
的电场分布 均匀带电无限大平面的电场分布
例:均匀带电球壳的电场强度
一半径为R , 均匀带电 Q 的薄
球壳 . 求球壳内外任意点的电场强
度. 解(1)0 r R
r S +
r +
+
O
+ 1+ + +
+R +
S
s (柱面)
h 0
2 rhE h 0
E
2 0 r
z
+
+
r h
+
+o
x+
E y en
E
O
r
讨论
o
E O
无限长均匀带电柱面的电场分布
对称性分析: 视为 无限长均匀带电直 线的集合;
r
P
dE '
选同轴圆柱型高斯 面;
由高斯定理计算
dE
dE dE'
0 rR
高斯 Carl Friedrich
Gauss 德国 1777~1855 数学家、天文学家
静电场的高斯定理

例7-10 求电荷呈“无限长”圆柱形轴对称均匀分布时 所激发的电场强度。
解:电场分布也应有柱对称性,方向沿径向。 作与带电圆柱同轴的圆柱形高斯面,
高为h,半径为r
•当r>R 时,
sE dS 侧面 E dS E 2 r h 为什么?
r h
E 2 r h h 0
P点的场强
E 2 0 r
1
0
d V
V
关于高斯定理的几点讨论
以上是通过用闭合曲面的电通量概念来说明高斯 定理,仅是为了便于理解而用的一种形象解释, 不是高斯定理的证明
高斯定理是在库仑定律基础上得到的,但是前者 适用范围比后者更广泛。后者只适用于真空中的 静电场,而前者适用于静电场和随时间变化的场, 高斯定理是电磁理论的基本方程之一。
③ 场源电荷为无限长均匀带电直线、均匀带电直圆柱面、直 圆柱体或同轴导体圆筒等,则电场的分布具有柱对称性。
(2) 选取高斯面
用高斯定理求场强时,选取恰当的高斯面是解题的关键。
选取高斯面的原则:
① 选取的高斯面必须通过所考查的场点。 ② 应使高斯面上各点的场强大小相等, 方向与该处面元 的
法线平行(这样则可将E提到积分号外,只对面积积分); 或者使高斯的部分面上各点场强大小相等,方向与 的法线 平行,另一部分面上各点场强为零或场强的方向与面元的 法线垂直(即通过这部分的E通量为零)。
高斯定理解题步骤: 总结
(1)分析电场的对称性
根据题意画出示意图,分析电场的分布情况 (最好画出电场 线),看是否具有某种特殊的对称性,这可从产生电场的场 源电荷的分布看出。
常见的情况有以下几种:
① 场源电荷为均匀带电球面、均匀带电球体、同心的均匀带 电导体球壳等,则电场的分布具有球对称性;
高斯定理求电场强度

高斯定理求电场强度
高斯定理是电学中的一项基本定理,用于求解电场强度。
它是由德国数学家卡尔·弗里德里希·高斯于18世纪末提出的。
在数学上,高斯定理也叫做散度定理,它可以将一个三维空间中的向量场在某个闭合曲面上的通量与该向量场在该曲面所包围的体积积分相联系。
在电学中,高斯定理用于求解电场强度。
它表明:一个电场从一个闭合曲面内通过的电通量等于该曲面内的电荷量的比值。
具体来说,高斯定理可以表示为:
∮S E·dS = Q/ε0
其中,S代表一个闭合曲面,E代表电场强度,Q代表该曲面内的总电荷量,ε0代表真空介电常数。
左侧的积分表示电场向曲面S的法向量的通量,右侧的比值表示该曲面内的总电荷量。
因此,如果我们已知一个由电荷产生的电场,并且想要求解该电场在一个闭合曲面内的通量,那么只需要使用高斯定理即可。
具体步骤是:选择一个适当的闭合曲面,计算该曲面内的总电荷量,然后代入高斯定理求解即可。
需要注意的是,高斯定理的适用范围是仅限于电场强度在曲面上处处连续的情况。
当电场强度在曲面上不连续时,需要使用其他方法进行求解。
高斯定理数学

高斯定理数学高斯定理,又称为高斯-奥斯特罗格雷定理(Gauss-Ostrogradsky theorem),是描述向量场通过曲面的流量密度与该曲面边界上环绕该曲面沿法向量方向的一圈线积分之间的关系的定理,是矢量分析的重要内容之一,也是工程中常用的理论。
$$\oint_S \textbf{F} \cdot \textbf{n} dS = \iiint_V \nabla \cdot \textbf{F} dV$$$\textbf{F}$ 表示某个向量场,$S$ 表示一个逐片光顺的曲面,$V$ 为该曲面所包围的立体。
$\textbf{n}$ 表示曲面上某一点的法向量,$\nabla \cdot \textbf{F}$ 为向量场 $\textbf{F}$ 的散度。
该式中左边表示 $\textbf{F}$ 向外通过曲面 $S$ 的流量密度。
左侧积分的意思是,对于曲面 $S$ 的每一点,对由该点到曲面外侧的垂直方向的投影所围成的小面积$dS$ 进行积分,得到整个曲面通过的总流量密度。
右边表示 $\textbf{F}$ 在立体$V$ 中的散度。
右侧积分的意思是,对于立体 $V$ 中的每一点,计算该点的散度,然后对整个立体进行积分,得到散度在整个立体中的总量。
高斯定理适用于任意的向量场,包括电场、磁场等。
它可以用来推导一些物理方程,并在基础数学领域中起到重要作用。
对于电场,高斯定理可以用来计算电通量,即电场向外通过一个立体的总电量。
对于静电场和恒定电场来说,高斯定理可以推导出库仑定律。
对于磁场,高斯定理可以用来推导出安培环路定理。
高斯定理在物理学和工程学中有非常广泛的应用,是理解和解决问题的重要工具之一。
高斯定理的证明可以通过追踪微小体积元素上的向外流量来完成。
假设该体积元素为$\Delta V$,体积元素表面上带有一小片面积为 $\Delta S$,该片面积的法向量表示为$\textbf{n}$。
向量场 $\textbf{F}$ 在该面积上的流量为 $\textbf{F} \cdot\textbf{n} \Delta S$,如果对所有该体积元素上的面积进行累计,则构成了整个曲面的流量,并得到了高斯定理的左侧积分:$$\oint_S \textbf{F} \cdot \textbf{n} dS$$接下来,可以通过施加散度定理来将该定理转化为该向量场的散度在这个立方体中的积分:证明中还需要使用到一些高等数学的知识,如积分中值定理等,具体证明过程相对复杂。
高斯定理总结

高斯定理总结高斯定理是电磁学中的一个重要定理,也称为高斯法则或高斯定律。
它是由德国数学家卡尔·弗里德里希·高斯在19世纪初提出的。
高斯定理描述了电场和磁场的性质以及它们与电荷和电流之间的关系。
通过应用高斯定理,我们可以更好地理解电磁学中的一些基本概念和现象。
让我们来了解一下什么是高斯定理。
高斯定理可以用来计算电场通过一个封闭曲面的总电通量。
电通量是电场线穿过一个面的数量的度量。
根据高斯定理,电通量正比于该曲面内包含的电荷量。
也就是说,如果一个封闭曲面内没有电荷,电通量将为零。
而如果有正电荷,则电通量将为正;如果有负电荷,则电通量将为负。
高斯定理的数学表达可以用以下公式来表示:∮E·dA = Q/ε₀在这个公式中,∮E·dA表示电场E对面元dA的积分,也即电场穿过曲面的总电通量;Q表示封闭曲面内的总电荷量;ε₀为真空介电常数。
高斯定理的应用非常广泛。
首先,它可以用来计算电场的分布。
通过选择合适的封闭曲面,我们可以根据高斯定理来计算电场通过该曲面的电通量,从而得到电场的强度。
这对于研究电场的分布规律以及解决与电场相关的问题非常有帮助。
高斯定理也可以用来计算电荷的分布。
如果我们已知电场分布,可以通过高斯定理来计算通过一个封闭曲面的电通量,从而推导出该曲面内的电荷量。
这对于研究电荷的分布规律以及解决与电荷相关的问题同样非常有用。
高斯定理还可以用来证明电场和电荷之间的关系。
根据高斯定理,电通量正比于封闭曲面内的电荷量,这意味着电荷是电场的源。
换句话说,电场是由电荷产生的,而电荷则受到电场的作用。
除了电场,高斯定理也适用于磁场。
对于磁场而言,高斯定理可以用来计算磁通量,即磁场通过一个封闭曲面的总磁通量。
磁通量与磁场线的穿过面元的数量有关。
通过应用高斯定理,我们可以计算磁通量,从而了解磁场的性质以及与电流之间的关系。
高斯定理是电磁学中的一个重要定理,它描述了电场和磁场的性质以及它们与电荷和电流之间的关系。
电通量真空中静电场的高斯定理

高斯定理的适用范围
真空环境
高斯定理适用于真空中静电场的情况,即没有电流和 变化的磁场。
静态场
高斯定理适用于描述静态场,即电场不随时间变化的 情况。
远场近似
对于远处的观察者或大尺度的空间区域,高斯定理提 供了一种近似描述电场分布的方法。
02 电通量与静电场的关系
电通量的概念
电通量是电场中穿过某一封闭曲面内 的电场线数,表示电场分布的强度和 方向。
详细描述
首先,根据微积分基本定理,电场E可以表示为电势V的负梯度,即E=-grad(V)。然后,对任意闭合曲面S 的体积分,有∫∫∫E⋅dV=∫∫(E⋅dS)⋅dV=∫∫∫grad(V)⋅dV=∫∫∫dV=∫∫V⋅dS。由于E⋅dS的方向与dS的方 向相同,因此高斯定理成立。
证明方法二:利用高斯公式
05 高斯定理的推广
推广到非均匀电场
总结词
在非均匀电场中,高斯定理的应用范围得到 扩展,可以描述电场分布的不均匀性。
详细描述
在非均匀电场中,电场线不再是均匀分布, 而是呈现出复杂的空间变化。高斯定理通过 引入电通量密度概念,能够准确描述这种非 均匀分布的电场特性。
推广到非线性电场
总结词
高斯定理在非线性电场中同样适用,可以描 述电场随空间和时间变化的非线性行为。
高斯定理是静电场的基本定理之一,它表明穿过任意封闭曲面的电通量等于该曲面 所包围的电荷量。
电通量与静电场的关系是相互依存的,电通量的计算需要依赖于静电场的分布,而 静电场的分布又受到电荷分布的影响。
03 高斯定理的证明
证明方法一:利用微积分基本定理
总结词
通过微积分基本定理,将电场分布表示为电势函数的梯度,再利用积分性质证明高斯定理。
静电场 高斯定理

静电场的高斯定理是静电学中的一个重要定理,它反映了静电场的一个基本性质,即静电场是有源场,其源即是电荷。
高斯定理也称为高斯通量理论,或称作散度定理、高斯散度定理、高斯-奥斯特罗格拉德斯基公式、奥氏定理或高-奥公式(通常情况的高斯定理都是指这个定理,也有其它同名定理)。
静电学上表示闭曲面内的电荷之和与产生的电场在该闭曲面上的电通量积分的关系,高斯定律表明了在闭合曲面中电荷分布与产生的电场之间的关系,高斯定律在静电场的情况下,类似于应用于磁场学的安培定律,两者都集中在麦克斯韦方程组中,由于数学上的相似性,高斯定律也适用于其它由平方反比律决定的物理量,例如引力或者辐照度。
高斯定理直接由库仑定律导出,完全依赖于电荷间作用力的平方反比定律,当高斯定理应用于静电平衡条件下的金属导体时,可以得出导体内部没有净电荷的结论,因此测量导体内部是否有净电荷是验证库仑定律的重要方法。
拓展:静电场,指的是观察者与电荷量不随时间发生变化的电荷相对静止时所观察到的电场。
它是电荷周围空间存在的一种特殊形态的物质,其基本特征是对置于其中的静止电荷有力的作用,库仑定律描述了这个力。
静电场高斯定理的积分形式

静电场高斯定理的积分形式
高斯定理是用于计算电场强度的重要定理,它可以用积分的形式表示。
通常,它表示为:
E = (1/4πε₀) ∫ρ(r')/|r-r'| dV'
其中,E 是电场强度,ρ(r') 是电荷密度,r 和r' 分别是电场点和电荷位置的矢量,ε₀是真空介电常数,dV' 是电荷所在体积单元的体积。
这个积分表示了电场点周围所有电荷对电场强度的贡献。
在计算电场强度时,可以将电荷分成若干个小体积单元,然后对每个单元分别求解上述积分,最后将所有单元的贡献相加起来,得到电场强度的总值。
注意,高斯定理仅适用于无电荷体积内的电场强度计算。
如果要计算电场强度在有电荷体积外的情况,则应使用莫尔定理。
