圆锥曲线培优讲义
圆锥曲线讲义

5.(2013浙江理)如图,点)1,0(-P 是椭圆)0(1:22
221>>=+b a b
y a x C 的一个顶点,1C 的长 轴是圆4:222=+y x C 的直径.21,l l 是过点P 且互相垂直的两条直线,其中1l 交圆2C 于两
点,2l 交椭圆于另一点
(1)求椭圆的方程; (2)求面积取最大值时直线的方程.
2.(2013新课标2理)平面直角坐标系
中,过椭圆的右焦点 作直
交于两点,为的中点,且的斜率为. (Ⅰ)求
的方程; (Ⅱ)
为上的两点,若四边形的对角线,求四边形面积的最大值.
1C D 1C ABD ∆1
l (第21题)
1. (2014全国1理) 已知点A(0,-2),椭圆E:
x 2a 2+y 2b 2=1 (a >b >0)的离心率为 32,F 是椭圆的右焦点,直线AF 的斜率为
2 33,O 为坐标原点.
(1) 求E 的方程; (2) 设过点A 的 动直线l 与E 相交于,P Q 两点,当OPQ ∆的面积最大时,求l 的方程.
4.(2008全国理) 设椭圆中心在坐标原点,(20)(01)A B ,,,是它的两个顶点,直线)0(>=k kx y 与AB 相交于点D ,与椭圆相交于E 、F 两点.
(Ⅰ)若6ED DF =,求k 的值;
(Ⅱ)求四边形AEBF 面积的最大值.。
高中数学圆锥曲线专题-暑假讲义(难得的好讲义)

第一讲 椭圆初步问题一 椭圆的定义【例1】求平面内与两个定点1F 、2F 的距离之和等于定长(大于12||F F )的点的轨迹方程。
【直观感觉】【严格求解】求平面内与两个定点1F (-c ,0)、2F (c ,0)的距离之和等于定长2a (a >c )的点的轨迹方程。
【反面验证】已知方程22221x y a b+= (0)a b >>,设P (x ,y )是该方程代表的曲线上任意一点,求证:P 到点1(F 和点2F 的距离之和等于2a 。
【经验小结】解析几何的最大特点就是通过建立平面直角坐标系,把一个难以解决的几何问题转化为代数问题,通过坐标和计算得出结论.坐标系建的好坏,直接影响到解题过程的繁简以及结果的好坏.通常建立平面直角坐标系时,可利用图形的对称性,或利用图形中的垂直关系,或使尽量多的点落在坐标轴上。
【要点总结】1、椭圆的定义和相关概念:平面内与两个定点1F 、2F 的距离之和等于定长(大于12||F F )的点的轨迹叫做椭圆,这两个定点 1F 、2F 叫做椭圆的焦点,两焦点的距离12||F F 叫做椭圆的焦距。
2、对椭圆定义的几点说明:⑴“在平面内”是前提,否则得不到平面图形(去掉这个条件,我们将得到一个椭球面); ⑵作为到这两个定点的距离的和的“常数”,必须满足大于| F 1F 2|这个条件。
若不然,当这个“常数”等于| F 1F 2|时,我们得到的是线段F 1F 2;当这个“常数”小于| F 1F 2|时,无轨迹。
⑶怎么看椭圆扁还是圆:椭圆的形状与两定点间距离、绳长有关。
在同样的绳长下,两定点间距离较长,则所画出的椭圆较扁,两定点间距离较短,则所画出的椭圆较圆,⑷对椭圆和它的方程进行进一步观察,发现它本身具备对称性,有两条对称轴和一个对称中心。
⑸如果建坐标系的方法不同,会得到以下两种椭圆的方程:中心在原点、焦点分别在x 轴上,y 轴上的椭圆标准方程分别为:22221x y a b += (0)a b >>;22221y x a b+= (0)a b >>;问题二 椭圆的基本几何性质归纳几点说明:⑴长轴:线段12A A ,长为2a ;短轴:线段12B B ,长为2b ;焦点在长轴上。
第三章 圆锥曲线复习讲义(精心整理、好用、经典)
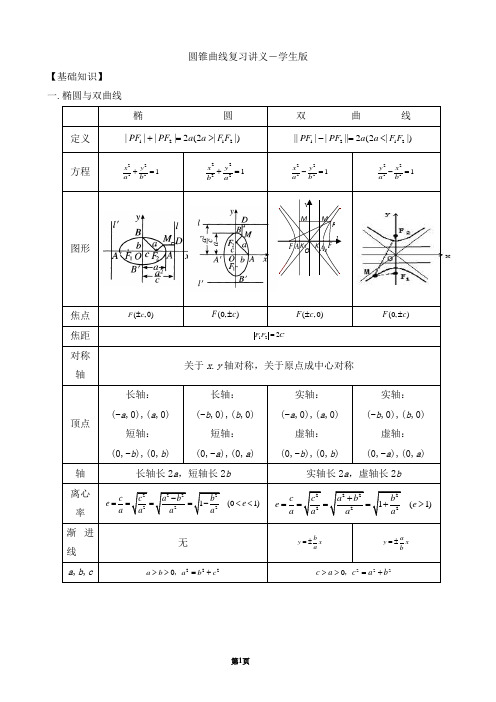
圆锥曲线复习讲义-学生版【基础知识】 一.椭圆与双曲线椭 圆双 曲 线定义 1212||||2(2||)PF PF a a F F +=>1212||||||2(2||)PF PF a a F F -=<方程22221x y a b += 22221x y b a+= 22221x y a b -= 22221y x a b -= 图形焦点 (,0)F c ± (0,)F c ±(,0)F c ± (0,)F c ±焦距 C F F 221=对称轴关于x .y 轴对称,关于原点成中心对称顶点长轴:(-a ,0),(a ,0) 短轴:(0,-b ),(0,b )长轴:(-b ,0),(b ,0) 短轴:(0,-a ),(0,a )实轴:(-a ,0),(a ,0) 虚轴:(0,-b ),(0,b )实轴:(-b ,0),(b ,0)虚轴:(0,-a ),(0,a )轴 长轴长2a ,短轴长2b实轴长2a ,虚轴长2b离心率 22222221(01)c c a b b e e a a a a-====-<< 22222221(1)c c a b be e a a a a+====+>渐进线无xab y ±= x ba y ±= a ,b ,c 2220c b a b a +=>>,2220b a c a c +=>>,M MPK K 1A A 2F F O yx二.抛物线的性质标准方程22(0)y px p => 22(0)y px p =->22(0)x py p => 22(0)x py p =-> 图形焦点坐标 (,0)2p(,0)2p-(0,)2p (0,)2p -准线方程 2p x =-2p x = 2p y =-2p y =范围 0x ≥ 0x ≤0y ≥ 0y ≤离心率1e = 1e = 1e = 1e = 三、弦长公式: ||14)(1||1||2212212212A k x x x x k x x k AB ∆⋅+=-+⋅+=-+= 其中,∆,A 分别是联立直线方程和圆锥曲线方程,消去 y 后所得关于x 的一元二次方程 的判别式和2x 的系数求弦长步骤:(1)求出或设出直线与圆锥曲线方程;(2)联立两方程,消去y,得关于x 的一元二次方程,02=++C Bx Ax 设),(11y x A ,),(22y x B ,由韦达定理求出AB x x -=+21,ACx x =21;(3)代入弦长公式计算。
高考一轮复习必备—圆锥曲线讲义

直线与圆锥曲 线一、直线l 与圆锥曲线C 的位置关系的判断判断直线l 与圆锥曲线C 的位置关系时,通常将直线l 的方程Ax By C 0 (A, B 不同时为0)代入圆 锥曲线C 的方程F (x, v) =0,消去y (也可以消去x)得到关丁一个变量的一元二次方程,即联立三、中点弦所在直线的斜率.22222-2 ;若椭圆方程为土号1(a b 0)时,相应结论为k —^-°(y 0 0),即kgk °p土 ;aab' by °b'2222若双曲线方程为七,1时,相应结论为k %~°(y 0 0),即kck op 旦^;a bb y ° bI 复习提问Ax By C 0 F (x, y) 0消去y 后得ax 2bx c 0(1) 当a 0时,即得到一个一元一次方程,贝U l 与C 相交,有且只有一个交点,此时,若 C 为双曲线,则直线l 与双曲线的渐近线平■行;若 C 为抛物线,则直线l 抛物线的对称轴平■行(2)当a 0时, 0,直线l 与曲线C 有两个不同的交点;公共点(切点); 0,直线l 与曲线C 相离。
二、圆锥曲线的弦长公式0,直线l 与曲线C 相切,即有唯相交弦AB 的弦长2 2(1)若椭圆方程为 1 土 1(a a b b 0)时,以P(x °,y °)为中点的弦所在直线斜率kb 2x。
a 2y(y 。
即 k*°p(2) P2(x 0,y 0)是双曲线 —2~ a 2yb 21部一点,以 P 为中点的弦所在直线斜率k 孕(y °a V 。
k*°pABk 2^ 7(x i x^74x 1x 21j I y i y 2(3)) P (x °,y 。
)是抛物线y 2 2px 部一点,以P 为中点的弦所在直线斜率n题型与方法一、直线与圆锥曲线的位置关系 (1)直线与圆锥曲线有两个不同的公共点的判断:通法为直线代入曲线判断0;另一方法就是数形结合,如直 线与双曲线有两个不同的公共点,可通过判定直线的斜率与双曲线渐近线的斜率大小得到。
高三培优讲义10---平移齐次化解决圆锥曲线中斜率和积问题与定点问题
专题2-2圆锥曲线中斜率和积为定值问题与定点问题(平移齐次化)【例题】已知椭圆2214xy+=,设直线l不经过2(0,1)P点且与C相交于A,B两点.若直线2P A与直线2P B的斜率的和为1−,证明:l过定点.【手电筒模型·1定+2动】直线y kx m =+与椭圆()2222=10x y a b a b +>>交于A ,B 两点,00(,)P x y 为椭圆上异于AB 的任意一点,若AP BP k k ⋅=定值或AP BP k k +=定值(不为0),则直线AB 会过定点. (因为三条直线形似手电筒,固名曰手电筒模型). 补充:若y kx m =+过定点,则AP BP k k ⋅=定值,AP BPk k k+=定值.【坐标平移+齐次化处理】(左加右减,上减下加为曲线平移)Step 1:平移点P 到原点,写出平移后的椭圆方程,设出直线方程,并齐次化处理 Step 2:根据斜率之积或斜率之和与韦达定理的关系得到等式,求得m ,n 之间的关系, Step 3:得出定点,此时别忘了,还要平移回去!【补充】椭圆2222:1(0),x y E a b a b +=>>00(,)P x y 是椭圆上一点,A ,B 为随圆E 上两个动点,PA 与PB 的斜率分别为k 1,k 2.(1)120k k +=,证明AB 斜率为定值2020:(x b y y a⋅≠0);(2)12)0(k k t t ≠+=,证明AB 过定点:20002022,y x b x y t t a ⎛⎫−−−⋅ ⎪⎝⎭; (3) 2122b k k a =⋅=,证明AB 的斜率为定值000(0)y x x −≠; (4)2122()b k k a λλ=≠⋅,证明AB 过定点:2222002222,a b a b x y a ba b λλλλ⎛⎫++− ⎪−−⎝⎭. 以上称为手电筒模型,注意点P 不在椭圆上时,上式并不适用,常数也需要齐次化乘“1²”O xyABP2020·新高考1卷·22已知椭圆C:22221(0)x ya ba b+=>>的离心率为22,且过点()2,1A.(1)求C的方程:(2)点M,N在C上,且AM AN⊥,AD MN⊥,D为垂足.证明:存在定点Q,使得DQ为定值.题型一 已知定点求定值1.已知抛物线2:4C y x =,过点(4,0)的直线与抛物线C 交于P ,Q 两点,O 为坐标原点.证明:90POQ ︒∠=.2.如图,椭圆22:12x E y +=,经过点(1,1)M ,且斜率为k 的直线与椭圆E 交于不同的两点P ,Q (均异于点(0,1)A −,证明:直线AP 与AQ 的斜率之和为2.3.已知点31,2A ⎛⎫ ⎪⎝⎭,O 为坐标原点,E ,F 是椭圆22:=143x y =C 上的两个动点,满足直线AE 与直线AF 关于直线x =1对称.证明直线EF 的斜率为定值,并求出这个定值;4.如图,点(1,0)F 为椭圆22143x y+=的右焦点,过F 且垂直于x 轴的直线与椭圆E 相交于C 、D 两点(C 在D 的上方),设点A 、B 是椭圆E 上位于直线CD 两侧的动点,且满足ACD BCD ∠=∠,试问直线AB 的斜率是否为定值,请说明理由.5.椭圆22:12x E y +=,()0,1A −,经过点()1,1,且斜率为k 的直线与椭圆E 交于不同的两点P ,Q (均重点题型·归类精讲异于点A ),证明:直线AP 与AQ 斜率之和为2.6.已知椭圆C :22143x y +=,过F 作斜率为(0)k k ≠的动直线l ,交椭圆C 于M ,N 两点,若A 为椭圆C 的左顶点,直线AM ,AN 的斜率分别为1k ,2k ,求证:12k kk k +为定值,并求出定值.题型二 已知定值求定点7.(2017·全国卷理)已知椭圆2214x y +=,设直线l 不经过2P 点且与C 相交于A ,B 两点.若直线2P A与直线2P B 的斜率的和为-1,证明:l 过定点.8.已知椭圆22:14x C y +=,设直线l 不经过点2(0,1)P 且与C 相交于A ,B 两点.若直线2P A 与直线2P B 的斜率的和为1−,证明:直线l 过定点.9.已知抛物线C :y 2=2px (p >0)上的点P (1,y 0)(y 0>0)到其焦点的距离为2. (1)求点P 的坐标及抛物线C 的方程; (2)若点M 、N 在抛物线C 上,且k PM •k PN =12-,证明:直线MN 过定点.10.已知椭圆22:143x y C +=,31,2P ⎛⎫ ⎪⎝⎭,若直线l 交椭圆C 于A ,B (A ,B 异于点P )两点,且直线P A 与PB 的斜率之积为94−,求点P 到直线l 距离的最大值.11.已知椭圆:的离心率为,椭圆的短轴长等于4.E 22221(0)x y a b a b +=>>33E(1)求椭圆的标准方程;(2)设,,过且斜率为的动直线与椭圆交于,两点,直线,分别交:于异于点的点,,设直线的斜率为,直线,的斜率分别为.①求证:为定值; ②求证:直线过定点.E 22164x y +=()0,1A −()0,2B A 1k l E M N BM BN C ()2211x y +−=B P Q PQ 2k BM BN 34k k ,34k k ⋅PQ专题2-2 圆锥曲线中斜率和积为定值问题与定点问题(平移齐次化)【例题】已知椭圆2214x y +=,设直线l 不经过2(0,1)P 点且与C 相交于A ,B 两点.若直线2P A 与直线2P B 的斜率的和为1−,证明:l 过定点.【平移+齐次化处理】Step 1:平移点P 到原点,写出平移后的椭圆方程,设出直线方程,并齐次化处理 将椭圆向下平移一个单位,(为了将2(0,1)P 平移到原点)椭圆方程化为22:(1)14x C y ++=,(左加右减,上减下加为曲线平移)设直线对应的直线为1mx ny +=,椭圆方程化简为221204x y y ++=,把一次项化成二次结构,将2y 乘上mx ny +即可此时椭圆方程变成:()()2222012021244x y y mx n x y n y y x m +++=1++⇒+=Step 2:根据斜率之积或斜率之和与韦达定理的关系得到等式,求得m ,n 之间的关系由于平移不会改变直线倾斜角,即斜率和仍然为-1,而P 2点此时为原点,设平移后的(,),(,)A A B B A x y B x y , 即00100A B A B y y x x −−+=−−−, (2,1)Q −l l '将椭圆方程两边同除以2x ,令y k x=,得()220214k n m k 1++=+,结合两直线斜率之和为,即122121mk k n +=−=−+,得,, Step 3:得出定点,此时别忘了,还要平移回去!直线恒过点,向上平移一个单位进行还原在原坐标系中,直线过点.【手电筒模型·1定+2动】直线y kx m =+与椭圆()2222=10x y a b a b +>>交于A ,B 两点,00(,)P x y 为椭圆上异于AB 的任意一点,若AP BP k k ⋅=定值或AP BP k k +=定值(不为0),则直线AB 会过定点. (因为三条直线形似手电筒,固名曰手电筒模型). 补充:若y kx m =+过定点,则AP BP k k ⋅=定值,AP BPk k k+=定值.【坐标平移+齐次化处理】(左加右减,上减下加为曲线平移)Step 1:平移点P 到原点,写出平移后的椭圆方程,设出直线方程,并齐次化处理 Step 2:根据斜率之积或斜率之和与韦达定理的关系得到等式,求得m ,n 之间的关系, Step 3:得出定点,此时别忘了,还要平移回去!【补充】椭圆2222:1(0),x y E a b a b +=>>00(,)P x y 是椭圆上一点,A ,B 为随圆E 上两个动点,PA 与PB 的斜率分别为k 1,k 2.(1)120k k +=,证明AB 斜率为定值2020:(x b y y a⋅≠0);1−221m n =+21m n ∴−=∴l '(2,2)Q '−l (2,1)Q −O xyABP(2)12)0(k k t t ≠+=,证明AB 过定点:20002022,y x b x y t t a ⎛⎫−−−⋅ ⎪⎝⎭; (3) 2122b k k a =⋅=,证明AB 的斜率为定值000(0)y x x −≠; (4)2122()b k k a λλ=≠⋅,证明AB 过定点:2222002222,a b a b x y a b a b λλλλ⎛⎫++− ⎪−−⎝⎭. 以上称为手电筒模型,注意点P 不在椭圆上时,上式并不适用,常数也需要齐次化乘“1²”2020·新高考1卷·22已知椭圆C :22221(0)x y a b a b +=>>的离心率为22,且过点()2,1A .(1)求C 的方程:(2)点M ,N 在C 上,且AM AN ⊥,AD MN ⊥,D 为垂足.证明:存在定点Q ,使得DQ 为定值.【详解】(1)由题意可得:2222222411c aa b a b c ⎧=⎪⎪⎪+=⎨⎪=+⎪⎪⎩,解得:2226,3a b c ===,故椭圆方程为:22163x y +=.(2)[方法一]:通性通法 设点()()1122,,,M x y N x y ,若直线MN 斜率存在时,设直线MN 的方程为:y kx m =+,代入椭圆方程消去y 并整理得:()222124260k x kmx m +++−=,可得122412km x x k +=−+,21222612m x x k −=+,因为AM AN ⊥,所以·0AM AN =,即()()()()121222110x x y y −−+−−=, 根据1122,kx m y kx m y =+=+,代入整理可得:()()()()22121212140x x km k x x km ++−−++−+=,所以()()()22222264121401212m km k km k m k k −⎛⎫++−−−+−+= ⎪++⎝⎭, 整理化简得()()231210k m k m +++−=, 因为(2,1)A 不在直线MN 上,所以210k m +−≠,故23101k m k ++=≠,,于是MN 的方程为2133y k x ⎛⎫=−− ⎪⎝⎭()1k ≠,所以直线过定点直线过定点21,33P ⎛⎫− ⎪⎝⎭.当直线MN 的斜率不存在时,可得()11,N x y −, 由·0AM AN =得:()()()()111122110x x y y −−+−−−=, 得()1221210x y −+−=,结合2211163x y +=可得:2113840x x −+=,解得:123x =或22x =(舍).此时直线MN 过点21,33P ⎛⎫− ⎪⎝⎭.令Q 为AP 的中点,即41,33Q ⎛⎫ ⎪⎝⎭,[方法二]【最优解】:平移坐标系将原坐标系平移,原来的O 点平移至点A 处,则在新的坐标系下椭圆的方程为22(2)(1)163x y +++=,设直线MN 的方程为4mx ny .将直线MN 方程与椭圆方程联立得224240x x y y +++=,即22()2()0x mx ny x y mx ny y +++++=,化简得22(2)()(1)0n y m n xy m x +++++=,即2(2)()(1)0y y n m n m x x ⎛⎫⎛⎫+++++= ⎪ ⎪⎝⎭⎝⎭.设()()1122,,,M x y N x y ,因为AM AN ⊥则1212AM AN y y k k x x ⋅=⋅112m n +==−+,即3m n =−−. 代入直线MN 方程中得()340n y x x −−−=.则在新坐标系下直线MN 过定点44,33⎛⎫−− ⎪⎝⎭,则在原坐标系下直线MN 过定点21,33P ⎛⎫− ⎪⎝⎭.又AD MN ⊥,D 在以AP 为直径的圆上.AP 的中点41,33⎛⎫⎪⎝⎭即为圆心Q .经检验,直线MN 垂直于x 轴时也成立.故存在41,33Q ⎛⎫ ⎪⎝⎭,使得122||||2DQ AP ==[方法三]:建立曲线系A 点处的切线方程为21163x y⨯⨯+=,即30x y +−=.设直线MA 的方程为11210k x y k −−+=,直线MB 的方程为22210k x y k −−+=,直线MN 的方程为0kx y m −+=.由题意得121k k .则过A ,M ,N 三点的二次曲线系方程用椭圆及直线,MA MB 可表示为()()22112212121063x y k x y k k x y k λ⎛⎫+−+−−+−−+= ⎪⎝⎭(其中λ为系数). 用直线MN 及点A 处的切线可表示为()(3)0kx y m x y μ−+⋅+−=(其中μ为系数).即()()22112212121()(3)63x y k x y k k x y k kx y m x y λμ⎛⎫+−+−−+−−+=−++− ⎪⎝⎭. 对比xy 项、x 项及y 项系数得()()()121212(1),4(3),21(3).k k k k k m k k k m λμλμλμ⎧+=−⎪++=−⎨⎪+−=+⎩①②③将①代入②③,消去,λμ并化简得3210m k ++=,即2133m k =−−.故直线MN 的方程为2133y k x ⎛⎫=−− ⎪⎝⎭,直线MN 过定点21,33P ⎛⎫− ⎪⎝⎭.又AD MN ⊥,D 在以AP 为直径的圆上.AP 中点41,33⎛⎫⎪⎝⎭即为圆心Q .经检验,直线MN 垂直于x 轴时也成立.故存在41,33Q ⎛⎫ ⎪⎝⎭,使得122||||2DQ AP ==[方法四]:设()()1122,,,M x y N x y .若直线MN 的斜率不存在,则()()1111,,,M x y N x y −. 因为AM AN ⊥,则0AM AN ⋅=,即()1221210x y −+−=.由2211163x y +=,解得123x =或12x =(舍).所以直线MN 的方程为23x =. 若直线MN 的斜率存在,设直线MN 的方程为y kx m =+,则()()()222122()6120x kx m k x x x x ++−=+−−=.令2x =,则()()1222(21)(21)2212k m k m x x k +−++−−=+.又()()221221262y m y y y y y k k −⎛⎫⎛⎫+−=+−− ⎪ ⎪⎝⎭⎝⎭,令1y =,则()()122(21)(21)1112k m k m y y k +−−+−−−=+. 因为AM AN ⊥,所以()()()()12122211AM AN x x y y ⋅=−−+−−2(21)(231)12k m k m k +−++=+0=,即21m k =−+或2133m k =−−.当21m k =−+时,直线MN 的方程为21(2)1y kx k k x =−+=−+.所以直线MN 恒过(2,1)A ,不合题意;当2133m k =−−时,直线MN 的方程为21213333y kx k k x ⎛⎫=−−=−− ⎪⎝⎭,所以直线MN 恒过21,33P ⎛⎫− ⎪⎝⎭.综上,直线MN 恒过21,33P ⎛⎫− ⎪⎝⎭,所以42||3AP =.又因为AD MN ⊥,即AD AP ⊥,所以点D 在以线段AP 为直径的圆上运动.取线段AP 的中点为41,33Q ⎛⎫ ⎪⎝⎭,则122||||23DQ AP ==.所以存在定点Q ,使得||DQ 为定值.【整体点评】(2)方法一:设出直线MN 方程,然后与椭圆方程联立,通过题目条件可知直线过定点P ,再根据平面几何知识可知定点Q 即为AP 的中点,该法也是本题的通性通法;方法二:通过坐标系平移,将原来的O 点平移至点A 处,设直线MN 的方程为4mx ny ,再通过与椭圆方程联立,构建齐次式,由韦达定理求出,m n 的关系,从而可知直线过定点P ,从而可知定点Q 即为AP 的中点,该法是本题的最优解;方法三:设直线:MN y kx m =+,再利用过点,,A M N 的曲线系,根据比较对应项系数可求出,m k 的关系,从而求出直线过定点P ,故可知定点Q 即为AP 的中点;方法四:同方法一,只不过中间运算时采用了一元二次方程的零点式赋值,简化了求解()()1222−−x x 以及()()1211y y −−的计算.题型一 已知定点求定值1.已知抛物线2:4C y x =,过点(4,0)的直线与抛物线C 交于P ,Q 两点,O 为坐标原点.证明:90POQ ︒∠=. 【解析】直线()()1122:4,,,,PQ x my P x y Q x y =+ 由4x my =+,得14x my−=则由244x my y x =+⎧⎨=⎩,得:244x my y x −=⋅,整理得:210y y m x x ⎛⎫+−= ⎪⎝⎭,即:12121y y x x ⋅=−.重点题型·归类精讲所以12121OP OQ y y k k x x ⋅==−, 则OP OQ ⊥,即:90POQ ︒∠=2.如图,椭圆22:12x E y +=,经过点(1,1)M ,且斜率为k 的直线与椭圆E 交于不同的两点P ,Q (均异于点(0,1)A −,证明:直线AP 与AQ 的斜率之和为2.【解析】设直线()()1122:(1)1,,,,PQ mx n y P x y Q x y ++= 则21m n +=. 由22(1)112mx n y x y ++=⎧⎪⎨+=⎪⎩, 得:22[(1)1]12x y ++−=.则22(1)2(1)[(1)]02x y y mx n y ++−+++=, 故2111(12)202y y n m x x ++⎛⎫⎛⎫−−+= ⎪ ⎪⎝⎭⎝⎭.所以1212112221y y m x x n +++==−. 即1212112AP AQ y y k k x x +++=+=.3.已知点31,2A ⎛⎫ ⎪⎝⎭,O 为坐标原点,E ,F 是椭圆22:=143x y =C 上的两个动点,满足直线AE 与直线AF 关于直线x =1对称.证明直线EF 的斜率为定值,并求出这个定值;【答案】(提示:120k k += 答案:12)4.如图,点(1,0)F 为椭圆22143x y+=的右焦点,过F 且垂直于x 轴的直线与椭圆E 相交于C 、D 两点(C 在D 的上方),设点A 、B 是椭圆E 上位于直线CD 两侧的动点,且满足ACD BCD ∠=∠,试问直线AB 的斜率是否为定值,请说明理由.解法1常规解法依题意知直线AB 的斜率存在,设AB 方程:y kx m =+()11,A x y ,()22,B x y代入椭圆方程22143x y +=得:()2224384120k x kmx m +++−=(*)122843km x x k ∴+=−+,212241243m x x k −=+ 由ACD BCD ∠=∠得0AC BC k k +=31,2C ⎫⎛ ⎪⎝⎭,121212123333222201111y y kx m kx m x x x x −−+−+−∴+=+=−−−− ()1212322302kx x m k x x m ⎫⎛∴+−−+−+= ⎪⎝⎭22241238223043243m km k m k m k k −⎛⎫⎛⎫∴⋅+−−−−+= ⎪⎪++⎝⎭⎝⎭整理得:(63)(223)0k k m −+−=2230k m ∴+−=或630k −=当2230k m +−=时,直线AB 过定点31,2C ⎛⎫⎪⎝⎭,不合题意 630k ∴−=,12k =,∴直线AB 的斜率是定值12 解法2齐次化:设直线AB 的方程为3(1)12m x n y ⎫⎛−+−= ⎪⎝⎭椭圆E 的方程即:22333[(1)1]41222x y ⎡⎤⎫⎛−++−+= ⎪⎢⎥⎝⎭⎣⎦即:22334126(1)3(1)022y y x x ⎫⎫⎛⎛−+−+−+−= ⎪ ⎪⎝⎝⎭⎭联立得:233(412)(126)22n y m n y ⎫⎫⎛⎛+−++− ⎪ ⎪⎝⎝⎭⎭2(1)(63)(1)0x m x −++−=即23322(412)(126)(63)011y y n m n m x x ⎛⎫−− ⎪+++++= ⎪−− ⎪⎝⎭∴由ACD BCD ∠=∠得121233(126)22011(412)AC BCy y m n k k x x n −−++=+=−=−−+即:2n m =− ∴直线AB 的斜率为12m n −=,是定值.5.椭圆22:12x E y +=,()0,1A −,经过点()1,1,且斜率为k 的直线与椭圆E 交于不同的两点P ,Q (均异于点A ),证明:直线AP 与AQ 斜率之和为2.解法1常规解法:证明:由题意设直线PQ 的方程为()()110y k x k =−+≠,代入椭圆方程2212xy +=,可得()()()221241220kxk k x k k +−−+−=,由已知得()1,1在椭圆外,设()11,P x y ,()22,Q x y ,120x x ≠,则()1224112k k x x k −+=+,()1222212k k x x k−=+, 且()()()22216182120kk k k k ∆=−−−+>,解得0k >或2k <−.则有直线AP ,AQ 的斜率之和为121211AP AQ y y k k x x +++=+()()121212121222112222kx k kx k x xk k k k x x x x x x ⎛⎫+−+−+=+=+−+=+−⋅ ⎪⎝⎭()()()()4122221222k k k k k k k k −=+−⋅=−−=−.即有直线AP 与AQ 斜率之和2.解法2齐次化:上移一个单位,椭圆E '和直线()2211:21x y L mx ny ⎧+−=⎪⎨⎪+=⎩',1mx ny +=过点()1,2,21m n +=,12m n =−,()22212x y +−=,22240x y y +−=,()22240y x y mx ny +−+=,()224240n y mxy x −+−+=,∵0x ≠,同除2x ,得()242410y yn m x x ⎛⎫−+−+= ⎪⎝⎭,1242224212m m mk k n n m+=−===−+−.6.已知椭圆C :22143x y +=,过F 作斜率为(0)k k ≠的动直线l ,交椭圆C 于M ,N 两点,若A 为椭圆C 的左顶点,直线AM ,AN 的斜率分别为1k ,2k ,求证:12k kk k +为定值,并求出定值.将椭圆沿着AO 方向平移,平移后的椭圆方程为034134)2(2222=++⇒=+−x y x y x设直线MN 方程为1=+ny mx ,代入椭圆方程得0)(3422=+++ny mx x yx ,两侧同时除以2x得0441)(312=−+−m x y n x y ,nmk k m k k n k k N M −==−==+'',343,32121,因为1=+ny mx 过定点31)0,3(=⇒'m F ,所以421=+k k k k题型二 已知定值求定点7.(2017·全国卷理)已知椭圆2214x y +=,设直线l 不经过2P 点且与C 相交于A ,B 两点.若直线2P A与直线2P B 的斜率的和为-1,证明:l 过定点. (1)根据椭圆的对称性,332P ⎛⎫− ⎪ ⎪⎝⎭,431,2P ⎛⎫⎪ ⎪⎝⎭两点必在椭圆C 上,又4P 的横坐标为1, ∴椭圆必不过()11,1P ,∴()20,1P ,33P ⎛− ⎝⎭,43P ⎛ ⎝⎭三点在椭圆C 上,把()20,1P ,33P ⎛− ⎝⎭代入椭圆C ,得:222111314b a b ⎧=⎪⎪⎨⎪+=⎪⎩,解得24a =,21b =,∴椭圆C 的方程为2214x y +=.(2):解法1常规解法:①当斜率不存在时,设:l x m =,(),A A m y ,(),A B m y −, ∵直线2P A 与直线2P B 的斜率的和为-1,∴221121A A P A P B y y k k m m m−−−−+=+==−, 解得2m =,此时l 过椭圆右顶点,不存在两个交点,故不满足.②当斜率存在时,设:l y kx t =+,1t,()11,A x y ,()22,B x y ,联立22440y kx tx y =+⎧⎨+−=⎩,整理,得()222148440k xktx t +++−=,122814ktx x k −+=+,21224414t x x k −=+,则()()()()()2222221212112212122888881111414441114P A P Bkt k kt ktx kx t x x kx t x k t y y k k k t x x x x t t k −−++−++−−−−++=+====−−+−+,又1t ≠,∴21t k =−−,此时64k ∆=−,存在k ,使得0∆>成立,∴直线l 的方程为21y kx k =−−,当2x =时,1y =−,∴l 过定点()2,1−.解法2齐次化:下移1个单位得()2222:112044x x E y y y '++=⇒++=,设平移后的直线::1A B mx ny ''+=,齐次化:()22480x y y mx ny +++=,()228480n y mxy x +++=,∵0x ≠同除以2x ,()284810y y n m x x ⎛⎫⎛⎫+++= ⎪ ⎪⎝⎭⎝⎭,()284810n k mk +++=,128184m k k n +=−=−+, 884m n =+,221m n −=,∴1mx ny +=过()2,2−,上移1个单位()2,1−.8.已知椭圆22:14x C y +=,设直线l 不经过点2(0,1)P 且与C 相交于A ,B 两点.若直线2P A 与直线2P B 的斜率的和为1−,证明:直线l 过定点. 不平移齐次化【解析】设直线:(1)1l mx n y +−=......(1) 由22:14x C y +=,得22[(1)1]14x y +−+=即:22(1)2(1)04x y y +−+−=......(2)由(1)(2)得:22(1)2(1)[(1)]04x y y mx n y +−+−+−=整理得:2111(12)204y y n m x x −−⎛⎫++⋅+= ⎪⎝⎭则221212112112P A P B y y m k k x x n−−+=+=−=−+, 则221m n =+,代入直线:(1)1l mx n y +−=,得::(21)2(1)2l n x n y ++−=显然,直线过定点(2,1)−.9.已知抛物线C :y 2=2px (p >0)上的点P (1,y 0)(y 0>0)到其焦点的距离为2. (1)求点P 的坐标及抛物线C 的方程; (2)若点M 、N 在抛物线C 上,且k PM •k PN =12-,证明:直线MN 过定点.答案:(2)(9,﹣2)10.已知椭圆22:143x y C +=,31,2P ⎛⎫ ⎪⎝⎭,若直线l 交椭圆C 于A ,B (A ,B 异于点P )两点,且直线P A 与PB 的斜率之积为94−,求点P 到直线l 距离的最大值. 解法1齐次化:公共点31,2P ⎛⎫ ⎪⎝⎭,左移1个单位,下移32个单位,()22312:143:1y x C A B mx ny ⎧⎛⎫+⎪ ⎪+⎪⎝⎭+='''⎨⎪⎪+=⎩,()2236430x x y y +++=,()()2243620y x x y mx ny ++++=,()()()2212462630n y m n xy m x +++++=,等式两边同时除以2x ,()()()212462630y yn m n m x x ⎛⎫+++++= ⎪⎝⎭,94PA PB k k ⋅=−,6391244m n +=−+,19124m n −−=, 1mx ny +=过19,24⎛⎫−− ⎪⎝⎭,右移1个单位,上移32个单位,过13,24Q ⎛⎫− ⎪⎝⎭,∴P 到直线l 的距离的最大值为PQ 221338512244⎡⎤⎛⎫⎛⎫−+−−= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 8512>,∴点P 到直线l 8511.已知椭圆:,椭圆的短轴长等于4.E 22221(0)x y a b a b +=>>3E(1)求椭圆的标准方程;(2)设,,过且斜率为的动直线与椭圆交于,两点,直线,分别交:于异于点的点,,设直线的斜率为,直线,的斜率分别为.①求证:为定值; ②求证:直线过定点.答案:(2)-2;(3)0,32⎛⎫⎪⎝⎭【小问1详解】由题意解得所以椭圆的标准方程为:;【小问2详解】① 设MN 的方程为,与联立得:,设,,则,【法二】平移坐标系+齐次化处理将坐标系中的图像整体向下平移2个单位,E 22164x y +=()0,1A −()0,2B A 1k l E M N BM BN C ()2211x y +−=B P Q PQ 2k BM BN 34k k ,34k k ⋅PQ 2222433b ca b c a=⎧⎪⎪=⎨⎪+=⎪⎩262b a c =⎧⎪=⎨⎪=⎩22164x y +=11y k x =−22164x y +=()221132690k x k x +−−=11(,)M x y 22(,)N x y ()11221122121163293272210k x x k x x k k ⎧+=⎪+⎪⎪=−⎨+⎪⎪∆=+>⎪⎩()()21122121121123412121233223()92k x k x y y k x x k x x k k x x x x x x −−−−−++∴⋅=⋅===−14 / 15平移后的椭圆方程为:()222164y x ++=,整理得:2212023y y x ++=,设平移后的直线MN 的方程为:1mx ny +=,代入点()0,3−得13ymx −=, 则有22023312y x y x y m ⎛⎫+ ⎝−=⎪⎭+,整理得:220212mxy y x ++=−令yk x=,将220212mxy y x ++=−两边同除2x ,得20212m k k ++=−,故342k k ⋅=− 说明:因为平移后'3'm m y k x =,'4'n n y k x =, 而式子220212mxy y x ++=−中x ,y 的值对应平移后的m ’和n ’ 所以同除2x 后得到的就是一个以3k 和4k 为根一个关于k 的一元二次方程.②设PQ 的方程为 ,与联立,设,则 由,即此时, 的方程为,故直线恒过定点.2y k x t =+()2211x y +−=()()()222212120k x k t x t t ++−+−=33P(,)x y 44(,)Q x y ()()()234223422222221121420k t x x k t t x x k k t t ⎧−+=−⎪+⎪⎪−⎪=⎨+⎪⎪∆=−+>⎪⎪⎩()()()()()22232423423434343412222222BP BQk x t k x t k x x k t x x t y y k k x x x x x x +−+−+−++−−−∴⋅=⋅==()()()()()()()()()2222222222222222112211222k t t k t t k t k t k t k t t t t tt−−−−++−−−++−−===−34BP BQ k k k k ⋅=⋅222,,3t t t −=−∴=2228409k ⎛⎫∆=+> ⎪⎝⎭PQ ∴223y k x =+PQ 203⎛⎫⎪⎝⎭,。
圆锥曲线培优讲义

一原点三角形面积公式1. 已知椭圆的离心率为,且过点.若点M (x 0,y 0)在椭圆C 上,则点称为点M 的一个“椭点”.(1)求椭圆C 的标准方程;(2)若直线l :y=kx +m 与椭圆C 相交于A ,B 两点,且A ,B 两点的“椭点”分别为P ,Q ,以PQ 为直径的圆经过坐标原点,试求△AOB 的面积.2. 己知椭圆x 2+2y 2=1,过原点的两条直线l 1和l 2分别与椭圆交于点A ,B 和C ,D .记△AOC 的面积为S .(1)设A (x 1,y 1),C (x 2,y 2).用A ,C 的坐标表示点C 到直线l 1的距离,并证明S =12∣x 1y 2−x 2y 1∣; (2)设l 1:y =kx ,C (√33,√33),S =13,求k 的值.(3)设l 1与l 2的斜率之积为m ,求m 的值,使得无论l 1与l 2如何变动,面积S保持不变.3. 已知椭圆()0,01:2222>>=+b by x C αα的左、右两焦点分别为()()0,1,0,121F F -,椭圆上有一点A 与两焦点的连线构成的21F AF ∆中,满足.127,121221ππ=∠=∠F AF F AF (1)求椭圆C 的方程;(2)设点D C B ,,是椭圆上不同于椭圆顶点的三点,点B 与点D 关于原点O 对称,设直线OC OB CD BC ,,,的斜率分别为4321,,,k k k k ,且4321k k k k ⋅=⋅,求22OC OB +的值.4. 在平面直角坐标系xoy 内,动点(,)M x y 与两定点(2,0),(2,0)-,连线的斜率之积为14-(1)求动点M 的轨迹C 的方程;(2)设点1122(,),(,)A x y B x y 是轨迹C 上相异的两点.(I)过点A ,B 分别作抛物线2y =的切线1l 、2l ,1l 与2l 两条切线相交于点()N t ,证明:0NA NB =u u u r u u u rg ;(Ⅱ)若直线OA 与直线OB 的斜率之积为14-,证明:AOB S ∆为定值,并求出这个定值·5. 已知A 、B 分别是x 轴和y 轴上的两个动点,满足∣AB∣=2,点P 在线段AB 上,且AP⃗⃗⃗⃗⃗ =tPB ⃗⃗⃗⃗⃗ (t 是不为0的常数),设点P 的轨迹方程为C . (1)求点P 的轨迹方程C ;(2)若曲线C 为焦点在x 轴上的椭圆,试求实数t 的取值范围;(3)若t =2,点M ,N 是曲线C 上关于原点对称的两个动点,点Q 的坐标为(32,3),求△QMN 的面积S 的最大值.6. 已知椭圆C 1的焦点在x 轴上,中心在坐标原点;抛物线C 2的焦点在y 轴上,顶点在坐标原点.在C 1,C 2上各取两个点,将其坐标记录于表格中:x 3−24√2y 9208√22(1)求C 1,C 2的标准方程;(2)已知定点C (0,18),P 为抛物线C 2上一动点,过点P 作抛物线C 2的切线交椭圆C 1于A ,B 两点,求△ABC 面积的最大值.7. 已知抛物线y 2=4x 的焦点为F ,过点F 的直线交抛物线于A ,B 两点.(1)若AF⃗⃗⃗⃗⃗ =2FB ⃗⃗⃗⃗⃗ ,求直线AB 的斜率; (2)设点M 在线段AB 上运动,原点O 关于点M 的对称点为C ,求四边形OACB 面积的最小值. 8. 设椭圆C 1:x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别是F 1、F 2,下顶点为A ,线段OA 的中点为B (O 为坐标原点),如图.若抛物线C 2:y =x 2−1与y 轴的交点为B ,且经过F 1,F 2点. (1)求椭圆C 1的方程;(2)设M (0,−45),N 为抛物线C 2上的一动点,过点N 作抛物线C 2的切线交椭圆C 1于P 、Q 两点,求△MPQ 面积的最大值.二定点定值问题9. 动点P 在圆E :22(1)16x y ++=上运动,定点(1,0)F ,线段PF 的垂直平分线与直线PE 的交点为Q . (Ⅰ)求Q 的轨迹T 的方程;x yNMAO (Ⅱ)过点F 的直线1l ,2l 分别交轨迹E 于A ,B 两点和C ,D 两点,且12l l ⊥.证明:过AB 和CD 中点的直线过定点.10. 在直角坐标系xOy 中,抛物线C 的顶点是双曲线D :22123y x -=的中心,抛物线C 的焦点与双曲线D 的焦点相同. (Ⅰ)求抛物线C 的方程;(Ⅱ)若点(,1)P t (0)t >为抛物线C 上的定点,A ,B 为抛物线C 上两个动点.且PA ⊥PB ,问直线AB 是否经过定点?若是,求出该定点,若不是,说明理由.11. 如图,在平面直角坐标系xOy 中,椭圆C:x 2a 2+y 2b 2=1(a >b >0)的离心率为√63,直线l 与x 轴交于点E ,与椭圆C 交于A,B 两点.当直线l 垂直于x 轴且点E 为椭圆C 的右焦点时,弦AB 的长为2√63. (1)求椭圆C 的方程;(2)若点E 的坐标为(√32,0),点A 在第一象限且横坐标为√3,连接点A 与原点O 的直线交椭圆C 于另一点P ,求△PAB 的面积;(3)是否存在点E ,使得1EA 2+1EB 2为定值若存在,请指出点E 的坐标,并求出该定值;若不存在,请说明理由.12. 已知椭圆的左焦点为F ,不垂直于x 轴且不过F 点的直线l 与椭圆C 相交于A ,B 两点.(1)如果直线FA ,FB 的斜率之和为0,则动直线l 是否一定经过一定点?若过一定点,则求出该定点的坐标;若不过定点,请说明理由. (2)如果FA ⊥FB ,原点到直线l 的距离为d ,求d 的取值范围.13. 如图,已知直线:1(0)l y kx k =+>关于直线1y x =+对称的直线为1l ,直线1,l l 与椭圆22:14x E y +=分别交于点A 、M 和A 、N ,记直线1l 的斜率为1k .(Ⅰ)求1k k ⋅的值;(Ⅱ)当k 变化时,试问直线MN 是否恒过定点若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.14. 如图,椭圆E:x 2a 2+y 2b 2=1(a >b >0)的离心率是√22,过点P (0,1)的动直线l与椭圆相交于A ,B 两点.当直线l 平行于x 轴时,直线l 被椭圆E 截得的线段长为2√2.(1)求椭圆E 的方程;(2)在平面直角坐标系xOy 中,是否存在与点P 不同的定点Q ,使得∣QA∣∣QB∣=∣PA∣∣PB∣恒成立若存在,求出点Q 的坐标;若不存在,请说明理由.15. 已知动圆过定点(p2,0),且与直线x =−p2相切,其中p >0.(1)求动圆圆心C 的轨迹的方程;(2)设A 、B 是轨迹C 上异于原点O 的两个不同点,直线OA 和OB 的倾斜角分别为α和β,当α,β变化且α+β为定值θ(0<θ<π)时,证明直线AB 恒过定点,并求出该定点的坐标.16. 已知抛物线E:y 2=2px (p >0)的准线与x 轴交于点K ,过点K 做圆C:(x −5)2+y 2=9的两条切线,切点为M ,N ,|MN|=3√3. (1)求抛物线E 的方程;(2)设A ,B 是抛物线E 上分别位于x 轴两侧的两个动点,且OA ⃗⃗⃗⃗⃗ OB⃗⃗⃗⃗⃗ =94(其中O 为坐标原点).①求证:直线AB 必过定点,并求出该定点Q 的坐标;②过点Q 作AB 的垂线与抛物线交于G ,D 两点,求四边形AGBD 面积的最小值.17. 如图,在平面直角坐标系xOy 中,设点M(x0,y0)是椭圆C :2212x y +=上一点,从原点O 向圆M:22002()()3x x y y -+-=作两条切线分别与椭圆C 交于点P 、Q ,直线OP 、OQ 的斜率分别记为k1,k2 (1)求证:k1k2为定值;(2)求四边形OPMQ 面积的最大值.18. 如图,在平面直角坐标系xOy 中,已知()00 R x y ,是椭圆22:12412x y C +=上的一点,从原点O 向圆()()2200:8R x x y y -+-=作两条切线,分别交椭圆于P ,Q . (1)若R 点在第一象限,且直线OP ,OQ 互相垂直,求圆R 的方程;(2)若直线OP ,OQ 的斜率存在,并记为12 k k ,,求12 k k ,的值; (3)试问22OP OQ +是否为定值?若是,求出该值;若不是,说明理由.三中点弦问题19. 椭圆()2222:10x y C a b a b+=>>的长轴长为22,P 为椭圆C 上异于顶点的一个动点,O 为坐标原点,2A 为椭圆C 的右顶点,点M 为线段2PA 的中点,且直线2PA 与直线OM 的斜率之积为12-.(1)求椭圆C 的方程;(2)过椭圆C 的左焦点1F 且不与坐标轴垂直的直线l 交椭圆C 于两点,A B ,线段AB 的垂直平分线与x 轴交于点N ,N 点的横坐标的取值范围是1,04⎛⎫- ⎪⎝⎭,求线段AB 的长的取值范围.20. 在平面直角坐标系xoy 中,过椭圆2222:1(0)x y C a b a b+=>>右焦点的直线20x y +-=交椭圆C 于,M N 两点,P 为,M N 的中点,且直线OP 的斜率为13. (Ⅰ)求椭圆C 的方程;(Ⅱ)设另一直线l 与椭圆C 交于,A B 两点,原点O 到直线l 的距离为3,求AOB ∆面积的最大值.21. 如图,椭圆2222:1(0)x y E a b a b+=>>左右顶点为A 、B ,左右焦点为1212,,4,23F F AB F F ==,直线(0)y kx m k =+>交椭圆E 于点C 、D 两点,与线段12F F 椭圆短轴分别交于M 、N 两点(M 、N 不重合),且CM DN =. (1)求椭圆E 的方程;(2)设直线,AD BC 的斜率分别为12,k k ,求12k k 的取值范围.22. 如图,在平面直角坐标系xoy 中,已知椭圆C :)0(12222>>=+b a bya x 的离心率21=e ,左顶点为)0,4(-A ,过点A 作斜率为)0(≠k k 的直线l 交椭圆C 于点D ,交y 轴于点E .(Ⅰ)求椭圆C 的方程;(Ⅱ)已知P 为AD 的中点,是否存在定点Q ,对于任意的)0(≠k k 都有EQ OP ⊥,若存在,求出点Q 的坐标;若不存在说明理由;(Ⅲ)若过O 点作直线l 的平行线交椭圆C 于点M ,求||||||OM AE AD +的最小值.23. 已知椭圆M:x 2a +y 2b =1(a >b >0)过点A (0,−1),且离心率e =√32. (1)求椭圆M 的方程;(2)若椭圆M 上存在点B,C 关于直线y =kx −1对称,求k 的所有取值构成的集合S ,并证明对于k ∈S ,BC 的中点恒在一条定直线上. 24. 如图,在直角坐标系xOy 中,点P (1,12)到抛物线C:y 2=2px (p >0)的准线的距离为54.点M (t,1)是C 上的定点,A ,B 是C 上的两动点,且线段AB 被直线OM平分.(1)求p ,t 的值;(2)求△ABP 面积的最大值.25. 已知抛物线C:y 2=4x ,过其焦点F 作两条相互垂直且不平行于x 轴的直线,分别交抛物线C 于点P 1,P 2和点P 3,P 4,线段P 1P 2,P 3P 4的中点分别记为M 1,M 2.(1)求△FM 1M 2面积的最小值;(2)求线段M 1M 2的中点P 满足的方程.26. 平面直角坐标系xOy 中,椭圆C :22221x y a b+=(0a b >>3抛物线E :22x y =的焦点F 是C 的一个顶点.(1)求椭圆C 的方程;(2)设P 是E 上动点,且位于第一象限,E 在点P 处的切线l 与C 交于不同的两点A ,B ,线段AB 的中点为D ,直线OD 与过P 且垂直于x 轴的直线交于点M . (i )求证:点M 在定直线上;PD MAOy E(ii )直线l 与y 轴交于点G ,记PFG ∆的面积为1S ,PDM ∆的面积为2S ,求12S S 的最大值及取得最大值时点P 的坐标. 四定比分点27. 已知点)0,2(-E ,点P 是椭圆F :36)2(22=+-y x 上任意一点,线段EP 的垂直平分线FP 交于点M ,点M 的轨迹记为曲线C . (Ⅰ)求曲线C 的方程;(Ⅱ)过F 的直线交曲线C 于不同的A ,B 两点,交y 轴于点N ,已知m =,n =,求n m +的值.28. 在直角坐标系xOy 上取两个定点12(6,0) ,(6,0),A A -再取两个动点1(0 , )N m ,2(0 , )N n ,且2mn =.(Ⅰ)求直线11A N 与22A N 交点M 的轨迹C 的方程;(Ⅱ)过(3 , 0)R 的直线与轨迹C 交于P ,Q ,过P 作PN x ⊥轴且与轨迹C 交于另一点N ,F 为轨迹C 的右焦点,若(1)RP RQ λλ=>u u u r u u u r ,求证:NF FQ λ=u u u r u u u r. 29. 如图,在平面直角坐标系xOy 中,椭圆C :22221x y a b+=()0a b >>的左、右焦点分别为1F ,2F ,P 为椭圆上一点(在x 轴上方),连结1PF 并延长交椭圆于另一点Q ,设11PF FQ λ=u u u r u u u r. (1)若点P 的坐标为3(1,)2,且2PQF △的周长为8,求椭圆C 的方程;(2)若2PF 垂直于x 轴,且椭圆C 的离心率12,2e ∈⎡⎢⎣,求实数λ的取值范围.五结论30. 已知椭圆20.已知椭圆()2222:10x y C a b a b+=>>经过点(2 2,且离心率等于2,点 A B ,分别为椭圆C 的左右顶点,点P 在椭圆C 上. (1)求椭圆C 的方程;(2) M N ,是椭圆C 上非顶点的两点,满足 OM AP ON BP ∥,∥,求证:三角形MON 的面积是定值.31. 过点(1,√32),离心率为√32.过椭圆右顶点A 的两条斜率乘积为−14的直线分别交椭圆C 于M ,N 两点.(1)求椭圆C 的标准方程;(2)直线MN 是否过定点D 若过定点D ,求出点D 的坐标,若不过点D ,请说明理由. 32. 已知椭圆的两个焦点为()15,0F -,)25,0F ,M 是椭圆上一点,若120MF MF ⋅=u u u u r u u u u r,128MF MF ⋅=u u u u r u u u u r .(1)求椭圆的方程;(2)点P 是椭圆上任意一点,12A A 、分别是椭圆的左、右顶点,直线12PA PA ,与直线352x =分别交于,E F 两点,试证:以EF 为直径的圆交x 轴于定点,并求该定点的坐标.33. 已知抛物线()220x py p =>的焦点为F ,直线4x =与x 轴的交点为P ,与抛物线的交点为Q,且5.4QF PQ =(1)求抛物线的方程;(2)如图所示,过F 的直线l 与抛物线相交于A,D 两点,与圆()2211x y +-=相交于B,C 两点(A ,B 两点相邻),过A,D 两点分别作我校的切线,两条切线相交于点M,求ABM ∆与CDM ∆的面积之积的最小值.34. 已知椭圆x 2a 2+y 2b 2=1(a >b >0),其右准线l 与x 轴交于点A ,椭圆的上顶点为B ,过它的右焦点F 且垂直于长轴的直线交椭圆于点P ,直线AB 恰经过线段FP 的中点D .(1)求椭圆的离心率;(2)设椭圆的左、右顶点分别是A 1、A 2,且BA 1⃗⃗⃗⃗⃗⃗⃗⃗ BA 2⃗⃗⃗⃗⃗⃗⃗⃗ =−3,求椭圆的方程;(3)在(2)的条件下,设Q 是椭圆右准线l 上异于A 的任意一点,直线QA 1,QA 2与椭圆的另一个交点分别为M 、N ,求证:直线MN 与x 轴交于定点. 35. 已知点(1,0)A -,(1,0)B ,直线AM 与直线BM 相交于点M ,直线AM 与直线BM 的斜率分别记为AM k 与BM k ,且2AM BM k k ⋅=-. (Ⅰ)求点M 的轨迹C 的方程;(Ⅱ)过定点(0,1)F 作直线PQ 与曲线C 交于,P Q 两点,OPQ ∆的面积是否存在最大值?若存在,求出OPQ ∆面积的最大值;若不存在,请说明理由.36. 已知一个动圆与两个定圆41)2(22=+-y x 和449)2(22=++y x 均相切,其圆心的轨迹为曲线C. (1) 求曲线C 的方程;(2) 过点F (0,2)做两条可相垂直的直线21,l l ,设1l 与曲线C 交于A,B 两点,2l 与曲线C 交于C,D 两点,线段AC ,BD 分别与直线2=x 交于M ,M,N 两点。
圆锥曲线培优讲义全

一 原点三角形面积公式 1. 已知椭圆的离心率为,且过点.若点M (x 0,y 0)在椭圆C 上,则点称为点M 的一个“椭点”.(1)求椭圆C 的标准方程;(2)若直线l :y=kx +m 与椭圆C 相交于A ,B 两点,且A ,B 两点的“椭点”分别为P ,Q ,以PQ 为直径的圆经过坐标原点,试求△AOB 的面积.2. 己知椭圆 x 2+2y 2=1,过原点的两条直线 l 1 和 l 2 分别与椭圆交于点 A ,B 和C ,D .记 △AOC 的面积为 S .(1)设 A (x 1,y 1),C (x 2,y 2).用 A ,C 的坐标表示点 C 到直线 l 1 的距离,并证明 S =12∣x 1y 2−x 2y 1∣; (2)设 l 1:y =kx ,C (√33,√33),S =13,求 k 的值.(3)设 l 1 与 l 2 的斜率之积为 m ,求 m 的值,使得无论 l 1 与 l 2 如何变动,面积 S 保持不变.3. 已知椭圆()0,01:2222>>=+b by x C αα的左、右两焦点分别为()()0,1,0,121F F -,椭圆上有一点A 与两焦点的连线构成的21F AF ∆中,满足.127,121221ππ=∠=∠F AF F AF (1)求椭圆C 的方程;(2)设点D C B ,,是椭圆上不同于椭圆顶点的三点,点B 与点D 关于原点O 对称,设直线OC OB CD BC ,,,的斜率分别为4321,,,k k k k ,且4321k k k k ⋅=⋅,求22OC OB +的值.4. 在平面直角坐标系,动点与两定点,连线的斜率之积为 (1)求动点的轨迹的方程;(2)设点是轨迹上相异的两点.(I)过点A ,B 分别作抛物线的切线、,与两条切线相交于点,证明:;xoy (,)M x y (2,0),(2,0)-14-M C 1122(,),(,)A x y B x yC 2y =1l 2l 1l 2l ()N t 0NA NB =(Ⅱ)若直线OA 与直线OB 的斜率之积为,证明:为定值,并求出这个定值·5. 已知 A 、 B 分别是 x 轴和 y 轴上的两个动点,满足 ∣AB∣=2,点 P 在线段 AB 上,且 AP ⃗⃗⃗⃗⃗ =tPB ⃗⃗⃗⃗⃗ (t 是不为 0 的常数),设点 P 的轨迹方程为 C .(1)求点 P 的轨迹方程 C ;(2)若曲线 C 为焦点在 x 轴上的椭圆,试数 t 的取值围;(3)若 t =2,点 M ,N 是曲线 C 上关于原点对称的两个动点,点 Q 的坐标为 (32,3),求 △QMN 的面积 S 的最大值.6. 已知椭圆 C 1 的焦点在 x 轴上,中心在坐标原点;抛物线 C 2 的焦点在 y轴上,顶点在坐标原点.在 C 1,C 2 上各取两个点,将其坐标记录于表格中: x3−24√2y908√2(1)求 C 1,C 2 的标准方程;(2)已知定点 C (0,18),P 为抛物线 C 2 上一动点,过点 P 作抛物线 C 2的切线交椭圆 C 1 于 A ,B 两点,求 △ABC 面积的最大值.7. 已知抛物线 y 2=4x 的焦点为 F ,过点 F 的直线交抛物线于 A ,B 两点.(1)若 AF⃗⃗⃗⃗⃗ =2FB ⃗⃗⃗⃗⃗ ,求直线 AB 的斜率; (2)设点 M 在线段 AB 上运动,原点 O 关于点 M 的对称点为 C ,求四边形 OACB 面积的最小值.8. 设椭圆 C 1:x 2a +y 2b =1 (a >b >0) 的左、右焦点分别是 F 1 、 F 2,下顶点为 A ,线段 OA 的中点为 B (O 为坐标原点),如图.若抛物线 C 2:y =x 2−1 与 y 轴的交点为 B ,且经过 F 1,F 2 点.(1)求椭圆 C 1 的方程;14-AOB S∆(2)设 M (0,−45),N 为抛物线 C 2 上的一动点,过点 N 作抛物线 C 2 的切线交椭圆 C 1 于 P 、 Q 两点,求 △MPQ 面积的最大值.二 定点定值问题9. 动点P 在圆E :22(1)16x y ++=上运动,定点(1,0)F ,线段PF 的垂直平分线与直线PE 的交点为Q . (Ⅰ)求Q 的轨迹T 的方程;(Ⅱ)过点F 的直线1l ,2l 分别交轨迹E 于A ,B 两点和C ,D 两点,且12l l ⊥.证明:过AB 和CD 中点的直线过定点.10. 在直角坐标系xOy 中,抛物线C 的顶点是双曲线D 抛物线C 的焦点与双曲线D 的焦点相同. (Ⅰ)求抛物线C 的方程;(Ⅱ)若点(,1)P t (0)t >为抛物线C 上的定点,A ,B 为抛物线C 上两个动点.且PA⊥PB ,问直线AB 是否经过定点?若是,求出该定点,若不是,说明理由.11. 如图,在平面直角坐标系 xOy 中,椭圆 C:x 2a 2+y 2b 2=1(a >b >0) 的离心率为√63,直线 l 与 x 轴交于点 E ,与椭圆 C 交于 A,B 两点.当直线 l 垂直于 x 轴且点 E 为椭圆 C 的右焦点时,弦 AB 的长为2√63.(1)求椭圆 C 的方程;(2)若点 E 的坐标为 (√32,0),点 A 在第一象限且横坐标为 √3,连接点 A 与原点 O 的直线交椭圆 C 于另一点 P ,求 △PAB 的面积; (3)是否存在点 E ,使得 1EA 2+1EB 2 为定值?若存在,请指出点 E 的坐标,并求出该定值;若不存在,请说明理由.12. 已知椭圆的左焦点为F ,不垂直于x 轴且不过F 点的直线l 与椭圆C 相交于A ,B 两点.(1)如果直线FA ,FB 的斜率之和为0,则动直线l 是否一定经过一定点?若过一定点,则求出该定点的坐标;若不过定点,请说明理由. (2)如果FA ⊥FB ,原点到直线l 的距离为d ,求d 的取值围.13. 如图,已知直线:1(0)l y kx k =+>关于直线1y x =+对称的直线为1l ,直线1,l l 与椭圆22:14x E y +=分别交于点A 、M 和A 、N ,记直线l 的斜率为k . (Ⅰ)求1k k ⋅的值;(Ⅱ)当k 变化时,试问直线MN 是否恒过定点恒过定点,请说明理由.14. 如图,椭圆 E:x 2a 2+y 2b 2=1(a >b >0)的离心率是√22,过点 P (0,1) 的动直线 l 与椭圆相交于 A ,B 两点.当直线 l 平行于x 轴时,直线 l 被椭圆 E 截得的线段长为 2√2.(1)求椭圆 E 的方程;(2)在平面直角坐标系 xOy 中,是否存在与点 P 不同的定点 Q ,使得∣QA∣∣QB∣=∣PA∣∣PB∣ 恒成立? 若存在,求出点 Q 的坐标;若不存在,请说明理由.15. 已知动圆过定点 (p2,0),且与直线 x =−p2 相切,其中 p >0.(1)求动圆圆心 C 的轨迹的方程;(2)设 A 、 B 是轨迹 C 上异于原点 O 的两个不同点,直线 OA 和 OB的倾斜角分别为 α 和 β,当 α,β 变化且 α+β 为定值 θ(0<θ<π) 时,证明直线 AB 恒过定点,并求出该定点的坐标.16. 已知抛物线 E:y 2=2px (p >0) 的准线与 x 轴交于点 K ,过点 K 做圆C:(x −5)2+y 2=9 的两条切线,切点为 M ,N ,|MN|=3√3. (1)求抛物线 E 的方程;(2)设 A ,B 是抛物线 E 上分别位于 x 轴两侧的两个动点,且 OA ⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗ =94 ( 其中 O 为坐标原点). ①求证:直线 AB 必过定点,并求出该定点 Q 的坐标;②过点 Q 作 AB 的垂线与抛物线交于 G ,D 两点,求四边形 AGBD 面积的最小值.17.18. 如图,在平面直角坐标系xOy 中,设点M(x0,y0)是椭圆C :2212x y +=上一点,从原点O 向圆M:22002()()3x x y y -+-=作两条切线分别与椭圆C 交于点P 、Q ,直线OP 、OQ 的斜率分别记为k1,k2 (1)求证:k1k2为定值;(2)求四边形OPMQ 面积的最大值.19. 如图,在平面直角坐标系xOy 中,已知()00 R x y ,是椭圆22:12412x y C +=上的一点,从原点O 向圆()()2200:8R x x y y -+-=作两条切线,分别交椭圆于P ,Q .(1)若R 点在第一象限,且直线OP ,OQ 互相垂直,求圆R 的方程; (2)若直线OP ,OQ 的斜率存在,并记为12 k k ,,求12 k k ,的值; (3)试问22OP OQ +是否为定值?若是,求出该值;若不是,说明理由.三 中点弦问题20. 椭圆()2222:10x y C a b a b+=>>的长轴长为P 为椭圆C 上异于顶点的一个动点,O 为坐标原点,2A 为椭圆C 的右顶点,点M 为线段2PA 的中点,且直线2PA 与直线OM 的斜率之积为12-. (1)求椭圆C 的方程;(2)过椭圆C 的左焦点1F 且不与坐标轴垂直的直线l 交椭圆C 于两点,A B ,线段AB 的垂直平分线与x 轴交于点N ,N 点的横坐标的取值围是1,04⎛⎫- ⎪⎝⎭,求线段AB 的长的取值围.21. 在平面直角坐标系xoy 中,过椭圆2222:1(0)x y C a b a b+=>>右焦点的直线20x y +-=交椭圆C 于,M N 两点,P 为,M N 的中点,且直线OP 的斜率为13. (Ⅰ)求椭圆C 的方程;(Ⅱ)设另一直线l 与椭圆C 交于,A B 两点,原点O 到直线l ,求AOB ∆面积的最大值.22. 如图,椭圆2222:1(0)x y E a b a b+=>>左右顶点为A 、B ,左右焦点为1212,,4,23F F AB F F ==,直线(0)y kx m k =+>交椭圆E 于点C 、D 两点,与线段12F F 椭圆短轴分别交于M 、N 两点(M 、N 不重合),且CM DN =.(1)求椭圆E 的方程;(2)设直线,AD BC 的斜率分别为12,k k ,求12k k 的取值围.23. 如图,在平面直角坐标系xoy 中,已知椭圆C :)0(12222>>=+b a bya x 的离心率21=e ,左顶点为)0,4(-A ,过点A 作斜率为)0(≠k k 的直线l 交椭圆C 于点D ,交y 轴于点E .(Ⅰ)求椭圆C 的方程;(Ⅱ)已知P 为AD 的中点,是否存在定点Q ,对于任意的)0(≠k k 都有EQ OP ⊥,若存在,求出点Q 的坐标;若不存在说明理由;(Ⅲ)若过O 点作直线l 的平行线交椭圆C 于点M ,求||||||OM AE AD +的最小值.24. 已知椭圆 M:x 2a 2+y 2b 2=1(a >b >0) 过点 A (0,−1),且离心率 e =√32. (1)求椭圆 M 的方程;(2)若椭圆 M 上存在点 B,C 关于直线 y =kx −1 对称,求 k 的所有取值构成的集合 S ,并证明对于 ∀k ∈S ,BC 的中点恒在一条定直线上.P DMA Oxy E25. 如图,在直角坐标系 xOy 中,点 P (1,12) 到抛物线 C:y 2=2px (p >0) 的准线的距离为 54.点 M (t,1) 是 C 上的定点,A ,B 是 C 上的两动点,且线段 AB 被直线 OM 平分.(1)求 p ,t 的值;(2)求 △ABP 面积的最大值.26. 已知抛物线 C:y 2=4x ,过其焦点 F 作两条相互垂直且不平行于 x 轴的直线,分别交抛物线 C 于点 P 1,P 2 和点 P 3,P 4,线段 P 1P 2,P 3P 4 的中点分别记为 M 1,M 2.(1)求 △FM 1M 2 面积的最小值;(2)求线段 M 1M 2 的中点 P 满足的方程.27. 平面直角坐标系xOy 中,椭圆C :22221x y a b+=(0a b >>3,抛物线E :22x y =的焦点F 是C 的一个顶点.(1)求椭圆C 的方程;(2)设P 是E 上动点,且位于第一象限,E 在点P 处的切线l 与C 交于不同的两点A ,B ,线段AB 的中点为D ,直线OD 与过P 且垂直于x 轴的直线交于点M . (i )求证:点M 在定直线上;(ii )直线l 与y 轴交于点G ,记PFG ∆的面积为1S ,PDM ∆的面积为2S ,求12S S 的最大值及取得最大值时点P 的坐标.四 定比分点28. 已知点)0,2(-E ,点P 是椭圆F :36)2(22=+-y x 上任意一点,线段EP 的垂直平分线FP 交于点M ,点M 的轨迹记为曲线C . (Ⅰ)求曲线C 的方程;(Ⅱ)过F 的直线交曲线C 于不同的A ,B 两点,交y 轴于点N ,已知m =,BF n NB =,求n m +的值.29. 在直角坐标系xOy 上取两个定点12(A A 再取两个动点1(0 , )N m ,2(0 , )N n ,且2mn =.(Ⅰ)求直线11A N 与22A N 交点M 的轨迹C 的方程;(Ⅱ)过(3 , 0)R 的直线与轨迹C 交于P ,Q ,过P 作PN x ⊥轴且与轨迹C 交于另一点N ,F 为轨迹C 的右焦点,若(1)RP RQ λλ=>,求证:NF FQ λ=.30. 如图,在平面直角坐标系xOy 中,椭圆C :22221x y a b+=()0a b >>的左、右焦点分别为1F ,2F ,P 为椭圆上一点(在x 轴上方),连结1PF 并延长交椭圆于另一点Q ,设11PF FQ λ=. (1)若点P 的坐标为3(1,)2,且2PQF △的周长为8,求椭圆C 的方程;(2)若2PF 垂直于x 轴,且椭圆C 的离心率1,2e ∈⎡⎢⎣,数λ的取值围.五 结论31. 已知椭圆 20.已知椭圆()2222:10x y C a b a b+=>>经过点(2 2,2,点 A B ,分别为椭圆C 的左右顶点,点P 在椭圆C 上. (1)求椭圆C 的方程;(2) M N ,是椭圆C 上非顶点的两点,满足 OM AP ON BP ∥,∥,求证:三角形MON 的面积是定值.32. 过点 (1,√32),离心率为 √32.过椭圆右顶点 A 的两条斜率乘积为 −14 的直线分别交椭圆 C 于 M ,N 两点. (1)求椭圆 C 的标准方程;(2)直线 MN 是否过定点 D ?若过定点 D ,求出点 D 的坐标,若不过点 D ,请说明理由.33. 已知椭圆的两个焦点为,,是椭圆上一点,若,.(1)求椭圆的方程;(2)点是椭圆上任意一点,分别是椭圆的左、右顶点,直线与直线分别交于两点,试证:以为直径的圆交轴于定点,并求该定点的坐标.34. 已知抛物线()220x py p =>的焦点为F ,直线4x =与x 轴的交点为P ,与抛物线的交点为Q,且5.4QF PQ =(1)求抛物线的方程;(2)如图所示,过F 的直线l 与抛物线相交于A,D 两点,与圆()2211x y +-=相交于B,C 两点(A ,B 两点相邻),过A,D 两点分别作我校的切线,两条切线相交于点M,求ABM ∆与CDM ∆的面积之积的最小值.()15,0F -)25,0F M 120MF MF ⋅=128MF MF ⋅=P 12A A 、12PA PA ,352x =,E F EF x35. 已知椭圆 x 2a 2+y 2b 2=1(a >b >0),其右准线 l 与 x 轴交于点 A ,椭圆的上顶点为 B ,过它的右焦点 F 且垂直于长轴的直线交椭圆于点 P ,直线 AB 恰经过线段 FP 的中点 D .(1)求椭圆的离心率;(2)设椭圆的左、右顶点分别是 A 1 、 A 2,且 BA 1⃗⃗⃗⃗⃗⃗⃗⃗ ⋅BA 2⃗⃗⃗⃗⃗⃗⃗⃗ =−3,求椭圆的方程;(3)在(2)的条件下,设 Q 是椭圆右准线 l 上异于 A 的任意一点,直线 QA 1,QA 2 与椭圆的另一个交点分别为 M 、 N ,求证:直线 MN 与 x 轴交于定点.36. 已知点(1,0)A -,(1,0)B ,直线AM 与直线BM 相交于点M ,直线AM 与直线BM的斜率分别记为AM k 与BM k ,且2AM BM k k ⋅=-.(Ⅰ)求点M 的轨迹C 的方程;(Ⅱ)过定点(0,1)F 作直线PQ 与曲线C 交于,P Q 两点,OPQ ∆的面积是否存在最大值?若存在,求出OPQ ∆面积的最大值;若不存在,请说明理由.37. 已知一个动圆与两个定圆41)2(22=+-y x 和449)2(22=++y x 均相切,其圆心的轨迹为曲线C.(1) 求曲线C 的方程;(2) 过点F (0,2)做两条可相垂直的直线21,l l ,设1l 与曲线C 交于A,B 两点, 2l 与曲线 C 交于C,D 两点,线段AC ,BD 分别与直线2=x 交于M ,M,N 两点。
圆锥曲线(课堂讲义和例题)

专题1 焦长与焦比体系】过椭圆的一个焦点的弦与另一个焦点围成的三角形的周长是 .【例2】 过椭圆的一个焦点F 作弦AB ,若,,则 的数值为( ) A . B .C .D .与、斜率有关【例3】设直线与椭圆相交于A 、B 两个不同的点,与x 轴相交于点F .(1)证明:;(2)若F 是椭圆的一个焦点,且,求椭圆的方程.【例4】设椭圆中心在坐标原点,焦点在轴上,一个顶点,离心率为. (1)求椭圆的方程;(2)若椭圆左焦点为,右焦点,过且斜率为1的直线交椭圆于,求的面积.秒杀秘籍:椭圆焦长以及焦比问题体:过椭圆的左焦点F 1的弦与右焦点F 2围成的三角形的周长是4a ;焦长公式:A 是椭圆上一点,、是左、右焦点,为,过,c 是椭圆半焦距,则(1);(2);(3).体面积:,. 证明:(1)如图所示,,故; (2)设由余弦定理得 ;整理得 ;整理得则过焦点的弦长.(焦长公式)焦比定理:过椭圆的左焦点F 1的弦,,令,即,代入弦长公式可得.yO F 2AB xF 1【例5】已知椭圆C:的左右顶点为A,B,点P为椭圆C上不同于A,B,的一点,且直线P A,PB的斜率之积为;(1)求椭圆的离心率;(2)设为椭圆C的左焦点,直线l过点F与椭圆C交与不同的两点M,N,且求直线l的斜率.【例6】(2014•安徽)设F1,F2分别是椭圆E:的左、右焦点,过点F1的直线交椭圆E于A、B两点,若,轴,则椭圆E的方程为.【例7】(2011•浙江)设F1,F2分别为椭圆的焦点,点A,B在椭圆上,若,则点A的坐标是.【例8】(2014•安徽)设F1,F2分别是椭圆E:的左、右焦点,过点F1的直线交椭圆E于A,B两点,.(1)若,的周长为16,求;(2)若,求椭圆E的离心率._________.【例10】过双曲线的左焦点F 1作倾斜角为的直线交双曲线于A 、B 两点,则=________.【例11】已知双曲线的左、右焦点分别为,.过的直线与双曲线的右支相交于,两点,若,若是以为顶角的等腰三角形,则双曲线的离心率为( ) A . B .C .D .注意:关于这类型焦比双曲线求离心率的题目很多,通常需要利用双曲线的几何性质把拥有焦比的较长的那段用关于的式子表示出来,再利用(交一支)或者(交两支)得出离心率.证明:1. ;同理. 2..3.设O 到AB 的距离为,则 ,故. 4.,. 5.;;;.关于抛物线的焦长公式及定理(A 为直线与抛物线右交点,B 为左交点,为AB 倾斜角) 1.;2. 3.;4.设,则; 5.设AB 交准线于点P ,.【例12】已知抛物线C :的焦点为F ,直线与C 交于A ,B (A 在x 轴上方)两点,若,则m 的值为( ) A .B .C .D .【例13】已知抛物线的方程为,过其焦点F 的直线与抛物线交于A 、B 两点,且,O 为坐标原点,则的面积和的面积之比为( ) A . B . C . D .【例14】过抛物线的焦点F 的直线l 交抛物线于点A 、B ,交其准线于点C ,若,且则此抛物线的方程为( )若交于两支时,,代入弦长公式可得.秒杀秘籍:抛物线焦长公式及性质 1..2..3..4.设,则.5.设AB 交准线于点P ,则;.秒杀秘籍:过焦点的弦与其中垂线的性质 1.设椭圆焦点弦的中垂线与长轴的交点为,则与之比是离心率的一半(如图)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一 原点三角形面积公式 1. 已知椭圆的离心率为,且过点.若点M (x 0,y 0)在椭圆C 上,则点称为点M 的一个“椭点”.(1)求椭圆C 的标准方程;(2)若直线l :y=kx +m 与椭圆C 相交于A ,B 两点,且A ,B 两点的“椭点”分别为P ,Q ,以PQ 为直径的圆经过坐标原点,试求△AOB 的面积.2. 己知椭圆 x 2+2y 2=1,过原点的两条直线 l 1 和 l 2 分别与椭圆交于点 A ,B 和C ,D .记 △AOC 的面积为 S .(1)设 A (x 1,y 1),C (x 2,y 2).用 A ,C 的坐标表示点 C 到直线 l 1 的距离,并证明 S =12∣x 1y 2−x 2y 1∣; (2)设 l 1:y =kx ,C (√33,√33),S =13,求 k 的值.(3)设 l 1 与 l 2 的斜率之积为 m ,求 m 的值,使得无论 l 1 与 l 2 如何变动,面积 S 保持不变.3. 已知椭圆()0,01:2222>>=+b by x C αα的左、右两焦点分别为()()0,1,0,121F F -,椭圆上有一点A 与两焦点的连线构成的21F AF ∆中,满足.127,121221ππ=∠=∠F AF F AF (1)求椭圆C 的方程;(2)设点D C B ,,是椭圆上不同于椭圆顶点的三点,点B 与点D 关于原点O 对称,设直线OC OB CD BC ,,,的斜率分别为4321,,,k k k k ,且4321k k k k ⋅=⋅,求22OC OB +的值.4. 在平面直角坐标系内,动点与两定点,连线的斜率之积为(1)求动点的轨迹的方程;(2)设点是轨迹上相异的两点.(I)过点A ,B 分别作抛物线的切线、,与两条切线相交于点,证明:;xoy (,)M x y (2,0),(2,0)-14-M C 1122(,),(,)A x y B x yC 2y =1l 2l 1l 2l ()N t 0NA NB =(Ⅱ)若直线OA 与直线OB 的斜率之积为,证明:为定值,并求出这个定值·5. 已知 A 、 B 分别是 x 轴和 y 轴上的两个动点,满足 ∣AB∣=2,点 P 在线段 AB 上,且 AP ⃗⃗⃗⃗⃗ =tPB ⃗⃗⃗⃗⃗ (t 是不为 0 的常数),设点 P 的轨迹方程为 C .(1)求点 P 的轨迹方程 C ;(2)若曲线 C 为焦点在 x 轴上的椭圆,试求实数 t 的取值范围; (3)若 t =2,点 M ,N 是曲线 C 上关于原点对称的两个动点,点 Q 的坐标为 (32,3),求 △QMN 的面积 S 的最大值.6. 已知椭圆 C 1 的焦点在 x 轴上,中心在坐标原点;抛物线 C 2 的焦点在 y轴上,顶点在坐标原点.在 C 1,C 2 上各取两个点,将其坐标记录于表格中: x3−24√2y908√2(1)求 C 1,C 2 的标准方程;(2)已知定点 C (0,18),P 为抛物线 C 2 上一动点,过点 P 作抛物线 C 2的切线交椭圆 C 1 于 A ,B 两点,求 △ABC 面积的最大值.7. 已知抛物线 y 2=4x 的焦点为 F ,过点 F 的直线交抛物线于 A ,B 两点.(1)若 AF⃗⃗⃗⃗⃗ =2FB ⃗⃗⃗⃗⃗ ,求直线 AB 的斜率; (2)设点 M 在线段 AB 上运动,原点 O 关于点 M 的对称点为 C ,求四边形 OACB 面积的最小值.8. 设椭圆 C 1:x 2a +y 2b =1 (a >b >0) 的左、右焦点分别是 F 1 、 F 2,下顶点为 A ,线段 OA 的中点为 B (O 为坐标原点),如图.若抛物线 C 2:y =x 2−1 与 y 轴的交点为 B ,且经过 F 1,F 2 点.(1)求椭圆 C 1 的方程;14-AOB S∆(2)设 M (0,−45),N 为抛物线 C 2 上的一动点,过点 N 作抛物线 C 2 的切线交椭圆 C 1 于 P 、 Q 两点,求 △MPQ 面积的最大值.二 定点定值问题9. 动点P 在圆E :22(1)16x y ++=上运动,定点(1,0)F ,线段PF 的垂直平分线与直线PE 的交点为Q . (Ⅰ)求Q 的轨迹T 的方程;(Ⅱ)过点F 的直线1l ,2l 分别交轨迹E 于A ,B 两点和C ,D 两点,且12l l ⊥.证明:过AB 和CD 中点的直线过定点.10. 在直角坐标系xOy 中,抛物线C 的顶点是双曲线D 抛物线C 的焦点与双曲线D 的焦点相同. (Ⅰ)求抛物线C 的方程;(Ⅱ)若点(,1)P t (0)t >为抛物线C 上的定点,A ,B 为抛物线C 上两个动点.且PA⊥PB ,问直线AB 是否经过定点?若是,求出该定点,若不是,说明理由.11. 如图,在平面直角坐标系 xOy 中,椭圆 C:x 2a 2+y 2b 2=1(a >b >0) 的离心率为√63,直线 l 与 x 轴交于点 E ,与椭圆 C 交于 A,B 两点.当直线 l 垂直于 x 轴且点 E 为椭圆 C 的右焦点时,弦 AB 的长为2√63.(1)求椭圆 C 的方程;(2)若点 E 的坐标为 (√32,0),点 A 在第一象限且横坐标为 √3,连接点 A 与原点 O 的直线交椭圆 C 于另一点 P ,求 △PAB 的面积; (3)是否存在点 E ,使得 1EA 2+1EB 2 为定值?若存在,请指出点 E 的坐标,并求出该定值;若不存在,请说明理由.12. 已知椭圆的左焦点为F ,不垂直于x 轴且不过F 点的直线l 与椭圆C 相交于A ,B 两点.(1)如果直线FA ,FB 的斜率之和为0,则动直线l 是否一定经过一定点?若过一定点,则求出该定点的坐标;若不过定点,请说明理由. (2)如果FA ⊥FB ,原点到直线l 的距离为d ,求d 的取值范围.13. 如图,已知直线:1(0)l y kx k =+>关于直线1y x =+对称的直线为1l ,直线1,l l 与椭圆22:14x E y +=分别交于点A 、M 和A 、N ,记直线l 的斜率为k . (Ⅰ)求1k k ⋅的值;(Ⅱ)当k 变化时,试问直线MN 是否恒过定点恒过定点,请说明理由.14. 如图,椭圆 E:x 2a 2+y 2b 2=1(a >b >0)的离心率是√22,过点 P (0,1) 的动直线 l 与椭圆相交于 A ,B 两点.当直线 l 平行于x 轴时,直线 l 被椭圆 E 截得的线段长为 2√2.(1)求椭圆 E 的方程;(2)在平面直角坐标系 xOy 中,是否存在与点 P 不同的定点 Q ,使得∣QA∣∣QB∣=∣PA∣∣PB∣ 恒成立? 若存在,求出点 Q 的坐标;若不存在,请说明理由.15. 已知动圆过定点 (p2,0),且与直线 x =−p2 相切,其中 p >0.(1)求动圆圆心 C 的轨迹的方程;(2)设 A 、 B 是轨迹 C 上异于原点 O 的两个不同点,直线 OA 和 OB的倾斜角分别为 α 和 β,当 α,β 变化且 α+β 为定值 θ(0<θ<π) 时,证明直线 AB 恒过定点,并求出该定点的坐标.16. 已知抛物线 E:y 2=2px (p >0) 的准线与 x 轴交于点 K ,过点 K 做圆C:(x −5)2+y 2=9 的两条切线,切点为 M ,N ,|MN|=3√3. (1)求抛物线 E 的方程;(2)设 A ,B 是抛物线 E 上分别位于 x 轴两侧的两个动点,且 OA ⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗ =94 ( 其中 O 为坐标原点). ①求证:直线 AB 必过定点,并求出该定点 Q 的坐标;②过点 Q 作 AB 的垂线与抛物线交于 G ,D 两点,求四边形 AGBD 面积的最小值.17.18. 如图,在平面直角坐标系xOy 中,设点M(x0,y0)是椭圆C :2212x y +=上一点,从原点O 向圆M:22002()()3x x y y -+-=作两条切线分别与椭圆C 交于点P 、Q ,直线OP 、OQ 的斜率分别记为k1,k2 (1)求证:k1k2为定值;(2)求四边形OPMQ 面积的最大值.19. 如图,在平面直角坐标系xOy 中,已知()00 R x y ,是椭圆22:12412x y C +=上的一点,从原点O 向圆()()2200:8R x x y y -+-=作两条切线,分别交椭圆于P ,Q .(1)若R 点在第一象限,且直线OP ,OQ 互相垂直,求圆R 的方程; (2)若直线OP ,OQ 的斜率存在,并记为12 k k ,,求12 k k ,的值; (3)试问22OP OQ +是否为定值?若是,求出该值;若不是,说明理由.三 中点弦问题20. 椭圆()2222:10x y C a b a b+=>>的长轴长为P 为椭圆C 上异于顶点的一个动点,O 为坐标原点,2A 为椭圆C 的右顶点,点M 为线段2PA 的中点,且直线2PA 与直线OM 的斜率之积为12-. (1)求椭圆C 的方程;(2)过椭圆C 的左焦点1F 且不与坐标轴垂直的直线l 交椭圆C 于两点,A B ,线段AB 的垂直平分线与x 轴交于点N ,N 点的横坐标的取值范围是1,04⎛⎫- ⎪⎝⎭,求线段AB 的长的取值范围.21. 在平面直角坐标系xoy 中,过椭圆2222:1(0)x y C a b a b+=>>右焦点的直线20x y +-=交椭圆C 于,M N 两点,P 为,M N 的中点,且直线OP 的斜率为13. (Ⅰ)求椭圆C 的方程;(Ⅱ)设另一直线l 与椭圆C 交于,A B 两点,原点O 到直线l 的距离为2,求AOB ∆面积的最大值.22. 如图,椭圆2222:1(0)x y E a b a b+=>>左右顶点为A 、B ,左右焦点为1212,,4,23F F AB F F ==,直线(0)y kx m k =+>交椭圆E 于点C 、D 两点,与线段12F F 椭圆短轴分别交于M 、N 两点(M 、N 不重合),且CM DN =.(1)求椭圆E 的方程;(2)设直线,AD BC 的斜率分别为12,k k ,求12k k 的取值范围.23. 如图,在平面直角坐标系xoy 中,已知椭圆C :)0(12222>>=+b a bya x 的离心率21=e ,左顶点为)0,4(-A ,过点A 作斜率为)0(≠k k 的直线l 交椭圆C 于点D ,交y 轴于点E . (Ⅰ)求椭圆C 的方程;(Ⅱ)已知P 为AD 的中点,是否存在定点Q ,对于任意的)0(≠k k 都有EQ OP ⊥,若存在,求出点Q 的坐标;若不存在说明理由;(Ⅲ)若过O 点作直线l 的平行线交椭圆C 于点M ,求||||||OM AE AD +的最小值.24. 已知椭圆 M:x 2a 2+y 2b 2=1(a >b >0) 过点 A (0,−1),且离心率 e =√32. (1)求椭圆 M 的方程;(2)若椭圆 M 上存在点 B,C 关于直线 y =kx −1 对称,求 k 的所有取值构成的集合 S ,并证明对于 ∀k ∈S ,BC 的中点恒在一条定直线上.P DMA Oxy E25. 如图,在直角坐标系 xOy 中,点 P (1,12) 到抛物线 C:y 2=2px (p >0) 的准线的距离为 54.点 M (t,1) 是 C 上的定点,A ,B 是 C 上的两动点,且线段 AB 被直线 OM 平分.(1)求 p ,t 的值;(2)求 △ABP 面积的最大值.26. 已知抛物线 C:y 2=4x ,过其焦点 F 作两条相互垂直且不平行于 x 轴的直线,分别交抛物线 C 于点 P 1,P 2 和点 P 3,P 4,线段 P 1P 2,P 3P 4 的中点分别记为 M 1,M 2.(1)求 △FM 1M 2 面积的最小值;(2)求线段 M 1M 2 的中点 P 满足的方程.27. 平面直角坐标系xOy 中,椭圆C :22221x y a b+=(0a b >>)的离心率是32,抛物线E :22x y =的焦点F 是C 的一个顶点.(1)求椭圆C 的方程;(2)设P 是E 上动点,且位于第一象限,E 在点P 处的切线l 与C 交于不同的两点A ,B ,线段AB 的中点为D ,直线OD 与过P 且垂直于x 轴的直线交于点M . (i )求证:点M 在定直线上;(ii )直线l 与y 轴交于点G ,记PFG ∆的面积为1S ,PDM ∆的面积为2S ,求12S S 的最大值及取得最大值时点P 的坐标.四 定比分点28. 已知点)0,2(-E ,点P 是椭圆F :36)2(22=+-y x 上任意一点,线段EP 的垂直平分线FP 交于点M ,点M 的轨迹记为曲线C . (Ⅰ)求曲线C 的方程;(Ⅱ)过F 的直线交曲线C 于不同的A ,B 两点,交y 轴于点N ,已知m =,BF n NB =,求n m +的值.29. 在直角坐标系xOy 上取两个定点12(A A 再取两个动点1(0 , )N m ,2(0 , )N n ,且2mn =.(Ⅰ)求直线11A N 与22A N 交点M 的轨迹C 的方程;(Ⅱ)过(3 , 0)R 的直线与轨迹C 交于P ,Q ,过P 作PN x ⊥轴且与轨迹C 交于另一点N ,F 为轨迹C 的右焦点,若(1)RP RQ λλ=>,求证:NF FQ λ=.30. 如图,在平面直角坐标系xOy 中,椭圆C :22221x y a b+=()0a b >>的左、右焦点分别为1F ,2F ,P 为椭圆上一点(在x 轴上方),连结1PF 并延长交椭圆于另一点Q ,设11PF FQ λ=. (1)若点P 的坐标为3(1,)2,且2PQF △的周长为8,求椭圆C 的方程;(2)若2PF 垂直于x 轴,且椭圆C 的离心率1,2e ∈⎡⎢⎣,求实数λ的取值范围.五 结论31. 已知椭圆 20.已知椭圆()2222:10x y C a b a b+=>>经过点()2 2,2,点 A B ,分别为椭圆C 的左右顶点,点P 在椭圆C 上. (1)求椭圆C 的方程;(2) M N ,是椭圆C 上非顶点的两点,满足 OM AP ON BP ∥,∥,求证:三角形MON 的面积是定值.32. 过点 (1,√32),离心率为 √32.过椭圆右顶点 A 的两条斜率乘积为 −14 的直线分别交椭圆 C 于 M ,N 两点. (1)求椭圆 C 的标准方程;(2)直线 MN 是否过定点 D ?若过定点 D ,求出点 D 的坐标,若不过点 D ,请说明理由.33. 已知椭圆的两个焦点为,,是椭圆上一点,若,.(1)求椭圆的方程;(2)点是椭圆上任意一点,分别是椭圆的左、右顶点,直线与直线分别交于两点,试证:以为直径的圆交轴于定点,并求该定点的坐标.34. 已知抛物线()220x py p =>的焦点为F ,直线4x =与x 轴的交点为P ,与抛物线的交点为Q,且5.4QF PQ =(1)求抛物线的方程;(2)如图所示,过F 的直线l 与抛物线相交于A,D 两点,与圆()2211x y +-=相交于B,C 两点(A ,B 两点相邻),过A,D 两点分别作我校的切线,两条切线相交于点M,求ABM ∆与CDM ∆的面积之积的最小值.()15,0F -)25,0F M 120MF MF ⋅=128MF MF ⋅=P 12A A 、12PA PA ,352x =,E F EF x35. 已知椭圆 x 2a 2+y 2b 2=1(a >b >0),其右准线 l 与 x 轴交于点 A ,椭圆的上顶点为 B ,过它的右焦点 F 且垂直于长轴的直线交椭圆于点 P ,直线 AB 恰经过线段 FP 的中点 D .(1)求椭圆的离心率;(2)设椭圆的左、右顶点分别是 A 1 、 A 2,且 BA 1⃗⃗⃗⃗⃗⃗⃗⃗ ⋅BA 2⃗⃗⃗⃗⃗⃗⃗⃗ =−3,求椭圆的方程;(3)在(2)的条件下,设 Q 是椭圆右准线 l 上异于 A 的任意一点,直线 QA 1,QA 2 与椭圆的另一个交点分别为 M 、 N ,求证:直线 MN 与 x 轴交于定点.36. 已知点(1,0)A -,(1,0)B ,直线AM 与直线BM 相交于点M ,直线AM 与直线BM的斜率分别记为AM k 与BM k ,且2AM BM k k ⋅=-.(Ⅰ)求点M 的轨迹C 的方程;(Ⅱ)过定点(0,1)F 作直线PQ 与曲线C 交于,P Q 两点,OPQ ∆的面积是否存在最大值?若存在,求出OPQ ∆面积的最大值;若不存在,请说明理由.37. 已知一个动圆与两个定圆41)2(22=+-y x 和449)2(22=++y x 均相切,其圆心的轨迹为曲线C.(1) 求曲线C 的方程;(2) 过点F (0,2)做两条可相垂直的直线21,l l ,设1l 与曲线C 交于A,B 两点, 2l 与曲线 C 交于C,D 两点,线段AC ,BD 分别与直线2=x 交于M ,M,N 两点。
