少儿编程NOIP2006提高组复赛试题
NOIP2006提高组复赛解题报告

1、DP,f表示合并区间内的珠子获得最大能源2、DP,可以先把主件和附件的搭配全部分出来,然后分阶段做背包3、模拟4、递推+高精度1.这题具有最优子结构的性质,与合并石子相似,所以可以用动态规划来做。
首先将数据存于c数组中,每次需要枚举一下起始点i和终点j的位置,还要枚举起点和终点之间一个断点k的位置,表示第i—k个珠子已经合并在了一起,第k—j个珠子也已经合并在了一起,当前要合并的是这两个已经合并在了一起的小珠子,这样就把一个问题分成了许多子问题。
当前一次操作所产生的能量K=c[i]*c[k]*c[j]具体做法是:开一个二维数组a,a[i,j]表示从i开始到j结束这一段中所有珠子合并所能产生的能量的最大值。
然后先枚举段的长度i(i为2到N),接着枚举开始位置j,由i, j 可推出结束位置k。
然后枚举断点位置v,v为j+1到k-1之间。
在每个断点处断开所能获得的能量为K=c[j]*c[v]*c[k]+a[j,v]+a[v,k]。
取这中间的一个最大值赋给a[j , k]。
这样做的时间复杂度为O(n3),因为N<=100,所以时间上肯定没有问题。
最后a[i,i]的最大值就是合并所有珠子后所能产生的能量的最大值。
constmaxn=100;varc:array[0..maxn] of longint;a:array[0..maxn,0..maxn] of longint;n,i,j,k,t,v,u,max:longint;beginassign(input,'energy.in'); reset(input);assign(output,'energy.out'); rewrite(output);readln(n);for i:=0 to n-1 do read(c[i]);fillchar(a,sizeof(a),0);for i:=2 to n do beginfor j:=0 to n-1 do begink:=(j+i) mod n;max:=0;for v:=j+1 to j+i-1 do beginu:=v mod n;t:=c[j]*c[u]*c[k]+a[j,u]+a[u,k];if t>max then max:=t;end;a[j,k]:=max;end;end;max:=0;for i:=0 to n-1 doif a[i,i]>max then max:=a[i,i];writeln(max);close(input); close(output)end.2、此题初看MS是01背包问题,只是多了附件这个条件。
2006年青少年信息学奥林匹克小学组复赛试题

2006年青少年信息学奥林匹克小学组复赛比赛时间3小时满分200分共4题注意事项:每道题目均有5组测试数据,每组测试数据均为10分,测试数据的范围均在题目中给出了描述。
每道题目都是文件输入、文件输出,屏幕的输入和输出无效。
题目的测试文件为xxx.in文件,请选手们注意,5组测试数据均放在同一个输入文件中,也就是你应该在你的程序最外层套一个循环,从而执行程序主体5次,对于每次运行程序主体,直接把本次结果输出到要求输出的xxx.out文件中,以方便评委的评测工作。
题目中一个样例就是对于一组数据的描述。
例如:给定两个整数a和b,求他们的和。
(假如输入文件文件:a.in , 输出文件:a.out)DIM a AS INTEGER, b AS INTEGERDIM casenum AS INTEGEROPEN "a.in" FOR INPUT AS #1OPEN "a.out" FOR OUTPUT AS #2FOR casenum = 1 TO 5 [ 注意此处循环了5次主体程序,就是为了解决5组数据] INPUT #1, a, b [ 程序主体]WRITE #2, a + b [ 程序主体]NEXT casenumCLOSE #1, #2上面的程序可以作为今天比赛的模板,[程序主体]部分可以替换为每道题目的具体代码。
提醒参赛选手,对于[程序主体]的开头要注意清空上一次循环存留下来的无用数据,以免造成这次运算的错误。
偶数世界源代码: even.bas输入文件: even.in输出文件: even.out假想我们生活在偶数世界里,在这个世界中只有正偶数。
下面就是这个世界中数的集合:Z = {2, 4, 6, 8, 10 ……};在偶数世界中,除法有它特殊的规则,如果数a能被数b整除,那么a除以b的商也一定是个偶数。
例如2能整除8, 因为2 * 4 = 8。
但是2却不能整除6,因为2 * 3 = 6。
NOIP2006 提高组 复赛试题
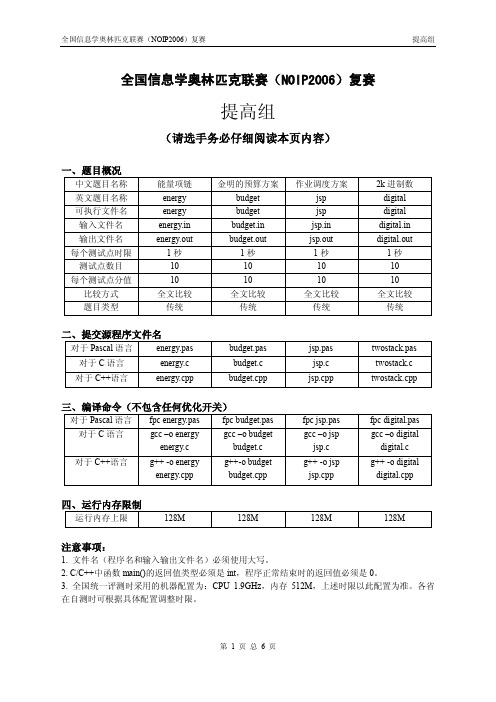
三、编译命令(不包含任何优化开关)
对于 Pascal 语言 对于 C 语言 对于 C++语言 fpc energy.pas gcc –o energy energy.c g++ -o energy energy.cpp fpc budget.pas gcc –o budget budget.c g++-o budget budget.cpp fpc jsp.pas gcc –o jsp jsp.c g++ -o jsp jsp.cpp fpc digital.pas gcc –o digital digital.c g++ -o digital digital.cpp
3.作业调度方案
(jsp.pas/c/cpp) 【问题描述】
我们现在要利用 m 台机器加工 n 个工件,每个工件都有 m 道工序,每道工序都在不同的指定 的机器上完成。每个工件的每道工序都有指定的加工时间。 每个工件的每个工序称为一个操作,我们用记号 j-k 表示一个操作,其中 j 为 1 到 n 中的某 个数字,为工件号;k 为 1 到 m 中的某个数字,为工序号,例如 2-4 表示第 2 个工件第 4 道工序 的这个操作。在本题中,我们还给定对于各操作的一个安排顺序。 例如,当 n=3,m=2 时, “1-1,1-2,2-1,3-1,3-2,2-2”就是一个给定的安排顺序, 即先安排第 1 个工件的第 1 个工序,再安排第 1 个工件的第 2 个工序,然后再安排第 2 个工件的 第 1 个工序,等等。 一方面,每个操作的安排都要满足以下的两个约束条件。 (1) 对同一个工件,每道工序必须在它前面的工序完成后才能开始; (2) 同一时刻每一台机器至多只能加工一个工件。 另一方面,在安排后面的操作时,不能改动前面已安排的操作的工作状态。 由于同一工件都是按工序的顺序安排的,因此,只按原顺序给出工件号,仍可得到同样的安排 顺序,于是,在输入数据中,我们将这个安排顺序简写为“1 1 2 3 3 2” 。 还要注意, “安排顺序”只要求按照给定的顺序安排每个操作。不一定是各机器上的实际操作 顺序。在具体实施时,有可能排在后面的某个操作比前面的某个操作先完成。 例如,取 n=3,m=2,已知数据如下: 机器号/加工时间 工件号 工序 1 工序 2 1 1/3 2/2 2 3 1/2 2/2 2/5 1/4
noip普及组复赛试题及答案

noip普及组复赛试题及答案一、选择题1. 在计算机科学中,以下哪个概念与数据结构最相关?A. 算法B. 操作系统C. 网络协议D. 编译原理答案:A2. 以下哪种排序算法的时间复杂度为O(n^2)?A. 快速排序B. 归并排序C. 堆排序D. 冒泡排序答案:D3. 在C++中,以下哪个关键字用于定义类?A. structB. unionC. enumD. typedef答案:A4. 以下哪个选项不是数据库管理系统(DBMS)的特性?A. 数据持久性B. 数据共享C. 数据加密D. 数据独立性答案:C5. 在计算机网络中,TCP和UDP协议分别属于哪一层?A. 传输层B. 应用层C. 网络层D. 物理层答案:A二、填空题1. 在计算机程序中,______ 用于定义数据的存储方式和组织形式。
答案:数据结构2. 一个算法的时间复杂度为O(1),表示该算法的执行时间与输入数据的规模______。
答案:无关3. 在C++中,______ 是一种特殊的类,它提供了一种方式来定义数据类型。
答案:typedef4. 数据库管理系统(DBMS)通常包含数据定义语言(DDL)、数据操纵语言(DML)和______。
答案:数据控制语言(DCL)5. 在计算机网络中,______ 协议负责在网络层进行数据包的路由选择。
答案:IP三、简答题1. 请简述面向对象编程(OOP)的三个基本特征。
答案:封装、继承、多态2. 描述二分查找算法的基本步骤。
答案:二分查找算法的基本步骤包括:首先确定数组是有序的,然后取中间元素与目标值比较,如果中间元素等于目标值,则查找成功;如果目标值小于中间元素,则在左半部分继续查找;如果目标值大于中间元素,则在右半部分继续查找,直到找到目标值或查找范围为空。
四、编程题1. 编写一个函数,实现对整数数组的排序。
答案:以下是一个简单的冒泡排序算法实现:```cppvoid bubbleSort(int arr[], int n) {for (int i = 0; i < n-1; i++) {for (int j = 0; j < n-i-1; j++) {if (arr[j] > arr[j+1]) {swap(arr[j], arr[j+1]);}}}}```2. 编写一个函数,实现计算一个整数的阶乘。
NOIP2006年题解解读

金明的预算方案
输入输出要求
【输入文件】 输入文件budget.in 的第1行,为两个正整数,用一个空格隔开: N m (其中N(<32000)表示总钱数,m(<60)为希望购买物品 的个数。) 从第2行到第m+1行,第j行给出了编号为j-1的物品的基本数据, 每行有3个非负整数 v p q (其中v表示该物品的价格(v<10000),p表示该物品的重要 度(1~5),q表示该物品是主件还是附件。如果q=0,表示该 物品为主件,如果q>0,表示该物品为附件,q是所属主件的 编号) 【输出文件】 输出文件budget.out只有一个正整数,为不超过总钱数的物品 的价格与重要度乘积的总和的最大值(<200000)。
2 3 4 5 6
i>=2,即对前i件物品,花费不超过k(0<=k<=10),价
7
8
9
10
1
2 3 4 5
0
0
0
0
0
0
0
0
0
0
0
0
16
16
16
If k>=w[i] then {第i件物品可要可不要, 不要 a[i,k]:=a[i-1,k]; 要 a[i,k]:=a[i-1,k-w[i]]+w[i]*v[i]} a[i,k]:=max(a[i-1,k], a[i-1,k-w[i]]+w[i]*v[i])
0 1 2 3 4 5 0 0 1 0 0 2 0 0 3 0 0 4 0 ? 5 0 6 0 7 0 8 16 9 16 10 16
W 8 4 3 4 2 V 2 5 5en {第i件物品可要可不要, 不要 a[2-1,4]=a[1,4]=0; 要 a[2-1,4-w[2]]+w[2]*v[2]=a[1,0]+4*5=20} max(a[2-1,k], a[2-1,k-w[2]]+w[2]*v[2])=max(0,20)
NOIP提高组复赛题解

样例 输入: 33 039 285 570 输出: 34 数据规模: 30%的数据满足:1<=m,n<=10 100%的数据满足:1<=m,n<=50
思路: 首先想到搜索,但是对于只考虑一条路线来说, 每一步有两种状态 一共要走m+n步,搜索整棵树的 时间复杂度为O(2^(m+n)),如果两条路线都考虑的 话,时间复杂度为O(4^(m+n)),即使是30%的数据, 即m+n=20,4^20≈10^12,这样的数据规模也还是太 大了。
4维动态规划 本题可以使用动态规划法解决。 设f[i,j,k,l]为第一条线走到(I,j),第二条线走到 (k,l)时的最优值(方便起见,两条线都看作从左上角 开始,右下角结束)。 动态转移方程: f[i-1,j,k-1,l] (i>1) f[i,j,k,l]=min f[i-1,j,k,l-1] (i>1) +s[i,j]+s[k,l] f[i,j-1,k-1,l] (j>1)且(k>i+1) f[I,j-1,k,j-1] (j>1) 同时,由于两条线不能交叉,有k>i。
输入格式: 输入文件matches.in共一行,有一个整数n(n<=24)。 * 输出格式: 输出文件matches.out共一行,表示能拼成的不同等 式的数目。
样例1 输入:
14 输出: 2 解释: 2个等式为0+1=1和1+0=1。
样例2 输入: 18 输出: 9 解释: 9个等式为: 0+4=4、0+11=11、1+10=11、2+2=4、 2+7=9、4+0=4、7+2=9、10+1=11、11+0=11
第十二年全国青少年信息学奥林匹克联赛提高组复赛试题
第十二年全国青少年信息学奥林匹克联赛提高组复赛试题联赛复赛试题〔NOIP2006提高组〕竞赛时间:2006年11月18日上午8:30—11:30关于竞赛中不同语言使用限制的说明一、关于使用Pascal语言与编译结果的说明1、关于Pascal语言的程序,当使用IDE和fpc编译结果不一致时,以fpc的编译结果为准。
2、同意使用数学库(usesmath子句),以及ansistring。
但不同意使用编译开关〔最后测试时pascal的范围检查开关默认关闭:{$R-,Q-,S-}〕,也不支持与优化相关的选项。
二、关于C++语言中模板使用的限制说明1、同意使用的部分:标准容器中的布尔集合,迭代器,串,流。
相关的头文件:2、禁止使用的部分:序列:vector,list,deque序列适配器:stack,queue,priority_queue关联容器:map,multimap,set,multiset拟容器:valarray散列容器:hash_map,hash_set,hash_multimap,hash_multiset 所有的标准库算法相关头文件:1、能量项链(energy.pas/c/cpp)【问题描述】在Mars星球上,每个Mars人都随身佩带着一串能量项链。
在项链上有N颗能量珠。
能量珠是一颗有头标记与尾标记的珠子,这些标记对应着某个正整数。
同时,关于相邻的两颗珠子,前一颗珠子的尾标记一定等于后一颗珠子的头标记。
因为只有如此,通过吸盘〔吸盘是Mars人吸收能量的一种器官〕的作用,这两颗珠子才能聚合成一颗珠子,同时释放出能够被吸盘吸收的能量。
假如前一颗能量珠的头标记为m,尾标记为r,后一颗能量珠的头标记为r,尾标记为n,那么聚合后释放的能量为〔Mars单位〕,新产生的珠子的头标记为m,尾标记为n。
需要时,Mars人就用吸盘夹住相邻的两颗珠子,通过聚合得到能量,直到项链上只剩下一颗珠子为止。
显然,不同的聚合顺序得到的总能量是不同的,请你设计一个聚合顺序,使一串项链释放出的总能量最大。
【精选资料】NOIP提高组复赛试题与简解转载
Day1铺地毯【问题描述】为了准备一个独特的颁奖典礼,组织者在会场的一片矩形区域(可看做是平面直角坐标系的第一象限)铺上一些矩形地毯。
一共有n 张地毯,编号从1 到n。
现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设,后铺的地毯覆盖在前面已经铺好的地毯之上。
地毯铺设完成后,组织者想知道覆盖地面某个点的最上面的那张地毯的编号。
注意:在矩形地毯边界和四个顶点上的点也算被地毯覆盖。
【输入】输入文件名为 carpet.in。
输入共 n+2 行。
第一行,一个整数 n,表示总共有n 张地毯。
接下来的 n 行中,第i+1 行表示编号i 的地毯的信息,包含四个正整数a,b,g,k,每两个整数之间用一个空格隔开,分别表示铺设地毯的左下角的坐标(a,b)以及地毯在x轴和y 轴方向的长度。
第 n+2 行包含两个正整数x 和y,表示所求的地面的点的坐标(x,y)。
【输出】输出文件名为 carpet.out。
输出共 1 行,一个整数,表示所求的地毯的编号;若此处没有被地毯覆盖则输出-1。
【输入输出样例 1】【输入输出样例说明】如下图,1 号地毯用实线表示,2 号地毯用虚线表示,3 号用双实线表示,覆盖点(2,2)的最上面一张地毯是3 号地毯。
【输入输出样例 2】【输入输出样例说明】如上图,1 号地毯用实线表示,2 号地毯用虚线表示,3 号用双实线表示,点(4,5)没有被地毯覆盖,所以输出-1。
【数据范围】对于 30%的数据,有n≤2;对于 50%的数据,0≤a, b, g, k≤100;对于 100%的数据,有0≤n≤10,000,0≤a, b, g, k≤100,000。
【一句话题意】给定n个按顺序覆盖的矩形,求某个点最上方的矩形编号。
【考察知识点】枚举【思路】好吧我承认看到图片的一瞬间想到过二维树状数组和二维线段树。
置答案ans=-1,按顺序枚举所有矩形,如果点在矩形内则更新ans。
注意题中给出的不是对角坐标,实际上是(a,b)与(a+g,b+k)。
NOIP复赛模拟试题2
NOIP复赛模拟试题2预览说明:预览图片所展示的格式为文档的源格式展示,下载源文件没有水印,内容可编辑和复制2013开明中学NOIP模拟试题2题目1、NBA总冠军(nba.pas/c/cpp)【问题描述】又要考试了,Ljw决定放松一下,就打开电视,看见了篮球赛,他立即想到了每年的NBA 总冠军队伍。
由于复习紧张,他只记起了一部分,记忆的内容是正确的,可能不是按时间顺序排列的,记忆的内容可能有重复。
现在请求学过编程的你帮助Ljw,按时间依次输出总冠军的球队(不能重复)。
(NBA 从1947A.D到2009A.D)【输入】输入文件nba.in的第一行是一个整数n(0<n<50)。
< bdsfid="75" p=""></n<50)。
<>接下来的n行,每行先是城市名(由大到小写字母、空格组成),后是时间(由数字组成)二者之间用空格隔开。
【输出】输出文件nba.out共n行,即排序后的NBA总冠军队伍。
每行先是时间,后是城市名。
【输入输出样例】2.买票(tickets.pas/c/cpp)【问题描述】周末Ztc想去剧场看演出,但他没有票。
这时,救世主Wzj出现了,他慷慨地愿意卖给Ztc 一些票。
Wzj手上共有n张票,但每张票的费用都不一样,贪心的ztc想要得到尽可能多的票,但又想花费最少,慷慨的wzj原意给连续的m张票。
Ztc 希望你能帮助他在花钱范围内取得最大的票数。
【输入】输入文件tickets.in的第一行是2个整数n,,f。
其中(2≤N≤1000000),表示票的数目,(10≤f≤10000),表示ztc身上的钱。
接下来的1行,有n个整数a(1≤a≤30),表示每一张票的票价。
【输出】输出文件tickets.out仅一行整数m,表示Ztc能得连续的最大票数。
【输入输出样例】【限制】50%的数据满足:2≤n≤10000100%的数据满足:2≤n≤10000003.逛街(shop.pas/c/cpp)【问题描述】某天,ZCL 在街上闲逛。
NOIP历年复赛提高组试题
全国信息学奥林匹克分区联赛(NOIP)复赛提高组试题第一届全国信息学奥林匹克分区联赛(NOIP1995)复赛试题(提高组竞赛用时:3.5小时)1、编码问题设有一个数组A:ARRAY[0..N-1]OFINTEGER;数组中存放的元素为0~N-1之间的整数,且A[i]≠A[j](当i≠j时)。
例如:N=6时,有:A=(4,3,0,5,1,2)此时,数组A的编码定义如下:A[0]的编码为0;A[i]的编码为:在A[0],A[1],…,A[i-1]中比A[i]的值小的个数(i=1,2,…,N-1)∴上面数组A的编码为:B=(0,0,0,3,1,2)程序要求解决以下问题:①给出数组A后,求出其编码。
②给出数组A的编码后,求出A中的原数据。
2、灯的排列问题设在一排上有N个格子(N≤20),若在格子中放置有不同颜色的灯,每种灯的个数记为N1,N2,……N k(k表示不同颜色灯的个数)。
放灯时要遵守下列规则:①同一种颜色的灯不能分开;②不同颜色的灯之间至少要有一个空位置。
例如:N=8(格子数);R=2(红灯数);B=3(蓝灯数),放置的方法有:R-B顺序B-R顺序放置的方法总数为12种。
数据输入的方式为:NP1(颜色,为一个字母)N1(灯的数量)P2 N2……Q(结束标记,Q本身不是灯的颜色)程序要求:求出一种顺序的放置(排列)方案及放置(排列)方案总数。
3、积木块上的数字设有一个四层的积木块,1~4层积木块的数量依次为:5,6,7,8,如下图所示放置:其中,给出第三层与第四层所标示的数字,并已知第三层的数据是由第四层的数据计算出来的。
计算的方法是:第三层的某个数据A是由第四层相邻的两个数据B,C经过某种计算后产生的:计算所用到的计算符为:+,-,⨯,且无优先级之分(自左向右计算),运算符最多为2个。
如:3+4⨯5=35 5⨯4+3=23可以看出,上图中的第三层的数据是由第四层的数据用以下计算公式计算出来的:A=B⨯C+B也就是:8=2⨯3+2,15=3⨯4+3,……14=2⨯6+2程序要求:给出第四层与第三层的数据后,将第一、二层的每块积木标上相应的数据,并输出整个完整的积木图及计算公式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
NOIP 2006 复赛试题 (提高组)第十二届全国青少年信息学奥林匹克联赛复赛试题(NOIP2006 提高组)竞赛时间:2006 年11 月18 日上午8:30—11:30关于竞赛中不同语言使用限制的说明一.关于使用Pascal 语言与编译结果的说明1.对于Pascal 语言的程序,当使用IDE 和fpc 编译结果不一致时,以fpc 的编译结果为准。
2.允许使用数学库(uses math 子句),以及ansistring。
但不允许使用编译开关(最后测试时pascal的范围检查开关默认关闭:{$R-,Q-,S-}),也不支持与优化相关的选项。
二.关于C++语言中模板使用的限制说明1.允许使用的部分:标准容器中的布尔集合,迭代器,串,流。
相关的头文件:<bitset > <iterator > <string > <iostream >2.禁止使用的部分:序列:vector,list,deque序列适配器:stack, queue, priority_queue关联容器:map, multimap, set, multiset拟容器:valarray散列容器:hash_map, hash_set, hash_multimap, hash_multiset所有的标准库算法相关头文件:<vector > <list > <deque > <stack > <map > <set > <algorithm >1.能量项链(energy.pas/c/cpp)【问题描述】在Mars 星球上,每个Mars 人都随身佩带着一串能量项链。
在项链上有N 颗能量珠。
能量珠是一颗有头标记与尾标记的珠子,这些标记对应着某个正整数。
并且,对于相邻的两颗珠子,前一颗珠子的尾标记一定等于后一颗珠子的头标记。
因为只有这样,通过吸盘(吸盘是Mars 人吸收能量的一种器官)的作用,这两颗珠子才能聚合成一颗珠子,同时释放出可以被吸盘吸收的能量。
如果前一颗能量珠的头标记为m,尾标记为r,后一颗能量珠的头标记为r,尾标记为n,则聚合后释放的能量为m⨯r⨯n(Mars 单位),新产生的珠子的头标记为m,尾标记为n。
需要时,Mars 人就用吸盘夹住相邻的两颗珠子,通过聚合得到能量,直到项链上只剩下一颗珠子为止。
显然,不同的聚合顺序得到的总能量是不同的,请你设计一个聚合顺序,使一串项链释放出的总能量最大。
例如:设N=4,4 颗珠子的头标记与尾标记依次为(2,3) (3,5) (5,10) (10,2)。
我们用记号⊕表示两颗珠子的聚合操作,(j⊕k)表示第j,k 两颗珠子聚合后所释放的能量。
则第4、1 两颗珠子聚合后释放的能量为:(4⊕1)=10*2*3=60。
这一串项链可以得到最优值的一个聚合顺序所释放的总能量为((4⊕1)⊕2)⊕3)=10*2*3+10*3*5+10*5*10=710。
【输入文件】输入文件energy.in 的第一行是一个正整数N(4≤N≤100),表示项链上珠子的个数。
第二行是N 个用空格隔开的正整数,所有的数均不超过1000。
第i 个数为第i 颗珠子的头标记(1 ≤i≤N),当i<N 时,第i 颗珠子的尾标记应该等于第i+1 颗珠子的头标记。
第N 颗珠子的尾标记应该等于第1 颗珠子的头标记。
至于珠子的顺序,你可以这样确定:将项链放到桌面上,不要出现交叉,随意指定第一颗珠子,然后按顺时针方向确定其他珠子的顺序。
【输出文件】输出文件energy.out 只有一行,是一个正整数E(E≤2.1*109),为一个最优聚合顺序所释放的总能量。
【输入样例】42 3 5 10【输出样例】7102.金明的预算方案(budget.pas/c/cpp)【问题描述】金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间金明自己专用的很宽敞的房间。
更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超过N 元钱就行”。
今天一早,金明就开始做预算了,他把想买的物品分为两类:主件与附件,附件是从属如果要买归类为附件的物品,必须先买该附件所属的主件。
每个主件可以有0 个、1 个或2 个附件。
附件不再有从属于自己的附件。
金明想买的东西很多,肯定会超过妈妈限定的N 元。
于是,他把每件物品规定了一个重要度,分为5 等:用整数1~5 表示,第5 等最重要。
他还从因特网上查到了每件物品的价格(都是10 元的整数倍)。
他希望在不超过N 元(可以等于N 元)的前提下,使每件物品的价格与重要度的乘积的总和最大。
设第j 件物品的价格为v[j],重要度为w[j],共选中了k 件物品,编号依次为j1,j2,……,j k,则所求的总和为:v[j1]*w[j1]+v[j2]*w[j2]+ …+v[j k]*w[j k]。
(其中*为乘号)请你帮助金明设计一个满足要求的购物单。
【输入文件】输入文件budget.in 的第1 行,为两个正整数,用一个空格隔开:N m(其中N(<32000)表示总钱数,m(<60)为希望购买物品的个数。
)从第2 行到第m+1 行,第j 行给出了编号为j-1 的物品的基本数据,每行有3 个非负整数v p q(其中v 表示该物品的价格(v<10000),p 表示该物品的重要度(1~5),q 表示该物品是主件还是附件。
如果q=0,表示该物品为主件,如果q>0,表示该物品为附件,q 是所属主件的编号)【输出文件】输出文件budget.out 只有一个正整数,为不超过总钱数的物品的价格与重要度乘积的总和的最大值(<200000)。
【输入样例】1000 5800 2 0400 5 1300 5 1400 3 0500 2 0【输出样例】22003.作业调度方案(jsp.pas/c/cpp)【问题描述】我们现在要利用m 台机器加工n 个工件,每个工件都有m 道工序,每道工序都在不同的指定的机器上完成。
每个工件的每道工序都有指定的加工时间。
每个工件的每个工序称为一个操作,我们用记号j-k 表示一个操作,其中j 为1 到n 中的某个数字,为工件号;k 为1 到m 中的某个数字,为工序号,例如2-4 表示第2 个工件第4 道工序的这个操作。
在本题中,我们还给定对于各操作的一个安排顺序。
例如,当n=3,m=2 时,“1-1,1-2,2-1,3-1,3-2,2-2”就是一个给定的安排顺序,即先安排第1 个工件的第1 个工序,再安排第1 个工件的第2 个工序,然后再安排第2 个工件的第1 个工序,等等。
一方面,每个操作的安排都要满足以下的两个约束条件。
(1)对同一个工件,每道工序必须在它前面的工序完成后才能开始;(2)同一时刻每一台机器至多只能加工一个工件。
另一方面,在安排后面的操作时,不能改动前面已安排的操作的工作状态。
由于同一工件都是按工序的顺序安排的,因此,只按原顺序给出工件号,仍可得到同样的安排顺序,于是,在输入数据中,我们将这个安排顺序简写为“1 1 2 3 3 2”。
还要注意,“安排顺序”只要求按照给定的顺序安排每个操作。
不一定是各机器上的实际操作顺序。
在具体实施时,有可能排在后面的某个操作比前面的某个操作先完成。
则对于安排顺序“1 1 2 3 3 2”,下图中的两个实施方案都是正确的。
但所需要的总时间分别是10 与12。
当一个操作插入到某台机器的某个空档时(机器上最后的尚未安排操作的部分也可以看作一个空档),可以靠前插入,也可以靠后或居中插入。
为了使问题简单一些,我们约定:在保证约束条件(1)(2)的条件下,尽量靠前插入。
并且,我们还约定,如果有多个空档可以插入,就在保证约束条件(1)(2)的条件下,插入到最前面的一个空档。
于是,在这些约定下,上例中的方案一是正确的,而方案二是不正确的。
显然,在这些约定下,对于给定的安排顺序,符合该安排顺序的实施方案是唯一的,请你计算出该方案完成全部任务所需的总时间。
【输入文件】输入文件 jsp.in 的第 1 行为两个正整数,用一个空格隔开:m n(其中m(<20)表示机器数,n(<20)表示工件数)第2 行:m n 个用空格隔开的数,为给定的安排顺序。
接下来的2n 行,每行都是用空格隔开的m 个正整数,每个数不超过20。
其中前n 行依次表示每个工件的每个工序所使用的机器号,第1 个数为第1 个工序的机器号,第2 个数为第2 个工序机器号,等等。
后n 行依次表示每个工件的每个工序的加工时间。
可以保证,以上各数据都是正确的,不必检验。
【输出文件】输出文件 jsp.out 只有一个正整数,为最少的加工时间。
【输入样例】2 31 123 3 21 21 22 13 22 52 4【输出样例】104.2k进制数(digital.pas/c/cpp)【问题描述】设r 是个2k进制数,并满足以下条件:(1)r 至少是个2 位的2k进制数。
(2)作为2k进制数,除最后一位外,r 的每一位严格小于它右边相邻的那一位。
(3)将r 转换为2 进制数q 后,则q 的总位数不超过w。
在这里,正整数k(1≤k≤9)和w(k<w≤30000)是事先给定的。
问:满足上述条件的不同的r 共有多少个?我们再从另一角度作些解释:设S 是长度为w 的01 字符串(即字符串S 由w 个“0”或“1” 组成),S 对应于上述条件(3)中的q。
将S 从右起划分为若干个长度为k 的段,每段对应一位2k进制的数,如果S 至少可分成2 段,则S 所对应的二进制数又可以转换为上述的2k进制数r。
例:设k=3,w=7。
则r 是个八进制数(23=8)。
由于w=7,长度为7 的01 字符串按3 位一段分,可分为3 段(即1,3,3,左边第一段只有一个二进制位),则满足条件的八进制数有:2 位数:高位为1:6 个(即12,13,14,15,16,17),高位为2:5 个,…,高位为6:1 个(即67)。
共6+5+…+1=21 个。
3 位数:高位只能是1,第2 位为2:5 个(即123,124,125,126,127),第2 位为3:4 个,…,第2 位为6:1 个(即167)。
共5+4+…+1=15 个。
所以,满足要求的r 共有36 个。
【输入文件】输入文件 digital.in 只有1 行,为两个正整数,用一个空格隔开:k W【输出文件】输出文件 digital.out 为1 行,是一个正整数,为所求的计算结果,即满足条件的不同的r 的个数(用十进制数表示),要求最高位不得为0,各数字之间不得插入数字以外的其他字符(例如空格、换行符、逗号等)。
