2024版新高考版高考总复习数学 5-1 三角函数的概念、同角三角函数的基本关系及诱导公式
2024年高考数学题源追溯专题05 三角函数(解析版)

专题05 三角函数目录一览2023真题展现考向一 三角函数的图象与性质考向二 三角恒等变换真题考查解读近年真题对比考向一 三角函数的图象与性质考向二 三角恒等变换考向三 同角三角函数间的基本关系命题规律解密名校模拟探源易错易混速记/二级结论速记考向一 三角函数的图象与性质1.(2023•新高考Ⅱ•第15题)已知函数f (x )=sin (ωx +φ),如图,A ,B 是直线y =12与曲线y =f (x )的两个交点,若|AB |=π6,则f (π)= .【答案】−32解:由题意:设A (x 1,12),B (x 2,12),则x 2﹣x 1=π6,由y =A sin (ωx +φ)的图象可知:ωx 2+φ﹣(ωx 1+φ)=5π6−π6=2π3,即ω(x 2﹣x 1)=2π3,∴ω=4,又f (2π3)=sin (8π3+φ)=0,∴8π3+φ=k π,k ∈Z ,即φ=−8π3+k π,k ∈Z ,观察图象,可知当k =2时,φ=−2π3满足条件,∴f (π)=sin (4π−2π3)=−32.故答案为:−32.2.(2023•新高考Ⅰ•第15题)已知函数f (x )=cos ωx ﹣1(ω>0)在区间[0,2π]有且仅有3个零点,则ω的取值范围是 .【答案】[2,3)【解答】解:x ∈[0,2π],函数的周期为2πω(ω>0),cos ωx ﹣1=0,可得cos ωx =1,函数f (x )=cos ωx ﹣1(ω>0)在区间[0,2π]有且仅有3个零点,可得2⋅2πω≤2π<3⋅2πω,所以2≤ω<3.考向二 三角恒等变换3.(2023•新高考Ⅱ•第7题)已知α为锐角,cos α=1+54,则sin α2=( )A .3−58B .−1+58C .3−54D .−1+54【答案】D 解:cos α=1+54,则cos α=1−2si n 2α2,故2si n 2α2=1﹣cos α=3−54,即si n 2α2=3−58=(5)2+12−2516=(5−1)216,∵α为锐角,∴sin α2>0,∴sin α2=−1+54.4.(2023•新高考Ⅰ•第8题)已知sin (α﹣β)=13,cos αsin β=16,则cos (2α+2β)=( )A .79B .19C .−19D .−79【答案】B解:因为sin (α﹣β)=sin αcos β﹣sin βcos α=13,cos αsin β=16,所以sin αcos β=12,所以sin (α+β)=sin αcos β+sin βcos α=12+16=23,则cos (2α+2β)=1﹣2sin 2(α+β)=1﹣2×49=19.【命题意图】考查同角三角函数的基本关系式、诱导公式、和角差角公式、三角函数的图象与性质、y=A sin (wx+ϕ)的图象与性质.应用三角公式进行化简、求值和恒等变形及恒等证明.【考查要点】三角函数高考必考.常考查和角差角公式、恒等变形化简求值、诱导公式、同角三角函数公式,辅助角公式等.常考查y=A sin (wx+ϕ)的图象与性质,涉及到增减性、周期性、对称性、图象平移、零点等.【得分要点】1.同角三角函数的基本关系(1)平方关系:sin 2α+cos 2α=1.(2)商数关系:sinαcosα=tan α.2.诱导公式公式一:sin (α+2k π)=sin α,cos (α+2k π)=cos_α,其中k ∈Z .公式二:sin (π+α)=﹣sin_α,cos (π+α)=﹣cos_α,tan (π+α)=tan α.公式三:sin (﹣α)=﹣sin_α,cos (﹣α)=cos_α.公式四:sin (π﹣α)=sin α,cos (π﹣α)=﹣cos_α.公式五:sin (π2−α)=cos α,cos (π2−α)=sin α.公式六:sin (π2+α)=cos α,cos (π2+α)=﹣sin α.3.两角和与差的正弦、余弦、正切公式(1)C (α﹣β):cos (α﹣β)=cos αcos β+sin αsin β.(2)C (α+β):cos (α+β)=cos αcos β﹣sin αsin β.(3)S (α+β):sin (α+β)=sin αcos β+cos αsin β.(4)S (α﹣β):sin (α﹣β)=sin αcos β﹣cos αsin β.(5)T (α+β):tan (α+β)=tanα+tanβ1−tanαtanβ.(6)T (α﹣β):tan (α﹣β)=tanα−tanβ1+tanαtanβ.4.二倍角的正弦、余弦、正切公式(1)S 2α:sin 2α=2sin αcos α.(2)C 2α:cos 2α=cos 2α﹣sin 2α=2cos 2α﹣1=1﹣2sin 2α.(3)T 2α:tan 2α=2tanα1−tan 2α.5.正弦函数、余弦函数、正切函数的图象和性质R R k ∈Z y =sin x 的图象变换得到y =A sin (ωx +φ)(A >0,ω>0)的图象的步骤7.由y=Asin(ωx+φ)的部分图象确定其解析式在由图象求三角函数解析式时,若最大值为M,最小值为m,则A=M−m2,k=M+m2,ω由周期T确定,即由2πω=T求出,φ由特殊点确定.考向一三角函数的图象与性质1.(2022•新高考Ⅰ)记函数f(x)=sin(ωx+)+b(ω>0)的最小正周期为T.若<T<π,且y=f(x)的图像关于点(,2)中心对称,则f()=( )A.1B.C.D.3【解答】解:函数f(x)=sin(ωx+)+b(ω>0)的最小正周期为T,则T=,由<T<π,得<<π,∴2<ω<3,∵y=f(x)的图像关于点(,2)中心对称,∴b=2,且sin(+)=0,则+=kπ,k∈Z.∴,k∈Z,取k=4,可得.∴f(x)=sin(x+)+2f()=sin(×+)+2=﹣1+2=1.故选:A.2.(多选)(2022•新高考Ⅱ)已知函数f(x)=sin(2x+φ)(0<φ<π)的图像关于点(,0)中心对称,则( )A.f(x)在区间(0,)单调递减B.f(x)在区间(﹣,)有两个极值点C.直线x=是曲线y=f(x)的对称轴D.直线y=﹣x是曲线y=f(x)的切线【解答】解:因为f(x)=sin(2x+φ)(0<φ<π)的图象关于点(,0)对称,所以+φ=kπ,k∈Z,所以φ=kπ﹣,因为0<φ<π,所以φ=,故f(x)=sin(2x+),令2x+,解得﹣<x<,故f(x)在(0,)单调递减,A正确;x∈(﹣,),2x+∈(,),根据函数的单调性,故函数f(x)在区间(﹣,)只有一个极值点,故B错误;令2x+=kπ+,k∈Z,得x=﹣,k∈Z,C显然错误;f(x)=sin(2x+),求导可得,f'(x)=,令f'(x)=﹣1,即,解得x=kπ或(k∈Z),故函数y=f(x)在点(0,)处的切线斜率为k=,故切线方程为y﹣,即y=,故D正确.故选:AD.3.(2021•新高考Ⅰ)下列区间中,函数f(x)=7sin(x﹣)单调递增的区间是( )A.(0,)B.(,π)C.(π,)D.(,2π)【解答】解:令,k∈Z.则,k∈Z.当k=0时,x∈[,],(0,)⊆[,],故选:A .考向二 三角恒等变换4.(2022•新高考Ⅱ)若sin (α+β)+cos (α+β)=2cos (α+)sin β,则( )A .tan (α﹣β)=1B .tan (α+β)=1C .tan (α﹣β)=﹣1D .tan (α+β)=﹣1【解答】解:解法一:因为sin (α+β)+cos (α+β)=2cos (α+)sin β,所以sin ()=2cos (α+)sin β,即sin ()=2cos (α+)sin β,所以sin ()cos β+sin βcos ()=2cos (α+)sin β,所以sin ()cos β﹣sin βcos ()=0,所以sin ()=0,所以=k π,k ∈Z ,所以α﹣β=k,所以tan (α﹣β)=﹣1.解法二:由题意可得,sin αcos β+cos αsin β+cos αcos β﹣sin αsin β=2(cos α﹣sin α)sin β,即sin αcos β﹣cos αsin β+cos αcos β+sin αsin β=0,所以sin (α﹣β)+cos (α﹣β)=0,故tan (α﹣β)=﹣1.故选:C .考向三 同角三角函数间的基本关系5.(2021•新高考Ⅰ)若tan θ=﹣2,则=( )A .﹣B .﹣C .D .【解答】解:由题意可得:===.故选:C.结合近三年命题规律,命制三角函数恒等变换题目,诸如“给值求角”“给值求值”“给角求值”,给定函数部分图象,求解函数解析式。
2024届全国新高考数学精准复习三角函数知识点总结

千里之行,始于足下。
2024届全国新高考数学精准复习三角函数知识点总结2024届全国新高考数学考试中,三角函数是一个重要的知识点。
以下是三角函数的主要内容和考点总结:1. 基本概念:- 弧度与角度的转换:1弧度=180°/π,1度=π/180弧度。
- 正弦、余弦、正切、余切、正割、余割的定义与关系。
2. 三角函数的图像与性质:- 正弦函数和余弦函数的图像特点:周期为2π,在x轴上的零点为kπ,振幅为1。
- 正切函数的图像特点:周期为π,在x轴上的零点为kπ,无振幅。
- 三角函数的奇偶性:正弦函数是奇函数、余弦函数是偶函数、正切函数是奇函数。
- 三角函数的周期性:正弦、余弦函数的周期为2π,正切函数的周期为π。
3. 三角函数的性质与关系:- 三角函数的基本关系:tanx=sinx/cosx,cotx=1/tanx,secx=1/cosx,cscx=1/sinx。
- 三角函数的倒数关系:sinx=1/cscx,cosx=1/secx,tanx=1/cotx。
- 三角函数的平方关系:sin^2x+cos^2x=1,1+tan^2x=sec^2x,1+cot^2x=csc^2x。
4. 三角函数的性质与特殊值:- 正弦函数和余弦函数的取值范围:-1≤sinx≤1,-1≤cosx≤1。
第1页/共2页锲而不舍,金石可镂。
- 正切函数和余切函数的取值范围:tanx属于R,cotx属于R。
- 三角函数的特殊值:sin0=0,cos0=1,sin90°=1,cos90°=0,tan45°=1,cot45°=1。
5. 三角函数的解析式与性质:- sin(x±y)=sinxcosy±cosxsiny。
- cos(x±y)=cosxcosy∓sinxsiny。
- tan(x±y)=(tanx±tany)/(1∓tanxtany)。
2025版高考数学一轮总复习第4章三角函数第2节同角三角函数的基本关系与诱导公式教师用书
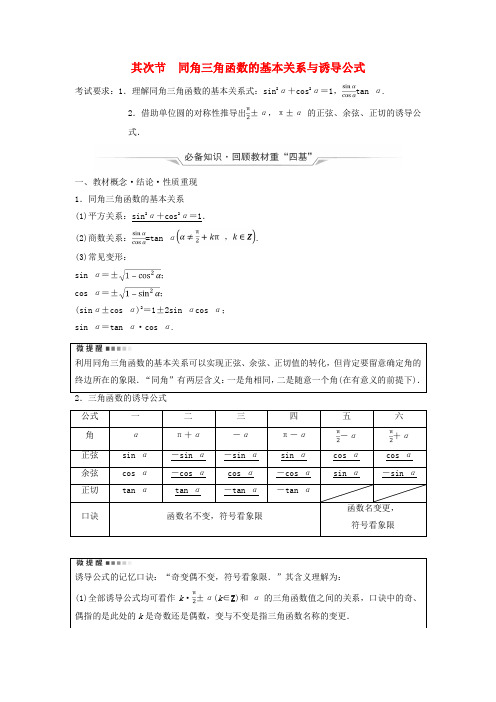
其次节同角三角函数的基本关系与诱导公式考试要求:1.理解同角三角函数的基本关系式:sin2α+cos2α=1,tan α.2.借助单位圆的对称性推导出±α,π±α的正弦、余弦、正切的诱导公式.一、教材概念·结论·性质重现1.同角三角函数的基本关系(1)平方关系:sin2α+cos2α=1.(2)商数关系:=tan α.(3)常见变形:sin α=±;cos α=±;(sinα±cos α)2=1±2sin αcos α;sin α=tan α·cos α.利用同角三角函数的基本关系可以实现正弦、余弦、正切值的转化,但肯定要留意确定角的终边所在的象限.“同角”有两层含义:一是角相同,二是随意一个角(在有意义的前提下).2.三角函数的诱导公式公式一二三四五六角απ+α-απ-α-α+α正弦sin α-sin α-sin αsin αcos αcos α余弦cos α-cos αcos α-cos αsin α-sin α正切tan αtan α-tan α-tan α口诀函数名不变,符号看象限函数名变更,符号看象限诱导公式的记忆口诀:“奇变偶不变,符号看象限.”其含义理解为:(1)全部诱导公式均可看作k·±α(k∈Z)和α的三角函数值之间的关系,口诀中的奇、偶指的是此处的k是奇数还是偶数,变与不变是指三角函数名称的变更.(2)结果的符号与把α当成锐角时角k·±α(k∈Z)的三角函数值的符号相同.二、基本技能·思想·活动阅历1.推断下列说法的正误,对的画“√”,错的画“×”.(1)对随意角α,sin23α+cos23α=1都成立.( √)(2)若cos(nπ-θ)=(n∈Z),则cos θ=.( ×)(3)已知sin θ=,cos θ=,其中θ∈,则m<-5或m≥3.(×) 2.若α是第四象限角,tan α=-,则sin α等于( )A.B.-C.D.-D解析:因为tan α==-,sin2α+cos2α=1,所以sinα=±.因为α是第四象限角,所以sin α=-.3.已知sin =,则cos =( )A.C.-D.-C解析:因为sin =,所以cos =cos =-sin =-.故选C.4.若α是第三象限角且cos α=-,则sin α=_______,tan α=_________.-解析:因为α是第三象限角且cos α=-,所以sin α=-=-,所以tanα==.5.已知sin α=,则·sin (α-π)·cos (2π-α)的值为_________.-解析:原式=·(-sin α)·cos (-α)=·(-sin α)·cos α=·(-sin α)·cos α=-sin2α=-.考点1 同角三角函数关系的基本应用——应用性考向1 知弦求弦、切或知切求弦(1)(2024·济南一模)已知α∈(0,π),若cosα=-,则tan α的值为( ) A.B.-C.D.-D解析:因为α∈(0,π),cos α=-,所以sin α=,则tan α=-.(2)已知3sin +sin (θ+π)=0,θ∈(-π,0),则sin θ=( )A.-B.-C.A解析:由3sin +sin (θ+π)=0,可得3cos θ=sin θ,可得tan θ=3. 而θ∈(-π,0),可得sin θ=-=-.本例(2)条件不变,求cos θ的值.解:由3sin +sin (θ+π)=0,可得3cos θ=sin θ,可得tan θ=3.而θ∈(-π,0),可得sin θ<0.又tan θ=3>0,所以cos θ<0,所以cos θ=-=-.1.利用sin 2α+cos2α=1可以实现正弦、余弦的互化,利用tanα=可以实现弦切互化.2.由一个角的随意一个三角函数值可以求出这个角的另外两个三角函数值,求值时要留意角所在的象限,以免出现符号错误.考向2 弦切互化求值(1)已知cos θ=,则sin θ·的值为( )A.B.-C.3 D.-3C解析:原式=sin θ=sin θ·=3.(2)(2024·新高考全国Ⅰ卷)若tan θ=-2,则=( )A.-B.-C.C解析:将式子进行齐次化处理,得=in θ(sin θ+cos θ)====.本例(2)条件不变,求cos2θ-sin2θ的值.解:cos2θ-sin2θ===1.1.弦化切的常见结构(1)形如“a sin2α+b sin αcos α+c cos2α”的二次式,分母看作1,利用1=sin2α+cos2α将原式转化为齐次式求值.(2)形如“次分式.2.切化弦当要化简的式子中同时出现正弦、余弦、正切时,一般利用公式tan α=,把式中的正切化为弦.考向3 sin α±cos α,sin αcos α之间的关系(1)已知sin α+cos α=,且α∈(0,π),则sin α-cos α=( )A.±B.-C.C解析:把sin α+cos α=,两边平方得(sin α+cos α)2=1+2sin αcos α=,即2sin αcos α=-<0.因为0<α<π,故sin α>0,cos α<0.所以sin α-cos α====.(2)已知sin x+cos x=,x∈(0,π),则tan x等于( )A.-C.D.-D解析:由题意可知sin x+cos x=,x∈(0,π),则(sin x+cos x)2=.因为sin2x+cos2x=1,所以2sin x cos x=-,即==-,得tan x=-或tan x=-. 当tan x=-时,sin x+cos x<0,不合题意,舍去.所以tan x=-.留意方程思想的应用:对于sin α+cos α,sin α·cos α,sin α-cos α这三个式子,利用(sin α±cos α)2=1±2sin αcos α,可以知一求二.1.已知tan θ+=4,则sin4θ+cos4θ=( )A.C.D解析:由tanθ+===4,得sin θcos θ=,所以sin4θ+cos4θ=(sin2θ+cos2θ)2-2sin2θcos2θ=1-2×=.2.若sinα+cos α=,α∈(0,π),则=( )A.B.-C.D.-B解析:因为sin α+cos α=,α∈(0,π),所以两边平方,可得1+2sin αcos α=,可得2sin αcos α=-<0,所以sin α>0,cos α<0,可得cos α-sin α=-==-=-,所以==-=-.考点2 诱导公式的应用——综合性(1)sin ·cos ·tan 的值是_________.-解析:原式=sin ·cos ·tan=··=×(-)=-.(2)(2024·北京卷)若P(cos θ,sin θ)与Q关于y轴对称,写出一个符合题意的θ值:_________.(答案不唯一)解析:因为P(cos θ,sin θ)与Q关于y轴对称,故其横坐标相反,纵坐标相等,即sin θ=sin 且cos θ=-cos ,由诱导公式sin θ=sin (π-θ),cos θ=-cos (π-θ),所以θ+=π-θ,解得θ=,则符合题意的θ值可以为.1.诱导公式的两个应用口诀(1)求值:负化正,大化小,化到锐角就终了.(2)化简:统一角,统一名,同角名少目的到.2.角的变更的通式特别角±已知角=所求角.1.下列各选项中与sin 2 022°最接近的是( )A.C.-D.-D解析:sin 2 022°=sin (1 800°+222°)=sin 222°=sin(180°+42°)=-sin 42°≈-.2.已知sin =-,则cos =( )A.C.-D.-B解析:cos =cos =-cos =-sin =.已知3cos x+4sin x=5,求tan x的值.[四字程序]读想算思求tan x的值1.同角的正弦、余弦和正切有什么关系?2.3cos x+4sin x 的最大值是多少?3.由已知条件联想点A(cosx,sin x)在哪条直线上1.求sin x和cos x.2.协助角公式1.方程思想.2.数形结合.3.转化与化归3cos x +4sinx=51.sin2x+cos2x=1,tan x=.2.3cos x +4sin x的最大值为5.3.点A(cos x,sin x)在直线3x+4y=5上1.联立3cos x+4sinx=5与sin2x+cos2x=1.2.3cos x+4sin x=5sin (x+φ)1.tan x可看作直线的斜率.2.将已知条件变为cos x+sinx=1思路参考:解方程组解:由消去cos x,整理得(5sin x-4)2=0,解得sin x=,cos x=.故tan x==.思路参考:留意到3cos x+4sin x的最大值为5,利用协助角公式推出x与协助角的关系.解:3cos x+4sin x=5=5sin (x+φ)=5,其中cos φ=,sin φ=,所以tan φ=,所以x+φ=2kπ+(k∈Z).于是tan x=tan ==.思路参考:令tan x=t,借助已知条件用t表示sin x和cos x.解:令tan x=t,即t cos x=sin x,代入3cos x+4sin x=5,得3cos x+4t cos x=5,所以cos x=,sin x=.再代入sin2x+cos2x=1,得+=1,解得t=,即tan x=.思路参考:设P(m,n)为角x终边上随意一点,r=,利用三角函数的定义求解.解:设P(m,n)为角x终边上随意一点,点P到原点O的距离为r,则r=.把sin x=,cos x=代入已知等式得3·+4·=5,即(3m+4n)2=(5r)2=25(m2+n2),整理得(4m-3n)2=0,所以4m=3n.明显m≠0,故tan x==.思路参考:设点A(cos x,sin x)是直线3x+4y=5与单位圆x2+y2=1的切点,而tan x =k OA.解:由3cos x+4sin x=5可知点A(cos x,sin x)在直线3x+4y=5上,同时也在单位圆x2+y2=1上,所以点A为直线3x+4y=5与单位圆的切点.由于直线3x+4y=5的斜率为-,所以OA的斜率为,即tan x=.思路参考:m=(cos x,sin x),n=,证明m∥n.解:因为cos x+sin x=1,不妨令m=(cos x,sin x),n=,可知|m|=1,|n|=1,所以m,n均为单位向量,且m·n=1.由|m||n|≥|m·n|,等号成立的条件为m∥n,则有cos x=sin x,即tan x=.1.本题考查同角三角函数基本关系的应用,基本解题方法是构建方程(组)、数形结合等.在求解过程中,应留意同角三角函数的基本关系本身是恒等式,也可以看作是方程.2.基于课程标准,解答本题一般须要有良好的运算求解实力、转化与化归的实力.本题的解答体现了数学运算的核心素养.3.基于高考数学评价体系,本题的多种解法中涉及同角三角函数基本关系式、方程、协助角公式、直线与圆、向量等学问,渗透着函数与方程、等价转换、数形结合等思想方法,对提升思维的敏捷性起到了主动的作用.已知θ是第一象限角,若sin θ-2cos θ=-,求sin θ+cos θ的值.解:因为sin θ-2cos θ=-,所以sin θ=2cos θ-,所以+cos2θ=1,所以5cos2θ-cosθ-=0,即=0.又因为θ为第一象限角,所以cos θ=,所以sin θ=,所以sin θ+cos θ=.课时质量评价(二十二)A组全考点巩固练1.已知sin α=,α∈,则tan α=( )A.B.-C.D.-D解析:因为sin α=,α∈,所以cos α=-=-,则tanα==-.2.已知α是其次象限角,sin (π-α)=,则cos (π+α)=( )A.-B.-C.D解析:因为α是其次象限角,sin (π-α)=,可得sin α=,所以cos α=-=-,则cos(π+α)=-cos α=.3.已知tan α=3,则=( )A.-C.±D解析:因为tanα=3,所以===.4.(2024·安徽模拟)已知cos+cos (π+α)=,则tan α+=( ) A.2 B.-2C.D.3A解析:因为cos +cos (π+α)=,所以-sin α-cos α=,即sin α+cos α=-,两边平方,可得1+2sin αcos α=2,所以sin αcos α=,所以tan α+===2.5.已知cos =,则cos =______,sin=_________.-解析:cos =cos =-cos =-.sin =sin =cos =.6.已知函数f(x)=a sin (πx+α)+b cos (πx+β),且f(4)=3,则f(2 021)=_________.-3解析:因为f(4)=a sin (4π+α)+b cos (4π+β)=a sin α+b cos β=3,所以f(2 021)=a sin (2 021π+α)+b cos (2 021π+β)=a sin (π+α)+b cos (π+β)=-(a sin α+b cos β)=-3.B组新高考培优练7.(多选题)已知α是三角形内角,若sin α+cos α=,则sin α-cos α的值可能为( )A.-B.-C.BC解析:因为α是三角形内角,所以α∈(0,π),又因为(sin α+cos α)2=sin2α+cos2α+2sinαcos α=1+2sin αcos α=,解得2sin αcos α=.因为sin αcos α>0且α∈(0,π),所以sin α>0,cos α>0,所以sin α-cos α符号不确定,所以(sin α-cos α)2=1-2sin αcos α=1-=,所以sin α-cos α=±.8.(2024·聊城模拟)已知α,β∈,且满意sin αcos β-2cos αsin β=0,则tan (2π+α)+tan 的最小值为( )A.2 B.C.1 D.2D解析:因为sin αcos β-2cos αsin β=0,α,β∈,所以tan α>0,tan β>0,tan α=2tan β,所以tan (2π+α)+tan =tan α+=2tan β+≥2,当且仅当tan β=时等号成立.9.(2024·承德二模)若α∈,2sin α+cos α=,则tan α=( )A.-2 B.2C.D.-A解析:由2sin α+cos α=,两边平方,可得(2sin α+cos α)2=,即4sin2α+4sinαcos α+cos2α=.所以,所以,则11tan2α+20tanα-4=0.解得tan α=-2或tan α=.因为α∈,所以tan α=-2.10.(2024·浙江卷)若3sin α-sin β=,α+β=,则sin α=________,cos 2β=_________.解析:因为3sin α-sin β=,α+β=,所以3sin α-cos α=,所以cos α=3sin α-.因为sin2α+cos2α=1,所以sin2α+(3sinα-)2=1,解得sin α=,cos β=sin α=,cos 2β=2cos2β-1=2×-1=.11.已知cos+sin =1,则cos2+cosβ-1的取值范围为_________.解析:由已知得cos β=1-sin α.因为-1≤cos β≤1,所以-1≤1-sin α≤1.又-1≤sin α≤1,可得0≤sin α≤1,所以cos2+cosβ-1=sin2α+1-sinα-1=sin2α-sinα=-.(*) 又0≤sin α≤1,所以当sin α=时,(*)式取得最小值-,当sin α=0或sin α=1时,(*)式取得最大值0,故所求范围是.12.已知-<α<0,且函数f(α)=cos -sin α·-1.(1)化简f(α);(2)若f(α)=,求sin αcos α和sin α-cos α的值.解:(1)因为-<α<0,所以sin α<0,所以f(α)=sin α-sin α·-1=sinα+sin α·-1=sin α+cos α.(2)法一:由f(α)=sin α+cos α=,平方可得sin2α+2sinα·cos α+cos2α=,即2sinαcos α=-.所以sin αcos α=-.又-<α<0,所以sin α<0,cos α>0,所以sin α-cos α<0,因为(sin α-cos α)2=1-2sin αcos α=,所以sin α-cos α=-.法二:联立方程解得或因为-<α<0,所以所以sin αcos α=-,sin α-cos α=-.。
2024年新高一数学初升高衔接《同角三角函数的基本关系》含答案解析
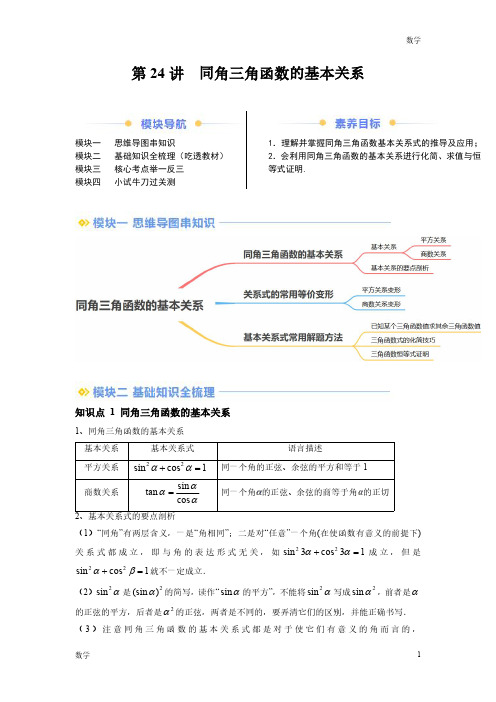
第24讲同角三角函数的基本关系模块一思维导图串知识模块二基础知识全梳理(吃透教材)模块三核心考点举一反三模块四小试牛刀过关测1.理解并掌握同角三角函数基本关系式的推导及应用;2.会利用同角三角函数的基本关系进行化简、求值与恒等式证明.知识点1同角三角函数的基本关系1、同角三角函数的基本关系基本关系基本关系式语言描述平方关系22sin cos 1αα+=同一个角的正弦、余弦的平方和等于1商数关系sin tan cos ααα=同一个角的正弦、余弦的商等于角的正切2、基本关系式的要点剖析(1)“同角”有两层含义,一是“角相同”;二是对“任意”一个角(在使函数有意义的前提下)关系式都成立,即与角的表达形式无关,如22sin 3cos 31αα+=成立,但是22sin cos 1αβ+=就不一定成立.(2)2sin α是2(sin )α的简写,读作“sin α的平方”,不能将2sin α写成2sin α,前者是α的正弦的平方,后者是2α的正弦,两者是不同的,要弄清它们的区别,并能正确书写.(3)注意同角三角函数的基本关系式都是对于使它们有意义的角而言的,22sin cos 1αα+=对一切R α∈恒成立,而sin tan cos ααα=仅对()2k k Z παπ≠+∈成立.知识点2关系式的常用等价变形1、2222222sin 1cos cos 1sin sin cos 1sin cos (sin cos )12sin cos αααααααααααα⎧=-⎪=-⎪⎪+=⇒=⎨⎪=⎪⎪+=±⎩2、sin tan cos sin tan sin cos cos tan ααααααααα=⎧⎪=⇒⎨=⎪⎩【注意】使用变形公式sin α=,cos α=时,“±”由α的终边所在的象限来确定,而对于其他形式的变形公式则不必考虑符号问题.知识点3基本关系式常用解题方法1、已知某个三角函数值求其余三角函数值的步骤第一步:由已知三角函数的符号,确定其角终边所在的象限;第二步:依据角的终边所在象限分类讨论;第三步:利用同角三角函数关系及其变形公式,求出其余三角函数值。
新高考数学复习基础知识专题讲义05 三角函数定义及同角三角函数(解析版)

新高考数学复习基础知识专题讲义 知识点05 三角函数定义及同角三角函数知识理解 一.任意角 (1)角的概念的推广①按旋转方向不同分为正角、负角、零角. ②按终边位置不同分为象限角和轴线角.(2)终边相同的角:终边与角α相同的角可写成α+k ·360°(k ∈Z). (3)弧度制①1弧度的角:长度等于半径长的弧所对的圆心角叫做1弧度的角.②规定:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零,|α|=lr ,l 是以角α作为圆心角时所对圆弧的长,r 为半径.③弧度与角度的换算:360°=2π rad ;180°=π rad ;1°=π180 rad ;1 rad =180π度. 二.任意角的三角函数1.定义:在平面直角坐标系中,设α的终边上任意一点P 的坐标是(x ,y ),它与原点的距离是r (r =x 2+y 2>0).则sin α=y r ,cos α=x r ,tan α=yx (x ≠0).2.三角函数在每个象限的正负如下表:三.同角三角函数的基本关系(1)平方关系:sin 2α+cos 2α=1(2)商数关系:sin αcos α=tan α⎝⎛⎭⎫α≠π2+k π,k ∈Z . 四.同角三角函数基本关系式的变形(1)sin 2α+cos 2α=1的变形公式:sin 2α=1-cos 2α;cos 2α=1-sin 2α; (2)tan α=sin αcos α的变形公式:sin α=cos_αtan_α;cos α=sin αtan α.考向一 角度制与弧度制的转换【例1-1】(2020·全国课时练习)填表(弧度数用含π的代数式表示),并在平面直角坐标系中作出角的终边.【答案】填表见解析,作图见解析 【解析】如表,如图:考向分析对应的角的终边分别为图中的射线OA ,OB ,OC ,OD ,OE ,OF ,OG ,OH ,OI. 【例1-2】(2020·全国课时练习)把下列各弧度化为角度. (1)12π;(2)53π;(3)310π;(4)8π;(5)32π-;(6)56π-. 【答案】(1)15︒;(2)300︒;(3)54︒;(4)22.5︒;(5)270︒-;(6)150︒-.【解析】(1)1801512ππ︒︒⨯=;(2)51803003ππ︒︒⨯=;(3)18054310ππ︒︒⨯=;(4)28180 2.5ππ︒︒⨯=;(5)31802702ππ︒︒-⨯=-;(6)51801506ππ︒︒-⨯=-.【例1-3】(2019·全国高三专题练习)将-1485°改写成2k π+α(0≤α<π,k ∈Z)的形式是( ) A .-8π+4πB .-10π-4πC .-8π+74πD .-10π+74π 【答案】D【解析】﹣1485°=﹣1800°+315°=﹣10π+74π.故选D【举一反三】1.(2020·全国课时练习)把下列角度化成弧度:(1)36︒; (2)150︒-; (3)1095︒; (4)1440︒. 【答案】(1)5π(2)56π-(3)7312π(4)8π 【解析】(1)361805ππ︒⨯=; (2)51501806ππ-︒⨯=-; (3)73109518012ππ︒⨯=; (4)14408180ππ︒⨯=. 2.(2020·全国课时练习)将下列角度与弧度进行互化. (1)20°;(2)-15°;(3)712π(4)-115π. 【答案】(1)20°=9π;(2)-15°=-12π;(3)712π=105°;(4)-115π=-396°.【解析】(1)20°=20180π=9π. (2)-15°=-15180π=-12π.(3)712π=712×180°=105°. (4)-115π=-115×180°=-396°.3.(2020·全国高三专题练习)把−1125°化成α+2k π(0≤α<2π,k ∈Z)的形式是( ) A .−π4−6πB .7π4−6πC .−π4−8πD .7π4−8π【答案】D【解析】−1125°=−1440°+315°=−8π+7π4,故选D.4.(2019·全国高三专题练习)将-1485°化成α+2k π(0≤α<2π,k ∈Z)的形式是( ) A .-4π-8πB .74π-8πC .4π-10πD .74π-10π【答案】D【解析】由题意,可知-1485°=-5×360°+315°,又π=180°,则315°=74π, 故-1485°化成α+2k π(0≤α<2π,k ∈Z)的形式是74π-10π. 考向二 三角函数定义【例2】(1)(2020·云南)已知角α的终边经过点34(,)55P -,则sin α等于( ) A .45B .35C .43-D .34- (2)(2020·广东)已知角θ的终边上一点(4,3)(0)P a a a ≠,则sin θ=( ) A .45B .35C .45±D .35± 【答案】(1)A (2)D【解析】(1)因为角α的终边经过点34(,)55P -,所以x 34,,155y r =-==,所以4sin 5y r α==,故选:A(2)5OP a == 由三角函数的定义可得333sin 55a a OP a θ===±故选:D 【举一反三】1.(2020·北京)在平面直角坐标系xOy 中,角α的顶点与原点O 重合,始边与x 轴的非负半轴重合,终边经过点(3,4)P ,那么sin α的值是( ) A .35B .34C .45D .43 【答案】C【解析】由已知5OP ==,所以4sin 5α.故选:C . 15.(2020·商南县高级中学)角α的终边过点()3,4P a ,若3cos 5α=-,则a 的值为( ) A .1B .1-C .±1D .5± 【答案】B【解析】由条件可知r OP ==, 由三角函数的定义可知3cos 5x r α===-,0a <,解得:1a =-.故选:B 3.(2019·吉林高三月考(文))若点cos ,sin36ππ⎛⎫⎪⎝⎭在角α的终边上,则tan α的值是( )A .-1B .1C .【答案】B【解析】据题意,得1sin62tan 11cos32παπ===.故选:B.考向三 三角函数正负判断【例3】(1)(2020·山东高三专题练习)已知cos tan 0θθ⋅>,那么θ是( ) A .第一、二象限角B .第二、三象限角C .第三、四象限角D .第一、四象限角(2)(2020·山东高三专题练习)若α是第二象限角,则点()sin ,cos P αα在 ( ) A .第一象限B .第二象限C .第三象限D .第四象限 【答案】(1)A (2)D【解析】(1)由cos tan 0θθ⋅>可知cos ,tan θθ同号,即cos tan =sin 0θθθ⋅>,从而θ为第一、二象限角,故选:A(2)因为α是第二象限角,所以sin 0,cos 0αα><,所以点()sin ,cos P αα在第四象限,故选D【举一反三】1.(2019·浙江高三专题练习)已知 sin 0θ>且cos 0θ<,则角的终边所在的象限是( ) A .第一象限B .第二象限C .第三象限D .第四象限 【答案】B【解析】依据题设及三角函数的定义可知角θ终边上的点的横坐标小于零,纵坐标大于零, 所以终边在第二象限,故选B.2.(2020·全国高三专题练习)若sin tan 0αα<,且cos 0tan αα<,则角α是( ) A .第一象限角B .第二象限角C .第三象限角D .第四象限角 【答案】 C【解析】2sin sin tan 0cos αααα=<,cos 0α∴<,又2cos cos 0tan sin αααα=<,则sin 0α<. 因此,角α为第三象限角.故选:C.3.(2020·全国高三专题练习)已知sin cos 0θθ<,且cos cos θθ=,则角θ是( ) A .第一象限角B .第二象限角C .第三象限角D .第四象限角 【答案】D【解析】由cos cos θθ=,可知cos 0θ≥,结合sin cos 0θθ<,得sin 0,cos 0θθ<>, 所以角θ是第四象限角,故选:D4.(多选)(2020·全国高三专题练习)对于①sin 0θ>,②sin 0θ<,③cos 0θ>,④cos 0θ<,⑤tan 0θ>,⑥tan 0θ<,则θ为第二象限角的充要条件为( ) A .①③B .①④C .④⑥D .②⑤ 【答案】BC【解析】若θ为第二象限角,则sin 0θ>,cos 0θ<,tan 0θ<.所以,θ为第二象限角sin 0cos 0θθ>⎧⇔⎨<⎩或sin 0tan 0θθ>⎧⎨<⎩或cos 0tan 0θθ<⎧⎨<⎩.故选:BC.考向四 同角三角公式【例4】(1)(2019·全国高三专题练习)已知α是第四象限角,cos α=1213,则sin α等于( ) A .513B .-513 C .512D .-512(2)(2020·江西景德镇一中)已知2tan 3α=,且2απ<<π,则cos α=( )A .13-B .13.13-D .13【答案】(1)B (2)A【解析】由条件知α是第四象限角,所以sin 0α<,即sin α===513-. 故选:B . (2)2tan 03α=>且2απ<<π,32ππα∴<<,cos 0α∴<, 由22sin 2tan cos 3sin cos 1ααααα⎧==⎪⎨⎪+=⎩得:cos 13α=-故选:A .【举一反三】1.(2020·海拉尔市蒙古族中学高三学业考试)已知α为第四象限的角,且3cos 5α=,则tan α的值为( ) A .34B .34-C .43D .43-【答案】D【解析】α为第四象限的角,且3cos 5α=,4sin 5α∴===-.4sin 45tan 3cos 35ααα-∴===-.故选:D .2.(2019·北京海淀·101中学高三月考)已知3,22ππα⎛⎫∈ ⎪⎝⎭,且tan α=那么sin α=( )A .-.D【答案】B【解析】因为3(,)22ππα∈,sin tan 0cos ααα==>,故3(,)2παπ∈, sin αα=,又22sin cos 1αα+=,解得:sin α=故选:B 3.已知tan α=43,且α是第三象限角,求sin α,cos α的值.【答案】见解析【解析】由tan α=sin αcos α=43,得sin α=43cos α①又sin 2α+cos 2α=1②由①②得169cos 2α+cos 2α=1,即cos 2α=925.又α是第三象限角,∴cos α=-35,sin α=43cos α=-45.考向五 弦的齐次【例5】(1)已知tan α=2,则sin α+cos αsin α-cos α的值为.(2)(2020·固原市五原中学高三)已知tan 2θ=,则2sin sin cos 2θθθ+-= 【答案】(1)3(2)45-(1)原式=tan α+1tan α-1=2+12-1=3. (2)因为22sin +cos 1θθ=,sin tan cos θθθ=所以222sin sin cos 2sin sin cos 2cos θθθθθθθ+-=-+-222222sin sin cos 2cos tan tan 2sin +cos tan +1θθθθθθθθθ-+--+-==42244+15-+-==-故选:D.【举一反三】1.(2020·全国高三专题练习)已知1tan 3α=-,则2cos sin cos ααα-+的值为( ) A .3-B .34-C .43-D .34【答案】A【解析】由1tan 3α=-,得2cos 2232sin cos 1tan 3αααα---===-++.故选:A.2.(2020·福建省武平县第一中学高三月考)已知tan 2θ=,则22sin sin cos 2cos θθθθ+-等于( ) A .43-B .54C .34-D .45【答案】D【解析】222222sin sin cos 2cos sin sin cos 2cos sin cos θθθθθθθθθθ+-+-=+22tan tan 24224tan 1415θθθ+-+-===++. 故选:D3.(2020·西藏拉萨中学高三)1tan 2α=,则sin 2α=( ) A .45-B .35C .45D .35【答案】C【解析】1tan 2α=,2222122sin cos 2tan 42sin 21151()2sin cos tan ααααααα⨯∴====+++.故选:C 4.(2020·江苏南京田家炳高级中学)已知tan 2α=,求:(1)sin 2cos sin cos αααα+-; (2)221sin sin cos 2cos αααα+-.【答案】(1) 4 (2)54【解析】(1)sin 2cos tan 2224sin cos tan 121αααααα+++===--- (2)2222221sin cos sin sin cos 2cos sin sin cos 2cos αααααααααα+=+-+-2222tan 1215tan tan 22224ααα++===+-+- 考向六 sin cos sin cos α±ααα与【例6】(1)(2020·永寿县中学高三开学考试)已知4sin cos 3αα-=,则sin 2α=( ). A .79-B .29-C .29D .79(2)(2020·广东华南师大附中高三月考)已知1sin cos 5αα+=,其中,2παπ⎛⎫∈ ⎪⎝⎭,则tan α=( )A .247B .43-或34-C .34-D .43- 【答案】(1)A (2)D【解析】()2sin cos 17sin 22sin cos 19ααααα--===--.所以选A.(2)由1sin cos 5αα+=,平方可得112sin cos 25αα+=,解得242sin cos 25αα=-, 又由2249(sin cos )sin cos 2sin cos 25αααααα-=+-=,因为,2παπ⎛⎫∈⎪⎝⎭,可得sin cos 0αα->,所以7sin cos 5αα-=,联立方程组1sin cos 57sin cos 5αααα⎧+=⎪⎪⎨⎪-=⎪⎩,解得43sin ,cos 55αα==-,所以sin tan s 43co ααα==-.故选:D.【举一反三】1.(2020·上海市奉贤区曙光中学高三期中)已知7sin cos17αα+=,()0,απ∈,则tanα=________.【答案】158-【解析】依题意7sin cos17αα+=,两边平方得4924012sin cos,2sin cos0289289αααα+==-<,而()0,απ∈,所以sin0,cos0αα><,所以23sin cos17αα-====.由7sin cos1723sin cos17αααα⎧+=⎪⎪⎨⎪-=⎪⎩解得158sin,cos1717αα==-,所以sin15tancos8ααα==-.故答案为:158-2.(2020·四川省南充高级中学高三月考(理))已知1sin cos5θθ+=,(0,)θπ∈,则tanθ=________. 【答案】43-【解析】已知1sin cos5θθ+=,平方得()2221sin cos sin cos2sin cos25θθθθθθ+=++=,得12sin cos25θθ=-,∴()222sin cos sin cos2sin cos125252449θθθθθθ-=+-=+=,(0,)θπ∈,sin0,cos0θθ><,7sin cos 5θθ∴-=,7ta sin cos 1sin cos n 571t n 51a θθθθθθ=-=-+=+,解得4tan 3θ=-. 故答案为:43-考向七 三角函数线运用【例7】(2020·全国高三专题练习)已知点(sin cos ,tan )P ααα-在第一象限,则在[0,2]π内α的取值范围是( ).A .35,,244ππππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭B .5,,424ππππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭C .353,,2442ππππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭D .3,,424ππππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭【答案】B【解析】由已知点(sin cos ,tan )P ααα-在第一象限得:sin cos 0αα->,tan 0α>,即sin cos αα>,tan 0α>,当sin cos αα>,可得52244k k πππαπ+<<+,k Z ∈. 当tan 0α>,可得222k k ππαπ<<+或3222k k πππαπ+<<+,k Z ∈. ∴2242k k πππαπ+<<+或5224k k πππαπ+<<+,k Z ∈. 当0k =时,42ππα<<或54ππα<<. 02απ,∴42ππα<<或54ππα<<.故选:B .【举一反三】1.(2020·全国高三专题练习)已知点()cos ,tan P αα在第二象限,则角α在( )A .第一象限B .第二象限C .第三象限D .第四象限 【答案】C【解析】点()cos ,tan P αα在第二象限,则cos 0tan 0αα<⎧⎨>⎩,所以角α在第三象限.故选:C2.(2020·海伦市第一中学高三期中(文))已知点()cos sin ,sin cos P αααα+-在第三象限,则α的取值范围是( ). A .()ππ2π,2π42k k k ⎛⎫++∈ ⎪⎝⎭Z B .()3π2π,2ππ4k k k ⎛⎫++∈ ⎪⎝⎭Z C .()3π5π2π,2π44k k k ⎛⎫++∈ ⎪⎝⎭Z D .()5π7π2π,2π44k k k ⎛⎫++∈ ⎪⎝⎭Z【答案】D 【解析】()cos sin ,sin cos P αααα+-在第三象限,cos sin 0sin cos 0αααα+<⎧∴⎨-<⎩,2222sin cos sin 1sin sin 0sin 0αααααα⎧⎧>>-∴⇒⎨⎨<<⎩⎩,21sin 2sin 0αα⎧>⎪∴⎨⎪<⎩,sin α∴<,()5π7π2π,2π44k k k α⎛⎫∴∈++∈ ⎪⎝⎭Z.故选:D. 3.(2020·贵州高三其他模拟)已知点(sin cos ,tan )P ααα-在第一象限,则在[]0,2π内的α的取值范围是( )A .35(,)(,)244ππππB .5(,)(,)424ππππC .353(,)(,)2442ππππD .33(,)(,)244ππππ 【答案】B【解析】由已知点(sin cos ,tan )P ααα-在第一象限得:sin cos 0αα->,tan 0α>,即sin cos αα>,tan 0α>,当sin cos αα>,可得52244k k πππαπ+<<+,k Z ∈.当tan 0α>,可得222k k ππαπ<<+或3222k k πππαπ+<<+,k Z ∈. ∴2242k k πππαπ+<<+或5224k k πππαπ+<<+,k Z ∈. 当0k =时,42ππα<<或54ππα<<.02απ≤≤,∴42ππα<<或54ππα<<.故选:B .1.(2020·重庆西南大学附中高三月考)下列转化结果正确的是( ) A .60化成弧度是rad 6πB .rad 12π化成角度是30 C .1化成弧度是180rad πD .1rad 化成角度是180π⎛⎫⎪⎝⎭【答案】D【解析】由180π=得,对于A 选项:60化成弧度是rad 3π,故A 不正确;对于B 选项:rad 12π化成角度是11801512⨯=,故B 不正确;对于C 选项:1化成弧度是180rad π,故C 错误;对于D 选项:1rad 化成角度是180π⎛⎫⎪⎝⎭,故D 正确,故选:D.2.(2020·天津市静海区大邱庄中学高三月考)下列转化结果错误的是( ) A .30化成弧度是6πB .103π-化成度是600-︒ C .6730'︒化成弧度是27πD .85π化成度是288︒ 【答案】C【解析】30化成弧度是6π,A 正确;103π-化成度是600-︒,B 正确; 6730'︒是367.567.51808ππ︒=⨯=,C 错误;85π化成度是288︒,D 正确.故选:C. 3.(2020·江苏高三专题练习)225-化为弧度为()强化练习A .34πB .74π-C .54π-D .34π- 【答案】C【解析】225225356024ππ=-⋅-=-.故选C 4.(2019·全国高三专题练习)下列结论不正确的是( )A .3πrad =60°B .10°=18πrad C .36°=5πradD .58πrad =115°【答案】D 【解析】 ∵π=180°,∴3πrad =60°正确,10°=18πrad 正确,36°=5πrad 正确,58πrad ==112.5°≠115°,D 不正确.故选D .5.(2020·浙江温州·高二期中)已知角α的终边上有一点()1,2P -,则tan α的值为( ) A .-2B .12-C D .【答案】A 【解析】角α的终边上有一点()1,2P -,2tan 21α-∴==-.故选:A. 6.(2020·江苏镇江·高三期中)已知点51,3tan6P π⎛⎫- ⎪⎝⎭是角θ终边上一点,则cosθ的值为( ) A .12B.12-D. 【答案】C【解析】因为53tan 36π⎛=⨯= ⎝⎭(1,P -,所以1cos 2θ==-,故选:C.7.(2020·河南高三月考(文))已知角α的顶点在坐标原点,始边在x 轴非负半轴上,终边与单位圆交于12P ⎛-⎝⎭,则sin α=( ) A.B .12-C..2【答案】D【解析】由三角函数的定义,sin y α==.故选:D. 8.(2020·北京人大附中高三月考)已知点5π2cos,16P ⎛⎫⎪⎝⎭是角α终边上一点,则sin α=( ) A .12B.2C .12-D.2- 【答案】A【解析】由5πcos62=-,可得点()P , 根据三角函数的定义,可得1sin 2α==.故选:A.9.(2020·浙江高二开学考试)已知角α的终边经过点(2,1)P -,则( )A .sin αB .sin α=C .cos α=D .tan 2α【答案】A【解析】角α的终边经过点(2,1)P -,所以P根据三角函数定义得到:sin 55a α====-,1tan 2α=-;故选A. 10.(2020·开鲁县第一中学高三月考(文))已知角α的终边经过点P (4,-3),则2sin cos αα+的值等于( ) A .25-B .45C .35D .25【答案】A【解析】因为角α的终边过点()4,3,5P r OP -==,所以利用三角函数的定义, 求得34,cos 55sin αα=-=,3422cos 2555sin αα∴+=-⨯+=-,故选A. 11.(2020·宁夏银川二中高三其他模拟)如果角α的终边过点(2sin30,2cos30)︒-︒,则sin α的值等于( )A .12B .12-C.D.-【答案】C【解析】由题意()(2sin30,2cos301,︒-︒= ,点(1,到原点的距离2r ==,由定义知sin 2y r α==-故选:C . 12.(2020·扶风县法门高中高三月考(文))已知α的值是( )A .3B .3-C .1D .12- 【答案】Ccos 2sin cos sin cos ααααα+=+, 因为α为第二象限角,所以sin 0,cos 0αα><,所以cos 2sin 2sin cos 211sin cos sin cos αααααααα-+=+=-=.故选:C. 13.(2020·安徽省蚌埠第三中学高一开学考试)已知点(tan ,cos )P αα在第三象限,则角α的终边位置在( )A .第一象限B .第二象限C .第三象限D .第四象限 【答案】B【解析】由于点(tan ,cos )P αα在第三象限,所以tan 0,cos 0αα<<, 所以α在第二象限.故选:B14.(2020·全国高三专题练习(文))已知点(tan ,cos )P αα在第三象限,则角α在第几象限( ) A .第一象限B .第二象限C .第三象限D .第四象限 【答案】B【解析】因为点(tan ,cos )P αα在第三象限,所以tan 0,cos 0αα<< 所以角α在第二象限故选:B15.(2020·江苏高三专题练习)若sin tan 0αα<,且cos 0tan αα<,则角α是第( )象限角. A .一B .二C .三D .四 【答案】C【解析】由条件知sin α与tan α异号,则α为第二或第三象限角;又cos α与tan α异号,则α为第三或第四象限角.综上可知,α为第三象限角.故选:C16.(2020·北京市第十三中学高三期中)已知()0,απ∈,且3cos 5α=-,则tan α=( ) A .43-B .34-C .34D .43 【答案】A【解析】由3cos 5α=-得4sin 5α===±,因为()0,απ∈,所以sin 0α>,所以4sin 5α, 所以4sin 45tan 3cos 35ααα===--,故选:A17.(2020·陕西省定边中学高三月考(文))已知tan 4α=,则21cos 28sin sin 2ααα++的值为( )A ..654C .4D .3【答案】B【解析】因为tan 4α=,所以21cos 28sin sin 2ααα++,222cos 8sin 2sin cos αααα+=,228tan 2tan αα+=,228424+⨯=⨯, 654=故选:B 18.(2020·重庆南开中学高三月考)已知tan 2α=,则2221sin 2cos sin 2cos αααα++=-( )A .32B .52C .4D .5 【答案】D 【解析】22222221sin 2cos sin 2sin cos 2cos sin 2cos sin 2cos αααααααααα++++=--22tan 2tan 25tan 2ααα++==-故选:D 19.(2020·全国高三专题练习(文))已知02πα-<<,1sin cos 5αα+=,则221cos sin αα-的值为( )A .75B .257C .725D .2425【答案】B【解析】由题意,因为1sin cos 5αα+=,所以112sin cos 25αα+=,所以242sin cos 25αα=-, 所以()249cos sin 12sin cos 25αααα-=-=,又因为02πα-<<,所以sin 0,cos 0αα<>,所以7cos sin 5αα-=,所以221125cos sin (cos sin )(cos sin )7αααααα==-+-,故选B.20.(2020·全国高三专题练习)(多选)下列转化结果正确的是( )A .6730'化成弧度是38πB .103π-化成角度是600-C .150-化成弧度是76π-D .12π化成角度是5 【答案】ABD【解析】对于A,3673067.51808ππ'=⨯=,正确;对于B,101018060033πππ-=-⨯=-,正确; 对于C,51501501806ππ⨯-=-=-,错误;对于D,180151212πππ=⨯=,正确.故选ABD 21.(2020·天津经济技术开发区第二中学高三期中)已知角θ的终边经过点(,3)P x (0x <)且cos 10x θ=,则x =___________. 【答案】1-【解析】由余弦函数的定义可得cos 10x θ==,解得0x =(舍去),或1x =(舍去),或1x =-, 1x ∴=-.故答案为:1-.22.(2020·湖南高二学业考试)已知角α的终边经过点(3,4),则cos α=______________.【答案】35【解析】因为角α的终边经过点(3,4),所以3cos 5x r α===,故答案:35 23(2020·天津经济技术开发区第二中学高三期中)已知2sin cos 0αα-=,则2sin 2sin cos ααα-=___________. 【答案】35【解析】由2sin cos 0αα-=,得1tan 2α=,则有222222sin 2sin cos sin 2sin cos tan 2tan 1sin cos tan 1ααααααααααα---==++221123225112⎛⎫-⨯ ⎪⎝⎭==-⎛⎫+ ⎪⎝⎭; 故答案为:35. 24.(2020·万载县第二中学高三月考(理))已知角α的终边经过点(,6)P x --,且3cos 5α=-,则11sin tan αα+=________. 【答案】12- 【解析】点P 的纵坐标为6-,且3cos 05α=-<.∴角α的终边落在第三象限,4sin 5α∴=-,4tan 3α= 115321sin tan 4442αα∴+=-+=-=-.故答案为:12-. 25.(2020·山东高三专题练习)已知sin 2cos 3sin 5cos αααα-+=-5,那么tan α=________. 【答案】-2316易知cos α≠0,由sin 2cos 3sin 5cos αααα-+=-5,得tan 23tan 5αα-+=-5,解得tan α=-2316.故答案为:-2316。
2024年高考数学 高三大一轮复习专题13 三角函数的基本概念、同角三角函数的基本关系与诱导公式

专题13 三角函数的基本概念、同角三角函数的基本关系与诱导公式【知识精讲】一、角的有关概念 1.定义角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形. 2.分类(1)按旋转方向不同分为正角、负角、零角. (2)按终边位置不同分为象限角和轴线角.(3)终边相同的角:所有与角α终边相同的角,连同角α在内,可构成一个集合·3{|}60,S k k ββα==+︒∈Z .3.象限角与轴线角第一象限角的集合为π2π2π,2k k k αα⎧⎫<<+∈⎨⎬⎩⎭Z ; 第二象限角的集合为π2π2ππ,2k k k αα⎧⎫+<<+∈⎨⎬⎩⎭Z ; 第三象限角的集合为3π2ππ2π,2k k k αα⎧⎫+<<+∈⎨⎬⎩⎭Z ; 第四象限角的集合为3π2π2π2π,.2k k k αα⎧⎫+<<+∈⎨⎬⎩⎭Z 终边与x 轴非负半轴重合的角的集合为{}2π,k k αα=∈Z ; 终边与x 轴非正半轴重合的角的集合为{}2ππ,k k αα=+∈Z ;终边与x 轴重合的角的集合为{}π,k k αα=∈Z ;终边与y 轴非负半轴重合的角的集合为π2π,2k k αα⎧⎫=+∈⎨⎬⎩⎭Z ; 终边与y 轴非正半轴重合的角的集合为π2π,2k k αα⎧⎫=−∈⎨⎬⎩⎭Z ;终边与y 轴重合的角的集合为ππ,2k k αα⎧⎫=+∈⎨⎬⎩⎭Z ; 终边与坐标轴重合的角的集合为π,2k k αα⎧⎫=∈⎨⎬⎩⎭Z . 二、弧度制1.1弧度的角把长度等于半径长的弧所对的圆心角叫做1弧度的角. 规定:,ll rα=是以角α作为圆心角时所对圆弧的长,r 为半径.正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零.2.弧度制用“弧度”做单位来度量角的单位制叫做弧度制.比值lr与所取的r 的大小无关,仅与角的大小有关.3.弧度与角度的换算180π180πrad ,1rad =57.3,1=rad π180⎛⎫︒=︒≈︒︒ ⎪⎝⎭. 4.弧长公式l r α=,其中α的单位是弧度,l 与r 的单位要统一.角度制下的弧长公式为:π180n rl =(其中n 为扇形圆心角的角度数). 5.扇形的面积公式21122S lr r α==.角度制下的扇形面积公式为:2π360n r S =(其中n 为扇形圆心角的角度数).三、任意角的三角函数 1.定义设α是一个任意角,它的顶点与原点重合,始边与x 轴非负半轴重合,点(),P x y 是角α的终边上任意一点,P 到原点的距离()0OP r r =>,那么角α的正弦、余弦、正切分别是sin ,cos ,tan y x y r r xααα===. 注意:正切函数tan y x α=的定义域是ππ,2k k αα⎧⎫≠+∈⎨⎬⎩⎭Z ,正弦函数和余弦函数的定义域都是R .2.三角函数值在各象限内的符号三角函数值在各象限内的符号口诀:一全正、二正弦、三正切、四余弦. 3.三角函数线设角α的顶点与原点重合,始边与x 轴非负半轴重合,终边与单位圆相交于点P ,过P 作PM 垂直于x 轴于M .由三角函数的定义知,点P 的坐标为()cos ,sin αα,即()cos ,sin P αα,其中cos ,sin ,OM MP αα==单位圆与x 轴的正半轴交于点A ,单位圆在A 点的切线与α的终边或其反向延长线相交于点T ,则tan AT α=.我们把有向线段,,OM MP AT 分别叫做α的余弦线、正弦线、正切线. 各象限内的三角函数线如下:角所在的象限第一象限第二象限第三象限第四象限图形4.特殊角的三角函数值补充:sin15cos 75,sin 75cos15,44︒=︒=︒=︒= tan152,tan 752︒=︒=+四、同角三角函数的基本关系式 1.平方关系22sin cos 1αα+=.2.商的关系sin cos tan ααα=. 3.同角三角函数基本关系式的变形(1)平方关系的变形:2222sin 1cos ,cos 1sin αααα=−=−; (2)商的关系的变形:sin sin tan cos ,cos tan αααααα=⋅=; (3)2222111tan 1,1cos sin tan αααα−=−=. 五、三角函数的诱导公式【题型精讲】题型一 角的有关概念【例1-1】在与495°角终边相同的角中,用弧度制表示满足下列条件的角. (1)最大的负角; (2)最小的正角; (3)在区间[)720,360−︒−︒内的角. 【答案】(1)54π− (2)34π (3)134π−【解析】 【分析】(1)与495°角终边相同的角为1124k ππ+,由11204k πππ−<2+<且k ∈Z ,求出k ,即可得解;(2)由110224k πππ<+<且k ∈Z ,求出k ,即可得解; (3)由11224k ππππ−4≤+<−且k ∈Z ,求出k ,即可得解. (1) ∵114954π︒=,∴与495°角终边相同的角为1124k ππ+,k ∈Z .由11204k πππ−<2+<且k ∈Z ,可得2k =−,故所求的最大负角为54π−; (2) 由110224k πππ<+<且k ∈Z ,可得1k =−,故所求的最小正角为34π; (3)由11224k ππππ−4≤+<−且k ∈Z ,可得3k =−,故所求的角为134π−. 【例1-2】将下列角度化为弧度,弧度转化为角度 (1)780︒ (2)1560−︒ (3)67.5︒ (4)103π− (5)12π(6)74π【答案】(1)133π弧度 (2)263−π弧度 (3)38π弧度 (4)600−︒ (5)15︒ (6)315︒ 【解析】 【分析】利用π弧度180=︒即可得出,即角度化弧度乘以180π,弧度化角度乘以180π,需注意单位为度. (1) 解:780780180π︒=⨯弧度133π=弧度, (2)解:15601560180π−︒=−⨯弧度263π=−弧度, (3) 解:67.567.5180π︒=弧度38π=弧度.(4) 解:103π−弧度101806003=−⨯︒=−︒,(5) 解:12π弧度1801512︒==︒, (6) 解:74π弧度71803154=⨯︒=︒.【例1-3】设α是第四象限的角. (1)试讨论2α是哪个象限的角; (2)写出3α的范围; (3)写出2α的范围.【答案】(1)第二或第四象限的角 (2)()222,33233k k k Z αππππ⎛⎫∈++∈ ⎪⎝⎭(3)()()243,44k k k Z αππππ∈++∈ 【解析】 【分析】(1)根据α是第四象限的角,先表达出α与2α,然后分k 为偶数和奇数,分别求出此时2α位于哪个象限;(2)利用α的范围,表达出3α的范围;(3)利用α的范围,表达出2α的范围 (1)α是第四象限的角,即()32222k k k Z ππαππ+<<+∈. ()342k k k Z παπππ+<<+∈, 当2k n =,n Z ∈时,32242n n παπππ+<<+,n Z ∈;此时2α是第二象限角; 当21k n =+,n Z ∈时,722242n n παπππ+<<+,n Z ∈,此时2α是第四象限角 所以,2α是第二或第四象限的角 (2) 因为()32222k k k Z ππαππ+<<+∈,所以()22232333k k k Z ππαππ+<<+∈,故()222,33233k k k Z αππππ⎛⎫∈++∈ ⎪⎝⎭(3) 因为()32222k k k Z ππαππ+<<+∈,所以()43244k k k Z ππαππ+<<+∈,故()()243,44k k k Z αππππ∈++∈【例1-4】用弧度制表示顶点在原点,始边重合于x 轴的非负半轴,终边落在阴影部分内的角的集合(包括边界,如图所示).【答案】π5π|2π2π,Z 612k k k αα⎧⎫−≤≤+∈⎨⎬⎩⎭,ππ|ππ,Z 62k k k αα⎧⎫+≤≤+∈⎨⎬⎩⎭【解析】 【分析】先利用弧度制写出边界角,再按逆时针顺序写出区域角即可. 【详解】 因为5π7512rad =,由图(1)知:以射线OA 为终边的角的集合为15π|2π,1Z 2k S k α∈⎧⎫=+⎨⎬⎩⎭,330角的终边与30−即π6rad −的角的终边相同,以OB 为终边的角为2π|2π,6Z S k k α⎧∈⎫=−⎨⎬⎩⎭,所以终边落在阴影部分内的角的集合为:π5π|2π2π,Z 612k k k αα⎧⎫−≤≤+∈⎨⎬⎩⎭.因为π306rad =,7π2106rad =, 由图(2)知:以射线OA 为终边的角为3πZ 6|2π,n S n ββ∈⎧⎫==+⎨⎬⎩⎭,以射线OB 为终边的角为47πZ 6|2π,S n n ββ∈⎧⎫==+⎨⎬⎩⎭,所以终边在直线AB 上的角为:()πππ2π,Z 21π|||666,Z π,Z n n n n k k S ββββββ+∈++⎧⎫∈+⎧⎫⎧⎫==⋃===⎨⎬⎨⎬⎨⎬⎩∈⎭⎩⎭⎩⎭,同理终边在y 轴上的角为ππ,Z |2k k ββ+∈⎧⎫=⎨⎬⎩⎭, 所以终边落在阴影部分内的角的集合ππ|ππ,Z 62k k k αα⎧⎫+≤≤+∈⎨⎬⎩⎭.【练习1-1】把375−︒表示成2πk θ+,k Z ∈的形式,则θ的值可以是( ) A .π12B .π12−C .5π12D .5π12−【解析】 【分析】由37515360−=−︒−︒︒结合弧度制求解即可. 【详解】∵37515360−=−︒−︒︒,∴π3752πrad 12⎛⎫−︒=−− ⎪⎝⎭故选:B【练习1-2】已知集合ππ,42k M x x k ⎧⎫==+∈⎨⎬⎩⎭Z ,ππ,24k N x x k ⎧⎫==+∈⎨⎬⎩⎭Z ,则( ) A .N M ⊆ B .M N ⊆ C .MND .M N ⋂=∅【答案】A 【解析】 【分析】利用集合的基本关系求解 【详解】解:因为()2πππ,,424k k M x x k x x k ⎧⎫+⎧⎫⎪⎪==+∈==∈⎨⎬⎨⎬⎩⎭⎪⎪⎩⎭Z Z ,()21π,4k N x x k ⎧⎫+⎪⎪==∈⎨⎬⎪⎪⎩⎭Z ,当k ∈Z 时,21k +是奇数,2k +是整数,所以N M ⊆. 故选:A .题型二 三角函数的定义【例2-1】已知角α的终边与单位圆的交点为P 1(,)2y −,则sin tan αα=______.【答案】32−【解析】 【分析】根据单位圆求出y ,然后由三角函数定义求得sin ,tan αα,再相乘可得.由题意2114y +=,2y =±,y =sin α=,tan α=,3sin tan 2αα=−,y =sin α=tan α=3sin tan 2αα=−, 综上,3sin tan 2αα=−.故答案为:32−.【例2-2】已知()2,P y −是角θ终边上一点,且sin 5θ=,则y 的值是( )A .BC .D 【答案】D 【解析】 【分析】根据sin 0θ>,可判断点()2,P y −位于第二象限,利用正弦函数的定义列方程求解即可. 【详解】解:因为()2,P y −是角θ终边上一点,sin 0θ=>,故点()2,P y −位于第二象限,所以0y >,sin θ==整理得:21732y =,因为0y >,所以y 故选:D.【练习2-1】已知角θ的顶点与原点重合,始边与x 轴的正半轴重合,终边在直线y =上,则tan θ=( )A.B .12−C .12D 【答案】D 【解析】 【分析】根据三角函数的定义可得答案.因为角θ的顶点与原点重合,始边与x 轴的正半轴重合,终边在直线y 上,所以tan yxθ== 故选:D【练习2-2】已知角α的终边经过点(,3)P x −,且3tan 4α=−,则cos sin αα+=( )A .15B .15±C D .15−【答案】A 【解析】 【分析】根据三角函数的定义求出x ,再根据三角函数的定义分别求出cos ,sin αα,即可得解. 【详解】解:角α的终边经过点(,3)P x −,由3tan 4α=−,可得334x −=−,所以4x =, 所以4cos 5α==,3sin 5α==−, 所以431cos sin 555αα+=−=. 故选:A .题型三 利用三角函数的定义解三角不等式【例3-1】集合A =[0,2π],B ={α|sin α<cos α},则A ∩B =_______.【答案】5[0,)(,2]44πππ⋃【解析】 【分析】由函数值的大小关系确定集合B 中α的范围,并在单位圆中画出其角度所在象限,再应用集合的交运算求A ∩B 即可. 【详解】由题设,3{|22,}44B k k k Z ππαπαπ=−<<+∈,如下图阴影部分所示(不含终边在y x =上∴5[0,)(,2]44A B πππ⋂=⋃.故答案为:5[0,)(,2]44πππ⋃.【例3-2】利用单位圆中的三角函数线 ,分别确定角θ的取值范围.(1)sin 2θ≥; (2)1cos 22θ−≤<.【答案】(1),32223k k k Z πππθπ+≤≤∈+ . (2)22362k k πππθπ<−−+≤+ 或22,326k k Z k ππθππ<≤+∈+ 【解析】 【分析】(1)按照三角函数的定义画出单位圆,再按图分析即可; (2)按照三角函数的定义画出单位圆,再按图分析即可. (1)下图中阴影部分就是满足条件的角θ 的范围, 即,32223k k k Z πππθπ+≤≤∈+ ;(2)下图中阴影部分就是满足条件的角θ 的范围, 即22362k k πππθπ<−−+≤+ 或22,326k k Z k ππθππ<≤+∈+ ;故答案为:,32223k k k Z πππθπ+≤≤∈+, 22362k k πππθπ<−−+≤+ 或22,326k k Z k ππθππ<≤+∈+.【练习3-1】设sin1,cos1,tan1a b c ===,则,,a b c 的大小关系为( ) A .a b c >> B .a c b >> C .c a b >> D .c b a >>【答案】C 【解析】 【分析】在单位圆中做出三角函数线即可比较大小. 【详解】以O 为圆心作单位圆,与x 轴正半轴交于点A ,作1POA ∠=交单位圆第一象限于点P ,做PB x ⊥轴,作AT x ⊥轴交OP 的延长线于点T ,如下图所示:由三角函数线的定义知,cos1OB =,sin1BP =,tan1AT =,因为ππ124>>, AT BP OB ∴>>∴tan1sin1cos1>> ∴c a b >> 故选:C 【点睛】本题主要考查三角函数值比较大小,借助三角函数线容易得出结果. 【练习3-2】求下列函数的定义域:(1)y = (2)lg(1)y x =.【答案】(1)22/,2cot ()33x k πππ⎡⎤∈++∈⎢⎥⎣⎦Z ; (2)3572,22,2()4444x k k k k ππππππππ⎛⎤⎡⎫∈++⋃++∈ ⎪⎥⎢⎝⎦⎣⎭Z . 【解析】 【分析】(1)由题可得2sin 0x ,即3sin 2x,在单位圆中作出满足该不等式的角的集合,即可得答案;(2)由题可得1010x x ⎧>⎪⎨+⎪⎩即cos x <,在单位圆中作出满足该不等式的角的集合,即可得答案. 【详解】(1)∵2sin 0x ≥,∴3sin 2x,在单位圆中作出满足该不等式的角的集合,如图①所示,可得22,2()33x k k k ππππ⎡⎤∈++∈⎢⎥⎣⎦Z .①(2)∵1010x x ⎧>⎪⎨⎪⎩∴cos x <,在单位圆中作出满足该不等式的角的集合,如图②所示,可得3572,22,2()4444x k k k k k ππππππππ⎛⎤⎡⎫∈++⋃++∈ ⎪⎥⎢⎝⎦⎣⎭Z .② 【点睛】本题考查借助三角函数线解三角不等式问题,属于基础题.题型四 弧度制的应用【例4-1】已知扇形的圆心角是α,半径是r ,弧长为l . (1)若100,2r α=︒=,求扇形的面积;(2)若扇形的周长为20,求扇形面积的最大值,并求此时扇形圆心角的弧度数. 【答案】(1)10π9(2)最大值为25;2α= 【解析】 【分析】(1)先把角度化为弧度,再利用扇形面积公式求解即可;(2)由题意可知扇形的面积为()()21120252522S lr r r r ==−⋅=−−+,利用二次函数的的性质,结合弧度的定义即可求解 (1)因为π5π1001001809α=︒=⨯=, 所以扇形的面积为21115π10π422299S lr r α===⨯⨯=;(2)由题意可知:220l r +=,即202l r =−,所以扇形的面积为()()21120252522S lr r r r ==−⋅=−−+,当=5r 时,扇形面积的最大值为25, 此时202510l =−⨯=,1025l r α=== 【例4-2】已知半径为6的圆O 中,弦AB 的长为6. (1)求弦AB 所对圆心角α的大小;(2)求圆心角α所在的扇形的弧长l 及弧所在的弓形..的面积.S 【答案】(1)π3(2)2l π=,6S π=−【解析】 【分析】(1)根据三角形形状得圆心角α的大小;(2)根据扇形的弧长以及面积公式求解. (1)解:半径为6的圆O 中,弦AB 的长为6, 所以三角形OAB 为正三角形, 所以弦AB 所对圆心角α为π3,(2)解:由弧长公式得:62,3l r παπ==⨯=扇形的面积11266.22S lr ππ==⨯⨯=扇形又1662AOBS=⨯⨯=所以6AOBS S Sπ=−=−扇形..的面积6S π=− 【例4-3】如图,扇环ABCD 中,弧4AD =,弧2BC =,1AB CD ==,则扇环ABCD 的面积S =__________.【答案】3 【解析】 【分析】根据弧长公式求出OB ,OA ,再由根据扇形的面积公式求解即可. 【详解】 设AOB θ∠=,因为弧4AD =,弧2BC =,1AB CD ==, 所以4OA θ⨯=,2OB θ⨯=, 所以2OA =,1OB =,又扇形AOD 的面积为12OA AD ⋅⋅,扇形BOC 的面积为12OB BC ⋅⋅,所以扇环ABCD 的面积1111241232222S OA AD OB BC =⋅⋅−⋅⋅=⨯⨯−⨯⨯=.故答案为:3【练习4-1】已知一扇形的圆心角为()0αα>,周长为C ,面积为S ,所在圆的半径为r . (1)若35α=︒,8r =cm ,求扇形的弧长;(2)若16C =cm ,求S 的最大值及此时扇形的半径和圆心角. 【答案】(1)149πcm ; (2)S 的最大值是216cm ,此时扇形的半径是4 cm ,圆心角为2. 【解析】 【分析】(1)根据弧长公式l r α=即可计算;(2)将S 表示成二次函数形式,利用二次函数性质即可求其最值. (1)35α=︒=735rad rad 18036ππ⨯=, 扇形的弧长7148369l r αππ==⨯=cm ; (2)设扇形的弧长为l ,半径为r , 则216r l +=,∴162l r =−()08r <<,则()()2211162841622S lr r r r r r ==−=−+=−−+,当4r =时,2max 16cm S =,16248l =−⨯=cm ,2l rα,∴S 的最大值是216cm ,此时扇形的半径是4 cm ,圆心角2α=.【练习4-2】我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何”现有一类似问题,不确定大小的圆柱形木材,部分埋在墙壁中,其截面如图所示.用锯去锯这木材,若锯口深2CD =2AB =,则图中ACB 与弦AB 围成的弓形的面积为( )A .22π−B .23πC .32π−D .33π−【答案】B 【解析】 【分析】设圆的半径为r ,利用勾股定理求出r ,再根据扇形的面积及三角形面积公式计算可得; 【详解】解:设圆的半径为r ,则(2OD r CD r =−=−,112AD AB ==,由勾股定理可得222ODADOA ,即(2221r r ⎡⎤−+=⎣⎦,解得2r =,所以2OA OB ==,2AB =,所以3AOB π∠=,因此2212222343MBBAOB S S Sππ=−=⨯⨯−=弓形扇形 故选:B【练习4-3】已知圆锥的表面积为28π,其侧面展开扇形的圆心角大小为3π,则这个圆锥的底面半径为______. 【答案】2 【解析】 【分析】根据圆锥展开图的特征列出关于半径r ,母线长l 的方程组,解出即可. 【详解】设圆锥的底面半径为r ,母线长为l , 由题意,有228rl r πππ+=①, 由于侧面展开扇形的圆心角大小为3π,所以23l r ππ=,即6l r =②,由①②得12l =,2r =, 即圆锥的底面半径为2, 故答案为:2.题型五 诱导公式【例5-1】已知角α的顶点在原点,始边与x 轴的非负半轴重合,终边经过点()3,4P −.(1)求cos()cos 2ππαα⎛⎫−++ ⎪⎝⎭的值; (2)求sin()cos sin()tan()2cos(2)sin cos()tan()2πααπαπαππααπαπα⎛⎫−−−+ ⎪⎝⎭⎛⎫−++− ⎪⎝⎭的值.【答案】(1)15−(2)6427【解析】 【分析】(1)根据三角函数的定义,求得cos ,sin αα的值,再利用诱导公式即可求解;(2)先求得tan α的值,利用诱导公式及商数关系化简即可求解. (1)解:∵角α的终边经过点()3,4P −,∴3cos 5α==−,4sin 5α==,∴341cos()cos cos sin 2555ππαααα⎛⎫−++=−−=−=− ⎪⎝⎭.(2)解:由(1)知:3cos 5α=−,4sin 5α, ∴4tan 3α=−,∴sin()cos sin()tan()2cos(2)sin cos()tan()2πααπαπαππααπαπα⎛⎫−−−+ ⎪⎝⎭⎛⎫−++− ⎪⎝⎭ sin sin sin tan cos cos (cos )(tan )αααααααα−=−−33464tan 327α⎛⎫=−=−−=⎪⎝⎭. 【例5-2】若1sin ,63a π⎛⎫+= ⎪⎝⎭则2cos 3a π⎛⎫+= ⎪⎝⎭( ) A .13 B .13−C .79D .79−【答案】B 【解析】 【分析】利用诱导公式计算可得; 【详解】解:因为1sin 63a π⎛⎫+= ⎪⎝⎭,所以21cos cos sin 32663ππππααα⎡⎤⎛⎫⎛⎫⎛⎫+=++=−+=− ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦, 故选:B.【练习5-1】已知()()()()()3sin cos tan cos 222sin 2tan sin f πππααπαααπααππα⎛⎫⎛⎫⎛⎫+−−+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=−−−+.(1)化简()f α;(2)若31cos 25πα⎛⎫−=− ⎪⎝⎭,求()f α的值. 【答案】(1)()f αcos α= (2)()5f α=±【解析】 【分析】(1)根据诱导公式化简即可;(2)由题知1sin 5α=,进而根据同角三角函数关系求解即可.(1)解:由题意得()()()()()3sin cos tan cos 222sin 2tan sin f πππααπαααπααππα⎛⎫⎛⎫⎛⎫+−−+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=−−−+()()()()()cos sin tan sin sin tan sin ααααααα−−−=−−−cos α=(2)解:∵31cos sin 25παα⎛⎫−=−=− ⎪⎝⎭,∴1sin 5α=. ∴α为第一或第二象限角,∴cos α== ∴()f α=【练习5-2】已知2sin 33πα⎛⎫−= ⎪⎝⎭,且α为锐角,则cos 6πα⎛⎫+= ⎪⎝⎭( )A .23B .23− C.D【答案】B 【解析】【分析】利用诱导公式直接求出. 【详解】因为2sin 33πα⎛⎫−= ⎪⎝⎭,所以2cos cos sin 63233ππππααα⎛⎫⎛⎫⎛⎫+=−+=−−=− ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.故选:B.题型六 同角三角函数的基本关系【例6-1】已知12tan 5α=,求sin α,cos α的值.【答案】答案见解析 【解析】 【分析】利用同角三角函数的基本关系即可求解. 【详解】 解 由sin 12tan cos 5ααα==,得12sin cos 5αα=. 又22sin cos 1αα+=,所以22212cos cos 15αα⎛⎫+= ⎪⎝⎭.解得225cos 169α=. 又由tan 0α>,知α是第一或第三象限角. 若α是第一象限角, 则5cos 13α=,12tan 5α=,12sin 13α=;若α是第三象限角, 则5cos 13α=−,12tan 5α=,12sin 13α=−.【例6-2】已知423sin ,cos 55−−==++m m m m αα,α是第四象限角.求: (1)m 的值; (2)1tan tan αα+的值. 【答案】(1)8;(2)16960−. 【解析】 【分析】(1)利用22sin cos 1αα+=即22423155−−⎛⎫⎛⎫+= ⎪ ⎪++⎝⎭⎝⎭m m m m ,解方程得到m 的值,再代入检验是否满足α是第四象限角即可; (2)因sin cos 1tan cot cos sin sin cos αααααααα+=+=,由(1)可得到125sin ,cos 1313=−=αα,代入计算即可. 【详解】(1)∵22sin cos 1αα+=,∴22423155−−⎛⎫⎛⎫+= ⎪ ⎪++⎝⎭⎝⎭m m m m .化简整理,得(8)0−=m m .解方程,得0m =或8m =.当0m =时,43sin ,cos 55αα==−,与α是第四象限角矛盾,舍去;当8m =时,125sin ,cos 1313=−=αα成立. 综上所述,8m =.(2)由(1)知,1258,sin ,cos 1313==−=m αα. ∴1sin cos 1169tan tan cos sin sin cos 60αααααααα+=+==−.【点晴】本题主要考查同角三角函数基本关系的应用,考查学生的数学运算能力,是一道容易题. 【练习6-1】已知3sin 5α=,且α为第一象限角,则cos α=( ) A .45B .45−C .34D .34−【答案】A 【解析】 【分析】根据三角函数值在各象限的符号以及平方关系即可解出. 【详解】因为α为第一象限角,3sin 5α=,所以4cos 5α=. 故选:A .【练习6-2】已知sin α,cos α是方程2220x kx k k −++=的两根,则k 的值为( )A B .12− C .1D .1【答案】B 【解析】 【分析】利用韦达定理得到sin cos αα+,sin cos αα,由同角三角函数平方关系可构造方程求得k ,由sin cos αα+的范围求得k 的范围,由此可得k 的取值. 【详解】由题意得:2sin cos 2sin cos kk kαααα+=⎧⎨=+⎩, ()()22222sin cos sin cos 2sin cos 421k k k αααααα+=+−=−+=,即22210k k −−=,解得:k =;sin cos 4πααα⎛⎫+=+ ⎪⎝⎭,sin cos αα⎡∴+∈⎣,即2k ⎡∈⎣,22k ⎡∴∈⎢⎣⎦,k ∴=. 故选:B.题型七 sinx+cosx 、sinx-cosx 、sinxcosx 之间的关系【例7-1】已知(0,π)α∈ ,且1sin cos 5αα+= ,给出下列结论:①ππ2α<<; ②12sin cos 25αα=− ; ③3cos 5α=; ④7cos sin 5αα−=− . 其中所有正确结论的序号是( ) A .①②④ B .②③④ C .①②③ D .①③④【答案】A 【解析】 【分析】由(0,π)α∈ ,且1sin cos 5αα+=,将等式两边平方可得12sin cos 025αα=−<,可判断ππ2α<<,即可判断①②③;继而利用2()cos sin 12sin cos αααα=−−求得7cos sin 5αα−=−,判断④,可得答案.【详解】∵(0,π)α∈, 1sin cos 5αα+=,等式两边平方得21sin cos 12sin cos 25()αααα+==+ , 解得12sin cos 25αα=−,故②正确; ∵(0,π)α∈,12sin cos 025αα=−<, ∴ππ2α<<,cos 0α<,故①正确,③错误; 由ππ2α<<可知,cos sin 0αα−< , 且212cos sin 12sin cos 12()252549()αααα−−=−⨯−== , 解得7cos sin 5αα−=−,故④正确,故选:A【例7-2】已知()221tan cos 5cos 4θθπθ−=⎛⎫+ ⎪⎝⎭,则sin 2θ=( )A .2425 B .2425−C .725D .725−【答案】A 【解析】 【分析】根据同角三角函数的基本关系和两角和的余弦公式化简可得()221tan cos cos 4θθπθ−=⎛⎫+ ⎪⎝⎭sin )θθ+,结合()21c 2sin cos os sin θθθθ=++和二倍角的正弦公式即可得出结果.【详解】()22221tan cos cos 42θθπθ−=⎛⎫+ ⎪⎝⎭sin )5θθ=+=,∴7cos sin 5θθ+=, ∴()24912sin cos sin cos 25θθθθ=+=+, ∴24sin 225θ=. 故选:A.【例7-3】求函数(sin 1)(cos 1)y x x =++,,122x ππ⎡⎤∈−⎢⎥⎣⎦的值域.【答案】3342⎡⎢⎣ 【解析】 【分析】利用sin cos ,sin cos x x x x +的关系,将目标函数化为二次函数,即可求其值域. 【详解】y =(sin 1)(cos 1)sin cos sin cos 1x x x x x x ++=+++令sin cos x x t +=,则211sin cos 22x x t =−,由sin cos 4t x x x π⎛⎫=+=+ ⎪⎝⎭,又,122x ππ⎡⎤∈−⎢⎥⎣⎦,则3,464x πππ⎡⎤+∈⎢⎥⎣⎦,则1sin ,142x π⎛⎫⎡⎤+∈ ⎪⎢⎥⎝⎭⎣⎦,故t ∈⎣,则()211,2y t t =+∈⎣故)2max13122y ==+2min 13124y ⎫==⎪⎪⎝⎭,即该函数值域为:33,422⎡+⎢⎣. 【练习7-1】已知sin α,cos α是关于x 的一元二次方程220x x m −−=的两根, (1)求sin cos αα+的值; (2)求m 的值; (3)若0απ<<,求sin cos αα−的值. 【答案】(1)12 (2)34(3)2【解析】 【分析】(1)利用根与系数的关系可求出结果,(2)利用根与系数的关系列方程组,结合22sin cos 1αα+=可求出m 的值,(3)先判断出2απ<<π,则sin cos αα−=,再代值计算即可 (1)因为sin α,cos α是关于x 的一元二次方程220x x m −−=的两根, 所以1sin cos 2αα+= (2)因为sin α,cos α是关于x 的一元二次方程220x x m −−=的两根, 所以1sin cos 2αα+=,sin cos 2mαα=−,且2(1)8()0m ∆=−−−≥,所以221sin cos 2sin cos 4αααα++=, 所以114m −=,得34m =,满足180m ∆=+≥,所以34m = (3)由(2)可得1sin cos 2αα+=,3sin cos 08αα=−<,因为0απ<<,所以sin 0,cos 0αα><,所以2απ<<π,所以sin cos αα−==【练习7-2】若ππ2α⎛⎫∈ ⎪⎝⎭,,且21cos sin 4αα−= ,则tan α=_____.【答案】3【解析】【分析】根据同角平方和关系可解得1sin 2α=,进而根据角的范围可得5π6α=,进而可求.【详解】因为21cos sin 4αα−=,所以()241sin 4sin 10αα=---即24sin 4sin 30αα+=- ,∴解得1sin 2α=或3sin 2α=− (舍去). ππ2α⎛⎫∈ ⎪⎝⎭,,5π6α∴=,因此5πtan tan 6α== .故答案为:题型八 齐次式下弦切互化【例8-1】已知3π4απ<<, 110ta tan n 3a α=−+. (1)求tan α的值; (2)求sin cos sin cos αααα+−的值; (3)求222sin sin co 3co s s αααα−− .的值【答案】(1)13−(2)12−(3)115【解析】 【分析】 (1)根据110ta tan n 3a α=−+可得210tan 33tan 0a α+=+,解方程并结合角的范围求得tan α;(2)利用弦化切,将sin cos sin cos αααα+−化为tan 1tan 1αα+−,可得答案;(3)利用221sin +cos αα=,将222sin sin co 3co s s αααα−−化为22222sin sin co 3co sin cos s s αααααα−−+,继而化为222tan tan 3tan 1ααα−−+,求得答案.(1) 由110ta tan n 3a α=−+得210tan 33tan 0a α+=+, 解得tan 3α=−或13− ,因为3π4απ<<,故1tan 0α−<<,则1tan 3α=−;(2)11sin cos tan 1131sin cos tan 1213αααααα−+++===−−−−−;(3)2222222sin sin co 3co 2sin sin co 3co sin cos s s s s αααααααααα−−−−=+ 222212()32tan tan 31131tan 1513()13ααα−−−−===−+−++.【例8-2】若1sin cos 2αα+=,则44sin cos αα+=( ) A .52B .18C .716D .2332【答案】D 【解析】 【分析】将已知等式平方,利用二倍角公式得出sin 2α的值,由同角三角函数的关系化简求值即可. 【详解】1sin cos 2αα+=,两边平方得11sin 24α+=,即3sin 24α=−则()24422222123sin cos sin cos 2sin cos 1sin 2232ααααααα+=+−=−= 故选: D【练习8-1】已知2απ<<π,3sin 5α=. (1)求tan α的值;(2)求()()()sin 2cos 2sin cos πααααπ⎛⎫+−− ⎪⎝⎭−−+π−的值.【答案】(1)34−;(2)97−. 【解析】【分析】(1)由平方关系及角的范围求得4cos 5α=−,再根据商数关系即可求tan α.(2)应用诱导公式化简目标式,由(1)所得结果代入求值即可. (1)因为sin α=35,则222316cos 1sin 1()525αα=−=−=,又2π<α<π,所以cos 0α<,则4cos 5α=−. 所以sin 3tan cos 4ααα==−. (2)原式=sin 2sin (sin )(cos )αααα−−−−+−=93sin 9534sin cos 7()55ααα−−==−−−−. 【练习8-2】已知 2sin cos 5sin 3cos θθθθ+=−−,求(1)tan θ 的值;(2)3cos24sin2θθ+ 的值. 【答案】(1)2;(2)75. 【解析】 【分析】(1)将已知等式分子分母同除cos θ,可构造关于tan θ的方程,求得tan θ;(2)将所求式子利用二倍角公式化为正余弦的二次式,配凑分母22sin cos 1θθ+=,分子分母同除2cos θ可构造出关于tan θ的方程,代入tan θ可求得结果. (1)2sin cos 5sin 3cos θθθθ+=−−,2tan 15tan 3θθ+∴=−−,解得:tan 2θ=.(2)()223cos 24sin 23cos sin 8sin cos θθθθθθ+=−+22223cos 3sin 8sin cos sin cos θθθθθθ−+=+ 2233tan 8tan tan 1θθθ−+=+ 3121641−+=+ 75=.。
2024年新高考版数学专题1_5.1 三角函数的概念、同角三角函数的基本关系及诱导公式

综合篇
考法一 三角函数定义的应用 1.已知角α终边上一点P的坐标,求三角函数值:先求出点P到原点的距离r, 然后利用三角函数的定义求解;若含参数,则需对参数进行讨论. 2.已知角α的终边所在直线的方程(角α的终边为射线,此处给的是直线方 程),求三角函数值:一般地,由于不确定终边所在象限,故在终边上任取一 个异于原点的点时应分两种情况,然后利用三角函数的定义求解;若直线 的倾斜角为特殊角,则可直接写出角α的三角函数值.
r
r
x
2)三角函数值在各象限内的符号
记忆口诀:一全正,二正弦,三正切,四余弦. 二、同角三角函数的基本关系 1.平方关系:sin2α+cos2α=1.
2.商数关系:tan
α=
sin α cos α
α
2
k
,
k
Z
.
三、三角函数的诱导公式
公式
角
正弦
Hale Waihona Puke 一2kπ+α
sin α
(k∈Z)
二
π+α
-sin α
三
-α
-sin α
四
π-α
sin α
五
-α
cos α
2
六
2 +α
cos α
七
3
2 π+α
-cos α
八
3
2 π-α
-cos α
余弦 cos α
-cos α cos α -cos α sin α -sin α sin α -sin α
正切 tan α
tan α -tan α -tan α
口诀 函数名不变,符 号看象限
高考 数学
2024版新教材高考数学总复习:第二节同角三角函数的基本关系及诱导公式课件

同角三角函数的基本关系及诱导公式
必备知识·夯实双基
关键能力·题型突破
【课标标准】
sinα
2
2
1.理解同角三角函数的基本关系式:sin α+cos α=1,
=tanα.
cos α
π
2.借助单位圆的对称性,利用定义推导出诱导公式( ±α,π±α的正
2
弦、余弦、正切).
必备知识·夯实双基
知识梳理
sin α+cos α
解析:
=
sin α−cos α
sin α
+1
cos α
sin α
−1
cos α
sin α+cos α
3
α=2,则
的值为________.
sin α−cos α
tan α+1 2+1
=
= =3.
tan α−1 2−1
sin kπ+α
4.(易错)已知A=
sin α
+
{2,-2}
是________.
=
所以f(-1 860°)=cos (-1 860°)=cos 1 860°
1
=cos (5×360°+60°)=cos 60°= .
2
=cos α,
题后师说
1.利用诱导公式把任意角的三角函数转化为锐角三角函数的步骤
2.常见的互余和互补的角
互余的角
互补的角
巩固训练1
4π
5
7π
(1)若cos (α+ )=- ,则sin ( -α)=(
3
5
sin π−α cos 2π−α tan −α+2π
(2)已知f(α)=
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题五三角函数与解三角形
5.1三角函数的概念、同角三角函数的基本关系及诱导
公式
考点三角函数的概念、同角三角函数的基本关系及诱导公式
1.(2022全国甲理,8,5分)沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”.如图,AB是以O为圆心,OA为半径的圆弧,C是AB的中点,D在AB上,CD⊥AB.“会圆术”给出AB的
弧长的近似值s的计算公式:s=AB+CD 2
OA
.当OA=2,∠AOB=60°时,s=( )
A.11−3√3
2B.11−4√3
2
C.9−3√3
2
D.9−4√3
2
答案 B 连接OC,如图.
∵C是AB的中点,OA=OB=2,∴OC⊥AB.又∵CD⊥AB,
∴D,C,O三点共线.
∵∠AOB=60°,∴AB=2,OC=√3,CD=2-√3,
∴s=2+(2−√3)2
2=11−4√3
2
,故选B.
2.(2019北京文,8,5分)如图,A,B是半径为2的圆周上的定点,P为圆周上的动点,∠APB是锐角,大小为β.图中阴影区域的面积的最大值为()
A.4β+4cos β
B.4β+4sin β
C.2β+2cos β
D.2β+2sin β
答案 B 本题主要考查扇形面积、三角形面积公式及应用;主要考查学生的推理论证能力和运算求解能力;考查的核心素养是数学运算.
由圆的性质易知,当|PA|=|PB|时,阴影部分的面积最大,其面积为△PAB 的面积与弓形的面积之和. 作PD ⊥AB 于D 点,由∠APB=β,知∠DOB=β(O 为圆心).所以|OD|=2cos β,|PD|=2+2cos β,|AB|=4sin β.所以S △PAB =1
2
·|AB|·|PD|=4sin β(1+cos β).S 弓形=S 扇形OAB -S △OAB =12
·2β·22
-12
·4sin β·2cos β=4β-4sin β· cos β.
故阴影部分的面积为S △PAB +S 弓形=4sin β+4sin βcos β+4β-4sin βcos β=4β+4sin β.故选B.
思路分析 本题阴影部分由一个三角形与一个弓形构成,当β确定时,弓形面积是确定的,故三角形面积最大时,阴影部分面积最大.
3.(2014课标Ⅰ文,2,5分)若tan α>0,则( ) A.sin α>0 B.cos α>0 C.sin 2α>0 D.cos 2α>0
答案 C 由tan α>0得α是第一或第三象限角,若α是第三象限角,则A,B 错;由sin 2α=2sin αcos α知
sin 2α>0,C 正确;α取π3时,cos 2α=2cos 2
α-1=2×(12)2-1=-12
<0,D 错.故选C.
评析 本题考查三角函数值的符号,判定时可运用基本知识、恒等变形及特殊值等多种方法,具有一定的灵活性.
4.(2014大纲全国文,2,5分)已知角α的终边经过点(-4,3),则cos α=( ) A.45
B.35
C.-35
D.-45
答案 D 由三角函数的定义知cos α=
√(−4)+3=-45
.故选D.
5.(2015福建文,6,5分)若sin α=-5
13
,且α为第四象限角,则tan α的值等于( ) A.
125 B.-125 C.512 D.-512
答案 D ∵sin α=-
5
13
,α为第四象限角,
∴cos α=√1−sin 2α=
1213,∴tan α=sinαcosα=-512
.故选D. 6.(2014大纲全国理,3,5分)设a=sin 33°,b=cos 55°,c=tan 35°,则( ) A.a>b>c B.b>c>a C.c>b>a D.c>a>b 答案 C ∵b=cos 55°=sin 35°>sin 33°=a,∴b>a.
又∵c=tan 35°=
sin35°
cos35°
>sin 35°=cos 55°=b,∴c>b.∴c>b>a.故选C.
7.(2013浙江理,6,5分)已知α∈R,sin α+2cos α=√10
2
,则tan 2α=( )
A.4
3
B.34
C.-34
D.-43
答案 C (sin α+2cos α)2
=52,展开得3cos 2
α+4sin αcos α=32,再由二倍角公式得32
cos 2α+2sin 2α=0,故
tan 2α=sin2αcos2α=-3
22=-3
4
,选C.
评析 本题考查同角三角函数的基本关系式和三角恒等变换,考查转化与化归思想,考查学生灵活应用公式的能力和运算求解能力.三角函数求值问题关键在于观察角与角之间的关系和三角函数名之间的关系. 8.(2013大纲全国文,2,5分)已知α是第二象限角,sin α=5
13
,则cos α=( ) A.-1213 B.-513 C.513 D.1213
答案 A ∵α是第二象限角,∴cos α<0. ∴cos α=-√1−sin 2α=-12
13
.故选A. 评析 本题考查三角函数值在各象限的符号,同角三角函数关系,属容易题. 9.(2013广东文,4,5分)已知sin (
5π2+α)=1
5,那么cos α=( ) A.-25
B.-15
C.15
D.25
答案 C ∵sin (
5π2+α)=sin (π2+α)=cos α,∴cos α=1
5
.故选C. 10.(2017北京文,9,5分)在平面直角坐标系xOy 中,角α与角β均以Ox 为始边,它们的终边关于y 轴对称.若sin α=13
,则sin β= . 答案
1
3 解析 本题考查三角函数的诱导公式.
由角α与角β的终边关于y 轴对称,可得β=(2k+1)π-α,k ∈Z,∵sin α=13
,∴sin β=sin[(2k+1)π-α]=sin α=13
.
11.(2011江西文,14,5分)已知角θ的顶点为坐标原点,始边为x 轴的正半轴.若P(4,y)是角θ终边上一点,且sin θ=-2√5
5
,则y= . 答案 -8
解析 P(4,y)是角θ终边上一点,由三角函数的定义知sin θ=
√16+y ,又sin θ=-
2√5
5
,∴√16+y =-
2√5
5
,解得y=-8.
评析 本题主要考查任意角三角函数的定义,考查运算求解能力,由题意得
√16+y 2
=-
2√5
5
是本题求解的关键.
12.(2016四川文,11,5分)sin 750°= . 答案
12
解析 sin 750°=sin(720°+30°)=sin 30°=12
. 解后反思 利用诱导公式把大角化为小角. 评析 本题考查了三角函数的诱导公式.
13.(2013课标Ⅱ理,15,5分)设θ为第二象限角,若tan (θ+π4)=1
2
,则sin θ+cos θ= . 答案 -√10
5
解析 tan θ=tan [(θ+π4)−π4]=1
2−11+12
=-1
3
,
∴sin θ=-1
3cos θ,将其代入sin 2
θ+cos 2
θ=1得
109cos 2θ=1,∴cos 2
θ=910,又易知cos θ<0,∴cos θ=-310
√10,∴sin θ=√10
10
,故sin θ+cos θ=-
√10
5
.。
