重庆大学《概率论与数理统计Ⅰ》课程试卷.
概率论与数理统计

重庆交通大学继续教育学院2008--2009学年第一学期考试A 卷《概率论与数理统计(经管类)》课程考核形式:闭卷 考试需用时间:120分钟在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.下列各函数中,可作为某随机变量概率密度的是( ) A .⎩⎨⎧<<=其他,0;10,2)(x x x fB .⎪⎩⎪⎨⎧<<=其他,0;10,21)(x x fC .⎩⎨⎧-<<=其他,1;10,3)(2x x x fD .⎩⎨⎧<<-=其他,0;11,4)(3x x x f2.设随机变量X~N(1,4),5.0)0(,8413.0)1(=Φ=Φ,则事件{13X ≤≤}的概率为( ) A.0.1385 B.0.2413 C.0.2934 D.0.34133.则P{XY=0}=( ) A. 41 B.125 C.43 D.14.某种电子元件的使用寿命X (单位:小时)的概率密度为⎪⎩⎪⎨⎧<≥=,100,0;100,100)(2x x x x f 任取一只电子元件,则它的使用寿命在150小时以内的概率为( )A .41 B .31 C .21 D .325.设E (X ),E (Y ),D (X ),D (Y )及Cov(X,Y )均存在,则D (X-Y )=( ) A .D (X )+D (Y ) B .D (X )-D (Y ) C .D (X )+D (Y )-2Cov(X,Y ) D .D (X )-D (Y )+2Cov(X,Y )7.设随机变量X 服从参数为3的泊松分布,Y~B (8,31),且X ,Y 相互独立,则D (X-3Y-4)=( )A .-13B .15C .19D .238.已知D (X )=1,D (Y )=25,ρXY =0.4,则D (X-Y )=( )A .6B .22C .30D .46 9.设总体X 服从[0,2θ]上的均匀分布(θ>0),x 1, x 2, …, x n 是来自该总体的样本,x 为样本均值,则θ的矩估计θˆ=( ) C .2xD .x2110.设n 1X ,,X 为正态总体N(2,σμ)的样本,记∑=--=ni i x x n S 122)(11,则下列选项中正确的是( ) A.)1(~)1(222--n S n χσB.)(~)1(222n S n χσ-C.)1(~)1(22--n S n χD.)1(~22-n S χσ二、填空题(本大题共15小题,每小题2分,共30分) 请在每小题的空格中填上正确答案。
重庆师范大学《概率论与数理统计》2020-2021学年期末试卷

重庆师范大学《概率论与数理统计》2020-2021学年第一学期期末试卷学号姓名年级专业成绩一、选择题(每小题3分,共15分):1.设随机变量X 的分布律为),2,1(}{ ===k b k X P kλ,则().(A)10<<λ,且11--=λb (B)10<<λ,且1-=λb (C)10<<λ,且11-=-λb (D)10<<λ,且11-+=λb 2.设随机变量X 的密度函数为xx Ae x f 22)(+-=,则().(A)πe(B)πe 1(C)πe 1(D)πe 23.设随机变量X 的概率密度和分布函数分别是)(xf 和)(x F ,且)()(x f x f -=,则对任意实数a ,有=-)(a F ().(A))(21a F -(B))(21a F +(C)1)(2-a F (D))(1a F -4.设相互独立的随机变量Y X ,具有同一分布,且都服从区间[0,1]上的均匀分布,则在区间或区域上服从均匀分布的随机变量是().(A)(Y X ,)(B)YX +(C)YX -(D)2X5.设)(1x F 与)(2x F 分别为随机变量1X 与2X 的分布函数,为使)()()(21x bF x aF x F -=是某随机变量的分布函数,在下列给定的各组数值中应取().(A)52,53-==b a (B)32,32==b a (C)23,21=-=b a (D)23,21-==b a二、填空题(每小题3分,共15分):1.二维随机变量(Y X ,)的联合分布律为:Y X121α0.22β0.3则α与β应满足的条件是,当Y X ,相互独立时,α=.2.二维随机变量(Y X ,)的联合密度为:])()[(212122221121),(σμσμσπσ-+--=y x e y x f ,则X的边缘概率密度为.3.连续型随机变量X 的概率密度为其它10,0,)(2<<⎩⎨⎧=x kx x f ,则常数=k .4.设)02.0,10(~2N X ,已知Φ(2.5)=0.9938,则=<≤}05.1095.9{X P .5.设Y X ,是相互独立的随机变量,),3(~),,2(~22σσ-N Y N X ,且95.0}7654.8|12{|=≤-+Y X P ,则σ=.三、计算题(3小题,共34分)1.(12分)随机变量X 的概率密度为⎪⎩⎪⎨⎧>≤=4||,04||,cos )(ππx x x A x f ,试求(1)系数A ;(2)X 的分布函数;(3)X 落在⎪⎭⎫⎝⎛6,0π内的概率.2.(10分)随机变量X 的概率密度为⎩⎨⎧≤>=-0,00)(,x x e x f x ;求2X Y =的概率密度.3.(12分)设Y X ,是两个相互独立的随机变量,其概率密度分别为:⎩⎨⎧≤≤=其它,010,1)(x x f x ⎩⎨⎧≤>=-0,00,)(y y e y f y Y 求随机变量Y X Z +=的概率密度函数.四、解答题(3小题,共36分)1.(12分)假设一设备开机后无故障工作的时间X 服从参数为5=θ的指数分布.设备定时开机,出现故障时自动关机,而在无故障的情况下工作2h 便关机,试求设备每次开机无故障工作的时间Y 的分布函数.2.(12分)随机变量X 和Y 均服从区间[0,1]上的均匀分布且相互独立.①写出二维随机变量(Y X ,)的边缘概率密度和联合概率密度.②求}23{≤+Y X P .3.(12分)已知随机变量Y X 与的分布律为:X -101P1/41/21/4且已知1}0{==XY P .(1)求(Y X ,)的联合分布律;(2)Y X 与是否相互独立?为什么?Y 01P1/21/2。
概率论与数理统计习题(含解答,答案)

概率论与数理统计习题(含解答,答案)概率论与数理统计复习题(1)⼀.填空.1.3.0)(,4.0)(==B P A P 。
若A 与B 独⽴,则=-)(B A P ;若已知B A ,中⾄少有⼀个事件发⽣的概率为6.0,则=-)(B A P 。
2.)()(B A p AB p =且2.0)(=A P ,则=)(B P 。
3.设),(~2σµN X ,且3.0}42{ },2{}2{=<<≥==>}0{X P 。
4.1)()(==X D X E 。
若X 服从泊松分布,则=≠}0{X P ;若X 服从均匀分布,则=≠}0{X P 。
5.设44.1)(,4.2)(),,(~==X D X E p n b X ,则==}{n X P6.,1)(,2)()(,0)()(=====XY E Y D X D Y E X E 则=+-)12(Y X D 。
7.)16,1(~),9,0(~N Y N X ,且X 与Y 独⽴,则=-<-<-}12{Y X P (⽤Φ表⽰),=XY ρ。
8.已知X 的期望为5,⽽均⽅差为2,估计≥<<}82{X P 。
9.设1?θ和2?θ均是未知参数θ的⽆偏估计量,且)?()?(2221θθE E >,则其中的统计量更有效。
10.在实际问题中求某参数的置信区间时,总是希望置信⽔平愈愈好,⽽置信区间的长度愈愈好。
但当增⼤置信⽔平时,则相应的置信区间长度总是。
⼆.假设某地区位于甲、⼄两河流的汇合处,当任⼀河流泛滥时,该地区即遭受⽔灾。
设某时期内甲河流泛滥的概率为0.1;⼄河流泛滥的概率为0.2;当甲河流泛滥时,⼄河流泛滥的概率为0.3,试求:(1)该时期内这个地区遭受⽔灾的概率;(2)当⼄河流泛滥时,甲河流泛滥的概率。
三.⾼射炮向敌机发射三发炮弹(每弹击中与否相互独⽴),每发炮弹击中敌机的概率均为0.3,⼜知若敌机中⼀弹,其坠毁的概率是0.2,若敌机中两弹,其坠毁的概率是0.6,若敌机中三弹则必坠毁。
概率论与数理统计期末试卷及答案(重庆大学)3

重庆大学《概率论与数理统计Ⅰ》课程试卷A 卷第1页共3页《概率论与数理统计Ⅰ》试卷评分标准及答案2016—2017学年第二学期开课学院:数统学院课程号:考试日期:2017.6.4.考试方式:考试时间:120分钟题号一二三四五六七八九十总分得分分位数:0.975 1.96u =,0.05(15) 1.753t =-,0.975(15) 2.131t =。
一、填空题(每空3分,共42分)1.设()()1,0.3P A B P A ==,()P B A =1。
2.学生做一道有4个选项的单项选择题时,如果他不知道问题的正确答案,就作随机猜测。
假设学生知道正确答案的概率为0.2,现从卷面上看题是答对了,试问学生确实知道正确答案的概率为:0.5。
3.某路口的显示屏由24块独立发光单元组成,每块发光单元的故障率为0.01,那么该发光显示屏正常显示的概率0.79or 240.99。
4.设连续型随机变量的密度函数为2, >100()0 , Ax f x xx ⎧⎪=⎨⎪≤⎩100则A =100,X 的分布函数()F x =0, x 1001001,100x x ≤⎧⎪⎨->⎪⎩,{1000}P X ≥=0.1。
5.设随机变量X 和Y 独立同分布,且2=3EX DX =,,则2(-)E X Y =6,根据切比雪夫不等式估计概率{|-|5}=P X Y ≥6/25。
6.设X 是样本容量为12且来自总体[]0,12X ~U 的样本均值,则2ES =_12_,2EX =37。
7.设128,,...,X X X 是来自总体(0,1)N 的样本,则822i i D X =⎛⎫=⎪⎝⎭∑14,常数a =3,统计量2212823()ii X X Y aX=+=∑~F (2,6)(注明分布)。
8.从正态总体N(3.4,36)中抽取容量为n 的样本,如果要求其样本均值位于区间(1.4,5.4)内的概率不小于0.95,问样本容量n 至少为35。
《概率论与数理统计》习题及答案

概率论与数理统计 第一部份 习题第一章 概率论基本概念一、填空题1、设A ,B ,C 为3事件,则这3事件中恰有2个事件发生可表示为 。
2、设3.0)(,1.0)(=⋃=B A P A P ,且A 与B 互不相容,则=)(B P 。
3、口袋中有4只白球,2只红球,从中随机抽取3只,则取得2只白球,1只红球的概率为 。
4、某人射击的命中率为0.7,现独立地重复射击5次,则恰有2次命中的概率为 。
5、某市有50%的住户订晚报,有60%的住户订日报,有80%的住户订这两种报纸中的一种,则同时订这两种报纸的百分比为 。
6、设A ,B 为两事件,3.0)(,7.0)(==B A P A P ,则=)(B A P 。
7、同时抛掷3枚均匀硬币,恰有1个正面的概率为 。
8、设A ,B 为两事件,2.0)(,5.0)(=-=B A P A P ,则=)(AB P 。
9、10个球中只有1个为红球,不放回地取球,每次1个,则第5次才取得红球的概率为 。
10、将一骰子独立地抛掷2次,以X 和Y 分别表示先后掷出的点数,{}10=+=Y X A{}Y X B >=,则=)|(A B P 。
11、设B A ,是两事件,则B A ,的差事件为 。
12、设C B A ,,构成一完备事件组,且,7.0)(,5.0)(==B P A P 则=)(C P ,=)(AB P 。
13、设A 与B 为互不相容的两事件,,0)(>B P 则=)|(B A P 。
14、设A 与B 为相互独立的两事件,且4.0)(,7.0)(==B P A P ,则=)(AB P 。
15、设B A ,是两事件,,36.0)(,9.0)(==AB P A P 则=)(B A P 。
16、设B A ,是两个相互独立的事件,,4.0)(,2.0)(==B P A P 则=)(B A P 。
17、设B A ,是两事件,如果B A ⊃,且2.0)(,7.0)(==B P A P ,则=)|(B A P 。
第二学期概率论与数理统计试卷 参考答案
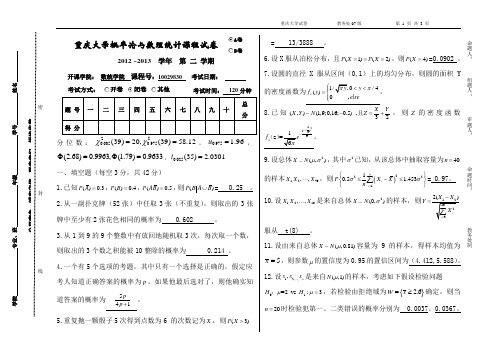
重庆大学概率论与数理统计课程试卷A卷B卷2012 ~2013 学年 第 二 学期开课学院: 数统学院 课程号:10029830 考试日期:考试方式:开卷闭卷 其他 考试时间: 120分钟分位数:220.0050.975(39)20,(39)58.12χχ==,0.975 1.96u =,(2.68)0.9963,(1.79)0.9633Φ=Φ=,0.025(35) 2.0301t =一、填空题(每空3分,共42分)1.已知()0.3P A =,()0.4P B =,()0.5P AB =,则()P B A B ⋃= 0.25 。
2.从一副扑克牌(52张)中任取3张(不重复),则取出的3张牌中至少有2张花色相同的概率为 0.602 。
3.从1到9的9个整数中有放回地随机取3次,每次取一个数,则取出的3个数之积能被10整除的概率为 0.214 。
4.一个有5个选项的考题,其中只有一个选择是正确的。
假定应 考人知道正确答案的概率为p 。
如果他最后选对了,则他确实知道答案的概率为541pp +。
5.重复抛一颗骰子5次得到点数为6 的次数记为X ,则(3)P X >= 13/3888 。
6.设X 服从泊松分布,且(1)(2)P X P X ===,则(4)P X ==0.0902 。
7.设圆的直径X 服从区间(0,1)上的均匀分布,则圆的面积Y 的密度函数为1//4()0 ,Y y f y elseπ⎧<<⎪=⎨⎪⎩。
8.已知(,)(1,9;0,16;0.5) ,32X YX Y N Z -=+且,则Z 的密度函数21()36z Z f --(z )。
9.设总体2(,)X N μσ,其中2σ已知,从该总体中抽取容量为40n =的样本1,240,,X X X ,则()222110.5 1.453nii P X X n σσ=⎧⎫≤-≤⎨⎬⎩⎭∑= 0.97。
10.设1,210,,X X X 是来自总体2(0,)XN σ的样本,则Y =服从 t(8) 。
重庆大学数理统计试题答案版

涉及到的有关分位数:()()()()()()()()()()()()20.950.950.950.9750.9750.9752222220.9750.0250.0250.9750.950.97520.95 1.645,16 1.746,15 1.753,16 2.12,15 2.131,1628.851527.49,16 6.91,15 6.26,1 5.02,1 3.84,27.382 5.99u t t t t χχχχχχχχ=============一、设123,,X X X 是来自总体~(0,3)X N 的样本。
记()2332i 1111,32i i i X X S X X====-∑∑,试确定下列统计量的分布:(1)3113i i X =∑;(2)23119i i X =⎛⎫⎪⎝⎭∑;(3)()23113i i X X=-∑;(4X解:(1)由抽样分布定理,311~(0,1)3i i X X N ==∑(2)因311~(0,1)3i i X N =∑,故223321111~(1)39i i i i X X χ==⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭∑∑(3)由抽样分布定理,()()()2223321131211~(2)3323i i i i S X X X X χ==-=⋅-=-∑∑(4)因()222~(0,1),~23X N S χ,X 与2S独立,故()~2X t 。
二、在某个电视节目的收视率调查中,随机调查了1000人,有633人收看了该节目,试根据调查结果,解答下列问题:(1)用矩估计法给出该节目收视率的估计量;(2)求出该节目收视率的最大似然估计量,并求出估计值;(3)判断该节目收视率的最大似然估计是否是无偏估计;(4)判断该节目收视率的最大似然估计是否是有效估计。
解:总体X 为调查任一人时是否收看,记为~(1,)X B p ,其中p 为收视率(1)因EX p =,而^E X X =,故收视率的矩估计量为^Xp =(2)总体X 的概率分布为()1()1,0,1xxf x p p x -=-=1111()(1)(1)(1)ln ()ln (1)ln(1)ln ()(1)01nniii ii i nx n x x x n X n n Xi L p p p pp p p L p nX p n X p d L p nX n X dp p p==---=∑∑=-=-=-=+---=-=-∏解得收视率p 的最大似然估计量为^Xp =现有一参量为1000的样本121000,,X X X ……,,且10001633ii X==∑则6330.6331000X ==,故收视率的极大似然估计值为0.633.(3)因E X p =,故^X p =是无偏估计(4)因()ln ()(1)1(1)d L p nX n X nX p dp p p p p -=-=---,又E X p=故收视率的最大似然估计X 是p 的有效估计。
概率论与数理统计试卷(计算)

题目部分,(卷面共有100题,845.0分,各大题标有题量和总分) 一、计算(43小题,共354.0分)(8分)[1]设随机变量ξ的分布函数为()2001 0xx F x e x -<⎧=⎨-≥⎩ (1)计算P{ξ≥2(2)计算P{- 3≤ξ<4}(3)求a,使得P{ξ≥a}=p{ξ<a}(8分)[2]从-1,0,1,2中随机地取出两个数字,设所取两个数字之和为ξ,求随机变量ξ的分布律和分布函数F(x)=P{ξ≤x} (13分)[3]设ξ,η相互独立,且都服从区间[0,a]上均匀分布,求ζ=η-ξ的分布函数和概率密度。
(5分)[4]在区间[0,a]上任意投掷一个质点,用ξ表示这个质点的坐标。
设这个质点落在[0,a]中任意小区间内的概率与这个小区间的长度成正比例,试求ξ的分布函数,(a>0)(10分)[5]甲、乙两篮球运动员,投篮命中率分别为0.8和0.7,每人投篮3次,求两人进球相等的概率。
(6分)[6]一袋中有3只白球,2只黑球,3只红球,在其中任取2只球,以ξ表示取到白球的只数,以η表示取到黑球的只数,求E ξ及E η (3分)[7]设随机变量ξ服从(0- 1)分布,其分布律为P(ξ=1)=p ,P(ξ=0)=q ,(0<p<1,p+q=1)求E ξ,D(ξ)。
(12分)[8]设系统L 是由两个相互独立的子系统1L 和2L 以串联方式联接而成,1L 与2L 的寿命分别为ξ与η,其概率密度分别为()1000x e x x x ααϕ-⎧>=⎨≤⎩()2000y e y y y ββϕ-⎧>=⎨≤⎩其中α>0,β>0,α≠β,试求系统L 的寿命ζ的概率密度。
(10分)[9]设二维连续型随机变量(ξ,η)的联合概率密度为 (23) 0,0(,)0 0,0x y Ae x y x y x y ϕ-+⎧>>=⎨≤≤⎩试求(1)系数A 的值,(2)(ξ,η)落在三角形区域D={(x,y)|x ≥0,y ≥0,2x+3y ≤6}的概率,(3)(ξ,η)的联合分布函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重庆大学《概率论与数理统计Ⅰ》课程试卷
2015—2016学年第一学期
1、填空题(共42分)
1.设P(A)=0.7,P(B)=0.5,P(A-B)=____________,=____________。
2.某学院在2014年招生的三个专业中,学生所占的比例分别为30%,
45%,25%。
在2015年评选优异生的过程中,学院决定专业打通按综
合成绩排序进行评选,其评选结果是三个专业占总人数的比例分别
为0.04,0.045,0.031,则该学院评选的优异生的比例(概率)为:
________________。
3.设连续性随机变量的分布函数为则A=____________,X的密度函数
=_________________,。
4.设随机变量X的密度函数,则EX=___________,随机变量Y=2X-1
的密度函数。
5.设则,根据切比雪夫不等式估计概率。
6.设是样本容量为15且来自总体P(3)(泊松分布)的样本均值,则。
7.设是来自总体N(0,4)的样本,则常数C=________,统计量(注:确
定分布),。
二、(10分)设一枚深水炸弹击沉一艘潜艇的概率为,击伤的概率为,
未击中的概率为,并设击伤潜艇两次也可导致其下沉,求施放3枚深水
炸弹能击沉潜艇的概率。
三、(14分)设二维随机变量的联合密度函数为:
求:(1)求随机变量X的边缘分布密度函数;
2)协方差;
(3)随机变量的密度函数。
四、(10分)经计算,神州号飞船返回舱将降落到内蒙古草原一个半
径3公里的圆形区域。
地面搜索队员在圆心处待命,飞船一旦降落,将
按直线以最快速度到达进行救援。
假设飞船着陆点在这个圆形区域内
服从均匀分布,求搜索队到达着陆点所需路程的期望值。
五、(12分)设总体是来自总体X的样本,求
(1)参数的矩估计量和最大似然估计量;
(2)判断估计量是否是参数的无偏估计量。
六、(12分)据环保条例规定,在排放的工业废水中,某有害物质的含量不得超过0.5,假定该有害物质含量,现取5份水样,测得该有害物质含量分别为0.530,0.542,0.510,0.495,0.515。
求
(1)参数的置信度为95%的置信区间;
(2)能否据此抽样结果说明该有害物质含量超过规定标准。
