初中数学 图形的相似 专题试题及答案
初中数学图形的相似练习题及参考答案

初中数学图形的相似练习题及参考答案相似是初中数学中的一个重要概念,它描述了两个图形在形状上的相似程度。
相似的图形具有相同的形状但不一定相等的大小。
在这篇文章中,我们将介绍几道关于相似图形的练习题,并提供参考答案供大家参考。
题目一:已知三角形ABC和三角形DEF相似,且比例系数为3:4。
若AB=6cm,BC=8cm,DE=12cm,求EF的长度。
解答一:根据相似三角形的定义,相似三角形的对应边长之比相等。
即AB/DE=BC/EF。
代入已知条件,得到以下等式:6/12=8/EF通过交叉乘法可以求解EF的长度:6*EF=12*8EF=16cm所以,EF的长度为16cm。
题目二:如果一个正方形的边长为6cm,那么和它相似的另一个正方形的边长是多少?解答二:由于两个正方形相似,所以它们的对应边长之比相等。
设另一个正方形的边长为x,则根据相似三角形的性质得到以下等式:x/6=6/6通过交叉乘法可以求解x的长度:x=6cm所以,和给定正方形相似的另一个正方形的边长也是6cm。
题目三:已知一个矩形的长为10cm,宽为5cm。
如果和它相似的另一个矩形的长为15cm,求这个矩形的宽。
解答三:根据相似矩形的性质,两个矩形的边长比相等。
设相似矩形的宽为x,则根据已知条件可以得到以下等式:10/x=15/5通过交叉乘法可以求解x的长度:10*5=15*x50=15*xx=50/15x=10/3 cm所以,这个矩形的宽为10/3 cm。
题目四:如果一个三角形的三边分别为3cm,4cm和5cm,那么和它相似的另一个三角形的三边分别是多少?解答四:根据相似三角形的性质,两个三角形的边长比相等。
设相似三角形的三边分别为x、y、z,则根据已知条件可以得到以下等式:x/3=y/4=z/5通过交叉乘法可以求解x、y、z的长度:x=3*(4/5)=12/5 cmy=4*(4/5)=16/5 cmz=5*(4/5)=20/5 cm所以,和给定三角形相似的另一个三角形的三边分别是:12/5 cm、16/5 cm和20/5 cm。
初中数学图形相似解答题专题训练含答案
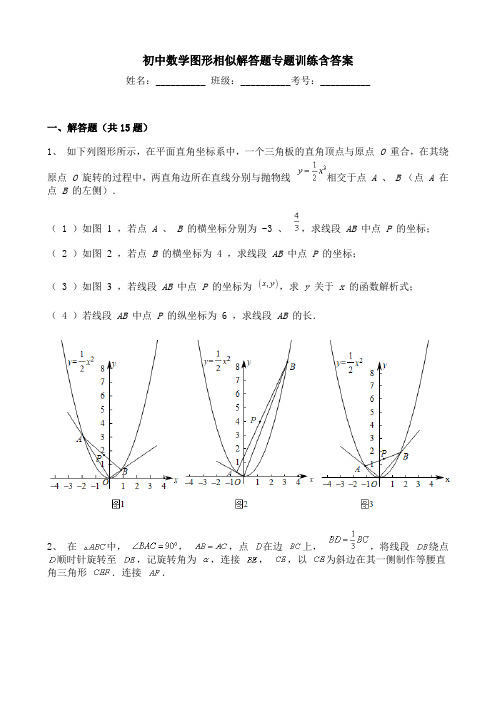
初中数学图形相似解答题专题训练含答案姓名:__________ 班级:__________考号:__________一、解答题(共15题)1、如下列图形所示,在平面直角坐标系中,一个三角板的直角顶点与原点O 重合,在其绕原点O 旋转的过程中,两直角边所在直线分别与抛物线相交于点A 、B (点A 在点B 的左侧).( 1 )如图1 ,若点A 、B 的横坐标分别为 -3 、,求线段AB 中点P 的坐标;( 2 )如图2 ,若点B 的横坐标为 4 ,求线段AB 中点P 的坐标;( 3 )如图3 ,若线段AB 中点P 的坐标为,求y 关于x 的函数解析式;( 4 )若线段AB 中点P 的纵坐标为 6 ,求线段AB 的长.2、在中,,,点在边上,,将线段绕点顺时针旋转至,记旋转角为,连接,,以为斜边在其一侧制作等腰直角三角形.连接.( 1 )如图1 ,当时,请直接写出线段与线段的数量关系;( 2 )当时,① 如图2 ,( 1 )中线段与线段的数量关系是否仍然成立?请说明理由;② 如图3 ,当,,三点共线时,连接,判断四边形的形状,并说明理由.3、如图,在四边形 ABCD 中,AD∥BC ,AC ,BD 交于点 E ,过点 E 作MN∥AD ,分别交AB ,CD 于点M ,N .( 1 )求证:△AME~△ABC ;( 2 )求证:;( 3 )若AD=5 ,BC=7 ,求MN 的长.4、如图,,试求和的值.5、已知,求的值.6、已知x:y=3:5,y:z=2:3,求的值.7、如图,AC是正方形ABCD的对角线,BE1⊥AC,E1F1⊥AB,F1E2⊥AC,E2F2⊥AB,F2E3⊥AC.(1)求AE3:AB的值.(2)作E3 F3⊥AB,F3E4⊥AC,…,Fn-lEn⊥AC,求AEn:AB的值.8、已知a+b+c=60,且,求a、b、c的值.9、已知:如图,l1∥l2∥l3,AB=3,BC=5,DF=12.求DE和EF的长.10、如图,△ABC中,DE//BC,EF//AB.求证:△ADE∽△EFC.11、如图,,CD为两个建筑物,两建筑物底部之间的水平地面上有一点.从建筑物的顶点测得点的俯角为45°,从建筑物的顶点测得点的俯角为75°,测得建筑物的顶点的俯角为30°.若已知建筑物的高度为20米,求两建筑物顶点、之间的距离(结果精确到,参考数据:,)12、我们知道,将一条线段AB分割成大小两条线段AP、PB,使AP>PB,点P把线段AB分成两条线段AP和BP,且,点P就是线段AB的黄金分割点,此时的值为 ________ (填一个实数):如图,Rt△ABC中,∠B=90°,AB=2BC,现以C为圆心、CB长为半径画弧交边AC于D,再以A为圆心、AD长为半径画弧交边AB于E.求证:点E是线段AB的黄金分割点13、如图F为平行四边形ABCD的AD延长线上一点,BF分别交CD、AC于G、E,若,求BE。
初中数学图形的相似难题汇编附答案

初中数学图形的相似难题汇编附答案一、选择题1.两个相似多边形的面积比是9∶16,其中小多边形的周长为36 cm,则较大多边形的周长为 )A.48 cm B.54 cm C.56 cm D.64 cm【答案】A【解析】试题分析:根据相似多边形对应边之比、周长之比等于相似比,而面积之比等于相似比的平方计算即可.解:两个相似多边形的面积比是9:16,面积比是周长比的平方,则大多边形与小多边形的相似比是4:3.相似多边形周长的比等于相似比,因而设大多边形的周长为x,则有=,解得:x=48.大多边形的周长为48cm.故选A.考点:相似多边形的性质.2.如果两个相似正五边形的边长比为1:10,则它们的面积比为()A.1:2 B.1:5 C.1:100 D.1:10【答案】C【解析】根据相似多边形的面积比等于相似比的平方,由两个相似正五边形的相似比是1:10,可知它们的面积为1:100.故选:C.点睛:此题主要考查了相似三角形的性质:相似三角形的面积比等于相似比的平方.3.如图所示,在△ABC中,∠C=90°,AB=8,CD是AB边上的中线,作CD的中垂线与CD交于点E,与BC交于点F.若CF=x,tanA=y,则x与y之间满足()A .2244x y +=B .2244x y -=C .2288x y -=D .2288x y+= 【答案】A【解析】【分析】由直角三角形斜边上的中线性质得出CD =12AB =AD =4,由等腰三角形的性质得出∠A =∠ACD ,得出tan ∠ACD =GE CE=tan A =y ,证明△CEG ∽△FEC ,得出GE CE CE FE =,得出y =2FE ,求出y 2=24FE ,得出24y=FE 2,再由勾股定理得出FE 2=CF 2﹣CE 2=x 2﹣4,即可得出答案.【详解】解:如图所示:∵在△ABC 中,∠C =90°,AB =8,CD 是AB 边上的中线,∴CD =12AB =AD =4, ∴∠A =∠ACD ,∵EF 垂直平分CD , ∴CE =12CD =2,∠CEF =∠CEG =90°, ∴tan ∠ACD =GE CE =tanA =y , ∵∠ACD+∠FCE =∠CFE+∠FCE =90°,∴∠ACD =∠FCE ,∴△CEG ∽△FEC , ∴GE CE =CE FE, ∴y =2FE, ∴y 2=24FE , ∴24y=FE 2, ∵FE 2=CF 2﹣CE 2=x 2﹣4, ∴24y=x 2﹣4, ∴24y+4=x 2,故选:A.【点睛】本题考查了解直角三角形、直角三角形斜边上的中线性质、等腰三角形的性质、相似三角形的判定与性质等知识;熟练掌握直角三角形的性质,证明三角形相似是解题的关键.4.如图,正方形OABC的边长为6,D为AB中点,OB交CD于点Q,Q是y=kx上一点,k的值是()A.4 B.8 C.16 D.24【答案】C【解析】【分析】延长根据相似三角形得到:1:2BQ OQ=,再过点Q作垂线,利用相似三角形的性质求出QF、OF,进而确定点Q的坐标,确定k的值.【详解】解:过点Q作QF OA⊥,垂足为F,OABCQ是正方形,6OA AB BC OC∴====,90ABC OAB DAE∠=∠=︒=∠,DQ是AB的中点,12BD AB ∴=, //BD OC Q , OCQ BDQ ∴∆∆∽,∴12BQ BD OQ OC ==, 又//QF AB Q ,OFQ OAB ∴∆∆∽,∴22213QF OF OQ AB OA OB ====+, 6AB =Q , 2643QF ∴=⨯=,2643OF =⨯=, (4,4)Q ∴,Q 点Q 在反比例函数的图象上,4416k ∴=⨯=,故选:C .【点睛】本题考查了待定系数法求反比例函数、相似三角形的性质和判定,利用相似三角形性质求出点Q 的坐标是解决问题的关键.5.如图,在△ABC 中,A ,B 两个顶点在x 轴的上方,点C 的坐标是(﹣1,0).以点C 为位似中心,在x 轴的下方作△ABC 的位似图形△A 'B 'C ,使得△A 'B 'C 的边长是△ABC 的边长的2倍.设点B 的横坐标是﹣3,则点B '的横坐标是( )A .2B .3C .4D .5【答案】B【解析】【分析】 作BD ⊥x 轴于D ,B′E ⊥x 轴于E ,根据位似图形的性质得到B′C =2BC ,再利用相似三角形的判定和性质计算即可.【详解】解:作BD ⊥x 轴于D ,B′E ⊥x 轴于E ,则BD∥B′E,由题意得CD=2,B′C=2BC,∵BD∥B′E,∴△BDC∽△B′EC,∴1'2 CD BCCE B C==,∴CE=4,则OE=CE−OC=3,∴点B'的横坐标是3,故选:B.【点睛】本题考查的是位似变换、相似三角形的判定和性质,掌握位似变换的概念是解题的关键.6.如图,正方形ABCD中,E、F分别为AB、BC的中点,AF与DE相交于点O,则AO DO=().A.13B25C.23D.12【答案】D【解析】【分析】由已知条件易证△ADE≌△BAF,从而进一步得△AOD∽△EAD.运用相似三角形的性质即可求解.【详解】∵四边形ABCD是正方形∴AE=BF,AD=AB,∠EAD=∠B=90︒∴△ADE≌△BAF∴∠ADE=∠BAF,∠AED=∠BFA∵∠DAO+∠FAB=90︒,∠FAB+∠BFA=90︒,∴∠DAO=∠BFA ,∴∠DAO=∠AED∴△AOD ∽△EAD ∴12AO AE DO AD == 故选:D 【点睛】 本题考查了正方形的性质,全等三角形的判定与性质,相似三角形的判定与性质.7.如图,在矩形ABCD 中,1AB =,在BC 上取一点E ,沿AE 将ABE ∆向上折叠,使B 点落在AD 上的F 点,若四边形EFDC 与矩形ABCD 相似,则AD 的长为( )A .2B 3C 15±D 15+ 【答案】D【解析】【分析】 可设AD=x ,由四边形EFDC 与矩形ABCD 相似,根据相似多边形对应边的比相等列出比例式,求解即可.【详解】解:∵1AB =, 设AD=x ,则FD=x-1,FE=1,∵四边形EFDC 与矩形ABCD 相似, ∴EF AD DF AB=,即111x x =-, 解得:1152x +=,2152x -=(不合题意,舍去) 经检验15x +=,是原方程的解. ∴15AD +=. 故选:D .【点睛】本题考查了翻折变换(折叠问题),相似多边形的性质,本题的关键是根据四边形EFDC 与矩形ABCD 相似得到比例式.8.如图,O是平行四边形ABCD的对角线交点,E为AB中点,DE交AC于点F,若平行四边形ABCD的面积为8,则DOE的面积是()A.2B.32C.1D.94【答案】C【解析】【分析】由平行四边形的面积,找到三角形底边和高与平行四边形底边和高的关系,利用面积公式以及线段间的关系求解.分别作△OED和△AOD的高,利用平行线的性质,得出高的关系,进而求解.【详解】解:如图,过A、E两点分别作AN⊥BD、EM⊥BD,垂足分别为M、N,则EM∥AN,∴EM:AN=BE:AB,∵E为AB中点,∴BE=12 AB,∴EM=12 AN,∵平行四边形ABCD的面积为8,∴2×12×AN×BD=8,∴AN×BD=8∴S△OED=12×OD×EM=12×12BD×12AN=18AN×BD=1.故选:C.【点睛】本题考查平行四边形的性质,综合了平行线分线段成比例以及面积公式.已知一个三角形的面积求另一个三角形的面积有以下几种做法:①面积比是边长比的平方比;②分别找到底和高的比.9.若△ABC ∽△DEF ,△ABC 与△DEF 的相似比为2︰3,则S △ABC ︰S △DEF 为( )A .2∶3B .4∶9C .2∶3 D .3∶2 【答案】B【解析】【分析】根据两相似三角形的面积比等于相似比的平方,所以224()39ABC DEF S S ==V V . 【详解】因为△ABC ∽△DEF ,所以△ABC 与△DEF 的面积比等于相似比的平方,所以S △ABC :S △DEF =(23)2=49,故选B . 【点睛】本题考查了相似三角形的性质,解题的关键是掌握:两个相似三角形面积比等于相似比的平方.10.如图,点E 为ABC ∆的内心,过点E 作MN BC P 交AB 于点M ,交AC 于点N ,若7AB =,5AC =,6BC =,则MN 的长为( )A .3.5B .4C .5D .5.5【答案】B【解析】【分析】 连接EB 、EC ,如图,利用三角形内心的性质得到∠1=∠2,利用平行线的性质得∠2=∠3,所以∠1=∠3,则BM=ME ,同理可得NC=NE ,接着证明△AMN ∽△ABC ,所以767MN BM -=,则BM=7-76MN①,同理可得CN=5-56MN②,把两式相加得到MN 的方程,然后解方程即可.【详解】连接EB 、EC ,如图,∵点E 为△ABC 的内心,∴EB 平分∠ABC ,EC 平分∠ACB ,∴∠1=∠2,∵MN∥BC,∴∠2=∠3,∴∠1=∠3,∴BM=ME,同理可得NC=NE,∵MN∥BC,∴△AMN∽△ABC,∴MN AMBC AB=,即767MN BM-=,则BM=7-76MN①,同理可得CN=5-56MN②,①+②得MN=12-2MN,∴MN=4.故选:B.【点睛】此题考查三角形的内切圆与内心,相似三角形的判定与性质,解题关键在于掌握与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.11.平面直角坐标系xOy中,点P(a,b)经过某种变换后得到的对应点为P′(12a+1,12b﹣1).已知A,B,C是不共线的三个点,它们经过这种变换后,得到的对应点分别为A′,B′,C′.若△ABC的面积为S1,△A′B′C′的面积为S2,则用等式表示S1与S2的关系为()A.S112=S2B.S114=S2C.S1=2S2D.S1=4S2【答案】D【解析】【分析】先根据点P及其对应点判断出变换的类型,再依据其性质可得答案.【详解】由点P(a,b)经过变换后得到的对应点为P′(12a+1,12b﹣1)知,此变换是以点(2,﹣2)为中心、2:1的位似变换,则△ABC的面积与△A′B′C′的面积比为4:1,∴S1=4S2,故选:D.【点睛】本题主要考查几何变换类型,解题的关键是根据对应点的坐标判断出其几何变换类型.12.如图,将图形用放大镜放大,应该属于( ).A.平移变换B.相似变换C.旋转变换D.对称变换【答案】B【解析】【分析】根据放大镜成像的特点,结合各变换的特点即可得出答案.【详解】解:根据相似图形的定义知,用放大镜将图形放大,属于图形的形状相同,大小不相同,所以属于相似变换.故选:B.【点睛】本题考查的是相似形的识别,关键要联系图形,根据相似图形的定义得出.13.如图,点E是矩形ABCD的边AD的中点,且BE⊥AC于点F,则下列结论中错误的是()A.AF=12 CFB.∠DCF=∠DFCC.图中与△AEF相似的三角形共有5个D.tan∠CAD3【答案】D【解析】【分析】由AE=12AD=12BC ,又AD ∥BC ,所以12AE AF BC FC ==,故A 正确,不符合题意; 过D 作DM ∥BE 交AC 于N ,得到四边形BMDE 是平行四边形,求出BM=DE=12BC ,得到CN=NF ,根据线段的垂直平分线的性质可得结论,故B 正确,不符合题意;根据相似三角形的判定即可求解,故C 正确,不符合题意;由△BAE ∽△ADC ,得到CD 与AD 的大小关系,根据正切函数可求tan ∠CAD 的值,故D 错误,符合题意.【详解】解:A 、∵AD ∥BC ,∴△AEF ∽△CBF , ∴AE BC =AF FC, ∵AE =12AD =12BC , ∴AF FC =12,故A 正确,不符合题意; B 、过D 作DM ∥BE 交AC 于N ,∵DE ∥BM ,BE ∥DM ,∴四边形BMDE 是平行四边形,∴BM =DE =12BC , ∴BM =CM ,∴CN =NF ,∵BE ⊥AC 于点F ,DM ∥BE ,∴DN ⊥CF ,∴DF =DC ,∴∠DCF =∠DFC ,故B 正确,不符合题意;C 、图中与△AEF 相似的三角形有△ACD ,△BAF ,△CBF ,△CAB ,△ABE 共有5个,故C 正确,不符合题意.D 、设AD =a ,AB =b 由△BAE ∽△ADC ,有b a =2a .∵tan ∠CAD =CD AD =b a =2,故D 错误,符合题意. 故选:D .【点睛】本题考查了相似三角形的判定和性质,矩形的性质,图形面积的计算,正确的作出辅助线是解题的关键.14.(2016山西省)宽与长的比是51-(约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:作正方形ABCD ,分别取AD 、BC 的中点E 、F ,连接EF :以点F 为圆心,以FD 为半径画弧,交BC 的延长线于点G ;作GH ⊥AD ,交AD 的延长线于点H ,则图中下列矩形是黄金矩形的是( )A .矩形ABFEB .矩形EFCDC .矩形EFGHD .矩形DCGH【答案】D【解析】【分析】 先根据正方形的性质以及勾股定理,求得DF 的长,再根据DF=GF 求得CG 的长,最后根据CG 与CD 的比值为黄金比,判断矩形DCGH 为黄金矩形.【详解】 解:设正方形的边长为2,则CD=2,CF=1在直角三角形DCF 中,22125DF +=5FG ∴=51CG ∴=512CG CD ∴= ∴矩形DCGH 为黄金矩形故选:D .【点睛】本题主要考查了黄金分割,解决问题的关键是掌握黄金矩形的概念.解题时注意,宽与长的比是512的矩形叫做黄金矩形,图中的矩形ABGH也为黄金矩形.15.如图,△ABC中,∠BAC=45°,∠ACB=30°,将△ABC绕点A顺时针旋转得到△AB1C1,当点C1、B1、C三点共线时,旋转角为α,连接BB1,交AC于点D.下列结论:①△AC1C 为等腰三角形;②△AB1D∽△BCD;③α=75°;④CA=CB1,其中正确的是()A.①③④B.①②④C.②③④D.①②③④【答案】B【解析】【分析】将△ABC绕点A顺时针旋转得到△AB1C1,得到△ABC≌△AB1C1,根据全等三角形的性质得到AC1=AC,于是得到△AC1C为等腰三角形;故①正确;根据等腰三角形的性质得到∠C1=∠ACC1=30°,由三角形的内角和得到∠C1AC=120°,得到∠B1AB=120°,根据等腰三角形的性质得到∠AB1B=30°=∠ACB,于是得到△AB1D∽△BCD;故②正确;由旋转角α=120°,故③错误;根据旋转的性质得到∠C1AB1=∠BAC=45°,推出∠B1AC=∠AB1C,于是得到CA=CB1;故④正确.【详解】解:∵将△ABC绕点A顺时针旋转得到△AB1C1,∴△ABC≌△AB1C1,∴AC1=AC,∴△AC1C为等腰三角形;故①正确;∴AC1=AC,∴∠C1=∠ACC1=30°,∴∠C1AC=120°,∴∠B1AB=120°,∵AB1=AB,∴∠AB1B=30°=∠ACB,∵∠ADB1=∠BDC,∴△AB1D∽△BCD;故②正确;∵旋转角为α,∴α=120°,故③错误;∵∠C1AB1=∠BAC=45°,∴∠B1AC=75°,∵∠AB1C1=∠BAC=105°,∴∠AB 1C =75°,∴∠B 1AC =∠AB 1C ,∴CA =CB 1;故④正确.故选:B .【点睛】本题考查了相似三角形的判定和性质,等腰三角形的判定和性质,旋转的性质,正确的识别图形是解题的关键.16.如图,网格中的两个三角形是位似图形,它们的位似中心是( )A .点AB .点BC .点CD .点D【答案】D【解析】【分析】 利用对应点的连线都经过同一点进行判断.【详解】如图,位似中心为点D .故选D .【点睛】本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.注意:两个图形必须是相似形;对应点的连线都经过同一点;对应边平行.17.如图,顶角为36o 的等腰三角形,其底边与腰之比等k ,这样的三角形称为黄金三角形,已知腰AB=1,ABC ∆为第一个黄金三角形,BCD ∆为第二个黄金三角形,CDE ∆为第三个黄金三角形以此类推,第2020个黄金三角形的周长()A .2018kB .2019kC .20182k k + D .2019(2)k k +【答案】D【解析】【分析】根据相似三角形对应角相等,对应边成比例,求出前几个三角形的周长,进而找出规律:第n 个黄金三角形的周长为k n-1(2+k ),从而得出答案.【详解】解:∵AB=AC=1,∴△ABC 的周长为2+k ;△BCD 的周长为k+k+k 2=k (2+k );△CDE 的周长为k 2+k 2+k 3=k 2(2+k );依此类推,第2020个黄金三角形的周长为k 2019(2+k ).故选:D .【点睛】此题考查黄金分割,相似三角形的性质,找出各个三角形周长之间的关系,得出规律是解题的关键.18.如图,已知一组平行线////a b c ,被直线m 、n 所截,交点分别为A 、B 、C 和D 、E 、F ,且 1.5AB =,2BC =, 1.8DE =,则EF =( )A .4.4B .4C .3.4D .2.4【答案】D【解析】【分析】 根据平行线等分线段定理列出比例式,然后代入求解即可.【详解】解:∵////a b c∴AB DEBC EF=即1.5 1.82EF=解得:EF=2.4故答案为D.【点睛】本题主要考查的是平行线分线段成比例定理,利用定理正确列出比例式是解答本题的关键.19.如图,点D是△ABC的边AB上的一点,过点D作BC的平行线交AC于点E,连接BE,过点D作BE的平行线交AC于点F,则下列结论错误的是()A.AD AEBD EC=B.AF DFAE BE=C.AE AFEC FE=D.DE AFBC FE=【答案】D【解析】【分析】由平行线分线段成比例和相似三角形的性质进行判断.【详解】∵DE//BC,∴AD AEBD EC=,故A正确;∵DF//BE,∴△ADF∽△ABF, ∴AF DFAE BE=,故B正确;∵DF//BE,∴AD AFBD FE=,∵AD AEBD EC=,∴AE AFEC FE=,故C正确;∵DE//BC,∴△ADE∽△ABC,∴DE ADBC AB=,∵DF//BE,∴AF ADAE AB=,∴DE AFBC AE=,故D错误.故选D.【点睛】本题考查平行线分线段成比例性质,相似三角形的性质,由平行线得出比例关系是关键.20.如图1,在Rt△ABC中,∠ACB=90°,点P以每秒1cm的速度从点A出发,沿折线AC -CB运动,到点B停止.过点P作PD⊥AB,垂足为D,PD的长y(cm)与点P的运动时间x(秒)的函数图象如图2所示.当点P运动5秒时,PD的长是()A .1.5cmB .1.2cmC .1.8cmD .2cm【答案】B【解析】【分析】【详解】 由图2知,点P 在AC 、CB 上的运动时间时间分别是3秒和4秒,∵点P 的运动速度是每秒1cm ,∴AC=3,BC=4.∵在Rt △ABC 中,∠ACB=90°,∴根据勾股定理得:AB=5.如图,过点C 作CH ⊥AB 于点H ,则易得△ABC ∽△ACH . ∴CH AC BC AB =,即AC BC 3412CH CH AB 55⋅⨯=⇒==. ∴如图,点E (3,125),F (7,0). 设直线EF 的解析式为y kx b =+,则 123k b {507k b=+=+, 解得:3k 5{21b 5=-=. ∴直线EF 的解析式为321y x 55=-+. ∴当x 5=时,()3216PD y 5 1.2cm 555==-⨯+==.故选B.。
(易错题精选)初中数学图形的相似知识点训练含答案

(易错题精选)初中数学图形的相似知识点训练含答案一、选择题1.如图,边长为4的等边ABC V 中,D 、E 分别为AB ,AC 的中点,则ADE V 的面积是( )A 3B .32C .334D .23【答案】A【解析】【分析】 由已知可得DE 是△ABC 的中位线,由此可得△ADE 和△ABC 相似,且相似比为1:2,再根据相似三角形的面积比等于相似比的平方,可求出△ABC 的面积.【详解】Q 等边ABC V 的边长为4,2ABC 3S 443∴==V Q 点D ,E 分别是ABC V 的边AB ,AC 的中点,DE ∴是ABC V 的中位线,DE //BC ∴,1DE BC 2=,1AD AB 2=,1AE AC 2=, 即AD AE DE 1AB AC BC 2===, ADE ∴V ∽ABC V ,相似比为12, 故ADE S V :ABC S 1=V :4, 即ADE ABC 11S S 43344==⨯=V V 故选A .【点睛】本题考查了等边三角形的性质、相似三角形的判定与性质、三角形中位线定理,解题的关键是熟练掌握等边三角形的面积公式、相似三角形的判定与性质及中位线定理.2.如图,AB 为O e 的直径,C 为O e 上一点,弦AD 平分BAC ∠,交弦BC 于点E ,4CD =,2DE =,则AE 的长为( )A .2B .4C .6D .8【答案】C【解析】【分析】 根据角平分线的定义得到∠CAD=∠BAD ,根据圆周角定理得到∠DCB=∠BAD ,证明△DCE ∽△DAC ,根据相似三角形的性质求出AD ,结合图形计算,得到答案.【详解】解:∵AD 平分∠BAC ,∴∠CAD=∠BAD ,由圆周角定理得,∠DCB=∠BAD ,∴∠CAD=∠DCB ,又∠D=∠D ,∴△DCE ∽△DAC , ∴DE DC DC DA =,即244AD=, 解得,AD=8,∴AE=AD -DE=8-2=6,故选:C .【点睛】本题考查的是相似三角形的判定和性质、圆周角定理,掌握相似三角形的判定定理和性质定理是解题的关键.3.若△ABC ∽△DEF ,△ABC 与△DEF 的相似比为2︰3,则S △ABC ︰S △DEF 为( )A .2∶3B .4∶9C 23D .3∶2 【答案】B【解析】【分析】 根据两相似三角形的面积比等于相似比的平方,所以224()39ABC DEF S S ==V V . 【详解】因为△ABC ∽△DEF ,所以△ABC 与△DEF 的面积比等于相似比的平方,所以S △ABC :S △DEF =(23)2=49,故选B . 【点睛】本题考查了相似三角形的性质,解题的关键是掌握:两个相似三角形面积比等于相似比的平方.4.如图,在平行四边形ABCD 中,点E 在边DC 上,DE :EC=3:1,连接AE 交BD 于点F ,则△DEF 的面积与△BAF 的面积之比为( )A .3:4B .9:16C .9:1D .3:1【答案】B【解析】【分析】 可证明△DFE ∽△BFA ,根据相似三角形的面积之比等于相似比的平方即可得出答案.【详解】∵四边形ABCD 为平行四边形,∴DC ∥AB ,∴△DFE ∽△BFA ,∵DE :EC=3:1,∴DE :DC=3:4,∴DE :AB=3:4,∴S △DFE :S △BFA =9:16.故选B .5.如图,已知////AB CD EF ,:3:5AD AF =,6BC =,CE 的长为( )A .2B .4C .3D .5【答案】B【解析】【分析】 根据平行线分线段成比例定理列出比例式,计算即可.【详解】∵AD :AF=3:5,∴AD :DF=3:2,∵AB ∥CD ∥EF ,∴AD BCDF CE=,即362CE=,解得,CE=4,故选B.【点睛】本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.6.如图所示,在正方形ABCD中,G为CD边中点,连接AG并延长交BC边的延长线于E 点,对角线BD交AG于F点.已知FG=2,则线段AE的长度为()A.6 B.8 C.10 D.12【答案】D【解析】分析:根据正方形的性质可得出AB∥CD,进而可得出△ABF∽△GDF,根据相似三角形的性质可得出AF ABGF GD==2,结合FG=2可求出AF、AG的长度,由CG∥AB、AB=2CG可得出CG为△EAB的中位线,再利用三角形中位线的性质可求出AE的长度,此题得解.详解:∵四边形ABCD为正方形,∴AB=CD,AB∥CD,∴∠ABF=∠GDF,∠BAF=∠DGF,∴△ABF∽△GDF,∴AF ABGF GD==2,∴AF=2GF=4,∴AG=6.∵CG∥AB,AB=2CG,∴CG为△EAB的中位线,∴AE=2AG=12.故选D.点睛:本题考查了相似三角形的判定与性质、正方形的性质以及三角形的中位线,利用相似三角形的性质求出AF的长度是解题的关键.7.如图,平行于BC的直线DE把△ABC分成面积相等的两部分,则的值为()A.1 B.C.D.【答案】C【解析】【分析】由平行于BC的直线DE把△ABC分成面积相等的两部分,可知△ADE与△ABC相似,且面积比为,则相似比为,的值为.【详解】∵DE∥BC,∴△ADE∽△ABC,∵DE把△ABC分成面积相等的两部分,∴S△ADE=S四边形DBCE,∴=,∴==,故选:C.【点睛】本题考查了相似三角形的判定,相似三角形的性质,面积比等于相似比的平方的逆用等.8.如图,正方形OABC的边长为6,D为AB中点,OB交CD于点Q,Q是y=kx上一点,k的值是()A.4 B.8 C.16 D.24【答案】C【解析】【分析】延长根据相似三角形得到:1:2BQ OQ =,再过点Q 作垂线,利用相似三角形的性质求出QF 、OF ,进而确定点Q 的坐标,确定k 的值.【详解】解:过点Q 作QF OA ⊥,垂足为F ,OABC Q 是正方形,6OA AB BC OC ∴====,90ABC OAB DAE ∠=∠=︒=∠,D Q 是AB 的中点,12BD AB ∴=, //BD OC Q ,OCQ BDQ ∴∆∆∽, ∴12BQ BD OQ OC ==, 又//QF AB Q ,OFQ OAB ∴∆∆∽, ∴22213QF OF OQ AB OA OB ====+, 6AB =Q , 2643QF ∴=⨯=,2643OF =⨯=, (4,4)Q ∴,Q 点Q 在反比例函数的图象上,4416k ∴=⨯=,故选:C .【点睛】本题考查了待定系数法求反比例函数、相似三角形的性质和判定,利用相似三角形性质求出点Q 的坐标是解决问题的关键.9.如图,在Rt △ABC 中,∠ACB=90°,CD ⊥AB 于点D ,如果AC=3,AB=6,那么AD 的值为( )A.32B.92C.33D.33【答案】A【解析】【分析】【详解】解:∵Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∴△ACD∽△ABC,∴AC:AB=AD:AC,∵AC=3,AB=6,∴AD=32.故选A.考点:相似三角形的判定与性质.10.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边40DE cm=,20EF cm=,测得边DF离地面的高度 1.5AC m=,8CD m=,则树高AB是()A.4米B.4.5米C.5米D.5.5米【答案】D【解析】【分析】利用直角三角形DEF和直角三角形BCD相似求得BC的长后加上小明的身高即可求得树高AB.【详解】解:∵∠DEF=∠BCD-90°∠D=∠D∴△ADEF∽△DCB∴BC DC EF DE=∴DE=40cm=0.4m,EF-20cm=0.2m,AC-1.5m,CD=8m∴80.20.4BC=解得:BC=4∴AB=AC+BC=1.5+4=5.5米故答案为:5.5.【点睛】本题考查了相似三角形的应用,解题的关键是从实际问题中整理出相似三角形的模型。
2022年九年级中考数学考点专题训练——专题五十八:图形的相似(含答案)

备战2022最新中考数学考点专题训练——专题五十八:图形的相似1.如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE 的比是()A.1:3 B.1:4 C.1:5 D.1:25 2.如图,点M在BC上,点N在AM上,CM=CN,AM BM,AN CM下列结论正确的是()A.△ABM∽△ACB B.△ANC∽△AMBC.△ANC∽△ACM D.△CMN∽△BCA3.如图,D是△ABC一边BC上一点,连接AD,使△ABC∽△DBA 的条件是()A.AC:BC=AD:BD B.AC:BC=AB:ADC.AB2=CD•BC D.AB2=BD•BC4.如图所示,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=CD,连接AE,AF,EF.给出下列结论:①∠BAE=30°,②△ABE∽△AEF,③AE⊥EF,④△ADF∽△ECF.其中正确的个数为()A.1B.2C.3D.45.如图,位似图形由三角板与其在灯光照射下的中心投影组成,已知灯到三角板的距离与灯到墙的距离的比为2∶5,且三角板的一边长为8 cm,则投影三角形的对应边长为()A.20 cmB.10 cmC.8 cmD.3.2cm6. 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AB=8,AD =3,BC=4,点P为AB边上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P 的个数是()A .1B .2C .3D .47. 如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O 为位似中心,相似比为13,把△ABO 缩小,则点A 的对应点A ′的坐标是()A .(-1,2)B .(-9,18)C .(-9,18)或(9,-18)D .(-1,2)或(1,-2)8.如图811-,已知等腰ABC ∆中,顶角︒=∠36A ,BD 为ABC ∠的平分线,则ACAD 的值等于()A 、21B 、215-C 、1D 、215+ 9.如图,在ABC ∆中,BC DE //,且分ABC ∆为面积相等的两部分,则BCDE :的值为():1B、2:1C、3:1D、1:2A、210.如果三角形的每条边都扩大为原来的5倍,那么三角形的每个角()A、都扩大为原来的5倍B、都扩大为原来的10倍C、都扩大为原来的25倍D、与原来相等11.有一个多边形的边长分别是4cm、5cm、6cm、4cm、5cm,和它相似的一个多边形最长边为8cm,那么这个多边形的周长是( )A.12cm B.18cm C. 32cm D. 48cm 12.如图,BE、CD相交于点O,且∠l=∠2,图中有几组相似三角形( )A.2组B.3组C. 5组D. 6组13.小红家的阳台上放置了一个晾衣架如图1,图2是晾衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点立于地面,经测量OE OF cm==,现将晾衣架完全稳OA OC cm==,34136AB CD cm==,51固张开,扣链E成一条线段,且32EF cm=.垂挂在衣架上的连衣裙总长度小于________cm时,连衣裙才不会拖到地面上.14.如图,在等边三角形ABC 中,D 为BC 边上一点,E 为AC 边上一点,且6AB =,2BD =,当CE =________时,ABD DCE ∽△△.15.顶角为36°的等腰三角形称为黄金三角形,如图,在△ABC 中,AB =AC =1,∠A =36°,BD 是三角形ABC 的角平分线,那么AD =.16. 在矩形ABCD 中,AB =6,BC =8.点P 在矩形ABCD 的内部,点E 在边BC 上,满足△PBE ∽△DBC.若△APD 是等腰三角形,则PE 的长为________.17. 如图,在△ABC 中,点D ,E ,F 分别在AB ,AC ,BC 上,DE ∥BC ,EF ∥AB.若AB =8,BD =3,BF =4,则FC 的长为________.18.如图,P 为正方形ABCD 内一点,将ABP ∆绕点B 顺时针方向旋转能与'CBP ∆重合,若3=PB ,则__________'=PP .19.如图,在等边△ABC 中,P 为BC 上一点,D 为AC 上一点,且∠APD=60°,BP=1,CD=32,则△ABC 的边长是。
初三数学图形的相似试题

初三数学图形的相似试题1.若,则= .【答案】.【解析】先用b表示出a,然后代入比例式进行计算即可得解;∵,∴.∴.【考点】比例的性质.2.如图,测得BD="120" m,DC="60" m,EC="50" m,则河宽AB为().A.120 m B.100 m C.75 m D.25 m【答案】B.【解析】根据题意易知:△ABD∽△ECD∴∴m.故选B.【考点】相似三角形的判定与性质.3.如图,在正方形ABCD中,E是BC上的一点,连结AE,作BF⊥AE,垂足为H,交CD于F,作CG∥AE,交BF于G.求证:(1)CG=BH,(2)FC2=BF·GF,(3)=.【答案】见解析【解析】证明:(1)∵BF⊥AE,CG∥AE,∴CG⊥BF.∵在正方形ABCD中,∠ABH+∠CBG=90°,∠CBG+∠BCG=90°,∠BAH+∠ABH=90°,∴∠BAH=∠CBG,∠ABH=∠BCG,AB=BC,∴△ABH≌△BCG,∴CG=BH;(2)∵∠BFC=∠CFG,∠BCF=∠CGF=90°,∴△CFG∽△BFC,∴=,即FC2=BF·GF;(3)由(2)可知,△BCG∽△BFC∴=,∴BC2=BG·BF,∵AB=BC,∴AB2=BG·BF,∴==即=.4.已知:如图9,在△ABC中,已知点D在BC上,联结AD,使得,DC=3且﹦1﹕2.(1)求AC的值;(2)若将△ADC沿着直线AD翻折,使点C落点E处,AE交边BC于点F,且AB∥DE,求的值.【答案】(1);(2).【解析】(1)根据等高的三角形的面积的比等于底边的比求出BD=2CD,然后求出BC,再根据两组角对应相等两三角形相似求出△ABC和△DAC相似,然后根据相似三角形对应边成比例可得AC:CD="BC:AC" ,代入数据计算即可得解;(2)根据翻折的性质可得∠E=∠C,DE=CD,再根据两直线平行,内错角相等可得∠B=∠EDF,然后求出∠EDF=∠CAD,再根据两组角对应相等两三角形相似求出△EFD和△ADC相似,根据相似三角形面积的比等于相似比的平方求解即可.试题解析:(1)∵﹦1﹕2∴CD:BD=1:2∵DC="3" ∴BD="6"在△ACD和△BCA中,∠CAD=∠B,∠C=∠C∴△ACD∽△BCA∴即∴.(2)∵翻折∴∠C=∠E,∠1=∠2,DE="DC=3"∵AB∥DE∴∠3=∠B∵∠1=∠B∴∠1=∠3∴△ACD∽△DEF∴.【考点】1.相似三角形的判定与性质;2.翻折变换(折叠问题).5.若x:y=6:5,则下列等式中不正确的是()A.B.C.D.【答案】D.【解析】∵x:y=6:5,∴设x=6k,y=5k,A.,故本选项错误;B.,故本选项错误;C.,故本选项错误;D.,故本选项正确.故选D.【考点】比例的性质.6.如图,直角三角形ABC中,∠ACB=90°,AB=10,BC=6,在线段AB上取一点D,作DF⊥AB交AC于点F.现将△ADF沿DF折叠,使点A落在线段DB上,对应点记为;AD的中点E的对应点记为.若∽,则AD=__________.【答案】.【解析】利用勾股定理列式求出AC,设AD=2x,得到AE=DE=DE1=A1E1=x,然后求出BE1,再利用相似三角形对应边成比例列式求出DF,然后利用勾股定理列式求出E1F,然后根据相似三角形对应边成比例列式求解得到x的值,从而可得AD的值.试题解析:∵∠ACB=90°,AB=10,BC=6,∴AC=,设AD=,∵点E为AD的中点,将△ADF沿DF折叠,点A对应点记为A1,点E的对应点为E1,∴AE=DE=DE1=A1E1=,∵DF⊥AB,∠ACB=90°,∠A=∠A,∴△ABC∽△AFD,∴=,即,解得DF=,在Rt△DE1F中,=,又∵BE1=AB﹣AE1=10﹣3x,△E1FA1∽△E1BF,∴,∴,即,解得,∴AD的长为.故答案为:.【考点】1.相似三角形的性质;2.坐标与图形性质;3.翻折变换(折叠问题).7.如图所示,图中的小方格都是边长为1的正方形,△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.(1)画出位似中心点O;(2)直接写出△ABC与△A′B′C′的位似比;(3)以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A′B′C′关于点O中心对称的△A″B″C″,并直接写出△A″B″C″各顶点的坐标.【答案】(1)作图见解析;(2)2:1 ;(3)(6,0),(3,-2),(4,-4),作图见解析.【解析】(1)对应点连线的交点即为位似中心点;(2)根据网格中的距离即可写出△ABC与△A′B'C'的位似比;(3)作出△A'B'C'关于点 O中心对称的△A″B″C″,根据平面直角坐标系中的位置写出△A″B″C″各顶点的坐标.试题解析:(1)图中点O为所求:(2)△ABC与△A'B'C'的位似比等于2:1 .(3)△A''B''C''为所求,A''(6,0);B''(3,-2); C''(4,-4).【考点】1.作图(位似和中心对称变换);2.平面直角坐标系和点的坐标.8.如图1,在Rt△ABC中,∠ACB=900,点P以每秒1cm的速度从点A出发,沿折线AC-CB运动,到点B停止。
(易错题精选)初中数学图形的相似知识点总复习含答案

(易错题精选)初中数学图形的相似知识点总复习含答案一、选择题1.如图,在平行四边形ABCD中,AC=4,BD=6,P是BD上的任一点,过点P作EF∥AC,与平行四边形的两条边分别交于点E、F,设BP=x,EF=y,则能反映y与x之间关系的图象是()A.B.C.D.【答案】C【解析】【分析】【详解】图象是函数关系的直观表现,因此须先求出函数关系式.分两段求:当P在BO上和P在OD上,分别求出两函数解析式,根据函数解析式的性质即可得出函数图象.解:设AC与BD交于O点,当P在BO上时,∵EF∥AC,∴EF BPAC BO=即43y x=,∴43y x =;当P 在OD 上时,有643DP EF y x DO AC -==即, ∴y=483x -+.故选C .2.如图,在Rt △ABC 中,∠ACB =90°,∠A =60°,AC =2,D 是AB 边上一个动点(不与点A 、B 重合),E 是BC 边上一点,且∠CDE =30°.设AD =x ,BE =y ,则下列图象中,能表示y 与x 的函数关系的图象大致是( )A .B .C .D .【答案】C【解析】【分析】根据题意可得出4,23,AB BC ==4,23,BD x CE y =-=然后判断△CDE ∽△CBD ,继而利用相似三角形的性质可得出y 与x 的关系式,结合选项即可得出答案.【详解】解:∵∠A =60°,AC =2,∴4,23,AB BC ==4,23,BD x CE y =-=-在△ACD 中,利用余弦定理可得CD 2=AC 2+AD 2﹣2AC •AD cos ∠A =4+x 2﹣2x ,故可得242CD x x =-+,又∵∠CDE =∠CBD =30°,∠ECD =∠DCB (同一个角),∴△CDE ∽△CBD ,即可得,CE CD CD CB= 即222342,2342yx x x x --+=-+ 故可得: 23343.y x x =-++ 即呈二次函数关系,且开口朝下. 故选C .【点睛】考查解直角三角形,相似三角形的判定与性质,掌握相似三角形的判定定理与性质定理是解题的关键.3.如图,点E 是ABCD Y 的边AD 上一点,2DE AE =,连接BE ,交AC 边于点F ,下列结论中错误的是( )A .3BC AE =B .4AC AF = C .3BF EF =D .2BC DE =【答案】D【解析】【分析】 由平行四边形的性质和相似三角形的性质分别判断即可.【详解】解:∵在ABCD Y 中,//AD BC ,AD BC =,∴AEF CBF V :V ,∴AE AF EF CB CF BF==, ∵2DE AE = ∴332BC DE AE ==,选项A 正确,选项D 错误, ∴133AF AE AE CF CB AE ===,即:3CF AF =, ∴4AC AF =,∴选项B 正确,∴133EF AE AE BF CB AE ===,即:3BF EF =, ∴选项C 正确,故选:D .【点睛】此题主要考查了平行四边形的性质以及相似三角形的判定与性质,能熟练利用相似三角形对应边成比例是解题关键.4.如图,已知在平面直角坐标系中,点O 是坐标原点,AOB V 是直角三角形,90AOB ∠=︒,2OB OA =,点B 在反比例函数2y x =上,若点A 在反比例函数k y x=上,则k 的值为( )A .12B .12-C .14D .14- 【答案】B【解析】【分析】通过添加辅助线构造出相似三角形,再根据相似三角形的性质可求得1,2x A x ⎛⎫- ⎪⎝⎭,然后由点的坐标即可求得答案.【详解】解:过点B 作BE x ⊥于点E ,过点A 作AF x ⊥于点F ,如图:∵点B 在反比例函数2y x=上∴设2,B x x ⎛⎫ ⎪⎝⎭∴OE x =,2BE x=∵90AOB ∠=︒ ∴90AOD BOD ∠+∠=︒∴90BOE AOF ∠+∠=︒∵BE x ⊥,AF x ⊥∴90BEO OFA ∠=∠=︒∴90OAF AOF ∠+∠=︒∴BOE OAF ∠=∠∴BOE OAF V V ∽∵2OB OA = ∴12OF AF OA BE OE BO === ∴121122OF BE x x =⋅=⋅=,11222x AF OE x =⋅=⋅= ∴1,2x A x ⎛⎫- ⎪⎝⎭∵点A 在反比例函数k y x=上 ∴12x k x=- ∴12k =-. 故选:B【点睛】本题考查了反比例函数与相似三角形的综合应用,点在函数图象上则点的坐标就满足函数解析式,结合已知条件能根据相似三角形的性质求得点A 的坐标是解决问题的关键.5.矩形ABCO 如图摆放,点B 在y 轴上,点C 在反比例函数y k x=(x >0)上,OA =2,AB =4,则k 的值为( )A.4 B.6 C.325D.425【答案】C【解析】【分析】根据矩形的性质得到∠A=∠AOC=90°,OC=AB,根据勾股定理得到OB22OA AB=+=5C作CD⊥x轴于D,根据相似三角形的性质得到CD85=,OD45=求得8545,)于是得到结论.【详解】解:∵四边形ABCO是矩形,∴∠A=∠AOC=90°,OC=AB,∵OA=2,AB=4,∴过C作CD⊥x轴于D,∴∠CDO=∠A=90°,∠COD+∠COB=∠COB+∠AOB=90°,∴∠COD=∠AOB,∴△AOB∽△DOC,∴OB AB OA OC CD OD==,∴25424CD OD==,∴CD855=,OD55=,∴C(455,855),∴k325 =,故选:C.【点睛】本题考查了反比例函数图象上点的坐标特征,反比例函数的性质,矩形的性质,相似三角形的判定和性质,正确的作出辅助线是解题的关键.6.如图,在正方形ABCD 中,3AB =,点M 在CD 的边上,且1DM =,AEM ∆与ADM ∆关于AM 所在直线对称,将ADM ∆按顺时针方向绕点A 旋转90°得到ABF ∆,连接EF ,则cos EFC ∠的值是 ( )A 171365B 61365C 71525D .617【答案】A【解析】【分析】 过点E 作//HG AD ,交AB 于H ,交CD 于G ,作EN BC ⊥于N ,首先证明AEH EMG V :V ,则有13EH AE MG EM == ,设MG x =,则3EH x =,1DG AH x ==+, 在Rt AEH V 中利用勾股定理求出x 的值,进而可求,,,EH BN CG EN 的长度,进而可求FN ,再利用勾股定理求出EF 的长度,最后利用cos FN EFC EF∠=即可求解. 【详解】 过点E 作//HG AD ,交AB 于H ,交CD 于G ,作EN BC ⊥于N ,则90AHG MGE ∠=∠=︒,∵四边形ABCD 是正方形,∴3,90AD AB ABC C D ==∠=∠=∠=︒ ,∴四边形AHGD,BHEN,ENCG 都是矩形.由折叠可得,90,3,1AEM D AE AD DM EM ∠=∠=︒====,90AEH MEG EMG MEG ∴∠+∠=∠+∠=︒ ,AEH EMG ∴∠=∠,AEH EMG ∴V :V ,13EH AE MG EM ∴== . 设MG x =,则3EH x =,1DG AH x ==+在Rt AEH V 中,222AH EH AE +=Q ,222(1)(3)3x x ∴++= ,解得45x =或1x =-(舍去), 125EH BN ∴==,65CG CD DG EN =-== . 1BF DM ==Q175FN BF BN ∴=+= . 在Rt EFN △ 中,由勾股定理得,2213EF EN FN =+= ,17cos 1365FN EFC EF ∴∠== . 故选:A .【点睛】 本题主要考查正方形,矩形的性质,相似三角形的判定及性质,勾股定理,锐角三角函数,能够作出辅助线是解题的关键.7.如图,点E 为ABC ∆的内心,过点E 作MN BC P 交AB 于点M ,交AC 于点N ,若7AB =,5AC =,6BC =,则MN 的长为( )A .3.5B .4C .5D .5.5【答案】B【解析】【分析】 连接EB 、EC ,如图,利用三角形内心的性质得到∠1=∠2,利用平行线的性质得∠2=∠3,所以∠1=∠3,则BM=ME ,同理可得NC=NE ,接着证明△AMN ∽△ABC ,所以767MN BM -=,则BM=7-76MN①,同理可得CN=5-56MN②,把两式相加得到MN 的方程,然后解方程即可.【详解】连接EB 、EC ,如图,∵点E 为△ABC 的内心,∴EB 平分∠ABC ,EC 平分∠ACB ,∴∠1=∠2,∵MN ∥BC ,∴∠2=∠3,∴∠1=∠3,∴BM=ME,同理可得NC=NE,∵MN∥BC,∴△AMN∽△ABC,∴MN AM BC AB=,即767MN BM-=,则BM=7-76MN①,同理可得CN=5-56MN②,①+②得MN=12-2MN,∴MN=4.故选:B.【点睛】此题考查三角形的内切圆与内心,相似三角形的判定与性质,解题关键在于掌握与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.8.如图,点A,B是双曲线18yx=图象上的两点,连接AB,线段AB经过点O,点C 为双曲线kyx=在第二象限的分支上一点,当ABCV满足AC BC=且:13:24AC AB=时,k的值为().A.2516-B.258-C.254-D.25-【答案】B【解析】【分析】如图作AE⊥x轴于E,CF⊥x轴于F.连接OC.首先证明△CFO∽△OEA,推出2()COFAOES OCS OA∆∆=,因为CA:AB=13:24,AO=OB,推出CA:OA=13:12,推出CO:OA=5:12,可得出2()COFAOES OCS OA∆∆==25144,因为S△AOE=9,可得S△COF=2516,再根据反比例函数的几何意义即可解决问题.【详解】解:如图作AE ⊥x 轴于E ,CF ⊥x 轴于F .连接OC .∵A 、B 关于原点对称,∴OA =OB ,∵AC =BC ,OA =OB ,∴OC ⊥AB ,∴∠CFO =∠COA =∠AEO =90°,∴∠COF +∠AOE =90°,∠AOE +∠EAO =90°,∴∠COF =∠OAE ,∴△CFO ∽△OEA , ∴2()COF AOE S OC S OA∆∆=, ∵CA :AB =13:24,AO =OB ,∴CA :OA =13:12,∴CO :OA =5:12, ∴2()COF AOE S OC S OA ∆∆==25144, ∵S △AOE =9,∴S △COF =2516, ∴||25216k =, ∵k <0, ∴258k =- 故选:B .【点睛】本题主要考查反比例函数图象上的点的特征、等腰三角形的性质、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,根据相似三角形解决问题,属于中考选择题中的压轴题.9.如图,已知////AB CD EF ,:3:5AD AF =,6BC =,CE 的长为( )A .2B .4C .3D .5【答案】B【解析】【分析】 根据平行线分线段成比例定理列出比例式,计算即可.【详解】∵AD :AF=3:5,∴AD :DF=3:2,∵AB ∥CD ∥EF , ∴AD BC DF CE =,即362CE=, 解得,CE=4,故选B .【点睛】 本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.10.如图,已知ABC ∆和ABD ∆都O e 是的内接三角形,AC 和BD 相交于点E ,则与ADE ∆的相似的三角形是( )A .BCE ∆B .ABC ∆ C .ABD ∆ D .ABE ∆【答案】A【解析】【分析】 根据同弧和等弧所对的圆周角相等, 则AB 弧所对的圆周角BCE BDA ∠=∠,CEB ∠和DEA ∠是对顶角,所以ADE BCE ∆∆∽.【详解】解:BCE BDA ∠=∠Q ,CEB DEA ∠=∠ADE BCE ∴∆∆∽,故选:A .【点睛】考查相似三角形的判定定理: 两角对应相等的两个三角形相似,关键就是牢记同弧所对的圆周角相等.11.如图,点D 是ABC V 的边BC 上一点,,2BAD C AC AD ∠=∠= ,如果ACD V 的面积为15,那么ABC V 的面积为( )A .20B .22.5C .25D .30 【答案】A【解析】【分析】先证明C ABD BA ∽△△,再根据相似比求出ABC V 的面积即可.【详解】∵,BAD C B B ∠=∠=∠∠∴C ABD BA ∽△△∵2AC AD =∴4S ABD S CBA =V V ∴43S ACD S CBA =V V ∵ACD V 的面积为15∴44152033S CBA S ACD ==⨯=VV 故答案为:A .【点睛】 本题考查了相似三角形的问题,掌握相似三角形的性质以及判定定理是解题的关键.12.如图,E 是矩形ABCD 中AD 边的中点,BE 交AC 于点,F ABF V 的面积为2,则四边形CDEF 的面积为()A .4B .5C .6D .7【答案】B【解析】【分析】设AEF S x =△,根据相似三角形的面积比等于相似比的平方,得出4BCF S x =V ,求出x 即可解答.【详解】解:∵AD ∥BC ,E 是矩形ABCD 中AD 边的中点,∴AEF ~CBF V V ,设AEF S x =△,那么4BCF S x =V ,∵2ABF S =V , ∴()1x 2422x +=+, 解得:x 1=, ∴325CDEF S x =+=四边形,故选:B.【点睛】此题主要考查相似三角形的相似比与面积比之间的关系,灵活运用关系是解题关键.13.如图,在ABC V 中,//,,30DE BC AF BC ADE ⊥∠=︒,2,33,DE BC BF ==则DF 的长为()A .4B .23C .33D .3【答案】D【解析】【分析】先利用相似三角形的相似比证明点D 是AB 的中点,再解直角三角形求得AB ,最后利用直角三角形斜边中线性质求出DF .【详解】解:∵//DE BC ,∴ADE ~ABC V V ,∵2DE BC =,∴点D 是AB 的中点,∵,30AF BC ADE ⊥∠=︒,33BF =,∴∠B =30°,∴AB 6cos30BF ==︒, ∴DF=3,故选:D . 【点睛】 此题主要考查相似三角形的判定与性质、解直角三角形和直角三角形斜边中线性质,熟练掌握性质的运用是解题关键.14.如图,△AOB 是直角三角形,∠AOB =90°,△AOB 的两边分别与函数12,y y x x=-=的图象交于B 、A 两点,则等于( )A 2B .12C .14D 3【答案】A【解析】【分析】过点A,B 作AC ⊥x 轴,BD ⊥x 轴,垂足分别为C,D.根据条件得到△ACO ∽△ODB.根据反比例函数比例系数k 的几何意义得出2()S OBD OB S AOC OA ∆=∆=121=12利用相似三角形面积比等于相似比的平方得出22OB OA = 【详解】 ∵∠AOB =90°,∴∠AOC +∠BOD =∠AOC +∠CAO =90°,∠CAO =∠BOD ,∴△ACO ∽△BDO , ∴2()S OBD OB S AOC OA ∆=∆ , ∵S △AOC =12 ×2=1,S △BOD =12×1=12, ∴2()OB OA =121=12 , ∴2OB OA =, 故选A .【点睛】此题考查了反比例函数图象上点的坐标特征和相似三角形的判定与性质,解题关键在于做辅助线,然后得到相似三角形再进行求解15.如图,△ABC 中,∠BAC =45°,∠ACB =30°,将△ABC 绕点A 顺时针旋转得到△AB 1C 1,当点C 1、B 1、C 三点共线时,旋转角为α,连接BB 1,交AC 于点D .下列结论:①△AC 1C 为等腰三角形;②△AB 1D ∽△BCD ;③α=75°;④CA =CB 1,其中正确的是( )A .①③④B .①②④C .②③④D .①②③④【答案】B【解析】【分析】 将△ABC 绕点A 顺时针旋转得到△AB 1C 1,得到△ABC ≌△AB 1C 1,根据全等三角形的性质得到AC 1=AC ,于是得到△AC 1C 为等腰三角形;故①正确;根据等腰三角形的性质得到∠C 1=∠ACC 1=30°,由三角形的内角和得到∠C 1AC=120°,得到∠B 1AB=120°,根据等腰三角形的性质得到∠AB 1B=30°=∠ACB ,于是得到△AB 1D ∽△BCD ;故②正确;由旋转角α=120°,故③错误;根据旋转的性质得到∠C 1AB 1=∠BAC=45°,推出∠B 1AC=∠AB 1C ,于是得到CA=CB 1;故④正确.【详解】解:∵将△ABC绕点A顺时针旋转得到△AB1C1,∴△ABC≌△AB1C1,∴AC1=AC,∴△AC1C为等腰三角形;故①正确;∴AC1=AC,∴∠C1=∠ACC1=30°,∴∠C1AC=120°,∴∠B1AB=120°,∵AB1=AB,∴∠AB1B=30°=∠ACB,∵∠ADB1=∠BDC,∴△AB1D∽△BCD;故②正确;∵旋转角为α,∴α=120°,故③错误;∵∠C1AB1=∠BAC=45°,∴∠B1AC=75°,∵∠AB1C1=∠BAC=105°,∴∠AB1C=75°,∴∠B1AC=∠AB1C,∴CA=CB1;故④正确.故选:B.【点睛】本题考查了相似三角形的判定和性质,等腰三角形的判定和性质,旋转的性质,正确的识别图形是解题的关键.16.如图,网格中的两个三角形是位似图形,它们的位似中心是()A.点A B.点B C.点C D.点D【答案】D【解析】【分析】利用对应点的连线都经过同一点进行判断.【详解】如图,位似中心为点D.故选D.【点睛】本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.注意:两个图形必须是相似形;对应点的连线都经过同一点;对应边平行.17.下列图形中,一定相似的是()A.两个正方形 B.两个菱形 C.两个直角三角形 D.两个等腰三角形【答案】A【解析】【分析】根据相似形的对应边成比例,对应角相等,结合正方形,菱形,直角三角形,等腰三角形的性质与特点对各选项分析判断后利用排除法.【详解】A、两个正方形角都是直角一定相等,四条边都相等一定成比例,所以一定相似,故本选项正确;B、两个菱形的对应边成比例,角不一定相等,所以不一定相似,故本选项错误;C、两个直角三角形的边不一定成比例,角不一定相等,所以不一定相似,故本选项错误;D、两个等腰三角形的边不一定成比例,角不一定相等,所以不一定相似,故本选项错误.故选A.【点睛】本题主要考查了相似图形的定义,比较简单,要从边与角两方面考虑.18.如图,点D在△ABC的边AC上,要判断△ADB与△ABC相似,添加一个条件,不正确的是()A .∠ABD=∠CB .∠ADB=∠ABC C .AB CB BD CD = D .AD AB AB AC= 【答案】C【解析】【分析】 由∠A 是公共角,利用有两角对应相等的三角形相似,即可得A 与B 正确;又由两组对应边的比相等且夹角对应相等的两个三角形相似,即可得D 正确,继而求得答案,注意排除法在解选择题中的应用.【详解】∵∠A 是公共角,∴当∠ABD=∠C 或∠ADB=∠ABC 时,△ADB ∽△ABC (有两角对应相等的三角形相似),故A 与B 正确,不符合题意要求;当AB :AD=AC :AB 时,△ADB ∽△ABC (两组对应边的比相等且夹角对应相等的两个三角形相似),故D 正确,不符合题意要求;AB :BD=CB :AC 时,∠A 不是夹角,故不能判定△ADB 与△ABC 相似,故C 错误,符合题意要求,故选C .19.如图,在四边形ABCD 中,,90,5,10AD BC ABC AB BC ∠=︒==P ,连接,AC BD ,以BD 为直径的圆交AC 于点E .若3DE =,则AD 的长为( )A .55B .45C .35D .25【答案】D【解析】【分析】先判断出△ABC 与△DBE 相似,求出BD ,最后用勾股定理即可得出结论.【详解】如图1,在Rt △ABC 中,AB=5,BC=10,∴AC=55,连接BE ,∵BD是圆的直径,∴∠BED=90°=∠CBA,∵∠BAC=∠EDB,∴△ABC∽△DEB,∴AB AC DE DB=,∴5355DB =,∴DB=35,在Rt△ABD中,AD=2225BD AB-=,故选:D.【点睛】此题考查勾股定理,相似三角形的判定和性质,正确作出辅助线是解题的关键.20.在Rt△ABC中,∠ACB=90°,CD是AB边上的高,则下列结论不正确的是()A.AC2=AD•AB B.CD2=AD•BD C.BC2=BD•AB D.CD•AD=AC•BC 【答案】D【解析】【分析】直接根据射影定理来分析、判断,结合三角形的面积公式问题即可解决.【详解】解:如图,∵∠ACB=90°,CD是AB边上的高,∴由射影定理得:AC2=AD•AB,BC2=BD•AB,CD2=AD•BD;∴CD BC AD AC=;∴CD•AC=AD•BC,∴A,B,C正确,D不正确.故选:D.【点睛】该题主要考查了射影定理及其应用问题;解题的关键是灵活运用射影定理来分析、判断、推理或解答.。
中考数学《图形的相似》专项练习题及答案

中考数学《图形的相似》专项练习题及答案一、单选题1.一块含30°角的直角三角板(如图),它的斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边的距离都是1cm,那么△DEF的周长是()A.5cm B.6cm C.(6-√3)cm D.(3+√3)cm2.如图,DE△BC,EF△AB,现得到下列结论:AEEC=BFFC,ADBF=ABBC,EFAB=DEBC,CECF=EABF其中正确的比例式的个数有()A.4个B.3个C.2个D.1个3.如图,△ABC与△ADE成位似图形,位似中心为点A,若AD:AB=1:3,则△ADE与△ABC面积之比为()A.1:2B.1:3C.1:9D.1:164.如图,△ABC中,三边互不相等,点P是AB上一点,有过点P的直线将△ABC切出一个小三角形与△ABC相似,这样的直线一共有()A.5条B.4条C.3条D.2条5.如图,已知△ABC和△EDC是以点C为位似中心的位似图形,且△ABC和△EDC的位似比为1:2,△ABC面积为2,则△EDC的面积是()A.2B.8C.16D.326.如图,△ADE△△ABC,若AD=2,BD=4,则△ADE与△ABC的相似比是()A.1:2B.1:3C.2:3D.3:27.如图,以A为位似中心,将△ADE放大2倍后,得位似图形△ABC,若s1表示△ADE的面积,s2表示四边形DBCE的面积,则s1:s2=()A.1︰2B.1︰3C.1︰4D.2︰38.如图,按如下方法,将△ABC的三边缩小到原来的12,任取一点O,连AO、BO、CO,并取它们的中点D、E、F得△DEF,则下列说法正确的是()①△ABC与△DEF是相似图形;②△ABC与△DEF的周长比为2:1;③△ABC与△DEF的面积比为4:1.A.①、②B.②、③C.①、③D.①、②、③9.如图,已知AB是半圆O的直径,弦AD,CB相交于点P,若∠DPB=45°,则S△CDP:S△ABP 的值()A.25B.23C.13D.1210.如图,AD△BE△CF,直线l1、l2这与三条平行线分别交于点A,B,C和点D,E,F.已知AB=1,BC=3,DE=2,则EF的长为()A.4B.5C.6D.811.一个三角形的三边长分别为3,4,5,另一个与它相似的三角形中有一条边长为6.则这个三角形的周长不可能是()A.725B.18C.48D.2412.如图,小正方形的边长为均为1,下列各图(图中小正方形的边长均为1)阴影部分所示的三角形中,与△ABC相似的三角形是()A.B.C.D.二、填空题13.勾股定理是一个基本的几何定理,有数百种证明方法.“青朱出入图”是我国古代数学家证明勾股定理的几何证明法.刘徽描述此图“勾自乘为朱方,股自乘为青方,令出入相补,各从其类,加就其余不动也,合成弦方之幂,开方除之,即弦也”.若图中BF=4,DF=2,则AE=.14.如图,矩形ABCD中,AB=3,BC=4,E是BC上一点,BE=1,AE与BD交于点F.则DF的长为.15.如图,点D在△ABC的边BC的延长线上,AD为△ABC的外角的平分线,AB=2BC,AC=3,CD=4,则AB的长为.16.如图,在△ABC中,△BAC=90°,AD△BC于D,BD=3,CD=12,则AD的长为17.在某一时刻,测得一根高为1m的竹竿的影长为2m,同时测得一栋高楼的影长为40m,这栋高楼的高度是m.18.如图,已知路灯离地面的高度AB为4.8m,身高为1.6m的小明站在D处的影长为2m,那么此时小明离电杆AB的距离BD为m.三、综合题19.如图,已知△BAC=90°,AD△BC于D,E是AC的中点,ED的延长线交AB的延长线于点F.求证:(1)△DFB△△AFD;(2)AB:AC=DF:AF.20.一次小组合作探究课上,小明将两个正方形按如图1所示的位置摆放(点E、A、D在同一条直线上).(1)发现BE与DG数量关系是,BE与DG的位置关系是.(2)将正方形AEFG绕点A按逆时针方向旋转(如图2),(1)中的结论还成立吗?若能,请给出证明;若不能,请说明理由.(3)把图1中的正方形分别改写成矩形AEFG和矩形ABCD,且AEAG=ABAD=23,AE=2,AB=4,将矩形AEFG绕点A按顺时针方向旋转(如图3),连接DE,BG.小组发现:在旋转过程中,DE2+BG2的值是定值,请直接写出这个定值.21.如图,已知点D在△ABC的外部,AD△BC,点E在边AB上,AB•AD=BC•AE.(1)求证:△BAC=△AED;(2)在边AC取一点F,如果△AFE=△D,求证:ADBC=AFAC.22.如图,在▱ABCD中,对角线AC,BD相交于点O,过点O作BD的垂线与边AD,BC分别交于点E,F,连接BE交AC于点K,连接DF。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九年级数学(下)自主学习达标检测
[图形的相似、相似三角形](时间60分钟 满分100分)
一、选择题(每题4分,共32分)
1.下列各种图形相似的是 ( )
A .(1)、(2)
B .(3)、(4)
C .(1)、(3)
D .(1)、(4)
2.下列图形相似的是 ( )
(1)放大镜下的图片与原来的图片;(2)幻灯的底片与投影在屏幕上的图象;(3)天空中两朵白云的照片;(4)卫星上拍摄的长城照片与相机拍摄的长城照片. A .4组 B .3组 C .2组 D .1组
3.下列说法不一定正确的是 ( )
A .所有的等边三角形都相似
B .有一个角是100°的等腰三角形相似
C .所有的正方形都相似
D .所有的矩形都相似 4.一根1.5米长的标杆直立在水平地面上,它在阳光下的影长为2.1米;此时一棵水杉树的影长为10.5米,这棵水杉树高为 ( ) A .7.5米 B .8米 C .14.7米 D .15.75米
5.两个相似三角形的周长比为4︰9,则面积比为 ( ) A .4︰9 B .8︰18 C .16︰81 D .2︰3
6.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下 ( ) A .小明的影子比小强的影子长 B .小明的影子比小强的影子短 C .小明的影子和小强的一样长 D .谁的影子长不确定 7.如图,能使△ACD ∽△BCA 全等的条件是( ) A .BC AB CD AC = B .CB CD AC ∙=2
C .CD
BD AC AB = D .BD AD CD ∙=2
8.如图所示的测量旗杆的方法,已知AB 是标杆,BC 表示AB 在太阳光下的影子,•叙述错误的是( )
A .可以利用在同一时刻,不同物体与其影长的比相等来计算旗杆的高
B .只需测量出标杆和旗杆的影长就可计算出旗杆的高
C .可以利用△ABC ∽△EDB ,来计算旗杆的高
D .需要测量出AB 、BC 和DB 的长,才能计算出旗杆 的高
二、填空题(每题4分,共32分)
9. 下列情形:①用眼睛看月亮和用望远镜看月亮,看到的图象是相似的图形;②用彩
笔在黑板上写上三个大字1、2、3,它们是相似图形;③用粉笔在黑板上写上“天”和用毛笔在纸上写上“天”,这两个字是相似图形;以上说法你认为正确的是 ,错误的是 .(填序号)
10. 若a , x ,b , y 成比例线段,则比例式为 ;若a =1,x =2,b =2.5
,则
(1)(2)(3)(4)B
C
D
A
第7题
E
D
C B
A
第8题
y = .
11.三角形三边之比为3︰5︰7,与它相似的三角形最长边为21cm ,那么与它相似的三
角形周长为 .
12.如图,∠ADC =∠ACB =90°,∠ACD =∠B ,AC =5,AB =6,则AD =____ __. 13.直线CD ∥EF ,若OC =3,CE =4,则
OD
OF
的值是 . 14.如图,AD ∥EF ∥BC ,则图的相似三角形共有_____对. 15.△ABC
2,△A'B'C '的两边为1和,若△ABC ∽△A'B'C',则△A'B'C'
的笫三边长为________.
16.两个相似三角形的面积之比为1∶5,小三角形的周长为4,则另一个三角形的周长
为___ __.
三、解答题(共36分)
17.在如图所附的格点图中画出两个相似的三角形.
18.两个相似三角形的一对对应边的长分别是35cm 和14cm ,它们的周长相差60cm ,
求这两个三角形的周长.
第12题
D
A 第14题
B
D A
E F
19.如图,△ABC 中,EF ∥BC ,FD ∥AB ,AE =18,BE =12,CD =14,求线段EF 的
长.
20.如图,有一路灯杆AB (底部B 不能直接到达),在灯光下,小明在点D 处测得自
己的影长DF =3m ,沿BD 方向到达点F 处再测得自己得影长FG =4m ,如果小明得身高为1.6m ,求路灯杆AB 的高度。
21.如图,点D 、E 分别在AC 、BC 上,如果测得CD =20m ,CE =40m ,AD =100m ,
BE =20m ,DE =45m ,求A 、B 两地间的距离。
A C
B D E F B D F
E
G
A
C
C
22.如图,零件的外径为16cm ,要求它的壁厚x ,需要先求出内径AB ,现用一个交叉钳
(AD 与BC 相等)去量,若测得O A ︰OD =OB ︰OC =3︰1,CD =5cm ,你能求零件的壁厚x 吗?
九年级数学(下)自主学习达标检测
一、填空题
1.A 2.C 3.D 4.A 5.C 6.D 7.B 8.B 二、选择题
9.①,②③ 10.a b
x y
,5 11.45 12.256 13.37 14.3 15. 16.三、解答题
17.图略. 18.100cm ,40cm . 19.21. 20.6.4cm . 21.135m . 22.0.5cm .。
