(完整版)反比例函数的图象与性质练习题
(完整word版)反比例函数的图象与性质练习题

反比例函数的图象与性质练习题一、填空题(每小题3分,共30分)1、近视眼镜的度数y (度)与镜片焦距x 成反比例.已知400度近视眼镜片的焦距为0.25米,则眼镜度数y 与镜片焦距x 之间的函数关系式是 .2、如果反比例函数xk y =的图象过点(2,-3),那么k = . 3、已知y 与x 成反比例,并且当x=2时,y=-1,则当y=3时,x 的值是 .4、已知y 与(2x+1)成反比例,且当x=1时,y=2,那么当x=0,y 的值是 .5、若点A (6,y 1)和B (5,y 2)在反比例函数x y 4-=的图象上,则y 1与y 2的大小关系是 . 6、已知函数xy 3=,当x <0时,函数图象在第 象限,y 随x 的增大而 . 7、若函数12)1(---=m m x m y 是反比例函数,则m 的值是 .8、直线y=-5x+b 与双曲线xy 2-=相交于 点P (-2,m ),则b= .9、如图1,点A 在反比例函数图象上,过点A 作AB 垂直于x 轴,垂足为B ,若S △AOB =2,则这个反比例函数的解析式为. 图 110、如图2,函数y=-kx(k≠0)与xy 4-=的图 象交于点A 、B ,过点A 作AC 垂直于y 轴,垂足为C ,则△BOC 的面积为 . 图 2二、选择题(每小题3分,共30分)1、如果反比例函数的图象经过点P (-2,-1),那么这个反比例函数的表达式为( )A 、x y 21=B 、x y 21-=C 、xy 2= D 、x y 2-= 2、已知y 与x 成反比例,当x=3时,y=4,那么当y=3时,x 的值等于( )A 、4B 、-4C 、3D 、-33、若点A (-1,y 1),B(2,y 2),C (3,y 3)都在反比例函数xy 5=的图象上,则下列关系式正确的是( ) A 、y 1<y 2<y 3 B 、y 2<y 1<y 3 C 、y 3<y 2<y 1 D 、y 1<y 3<y 24、反比例函数xm y 5-=的图象的两个分支分别在第二、四象限内,那么m 的取值范围是( ) A 、m <0 B 、m >0 C 、m <5 D 、m >55、已知反比例函数的图象经过点(1,2),则它的图象也一定经过( )A 、(-1,-2)B 、(-1,2)C 、(1,-2)D 、(-2,1)6、若一次函数b kx y +=与反比例函数x k y =的图象都经过点(-2,1),则b 的值是( ) A 、3 B 、-3 C 、5 D 、-57、若直线y=k 1x(k 1≠0)和双曲线xk y 2=(k 2≠0)在同一坐标系内的图象无交点,则k 1、k 2的关系是( ) A 、k 1与k 2异号 B 、k 1与k 2同号 C 、k 1与k 2互为倒数 D 、k 1与k 2的值相等8、已知点A 是反比例函数图象上一点,它到原点的距离为5,到x 轴的距离为3,若点A 在第二象限内,则这个反比例函数的表达式为( )A 、x y 12=B 、x y 12-=C 、x y 121=D 、xy 121-= 9、如果点P 为反比例函数x y 6=的图像上的一点,PQ 垂直于x 轴,垂足为Q ,那么 △POQ 的面积为( )A 、12B 、6C 、3D 、1.510、已知反比例函数xk y =(k≠0),当x >0时,y 随x 的增大而增大,那么一次函数y=kx-k 的图象经过( )A 、第一、第二、三象限B 、第一、二、三象限C 、第一、三、四象限D 、第二、三、四象限三、解答题1、(7分)如图3,点A是双曲线x k y =与直线y=-x-(k+1)在第二象限内的交点, AB⊥x 轴于B ,且S△ABO =23. (1)求这两个函数的解析式;(2)求直线与双曲线的两个交点A、C的坐标和△AOC 的面积.2、(7分)已知反比例函数xk y 2=和一次函数y=2x-1,其中一次函数的图象经过(a,b ),(a+1,b+k )两点.(1)求反比例函数的解析式;(2)如图4,已知点A 在第一象限,且同时在上述两个函数的图象上,求点A 的坐标;(3)利用(2)的结果,请问:在x 轴上是否存在点P ,使△AOP 为等腰三角形?若存在,把符合条件的P 点坐标都求出来;若不存在,请说明理由.。
第11章 11.2 反比例函数的图像和性质(解答题)

11.2 反比例函数的图像和性质(解答题)1.(2017•北京)如图,在平面直角坐标系xOy中,函数y=(x>0)的图象与直线y=x﹣2交于点A(3,m).(1)求k、m的值;(2)已知点P(n,n)(n>0),过点P作平行于x轴的直线,交直线y=x﹣2于点M,过点P作平行于y轴的直线,交函数y=(x>0)的图象于点N.①当n=1时,判断线段PM与PN的数量关系,并说明理由;②若PN≥PM,结合函数的图象,直接写出n的取值范围.2.(2017•宁波)如图,正比例函数y1=﹣3x的图象与反比例函数y2=的图象交于A、B两点.点C在x轴负半轴上,AC=AO,△ACO的面积为12.(1)求k的值;(2)根据图象,当y1>y2时,写出x的取值范围.3.(2017•成都)如图,在平面直角坐标系xOy中,已知正比例函数y=x的图象与反比例函数y=的图象交于A(a,﹣2),B两点.(1)求反比例函数的表达式和点B的坐标;(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连接PO,若△POC的面积为3,求点P的坐标.4.(2017•株洲)如图所示,Rt△PAB的直角顶点P(3,4)在函数y=(x>0)的图象上,顶点A、B在函数y=(x>0,0<t<k)的图象上,PA∥y轴,连接OP,OA,记△OPA 的面积为S△OPA,△PAB的面积为S△PAB,设w=S△OPA﹣S△PAB.①求k的值以及w关于t的表达式;②若用w max和w min分别表示函数w的最大值和最小值,令T=w max+a2﹣a,其中a为实数,求T min.5.(2017•绵阳)如图,设反比例函数的解析式为y=(k>0).(1)若该反比例函数与正比例函数y=2x的图象有一个交点的纵坐标为2,求k的值;(2)若该反比例函数与过点M(﹣2,0)的直线l:y=kx+b的图象交于A,B两点,如图所示,当△ABO的面积为时,求直线l的解析式.6.(2017•贵阳)如图,直线y=2x+6与反比例函数y=(k>0)的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB 于点N,连接BM.(1)求m的值和反比例函数的表达式;(2)直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?7.(2017•随州)如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数y=的图象于点B,AB=.(1)求反比例函数的解析式;(2)若P(x1,y1)、Q(x2,y2)是该反比例函数图象上的两点,且x1<x2时,y1>y2,指出点P、Q各位于哪个象限?并简要说明理由.8.(2017•常德)如图,已知反比例函数y=的图象经过点A(4,m),AB⊥x轴,且△AOB 的面积为2.(1)求k和m的值;(2)若点C(x,y)也在反比例函数y=的图象上,当﹣3≤x≤﹣1时,求函数值y的取值范围.9.(2017•安顺)已知反比例函数y1=的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2).(1)求这两个函数的表达式;(2)根据图象直接写出一次函数的值大于反比例函数的值的x的取值范围.10.(2017•巴彦淖尔)如图,反比例函数y=与一次函数y=k2x+b的图象交于A(2,4),B(﹣4,m)两点.(1)求k1,k2,b的值;(2)求△AOB的面积;(3)若M(x1,y1),N(x2,y2)是反比例函数y=的图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限.11.(2017•深圳)如图,一次函数y=kx+b与反比例函数y=(x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.(1)直接写出一次函数y=kx+b的表达式和反比例函数y=(x>0)的表达式;(2)求证:AD=BC.12.(2017•广元)如图,一次函数y=ax+b的图象与反比例函数y=的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=,OB=4,OE=2.(1)求一次函数的解析式和反比例函数的解析式;(2)求△OCD的面积;(3)根据图象直接写出一次函数的值大于反比例函数的值时,自变量x的取值范围.13.(2017•聊城)如图,分别位于反比例函数y=,y=在第一象限图象上的两点A、B,与原点O在同一直线上,且=.(1)求反比例函数y=的表达式;(2)过点A作x轴的平行线交y=的图象于点C,连接BC,求△ABC的面积.14.(2017•广安)如图,一次函数y=kx+b的图象与反比例函数y=的图象在第一象限交于点A(4,2),与y轴的负半轴交于点B,且OB=6,(1)求函数y=和y=kx+b的解析式.(2)已知直线AB与x轴相交于点C,在第一象限内,求反比例函数y=的图象上一点P,使得S△POC=9.15.(2017•巴中)如图,一次函数y=kx+b与反比例函数y=(x>0)的图象交于A(m,4),B(2,n)两点,与坐标轴分别交于M、N两点.(1)求一次函数的解析式;(2)根据图象直接写出kx+b﹣>0中x的取值范围;(3)求△AOB的面积.16.(2017•武汉)如图,直线y=2x+4与反比例函数y=的图象相交于A(﹣3,a)和B两点(1)求k的值;(2)直线y=m(m>0)与直线AB相交于点M,与反比例函数的图象相交于点N.若MN=4,求m的值;(3)直接写出不等式>x的解集.17.(2017•岳阳)如图,直线y=x+b与双曲线y=(k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.(1)求直线和双曲线的解析式;(2)点P在x轴上,且△BCP的面积等于2,求P点的坐标.18.(2017•常州)如图,已知一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=(x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.(1)求m的值;(2)若∠DBC=∠ABC,求一次函数y=kx+b的表达式.19.(2017•黄冈)已知:如图,一次函数y=﹣2x+1与反比例函数y=的图象有两个交点A (﹣1,m)和B,过点A作AE⊥x轴,垂足为点E;过点B作BD⊥y轴,垂足为点D,且点D的坐标为(0,﹣2),连接DE.(1)求k的值;(2)求四边形AEDB的面积.20.(2017•菏泽)如图,一次函数y=kx+b与反比例函数y=的图象在第一象限交于A、B 两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.(1)求一次函数和反比例函数的表达式;(2)求△AOB的面积.21.(2017•宜宾)如图,一次函数y=kx+b的图象与反比例函数y=的图象交于点A(﹣3,m+8),B(n,﹣6)两点.(1)求一次函数与反比例函数的解析式;(2)求△AOB的面积.22.(2017•吉林)如图,在平面直角坐标系中,直线AB与函数y=(x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=OC,且△ACD的面积是6,连接BC.(1)求m,k,n的值;(2)求△ABC的面积.23.(2017•柳州)如图,直线y=﹣x+2与反比例函数(k≠0)的图象交于A(﹣1,m),B(m,﹣1)两点,过A作AC⊥x轴于点C,过B作BD⊥x轴于点D,(1)求m,n的值及反比例函数的解析式;(2)请问:在直线y=﹣x+2上是否存在点P,使得S△PAC=S△PBD?若存在,求出点P的坐标;若不存在,请说明理由.24.(2017•襄阳)如图,直线y1=ax+b与双曲线y2=交于A、B两点,与x轴交于点C,点A的纵坐标为6,点B的坐标为(﹣3,﹣2).(1)求直线和双曲线的解析式;(2)求点C的坐标,并结合图象直接写出y1<0时x的取值范围.25.(2017•重庆)如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2,点A的纵坐标为4.(1)求该反比例函数和一次函数的解析式;(2)连接MC,求四边形MBOC的面积.26.(2017•湘西州)如图所示,一次函数y1=x+b(b为常数)的图象与反比例函数y2=的图象都经过点A(2,m).(1)求点A的坐标及一次函数的解析式;(2)根据图象直接回答:在第一象限内,当x取何值时y1<y2.27.(2017•六盘水)已知函数y=kx+b,y=,b、k为整数且|bk|=1.(1)讨论b,k的取值.(2)分别画出两种函数的所有图象.(不需列表)(3)求y=kx+b与y=的交点个数.28.(2017•资阳)如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=(m≠0,x<0)的图象交于点A(﹣3,1)和点C,与y轴交于点B,△AOB的面积是6.(1)求一次函数与反比例函数的解析式;(2)当x<0时,比较y1与y2的大小.29.(2017•百色)已知反比例函数y=(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.(1)求这个反比函数的解析式;(2)求△ACD的面积.30.(2017•攀枝花)如图,在平面直角坐标系中,坐标原点O是菱形ABCD的对称中心.边AB与x轴平行,点B(1,﹣2),反比例函数y=(k≠0)的图象经过A,C两点.(1)求点C的坐标及反比例函数的解析式.(2)直线BC与反比例函数图象的另一交点为E,求以O,C,E为顶点的三角形的面积.31.(2017•河南)如图,一次函数y=﹣x+b与反比例函数y=(x>0)的图象交于点A(m,3)和B(3,1).(1)填空:一次函数的解析式为,反比例函数的解析式为;(2)点P是线段AB上一点,过点P作PD⊥x轴于点D,连接OP,若△POD的面积为S,求S的取值范围.32.(2017•葫芦岛)如图,直线y=3x与双曲线y=(k≠0,且x>0)交于点A,点A的横坐标是1.(1)求点A的坐标及双曲线的解析式;(2)点B是双曲线上一点,且点B的纵坐标是1,连接OB,AB,求△AOB的面积.33.(2017•来宾)如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=(k≠0)的图象交于点A(﹣2,1),B(1,﹣2).(1)求一次函数和反比例函数的解析式;(2)观察图象,直接写出不等式ax+b≤的解集.34.(2017•山西)如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,其边长为2,点A,点C分别在x轴,y轴的正半轴上,函数y=2x的图象与CB交于点D,函数y=(k为常数,k≠0)的图象经过点D,与AB交于点E,与函数y=2x的图象在第三象限内交于点F,连接AF、EF.(1)求函数y=的表达式,并直接写出E、F两点的坐标;(2)求△AEF的面积.35.(2017•兰州)如图,在平面直角坐标系xOy中,直线y=﹣x+3交y轴于点A,交反比例函数y=(k<0)的图象于点D,y=(k<0)的图象过矩形OABC的顶点B,矩形OABC 的面积为4,连接OD.(1)求反比例函数y=的表达式;(2)求△AOD的面积.36.(2017•恩施州)如图,∠AOB=90°,反比例函数y=﹣(x<0)的图象过点A(﹣1,a),反比例函数y=(k>0,x>0)的图象过点B,且AB∥x轴.(1)求a和k的值;(2)过点B作MN∥OA,交x轴于点M,交y轴于点N,交双曲线y=于另一点C,求△OBC的面积.37.(2017•天水)如图所示,一次函数y=kx+b与反比例函数y=的图象交于A(2,4),B (﹣4,n)两点.(1)分别求出一次函数与反比例函数的表达式;(2)过点B作BC⊥x轴,垂足为点C,连接AC,求△ACB的面积.38.(2017•苏州)如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=(x >0)的图象经过点C,交AB于点D.已知AB=4,BC=.(1)若OA=4,求k的值;(2)连接OC,若BD=BC,求OC的长.39.(2017•东营)如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y=的图象在第一象限的交点为C,CD⊥x轴,垂足为D,若OB=3,OD=6,△AOB 的面积为3.(1)求一次函数与反比例函数的解析式;(2)直接写出当x>0时,kx+b﹣<0的解集.40.已知直线y=x上点C,过点C作CD∥y轴交x轴于点D,交双曲线y=于点B,过点C作NC∥x轴交y轴于点N,交双曲线y=于点E,若B是CD的中点,且四边形OBCE 的面积为.(1)求k的值;(2)若A(3,3),M是双曲线y=第一象限上的任一点,求证:|MC|﹣|MA|为常数6.(3)现在双曲线y=上选一处M建一座码头,向A(3,3),P(9,6)两地转运货物,经测算,从M到A,从M到P修建公路的费用都是每单位长度a万元,则码头M应建在何处,才能使修建两条公路的总费用最低?(提示:利用(2)的结论转化)参考答案与解析1.(2017•北京)如图,在平面直角坐标系xOy中,函数y=(x>0)的图象与直线y=x﹣2交于点A(3,m).(1)求k、m的值;(2)已知点P(n,n)(n>0),过点P作平行于x轴的直线,交直线y=x﹣2于点M,过点P作平行于y轴的直线,交函数y=(x>0)的图象于点N.①当n=1时,判断线段PM与PN的数量关系,并说明理由;②若PN≥PM,结合函数的图象,直接写出n的取值范围.【分析】(1)将A点代入y=x﹣2中即可求出m的值,然后将A的坐标代入反比例函数中即可求出k的值.(2)①当n=1时,分别求出M、N两点的坐标即可求出PM与PN的关系;②由题意可知:P的坐标为(n,n),由于PN≥PM,从而可知PN≥2,根据图象可求出n的范围.【解答】解:(1)将A(3,m)代入y=x﹣2,∴m=3﹣2=1,∴A(3,1),将A(3,1)代入y=,∴k=3×1=3,(2)①当n=1时,P(1,1),令y=1,代入y=x﹣2,x﹣2=1,∴x=3,∴M(3,1),∴PM=2,令x=1代入y=,∴y=3,∴N(1,3),∴PN=2∴PM=PN,②P(n,n),n>0点P在直线y=x上,过点P作平行于x轴的直线,交直线y=x﹣2于点M,M(n+2,n),∴PM=2,∵PN≥PM,即PN≥2,∵PN=|﹣n|,||≥2∴0<n≤1或n≥3【点评】本题考查反比例函数与一次函数的综合问题,解题的关键是求出反比例函数与一次函数的解析式,本题属于基础题型.2.(2017•宁波)如图,正比例函数y1=﹣3x的图象与反比例函数y2=的图象交于A、B两点.点C在x轴负半轴上,AC=AO,△ACO的面积为12.(1)求k的值;(2)根据图象,当y1>y2时,写出x的取值范围.【分析】(1)过点A作AD垂直于OC,由AC=AO,得到CD=DO,确定出三角形ADO与三角形ACD面积,即可求出k的值;(2)根据函数图象,找出满足题意x的范围即可.【解答】解:(1)如图,过点A作AD⊥OC,∵AC=AO,∴CD=DO,∴S△ADO=S△ACD=6,∴k=﹣12;(2)联立得:,解得:或,即A(﹣2,6),B(2,﹣6),根据图象得:当y1>y2时,x的范围为x<﹣2或0<x<2.【点评】此题考查了反比例函数与一次函数的交点问题,利用了数形结合的思想,熟练掌握各函数的性质是解本题的关键.3.(2017•成都)如图,在平面直角坐标系xOy中,已知正比例函数y=x的图象与反比例函数y=的图象交于A(a,﹣2),B两点.(1)求反比例函数的表达式和点B的坐标;(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连接PO,若△POC的面积为3,求点P的坐标.【分析】(1)把A(a,﹣2)代入y=x,可得A(﹣4,﹣2),把A(﹣4,﹣2)代入y=,可得反比例函数的表达式为y=,再根据点B与点A关于原点对称,即可得到B的坐标;(2)过P作PE⊥x轴于E,交AB于C,先设P(m,),则C(m,m),根据△POC 的面积为3,可得方程m×|m﹣|=3,求得m的值,即可得到点P的坐标.【解答】解:(1)把A(a,﹣2)代入y=x,可得a=﹣4,∴A(﹣4,﹣2),把A(﹣4,﹣2)代入y=,可得k=8,∴反比例函数的表达式为y=,∵点B与点A关于原点对称,∴B(4,2);(2)如图所示,过P作PE⊥x轴于E,交AB于C,设P(m,),则C(m,m),∵△POC的面积为3,∴m×|m﹣|=3,解得m=2或2,∴P(2,)或(2,4).【点评】本题主要考查了反比例函数与一次函数的交点问题,解题时注意:反比例函数与一次函数的图象的交点坐标满足两函数的解析式.4.(2017•株洲)如图所示,Rt△PAB的直角顶点P(3,4)在函数y=(x>0)的图象上,顶点A、B在函数y=(x>0,0<t<k)的图象上,PA∥y轴,连接OP,OA,记△OPA 的面积为S△OPA,△PAB的面积为S△PAB,设w=S△OPA﹣S△PAB.①求k的值以及w关于t的表达式;②若用w max和w min分别表示函数w的最大值和最小值,令T=w max+a2﹣a,其中a为实数,求T min.【分析】(1)由点P的坐标表示出点A、点B的坐标,从而得S△PAB=•PA•PB=(4﹣)(3﹣),再根据反比例系数k的几何意义知S△OPA=S△OPC﹣S△OAC=6﹣t,由w=S△OPA﹣S可得答案;△PAB(2)将(1)中所得解析式配方求得w max=,代入T=w max+a2﹣a配方即可得出答案.【解答】解:(1)∵点P(3,4),∴k=3×4=12,在y=中,当x=3时,y=,即点A(3,),当y=4时,x=,即点B(,4),则S△PAB=•PA•PB=(4﹣)(3﹣),如图,延长PA交x轴于点C,则PC⊥x轴,又S△OPA=S△OPC﹣S△OAC=×3×4﹣t=6﹣t,∴w=6﹣t﹣(4﹣)(3﹣)=﹣t2+t;(2)∵w=﹣t2+t=﹣(t﹣6)2+,∴w max=,则T=w max+a2﹣a=a2﹣a+=(a﹣)2+,∴当a=时,T min=.【点评】本题主要考查反比例函数系数k的几何意义及二次函数的性质,熟练掌握反比例系数k的几何意义及配方法求二次函数的最值是解题的关键.5.(2017•绵阳)如图,设反比例函数的解析式为y=(k>0).(1)若该反比例函数与正比例函数y=2x的图象有一个交点的纵坐标为2,求k的值;(2)若该反比例函数与过点M(﹣2,0)的直线l:y=kx+b的图象交于A,B两点,如图所示,当△ABO的面积为时,求直线l的解析式.【分析】(1)由题意可得A(1,2),利用待定系数法即可解决问题;(2)把M(﹣2,0)代入y=kx+b,可得b=2k,可得y=kx+2k,由消去y得到x2+2x﹣3=0,解得x=﹣3或1,推出B(﹣3,﹣k),A(1,3k),根据△ABO的面积为,可得•2•3k+•2•k=,解方程即可解决问题;【解答】解:(1)由题意A(1,2),把A(1,2)代入y=,得到3k=2,∴k=.(2)把M(﹣2,0)代入y=kx+b,可得b=2k,∴y=kx+2k,由消去y得到x2+2x﹣3=0,解得x=﹣3或1,∴B(﹣3,﹣k),A(1,3k),∵△ABO的面积为,∴•2•3k+•2•k=,解得k=,∴直线l的解析式为y=x+.【点评】本题考查一次函数与反比例函数图象的交点、待定系数法、二元一次方程组等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.6.(2017•贵阳)如图,直线y=2x+6与反比例函数y=(k>0)的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB 于点N,连接BM.(1)求m的值和反比例函数的表达式;(2)直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?【分析】(1)求出点A的坐标,利用待定系数法即可解决问题;(2)构建二次函数,利用二次函数的性质即可解决问题;【解答】解:(1)∵直线y=2x+6经过点A(1,m),∴m=2×1+6=8,∴A(1,8),∵反比例函数经过点A(1,8),∴8=,∴k=8,∴反比例函数的解析式为y=.(2)由题意,点M,N的坐标为M(,n),N(,n),∵0<n<6,∴<0,∴S△BMN=×(||+||)×n=×(﹣+)×n=﹣(n﹣3)2+,∴n=3时,△BMN的面积最大.【点评】本题考查反比例函数与一次函数的交点问题,解题的关键是灵活运用所学知识解决问题,学会构建二次函数,解决最值问题,属于中考常考题型.7.(2017•随州)如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数y=的图象于点B,AB=.(1)求反比例函数的解析式;(2)若P(x1,y1)、Q(x2,y2)是该反比例函数图象上的两点,且x1<x2时,y1>y2,指出点P、Q各位于哪个象限?并简要说明理由.【分析】(1)求出点B坐标即可解决问题;(2)结论:P在第二象限,Q在第四象限.利用反比例函数的性质即可解决问题;【解答】解:(1)由题意B(﹣2,),把B(﹣2,)代入y=中,得到k=﹣3,∴反比例函数的解析式为y=﹣.(2)结论:P在第二象限,Q在第四象限.理由:∵k=﹣3<0,∴反比例函数y在每个象限y随x的增大而增大,∵P(x1,y1)、Q(x2,y2)是该反比例函数图象上的两点,且x1<x2时,y1>y2,∴P、Q在不同的象限,∴P在第二象限,Q在第四象限.【点评】此题考查待定系数法、反比例函数的性质、坐标与图形的变化等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.8.(2017•常德)如图,已知反比例函数y=的图象经过点A(4,m),AB⊥x轴,且△AOB 的面积为2.(1)求k和m的值;(2)若点C(x,y)也在反比例函数y=的图象上,当﹣3≤x≤﹣1时,求函数值y的取值范围.【分析】(1)根据反比例函数系数k的几何意义先得到k的值,然后把点A的坐标代入反比例函数解析式,可求出k的值;(2)先分别求出x=﹣3和﹣1时y的值,再根据反比例函数的性质求解.【解答】解:(1)∵△AOB的面积为2,∴k=4,∴反比例函数解析式为y=,∵A(4,m),∴m==1;(2)∵当x=﹣3时,y=﹣;当x=﹣1时,y=﹣4,又∵反比例函数y=在x<0时,y随x的增大而减小,∴当﹣3≤x≤﹣1时,y的取值范围为﹣4≤y≤﹣.【点评】本题考查了反比例函数系数k的几何意义,反比例函数图象上点的坐标特征,点在图象上,点的横纵坐标满足图象的解析式;也考查了反比例函数的性质以及代数式的变形能力.9.(2017•安顺)已知反比例函数y1=的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2).(1)求这两个函数的表达式;(2)根据图象直接写出一次函数的值大于反比例函数的值的x的取值范围.【分析】(1)由A在反比例函数图象上,把A的坐标代入反比例解析式,即可得出反比例函数解析式,又B也在反比例函数图象上,把B的坐标代入确定出的反比例解析式即可确定出m的值,从而得到B的坐标,由待定系数法即可求出一次函数解析式;(2)根据题意,结合图象,找一次函数的图象在反比例函数图象上方的区域,易得答案.【解答】解:(1)∵A(1,4)在反比例函数图象上,∴把A(1,4)代入反比例函数y1=得:4=,解得k1=4,∴反比例函数解析式为y1=的,又B(m,﹣2)在反比例函数图象上,∴把B(m,﹣2)代入反比例函数解析式,解得m=﹣2,即B(﹣2,﹣2),把A(1,4)和B坐标(﹣2,﹣2)代入一次函数解析式y2=ax+b得:,解得:,∴一次函数解析式为y2=2x+2;(2)根据图象得:﹣2<x<0或x>1.【点评】此题主要考查了反比例函数和一次函数的图象性质及待定系数法求解析式,要掌握它们的性质才能灵活解题.10.(2017•巴彦淖尔)如图,反比例函数y=与一次函数y=k2x+b的图象交于A(2,4),B(﹣4,m)两点.(1)求k1,k2,b的值;(2)求△AOB的面积;(3)若M(x1,y1),N(x2,y2)是反比例函数y=的图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限.【分析】(1)利用待定系数法即可解决问题;(2)直线y=x+2,交y轴与D(0,2),可以根据S△AOB=S△BOD+S△AOD计算即可;(3)利用图象法解决问题即可;【解答】解:(1)∵y=与一次函数y=k2x+b的图象交于A(2,4),B(﹣4,m)两点∴k1=8,m=﹣2,∴B(﹣4,﹣2),则有解得,∴k1=8,k2=1,b=2;(2)∵直线y=x+2,交y轴与D(0,2),∴S△AOB=S△BOD+S△AOD=×2×6=6.(3)观察图象可知,点M在第三象限,点N在第四象限;【点评】本题考查反比例函数的性质、一次函数的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.11.(2017•深圳)如图,一次函数y=kx+b与反比例函数y=(x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.(1)直接写出一次函数y=kx+b的表达式和反比例函数y=(x>0)的表达式;(2)求证:AD=BC.【分析】(1)先确定出反比例函数的解析式,进而求出点B的坐标,最后用待定系数法求出直线AB的解析式;(2)由(1)知,直线AB的解析式,进而求出C,D坐标,构造直角三角形,利用勾股定理即可得出结论.【解答】解:(1)将点A(2,4)代入y=中,得,m=2×4=8,∴反比例函数的解析式为y=,将点B(a,1)代入y=中,得,a=8,∴B(8,1),将点A(2,4),B(8,1)代入y=kx+b中,得,,∴,∴一次函数解析式为y=﹣x+5;(2)∵直线AB的解析式为y=﹣x+5,∴C(10,0),D(0,5),如图,过点A作AE⊥y轴于E,过点B作BF⊥x轴于F,∴E(0,4),F(8,0),∴AE=2,DE=1,BF=1,CF=2,在Rt△ADE中,根据勾股定理得,AD==,在Rt△BCF中,根据勾股定理得,BC==,∴AD=BC.【点评】此题是反比例函数与一次函数交点坐标问题,主要考查了待定系数法,勾股定理,解(1)的关键是掌握待定系数法求函数的解析式,解(2)的关键是构造直角三角形.12.(2017•广元)如图,一次函数y=ax+b的图象与反比例函数y=的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=,OB=4,OE=2.(1)求一次函数的解析式和反比例函数的解析式;(2)求△OCD的面积;(3)根据图象直接写出一次函数的值大于反比例函数的值时,自变量x的取值范围.【分析】(1)根据已知条件求出A、B、C点坐标,用待定系数法求出直线AB和反比例函数的解析式;(2)联立一次函数的解析式和反比例的函数解析式可得交点D的坐标,从而根据三角形面积公式求解;(3)根据函数的图象和交点坐标即可求解.【解答】解:(1)∵OB=4,OE=2,∴BE=2+4=6.∵CE⊥x轴于点E,tan∠ABO===,∴OA=2,CE=3.∴点A的坐标为(0,2)、点B的坐标为C(4,0)、点C的坐标为(﹣2,3).∵一次函数y=ax+b的图象与x,y轴交于B,A两点,∴,解得.故直线AB的解析式为y=﹣x+2.∵反比例函数y=的图象过C,∴3=,∴k=﹣6.∴该反比例函数的解析式为y=﹣;(2)联立反比例函数的解析式和直线AB的解析式可得,可得交点D的坐标为(6,﹣1),则△BOD的面积=4×1÷2=2,△BOC的面积=4×3÷2=6,故△OCD的面积为2+6=8;(3)由图象得,一次函数的值大于反比例函数的值时x的取值范围:x<﹣2或0<x<6.【点评】本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.13.(2017•聊城)如图,分别位于反比例函数y=,y=在第一象限图象上的两点A、B,与原点O在同一直线上,且=.(1)求反比例函数y=的表达式;(2)过点A作x轴的平行线交y=的图象于点C,连接BC,求△ABC的面积.【分析】(1)作AE、BF分别垂直于x轴,垂足为E、F,根据△AOE∽△BOF,则设A的横坐标是m,则可利用m表示出A和B的坐标,利用待定系数法求得k的值;(2)根据AC∥x轴,则可利用m表示出C的坐标,利用三角形的面积公式求解.【解答】解:(1)作AE、BF分别垂直于x轴,垂足为E、F.∵△AOE∽△BOF,又=,∴===.由点A在函数y=的图象上,设A的坐标是(m,),∴==,==,∴OF=3m,BF=,即B的坐标是(3m,).又点B在y=的图象上,∴=,解得k=9,则反比例函数y=的表达式是y=;(2)由(1)可知,A(m,),B(3m,),又已知过A作x轴的平行线交y=的图象于点C.∴C的纵坐标是,把y=代入y=得x=9m,∴C的坐标是(9m,),∴AC=9m﹣m=8m.∴S△ABC=×8m×=8.【点评】本题考查了待定系数法确定函数关系式以及相似三角形的判定与性质,正确利用m 表示出个点的坐标是关键.14.(2017•广安)如图,一次函数y=kx+b的图象与反比例函数y=的图象在第一象限交于点A(4,2),与y轴的负半轴交于点B,且OB=6,(1)求函数y=和y=kx+b的解析式.(2)已知直线AB与x轴相交于点C,在第一象限内,求反比例函数y=的图象上一点P,使得S△POC=9.【分析】(1)把点A(4,2)代入反比例函数y=,可得反比例函数解析式,把点A(4,2),B(0,﹣6)代入一次函数y=kx+b,可得一次函数解析式;(2)根据C(3,0),可得CO=3,设P(a,),根据S△POC=9,可得×3×=9,解得a=,即可得到点P的坐标.【解答】解:(1)把点A(4,2)代入反比例函数y=,可得m=8,∴反比例函数解析式为y=,∵OB=6,∴B(0,﹣6),把点A(4,2),B(0,﹣6)代入一次函数y=kx+b,可得,解得,∴一次函数解析式为y=2x﹣6;(2)在y=2x﹣6中,令y=0,则x=3,即C(3,0),∴CO=3,设P(a,),则由S△POC=9,可得×3×=9,解得a=,∴P(,6).【点评】本题主要考查了反比例函数与一次函数交点问题,解题时注意:反比例函数与一次函数交点坐标同时满足两个函数解析式.15.(2017•巴中)如图,一次函数y=kx+b与反比例函数y=(x>0)的图象交于A(m,4),B(2,n)两点,与坐标轴分别交于M、N两点.(1)求一次函数的解析式;(2)根据图象直接写出kx+b﹣>0中x的取值范围;(3)求△AOB的面积.【分析】(1)将点A、点B的坐标分别代入解析式即可求出m、n的值,从而求出两点坐标;(2)由图直接解答;(3)将△AOB的面积转化为S△AON﹣S△BON的面积即可.【解答】解:(1)∵点A 在反比例函数y=上,∴=4,解得m=1,∴点A的坐标为(1,4),又∵点B也在反比例函数y=上,∴=n,解得n=2,∴点B的坐标为(2,2),又∵点A、B在y=kx+b的图象上,∴,解得,∴一次函数的解析式为y=﹣2x+6.(2)x的取值范围为1<x<2;(3)∵直线y=﹣2x+6与x轴的交点为N,∴点N的坐标为(3,0),S△AOB=S△AON﹣S△BON=×3×4﹣×3×2=3.【点评】本题考查了反比例函数与一次函数的交点问题,数形结合是解题的关键.16.(2017•武汉)如图,直线y=2x+4与反比例函数y=的图象相交于A(﹣3,a)和B两点(1)求k的值;(2)直线y=m(m>0)与直线AB相交于点M,与反比例函数的图象相交于点N.若MN=4,求m的值;(3)直接写出不等式>x的解集.【分析】(1)把点A(﹣3,a)代入y=2x+4与y=即可得到结论;(2)根据已知条件得到M(,m),N(,m),根据MN=4列方程即可得到结论;(3)根据>x得到>0解不等式组即可得到结论.【解答】(1)∵点A(﹣3,a)在y=2x+4与y=的图象上,∴2×(﹣3)+4=a,∴a=﹣2,∴k=(﹣3)×(﹣2)=6;(2)∵M在直线AB上,∴M(,m),N在反比例函数y=上,∴N(,m),∴MN=x N﹣x M=﹣=4或x M﹣x N=﹣=4,解得:∵m>0,∴m=2或m=6+4;(3)x<﹣1或5<x<6,方法1:x﹣5=m,则x=m+5,<m+5,反比例函数y=与一次函数y=m+5的交点是(﹣6,﹣1),(1,6),函数y=与函数y=x的交点是(﹣1,﹣1),(6,6),综上,原不等式的解集是:x<﹣1或5<x<6.方法:2:由>x得:﹣x>0,∴>0,∴<0,∴或,结合抛物线y=x2﹣5x﹣6的图象可知,由得,∴或,∴此时x<﹣1,由得,,∴,解得:5<x<6,综上,原不等式的解集是:x<﹣1或5<x<6.【点评】本题考查了反比例函数与一次函数的交点问题,求不等式组的解集,正确的理解题意是解题的关键17.(2017•岳阳)如图,直线y=x+b与双曲线y=(k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.(1)求直线和双曲线的解析式;(2)点P在x轴上,且△BCP的面积等于2,求P点的坐标.【分析】(1)把A(1,2)代入双曲线以及直线y=x+b,分别可得k,b的值;(2)先根据直线解析式得到BO=CO=1,再根据△BCP的面积等于2,即可得到P的坐标.【解答】解:(1)把A(1,2)代入双曲线y=,可得k=2,∴双曲线的解析式为y=;把A(1,2)代入直线y=x+b,可得b=1,∴直线的解析式为y=x+1;(2)设P点的坐标为(x,0),在y=x+1中,令y=0,则x=﹣1;令x=0,则y=1,∴B(﹣1,0),C(0,1),即BO=1=CO,∵△BCP的面积等于2,∴BP×CO=2,即|x﹣(﹣1)|×1=2,解得x=3或﹣5,∴P点的坐标为(3,0)或(﹣5,0).【点评】本题主要考查了反比例函数与一次函数交点问题,解题时注意:反比例函数与一次函数交点的坐标同时满足两个函数解析式.。
反比例函数的图像与性质训练卷

反比例函数的图像与性质训练卷一.选择题(共15小题)1.如图,正比例函数y=k1x与反比例函数y=的图象交于A(1,m)、B两点,当k1x ≤时,x的取值范围是()A.﹣1≤x<0或x≥1B.x≤﹣1或0<x≤1C.x≤﹣1或x≥1D.﹣1≤x<0或0<x≤12.已知反比例函数y=(k≠0)的图象经过点(﹣2,4),那么该反比例函数图象也一定经过点()A.(4,2)B.(1,8)C.(﹣1,8)D.(﹣1,﹣8)3.若点A(﹣2,y1),B(﹣1,y2)都在反比例函数y=的图象上,则y1,y2的大小关系是()A.y1<y2B.y1=y2C.y1>y2D.不能确定4.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则一次函数y=ax+b和反比例函数y=(c≠0)在同一直角坐标系中的图象可能是()A.B.C.D.5.如图,等边三角形OAB,点B在x轴正半轴上,S△OAB=4,若反比例函数y=(k ≠0)图象的一支经过点A,则k的值是()A.B.C.D.6.如图,矩形OABC与反比例函数y1=(k1是非零常数,x>0)的图象交于点M,N,与反比例函数y2=(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1﹣k2=()A.3B.﹣3C.D.7.如图,在平面直角坐标系中,点O为坐标原点,平行四边形OBAD的顶点B在反比例函数y=的图象上,顶点A在反比例函数y=的图象上,顶点D在x轴的负半轴上.若平行四边形OBAD的面积是5,则k的值是()A.2B.1C.﹣1D.﹣28.点(1,y1),(2,y2),(3,y3),(4,y4)在反比例函数y=图象上,则y1,y2,y3,y4中最小的是()A.y1B.y2C.y3D.y49.如图是同一直角坐标系中函数y1=2x和y2=的图象.观察图象可得不等式2x>的解集为()A.﹣1<x<1B.x<﹣1或x>1C.x<﹣1或0<x<1D.﹣1<x<0或x>110.若点A(x1,2),B(x2,﹣1),C(x3,4)都在反比例函数y=的图象上,则x1,x2,x3的大小关系是()A.x1<x2<x3B.x2<x3<x1C.x1<x3<x2D.x2<x1<x3 11.如图是反比例函数y=的图象,点A(x,y)是反比例函数图象上任意一点,过点A 作AB⊥x轴于点B,连接OA,则△AOB的面积是()A.1B.C.2D.12.反比例函数y=的图象分别位于()A.第一、第三象限B.第一、第四象限C.第二、第三象限D.第二、第四象限13.一次函数y=ax+1与反比例函数y=﹣在同一坐标系中的大致图象是()A.B.C.D.14.某市举行中学生党史知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)y与该校参加竞赛人数x的情况,其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上,则这四所学校在这次党史知识竞赛中成绩优秀人数最多的是()A.甲B.乙C.丙D.丁15.已知一次函数y=kx+b的图象如图所示,则y=﹣kx+b与y=的图象为()A.B.C.D.二.填空题(共8小题)16.如图,反比例函数y=的图象经过矩形ABCD对角线的交点E和点A,点B、C在x 轴上,△OCE的面积为6,则k=.17.如图,点P(x,y)在双曲线y=的图象上,P A⊥x轴,垂足为A,若S△AOP=2,则该反比例函数的解析式为.18.反比例函数y=的图象分布情况如图所示,则k的值可以是(写出一个符合条件的k值即可).19.根据物理学知识,在压力不变的情况下,某物体承受的压强p(Pa)是它的受力面积S (m2)的反比例函数,其函数图象如图所示.当S=0.25m2时,该物体承受的压强p的值为Pa.20.如图,△OMN是边长为10的等边三角形,反比例函数y=(x>0)的图象与边MN、OM分别交于点A、B(点B不与点M重合).若AB⊥OM于点B,则k的值为.21.在平面直角坐标系xOy中,若反比例函数y=的图象位于第二、四象限,则k的取值范围是.22.如图,正比例函数y=k1x和反比例函数y=图象相交于A、B两点,若点A的坐标是(3,2),则点B的坐标是.23.在反比例函数y=的图象的每一支曲线上,函数值y随自变量x的增大而增大,则m的取值范围是.三.解答题(共12小题)24.已知反比例函数y=(k为常数,k≠0)的图象经过点A(﹣2,).(1)求这个函数的解析式;(2)若点B(m+2,m)在这个函数的图象上,求m的值.25.如图,在平面直角坐标系中,一次函数y1=kx+b的图象与反比例函数y2=的图象交于A(4,1),B(﹣2,n)两点,与y轴交于点C.(1)求一次函数与反比例函数的解析式;(2)若点D在y轴上,且S△ABD=12,求点D的坐标;(3)当y1>y2时,自变量x的取值范围为.26.如图,一次函数y=﹣x+3的图象与反比例函数y=(x>0)的图象交于A(1,a),B两点,与x轴交于点C.(1)求反比例函数的解析式和点B的坐标;(2)根据图象,直接写出关于x的不等式﹣x+3<的解集;(3)若点P在x轴上,且S△APC=5,求点P的坐标.27.已知一次函数y=kx+b(k≠0)与反比例函数(m≠0)的图象交于A(2,3),B (﹣6,n)两点.(1)求一次函数和反比例函数的解析式;(2)求△AOB的面积.28.如图,一次函数y=x+5的图象与反比例函数的图象交于A、B两点,其中A(﹣1,a).(1)求k的值及点B的坐标;(2)请根据图象直接写出不等式的解集.29.如图,一次函数y=ax+1(a≠0)的图象与x轴交于点A,与反比例函数y=的图象在第一象限交于点B(1,3),过点B作BC⊥x轴于点C.(1)求一次函数和反比例函数的解析式.(2)求△ABC的面积.30.如图,在平面直角坐标系中,一次函数y=k1x+b(k1≠0)的图象与反比例函数y=(k2≠0)的图象相交于A(3,4),B(﹣4,m)两点.(1)求一次函数和反比例函数的解析式;(2)若点D在x轴上,位于原点右侧,且OA=OD,求△AOD的面积.31.如图,直线AB与反比例函数y=(k>0,x>0)的图象相交于点A和点C(3,2),与x轴的正半轴相交于点B.(1)求k的值;(2)连接OA,OC,若点C为线段AB的中点,求△AOC的面积.32.已知反比例函数y=(k≠0)的图象的一支如图所示,它经过点(3,﹣2).(1)求这个反比例函数的表达式,并补画该函数图象的另一支.(2)求当y≤5,且y≠0时自变量x的取值范围.33.如图,点A(m,4)在反比例函数y=(x>0)的图象上,点B在y轴上,OB=2,将线段AB向右下方平移,得到线段CD,此时点C落在反比例函数的图象上,点D落在x轴正半轴上,且OD=1.(1)点B的坐标为,点D的坐标为,点C的坐标为(用含m的式子表示);(2)求k的值和直线AC的表达式.34.如图,在平面直角坐标系xOy中,一次函数y=ax+b(a≠0)的图象与反比例函数y=(k≠0)的图象交于P、Q两点.点P(﹣4,3),点Q的纵坐标为﹣2.(1)求反比例函数与一次函数的表达式;(2)求△POQ的面积.35.如图,一次函数y=x+1与反比例函数y=的图象相交于A(m,2),B两点,分别连接OA,OB.(1)求这个反比例函数的表达式;(2)求△AOB的面积;(3)在平面内是否存在一点P,使以点O,B,A,P为顶点的四边形为平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.。
(完整版)反比例函数基础练习题及答案

反比例函数练习一一.选择题(共22小题)1.(2015春•泉州校级期中)下列函数中,y是x的反比例函数的为()A.y=2x+1 B.C.D.2y=x2.(2015春•兴化市校级期中)函数y=k是反比例函数,则k的值是()A.﹣1 B.2 C.±2 D.±3.(2015春•衡阳县期中)若y=(m﹣1)x|m|﹣2是反比例函数,则m的值为()A.m=2 B.m=﹣1 C.m=1 D.m=04.(2014•汕尾校级模拟)若y与x成反比例,x与z成反比例,则y是z的()A.正比例函数B.反比例函数C.一次函数D.不能确定5.(2014春•常州期末)反比例函数(m为常数)当x<0时,y随x的增大而增大,则m的取值范围是()A.m<0 B.C.D.m≥6.(2015•贺州)已知k1<0<k2,则函数y=和y=k2x﹣1的图象大致是()A.B. C.D.7.(2015•滦平县二模)在同一直角坐标系中,函数y=kx+k与y=(k≠0)的图象大致为()A.B.C.D.8.(2015•上海模拟)下列函数的图象中,与坐标轴没有公共点的是()A.B.y=2x+1 C.y=﹣x D.y=﹣x2+19.(2015•宝安区二模)若ab>0,则函数y=ax+b与函数在同一坐标系中的大致图象可能是()A.B.C.D.10.(2015•鱼峰区二模)若方程=x+1的解x0满足1<x0<2,则k可能是()A.1 B.2 C.3 D.611.(2012•颍泉区模拟)如图,有反比例函数y=,y=﹣的图象和一个圆,则图中阴影部分的面积是()第11题图第12题图A.πB.2πC.4πD.条件不足,无法求12.(2010•深圳)如图所示,点P(3a,a)是反比例函数y=(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为()A.y=B.y=C.y=D.y=13.(2014•随州)关于反比例函数y=的图象,下列说法正确的是()A.图象经过点(1,1)B.两个分支分布在第二、四象限C.两个分支关于x轴成轴对称D.当x<0时,y随x的增大而减小14.(2014•昆明)如图是反比例函数y=(k为常数,k≠0)的图象,则一次函数y=kx﹣k 的图象大致是()A.B.C.D.15.(2014•天水)已知函数y=的图象如图,以下结论:①m<0;②在每个分支上y随x的增大而增大;③若点A(﹣1,a)、点B(2,b)在图象上,则a<b;④若点P(x,y)在图象上,则点P1(﹣x,﹣y)也在图象上.其中正确的个数是()A.4个B.3个C.2个D.1个16.(2014•杭州)函数的自变量x满足≤x≤2时,函数值y满足≤y≤1,则这个函数可以是()A.y=B.y=C.y=D.y=17.(2014•阜新)反比例函数y=在每个象限内的函数值y随x的增大而增大,则m的取值范围是()A.m<0 B.m>0 C.m>﹣1 D.m<﹣118.(2015•凉山州)以正方形ABCD两条对角线的交点O为坐标原点,建立如图所示的平面直角坐标系,双曲线y=经过点D,则正方形ABCD的面积是()第18题图第19题图A.10 B.11 C.12 D.1319.(2015•眉山)如图,A、B是双曲线y=上的两点,过A点作AC⊥x轴,交OB于D 点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为()A.B.C.3 D.420.(2014•绥化)如图,过点O作直线与双曲线y=(k≠0)交于A、B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴上分别取点E、F,使点A、E、F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1、S2的数量关系是()第20题图第21题图A.S1=S2B.2S1=S2C.3S1=S2D.4S1=S2 21.(2014•抚顺)如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线y=(x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会()A.逐渐增大B.不变C.逐渐减小D.先增大后减小22.(2014•重庆)如图,反比例函数y=﹣在第二象限的图象上有两点A、B,它们的横坐标分别为﹣1,﹣3,直线AB与x轴交于点C,则△AOC的面积为()A.8 B.10 C.12 D.24二.填空题(共4小题)23.(2015•锦江区一模)已知y=(a﹣1)是反比例函数,则a=.24.(2014•江西模拟)已知反比例函数的解析式为y=,则最小整数k=.25.(2013•路北区二模)函数y=,当y≥﹣2时,x的取值范围是(可结合图象求解).26.(2014•贵阳)若反比例函数的图象在其每个象限内,y随x的增大而增大,则k的值可以是.(写出一个符合条件的值即可)三.解答题(共4小题)27.(2014春•东城区校级期中)已知反比例函数y=﹣(1)说出这个函数的比例系数;(2)求当x=﹣10时函数y的值;(3)求当y=6时自变量x的值.28.(2013春•汉阳区校级期中)已知函数y=(5m﹣3)x2﹣n+(n+m),(1)当m,n为何值时是一次函数?(2)当m,n为何值时,为正比例函数?(3)当m,n为何值时,为反比例函数?29.(2013•德宏州)如图,是反比例函数y=的图象的一支.根据给出的图象回答下列问题:(1)该函数的图象位于哪几个象限?请确定m的取值范围;(2)在这个函数图象的某一支上取点A(x1,y1)、B(x2,y2).如果y1<y2,那么x1与x2有怎样的大小关系?30.(2014•苏州)如图,已知函数y=(x>0)的图象经过点A、B,点A的坐标为(1,2),过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC、OD.(1)求△OCD的面积;(2)当BE=AC时,求CE的长.答案:一.选择题(共22小题)1.C 2.D 3.B 4.A 5.C 6.C 7.B 8.A 9.C 10.C 11.B 12.D 13.D 14.B 15.B 16.A 17.D 18.C 19.B20.B 21.C 22.C二.填空题(共4小题)23.-1 24.1 25.x≤-2或x>0 26.-1(答案不唯一)三.解答题(共4小题)27.28.29.30.。
反比例函数的图象与性质 能力提升专题训练 2021-2022学年湘教版九年级数学上册
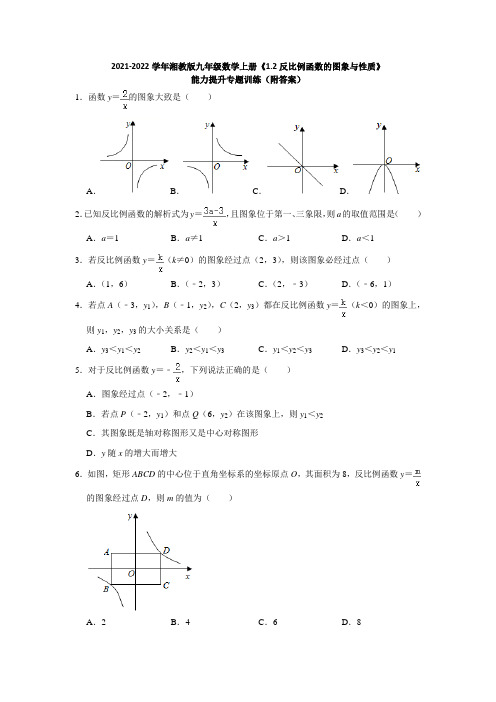
2021-2022学年湘教版九年级数学上册《1.2反比例函数的图象与性质》能力提升专题训练(附答案)1.函数y=的图象大致是()A.B.C.D.2.已知反比例函数的解析式为y=,且图象位于第一、三象限,则a的取值范围是()A.a=1B.a≠1C.a>1D.a<13.若反比例函数y=(k≠0)的图象经过点(2,3),则该图象必经过点()A.(1,6)B.(﹣2,3)C.(2,﹣3)D.(﹣6,1)4.若点A(﹣3,y1),B(﹣1,y2),C(2,y3)都在反比例函数y=(k<0)的图象上,则y1,y2,y3的大小关系是()A.y3<y1<y2B.y2<y1<y3C.y1<y2<y3D.y3<y2<y15.对于反比例函数y=﹣,下列说法正确的是()A.图象经过点(﹣2,﹣1)B.若点P(﹣2,y1)和点Q(6,y2)在该图象上,则y1<y2C.其图象既是轴对称图形又是中心对称图形D.y随x的增大而增大6.如图,矩形ABCD的中心位于直角坐标系的坐标原点O,其面积为8,反比例函数y=的图象经过点D,则m的值为()A.2B.4C.6D.87.如图,在△AOB中,S△AOB=2,AB∥x轴,点A在反比例函数y=的图象上,若点B 在反比例函数y=的图象上,则k的值为()A.﹣B.C.3D.﹣38.如图,A、B是曲线y=上的点,经过A、B两点向x轴、y轴作垂线段,若S阴影=1.5,则S1+S2=()A.4B.5C.6D.79.如图,正比例函数y1=k1x(k1<0)的图象与反比例函数y2=(k2<0)的图象相交于A,B两点,点B的横坐标为2,当y1>y2时,x的取值范围是()A.x<﹣2或x>2B.﹣2<x<0或x>2C.x<﹣2或0<x<2D.﹣2<x<0或0<x<210.如图,已知直线y=mx与双曲线y=的一个交点坐标为(3,4),则它们的另一个交点坐标是.11.如图是三个反比例函数的图象的分支,其中k1,k2,k3的大小关系是.12.如图,矩形ABCD的两边AD,AB的长分别为3,8,E是DC的中点,反比例函数y =(x<0)的图象经过点E,与AB交于点F,连接AE,若AF﹣AE=2,则k的值为.13.如图,在平面直角坐标系中,△ABC的边BC⊥y轴于点D,点B在双曲线y=(x<0)上,点C在双曲线y=(x>0)上,若△ABC的面积为9,OD=2AO,则k=.14.在平面直角坐标系中,A为反比例函数y=﹣(x>0)图象上一点,点B的坐标为(4,0),O为坐标原点,若△AOB的面积为6,则点A的坐标为.15.如图,点A是反比例函数y=(x<0)图象上一点,AC⊥x轴于点C且与反比例函数y=(x<0)的图象交于点B,AB=3BC,连接OA,OB.若△OAB的面积为6,则k1+k2=.16.如图,在平面直角坐标系中,直线AB经过点A(8,0)、B(0,6),反比例函数y=的图象与直线AB交于C、D两点,分别连接OC、OD.当△AOC、△COD、△DOB的面积都相等时,则k=.三.解答题(共4小题)17.已知图中的曲线是反比例函数y=(m为常数)图象的一支.(1)根据图象位置,求m的取值范围;(2)若该函数的图象任取一点A,过A点作x轴的垂线,垂足为B,当△OAB的面积为4时,求m的值.18.如图,一次函数y=kx+1的图象与反比例函数y=的图象交于点A、B,点A在第一象限,过点A作AC⊥x轴于点C,AD⊥y轴于点D,点B的纵坐标为﹣2,一次函数的图象分别交x轴、y轴于点E、F,连接DB、DE,已知S△ADF=4,AC=3OF.(1)求一次函数与反比例函数的解析式;(2)求△DBE的面积;(3)直接写出反比例函数的值大于一次函数的值的x的取值范围.19.如图,已知点A(2,4)、B(4,a)都在反比例函数y=的图象上.(1)求k和a的值;(2)以AB为一边在第一象限内作▱ABCD,若点C的横坐标为8,且▱ABCD的面积为10,求点D的坐标.20.如图,反比例函数y=(k>0)与长方形OABC在第一象限相交于D、E两点,OA=2,OC=4,连接OD、OE、DE.记△OAD、△OCE的面积分别为S1、S2.(1)填空:①点B坐标为;②S1S2(填“>”、“<”、“=”);(2)当S1+S2=2时,求:k的值及点D、E的坐标;试判断△ODE的形状,并求△ODE 的面积.参考答案1.解:∵y=,k=2,∴该函数的图象是位于第一、三象限的双曲线,故选:B.2.解:∵反比例函数的解析式为y=,且图象位于第一、三象限,∴3a﹣3>0,解得a>1,故选:C.3.解:∵反比例函数y=(k≠0)的图象经过点(2,3),∴k=2×3=6,A选项中(1,6),1×6=6.故选:A.4.解:∵反比例函数中k<0,∴函数图象的两个分支分别位于二、四象限,且在每一象限内y随x的增大而增大.∵﹣3<0,﹣1<0,∴点A(﹣3,y1),B(﹣1,y2)位于第二象限,∴y1>0,y2>0,∵﹣3<﹣1<0,∴0<y1<y2.∵2>0,∴点C(2,y3)位于第四象限,∴y3<0,∴y3<y1<y2.故选:A.5.解:∵k=﹣2,∴A.图象经过点(﹣2,﹣1)不合题意;B.y1=1,y2=﹣,故不合题意;C.图象既是轴对称图形又是中心对称图形,符合题意;D.在每一象限内,y随x的增大而增大,故不合题意.6.解:∵矩形的中心为直角坐标系的原点O,∴矩形ABCD的面积是8,设D(x,y),则4xy=8,xy=2,反比例函数的解析式为y=,∴m=2.故选:A.7.解:设AB与y轴交于C,∵A在反比例函数y=的图象上,AB∥x轴,∴OC•AC=1,∴S△AOC=OC•AC=,∵S△AOB=2,∴S△BOC=,∴BC•OC=,∴BC•OC=3,∵点B在反比例函数y=的图象上且B在第二象限,∴k=﹣3,故选:D.8.解:∵A、B是曲线y=上的点,经过A、B两点向x轴、y轴作垂线段,∴S1+S阴影=S2+S阴影=5,又∵S阴影=1.5,∴S1=S2=5﹣1.5=3.5,故选:D.9.解:由反比例函数与正比例函数相交于点A、B,可得点A坐标与点B坐标关于原点对称.故点A的横坐标为﹣2.当y1>y2时,即正比例函数图象在反比例图象上方,观察图象可得,当x<﹣2或0<x<2时满足题意.故选:C.10.解:因为直线y=mx过原点,双曲线y=的两个分支关于原点对称,所以其交点坐标关于原点对称,一个交点坐标为(3,4),另一个交点的坐标为(﹣3,﹣4).故答案是:(﹣3,﹣4).11.解:由图象可得,k1>0,k2<0,k3<0,∵点(﹣1,﹣)在y2=的图象上,点(﹣1,)在y3=的图象上,∴﹣<,∴k2>k3,由上可得,k1>k2>k3,故答案为:k1>k2>k3.12.解:矩形ABCD中,AD=3,AB=8,E为CD的中点,∴DE=CE=4,∴AE==5,∵AF﹣AE=2,∴AF=7,∴BF=1,设E点坐标为(a,4),则F点坐标为(a﹣3,1),∵E,F两点在反比例函数y=(x<0)的图象上,∴4a=a﹣3,解得a=﹣1,∴E(﹣1,4),∴k=﹣1×4=﹣4,故答案为﹣4.13.解:如图,连接OB、OC,∵点B在双曲线y=(x<0)上,且BC⊥y轴,∴S△OBD==4,又∵OD=2AO,∴S△OBA=S△OBD=2,∴S△ABD=6,∴S△ACD=S△ABC﹣S△ABD=9﹣6=3,由OD=2AO可知S△OCD=2S△AOC,∴S△BCD=S△ACD=×3=2,∵点C在双曲线y=(x>0)上,且BC⊥y轴,∴=2,∴|k|=4,由函数图象可知k<0,∴k=﹣4.故答案为﹣4.14.解:设点A的坐标为(﹣,a),∵点B的坐标为(4,0).若△AOB的面积为6,∴S△AOB=4×|a|=6,解得:a=±3,∵x>0∴点A的坐标为2,﹣3).故答案为:(2,﹣3).15.解:∵S△AOB=AB•OC=6,S△BOC=BC•OC,AB=3BC,∴S△BOC=2,∴S△AOC=2+6=8,又∵|k1|=8,|k2|=2,k1<0,k2<0,∴k1=﹣16,k2=﹣4,∴k1+k2=﹣16﹣4=﹣20,故答案为:﹣20.16.解:设直线AB的解析式为y=kx+b,∵直线AB过点A(8,0)、B(0,6),∴,解得:,∴直线AB的解析式为y=﹣x+6;过点C分别作x轴的垂线,垂足是点F,当△AOC、△COD、△DOB的面积都相等时,有S△AOC=S△AOB,即OA×CF=OA×OB,×8×CF=×8×6,解得:CF=2,即C点的纵坐标为2,把C点的纵坐标代入y=﹣x+6中,﹣x+6=2,解得:x=,∴C(,2),反比例函数y=的图象经过点C,∴k=×2=故答案为.17.解:(1)∵这个反比例函数的图象分布在第一、第三象限,∴m﹣5>0,解得m>5.(2)∵S△OAB=|k|,△OAB的面积为4,∴(m﹣5)=4,∴m=13.18.解:(1)对于y=kx+1,令x=0,则y=1,故点F(0,1),则OF=1,而AC=3OF=3,故点D(0,3),∵A的纵坐标为3,点A在反比例函数上,故点A(,3),S△ADF=×AD×DF=××(3﹣1)=4,解得m=12,故点A(4,3),反比例函数表达式为y=,将点B的纵坐标代入上式得,﹣2=,解得x=﹣6,故B(﹣6,﹣2),将点B的坐标代入y=kx+1得,﹣2=﹣6k+1,解得k=,故一次函数表达式为y=x+1;(2)对于y=x+1,令y=0,则x+1=0,解得x=﹣2,故点E(﹣2,0),△DBE的面积=S△DFB﹣S△DFE=×DF×(x E﹣x B)=×2×(﹣2+6)=4;(3)由(1)知,点A、B的坐标分别为(4,3)、(﹣6,﹣2),观察函数图象知,反比例函数的值大于一次函数的值的x的取值范围为:x<﹣6或0<x <4.19.解:(1)∵点A(2,4)在反比例函数y=的图象上,∴k=2×4=8,∵B(4,a)在反比例函数y=的图象上,∴a==2;(2)∵A(2,4),B(4,2),四边形ABCD是平行四边形,点C的横坐标为8,∴点D的横坐标为:8﹣(4﹣2)=6,设D(6,m),连接BD,过A作EF∥y轴,作DE⊥EF,BF⊥EF,如图所示:则E(2,m),F(2,2),∵▱ABCD的面积为10,∴S△ABD=×10=5,∵S梯形DEFB﹣S△DEA﹣S△AFB=S△ABD,或S梯形DEFB+S△DEA﹣S△AFB=S△ABD,∴(2+4)(m﹣2)﹣×4×(m﹣4)﹣×2×2=5,或(2+4)(m﹣2)+×4×(4﹣m)﹣×2×2=5,解得:m=5,∴点D的坐标为:(6,5).20.解:(1)①根据长方形OABC中,OA=2,OC=4,则点B坐标为(4,2),②∵反比例函数(k>0)与长方形OABC在第一象限相交于D、E两点,利用△OAD、△OCE的面积分别为S1=AD•AO,S2=•CO•EC,xy=k,得出,S1=AD•AO=k,S2=•CO•EC=k,∴S1=S2;(2)当S1+S2=2时,∵S1=S2,∴S1=S2=1=,∴k=2,∵S1=AD•AO=AD×2=1,∴AD=1,∵S2=•CO•EC=×4×EC=1,∴EC=,∵OA=2,OC=4,∴BD=4﹣1=3,BE=2﹣=,∴DO2=AO2+AD2=4+1=5,DE2=DB2+BE2=9+=,OE2=CO2+CE2=16+=,∴D的坐标为(1,2),E的坐标为(4,)∴DO2+DE2=OE2,∴△ODE是直角三角形,∵DO2=5,∴DO=,∵DE2=,∴DE=,∴△ODE的面积为:×DO×DE=××=,故答案为:(1)①(4,2);②=.。
中考数学总复习《反比例函数的性质》练习题及答案

中考数学总复习《反比例函数的性质》练习题及答案班级:___________姓名:___________考号:_____________一、单选题1.对于反比例函数y=2x,下列说法正确是()A.图象经过点(2,﹣1)B.图象位于第二、四象限C.图象是中心对称图形D.当x<0时,y随x的增大而增大2.对于反比例函数y=2x,下列说法不正确的是()A.当x<0时,y随x的增大而减小B.点(-2,-1)在它的图象上C.它的图象在第一、三象限D.当x>0时,y随x的增大而增大3.如图,过y轴上任意一点P,作x轴的平行线,分别与反比例函数y=4x和y=2x的图象交于A点和B点,若C为x轴上任意一点,连接AC,BC,则△ABC的面积为()A.3B.4C.5D.64.已知反比例函数y=k x的图象如图所示,则一次函数y=kx+k的图象经过()A.第一、二、三象限B.第二、三、四象限C.第一、二、四象限D.第一、三、四象限5.若点M(﹣3,a),N(4,﹣6)在同一个反比例函数的图象上,则a的值为()A.8B.﹣8C.﹣7D.56.函数y=1x+√x的图象在()A.第一象限B.第一、三象限C.第二象限D.第二、四象限7.图所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是A.当x=3时,EC<EM B.当y=9时,EC>EMC.当x增大时,EC·CF的值增大。
D.当y增大时,BE·DF的值不变。
8.已知函数y=−k 2+1x的图象经过点P1(x1,y1),P2(x2,y2),如果x2<0<x1,那么()A.0<y2<y1B.y1>0>y2C.y2<y1<0D.y1<0<y29.已知双曲线y=k−1x向右平移2个单位后经过点(4,1),则k的值等于()A.1B.2C.3D.510.对于反比例函数y=k x(k≠0),下列说法正确的是()A.当k>0时,y随x增大而增大B.当k<0时,y随x增大而增大C.当k>0时,该函数图象在二、四象限D.若点(1,2)在该函数图象上,则点(2,1)也必在该函数图象上11.下列关于反比例函数y=8x的描述,正确的是()A.它的图象经过点(12,4)B.图象的两支分别在第二、四象限C.当x>2时,0<y<4D.x>0时,y随x的增大而增大12.反比例函数y= 1x的图象的两个分支分别位于()象限.A.一、二B.一、三C.二、四D.一、四二、填空题13.如图,已知点A、B在双曲线y= k x(x>0)上,AC△x轴于点C,BD△y轴于点D,AC与BD 交于点P,P是AC的中点,若△ABP的面积为3,则k=.14.如图,矩形ABCD的顶点A和对称中心在反比例函数y=k x(k≠0,x>0)的图象上,若矩形ABCD的面积为16,则k的值为.15.已知反比例函数y= k x(k为常数,k≠0)的图象位于第一、第三象限,写出一个符合条件的k的值为.16.若反比例函数y=﹣mx的图象经过点(﹣3,﹣2),则当x<0时,y随x的增大而.17.若点(4,m)与点(5,n)都在反比例函数y=8x(x≠0)的图象上,则m n(填>,<或=).18.如图,A(1,1),B(2,2),双曲线y= k x与线段AB有公共点,则k的取值范围是。
人教版九年级数学第二十六章第1节《反比例函数的图象和性质》提升练习卷 (16)(含答案解析)

二、填空题
6.对于函数 ,当函数值 时,自变量 的取值范围是_________.
7.如图,已知双曲线 ( )经过 斜边 的中点 ,与直角边 相交于点 ,点 在 轴上.若 的面积为3,则 _________.
8.如图,在平面直角坐标系中,平行四边形OABC的顶点A在反比例函数 的图象上,顶点B在反比例函数 的图象上,点C在x轴的正半轴上,则□OABC的面积是__________
解得k=2.
本题考查了反比例函数中K的几何意义,过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值,即S= |k|,这是常考题型,解这类题一定要正确理解K的几何意义.
8.5-k
【解析】
由A、B点所在函数解析式可以写出A、B的坐标,再结合平行四边形的面积计算公式可以得到答案.
(1)利用图中条件,求该反比例函数和一次函数的表达式;
(2)看图,指出方程组 的解;
(3)观察图象,当 在什么范围时, < ?
24.已知正比例函数 与反比例函数 的图象交于A、B两点,点A的坐标为(2,1),点B的坐标为(n,-1)
(1)求正比例函数、反比例函数的表达式;
(2)求点B的坐标.
25.在平面直角坐标系 中,直线 : 与双曲线 相交于点 .
(1)求点 坐标及反比例函数的表达式;
(2)若直线 与 轴交于点 ,点 在反比例函数的图象上,当 的面积为1时,求点 的坐标.
26.如图,在平面直角坐标系xOy中,一次函数y=ax+b(a≠0)的图象与反比例函数 (k≠0,x>0)的图象相交于A(1,5),B(m,1)两点,与x轴,y轴分别交于点C,D,连接OA,OB.
解:由题意,可设A、B点的坐标分别为(m,y)、(n,y),则:
(完整版)反比例函数的图像和性质练习题

A.x<﹣1或0<x<3B.﹣1<x<0或x>3C.﹣1<x<0D.x>3
10、如图,点P是x轴正半轴上一个动点,过点P作x轴的垂线PQ交双曲线y= 于点Q,连结OQ,点P沿x轴正方向运动时,Rt△QOP的面积( ).
A、逐渐增大 B、逐渐减小 C、保持不变 D、无法确定
(第10题图) (第11题图) (第12题图)
(3)当气球内的气压大于144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于多少立方米?
24、如图, 已知反比例函数y= 的图象与一次函数y=ax+b的图象交于M(2,m)和N(-1,-4)两点.
(1)求这两个函数的解析式;
(2)求△MON的面积;
(3)请判断点P(4,1)是否在这个反比例函数的图象上,
反比例函数的图像和性质练习题
一、选择题
1.下列函数中,y与x成反比例函数是( )
A、 B、 C、 D、
2.反比例函数 的图象两支分布在第二、四象限,则k取值范围为( )
A.k<2B.k>2C. D.
3.如果双曲线y= 经过点(-2,3),那么此双曲线也经过点( )
A.(-2,-3)B.(3,2)C.(3,-2)D.(-3,-2)
7.一次函数 与反比例函数 在同一坐标系中的图像大致是( )
(第6题图) (第7题图)
8.面积为2的△ABC,一边长为x,这边上的高为y,则y与x的变化规律用图象表示大致是()
(第8题图) (第9题图)
9、已知一次函数y1=kx+b与反比例函数y2= 在同一直角坐标系中的图象如图所示,则当y1<y2时,x的取值范围是()
19、如图,点A是反比例函数 图象上一点,AB⊥y轴于点B, 那么△AOB的面积是。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反比例函数的图象与性质练习题
一、填空题(每小题3分,共30分)
1、近视眼镜的度数y (度)与镜片焦距x 成反比例.已知400度近视眼镜片的焦距为0.25米,则眼镜度数y 与镜片焦距x 之间的函数关系式是 .
2、如果反比例函数x
k y =的图象过点(2,-3),那么k = . 3、已知y 与x 成反比例,并且当x=2时,y=-1,则当y=3时,x 的值是 .
4、已知y 与(2x+1)成反比例,且当x=1时,y=2,那么当x=0,y 的值是 .
5、若点A (6,y 1)和B (5,y 2)在反比例函数x y 4-
=的图象上,则y 1与y 2的大小关系是 . 6、已知函数x
y 3=,当x <0时,函数图象在第 象限,y 随x 的增大而 . 7、若函数12)1(---=m m x m y 是反比例函数,则m 的值是 .
8、直线y=-5x+b 与双曲线x
y 2-=相交于 点P (-2,m ),则b= .
9、如图1,点A 在反比例函数图象上,
过点A 作AB 垂直于x 轴,垂足为B ,
若S △AOB =2,则这个反比例函数的解析式为
. 图 1
10、如图2,函数y=-kx(k≠0)与x
y 4-=的图 象交于点A 、B ,过点A 作AC 垂直于y 轴,垂
足为C ,则△BOC 的面积为 . 图 2
二、选择题(每小题3分,共30分)
1、如果反比例函数的图象经过点P (-2,-1),那么这个反比例函数的表达式为( )
A 、x y 21=
B 、x y 21-=
C 、x
y 2= D 、x y 2-= 2、已知y 与x 成反比例,当x=3时,y=4,那么当y=3时,x 的值等于( )
A 、4
B 、-4
C 、3
D 、-3
3、若点A (-1,y 1),B(2,y 2),C (3,y 3)都在反比例函数x
y 5=的图象上,则下列关系式正确的是( ) A 、y 1<y 2<y 3 B 、y 2<y 1<y 3 C 、y 3<y 2<y 1 D 、y 1<y 3<y 2
4、反比例函数x
m y 5-=的图象的两个分支分别在第二、四象限内,那么m 的取值范围是( ) A 、m <0 B 、m >0 C 、m <5 D 、m >5
5、已知反比例函数的图象经过点(1,2),则它的图象也一定经过( )
A 、(-1,-2)
B 、(-1,2)
C 、(1,-2)
D 、(-2,1)
6、若一次函数b kx y +=与反比例函数x k y =的图象都经过点(-2,1),则b 的值是( ) A 、3 B 、-3 C 、5 D 、-5
7、若直线y=k 1x(k 1≠0)和双曲线x
k y 2=(k 2≠0)在同一坐标系内的图象无交点,则k 1、k 2的关系是( ) A 、k 1与k 2异号 B 、k 1与k 2同号 C 、k 1与k 2互为倒数 D 、k 1与k 2的值相等
8、已知点A 是反比例函数图象上一点,它到原点的距离为5,到x 轴的距离为3,若点A 在第二象限内,则这个反比例函数的表达式为( )
A 、x y 12=
B 、x y 12-=
C 、x y 121=
D 、x
y 121-= 9、如果点P 为反比例函数x y 6=的图像上的一点,PQ 垂直于x 轴,垂足为Q ,那么 △POQ 的面积为( )
A 、12
B 、6
C 、3
D 、1.5
10、已知反比例函数x
k y =(k≠0),当x >0时,y 随x 的增大而增大,那么一次函数y=kx-k 的图象经过( )
A 、第一、第二、三象限
B 、第一、二、三象限
C 、第一、三、四象限
D 、第二、三、四象限
三、解答题
1、(7分)如图3,点A是双曲线x k y =
与直线y=-x-(k+1)在第二象限内的交点, AB⊥x 轴于B ,且S△ABO =2
3. (1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A、C的坐标
和△AOC 的面积.
2、(7分)已知反比例函数x
k y 2=和一次函数y=2x-1,其中一次函数的图象经过(a,b ),(a+1,b+k )两点.
(1)求反比例函数的解析式;
(2)如图4,已知点A 在第一象限,且同时在上述两个函数的图象上,求点A 的坐标;
(3)利用(2)的结果,请问:在x 轴上是否存在点P ,使△AOP 为等腰三角形?若存在,把符合条件
的P 点坐标都求出来;若不存在,请说明理由.。
