2020年深国交G1入学考试数学复习资料： 圆的综合计算与证明(含答案)
2020年最新深圳国际交流学院G1入学考试数学训练2
2020年最新深圳国际交流学院G1入学考试数学训练一．选择题（共8小题）1．若a≠b，且a2﹣4a+1＝0，b2﹣4b+1＝0，则的值为（）A．B．1 C．.4 D．32．关于x的方程kx2+2x﹣1＝0有实数根，则k的取值范围是（）A．k≥﹣1 B．k≥﹣1且k≠0 C．k≤﹣1 D．k≤1且k≠0 3．函数y＝与y＝﹣kx2+k（k≠0）在同一直角坐标系中的图象可能是（）A．B．C．D．4．如图，某小区计划在一块长为32m，宽为20m的矩形空地上修建三条同样宽的道路，剩余的空地上种植草坪，使草坪的面积为570m2．若设道路的宽为xm，则下面所列方程正确的是（）A．（32﹣2x）（20﹣x）＝570B．32x+2×20x＝32×20﹣570C．（32﹣x）（20﹣x）＝32×20﹣570D．32x+2×20x﹣2x2＝5705．如图是抛物线y＝ax2+bx+c（a≠0）的部分图象，其顶点坐标为（1，n），且与x轴的一个交点在点（3，0）和（4，0）之间．则下列结论：①a﹣b+c＞0；②3a+b＝0；③b2＝4a（c﹣n）；④一元二次方程ax2+bx+c＝n﹣1有两个不相等的实数根．其中正确结论的个数是（）A．1 B．2 C．3 D．46．甲、乙两车间同时开始加工一批服装．从开始加工到加工完这批服装甲车间工作了9小时，乙车间在中途停工一段时间维修设备，然后按停工前的工作效率继续加工，直到与甲车间同时完成这批服装的加工任务为止．设甲、乙两车间各自加工服装的数量为y （件）．甲车间加工的时间为x（时），y与x之间的函数图象如图所示，则下列结论错误的是（）A．甲车间每小时加工服装80件B．这批服装的总件数为1140件C．乙车间每小时加工服装为60件D．乙车间维修设备用了4小时7．如图，在平面直角坐标系中，A（1，2），B（1，﹣1），C（2，2），抛物线y＝ax2（a≠0）经过△ABC区域（包括边界），则a的取值范围是（）A．a≤﹣1或a≥2 B．≤a≤2C．﹣1≤a＜0或1＜a≤D．﹣1≤a＜0或0＜a≤28．如图，在单位为1的方格纸上，△A1A2A3，△A3A4A5，△A5A6A7，…，都是斜边在x轴上，斜边长分别为2，4，6，…的等腰直角三角形，若△A1A2A3的顶点坐标分别为A1（2，0），A2（1，1），A3（0，0），则依图中所示规律，A2019的坐标为（）A．（﹣1008，0）B．（﹣1006，0）C．（2，﹣504）D．（1，505）二．填空题（共5小题）9．因式分解：x3﹣9x＝．10．已知＝+，则实数A＝．11．如图，菱形ABCD的顶点A，B的横坐标分别为1，4，BD∥x轴、双曲线y＝（x＞0）经过A，B两点，则菱形ABCD的面积为．12．如图是抛物线型拱桥，当拱顶离水面2m时，水面宽4m，水面下降2m，水面宽度增加m．13．已知直线y＝kx（k≠0）经过点（12，﹣5），将直线向上平移m（m＞0）个单位，若平移后得到的直线与半径为6的⊙O相交（点O为坐标原点），则m的取值范围为．三．解答题（共4小题）14．计算：+﹣﹣（）﹣1．15．如图，AB为⊙O的直径，弦CD∥AB，E是AB延长线上一点，∠CDB＝∠ADE．（1）DE是⊙O的切线吗？请说明理由；（2）求证：AC2＝CD•BE．16．某中学计划购买A型和B型课桌凳共200套．经招标，购买一套A型课桌凳比购买一套B型课桌凳少用40元，且购买4套A型和5套B型课桌凳共需1820元．（1）求购买一套A型课桌凳和一套B型课桌凳各需多少元？（2）学校根据实际情况，要求购买这两种课桌凳总费用不能超过40880元，并且购买A 型课桌凳的数量不能超过B型课桌凳数量的，求该校本次购买A型和B型课桌凳共有几种方案？哪种方案的总费用最低？17．如图，二次函数y＝ax2+2x+c的图象与x轴交于点A（﹣1，0）和点B，与y轴交于点C（0，3）．（1）求该二次函数的表达式；（2）过点A的直线AD∥BC且交抛物线于另一点D，求直线AD的函数表达式；（3）在（2）的条件下，在x轴上是否存在一点P，使得以B、C、P为顶点的三角形与△ABD相似？若存在，求出点P的坐标；若不存在，请说明理由．参考答案与试题解析一．选择题（共8小题）1．若a≠b，且a2﹣4a+1＝0，b2﹣4b+1＝0，则的值为（）A．B．1 C．.4 D．3【分析】根据根与系数的关系即可求出答案．【解答】解：由题意可知：a、b是方程x2﹣4x+1＝0的两个不同的实数根，∴由根与系数的关系可知：ab＝1，a+b＝4，∴a2+1＝4a，b2+1＝4b，∴原式＝+＝＝＝1，故选：B．2．关于x的方程kx2+2x﹣1＝0有实数根，则k的取值范围是（）A．k≥﹣1 B．k≥﹣1且k≠0 C．k≤﹣1 D．k≤1且k≠0 【分析】由于k的取值范围不能确定，故应分k＝0和k≠0两种情况进行解答．【解答】解：（1）当k＝0时，﹣6x+9＝0，解得x＝；（2）当k≠0时，此方程是一元二次方程，∵关于x的方程kx2+2x﹣1＝0有实数根，∴△＝22﹣4k×（﹣1）≥0，解得k≥﹣1，由（1）、（2）得，k的取值范围是k≥﹣1．故选：A．3．函数y＝与y＝﹣kx2+k（k≠0）在同一直角坐标系中的图象可能是（）。
2020年深国交G1入学考试数学复习资料：综合专题 精讲精练(解析版)
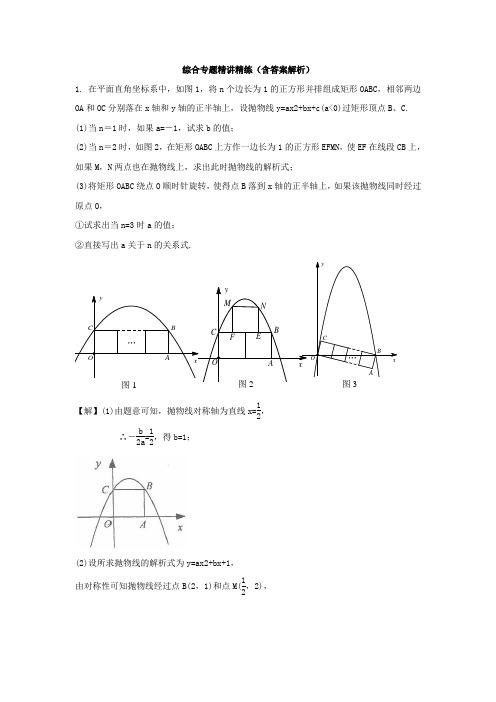
综合专题精讲精练（含答案解析）1. 在平面直角坐标系中，如图1，将n 个边长为1的正方形并排组成矩形OABC ，相邻两边OA 和OC 分别落在x 轴和y 轴的正半轴上，设抛物线y=ax2+bx+c(a<0)过矩形顶点B 、C. (1)当n ＝1时，如果a=－1，试求b 的值；(2)当n ＝2时，如图2，在矩形OABC 上方作一边长为1的正方形EFMN ，使EF 在线段CB 上，如果M ，N 两点也在抛物线上，求出此时抛物线的解析式；(3)将矩形OABC 绕点O 顺时针旋转，使得点B 落到x 轴的正半轴上，如果该抛物线同时经过原点O ，①试求出当n=3时a 的值； ②直接写出a 关于n 的关系式.(2)设所求抛物线的解析式为y=ax2+bx+1， 由对称性可知抛物线经过点B(2，1)和点M(12，2)，∴⎩⎪⎨⎪⎧1=4a+2b+1，2=14a+12b+1.解得⎩⎨⎧a=－43，b=83.∴所求抛物线解析式为y=－43x2+83x+1；(3)①当n=3时，OC=1，BC=3， 设所求抛物线的解析式为y=ax2+bx ，过C 作CD⊥OB 于点D ，则Rt△OCD∽Rt△CBD， ∴OD CD =OC BC =13，设OD=t ，则CD=3t ， ∵OD 2+CD2=OC2， ∴（3t ）2+ t 2=12，∴ t=110=1010， ∴C(1010，31010)，又B(10，0)， ∴把B 、C 坐标代入抛物线解析式，得⎩⎪⎨⎪⎧0=10a+10b ，31010=110a+1010b.解得：a=－103；②a=－n2+1n.2. 将抛物线c1：y=-3x2+3沿x 轴翻折，得抛物线c2,如图所示.（1）请直接写出抛物线c2的表达式.（2）现将抛物线c1向左平移m 个单位长度，平移后得的新抛物线的顶点为M ，与x 轴的交点从左到右依次为A ，B ；将抛物线c2向右也平移m 个单位长度，平移后得到的新抛物线的顶点为N ，与x 轴交点从左到右依次为D ，E. ①当B ，D 是线段AE 的三等分点时，求m 的值；②在平移过程中，是否存在以点A ，N ，E ，M 为顶点的四边形是矩形的情形？若存在，请求出此时m 的值；若不存在，请说明理由.【答案】【答案】解：(1)y=3x2-3.(2)①令-3x2+3=0，得x1=-1,x2=1,则抛物线c1与x 轴的两个交点坐标为（-1，0），（1，0）.∴A（-1-m ，0），B （1+m,0）.当AD=31AE 时，如图①，（-1+m ）-（-1-m ）=31, ∴m=21 当AB=31AE 时，如图②，（1-m ）-（-1-m ）=31, ∴m=2.∴当m=21或2时，B ，D 是线段AE 的三等分点.②存在.理由：连接AN、NE、EM、MA.依题意可得：M（-m，-3）.即M，N关于原点O对称，∴OM=ON.∵A（-1-m，0），E（1+m，0），∴A，E关于原点O对称，∴OA=OE，∴四边形ANEM 为平行四边形.要使平行四边形ANEM为矩形，必需满足OM=OA，即m2+(3）2=2, ∴m=1.∴当m=1时，以点A，N，E，M为顶点的四边形是矩形.3. （2011甘肃兰州，28，12分）如图所示，在平面直角坐标系xoy中，正方形OABC的边长为2cm，点A、C分别在y轴的负半轴和x轴的正半轴上，抛物线2y ax bx c=++经过点A、B和D（4，23-）。
2020年深国交G1考试数学复习资料：限时训练25 圆的有关计算
限时训练25 圆的有关计算(时间：30分钟 总分：37分）一、选择题(每小题3分，共15分)1．120°的圆心角所对的弧长是6π，则此弧所在圆的半径是( C )A ．3B ．4C ．9D ．182．如图，⊙O 是△ABC 的外接圆，BC ＝2，∠BAC ＝30°，则劣弧BC ︵的长等于( A )A .2π3B .π3C .23π3D .3π3(第2题图)(第3题图)3．(2019·南充中考)如图，在半径为6的⊙O 中，点A ，B ，C 都在⊙O 上，四边形OABC 是平行四边形，则图中阴影部分的面积为 ( A )A ．6πB ．33πC ．23πD ．2π4．(2019·山西中考)如图，在Rt △ABC 中，∠ABC ＝90°，AB ＝23，BC ＝2，以AB 的中点O 为圆心，OA 的长为半径作半圆交AC 于点D ，则图中阴影部分的面积为( A ) A .534－π2 B .534＋π2C ．23－πD ．43－π2(第4题图)(第5题图)5．(2019·泰安中考)如图，将⊙O 沿弦AB 折叠，AB ︵恰好经过圆心O ，若⊙O 的半径为3，则AB ︵的长为( C )A .12π B ．π C ．2π D ．3π 二、填空题(每小题3分，共12分)6．(2019·衡阳中考)已知圆的半径是6，则圆内接正三角形的边长是__63__.7．(2019·泰州中考)如图，分别以正三角形的3个顶点为圆心，边长为半径画弧，三段弧围成的图形称为莱洛三角形，若正三角形边长为6 cm ，则该莱洛三角形的周长为__6π__cm .,(第7题图)) ,(第9题图))8．(2019·无锡中考)已知圆锥的母线长为5 cm ，侧面积为15 π cm 2，则这个圆锥的底面圆半径为__3__cm .9．(2019·徐州中考)如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形，若圆锥的底面圆的半径 r ＝2 cm ，扇形的圆心角θ＝120°，则该圆锥的母线长l 为__6__cm .三、解答题(共10分)10．如图，⊙O 是△ABC 的外接圆，AB 为直径，∠BAC 的平分线交⊙O 于点D ，过点D 作DE ⊥AC 分别交AC ，AB 的延长线于点E ，F.(1)求证：EF 是⊙O 的切线；(2)若AC ＝4，CE ＝2，求BD ︵的长度．(结果保留π)(1)证明：连接OD ，交BC 于点P.∵AD 平分∠BAC ，∴∠EAD ＝∠BAD.又∵OA ＝OD ，∴∠OAD ＝∠ODA.∴∠EAD ＝∠ODA.∴OD ∥AE.又∵EF ⊥AC ，∴OD ⊥EF.又∵点D 在⊙O 上，∴EF 是⊙O 的切线；(2)解：∵AB 是⊙O 的直径，∴ ∠ACB ＝90°.又∵∠E ＝∠PDE ＝90°，∴四边形CEDP 是矩形． ∴PD ＝CE ＝2.又∵OD ∥AE ，点O 是AB 的中点， ∴OP 是△BAC 的中位线．∴OP ＝12AC ＝12×4＝2. ∴OD ＝OB ＝2＋2＝4.在Rt △OPB 中，OP ＝2，OB ＝4， ∴∠OBP ＝30°.∴∠POB ＝60°.∴BD ︵的长为60×4×π180＝43π.。
2020年深国交G1入学考试数学冲刺 题型专练 几何综合与实践专题(含答案)
2020年深国交G1入学考试数学冲刺 题型专练 几何综合与实践专题（1. 综合与实践问题探究：(1)如图①，点A 是线段BC 外一动点，若AB ＝a ，BC ＝b ，求线段AC 长的最大值(用含a ，b 的式子表示)；(2)如图①，点A 是线段BC 外一动点，且AB ＝1，BC ＝4，分别以AB 、AC 为边作等边①ABD 、等边①ACE ，连接CD 、BE .①求证：CD ＝BE ；①求线段BE 长的最大值；问题解决：(3)如图①，在平面直角坐标系中，已知点A (2，0)、B (5，0)，点P 、M 是线段AB 外的两个动点，且P A ＝2，PM ＝PB ，①BPM ＝90°，求线段AM 长的最大值及此时点P 的坐标．第1题图(1)解：①点A 是线段BC 外一动点，且AB ＝a ，BC ＝b ， 则AC ≤AB ＋BC ，且当点A 位于CB 的延长线上时，线段AC 的长取得最大值，此时AC 的长的最大值为：AB ＋BC ＝a ＋b ；(2)①证明：①①ABD ，①ACE 都是等边三角形，①AD ＝AB ，AC ＝AE ，①BAD ＝①EAC ＝60°，①①DAC ＝①BAE ，在①CAD 和①EAB 中，⎩⎪⎨⎪⎧AD ＝AB ①CAD ＝①EAB AC ＝AE，①①CAD ①①EAB (SAS)，①CD ＝BE ；①解：①CD ＝BE ，①线段BE 长的值最大值即为线段CD 长的最大值，此时BE 的最大值为：BD ＋BC＝AB ＋BC ＝5；(3)解：如解图①，连接BM ，①PB ＝PM ，①MPB ＝90°，第1题解图①①可以将①APM 绕点P 顺时针旋转90°得到①PBN ，连接AN ，则①APN 是等腰直角三角形，①PN ＝P A ＝2，BN ＝AM ，①线段AM 的长的最大值即为线段BN 长的最大值， 由(1)的结论可知，当点N 在线段BA 的延长线上时，线段BN 的值最大，且此时的最大值为AB ＋AN 的值．①A (2，0)，B (5，0)，①OA ＝2，OB ＝5，AB ＝3，①AN ＝2AP ＝22，①最大值为22＋3；如解图①中，作PE ①x 轴于点E ，第1题解图①①①APN 是等腰直角三角形，①PE ＝AE ＝12AN ＝2， ①OE ＝OA －AE ＝2－2，①P (2－2，2)， 即线段AM 的最大值为22＋3，此时P 的坐标为(2－2，2)．2.综合与探究问题背景在综合实践课上，老师让同学们根据如下问题情境，写出两个教学结论：如图①，点C在线段BD上，点E在线段AC上．①ACB=①ACD=90°，AC=BC；DC=CE，M，N分别是线段BE，AD上的点．“兴趣小组”写出的两个教学结论是：①①BCE①①ACD；①当CM，CN分别是①BCE和①ACD 的中线时，①MCN是等腰直角三角形．解决问题（1）请证明“兴趣小组”所写的两个结论的正确性．类比探究受到“兴趣小组”的启发，“实践小组”的同学们写出如下结论：如图②，当①BCM=①ACN时，①MCN是等腰直角三角形．（2）“实践小组”所写的结论是否正确？请说明理由．感悟发现“奋进小组”认为：当点M，N分别是BE，AD的三等分点时，①MCN仍然是等腰直角三角形请你思考：（3）“奋进小组”所提结论是否正确？答：．（填“正确”、“不正确”或“不一定正确”．）（4）反思上面的探究过程，请你添加适当的条作，再写出使得①MCN是等腰直角三角形的数学结论．（所写结论必须正确，写出1个即可，不要求证明）图①图②备用图。
2020年深国交G1入学考试 数学模拟试卷9(初三)
3．若方程组
的解 x 与 y 的和为 0，则 m 的值为（ ）
A．﹣2 B．0 C．2 D．4
4．如图，有四个平面图形分别是三角形、平行四边形、直角梯形、圆，垂直于 x 轴的直线 l：x=t（0≤t≤a）从原点 O 向右平行移动，l 在移动过程中扫过平面图形的面积为 y（图中阴 影部分），若 y 关于 t 函数的图象大致如图，那么平面图形的形状不可能是 （）
A． a（x1﹣x2）=d C． a（x1﹣x2）2=d
B． a（x2﹣x1）=d D． a（x1+x2）2=d
10．在平面直角坐标系中，函数 y=x2﹣2x（x≥0）的图象为 C1，C1 关于原点对称的图象为 C2，则直线 y=a（a 为常数）与 C1、C2 的交点共有（ ） A．1 个 B．1 个或 2 个 C．1 个或 2 个或 3 个 D．1 个或 2 个或 3 个或 4 个
中阴影部分的面积为
．
16．方程 x=
的解是
三．解答题（共 3 小题，共 36 分） 17．（10 分）若 x1，x2 是关于 x 的方程 x2+bx+c=0 的两个实数根，且|x1|+|x2|=2|k（| k 是整数）， 则称方程 x2+bx+c=0 为“偶系二次方程”．如方程 x2﹣6x﹣27=0，x2﹣2x﹣8=0，x2+3x﹣ =0， x2+6x﹣27=0，x2+4x+4=0，都是“偶系二次方程”． （1）判断方程 x2+x﹣12=0 是否是“偶系二次方程”，并说明理由； （2）对于任意一个整数 b，是否存在实数 c，使得关于 x 的方程 x2+bx+c=0 是“偶系二次方 程”，并说明理由．
二．填空题（共 6 小题，每题 4 分）
2020年深国交G1入学考试 数学模拟试卷2答案(初二新版)
19.(1)如图所示，设第一次落地时，抛物线的表达式为 y a(x 6)2 4 ．由已知 当 x＝0 时，y＝1．即1 36a 4，∴ a 1 ．
12 ∴ 表达式为 y 1 (x 6)2 4 ．
12
(2)令 y＝0， 1 (x 6)2 4 0 ． 12
∴ (x 6)2 48． 解得 x1 4 3 6 ≈13 ， x2 4 3 6 0 (舍去)． ∴ 足球第一次落地距守门员约 13 米． (3)如图所示，第二次足球弹出后的距离为 CD， 根据题意得 CD＝EF(即相当于将抛物线 AEMFC 向下平移了 2 个单位)， ∴ 2 1 ( x 6)2 4 ，
x1
1 时，原方程无意义．∴
x
3 2
是原方程的解．
（2） x4 x2 6 0 ．
解：设 x2 y ，那么原方程可化为 y2 y 6 0
解得 y1 3 ； y2 2 当 y 3 时， x2 3 ； x 3
当 y 2 时， x2 2 不符合题意，舍去．
所以原方程的解为 x1 3 ， x2 3 ．
2020年深国交入学考试
G1 数学试题模拟2（初二新版）
一、 选择题（共 10 小题，每小题 4 分，共 40 分）
1-5 BABBA 6-10 DACCA
二、填空题（共 6 小题，每小题 4 分，共 24 分）
11．18
12．－2
13．300°
14．y1＜y21）设生产 A 型桌椅 x 套，则生产 B 型桌椅 (500 x) 套，由题意得 0.5x 0.7 (500 x) ≤302 2x 3 (500 x) ≥1250
2020年中考复习 圆的证明 及计算
1. 如图，在等腰三角形△ABC 中，AB=BC ，以BC 为直径的⊙O 与AC 相交于点D ，过点D 作DE ⊥AB 交CB 延长线于点E ，垂足为点F 。
（1）判断DE 与⊙O 的位置关系，并说明理由； （2）若⊙O 的半径R=5，tanC=21，求EF 的长。
解析：（1）有交点连半径，证垂直。
连接OD ，由BC 是直径可得∠CDB 是直角，又AB=AC 可得D 是AC 中点，就能得出OD ∥AB,又知DE ⊥AB,可得出OD ⊥DE ，即DE 与⊙O 相切.（3）连接DB ，作DH ⊥BC 。
由BC=10,tanC=21,可求得CD 、DB 的长，再利用面积可求DH 长，知道OD 、DH 应用勾股定理可得OH ，利用相似可求得OE 及BE 、DE 。
再利用相似可求EF 长。
2. 如图，AB 、CD 是⊙O 的直径，点E 在AB 延长线上，FE ⊥AB ，BE=EF=2，FE 的延长线交CD 延长线于点G ，DG=GE=3，连接FD 。
（1）求⊙O 的半径（2）求证：DF 是⊙O 的切线解析：（1）设⊙O 的半径为r ，则OE=r+2,OG=r+3，EG=3.利用勾股定理可求r 。
（2）由∠HOD=∠GOE,∠OHD=∠OGE,可得△ODH ∽△OEH,可得∠ODH=∠OEG=900,即DF 是⊙O 的切线。
3. 如图，△ABC 内接于⊙O ，AD 与BC 是⊙O 的直径，延长线段AC 至点G ，使AG=AD ，连接DG 交⊙O 于点E ，EF ∥AB 交AG 于点F 。
（1）求证：EF 与⊙O 相切。
（2）若EF=32，AC=4.求扇形OAC 的面积。
解析：（1）由BC 是直径可知∠BAC=900，又EF ∥AB,得∠AFE=900。
连接OE ，得∠OED=∠ODE=∠AGD,所以OE ∥AG ，得∠OEF=∠AFE=900,即EF 与⊙O 相切。
（2）过点O 作OH ⊥AC ，垂足为H ，则OH=EF=32。
2020年最新深圳国际交流学院G1入学考试数学训练试题
2020年最新深圳国际交流学院G1入学考试数学训练知识点1 :函数的定义与自变量的取值范围1．（3分）下列图象能表示y是x的函数的是（）A．B．C．D．2．（3分）在函数y＝+中，自变量x的取值范围是（）A．x≥1B．x≥1且x≠3C．x≠3D．1≤x≤3知识点2 :一次函数的定义，图像与性质3．（3分）若y＝（m﹣1）x2﹣|m| +3是关于x的一次函数，则m的值为（）A．1 B．﹣1 C．±1 D．±24．（3分）以下关于直线y＝2x﹣4的说法正确的是（）A．直线y＝2x﹣4与x轴的交点坐标为（0，﹣4）B．坐标为（3，3）的点不在直线y＝2x﹣4上C．直线y＝2x﹣4不经过第四象限D．函数y＝2x﹣4中，y的值随x的增大而减小5．（3分）A（x1，y1）和B（x2，y2）是一次函数y＝（k2+1）x+2图象上的两点,且x1＜x2，则y与y2的大小关系是（）1A．y1＝y2B．y1＜y2C．y1＞y2D．不确定6．（3分）已知正比例函数y＝kx（k≠0）的图象经过二、四象限，则一次函数y＝kx﹣k的图象大致是（）A．B．C．D．7. （3分）将函数y=2x-3的图象向上平移2个单位得到的函数解析式为。
知识点3 :一次函数图像与不等式，方程（组）的关系8．（3分）函数y＝kx+b（k、b为常数，k≠0）的图象如图，则关于x的不等式kx+b＜0的解集为（）A．x＞0 B．x＜0 C．x＜2 D．x＞29．（3分）如图，一次函数y＝x+1与y＝2x﹣1图象的交点是（2，3），观察图像，直接写出方程组 y＝x+1 的解为（）y＝2x﹣1A． B．C． D．知识点4 :观察图像，获取信息10．（3分）电话卡上存有4元话费，通话时每分钟话费0.4元，则电话卡上的余额y（元）与通话时间t（分钟）之间的函数图象是图中的（）A．B．C．D．11．（3分）甲、乙两同学骑自行车从A地沿同一条路到B地，已知乙比甲先出发，他们离出发地的距离s/km和骑行时间t/h之间的函数关系如图所示．根据图象信息，以下说法错误的是（）A．他们都骑了20kmB．两人在各自出发后半小时内的速度相同C．甲和乙两人同时到达目的地D．相遇后，甲的速度大于乙的速度12. （3分）一台印刷机每年可印刷的书本数量y（万册）与它的使用时间x（年）成反比例关系，当x=2时，y=20．则y与x的函数图象大致是（）A． B． C． D．知识点5: 分段函数的定义与图像13．（3分）如图是一个运算程序的示意图，若输出y的值为2，则输入的x值可能为（）A．3 B．±1C．1或3 D．±1或314．（3分）小刘下午5点30分放学匀速步行回家，途中路过鲜花店为过生日的妈妈选购了一束鲜花，6点20分到家，已知小刘家距学校3千米，下列图象中能大致表示小刘离学校的距离S（千米）与离校的时间t（分钟）之间的关系的是（）A． B．C． D．15．（9分）某城市出租车的收费标准为：3千米以内（含3千米）收费8元，超过3千米时，超过的部分每千米收费1.4元．（1）写出车费y（元）和行车里程x（千米）之间的关系式；（2）甲乘坐13千米需付多少元钱？若乙付的车费是36元，则他乘坐了多少里程？知识点6: 反比例函数的定义，图像与性质16. （3分）在下列函数中，y是x的反比例函数的是（）A．y＝3x B．y＝C．y＝D．y＝17．（3分）已知函数是反比例函数，且当x＜0时，y随着x的增大而增大，则m的取值是．18．（3分）若点A（﹣3，y1），B（﹣2，y2），C（1，y3）都在反比例函数y＝（k<0）的图象上，则y1，y2，y3的大小关系是（）A．y2＜y1＜y3B．y3＜y2＜y1C．y1＜y2＜y3D．y3＜y1＜y219．（3分）对于反比例函数y＝，下列说法不正确的是（）A．图象分布在第一、三象限B．当x＞0时，y随x的增大而减小C．图象经过点（2，3）D．若点A（x1，y1），B（x2，y2）都在图象上，且x1＜x2，则y1＜y220．（3分）已知函数y＝图象如图，以下结论，其中正确的有（）个：①k＜0；②y随x的增大而增大；③若A（﹣1，a），点B（2，b）在图象上，则a＜b（﹣x，﹣y）也在图象上．④若P（x，y）在图象上，则点P1A．4个 B．3个 C．2个 D．1个21．（3分）已知A（m+3，2），B（3，）是同一个反比例函数图象上的两个点，则m＝知识点7: 反比例函数中K的几何意义22．（3分）反比例函数图象的一支如图所示，△POM的面积为2，则该函数的解析式是（）A．y＝ B．y＝C．y＝﹣ D．y＝﹣23．（3分）如图，在反比例函数y＝（x＞0）的图象上，有点P1、P2、P3、P4，它们的横坐标依次为1，2，3，4．分别过这些点作x轴与y轴作垂线，图中所构成的阴影部分的面积从左到右依次为S1、S2、S3，则S1+S2+S3＝（）A．2 B．2.5C．3 D．无法确定知识点 8:反比例函数的应用24. （3分）某种气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P（kPa）是气球体积V的反比例函数，其图象如图所示，当气球内的气压大于160kPa时，气球将爆炸，为了安全，气球的体积应该（）A．不小于m3 B．小于m3C．不大于m3 D．小于m3知识点 9: 反比例函数与一次函数结合25．（3分）函数y＝﹣2x与函数y＝﹣在同一坐标系中的大致图象是（）A．B．C．D．26．（3分）如图，正比例函数y1=k1x的图象与反比例函数y2=的图象相交于A，B两点，其中点A的横坐标为2，当y1＞y2时，x的取值范围是（）A．x＜﹣2或x＞2 B．x＜﹣2或0＜x＜2C ．﹣2＜x ＜0或0＜x ＜2D ．﹣2＜x ＜0或x ＞227．（12分）如图，直线y ＝kx +b 与反比例函数的图象分别交于点A （﹣1，2），点B （﹣4，n ），直线与x 轴，y 轴分别交于点C ，点D ． （1）求此一次函数和反比例函数的解析式； （2）求△AOB 的面积．28．（10分）如图所示,已知一次函数y=kx+b(k≠0)的图象与x 轴、y 轴分别交于A 、B 两点,且与反比例函数y=mx (m≠0)的图象在第一象限交于C 点, CD 垂直于x 轴,垂足为 D.若OA=OB=OD=1,(1)求点A 、B 、D 的坐标；(2)求一次函数和反比例函数的解析式.yOxDC B A29．（14分）为了预防传染病,某学校对教室采用药薰消毒法进行消毒. 已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧完后,y与x成反比例(如图所示),现测得药物8分钟燃毕, 此时室内空气中每立方米的含药量为6毫克.请根据题中所提供的信息,解答下列问题:(1)分别求出药物燃烧时及药物燃烧后y 关于x 的函数关系式, 并写出自变量x 的取值范围，(2)研究表明,当空气中每立方米的含药量低于 1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过几分钟后,学生才能回到教室？(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10 分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?参考答案1.D2.B3.B4.B5.B6.C7.y=2x-1,8.D 9.B 10.D 11.C 12.C 13.C 14.C8 x≤315.(1)y = (2)甲需付22元，乙乘坐了23千米。
2020年中考数学复习 圆的有关计算与证明问题(解析版)
【考点1】圆中有关角的计算问题【例1】（2019•台州）如图，AC是圆内接四边形ABCD的一条对角线，点D关于AC的对称点E在边BC 上，连接AE．若∠ABC＝64°，则∠BAE的度数为．【分析】直接利用圆内接四边形的性质结合三角形外角的性质得出答案．【解析】∵圆内接四边形ABCD，∴∠D＝180°﹣∠ABC＝116°，∵点D关于AC的对称点E在边BC上，∴∠D＝∠AEC＝116°，∴∠BAE＝116°﹣64°＝52°．故答案为：52°．点评：此题主要考查了圆内接四边形的性质以及三角形的外角，正确得出∠AEC的度数是解题关键．̂）上，若∠【例2】（2019•温州）如图，⊙O分别切∠BAC的两边AB，AC于点E，F，点P在优弧（EDFBAC＝66°，则∠EPF等于度．【分析】连接OE，OF，由切线的性质可得OE⊥AB，OF⊥AC，由四边形内角和定理可求∠EOF＝114°，即可求∠EPF的度数．【解析】连接OE，OF∵⊙O分别切∠BAC的两边AB，AC于点E，F∴OE⊥AB，OF⊥AC又∵∠BAC＝66°∴∠EOF＝114°∵∠EOF＝2∠EPF∴∠EPF＝57°故答案为：57点评：本题考查了切线的性质，圆周角定理，四边形内角和定理，熟练运用切线的性质是本题的关键．【考点2】切线的有关线段计算问题【例3】（2019•舟山）如图，已知⊙O上三点A，B，C，半径OC＝1，∠ABC＝30°，切线P A交OC延长线于点P ，则P A 的长为（ ）A ．2B ．√3C ．√2D ．12【分析】连接OA ，根据圆周角定理求出∠AOP ，根据切线的性质求出∠OAP ＝90°，解直角三角形求出AP 即可．【解析】连接OA ，∵∠ABC ＝30°，∴∠AOC ＝2∠ABC ＝60°，∵过点A 作⊙O 的切线交OC 的延长线于点P ， ∴∠OAP ＝90°， ∵OA ＝OC ＝1，∴AP ＝OA tan60°＝1×√3=√3， 故选：B ．点评：本题考查了切线的性质和圆周角定理、解直角三角形等知识点，能熟记切线的性质是解此题的关键，注意：圆的切线垂直于过切点的半径．【例4】（2019•台州）如图，等边三角形ABC 的边长为8，以BC 上一点O 为圆心的圆分别与边AB ，AC 相切，则⊙O 的半径为（ ）A ．2√3B ．3C ．4D ．4−√3【分析】设⊙O与AC的切点为E，连接AO，OE，根据等边三角形的性质得到AC＝8，∠C＝∠BAC＝60°，由切线的性质得到∠BAO＝∠CAO=12∠BAC＝30°，求得∠AOC＝90°，解直角三角形即可得到结论．【解析】设⊙O与AC的切点为E，连接AO，OE，∵等边三角形ABC的边长为8，∴AC＝8，∠C＝∠BAC＝60°，∵圆分别与边AB，AC相切，∴∠BAO＝∠CAO=12∠BAC＝30°，∴∠AOC＝90°，∴OC=12AC＝4，∵OE⊥AC，∴OE=√32OC＝2√3，∴⊙O的半径为2√3，故选：A．点评：本题考查了切线的性质，等边三角形的性质，解直角三角形，正确的作出辅助线是解题的关键．【考点3】扇形与弧长的有关计算问题【例5】（2019•宁波）如图所示，矩形纸片ABCD中，AD＝6cm，把它分割成正方形纸片ABFE和矩形纸片EFCD后，分别裁出扇形ABF和半径最大的圆，恰好能作为一个圆锥的侧面和底面，则AB的长为（）A ．3.5cmB ．4cmC ．4.5cmD ．5cm【分析】设AB ＝xcm ，则DE ＝（6﹣x ）cm ，根据扇形的弧长等于圆锥底面圆的周长列出方程，求解即可．【解析】设AB ＝xcm ，则DE ＝（6﹣x ）cm ， 根据题意，得90πx 180=π（6﹣x ），解得x ＝4． 故选：B ．点评：本题考查了圆锥的计算，矩形的性质，正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．【例6】（2019•绍兴）如图，△ABC 内接于⊙O ，∠B ＝65°，∠C ＝70°．若BC ＝2√2，则BC ̂的长为（ ）A ．πB ．√2πC ．2πD ．2√2π【分析】连接OB ，OC ．首先证明△OBC 是等腰直角三角形，求出OB 即可解决问题． 【解析】连接OB ，OC ．∵∠A ＝180°﹣∠ABC ﹣∠ACB ＝180°﹣65°﹣70°＝45°， ∴∠BOC ＝90°， ∵BC ＝2√2，∴BC ̂的长为90⋅π⋅2180=π，故选：A ．点评：本题考查圆周角定理，弧长公式，等腰直角三角形的性质的等知识，解题的关键是熟练掌握基本知识，属于中考常考题型． 【考点4】圆锥的有关计算问题【例7】（2019•湖州）已知圆锥的底面半径为5cm ，母线长为13cm ，则这个圆锥的侧面积是（ ） A ．60πcm 2B ．65πcm 2C ．120πcm 2D ．130πcm 2【分析】利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形面积公式计算． 【解析】这个圆锥的侧面积=12×2π×5×13＝65π（cm 2）． 故选：B ．点评：本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．【例8】（2019•金华）如图物体由两个圆锥组成．其主视图中，∠A ＝90°，∠ABC ＝105°，若上面圆锥的侧面积为1，则下面圆锥的侧面积为（ ）A ．2B ．√3C ．32D ．√2【分析】先证明△ABD 为等腰直角三角形得到∠ABD ＝45°，BD =√2AB ，再证明△CBD 为等边三角形得到BC ＝BD =√2AB ，利用圆锥的侧面积的计算方法得到上面圆锥的侧面积与下面圆锥的侧面积的比等于AB ：CB ，从而得到下面圆锥的侧面积． 【解析】∵∠A ＝90°，AB ＝AD ， ∴△ABD 为等腰直角三角形， ∴∠ABD ＝45°，BD =√2AB ，∴∠CBD＝60°，而CB＝CD，∴△CBD为等边三角形，∴BC＝BD=√2AB，∵上面圆锥与下面圆锥的底面相同，∴上面圆锥的侧面积与下面圆锥的侧面积的比等于AB：CB，∴下面圆锥的侧面积=√2×1=√2．故选：D．点评：本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．也考查了等腰直角三角形和等边三角形的性质．【考点5】圆与多边形的有关计算问题【例9】（2019•湖州）如图，已知正五边形ABCDE内接于⊙O，连结BD，则∠ABD的度数是（）A．60°B．70°C．72°D．144°【分析】根据多边形内角和定理、正五边形的性质求出∠ABC、CD＝CB，根据等腰三角形的性质求出∠CBD，计算即可．【解析】∵五边形ABCDE为正五边形，∴∠ABC＝∠C=(5−2)×180°5=108°，∵CD＝CB，∴∠CBD=180°−108°2=36°，∴∠ABD＝∠ABC﹣∠CBD＝72°，故选：C．点评：本题考查的是正多边形和圆、多边形的内角和定理，掌握正多边形和圆的关系、多边形内角和等于（n﹣2）×180°是解题的关键．【例10】（2018•温州）小明发现相机快门打开过程中，光圈大小变化如图1所示，于是他绘制了如图2所示的图形．图2中六个形状大小都相同的四边形围成一个圆的内接正六边形和一个小正六边形，若PQ 所在的直线经过点M ，PB ＝5cm ，小正六边形的面积为49√32cm 2，则该圆的半径为 8 cm ．【分析】设两个正六边形的中心为O ，连接OP ，OB ，过O 作OG ⊥PM ，OH ⊥AB ，由正六边形的性质及邻补角性质得到三角形PMN 为等边三角形，由小正六边形的面积求出边长，确定出PM 的长，进而求出三角形PMN 的面积，利用垂径定理求出PG 的长，在直角三角形OPG 中，利用勾股定理求出OP 的长，设OB ＝xcm ，根据勾股定理列出关于x 的方程，求出方程的解即可得到结果． 【解析】设两个正六边形的中心为O ，连接OP ，OB ，过O 作OG ⊥PM ，OH ⊥AB ， 由题意得：∠MNP ＝∠NMP ＝∠MPN ＝60°， ∵小正六边形的面积为49√32cm 2，∴小正六边形的边长为7√33cm ，即PM ＝7√3cm ， ∴S △MPN =147√34cm 2， ∵OG ⊥PM ，且O 为正六边形的中心， ∴PG =12PM =7√32cm ，OG =√36PM =72， 在Rt △OPG 中，根据勾股定理得：OP =(72)2+(7√32)2=7cm ， 设OB ＝xcm ，∵OH ⊥AB ，且O 为正六边形的中心， ∴BH =12x ，OH =√32x ，∴PH ＝（5−12x ）cm ，在Rt △PHO 中，根据勾股定理得：OP 2＝（√32x ）2+（5−12x ）2＝49， 解得：x ＝8（负值舍去），则该圆的半径为8cm．故答案为：8点评：此题考查了正多边形与圆，熟练掌握正多边形的性质是解本题的关键．【考点6】圆中有关线段的最值问题【例11】（2019•嘉兴）如图，在⊙O中，弦AB＝1，点C在AB上移动，连结OC，过点C作CD⊥OC交⊙O于点D，则CD的最大值为12．【分析】连接OD，如图，利用勾股定理得到CD，利用垂线段最短得到当OC⊥AB时，OC最小，再求出即可．【解析】连接OD，如图，∵CD⊥OC，∴∠DCO＝90°，∴CD=√OD2−OC2=√r2−OC2，当OC的值最小时，CD的值最大，而OC⊥AB时，OC最小，此时D、B两点重合，∴CD ＝CB =12AB =12×1=12， 即CD 的最大值为12， 故答案为：12．点评：本题考查了垂线段最短，勾股定理和垂径定理等知识点，能求出点C 的位置是解此题的关键． 【考点7】圆中有关计算与证明综合问题【例12】（2019•金华）如图，在▱OABC 中，以O 为圆心，OA 为半径的圆与BC 相切于点B ，与OC 相交于点D ．（1）求BD̂的度数． （2）如图，点E 在⊙O 上，连结CE 与⊙O 交于点F ，若EF ＝AB ，求∠OCE 的度数．【分析】（1）连接OB ，证明△AOB 是等腰直角三角形，即可求解；（2）△AOB 是等腰直角三角形，则OA =√2t ，HO =√OE 2−EH 2=√2t 2−t 2=t ，即可求解． 【解析】（1）连接OB ，∵BC 是圆的切线，∴OB ⊥BC ， ∵四边形OABC 是平行四边形， ∴OA ∥BC ，∴OB ⊥OA ， ∴△AOB 是等腰直角三角形， ∴∠ABO ＝45°， ∴BD̂的度数为45°；（2）连接OE，过点O作OH⊥EC于点H，设EH＝t，∵OH⊥EC，∴EF＝2HE＝2t，∵四边形OABC是平行四边形，∴AB＝CO＝EF＝2t，∵△AOB是等腰直角三角形，∴OA=√2t，则HO=√OE2−EH2=√2t2−t2=t，∵OC＝2OH，∴∠OCE＝30°．点评：本题主要利用了切线和平行四边形的性质，其中（2），要利用（1）中△AOB是等腰直角三角形结论．【例13】（2019•衢州）如图，在等腰△ABC中，AB＝AC，以AC为直径作⊙O交BC于点D，过点D作DE⊥AB，垂足为E．（1）求证：DE是⊙O的切线．̂的长．（2）若DE=√3，∠C＝30°，求AD【分析】（1）连接OD，只要证明OD⊥DE即可；（2）连接AD，根据AC是直径，得到∠ADC＝90°，利用AB＝AC得到BD＝CD，解直角三角形求得BD，在Rt△ABD中，解直角三角形求得AD，根据题意证得△AOD是等边三角形，即可OD＝AD，然后利用弧长公式求得即可．【解答】（1）证明：连接OD；∵OD＝OC，∴∠C＝∠ODC，∵AB＝AC，∴∠B＝∠C，∴∠B＝∠ODC，∴OD∥AB，∴∠ODE＝∠DEB；∵DE⊥AB，∴∠DEB＝90°，∴∠ODE＝90°，即DE⊥OD，∴DE是⊙O的切线．（2）解：连接AD，∵AC是直径，∴∠ADC＝90°，∵AB＝AC，∠C＝30°，∴∠B＝∠C＝30°，BD＝CD，∴∠OAD＝60°，∵OA＝OD，∴△AOD是等边三角形，∴∠AOD＝60°，∵DE=√3，∠B＝30°，∠BED＝90°，∴CD＝BD＝2DE＝2√3，∴OD＝AD＝tan30°•CD=√33×2√3=2，∴AD̂的长为：60π⋅2180=2π3．点评：本题考查了切线的判定．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．一．选择题（共5小题）1．（2020•温岭市一模）如图物体由两个圆锥组成．其主视图中，∠A ＝90°，∠ABC ＝105°，则上下两圆锥的侧面积之比为（ ）A ．1：2B ．1：√3C ．2：3D ．1：√2【分析】设BD ＝2r ，先利用∠A ＝90°得到AB =√2r ，再计算∠CBD ＝60°，则BC ＝BD ＝2r ，然后利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形的面积公式计算上下两圆锥的侧面积的比值． 【解析】设BD ＝2r ， ∵AB ＝AD ，∠A ＝90°， ∴AB =√2r ， ∵∠ABC ＝105°， ∴∠CBD ＝60°， ∴BC ＝BD ＝2r ，∴上下两圆锥的侧面积之比＝（12×2πr ×√2r ）：（12×2πr ×2r ）＝1：√2．故选：D ．2．（2020•金华模拟）如图，一只蚂蚁要从圆柱体下底面的A 点，沿圆柱表面爬到与A 相对的上底面的B 点，圆柱底面直径为4，母线为6，则蚂蚁爬行的最短路线长为（ ）A．√36+4π2B．√4+36π2C．4πD．6π【分析】要求最短路线，首先要把圆柱的侧面展开，利用两点之间线段最短，再利用勾股定理来求．【解析】把圆柱侧面展开，展开图如图所示，点A，B的最短距离为线段AB的长，BC＝6，AC为底面半圆弧长，AC＝2π，所以AB=√62+(2π)2=√36+4π2．故选：A．3．（2020•杭州模拟）如图，在△ABC中，以BC为直径的⊙O，交AB的延长线于点D，交AC于点E，连接OD，OE．若∠A＝α，则∠DOE的度数为（）A．180°﹣2αB．180°﹣αC．90°﹣αD．2α【分析】连接CD，如图，根据圆周角定理得到∠BDC＝90°，利用互余得到∠ACD＝90°﹣α，然后根据圆周角定理得到∠DOE＝2（90°﹣α）．【解析】连接CD，如图，∵BC为直径，∴∠BDC＝90°，∴∠ACD＝90°﹣∠A＝90°﹣α，∴∠DOE＝2∠ACD＝2（90°﹣α）＝180°﹣2α．故选：A．4．（2020•温州模拟）如图，△ABC，AC＝3，BC＝4√3，∠ACB＝60°，过点A作BC的平行线1，P为直线l上一动点，⊙O为△APC的外接圆，直线BP交⊙O于E点，则AE的最小值为（）A．√3−1B．7﹣4√3C．√3D．1̂上运【分析】如图，连接CE．首先证明∠BEC＝120°，由此推出点E在以O'为圆心，O'B为半径的BĈ于E′，此时AE′的值最小．动，连接O'A交BC【解析】如图，连接CE．∵AP∥BC，∴∠P AC＝∠ACB＝60°，∴∠CEP＝∠CAP＝60°，∴∠BEC＝120°，̂上运动，∴点E在以O'为圆心，O'B为半径的BĈ于E′，此时AE′的值最小．此时⊙O与⊙O'交点为E'．连接OA交BC∵∠BE'C＝120°̂所对圆周角为60°，∴BC∴BOC＝2×60°＝120°，∵△BOC是等腰三角形，BC＝4√3，OB＝OC＝4，∵∠ACB＝60°，∠BCO'＝30°，∴∠ACO；＝90°∴O'A=√O′C2+AC2=√42+32=5，∴AE′＝O'A﹣O'E′＝5﹣4＝1．故选：D．5．（2020•绍兴一模）如图，AB是⊙O的直径，DB，DE分别切⊙O于点B、C，若∠ACE＝20°，则∠D 的度数是（）A．40°B．50°C．60°D．70°【分析】连OC，根据切线的性质得到∠OBD＝∠OCD＝90°，根据∠ACE＝20°和OA＝OC求出∠OAC ＝∠OCA＝70°，可得∠BOC＝2×70°＝140°，再根据四边形的内角和为360°即可计算出∠D的度数．【解析】连OC，如图，∵DB、DE分别切⊙O于点B、C，∴∠OBD＝∠OCD＝∠OCE＝90°，∵∠ACE＝20°，∴∠OCA＝90°﹣20°＝70°，∵OC＝OA，∴∠OAC＝∠OCA＝70°，∴∠BOC＝2×70°＝140°，∴∠D＝360°﹣90°﹣90°﹣140°＝40°．故选：A．二．填空题（共5小题）6．（2020•金华模拟）如图，BC是⊙O的弦，以BC为边作等边三角形ABC，圆心O在△ABC的内部，若BC＝6，OA=√3，则⊙O的半径为√21．【分析】过O作OD⊥BC于D，由垂径定理可知BD＝CD=12BC，根据△ABC是等边三角形可知∠ABC＝60°，故△ABD也是直角三角形，BD＝DD，在Rt△OBD中利用勾股定理求出OB的长即可．【解析】过O作OD⊥BC于D，连接OB，∵BC是⊙O的一条弦，且BC＝6，∴BD＝CD=12BC=12×6＝3，∴OD垂直平分BC，又AB＝AC，∴点A在BC的垂直平分线上，即A，O及D三点共线，∵△ABC是等边三角形，∴∠ABC＝60°，∴AD=√3BD＝3√3，∵OA=√3，∴OD＝AD﹣OA＝2√3在Rt △OBD 中，OB =√BD 2+OD 2=√32+(2√3)2=√21； 故答案为：√21．7．（2020•天台县模拟）如图，已知等边△ABC 的边长为8，以AB 为直径的⊙O 与边AC 、BC 分别交于D 、E 两点，则劣弧DÊ的长为 43π ．【分析】连接OD 、OE ，先证明△AOD 、△BOE 是等边三角形，得出∠AOD ＝∠BOE ＝60°，求出∠DOE ＝60°，再由弧长公式即可得出答案． 【解析】连接OD 、OE ，如图所示：∵△ABC 是等边三角形， ∴∠A ＝∠B ＝∠C ＝60°， ∵OA ＝OD ，OB ＝OE ，∴△AOD 、△BOE 是等边三角形， ∴∠AOD ＝∠BOE ＝60°， ∴∠DOE ＝60°， ∵OA =12AB ＝4， ∴DÊ长=60π×4180=43π； 故答案为：43π．8．（2020•绍兴一模）如图所示，在Rt △ABC 中，∠ACB ＝90°，AC ＝6，BC ＝8，若以点C 为圆心，r 为半径的圆与边AB 所在直线有公共点，则r 的取值范围为 r ≥245 ．【分析】如图，作CH⊥AB于H．利用勾股定理求出AB，再利用面积法求出CH即可判断．【解析】如图，作CH⊥AB于H．在Rt△ABC中，∵∠ACB＝90°，BC＝8，AC＝6，∴AB=√AC2+BC2=√62+82=10，∵S△ABC=12•AC•BC=12•AB•CH，∴CH=24 5，∵以点C为圆心，r为半径的圆与边AB所在直线有公共点，∴r≥24 5，故答案为r≥24 5．9．（2020•拱墅区校级模拟）如图，P A，PB是⊙O的两条切线，A，B为切点，点D，E，F分别在线段AB，BP，AP上，且AD＝BE，BD＝AF，∠P＝54°，则∠EDF＝63度．【分析】根据切线长定理得到P A＝PB，根据三角形内角和定理得到∠P AB＝∠PBA＝63°，证明△AFD ≌△BDE，根据全等三角形的性质得到∠AFD＝∠BDE，结合图形计算，得到答案．【解析】∵P A，PB是⊙O的两条切线，∴P A ＝PB ， ∴∠P AB ＝∠PBA =180°−54°2=63°， 在△AFD 和△BDE 中， {AD =BE∠FAD =∠DBE AD =BD， ∴△AFD ≌△BDE （SAS ） ∴∠AFD ＝∠BDE ，∴∠EDF ＝180°﹣∠BDE ﹣∠ADF ＝180°﹣∠AFD ﹣∠ADF ＝∠F AD ＝63°， 故答案为：63．10．（2020•衢州模拟）如图，小圆O 的半径为1，△A 1B 1C 1，△A 2B 2C 2，△A 3B 3C 3，…，△A n B n ∁n 依次为同心圆O 的内接正三角形和外切正三角形，由弦A 1C 1和弧A 1C 1围成的弓形面积记为S 1，由弦A 2C 2和弧A 2C 2围成的弓形面积记为S 2，…，以此下去，由弦A n ∁n 和弧A n ∁n 围成的弓形面积记为S n ，其中S 2020的面积为 24036（4π3−√3） ．【分析】根据正三角形和圆的关系可依次求出弓形面积，再根据弓形面积寻找规律即可得结论． 【解析】∵小圆O 的半径为1，△A 1B 1C 1，△A 2B 2C 2，△A 3B 3C 3，…，△A n B n ∁n 依次为同心圆O 的内接正三角形和外切正三角形， ∴S 1＝S扇形A 1OC 1−S△A 1OC 1=120π×12360−12×√3×12，S 2=120π×22360−12×2√3×1 S 3=120π×42360−12×4√3×2… 发现规律：S n =120π×(2n−1)2360−12×（2n ﹣1） √3×2n ﹣2 =π3×22n ﹣2﹣22n ﹣4×√3＝22n ﹣4 （4π3−√3）∴S 2020的面积为：24036（4π3−√3）．故答案为：24036（4π3−√3）．三．解答题（共10小题）11．（2020•金华模拟）如图，在Rt △ABC 中，∠C ＝90°，AC ＝BC ，点O 在AB 上，以O 为圆心，OA 为半径作⊙O ，与BC 相切于点D ，且交AB 于点E ． （1）连结AD ，求证：AD 平分∠CAB ； （2）若BE =√2−1，求阴影部分的面积．【分析】（1）连接OD ，证OD ∥AC ，求出∠OAD ＝∠ODA ＝∠CAD 即可； （2）证明△BOD 是等腰直角三角形，分别求出△BOD 和扇形EOD 的面积即可． 【解答】（1）证明：如图，连结OD ，∵⊙O 与BC 相切于点D ， ∴OD ⊥BC ， 即∠ODB ＝90°． 又∵∠C ＝90°， ∴OD ∥AC ， ∴∠ODA ＝∠CAD ．在⊙O中，OA＝OD，∴∠ODA＝∠OAD，∴∠OAD＝∠CAD，∴AD平分∠CAB．（2）解：在Rt△ABC中，∠C＝90°，AC＝BC，∴∠B＝45°，∴∠BOD＝45°，∴△BOD是等腰直角三角形，∴OB=√2OD，BD＝OD，设⊙O的半径为r，则OD＝BD＝r，OB=√2r，∴BE=(√2−1)r=√2−1，∴r＝1，∴S阴影=12r2−45360πr2=12−π8．12．（2020•鹿城区校级模拟）如图，在Rt△ABC中，∠BAC＝90°，D是BC边上的一点，过A，B，D三点的⊙O交AC于点E，作直径AF，连结FD并延长交AC于点G，且FG∥BE，连结BE，BF﹒（1）求证：AB＝BD；（2）若BD＝2CD，AC＝5，求⊙O的直径长﹒【分析】（1）连接EF、DE，然后证明四边形ABFE和四边形BFDE分别为矩形和等腰梯形即可．（2）设CD为x，在Rt△ABC中，利用勾股定理可求得CD长度，然后设BF＝DE＝AE＝y，在Rt△CDE 中利用勾股定理求得BF的长，最后在Rt△ABF中，利用勾股定理算出直径．【解析】（1）如图，连接EF、ED．∵AF为直径，∴∠ABF＝∠AEF＝90°，∵∠BAC＝90°，∴四边形ABFE是矩形，∴AB＝EF，AE＝BF，∵DF∥BE，̂=DÊ，∴BF∴BF＝DE，∴四边形BFDE是等腰梯形，∴BD＝EF，∴AB＝BD．（2）设CD＝x，则AB＝BD＝2CD＝2x，BC＝3x．在Rt△ABC中：AB2+AC2＝BC2，∴（2x）2+52＝（3x）2，解得x1=√5，x2=−√5（舍），∴CD=√5，AB＝BD＝2√5，设BF＝AE＝DE＝y，则CE＝5﹣y，在Rt△CED中：DE2+CD2＝CE2，∴y2+5＝（5﹣y）2，解得y＝2，∴BF＝DE＝AE＝2，∴AF=√AB2+BF2=√20+4=2√6，即⊙O的直径长为2√6．13．（2020•绍兴一模）如图，在正方形网格图中建立平面直角坐标系，一条圆弧经过格点A（0，4）、B（﹣4，4）、C（﹣6，2），若该圆弧所在圆的圆心为D点，请你利用网格图回答下列问题：（1）圆心D的坐标为（﹣2，0）；（2）若扇形ADC是一个圆锥的侧面展开图，求该圆锥底面圆的半径长（结果保留根号）．【分析】（1）分别作AB、BC的垂直平分线，两直线交于点D，则点D即为该圆弧所在圆的圆心，可知点D的坐标为（﹣2，0）．（2）连接AC、AD和CD，根据勾股定理的逆定理求出∠CDA＝90°，根据弧长公式和圆的周长求出答案即可．【解析】（1）分别作线段AB和线段BC的垂直平分线，两垂直平分线的交点，就是圆心D，如图，D点正好在x轴上，D点的坐标是（﹣2，0），故答案为：（﹣2，0）；（2）连接AC、AD、CD，⊙D的半径长=√22+42=2√5，AC=√22+62=2√10，∵AD 2+CD 2＝20+20＝40，AC 2＝40， ∴AD 2+CD 2＝AC 2， ∴∠ADC ＝90°．设圆锥的底面圆的半径长为r ， 则2πr =90π×2√5180， 解得：r =√52，所以该圆锥底面圆的半径长为√52． 14．（2020•上虞区校级一模）如图1 （1）已知△ABC 中AB ＝AC ，∠BAC ＝36°，BD 是角平分线，求证：点D 是线段AC 的黄金分割点；（2）如图2，正五边形的边长为2，连结对角线AD 、BE 、CE ，线段AD 分别与BE 和CE 相交于点M 、N ，求MN 的长；（3）设⊙O 的半径为r ，直接写出它的内接正十边形的边长＝√5−12r （用r 的代数式表示）．【分析】（1）如图1，先证AD ＝BD ＝BC ，再证△BCD ∽△ACB ，即可得出点D 是线段AC 的黄金分割点；（2）利用正五边形的性质，证BM ＝BA ＝AE ，再证△AEM ∽△BEA ，推出EM EB=3−√52，再证△EMN ∽△EBC ，即可求出MN 的长； （3）正十边形的中心角为：360°10=36°，利用图1，可设∠BAC 是正十边形的一个中心角，则AB ，AC为正十边形外接圆的半径r ，BD 是∠ABC 的平分线，由（1）知CDAD=AD AC，可用含r 的代数式表示出AD的长，即正十边形的边长． 【解答】（1）证明：如图1，∵在△ABC 中AB ＝AC ，∠BAC ＝36°，∴∠ABC ＝∠C =12（180°﹣36°）＝72°， ∵BD 是角平分线，∴∠CBD ＝∠ABD =12∠ABC ＝36°， ∴AD ＝BD ＝BC ，∴在△BCD 中，∠BDC ＝180°﹣∠C ﹣∠CBD ＝72°， ∴BD ＝BC ，∵∠A ＝∠CBD ＝36°，∠C ＝∠C ， ∴△BCD ∽△ACB ， ∴CD BC=BC AC，∵AD ＝BD ＝BC ， ∴CD AD=AD AC，∴点D 是线段AC 的黄金分割点； （2）在正五边形ABCDE 中， ∠AED =180°×(5−2)5=108°，AE ＝DE ，∴∠EAD ＝∠EDA =12（180°﹣108°）＝36°， 同理可求，∠AEB ＝∠ABE ＝36°， ∵∠EAM ＝∠∠EBA ，∠AEM ＝∠BEA ， ∴△AEM ∽△BEA ， ∴EM AE=AE BE，∵∠AMB ＝∠MAE +∠AEM ＝72°，∠MAB ＝∠BAE ﹣∠MAE ＝72°， ∴∠BAM ＝∠BMA ， ∴BM ＝BA ＝AE ＝2， ∴EM BM =BM BE， ∴EM 2=2EM+2，∴EM =√5−1（取正值）， ∴EM EB=√5−15−1+2=3−√52，∵∠BAM +∠ABC ＝72°+108°＝180°， ∴AD ∥BC ， ∴△EMN ∽△EBC ， ∴EM EB=MN BC=3−√52， ∵BC ＝2， ∴MN ＝3−√5；（3）正十边形的中心角为：360°10=36°，如图1，可设∠BAC 是正十边形的一个中心角，则AB ，AC 为正十边形外接圆的半径r ，BD 是∠ABC 的平分线， 由（1）知CD AD =AD AC，∴r−AD AD=ADr，∴AD =√5−12r ，∴BC ＝BD =√5−12r ，故答案为：√5−12r ．15．（2020•长安区模拟）如图1，在△ABC中，AC＝BC，以BC为直径的⊙O交AB于点D．（1）求证：点D是AB的中点；（2）如图2，过点D作DE⊥AC于点E，求证：DE是⊙O的切线．【分析】（1）由于AC＝AB，如果连接CD，那么只要证明出CD⊥AB，根据等腰三角形三线合一的特点，我们就可以得出AD＝BD，由于BC是圆的直径，那么CD⊥AB，由此可证得．（2）连接OD，再证明OD⊥DE即可．【解答】证明：（1）如图1，连接CD，∵BC为⊙O的直径，∴CD⊥AB．∵AC＝BC，∴AD＝BD．（2）如图2，连接OD；∵AD＝BD，OB＝OC，∴OD是△BCA的中位线，∴OD∥AC．∵DE⊥AC，∴DF⊥OD．∵OD为半径，∴DE是⊙O的切线．16．（2020•衢州模拟）如图，以△ABC的BC边上一点O为圆心的圆，经过A、B两点，且与BC边交于点E，D为BE的下半圆弧的中点，连接AD交BC于F，若AC＝FC．（1）求证：AC是⊙O的切线；（2）若BF＝4，DF=√10，求⊙O的半径．【分析】（1）由等腰三角形的性质和垂径定理可求∠OAC＝90°，可得结论；（2）由勾股定理可求解．【解答】证明：（1）连接AO，∵OA＝OD，∴∠OAD＝∠ODA，∵AC＝FC，∴∠CAF＝∠CF A＝∠OFD，∵D为BE的下半圆弧的中点，∴OD⊥BE，∴∠ODA+∠OFD＝90°，∴∠CF A+∠DAO＝90°，∴∠OAC＝90°，且OA是半径，∴AC是⊙O的切线；（2）在Rt△ODF中，DF2＝OD2+OF2，∴10＝OD2+（4﹣OD）2，∴OD＝1（不合题意舍去），OD＝3，∴⊙O的半径为3．17．（2020•温州模拟）如图，AB是O的直径，C是弧BD的中点，CE⊥AB，垂足为E，BD交CE于点F．（1）求证：CF＝BF；（2）若AD＝6，⊙O的半径为5，求BC的长．【分析】（1）连接ACAC，由圆周角定理得出∠ACB＝90°，证出∠BAC＝∠BCE；由C是弧BD的中点，得到∠DBC＝∠BAC，延长∠BCE＝∠DBC，即可得到结论；CF＝BF．（2）连接OC交BD于G，由圆周角定理得出∠ADB＝90°，由勾股定理得出BD=√AB2−AD2=8，由垂径定理得出OC⊥BD，DG＝BG=12BD＝4，证出OG是△ABD的中位线，得出OG=12AD＝3，求出CG＝OC﹣OG＝2，在Rt△BCG中，由勾股定理即可得出答案．【解答】（1）证明：连接AC，如图1所示：∵C是弧BD的中点，∴∠DBC＝∠BAC，在ABC中，∠ACB＝90°，CE⊥AB，∴∠BCE+∠ECA＝∠BAC+∠ECA＝90°，∴∠BCE＝∠BAC，又C是弧BD的中点，∴∠DBC＝∠CDB，∴∠BCE＝∠DBC，∴CF＝BF．（2）解：连接OC交BD于G，如图2所示：∵AB是O的直径，AB＝2OC＝10，∴∠ADB＝90°，∴BD=√AB2−AD2=√102−62=8，∵C是弧BD的中点，∴OC⊥BD，DG＝BG=12BD＝4，∵OA＝OB，∴OG是△ABD的中位线，∴OG=12AD＝3，∴CG＝OC﹣OG＝5﹣3＝2，在Rt△BCG中，由勾股定理得：BC=√CG2+BG2=√22+42=2√5．18．（2020•拱墅区校级模拟）如图，△ABC是的内接三角形，点C是优弧AB上一点，设∠OAB＝α，∠C ＝β．（1）猜想：β关于α的函数表达式，并给出证明；（2）若α＝30°，AB＝6，S△ABC＝6√3，求AC的长．【分析】（1）连接OB，理由等腰三角形的性质圆周角定理即可解决问题．（2）如图，延长AO交⊙O于E，连接EB，作EF∥AB交⊙O于F，连接AF．证明点C与点E重合即可解决问题．【解析】（1）如图，结论：β＝90°﹣α．理由：连接OB．∵OA＝OB，∴∠OAB＝∠OBA＝α，∴∠AOB＝180°﹣2α，∴∠C=12∠AOB＝90°﹣α，即β＝90°﹣α．（2）如图，延长AO交⊙O于E，连接EB，作EF∥AB交⊙O于F，连接AF．∵AE是直径，∴∠ABE＝90°，∵∠EAB＝30°，AB＝6，∴BE＝AB•tan30°＝2√3，∴S△EAB=12•AB•EB＝6√3，∵S△ABC＝6√3，∴点C与E重合，或与F重合，∴AC＝2BE＝4√3或AC′＝AF＝BE＝2√3．综上所述，AC的长度为4√3或2√3．19．（2019•泸县模拟）如图，已知⊙O的直径AB＝10，弦AC＝6，∠BAC的平分线交⊙O于点D，过点D 作DE⊥AC交AC的延长线于点E．（1）求证：DE是⊙O的切线；（2）求DE的长．【分析】（1）连接OD，欲证明DE是⊙O的切线，只要证明OD⊥DE即可．（2）过点O作OF⊥AC于点F，只要证明四边形OFED是矩形即可得到DE＝OF，在RT△AOF中利用勾股定理求出OF即可．【解答】证明：（1）连接OD，∵AD平分∠BAC，∴∠DAE＝∠DAB，∵OA＝OD，∴∠ODA＝∠DAO，∴∠ODA＝∠DAE，∴OD∥AE，∵DE⊥AC，∴OD⊥DE，∴DE是⊙O切线．（2）过点O作OF⊥AC于点F，∴AF＝CF＝3，∴OF=√AO2−AF2=√52−32=4．∵∠OFE＝∠DEF＝∠ODE＝90°，∴四边形OFED是矩形，∴DE＝OF＝4．20．（2019•泰顺县模拟）已知矩形ABCD，AB＝10，AD＝8，G为边DC上任意一点，连结AG，BG以AG 为直径作⊙P分别交BG，AB于点E，H，连结AE，DE．（1）若点E为GĤ的中点，证明：AG＝AB．（2）若△ADE为等腰三角形时，求DG的长．（3）作点C关于直线BG的对称点C′．①当点C落在线段AG上时，设线段AG，DE交于点F，求△ADF与△AEF的面积之比；②在点G的运动过程中，当点C′落在四边形ADGE内时（不包括边界），则DG的范围是185＜DG＜10（直接写出答案）【分析】（1）由AG 为⊙P 直径可得：∠AEG ＝∠AEB ＝90°，由点E 为DĤ的中点，可得：∠BAE ＝∠GAE ，由此易证：△AEB ≌△AEG ；（2）△ADE 为等腰三角形，要分类讨论：①AE ＝AD ，②AE ＝DE ，③AD ＝DE ；（3）①△ADF 与△AEF 的高相等，面积之比等于底之比；连接PE ，证明PE ∥CD ，再利用相似三角形性质易求得结论，②点C ′落在AE 上时可求得DG 的最小值，最大值很容易看出为10．【解析】（1）∵AG 为⊙P 直径∴∠AEG ＝∠AEB ＝90°∵点E 为GĤ的中点， ∴∠BAE ＝∠GAE在△AEB 和△AEG 中{∠BAE =∠GAEAE =AE ∠AEB =∠AEG∴△AEB ≌△AEG （ASA ）∴AG ＝AB ；（2）如图1，△ADE 为等腰三角形，分三种情况：①AE ＝AD ＝8∵AG 为⊙P 直径∴∠AEG ＝∠AEB ＝90°∴BE =√AB 2−AE 2=√102−82=6∵ABCD 是矩形∴∠ABC ＝∠BCD ＝∠BAD ＝∠ADC ＝90°，BC ＝AD ＝8，CD ＝AB ＝10∴∠ABE +∠CBG ＝90°，∠BAE +∠ABE ＝90°∴∠CBG ＝∠BAE在△BCG 和△AEB 中，{∠CBG =∠BAEBC =AE ∠BCG =∠AEB∴△BCG ≌△AEB （ASA ）∴CG ＝BE ＝6∴DG ＝CD ﹣CG ＝10﹣6＝4②AE ＝DE ，过点E 作EM ⊥AD 于M ，∵AE ＝DE ，EM ⊥AD∴∠AEM ＝∠DEM ，∠AME ＝∠DME ＝90°∴AB ∥CD ∥EM∴∠BAE ＝∠AEM ＝∠DEM ＝∠EDG∴EH ̂=EG ̂由（1）得AG ＝AB ＝10∴DG =2−AD 2=√102−82=6；③AD ＝DE ，过D 作DN ⊥AE 于N ，∴∠AND ＝∠AEB ＝90°，AN ＝NE∵∠DAE +∠BAE ＝∠ADN +∠DAE ＝90°∴∠BAE ＝∠ADN∴△ADN ∽△BAE∴AN BE =AD AB =810，即：AN BE =45∴AE BE =85∵∠ABE +∠CBG ＝∠CGB +∠CBG ＝90°∴∠ABE ＝∠CGB∵∠AEB ＝∠BCG ＝90°∴△BCG ∽AEB∴BC CG =AE BE =85，即：8CG =85∴CG ＝5∴DG ＝CD ﹣CG ＝10﹣5＝5综上所述，DG ＝4或6或5．（3）①如图2，点C ′，C 关于直线BG 对称，连接BC ′，连接PE ，由轴对称性质得：BC ′＝BC ，∠C ′BG ＝∠CBG ，GC ＝GC ′，∠BGC ′＝∠BGC ∴∠BC ′G ＝∠BCG ＝90°∴△ABC ′≌△GAD （AAS ）∴AG ＝AB ＝10，DG =√AG 2−AD 2=√102−82=6∵AB ∥CD∴∠BGC ＝∠ABG ＝∠AGB∵AE ⊥BG∴BE ＝EG∵AP ＝PG∴PE ∥AB ∥CD ，PE =12AB ＝5∴△DFG ∽△EFP∴DF EF =DG PE =65∴S △ADF S △AEF =DF EF =65②如图3，当点C ′落在矩形ABCD 对角线AC 上时，∵∠AEB ＝∠BEC ＝∠ABC ＝∠BCG ＝90°∴∠BAC +∠ACB ＝∠CBG +∠ACB ＝90°∴∠BAC ＝∠CBG∴△ABC ∽△BCG ，∴CG BC =BC AB ，即CG =BC 2AB =8210=325∴DG ＝CD ﹣CG ＝10−325=185，当点G 向右运动且不与点C 时，C ′始终落在四边形ADGE 内部， ∴DG ＜10故答案为：185＜DG ＜10．。
2020年深国交G1入学考试数学复习资料：新定义问题专题训练(有答案)
例如：因为 ，所以 ， ．
根据上述规定填空： ， ____________， ， _____________；
已知 ， ， ， ，求 ， 用含m、n的代数式表示 ；
若 ， ， ， ，则a、b的大小关系是：a_______ 填“ ”、“ ”或“ ” ．
【学习新知】定义：如果 且 ，即a的n次方等于 且 ，那么数n叫做以a为底M的对数 ，记作 其中a叫做对数的底数，M叫做真数，n叫做以a为底M的对数．例如：因为 ，所以 ；因为 ，所以 ；因为 ，所以 其中零没有对数；在有理数范围内，负数没有对数．
【应用新知】
根据定义计算： _______； _______； ______．
如果 ，那么 _________．
结合上面的知识计算： ．
已知 ， M、N均为正数 ，求 的值．
答案和解析
1.D
解：由题意可知，原式可化为方程
，
解得 ．
2.C
解：由题意可得： ，
3.A
解：由题意得 ，
，
，
，
，
4.C
解：根据题中的新定义得： ，
5.D
解：由题意可得 只有D符合．
6.B
解：由函数 得 ，则 ，
材料二：劳格数有如下运算性质：若m、n为正数，则
根据劳格数的定义，填空： ____， ____；
若 ，求 的值；
已知 ， ， ，证明： ．
24.【知识重现】在七上数学教材p58中，我们已经学习：求n个相同因数a的积的运算叫做乘方 ，乘方的结果叫做幂 ，a叫做底数 ，n叫做指数 ， 读作“a的n次幂” 或“a的n次方” ；在 中，已知底数a，指数n，求幂M的运算叫做乘方运算．例如 ， ．
2020年深国交G1考试数学复习资料：限时训练23 圆的基本性质
限时训练23圆的基本性质(时间：45分钟总分：54分)一、选择题(每小题3分，共21分)1．(2019·柳州中考)如图，A，B，C，D是⊙O上的点，则图中与∠A相等的角是(D)A．∠B B．∠C C．∠DEB D．∠D(第1题图)(第2题图)2．如图，点A，B，C都在⊙O上，且点C在弦AB所对的优弧上，如果∠AOB＝64°，那么∠ACB的度数是(C)A．26°B．30°C．32°D．64°3．(2019·宜昌中考)如图，点A，B，C均在⊙O上，当∠OBC＝40°时，∠A的度数是(A)A．50°B．55°C．60°D．65°(第3题图)(第4题图)4．如图，AB是⊙O的直径，弦CD⊥AB于点E.若AB＝8，AE＝1，则弦CD的长是(B)A.7 B．27 C．6 D．85．如图，⊙O的半径OD垂直于弦AB，垂足为点C，连接AO并延长交⊙O于点E，连接BE，CE.若AB＝8，CD＝2，则△BCE的面积为(A)A．12 B．15 C．16 D．18(第5题图)(第6题图)6．(2019·滨州中考)如图，AB 为⊙O 的直径，C ，D 为⊙O 上两点，若∠BCD ＝40°，则∠ABD 的大小为( B )A ．60°B ．50°C ．40°D ．20°7．(2019·唐山路南区三模)如图，O 为锐角三角形ABC 的外心，四边形OCDE 为正方形，其中E 点在△ABC 的外部，判断下列叙述何者正确( B )A ．O 是△AEB 的外心，O 是△AED 的外心 B ．O 是△AEB 的外心，O 不是△AED 的外心C ．O 不是△AEB 的外心，O 是△AED 的外心 D ．O 不是△AEB 的外心，O 不是△AED 的外心(第7题图)(第9题图)二、填空题(每小题3分，共12分)8．直径为10 cm 的⊙O 中，弦AB ＝5 cm ，则弦AB 所对的圆周角是__30°或150°__．9．如图，边长为1的小正方形构成的网格中，半径为1的⊙O 的圆心O 在格点上，则∠AED 的正切值为__12__.10．(2019·凉山中考)如图所示，AB 是⊙O 的直径，弦CD ⊥AB 于H ，∠A ＝30°，CD ＝23，则⊙O 的半径是__2__．(第10题图)(第11题图)11．(2019·德州中考)如图，CD 为⊙O 的直径，弦AB ⊥CD ，垂足为E ，AB ︵＝BF ︵，CE ＝1，AB ＝6，则弦AF 的长度为__485__．三、解答题(共21分)12．(10分)(2019·包头中考)如图，在⊙O 中，B 是⊙O 上一点，∠ABC ＝120°，弦AC ＝23，弦BM 平分∠ABC 交AC 于点D ，连接MA ，MC.(1)求⊙O 半径的长； (2)求证：AB ＋BC ＝BM.(1)解：连接OA ，OC.∵∠ABC ＝120°，BM 平分∠ABC ， ∴∠MBA ＝∠MBC ＝12∠ABC ＝60°.∴∠ACM ＝∠ABM ＝60°， ∠MAC ＝∠MBC ＝60°. ∴在△AMC 中，∠AMC ＝∠MAC ＝∠ACM ＝60°. ∴△AMC 是等边三角形．∵AO ＝CO ，∠AOC ＝2∠AMC ＝120°， ∴∠OAC ＝∠OCA ＝30°. 作OH ⊥AC 交AC 于点H. ∴AH ＝CH ＝12AC ＝ 3.∵在Rt △AOH 中，cos ∠OAH ＝AHAO ，∴3AO ＝32.∴AO ＝2. ∴⊙O 的半径长为2；(2)证明：在BM 上截取BE ＝BC ，连接CE. ∵∠MBC ＝60°，BE ＝BC ， ∴△EBC 为等边三角形． ∴CE ＝CB ＝BE ，∠BCE ＝60°. ∴∠BCD ＋∠DCE ＝60°. ∵∠ACM ＝60°，∴∠ECM ＋∠DCE ＝60°. ∴∠ECM ＝∠BCD. ∵△AMC 为等边三角形， ∴AC ＝MC.∴△ACB ≌△MCE(SAS )． ∴AB ＝ME. ∵ME ＋EB ＝BM ， ∴AB ＋BC ＝BM.13．(11分)(2019·绵阳中考)如图，AB 是⊙O 的直径，点C 为BD ︵的中点，CF 为⊙O 的弦，且CF ⊥AB ，垂足为E ，连接BD 交CF 于点G ，连接CD ，AD ，BF.(1)求证：△BFG ≌△CDG ； (2)若AD ＝BE ＝2，求BF 的长．(1)证明：连接BC.∵∠BDC 与∠CFB 都是BC ︵对应的圆周角， ∴∠BDC ＝∠CFB.∵点C 是BD ︵的中点，∴BC ＝CD. 又∵直径AB 垂直于弦CF ， ∴AB 垂直平分弦CF.∴BC ＝BF. ∴CD ＝BF.又∵∠CGD ＝∠BGF ， ∴△BFG ≌△CDG(AAS )；(2)解：连接AC ，过点C 作AD 延长线的垂线，垂足为H ，连接OC. ∵点C 是BD ︵的中点， ∴∠HAC ＝∠BAC ， 即AC 为∠BAD 的平分线． ∵CH ⊥AD ，CE ⊥AB ，∴CH ＝CE. 又∵AC ＝AC ，∴Rt △ACE ≌Rt △ACH(HL )．∴AH ＝AE. 又∵在Rt △CDH 和Rt △CBE 中， BC ＝CD ，CH ＝CE ，∴△CDH ≌△CBE(HL )．∴DH ＝BE ＝2. ∴AE ＝AH ＝AD ＋DH ＝2＋2＝4.∴AB＝AE＋BE＝4＋2＝6.∴OC＝OB＝3.∵BE＝2，∴OE＝OB－BE＝3－2＝1.∴在Rt△COE中，CE2＝OC2－OE2＝9－1＝8.在Rt△BCE中，BC＝CE2＋BE2＝23，∴BF＝2 3.。
2020年深国交G1入学考试数学复习资料：限时训练二(2套)
2020年深国交G1入学考试数学复习资料：限时练习题11、如图，将3个12cm×12cm的正方形沿邻边中点剪开，分成两部分，把所得的六片纸片粘在一个边长为62cm正六边形的外面，然后折成多面体，则此多面体的表面积是2、从图形的几何性质考虑，下列字母图形有一个与其他几个不同的是W S T X H3、方程x2+2x-3=0的实数根的和为4、如图，在平行四边形ABCD中，E、F分别是BC边，CD边的中点，AE、AF分别交BD于点G，H，设∆AGH 的面积为S1S1，五边形GHFCE的面积为S2，则S1:S2的值为5、规定[x]表示不大于x的最大整数，例如[2.3]＝2，[3]＝3，[﹣2.5]＝﹣3．那么函数y=x-[x]的图象为(1)(2)（3）（4）⎧，⎬6、一组数据由5个整数组成，中位数是6，唯一的众数是7，那么这5个整数的和最大只可能是7、如图，在正方形ABCD 中，AE ＝ED ，且EF ＝2FC ，正方形ABCD 的面积是20，则△ABF 的面积是．8、如图，正方形ABCD 的边长为5，点A 的坐标为(-4,0)，点B 在y 轴上，若反比例函数y =k (k >0)的x 图象过点C ，则k =9、如图，直角三角形纸片的两直角边长分别为6，8，按如图所示折叠，使点A 与点B 重合，折痕为DE ，则S △BCE :S △BDE=10、已知函数y ＝ax 2＋2x ＋1．（1）若函数图象与x 轴只有一个交点，则a ＝；（2）若方程ax 2＋2x ＋1＝0至少有一正根，则a 的取值范围是．11、用min {a ,b ,c }表示a ,b ,c 个数中的最小值，设y =min ⎨-x 2⎩+4x ,-x +43⎫x ⎭(x >0)，则y 的最大值是3312、如图，在Rt △ABC 中，∠ACB ＝90°，sin B ＝5，D 是BC 上一点，DE ⊥AB 于E ，CD ＝DE ，AC +CD ＝9．则BC ＝．13、如图，点A ，B 为直线y ＝x 上的两点，过A ，B 两点分别作y 轴的平行线交双曲线y =D 两点．若BD ＝2AC ，则4OC 2﹣OD 2的值为．1（x ＞0）于C ，x 14、若关于x的方程（x ﹣4）（x 2﹣6x +m ）＝0的三个根恰好可以组成某直角三角形的三边长，则m 的值为．15、在n 凸多边形中，除了两个内角外，其余内角之和为2380°，则n =16、如图，AB 为 O 的直径，AB =4，点C 为半圆弧的中点：（1）若 O 的另一条弦AD 长等于2，∠CAD 的度数为；（2）在（1）的条件下，若在直径AB 另一侧有一点E （C ,E 在直线AB 两侧），tan ∠BAE =3，则4CE = ．。
2020年最新深圳国际交流学院G1入学考试数学训
2020年最新深圳国际交流学院G1入学考试数学训练1．如图是由 4 个完全一样的小正方体组成的几何体，这个几何体的主视图是（）A ．B ．C ．D ．2．设 a 为正整数，且 ＜a +1，则 a 的值为（ ）A ．5B ．6C ．7D ．83．下列图形中，不是轴对称图形的是（）A ．B ．C ．D ．4．九年级参展作品中有 4 件获得一等奖，其中有 2 名作者是男生，2 名作者是女生．现在要在抽两人去参加学校总结表彰座谈会，求恰好抽中一男一女的概率（）A ．B ．C ．D ． 5．若在实数范围内有意义，则 x 的取值范围是（）A ．B ．x ＜ 2D ．x ≥06．下列事件中，是必然事件的是（）A ．掷一次骰子，向上一面的点数是 6B ．13 个同学参加一个聚会，他们中至少有两个同学的生日在同一个月C ．射击运动员射击一次，命中靶心D ．经过有交通信号灯的路口，遇到红灯7．如图，l 1∥l 2，等边△ABC 的顶点 A 、B 分别在直线 l 1、l 2，则∠1+∠2＝（ ）A ．30°B ．40°C ．50°D ．60°第 7 题 第 8 题第 10 题8．Rt △ABC 中，AB ＝4，则 cos B 的值是（）A ．B ．C ．D ．9．《九章算术》是我国古代数学名著，有题译文如下：今有门，不知其高宽；有竿，不知其长短．横放，竿比门宽长出 4 尺；竖放，竿比门高长出 2 尺；斜放，竿与门对角线长恰好相等．问门高、宽和对角线的长各是多少？设门对角线的长为 x 尺，下列方程符合题意的是（ ） A ．（x +2）2+（x ﹣4）2＝x 2 B ．（x ﹣2）2+（x ﹣4）2＝x 2 C ．x 2+（x ﹣4）2＝（x ﹣4）2D ．（x ﹣2）2+x 2＝（x +4）210．如图所示，在平面直角坐标系中，直线 y 1＝2x +4 分别与 x 轴，y 轴交于 A ，B 两点，以线段 OB 为一条边向右侧作矩形 OCDB ，且点 D 在直线 y 2＝﹣x +b 上，若矩形 OCDB 的面积为 20，直线 y 1＝2x +4 与直线 y 2＝﹣x +b 交于点 P ．则 P 的坐标为（ ） A ．（2，8）B ．C ．D ．（4，12）11．3x （x ﹣5）+2（5﹣x ）分解因式的结果为．12．将抛物线 y ＝2x 2 向下平移 1 个单位，再向左平移 3 个单位得到的抛物线的解析式是．13．如图：在 Rt △ABC 中，∠B ＝90°，以顶点 C 为圆心，适当长为半径画弧，分别交 AC 、BC 于点 E 、F ，再分别以点 E 、F 为圆心，大于 EF 的长为半径画弧，两弧交于点 P ，作射线 CP 交 AB 于点 D ，若 BD ＝ 2，AC ＝6，则△ACD 的面积为．第 13 题 第 14 题14．如图，若△ABC 内接于半径为 6 的⊙O ，且∠A ＝60°，连接 OB 、OC ，则边 BC 的长为 ．15.（每小题 6 分，共 12 分）（2）解不等式组：，并求出所有整数解之和．16.（6 分）已知 x ，y 满足方程组，求代数式（x ﹣y ）2﹣（x +2y ）（x ﹣2y ）的值．17.（本小题 8 分）某校组织学生到恩格贝 A 和康镇 B 进行研学活动，澄澄老师在网上查得，A 和 B 分 别位于学校 D 的正北和正东方向，B 位于 A 南偏东 37°方向，校车从 D 出发，沿正北方向前往 A 地， 行驶到 15 千米的 E 处时，导航显示，在 E 处北偏东 45°方向有一服务区 C ，且 C 位于 A ，B 两地中点处．（1）求 E ，A 两地之间的距离；（2）校车从A地匀速行驶 1 小时 40 分钟到达 B 地，若这段路程限速 100 千米/时，计算校车是否超速？ （参考数据 ，cos37°＝，tan37°＝）18.（本小题 8 分）为了了解本校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，课题小组随机选取该校部分学生进行了问卷调査（问卷调査表如图 1 所示），并根据调查结果绘制了图 2、图 3两幅统计图（均不完整），请根据统计图解答下列问题．（1）本次接受问卷调查的学生有 名．（2）补全条形统计图．（3）扇形统计图中 B 类节目对应扇形的圆心角的度数为．（4）该校共有 2000 名学生，根据调查结果估计该校最喜爱新闻节目的学生人数．19.（10 分）如图，在平面直角坐标系中，直线 AB 与 y 轴交于点 B （0，7），与反比例函数 y ＝在第二象限内的图象相交于点 A （﹣1，a ）．（1）求直线 AB的解析式；（2）将直线 AB 向下平移 9 个单位后与反比例函数的图象交于点 C 和点 E ，与 y 轴交于点 D ，求△ACD 的面积；（3）设直线 CD 的解析式为 y ＝mx +n ，根据图象直接写出不等式 mx +n ≤ 的解集．20.（本题10 分）如图，△ABC 内接于⊙O，∠CBG＝∠A，CD 为直径，OC 与AB 相交于点E，过点E 作EF⊥BC，垂足为F，延长CD 交GB 的延长线于点P，连接BD．（1）求证：PG 与⊙O 相切；（2）＝，的值；（3）在（2）的条件下，若⊙O 的半径为8，PD＝OD，求OE 的长．21．已知关于x 的方程a（x+m）2+b＝0（a、b、m 为常数，a≠0）的解是x1＝2，x2＝﹣1，那么方程a（x+m+2）2+b＝0 的解．22．有六张正面分别标有数字﹣2，﹣1，0，2，3，4 的不透明卡片，它们除数字不同外其余均相同．现它们背面朝上，洗匀后从中任取一张，将该卡片上的数字记为m，则使关于x 的分式方程有正整数解的概率为．23．如图，在△ABC 中，AB＝AC，点A 在y 轴上，点C 在x 轴上，BC⊥x 轴．延长AC 到点D，过点D 作DE⊥x 轴于点G，且DG＝GE，连接CE，反比例函数（k≠0）的图象经过点B，和CE 交于点F，且CF：FE＝2：1．若△ABE 面积为6，则点D 的坐标为．第23 题第24 题第25 题24．如图，在菱形ABCD 中，∠B＝60°，点P 是△ACD 内一点，连接PA、PC、PD，若PA＝5，PD＝12，PC＝13，则AC•BD＝．25．矩形ABCD 的边AB＝4，边AD 上有一点M，连接BM，将MB 绕M 点逆时针旋转90°得MN，N 恰好落在CD 上，过M、D、N 作⊙O，⊙O 与BC 相切，Q 为⊙O 上的动点，连BQ，P 为BQ 中点，连AP，则AP 的最小值为．26.（本题 8 分）为响应成都市“创建全国文明城市”号召，某单位不断美化环境，拟在一块矩形空地上修建绿色植物园，其中一边靠墙，可利用的墙长不超过18m，另外三边由36m 长的栅栏围成．设矩形ABCD 空地中，垂直于墙的边AB＝xm，面积为ym2（如图）．（1）求y 与x 之间的函数关系式，并写出自变量x 的取值范围；（2）若矩形空地的面积为160m2，求x 的值；（3）若该单位用8600 元购买了甲、乙、丙三种绿色植物共400 棵（每种植物的单价和每棵栽种的合理用地面积如下表）．问丙种植物最多可以购买多少棵？此时，这批植物可以全部栽种到这块空地上吗？请说明理由．甲乙丙单价（元/棵）141628合理用地（m2/棵）0.410.427.（10分）（1）证明推断：如图（1），在正方形ABCD中，点E，Q分别在边BC，AB上，DQ⊥AE于点O，点G，F 分别在边CD，AB 上，GF⊥AE．①求证：DQ＝AE；②推断的值为；（2）类比探究：如图（2），在矩形ABCD中，＝k（k为常数）．将矩形ABCD沿GF折叠，使点A 落在BC 边上的点E 处，得到四边形FEPG，EP 交CD 于点H，连接AE 交GF 于点O．试探究GF 与AE 之间的数量关系，并说明理由；（3）拓展应用：在（2）的条件下，连接CP，当k＝时，若tan∠CGP＝，GF＝2 ，求CP 的长．。
2020年深国交G1入学考试数学复习资料：填空综合训练-4(25题)
填空综合题-41.化简：=----2222a ab b ab ab b a 2.有一组数4，6，8，17，x ，若这组数的中位数等于平均数，则符合题意的=x 3.已知x 为实数，且3122=+x x ，则=+331x x 4.若代数式113+x 被代数式1-x 除，余数是5.若y x ,满足方程组⎩⎨⎧=++=+++032015622y x y x x ,则我们也可用只含y 方程表示为6.如图，在平面直角坐标系中，直线12y x =-与反比例函数(0)k y k x=≠在第二象限内的图象相交于点(,1)A m ．将直线12y x =-向上平移后与反比例函数图象在第二象限内交于点B ，与y 轴交于点C ，且ABO ∆的面积为32，求直线BC 的解析式为7.已知实数y x ,满足⎪⎩⎪⎨⎧+=+=525222x y y x ，且y x ≠，则=+-3223222y y x x 8.关于x ，y 的二元一次方程组237328x y t x y t +=⎧⎨+=⎩的解x ，y 满足435x y -=，则t 的值为9.如图，P 是等边三角形ABC 中的一个点，2PA =，23PB =，4PC =，则三角形ABC 的边长为10.如图所示的飞镖游戏板是顺次连接正六边形的三个不相邻的顶点后得到的，若某人向该游戏板投掷镖一次（假设飞镖落在游戏板上），则飞镖落在阴影部分的概率是11.若322255(21)()3x ax x x ax x b --+=+--+，其中a ，b 为整数，则ab 的值为12.如图，在ABC ∆中，60A ∠=︒，BE 、CF 分别是AC 、AB 边上的高，连接EF ，则:EF BC 的值为13.如图，在边长为2的正方形ABCD 中，以点D 为圆心，AD 为半径画 AC ，再以BC 为直径画半圆，若阴影部分①的面积为1S ，阴影部分②的面积为2S ，则图中21S S -的值为14.从1，2，3，5，7，8中任取两数相加，在不同的和数中，是2的倍数的个数为a ，是3的倍数的个数为b ，则样本6、a 、b 、9的中位数是．15.如图，AB 是圆O 的直径，AB ＝8，点M 在圆O 上，∠MOB ＝60°，N 是MB 的中点，P 为AB 上一动点，则PM +PN 的最小值是．16.如下图所示，矩形纸片ABCD 中，2AB =，6AD =，将其折叠，使点D 与点B 重合，得折痕EF ，则tan BFE ∠的值是．17.有依次排列的3个数：3，9，8，对任意相邻的两个数，都用右边的数减去左边的数，所得之差写在这两个数之间，可产生一个新数串：3，6，9，1-，8，这称为第一次操作；做第二次同样的操作后也可产生一个新数串：3，3，6，3，9，10-，1-，9，8，继续依次操作下去，问：从数串3，9，8开始操作第100次以后所产生的那个新数串的所有数之和是多少？．18.满足不等式3002005<n 的最大整数n 等于．19.甲、乙两车分别从A ，B 两车站同时开出相向而行，相遇后甲驶1小时到达B 站，乙再驶4小时到达A 站.那么，甲车速是乙车速的倍。
圆的计算与证明(答案)
圆的计算与证明参考答案与试题解析一．解答题（共40小题）1．如图，已知AB是⊙O的直径，PB切⊙O于点B，过点B作BC⊥PO于点D，交⊙O于点C，连接AC、PC（1）求证：PC是⊙O的切线；（2）若∠BPC＝60°，PB＝3，求阴影部分面积．【解答】（1）证明：连接OC，如图：}∵OB＝OC，∴∠OBC＝∠OCB，∵AB是⊙O的直径，PB切⊙O于点B，∴AB⊥PB，∠PBO＝∠OBC+∠PBC＝90°，∵BC⊥PO，∴BD＝CD，∴PO是BC的垂直平分线，∴PB＝PC，【∴∠PBC＝∠PCB，∴∠OCB+∠PCB＝∠OBC+∠PBC＝90°，即OC⊥PC，∴PC是⊙O的切线；（2）解：由（1）知，PB、PC为⊙O的切线，∴PB＝PC，∵∠BPC＝60°，PB＝3，∴△PBC是等边三角形，)∴BC＝PB＝3，∠PBC＝60°，∴∠OBC＝30°，∵AB是⊙O的直径，∴∠ACB＝90°，∴∠AOC＝60°，∵OA＝OC，∴△AOC是等边三角形，∴AC＝OC＝OB＝PB＝，,∴扇形OAC的面积＝＝，△OAC的面积＝×（）2＝，∴阴影部分面积＝﹣．2．如图，已知AB为⊙O的直径，CD切⊙O于C点，弦CF⊥AB于E点，连结AC．（1）求证：∠ACD＝∠ACF；（2）当AD⊥CD，BE＝2cm，CF＝8cm，求AD的长．【解答】（1）证明：连接OC，（∵CD切⊙O于C点，∴∠OCD＝90°，∴∠ACD+∠ACO＝90°，∵CF⊥AB，∴∠AEC＝90°，∴∠ACF+∠CAE＝90°，∵OA＝OC，∴∠ACO＝∠CAE，^∴∠ACD＝∠ACF；（2）解：由（1）可知，∠ACD＝∠ACF，∵CF⊥AB，∴CE＝CF＝4，设⊙O的半径为r，则OE＝r﹣2，在Rt△OEC中，OC2＝OE2+CE2，即r2＝（r﹣2）2+42，解得，r＝5，∴AE＝AB﹣BE＝8，?∵∠ACD＝∠ACF，AD⊥CD，CF⊥AB，∴AD＝AE＝8（cm）．3．如图，O为∠MBN角平分线上一点，⊙O与BN相切于点C，连结CO并延长交BM于点A，过点A作AD⊥BO于点D．（1）求证：AB为⊙O的切线；（2）若BC＝6，tan∠ABC＝，求AD的长．【解答】解：（1）过点O作OE⊥AB于点E，~∵O为∠MBN角平分线上一点，∴∠ABD＝∠CBD，又∵BC为⊙O的切线，∴AC⊥BC，∵AD⊥BO于点D，∴∠D＝90°，∴∠BCO＝∠D＝90°，∵∠BOC＝∠AOD，∴∠BAD+∠ABD＝90°，∠AOD+∠OAD＝90°，∵∠AOD＝∠BAD，∴∠ABD＝∠OAD，∴∠OBC＝∠OAD＝∠ABD，在△BOC和△BOE中，∵，∴△BOC≌△BOE（AAS），&∴OE＝OC，∵OE⊥AB，∴AB是⊙O的切线；（2）∵∠ABC+∠BAC＝90°，∠EOA+∠BAC＝90°，∴∠EOA＝∠ABC，∵tan∠ABC＝、BC＝6，∴AC＝BC?tan∠ABC＝8，|则AB＝10，由（1）知BE＝BC＝6，∴AE＝4，∵tan∠EOA＝tan∠ABC＝，∴，∴OE＝3，OB＝＝3，∵∠ABD＝∠OBC，∠D＝∠ACB＝90°，∴△ABD∽△OBC，∴，即＝，∴AD＝2．4．如图，直线MN交⊙O于A，B两点，AC是⊙O直径，∠CAM的平分线交⊙O于点D，过点D 作DE⊥MN于点E．（1）求证：DE是⊙O的切线；（2）若DE＝6cm，AE＝3cm，求⊙O的半径．【解答】（1）证明：连接OD，如图所示：∵OA＝OD，[∴∠3＝∠2，∵AD平分∠CAM，∴∠2＝∠1，∴∠1＝∠3，∴MN∥OD，∵DE⊥MN，∴DE⊥OD，∴DE是⊙O的切线；）（2）解：连接CD，如图所示：∵AC是⊙O的直径，∴∠ADC＝90°，∴AD＝＝＝3（cm），∵DE⊥MN，∴∠AED＝90°，∴∠ADC＝∠AED，又∵∠2＝∠1，-∴△ADC∽△AED，∴＝，即＝，∴AC＝15（cm），∴OA＝AC＝cm，即⊙O的半径为cm．5．如图，AB是⊙O的直径，弦DE垂直平分半径OA，C为垂足，弦DF与半径OB相交于点P，连接EF、EO．若DE＝2，∠DP A＝45°．《（1）求⊙O的半径；（2）求图中阴影部分及△PBF的面积．【解答】解：（1）∵OC⊥DE，∴DC＝EC＝DE＝×2＝，∵弦DE垂直平分半径OA，∴OC＝OA＝OE，在Rt△OCE中，∵OE＝2OC，^∴∠E＝30°，∴OC＝CE＝1，∴OE＝2，即⊙O的半径为2；（2）连结OF，BF，BE，作BH⊥DF于H，如图，∵∠DP A＝45°，∴∠DDC＝45°，∴∠EOF＝2∠EPF＝90°，△PCD为等腰直角三角形，|∴图中阴影部分的面积＝S扇形EOF﹣S△OEF＝﹣?2?2＝π﹣2；∵BC＝AB﹣AC＝4﹣1＝3，而DC＝，∴BD＝＝2，∵BC垂直平分DE，∴BD＝BE＝2，；∵BD＝DE＝BE，∴△BED为等边三角形，∴∠BED＝60°，∴∠BFD＝∠BED＝60°，∵△PCD为等腰直角三角形，∴PC＝DC＝，∴OP＝PC﹣OC＝﹣1，∴PB＝2﹣（﹣1）＝3﹣，@在Rt△PBH中，∠BPH＝∠DPC＝45°，∴BH＝PH＝PB＝，在Rt△BHF中，∠HBF＝30°，∴HF＝BH＝?＝，∴PF＝PH+HF＝+＝，∴S△PBF＝??＝．6．如图，AB是⊙O直径，弦CD⊥AB于点E，过点C作DB的垂线，交AB的延长线于点G，垂足为点F，连结AC．\（1）求证：AC＝CG；（2）若CD＝8，OG＝10，求⊙O的半径．【解答】（1）证明：∵DF⊥CG，CD⊥AB，∴∠DEB＝∠BFG＝90°，∵∠DBE＝∠GBF，∴∠D＝∠G，∵∠A＝∠D，，∴∠A＝∠G，∴AC＝CG．（2）解：设⊙O的半径为r．则AG＝OA+OG＝r+10，∵CA＝CG，CD⊥AB，∴AE＝EG＝，EC＝ED＝4，∴OE＝AE﹣OA＝，在Rt△OEC中，∵OC2＝OE2+EC2，'∴r2＝（）2+42，解得r＝或（舍弃），∴⊙O的半径为．7．如图，射线PG平分∠EPF，O为射线PG上一点，以O为圆心，13为半径作⊙O，分别与∠EPF的两边相交于A、B和C、D，连结OA，且OA∥PE．（1）求证：AP＝AO；（2）若弦AB＝24，求OP的长．<【解答】（1）证明：如图，∵PG平分∠EPF，∴∠CPO＝∠APO．∵AO∥PE，∴∠CPO＝∠AOP，∴∠APO＝∠AOP，∴AP＝AO．[（2）解：过点O作OH⊥AB于H，如图．根据垂径定理可得AH＝BH＝AB＝12，∴PH＝P A+AH＝AO+AH＝13+12＝25．在Rt△AHO中，OH＝＝＝5，由勾股定理得：OP＝＝＝＝5．则OP的长为5．.8．如图，Rt△ABC中，∠ACB＝90°，O为△ABC角平分线的交点，以OC为半径的⊙O交△ABC 于D、E、F、G．（1）求证：CD＝EF；（2）若⊙O的半径为4，AE＝2，求AB的长．【解答】（1）证明：作OM⊥AB于M，ON⊥AC于N，OH⊥CG于G，连接OE、OD，∵点O为△ABC的角平分线交点，∴OM＝ON，∵OE＝OD＝OC，·∴RT△OME≌RT△OND（HL），∴ME＝ND，∵EF＝2ME，CD＝2ND，∴CD＝EF；（2）解：由（1）可知CD＝EF＝CG，∵点O为△ABC的角平分线交点，∴OM＝ON＝OH，∵∠ACB＝90°，)∴四边形ONCH是正方形，∴OM＝ON＝OH＝CD＝EF＝CG，∵OC＝4，∴OH＝OC＝4，∴EF＝CD＝CG＝8，易证得AM＝AN＝6，BM＝BH，∴AC＝10，设BM＝BH＝x，则BC＝x+4，AB＝x+6，\∵∠ACB＝90°，∴AB2＝AC2+BC2，即（6+x）2＝102+（4+x）2，解得x＝20，∴BM＝20，∴AB＝AM+BM＝20+6＝26．9．如图，在圆O中，弦AB＝8，点C在圆O上（C与A，B不重合），连接CA、CB，过点O分别作OD⊥AC，OE⊥BC，垂足分别是点D、E．（1）求线段DE的长；、（2）点O到AB的距离为3，求圆O的半径．【解答】解：（1）∵OD经过圆心O，OD⊥AC，∴AD＝DC，同理：CE＝EB，∴DE是△ABC的中位线，∴DE＝AB，∵AB＝8，,∴DE＝4．（2）过点O作OH⊥AB，垂足为点H，OH＝3，连接OA，∵OH经过圆心O，∴AH＝BH＝AB，∵AB＝8，∴AH＝4，？在Rt△AHO中，AH2+OH2＝AO2，∴AO＝5，即圆O的半径为5．10．如图，Rt△OAB中，∠OAB＝90°，以OA为半径的⊙O交BO于点C，交BO延长线于点D．在⊙O上取一点E，且＝，延长DE与BA交于点F．（1）求证：△BDF是直角三角形；（2）连接AC，AC＝2，OC＝2BC，求AF的长．【解答】（1）证明：如图连接EC交OA于H．`∵＝，∴OA⊥EC，∵CD是⊙O的直径，∴∠DEC＝90°，∴DF⊥EC，∴OA∥DF，∵BF是⊙O的切线，∴OA⊥BF，、∴DF⊥BF，∴∠F＝90°，∴△DFB是直角三角形．（2）解：∵∠DEC＝∠F＝90°，∴EC∥FB，∴＝＝2，∴OH＝2AH，设AH＝m，则OH＝2m，OC＝3m，#∵CH2＝OC2﹣OH2＝AC2﹣AH2，∴9m2﹣4m2＝40﹣m2，∴m＝（负根已经舍弃），∴CH＝，∵OA⊥EC，∴EH＝HC＝，∵∠F＝∠F AH＝∠AHE＝90°，∴四边形AFEH是矩形，"∴AF＝EH＝．11．如图，在等腰△ABC中，AB＝BC，以AB为直径的⊙O，分别与AC和BC相交于点D和E，连接OD．（1）求证：OD∥BC；（2）求证：AD＝DE．【解答】证明：（1）∵OA＝OD，∴∠OAD＝∠ODA，∵AB＝BC，~∴∠BAC＝∠OAD＝∠C，∴∠ODA＝∠C，∴OD∥BC；（2）连接半径OE，如图，∴OB＝OE，∴∠B＝∠OEB，由（1）知OD∥BC，∴∠AOD＝∠B，"∴∠OEB＝∠EOD，∴∠EOD＝∠B，∴∠AOD＝∠EOD，∴AD＝DE．12．如图，点C在以线段AB为直径的圆上，且，点D在AC上，且DE⊥AB于点E，F是线段BD的中点，连接CE、FE．（1）若AD＝6，BE＝8，求EF的长；（2）求证：CE＝EF．】【解答】解：（1）∵点C在以线段AB为直径的圆上，且∴∠ACB＝90°，且AC＝BC，∴△ABC为等腰直角三角形，∴∠A＝∠ABC＝45°，∵DE⊥AB，∴AE＝DE＝AD＝×6＝6，在Rt△BDE中，;∵DE＝6，BE＝8，∴BD＝＝10，又∵F是线段BD的中点，∴EF＝BC＝5；（2）如图，连接CF，∵∠BED＝∠AED＝∠ACB＝90°，∵点F是BD的中点，∴CF＝EF＝FB＝FD，{∴B、C、D、E在以BD为直径的圆上，∴∠EFC＝2∠EBC＝2×45°＝90°，∴△EFC为等腰直角三角形，∴CE＝EF．13．如图，⊙O的半径OA⊥弦BC于E，D是⊙O上一点．（1）求证：∠ADC＝∠AOB；（2）求AE＝2，BC＝6，求OA的长．…【解答】（1）证明：∵OA⊥BC，∴＝，∴∠ADC＝∠AOB；（2）解：∵OA⊥BC，∴BE＝CE＝BC＝×6＝3，设⊙O的半径为r，则OA＝OB＝r，OE＝r﹣2，在Rt△OBE中，32+（r﹣2）2＝r2，解得r＝，-即OA的长为．14．如图，BD是⊙O的直径．弦AC垂直平分OD，垂足为E．（1）求∠DAC的度数；（2）若AC＝6，求BE的长．【解答】解：（1）连接OA．∵AC垂直平分OD，∴AO＝AD，^又OA＝OD，∴△OAD是等边三角形，∴∠DAO＝60°．∵AC⊥OD，AO＝AD，∴∠DAC＝∠OAC＝×60°＝30°，（2）∵OD⊥AC，AC＝6，∴AE＝AC＝3，∵AC垂直平分OD，垂足为E，>∴∠AEO＝90°，OE＝OD，∴OE＝OA，设OE＝x，则OA＝OB＝2x，在Rt△AEO中，AE2+EO2＝AO2，即：32+x2＝（2x）2，解得，x＝．∴BE＝OE+OB＝x+2x＝3x＝3．…15．如图所示，已知AB为⊙O的直径，CD是弦，且AB⊥CD于点E．连接AC、OC、BC．（1）求证：∠ACO＝∠BCD；（2）若tan∠ACO＝，CD＝6，求⊙O的直径．【解答】（1）证明：∵AB⊥CD，∴＝，∴∠A＝∠BCD，∵OA＝OC，【∴∠ACO＝∠A，∴∠ACO＝∠BCD；（2）解：∵AB⊥CD，∴CE＝DE＝CD＝3，在Rt△BCE中，∵tan∠BCD＝tan∠ACO＝＝，∴BE＝1，设⊙O的半径为r，则OC＝r，OE＝r﹣1，在Rt△OCE中，32+（r﹣1）2＝r2，解得r＝5，《∴⊙O的直径为10．16．已知如图，⊙O的半径为4，四边形ABCD为⊙O的内接四边形，且∠C＝2∠A．（1）求∠A的度数．（2）求BD的长．【解答】解：（1）∵四边形ABCD为⊙O的内接四边形，∴∠C+∠A＝180°，∵∠C＝2∠A，…∴∠A＝60°；（2）连接OB，OD，作OH⊥BD于H∵∠A＝60°，∠BOD＝2∠A，∴∠BOD＝120°；又∵OB＝OD，∴∠OBD＝∠ODB＝30°，∵OH⊥BD于H，在Rt△DCP中，，》∴，∵OH⊥BD于H，∴．17．已知在△ABC中，AB＝BC，以AB为直径的⊙O分别交AC于D，BC于E，连接ED．（1）求证：ED＝DC；（2）若CD＝6，EC＝4，求AB的长．·【解答】（1）证明：∵A、B、E、D四点共圆，∴∠DEC＝∠A，∵AB＝BC，∴∠A＝∠C，∴∠DEC＝∠C，∴ED＝DC；（2）解：连接BD，·∵AB为⊙O的直径，∴∠ADB＝90°，即BD⊥AC，∵AB＝BC，CD＝6，∴AD＝DC＝6，∴AC＝12，∵∠A＝∠DEC，∠C＝∠C，∴△DEC∽△BAC，…∴＝，∴＝，解得：BC＝6，∵AB＝BC，∴AB＝6．18．如图，在△ABC中，AB＝AC，以AB为直径的⊙O与边BC，AC分别交于D，E两点，过点D 作DH⊥AC于点H．（1）求证：BD＝CD；（2）连结OD若四边形AODE为菱形，BC＝8，求DH的长．]【解答】（1）证明：如图，连接AD．∵AB是直径，∴∠ADB＝90°，∴AD⊥BC，∵AB＝AC，∴BD＝CD．：（2）解：如图，连接OE．∵四边形AODE是菱形，∴OA＝OE＝AE，∴△AOE是等边三角形，∴∠A＝60°，∵AB＝AC，∴△ABC是等边三角形，【∵OA＝OB＝BD＝CD∴AE＝EC，∴CD＝CE，∵∠C＝60°，∴△EDC是等边三角形，∵DH⊥EC，CD＝4，∴DH＝CD?sin60°＝2．19．如图，AB是⊙O的直径，CD是⊙O的一条弦，且CD⊥AB于点E．（1）求证：∠BCO＝∠D；#（2）若CD＝，AE＝2，求⊙O的半径．【解答】（1）证明：如图．∵OC＝OB，∴∠BCO＝∠B．∵∠B＝∠D，∴∠BCO＝∠D；（2）解：∵AB是⊙O的直径，且CD⊥AB于点E，、∴CE＝CD＝×4＝2，在Rt△OCE中，OC2＝CE2+OE2，设⊙O的半径为r，则OC＝r，OE＝OA﹣AE＝r﹣2，∴r2＝（2）2+（r﹣2）2，解得：r＝3，∴⊙O的半径为3．20．如图，△ABC内接于⊙O，∠BAC＝60°，高AD的延长线交⊙O于点E，BC＝6，AD＝5．!（1）求⊙O的半径；（2）求DE的长．【解答】解：（1）如图，作直径BF，连接CF，∴∠BCF＝90°，∵∠F＝∠BAC＝60°，∴BF＝＝＝4，∴⊙O的半径为；$（2）如图，过O作OG⊥AD于G，OH⊥BC于H，∴GE＝GA，四边形OHDG是矩形，∴OH＝DG，∵OB＝，∠FBC＝30°，∴OH＝，∴DG＝，∴AG＝AD﹣GD＝5﹣，】∴EG＝5﹣，∴DE＝EG﹣GD＝＝．21．如图，Rt△ABC中，∠C＝90°，在BC上取一点D使AD＝BD，连结AD，作△ACD的外接圆⊙O，交AB于点E．（1）求证：AE＝BE；（2）若CD＝3，AB＝4，求AC的长．【解答】解：（1）证明：连结DE，、∵∠C＝90°，∴AD为直径，∴DE⊥AB，∵AD＝BD，∴AE＝BE；（2）设BD＝x，∵∠B＝∠B，∠C＝∠DEB＝90°∴△ABC～△DBE，~∴＝，∴，∴x＝5．∴AD＝BD＝5，∴AC＝＝4．22．如图，△ABC内接于⊙O，OE⊥BC于E，延长EO交AB于F，交⊙O于D，A为的中点，连接BD．（1）求证：∠ACB＝3∠ABC；）（2）若OF＝5，EO＝7，求△BDF的面积．【解答】（1）证明：∵OE⊥BC，∴＝＝，∵A为的中点，∴＝＝，∴＝，∴＝，~∴∠ACB＝3∠ABC；（2）连接OB，设OB＝OD＝r，∵OE⊥BC，OF＝5，EO＝7，∴DF＝r﹣5，BE＝，过F作FH⊥BD于H，∴FH＝FE＝12，∠DHF＝∠DEB＝90°，DH＝＝，∵∠FDH＝∠BDE，|∴△DHF∽△DEB，∴＝，∴＝，∴r＝25，∴DE＝32，BE＝24，∴BD＝＝＝40，∴△BDF的面积＝＝240．)23．如图，△ABC内接于⊙O，∠ABC和∠BAC的平分线交于点E，延长AE分别交BC，⊙O于点F，D，连接BD．（1）求证：BD＝DE．（2）若BD＝6，AD＝10，求EF的长．【解答】（1）证明：∵AD平分∠BAC，∴∠BAD＝∠CAD．∴＝．∴∠DBC＝∠CAD，；∵BE平分∠ABC，∴∠ABE＝∠CBE，由∠BED＝∠BAD+∠ABE，∠DBE＝∠DBC+∠CBE，∴∠BED＝∠DBE，∴DB＝DE；（2）解：由（1）得∠DBC＝∠CAD，∠D＝∠D，*∴△DBF∽△DAB，∴＝，∵BD＝6，AD＝10，∴＝，∴DF＝3.6，且由（1）得：DE＝BD＝6，∴EF＝DE﹣DF＝6﹣3.6＝2.4．24．如图，△ABC内接于⊙O，直径AD⊥BC于点E，连结CO．<（1）求证：∠COD＝∠CAB；（2）若＝2，AB＝3，求图中阴影部分面积．【解答】（1）证明：∵AD是⊙O的直径，AD⊥BC，∴＝＝，∵∠CAB的度数＝的度数，∠COD的度数＝的度数，∴∠COD＝∠CAB；（2）解：∵＝2，$∴∠AOC＝COD，∵直径AD⊥BC于点E，∴＝，∴AC＝AB＝3，∴OC＝2，∴S阴影＝2×（﹣×32）＝．25．如图，⊙O是△ABC的外接圆，AE平分∠BAC交⊙O于点E，∠ABC的平分线BF交AD于点F，交BC于点D．（1）求证：BE＝EF；}（2）若DE＝4，DF＝3，求AF的长．【解答】（1）证明：∵AE平分∠BAC，∴∠1＝∠4，∵∠1＝∠5，∴∠4＝∠5，∵BF平分∠ABC，∴∠2＝∠3，~∵∠6＝∠3+∠4＝∠2+∠5，即∠6＝∠EBF，∴EB＝EF；（2）解：∵DE＝4，DF＝3，∴BE＝EF＝DE+DF＝7，∵∠5＝∠4，∠BED＝∠AEB，∴△EBD∽△EAB，∴＝，即＝，(∴EA＝，∴AF＝AE﹣EF＝﹣7＝．26．如图，CD是⊙O的直径，弦AB⊥CD，垂足为H，FG是⊙O的切线，FG∥BD，DF与AB交于点E．（1）求证：BE＝BD；（2）若AB＝8，DH＝3，求EH的长．【解答】解：（1）如图，连接OF，/∵FG是⊙O的切线，∴∠GFD+∠OFD＝90°，∵AB⊥CD，∴∠DEH+∠ODE＝90°，∵OF＝OD，∴∠OFD＝∠ODF．∴∠DEH＝∠GFD，#∵FG∥BD，∴∠GFD＝∠BDF，∴∠DEH＝∠BDF，∴BE＝BD；（2）∵CD是⊙O的直径，弦AB⊥CD，垂足为H，∴，∵DH＝3，∴BD＝5，"∵BE＝BD，∴BE＝5，∴EH＝BE﹣BH＝1，答：EH的长为1．27．如图，AB是⊙O的直径，C点在⊙O上，AD平分角∠BAC交⊙O于D，过D作直线AC的垂线，交AC的延长线于E，连接BD，CD．（1）求证：BD＝CD；（2）求证：直线DE是⊙O的切线；（3）若DE＝，AB＝4，求AD的长．'【解答】（1）证明：∵在⊙O中，AD平分角∠BAC，∴∠CAD＝∠BAD，∴BD＝CD；（2）证明：连接半径OD，如图1所示：则OD＝OA，∴∠OAD＝∠ODA，∵DE⊥AC于E，在Rt△ADE中，）∴∠EAD+∠ADE＝90°，由（1）知∠EAD＝∠BAD，∴∠BAD+∠ADE＝90°，即∠ODA+∠ADE＝90°，∴OD⊥DE，∴DE是⊙O的切线；（3）解：过点D作DF⊥AB于F，如图2所示：则DF＝DE＝，∵AB＝4，·∴半径OD＝2，在Rt△ODF中，OF＝＝＝1，∴∠ODF＝30°，∴∠DOB＝60°，∵OD＝OB，∴△OBD是等边三角形，∴OF＝FB＝1，∴AF＝AB﹣FB＝4﹣1＝3，\在Rt△ADF中，AD＝＝＝2．28．如图，AB是⊙O的直径，AC⊥AB，E为⊙O上的一点，AC＝EC，延长CE交AB的延长线于点D．（1）求证：CE为⊙O的切线；（2）若OF⊥AE，AE＝4，∠OAF＝30°，求图中阴影部分的面积．（结果保留π）【解答】（1）证明：连接OE，：∵AC＝EC，OA＝OE，∴∠CAE＝∠CEA，∠F AO＝∠FEO，∵AC⊥AB，∴∠CAD＝90°，∴∠CAE+∠EAO＝90°，∴∠CEA+∠AEO＝90°，即∠CEO＝90°，∴OE⊥CD，^∴CE为⊙O的切线；（2）解：设OF＝x，∵∠OAF＝30°，OF⊥AF，∴OA＝2OF＝2x，在Rt△OEF中，由勾股定理得：，解得x＝2，∴OA＝4，∴，、∵∠AOE＝120°，AO＝4；∴，∴．29．如图，点D是以AB为直径的⊙O上一点，过点B作⊙O的切线，交AD的延长线于点C，E 为BC的中点，连接DE交BA的延长线于点F．（1）求证：DE是⊙O的切线；（2）若OA＝AF，DF＝4，求阴影部分面积．~【解答】解：（1）连接OD，OE，∵E为BC的中点，∴BE＝CE，∵AO＝OB，∴OE∥AC，∴∠OAD＝∠BOE，∠ADO＝∠DOE，∵OD＝OA，∴∠OAD＝∠ADO，：∴∠DOE＝∠BOE，∵OD＝OB，∴△DOE≌△BOE（SAS），∴∠ODE＝∠OBE，∵BC是⊙O的切线，∴∠OBE＝90°，∴∠ODE＝90°，∴DE是⊙O的切线；)（2）解：∵OA＝AF，∴OD＝OF，∵∠ODF＝90°，∴AD＝OA，∴△ADO是等边三角形，∴∠DOF＝60°，∵DF＝4，∴OD＝DF＝，-∴阴影部分面积＝S△ODF﹣S扇形AOD＝﹣＝﹣．30．如图，点O为Rt△ABC斜边AB上的一点，∠C＝90°，以OA为半径的⊙O与BC交于点D，与AC交于点E，连接AD且AD平分∠BAC．（1）求证：BC是⊙O的切线；（2）若∠BAC＝60°，OA＝2，求阴影部分的面积（结果保留π）【解答】（1）证明：连接OD，]∵AD平分∠BAC，∴∠BAD＝∠DAC，∵AO＝DO，∴∠BAD＝∠ADO，∴∠CAD＝∠ADO，∴AC∥OD，∵∠ACD＝90°，∴OD⊥BC，(∴BC与⊙O相切；（2）解：连接OE，ED，OE与AD交于点M．∵∠BAC＝60°，OE＝OA，∴△OAE为等边三角形，∴∠AOE＝60°，∴∠ADE＝30°，又∵∠OAD＝∠BAC＝30°，.∴∠ADE＝∠OAD，∴ED∥AO，∴四边形OAED是菱形，∴OE⊥AD，且AM＝DM，EM＝OM，∴S△AED＝S△AOD，∴阴影部分的面积＝S扇形ODE＝＝π．31．如图，正六边形ABCDEF内接于⊙O，BE是⊙O的直径，连接BF，延长BA，过F作FG⊥BA，垂足为G．（1）求证：FG是⊙O的切线；{（2）已知FG＝2，求图中阴影部分的面积．【解答】（1）证明：连接OF，AO，∵AB＝AF＝EF，∴＝＝，∴∠ABF＝∠AFB＝∠EBF＝30°，∵OB＝OF，∴∠OBF＝∠BFO＝30°，】∴∠ABF＝∠OFB，∴AB∥OF，∵FG⊥BA，∴OF⊥FG，∴FG是⊙O的切线；（2）解：∵＝＝，∴∠AOF＝60°，∵OA＝OF，（∴△AOF是等边三角形，∴∠AFO＝60°，∴∠AFG＝30°，∵FG＝2，∴AF＝4，∴AO＝4，∵AF∥BE，∴S△ABF＝S△AOF，-∴图中阴影部分的面积＝＝．32．如图，正方形ABCD的外接圆为⊙O，点P在劣弧BC上（不与B、C点重合）．（1）求∠BPC的度数；（2）若正方形ABCD的边长为2cm，求⊙O的半径及阴影部分的面积．【解答】解：（1）连结AC，∵四边形ABCD为正方形，$∴∠BAC＝45°，∵四边形ABPC是圆内接四边形，∴∠BPC+∠BAC＝180°，∴∠BPC＝180°﹣45°＝135°；（2）连结OC、OD，则OC＝OD，∵正方形ABCD为⊙O的内接四边形，∠COD＝90°，在Rt△COD中，OC＝CD＝，@阴影部分的面积＝﹣××＝﹣1．33．如图，正方形ABCD的外接圆为⊙O，点P在劣弧上（不与C点重合）．（1）求∠BPC的度数；（2）若⊙O的半径为8，求正方形ABCD的边长．【解答】解：（1）连接OB，OC，∵四边形ABCD为正方形，…∴∠BOC＝90°，∴∠P＝∠BOC＝45°；（2）过点O作OE⊥BC于点E，∵OB＝OC，∠BOC＝90°，∴∠OBE＝45°，∴OE＝BE，∵OE2+BE2＝OB2，∴BE＝＝＝4【∴BC＝2BE＝2×4＝8．34．如图，P A，PB分别与⊙O相切于点A，B，AC为弦，BC为⊙O的直径，若∠P＝60°，PB＝2cm．（1）求证：△P AB是等边三角形；（2）求AC的长．【解答】解：（1）∵P A，PB分别与⊙O相切于点A，B，∴P A＝PB，且∠P＝60°，|∴△P AB是等边三角形；（2）∵△P AB是等边三角形；∴PB＝AB＝2cm，∠PBA＝60°，∵BC是直径，PB是⊙O切线，∴∠CAB＝90°，∠PBC＝90°，∴∠ABC＝30°，∴tan∠ABC＝＝，∴AC＝2×＝cm．￥35．如图，AB为⊙O直径，P A、PC分别与⊙O相切于点A、C，PQ⊥P A，PQ交OC的延长线于点Q．（1）求证：OQ＝PQ；（2）连BC并延长交PQ于点D，P A＝AB，且CQ＝6，求BD的长．【解答】（1）证明：连接OP．∵P A、PC分别与⊙O相切于点A，C，∵OA＝OC，OP＝OP，、∴△OP A≌△OPC（SSS），∴∠AOP＝∠POC，∵QP⊥P A，∴QP∥BA，∴∠QPO＝∠AOP，∴∠QOP＝∠QPO，∴OQ＝PQ．&（2）设OA＝r．∵OB＝OC，∴∠OBC＝∠OCB，∵OB∥QD，∴∠QDC＝∠B，∵∠OCB＝∠QCD，∴∠QCD＝∠QDC，∴QC＝QD＝6，∵QO＝QP，{∴OC＝DP＝r，∵PC是⊙O的切线，∴OC⊥PC，∴∠OCP＝∠PCQ＝90°，在Rt△PCQ中，∵PQ2＝PC2+QC2，∴（6+r）2＝62+（2r）2，r＝4或0（舍弃），∴OP＝＝4，∴四边形OBDP是平行四边形，∴BD＝OP＝4．36．已知P A、PB分别切⊙O于A、B，E为劣弧AB上一点，过E点的切线交P A于C、交PB于D．（1）若P A＝6，求△PCD的周长．（2）若∠P＝50°求∠DOC．【解答】解：（1）连接OE，∵P A、PB与圆O相切，∴P A＝PB＝6，同理可得：AC＝CE，BD＝DE，△PCD的周长＝PC+PD+CD＝PC+PD+CE+DE＝P A+PB＝12；（2）∵P A PB与圆O相切，∴∠OAP＝∠OBP＝90°∠P＝50°，∴∠AOB＝360°﹣90°﹣90°﹣50°＝130°，在Rt△AOC和Rt△EOC中，，∴Rt△AOC≌Rt△EOC（HL），∴∠AOC＝∠COE，同理：∠DOE＝∠BOD，∴∠COD＝∠AOB＝65°．37．如图，P A，PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠P＝60°．（1）求∠BAC的度数；（2）当OA＝2时，求AB的长．【解答】解：（1）∵P A，PB是⊙O的切线，∴AP＝BP，∵∠P＝60°，∴∠P AB＝60°，∵AC是⊙O的直径，∴∠P AC＝90°，∴∠BAC＝90°﹣60°＝30°．（2）连接OP，则在Rt△AOP中，OA＝2，∠APO＝30°，∴OP＝4，由勾股定理得：，∵AP＝BP，∠APB＝60°，∴△APB是等边三角形，∴．38．如图，已知AB为⊙O的直径，P A，PC是⊙O的切线，A，C为切点，∠BAC＝30°．（Ⅰ）求∠P的大小；（Ⅱ）若AB＝2，求P A的长（结果保留根号）．【解答】解：（Ⅰ）∵P A是⊙O的切线，AB为⊙O的直径，∴P A⊥AB，∴∠BAP＝90°；∵∠BAC＝30°，∴∠CAP＝90°﹣∠BAC＝60°．又∵P A、PC切⊙O于点A、C，∴P A＝PC，∴△P AC为等边三角形，∴∠P＝60°．（Ⅱ）如图，连接BC，则∠ACB＝90°．在Rt△ACB中，AB＝2，∠BAC＝30°，∵cos∠BAC＝，∴AC＝AB?cos∠BAC＝2cos30°＝．∵△P AC为等边三角形，∴P A＝AC，∴P A＝．39．如图，在⊙O中，弦BC垂直于半径OA，垂足为E，D是优弧BC上一点，连接BD，AD，OC，∠ADB＝30°．（1）求∠AOC的度数；（2）若弦BC＝8cm，求图中劣弧BC的长．【解答】解：（1）连接OB，∵OA⊥BC，∴＝，∴∠AOC＝∠AOB，由圆周角定理得，∠AOB＝2∠ADB＝60°，∴∠AOC＝∠AOB＝60°；（2）∵OA⊥BC，∴BE＝BC＝4，在Rt△BOE中，∠AOB＝60°，∴OB＝＝，∴劣弧BC的长＝＝π（cm）．40．如图，已知AB是⊙O的直径，点C在⊙O上，延长BC至点D，使得DC＝BC，直线DA与⊙O的另一个交点为E，连结AC，CE．（1）求证：CD＝CE；（2）若AC＝2，∠E＝30°，求阴影部分（弓形）面积．【解答】（1）证明：∵AB是直径，∴∠ACB＝90°，∵DC＝BC，∴AD＝AB，∴∠D＝∠ABC，∵∠E＝∠ABC，∴∠E＝∠D，∴CD＝CE．（2）解：由（1）可知：∠ABC＝∠E＝30°，∠ACB＝90°，∴∠CAB＝60°，AB＝2AC＝4，在Rt△ABC中，由勾股定理得到BC＝2，连接OC，则∠COB＝120°，∴S阴＝S扇形OBC﹣S△OBC＝﹣×××2＝﹣．。
2024年中考数学复习重难点题型训练—圆的相关证明与计算(含答案解析)
2024年中考数学复习重难点题型训练—圆的相关证明与计算（含答案解析）类型一基本性质有关的1.(2022·湖南省郴州市)如图，在△ABC中，AB=AC.以AB为直径的⊙O与线段BC交于点D，过点D作DE⊥AC，垂足为E，ED的延长线与AB的延长线交于点P．(1)求证：直线PE是⊙O的切线；(2)若⊙O的半径为6，∠P=30°，求CE的长．【答案】(1)连接OD，根据AB=AC，OB=OD，得∠ACB=∠ODB，从而OD//AC，由DE⊥AC，即可得PE⊥OD，故PE是⊙O的切线；(2)连接AD，连接OD，由DE⊥AC，∠P=30°，得∠PAE=60°，又AB=AC，可得△ABC 是等边三角形，即可得BC=AB=12，∠C=60°，而AB是⊙O的直径，得∠ADB=90°，可得BD=CD=12BC=6，在Rt△CDE中，即得CE的长是3．本题考查圆的综合应用，涉及圆的切线，等腰三角形性质及应用，含特殊角的直角三角形三边关系等，解题的关键是判定△ABC是等边三角形．2.(2022·辽宁省盘锦市)如图，△ABC内接于⊙O，∠ABC=45°，连接AO并延长交⊙O于点D，连接BD，过点C作CE//AD与BA的延长线交于点E．(1)求证：CE与⊙O相切；(2)若AD=4，∠D=60°，求线段AB，BC的长．【答案】(1)连接OC，根据圆周角定理得∠AOC=90°，再根据AD//EC，可得∠OCE=90°，从而证明结论；(2)过点A作AF⊥EC交EC于F，由AD是圆O的直径，得∠ABD=90°，又AD=4，60°，即得AB=3BD=23，根据∠ABC=45°，知△ABF是等腰直角三角形，AF=BF=2AB= 6，又△AOC是等腰直角三角形，OA=OC=2，得AC=22，故CF=AC2−AF2=2，从而BC=BF+CF=6+2．本题主要考查了圆周角定理，切线的判定与性质，含30°角的直角三角形的性质等知识，作辅助线构造特殊的直角三角形是解题的关键．3.（2021·山东临沂市·中考真题）如图，已知在⊙O中，＝＝，OC与AD相交于点AB BC CDE．求证：（1）AD∥BC（2）四边形BCDE为菱形．【答案】（1）见解析；（2）见解析【分析】（1）连接BD ，根据圆周角定理可得∠ADB=∠CBD ，根据平行线的判定可得结论；（2）证明△DEF ≌△BCF ，得到DE=BC ，证明四边形BCDE 为平行四边形，再根据 BCCD =得到BC=CD ，从而证明菱形．【详解】解：（1）连接BD ，∵ AB BCCD ==，∴∠ADB=∠CBD ，∴AD ∥BC ；（2）连接CD ，∵AD ∥BC ，∴∠EDF=∠CBF ，∵ BCCD =，∴BC=CD ，∴BF=DF ，又∠DFE=∠BFC ，∴△DEF ≌△BCF （ASA ），∴DE=BC ，∴四边形BCDE 是平行四边形，又BC=CD ，∴四边形BCDE 是菱形．【点睛】本题考查了垂径定理，圆周角定理，弧、弦、圆心角的关系，全等三角形的判定和性质，菱形的判定，解题的关键是合理运用垂径定理得到BF=DF ．4.（2021·四川南充市·中考真题）如图，A ，B 是O 上两点，且AB OA =，连接OB 并延长到点C ，使BC OB =，连接AC ．（1）求证：AC 是O 的切线．（2）点D ，E 分别是AC ，OA 的中点，DE 所在直线交O 于点F ，G ，4OA =，求GF 的长．【答案】（1）见解析；（2）【分析】（1）先证得△AOB 为等边三角形，从而得出∠OAB=60°，利用三角形外角的性质得出∠C=∠CAB=30°，由此可得∠OAC=90°即可得出结论；（2）过O 作OM ⊥DF 于M ，DN ⊥OC 于N ，利用勾股定理得出AC=30°的直角三角形的性质得出DN ，再根据垂径定理和勾股定理即可求出GF 的长．【详解】（1）证明：∵AB=OA ，OA=OB∴AB=OA=OB∴△AOB 为等边三角形∴∠OAB=60°，∠OBA=60°∵BC=OB∴BC=AB∴∠C=∠CAB又∵∠OBA=60°=∠C+∠CAB∴∠C=∠CAB=30°∴∠OAC=∠OAB+∠CAB=90°∴AC 是⊙O 的切线；（2）∵OA=4∴OB=AB=BC=4∴OC=8∴AC=∵D 、E 分别为AC 、OA 的中点，∴OE//BC ，DC=过O 作OM ⊥DF 于M ，DN ⊥OC 于N则四边形OMDN 为矩形∴DN=OM在Rt △CDN 中，∠C=30°，∴DN=12DC=∴OM=3连接OG ，∵OM ⊥GF∴GF=2MG=222OG OM -=()22243-=213【点睛】本题考查了切线的判定、垂径定理、等边三角形的性质和判定，熟练掌握相关的知识是解题的关键．5.（2021·安徽中考真题）如图，圆O 中两条互相垂直的弦AB ，CD 交于点E ．（1）M 是CD 的中点，OM ＝3，CD ＝12，求圆O 的半径长；（2）点F 在CD 上，且CE ＝EF ，求证：AF BD ⊥．【答案】（1）35；（2）见解析．【分析】（1）根据M 是CD 的中点，OM 与圆O 直径共线可得OM CD ⊥，OM 平分CD ，则有6MC =，利用勾股定理可求得半径的长；（2）连接AC ，延长AF 交BD 于G ，根据CE EF =，AE FC ⊥，可得AF AC =，12∠=∠，利用圆周角定理可得2D ∠=∠，可得1D ∠=∠，利用直角三角形的两锐角互余，可证得90AGB ∠=︒，即有AF BD ⊥．【详解】（1）解：连接OC ，∵M 是CD 的中点，OM 与圆O 直径共线∴OM CD ⊥，OM 平分CD ，90OMC ∴∠=︒12CD = 6MC ∴=．在Rt OMC △中．OC ===∴圆O 的半径为（2）证明：连接AC ，延长AF 交BD 于G ．CE EF = ，AE FC⊥AF AC∴=又CE EF= 12∠∠∴= BCBC = 2D∴∠=∠1D∴∠=∠中在Rt BED∠+∠=︒90D B∴∠+∠=︒B190AGB∴∠=︒90∴⊥AF BD【点睛】本题考查了垂径定理，圆周角定理，直角三角形的两锐角互余，勾股定理等知识点，熟练应用相关知识点是解题的关键．∠是 AD所对的圆周角，6.（2021·浙江中考真题）如图，已知AB是⊙O的直径，ACD∠=︒．30ACD∠的度数；（1）求DABAB=，求DF的（2）过点D作DE AB⊥，垂足为E，DE的延长线交⊙O于点F．若4长．【答案】（1）60︒；（2）23【分析】（1）连结BD ，根据圆周角性质，得B ACD ∠=∠；根据直径所对圆周角为直角、直角三角形两锐角互余的性质计算，即可得到答案；（2）根据含30°角的直角三角形性质，得12AD AB =；根据垂径定理、特殊角度三角函数的性质计算，即可得到答案．【详解】（1）连结BD ，30ACD ∠=︒30B ACD \Ð=Ð=°AB Q 是O 的直径，90ADB ∴∠=︒，9060DAB B ∴∠=︒-∠=︒（2）90ADB ∠=︒ ，30B ∠=︒，4AB =∴122AD AB ==60DAB ∠=︒ ，DE AB ⊥，且AB 是直径sin 60EF DE AD︒∴===2DF DE =∴=．【点睛】本题考查了圆、含30°角的直角三角形、三角函数的知识；解题的关键是熟练掌握圆周角、垂径定理、含30°角的直角三角形、三角函数、直角三角形两锐角互余的性质，从而完成求解．7.（2021·湖南中考真题）如图，ABC 是O 的内接三角形，AC 是O 的直径，点D 是 BC的中点，//DE BC 交AC 的延长线于点E ．（1）求证：直线DE 与O 相切；（2）若O 的直径是10，45A ∠=︒，求CE 的长．【答案】（1）见解析；（2）5CE =．【分析】（1）连接OD ，由点D 是 BC的中点得OD ⊥BC ，由DE//BC 得OD ⊥DE ，由OD 是半径可得DE 是切线；（2）证明△ODE 是等腰直角三角形，可求出OE 的长，从而可求得结论．【详解】解：（1）连接OD 交BC 于点F ，如图，∵点D 是 BC的中点，∴OD ⊥BC ，∵DE//BC∴OD ⊥DE∵OD 是O 的半径∴直线DE 与O 相切；（2）∵AC 是O 的直径，且AB=10,∴∠ABC=90°，152OC OA AB ===∵OD ⊥BC∴∠OFC=90°∴OD//AB 45BAC ∠=︒∴45DOE ∠=︒∵90ODE ∠=︒∴45OED ∠=∴5DE OD OC ===由勾股定理得，OE =∴5CE OE OC =-=．【点睛】此题主要考查了切线的判定与性质的综合运用，熟练掌握切线的判定与性质是解答此题的关键．8.（2021·湖南张家界市·中考真题）如图，在Rt AOB 中，90∠=︒ABO ，30OAB ∠=︒，以点O 为圆心，OB 为半径的圆交BO 的延长线于点C ，过点C 作OA 的平行线，交O 于点D ，连接AD ．（1）求证：AD 为O 的切线；（2）若2OB =，求弧CD 的长．【答案】（1）见解析；（2）23π【分析】（1）连接OB ，先根据直角三角形的性质得到∠AOB=60°，再运用平行线的性质结合已知条件可得60AOD ∠=︒，再证明AOB AOD △≌△可得90ADO ABO ∠=∠=︒即可；（2）先求出∠COD ，然后再运用弧长公式计算即可．【详解】（1）证明：连接OD∵30OAB ∠=︒，90B ∠=︒∴60AOB ∠=︒又∵//CD AO∴60C AOB ∠=∠=︒∴2120BOD C ∠=∠=︒∴60AOD ∠=︒又∵,OB OD AO AO==∴()AOB AOD SAS ≌∴90ADO ABO ∠=∠=︒又∵点D 在O 上∴AD 是O 的切线；（2）∵120BOD ∠=︒∴60COD ∠=︒∴602223603l ππ=⨯⨯=．【点睛】本题主要考查了圆的切线的证明、弧长公式等知识点，掌握圆的切线的证明方法成为解答本题的关键．9.（2020•齐齐哈尔）如图，AB 为⊙O 的直径，C 、D 为⊙O 上的两个点，AC=CD =DB ，连接AD ，过点D 作DE ⊥AC 交AC 的延长线于点E ．（1）求证：DE 是⊙O 的切线．（2）若直径AB ＝6，求AD 的长．【分析】（1）连接OD ，根据已知条件得到∠BOD =13×180°＝60°，根据等腰三角形的性质得到∠ADO＝∠DAB＝30°，得到∠EDA＝60°，求得OD⊥DE，于是得到结论；（2）连接BD，根据圆周角定理得到∠ADB＝90°，解直角三角形即可得到结论．【解析】（1）证明：连接OD，=CD =DB ，∵AC∴∠BOD=13×180°＝60°，=DB ，∵CD∴∠EAD＝∠DAB=12∠BOD＝30°，∵OA＝OD，∴∠ADO＝∠DAB＝30°，∵DE⊥AC，∴∠E＝90°，∴∠EAD+∠EDA＝90°，∴∠EDA＝60°，∴∠EDO＝∠EDA+∠ADO＝90°，∴OD⊥DE，∴DE是⊙O的切线；（2）解：连接BD，∵AB为⊙O的直径，∴∠ADB＝90°，∵∠DAB＝30°，AB＝6，∴BD=12AB＝3，∴AD=62−32=33．10.（2020•深圳）如图，AB为⊙O的直径，点C在⊙O上，AD与过点C的切线互相垂直，垂足为D．连接BC并延长，交AD的延长线于点E．（1）求证：AE＝AB；（2）若AB＝10，BC＝6，求CD的长．【分析】（1）证明：连接AC、OC，如图，根据切线的性质得到OC⊥CD，则可判断OC∥AD，所以∠OCB＝∠E，然后证明∠B＝∠E，从而得到结论；（2）利用圆周角定理得到∠ACB＝90°，则利用勾股定理可计算出AC＝8，再根据等腰三角形的性质得到CE＝BC＝6，然后利用面积法求出CD的长．【解析】（1）证明：连接AC、OC，如图，∵CD为切线，∴OC⊥CD，∴CD⊥AD，∴OC∥AD，∴∠OCB＝∠E，∵OB＝OC，∴∠OCB＝∠B，∴∠B＝∠E，∴AE＝AB；（2）解：∵AB为直径，∴∠ACB＝90°，∴AC=102−62=8，∵AB＝AE＝10，AC⊥BE，∴CE＝BC＝6，∵12CD•AE=12AC•CE，∴CD=6×810=245．11.（2020•陕西）如图，△ABC是⊙O的内接三角形，∠BAC＝75°，∠ABC＝45°．连接AO并延长，交⊙O于点D，连接BD．过点C作⊙O的切线，与BA的延长线相交于点E．（1）求证：AD∥EC；（2）若AB＝12，求线段EC的长．【分析】（1）连接OC，由切线的性质可得∠OCE＝90°，由圆周角定理可得∠AOC＝90°，可得结论；（2）过点A作AF⊥EC交EC于F，由锐角三角函数可求AD＝83，可证四边形OAFC是正方形，可得CF＝AF＝43，由锐角三角函数可求EF＝12，即可求解．【解析】证明：（1）连接OC，∵CE与⊙O相切于点C，∴∠OCE＝90°，∵∠ABC＝45°，∴∠AOC＝90°，∵∠AOC+∠OCE＝180°，∴∴AD∥EC（2）如图，过点A作AF⊥EC交EC于F，∵∠BAC＝75°，∠ABC＝45°，∴∠ACB＝60°，∴∠D＝∠ACB＝60°，∴sin∠ADB=AB AD==83，∴AD=∴OA＝OC＝43，∵AF⊥EC，∠OCE＝90°，∠AOC＝90°，∴四边形OAFC是矩形，又∵OA＝OC，∴四边形OAFC是正方形，∴CF＝AF＝43，∵∠BAD＝90°﹣∠D＝30°，∴∠EAF＝180°﹣90°﹣30°＝60°，∵tan∠EAF=EF AF=3，∴EF=3AF＝12，∴CE＝CF+EF＝12+43．类型二与三角形全等、相似有关的12.(2022·辽宁省营口市)如图，在△ABC中，AB=AC，以AB为直径作⊙O与AC交于点E，过点A作⊙O的切线交BC的延长线于点D．(1)求证：∠D=∠EBC；(2)若CD=2BC，AE=3，求⊙O的半径．【答案】(1)根据切线的性质可得∠DAO=90°，从而可得∠D+∠ABD=90°，根据直径所对的圆周角是直角可得∠BEC=90°，从而可得∠ACB+∠EBC=90°，然后利用等腰三角形的性质可得∠ACB=∠ABC，从而利用等角的余角相等即可解答；(2)根据已知可得BD=3BC，然后利用(1)的结论可得△DAB∽△BEC，从而利用相似三角形的性质可得AB=3EC，然后根据AB=AC，进行计算即可解答．本题考查了圆周角定理，等腰三角形的性质，切线的性质，相似三角形的判定与性质，熟练掌握切线的性质，以及相似三角形的判定与性质是解题的关键．13.（2022·北部湾）如图，在△ABC中，AB=AC，以AC为直径作⊙O交BC于点D，过点D作DE⊥AB，垂足为E，延长BA交⊙O于点F.（1）求证：DE是⊙O的切线（2）若AE DE=23，AF=10，求⊙O的半径.【答案】（1）证明：连接OD；∵OD=OC，∴∠C=∠ODC，∵AB=AC，∴∠B=∠C，∴∠B=∠ODC，∴OD∥AB，∴∠ODE=∠DEB；∵DE⊥AB，∴∠DEB=90°，∴∠ODE=90°，即DE⊥OD，∴DE是⊙O的切线（2）解：连接CF，由（1）知OD⊥DE，∵DE⊥AB，∴OD∥AB，∵OA=OC，∴BD=CD，即OD是△ABC的中位线，∵AC是⊙O的直径，∴∠CFA=90°，∵DE⊥AB，∴∠BED=90°，∴∠CFA=∠BED=90°，∴DE∥CF，∴BE=EF，即DE是△FBC的中位线，∴CF=2DE，∵AE DE=23，∴设AE=2x，DE=3k，CF=6k，∵AF=10，∴BE=EF=AE+AF=2k+10，∴AC=BA=EF+AE=4k+10，在Rt△ACF中，由勾股定理，得AC2=AF2+CF2，即(4k+10)2=102+(6k)2，解得：k=4，∴AC=4k+10=4×4+10=26，∴OA=13，即⊙O的半径为13.【知识点】平行线的判定与性质；等腰三角形的性质；圆周角定理；切线的判定；三角形的中位线定理【解析】【分析】（1）连接OD ，根据等腰三角形的性质可得∠C=∠ODC ，∠B=∠C ，则∠B=∠ODC ，推出OD ∥AB ，由平行线的性质可得∠ODE=∠DEB=90°，即DE ⊥OD ，据此证明；（2）连接CF ，由（1）知OD ⊥DE ，则OD ∥AB ，易得OD 是△ABC 的中位线，根据圆周角定理可得∠CFA=90°，根据垂直的概念可得∠BED=90°，则DE ∥CF ，推出DE 是△FBC的中位线，得CF=2DE ，设AE=2x ，DE=3k ，CF=6k ，则BE=EF=2k+10，AC=BA=4k+10，根据勾股定理可得k 的值，然后求出AC 、OA ，据此可得半径.14.（2021·江苏无锡市·中考真题）如图，四边形ABCD 内接于O ，AC 是O 的直径，AC 与BD 交于点E ，PB 切O 于点B ．（1）求证：PBA OBC ∠=∠；（2）若20PBA Ð=°，40ACD ∠=︒，求证：OAB CDE V V ∽．【答案】（1）见详解；（2）见详解【分析】（1）由圆周角定理的推论，可知∠ABC=90°，由切线的性质可知∠OBP=90°，进而即可得到结论；（2）先推出20OCB OBC ∠=∠=︒，从而得∠AOB=40°，继而得∠OAB=70°，再推出∠CDE=70°，进而即可得到结论．【详解】证明：（1）∵AC 是O 的直径，∴∠ABC=90°，∵PB 切O 于点B ，∴∠OBP=90°，∴90PBA ABO OBC ABO ∠+∠=∠+∠=︒，∴PBA OBC ∠=∠；（2）∵20PBA Ð=°，PBA OBC ∠=∠，∴20OBC ∠=︒，∵OB=OC ，∴20OCB OBC ∠=∠=︒，∴∠AOB=20°+20°=40°，∵OB=OA ，∴∠OAB=∠OBA=(180°-40°)÷2=70°，∴∠ADB=12∠AOB=20°，∵AC 是O 的直径，∴∠ADC=90°，∴∠CDE=90°-20°=70°，∴∠CDE=∠OAB ，∵40ACD ∠=︒，∴40ACD AOB ∠=∠=︒，∴OAB CDE V V ∽．【点睛】本题主要考查圆的性质以及相似三角形的判定定理，掌握圆周角定理的推论，相似三角形的判定定理，切线的性质定理，是解题的关键．15.（2020•衢州）如图，△ABC 内接于⊙O ，AB 为⊙O 的直径，AB ＝10，AC ＝6，连结OC ，弦AD分别交OC，BC于点E，F，其中点E是AD的中点．（1）求证：∠CAD＝∠CBA．（2）求OE的长．【分析】（1）利用垂径定理以及圆周角定理解决问题即可．（2）证明△AEC∽△BCA，推出CE AC=AC AB，求出EC即可解决问题．【解析】（1）证明：∵AE＝DE，OC是半径，=CD ，∴AC∴∠CAD＝∠CBA．（2）解：∵AB是直径，∴∠ACB＝90°，∵AE＝DE，∴OC⊥AD，∴∠AEC＝90°，∴∠AEC＝∠ACB，∴△AEC∽△BCA，∴CE AC=AC AB，∴CE6=610，∴CE＝3.6，∵OC=12AB＝5，∴OE＝OC﹣EC＝5﹣3.6＝1.4．16.（2020•铜仁市）如图，AB是⊙O的直径，C为⊙O上一点，连接AC，CE⊥AB于点E，D 是直径AB延长线上一点，且∠BCE＝∠BCD．（1）求证：CD是⊙O的切线；（2）若AD＝8，BE CE=12，求CD的长．【分析】（1）连接OC，根据圆周角定理得到∠ACB＝90°，根据余角的性质得到∠A＝∠ECB，求得∠A＝∠BCD，根据等腰三角形的性质得到∠A＝∠ACO，等量代换得到∠ACO＝∠BCD，求得∠DCO＝90°，于是得到结论；（2）设BC＝k，AC＝2k，根据相似三角形的性质即可得到结论．【解析】（1）证明：连接OC，∵AB是⊙O的直径，∴∠ACB＝90°，∵CE⊥AB，∴∠CEB＝90°，∴∠ECB+∠ABC＝∠ABC+∠CAB＝90°，∴∠A＝∠ECB，∵∠BCE＝∠BCD，∴∠A＝∠BCD，∵OC＝OA，∴∠A＝∠ACO，∴∠ACO＝∠BCD，∴∠ACO+∠BCO＝∠BCO+∠BCD＝90°，∴∠DCO＝90°，∴CD是⊙O的切线；（2）解：∵∠A＝∠BCE，∴tanA=BC AC=tan∠BCE=BE CE=12，设BC＝k，AC＝2k，∵∠D＝∠D，∠A＝∠BCD，∴△ACD∽△CBD，∴BC AC=CD AD=12，∵AD＝8，∴CD＝4．17.（2020•衡阳）如图，在△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，过点A和点D的圆，圆心O在线段AB上，⊙O交AB于点E，交AC于点F．（1）判断BC与⊙O的位置关系，并说明理由；（2）若AD＝8，AE＝10，求BD的长．【分析】（1）连接OD，根据平行线判定推出OD∥AC，推出OD⊥BC，根据切线的判定推出即可；（2）连接DE，根据圆周角定理得到∠ADE＝90°，根据相似三角形的性质得到AC=325，根据勾股定理得到CD=AD2−AC2==根据相似三角形的性质即可得到结论．【解析】（1）BC与⊙O相切，理由：连接OD，∵OA＝OD，∴∠OAD＝∠ODA，∵AD平分∠BAC，∴∠BAD＝∠CAD，∴∠ODA＝∠CAD，∴OD∥AC，∵∠C＝90°，∴∠ODC＝90°，∴OD⊥BC，∵OD为半径，∴BC是⊙O切线；（2）连接DE，∵AE是⊙O的直径，∴∠ADE＝90°，∵∠C＝90°，∴∠ADE＝∠C，∵∠EAD＝∠DAC，∴△ADE∽△ACD，∴AE AD=AD AC，108=8AC，∴AC=325，∴CD=AD2−AC2==245，∵OD⊥BC，AC⊥BC，∴△OBD∽△ABC，∴OD AC=BD BC，∴5325=BD BD+245，∴BD=1207．18.（2020•遵义）如图，AB是⊙O的直径，点C是⊙O上一点，∠CAB的平分线AD交BC 于点D，过点D作DE∥BC交AC的延长线于点E．（1）求证：DE是⊙O的切线；（2）过点D作DF⊥AB于点F，连接BD．若OF＝1，BF＝2，求BD的长度．【分析】（1）连接OD，由等腰三角形的性质及角平分线的性质得出∠ADO＝∠DAE，从而OD∥AE，由DE∥BC得∠E＝90°，由两直线平行，同旁内角互补得出∠ODE＝90°，由切线的判定定理得出答案；（2）先由直径所对的圆周角是直角得出∠ADB＝90°，再由OF＝1，BF＝2得出OB的值，进而得出AF和BA的值，然后证明△DBF∽△ABD，由相似三角形的性质得比例式，从而求得BD2的值，求算术平方根即可得出BD的值．【解析】（1）连接OD，如图：∵OA＝OD，∴∠OAD＝∠ADO，∵AD平分∠CAB，∴∠DAE＝∠OAD，∴∠ADO＝∠DAE，∴OD∥AE，∵DE∥BC，∴∠E＝90°，∴∠ODE＝180°﹣∠E＝90°，∴DE是⊙O的切线；（2）∵AB是⊙O的直径，∴∠ADB＝90°，∵OF＝1，BF＝2，∴OB＝3，∴AF＝4，BA＝6．∵DF⊥AB，∴∠DFB＝90°，∴∠ADB＝∠DFB，又∵∠DBF＝∠ABD，∴△DBF∽△ABD，∴BD BA=BF BD，∴BD2＝BF•BA＝2×6＝12．∴BD＝23．19.（2019•陕西）如图，⊙O的半径OA＝6，过点A作⊙O的切线AP，且AP＝8，连接PO 并延长，与⊙O交于点B、D，过点B作BC∥OA，并与⊙O交于点C，连接AC、CD．（1）求证：DC∥AP；（2）求AC的长．【分析】（1）根据切线的性质得到∠OAP＝90°，根据圆周角定理得到∠BCD＝90°，根据平行线的性质和判定定理即可得到结论；（2）根据勾股定理和相似三角形的判定和性质定理即可得到结论．【解析】（1）证明：∵AP是⊙O的切线，∴∠OAP＝90°，∵BD是⊙O的直径，∴∠BCD＝90°，∵OA∥CB，∴∠AOP＝∠DBC，∴∠BDC＝∠APO，∴DC∥AP；（2）解：∵AO∥BC，OD＝OB，∴延长AO交DC于点E，则AE⊥DC，OE=12BC，CE=12CD，在Rt△AOP中，OP=62+82=10，由（1）知，△AOP∽△CBD，∴DB OP=BC OA=DC AP，即1210=BC6=DC8，∴BC=365，DC=485，∴OE=185，CE=245，在Rt△AEC中，AC=AE2+CE2==20（2021·云南中考真题）如图，AB 是O 的直径，点C 是O 上异于A 、B 的点，连接AC 、BC ，点D 在BA 的延长线上，且DCA ABC ∠=∠，点E 在DC 的延长线上，且BE DC ⊥．（1）求证：DC 是O 的切线：（2）若2,33OA BE OD ==，求DA 的长．【答案】（1）见解析；（2）910【分析】（1）连接OC ，根据圆周角定理得到∠ACB=90°，根据等量代换得到∠DCO=90°，即可证明DC 是圆O 的切线；（2）根据已知得到OA=2DA ，证明△DCO ∽△DEB ，得到DO CO DB EB =，可得DA=310EB ，即可求出DA 的长．【详解】解：（1）如图，连接OC ，由题意可知：∠ACB 是直径AB 所对的圆周角，∴∠ACB=90°，∵OC ，OB 是圆O 的半径，∴OC=OB ，∴∠OCB=∠ABC ，又∵∠DCA=∠ABC ，∴∠DCA=∠OCB ，∴∠DCO=∠DCA+∠ACO=∠OCB+∠ACO=∠ACB=90°，∴OC ⊥DC ，又∵OC 是圆O 的半径，∴DC 是圆O 的切线；（2）∵23OA OD =，∴23OA OA DA =+，化简得OA=2DA ，由（1）知，∠DCO=90°，∵BE ⊥DC ，即∠DEB=90°，∴∠DCO=∠DEB ，∴OC ∥BE ，∴△DCO ∽△DEB ，∴DO CO DB EB =，即33255DA OA DA DA DA OA OB DA EB+===++，∴DA=310EB ，∵BE=3，∴DA=310EB=3931010⨯=，经检验：DA=910是分式方程的解，∴DA=910．【点睛】本题考查了圆周角定理，相似三角形的判定和性质，切线的判定，正确的作出辅助线，证明切线，得到相似三角形是解题的关键．21.（2021·江苏扬州市·中考真题）如图，四边形ABCD 中，//AD BC ，90BAD ∠=︒，CB CD =，连接BD ，以点B 为圆心，BA 长为半径作B ，交BD 于点E ．（1）试判断CD 与B 的位置关系，并说明理由；（2）若AB =，60BCD ∠=︒，求图中阴影部分的面积．【答案】（1）相切，理由见解析；（2）π-【分析】（1）过点B 作BF ⊥CD ，证明△ABD ≌△FBD ，得到BF=BA ，即可证明CD 与圆B 相切；（2）先证明△BCD 是等边三角形，根据三线合一得到∠ABD=30°，求出AD ，再利用S △ABD -S 扇形ABE 求出阴影部分面积．【详解】解：（1）过点B 作BF ⊥CD ，∵AD ∥BC ，∴∠ADB=∠CBD ，∵CB=CD ，∴∠CBD=∠CDB ，∴∠ADB=∠CDB ，又BD=BD ，∠BAD=∠BFD=90°，∴△ABD ≌△FBD （AAS ），∴BF=BA ，则点F 在圆B 上，∴CD 与圆B 相切；（2）∵∠BCD=60°，CB=CD ，∴△BCD 是等边三角形，∴∠CBD=60°∵BF ⊥CD ，∴∠ABD=∠DBF=∠CBF=30°，∴∠ABF=60°，∵AB=BF=，∴AD=DF=tan30AB ⋅︒=2，∴阴影部分的面积=S △ABD -S 扇形ABE=(230122360π⨯⨯⨯-=π-．【点睛】本题考查了切线的判定，全等三角形的判定和性质，等边三角形的判定和性质，扇形面积，三角函数的定义，题目的综合性较强，难度不小，解题的关键是正确做出辅助线．22.（2020•上海）如图，△ABC中，AB＝AC，⊙O是△ABC的外接圆，BO的延长线交边AC 于点D．（1）求证：∠BAC＝2∠ABD；（2）当△BCD是等腰三角形时，求∠BCD的大小；（3）当AD＝2，CD＝3时，求边BC的长．【分析】（1）连接OA．利用垂径定理以及等腰三角形的性质解决问题即可．（2）分三种情形：①若BD＝CB，则∠C＝∠BDC＝∠ABD+∠BAC＝3∠ABD．②若CD＝CB，则∠CBD＝∠CDB＝3∠ABD．③若DB＝DC，则D与A重合，这种情形不存在．分别利用三角形内角和定理构建方程求解即可．（3）如图3中，作AE∥BC交BD的延长线于E．则AE BC=AD DC=23，推出AO OH=AE BH=43，设OB＝OA＝4a，OH＝3a，根据BH2＝AB2﹣AH2＝OB2﹣OH2，构建方程求出a即可解决问题．【解析】（1）证明：连接OA．A∵AB＝AC，=AC ，∴AB∴OA⊥BC，∴∠BAO＝∠CAO，∵OA＝OB，∴∠ABD＝∠BAO，∴∠BAC＝2∠BAD．（2）解：如图2中，延长AO交BC于H．①若BD＝CB，则∠C＝∠BDC＝∠ABD+∠BAC＝3∠ABD，∵AB＝AC，∴∠ABC＝∠C，∴∠DBC＝2∠ABD，∵∠DBC+∠C+∠BDC＝180°，∴8∠ABD＝180°，∴∠C＝3∠ABD＝67.5°．②若CD＝CB，则∠CBD＝∠CDB＝3∠ABD，∴∠C ＝4∠ABD ，∵∠DBC+∠C+∠CDB ＝180°，∴10∠ABD ＝180°，∴∠BCD ＝4∠ABD ＝72°．③若DB ＝DC ，则D 与A 重合，这种情形不存在．综上所述，∠C 的值为67.5°或72°．（3）如图3中，作AE ∥BC 交BD 的延长线于E ．则AE BC =AD DC =23，∴AO OH =AE BH =43，设OB ＝OA ＝4a ，OH ＝3a ，∵BH 2＝AB 2﹣AH 2＝OB 2﹣OH 2，∴25﹣49a 2＝16a 2﹣9a 2，∴a 2=2556，∴BH =∴BC ＝2BH =23.（2021·云南中考真题）如图，AB 是O 的直径，点C 是O 上异于A 、B 的点，连接AC 、BC ，点D 在BA 的延长线上，且DCA ABC ∠=∠，点E 在DC 的延长线上，且BE DC ⊥．（1）求证：DC是O的切线：（2）若2,33OA BEOD==，求DA的长．【答案】（1）见解析；（2）9 10【分析】（1）连接OC，根据圆周角定理得到∠ACB=90°，根据等量代换得到∠DCO=90°，即可证明DC是圆O的切线；（2）根据已知得到OA=2DA，证明△DCO∽△DEB，得到DO CODB EB=，可得DA=310EB，即可求出DA的长．【详解】解：（1）如图，连接OC，由题意可知：∠ACB是直径AB所对的圆周角，∴∠ACB=90°，∵OC，OB是圆O的半径，∴OC=OB，∴∠OCB=∠ABC，又∵∠DCA=∠ABC，∴∠DCA=∠OCB，∴∠DCO=∠DCA+∠ACO=∠OCB+∠ACO=∠ACB=90°，∴OC⊥DC，又∵OC 是圆O 的半径，∴DC 是圆O 的切线；（2）∵23OA OD =，∴23OA OA DA =+，化简得OA=2DA ，由（1）知，∠DCO=90°，∵BE ⊥DC ，即∠DEB=90°，∴∠DCO=∠DEB ，∴OC ∥BE ，∴△DCO ∽△DEB ，∴DO CO DB EB =，即33255DA OA DA DA DA OA OB DA EB +===++，∴DA=310EB ，∵BE=3，∴DA=310EB=3931010⨯=，经检验：DA=910是分式方程的解，∴DA=910．【点睛】本题考查了圆周角定理，相似三角形的判定和性质，切线的判定，正确的作出辅助线，证明切线，得到相似三角形是解题的关键．类型三与锐角三角函数有关24.(2022·辽宁省铁岭市)如图，△ABC内接于⊙O，AC是⊙O的直径，过OA上的点P作PD⊥AC，交CB的延长线于点D，交AB于点E，点F为DE的中点，连接BF．(1)求证：BF与⊙O相切；(2)若AP=OP，cosA=45，AP=4，求BF的长．【答案】(1)连接OB，根据直径所对的圆周角是直角可得∠ABC=90°，从而可得∠ABD=90°，进而利用直角三角形三角形斜边上的中线可得BF=EF=12AD，然后利用等腰三角形的性质可得∠FEB=∠FBE，从而可得∠FBE=∠AEP，最后根据垂直定义可得∠EPA=90°，从而可得∠A+∠AEP=90°，再利用等腰三角形的性质可得∠A=∠OBA，从而可得∠OBA+∠FBE= 90°，进而可得∠OBF=90°，即可解答；(2)在Rt△AEP中，利用锐角三角函数的定义求出AE的长，从而利用勾股定理求出PE的长，然后利用同角的余角相等可得∠AEP=∠C，从而可证△APE∽△DPC，进而利用相似三角形的性质可求出DP的长，最后求出DE的长，即可解答．本题考查了解直角三角形，切线的判定与性质，圆周角定理，三角形的外接圆与外心，直线与圆的位置关系，熟练掌握解直角三角形，以及切线的判定与性质是解题的关键．25.(2022·四川省广安市)如图，AB为⊙O的直径，D、E是⊙O上的两点，延长AB至点C，连接CD ，∠BDC =∠BAD ．(1)求证：CD 是⊙O 的切线．(2)若tan∠BED =23，AC =9，求⊙O 的半径．【答案】（1）连接OD ，由圆周角定理得出∠ADB =90°，证出OD ⊥CD ，由切线的判定可得出结论；(2)证明△BDC∽△DAC ，由相似三角形的性质得出CD AC =BC CD =BD DA =23，由比例线段求出CD 和BC 的长，可求出AB 的长，则可得出答案．本题考查了切线的判定，相似三角形的判定与性质，锐角三角函数的定义，圆周角定理，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．26.（2021·山东菏泽市·中考真题）如图，在O 中，AB 是直径，弦CD AB ⊥，垂足为H ，E 为 BC上一点，F 为弦DC 延长线上一点，连接FE 并延长交直径AB 的延长线于点G ，连接AE 交CD 于点P ，若FE FP =．（1）求证：FE 是O 的切线；（2）若O 的半径为8，3sin 5F =，求BG 的长．【答案】（1）见解析；（2）=2BG 【分析】（1）连接OE ，证明OE ⊥EF 即可；（2）由3sin 5F =证得4sin 5G =，运用正弦的概念可得结论．【详解】解：（1）证明：连接OE ，如图，∵OA=OE∴∠OAE=∠OEA ．∵EF=PF ，∴∠EPF=∠PEF∵∠APH=∠EPF ，∴∠APH=∠EPF ，∴∠AEF=∠APH ．∵CD ⊥AB ，∴∠AHC=90°．∴∠OAE+∠APH=90°．∴∠OEA+∠AEF=90°∴∠OEF=90°∴OE ⊥EF ．∵OE 是O 的半径∴EF 是圆的切线，（2）∵CD ⊥AB∴FHG ∆是直角三角形∵3sin 5F =∴35GH FG =设3GH x =，则5FG x=由勾股定理得，4FH x=由（1）得，OEG ∆是直角三角形∴4sin 5OE FH x G OG FG x===∴45OE OG =，即45OE OE BG =+∵8OE =∴8485BG =+解得，2BG =【点睛】此题主要考查了圆的切线的判定，勾股定理和解直角三角形等知识，熟练掌握切线的判定是解答此题的关键．27.（2022·黔东南）（1）请在图中作出△ABC 的外接圆⊙O （尺规作图，保留作图痕迹，不写作法）；的中点，过点B的（2）如图，⊙O是△ABC的外接圆，AE是⊙O的直径，点B是CE切线与AC的延长线交于点D.①求证：BD⊥AD；②若AC=6，tan∠ABC=34，求⊙O的半径.【答案】（1）解：如下图所示（2）解：①如下图所示，连接OC、OB∵BD是⊙O的切线∴OB⊥BD对应的圆周角，∠COE是CE 对应的圆心角∵∠CAE是CE∴∠COE=2∠CAE的中点∵点B是CE∴∠COE=2∠BOE∴∠CAE=∠BOE∴∠CAE=∠BOE∴AD//OB∴BD⊥AD②如下图所示，连接CE对应的圆周角∵∠ABC与∠AEC是AC∴∠ABC=∠AEC∵AE是⊙O的直径∴∠ACE=90°∴tan∠AEC=AC CE=34∴CE=8∵AE2=CE2+AC2∴AE=10∴⊙O的半径为5.【知识点】圆周角定理；三角形的外接圆与外心；切线的性质；解直角三角形；作图-线段垂直平分线【解析】【解答】（1）∵△ABC的外接圆⊙O的圆心为任意两边的垂直平分线的交点，半径为交点到任意顶点的距离，∴做AB、AC的垂直平分线交于点O，以OB为半径，以O为圆心做圆即可得到△ABC 的外接圆；【分析】（1）利用尺规作图分别作出AC，AB的垂直平分线，两垂直平分线交于点O，然后以点O为圆心，OB的长为半径画圆即可.（2）①连接OC，OB，利用切线的性质可证得OB⊥BD，利用圆周角定理可证得∠COE=2∠CAE，由点B是弧CE的中点，可推出∠CAE=∠BOE，利用平行线的判定定理可证得AD∥OB，由此可证得结论；②连接CE，利用同弧所对的圆周角相等，可证得∠ABC=∠AEC，利用直径所对的圆周角是直角，可推出∠ACE=90°；再利用解直角三角形求出CE的长，利用勾股定理求出AE的长.28.（2022·鄂州）如图，△ABC内接于⊙O，P是⊙O的直径AB延长线上一点，∠PCB=∠OAC，过点O作BC的平行线交PC的延长线于点D.（1）试判断PC与⊙O的位置关系，并说明理由；（2）若PC＝4，tanA＝12，求△OCD的面积.【答案】（1）解：PC与⊙O相切，理由如下：∵AB是圆O的直径，∴∠ACB=90°，∴∠OCB+∠OCA=90°，∵OA=OC，∴∠OCA=∠OAC，∵∠PCB=∠OAC，∴∠PCB=∠OCA，∴∠PCB+∠OCB=∠OCA+∠OCB=90°，即∠PCO=90°，∴PC与⊙O相切（2）解：∵∠ACB=90°，tanA=12，∴BC AC=12，∵∠PCB=∠OAC，∠P=∠P，∴△PBC∽△PCA，∴PC PA=PB PC=BC CA=12，∴PA=8，PB=2，∴AB=6，∴OC=OB=3，∴OP=5，∵BC∥OD，∴△PBC∽△POD，∴PB OP=PC PD，即25=4PD，∴PD=10，∴CD=6，∴S△OCD=12OC⋅CD=9【知识点】等腰三角形的性质；圆周角定理；切线的判定；相似三角形的判定与性质；锐角三角函数的定义【解析】【分析】（1）由圆周角定理得∠ACB=90°，根据等腰三角形的性质可得∠OCA=∠OAC，结合∠PCB=∠OAC得PCB=∠OCA，结合∠OCB+∠OCA=90°可得∠PCO=90°，据此证明；（2）根据三角函数的概念可得BC AC=12，易证△PBC∽△PCA，根据相似三角形的性质可得PA、PB，然后求出AB、OP，证明△PBC∽△POD，根据相似三角形的性质可得PD，由PD-PC=CD可得CD，然后根据三角形的面积公式进行计算.29.（2022·毕节）如图，在△ABC中，∠ACB=90∘，D是AB边上一点，以BD为直径的⊙O与AC相切于点E，连接DE并延长交BC的延长线于点F.（1）求证：BF=BD；（2）若CF=1，tan∠EDB=2，求⊙O直径.【答案】（1）证明：连接OE，如下图所示：∵AC为圆O的切线，∴∠AEO=90°，∵AC⊥BC，∴∠ACB=90°，∴OE∥BC，∴∠F=∠DEO，又∵OD=OE，∴∠ODE=∠DEO，∴∠F=∠ODE，∴BD=BF.（2）解：连接BE，如下图所示：由(1)中证明过程可知：∠EDB=∠F，。
2020年最新深圳国际交流学院G1入学考试数学模拟试卷7
2020年最新深圳国际交流学院G1入学考试数学模拟试卷7一、选择题（ ） 1. 2019-的倒数是 A ．20191 B ．20191- C ．2019 D ．－2019（ ）2．下列运算正确的是 A ． 1055x x x=+B ．633)(x x= C ．523x x x =⋅ D ．336x x x=-（ ） 3．下面几何体中，其主视图与俯视图相同的是（ ）（ ）4. 如图，直线a ，b 被直线c 所截，a ∥b ，∠1=∠2，若∠3=40°，则∠4等于 A ．40° B ．50° C ．70° D ．80° （ ）5．下列图形是中心对称图形的是（ ）（ ）6．不等式组⎩⎨⎧≤->+13202x x 的解集在数轴上表示正确的是（ ）A B C D（ ）7.我国明代数学读本《算法统宗》一书中有这样一道题：一支竿子一条索，索比竿子长一托，对折索子来量竿，却比竿子短一托，如果一托为5尺，那么索长（ ）尺. A.25 B.20 C.15 D.10（ ）8.如图，在平行四边形ABCD 中，用直尺和圆规作∠BAD 的平分线AG 交BC 于点E 。
若BF=8，AB=5，则AE 的长为（ ）. A.5 B.6 C.8 D.12（ ）9.如图，P 是正△ABC 内的一点，若将△PBC 绕点B 旋转到△P ’BA ，则∠PBP ’的度数是( ). A ．45° B ．60° C ．90° D ．120°（ ）10.函数1+=ax y 与12++=bx ax y （0≠a ）的图象可能是（ ）A. B. C. D.二．填空题11.中国倡导的“一带一路”建设将促进我国与世界各国的互利合作。
根据规划，“一带一路”地区覆盖总人口 约为4400 000 000人，这个数用科学记数法表示为_______________.12. 分式方程275-=x x 的解是＿＿＿＿＿＿＿． 13. 一个不透明的口袋中放着若干只红球和白球，这两种球除了颜色以外没有任何其他区别，袋中的球已经搅匀，从口袋中随机取出一只球，取出红球的概率是41．如果袋中的白球有24只，那么袋中的红球有＿＿＿＿个． 14. 如图，△ABC 的顶点是正方形网格的格点，则A sin ＝＿＿＿＿＿．15. ⊙Ｏ的直径AE ＝cm 10，弦BC ＝cm 8，且BC ⊥AE 于D ，则△ABC 的面积为＿＿＿＿＿＿．16.如图，在矩形ABCD 中，将∠ABC 绕点A 按逆时针方向旋转一定角度后，BC 的对应边B ′C ′交CD 边于点G.连接BB ′、CC ′.若AD=7,CG=4,AB ′=B ′G,则''BB CC = .三、解答题 17. 先化简，再求值：aa a a a a 2482222-÷-+-+）（，其中260tan -︒=a .18. 某校八年级为了解学生课堂发言情况，随机抽取该年级部分学生，对他们某天在课堂上发言的次数进行了统计，其结果如下表，并绘制了如图所示的两幅不完整的统计图，已知B 、E 两组发言人数的比为5:2,请结合 图中相关数据回答下列问题： （1）求出样本容量，并补全直方图； （2）该年级共有学生500人，请估计全年级在这天里发言次数不少于12的人数； （3）在扇形统计图中，“B ”所对应的圆心角的度数是 .19.如图，一枚运载火箭从o 处发射，当火箭到达点A 、B 时，在雷达站C 处测得点A 、B 的仰角分别为34°、45°，其中点O 、A 、B 在同一条直线上，A 、B 两点间的距离是1.65km.求发射地O 距雷达站C 的距离（结果保留整数）。
圆的相关定理及其几何证明(含答案)
圆的相关定理及其几何证明典题探究例1：如图，圆O 是ABC ∆的外接圆，过点C 作圆O 的切线交BA 的延长线于点D.若CD =2AB AC ==，则线段AD 的长是 ；圆O 的半径是 .例2：如图，在圆O 中，直径AB 与弦CD 垂直，垂足为E （E 在A ,O 之间），,垂足为F ．若，，则EF BC ^6AB =5CF CB ?AE =例3：如图已知PA 与圆O 相切于A ，半径OC OP ⊥，AC 交PO 于B ，若1OC =,2OP =，则PA = ，=PB ．例4：如图，从圆O 外一点P 引圆O 的切线PA 和割线PBC ，已知30BPA ∠=︒，11BC =，1PB =, 则PA = ,圆O 的半径等于演练方阵A 档（巩固专练）1．如图，已知直线PD 切⊙O 于点D ，直线PO 交⊙O 于点E,F.若21PF PD ==，则⊙O 的半径为 ；EFD ∠= .AB COPPA2. 如图，与切于点，交弦的延长线于点，过点作圆的切线交于点. 若，，则弦的长为_______.3. 如图：圆O 的割线PAB 经过圆心O ，C 是圆上一点，PA ＝AC ＝12AB ，则以下结论不正确．．．的是( )A.CB CP =B. PCAC PABC =C. PC 是圆O 的切线D. BC BABP =4．如图，已知AB 是圆O 的直径，P 在AB 的延长线上，PC 切圆O 于点C ，CD OP ⊥于D ．若6CD =，10CP =，则圆O 的半径长为______；BP =______．AP O A DB P B O AP C 90ACB ∠=︒3,4BC CP ==DBD CB PA OCBA5．如图所示，以直角三角形ABC 的直角边AC 为直径作⊙O ，交斜边AB 于点D ，过点D 作⊙O 的切线，交BC 边于点E .则=BCBE.6．如图，直线AM 与圆相切于点M, ABC 与ADE 是圆的两条割线，且BD ⊥AD ，连接MD 、 EC 。
2020年深国交G1入学考试数学复习资料：方法与策略专题训练(有答案)
方法与策略专题训练班级：___________姓名：___________ 得分：___________一、选择题1.小学时候大家喜欢玩的幻方游戏，老师稍加创新改成了“幻圆”游戏，现在将−1、2、−3、4、−5、6、−7、8分别填入图中的圆圈内，使横、竖以及内外两圈上的4个数字之和都相等，老师已经帮助同学们完成了部分填空，则图中a+b的值为()A. −6或−3B. −8或1C. −1或−4D. 1或−12.用反证法证明“两条直线相交只有一个交点”，应该先假设()A. 两条直线相交至少有两个交点B. 两条直线相交没有两个交点C. 两条直线平行时也有一个交点D. 两条直线平行没有交点3.如图是琳琳6个装好糖果的礼包盒，每盒上面的数字代表这盒礼包实际装有的糖果数量．她把其中的5盒送给好朋友小芬和小红。
自己留下l盒．已知送的都是整盒，包装没拆过，送给小芬的糖果数量是小红的2倍．则琳琳自己留下的这盒有糖果()A. 15粒B. 18粒C. 20粒D. 31粒4.要将9个参加数学竞赛的名额分配给6所学校，每所学校至少要分得一个名额，那么不同的分配方案共有()A. 56种B. 36种C. 28种D. 72种5.小明训练上楼梯赛跑．他每步可上2阶或3阶(不上1阶)，那么小明上12阶楼梯的不同方法共有()(注：两种上楼梯的方法，只要有1步所踏楼梯阶数不相同，便认为是不同的上法．)A. 15种B. 14种C. 13种D. 12种6.小华家要进行室内装修，设计师提供了如下四种图案的地砖，爸爸希望灰白两种颜色的地砖面积比例大致相同，那么下面最符合要求的是()A. B.C. D.7.如图所示，从小明家到学校要穿过一个居民小区，小区的道路均是北南或西东方向，小明走下面哪条线路最短()A. (1,3)→(1,2)→(1,1)→(1,0)→(2,0)→(3,0)→(4,0)B. (1,3)→(0,3)→(2,3)→(0,0)→(1,0)→(2,0)→(4,0)C. (1,3)→(1,4)→(2,4)→(3,4)→(4,4)→(4,3)→(4,2)→(4,0)D. 以上都不对8.中国有个名句“运筹帷幄之中，决胜千里之外”.其中的“筹”原意是指《孙子算经》中记载的“算筹”.算筹是古代用来进行计算的工具，它是将几寸长的小竹棍摆在平面上进行运算，算筹的摆放形式有纵横两种形式(如图).当表示一个多位数时，像阿拉伯计数一样，把各个数位的数码从左到右排列，但各位数码的筹式需要纵横相间：个位、百位、万位数用纵式表示；十位，千位，十万位数用横式表示；“0”用空位来代替，以此类推．例如3306用算筹表示就是，则2022用算筹可表示为()A. B. C. D.二、填空题9.如图，为了测量一个池塘的宽BC，小明在池塘一侧的平地上选一点A，再分别找出线段AB，AC的中点D，E，若小明测得DE的长是20米，则池塘宽BC=________米．10.现定义一种新运算：a∗b=(a+b)(a−b)，其中a、b均为有理数，则a∗b+(b−a)∗b=．11.在一个边长为a的正方形地块上，辟出一部分作为花坛，小明设计一种方案，请你写出花坛(图中阴影部分，其中中间阴影部分为一小正方形)面积S的表达式______________．12.将四张花纹面相同的扑克牌的花纹面都朝上，两张一叠放成两堆不变，若每次可任选一堆的最上面的一张翻看(看后不放回)，并全部看完，则共有_________种不同的翻牌方式．13.武广高铁连通湖北、湖南、广东三省，北起武汉站，南到广州站，中途共停靠12个车站。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
则FD=3x,
连接AE,易证△ADE∽△FDA,
所以 = = ,
所以ED= AD= x,
所以EF= x,EO= x,DO= x,
在△ABC中,DO为中位线,
所以DO= BC=4,
所以 x=4,x= ,所以ED= x= .
3.解:(1)证明:连接OC.
∵CE是☉O的切线,∴OC⊥CE.
①当∠D的度数为时,四边形ECFG为菱形;
②当∠D的度数为时,四边形ECOG为正方形.
图3
4.如图4,在△ABC中,AB=AC,过AC延长线上的点O作OD⊥AO,交BC的延长线于点D,以O为圆心,OD长为半径的圆过点B.
(1)求证:直线AB与☉O相切;
(2)若AB=5,☉O的半径为12,则tan∠BDO=.
所以∠ACB=90°,所以∠ABC+∠BAC=90°,
因为∠PCA=∠ABC,所以∠PAC=∠ABC,
所以∠PAC+∠BAC=90°,所以PA⊥AB,所以PA是☉O的切线.
(2)因为∠PAO=∠ADO=90°,∠AOD=∠POA,所以△PAO∽△ADO,所以 = ,
所以AO2=OD·OP,
所以EF2=AB2=(2AO)2=4AO2=4OD·OP.
∴∠FCO+∠ECF=90°.
∵DO⊥AB,∴∠B+∠BFO=90°.
∵∠CFE=∠BFO,
∴∠B+∠CFE=90°.
∵OC=OB,∴∠FCO=∠B.
∴∠ECF=∠CFE.
∴CE=EF.
(2)∵AB是☉O的直径,∴∠ACB=90°.
∴∠DCF=90°.
∴∠DCE+∠ECF=90°,∠D+∠EFC=90°.
由(1)得∠ECF=∠CFE,
∴∠D=∠DCE.
∴ED=EC.
∴ED=EC=EF.
即点E为线段DF的中点.
①四边形ECFG为菱形时,CF=CE.
∵CE=EF,∴CE=CF=EF.
∴△CEF为等边三角形.
∴∠CFE=60°.
∴∠D=30°.
故填30°.
②四边形ECOG为正方形时,△ECO为等腰直角三角形.
∵AB=AC,∴BE=EC,∠BAE=∠CAE.
∵∠BAC=2∠CBF,∴∠BAE=∠CBF.
∵∠BAE+∠ABE=90°,
∴∠CBF+∠ABE=90°,
∴AB⊥BF,∴BF是☉O的切线.
(2)由(1)得∠BAE=∠CBF,
∴sin∠CBF=sin∠BAE= ,
∵∠AEB=90°,AB=3,
∴BE=ABsin∠BAE= ,
∴∠OBD+∠ABC=90°,
即∠ABO=90°,
∴AB⊥OB,
∵点B在☉O上,
∴直线AB与☉O相切.
(2)∵∠ABO=90°,
∴OA= = =13,
∵AC=AB=5,
∴OC=OA-AC=8,
∴tan∠BDO= = = .
故答案为: .
5.解:(1)证明:连接AE,
∵AB为直径,∴∠AEB=90°,∴AE⊥BC.
∴∠CEF=45°.
∵∠CEF=∠D+∠DCE,
∴∠D=∠DCE=22.5°.
故填22.5°.
4.解:(1)证明:连接OB,如图所示.
∵AB=AC,
∴∠ABC=∠ACB.
∵∠ACB=∠OCD,
∴∠ABC=∠OCD.
∵OD⊥AO,
∴∠COD=90°,
∴∠D+∠OCD=90°.
∵OB=OD,
∴∠OBD=∠D,
∴BC=2BE=2 .
过点C作CH⊥BF于H点,
在Rt△CBH中,CH=BCsin∠CBF=2,BH=2 ,
∵CH⊥BF,AB⊥BF,∴AB∥CH,
∴△FCH∽△FAB,∴ = ,
∴ = ,
∴BF=6 .
6.(1)连接OD,根据同圆半径相等及角平分线条件得到∠DAC=∠ODA,得OD∥AC,切线得证;(2)连接EF,DF,根据直径所对圆周角为直角,证明∠AFE=90°,可得EF∥BC,因此∠B=∠AEF,再利用同弧所对圆周角相等可得∠B=∠ADF,从而证明△ABD∽△ADF,可得AD与AB,AF的关系;(3)根据∠AEF=∠B,利用三角函数,分别在Rt△DOB和Rt△AFE中求出半径和AF,代入(2)的结论中,求出AD,再利用两角对应相等,证明△OGD∽△FGA,再利用对应边成比例,求出DG∶AG的值,即可求得DG的长.
1.如图1所示,☉O的半径为4,点A是☉O上一点,直线l经过点A.P是☉O上的一个动点(不与点A重合),过点P作PB⊥l于点B,交☉O于点E,直径PD的延长线交直线l于点F,点A是 的中点.
(1)求证:直线l是☉O的切线;
(2பைடு நூலகம்若PA=6,求PB的长.
图1
2.如图2,☉O是△ABC的外接圆,AB是直径,D是AC中点,直线OD与☉O相交于E,F两点,P是☉O外一点,且P在直线OD上,连接PA,PC,AF,满足∠PCA=∠ABC.
图7
8.如图8,四边形ABCD是正方形,以边AB为直径作☉O,点E在BC边上,连接AE交☉O于点F,连接BF并延长交CD于点G.
(1)求证:△ABE≌△BCG.
(2)若∠AEB=55°,OA=3,求 的长.(结果保留π)
图8
【参考答案】
1.解:(1)证明:连接OA.
∵OA=OP,
∴∠OAP=∠OPA.
(1)求证:PA是☉O的切线;
(2)证明:EF2=4OD·OP;
(3)若BC=8,tan∠AFP= ,求DE的长.
图2
3.如图3,AB是☉O的直径,DO⊥AB于点O,连接DA交☉O于点C,过点C作☉O的切线交DO于点E,连接BC交DO于点F.
(1)求证:CE=EF.
(2)连接AF并延长,交☉O于点G.填空:
(1)求证:BC是☉O的切线;
(2)设AB=x,AF=y,试用含x,y的代数式表示线段AD的长;
(3)若BE=8,sinB= ,求DG的长.
图6
7.如图7,AB是☉O的直径,点C,D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.
(1)求证:CE为☉O的切线.
(2)判断四边形AOCD是否为菱形?并说明理由.
图4
5.如图5,在△ABC中,AB=AC,以AB为直径的☉O分别交AC,BC于点D,E,点F在AC的延长线上,且∠BAC=2∠CBF.
(1)求证:BF是☉O的切线;
(2)若☉O的直径为3,sin∠CBF= ,求BC和BF的长.
图5
6.如图6,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的☉O分别交AB,AC于点E,F,连接OF交AD于点G.
∵点A是 的中点,
∴ = ,
∴∠DPA=∠APB,
∴∠OAP=∠APB.∴OA∥PB.
∵PB⊥l,∴OA⊥l,
∴直线l是☉O的切线.
(2)连接AD,∵PD是直径,
∴∠PAD=90°,∴∠PAD=∠PBA.
又∵∠DPA=∠APB,
∴△PAD∽△PBA,
∴ = ,即 = ,∴PB= .
2.解:(1)因为点D是AC中点,所以OD⊥AC,所以PA=PC,所以∠PCA=∠PAC,因为AB是☉O的直径,