根轨迹法习题和答案
第4章 控制系统根轨迹法习题

即: (s −s2)(s −s3) = s2 + s +1
−1+ j 3 则:s2 = 2 −1− j 3 s2 = 2
为系统另外
两个极点的值。 两个极点的值。
(s +2)(s +1 ) (s +2)(s +1 ) s(s +1 ) ϕ(s) = = (s +2)(s +1 s(s +1 +(s +2)(s +1 ) ) ) 1+ s(s +1 ) (s +2)(s +1 ) s +2 = = (2s +2)(s +1 2s +2 )
三.绘制下图所示系统的概略根轨迹,并用根轨迹 绘制下图所示系统的概略根轨迹, 的模值方程确定使系统的三个根均为负实根的 k* 取值范围。 取值范围。
2.系统在欠阻尼状态下,也就是根轨迹在复平面 2.系统在欠阻尼状态下, 系统在欠阻尼状态下 上变化, 上变化,而不在实轴上变化 0 <T <1 3.闭环极点出现重根时,也就是根轨迹在分离点 3.闭环极点出现重根时 闭环极点出现重根时, s1 = s2 =−1 系统此时为临 处,此时闭环极点 界阻尼 T =1 。 则闭环传递函数为: 则闭环传递函数为:
二.系统结构如下图所示: 系统结构如下图所示: 1.绘制T从 0 →∞ 变化的根轨迹。 1.绘制 绘制T 变化的根轨迹。 2.确定系统在欠阻尼状态下T的取值范围。 2.确定系统在欠阻尼状态下 的取值范围。 确定系统在欠阻尼状态下T 3.求闭环极点出现重根时的闭环传递函数。 3.求闭环极点出现重根时的闭环传递函数 求闭环极点出现重根时的闭环传递函数。
解:特征方程为: 特征方程为:
自动控制原理简明教程 第四章 根轨迹法 习题答案

(S S3 )(S 1)2 S (S 3)2 4
则解得:
(S S3 )(S 1)2 S (S 1)2 4(S 1)2 (S 4)(S 1)2
则 (S S3) S 4 S3 4 (另外一个闭环极点) 临界阻尼时的闭环传递函数为
(S)
(S
4(S 1) 4)(S 1)2
d d 2 d 1 j d 1 j
n
(
1
m
1 ) 求分离点的坐标公式
i1 d Pi i1 d Zi
解得:d 1
分离角: l
180 l
180 2
900
此时对应为T值:
(应使用模值方程求得)
T S S2 1T 1
S 1 j S 1 j
P1(-1,j)
T=0
Z2
Z1
-2
-1
0
T=∞
传递函数(写成零极点乘积形式) 解:系统结构图如下:
R(S) -
G(S)
C(S)
如果没有特别强调是正反馈,则单位反馈系统都 是单位负反馈系统。该题为参量根轨迹。 根轨迹方程:1 G(S) 1 4(S k) 0
S(S 1)(S 5)
特征方程:
D(S) S 3 6S 2 9S 4k 0
等效开环传递函数为:
G开 (S)
4k S(S
3)2
1
4k S (S 3)2
0
开环零点: m 0
开环极点: n 3, P1 0, P2 3, P3 3 则根轨迹有3条分支,有3条渐近线。
根轨迹与实轴的交点:
n
m
a
Pi Zi
i 1
i 1
nm
3 3 2 3
渐近线与实轴正方向夹角
根轨迹例题——精选推荐

根轨迹例题题4-1 求下列各环传递函数所对应的负反馈系统根轨迹。
(1)2(2)()23g K K s W s s s +=++解1)起点:两个开环极点1211p p -=-+-=--。
终点:系统有一个 2 z -=-开环零点。
2)实轴上根轨迹区间为 (2]-∞-,。
3)渐近线计算由公式()()1118012 0,1,2,n mj i j i k n m p z n m μϕμσ==⎧+==⎪-⎪⎪⎨-⎪⎪-=-⎪-⎩∑∑ 求得根轨迹的渐近线倾角和渐近线与实轴的交点为180(12)18021μϕ+==-22021k σ--=-=- 4)求分离点,会合点 由'()()'()()0D s N s N s D s -=得223(2)(22)0s s s s ++-++=整理得2410s s ++=解得12s =--22s =-+。
由于实轴上的根轨迹在()2-∞,区间内,所以分离点应为12 3.7s =-≈-。
5)出射角计算由111180n m sc j i j i ββα-==⎛⎫=-- ⎪⎝⎭∑∑得()11809054.7144.7sc β=--=同理,2144.7sc β=- 。
根轨迹如图4-1所示。
图4-1 题4-1(1) 根轨迹图(2))22)(2()(2+++=s s s s K s W gK解1) 起点:系统四个开环极点为12340,2,1,1p p p j p j -=-=--=---=-+;终点:四个无限零点。
2) 渐近线计算由公式()()1118012 0,1,2,n mj i j i k n m p z n m μϕμσ==⎧+==⎪-⎪⎪⎨-⎪⎪-=-⎪-⎩∑∑求得根轨迹的渐近线倾角和渐近线与实轴的交点为180(12)451354o μϕ+==±± 、21114k σ+-=-=-+ 3) 分离点,会合点计算'()()'()()0D s N s N s D s -=整理得 3 (1)0s += 解得1,2,3 1s =- 4) 出射角计算由111180n m sc j i j i ββα-==⎛⎫=-- ⎪⎝⎭∑∑得()1180901354590sc β=-++=-同理,290sc β=+ 。
第四章 根轨迹法 习题

第四章 根轨迹法4-1试粗略画出对应反馈控制系统具有以下前向和反馈传递函数的根轨迹图: ()()()()s s H s s s K s G 6.01,01.01.02+=++=4-2 试粗略地画出反馈系统函数 ()()()()2411+-+=s s s Ks G 的根轨迹。
4-3 对应负反馈控制系统,其前向和反馈传递函数为 ()()()()1,42)1(2=+++=s H s s s s K s G 试粗略地画出系统的根轨迹。
4-4 对应正反馈重做习题4-3,试问从你的结果中得出什么结论?4-5 试画出具有以下前向和反馈传递函数的,正反馈系统根轨迹的粗略图。
()()()()1,4122=++=s H s s Ks G4-6 试确定反馈系统开环传递函数为 ()()()()()5284)2(2+++++=s s s s s s K s H s G 对应-∞<K<∞的根轨迹。
指明所有根轨迹上的相应特征。
4-7 设一负反馈系统,其开环传递函数 ()()()()()90020040)4(2++++=s s s s s K s H s G a) 画出根轨迹并表明根轨迹上全部特征值。
b) 增益值在一个什么样的范围内,系统才是稳定的? c) 画出系统的伯德图,并使其稳定性和不稳定性区域,与根轨迹图连系起来说明。
4-8 对应负反馈情况,重做习题4-7.4-9 对应如下的负反馈控制系统,粗略地作出根轨迹,并确定系统稳定下K 的范围。
()()()()1,41)6(=+++=s H s s s s K s G4-10 对应习题4-10图所示系统,根据以下条件,试确定导致系统稳定的正实数增益K 的范围:a) 具有负反馈的系统。
b) 具有正反馈的系统。
习题4-10图4-11 已知反馈系统的开环传递函数*()()(1)(2)K G s H s s s s =++ 试绘制系统的根轨迹图,详细列写根轨迹的计算过程,其中包括零点、极点、渐近线及与实轴交点,根轨迹分离点及与虚轴的交点、渐近线与实轴夹角。
自控-第四章根轨迹法习题课

1 已知系统的开环传递函数为()()()()21++=s s s ks H s G ,(1)试绘制该系统的概略根轨迹图;(2)利用根轨迹图分析系统稳定时K 的取值范围。
解:(1)根据绘制根轨迹的基本法则,可知: ① 实轴上的根轨迹区域为:(-∞,-2]和[0.-1]。
② 根轨迹总共有三条,其中二条将趋向无穷远处,其渐近线为: a 与实轴的交点坐标(a δ,0j )()()1321011-=-+-+=--=∑∑==mn zp n i mj ji a δb 与实轴的夹角:()⎪⎩⎪⎨⎧-=-===+=-+=1601180060318012180)12(0000k k k k m n k o a ϕ③ 根轨迹的分离点()()()()()(){}()423.0,578.121210211)(121-=-=⇒++-=⇒++-=⇒=+++=+s s dss s s d ds dk s s s k s s s k s G g g g舍去④ 根轨迹与虚轴的交点()()()()0,6,0,20210211)(1=±=⇒=+++⇒=⇒=+++=+g g gk k j j j j s s s k s G 对应的代入上式:令s ωωωωω系统稳定的充要条件为所有的闭环极点都要复平面的左半平面,根据以上绘制根轨迹的第4点,系统稳定时K 的取值范围为60<<K 。
2 已知系统的开环传递函数为)3)(2()5()(*+++=s s s s K s G ,(1)试绘制该系统的概略根轨迹图;(2)利用根轨迹图分析系统稳定时K*的取值范围。
(1)根据根轨迹的绘制法则,可知:① 实轴上的根轨迹:[]3,5--, []0,2--1-2j② 渐近线: ⎪⎪⎩⎪⎪⎨⎧±=+==----=22)12(02)5(320ππϕσk a a③ 分离点: 5131211+=++++d d d d 用试探法可得886.0-=d 。
自动控制_根轨迹(例题)

n
m
n
m
nm
j 1
i 1
nm
这是与实轴交点为-,斜率为 tg
(2k 1) nm
是渐近线方程。渐近线与实轴的夹角(称为渐近线的倾斜角为
k 0,1,2
( 2k 1) 的直线方程。也就 nm
180
0
n m 1
nm 2
90 0
和
实轴上的会合点和分离点的求法
由此得: D( d ) K gd N ( d ) 0 ' ' D ( ) K N ( d ) 0 d gd 即:
N ' ( s ) D( s ) N ( s ) D ' ( s ) 0 D( s ) K gd N ( s) s d
二.根据相角条件确定根轨迹上的点
设某一系统的开环零极点如图,在S 平面中的任意一点 S0 ,用相角条件可
s0
O
× p2
以判断 S0 是不是根轨迹的点。
1、从 S0 到各零极点连直线
2、用量角器量 (s0 p1 ),…等各个角 3、将量好的值代入(**)式,若等
式成立,则 S0 就是根轨迹上的点
j 1 i 1 i
当 Kg= 0 时,有 s = pj ( j =1, 2, … , n) 上式说明Kg= 0时,闭环特征方程的根就是开环极点。
将特征方程改写为:
1 Kg
(s p ) (s z ) 0
j 1 j i 1 i
n
m
当 Kg 时,有
s = zi
( i =1, 2, … , m)
z1
o
根轨迹法习题及答案

第四章 根轨迹法习题及答案4-1 系统的开环传递函数为)4)(2)(1()()(*+++=s s s K s H s G 试证明点311j s +−=在根轨迹上,并求出相应的根轨迹增益*K 和开环增益K 。
解 若点在根轨迹上,则点应满足相角条件1s 1s π)12()()(+±=∠k s H s G ,如图解4-1所示。
对于31j s +−=,由相角条件=∠)()(11s H s G=++−∠−++−∠−++−∠−)431()231()131(0j j jππππ−=−−−632满足相角条件,因此311j s +−=在根轨迹上。
将代入幅值条件:1s 1431231131)(*11=++−⋅++−⋅++−=j j j K s H s G )(解出 : 12*=K , 238*==K K4-2 已知开环零、极点如图4-22所示,试绘制相应的根轨迹。
1(e) (f) (g) (h) 题4-22图 开环零、极点分布图解 根轨如图解4-2所示:4-3 已知单位反馈系统的开环传递函数,试概略绘出系统根轨迹。
⑴ )15.0)(12.0()(++=s s s Ks G⑵ )3)(2()5()(*+++=s s s s K s G⑶ )12()1()(++=s s s K s G2解 ⑴ )2)(5(10)15.0)(12.0()(++=++=s s s Ks s s K s G系统有三个开环极点:,01=p 22−=p ,53−=p① 实轴上的根轨迹:,(]5,−∞−[0,2−]② 渐近线: ⎪⎪⎩⎪⎪⎨⎧±=+=−=−−=πππϕσ,33)12(373520k a a③ 分离点:021511=++++d d d 解之得:,(舍去)。
88.01−=d 7863.32−d ④ 与虚轴的交点:特征方程为010107)(23=+++=k s s s s D 令 ⎩⎨⎧=+−==+−=010)](Im[0107)](Re[32ωωωωωj D k j D 解得⎩⎨⎧==710k ω 与虚轴的交点(0,j 10±)。
自控 根轨迹法习题及答案
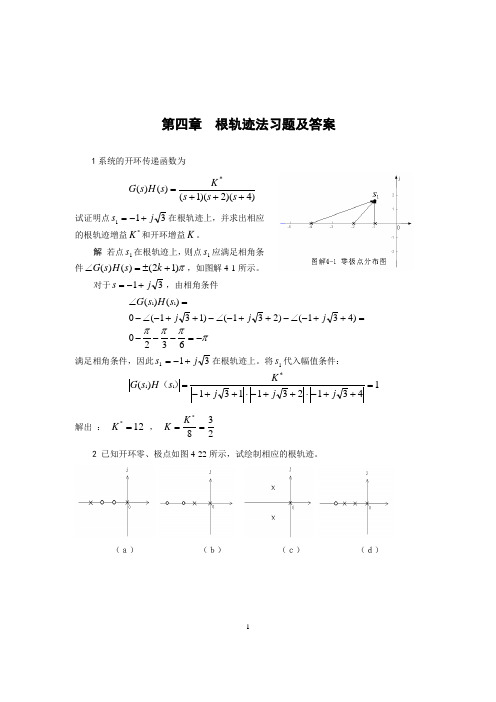
1第四章 根轨迹法习题及答案1系统的开环传递函数为)4)(2)(1()()(*+++=s s s K s H s G试证明点311j s +-=在根轨迹上,并求出相应的根轨迹增益*K 和开环增益K 。
解 若点1s 在根轨迹上,则点1s 应满足相角条件π)12()()(+±=∠k s H s G ,如图解4-1所示。
对于31j s +-=,由相角条件=∠)()(11s H s G=++-∠-++-∠-++-∠-)431()231()131(0j j jππππ-=---6320满足相角条件,因此311j s +-=在根轨迹上。
将1s 代入幅值条件:1431231131)(*11=++-⋅++-⋅++-=j j j K s H s G )(解出 : 12*=K , 238*==K K 2 已知开环零、极点如图4-22所示,试绘制相应的根轨迹。
2解根轨如图解4-2所示:3已知单位反馈系统的开环传递函数,要求:(1)确定)20)(10()()(2+++=*ssszsKsG产生纯虚根为1j±的z值和*K值;(2)概略绘出)23)(23)(5.3)(1()(jsjssssKsG-+++++=*的闭环根轨迹图(要求3确定根轨迹的渐近线、分离点、与虚轴交点和起始角)。
解(1)闭环特征方程020030)()20)(10()(2342=++++=++++=***z K s K s s s z s K s s s s D有 0)30()200()(324=-++-=**ωωωωωK j z K j D令实虚部分别等于零即: ⎪⎩⎪⎨⎧=-=+-**0300200324ωωωωK z K 把1=ω代入得: 30=*K , 30199=z 。
(2)系统有五个开环极点:23,23,5.3,1,054321j p j p p p p --=+-=-=-==① 实轴上的根轨迹:[],5.3,-∞- []0,1-② 渐近线: 1 3.5(32)(32) 2.15(21)3,,555a a j j k σπππϕπ--+-++--⎧==-⎪⎪⎨+⎪==±±⎪⎩③ 分离点:02312315.31111=+++-++++++j d j d d d d 解得: 45.01-=d , 4.22-d (舍去) , 90.125.343j d ±-=、 (舍去)④ 与虚轴交点:闭环特征方程为0)23)(23)(5.3)(1()(=+-+++++=*K j s j s s s s s D把ωj s =代入上方程,整理,令实虚部分别为零得:⎪⎩⎪⎨⎧=+-==-+=*05.455.43 )Im(05.795.10)Re(3524ωωωωωωωj K j解得:⎩⎨⎧==*00K ω ,⎩⎨⎧=±=*90.7102.1K ω,⎩⎨⎧-=±=*3.1554652.6K ω(舍去)⑤ 起始角:根据法则七(相角条件),根轨迹的起始角为74..923..1461359096..751804=----=p θ由对称性得,另一起始角为74.92,根轨迹如图解4-6所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 根轨迹法习题及答案4-1 系统的开环传递函数为)4s )(2s )(1s (K )s (H )s (G *+++=试证明3j 1s 1+-=在根轨迹上,并求出相应的根轨迹增益*K 和开环增益K 。
解 若点1s 在根轨迹上,则点1s 应满足相角条件π)12()()(+±=∠k s H s G ,如图所示。
对于31j s +-=,由相角条件=∠)s (H )s (G 11-++-∠-)13j 1(0=++-∠-++-∠)43j 1()23j 1(ππππ-=---632满足相角条件,因此311j s +-=在根轨迹上。
将1s 代入幅值条件:143j 123j 113j 1K s H )s (G *11=++-⋅++-⋅++-=)(解出 : 12K *= , 238K K *==4-2 已知单位反馈系统的开环传递函数如下,试求参数b 从零变化到无穷大时的根轨迹方程,并写出2b =时系统的闭环传递函数。
(1))b s )(4s (02)s (G ++=(2))b s )(2s (s )b 2s (01)s (G +++=解 (1) )4j 2s )(4j 2s ()4s (b 20s 4s )4s (b )s (G 2-++++=+++=' 28s 6s 20)s (G 1)s (G )s (2++=+=Φ(2) )10s 2s (s )20s 2s (b )s (G 22++++='=)3j 1s )(3j 1s (s )19j 1s )(19j 1s (b -+++-+++ 40s 14s 4s )4s (10)s (G 1)s (G )s (23++++=+=Φ 4-3 已知单位反馈系统的开环传递函数)b s )(4s (s2)s (G ++=,试绘制参数b 从零变化到无穷大时的根轨迹,并写出s=-2这一点对应的闭环传递函数。
解 )6s (s )4s (b )s (G ++='根轨迹如图。
2s -=时4b =, )8s )(2s (s216s 10s s 2)s (2++=++=Φ4-4 已知单位反馈系统的开环传递函数,试概略绘出系统根轨迹。
⑴ )1s 5.0)(1s 2.0(s k)s (G ++=(2) )1s 2(s )1s (k )s (G ++=(3) )3s )(2s (s )5s (k )s (G *+++= (4) )1s (s )2s )(1s (*k )s (G -++=解 ⑴ )2s )(5s (s K10)1s 5.0)(1s 2.0(s K )s (G ++=++=三个开环极点:0p 1=,2p 2-=,5p 3-= ① 实轴上的根轨迹:(]5,-∞-, []0,2-② 渐近线: ⎪⎪⎩⎪⎪⎨⎧ππ±=π+=ϕ-=--=σ,33)1k 2(373520a a③ 分离点:02d 15d 1d 1=++++ 解之得:88.0d 1-=,7863.3d 2-(舍去)。
④ 与虚轴的交点: 特征方程为0k 10s 10s 7s )s (D 23=+++=令 ⎩⎨⎧=ω+ω-=ω=+ω-=ω010)]j (D Im[0k 107)]j (D Re[32 解得⎩⎨⎧==ω7k 10与虚轴的交点(0,j 10±)。
根轨迹如图所示。
⑵ )21s (s 2)1s (K )1s 2(s )1s (K )s (G ++=++=根轨迹绘制如下:① 实轴上的根轨迹:(]1,-∞-, []0,5.0- ② 分离点:1d 15.0d 1d 1+=++ 解之得:707.1d ,293.0d -=-=。
根轨迹如图所示。
⑶根轨迹绘制如下:① 实轴上的根轨迹:[]3,5--, []0,2-② 渐近线: ⎪⎪⎩⎪⎪⎨⎧±=+==----=22)12(02)5(320ππϕσk a a③ 分离点:5131211+=++++d d d d用试探法可得886.0-=d 。
根轨迹如图所示。
(4) 根轨迹绘制如下:① 实轴上的根轨迹:[0, 1],[-1,-2] ②分离点:2d 11d 11d 1d 1+++=-+ 求解得:37.1d 37.0d 21-==, 根轨迹如图所示。
4-5 已知单位反馈系统的开环传递函数为 )101s .0)(102s .0(s k)s (G ++=要求:(1) 绘制系统的根轨迹;(2) 确定系统临界稳定时开环增益k 的值; (3) 确定系统临界阻尼比时开环增益k 的值。
解 (1) )100s )(50s (s k5000)1s 01.0)(1s 02.0(s k )s (G ++=++=① 实轴上的根轨迹:[0, -50],[-100,-∞] ② 分离点:0100d 150d 1d 1=++++ 求解得87.78d 13.21d 21-=-=,③ 渐近线:o oa a 1806050,,±=ϕ-=σ 根轨迹如图所示。
(2) 系统临界稳定时150k 750000k *==, (3) 系统临界阻尼比时62.9k 5.48112k *==,4-6 已知系统的开环传递函数为)20s 8s (s k )s (H )s (G 2*++=,要求绘制根轨迹并确定系统阶跃响应无超调时开环增益k 的取值范围。
解 )20s 8s (s K )s (H )s (G 2++=*① 实轴上的根轨迹: (]0,∞-② 渐近线:⎪⎪⎩⎪⎪⎨⎧ππ±=π+=ϕ-=--++-+=σ,33)1k 2(383)2j 4()2j 4(0a a ③分离点:02j 4d 12j 4d 1d 1=-+++++ 解之得:33.3d ,2d -=-=。
④与虚轴交点:*+++=ks 20s 8s )s (D 23把ω=j s 代入上方程,整理,令其实、虚部分别为零得:⎩⎨⎧=ω-ω=ω=ω-=ω*020))j (D Im(08k ))j (D Re(32 解得:⎩⎨⎧==ω*0k 0⎪⎩⎪⎨⎧=±=ω*160k 52⑤起始角:由相角条件632p -=θ,633p =θ。
根轨迹如图所示。
所有根为负实根时阶跃响应无超调,此时,16k 8.14*≤≤ 所以8.0k 74.0≤≤4-7 单位反馈系统的开环传递函数为)1s 74()1s ()1s 2(k )s (G 2-++=,试绘制系统根轨迹,并确定使系统稳定的k 值范围。
解 :根轨迹绘制如下:① 实轴上的根轨迹: []4/75.0,- ② 渐近线:⎪⎪⎩⎪⎪⎨⎧π±=π+=ϕ=--+--=σ22)1k 2(812)5.0(4/711a a③ 与虚轴交点:闭环特征方程为01k s )710k 2(s 71s 74)s (D 23=-+-++=把ω=j s 代入上方程,令⎪⎩⎪⎨⎧=ω-ω-=ω=ω--=ω074)710K 2())j (D Im(0711K ))j (D Re(32解得: ⎩⎨⎧==ω1K 0,⎪⎩⎪⎨⎧=±=ω79K 2 根轨迹如图所示。
由图可知使系统稳定的K 值范围为 79K 1<<。
4-8 已知控制系统的开环传递函数如下,试绘制系统根轨迹(要求求出起始角)。
22)9s 4s (2s K )s (H )s (G +++=*)( 解 根轨迹绘制如下:① 实轴上的根轨迹: []2,-∞-② 渐近线:⎪⎪⎩⎪⎪⎨⎧ππ±=π+=ϕ-=--+---=σ,33)1k 2(323)2(5j 25j 2a a ③ 分离点:2d 15j 2d 25j 2d 2+=-++++ 解之得:29.3d -= 71.0d = (舍去) ④ 与虚轴交点:闭环特征方程为02s K )9s 4s ()s (D 22=++++=*)(把ωj s =代入上方程,令⎪⎩⎪⎨⎧=ω-ω+=ω=++ω-ω=ω**8)K 72())j (D Im(0K 28134))j (D Re(324解得: ⎩⎨⎧=±=ω*96K 21⑤ 起始角: π+=⨯-θ-)()(1k 29022901p解出135,4521p p -=θ=θ 根轨迹如图所示。
4-9 已知系统开环传递函数如下,试分别绘制以a 和T 为变化参数的根轨迹。
(1) )1s (s )a s (4/1)s (G 2++=,0a >;(2) )1Ts )(11s .0(s 6.2)s (G ++=,0T > 解 (1) 2)5.0s (s 4/a )s (G +=' ① 实轴上的根轨迹: )0(,-∞ ② 渐近线:o oa a 180603/1,,±=ϕ-=σ ③ 分离点:6/1d -= 根轨迹如图所示。
(2) 26s 10s )10s (Ts )s (G 22+++='① 实轴上的根轨迹: )0(,-∞ ② 起始角终止角:o o p 11o 180)90(51tg )51tg 180(2=+θ-+---解得起始角o p 7.78±=θ o 11oz 180)51tg 51tg(02=+--+θ-- 解得终止角oz 90±=θ 根轨迹如图所示。
4-10 已知系统的开环传递函数如下,试概略绘出相应的根轨迹, 并求出所有根为负实根时开环增益k 的取值范围及系统稳定时k 的值。
)18s ()1s ()1s (k )s (H )s (G 2+-+=* 解① 实轴上的根轨迹: ]118[--, ② 分离点:22.4d 1-=,28.6d 2-=③ 渐近线:5.7a -=σ,o a 90±=ϕ④ 与虚轴交点:j 86.1s 2,1±=,7.37k *=根轨迹如图所示。
6.116k d *1=处,6.117k d *2=处,18/k k *=结论:53.6k 48.6<<时所有根为负实根,095.2k >时系统稳定。
4-11 已知系统结构图如图所示,试绘制时间常数T 变化时系统的根轨迹,并分析参数T 的变化对系统动态性能的影响。
解:s20s Ts 100)s (G 23++=作等效开环传递函数32*s )100s 20s (T 1)s (G ++=根轨迹绘制如下: (注意:)T /1k *= ① 实轴上的根轨迹:]10,(--∞,[]0,10- ② 分离点:10d 2d 3+=解得30d -=。
根据幅值条件,对应的015.0T =。
③ 虚轴交点:闭环特征方程为0100s 20s Ts )s (D 23=+++=把ω=j s 代入上方程,整理,令实虚部分别为零得:⎪⎩⎪⎨⎧=ω-ω=ω=ω-=ω0T 20))j (D Im(0100))j (D Re(32解得: ⎩⎨⎧=±=ω2.0T 10④ 起始角:︒=θ601p参数T 从零到无穷大变化时的根轨迹如图所示。
