大学物理安培定律
大学物理-安培定律3
B
R
B
R
B
R
B
R
B
R
7-8 载流导线在磁场中所受的力
一、 安培力
Ⅰ、带电粒子在磁场中所受的
f
洛 仑兹力 :
f q B
Ⅱ、所有粒子受力的宏观表现：
s n+ v
dl
×××
d F dN f
ns dl qv B
dN
ndV nsdl
V是指粒子作定向 运动的方向.
nqvsdl B I qnvs
（A）向着长直导线平移 （C）转动
（B）离开长直导线平移
（D）不动
dF
无限长直导线产生的磁感应强度为：
B 0I 2r
I1
若在均匀磁场中？
B
60
I2
C
A B
五、 磁场对载流线圈的作用
1、磁场对载流线圈作用的磁力矩
F1
a
r1 θ
I
θdF2 θ
cn
B
r2
M
合力=0 F2和
F2 F2
ad l1 ab
Idl1
df1
df2
B1I2dl2 B1
0 I1 2a
I1
导线1、2单位长度上所受的磁场力为：
df1 0 I1I2 df2 0 I1 I2 dl1 2a dl2 2a
安培的定义 : a 1m，df dl
2 107
N m
o 4 107 (N / A2 )
a
df2
Idl2
I2 B1
练习：如图，无限长直载流导线与正三角形载流线圈在同一平面内， 若长直导线固定不动，则载流三角形线圈将 [ ] A
设粒子的质量为m,圆周轨道的半径为R:
大学物理安培环路定理
10-4 安培环路定理静电场的一个重要特征是电场强度E 沿任意闭合路径的积分等于零，即0d =⋅⎰l E l，那么，磁场中的磁感强度B 沿任意闭合路径的积分⎰⋅ld lB 等于多少呢？可以证明：在真空的稳恒磁场中，磁感强度B 沿任一闭合路径的积分（即B 的环流）的值，等于0μ乘以该闭合路径所包围的各电流的代数和，即∑⎰==⋅ni lI10 d il B μ （10-8）安培环路定理与静电场环路定理的比较 讨论：安培环路定理的证明如图(a)所示，有一通有电流I 的长直载流导线垂直于屏幕平面，且电流流向垂直屏幕平面向内. 在屏幕平面上取两个闭合路径1C 和2C ，其中闭合路径1C 内包围的电流为I ，而在闭合路径2C 内没有电流. 从图（b ）可以看出，由于磁感强度B 的方向总是沿着环绕直导线的圆形回路的切线方向，所以对闭合路径1C 或2C 上任意一线元l d ，磁感强度B 与l d 的点积为ϕαd cos d d Br l B ==⋅l B式中r 为载流导线至线元l d 的距离. 由第10-2节二中例1的式（2），上式可写成ϕμϕμd π2d π2d 00Ir rI==⋅l B （1）对于图（a ）的闭合回路1C ，ϕ将由0增至π2. 于是，磁感强度B 沿闭合路径1C 的环流为这就是真空中磁场的环路定理，也称安培环路定理。
它是电流与磁场之间的基本规律之一。
在式（10-8）中，若电流流向与积分回路呈右螺旋关系，电流取正值；反之则取负值。
⎰⎰===⋅1000π2π2d π2d CIIIμμϕμl B （2）可见，真空中磁感强度B 沿闭合路径的环流等于闭合路径所包围的电流乘以0μ，而与闭合路径的形状无关.然而，对于图（a ）中的闭合路径2C ，将得到不同的结果，当我们从闭合路径2C 上某一点出发，绕行一周后，角ϕ的净增量为零，即⎰=0d ϕ于是，由式（1）可得⎰=⋅20d c l B （3）比较式（2）和式（3）可以看出，它们是有差别的. 这是由于闭合路径1C 包围了电流，而闭合路径2C 却未包围电流. 于是我们可以得到普遍的安培环路定理：沿任意闭合路径的磁感强度B 的环流为⎰∑=⋅20d c I μl B式中∑I 是该闭合路径所包围电流的代数和 人物简介：安培简介安培(Andre Marie Ampere,1775-1855)，法国物理学家，对数学和化学也有贡献，他在电磁理论的建立和发展方面建树颇丰。
大学物理10.4安培环路定理及其应用Xiao
实验设备与材料
01
02
磁场测量仪
用于测量磁场强度和方向。
导线
用于产生电流，形成磁场。
03
电源
为导线提供电流。
04
磁力计
用于测量磁力大小。
实验步骤与操作
步骤2
连接电源，使导线通电，产生 电流。
步骤4
使用磁力计测量导线受到的磁 力大小。
步骤1
将导线绕制成一定形状，如圆 形或矩形，并固定在实验台上。
步骤3
02
安培环路定理的数学表达式为： ∮B·dl = μ₀I，其中B表示磁场强度， dl表示微小线段，I表示穿过曲线的 电流，μ₀表示真空中的磁导率。
安培环路定理的推导过程
安培环路定理的推导基于电磁场的基 本理论，通过应用高斯定理和斯托克 斯定理，结合电流连续性和电荷守恒 定律，逐步推导出安培环路定理。
大学物理10.4安培环路定理及其 应用
目 录
• 安培环路定理的概述 • 安培环路定理的应用场景 • 安培环路定理在实践中的应用 • 安培环路定理的实验验证 • 安培环路定理的扩展与思考
01 安培环路定理的概述
安培环路定理的定义
01
安培环路定理是描述磁场与电流 之间关系的物理定理，它指出磁 场对电流的作用力与电流分布及 路径有关。
03
电磁场仿真
安培环路定理是电磁场仿真的基础之一，通过仿真软件实现安培环路定
理的算法，可以模拟电机的电磁场行为，预测电机的性能，并为实际电
机设计提供理论依据。
电磁场仿真软件的安培环路定理实现
有限元法（FEM）
有限元法是一种常用的电磁场仿真方法，通过将连续的电磁场离散化为有限个小的单元，并应用安培环路定理进行求 解。这种方法可以处理复杂的几何形状和边界条件，得到高精度的仿真结果。
大学物理-磁场 安培环路定律
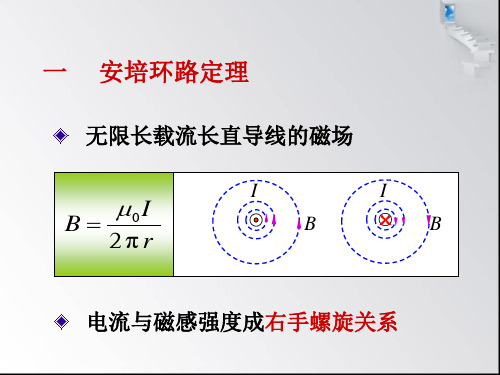
Φ BS cos BS
s
一般情况 Φ s BdS
dS2
B
S 2
dS1
1
B1
dΦ1 B1 dS1 0
dΦ2 B2 dS2 0
B2
SB cosdS 0
磁场高斯定理
S B d S 0
物理意义：通过任意闭合曲面的磁通
量必等于零（故磁场是无源的）.
B B1 B2 B3
Bdl
l
0(I2 I3)
推广：
➢ 安培环路定理
n
B dl 0 Ii
i 1
n
安培环路定理
B dl 0 Ii
i 1
在真空的恒定磁场中，磁感强度 B沿任
一闭合路径的积分的值，等于 0乘以该闭合
路径所穿过的各电流的代数和.
注意
电流 I 正负的规定： I 与 L 成右螺旋
而与环路外电流无关。
3. B为环路上一点的磁感应强度，它与环路内外电流
都有关。
若
B
dl
0
并不一定说明环路上各点的 B 都为 0。
若 B dl 0 环路内并不一定无电流。
4.环路定理只适用于闭合电流或无限电流，
应用 安培环路定理的应用举例
例1
求载流螺绕环内的磁场
解 （1）对称性分析：环内B 线为同心
B dl B 2r 0 I
B 0 I 1 2r r
I
r LR
r L
分布曲线
B
0 I 2R B r
B 1 r
o
R
r
例4 无限大均匀带电(线密度为i)平面的磁场
解 如图，作安培环路
abcda，应用安培环路 定理
b
l B d l 2a B dl
朱卫华《大学物理》2-安培环路定律与安培定律和带电粒子的作用和磁介质2014
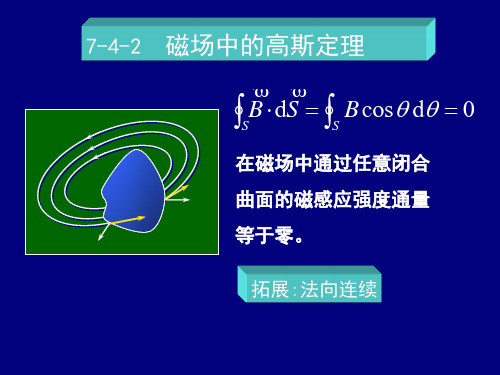
v 2eV m
电子束打在屏幕中央的条件： v E B
E 2eV Bm
e m
E2 2VB 2
电子的比荷： e 1.75881962(53) 1011 C kg 1 m
电子的质量： m 9.1093897(54) 1031 kg
v E B
7 质谱仪原理
R mv qB0
mE qB0 B
不同的粒子质量分布在不同的位置
液体中观察原子图象
下图所示的是在电解液中得到的硫酸根离子吸附在 铜单晶(111)表面的STM图象。
5 . 电子荷质比的测定
控制极 阳极
阴
极
U
⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙
B l
调节B 使比值
l n v0 xT
控制极 阳极
阴
极
U
⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙
B l
T 2π m qB
安培环路定理：
B B onI
a
bB
d
c
2. 螺线环内的磁感应强度
B dl L
o I
B 2 r oNI
B oNI 2 r
环路 L
磁感应 线
无限大电流平面的磁场----与电场作类比
E
2 0
B
0
j 2
???
电场高斯定理和磁场安培环 路定理应用总结
注意
B dl L
0
Ii
1. 安培环路定理表达式中的
电流强度是指闭合曲线所包
I4
围，并穿过的电流强度，不
包括闭合曲线以外的电流。
I3 I2 I1
L
2. 安培环路定理表达式中的磁感应强度B是闭合曲线
内外所有电流产生的磁感应强度。
大学物理8-8有磁介质时的安培环路定理磁场强度
例题8-8 在均匀密绕的螺绕环内充满均匀的顺磁介 质，已知螺绕环中的传导电流为 I ，单位长度内匝 数 n ，环的横截面半径比环的平均半径小得多，磁介 质的相对磁导率和磁导率分别为 r 和 。 求环内的 磁场强度和磁感应强度。 解：在环内任取一点， 过该点作一和环同心、 r 半径为 r的圆形回路。
§8-8 有磁介质时的安培环路定理磁场强度
一、磁化强度
反映磁介质磁化程度(大小与方向)的物理量。 磁化强度：单位体积内所有分子固有磁矩的 矢量和 m 加上附加磁矩的矢量和 m分子 ，称 分子 为磁化强度，用 M 表示。 m分子 m分子 均匀磁化 M V m分子 m分子 非均匀磁化 M lim V 0 V 磁化强度的单位： A/m
上页 下页 返回 退出
0 H dl I
M ) dl I
有磁介质时的 安培环路定理
H
B
0
此式说明了介质中任一点磁场强度、 M 磁感应强度、磁化强度之间的普遍
关系，不论介质是否均匀。
实验证明：对于各向同性的介质，在磁介质 中任意一点磁化强度和磁场强度成正比。
R2
2 πr3 H d l H d l 0
即
H 0
0
I
I I
或
B0
上页 下页 返回 退出
选择进入下一节 §8-0 教学基本要求 §8-1 恒定电流 §8-2 磁感应强度 §8-3 毕奥-萨伐尔定律 §8-4 稳恒磁场的高斯定理与安培环路定理 §8-5 带电粒子在电场和磁场中的运动 §8-6 磁场对载流导线的作用 §8-7 磁场中的磁介质 §8-8 有磁介质时的安培环路定理 磁场强度 *§8-9 铁磁质
大学常用的物理公式(二)2024
大学常用的物理公式（二）引言概述：大学物理是大多数理工科专业学生所学的一门基础课程。
在学习物理过程中，常用的物理公式是不可或缺的工具。
本文将介绍大学常用的物理公式（二）。
根据其应用领域，这些公式可分为五个大点：力学、热学、电磁学、光学和量子物理。
每个大点都包含了几个小点，总共提供了全面的物理公式知识。
正文：一、力学1. 速度公式：速度（v）等于物体位移（s）除以物体经过的时间（t），即v = s/t。
2. 加速度公式：加速度（a）等于物体速度（v）变化的量除以时间（t），即a = Δv / t。
3. 牛顿第二定律：力（F）等于物体质量（m）乘以物体加速度（a），即F = ma。
4. 动能公式：物体的动能（K）等于质量（m）乘以速度（v）的平方的一半，即K = 1/2 mv²。
5. 万有引力公式：物体间的引力（F）等于物体质量（m₁）乘以另一物体质量（m₂），再除以二者间的距离（r）的平方，即F = G(m₁m₂)/r²。
（G为万有引力常数）二、热学1. 热传导公式：热传导（Q）等于热传导系数（k）乘以温度差（ΔT）除以物体的厚度（d），即Q = kΔT / d。
2. 热容量公式：物体的热容量（C）等于物体的质量（m）乘以物体的比热容（c），即C = mc。
3. 理想气体状态方程：理想气体的压强（P）等于气体物质的摩尔数（n）乘以气体的温度（T）除以气体的体积（V），即P = nRT/V。
（R为气体常数）4. 熵变公式：系统的熵变（ΔS）等于系统吸收的热量（Q）除以温度（T），即ΔS = Q/T。
5. 热力学第二定律：热不会自发从低温物体传递到高温物体，即熵在自然过程中总是增加的。
三、电磁学1. 电场力公式：电场力（F）等于电荷（q）乘以电场强度（E），即F = qE。
2. 磁场力公式：磁场力（F）等于带电粒子的电荷（q）乘以其速度（v）乘以磁场（B）的正弦角（θ），即F = qvBsinθ。
有磁介质的安培环路定律(大学物理下)
(2)硬磁材料——作永久磁铁 钨钢，碳钢，铝镍钴合金
B
HC
HC H
矫顽力(Hc)大（>102A/m)，剩磁Br大 磁滞回线的面积大，损耗大。
还用于磁电式电表中的永磁铁。 耳机中的永久磁铁，永磁扬声器。
(3)矩磁材料——作存储元件
锰镁铁氧体，锂锰铁氧体
B
HC
H
HC
Br=BS ，Hc不大，磁滞回线是矩形。 用于记忆元件，当+脉冲产生H>HC使磁芯呈+B态， 则–脉冲产生H< – HC使磁芯呈– B态，可做为二进制 的两个态。
人有了知识，就会具备各种分析能力， 明辨是非的能力。
所以我们要勤恳读书，广泛阅读， 古人说“书中自有黄金屋。
”通过阅读科技书籍，我们能丰富知识， 培养逻辑思维能力；
通过阅读文学作品，我们能提高文学鉴赏水平， 培养文学情趣；
通过阅读报刊，我们能增长见识，扩大自己的知识面。 有许多书籍还能培养我们的道德情操， 给我们巨大的精神力量， 鼓舞我们前进。
2r
O
B H 0r H
例2 一无限长载流圆柱体，通有电流I ，设电流 I
均匀分布在整个横截面上。柱体的相对磁导率μr， 柱外为真空。求：柱内外各区域的磁场强度和磁感
应强度。
I
解： r R
LH dl H 2r I
r2 R2 I
Ir
Ir
H 2R2 B 2R2
四、磁化强度
定义: 磁化强度
l
M
pm
V
A m1
Is
S
Is
Is
Is——沿轴线单位长度上的磁化电流（磁化面电流密度）
大学物理安培环路定律教案
一、教学目标1. 理解安培环路定律的基本概念和原理。
2. 掌握安培环路定律的应用方法。
3. 培养学生的逻辑思维能力和分析问题的能力。
二、教学重点1. 安培环路定律的基本概念和原理。
2. 安培环路定律的应用方法。
三、教学难点1. 理解安培环路定律中的积分运算。
2. 掌握安培环路定律在不同情况下的应用。
四、教学过程一、导入1. 介绍安培环路定律的背景和意义。
2. 提出问题：如何计算载流导线产生的磁场？二、讲解安培环路定律1. 介绍安培环路定律的基本概念和原理，包括磁感应强度B、闭合路径l、微小线元素dl、磁常数μ0、闭合路径所包围的电流I等。
2. 解释安培环路定律的表达式：∮B·dl = μ0I3. 分析安培环路定律的物理意义：在稳恒磁场中，磁感应强度B沿任何闭合路径的线积分等于闭合路径所包围的电流乘以磁导率。
三、讲解安培环路定律的应用方法1. 应用安培环路定律计算载流导线产生的磁场。
2. 应用安培环路定律分析复杂电流分布产生的磁场。
3. 通过实例讲解如何确定闭合路径和计算积分。
四、讲解安培环路定律的局限性1. 介绍安培环路定律的适用范围：仅适用于稳恒磁场。
2. 说明安培环路定律在含时电场中的局限性。
五、课堂练习1. 列举安培环路定律的典型应用实例。
2. 分析并解决相关计算问题。
六、总结与拓展1. 总结安培环路定律的基本概念和原理。
2. 拓展安培环路定律在电磁学领域的应用。
七、作业1. 完成课后习题，巩固所学知识。
2. 查阅资料，了解安培环路定律在工程和科研中的应用。
八、教学反思1. 分析学生在学习安培环路定律过程中的难点和困惑。
2. 优化教学方法和手段，提高学生的学习效果。
大学物理安培定理
I1
I2
I1dl1 B2
I2dl2
dF1
dF2
B1
d
dF2 dF1 0I1I2
dl2 dl1 2π d
B1
0 I1
2π d
B2
0I2
2π d
dF2 B1I2dl2 sin
90,sin 1
dF2
B1I 2dl2
0 I1I 2dl2
2π d
dF1
B2 I1dl1
0 I 2 I1dl1
与 Idl B 同向 .
有限长载流导线 所受的安培力
F ldF l Idl B
dF Idl
Idl
dF
B
B
度为例B1的均如匀图磁一场通中有，电回流路I平的面闭与合磁回感路强放度在磁B感垂应直强.
r 回路由直导线 AB 和半径为 的圆弧导线 BCA 组成 ，
电流为顺时针方向, 求磁场作用于闭合导线的力.
§9.4 安培定律
一、安培定律(Ampere law)
洛伦兹力
fm
evd
B
vd
fm evd B sin
fm
Idl
I
S
dF nevdSdlB sin
B
dl
dF IdlBsin IdlB sin I nevdS
由于自由电子与晶格之间的相互作用，使导线在
宏观上看起来受到了磁场的作用力 .
2π d
国际单位制中电流单位安培的定义
I1
I2
B2
dF1
dF2
d
在真空中两平行长直导线相
距 1 m ，通有大小相等、方向相
同的电流，当两导线每单位长度
上的受力为 2107 N m1 时，规
6.磁场的安培环路定理
《大学物理》作业 No.6 磁场的安培环路定理班级 ___________ 学号 __________ 姓名 ____________ 成绩 __________说明：字母为黑体者表示矢量内容提要：安培环路定理 ∑⎰=⋅I l d B L0μ1. 安培环路定理的理解：①B是环路上各点的磁感应强度，是环路内外所有电流共同激发的磁场。
②∑I 只是被环路包围的电流的代数和。
③不被环路包围的电流在环路上激发的磁场在环路的线积分中抵消掉了。
④环路上各点0=B 时，必有0=∑I ；但0=∑I 时，未必环路上各点的B 一定都为零。
⑤对于电流的正负的规定：当电流的方向与环路积分的方向符合右手螺旋关系时，电流为正，否则为负。
⑥安培环路定理中的电流应该是闭合（或无限长）恒定电流，对于一段恒定电流的磁场，安培环路定理不成立。
2. 安培环路定理的应用：①只有在磁场具有较好的对称性时才能用安培环路定理求解B ，但安培环路定理是普遍成立的，不具有较好对称性的磁场不能用安培环路定理求解B ，但定理依然成立。
②利用安培环路定理求磁场分布一般包含两步：首先依据电流的对称性分析磁场分布的对称性，然后再利用安培环路定理计算磁感应强度的数值和方向。
此过程中决定性的技巧是选取合适的闭合路径L （环路），以便⎰⋅Ll d B 中的B 能以标量形式从积分号内提出来。
基本要求：1.掌握安培环路定理：2.掌握安培环路定理分析计算磁感应强度的条件和方法，并能熟练运用。
一、选择题1.如图6.1所示,有两根无限长直载流导线平行放置,电流分别为I 1和I 2, LI 1在L 内,I 2在L 外,P 是L 上的一点,今将I 2 在L 外向I 1移近时,则有 [ ] (A)l B d ⋅⎰L与B P同时改变. (B) l B d ⋅⎰L与B P都不改变. (C) l B d ⋅⎰L不变,B P改变.(D)l B d ⋅⎰L改变,BP不变.2.对于某一回路l ，积分l B d ⋅⎰l等于零，则可以断定I 图6.1[ ] (A) 回路l 内一定有电流. (B) 回路l 内可能有电流.(C) 回路l 内一定无电流. (D) 回路l 内可能有电流，但代数和为零.3. 如图6.2所示，两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上，稳恒电流I 从a 端流入而从d 端流出，则磁感应强度B 沿图中闭合路径L 的积分l B d ⋅⎰l等于[ ] (A) I u 0(B) I u 031(C)I u 041(D) I u 0324. 用相同细导线分别均匀密绕成两个单位长度匝数相等的半径为R 和r 的长直螺线管(R =2r )，螺线管长度远大于半径.今让两螺线管载有电流均为I ，则两螺线管中的磁感强度大小B R 和B r 应满足：[ ] (A) B R = 2B r . (B) B R = B r . (C) 2B R = B r . (D) B R = 4B r .二、填空题1.在安培环路定理中iLI∑=⋅⎰0d μl B , 其中∑I i 是指 ;B 是由 的电流产生的.2. 两根长直导线通有电流I ,图6.3所示有三种环路,对于环路a ,=⋅⎰a L l B d ;对于环路b , =⋅⎰b L l B d 。
大学物理10.5磁场对载流导线作用安培定律Xiao
若d=1m, 则当
B2
dF1
dF2
B1
dF1 dF2 0 2 10 7 N / m
dl1 dl2 2 π
d
时，有 I1 I2 1A
在真空中两平行长直导线相距 1 m ，通有大小相等、 方向相同的电流，当两导线每单位长度上的吸引力 为 2 107 N m1 时，规定这时的电流为 1 A（安培）.
10.5 磁场对载流导线的作用
——安培定律
南京理工大学应用物理系
10.5 磁场对载流导线的作用—安培定律
一、安培定律
描写电流元在磁场中受安培力的规律. Idl
安培定律的表述：
dF
B
一个电流元在磁场中所受磁场力为电流元 Idl 与磁感
应强度 B 的矢量积。
用矢量式表示： dF Idl B
大小：dF IdlBsin
I2 导线左端距 I1 为 a，求导线 I2 所 受到的安培力。
I 1o
x
I 2 dx x
解：建立坐标系,坐标原点选在 I1上， 分割电流元， 长度为 dx ,
a L B1
电流元受安培力大小为：dF I 2dxB 1 sin
其中
B1
0 I1 2x
,
2
南京理工大学应用物理系
10.5 磁场对载流导线的作用—安培定律
Idl
Fx dFx BI 00dy 0
L
dFy
dy x
dFx dx
Fy
dFy
BI0
dx
BIL
F
Fy
BILj
F OP
与前面的普遍结论一致.
南京理工大学应用物理系
10.5 磁场对载流导线的作用—安培定律
10.4磁场安培环路定理
II
若电流方向与积分环路方向 呈右手螺旋法则，则有:
I
l
B dl μ I
0 l
电流为正
若电流方向与积分环路方向 不呈右手螺旋关系,则有:
l
B dl μ0 I
I
l
判断：
电流为负
2.无限长直线电流，任意积分回路
B dl B cos θdl
B 0nI
无限大平板电流的磁场分布。设一无限大导体薄 例题4 ： 平板垂直于纸面放置，其上有方向垂直于纸面朝外的 电流通过，面电流密度（即指通过与电流方向垂直的 单位长度的电流）处处均匀,大小为 i . 解：可视为无限多平行 长直电流产生的磁场。
dB
dB ' dB' '
dl '
p
l
μ0 ( I1 I 2 I 3 )
3.电流在回路之外IBl dl
l
0 I d 2
dl
0 I 2
0
0 I d 2
0
d 0
可见，电流若不在安培环路内，由它激发的磁 场在这个环路上的路径积分就是零。
其实并不局限于无限长直线电流，严格的理论分析证明， 对任意形式的闭合稳恒电流，上述结果也都正确。
已知：I 、R，电流沿轴向在截面上均匀分布， 例题1 ： 求“无限长”载流圆柱导体内外磁场的分布 解： 首先分析对称性 电流分布——轴对称 磁场分布——轴对称 I R
r
O
dS1
dB
dB2
dB1
l
P
dS 2
电流及其产生的磁场具有轴对称分布时
大学物理学：高斯定理和安培环路定律
R3
R1 R2
I I
r
R1< r < R2 , 同理
B dl 0 I
B 2r 0 I
B 0I 2r
R3
R1 R2
I I
r
R2< r < R3 ,
B dl 0 I
R3
R1 R2
I I
r
R2< r < R3 ,
B dl 0 I
B 2r
0 I
I (r 2 ( R32
I l
电流为负
2、说明
•符号规定：电流方向与L的环绕方向服从右手关系的 I为正，否 则为负。 •安培环路定律对于任一形状的闭合回路均成立。 •B的环流与电流分布有关，但路径上B仍是闭合路径内外电流的 合贡献。 •物理意义：磁场是非保守场，不能引入势能。
二、安培环路定理的应用
1.分析磁场的对称性：根据电流的分布来分析； 2.过场点选取合适的闭合积分路径； 3.选好积分回路的取向，确定回路内电流的正负； 4.由安培环路定理求出B。
B dS 0
S
二、 高斯定律
1、内容
通过任意闭合曲面的磁通量必等于零。
B dS 0
S
2、解释
磁感应线是闭合的，因此 有多少条磁感应线进入闭 合曲面，就一定有多少条 磁感应线穿出该曲面。
B
S
B
4 安培环路定理
安培 (Ampere, 1775-1836)
法国物理学家，电动力学的创始人。1805年 担任法兰西学院的物理教授，1814年参加了 法国科学会，1818年担任巴黎大学总督学， 1827年被选为英国皇家学会会员。他还是柏 林科学院和斯德哥尔摩科学院院士。
安培在电磁学方面的贡献卓著，发现了一系 列的重要定律、定理，推动了电磁学的迅速 发展。1827年他首先推导出了电动力学的基 本公式，建立了电动力学的基本理论，成为 电动力学的创始人。
安培定律计算公式如何计算
安培定律计算公式如何计算
安培定律是电磁学中的基本定律之一，用来描述电流对磁场的作用。
根据安培定律，电流元产生的磁场可以通过以下公式计算：
B = (μ0/4π) * (I * dl * sinθ) / r^2
其中
B表示磁场强度，单位为特斯拉(T)；
μ0表示真空中的磁导率，其数值为4π*10^-7特斯拉·米/安培；
I表示电流强度，单位为安培(A)；
dl表示电流元的长度；
θ表示电流元与观察点的夹角，一般取为电流元与径向的夹角；
r表示观察点到电流元的距离。
根据这个公式，可以计算出特定电流元产生的磁场强度。
如果需要计算复杂电流分布的磁场，可以通过对整个电流路径进行积分来得到磁场。
需要注意的是，安培定律适用于静电场情况下的电流分布。
如果电流随时间变化，则需要结合法拉第定律和麦克斯韦方程组，采用更复杂的数学方法进行计算。
6安培定律(大学物理-磁场部分)
二、一段电流在磁场中受力
计算一段电流
在磁场中受到的安 培力时，应先将其 分割成无限多电流 元，将所有电流元 受到的安培力矢量 求和----矢量积分。
B Id l
F d F Id l B
三、均匀磁场中曲线电流受力
均匀磁场中曲线电流受的安培力，等 于从起点到终点的直线电流所受的安培力。
F ab d F ab Id l B
0 I1 2x
,
2
I1 dF x dx
aL B1
I2 x
分割的所有电流
元受力方向都向上， 离 I1 近的电流元受力 大，离 I1 远的电流元 受力小，所以 I2 受到 o 的安培力为：
F
dF
a L
a
I 2B1
sin
2
dx
I1 dF x dx
aL B1 a LaI20 I1 2
dx x
0 I1I 2 ln a L
第四节 安培定律
一、安培定律
描写电流元在磁场中受安培力的规律。
由实验发现，
电流元在磁场中受
到的安培力大小： Id l
B
dF I dl B sin
dF I dl B sin
用矢量式表示：
dF Id l B 外磁场
方向：从 dl 右旋到 B，大拇指指向。
Id l
B
dF
dF B
Id l
I2 受到的安培力方 向如图所示，安培
力大小：
F I 2LB 1 sin
其中
B1
0 I1 2a
2
I2
I1 F
L
a B1
F I 2LB 1 sin
F
I 2L
0 I1 sin 2a
安培环路定理(大学物理)
lI
2π r
哈尔滨工程大学 姜海丽
安培环路定理
第1章 稳恒磁场
练习题 1、如图，流出纸面的电流为2I，流进纸面的电流为I， 则下述各式中哪一个是正确的？ (B) H d l I (A) H d l 2 I 答案：D L L
稳恒磁场安培环路定理16安培环路定理设闭合回路为圆形回路载流长直导线的磁感强度为哈尔滨工程大学稳恒磁场安培环路定理若回路绕向化为逆时针时则对任意形状的回路稳恒磁场安培环路定理稳恒磁场安培环路定理多电流情况以上结果对任意形状的闭合电流伸向无限远的电流均成立
安培环路定理
第1章 稳恒磁场
1.6 安培环路定理 载流长直导线的磁感强度为
c a I c I⊙
．
I1 L
I1 I2
0 ( I 2 2I1 ) 4、如图所示，磁感强度沿闭合曲线L的环流________．
哈尔滨工程大学 姜海丽
安培环路定理
第1章 稳恒磁场
5、半径为R的圆柱体上载有电流I，电流在其横截面上均 匀分布，一回路L通过圆柱内部将圆柱体横截面分为两部 dl 分，其面积大小分别为S1、S2如图所示，则 H _______．
安培环路定理
哈尔滨工程大学 姜海丽
安培环路定理
第1章 稳恒磁场
安培环路定理
n B dl 0 Ii i 1
即在真空的稳恒磁场中，磁感应强度 B 沿任 一闭合路径的积分的值，等于 0 乘以该闭合路径 所包围的各电流的代数和.
注意 电流 I 正负的规定 ：I 与 L 成右螺旋时， I 为正；反之为负.
PM
B MN 0 n MN I
B 0 nI
大学物理安培定律3
，初步体会词语的意义；能用部分学过的词语写句子；在阅读中积累优美的 词语、精彩的句段及自己喜欢的成语警句等提高语言的感悟能力。能结合上下文 和生活实际理解课文中的词句的意思；学习结合上下文和生活实际理解课文中的 词句的意思；学习结
合上下文和生活实际理解课文中的词句的意思；学习辨析句子中的重点词语， 学习体会词语的含意；在阅读中体会叙事及记人叙事文章的写作特点；学习较浅 显的记叙方法及阅读方法；在阅读实践中积累语言；能在阅读中展开想象；能用 自己的话说出
3、培养学生良好的语文学习习 惯和正确的读写姿势。
4、培养学生热爱祖国语言文字 的热情。
5、积累课文中的优美词语、精 彩句段，培养初步的语感。
6、鼓励学生观察大自然、观察社会生活，提高观察能力、分析能力、表达 能力。
7、引导学生进行简单的仿写和想象创造，培养他们的想象力创造力。
8、引导学生积累好词好句好段 和成语故事。
三、牛顿第二定律
牛顿第二定律是指物体的加速度与作用力成正比，与质量成反比。其数学表 达为F=ma（F代表作用力，m代表物体的质量，a代表物体的加速度）。这个公式 揭示了力、质量和加速度之间的关系。
四、重力公式
重力是指地球对物体的吸引力，其计算公式为：重力 =质量 ×重力加速度 （G = mg）。这个公式表明，重力的大小是由物体的质量和重力加速度的乘积决 定的。
此外，我们还可以利用高斯定理来求解静电场的分布。高斯定理表明，通过 一个闭合曲面的电场线数等于该闭合曲面所包围的电荷量与真空中的介电常数的 比值。这个定理提供了一种在复杂情况下求解电场分布的有效方法。
最后，静电场的能量储存也是一个重要的概念。在静电平衡状态下，系统的 总能量是最低的，这是稳定系统的一个重要特性。这个概念对于理解如电容和电 感等电子元件的工作原理非常重要。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
b
fy
df y
BI
dx BI ab
a
练 1、如图 均匀磁场中求半圆导线所受安培力
习
f BI ab 2BIR
c
B
方向竖直向上
I
R
a b
2、任意形状闭合载流线圈在均匀磁场中所受力
合磁力为零
三、*非均匀磁场中载流导线所受安培力 如图：求导线ab所受安培力，直
复
习
B dl 0 Ii
电流的流向与环路的环绕 方向成右旋关系的电 流为正, 否则为负.
I1 I 2
I4
I3
l
B dl 0
Ii 0(I2 I3 )
B dl 0 Ii
i
安培环路定理的应用步骤:
1、根据电流分布的对称性分析磁场分布（磁场线）的对称性； 2、根据磁场分布（磁场线）的对称性，选取合适的回路：
（1）沿回路上磁感大小相等(或为零），
（2）回路方向与 磁场 线相同或垂直。
3、计算磁感沿该回路的线积分： B dl
4、计算该回路包围的电流的代数和： Ii
i
5、求出磁感B 。
7-7 带电粒子在电场和磁场中的运动
一、运动电荷在磁场中所受的磁场力
F
q
B
v
B
F qvB sin
F2’产生力矩。
BIl2
l2 r1 r2
2
d
四、平行电流的相互作用力
两无限长平行导线，相距为a，各自通 B2
有电流I1和I2 ，则单位长度上的磁场力
df1
B2 I1dl1
B2
0I2 2a
Idl1
df1
df2
B1I2dl2 B1
0 I1 2a
I1
导线1、2单位长度上所受的磁场力为：
df1 0 I1I2 df2 0 I1 I2 dl1 2a dl2 2a
大小: df IdlB sin
B
a
I
方向判断:
右手螺旋
Idl
I
df
载流导线受到的磁力: f L Idl B
二、均匀磁场中载流直导线所受安培力
取电流元 Idl
df Idl B
Idl
B
df BIdl sin
f LBIdl sin BILsin
导线ab垂直于长直导线
已知：I1, I2, L,d
df
求：导线ab所受的安培力 解：如图取微元
I1
B 0 I1 方向垂直板面向里。 2x
a
b
x Idx I 2
df
BI2dl
0 I1 I 2 2x
dx
d
L
方向：竖直向上
f
d L 0 I1 I2 dx d 2x
0 I1I2 ln d L
X
dfx df sin BIdl sinOa dy dl sin b
dfy df cos BIdl cos dx dl cos
df x BIdy df y BIdx
0
fx
df x
BI
dy 0
0
整个弯曲导线受的磁场力 的总和等于从起点到终点 连的直导线通过相同的电 流时受的磁场力。
Ⅰ、带电粒子在磁场中所受的
f
洛f 仑 兹q力 :
B
Ⅱ、所有粒子受力的宏观表现：
s n+ v
dl
×××
d
Fns ddlNqfv
B
dN
ndV nsdl
V是指粒子作定向 运动的方向.
nqvsdl B I qnvs
Idl B
安培定律——电流元在磁 场中受力的规律 安培力: df Idl B
周期没关系。
(3) 与B 成角
// cos sin
//
B
回转 半径:
R m qB
m sin qB
B
回转周期: T 2R 2m
qB
带电粒子做螺旋线运动:
//
h 螺距 h ： h
注：粒子每回
//T
方向 f L IL B
结论： f BLI sin
0
f 0
2
fmax BLI
B
I
B
I
任意取形电状流导元线在I均dl匀 磁场中受力：dYf
df BIdl
建坐标系，取分 量
Idl
B
安培的定义 : a 1m，df dl
2 107
N m
o 4 107 (N / A2 )
a
df2
Idl2
I2 B1
练习：如图，无限长直载流导线与正三角形载流线圈在同一平面内， 若长直导线固定不动，则载流三角形线圈将 [ ] A
（A）向着长直导线平移 （C）转动
（B）离开长直导线平移
cos
T
转一周时前进 的距离。
2m cos
qB
q R
B
R
B
R
B
R
B
R
B
R
B
R
B
R
B
R
B
R
B
R
B
R
B
R
B
R
B
R
B
R
B
R
B
Rபைடு நூலகம்
7-8 载流导线在磁场中所受的力
一、 安培力
洛伦兹力的方向由电荷的正负
q F
B
和右手螺旋法则决定。
洛伦兹力的特点：力恒与电荷
速度方向垂直，故洛伦兹力不作功。
v
二、 F带电q粒 子 B在磁场中的运动
下面分三种情形来讨论带电粒子在均匀磁场
(当1)中平的 行运B动 或。反 平行B
F q B 0 0
（D）不动
dF
无限长直导线产生的磁感应强度为：
B
60
B 0I 2r
I1 I2
C
若在均匀磁场中？
A B
五、 磁场对载流线圈的作用
1、磁场对载流线圈作用的磁力矩
F1
a
r1 θ I
θdF2 θ
cn
B
r2
M
合力=0 F2和
F2 F2
ad l1 ab
2F2r1 sin BIl2l1 sin
B
粒子做匀速直线运动
(2)
B*
F qB
设粒子的质量为m,圆周轨道的半径为R:
× ×× × ××
F qB m 2
R
R m qB
× ×
× × × × ×Fm×
×
×
B
××
T 2R 2m qB
× ×
×× ×
× ×q ×
× ×
××
粒子的速度和回旋