2017届山东省青岛市即墨市第一中学高三上学期期中考试数学(文)试题

合集下载

【最新经典文档】2017-2018学年山东省青岛市胶州市高三(上)期中数学试卷和答案(文科)

第 4 页（共 18 页）
2017-2018 学年山东省青岛市胶州市高三（上）试卷（文科）
参考答案与试题解析
期中数学
一、选择题：本大题共 12 个小题，每小题 5 分，共 60 分.在每小题给出的四个选项中，只有一项是符合题目要求的 . 1．（5 分）已知集合 A={ 1，2，3，4，5，6} ，B={ x| （3x+1）（2x﹣7）＜ 0} ，则 A∩B=（） A．{ 5} B．{ 1， 6} C． { 1，2，3} D．{ 1， 2， 3， 4} 【解答】解：集合 A={ 1，2，3，4，5，6} ， B={ x| （3x+1）（2x﹣7）＜ 0} ={ x| ﹣ ＜ x＜ } ，
7．（5 分）设 x，y 满足约束条件
为（） A．34 B．32 C．30 D．15
【解答】解：作出 x，y 满足约束条件
，则目标函数 z=12x+3y 的最大值，对应的平面区域内的 x，y
第 7 页（共 18 页）
∈ Z 点，如图：由 z=12x+3y 得 y=﹣4x+ z，平移直线 y=﹣4x+ z，
（ 2）若
=6，求 a 的最小值．
20．（ 12 分）已知函数 f （x）=alnx﹣x2+ （a+4）（a∈R）．
（ 1）讨论 f（x）的单调性；（ 2）若 a＜2e2，且 f（ x）在 [ 1，e] 上有零点，求 a 的取值范围． 21．（ 12 分）已知函数 f （x）=（x﹣1）（x2+2）ex﹣2x，g（x）=f'（x）+3x+1．（ 1）求曲线 y=f（ x）在点（ 0，f（ 0））处的切线与曲线 y=g（ x）在点（ 0，f（ 0））处的切线的交点坐标．（ 2）证明： f（x）＞﹣ x2﹣4．

2024-2025学年山东省青岛市高三上学期期中数学质量检测试题(含解析)

2024-2025学年山东省青岛市高三上学期期中数学质量检测试题注意事项：1.答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置.2.回答选择题时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需要改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上无效.第Ⅰ卷一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合，，则（）6,1P x y y x ⎧⎫=∈=∈⎨⎬+⎩⎭N N {}15Q x x =-≤<P Q = A.B.C.D.{}1,2,3{}0,1,2{}1,2,5{}0,1,2,52. 已知，则＝（）i22i z =-z A. 2 B. 13. 已知．若，则（）a = ()2a b a+⊥ cos ,a b=A.B.D. 4. 已知等比数列的前n 项和为，且，则“”是“的公比为2”的（{}n a n S 31S ma =7m ={}n a ）A. 必要不充分条件B. 充分不必要条件C .充要条件D. 既不充分也不必要条件5.此正四棱锥的体积为（）A. B. C.D.6. 已知函数则图象上关于原点对称的点有（）()21,0,22,0,xx f x x x x ⎧⎛⎫≥⎪ ⎪=⎝⎭⎨⎪-+<⎩()f x A. 1对B. 2对C. 3对D. 4对7. 已知函数，函数的图象各点的横坐标缩()2211cos sin cos 222222x x x xf x =-f (x )小为原来的（纵坐标不变），再向左平移个单位长度，得到函数的图象.若方程12π12y =g (x )在上有两个不同的解，，则的值为（）()21g x m -=7π0,12x ⎡⎤∈⎢⎥⎣⎦1x 2x 12x x +A. B. C. D. π6π3π2π8. 若关于不等式恒成立，则当时，的最小值为（）x ()ln ax x b ≤+1e e a ≤≤1e ln b a +-A. B. C. 1D. 11e+e 1-e二.多项选择题（本大题共3小题，每小题6分，共18分.在每小题给出的四个选项中，有多项符合题目要求.全部选对的得6分，部分选对得部分分，有选错的得0分）9. 已知，则下列结论正确的是（）3515ab==A. B. C. D.lg lg a b>a b ab+=1122a b⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭49a b +>10. 若数列满足，，，则称数列为斐波那{a n }11a =21a =12n n n a a a --=+3n ≥n +∈N {a n }契数列，又称黄金分割数列，则下列结论成立的是（）A. B. 713a =222n n n a a a -+=+3n ≥n +∈N C.D.135********a a a a a ++++= 24620242025a a a a a ++++= 11. 如图，在边长为4的正方体中，E ，F 分别是棱，的中点，1111ABCD A B C D -11B C 11C D P 是正方形内的动点，则下列结论正确的是（）1111D C B AA. 若平面，则点P 的轨迹长度为//DP CEFB. 若P 的轨迹长度为AP =2πC. 若P 是正方形的中心，Q 在线段EF 上，则的最小值为1111D C B A PQ CQ +D. 若P 是棱的中点，则三棱锥的外接球的表面积是11A B P CEF -41π第Ⅱ卷三.填空题（本大题共3小题，每小题5分，共15分）12. 曲线的所有切线中，斜率最小的切线的方程是_______.32374y x x x =+++13. 为测量某塔的高度，在塔旁的水平地面上共线的三点A ，B ，C 处测得其顶点P 的仰角分别为30°，60°，45°，且米，则塔的高度________米.50AB BC ==OP =14. 已知，当，时，是线段的中点，点在所有的线段121A A =2n ≥*N n ∈1n A +1n n A A -P 上，若，则的最小值是________．1n n A A +1A P λ≤λ四.解答题（本大题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤）15. 已知数列的前项和为，且.{}n a n n S 22n n S a +=（1）求及数列的通项公式；2a {}n a （2）在与之间插入个数，使得这个数依次组成公差为的等差数列，求n a 1n a +n ()2+n n d数列的前项和.1n d⎧⎫⎨⎬⎩⎭n n T 16. 设的内角A ，B ，C 所对的边分别为a ，b ，c ，且有，ABC V π2cos 3b A a c⎛⎫-=+ ⎪⎝⎭（1）求角B ：（2）若AC 边上的高，求.h =cos cos A C 17. 如图1，在平行四边形中，，，E 为的中点，ABCD 24AB BC ==60ABC ∠=︒CD 将沿折起，连结，，且，如图2．ADE V AE BD CD 4BD=（1）求证：图2中的平面平面；ADE ⊥ABCE （2）在图2中，若点在棱上，直线与平面F BD AF ABCE 点到平面的距离．F DEC 18. 已知函数，且与轴相切于坐标原点．()sin ln(1)f x x x ax =++-()y f x =x （1）求实数的值及的最大值；a ()f x （2）证明：当时，；π,π6x ⎡⎤∈⎢⎥⎣⎦1()22f x x +>（3）判断关于的方程实数根的个数，并证明．x ()0f x x +=19. 对于任意正整数n ，进行如下操作：若n 为偶数，则对n 不断地除以2，直到得到一个奇数，记这个奇数为；若n 为奇数，则对不断地除以2，直到得出一个奇数，记这个n a 31n +奇数为.若，则称正整数n 为“理想数”.n a 1n a =（1）求20以内的质数“理想数”；（2）已知.求m 的值；9m a m =-（3）将所有“理想数”从小至大依次排列，逐一取倒数后得到数列，记的前n 项和{}n b {}n b 为，证明.n S ()*7N 3n S n <∈2024-2025学年山东省青岛市高三上学期期中数学质量检测试题注意事项：1.答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置.2.回答选择题时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需要改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上无效.第Ⅰ卷一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合，，则（）6,1P x y y x ⎧⎫=∈=∈⎨⎬+⎩⎭N N {}15Q x x =-≤<P Q = A.B.C.D.{}1,2,3{}0,1,2{}1,2,5{}0,1,2,5【正确答案】B【分析】首先把集合用列举法表示出来，再运用交集的运算进行求解即可.P 【详解】若，，则是的正因数，而的正因数有，，，，61y x =+y ∈N 1x +661236所以，{}6,0,1,2,51P x y y x ⎧⎫=∈=∈=⎨⎬+⎩⎭N N 因为，{}15Q x x =-≤<所以，{}0,1,2P Q ⋂=故选：B.2. 已知，则＝（）i22i z =-z A. 2 B. 1【正确答案】C【分析】根据复数的运算法则计算出复数，再计算复数的模.z 【详解】由题意知，()()()i 22i i 22i 22i 22i z +==--+2i 28-=11i 44=-+所以，z ==故选：C.3. 已知．若，则（）a = ()2a b a+⊥ cos ,a b =A.B.D. 【正确答案】B【分析】根据向量垂直可得，代入向量夹角公式即可得结果.32a b ⋅=-【详解】因为，且，()2a b a+⊥1a = 则，可得，()2220a a a ab b +⋅=+⋅= 21322a b a⋅=-=-rr r 所以.cos ,a b a b a b⋅===⋅r r r r r r 故选：B.4. 已知等比数列的前n 项和为，且，则“”是“的公比为2”的（{}n a n S 31S ma =7m ={}n a ）A. 必要不充分条件B. 充分不必要条件C. 充要条件D. 既不充分也不必要条件【正确答案】A【分析】利用等比数列的性质，分别判断充分性与必要性即可.【详解】设等比数列的公比为，{}n a q 由，得，()223123111111S a a a a a q a q a q q ma =++=++=++=21q q m ++=当时，，解得或，充分性不成立；7m =217q q ++=2q =3q =-当时，，必要性成立.2q =217q q m ++==所以“”是“的公比为2” 的必要不充分条件.7m ={}n a 故选：A5. 此正四棱锥的体积为（）A. B. C. D. 【正确答案】B【分析】根据正四棱柱及正四棱锥的体积公式可得正四棱锥的高与斜高的关系式，进而可得解.【详解】如图所示，正四棱柱为，正四棱锥，1111ABCD A B C D -1O ABCD -设底边边长，高AB a =1OO =则，1O E ==又正四棱柱的侧面积，114S AB OO =⋅=正四棱锥的侧面积，21142S AB O E a=⋅⋅=则，解得，a=a =所以正四棱锥体积，2113ABCD V S OO =⋅==故选：B.6. 已知函数则图象上关于原点对称的点有（）()21,0,22,0,xx f x x x x ⎧⎛⎫≥⎪ ⎪=⎝⎭⎨⎪-+<⎩()f x A. 1对 B. 2对C. 3对D. 4对【正确答案】C【分析】作出的图象，再作出函数关于原点对称的图象，进而数形结()f x 1,0,2xy x ⎛⎫=≥ ⎪⎝⎭合判断即可.【详解】作出的图象，再作出函数关于原点对称的图象如图所示.()f x 1,0,2xy x ⎛⎫=≥ ⎪⎝⎭因为函数关于原点对称的图象与图象有三个交点，故1,0,2xy x ⎛⎫=≥ ⎪⎝⎭22,0,y x x x =-+<图象上关于原点对称的点有3对.()fx故选：C7. 已知函数，函数的图象各点的横坐标缩()2211cos sin cos 222222x x x xf x =-f (x )小为原来的（纵坐标不变），再向左平移个单位长度，得到函数的图象.若方程12π12y =g (x )在上有两个不同的解，，则的值为（）()21g x m -=7π0,12x ⎡⎤∈⎢⎥⎣⎦1x 2x 12x x +A. B. C. D. π6π3π2π【正确答案】A【分析】先化简，根据图象变换求出，将方程转化为()f x ()g x ()21g x m -=，由函数图象的对称性求出答案.()12m g x +=()g x 【详解】根据题意可得，()1πcos sin 26f x x x x ⎛⎫=+=+ ⎪⎝⎭所以，()πππsin 2sin 21263g x x x ⎡⎤⎛⎫⎛⎫=++=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，，7π012x ≤≤ππ3π2332x ∴≤+≤所以在上单调递增，在上单调递减，关于对称，()g x π0,12⎡⎤⎢⎥⎣⎦π7π,1212⎡⎤⎢⎥⎣⎦()g x π12x =且，，()π06g g ⎛⎫== ⎪⎝⎭π112g ⎛⎫= ⎪⎝⎭7π112g ⎛⎫=- ⎪⎝⎭方程等价于有两个不同的解，()21g x m -=()12m g x +=12,x x .12ππ2126x x ∴+=⨯=故选：A.8. 若关于不等式恒成立，则当时，的最小值为（）x ()ln ax x b ≤+1e e a ≤≤1e ln b a +-A.B. C. 1D. 11e +e 1-e【正确答案】C【分析】构建，分析可知的定义域为，且在()()ln f x ax x b=--()f x (0,+∞)()0f x ≤内恒成立，利用导数可得，整理可得，构建(0,+∞)ln 1a b ≤+1e ln ln b a a a +-≥-，利用导数求其最值即可.()1ln ,ee g a a a a =-≤≤【详解】设，()()ln f x ax x b=--因为，可知的定义域为，所以在内恒成立，1e e a ≤≤()f x (0,+∞)()0f x ≤(0,+∞)又因为，()111xf x x x -=-='令，解得；令，解得；f ′(x )>001x <<f ′(x )<01x >可知在内单调递增，在内单调递减，()f x (0,1)(1,+∞)则，可得，则，()()1ln 10f x f a b ≤=--≤ln 1a b ≤+1ln e e b aa +≥=可得，当且仅当时，等号成立，1e ln ln b a a a +-≥-ln 1a b =+令，则，()1ln ,e e g a a a a =-≤≤()111a g a a a '-=-=令，解得；令，解得；()0g a '>1e a <≤()0g a '<11e a <≤可知在内单调递增，在内单调递减，则，()g a (]1,e 1,1e ⎡⎫⎪⎢⎣⎭()()11g a g ≥=即，当且仅当时，等号成立，1eln ln 1b a a a +-≥-≥1,1a b ==-所以的最小值为1.1eln b a +-故选：C.方法点睛：两招破解不等式的恒成立问题（1）分离参数法第一步：将原不等式分离参数，转化为不含参数的函数的最值问题；第二步：利用导数求该函数的最值；第三步：根据要求得所求范围．（2）函数思想法第一步：将不等式转化为含待求参数的函数的最值问题；第二步：利用导数求该函数的极值；第三步：构建不等式求解．二.多项选择题（本大题共3小题，每小题6分，共18分.在每小题给出的四个选项中，有多项符合题目要求.全部选对的得6分，部分选对得部分分，有选错的得0分）9. 已知，则下列结论正确的是（）3515ab==A. B. C. D.lg lg a b>a b ab+=1122a b⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭49a b +>【正确答案】ABD【分析】根据指对互化与运算以及指数函数、对数函数单调性即可判断ABC ，利用基本不等式即可判断D.【详解】由题可得，，33log 15log 310a =>=>55log 15log 510b =>=>，即，所以，1515110log 3log 5a b ∴<=<=110a b <<0a b >>对于A ，因为，所以，故A 正确；0a b >>lg lg a b >对于B ，，，故B 正确；15151511log 3log 5log 151a b +=+== a b ab ∴+=对于C ，因为，所以，故C 错误；0a b >>1122a b⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭对于D ，因为，，0a b >>111a b +=所以，()11444559b a a b a b a b a b ⎛⎫+=++=++≥+= ⎪⎝⎭当且仅当，即时等号成立，这与已知矛盾，所以，故D 正4b aa b =2a b =35a b =49a b +>确.故选：ABD.10. 若数列满足，，，则称数列为斐波那{a n }11a =21a =12n n n a a a --=+3n ≥n +∈N {a n }契数列，又称黄金分割数列，则下列结论成立的是（）A. B. 713a =222n n n a a a -+=+3n ≥n +∈N C.D.135********a a a a a ++++= 24620242025a a a a a ++++= 【正确答案】AC【分析】利用斐波那契数列的定义结合递推关系一一判定选项即可.【详解】对于A ，由题可得，，，，，故A 正确；32a =43a =55a =68a =713a =对于B ，因为，又，21112n n n n n n n n a a a a a a a a ++--=+=++=+12n n n a a a --=+所以，即，故B 错误；21213n n n n n a a a a a +---++=+223n n n a a a +-=+对于C ，2024202320222023202120202023202132a a a a a a a a a a =+=++==++++ ，故C 正确；2023202131a a a a =++++ 对于D ，2025202420232024202220212024202243a a a a a a a a a a =+=++=++++ ，故D 错误.20242022421a a a a a =+++++ 故选：AC.11. 如图，在边长为4的正方体中，E ，F 分别是棱，的中点，1111ABCD A B C D -11B C 11C D P 是正方形内的动点，则下列结论正确的是（）1111D C B AA. 若平面，则点P 的轨迹长度为//DP CEFB. 若P 的轨迹长度为AP =2πC. 若P 是正方形的中心，Q 在线段EF 上，则的最小值为1111D C B A PQ CQ +D. 若P 是棱的中点，则三棱锥的外接球的表面积是11A B P CEF -41π【正确答案】ACD【分析】作出相应图形，先证明平面平面，再结合给定条件确定动点轨迹，//BDNM CEF 求出长度即可判断；建立空间直角坐标系，根据题意确定动点轨迹，求解长度即可判断，A B 将平面翻折到与平面共面，连接，与交于点，此时取到CEF 1111D C B A PC EF Q PQ CQ +最小值，利用勾股定理求出即可判断，先找到球心，利用勾股定理得出半径，求,PQ CQ C 出外接球的表面积即可判断.D 【详解】如图，取，的中点为，连接，，11A D 11A B ,N M ,,,,MN DN BD BM NE 11B D所以，又E ，F 分别是棱，的中点，11//MN B D 11B C 11C D 所以，所以，11//EF B D //MN EF 平面，平面，MN ⊄CEF EF ⊂CEF 平面，//MN ∴CEF 因为分别是棱，的中点，所以，且，,N E 11A D 11B C //NE CD NE CD =所以四边形为平行四边形，CDNE 所以，又平面，平面，//ND CE ND ⊄CEF CE ⊂CEF 平面，//ND ∴CEF 又，平面，MN ND N = ,MN ND ⊂BDNM 所以平面平面，//BDNM CEF点P 是正方形内的动点，且平面，1111D C B A //DP CEF 所以点P 的轨迹为线段，由勾股定理得，故正确；MN MN ==A 如图，以为原点，以所在直线为轴，轴，轴，A 1,,AB AD AA x y z 由题意得，设，(0,0,0)A (,,4)P x y，AP ==所以，所以点的轨迹为为圆心，半径为1的个圆，221x y +=P 1A 14所以点P 的轨迹长度为.故错误；1π2π42⋅=B 如图，将平面翻折到与平面共面，CEF 1111DC B A 连接，与交于点，此时取到最小值，PC EF Q PQ CQ+，且，CE CF === 2PE PF ==所以点为的中点，所以Q EFPQ EQ ===所以，CQ ===即的最小值为，故正确；PQ CQ +C如图，连接，交于点，连接，PF 11B D 1O PE 若P 是棱的中点，则，11A B 90FEP ∠= 所以是外接圆的一条直径，所以是外接圆的圆心，FP PEF !1O PEF !过点作平面的垂线，则三棱锥的外接球的球心一定在该垂线上，1O ABCD P CEF -O 连接，设，则，OP 1OO t =2222t R +=连接，，所以，OC 12AC ==()(2224t R -+=所以，解得，()(222224t t +=-+52=t 所以，222541244R =+=所以三棱锥的外接球的表面积为，故正确.P CEF -24π41πS R ==D 故选.ACD方法点睛：三棱锥外接球的半径的求法：（1）先找两个面的外心；（2）过外心作所在平面的垂线，两垂线的交点即为球心；（3）构造直角三角形，利用勾股定理求出半径.有时无须确定球心的具体位置，即只用找一个面的外心，则球心一定在过该外心与所在平面的垂线上.第Ⅱ卷三.填空题（本大题共3小题，每小题5分，共15分）12. 曲线的所有切线中，斜率最小的切线的方程是_______.32374y x x x =+++【正确答案】.430x y -+=【分析】首先求函数的导数，再根据二次函数求最小值，即可求切线的斜率，以及代入切线方程，即可求解.【详解】由题意，223673(1)4y x x x '=++=++所以时，，又时，，1x =-min4y '=1x =-1y =-所以所求切线的方程为，即．14(1)y x +=+430x y -+=故．430x y -+=13. 为测量某塔的高度，在塔旁的水平地面上共线的三点A ，B ，C 处测得其顶点P 的仰角分别为30°，60°，45°，且米，则塔的高度________米.50AB BC ==OP =【正确答案】【分析】设，在，，分别根据锐角三角函数定义求PO h =Rt POA △Rt POB △Rt POC △出，最后利用余弦定理进行求解即可.,,OA OB OC 【详解】设塔的高，PO h =在中，，同理可得，，Rt POA △otan 30OP OA ==OB =OC h =在中，，则，OAC πOBA OBC ∠+∠=cos cos OBA OBC ∠=-∠，22222222OB AB OA OB BC OC OB AB OB BC +-+-∴=-⋅⋅.=h =所以塔的高度为米.故答案为.14. 已知，当，时，是线段的中点，点在所有的线段121A A =2n ≥*N n ∈1n A +1n n A A -P 上，若，则的最小值是________．1n n A A +1A P λ≤λ【正确答案】23【分析】根据中点坐标公式可得，进而可得为等比数列，()*122n n n a a a n +++=∈N {}1n n a a +-即可利用累加法求解,由极限即可求解.121132n n a -⎡⎤⎛⎫=--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦【详解】不妨设点、，设点，()10,0A ()21,0A ()(),0n n A a n *∈N 则数列满足，，，{a n }10a =21a =()*122n n n a a a n +++=∈N 所以，，1212n nn n a a a a +++--=-所以，数列是首项为，公比为的等比数列，{}1n n a a +-211a a -=12-所以，，11111122n n n n a a --+⎛⎫⎛⎫-=⨯-=- ⎪⎪⎝⎭⎝⎭当时，2n ≥()()()2121321110122n n n n a a a a a a a a --⎛⎫⎛⎫=+-+-++-=++-++- ⎪ ⎪⎝⎭⎝⎭ ，1111212113212n n --⎛⎫-- ⎪⎡⎤⎛⎫⎝⎭==--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦+也满足，故对任意的，.10a =121132n n a -⎡⎤⎛⎫=--⎢⎥⎪⎝⎭⎢⎥⎣⎦n *∈N 121132n n a -⎡⎤⎛⎫=--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦所以，，故11212lim 1323n n A P ∞-→+⎧⎫⎡⎤⎪⎪⎛⎫=--=⎢⎥⎨⎬ ⎪⎝⎭⎢⎥⎪⎪⎣⎦⎩⎭23λ≥故答案为.23四.解答题（本大题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤）15. 已知数列的前项和为，且.{}n a n n S 22n n S a +=（1）求及数列的通项公式；2a {}n a （2）在与之间插入个数，使得这个数依次组成公差为的等差数列，求n a 1n a +n ()2+n n d 数列的前项和.1n d⎧⎫⎨⎬⎩⎭n n T 【正确答案】（1），，24a =2n n a =*N n ∈（2）332n nn T +=-【分析】（1）先将代入题干表达式计算出，再将代入题干表达式即可计算1n =12a =2n =出的值，当时，由，可得，两式相减进一步推导即可2a 2n ≥22n n S a +=1122n n S a --+=发现数列是以为首项，为公比的等比数列，从而计算出数列的通项公式；{}n a 22{}n a （2）先根据第题的结果写出与的表达式，再根据题意可得，()1n a 1n a +()11n n n a a n d +-=+通过计算出的表达式即可计算出数列的通项公式，最后运用错位相减法即可计算出n d 1n d ⎧⎫⎨⎬⎩⎭前项和．n n T 【小问1详解】由题意，当时，，解得，1n =111222S a a +=+=12a =当时，，即，解得，2n =2222S a +=12222a a a ++=24a =当时，由，可得，两式相减，可得，2n ≥22n n S a +=1122n n S a --+=122n n n a a a -=-整理，得，∴数列是以2为首项，2为公比的等比数列，12n n a a -={}n a ∴，.1222n n n a -=⋅=*N n ∈【小问2详解】由（1）可得，，，2nn a =112n n a ++=在与之间插入个数，使得这个数依次组成公差为的等差数列，n a 1n a +n ()2+n n d 则有，()11n n na a n d +-=+∴，∴，1211nn n n a a d n n +-==++112n n n d +=∴，1231211123412222n n n n T d d d +=++⋅⋅⋅+=+++⋅⋅⋅+，()2311111123122222nn n T n n +⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯+⋅⋅⋅+⋅++⋅ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭两式相减得，2112311111121111133221122222222212n n n n n n n n n T ++++-+++=+++⋅⋅⋅+-=+-=--∴.332n n n T +=-16. 设的内角A ，B ，C 所对的边分别为a ，b ，c ，且有，ABC V π2cos 3b A a c⎛⎫-=+ ⎪⎝⎭（1）求角B ：（2）若AC 边上的高，求.h =cos cos A C【正确答案】（1）π3B =（2）18-【分析】（1）由正弦定理及两角和的正弦公式可得角的大小;B （2）由等面积法可得，再由正弦定理可得的值，再由22b ac =sin sin A C ，可得的值.cos cos()B A C =-+cos cos A C 【小问1详解】因为，π2cos 3b A a c⎛⎫-=+ ⎪⎝⎭由正弦定理可得，12sin cos sin sin 2B A A A C ⎛⎫+=+ ⎪ ⎪⎝⎭即sin cos sin sin sin()B A A B A A B +=++即，sin cos sin sin sin cos cos sin B A A B A A B A B +=++，sin sin sin cos B A A A B =+在三角形中，，sin 0A >，cos 1B B -=即，因为，则π1sin 62B ⎛⎫-= ⎪⎝⎭(0,)B π∈ππ5π,666B ⎛⎫-∈- ⎪⎝⎭可得，则.ππ66B -=π3B =【小问2详解】因为边上的高，AC h =所以①21122ABC S b h b =⋅==又②11sin 22ABC S ac B ac === 由①②可得，22b ac =由正弦定理可得，2sin 2sin sin B A C =结合（1）中可得，π3B =3sin sin 8A C =因为，()1cos cos cos cos sin sin 2B A C A C A C =-+=-+=所以.1311cos cos sin sin 2828A C A C =-=-=-17. 如图1，在平行四边形中，，，E 为的中点，ABCD 24AB BC ==60ABC ∠=︒CD 将沿折起，连结，，且，如图2．ADE VAE BD CD 4BD =（1）求证：图2中的平面平面；ADE ⊥ABCE （2）在图2中，若点在棱上，直线与平面F BD AF ABCE 点到平面的距离．F DEC 【正确答案】（1）证明见解析（2【分析】（1）连接，利用勾股定理证明，再根据线面垂直的判定定BE ,BE DE BE AE ⊥⊥理证得平面，再根据面面垂直的判定定理即可得证；BE ⊥ADE （2）以点为原点，建立空间直角坐标系，利用向量法求解即可.E【小问1详解】连接，BE 由题意，2,60,120AD DE ADE BCE ==∠=︒∠=︒则为等边三角形，ADE V 由余弦定理得，所以2144222122BE ⎛⎫=+-⨯⨯⨯-= ⎪⎝⎭BE =则，222222,DE BE BD AE BE BD +=+=所以，,BE DE BE AE ⊥⊥又平面，,,AE DE E AE DE ⋂=⊂ADE 所以平面，BE ⊥ADE 又平面，所以平面平面；BE ⊂ABCE ADE ⊥ABCE 【小问2详解】如图，以点为原点，建立空间直角坐标系，E 则，()()()(()2,0,0,0,,,,0,0,0A B CD E -设，()01DF DB λλ=≤≤故，()((,,1,EC ED DB=-==-，((()1,1,AD AD DF λλ=+=-+-=--因为轴垂直平面，故可取平面的一条法向量为，z ABCE ABCE ()0,0,1m =所以，cos ,m AF m AF m AF⋅===化简得，解得或（舍去），23830λλ+-=13λ=3λ=-所以，1133DF DB ⎛==- ⎝ 设平面的法向量为，DEC (),,n x y z =则有，可取，00n EC x n ED x ⎧⋅=-=⎪⎨⋅=+=⎪⎩)1n =- 所以点到平面FDEC18. 已知函数，且与轴相切于坐标原点．()sin ln(1)f x x x ax =++-()y f x =x （1）求实数的值及的最大值；a ()f x （2）证明：当时，；π,π6x ⎡⎤∈⎢⎥⎣⎦1()22f x x +>（3）判断关于的方程实数根的个数，并证明．x ()0f x x +=【正确答案】（1），最大值为0 2a =（2）证明见解析（3）2个，证明见解析【分析】（1）由求出的值，即可得到解析式，再利用导数求出函数的单调(0)0f '=a ()f x 区间，从而求出函数的最大值；（2）依题意即证当时，记，π,π6x ⎡⎤∈⎢⎥⎣⎦1sin ln(1)2x x ++>1()sin ln(1)2m x x x =++-，当时直接说明即可，当，利用导数说明函数的单调π,π6x ⎡⎤∈⎢⎥⎣⎦π5π,66x ⎡⎤∈⎢⎥⎣⎦5π,π6x ⎛⎤∈ ⎥⎝⎦性，即可得证；（3）设，，当时，由（1）知，()()h x f x x =+()1,x ∞∈-+(1,0)x ∈-()(0)0f x f <=则，当时，利用导数说明函数的单调性，结合零点存在性定理判断函()0f x x +<π()0,x ∈数的零点，当时，，令，[π,)x ∈+∞()1ln(1)h x x x ≤++-()1ln(1)(π)l x x x x =++-≥利用导数说明在区间上单调递减，即可得到，从而说明函数在()l x [π,)+∞()0l x <无零点，即可得解.[π,)+∞【小问1详解】由题意知，且，(0)0f =(0)0f '=，1()cos 1f x x a x '=+-+ ，解得，(0)20f a '∴=-=2a =，，()sin ln(1)2f x x x x ∴=++-()1,x ∞∈-+则，1()cos 21f x x x '=+-+当时，，．故，0x ≥cos 1≤x 111x ≤+()0f x '≤所以在区间上单调递减，所以．()f x [0,)+∞()(0)0f x f £=当时，令，10x -<<1()cos 21g x x x =+-+则，21()sin (1)g x x x '=--+，，，sin (0,1)x -∈ 211(1)x >+()0g x '∴<在区间上单调递减，则，()f x '∴(1,0)-()(0)0f x f ''>=在区间上单调递增，则，则．()f x ∴(1,0)-()(0)0f x f <=()()max 00f x f ==综上所述，，的最大值为．2a =()f x 0【小问2详解】因为，()sin ln(1)2f x x x x =++-要证当时，即证，π,π6x ⎡⎤∈⎢⎥⎣⎦1()22f x x +>1sin ln(1)2x x ++>记，，1()sin ln(1)2m x x x =++-π,π6x ⎡⎤∈⎢⎥⎣⎦当时，，，π5π,66x ⎡⎤∈⎢⎥⎣⎦1sin 12x ≤≤ln(1)0x +>；1()sin ln(1)02m x x x ∴=++->当时，，5π,π6x ⎛⎤∈ ⎥⎝⎦1()cos 1m x x x '=++记，则，1()()cos 1n x m x x x '==++21()sin 0(1)n x x x '=--<+在区间上单调递减，则，()m x '∴5π,π6⎛⎤ ⎥⎝⎦5π6()065π6m x m ⎛⎫<=+< '+⎝'⎪⎭则在区间上单调递减，()m x 5π,π6⎛⎤⎥⎝⎦，()11()(π)sin πln(π1)ln π1022m x m ∴≥=++-=+->综上所述，当时，．π,π6x ⎡⎤∈⎢⎥⎣⎦1()22f x x +>【小问3详解】设，，()()sin ln(1)h x f x x x x x =+=++-()1,x ∞∈-+，1()cos 11h x x x '∴=+-+当时，由（1）知，(1,0)x ∈-()(0)0f x f <=故，()()0f x x f x +<<故在区间上无实数根．()0f x x +=(1,0)-当时，，因此为的一个实数根．0x =(0)0h =0()0f x x +=当时，单调递减，π()0,x ∈1()cos 11h x x x '=+-+又，，(0)10h '=>1(π)20π1h '=-<+存在，使得，∴0(0,π)x ∈()00h x '=所以当时，当时，00x x <<ℎ′(x )>00πx x <<ℎ′(x )<0在区间上单调递增，在区间上单调递减，()h x ∴()00,x ()0,πx ，又，()0(0)0h x h ∴>=(π)ln(π1)π2π0h =+-<-<在区间上有且只有一个实数根，在区间上无实数根．()0f x x ∴+=()0,πx (]00,x 当时，，[π,)x ∈+∞()1ln(1)h x x x ≤++-令，()1ln(1)(π)l x x x x =++-≥，1()1011x l x x x -'∴=-=<++故在区间上单调递减，，()l x [π,)+∞()(π)ln(1π)π13π0l x l ≤=+-+<-<于是恒成立．故在区间上无实数根，()0f x x +<()0f x x +=[π,)+∞综上所述，有2个不相等的实数根．()0f x x +=方法点睛：导函数中常用的两种常用的转化方法：一是利用导数研究含参函数的单调性，常化为不等式恒成立问题．注意分类讨论与数形结合思想的应用；二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问题处理．19. 对于任意正整数n ，进行如下操作：若n 为偶数，则对n 不断地除以2，直到得到一个奇数，记这个奇数为；若n 为奇数，则对不断地除以2，直到得出一个奇数，记这个n a 31n +奇数为.若，则称正整数n 为“理想数”.n a 1n a =（1）求20以内的质数“理想数”；（2）已知.求m 的值；9m a m =-（3）将所有“理想数”从小至大依次排列，逐一取倒数后得到数列，记的前n 项和{}n b {}n b 为，证明.n S ()*7N 3n S n <∈【正确答案】（1）2和5为两个质数“理想数” （2）的值为12或18m（3）证明见解析【分析】（1）根据“理想数”概念，结合列举法可解；（2）分析题意知道必为奇数，则必为偶数，结合整除知识得解；9m a m =-m （3）将数列适当放缩，后分组，结合等比数列求和公式计算即可.【小问1详解】以内的质数为，202,3,5,7,11,13,17,19，故，所以为“理想数”；212=21a =2，而，故不是“理想数”；33110⨯+=1052=3，而，故是“理想数”；35116⨯+=41612=5，而，故不是“理想数”；37122⨯+=22112=7，而，故不是“理想数”；311134⨯+=34172=11，而，故不是“理想数”；313140⨯+=4058=13，而，故不是“理想数”；317152⨯+=52134=17，而，故不是“理想数”；319158⨯+=58292=19和5为两个质数“理想数”；2∴【小问2详解】由题设可知必为奇数，必为偶数，9m a m =-m ∴存在正整数，使得，即：∴p 92p m m =-9921p m =+-，且，921p ∈-Z211p-≥，或，或，解得，或，211p ∴-=213p -=219p-=1p =2p =，或，即的值为12或18．1991821m ∴=+=-2991221m =+=-m 【小问3详解】显然偶数"理想数"必为形如的整数，()*2k k ∈N 下面探究奇数"理想数"，不妨设置如下区间：，((((0224462222,2,2,2,2,2,,2,2k k -⎤⎤⎤⎤⎦⎦⎦⎦若奇数，不妨设，1m >(2222,2k k m -⎤∈⎦若为"理想数"，则，且，即，且，m (*3112s m s +=∈N )2s >(*213s m s -=∈N )2s >①当，且时，；(*2s t t =∈N )1t >41(31)133t t m -+-==∈Z ②当时，；()*21s t t =+∈N 2412(31)133t t m ⨯-⨯+-==∉Z ，且，(*413t m t -∴=∈N )1t >又，即，22241223t k k--<<1344134k t k-⨯<-≤⨯易知为上述不等式的唯一整数解，t k =区间]存在唯一的奇数"理想数"，且，(2222,2k k -(*413k m k -=∈N )1k >显然1为奇数"理想数"，所有的奇数"理想数"为，()*413k m k -=∈N 所有的奇数"理想数"的倒数为，∴()*341kk ∈-N 1133134144441k k k ++<=⨯---1212123111111222521n n n n S b b b b b b b +⎛⎫⎛⎫∴=+++<+++++<+++++++ ⎪ ⎪⎝⎭⎝⎭，即．21111171111124431124⎛⎫<⨯++++<+⨯=⎪⎝⎭-- ()*73n S n <∈N 知识点点睛：本题属于新定义的题目，综合了整除，数列的放缩，分组求和和等比数列公式.属于难题.。

山东省青岛市即墨市第一中学高三上学期期中考试——物

山东省青岛市即墨市第一中学2017届高三上学期期中考试物理试题第Ⅰ卷（选择题共52分）注意事项：1、选择题答案涂在答题卡的相应位置上；2、实验题、解答题的答案写在各题目的指定区域内的位置上，不按要求作答的答案无效3、交卷时只交答题卡和答题纸。

一、选择题：（1－7题为单选题，8－13题为多选题。

每题4分，共52分，其中多选题全部选对得4分，选对但不全得2分，有选错得0分）1．下列关于物理学史和物理研究方法的叙述中正确的是A．根据速度的定义式，当Δt取不同的时间段时，v都可以表示物体的瞬时速度B．牛顿发现了万有引力定律，并准确的测定了万有引力常量C．伽利略借助实验研究和逻辑推理得出了自由落体运动规律D．用比值定义的物理概念在物理学中占有相当大的比例，例如场强就是采用比值定义的2．如图所示，在水平地面上竖直固定一直杆，质量为m 的气球用轻质细线悬于杆顶端O，当水平风吹来时，气球在水平风力的作用下飘起来．已知风力大小正比于风速，当风速v0=3m/s时，测得球平衡时细线与竖直方向的夹角θ=30°．下列说法正确的是A．细线拉力与风力的合力大于mgB．θ=60°时，风速v=9m/sC．若风速增大到某一值时，θ可能等于90°D．若风力方向发生变化，θ仍为30o，则风力可能小于0.5mg3．质点做匀加速直线运动，相继经过两端距离为16 m的路程，第一段用时4 s，第二段用时2 s，则质点运动的加速度是（）A．B．C．D．4．如图所示，水平地面上有一车厢，车厢内固定的平台通过相同的弹簧把相同的物块A、B压在竖直侧壁和水平的顶板上，已知A、B与接触面间的动摩擦因数均为μ，车厢静止时，两弹簧长度相同，A恰好不下滑，最大静摩擦力等于滑动摩擦力，重力加速度为g．现使车厢沿水平方向加速运动，为保证A、B仍相对车厢静止，则A．速度可能向左，加速度可大于（1+μ）gB．加速度一定向左，不能超过μgC．加速度一定向右，不能超过（1－μ）gD．加速度一定向左，不能超过（1－μ）g5．如图，水平传送带两端点A、B间距离L= 5m，传送带以v0=2m／s的速度（始终保持不变）顺时针运转。

即墨市第一中学2018-2019学年上学期期中高考数学模拟题

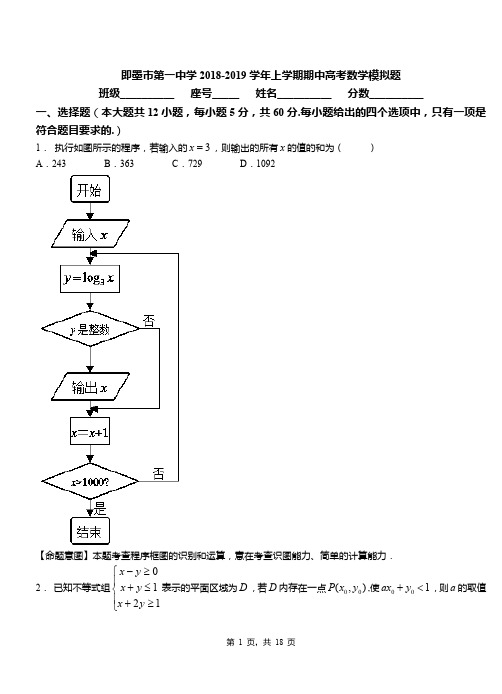
即墨市第一中学2018-2019学年上学期期中高考数学模拟题班级__________ 座号_____ 姓名__________ 分数__________一、选择题（本大题共12小题，每小题5分，共60分.每小题给出的四个选项中，只有一项是符合题目要求的.）1．执行如图所示的程序，若输入的，则输出的所有的值的和为（）3x =x A ．243 B ．363 C ．729 D ．1092【命题意图】本题考查程序框图的识别和运算，意在考查识图能力、简单的计算能力．2．已知不等式组表示的平面区域为，若内存在一点,使，则的取值⎪⎩⎪⎨⎧≥+≤+≥-1210y x y x y x D D 00(,)P x y 001ax y +<a范围为（）A ．B ．C ．D ．(,2)-∞(,1)-∞(2,)+∞(1,)+∞3．某大学的名同学准备拼车去旅游，其中大一、大二、大三、大四每个年级各两名，分乘甲、乙两辆汽8车，每车限坐名同学（乘同一辆车的名同学不考虑位置），其中大一的孪生姐妹需乘同一辆车，则乘44坐甲车的名同学中恰有名同学是来自同一年级的乘坐方式共有（）种.42A ．B ．C ．D ．24184836【命题意图】本题考查排列与组合的基础知识，考查学生分类讨论，运算能力以及逻辑推理能力．4．已知实数满足不等式组，若目标函数取得最大值时有唯一的最优解，则y x ,⎪⎩⎪⎨⎧≤-≥+≤-5342y x y x x y mx y z -=)3,1(实数的取值范围是（）m A ．B ．C ．D ．1-<m 10<<m 1>m 1≥m 【命题意图】本题考查了线性规划知识，突出了对线性目标函数在给定可行域上最值的探讨，该题属于逆向问题，重点把握好作图的准确性及几何意义的转化，难度中等.5．已知点是双曲线C ：左支上一点，，是双曲线的左、右两个焦点，且P 22221(0,0)x y a b a b-=>>1F 2F ，与两条渐近线相交于，两点（如图），点恰好平分线段，则双曲线的离心率12PF PF ⊥2PF M N N 2PF 是（）A.B.2D.52【命题意图】本题考查双曲线的标准方程及其性质等基础知识知识，意在考查运算求解能力.6．已知向量=（1，2），=（x ，﹣4），若∥，则x=（）A ． 4B ． ﹣4C ． 2D ． ﹣27．复数（为虚数单位），则的共轭复数为（）2(2)i z i-=i z A ． B ． C ． D ．43i -+43i +34i +34i-【命题意图】本题考查复数的运算和复数的概念等基础知识，意在考查基本运算能力．8．中，“”是“”的（）ABC ∆A B >cos 2cos 2B A >A. 充分必要条件B. 充分不必要条件C. 必要不充分条件D. 既不充分也不必要条件【命题意图】本题考查三角函数的性质与充分必要条件等基础知识，意在考查构造函数的思想与运算求解能力.9．已知函数，，若，则（）A1B2C3D-110．我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大的创举，这个伟大创举与我国古老的算法——“辗转相除法”实质一样，如图的程序框图源于“辗转相除法”．当输入a＝6 102，b＝2 016时，输出的a为（）A．6B．9C．12D．1811．如图，AB是半圆O的直径，AB＝2，点P从A点沿半圆弧运动至B点，设∠AOP＝x，将动点P到A，B 两点的距离之和表示为x的函数f（x），则y＝f（x）的图象大致为（）12．已知集合，{2,1,1,2,4}A =--，则2{|log ||1,}B y y x x A ==-∈（）A B = A ．B ．{2,1,1}--{1,1,2}-C ．D ．{1,1}-{2,1}--【命题意图】本题考查集合的交集运算，意在考查计算能力．二、填空题（本大题共4小题，每小题5分，共20分.把答案填写在横线上）13．已知，为实数，代数式的最小值是.x y 2222)3(9)2(1y x x y ++-++-+【命题意图】本题考查两点之间距离公式的运用基础知识，意在考查构造的数学思想与运算求解能力.14．已知函数的一条对称轴方程为，则函数的最大值为21()sin cos sin 2f x a x x x =-+6x π=()f x ___________．【命题意图】本题考查三角变换、三角函数的对称性与最值，意在考查逻辑思维能力、运算求解能力、转化思想与方程思想．15．曲线y ＝x 2＋3x 在点（－1，－2）处的切线与曲线y ＝ax ＋ln x 相切，则a ＝________．16．已知等差数列的前项和为，若，则.}{n a n n S 564318a a a a --=+=8S 三、解答题（本大共6小题，共70分。

2017届高三上学期期中考试数学(文)试题 Word版含答案

高三数学期中测试卷(文)试卷满分共计150分考试时间：120分钟一、选择题：本大题共8小题，每小题5分，共40分 1．若集合{1,2,3}A =，{0,1,2}B =，则A B =A ．{0,1,2,3}B ．{0,1,2}C ．{1,2}D ．{1,2,3}2．设3log 2a =，21log 8b =，c = A ．a b c >> B ．c b a >> C ．a c b >> D ．c a b >>3．“数列{}n a 既是等差数列又是等比数列”是“数列{}n a 是常数列”的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．若实数,x y 满足010x y x y x -≤⎧⎪+≤⎨⎪≥⎩，则2z x y =+的最大值为A ．0B ．1C ．32D ．2 5．从,,,,A B C DE 5名学生中随机选出2人，A 被选中的概率为A ．15B ．25C ．825D ．9256. 下列函数中，其定义域和值域分别与函数lg 10x y =的定义域和值域相同的是A ．y x =B ．lg y x =C ．2x y = D．y =7．执行如图所示的程序框图，输出的k 的值为A ．3B ．4C ．5D ．68．函数()2sin()(0,)22f x x ππωϕωϕ=+>-<<的部分图象如图所示，则,ωϕ的值分别是（）A ．2,3π- B ．2,6π-C ．4,6π-D ．4,3π二、填空题：本大题共6小题，每小题5分，共30分 9．设命题p ：∃n ∈N ，2n >2n ，则p ⌝为______ .10．若i 为虚数单位，则21i=+______ .11．数列}{n a 中，若11=a ，211+=-n n a a （2≥n ），则数列}{n a 的前9项和等于______ .12．曲线ln y x x =+在点()1,1处的切线方程为______ .13．ABC ∆中，角,,A B C 所对的边分别为,,a b c . 若3a =，2b =，1cos()3A B +=，则边c =______ .14．设函数21()4()(2)1x a x f x x a x a x ⎧-<=⎨--≥⎩，①若1a =，则()f x 的最小值为______；②若()f x 恰有2个零点，则实数a 的取值范围是______ .三、解答题：本大题共6小题，共80分. 解答应写出文字说明，验算步骤或证明过程. 15．（本小题满分13分）已知：ABC ∆中，角,,A B C 所对的边分别为,,a b c，且sin 2sin a B A =．（Ⅰ）求角B 的大小；（Ⅱ）若1cos 3A =，求sin C 的值．16．（本小题满分13分）某超市随机选取1000位顾客，记录了他们购买甲、乙、丙、丁四种商品的情况，整理成如下统计表，其中“√”表示购买，“×”表示未购买．（Ⅰ）估计顾客同时购买乙和丙的概率；（Ⅱ）估计顾客在甲、乙、丙、丁中同时购买3种商品的概率；（Ⅲ）如果顾客购买了甲，则该顾客同时购买乙、丙、丁中哪种商品的可能性最大？17．（本小题满分13分）已知：函数2()sin 2f x x x =+. （Ⅰ）求()f x 的最小正周期；（Ⅱ）求()f x 的单调递增区间；（Ⅲ）把函数()y f x =的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再把得到的图象向左平移3π个单位，得到函数()y g x =的图象，求()6g π的值．18．（本小题满分13分）已知：函数2()()(0)x f x ax bx c e a =++>的导函数'()y f x =的两个零点为3-和0．（Ⅰ）求()f x 的单调区间；（Ⅱ）若()f x 的极小值为1-，求()f x 的极大值．19.（本小题满分14分）已知：()f x 是定义在[1,1]-上的奇函数，且(1)1f =，若,[1,1]a b ∈-，且0a b +≠时，有()()0f a f b a b+>+恒成立．（Ⅰ）用定义证明函数()f x 在[1,1]-上是增函数；（Ⅱ）解不等式：1()(1)2f x f x +<-；（Ⅲ）若2()21f x m m ≤-+对所有[1,1]x ∈-恒成立，求：实数m 的取值范围．20．（本小题满分14分）已知：对于无穷数列{}n a 与{}n b ，记*{|,}n A x x a n ==∈N ，*{|,}n B x x b n ==∈N ，若同时满足条件：①{}n a ，{}n b 均单调递增；②A B =∅ 且*A B =N ，则称{}n a 与{}n b 是无穷互补数列．（Ⅰ）若21n a n =-， 42n b n =-，判断{}n a 与{}n b 是否为无穷互补数列，并说明理由；（Ⅱ）若2n n a =且{}n a 与{}n b 是无穷互补数列，求数列{}n b 的前16项的和；（Ⅲ）若{}n a 与{}n b 是无穷互补数列，{}n a 为等差数列且1636a =，求{}n a 与{}n b 的通项公式．高三数学期中测试卷(文)参考答案：CDAD BDBA9．p ⌝：2,2n n N n ∀∈≤； 10．1i -； 11．27；12．21y x =-； 13； 14． 1-；11[2)2，，⎡⎫+∞⎪⎢⎣⎭；15．解：（Ⅰ）ABC ∆中，由正弦定理BbA a sin sin =，可得A bB a sin sin =，又由A b B a sin 32sin =得B a A b B B a sin 3sin 3cos sin 2==，所以23cos =B ，因为0B π<<，6π=B ； ………7分（Ⅱ）由31cos =A 及0A π<<得322sin =A ，则)sin()](sin[sin B A B A C +=+-=π，所以)6sin(sin π+=A C 6162cos 21sin 23+=+=A A ． ………13分16．解：（Ⅰ）从统计表可以看出，在这1000位顾客中，有200位顾客同时购买了乙和丙，所以顾客同时购买乙和丙的概率可以估计为2000.21000=； ………4分（Ⅱ）从统计表可以看出，在这1000位顾客中，有100位顾客同时购买了甲、丙、丁，另有200位顾客同时购买了甲、乙、丙，其他顾客最多购买了2种商品．所以顾客在甲、乙、丙、丁中同时购买3种商品的概率可以估计为1002000.31000+=； ………8分（Ⅲ）与（Ⅰ）同理，可得：顾客同时购买甲和乙的概率可以估计为2000.21000=，顾客同时购买甲和丙的概率可以估计为1002003000.61000++=，顾客同时购买甲和丁的概率可以估计为1000.11000=，所以，如果顾客购买了甲，则该顾客同时购买丙的可能性最大． ………13分17．解：2()sin 2f x x x =+cos2)sin 2x x =-+sin 2x x =2sin(2)3x π=-………3分（Ⅰ）22T ππ==； ………5分（Ⅱ）由222232k x k πππππ-≤-≤+（k ∈Z ）得51212k x k ππππ-≤≤+（k ∈Z ），则()f x 的单调递增区间是5[,]1212k k ππππ-+（k ∈Z ）； ………8分（Ⅲ）函数()y f x =的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变）得到函数2sin()3y x π=-+3π个单位得到函数2sin y x =象，即()2sin g x x =()2sin 166g ππ=+=． ………13分18．解：（Ⅰ）2()()x f x ax bx c e =++，定义域：R22()(2)()[(2)]x x x f x ax b e ax bx c e ax a b x b c e '=++++=++++．令()0f x '=，则3x =-和0x =，由0x e >，0a >，则则()f x 的单调增区间是(,3)-∞-，(0,)+∞，单调减区间是(3,0)-， ………7分（Ⅱ）由（Ⅰ）知，()(0)f x f c ==极小值，3-和0是2(2)0ax a b x b c ++++=的根，则1230(3)0c a b a b c a ⎧⎪=-⎪+⎪-+=-⎨⎪+⎪-⨯=⎪⎩，解得111a b c =⎧⎪=⎨⎪=-⎩，所以2()(1)x f x x x e =+-，又由（Ⅰ）知，335()(3)(931)f x f e e -=-=--=极大值 ………13分19．解：（Ⅰ）证明：设任意12,[1,1]x x ∈-且12x x <，由于()f x 是定义在[1,1]-上的奇函数，∴2121()()()()f x f x f x f x -=+- 因为12x x <，所以21()0x x +-≠，由已知有2121()()0()f x f x x x +->+-,∵2121()0x x x x +-=->，∴21()()0f x f x +->，即21()()f x f x >，所以函数()f x 在[1,1]-上是增函数. ………5分（Ⅱ）由不等式1()(1)2f x f x +<-得1112111112x x x x⎧-≤+≤⎪⎪-≤-≤⎨⎪⎪+<-⎩，解得104x ≤< ………9分（Ⅲ）由以上知()f x 最大值为(1)1f =，所以要使2()21f x m m ≤-+对所有[1,1]x ∈-，只需2121m m ≤-+恒成立，得实数m 的取值范围为0m ≤或2m ≥. ………14分20．解：（Ⅰ）若21n a n =-， 42n b n =-，则*{|,}{1,3,5,7,}n A x x a n ==∈=N ，*{|,}{2,6,10,14,}n B x x b n ==∈=N因为4∉A ，4∉B ，所以4∉A B ，从而{}n a 与{}n b 不是无穷互补数列； ………4分（Ⅱ）若2n n a =，*{|,}{2,4,8,16,32,}n A x x a n ==∈=N ，则当{1,3,5,6,7,9,10,11,12,13,14,15,17,18,19,20,}B = 时满足条件，则数列{}n b 的前16项的和为()()23412202222++⋅⋅⋅+-+++()512020221802+=⨯--=； ………9分（Ⅲ）设{}n a 的公差为d ，d *∈N ，则1611536a a d =+=，由136151a d =-≥，得1d =或2，若1d =，则121a =，20n a n =+，则{}n b 中只有20项与{}n b 是无穷数列矛盾；若2d =，则16a =，24n a n =+，5255n nn b n n ≤⎧=⎨->⎩． ………14分。

山东省青岛市即墨市第一中学高三语文上学期期中试题

山东省青岛市即墨市第一中学2017届高三语文上学期期中试题本试卷分第Ⅰ卷和第Ⅱ卷两部分，共８页，满分150分。

考试时间150分钟。

考试结束后，将答题纸交回。

注意事项：1．答卷前，将学校、班级、姓名、准考证号填写在答题纸规定的位置上。

2．必须用0.5毫米黑色签字笔作答，答案必须写在答题纸各题目指定区域内相应的位置，不能写在试卷上；如需改动，先划掉原来的答案，然后再写上新的答案。

不能使用涂改液、胶带纸、修正带。

不按以上要求作答的答案无效。

第Ⅰ卷（共36分）一、（15分。

共5小题，每小题3分）阅读下面的文字，完成1～3题。

看呐，百十个斜背腰鼓的后生，如百十块被强震不断击起的石头，狂舞在你面前。

这腰鼓，使冰冷的空气立即变得躁热．．了，恬静的阳光立即变得飞溅了，困倦的世界立即变得（亢奋/兴奋）了。

容不得束缚，容不得羁绊．．。

骤雨一样，如急促的鼓点；①；火花一样，如闪射的瞳．．，容不得闭塞仁。

它震憾．．着你，烧灼着你，威逼着你。

它使你（惊诧/惊异）于那农民衣着包裹着的躯体，居然可以释放出那么奇伟磅礴．．淋漓的后生。

每一个舞姿都充满了．．的能量。

黄土高原呐，你生养了这些元气力量，每一个舞姿都呼呼作响，每一个舞姿都是光与影的匆匆（变幻/变换），每一个舞姿都使人颤．栗．在浓烈的艺术享受中。

当它戛然．．而止的时候，世界出奇的寂静，以致使人对她感到十分陌生了，简直像来到另一个星球，②。

1.文中加点字的字形和注音全都正确的一项是（）A．躁热羁绊．（bàn） B．震憾闭塞．（sè）C．磅礴颤．栗（chàn） D．元气戛．然（jiá）2.依次选用文中括号中的词语，最恰当的一项是（）A．亢奋惊异变幻 B．兴奋惊异变换C．兴奋惊诧变幻 D．亢奋惊诧变换3.在文中两处横线上依次填入语句，衔接最恰当的一项是（）A．①旋风一样，如飞扬的流苏②耳畔是一声渺远的鸡啼B．①旋风一样，如飞扬的流苏②一声渺远的鸡啼回响耳畔C．①旋风一样，如流苏的飞扬②耳畔是一声渺远的鸡啼D．①旋风一样，如流苏的飞扬②一声渺远的鸡啼回响耳畔4．下列各句中，加点的成语使用正确的一项是（）A．大自然希望儿童在成人以前就要像儿童的样子，如果我们违背了这个规律，就会催生出一些年纪轻轻的学究和老态龙钟．．．．的儿童。

山东省青岛市即墨北中学高三数学文测试题含解析

山东省青岛市即墨北中学高三数学文测试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 若等差数列{a n}的前三项为x﹣1，x+1，2x+3，则这数列的通项公式为( )A．a n=2n﹣5 B．a n=2n﹣3 C．a n=2n﹣1 D．a n=2n+1参考答案：B【考点】等差数列的通项公式．【专题】计算题．【分析】由等差数列{a n}的前三项为x﹣1，x+1，2x+3，知（x+1）﹣（x﹣1）=（2x+3）﹣（x+1），解得x=0．故a1=﹣1，d=2，由此能求出这数列的通项公式．【解答】解：∵等差数列{a n}的前三项为x﹣1，x+1，2x+3，∴（x+1）﹣（x﹣1）=（2x+3）﹣（x+1），解得x=0．∴a1=﹣1，d=2，a n=﹣1+（n﹣1）×2=2n﹣3．故选B．【点评】本题考查等差数列的通项公式，解题时要认真审题，注意等差数列的性质的灵活运用．2. 下列函数中，满足“”的单调递增函数是（）（A）（B）（C）（D）参考答案：D3. 命题“若，则”的逆否命题是（）A．若，则B．若，则C．若，则D．若，则参考答案：D 略4. 设不等式组表示的平面区域为D.若圆经过区域D上的点，则r的取值范围是A. B.C. D.参考答案：B5.在等差数列中，则=（）（A）24 （B）22（C）20 （D）－8参考答案：答案：A6. 已知直线，平面，且，，则（）A．若平面不平行于平面，则不可能垂直于；B．若平面平行于平面，则不可能垂直于；C．若平面不垂直于平面，则不可能平行于；D．若平面垂直于平面，则不可能平行于；参考答案：A中，有可能与垂直，B中，必与垂直，D中，可能平行于，C正确，选C．7. 如图，点A，B在函数y=log2x+2的图象上，点C在函数y=log2x的图象上，若△ABC为等边三角形，且直线BC∥y轴，设点A的坐标为（m，n），则m=（）A．2 B．3 C．D．参考答案：D【考点】4N：对数函数的图象与性质．【分析】根据题意，设出A、B、C的坐标，由线段BC∥y轴，△ABC是等边三角形，得出AB、AC与BC的关系，求出m、n的值，计算出结果．【解答】解：根据题意，设B（x0，2+log2x0），A（m，n），C（x0，log2x0），∵线段BC∥y轴，△ABC是等边三角形，∴BC=2，2+log2m=n，∴m=2n﹣2，∴4m=2n；又x0﹣m=，∴m=x0﹣，∴x0=m+；又2+log2x0﹣n=1，∴log2x0=n﹣1，x0=2n﹣1；∴m+=2n﹣1；2m+2=2n=4m，∴m=，故选：D．【点评】本题考查了指数函数与对数函数的图象与性质的应用问题，也考查了指数，对数的运算问题，属于中档题．8. 不等式的解集为A．[-4，2] B．C． D．参考答案：A9. 已知点P在以为左右焦点的椭圆上，椭圆内一点Q在的延长线上，满足，若，则该椭圆离心率取值范围是（）A．B．C．D．参考答案：A10. 已知,则“”是“”的（）A．充分不必要条件 B．必要不充分条件C．充要条件 D．即不充分又不必要条件参考答案：A考点：充分必要条件的判定.二、填空题:本大题共7小题,每小题4分,共28分11. 一个几何体的三视图如图所示，则这个几何体的体积为。

2017届山东省青岛市即墨市第一中学高三上学期期中考试生物试题

2015—2016学年度第二学期期中模块检测高三生物试题（Ⅰ卷）注意事项：1、选择题答案涂在答题卡的相应位臵上；2、填空题、解答题的答案写在各题目的指定区域内的位臵上，不按要求作答的答案无效3、交卷时只交答题卡和答题纸。

一、选择题：(本大题共24小题，每小题2分，共48分，在每小题给出的四个选项中，只有一项是符合题目要求的。

)1、下列关于性染色体及其上面的基因遗传方式和特点的说法，正确的是( )A．具有同型性染色体的生物，发育成雌性个体，具有异型性染色体的生物发育成雄性个体B．X、Y染色体在减数第一次分裂后期分离，X、X染色体在减数第一次分裂后期或减数第二次分裂后期分离C．伴X染色体隐性遗传，男性发病率高，且女性患者的母亲和儿子均为患者D．性染色体上的基因只符合伴性遗传的特点，而不遵循孟德尔定律2、下图甲、乙、丙、丁表示四株豌豆体细胞中的控制种子的圆粒与皱粒(Y、y)及黄色与绿色(R、r)两对基因及其在染色体上的位臵，下列分析正确的是( )A．甲、乙豌豆杂交后代的性状分离比为9∶3∶3∶1B．乙、丙豌豆杂交后代有4种基因型、1种表现型C．甲、丙豌豆杂交后代的性状分离比为1∶2∶1D．甲、丁豌豆杂交后代有6种基因型、4种表现型3、下列是某同学关于真核生物基因的叙述( )①携带遗传信息②能转运氨基酸③能与核糖体结合④能转录产生RNA ⑤每三个相邻的碱基组成一个反密码子⑥可能发生碱基对的增添、缺失或替换其中正确的是( )A．①③⑤B．①④⑥C．②③⑥D．②④⑤4、美国科学家安德鲁〃菲尔和克雷格〃梅洛发现了RNA干扰现象，这是一个有关控制基因信息流程的关键机制。

下列有关RNA的叙述错误的是( )A．有的RNA具有生物催化作用B．tRNA、rRNA和mRNA都是基因转录的产物C．mRNA上有多少个密码子就有多少个tRNA与之对应D．分化后的不同形态的细胞中mRNA的种类和数量有所不同5、下列关于转录和翻译的叙述正确的是( )A．RNA聚合酶能与信使RNA的特定位点结合，催化转录B．不同密码子编码同种氨基酸可保证翻译的速度C．真核细胞的转录主要在细胞核内进行，翻译主要在细胞质基质中进行D．转录时的碱基互补配对类型有4种，翻译时有3种6、下列有关基因、蛋白质和核酸之间关系的叙述，错误的是( )A．同一生物不同的体细胞中核DNA分子是相同的，蛋白质和RNA不完全相同B．基因中的遗传信息通过mRNA决定蛋白质中的氨基酸排列顺序C．蛋白质合成旺盛的细胞中，DNA分子较多，转录成的mRNA分子也较多D．真核细胞中，转录主要在细胞核中进行，蛋白质的合成在细胞质中进行7、下图表示人体基因Y的表达过程，①～④表示过程。

山东省即墨市第一中学高三数学10月月考试题文

即墨市一中高二数学文科10月月考试题一、选择题：1．ii i i +---+1)2(1)21(22等于（）A ．i 43-B ．i 43+-C ．i 43+D ．i 43--2、已知集合},21|1||{R x x x P ∈≤-=，Q P N x x Q 则},|{∈=等于（）A ．]1,0[B ．}1,0{C ．}1{D ．}0{3、在△ABC 中，边a 、b 、c 所对角分别为A 、B 、C ，且cCb B a A cos cos sin ==，则△ABC 的形状为（）A ．等边三角形B ．有一个角为30°的直角三角形C ．等腰直角三角形D ．有一个角为30°的等腰三角形4、函数y=log 2(| x|+1)的图象大致是5、在200m 高的山顶上，测得山下一塔顶与塔底的俯角分别是30°、60°,则塔高为（） A ．3400m B ．33200m C ．33400m D ．3200m 6、对下列命题的否定，其中说法错误的是：（）A ．P ：能被3整除的整数是奇数；⌝P ：存在一个能被3整除的整数不是奇数B ．P ：每一个四边形的四个顶点共圆；⌝P ：每一个四边形的四个顶点不共圆C ．P ：有的三角形为正三角形：⌝P ：所有的三角形都不是正三角形D ．P ：022,:;022,22≤++∈∀⌝≤++∈∃x x R x p x x R x 7 、若011<<b a ，则下列不等式：①a ＋b <ab ②|a |>|b | ③a <b ④2>+baa b 中，正确的不等式有 A ．①②B ．②③C ．①④D ．③④8、已知函数()2,0,2,0,x f x x x ≥⎧=⎨-+<⎩则满足不等式()()232f x f x -<的x 的取值范围为9、已知x 和y 是正整数，且满足约束条件y x z x y x y x 32,72210+=⎪⎩⎪⎨⎧≥≤-≤+则的最小值是A ．24B ．14C ．13D ．11.510、已知函数()y f x =的导函数()y f x '=的图象如图所示，则关于函数()y f x =，下列说法正确的是A ．在1x =-处取得极大值B ．在区间[1,4]-上是增函数C ．在1x =处取得极大值D ．在区间[1,)+∞上是减函数11、给出下列命题：①在区间(0,)+∞上，函数1y x -=,12y x =,2(1)y x =-,3y x =中有三个是增函数；②若log 3log 30m n <<，则01n m <<<；③若函数()f x 是奇函数，则(1)f x -的图象关于点(1,0)A 对称；④已知函数233,2,()log (1),2,x x f x x x -⎧≤=⎨->⎩则方程 1()2f x =有2个实数根，其中正确命题的个数为（A ）1 （B ）2 （C ）3 （D ）4 12、函数()xf x ln x e =+的零点所在的区间是A.10,e ⎛⎫ ⎪⎝⎭B.1,1e ⎛⎫ ⎪⎝⎭C.（1，e ）D.()e,+∞二、填空题：（本大题共4个小题，每小题4分，共16分） 13、在ABC ∆中，若π32,3,1=∠==C c b ，则=∆ABC S .14.若x >1时，不等式x +k x ≥-11恒成立，则实数k 的取值范围是_________________. 15若316sin =⎪⎭⎫ ⎝⎛-απ，则⎪⎭⎫ ⎝⎛+απ232cos =_____________16第10题图第16题图三、解答题：本大题共6个小题，共74分。

人教A版数学必修一即墨市第一高级中学—年第一学期期中考试.doc

高中数学学习材料唐玲出品即墨市第一高级中学2012—2013年第一学期期中考试高一数学试题一、选择题（共12小题，每小题5分）1、下列表示错误的是（）A 、∅∉0B 、}{4,353102),(=⎪⎩⎪⎨⎧⎭⎬⎫=-=+y x y x y xC 、}{2,1∉φ D 、若B A ⊆，则A B A = 2、设集合}{2,1=M ，则满足条件}{4,3,2,1=N M 的集合N 的个数是（） A 、1 B 、3 C 、4 D 、83、已知集合}{81≤≤-=x x A ，}{133-+=m x m x B 且φ≠B ，若A B A = ，则（）A 、34≤≤-mB 、34 m -C 、32≤mD 、32 m4、已知两个函数()x f 和()x g 的定义域和值域都是集合}{3,2,1，其定义如下表x 1 2 3 x 1 2 3 F(x)213g(x)321填写下列()[]x f g 的表格，其三个数依次为（） A 、3,2,1 B 、1,2,3 C 、2,1,3 D 、2,3,15、函数113--=x x y 的定义域为（） A 、⎪⎭⎫⎢⎣⎡+∞,31 B 、()+∞,1 C 、⎪⎭⎫⎢⎣⎡1,31 D 、⎪⎭⎫⎢⎣⎡1,31 ()+∞,1 6、下列函数在区间()3,0上是增函数的是（）A 、xy 1= B 、21x y = C 、x y -=3 D 、1522--=x x y7、已知3153-⎪⎭⎫ ⎝⎛=a ，2153-⎪⎭⎫ ⎝⎛=b ，2134-⎪⎭⎫⎝⎛=c ，则a,b,c 三个数的大小关系是（） A 、b a c << B 、a b c << C 、c b a << D 、c a b << 8、已知()()m f bx ax x x f =--++=2235且，那么()()=-+22f f （）A 、0B 、2mC 、-4D 、4-m 9、已知函数()()[)()()20R -≥∞+=f a f x f x f y 上是减函数，若，在上的偶函数，且是，则a 的取值范围是（）A 、2-≤aB 、2-≥aC 、2-≤a 或2-≥aD 、22≤≤-a10、已知函数()[]()()的取值范围则且m m f x f m x x x x f ,,0,34max 2=∈-+-=（）A 、2≥mB 、20≤<mC 、2≤mD 、20≤≤m 11、当0≠a 时，函数axb y b ax y =+=和的图像只可能是（）x 123()[]x f gA B C D 12、给出下列各题（1）已知幂函数的图像经过点（9,3），则()10100=f （2）函数的图像关于原点对称2422xx y ---=（3）是同一函数与2x y x y ==（4）若函数()1R ＞上是增函数，则在a a x f x-= （5）函数()[]()是偶函数，则且x f x x x f 2,12-∈= 则正确的个数为（）A 、1B 、2C 、 3D 、4 二、填空题（本大题共4小题，每小题4分） 13、设全集}}{{06|R ,10x 1|N ,2=-+∈=≤≤∈==x x x B x A R U，则右图中阴影部分表示的集合为 14、计算()=--⨯44425.03232715、定义在R 上的奇函数()()()=-=x f x x x x f x x f 时＜则时＞若当0,20,216、已知定义在R 上的奇函数()x f 在(]0,∞-上是增函数且(),42=f 则不等式()042＞x x f -+的解集为三、解答题17、（本题共2小题，每题6分，共12分）（1）已知二次函数()()()()8,11,12的最大值为且满足：x f f f x f -=--=，求此二次函数的解析式。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2016—2017学年度第一学期期中检测高三数学（文）试题注意事项：1．本试卷分第Ⅰ卷和第Ⅱ卷两部分。

第Ⅰ卷为选择题，共50分；第Ⅱ卷为非选择题，共100分，满分150分，考试时间为120分钟。

2．第Ⅰ卷请按照题目要求将选出的答案标号（A、B、C、D）涂在答题卡上。

第Ⅱ卷将答案用黑色签字笔（0.5mm）写在答题卡上，不按要求作答的答案无效。

第Ⅰ卷（共50分）一、选择题：(本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的。

)1．集合{}{}R x y y B x x x A x ∈==>-=,2,022，R 是实数集，则()R C B A ⋃等于（）A．R B．]),2(0,(+∞⋃-∞C．(]10，D．(],1(2,)-∞⋃+∞2.已知向量(1,2)a =-,,R m ∈,则“6m =-”是“)//(b a a +”的（）A．充要条件B．充分不必要条件C．必要不充分条件D．既不充分也不必要条件3．已知角α的终边经过点(1,2)P -，则tan 4πα⎛⎫+ ⎪⎝⎭的值是（）．A．3B．3-C．13D．13-4．在ABC ∆中，已知8,60,75a B C =∠=∠=,则b 等于A．43B．45C．46D．2235.下列命题错误的是（）A．命题“若022=+y x ，则0==y x ”的逆否命题为“若y x ,至少一个不为0,则022≠+y x ”B．若命题01,:0200≤+-∈∃x x R x p ，则01,:2>+-∈∀⌝x x R x p C．若向量a b 满足0<⋅b a ，则a 与b 的夹角为钝角D．ABC ∆中，B A sin sin >是B A >的充要条件6．已知等差数列{n a }的前n 项和为n S ，且1012S =，则56a a +=A．125B．12C．6D．657.若函数a ax x f 213)(-+=在区间)1,1(-上存在一个零点，则a 的取值范围是A．51>a B．51>a 或1-<a C．511<<-a D．1-<a 8．已知函数()sin()f x A x ωϕ=+（其中0,2A πϕ><）的图象如图所示，则函数()f x 的解析式为A．()sin(2)3f x x π=-B．()sin(2)6f x x π=+C．()sin(2)3f x x π=+D.()sin(4)6f x x π=+9.在ABC ∆中，90C =o，且3CA CB ==，点M 满足MA 2BM =，则CB CM ⋅等于（）A．3B．4C．5D．610.已知O 是坐标原点，点(1,1)A -，若点(,)M x y 为平面区域2,1,2,x y x y +≥⎧⎪≤⎨⎪≤⎩上一个动点，则OA OM ⋅的取值范围是（）A.[1,0]-B.[0,2]C.[1,2]D.[1,1]-第Ⅱ卷（非选择题共100分）二、填空题：（本大题共5小题，每小题5分，共25分。

）11．已知函数21,0(),0xx f x x x -⎧-≤⎪=⎨>⎪⎩，则[(2)]f f -=;12．设正项等比数列{}n a 的前n 项和为n S ，若12,3693=-=S S S ，则=6S ;13.函数()xy x a e =+在0x =处的切线与直线10x y ++=垂直，则a 的值为_______.14．已知0,0,lg 2lg8lg 2x yx y >>+=，则113x y+的最小值是.15.有下列命题：①cos()cos()44y x x ππ=-+的图象关于直线2x π=对称；②31x y x +=-的图象关于点(1,1)-对称；③关于x 的方程2210ax ax --=有且仅有一个实根，则1a =-；④满足条件3,60AC B =∠=︒，1AB =的三角形有两个．其中真命题的序号是_________________________.三、解答题：本大题6小题，共75分．解答应写出文字说明，证明过程或演算步骤．16．（本小题满分12分）已知a =2 ，1b = ，3)()9a b a b (2-⋅2+=．（1）求向量a 与b 的夹角θ；（2）求a b +及向量a 在a b + 方向上的投影．17．（本小题满分12分）设函数xx f 121)(+=，正项数列{}n a 满足)1(,111-==n n a f a a ，*N n ∈，且2≥n .（1）求数列{}n a 的通项公式；（2）对*N n ∈，求14332211111+++++=n n n a a a a a a a a S ．18．（本小题满分12分）已知向量)2,cos (sin ),1,cos 2(x x n x m ωωω-=-=)0(>ω，函数3)(+⋅=n m x f ，若函数)(x f 的图象的两个相邻对称中心的距离为2π.（1）求函数)(x f 的单调增区间；（2）若将函数)(x f 的图象先向左平移4π个单位，然后纵坐标不变，横坐标缩短为原来的21倍，得到函数)(x g 的图象，当[,]42x ππ∈时，求函数)(x g 的值域.19.（本小题满分12分）在锐角ABC ∆中，角A,B,C 的对边分别为,,a b c ，向量)3),sin(2(C A m +=,向量)2cos 21,2(cos 2BB n -=，且n m //（1）求角B 的大小；（2）若2sin sin sin A C B =，求a c -的值.20.（本小题满分13分）“地沟油”严重危害了人民群众的身体健康，某企业在政府部门的支持下，进行技术攻关，新上了一种从“食品残渣”中提炼出生物柴油的项目，经测算，该项目月处理总成本y(元)与月处理总量x(吨)之间的函数关系可以近似的表示为：3221x 80x 5 040x,x 120,144)3y ,1x 200x 80 000,x 144,500)2⎧-+∈⎪⎪=⎨⎪-+∈⎪⎩［［且每处理一吨“食品残渣”，可得到能利用的生物柴油价值为200元，若该项目不获利，政府将补贴.（1）当x∈[200,300]时，判断该项目能否获利？如果获利，求出最大利润；如果不获利，则政府每月至少需要补贴多少元才能使该项目不亏损.（2）该项目每月处理总量为多少吨时，才能使每吨的平均处理成本最低？21.（本小题满分14分）设函数()21ln 2f x x ax bx =--.（1）当3,2=-=b a 时，求函数()f x 的极值；（2）令()()()21032a F x f x ax bx x x =+++<≤，其图象上任意一点()00,P x y 处切线的斜率12k ≤恒成立，求实数a 的取值范围；（3）当0,1a b ==-时，方程()f x mx =在区间21,e ⎡⎤⎣⎦内恰有两个实数解，求实数m 的取值范围.2016-2017上学期高三数学(文科)期中(答案)一、选择题：BADCC ABCAB二、填空题：11、312、913、014、415、①③16．（Ⅰ）()()2,1,2329a b a b a b ==-⋅+=224439a a b b ∴-⋅-= …………………………………………(2分)21428cos 39cos 2θθ∴⨯--=∴=……………………………(4分)[]0,3πθπθ∈∴=……………………………(6分)（Ⅱ）由（Ⅰ）知1cos 2112a b a b θ⋅==⨯⨯= ()2415a a b a a b ∴⋅+=+⋅=+=………………………(8分)2224127a b a b a b ∴+=++⋅=++=………………………(10分)向量a 在a b + 方向上的投影为()557cos ,77a a b a a a b a b⋅++===+ …………(12分)17.解：（1）由，所以，，且由等差数列定义可知：数列是以1为首项，以为公差的等差数列所以：（2）由（1）可知]18.解:(1)()2cos (sin cos )23f x x x x ωωω=--+sin 2cos 2x xωω=-2sin(2)4x πω=-……………………(2分)212T πππωω=∴=∴= ()2sin(2)4f x x π∴=-…………………(4分)增区间:222242k x k πππππ-+≤-≤+,3,88k k k z ππππ⎡⎤-++∈⎢⎥⎣⎦……………………(6分)(2)()2sin(4)4g x x π=+………………………(8分)59442444x x πππππ≤≤∴≤+≤21sin(4)42x π∴-≤+≤……………………(10分)函数()g x 的值域是2,1⎡⎤-⎣⎦…………………(12分)19.(1)解3)2,0(0)32sin(02cos 32sin 02cos 3cos sin 202cos 3)2cos 21)(sin(2//2πππ=∴∈=+=+=--=--+∴B B B B B B B B B BC A nm (2)由正弦定理得2b ac =由余弦定理得Bac a c b cos 2222-+=00)(222=-∴=--+=∴c a c a ac a c ac 20．(1)当x∈[200,300]时，设该项目获利为S，则S＝200x－(12x 2－200x＋80000)＝－12x 2＋400x－80000＝－12(x－400)2，所以当x∈[200,300]时，S<0.因此，该项目不会获利.当x＝300时，S 取得最大值－5000，所以政府每月至少需要补贴5000元才能使该项目不亏损.…………………………6分(2)由题意可知，食品残渣的每吨平均处理成本为：21x 80x 5 040,x 120,144)y 3.1x x 80 000x 200,x 144,500)2⎧-+∈⎪⎪=⎨⎪+-∈⎪⎩［［①当x∈[120,144)时，y x ＝13x 2－80x＋5040＝13(x－120)2＋240，∴当x＝120时，yx 取得最小值240；…………………………………8分②当x∈[144,500)时，y x ＝12x＋80000x －200≥212x·80000x－200＝200.当且仅当12x＝80000x ，即x＝400时，yx 取得最小值200.∵200<240，∴当每月处理量为400吨时，才能使每吨的平均处理成本最低……………………12分21.(Ⅰ)依题意，()f x 的定义域为(0,)+∞，当3,2=-=b a 时，)0(,3ln )(2>-+=x x x x x f ，121,0)1)(12()(/===--=x x x x x x f 或得列表()f x 的极大值为452ln )21(--=f ，()f x 的极小值为2)1(-=f (Ⅱ)]3,0(,ln )(∈+=x x ax x F ，则有00201(),2x a k F x x -'==≤在]3,0(上有解，∴a ≥200min 1()2x x -+所以当1=x 时，02021x x +-取得最小值2121≥∴a (Ⅲ)当1,0-==b a 时，[]),1(,ln )(2e x mx x x xf ∈=+=得[]有两个实数解，在21ln 1e x xm +=)11,12[2++∈e e m 时方程有两个实数解。