菱形的判定方法的应用
菱形的判定定理

菱形的判定定理菱形的判定定理是数学中一个重要的定理,它用于判断一个四边形是否为菱形。
菱形是一种特殊的四边形,具有四条边相等且对角线互相垂直的特点。
下面我们将详细介绍菱形的判定定理,并解释其原理及应用。
为了简化问题,首先我们需要明确菱形的定义。
一个四边形如果满足以下条件之一,即可被称为菱形:1. 四条边相等。
2. 对角线互相垂直。
在实际应用中,判断一个四边形是否为菱形,通常使用以下几种方法:方法一:边长判定法通过测量四边形的四条边的长度,如果四条边的长度都相等,则可以判断这个四边形是一个菱形。
方法二:对角线判定法通过测量四边形的两条对角线的长度,如果两条对角线的长度相等,则可以判断这个四边形是一个菱形。
方法三:边长和角度判定法通过测量四边形的四条边的长度以及四个内角的大小,如果四条边的长度都相等且四个内角都为直角(90度),则可以判断这个四边形是一个菱形。
菱形的判定定理的原理是基于上述三种方法,通过测量边长、对角线长度和角度来判断四边形是否为菱形。
这些方法都是基于几何学中关于菱形的定义和特性而来。
在实际应用中,菱形的判定定理可以用于解决一些几何问题,例如:1. 判断建筑物的平面图中是否存在菱形结构。
2. 在设计家具或装饰品时,判断其形状是否为菱形以便于制造。
3. 在地理学中,判断地图上的区域是否为菱形以便于计算面积或边界。
总结起来,菱形的判定定理是数学中用于判断一个四边形是否为菱形的定理。
通过测量边长、对角线长度和角度可以判断一个四边形是否满足菱形的定义。
这个定理在实际应用中有着广泛的应用,可以用于解决各种几何问题。
但需要注意的是,判定菱形的时候需要严格按照定义和条件进行测量和判断,以免出现错误的结果。
【初中数学知识点解析】 菱形性质与判定的应用

∵∠ABD=90°,AE=DE,∴BE=DE.
∴四边形BCDE是菱形.
类型1
利用菱形的性质与判定判断图形的形状
1.如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD
=90°,E为AD的中点,连接BE.
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,BC=1,求AC的长.
解:(2)∵AD∥BC,AC平分∠BAD,∴∠BAC=∠DAC=∠BCA.∴AB=BC=1.
1
2
∵∠ABD=90°,E为AD的中点,∴BE=AE= AD.
∵AD=2BC=2,∴BE=AE=AB=1.∴△ABE为等边三角形,∴∠BAE=60°.
3.如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE∥BA交
AC于点E,DF∥CA交AB于点F,已知CD=3.
(1)求AD的长;
(2)求四边形AEDF的周长.(注意:本题中的计算过程和结果均保留根号)
(2)∵DE∥BA交AC于点E,DF∥CA交AB于点F,
∴四边形AEDF是平行四边形,∠EAD=∠ADF.
类型4
利用菱形的性质与判定解决面积问题
4.如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E、F分别是AB、AC
的中点.
(1)求证:四边形AEDF是菱形;
(2)如果四边形AEDF的周长为12,两条对角线的和等于7,求四边形AEDF的面积S.
证明:(1)∵AD⊥BC,点E、F分别是AB、AC的中点,
∴∠DAC=30°,∠ADB=30°.∴∠ADC=60°.∴∠ACD=90°.
在Rt△ACD中,∵AD=2,∠DAC=30°,∴CD=1. ∴AC= 3
菱形的判定及应用
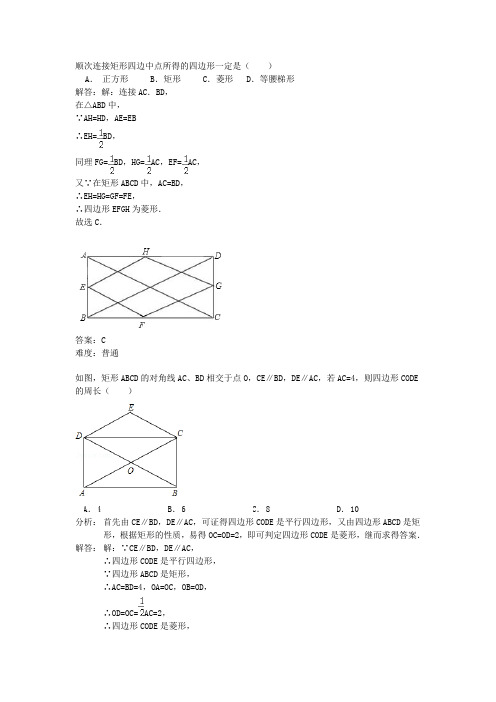
顺次连接矩形四边中点所得的四边形一定是()A.正方形 B.矩形 C.菱形 D.等腰梯形解答:解:连接AC.BD,在△ABD中,∵AH=HD,AE=EB∴EH=BD,同理FG=BD,HG=AC,EF=AC,又∵在矩形ABCD中,AC=BD,∴EH=HG=GF=FE,∴四边形EFGH为菱形.故选C.答案:C难度:普通如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE 的周长()A.4B.6C.8D.10分析:首先由CE∥BD,DE∥AC,可证得四边形CODE是平行四边形,又由四边形ABCD是矩形,根据矩形的性质,易得OC=OD=2,即可判定四边形CODE是菱形,继而求得答案.解答:解:∵CE∥BD,DE∥AC,∴四边形CODE是平行四边形,∵四边形ABCD是矩形,∴AC=BD=4,OA=OC,OB=OD,∴OD=OC=AC=2,∴四边形CODE是菱形,∴四边形CODE 的周长为:4OC=4×2=8. 故选C .答案:C 难度:普通已知:菱形ABCD 中,对角线AC 与BD 相交于点O ,OE∥DC 交BC 于点E ,AD=6cm ,则OE 的长为( )A . 6cmB . 4cmC . 3cmD . 2cm解答: 解:∵四边形ABCD 是菱形, ∴OB=OD,CD=AD=6cm , ∵OE∥DC, ∴BE=CE, ∴OE=CD=3cm . 故选C .答案:C 难度:普通如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH (不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm 2,四边形ABCD 面积是11cm 2,则①②③④四个平行四边形周长的总和为( ) (A )48cm (B )36cm (C )24cm(D )18cm答案:A 难度:普通如图,小聪在作线段AB 的垂直平分线时,他是这样操作的:分别以A 和B 为圆心,大于12AB 的长为半径画弧,两弧相交于C 、D ,则直线CD 即为所求.根据他的作图方法可知四边形ADBC 一定是... A .矩形 B .菱形C .正方形D .等腰梯形答案:B 难度:普通FAB CDH EG①②③④⑤BACD如图,点E 、F 、G 、H 分别是任意四边形ABCD 中AD 、BD 、BC 、CA 的中点,当四边形ABCD 的边至少满足 条件时,四边形EFGH 是菱形.答案:AB=CD 难度:普通如图6,已知菱形ABCD ,其顶点A ,B 在数轴对应的数分别为-4和1,则BC=__.图60D ABC答案:5 难度:普通如图,四边形ABCD 的对角线AC 、BD 互相垂直,则下列条件能判定四边形ABCD 为菱形的是( ) A .BA =BC B .AC 、BD 互相平分 C .AC =BD D .AB ∥CD 答案:B 难度:普通已知菱形ABCD 中,对角线AC=8cm ,BD=6cm ,在菱形内部(包括边界)任取一点P ,使△A CP 的面积大于6 cm 2的概率为 .【答案】0.25如图,若要使平行四边形 ABCD 成为菱形,则需要添加的条件是 A .AB =CDB .AD =BCC .AB =BCD .AC =BDAB CD EFG H A B C D答案:C 。
《菱形的判定》教案

《菱形的判定》教案教案:菱形的判定一、教学目标1.理解菱形的定义和性质。
2.能够判断一个四边形是否为菱形。
3.能够根据菱形的性质解决一些几何问题。
二、教学重难点1.菱形的定义和性质。
2.如何判断四边形是否为菱形。
3.如何应用菱形的性质解决几何问题。
三、教学方法1.理论授课相结合的方法。
2.案例分析法和讨论法,培养学生的分析和解决问题的能力。
四、教学步骤1.导入(5分钟)通过展示一些几何图形,让学生回答这些图形是否为菱形,引起学生对菱形的兴趣和思考。
2.理论讲解(20分钟)a)定义:什么是菱形?菱形是指四条边相等的四边形。
b)性质:-对角线的长度相等。
-对角线相互垂直。
-相邻角的和为180度。
-具有对称性。
-内角均是直角。
-具有平移不变性。
3.判断菱形的方法(15分钟)a)根据定义:判断四边形的四条边是否相等。
b)根据性质:判断四边形的对角线是否相等,是否互相垂直。
4.案例分析(20分钟)给出一些几何图形,让学生判断是否为菱形,并解释判断的过程和原因。
5.拓展应用(20分钟)a)设计一些菱形的几何问题,让学生应用菱形的性质解决。
b)分组讨论,学生互相出题并进行解答。
五、教学反思本节课通过对菱形的定义和性质的讲解,让学生对菱形有了初步的了解。
通过判断菱形的方法和解决菱形相关问题的练习,培养了学生的观察能力、分析和解决问题的能力。
此外,通过案例分析和拓展应用,提高了学生的思维能力和创造能力。
总之,本节课通过理论讲解和实际应用相结合的方法,使学生对菱形的理解更加深入,能够灵活运用菱形的性质解决几何问题。
数学菱形判定

数学菱形判定全文共四篇示例,供读者参考第一篇示例:数学中的菱形判定是一个重要的几何学概念,它涉及到平面几何中的图形判断和证明。
一个菱形是一个有四个相等边长的四边形,同时每两个相邻边之间的夹角是直角。
在实际生活和数学题目中,我们经常需要判断一个给定的四边形是否为菱形,这就需要运用一些基本的几何学知识和推理能力。
菱形判定的主要原理是根据菱形的定义来判断一个四边形是否满足菱形的性质。
也就是说,要判断一个四边形是否为菱形,就需要证明它有相等的四条边和四个直角。
我们来看一个简单的例子。
如图所示,有一个四边形ABCD,我们要判断它是否为菱形。
[图]我们需要证明四边形ABCD的四条边相等。
根据几何学知识,如果一个四边形的对边相等,那么这个四边形就是平行四边形。
所以我们可以先证明AB平行于CD,同时AD平行于BC。
如果AB平行于CD,我们可以用平行线的性质来证明AB等于CD。
同理,如果AD平行于BC,我们可以用同样的方法证明AD等于BC。
经过以上步骤,我们可以得出结论:四边形ABCD是一个菱形,因为它有四个相等的边长和四个直角。
除了上述方法,我们还可以通过另一种方法来判断一个四边形是否为菱形。
这种方法利用了菱形的特殊性质:对角线相互垂直且相等。
我们需要绘制对角线AC和BD。
接着,我们可以利用直角的定义和垂直线的性质来判断对角线AC和BD是否相互垂直。
如果AC和BD 相互垂直,那么我们可以通过勾股定理来证明AC等于BD。
同理,如果AC和BD相互垂直,那么我们可以通过同样的方法证明BD等于AC。
菱形判定是一个基础且重要的几何学概念,它需要我们熟练掌握几何学知识和推理能力。
在实际生活和数学题目中,要判断一个四边形是否为菱形,我们可以通过证明它有相等的四条边和四个直角,或者证明它有对角线相互垂直且相等来判断。
通过不断练习和思考,我们可以提高自己的数学水平和解题能力。
【这篇文章总结了数学中菱形判定的原理和方法,希望对读者有所帮助。
证明菱形的四种方法

证明菱形的四种方法方法一:利用图形的定义菱形是一个具有以下特征的四边形:它的四条边都相等,且相邻两条边之间的夹角都是90度。
我们可以通过证明这些特征来证明菱形。
(1)证明四边相等:设菱形的四个顶点分别为A、B、C、D,连接AC 和BD两条对角线。
由于AC和BD是菱形的对角线,所以AC=BD。
同时,由于AB和CD是菱形的边,所以AB=CD。
结合这两个等式,可以得出AB=BC=CD=DA,即菱形的四边相等。
(2)证明相邻两边夹角为90度:继续观察图形,可以发现△ABC和△CDA是两个直角三角形,其中∠CAB和∠CDA都是直角。
由于两个直角三角形共边AC相等,所以可得∠ABC≅∠CDA。
同理,也可以证明∠BCD≅∠DAB。
由于两个角均为直角,所以它们的和为180度。
综上所述,根据菱形的定义和证明,可以得出菱形的四个边相等且相邻两边夹角为90度。
因此,该图形是菱形。
方法二:利用对角线性质利用菱形对角线的性质来证明该图形是菱形。
设菱形的对角线分别为AC和BD,交于点O。
(1)证明四边相等:根据对角线性质,AC=BD。
将菱形的边再连接起来,可以得到四个三角形:△ABC、△ACD、△BAD和△BCD。
由于对角线相等,所以可以得出AB=BC、BC=CD和CD=DA。
这样就证明了菱形的四边相等。
(2)证明相邻两边夹角为90度:根据菱形的定义,对角线相等且相邻两边夹角为90度。
所以可以得出∠ABC=∠ACD=∠BAD=∠BCD=90度。
因此,该图形是菱形。
方法三:利用正方形性质正方形是一种特殊的菱形,它的特点是四个边相等且相邻两边夹角为90度。
可以通过正方形的性质来证明菱形。
(1)证明四边相等:将正方形的一条对角线,如AC连接起来,可以得到两个等腰直角三角形△ABC和△ACD。
由于直角三角形的两个直角边相等,所以可以得出AB=BC。
类似地,也可以证明AD=DC。
因此,正方形的四边相等。
(2)证明相邻两边夹角为90度:由正方形的性质可知,相邻两边夹角为90度。
《菱形》教学教案

《菱形》教学教案一、教学目标:1. 让学生理解菱形的定义和性质,能够识别和描述生活中的菱形实例。
2. 培养学生运用菱形性质解决实际问题的能力,提高学生的空间想象和逻辑思维能力。
3. 通过对菱形的学习,培养学生热爱数学、探索数学的兴趣。
二、教学内容:1. 菱形的定义及性质2. 菱形的判定方法3. 菱形的应用与实践三、教学重点与难点:1. 重点:菱形的定义、性质和判定方法。
2. 难点:菱形性质在实际问题中的应用。
四、教学方法:1. 采用问题驱动的教学方法,引导学生主动探究菱形的性质。
2. 运用多媒体课件辅助教学,直观展示菱形的形成和性质。
3. 组织学生进行小组讨论和合作交流,提高学生的动手能力和团队协作能力。
4. 结合生活实例,培养学生学以致用的能力。
五、教学过程:1. 导入新课:通过展示生活中的菱形实例,引导学生发现并提出菱形的问题。
2. 探究菱形的定义与性质:学生自主探究菱形的定义,教师引导学生发现菱形的性质,并通过多媒体课件进行展示。
3. 菱形的判定方法:学生总结菱形的判定方法,教师进行点评和讲解。
4. 实践与应用:学生分组进行实践活动,运用菱形的性质解决实际问题,教师进行指导和点评。
5. 课堂小结:学生总结本节课所学内容,教师进行补充和总结。
6. 布置作业:设计有关菱形的练习题,巩固所学知识。
六、教学评价:1. 通过课堂问答、作业批改等方式,了解学生对菱形定义、性质和判定方法的掌握情况。
2. 观察学生在实践活动中运用菱形知识解决实际问题的能力,评价学生的学以致用能力。
3. 搜集学生的小组讨论报告,评价学生的合作交流和动手操作能力。
七、教学拓展:1. 引导学生思考:还有哪些几何图形具有特殊的性质和应用?2. 推荐学生阅读有关几何图形的书籍和文章,扩大学生的知识面。
3. 鼓励学生参加数学竞赛和相关活动,提高学生的数学素养。
八、教学资源:1. 多媒体课件:展示菱形的定义、性质、判定方法及实际应用。
菱形判断方法

菱形判断方法菱形判断法是一种流程控制结构,主要用于解决特定问题的计算机程序中。
通过菱形判断法,程序可以根据条件进行不同的操作。
在菱形判断法中,程序会判断给定的条件是否成立,如果成立就执行一段操作;否则就执行另一段操作。
这种判断方式可以让程序更加灵活和智能,从而提高计算机程序的效率和可靠性。
菱形判断法的基本形式为 if-else 语句。
在 if-else 语句中,程序会根据给定的条件进行判断,如果条件成立就执行某个操作;否则就执行另一个操作。
if-else 语句的基本语法为:if (条件){// 如果条件成立就执行这里的代码}else{// 如果条件不成立就执行这里的代码}在上面的代码中,条件可以是任何可以被计算得出的值,比如变量、常量、表达式等。
如果条件成立,就会执行 if 后面的代码块;否则就会执行 else 后面的代码块。
1. 判断闰年int year = 2020;if ((year % 4 == 0 && year % 100 != 0) || year % 400 == 0){printf("%d 是闰年。
\n", year);}else{printf("%d 不是闰年。
\n", year); }2. 判断成绩等级int score = 85;if (score >= 90){printf("等级为 A\n");}else if (score >= 80 && score < 90) {printf("等级为 B\n");}else if (score >= 70 && score < 80) {printf("等级为 C\n");}else if (score >= 60 && score < 70) {printf("等级为 D\n");}else{printf("等级为 E\n");}在上面的代码中,根据不同的成绩范围来判断学生的等级。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
菱形的判定方法的应用(1)
菱形是特殊的平行四边形,它的常用判定方法有:
(1)四条边都相等的四边形是菱形;
(2)有一组临边相等的平行四边形是菱形;
(3)对角线互相垂直的平行四边形是菱形;
下面,就给同学们说说如何应用这些方法进行判定一个四边形是菱形。
一、四条边都相等的四边形是菱形
例1(08年,郴州)如图1,ΔABC 为等腰三角形,把它沿底边BC 翻折后,得到ΔDBC .请你判断四边形ABDC 的形状,并说出你的理由.
分析:翻折就是对称,也就是全等。
解:四边形ABCD 为菱形。
理由是:
由翻折,得:△ABC ≌△DBC .
所以,,AC CD AB BD ==
因为,△ABC 为等腰三角形, 所以,AB AC =
所以,AC =CD =AB =BD ,
故,四边形ABCD 为菱形
点评:本题主要是应用对称的知识得出一组临边相等,在运用等腰三角形的两腰相等得到四条边都相等来解答。
二、有一组临边相等的平行四边形是菱形
例2(08年,永州)如图△ABC 与△CDE 都是等边三角形,点E 、F 分别在AC 、BC 上,且EF∥AB
(1)求证:四边形EFCD 是菱形;
(2)设CD =4,求D 、F 两点间的距离.
分析:在四边形EFCD 中,由题意我们知道有一组临边ED 和CD 相等是很容易得到的,只要在说明这个四边形是平行四边形即可以。
(1)证明:
ABC Q △与CDE △都是等边三角形
ED CD ∴= 60A DCE BCA DCE ∴∠=∠=∠=∠=o
AB CD DE CF ∴∥,∥
又Q EF AB ∥
∴EF ∥CD ,
四边形EFCD 是平行四边形,
∴平行四边形EFCD 是菱形。
(2)解:连结DF ,与CE 相交于点G
由4CD =,可知2CG = ∴224223DG =-=
43DF ∴=
点评:观察是解答问题的途径和窗口。
三、对角线互相垂直的平行四边形是菱形
例3(08年,上海)如图11,已知平行四边形ABCD 中,对角线AC BD ,交于点O ,E 是BD 延长线
C A
B D 图1
上的点,且ACE △是等边三角形.
求证:四边形ABCD 是菱形;
分析:本题主要是利用等边三角形顶角的平分线、底边上的高和中线三线合一,得出AC ⊥BD ,然后在利用对角线互相垂直的平行四边形是菱形。
证明:在平行四边形ABCD 中,
AO=OC, 又因为,ACE △是等边三角形,
所以,OC 是底边AC 上的中线,也是底边上的高
即AC ⊥BD , 所以,平行四边形ABCD 是菱形。
点评:判定方法的确定要依据题目的特征来选择,要因题而宜,灵活运用。
以一当十:
1、(08年,赣州) 如图,等腰梯形ABCD 中,AD ∥BC ,M 、N 分别是AD 、BC 的中点,E 、F 分别是BM 、CM 的中点.
(1)在不添加线段的前提下,图中有哪几对全等三角形请直接写出结论;
(2)判断并证明四边形MENF 是何种特殊的四边形
2、(08年,无锡)如图,四边形ABCD 中,AB CD ∥,AC 平分BAD ∠,CE AD ∥交AB 于E .
(1)求证:四边形AECD 是菱形;
(2)若点E 是AB 的中点,试判断ABC △的形状,并说明理由.
参考答案:(1)△AMB ≌△DMC ;△BEN ≌△CFN
(2)判断四边形MENF 为菱形;
证明:∵ABCD 为等腰梯形,
∴AB =CD ,∠A =∠D , 又∵M 为AD 的中点, ∴MA =MD
∴△AMB ≌△DMC ,∴BM =CM ;
又∵E 、F 、N 分别为BM 、CM 、BC 中点,
∴MF =NE =12MC ,ME =NF =12
BM ,(或MF ∥NE , ME ∥NF ;) ∴EM =NF =MF =NE ;
∴四边形MENF 为菱形.
2、(1)AB CD Q ∥,即AE CD ∥,又CE AD Q ∥,∴四边形AECD 是平行四边形.
AC Q 平分BAD ∠,CAE CAD ∴∠=∠,
又AD CE Q ∥,ACE CAD ∴∠=∠,ACE CAE ∴∠=∠,AE CE ∴=,
∴四边形AECD 是菱形.
(2)E Q 是AB 中点,AE BE ∴=.又AE CE =Q ,BE CE ∴=,B BCE ∴∠=∠,
180B BCA BAC ∠+∠+∠=o Q ,22180BCE ACE ∴∠+∠=o ,90BCE ACE ∴∠+∠=o . 即90ACB ∠=o ,ABC ∴△是直角三角形. M F E
N D C A B E
D
B A O 例3。
