重庆市高2010级高三上期一诊考试题(数学理)参考答案
重庆市2010年高三上大部分区县期末联考试题(数学理)扫描版

高2011级(上)期末测试卷 数学(理工类)参考答案一.选择题:本大题10小题,每小题5分,共50分。
1~5 CBACB6~10 CAABD6.C根据定义有()sin 2cos()6f x x x x π=-=+,则至少向左平移56π个单位是偶函数.7.A 根据已知条件可得1ABC S ∆=,则12x y +=,且0,0x y >>.8.A 由可行域知当4,6x y ==时有最大值,则2323231325236,3266a b a b b a a b a b abab+++=+=+=++≥.9.B 易证)(x f 是R 上的奇函数与增函数. 10.D 如图:因为CD 弧长=2R πα⋅=,所以2πα=,故图中阴影部分的面积为142π-.所以可得原题中 阴影部分的面积为1333[2()]3422πππ-⨯⨯-=+.二.填空题:本大题共5小题,共25分。
11. )25,21(12. )2,1( 13.2 14.1)21(34--n 15. p 2 14.由⎩⎨⎧>==⇒+=-1213121n n a S n nnn , 所以11221)21(3421212131111---=++++=+++n n na a a . 15.设θ=∠AFB ,则由圆锥曲线的第二定义得θθcos 1||,cos 1||+=-=p BF pAF ,OCDα由 90=∠QBF 知:θθθ2cos 1cos cos ||-=⇒=pBF , p p BF AF 2cos 1cos 2||||2=-=-θθ.三.解答题:本大题共6小题,共75分。
16.(本小题满分13分)解: (Ⅰ)由余弦定理,2124122cos 222==-+=acbc a B 3π=⇒B …………6分.(Ⅱ)由面积法有,13396132334sin 21sin 21=⨯⨯==⇒==∆bBac h bh B ac S …………13分.17.(本小题满分13分)解:(Ⅰ)A ={}|12x x x ≤->或…………3分B ={}|1x x a x a <>+或…………6分.(Ⅱ)由A B =B 得A ⊆B ,因此112a a >-⎧⎨+≤⎩…………10分所以11a -<≤,所以实数a 的取值范围是]1,1(-…………13分.18.(本小题满分13分)解: (Ⅰ)设它们的夹角为θ,则(cos sin sin cos )cos sin()O A O B m m O A O Bαβαβθαβ⋅-+===-=1sin 62π=, 故3πθ=……6分.≥得22(cos sin )(sin cos )4m m αβαβ++-≥即212sin()4m m βα++-≥对任意的,αβ恒成立…………9分则2214m m m >⎧⎨-+≥⎩或2214m m m <⎧⎨++≥⎩,解得33m m ≤-≥或…………13分.19. (本小题满分12分)解:(Ⅰ)当1a >时,x y a =在R 上单调递增,1()xxy aa-==在R 上单调递减 所以,原函数在R 上单调递增;同理,当01a <<时,原函数在R 上单调递减.…………6分 (Ⅱ)313(1),22f a a=∴-=,即212320,22a a a a --=∴==-或(舍去)222()222(22)(22)2(22)2xxx xx xxxg x m m ----∴=+--=---+………8分 令()22xxt f x -==-22231,(1),()22()22x t f g t t m t t m m ≥∴≥=∴=-+=-+-当32m ≥时,2m in ()()22g t g m m ==-=-,22m m ∴==-或(舍) 当32m <时,m in 317()()3224g t g m ==-=-,253122m ∴=>(舍)综上可知2m =…………12分.20. (本小题满分12分)解:依题意得:)0,1(-Q ,直线l 斜率存在,设其斜率为k ,则l 的方程为)1(+=x k y ,代入抛物线方程有:0)42(2222=+-+kx k x k …………2分(Ⅰ)若0≠k ,令0=∆得,1±=k ,此时l 的方程为1,1--=+=x y x y .若0=k ,方程有唯一解.此时l 的方程为0=y …………4分(Ⅱ)显然0≠k ,记),(),,(2211y x B y x A ,则1,24212221=-=+x x kk x x ,ky y 421=+,4)1(2121221=+++=x x x x k y y …………6分(ⅰ)0)1)(1()1(2112121221121=---=-+-=+x x x x k x y x y k k …………8分(ⅱ)设点R 的坐标为),(y x ,∵||||||||QB AQ RB AR =, ∴02121--=--y y yy y y ,k ky y y y y 244222121=⨯=+=∴11211=-=-=∴y kx …………10分由0>∆得,11<<-k ,又0≠k ,∴)2,0()0,2( -∈y . 综上,点R 的轨迹为,1=x )2,0()0,2( -∈y ……………………12分21. (本小题满分12分)解:(Ⅰ)12sin 3n a n ≤=+≤,故{}n a 为有界数列…………2分 (Ⅱ)设公比为q ,当01q <<时,11(1)11nn a q a S qq-=<--,则正数数列{}n S 满足11n a S q<-,即为有界数列;当1q =时,1n S na =→+∞,故为无界数列;当1q >时,121......n n S a a a na =+++>→+∞,此时为无界数列.综上:当且仅当01q <<时,{}n S 为有界数列…………6分.(Ⅲ){}n a 为无界数列,事实上 11111111 (3)57214682na n n=++++>++++-1111112 (3456)212n a n n∴>++++++-2111112 (3)45622nna ∴>+++++⋅11111111111()()(....)....(....)345678916212222nnnn=++++++++++++++++1111248 (24)816222n nn >⨯+⨯+⨯++⨯=⨯24nn a ∴>故当n 无限增大时n a 也无限增大,所以{}n a 无界…………12分.。
重庆市2010届高三上学期期末测试(数学理)

高2010级(上)期末测试卷数学(理工类)数学试题卷(理工农医类)共4页。
满分150分。
考试时间120分钟。
注意事项:1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2.答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦擦干净后,再选涂其它答案标号。
3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4.所有题目必须在答题卡上作答,在试卷上答题无效。
5.考试结束,将试卷和答题卡一并收回。
参考公式:当事件A 、B 互斥时,那么P(A+B) = P(A)+P(B) 当事件A 、B 互相独立时,那么P(A ·B) = P(A)·P(B)如果事件A 在一次实验中发生的概率是P ,那么n 次独立重复实验中恰好发生K 次的概率k n kk n n p p c k p --=)1()(.一.选择题:本大题10小题,每小题5分,共50分.在每小题给出的四个备选项中,只有一项符合题目要求.1. 设集合A={a ,b },则满足A B={a ,b ,c ,d }的所有集合B 的个数是A.1B.4C.8D.162. 函数lg(1)y x =+的反函数的图像为3. 在等差数列{n a }中, 1328,3a a a ⋅== , 则公差d =DxCABA. 1B. -1C. ±1D. ±24. 直线1l 在x 轴和y 轴上的截距分别为3和1,直线2l 的方程为022=+-y x ,则直线1l 到2l 的角为A .71arctanB .45C .135D .45或1355. 已知3sin tan 2=⋅αα,02<<-απ,则)6cos(πα-的值是A .0B .23C .1D .216. 把函数)(x y 3lg =的图像按向量a 平移,得到函数)1lg(+=x y 的图像,则a为A . )3lg ,1(-B . )3lg ,1(-C .)3lg ,1(--D .)0,31(7. 已知x a x f =)(,x b x g =)(,当3)()(21==x g x f 时,21x x >,则a 与b 的大小关系不可能成立.....的是 A .1>>a bB .01>>>b aC.10<<<b aD .01>>>a b8. 双曲线)1(122>=-n y nx 的两焦点为21,F F ,点P 在双曲线上,且满足:2221+=+n PF PF ,则21F PF ∆的面积是A .1B .21C .2D .49. 称||),(d -=为两个向量、间的“距离”.若向量、满足: ① 1||=; ② ≠;③ 对任意的R t ∈,恒有),(),(d t d ≥则 A. ⊥B. )(-⊥C. )(-⊥D.)()(-⊥+10. 关于x 的方程0)1(122=++++b x x a xx 有实数根,则22b a +的最小值是 A.52B. 1C. 54D. 52二.填空题:(本大题共5小题,共25分,把答案填写在答题卡相应位置上) 11. 抛物线022=+y x 的焦点坐标是_____________. 12. 不等式2|log 1|2>+x 的解集是_____________.13.已知正数x 、y 满足⎩⎨⎧≥+-≤-05302y x y x ,则yx z )21()41(⋅=的最小值为_____________.14. 已知数列}{n a 满足11,211221++-==-n na n n a a n n ,则数列}{n a 的通项=n a _____________.15. 如图,一条螺旋线是用以下方法画成:ΔABC 是边长为1的正三角形,曲线11223,,CA A A A A 分别以A 、B 、C 为圆心,AC 、1BA 、2CA 为半径画的弧,曲线123CA A A 称为螺旋线旋转一圈.然后又以A 为圆心3AA 为半径画弧,这样画到第n 圈,则所得螺旋线的长度n l =_____________.(用π表示即可)三. 解答题:(本大题共6小题,共75分)(各题解答必须写出必要的文字说明、演算步骤和推理过程). 16. (本小题满分13分)已知向量)3,5(),3,6(),4,3(m m ---=-=-=. (Ⅰ)若C B A ,,三点共线,求实数m 的值; (Ⅱ)若ABC ∠为锐角,求实数m 的取值范围.A 3A 2A 1CA B17. (本小题满分13分)已知函数x x b x a x f cos sin cos 2)(2+=)0,0>>b a (,)(x f 的最大值为a +1,最小值为21-. (Ⅰ)求)(x f 的最小正周期; (Ⅱ)求)(x f 的单调递增区间.18. (本小题满分13分)已知数列}{n a 中,11=a ,113--⋅=n n n a a ),2(*N n n ∈≥.数列}{n b 的前n 项和)9(log 3n nn a S =)(*N n ∈. (Ⅰ)求数列}{n b 的通项公式; (Ⅱ)求数列|}{|n b 的前n 项和. 19. (本小题满分12分)已知22()log a xf x x a--=-是奇函数.(Ⅰ) 求a 的值;(Ⅱ) 若关于x 的方程1()2x f x m --=⋅有实解,求m 的取值范围.20. (本小题满分12分)已知点()1,1A 是椭圆()012222>>=+b a by a x 上一点,21,F F 是椭圆的两焦点,且满足421=+AF AF .(Ⅰ)求椭圆的两焦点坐标;(Ⅱ)设点B 是椭圆上任意一点,如果AB 最大时,求证A 、B 两点关于原点O 不对称;(Ⅲ)设点C 、D 是椭圆上两点,直线AC 、AD 的倾斜角互补,试判断直线CD 的斜率是否为定值?若是定值,求出定值;若不是定值,说明理由.21. (本小题满分12分)已知曲线C :xy =1,过C 上一点),(n n n y x A 作一斜率为21+-=n n x k 的直线交曲线C 于另一点),(111+++n n n y x A ,点列),3,2,1( =n A n 的横坐标构成数列{n x },其中7111=x . (Ⅰ)求证:{3121+-n x }是等比数列;(Ⅱ)求证:)1,(1)1()1()1()1(33221≥∈<-++-+-+-n N n x x x x n n .高2010级(上)期末测试卷 数学(理工类)(参考答案)一.选择题:本大题10小题,每小题5分,共50分. 1~5 BDCBA 6~10 CDACC 10. 令t xx =+1,则原方程化为022=-++b at t ,其中2||≥t ,此方程有根有以下情形对于图)(),(),(c b a ,易知0)2(≤-f 和0)2(≤f 中至少有一个成立 即有022≤++-b a 或022≤++b a由线性规划知识可知,),(b a 满足的平面区域如图阴影部分所示且点O 到直线的距离为5252002=++⨯Oxyxyxxxx)(a )(b )(c )(d )(e故此时5422≥+b a ,其中当52,54-=±=b a 时取等号 对于图)(),(e d ,显然有4≥a ,此时1622≥+b a ,故有22b a +的最小值为54. 二.填空题:本大题共5小题,共25分.11. )81,0(- 12. ),2()81,0(+∞ 13.116 14. 12+n n 15.π)3(2n n +三. 解答题:本大题共6小题,共75分. 16.(13分)解:(1)已知向量))3(,5(),3,6(),4,3(m m OC OB OA +--=-=-=),1,2(),1,3(m m AC AB --== 由三点共线知m m -=-2)1(3∴实数21=m 时,满足的条件…………6分(2)由题设知),1(),1,3(m m BC BA ---=--=ABC ∠ 为锐角,43033->⇒>++=⋅∴m m m …………12分又由(1)可知,当21=m 时, 0=∠ABC ,故),21()21,43(∞+-∈ m …………13分17.(13分)解:(1)a x b a x b x a x f +++=++=)2sin(42sin 2)2cos 1()(22ϕ,由题设知214,142222-=+-=+b a a b a ,所以21=a ,3=b (4)分所以21)62sin(212cos 212sin 23)(++=++=πx x x x f , 所以)(x f 的最小正周期为π…………7分 (2)由63226222πππππππππ+≤≤-⇒+≤+≤-k x k k x k ,所以)(x f 单调增区间为]6,3[ππππ+-k k )(Z k ∈…………13分18.(13分)解:(1)11333log log --⋅=n n n a a ,)1(log log 133-+=-n a a n n)1(21log log 133-+++=-n a a n 2)1(-=n n ,n a 3log 2)1(-=n n , )9(log 3n n n a S =252nn -=)(*N n ∈…………4分211-==S b ,当2≥n 时,31-=-=-n S S b n n n ,∴数列}{n b 的通项公式3-=n b n )(*N n ∈.…………7分(2)设数列|}{|n b 的前n 项和为n T ,当03≤-=n b n 即3≤n 时,n n S T -=252n n -=; 当3>n 时,32S S T n n -=21252+-=n n .…………13分19(12分)解: (Ⅰ)由20a xx a-->-得:2a x a -<<…………2分()f x 为奇函数,2 1.a a a ∴-=-⇒=经验证可知:1=a 时,)(x f 是奇函数,1=a 为所求…………5分(Ⅱ)12121()log ,().121x x x f x f x x -+-=∴=-+ …………8分 法一:由1()2x f x m --=⋅得:22(2)2(21)3(21)22121x x x x x xm -+-++==++ 2(21)3 3.21xx =++-≥+当且仅当2log 1)x =时,min 3m =所以m 的取值范围是3,)+∞…………12分 法二:原方程即2(2)(1)20x xm m -+-=设2xt =,则2(1)0t m t m -+-=原方程有实解,等价于方程2(1)0t m t m -+-=有正实解…………6分令2()(1)g t t m t m =-+-则(0)0g <或(0)0102g m =⎧⎪⎨+>⎪⎩或⎪⎪⎩⎪⎪⎨⎧>+≥++=∆>02104)1(0)0(2m m m g …………10分 0m ⇒>或0m =或30m ≤<所以m的取值范围是3,)+∞…………12分20.(12分) 解:(I )由椭圆定义知:42=a ∴2=a ∴14222=+b y x 把()1,1代入得11412=+b∴ 342=b 则椭圆方程为134422=+y x ∴ 38344222=-=-=b a c ∴ 362=c 故两焦点坐标为)0,362(),0,362(-.…………3分 (II ) 用反证法 : 假设A 、B 两点关于原点O 对称,则B 点坐标为()1,1-- ,此时22=AB 取椭圆上一点()0,2-M ,则10=AM ∴AB AM >.从而此时AB 不是最大,这与AB 最大矛盾,所以命题成立.…………7分(III )设AC 方程为:()11+-=x k y 联立⎪⎩⎪⎨⎧=++-=14341)1(22y x x k y 消去y 得()()01631631222=--+--+k k x k k xk ∵点()1,1A 在椭圆上∴1316322+--=k k k x C …………9分∵ 直线AC 、AD 倾斜角互补 ∴ AD 的方程为()11+--=x k y同理 1316322+-+=k k k x D …………10分又()()11,11+--=+-=D D C C x k y x k y()k x x k y y D C D C 2-+=-所以31=--=D C D C CD x x y y k 即直线CD 的斜率为定值31.…………12分21.(12分)过C :xy 1=上一点),(n n n y x A 作斜率为n k 的直线交C 于另一点1+n A , 则2111111111+-=⋅-=--=--=+++++n n n n n n n n n n n n x x x x x x x x x y y k , 于是有:21+=+n n n x x x . …………2分记3121+-=n n x a ,则n n nn n n a x x x x a 2)3121(231221312111-=+--=+-+=+-=++,因为023121,711111≠-=+-==x a x 而, 因此数列{3121+-n x }是等比数列. ………… 6分(3)由(2)可知:31)2(12,)2(--+=-=n n nn x a 则,31)1(212)1()1(⋅--+⋅-=-n n n n n x .当n 为偶数时有:- 11 - =-+---n n n n x x )1()1(11 =n n n n n n n n n n n n 21212222)312)(312(2231213121111111+<⋅+<-++=-++------, 于是①在n 为偶数时有:12121212121)1()1()1(432221<+++++<-++-+-n n n x x x .…………10分 ②在n 为奇数时,前n -1项为偶数项,于是有: n n n n x x x x )1()1()1()1(11221-+-++-+--- 131211)31)2(12(11)1(1<++-=--+-=-=-+<n n n n n x x .…………12分综合①②可知原不等式得证.。
最新高三数学题库 2010学高三年级第一次练习数学试卷理参考答案

嘉定区2010学年高三年级第一次质量调研 数学试卷(理)参考答案与评分标准一.填空题(本大题满分56分)本大题共有14题,考生必须在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分. 1.答案:1.因i a a ai i )1(1)1)(1(-++=-+是实数,所以=a 1. 2.答案:]2,0[.由022≥-x x ,得022≤-x x ,所以]2,0[∈x . 3.答案:1.112+=a a ,314+=a a ,由已知得4122a a a =,即)3()1(1121+=+a a a ,解得11=a . 4.答案:257-.由532sin =⎪⎭⎫ ⎝⎛+θπ,得53cos =θ,所以2571cos 22cos 2-=-=θθ.5.答案:2-.解法一:函数x x f -=)(的反函数为21)(x x f =-(0≤x ),由4)(1=-x f 得42=x ,因为0<x ,故2-=x .解法二:由4)(1=-x f ,得2)4(-==f x .6.答案:105arccos. 因为AB ∥11B A ,故1BAC ∠就是异面直线1AC 与11B A 所成的角,连结1BC ,在1ABC 中,1=AB ,511==BC AC ,所以10552121cos 11===∠AC ABBAC .7.答案:0.因)(x f 是定义在R 上的奇函数,所以0)0(=f ,在等式)()2(x f x f -=+中令2-=x ,得0)2(=-f . 8.答案:2.9)21(x -展开式的第3项为288)2(2293=-=x C T ,解得23=x ,所以232132132lim 323232lim 111lim 22=-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+++∞→∞→∞→nn nn n n x x x .9.答案:1.三阶行列式xa x 1214532+中元素3的余子式为xa x x f 21)(+=,由0)(<x f 得022<-+ax x ,由题意得a b -=+-1,所以1=+b a .10.答案:16.1=a ,满足3≤a ,于是4211==+b ;2=a ,满足3≤a ,8212==+b ;3=a ,满足3≤a ,则16213==+b ;4=a ,不满足3≤a ,则输出b ,16=b .11.答案:21.满足条件的选法可分为三类:A 组2人,B 、C 组各1人,有121325C C C 种选法;B 组2人,A 、C 组各1人,有122315C C C 种选法;C 组2人,A 、B 组各1人,有221315C C C 种选法.所以A 、B 、C 三组的学生都有的概率21210105410221315122315121325==++=C C C C C C C C C C P . 12.答案:65π.由题意,612cos 2>θ且212sin 2>θ,⎩⎨⎧==+22cos 34ab b a θ,⎪⎪⎩⎪⎪⎨⎧=⋅-=+21112sin 211a b a b θ,所以θθ2sin 22cos 32-=,32tan -=θ,因)2,(2ππθ∈,故352πθ=,65πθ=.13.答案:①③④.由y x y f x f ⋅=⋅)()(,得y x a y a y a x a x⋅=⋅⋅-⋅⋅⋅-])(2[])(2[,化简得)()()()(2y a x a a y a x a ⋅⋅⋅=⋅⋅⋅⋅,当0 =a 时,等式成立;当0 ≠a 时,有12=a ,即1||=a,所以①、③、④都能使等式成立. 14.答案:4.11+<<t a t ,则t t a a <<-=112,t t a t a t a >+>-+=-+=1222123,t a t t a a <-+=-=1342,1452a a t a =-+=.所以}{n a 是以4为周期的周期数列.(第14题也可取满足条件的t 和1a 的特殊值求解)二.选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案,考生必须在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分. 15.C .16.A .17.D .16.B .15.由5:4:3::=c b a 可得a ,b ,c 成等差数列;若a ,b ,c 成等差数列,则c a b +=2,由勾股定理,222c b a =+,得2222c c a a =⎪⎭⎫ ⎝⎛++,032522=-+c ac a ,解得53=c a ,令k a 3=(0>k ),则k c 5=,得k b 4=.所以5:4:3::=c b a .16.①错.不在同一直线上的三点才能确定一个平面;②错.若圆锥的侧面展开图是一个圆面,则可得圆锥底面半径的长等于圆锥母线的长;③错.如果三棱锥的底面是等边三角形,一条侧棱垂直于底面且长度等于底面边长,则三个侧面都是等腰三角形;④错.若这两点是球的直径的两个端点,过这两点可作无数个大圆.17.作出函数xy 2=与2x y =,可发现两函数图像在第二象限有一个交点,在第一象限有两个交点(第一象限的两个交点是)4,2(和)16,4().18.若取1x 、2x 为区间]4,2[的两个`端点,则8)()(21=x f x f .若8>C ,取21=x ,4)(1=x f ,对任意]4,2[2∈x ,16)(2≤x f ,于是8)(4)()(221≤=x f x f x f ;若8<C ,取41=x ,16)(1=x f ,对任意]4,2[2∈x ,4)(2≥x f ,于是8)(16)()(221≥=x f x f x f .所以8=C .三.解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤. 19.(本题满分12分) 解:设半圆的半径为r ,在△ABC 中,090=∠ACB ,030=∠ABC ,3=BC , 连结OM ,则AB OM ⊥,……(2分) 设r OM =,则r OB 2=,…………(4分) 因为OB OC BC +=,所以r BC 3=,即33=r .………………(6分)130tan 0=⋅=BC AC .阴影部分绕直线BC 旋转一周所得旋转体为底面半径1=AC ,高3=BC 的圆锥中间挖掉一个半径33=r 的球.………………(8分) 所以,圆锥V V =球V -πππ27353334313132=⎪⎪⎭⎫ ⎝⎛⋅⋅-⋅⋅⋅=.…………(12分)20.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.解:(1)若1=ω,则⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-=6cos ,1πx a ,⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-=6sin 2,2πx b ,由a ∥b 的充要条件知,存在非零实数λ,使得a b ⋅=λ,即⎪⎩⎪⎨⎧⎪⎭⎫ ⎝⎛-⋅=⎪⎭⎫ ⎝⎛-=6cos 6sin 22πλπλx x , 所以⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-6cos 6sin ππx x ,16tan =⎪⎭⎫ ⎝⎛-πx ,…………(3分)(以下有两种解法:)解法一:46πππ+=-k x ,Z k ∈,125ππ+=k x ,Z k ∈,32333333133164tan 125tan 125tan tan +=-+=-+=⎪⎭⎫ ⎝⎛+==⎪⎭⎫ ⎝⎛+=πππππk x .…(6分) 解法二:323313316tan 6tan 16tan 6tan 66tan tan +=-+=⎪⎭⎫ ⎝⎛--+⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-=ππππππx x x x . 所以321313tan +=-+=x .…………(6分)(2)⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-+=6cos 6sin 226cos 6sin 22)(πωπωπωπωx x x x x f⎪⎭⎫⎝⎛-=32sin πωx ,…………(8分) 因为)(x f 的最小正周期为π,所以πωπ=22,1=ω,所以⎪⎭⎫ ⎝⎛-=32sin )(πx x f ,…………(10分)当⎥⎦⎤⎢⎣⎡∈2,0πx 时,⎥⎦⎤⎢⎣⎡-∈-32,332πππx ,…………(12分) 所以函数)(x f 的值域为⎥⎦⎤⎢⎣⎡-1,23.…………(14分)21.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分. 解:(1)由已知,当0=x 时,8)(=x C ,即85=k,所以40=k ,……(1分) 所以5340)(+=x x C ,…………(2分)又加装隔热层的费用为x x C 6)(1=.所以5380066534020)()(20)(1++=++⨯=+⋅=x x x x x C x C x f ,…………(5分) )(x f 定义域为]10,0[.…………(6分)(2)10380062103538003563538006538006)(-⨯≥-⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛++=++=x x x x x x x f70=,…………(10分)当且仅当⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+353800356x x ,18800352=⎪⎭⎫ ⎝⎛+x ,32035=+x ,即5=x 时取等号.…………(13分) 所以当隔热层加装厚度为5厘米时,总费用)(x f 最小.最小总费用为70万元.…(14分)22.(本题满分16分)本题共有3个小题,第1小题满分3分,第2小题满分7分,第3小题满分6分.解:(1)1=m 时,1)(2+=x x f ,因为01=a ,所以1)0()(12===f a f a ,2)(23==a f a ,5)(34==a f a .…………(3分,每求对一项得1分)(2)m x x f +=2)(,则m a =2,m m a +=23,m m m m m m m a +++=++=2342242)(,…………(5分) 如果2a ,3a ,4a 成等比数列,则)2()(23422m m m m m m m +++=+,234523422m m m m m m m +++=++,0345=-+m m m ,…………(6分)因为02≠=m a ,所以012=-+m m ,251+-=m 或251--=m .……(8分)当251+-=m 时,数列的公比2511223+=+=+==m m m m a a q .……(9分) 当251--=m ,251-=q .…………(10分) (3)1)(2-=x x f ,),0[+∞∈x ,所以1)(1+=-x x f (1-≥x ),……(11分)11=b ,121+=+n n b b ,所以1221+=+n n b b ,而121=b ,所以{}2n b 是以1为首项,1为公比的等比数列,n b n =2,…………(13分)所以2)1(21+=+++=n n n S n ,…………(14分) 由2010>n S ,即20102)1(>+n n ,解得63≥n ,所以所求的最小正整数n 的值是63.…………(16分) 23.(本题满分18分)本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分7分. 23.解:(1)设点),(y x P 是函数)(x f 图像上任意一点,P 关于点A 对称的点为),(y x P ''',则12='+x x ,22='+y y ,于是x x -='2,y y -='4,…………(2分) 因为),(y x P '''在函数)(x g 的图像上,所以2|2|24-'-'⋅--='x x a ay ,……(3分) 即x x a a y --⋅--=-244||,x x a a y -⋅+=2||,所以x x a a x f -⋅+=2)(||(或xx a a x f 2)(||+=).………………(5分)(2)令t a x=,因为1>a ,0>x ,所以1>t ,所以方程m x f =)(可化为m tt =+2, 即关于t 的方程022=+-mt t 有大于1的相异两实数解.…………(8分)作2)(2+-=mt t t h ,则⎪⎪⎩⎪⎪⎨⎧>->>08120)1(2m m h ,…………(11分)解得322<<m .所以m 的取值范围是)3,22(.…………(12分) (3)x x a ax g 2)(||+=,),2[∞+-∈x .当0≥x 时,因为1>a ,所以1≥xa ,),3[3)(∞+∈=xa x g ,所以函数)(x g 不存在最大值.…………(13分)当02<≤-x 时,x xa a x g 12)(+=,令xt 2=,则t t t h x g 12)()(+==,⎪⎭⎫⎢⎣⎡∈1,12a t , 当2212>a ,即421<<a 时,)(t h 在⎪⎭⎫⎢⎣⎡1,12a 上是增函数,存在最小值222a a +,与a 有关,不符合题意.…………(15分)当22102≤<a ,即42≥a 时,)(t h 在⎥⎦⎤⎢⎣⎡22,12a 上是减函数,在⎪⎪⎭⎫⎢⎣⎡1,22上是增函数,当22=t 即2log 21a x -=时,)(t h 取最小值22,与a 无关.…………(17分)综上所述,a 的取值范围是),2[4∞+.…………(18分)。
重庆一中2010届高三上学期第四次月考(数学理)

秘密★启用前重庆一中高2010级高三上期第四次月考数学试题卷(理科)2009.12数学试题共3页。
满分150分。
考试时间120分钟。
注意事项:1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2.答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案标号。
3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4.所有题目必须在答题卡上作答,在试题卷上答题无效。
一.选择题.(每小题5分,共50分)1.已知集合,集合,则=( )A. B. C. D.2.若,且,则锐角=( )A. B. C. D.3.下列命题中正确的是( )A.若实数满,则B.若实数满足,则C.若,则D.若,则4.等差数列满足:,则=( )A. B.0 C.1 D.25.已知,则“”是“”的( )条件.A. 充要B. 既不充分也不必要C. 必要不充分D. 充分不必要6.△ABC中, ,则∠C=( )A. B. C.或 D.或7.已知,与的夹角为,如下图所示,若, ,且为的中点,则=( )A. B.C. D.8.已知.且当时, ,则的解集是( )A. B. C. D.9.定义域为R的函数对任意都有,且其导函数满足,则当时,有( )A. B.C. D.10.若实数满足,则的最大值是( )A. B. C. D.二.填空题.(每小题5分,共25分)11.若,则= .12.分有向线段所成的比为,则分有向线段所成的比为.13.手表的表面在一平面上,整点1,2,…,12这12个数字等间隔地分布在半径为的圆周上,从整点到整点的向量记作,则=.14.设函数,且,则.15.设的内角满足成等比数列,则的取值范围是.三.解答题.(共75分)16. (13分)已知向量(其中).设,且的最小正周期为.(1)求;(2)若,求的值域.17. (13分)△ABC中,分别是角A,B,C的对边,且.(1)求;(2)若,且,求△ABC的面积.18. (13分)已知数列的前项和为,且.(1) 求证:为等差数列;(2)求;(3)若, 求19. (12分)已知,满足.且在R上恒成立.(1)求;(2)若,解关于的不等式:.20. (12分)设.(1)若,与在同一个值时都取极值,求;(2)对于给定的负数,当时有一个最大的正数,使得时,恒有.(i)求的表达式;(ii)求的最大值及相应的的值.21. (12分)已知数列满足,其中,函数.(1)若数列满足, ,求;(2)若数列满足.数列满足,求证:.重庆一中高2010级高三上期第四次月考答案数学试题卷(理科)2009.12二.填空题.(每题5分,共25分)11.;12.1 ;13. ;14.;15.三.解答题.(共75分)16.解:(1)∵∴∴(2)由(1)得: ∵∴∴∴的值域为17.解:(1)由正弦定理及有:即∴又∴∴又∴又∴(2)在△ABC中,由余弦定理可得:,又∴∴∴18.解:(1)当时,由已知有易知故∴为首项为2,公差为2的等差数列. (2)易知,当时, ∴(3)易知,时.∴19.解:(1) ∴∴由有,∵在R上恒成立, 即:恒成立显然时不满足条件,∴即∴∴(2) ∴即,即,∴当时,即时,解集为;当时,即时,解集为;当时,即时,解集为.20.解: (1)易知在时取得极值.由得由题意得:. 故.经检验时满足题意.(2) (i)因. ∴.情形一:当,即时,此时不满足条件。
重庆市高2010级高三上期一诊考试题(数学理)
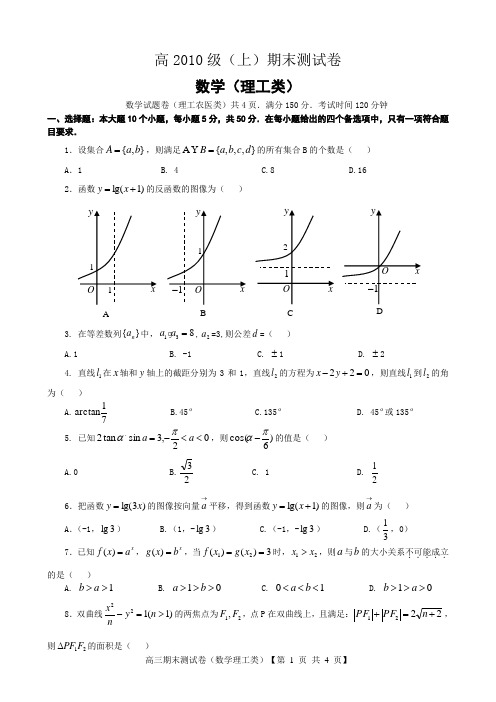
高2010级(上)期末测试卷数学(理工类)数学试题卷(理工农医类)共4页.满分150分.考试时间120分钟一、选择题:本大题10个小题,每小题5分,共50分.在每小题给出的四个备选项中,只有一项符合题目要求.1.设集合},{b a A =,则满足},,,{A d c b a B = 的所有集合B 的个数是( ) A . 1 B. 4 C.8 D.162.函数)1lg(+=x y 的反函数的图像为( )3. 在等差数列}{n a 中,138a a =,2a =3,则公差d =( )A.1B. -1C. ±1D. ±24. 直线1l 在x 轴和y 轴上的截距分别为3和1,直线2l 的方程为022=+-y x ,则直线1l 到2l 的角为( )A.71arctanB.45C.135D. 45 或135 5. 已知αtan 2.02,3sin <<-=a a π,则)6cos(πα-的值是( ) A.0 B.23C. 1D. 216.把函数)3lg(x y =的图像按向量→a 平移,得到函数)1lg(+=x y 的图像,则→a 为( ) A .(-1,3lg ) B.(1,-3lg ) C.(-1,-3lg ) D.(31,0) 7.已知xa x f =)(,xb x g =)(,当3)()(21==x g x f 时,21x x >,则a 与b 的大小关系不可能成立.....的是( )A. 1>>a bB. 01>>>b aC. 10<<<b a D. 01>>>a b8.双曲线)1(122>=-n y nx 的两焦点为21,F F ,点P 在双曲线上,且满足:2221+=+n F P F P ,ABCDA .1B .21C .2D .4 9.称→→→→-=b a b a d ),(为两个向量→a 、→b 间的“距离”.若向量→a 、→b 满足:①1=→b ;②→→≠b a ;③对任意的R t ∈,恒有),(),(→→→→≥b a d b t a d 则( )A .→→⊥b a B.)(→→→-⊥b a a C. )(→→→-⊥b a b D. )()(→→→→-⊥+b a b a10.关于x 的方程0)1(122=++++b xx a x x 有实数根,则22b a +的最小值是( ) A .52B .1C .54D .52二、填空题:(本大题共5个小题,共25分,把答案填写在答题卡相应位置上)11.抛物线022=+y x 的焦点坐标是________ ____. 12.不等式2log 12>+x 的解集是____ ________.13.已知正数x 、y 满足⎩⎨⎧≥+-≤-05302y x y x ,则x z )41(=.y)21(的最小值为__________.14.已知数列}{n a 满足,11,211221++-==-n na n n a a n n 则数列}{n a 的通项n a =__________ . 15 如图,一条螺旋线是用以下办法画成:ABC ∆是边长为1的正三角形,曲线32211,,A A A A CA 分别以A 、B 、C 为圆心,AC 、1BA 、2CA 为半径画弧,曲线321A A CA 称为螺旋线旋转一圈.然后又以A 为圆心3AA 为半径画弧,这样画到第n 圈,所得的螺旋线的长度n l =_____ _____.(用π表示即可)三、解答题:(本大题共6个小题,共75分)(各题解答必须写出必要的文字说明、演算步骤和推理过程).16.(本小题满分13分)已知向量)4,3(-=−→−OA ,)3,6(-=−→−OB ,)3,5(m m OC ---=−→−.(Ⅰ)若C B A ,,三点共线,求实数m 的值; (Ⅱ)若ABC ∠为锐角,求实数m 的取值范围.已知函数)0,0(cos sin cos 2)(2>>+=b a x x b x a x f ,)(x f 的最大值为a +1,最小值为21-. (Ⅰ)求)(x f 的最小正周期;(Ⅱ)求)(x f 的单调递增区间.18.(本小题满分13分) 已知数列}{n a 中,11=a ,113--⋅=n n n a a ).,2(*N n n ∈≥数列}{nb 的前n 项和))(9(log *3N n a S n n n ∈=. (Ⅰ)求数列}{n b 的通项公式;(Ⅱ)求数列{}n b 的前n 项和.19.(本小题满分12分) 已知ax xa x f ---=2log )(2是奇函数.(Ⅰ)求a 的值;(Ⅱ)若关于x 的方程x m x f --⋅=2)(1有实解,求m 的取值范围.已知点)1,1(A 是椭圆)0(12222>>=+b a b y a x 上一点,21,F F 是椭圆的两焦点,且满足421=+AF AF .(Ⅰ)求椭圆的两焦点坐标;(Ⅱ)设点B 是椭圆上任意一点,如果AB 最大时,求证A 、B 两点关于原点O 不对称; (Ⅲ)设点C 、D 是椭圆上两点,直线AC 、AD 的倾斜角互补,试判断直线CD 的斜率是否为定值?若是定值,求出定值;若不是定值,说明理由.21.(本小题满分12分)已知曲线C :1xy =过C 上一点(n n A x ,)n y 作一斜率21+-=n n x k 的直线交曲线C 于另一点11(n n A x ++,1)n y +,点列*()n A n N ∈的横坐标构成数列}{n x ,其中7111=x . (Ⅰ)求证:}3121{+-n x 是等比数列; (Ⅱ)求证:23123(1)(1)(1)x x x -+-+-+…*(1)1()n n x n N +-<∈.。
重庆一中2010届高三上学期第一次月考(数学理)

绝密★启用前重庆一中高2010级高三上期第一次月考数学试题(理科)2009.9数学试题共 4页。
满分150分。
考试时间120分钟。
注意事项:1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2.答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案标号。
3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4.所有题目必须在答题卡上作答,在试题卷上答题无效。
一、选择题(每小题只有一个正确答案。
每题5分,共50分)1.函数的定义域为()A.B.C.D.2.若集合,则()A.B.C.D.3.下列函数中,满足对任意,(0,),当<时,都有>的是()A.= B. = C . = D.4.若条件,条件,则是的()条件A.充分不必要B.必要不充分C.充要D.既不充分也不必要5.已知函数,当时,则的值为()A.B.C.D.26.设是函数的反函数,则的解集为()A.B.C.D.7.若关于的方程有实数解,则实数的范围是()A.B.C.D.8.已知偶函数在区间单调递增,则满足<的取值范围是()A.(,)B. [,)C.(,)D. [,)9.函数的最小值...为()A.0 B. 2 C. D.10.二次函数方程有两个小于1的不等正根,则a的最小值为()A. 2 B. 3 C. 4 D. 5二、填空题(每小题5分,共25分)11.已知函数若,则;12.已知函数的定义域为,则函数的定义域为;13.命题“两组对边都相等的四边形是平行四边形”的否命题为;14.函数在区间上有单调性,则实数的范围是;15.给出以下命题:①若为奇函数,则;②若函数对任意的均有,则函数的图像关于直线对称;③设定义在上的函数的反函数为,且对于任意的,都有,则=0;④函数为R上的奇函数,对均有成立,则是以4为周期的周期函数。
其中正确命题的序号是。
三、解答题(共75分)16.(13分)记集合A=,的定义域为集合B.⑴求B .⑵若,求实数的范围。
2010一诊理科数学参考答桉

2010兰州高三诊断试题数学(理科)参考答案一、选择题(本题共12小题,每小题5分,共60分。
)12. 解析:当0m <且1m≠-时,曲线为椭圆,则不经过区域M ;当1m =-时,曲线为以原点为圆心,1为半径的圆,不经过区域M 当0m =时,1x =±,不经过区域M当0m >时,曲线为焦点在x总经过区域M ,则有441m -=解得34m =故离心率2173e =和161m -=解得15m = 故离心率221615e =根据双曲线的性质可得: 22221e e e ≤≤ 即有16171153m ≤+≤ 所以3154m ≤≤二、填空题(本大题共4小题,每小题5分,共20分。
) 13.8 14.33 15.312R 16.5a .解析:依题意知曲线PQ 是以A 、B 为焦点、实轴长为2的双曲线的一支,此双曲线的离心率为2,以直线AB 为x 轴、AB 的中点为原点建立平面直角坐标系,则该双曲线的方程为2213y x -=,点C 的坐标为(3,).则修建这条公路的总费用||2||W a MB a MC =+=12(||||)2a MB MC +,设点M 、C 在双曲线右准线上射影分别为点1M 、1C ,根据双曲线的定义有11||||2M M M B =,所以11112(||||)2(|||)2||2(3)522W a MB MC a MM MC a CC a a =+=+≥=⨯-=当且仅当点M 为曲线PQ 与线段1CC 的交点时取等号,故W 的最小值是5a . 三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.) 17.解:(Ⅰ) 由p ∥q得1cos2A A -=,所以22sin A A又A为锐角∴sin A =,1cos 2A = …………3分而222a cb mbc -=-可以变形为22222b c a mbc +-= 即1cos 22m A ==,所以1m = ……………5分(Ⅱ)由(Ⅰ)知 1cos 2A =,sin A = 又222122b c a bc +-= 所以22222bc b c a bc a =+-≥-即2bc a ≤故211sin 22ABC S bc A a ∆=≤=当且仅当b c ==ABC ∆……………10分 18.解:(Ⅰ)依题意,0≠n a ,故可将110(2)n n n n a a a a n --+-=≥整理得:1111(2)n n n a a --=≥ ………3分 所以111(1)nn n a =+⨯-= 即1n a n = …………………5分1n =,上式也成立,所以1n a n= …………………6分 (Ⅱ)∵1n n n b a a += ∴ 111111(1)1n b n n n n n n =⨯==-+++ …………………9分∴12311111111()()()()1223341n n S b b b b n n =++++=-+-+-++-+ 1111n n n =-=++ …………………10分 ∴lim lim11n n n n S n→∞→∞=+= …………………12分 19. 解:(Ⅰ)∵各棵树成活与否是相互独立的,每棵树成活的概率均为p∴333620(1)64C p p -= …………2分解得12p =…………4分 (Ⅱ)记“需要补种”为事件A ,则包括有1A :3颗未成活、2A :有4颗未成活、3A :有5颗未成活、4A :有6颗未成活共四种情况 …………5分333161120()()()2264==P A C ,442261115()()()2264==P A C 55136116()()()2264==P A C ,66046111()()()2264==P A C …………7分 ∴20156121()6432+++==P A …………8分(Ⅲ)由题意知,ξ服从二项分布1(6,)2B …………10分∴3E np ξ== …………12分 或ξ的分布列为∴16152015610123456364646464646464E ξ=⨯+⨯+⨯+⨯+⨯+⨯+⨯= 20.解法一:依题意有AD ∥BC ,所以4MAD π∠=所以点M 是SD 的中点,且AM SD ⊥ …………3分 (Ⅰ)证明:连结BD 交AC 于E ,连结ME …………4分ABCD 是正方形,∴ E 是BD 的中点 M 是SD 的中点,∴ME 是DSB ∆的中位线∴//ME SB …………5分 又∵ME ⊂平面ACM , SB ⊄平面ACM ,∴SB //平面ACM . …………6分 (Ⅱ)由题可得,CD ⊥平面SAD ,所以有CD AM ⊥,又⊥SD AM∴AM ⊥平面SCD ,∴ACM ∠为直线AC 与平面SDC 所成的角 …………8分 在Rt AMC ∆中,12AM SD AD ==,AC = ∴6ACM π∠=,即直线AC 于平面SDC 所成的角为6π…………9分 (Ⅲ)∵AM ⊥平面SCD ∴NMC ∠为二面角N AM C --的一个平面角 …10分且AM SC ⊥,又⊥AN SC∴SC ⊥平面AMN ∴SC MN ⊥. 在Rt MNC ∆中2==CM AD , ∆ Rt SNM ∽∆Rt SDC∴6AD ADCD SMMN AD SC⋅===∴1cos 3ADMN NMC CM ∠=== ∴二面角N AM C --的大小为1arccos3…………12分 解法二:依题意有AD ∥BC ,所以4MAD π∠=所以点M 是SD 的中点,且AM SD ⊥如图,以A 为坐标原点,建立空间直角坐标系O xyz -,由S A A B =故设1AB AD AS === 则(0,0,0),(0,1,0),(1,1,0),A B C 11(1,0,0),(0,0,1),(,0,)22D S M …………3分(Ⅰ)连结BD 交AC 于E ,则11(,,0)22E ∵11(0,1,1),(0,,)22SB ME =-=-∴12ME SB = ∴SB ∥ME∴//SB 平面ACM …………6分(Ⅱ)由题可得,CD ⊥平面SAD ,所以有CD AM ⊥又⊥SD AM∴AM ⊥平面SCD∴AM为平面SCD 的一个法向量∴1cos ,2||||AM AC AM AC AM AC ⋅<>==⋅∴,3AM AC π<>=∴直线AC 于平面SDC 所成的角为236πππ-= …………9分(Ⅲ)∵AM ⊥平面SCD ∴AM SC ⊥,又AN SC ⊥∴SC ⊥平面AMN ∴(1,1,1)SC =-为平面AMN 的一个法向量。
2010学年高三年级第一次练习数学试卷理参考答案(打印版)

嘉定区2010学年高三年级第一次质量调研数学试卷(理)参考答案与评分标准一.填空题(本大题满分56分)本大题共有14题,考生必须在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分. 1.答案:1.因i a a ai i )1(1)1)(1(-++=-+是实数,所以=a 1. 2.答案:]2,0[.由022≥-x x ,得022≤-x x ,所以]2,0[∈x . 3.答案:1.112+=a a ,314+=a a ,由已知得4122a a a =,即)3()1(1121+=+a a a ,解得11=a . 4.答案:257-.由532sin =⎪⎭⎫ ⎝⎛+θπ,得53cos =θ,所以2571cos 22cos 2-=-=θθ.5.答案:2-.解法一:函数x x f -=)(的反函数为21)(x x f =-(0≤x ),由4)(1=-x f 得42=x ,因为0<x ,故2-=x .解法二:由4)(1=-x f ,得2)4(-==f x .6.答案:105arccos. 因为AB ∥11B A ,故1BAC ∠就是异面直线1AC 与11B A 所成的角,连结1BC ,在1ABC 中,1=AB ,511==BC AC ,所以10552121cos 11===∠AC ABBAC . 7.答案:0.因)(x f 是定义在R 上的奇函数,所以0)0(=f ,在等式)()2(x f x f -=+中令2-=x ,得0)2(=-f . 8.答案:2.9)21(x -展开式的第3项为288)2(2293=-=x C T ,解得23=x ,所以232132132lim 323232lim 111lim 22=-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+++∞→∞→∞→nn nn n n x x x .9.答案:1.三阶行列式xa x 1214532+中元素3的余子式为xa x x f 21)(+=,由0)(<x f 得022<-+ax x ,由题意得a b -=+-1,所以1=+b a .10.答案:16.1=a ,满足3≤a ,于是4211==+b ;2=a ,满足3≤a ,8212==+b ;3=a ,满足3≤a ,则16213==+b ;4=a ,不满足3≤a ,则输出b ,16=b .11.答案:21.满足条件的选法可分为三类:A 组2人,B 、C 组各1人,有121325C C C 种选法;B 组2人,A 、C 组各1人,有122315C C C 种选法;C 组2人,A 、B 组各1人,有221315C C C 种选法.所以A 、B 、C 三组的学生都有的概率21210105410221315122315121325==++=C C C C C C C C C C P . 12.答案:65π.由题意,612cos 2>θ且212sin 2>θ,⎩⎨⎧==+22cos 34ab b a θ,⎪⎪⎩⎪⎪⎨⎧=⋅-=+21112sin 211a b a b θ,所以θθ2sin 22cos 32-=,32tan -=θ,因)2,(2ππθ∈,故352πθ=,65πθ=.13.答案:①③④.由y x y f x f ⋅=⋅)()(,得y x a y a y a x a x⋅=⋅⋅-⋅⋅⋅-])(2[])(2[,化简得)()()()(2y a x a a y a x a ⋅⋅⋅=⋅⋅⋅⋅,当0 =a 时,等式成立;当0 ≠a 时,有12=a,即1||=a,所以①、③、④都能使等式成立. 14.答案:4.11+<<t a t ,则t t a a <<-=112,t t a t a t a >+>-+=-+=1222123, t a t t a a <-+=-=1342,1452a a t a =-+=.所以}{n a 是以4为周期的周期数列.(第14题也可取满足条件的t 和1a 的特殊值求解)二.选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案,考生必须在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分. 15.C .16.A .17.D .16.B . 15.由5:4:3::=c b a 可得a ,b ,c 成等差数列;若a ,b ,c 成等差数列,则c a b +=2,由勾股定理,222c b a =+,得2222c c a a =⎪⎭⎫ ⎝⎛++,032522=-+c ac a ,解得53=c a ,令k a 3=(0>k ),则k c 5=,得k b 4=.所以5:4:3::=c b a .16.①错.不在同一直线上的三点才能确定一个平面;②错.若圆锥的侧面展开图是一个圆面,则可得圆锥底面半径的长等于圆锥母线的长;③错.如果三棱锥的底面是等边三角形,一条侧棱垂直于底面且长度等于底面边长,则三个侧面都是等腰三角形;④错.若这两点是球的直径的两个端点,过这两点可作无数个大圆.17.作出函数xy 2=与2x y =,可发现两函数图像在第二象限有一个交点,在第一象限有两个交点(第一象限的两个交点是)4,2(和)16,4().18.若取1x 、2x 为区间]4,2[的两个`端点,则8)()(21=x f x f .若8>C ,取21=x ,4)(1=x f ,对任意]4,2[2∈x ,16)(2≤x f ,于是8)(4)()(221≤=x f x f x f ;若8<C ,取41=x ,16)(1=x f ,对任意]4,2[2∈x ,4)(2≥x f ,于是8)(16)()(221≥=x f x f x f .所以8=C .三.解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤. 19.(本题满分12分) 解:设半圆的半径为r ,在△ABC 中,090=∠ACB ,030=∠ABC ,3=BC ,连结OM ,则AB OM ⊥,……(2分) 设r OM =,则r OB 2=,…………(4分) 因为OB OC BC +=,所以r BC 3=,即33=r .………………(6分)130tan 0=⋅=BC AC .阴影部分绕直线BC 旋转一周所得旋转体为底面半径1=AC ,高3=BC 的圆锥中间挖掉一个半径33=r 的球.………………(8分) 所以,圆锥V V =球V -πππ27353334313132=⎪⎪⎭⎫ ⎝⎛⋅⋅-⋅⋅⋅=.…………(12分)20.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.解:(1)若1=ω,则⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-=6cos ,1πx a ,⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-=6sin 2,2πx b ,由a ∥b 的充要条件知,存在非零实数λ,使得a b ⋅=λ,即⎪⎩⎪⎨⎧⎪⎭⎫ ⎝⎛-⋅=⎪⎭⎫ ⎝⎛-=6cos 6sin 22πλπλx x , 所以⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-6cos 6sin ππx x ,16tan =⎪⎭⎫ ⎝⎛-πx ,…………(3分)(以下有两种解法:) 解法一:46πππ+=-k x ,Z k ∈,125ππ+=k x ,Z k ∈,32333333133164tan 125tan 125tan tan +=-+=-+=⎪⎭⎫ ⎝⎛+==⎪⎭⎫ ⎝⎛+=πππππk x .…(6分)解法二:323313316tan 6tan 16tan 6tan 66tan tan +=-+=⎪⎭⎫ ⎝⎛--+⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-=ππππππx x x x . 所以321313tan +=-+=x .…………(6分)(2)⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-+=6cos 6sin 226cos 6sin 22)(πωπωπωπωx x x x x f⎪⎭⎫ ⎝⎛-=32sin πωx ,…………(8分)因为)(x f 的最小正周期为π,所以πωπ=22,1=ω,所以⎪⎭⎫ ⎝⎛-=32sin )(πx x f ,…………(10分)当⎥⎦⎤⎢⎣⎡∈2,0πx 时,⎥⎦⎤⎢⎣⎡-∈-32,332πππx ,…………(12分) 所以函数)(x f 的值域为⎥⎦⎤⎢⎣⎡-1,23.…………(14分)21.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.解:(1)由已知,当0=x 时,8)(=x C ,即85=k,所以40=k ,……(1分) 所以5340)(+=x x C ,…………(2分)又加装隔热层的费用为x x C 6)(1=.所以5380066534020)()(20)(1++=++⨯=+⋅=x x x x x C x C x f ,…………(5分) )(x f 定义域为]10,0[.…………(6分)(2)10380062103538003563538006538006)(-⨯≥-⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛++=++=x x x x x x x f70=,…………(10分)当且仅当⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+353800356x x ,18800352=⎪⎭⎫ ⎝⎛+x ,32035=+x ,即5=x 时取等号.…………(13分) 所以当隔热层加装厚度为5厘米时,总费用)(x f 最小.最小总费用为70万元.…(14分)22.(本题满分16分)本题共有3个小题,第1小题满分3分,第2小题满分7分,第3小题满分6分.解:(1)1=m 时,1)(2+=x x f ,因为01=a ,所以1)0()(12===f a f a ,2)(23==a f a ,5)(34==a f a .…………(3分,每求对一项得1分)(2)m x x f +=2)(,则m a =2,m m a +=23,m m m m m m m a +++=++=2342242)(,…………(5分) 如果2a ,3a ,4a 成等比数列,则)2()(23422m m m m m m m +++=+,234523422m m m m m m m +++=++,0345=-+m m m ,…………(6分)因为02≠=m a ,所以012=-+m m ,251+-=m 或251--=m .……(8分) 当251+-=m 时,数列的公比2511223+=+=+==m m m m a a q .……(9分) 当251--=m ,251-=q .…………(10分)(3)1)(2-=x x f ,),0[+∞∈x ,所以1)(1+=-x x f (1-≥x ),……(11分)11=b ,121+=+n n b b ,所以1221+=+n n b b ,而121=b ,所以{}2n b 是以1为首项,1为公比的等比数列,n b n =2,…………(13分)所以2)1(21+=+++=n n n S n ,…………(14分) 由2010>n S ,即20102)1(>+n n ,解得63≥n ,所以所求的最小正整数n 的值是63.…………(16分)23.(本题满分18分)本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分7分.23.解:(1)设点),(y x P 是函数)(x f 图像上任意一点,P 关于点A 对称的点为),(y x P ''',则12='+x x ,22='+y y ,于是x x -='2,y y -='4,…………(2分) 因为),(y x P '''在函数)(x g 的图像上,所以2|2|24-'-'⋅--='x x a ay ,……(3分) 即x x a a y --⋅--=-244||,x x a a y -⋅+=2||,所以xx a a x f -⋅+=2)(||(或x x aa x f 2)(||+=).………………(5分)(2)令t a x=,因为1>a ,0>x ,所以1>t ,所以方程m x f =)(可化为m tt =+2,即关于t 的方程022=+-mt t 有大于1的相异两实数解.…………(8分)作2)(2+-=mt t t h ,则⎪⎪⎩⎪⎪⎨⎧>->>08120)1(2m m h ,…………(11分)解得322<<m .所以m 的取值范围是)3,22(.…………(12分) (3)x x a ax g 2)(||+=,),2[∞+-∈x .当0≥x 时,因为1>a ,所以1≥xa ,),3[3)(∞+∈=xa x g ,所以函数)(x g 不存在最大值.…………(13分)当02<≤-x 时,x xa a x g 12)(+=,令xt 2=,则t t t h x g 12)()(+==,⎪⎭⎫⎢⎣⎡∈1,12a t , 当2212>a ,即421<<a 时,)(t h 在⎪⎭⎫⎢⎣⎡1,12a 上是增函数,存在最小值222a a +,与a有关,不符合题意.…………(15分) 当22102≤<a ,即42≥a 时,)(t h 在⎥⎦⎤⎢⎣⎡22,12a 上是减函数,在⎪⎪⎭⎫⎢⎣⎡1,22上是增函数,当22=t 即2log 21a x -=时,)(t h 取最小值22,与a 无关.…………(17分) 综上所述,a 的取值范围是),2[4∞+.…………(18分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高2010级(上)期末测试卷 数学(理工类)参考答案
11.)81,0(- 12.),2()81
,0(+∞ 13. 161 14. 1
2+n n 15. π)3(2n n +
三:解答题
16.(13分)解:
(Ⅰ)已知向量))3(,5(),3,6(),4,3(m m OC OB OA +--=-=-=−→
−−→
−−→
−
),1,2(),1,3(m m AC AB --==−→
−−→− 由三点共线知m m -=-2)1(3
∴实数2
1
=
m 时,满足条件…………………………………………………………………………6分 (Ⅱ)由题设知),1(),1,3(m m BC BA ---=--=−→
−−→
−
ABC ∠ 为锐角,4
3
033->⇒>++=⋅∴−→
−−→−m m m BC BA ……………………………………12分
又由(1)可知,当21=m 时,,0
=∠ABC 故),2
1()21,43(+∞-∈ m …………………………13分 17.(13分)解:
(Ⅰ)()(1cos 2)sin 2)2b f x a x x x a φ=++=++
由题设知,2
14,1422
22
-=+-=+b a a b a 所以3,21==b a ……………………………………4分
所以2
1
)62sin(212cos 212sin 23)(++=++=
πx x x x f 所以)(x f 的最小正周期为π…………………………………………………………………………7分 (Ⅱ)由,6
3
2
26
22
2π
ππ
ππ
ππ
π
π+
≤≤-
⇒+
≤+
≤-
k x k k x k
所以)(x f 单调增区间为)(6,3
Z k k k ∈⎥⎦
⎤
+
⎢⎣
⎡
-πππ
π………………………………………………13分 18(13分)解:
(Ⅰ))1(log log ,3log log 1331133-+=⋅=---n a a a a n n n n n ∴2
)
1(log ,2)1()1(21log log 3133-=-=
-+++=-n n a n n n a a n n )(25)9
(log *23N n n
n a S n n n ∈-==…………………………………………………………………4分
,211-==S b 当2≥n 时,,31-=-=-n S S b n n n
∴数列}{n b 的通项公式)(3*N n n b n ∈-=…………………………………………………………7分
(Ⅱ)设数列}{n b 的前n 项和为n T ,当03≤-=n b n 即3≤n 时,252
n n S T n n -=-=;
当3>n 时,2
12
5223+-=-=n n S S T n n .…………………………………………………………13分
19(本小题满分12分)解: (Ⅰ)由
02>---a
x x
a 得:a x a <<-2 ……………………………………………………………2分
)(x f 为奇函数,∴12=⇒-=-a a a
经验证可知:1=a 时,)(x f 是奇函数,1=a 为所求……………………………………………5分
(Ⅱ)1
212)(,11log )(1
2+-=∴-+=-x x x f x x x f ………………………………………………………8分 法一:由x m x f
--⋅=2)(1
得:
32231
22)12(122)12(3)12(122)2(22-≥-+++=+++-+=+-=x x
x x x x x x m
当且仅当)12(log 2-=x 时,322min -=m
所以m 的取值范围[)
+∞-,322………………………………………………………………………12分 法二:原方程即02)1()2(2=-+-m m x
x
设t x
=2,则0)1(2
=-+-m t m t
原方程有实解,等价于方程0)1(2
=-+-m t m t 有正实解……………………………………………6分 令m t m t t g -+-=)1()(2
则
0)0(<g 或⎪⎩⎪⎨⎧>+=0210)0(m g 或2
(0)0
(1)4010
2g m m m ⎧
⎪>⎪∆=++≥⎨⎪+⎪>⎩…………………………………………………10分
0>⇒m 或0=m 或0322<≤-m
所以m 的取值范围是[)
+∞-,322……………………………………………………………………12分 20.(12分)解:
(Ⅰ)由椭圆定义知:42=a ,∴2=a ,故椭圆方程为1422
2=+b y x ,
把)1,1(代入得11412=+b 得342
=b ,则椭圆方程为
14
422=+y x , ∴383442
2
2
=-
=-=b a c ,∴3
6
2=c ,故两焦点坐标为)0,362(),0,362(-.…………3分 (Ⅱ)用反证法:假设A 、B 两点关于原点O 对称,则B 点的坐标为)1,1(--,此时22=AB ,取椭圆上一点)0,2(-M ,则10=AM ,∴AB AM >,从而此时AB 不是最大,这与AB 最大矛盾,所以命题成立.………………………………………………………………………………………………7分
(Ⅲ)设AC 方程为:1)1(+-=x k y ,联立⎪⎩⎪
⎨⎧=++-=14
341
)1(22y x x k y 消去y 得
0163)1(6)31(222=--+--+k k x k k x k ,
点A (1,1)在椭圆上,∴1
31
6322+--=
k k k x c ……………………………………………………9分 直线AC 、AD 倾斜角互补,∴AD 的方程为1)1(+--=x k y ,
同理1
31
6322+-+=k k k x D ,………………………………………………………………………………11分
又1)1(,1)1(+--=+-=D D C C x k y x k y ,k x x k y y D C D C 2)(-+=- 所以3
1
=--=
D C D C CD x x y y k ,即直线CD 的斜率为定值31.…………………………………………12分
21.(12分)
解:(Ⅰ)过x
y C 1
:=
上一点),(n n n y x A 作斜率为n k 的直线交C 于另一点1+n A , 则2
1
11111111+-
=⋅-=--
=--=+++++n n n n n n n n n n n n x x x x x x x x x y y k , 于是有:21+=+n n n x x x ………………………………………………………………………………2分 记31
21+-=
n n x a ,则n n n
n n n a x x x x a 2)3121(2312
21312111-=+--=+-+=+-=
++, 因为7111=
x ,而02312111≠-=+-=x a ,因此数列}3
121{+-n x 是等比数列.………………6分 (Ⅱ)由(Ⅰ)可知:n n a )2(-=,则3
1
)2(12-
-+=n n x ,3
1
)1(212)1()1(⋅
--+
⋅-=-n n n n n x .
当n 为偶数时有:
n n
n n x x )1()
1(11
-+---n n n n n n n n n n n n 21
212222)3
12)(312(223121
3121111111+<⋅+<-++=-++=
------, 于是:①在n 为偶数时有:
12
1
21212121)1()1()1(432221<+++++<
-++-+-n n n x x x ……………………………10分 ②在n 为奇数时,前1-n 项为偶数项,于是有:
n n n n x x x x )1()1()1()1(11221-+-++-+---
13
1211)3
1)2(12(11)1(1<+
+
-=-
-+
-=-=-+<n n n n n x x …………………………………12分
综合①②可知原不等式得证.。
