作业答案
作业练习题有答案

作业练习题有答案一、选择题(每题2分,共20分)1. 地球的自转周期是多久?A. 1天B. 1个月C. 1年D. 1世纪答案:A2. 以下哪个不是哺乳动物的特征?A. 胎生B. 哺乳C. 有羽毛D. 体表被毛答案:C3. 光合作用主要发生在植物的哪个部位?A. 根B. 茎C. 叶D. 花答案:C二、填空题(每空1分,共10分)4. 牛顿第三定律指出,作用力和反作用力大小相等、方向相反,且作用在________上。
答案:不同物体5. 化学方程式 \( \text{Mg} + 2\text{H}_2\text{O} \rightarrow\text{Mg(OH)}_2 + \text{H}_2 \uparrow \) 表示的是________。
答案:镁与水反应生成氢氧化镁和氢气三、简答题(每题10分,共20分)6. 请简述什么是生态系统,并说明其组成部分。
答案:生态系统是指自然界中生物群落与其生存环境相互作用形成的一个统一整体。
它包括生物部分和非生物部分。
生物部分包括生产者、消费者和分解者,非生物部分包括阳光、空气、水和土壤等。
7. 解释什么是牛顿第一定律,并举例说明。
答案:牛顿第一定律,也称为惯性定律,指出如果一个物体不受外力作用,它将保持静止状态或匀速直线运动状态。
例如,当一个滑冰运动员在冰面上滑行时,如果没有摩擦力,他将保持匀速直线运动。
四、计算题(每题15分,共30分)8. 一个物体的质量为2千克,受到的重力为多少牛顿?答案:根据重力公式 \( F = m \times g \),其中 \( m \) 是质量,\( g \) 是重力加速度(约为9.8 m/s²),计算得 \( F = 2 \times 9.8 = 19.6 \) 牛顿。
9. 如果一个化学反应的速率常数 \( k \) 为0.05秒⁻¹,初始浓度为0.1摩尔/升,求10秒后的反应物浓度。
答案:使用一级反应方程 \( [A] = [A]_0 \times e^{-kt} \),其中\( [A]_0 \) 是初始浓度,\( t \) 是时间。
作业(答案)

布置作业:
1、相切两圆半径分别是4和6,求圆心距。
(分内切、外切两种情况,圆心距是6-4或6+4)
2、相交两圆半径分别是25和39,公共弦长30,求圆心距。
(分两圆心在公共弦的同旁和两旁两种情况,是36-20或36+20)
3、三角形ABC的外接圆半径是4,BC=4,求角A的度数。
(分圆心在三角形内部和外部两种情况,是30度或150度)
4、绝对值是5的数与平方根是3的数的和是几?(绝对值是正数的数有两个,和是8或-2)
5、数轴上,与表示2的点距离等于6的点表示的数,是倒数等于1.5的数的多少倍?(距离是6的点表示的数是原数加上6或减去6,结果是-6倍或12倍)
6、三角形的一个30°角对的边为5,一条邻边是8,求面积。
(分锐角三角形和钝角三角形两种情况,面积是2(4根号3+3)或2(4根号3-3)
7、等腰三角形一个角是另一个角的2倍,求底角。
(有底角大于顶角和底角小于顶角两种情况,底角是72°或45°)
8、画图找出到三角形三边距离相等的点。
(分形内形外两种情况,有4个点:内角平分线交点一个,外角平分线交点3个)
9、平行四边形ABCD中,AB=5,BC边上高AE=3,CE=2,求BC。
(点E 可在C点的左和右,BC=6或2)。
第一次作业参考答案

1
A A
8
1
f ,5
5 a,8
1
a,5
1
238 1 2.416 583.5
235
2.7
1.692
680.9 1 1.72%
9、设核燃料中 235U 的富集度为 3.2%(重量),试求其 235U 与 238U 的核子数之比。
解:设 235U 与 238U 的核子数之比为 ,则富集度为
解:查表得: f ,5 583.5 b,a,5 680.9 b,a,8 2.70 b, a,c 0.0034 b
a,
f
5
N A
A5
a,5 8
N A
A8
a,8
a
a,C
a, f
C
N A
AC
a,C
5
N A
A5
a,5 8
N A
A8
a,8
热中子利用系数:
f a, f
5
N A5
A
a,5
235
故消耗的 U 量为
m (1 ) 3.125 1010 Eth A103 NA
(1 0.169) 3.125 1010 1.8 1012 235 103
0.0257kg
6.022 1023
8.(1) 计算并画出中子能量为 0.0253eV 时的富集铀的参数 与富集度的函数关系。
8
N A
A8
a,8
a
C
N A
AC
a,C
5
N A
A5
a,5
8
N A
A8
a,8
a,5
1
A5
A8
a,8
A5 AC
作业及其答案

现代保险学教程第二版作业参考答案第一章一、√××√√二、ABC,C,CD,ABCD,D,D,BC,AC第二章一、×××√×二、A,ABD,A,AC第三章一、××√××二、ABCD,ABCD,ABC,ABC,ABCD,BC,A第四章一×√√××二 AC,A,D,A,ABC,D,B,A,AB第五章一、√×××√二、A,ABCD,ABC,ABCD ,D,C第六章一、×√××√√√×√√二、BCD,ABCD,B,ABC,ABD,AD,B,ABCD,AC,AD,ABC,AB第七章一、√√√×二、ABD,ABCD,ABCD,AC,ABCD,AC三、案例分析题20世纪80年代前期日本经历了经济的高速增长;房地产和股市表现出一派繁荣景象,投资者包括各大保险公司从中获得高回报率,他们尝到甜头后继续深度介入;然而在80年代后期房地产和股市泡沫纷纷破灭,资产大幅贬值,许多金融机构由此产生巨额不良资产,即流动性、收益性都得不到既定保证的资产;日本开始饱尝泡沫经济的恶果;所谓泡沫经济,是指一种或一系列资产在经历一个连续的涨价过程后,其市场价格远远高于实际价值的经济现象;在泡沫经济的形成过程中,开始的价格上升会使人们产生还要涨价的预期,于是又吸引了新的买主,这些新的买主一般只是想通过未来价格的提高牟取利润,并不关心这些资产本身的状况和盈利能力;当这种行为成为一种普遍的社会现象时,社会资产所表现的账面价值远高于其实际价值,于是就形成一种所谓的“泡沫经济”;20世纪80年代,为了获得更多的客户,日本寿险公司以高利率回报作为诱饵,一味追求规模扩张,大肆销售高利率的个人养老金等保险品种,这些品种以储蓄型为主,在一定条件下需要向被保险人支付固定利率,比如我们学过的定期生存保险;日本保险产品的预定利率曾高达8%左右,这也对保险公司资金的投资收益率提出了很高的要求,而当时日本的保险公司在股票和房地产的投资比例很高,平均在22%左右;不久,经济泡沫破灭、经济出现通缩,股价和地价暴跌,日本进入低利率和零利率时期,保险资产的收益率随着日本贴现率水平的降低而下降;利差损开始出现,保险公司资产负债表上一边是高利率待支付的保险负债,另一边是有着低于约定利率的收益率的公司资产,二者的不匹配给公司带来沉重的负债,开始影响公司的资本金、所有者权益;同样的情况也发生在财产保险公司身上;本来财产保险公司合同期限多为一年,期限短,收益快,资金周转灵活,按理说应能使财险公司财务状况较为稳定,但第一火灾却以合同期长的累积性业务为主,这样一来,随后的超低利率使其资金运用业绩低于向合同对方保证的预定利率,从而形成巨亏;利差损是将一些保险公司推向破产边缘的主要原因;同时,我们也能清晰地体会到资本市场的成熟程度对保险投资的影响;成熟的资本市场稳定性强,投机性弱,泡沫少,能较真实反映发行公司的价值,有利于进行长期投资,适合拥有大量中长期寿险资金的寿险公司投资,因为在这类市场中利率波动幅度较小,易于减少保险公司利率估计失误;经济泡沫的破灭不仅通过房地产和股市引起利差损,影响保险公司,也通过公司的实业投资打击着他们;日本战后实行的是“以政府为主导”的经济模式;在经济高速增长和繁荣时期,保险企业大量直接投资和参股日本企业,被投资企业又大量购买保险公司的保单,两者形成了相互促进的良性关系;但是,在泡沫经济过后,这种良性循环被打破;企业为降低经营成本,竞相削减保险计划,而保险公司面对保费的负增长,又不得不减持企业股份,从而导致企业保单的进一步减少,形成了恶性循环;第八章一、√√√二、ABCD,C ,BC,ABC,ABC,ABD,AB,ABC三、案例分析题本案争议的焦点是导致客车公司赔偿肖某家属的事故是否属于保险事故,双方在对相关条款的解释上有争议;我国保险法第31条规定:“对于保险合同的条款,保险人与投保人、被保险人或者受益人有争议时,人民法院或者仲裁机关应当作有利于被保险人和受益人的解释;”合同法第41条规定:“对格式条款的理解发生争议的,应当按通常理解予以解释;对格式条款有两种以上解释的,应当作出不利于提供格式条款一方的解释;格式条款和非格式条款不一致的,应当采用非格式条款;”这两条法律规定确立了我国对保险合同条款解释的原则——“不利解释”原则;“不利解释”原则为在有争议时解释保险合同条款提供了一种原则,但其本身并没有提供解释保险合同的方法;合同法确立的合同解释的一般原则是:“当事人对合同条款的理解有争议的,应当按照合同所使用的词语、合同有关的条款、合同的目的、交易习惯以及诚实信用原则,确定该条款的真实意思”;这一原则同样适用于对保险合同的解释;因此,“不利解释”原则不能排除合同解释的一般原则或方法,不能对保险合同任意作不利于保险人的解释;也就是说,并不是只要对保险条款发生争议,就必须作不利于保险人的解释;如果保险条款的含义清楚、意图明确,只是由于投保人、被保险人或受益人的理解错误而与保险人发生争议,就应该按保险条款的真实含义进行解释;第三者责任险的保险责任条款的含义是很明确的:由于保险车辆自身发生的保险事故,给第三者造成了人身损害或直接的财产损毁,被保险人依法应当承担赔偿责任;在本案中,王某的死亡是迎面而来的小轿车直接撞击造成的,尽管客车司机违反有关道路交通管理规定应承担事故的全部责任,但由于大客车本身并未发生交通事故,所以并没有发生保险事故;因此保险公司不应当承担客运公司对王某的赔偿责任;第九章一、√√√二、A,B,D,ABCD ,B,ABCD,ABC,BCD,ABCD四、140×80/100=32万元, 赔32万元;2地震损失为除外责任,故不赔;3min{80,70}=70,损失70,赔70万元第十章一、√√×××二、B,ABC,ABC,ABD,ABC,AB三、案例分析题雇员忠诚保证保险是诚实保证保险的一种,以被保险人的雇员在受雇期间,因欺骗或不忠诚行为贪污、挪用款项、伪造账目、偷窃钱财等而导致其直接经济损失为保障内容的一种保险;雇员的忠诚信用是保障的基础;被保险人转嫁给保险公司的是其雇员在被雇佣期间可能发生不忠诚行为的潜在风险;参照国际上的习惯做法,我国保险公司现行使用的雇员忠诚保证保险条款都列明,被保险人必须对其雇员受雇前的情况进行查询,并保存查询资料,在索赔时,如有必要应提供给保险公司;通过对其雇员受雇前情况的必要查询来防范被雇佣者在忠诚信用方面潜在的风险,这是被保险人的义务之一,也是保险公司提供雇员忠诚保证保障的前提;本案中的投保公司对其雇员受雇前的情况没有作必要的查询来防范雇员在忠诚信用方面的潜在风险,不应得到赔偿,保险公司的拒赔理由是充分的;第十一章一、×××二、AB,ABD,ABC,ABCD,AC ,AC, ABCD三、案例分析题根据保险法第36条规定:“在合同有效期内,保险标的风险程度增加的,被保险人按照合同约定应当及时通知保险人,保险人有权要求增加保险费或者解除合同;这是最大诚信原则中所说的“重要事实”问题;在本案中,承保货物装载在舱面上,背离了原约定保险标的应全部装载在船舱内;被保险人未履行标的装载在舱面的这一风险增加的告知义务,保险公司不能赔偿;保险条款中倾覆险的解释是指“运输工具在行驶或航行中,车身、船体翻倒或倾侧,失去正常状态,非经施救不能继续行驶或航行”;涉案承运船舶在航行条件正常的情况下,避让他船,虽大幅度倾斜,但驾驶员迅速拨正航向后,该船即脱险恢复常态;由于驾驶员拨正航向的行为系驾驶船舶的连续行为,而非专门的施救,故从另一方面证实这起海上事故不属倾覆险的保险责任范围,保险公司同样可以拒赔;四、对于定值保险1货物全损,按约定价值24万元补偿;2货物部分损失,则补偿额为24×80%=万元第十二章一、×√×√二、A,A,C,CD,ABC,AC三、案例分析题1、不可抗争条款是指人寿保险合同生效满一定时期一般为一年或两年以后,就成为无可争议的文件,保险人不能再以投保人在投保时违反最大诚信原则,未履行告知义务等理由而主张保险合同自始无效;此案中,保险合同订立已超过两年,应适用不可争条款;保险法第17条规定:“订立保险合同,保险人应当向投保人说明保险合同的条款内容,并可以就保险标的或者被保险人的有关情况提出询问,投保人应当如实告知;投保人故意隐瞒事实,不履行如实告知义务的,或者因过失未履行如实告知义务,足以影响保险人决定是否同意承保或者提高保险费率的,保险人有权解除保险合同;”这一条更多的体现了对保险人权益的保护;在国外,一般来讲,对保险人的这项权益的保护是有所限制的,即保险公司只能在一定期限内行使这项权利;在此期间,保险公司只要查明真相,均可行使保险合同解除权,超过了这个期限就意味着保险公司主动放弃了保险合同解除权;美国法律规定:要约人不管是由于过失,还是故意甚至欺诈订立了合同,只要过了不可争议期间,即为不可抗争;英国、法国、日本等国保险法都有不可抗争条款的规定;加拿大的保险法律也有不可争之规定,但规定“若有欺诈行为,不论契约经过期间如何,均为可争”,即只要是有欺诈行为的,就不适用不可抗争条款;不可抗争条款有一定的使用范围;一般而言,不可抗争条款包括的范围是年龄和健康;我国的保险法在不可抗争条款规定中,对年龄的误报有明确说法,而对于保险实务中争议最多的“健康”情况不如实告知却无相应规定,在现有的寿险、健康险条款中也未有对健康方面不可抗争的内容;本案中,王某故意隐瞒健康状况,而保险合同条款中的除外责任有“投保人或被保险人对投保隐瞒或欺骗行为”一条,因此,保险公司的拒赔有其法律依据;2、本案主要涉及人身保险的受益人问题;1保险法第61条规定:“人身保险的受益人由被保险人或者投保人指定;”第64条规定:“被保险人死亡后,遇有下列情形之一的,保险金作为被保险人的遗产,由保险人向被保险人的继承人履行给付保险金的义务:一没有指定受益人的;二受益人先于被保险人死亡,没有其他受益人的;三受益人依法丧失受益权或者放弃受益权,没有其他受益人的;”此案中投保人某企业以及被保险人张某并未指定受益人,因此保险金应该作为被保险人的遗产由被保险人张某的继承人获得;2根据继承法的规定,遗产的继承顺序应为:配偶、子女为第一顺序继承人;父母亲为第二顺序继承人;因此,此案中遗产的第一顺序继承人为张的配偶及子女,第二顺序继承人为张的父母亲;张的哥哥不属于继承人范畴;作为第一继承人,张的妻子有权全额领取并支配保险金,张的父母有获得部分保险金的权利其父母已丧失劳动能力;3保险法第53条规定,除亲属外,“被保险人同意投保人为其订立合同的,视为投保人对被保险人具有可保利益;”投保人某企业出资为张某投保,可视为对张某具有可保利益;但具有可保利益并不等同于能获得保险金;根据保险的基本原则,购买保险是为了获得经济补偿和风险保障,不能因此获得额外收益;该企业不能因为是投保人而作为受益人领取保险金;综合以上三点,张某的妻子应该是保险金的受益人,对保险金具有支配权;第十三章一、√××√二、C ,C ,A,B,D,BCD,BCD,BC三、案例分析题从上述简单介绍中,我们可以具体了解到再保险的两种责任分担方式:成数再保险和溢额再保险;按各公司的约定,入股公司每签订一张综合保险火险、水险和车险等的保单,便要采取成数再保险方式,即向泰国再保险公司分出该保单金额的5%,也就是再保险金额为5%,自留保费为95%,如果发生保险事故,则再保险公司应承担5%的赔偿责任;这种方式无需按保险风险逐个确定保费和赔款的分配比例,而是按约定统一结算,手续简单,节省人力和费用;寿险公司采取溢额再保险方式;对于不同风险的业务,入股公司与该再保险公司签订再保险合同时可商定不同的自留额和限额;如果业务损失率大,出险机会多,则要考虑分保同时自留额不宜太大,但对于某些低风险的业务甚至可考虑不分保;每签订一张寿险合同,入股公司应根据该业务的风险和与再保险公司的合同约定来判断是否分出保费,该保额是否在自留额之内,是否有溢额,如有溢额分出,则应按合同约定比例分出;一旦泰国再保险公司接受分保,保险事故发生时它就应当按所收取的保费比例分摊赔款;另外,泰国再保险公司的产生其实也是各入股公司采取的一种再保险方式,它生动的印证了“再保险公司是保险人的保险”这句话;同时,我们看到在整个保险市场中,尽管竞争激烈,但合作也是不可少的,75家保险公司的合作产生了泰国再保险公司;第十四章一、√√√√二、B,D,C,A,AD,ABD,A,A,B,BD三、案例分析题可以要求厂方再赔偿5万元,因为保险公司支付的是人身意外伤害赔偿金,不能代替工伤赔偿;人身无价,补偿原则不适用于人身伤害赔偿,王某可以获得两次赔偿给付;补充计算题1——财产保险1、张某于2005年6月1日向某保险公司投保财产保险,双方签订了一份不定值保险合同,保险期限从2005年6月1日至2006年6月1日,保险金额为20万元;2005年8月6日遭受火灾;在以下几种情形下,保险公司应当如何赔偿;1如果出险时保险财产的保险价值为24万元,实际遭受的损失为6万元,保险公司的赔偿额是多少2如果出险时保险财产的保险价值是20万元,实际遭受的损失是6万元,保险公司的赔偿额是多少3如果出险时保险财产的保险价值是16万元,实际遭受的损失是6万元,保险公司的赔偿额是多少实际遭受的损失是16万元,保险公司的赔偿额是多少2、龙门钢铁厂投保企业财产保险,固定资产保险金额300万元,流动资产保险金额100万元;在保险期间内发生保险事故,固定资产损失150万元,流动资产损失50万元;出险时,固定资产的重置价值280万元,流动资产的账面余额110万元;保险公司应如何赔付3、新车购置价100000元,投保时实际价值80000元,出险时实际价值75000元;1若发生全损,保险金额分别为为100000元、80000元、70000元时,保险公司各应赔偿多少2若发生部分损失,施救费用2000元,实际修理费用15000元,则上述即1情况下保险公司又各应赔偿多少1、解不定值保险的保险金额在投保时确定,保险价值则是在出险时才确定,因此,保险金额与保险价值常常不相等;1如果出险时保险财产的保险价值为24万元,保险金额为20万元,少于保险价值,因此,采取不足额赔偿方式赔偿;实际遭受损失为6万元,则保险公司赔偿额=实际损失额×保险金额/保险价值=6×20/24=5万元2如果出险时保险价值是20万元,保险金额为20万元,因此,采取足额赔偿方式赔偿;实际遭受的损失是6万元,保险公司赔偿额与实际损失相等,即保险公司赔偿6万元; 3如果出险时保险价值是16万元,保险金额为20万元;因此,采取超额赔偿方式赔偿,保险公司赔偿额与实际损失相等,超额部分无效,则实际遭受的损失是6万元,保险公司赔偿6万元;实际遭受的损失是16万元,保险公司赔偿16万元;2、解固定资产赔偿:保险金额>保险价值属超额投保,应按实际损失赔偿赔款=150万元流动资产赔偿:保险金额<保险价值属不足额投保,应按比例赔偿;赔款为100÷110×50=500/11= 万元3、解1保险公司依次赔偿万元,万元和7万元;2施救费用和实际修理费用合计+=万元保险公司依次赔偿×80000/100000=万元;同上×70000/100000=万元;补充计算题2——再保险1、一份再保险合同,双方约定,分出公司自留额100万元,分入公司分保限额10线;有一笔1000万元的再保险业务符合此约定,保费100万元,赔款50万元,那末,对于分出公司与分入公司,自留额与分保额、保费与分保费、分摊赔款分别为多少2、某分出、分入两公司签订一份海上运输成数分保合同,合同规定货船最高责任限额1000万元、保费10万元,分出公司自留额比例20%,结果发生赔款30万元;试求分入公司应接受的分保额、分保费,摊多少赔款3、假如有一超过5万元以后的25万元的超赔再保险合同;在合同有效期内发生一次赔款10万元,赔付时的通货膨胀率较合同生效时的通货膨胀率增加了40%;规定赔付时的通货膨胀率与合同生效时的通货膨胀率相比较,若增幅在10%的范围内,分出公司的自负责任额和接受公司的分保责任额无须进行调整,若增幅超过10%,则必须进行调整;试计算分出公司和分入公司各自的赔付额;1、解分出公司:自留额100万,保费 100ⅹ100/1000=10万元,分摊赔款 50ⅹ100/1000=5万元;分入公司:分保额 1000-100=900万,保费 100ⅹ900/1000=90万元,赔款 50ⅹ900/1000=45万元2、解分入公司应接受分保额10001-20%=800万元;分保费 101-20%=8万元;分摊赔款 301-20%=24万元3、解由于通货膨胀率的增幅超过了10%,因此需对分出公司的自负责任额和接受公司的分保责任额作调整,计算如下:分出公司的自负责任额5×1+40%=7万元接受公司的分保责任额25×1+40%=35万元因为分出公司的自负责任额由5万元提高到7万元,所以对于10万元的赔款,分出公司应赔付7万元,接受公司赔付超过7万元以上的3万元;一、单项选择题共10小题,每题 1分,共计10 分二、多项选择题共5小题,每题2分,共计10 分三、判断题共10 小题,每题1分,共计10分四、概念比较题共2小题,每题6分,共计12分五、简答题共3 小题,每题6分,共计18分六、计算题共3 小题,第1题6分,第2、3题各7分,共计20分七、案例分析题共2 小题,每题10分,共计20分。
(完整版)作业题答案

作业题答案试述电弧中带电粒子的产生方式:电弧中的带电粒子主要是指电子正离子和负离子,这些带电粒子主要依靠电弧气体空间的电离和电极的电子发射两个物理过程所产生,同时伴随着解离、激励、扩散、复合、负离子的产生等一些其他过程。
产生电弧的两个基本条件是有带电粒子和电极之间有一定的电场强度。
产生方式有解离、电离(热电离电场作用电离光电离) 激励(碰撞传递光辐射传递)电子发射(热发射电场发射光发射粒子碰撞发射)。
最小电压原理:在给定电流和周围条件一定的情况下,电弧稳定燃烧时其导电区的半径或温度应使电弧电场强度具有最小的数值,就是说电弧具有保持最小能量消耗的特性。
什么是焊接静特性:是指稳定状态下(弧长一定,稳定的保护气流量和电极)焊接电弧的焊接电流和电弧电压特性。
什么是焊接动特性,为什么交流电弧和直流变动的直流电弧的动特性呈回线特性?是指的那个电弧的长度一定,电弧电流发生连续快速变化时,电弧电压与焊接电流瞬时值之间的关系。
它反映了电弧的导电性对电流变化的响应能力。
在焊接电流的上升过程中,由于电弧先前处于相对低温状态,电流的增加需要有较高的电场,因此表现出电弧电压有某种程度的增加;在电流下降过程中,由于电弧先前已处于较高温度状态,电弧等离子体的热惯性不能马上对电流降低做出反应,电弧中仍然有较多的游离带电粒子,电弧导电性仍然很强,使电弧电压处于相对较低的水平,从而形成回线状的电弧动特性。
试述焊接电弧的产热机构以及焊接电流T分布: 焊接电流是一个能量输出很强的导体,其能量通过电弧转换,由于弧柱、阴极区、阳极区组成,因此焊接电弧总的能量来自这三个部分。
(1)阴极区的产热本质是产生电子(消耗能量)、接收正离子的过程有能量变化,这些能量的平衡结果就是产热。
产热产热量是PK=I*(UK-Uw-UT),作用是用于加热阴极。
(2) 阳极区的产热本质是接收电子、产生A、过程中伴随能量的转换。
产热量是PA=I*(UA-UK-Tt), 用于加热阳极。
第一次作业及参考答案

第一次作业:第一章一.名词解释:1.饱和空气2.未饱和空气3.制冷4.露点温度5.含湿量6.绝对湿度7. 相对湿度二.简答题:1.空气调节的定义与客车空调装置的任务2.说明制冷与空调的区别和联系3.空气的干球温度、湿球温度和露点温度有什么区别?三者之间的关系如何?4.确定空调装置外气计算参数的方法是什么?5.空气的相对湿度与含湿量有何区别?空气的枯燥程度与吸湿能力大小由那个参数反映?6.白天空气的温度为30℃,相对湿度为50%,夜间温度下降至20℃,夜间会出现结露吗?夜间的相对湿度是多少?7.冷却、冷藏、冷冻都有什么区别?8.焓湿图由哪几种线群组成?9.列车空调系统主要由哪几个根本局部组成?各局部的用作是什么?第一次作业参考答案一.名词解释:1.饱和空气:干空气和饱和水蒸汽的混合物称为饱和空气。
2.未饱和空气:干空气和过热水蒸汽的混合物称为过饱和空气。
3.制冷:用一定的方法使某物体或空间的温度低于周围环境介质的温度,并且使其维持在某一范围内,这个过程称为制冷。
4.露点温度:指某一状态的空气,在含湿量不变时,降温至饱和状态时的温度。
5.含湿量:随一公斤干空气同时存在的水蒸汽质量,称为湿空气的含湿量〔g〕。
6.绝对湿度:每立方米湿空气中所含水蒸汽的质量,称为空气的绝对湿度。
7.相对湿度:一立方米湿空气中所含水蒸汽的质量,与同一温度下饱和空气中所含水蒸汽质量的比值称为相对湿度。
二.简答题:1. 空气调节的定义与客车空调装置的任务答:空气调节:把经过一定处理后的空气,以一定的方式送入室内,使室内空气的温度、相对湿度、气流速度和干净度等控制在适当范围内的专门技术。
客车空调装置的任务是将一定量的车外新鲜空气和车内再循环空气混合后,经过过滤、冷却或加热、减湿或加湿等处理,以一定的流速送入车内,并将车内一定量的污浊空气排出车外。
答:制冷:用人工的方法在一定时间和空间内将某物体或流体冷却,使其温度低于周围环境介质的温度,并保持这个低温的过程。
作业一参考答案
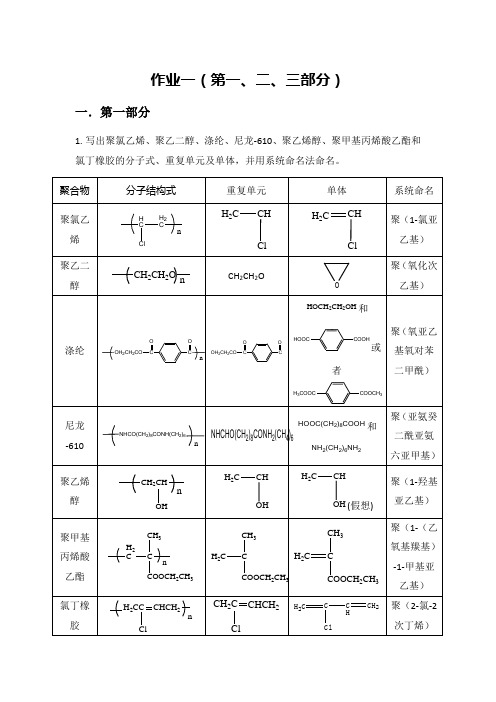
作业一(第一、二、三部分)一.第一部分1.写出聚氯乙烯、聚乙二醇、涤纶、尼龙-610、聚乙烯醇、聚甲基丙烯酸乙酯和氯丁橡胶的分子式、重复单元及单体,并用系统命名法命名。
2. (1)数均分子量M n 和重均分子量M w 的物理意义是什么试证明多分散系数d ≥1。
(2)某聚合物试样由下列级分组成,试计算该试样的数均分子量M n 和重均分子量M w 以及多分散系数d 。
解:(1)数均分子量的物理意义是各种不同分子量的分子所占的分数与其相对应的分子量乘积的总和。
重均分子量的物理意义是各种不同分子量的分子所占的重量分数与其相对应的分子量乘积的总和。
设i M 为i 聚体的分子量,则()22220i n i i i nin i i M M N M N M NM M N -=+-≥∑∑∑∑亦即20w n n M M M -≥故当i n M M ≡时,则w n M M ≡,当i n M M ≠时,则w n M M 。
(2)456118484.30.50.40.1101010i ini n M M n===++∑∑45650.5100.4100.110 1.45101i iwiw M M w⨯+⨯+⨯===⨯∑∑51.45107.8418484.3w n M d M ⨯===二.第二部分3. 多少乙酸加到等摩尔比的己二酸和己二胺中才能使聚酰胺的分子量为11318,反应程度为 %,求乙酸和己二酸的摩尔比解:设己二酸加料为1mol 时,乙酸为N mol ,将P =,11318,113n X =代入112n r X r r ϕ'+='+-中,解得0.99r '=。
由120.99122b b b N r N N N ⨯'==='+⨯+, 得N =。
所以乙酸和己二酸得摩尔比为:1。
4. 计算下列体形缩聚反应体系的凝胶点:(1)邻苯二甲酸和甘油的摩尔比为:;(2)邻苯二甲酸、甘油和乙二醇的摩尔比为::解:(1)30.982 2.371.500.98f ⨯⨯==+,220.8442.39c P f ===(2)(30.990.0022)2 2.391.500.990.005f ⨯+⨯⨯==++;220.8382.39c P f === 。
课后作业 含答案

5.10 课后作业一、单项选择题1.一物体做斜上抛运动(不计空气阻力),在由抛出到落地的过程中,下列表述中正确的是( ) A .物体的加速度是不断变化的 B .物体的速度不断减小C .物体到达最高点时的速度等于零D .物体到达最高点时的速度沿水平方向解析:选D.加速度决定于物体受到的重力,所以加速度是不变的,速度是先变小再变大,所以A 、B 选项均错.在最高点的速度不为零且沿水平方向,所以C 错,D 对.2.物体做平抛运动时,它的速度方向和水平方向间的夹角α的正切tan α随时间t 变化的图象是图中的( )解析:选B.平抛运动的合速度v 与两个分速度v 0、v y 的关系如图所示.则tan α=v y v 0=gv 0·t ,故正切tan α与时间t 成正比,B 正确.3.一个物体以初速度v 0水平抛出,经时间t ,竖直方向的速度大小也为v 0,则t 为( ) A.v 0g B.2v 0g C.v 02g D.2v 0g解析:选A.平抛运动可分解为水平方向的匀速直线运动和竖直方向的自由落体运动,在竖直方向上v 0=gt ,故t =v 0g,A 正确. 4.飞机以150 m/s 的水平速度匀速飞行,某时刻让A 球落下,相隔1 s 又让B 球落下,不计空气阻力.在以后的运动中,关于A 球与B 球的相对位置关系,正确的是(取g =10 m/s 2)( )A .A 球在B 球前下方 B .A 球在B 球后下方C .A 球在B 球正下方5 m 处D .A 球在B 球的正下方,距离随时间增加而增加 解析:选D.A 、B 球离开飞机后都做平抛运动,它们在水平方向与飞机的运动同步,即在空中A 、B 一定在飞机的正下方,B 球落下t 秒时A 、B 相距Δh =12g (t +1)2-12gt 2=12g (2t +1),即A 、B 球间的距离随时间增加而增加,D 项正确.二、多项选择题5.一架水平匀速飞行的飞机每隔1 s 投下一颗小球,共投下5颗,若不计空气阻力及风的影响,则( )A .这5颗小球在空中排列成一条抛物线B .这5颗小球及飞机在小球落地前,在空中排列成一条竖直线C .这5颗小球在空中各自运动的轨迹均是抛物线D .这5颗小球在地面的落点间的距离是相等的解析:选BCD.空中小球与飞机在水平方向上速度相同,即水平方向上相对静止,都在飞机的正下方,故A 错误B 正确;每个小球都做平抛运动,故轨迹均是抛物线,C 正确;落地点间的距离由Δx =v Δt 知,间距相等,故D 正确.6.如图,x 轴在水平地面内,y 轴沿竖直方向.图中画出了从y 轴上沿x 轴正向抛出的三个小球a 、b 和c 的运动轨迹,其中b 和c 是从同一点抛出的.不计空气阻力,则( )A .a 的飞行时间比b 的长B .b 和c 的飞行时间相同C .a 的水平速度比b 的小D .b 的初速度比c 的大解析:选BD.小球做平抛运动,在竖直方向上满足h =12gt 2,得t =2hg,可知A 错误B 正确.在水平方向上x =v 0t 即v 0=x ·g2h,且由题图可知h b =h c >h a ,x a >x b >x c ,则D 正确,C 错误.7. 某人向放在水平地面的正前方小桶中水平抛球,结果球划着一条弧线飞到小桶的右侧(如图所示).不计空气阻力,为了能把小球抛进小桶中,则下次再水平抛球时,他可能作出的调整为( )A .减小初速度,抛出点高度不变B .增大初速度,抛出点高度不变C .初速度大小不变,降低抛出点高度D .初速度大小不变,提高抛出点高度解析:选AC.设小球被抛出时的高度为h ,则h =12gt 2,小球从抛出到落地的水平位移x =v 0t ,两式联立得x =v 02hg,根据题意,再次抛小球时,要使小球运动的水平位移x 减小,可以采用减小初速度v 0或降低抛出点高度h 的方法,故A 、C 正确.三、非选择题8.如图所示,飞机距地面高度h =500 m ,水平飞行速度v 1=100 m/s ,追击一辆速度为v 2=20 m/s 同向行驶的汽车,欲使炸弹击中汽车,飞机应在距汽车水平距离多远处投弹?(g 取10 m/s 2).解析:炸弹离开飞机后做平抛运动,由h =12gt 2得下落时间t =2h g= 2×50010s =10 s. 设距离为x 时投弹,由位移关系知 v 1t =x +v 2t所以x =(v 1-v 2)t =(100-20)×10 m =800 m. 答案:800 m9. 如图所示,一个斜面固定在水平面上,从斜面顶端以不同初速度v 0水平抛出小物体,得到小物体在空中运动时间t 与初速度v 0的关系如下表,g 取10 m/s 2,试求:v 0/(m·s -1)… 2 … 9 10 … t /s… 0.400 … 1.000 1.000 …(1)v 0=2 m/s 时平抛水平位移x ; (2)斜面的高度h ; (3)斜面的倾角θ.解析:(1)x 1=v 0t 1=0.80 m.(2)初速度达到9 m/s 以后,运动时间保持t =1 s 不变,故小物体落地点在水平面上.竖直位移h =12gt 2=5 m.(3)小物体初速度为2 m/s 时,运动时间t =0.400 s ,落至斜面上,水平位移x 1=v 0t 1=0.80 m ,竖直位移h 1=12gt 21=0.80 m ,故tan θ=h 1x 1,θ=45°. 答案:(1)0.80 m (2)5 m (3)45°1234。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作业11.什么是白噪声?白噪声有何特点?答:白噪声是均值为0,自相关函数为冲击响应的随机过程。
白噪声的功率谱为常数。
2. 一个离散时间的随机信号由两个正弦波信号叠加而成,即()x t =1sin()A t ω+ 2cos()B t ω,i ω=2i f π,i =1,2,其中幅值A 和B 为独立的高斯随机变量,具有以下概率密度221/(2)()a A f a σ-=,222/(2)()b B f a σ-= 求离散时间信号()x t 为严格平稳随机信号的条件。
解:由于()x t 为两个正弦信号的线性叠加,因此()x t 也是正弦信号。
又因为{()}E x t =1{sin()}E A t ω+ 2{cos()}E B t ω=0{()}D x t =1{sin()}D A t ω+ 2{cos()}D B t ω=2211sin ()t σω+2222cos ()t σω 所以,()x t 的概率密度函数可以表示为222221122/2[sin ()cos ()](,)x t t f x t σωσω-+=若1σ=2σ=σ,1ω=2ω,则{()}D x t =2σ此时的()x t 的概率密度函数可以表示为22/2(,)x f x t σ-=因此(,)f x t 将与t 无关,因此()x t 为严格平稳的条件为1σ=2σ,1ω=2ω作业21. 在一个3发射4接收的MIMO 无线通信系统中,系统在白噪声的环境下采用训练序列估计信道00h ,10h 和20h ,其中ij h 表示用户i 的数据发射到天线j 时经过的单径信道,训练序列的块长为16,请用最小二乘估计方法估计这三个信道。
解:信道0H =[00h , 10h , 20h ]T ,第0个用户的发射数据为0X =[0,0x , 0,1x , …0,15x ]T 第1个用户的发射数据为1X =[1,0x , 1,1x , …1,15x ]T 第2个用户的发射数据为2X =[2,0x , 2,1x , …2,15x ]T 则我们在第0个天线处接收到的数据为 0Y =0XH +N其中X =[0X , 1X , 2X ], N 为白噪声向量 因此最后的0H 的最小二乘估计表达式为 0ˆH =0+X Y作业31.若一条件概率密度函数为高斯分布,则采用该分布函数所获得的绝对损失型、二次型和均匀型Bayes 估计的结果之间有何关系?为什么? 答:估计结果相等。
绝对损失型、二次型和均匀型的Bayes 估计结果分别是概率密度函数的中值,均值和极值,因此,当条件概率密度函数为高斯分布,这三个值重合。
2. 在一个被动RFID 系统中,阅读器采用动态帧时隙Aloha 协议识别标签,若阅读器在一个时隙数为L 的的帧内观察到0c 个空时隙、1c 个可读时隙和c κ个冲突时隙,请用Bayes 的绝对型,二次型和均匀型代价函数估计这个帧内的标签数n 。
解:一个信息帧的时隙数为L , 若阅读的标签数为n , 那么帧中的每个时隙内有r 个标签应答的概率为[11, 12, 15-17, 19],...1,0,111=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=-r L L r n p rn rr由式(1)可得, 发生空时隙, 可读时隙和冲突时隙的概率分别为nL p ⎪⎭⎫⎝⎛-=1101111-⎪⎭⎫ ⎝⎛-=n L L n p111111-⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛--=n nL L n L p κ由式(2)我们可以得到, 在一个长为L 的信息帧内发生了0c 个空时隙, 1c 个成功时隙, κc 个冲突时隙下有n 个标签的条件概率为[19]010101!(|)!!!c c c L p n c p p p c c c κκκ=二次型:代价函数表示为[25]2)~(),~(n n n nJ -= 相应的贝叶斯估计为∑∑∑=====Nn Nn Nn c n p c n np c n p n n111)|()|()|(ˆ绝对型:代价函数表示为[25]n n n nJ -=~),~( 相应的贝叶斯估计为⎪⎭⎫⎝⎛-=∑∑==Ω∈N n n n n n c n p c n p n ~~1~)|()|(min arg ˆ 均匀型代价函数取为⎪⎩⎪⎨⎧∆≤-∆≥-=2/~ 02/~ 1),~(n n n n n n J 其中, ∆为很小的常数. 相应的贝叶斯估计为)|~(max arg ˆ~c n p n n Ω∈=作业41.有时在采用非参数化谱估计的直接法计算功率谱时,为何不用Fourier 变换而是用短时Fourier 变换对信号作变换?在采用非参数化谱估计的间接法中,使用了Wienier-Khinchine 定理来计算功率谱,在使用该定理时,信号必须满足什么条件?答:因为非参数化估计的前提是,该随机过程为平稳过程,而Fourier 变换只能针对平稳过程,而短时Fourier 变换可以对非平稳过程进行处理。
使用Wienier-Khinchine 定理时,信号必须满足平稳随机过程的特性,而且该随机过程的均值应为0.2. 假定一平稳分布的离散随机过程有N 个数据样本(0)x , (1)x ,… (1)x N -,且均值{}()E x t =0,请用非参数化谱估计的直接法和间接法估计该随机过程的功率谱。
解:1)直接法定义信号x (n )的周期图为:22)()2()1(1)(jwN w j jw e N x e x e x Ns ---+++= ω 根据功率谱的定义:])(1[lim )(2jw N x e X NE S ∞→=ω 如果信号是各态历经的,则:212)(1lim])(1[lim )(∑-=-∞→∞→==N n jwnN jw N x en x N e X NE S ω在实际中,信号的观察值是有限的,记为x (0),x (1),…,x (N -1),用这些观察序列对功率谱S x (w )进行估计,有:2102)(1)(1)(ˆ∑-=-==N n jwnjw N x en x Ne X N S ω2)间接法211ˆ()()()N xn R k x n k x n N -*==+∑ˆˆ()()Mjkw xxk MS R k e ω-=-=∑作业51.请列出梯度算法(也称最陡下降法)的统一表达形式。
当梯度算法的代价函数()J n 为什么时,梯度梯度算法变化为LMS 算法? 答:()(1)()()J k W k W k W k μ∂+=-∂,其中k 为迭代次数,W 为滤波器系数向量,μ为步长,()J k 为代价函数2ˆ()|()()|J k y k yk =-,其中()y k 为真实信号,ˆ()y k 为通过Lms 滤波器的信号2. 已知有下列两类模式:A :1X =(0, 0, 0)T , 2X =(1, 0, 0)T , 3X =(1, 0, 1)T , 4X =(1, 1, 0)T ;B :5X =(0, 0, 1)T , 6X =(0, 1, 1)T , 7X =(0, 1, 0)T , 8X =(1, 1, 1)T 。
请用梯度算法求解判决函数:(1)选择代价函数(,)J W X ,并给出相应的梯度算法表达式;(2) 选择合适的迭代步长μ,计算出最后的权向量W ;(3) 给出该梯度算法的伪代码。
解:(1)T TT T|| (,)|| A J B ⎧-⎪=⎨+⎪⎩W X W X W X W X W X ,对于类,对于类 因此A 类:T T() ()0(1)() ()0i i i n n k n n u n k ⎧+>⎪+=⎨++≤⎪⎩W W X W W X W X ,,因此B 类:T T() ()0(1)() ()0i i i n n k n n u n k ⎧+<⎪+=⎨-+≥⎪⎩W W X W W X W X ,,其中n 为迭代次数,W 为判决函数的系数向量,μ为步长,k 为任意系数(2)取μ=0.5,k =1, 则经计算W =[1, -1.5, -1.5]所以最后的判决函数为d T()d k =+X W X 。
(3)for n=1:100; for i=1:4if W(:,n).'*X(:,i)+k<=0W(:,n)=W(:,n)+u*X(:,i); end endfor i=5:8if W(:,n).'*X(:,i)+k>=0 W(:,n)=W(:,n)-u*X(:,i); end endW(:,n+1)=W(:,n); end作业6.1.若一随机过程可以表示为ARMA 过程,其必要条件是输入激励为什么信号? ARMA 模型与AR 和MA 模型有何关系?LMS 滤波器与方程误差(EEA )滤波器分别是以上的什么模型?答:必要条件为输入激励应为高斯白噪声。
当ARMA 模型的AR 系数为0时,该模型为MA 模型,当MA 系数为0时,该模型为AR 模型。
——3分LMS 为MA 模型,EEA 为ARMA 模型。
作业71. 已知一滤波器的递归差分方程形式如下:∑∑-=-=-+-=1011)()()()()(M m m N n n m t x t b n t y t a t y若定义代价函数2ˆ()|()()|J t y t y t =-,其中ˆ()y t 为构造滤波器的输出信号。
(1)计算梯度向量()J t ∇;(2)给出相应梯度算法表达式;(3)列出该梯度算法步骤。
解:1) 令)()()(t y t d t e -=,则2()()J t e t =,因此()J t ∇可以表示为211()()()2()2()[()()],1,...1()()()N n n n n n e t y t y t n e t e t y t n a t n N a t a t a t -=∂∂∂-==-+=-∂∂∂∑211()()()2()2()[()()],0,...1()()()M m m m m m e t y t y t m e t e t x t m a t m M b t b t b t -=∂∂∂-==-+=-∂∂∂∑2)相应的梯度算法可表示为⎪⎪⎩⎪⎪⎨⎧∂-∂+-+-=∂-∂+-+-=∑∑-=-=])()()()()[()1()(])()()()()[()1()(1111M m m mm m N n n n n nt b m t y t a m t x t e t b t b t a n t y t a n t y t e t a t a μμ 令T m N t b t b t a t a t )](),...(),(),...([)(01=θT M t x t x N t y t y t Y )]1('),...('),('),...('[)('+--=则式最后的梯度算法可表示为)(')()1()(t Y t e t t μθθ+-=3)算法步骤: 步骤1 初始化)(')()1()(t Y t e t t μθθ+-=; 步骤 2 更新:t =1, 2, ….T ()()()()e t d t t Y t θ'=-)(')()1()(t Y t e t t μθθ+-=作业7.在一盲均衡仿真实验中,信道()h n 用L =6个抽头,信号源采用PAM 调制方式,选用的值分别为:7.0±, 5.0±, 3.0±, 1.0±,均衡器()w n 也选用6个抽头,第三个点的初始值设为1,其余的设为0。
