单缝衍射夫琅禾费单缝衍射衍射角
合集下载
夫琅禾费单缝衍射
中央明纹线宽度
x
xk
中央 O 明纹
k2
k 1
(a , )
其他明纹宽度
a sin k k xk tg k f tg k sin k
f
f xk k a
x k f a
中央亮纹的边缘对应的衍射角1，称为
中央亮纹的半角宽
sin 1
总结： ——中央明纹(中心) a sin 0 a sin k，k 1,2,3„ ——暗纹(中心) （注意k 0）
0.017 0.047
1
I / I0
0.047
0.017
-2( /a) -( /a) 0 /a 2( /a)
sin
中央极大值对应的明条纹称 中央明纹。 中央极大值两侧的其他明条纹称 次极大。
sin Δ x / f
明纹暗纹的图示
中央亮纹的半角宽
1
f
x
（1）明纹宽度
中央明纹：两个一级暗纹间的距离，
b sin ( 2k 1)
——暗纹
2
, ( k 1,2)
——明纹(中心) ——中央明纹中心
b sin 0 0
上述暗纹和中央明纹(中心)的位置是准确的，其余 明纹中心的实际位置较上稍有偏离。
四、衍射图样的特点
衍射图样中各级条纹的相对光强如图所示.
相对光强曲线
惠更斯-菲涅尔积分公式
K ( ) E dE C dS cos(wt ) r
P
Hale Waihona Puke a
为衍射角
f
P点的光强取决于狭缝上各子波源 到此的光程差。光强分布？
为缝边缘两条光线在 p 点的光程差
单缝和圆孔夫琅禾费衍射介绍
三、入射光非垂直入射时光程差的计算
DB BC A
b(si n sin ) b
（中央明纹向下移动）
D
B
C
BC DA
b(si n sin )
（中央明纹向上移动）
D A
b
C
B
例1 在单缝衍射中，=600nm, a=0.60mm, f=60cm, 则（1）中央明纹宽度为多少？（2）两 个第三级暗纹之间的距离？
单缝和圆孔的夫琅 禾费衍射介绍
一、单缝夫琅禾费衍射
1.衍射装置及图样
单缝 透镜
衍射角
f
衍射屏
I
衍射图样
（1） 衍射条纹与狭缝平行。 （2）中心条纹很亮，两侧明条纹对称分布， 亮度减弱。 （3）中央亮斑的宽度为其他亮斑的两倍。
由惠更斯——菲涅耳原理：
单缝处波面看作无穷多个相干波源，屏上一点是 (无穷)多光束干涉的结果。
解 ⑴ 中央明纹的宽度
⑵第三级暗纹在屏上的位置
x3ftanf3a3l0
两个第三级暗纹之间的距离
x6l 7.2mm 0
例2 已知：一雷达位于路边d =15m处,射束与公路成 15°角，天线宽度a =0.20m，射束波长=30mm。
求：该雷达监视范围内公路长L =?
L
d
a
θ1
β
150
解：将雷达波束看成是单缝衍射的0级明纹
越大，
越大，衍射效应越明显.
1
二、用振幅矢量推导光强公式
1.振幅矢量法 将缝AB的面积S等分成N(很大)个等宽的窄带,
每个窄带宽度a/N.
每个窄带发的子波在P点振
A
幅近似相等，设为A1，相邻
窄带所发子波在P点引起的振
20.2 单缝的夫琅禾费衍射
B
A C
·P
0
f
AC = a sinϕ = (2k +1)
(3) OP间有几条暗纹？ 间有几条暗纹？ 间有几条暗纹
λ
2 0 1 1 2
= 2.5λ
∴ k =2
2
两条暗纹
单缝可分成几个半波带？ (4) 单缝可分成几个半波带？
5个半波带
点为第二级暗纹，则缝可分成几个半波带？ (5) 若P点为第二级暗纹，则缝可分成几个半波带？ 缝可分成4 AC = a sinϕ = 2k ⋅ = 4⋅ 缝可分成4个半波带 2 2
§20.2 单缝的夫琅禾费衍射
一、实验装置 二、 用半波带法分析条纹的形成 三、用旋矢法求解强度分布 四、条纹分析 五、其他衍射现象 六、光学仪器的分辨本领
1
第20章光的衍射
2
第20章光的衍射
一、实验装置
P
O
*
f′
ϕ
B
ϕ
A
·x
0
正一级 中央亮纹 负一级
C
f
( 单缝夫琅和费衍射 )
单缝处波面看作无穷多个相干波源 P点是 (无穷)多光束干涉的结果 点是 无穷)
λ
D
物点 一一对应 物点
第20章光的衍射
像点 像斑
ϕ1
可分辨
ϕ1 > δϕ
ϕ2
刚可分辨
ϕ2 = δϕ
ϕ3 < δϕ
ϕ3
不可分辨
瑞利判据: 对于两个等光强的非相干物点,如果一个像斑中心 瑞利判据 对于两个等光强的非相干物点 如果一个像斑中心 恰好落在另一像斑的边缘(第一暗纹处 第一暗纹处),则此两像被认为是刚 恰好落在另一像斑的边缘 第一暗纹处 则此两像被认为是刚 好能分辨。 好能分辨。此时两像斑中心角距离为最小分辨角
18-2 夫琅禾费单缝衍射
第十八章 光的衍射与偏振
18-2 夫琅禾费单缝衍射 18-
夫 琅 禾 费 单
R
L
衍射角
f
Q
P
A b B
θ
C
bsinθ
δ = BC = b sinθ
o
(衍射角θ ：向上为正，向下为负。) 衍射角 向上为正，向下为负。 A→P和B→P的光程差 和 的光程差
第十八章 光的衍射与偏振
18-2 夫琅禾费单缝衍射 18-
b sin θ = ± 2 k
λ
干涉相消（暗纹） = ± kλ 干涉相消（暗纹） 干涉加强（明纹） 干涉加强（明纹） 除了中央明纹外的其 它明纹、 它明纹、暗纹的宽度
l = θ k +1 f − θ k f =
λ f
b
（4）单缝衍射的动态变化 ） 单缝上下移动，根据透镜成像原理衍射图不变。 单缝上下移动，根据透镜成像原理衍射图不 上下移动
b A θ
总体上说： 总体上说：
k≠0
λ
? 中央明纹中心
B
b sin θ = 0
b sin θ = ±2k
λ/2
2 λ b sin θ = ± ( 2k + 1) 干涉加强（明纹） 2k + 1 干涉加强（明纹） 个半波带 2
= ± kλ 干涉相消（暗纹） 2k个半波带 干涉相消（暗纹）
b sinθ ≠ k
I0
I
0.047I0 0.017I0
0.017I0
0.047I0
−3
λ
b
−2
λ
b
−
λ
b
o
λ
b
2
λ
b
3
λ
b
sinθ
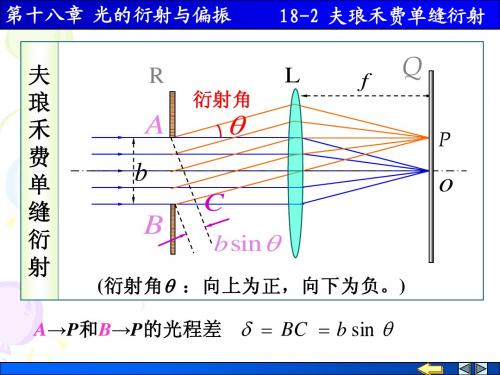
18-2 夫琅禾费单缝衍射 18-
夫 琅 禾 费 单
R
L
衍射角
f
Q
P
A b B
θ
C
bsinθ
δ = BC = b sinθ
o
(衍射角θ ：向上为正，向下为负。) 衍射角 向上为正，向下为负。 A→P和B→P的光程差 和 的光程差
第十八章 光的衍射与偏振
18-2 夫琅禾费单缝衍射 18-
b sin θ = ± 2 k
λ
干涉相消（暗纹） = ± kλ 干涉相消（暗纹） 干涉加强（明纹） 干涉加强（明纹） 除了中央明纹外的其 它明纹、 它明纹、暗纹的宽度
l = θ k +1 f − θ k f =
λ f
b
（4）单缝衍射的动态变化 ） 单缝上下移动，根据透镜成像原理衍射图不变。 单缝上下移动，根据透镜成像原理衍射图不 上下移动
b A θ
总体上说： 总体上说：
k≠0
λ
? 中央明纹中心
B
b sin θ = 0
b sin θ = ±2k
λ/2
2 λ b sin θ = ± ( 2k + 1) 干涉加强（明纹） 2k + 1 干涉加强（明纹） 个半波带 2
= ± kλ 干涉相消（暗纹） 2k个半波带 干涉相消（暗纹）
b sinθ ≠ k
I0
I
0.047I0 0.017I0
0.017I0
0.047I0
−3
λ
b
−2
λ
b
−
λ
b
o
λ
b
2
λ
b
3
λ
b
sinθ
光的干涉与衍射现象比较
光的干涉与衍射现象比较光的干涉和衍射是光学领域中两个基本的波动现象。
它们都是由光波的传播性质引起的，但在具体的表现形式上有所不同。
本文将对光的干涉和衍射现象进行比较，以便更好地理解它们之间的区别和联系。
一、光的干涉光的干涉是指两束或多束光波相互叠加而形成明暗条纹的现象。
两束或多束光波在空间中相遇时，会相互干涉，产生干涉条纹。
干涉的条件包括光源的相干性、干涉物（如刀口、薄膜等）的形状和间距。
典型的干涉现象有杨氏双缝干涉和牛顿环干涉。
1. 杨氏双缝干涉杨氏双缝干涉是将一束单色光通过两个非常接近的狭缝所形成的干涉现象。
在干涉屏幕上可以观察到一系列明暗相间的条纹，这些条纹可以用来测量光波的波长。
杨氏双缝干涉说明了干涉现象是由光波的波动性质引起的。
2. 牛顿环干涉牛顿环干涉是利用光在凸透镜和平板玻璃之间的干涉现象。
当光波在平板玻璃上反射和折射后再与原来的光波相遇时，会产生明暗相间的环形条纹。
利用牛顿环干涉可以测量透镜的曲率半径和介质的折射率。
二、光的衍射光的衍射是光波传播时遇到物体缝隙、边缘等障碍物时发生的波动现象。
衍射的结果是光波传播到屏幕上时形成弧形或直线条纹的图案。
典型的衍射现象有单缝衍射和夫琅禾费衍射。
1. 单缝衍射单缝衍射是将单色光波通过一个细缝后形成的衍射现象。
在屏幕上可以观察到中央明亮、两侧暗化的衍射条纹。
根据衍射条纹的形状和间距，可以推断出光波的波长和衍射角。
单缝衍射是衍射现象的一种基本表现形式。
2. 夫琅禾费衍射夫琅禾费衍射是指光通过一个具有圆形或方形孔径的屏幕后产生的衍射现象。
夫琅禾费衍射的特点是在中央有明亮的中心区域，并伴随着一系列的环形和直线衍射条纹。
夫琅禾费衍射是衍射现象中的典型例子，也被广泛应用于光学实验和光学仪器中。
三、干涉与衍射的比较尽管干涉和衍射两者都是光的波动现象，但在具体表现形式上有所区别。
1. 形成条件：干涉需要两束或多束光波的相互叠加，而衍射则是光波传播时通过物体缝隙或边缘发生的波动现象。
光的衍射问题
ba
1500（nm） 4500（nm）
(a b)sin
(2) k
2 10 理论上观察到最高
max
级次是第十级, 但最多只能观察到第九级。
(3) 由k a b k k 1,2, a k 4,8缺级 即第八级也缺级
实际呈现的条纹共15条：0， 1， 2， 3， 5， 6， 7， 9
※分辨率： 最小分辨角的倒数.
1
/
0
[ 1.22
D
] 1
•可见提高分辨率： ※增大孔径（天文、摄影） ※用紫光或紫外线作光源 ※电子显微镜（利用电子束的波动性成像）
X射线的衍射
# X 射线是波长很短的电磁波。
# 在电磁场中不发生偏转。 # X 射线的波长： 0.01 ~ 10nm
X射线管
阴极
阳极 （对阴极）
光的衍射问题的历史由来：
➢1818 年,巴 黎 科 学 院 举 行 了 一 次 以 解 释 衍 射 现 象 为 内 容 的 科 学 竞赛。 菲 涅 耳以惠更斯的波振面作图以及杨的 干涉原理相结合方式建立了一般的衍射理 论。
惠更斯-菲涅耳原理： 1）子波只能向前传播，且传播方向上任
一点的振幅与距离成反比； 2）传播方向上任一点的强度，决定于所
2
➢干涉与衍射的区别与联系
1、从根本上讲，都是波的相干叠加，没 有原则区别。
n
2、干涉：E Ei ，衍射：E dE
i 1
s
例：在单缝夫朗和费衍射实验中，屏上第3级暗纹 对应的单缝处波面可划分为——6 —个半波带？若 将缝宽缩小一半，原来第3级暗纹处将是明——纹。
例：波长为600nm的单色平行光，垂直入射到 缝宽为b=0.60mm的单缝上，缝后有一焦距 f=60cm的透镜。在透镜焦平面上观察衍射图 样.
单缝夫琅禾费衍射明暗纹公式
单缝夫琅禾费衍射明暗纹公式
夫琅禾费衍射是物理学的一个重要分支，用于研究光的衍射现象。
夫琅禾费衍射的基本原理是：当通过一条狭缝或一些微小孔洞的光线照射一个物体时，会发生弯曲和散射。
这种现象被称为衍射。
夫琅禾费衍射明暗纹的公式是：
dsin(θ) = mλ
其中，d是狭缝孔径的宽度，θ是散射光线和中心光线之间的夹角，m是干涉级数，λ是波长。
夫琅禾费衍射明暗纹公式的含义是，照射物体的光线被散射，形成明暗不同的衍射纹。
这些纹理取决于狭缝孔径宽度与照射光线波长之比、衍射角度等因素。
在实际应用中，夫琅禾费衍射广泛用于光学、激光技术、人体健康、科学研究等领域。
例如，科学家们能够通过夫琅禾费衍射技术，在人体细胞和组织中观察到各种有用信息，以帮助研究人类疾病的发病机理和治疗方法。
总之，夫琅禾费衍射明暗纹公式是物理学中重要的公式，用于描述狭缝或孔洞光散射过程中形成的明暗纹的特征。
7.6 单缝夫琅禾费衍射解析
( k 1,2 , ) 暗纹 ( k 1,2 , ) 明纹 中央明纹
正、负号表示衍射条纹对称分布于中央明纹的两侧
对于任意衍射角，单缝不能分成整数个半波带，
在屏幕上光强介于最明与最暗之间。
讨论
1. 光强分布 当 增加时,为什么光强的 极大值迅速衰减？
I
5 3 2a 2a
0
(2)由单缝衍射明纹所满足的条件
a sin (2k 1)
第1级明纹所对应的衍射角满足
2
600 109 3 sin (2k 1) (2 1 1) 4 . 5 10 2a 2 0.2 103
600 109 3 sin (2k 1) (2 1 1) 4 . 5 10 2a 2 0.2 103
第一级暗纹 k=1,1=300
a
sin 1
0.5 2 1.0m
例、一束波长为 =5000Å的平行光垂直照射在一个 单缝上。(2)如果所用的单缝的宽度a=0.5mm，缝后 紧挨着的薄透镜焦距f=1m，求：(a)中央明条纹的角 宽度；(b)中央亮纹的线宽度；(c) 第一级与第二级暗 纹的距离； (a)
3 2a
5 sin 2a
当 角增加时，半波带数增加，未被抵消的半 波带面积减少，所以光强变小； 另外，当： K ( ) I
2. 中央亮纹宽度
中央两侧第一暗条纹之间的区域，称做零极 （或中央）明条纹，它满足条件：
I
a
a sin
a 3 2a 5 sin 2a
a sin 2k
2
k 1
则
a sin0
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
射束与公路成 15角.发射的微波波长是18 mm ，假如发
射天线的输出口宽度 b 0.10 m，则在它监视范围内
的公路长度大约是多少？
解 将雷达天线输出口看成是发出衍射波的单缝，
衍射波能量主要集中在中央明纹范围内.
d 15 m
15 b 0.10 m
14 – 6 单缝衍射
s
s1
s2
1 15
bsin 2k k
b sin
(2k
2 1)
2
干涉相消（暗纹） 干涉加强（明纹）
I
3 2
bb b
O 2 3 sin
b
b
b
14 – 6 单缝衍射
S
L1 R
L2
b
Px
f
x
O
I
当 较小时，sin
x f
3 2 O 2 3 sin
答：根据透镜成像原理衍射图不变 .
R
单缝上移，零
f
o 级明纹中心仍在透 镜光轴上.
14 – 6 单缝衍射 讨论：下面单缝衍射图中，各条入射光线间距相 等，问：（1）光线 1 与 3 在幕上 P 点相遇时, 两光 振动的相位差是多少？ （2）P 点是明还是暗？
b
缝长
R
1
3
5 2
1
3
P
5
o
答：（1） 1，3光线 在P 点相遇时, 两光振
b
b
b
b
b
b
3 f 2 f f
bbb
f 2 f 3 f x
b
b
b
14 – 6 单缝衍射
bsin 2k k 干涉相消（暗纹）
讨论
b sin
(2k
2 1)
干涉加强（明纹）
sin ,
2
x f ,
bsin b x
f
（1）第一暗纹距中心的距离
动的位相差为 2π .
bsin 2k
2
（2） P 点是暗点.
14 – 6 单缝衍射 不同缝宽的单缝衍射条纹的比较
0.16 mm 0.08 mm 0.04 mm 0.02 mm
14 – 6 单缝衍射
例1 一单色平行光垂直入射一单缝，其衍射第
三级明纹位置恰好与波长为 600 nm 的单色光垂直入 射该缝时衍射的第二级位置重合，试求该单色光的波
长. 解
b sin (2k1源自 1) 12b sin
(2k2
1) 2
2
k1 3, k2 2, 2 600 nm
1
2k2 2k1
1 1
2
5 600 7
nm
428 .6 nm
14 – 6 单缝衍射 例2 如图所示，一雷达位于路边 15 m 处，它的
x1 f
b
f
第一暗纹的衍射角
1
arcsin
b
RL
b
P
x
O
f
14 – 6 单缝衍射
第一暗纹的衍射角
一定 b增大，1减小
b
减小，
增大
1
bb10a,,rc11sin bπ02
光直线传播 衍射最大
b 一定，越大，1越大，衍射效应越明显.
（2）中央明纹 （ k 1的两暗纹间）
角范围 sin 线范围 f x f
b
b
b
b
中央明纹的宽度
l0
2x1
2
b
f
14 – 6 单缝衍射 单缝宽度变化，中央明纹宽度如何变化？
14 – 6 单缝衍射 单缝实验（缝宽度变化对条纹的影响）
14 – 6 单缝衍射 入射波长变化，衍射效应如何变化 ?
14 – 6 单缝衍射
一 半波带法
A
b
B
缝长
R
A
L
A1
C
P Q
O
bsin 2k / 2
B /2
b
A
R
L
A
P Q
B
A1
bsin (2k 1) / 2 A2 C
O
k 1,2,3,
B /2
14 – 6 单缝衍射
R
L
A
A1
A2 C
B /2
P
BC bsin
Q
k
O
2
（ k 个半波带）
bsin 0
中央明纹中心
bsin 2k k 干涉相消（暗纹）2k个半波带
b sin
b sin
k (22k2（介1)于2明干暗涉之加间强）（明(k纹）1,个22,k半3波,1带)
14 – 6 单缝衍射
二 光强分布
mm的单缝上，缝后有焦距为40 cm的凸透镜，求透镜焦
平面上出现的衍射中央明纹的宽度。
解： bsin
sin
b
L 2x 2D tan
2D 2 D
D
b
25.460107 0.40 0.437 103
m
1.0103 m
2
d 15 m
b 0.10 m
根据暗纹条件 b sin , arcsin 10.37
b
s2 s s1 d(cot2 cot1)
d[cot(15 ) cot(15 )] 153 m
14 – 6 单缝衍射
例3 波长为546 nm的平行光垂直照射在 b = 0.437
越大，
越大，衍射效应越明显.
1
14 – 6 单缝衍射
（3）条纹宽度（相邻条纹间距）
bsin 2k k 干涉相消（暗纹）
b sin
(2k
2 1)
干涉加强（明纹）
2
l
k1 f
k
f
f
b
除了中央明纹外的其 他明纹、暗纹的宽度
问：单缝上下微小移动时，衍射图有否变化？
射天线的输出口宽度 b 0.10 m，则在它监视范围内
的公路长度大约是多少？
解 将雷达天线输出口看成是发出衍射波的单缝，
衍射波能量主要集中在中央明纹范围内.
d 15 m
15 b 0.10 m
14 – 6 单缝衍射
s
s1
s2
1 15
bsin 2k k
b sin
(2k
2 1)
2
干涉相消（暗纹） 干涉加强（明纹）
I
3 2
bb b
O 2 3 sin
b
b
b
14 – 6 单缝衍射
S
L1 R
L2
b
Px
f
x
O
I
当 较小时，sin
x f
3 2 O 2 3 sin
答：根据透镜成像原理衍射图不变 .
R
单缝上移，零
f
o 级明纹中心仍在透 镜光轴上.
14 – 6 单缝衍射 讨论：下面单缝衍射图中，各条入射光线间距相 等，问：（1）光线 1 与 3 在幕上 P 点相遇时, 两光 振动的相位差是多少？ （2）P 点是明还是暗？
b
缝长
R
1
3
5 2
1
3
P
5
o
答：（1） 1，3光线 在P 点相遇时, 两光振
b
b
b
b
b
b
3 f 2 f f
bbb
f 2 f 3 f x
b
b
b
14 – 6 单缝衍射
bsin 2k k 干涉相消（暗纹）
讨论
b sin
(2k
2 1)
干涉加强（明纹）
sin ,
2
x f ,
bsin b x
f
（1）第一暗纹距中心的距离
动的位相差为 2π .
bsin 2k
2
（2） P 点是暗点.
14 – 6 单缝衍射 不同缝宽的单缝衍射条纹的比较
0.16 mm 0.08 mm 0.04 mm 0.02 mm
14 – 6 单缝衍射
例1 一单色平行光垂直入射一单缝，其衍射第
三级明纹位置恰好与波长为 600 nm 的单色光垂直入 射该缝时衍射的第二级位置重合，试求该单色光的波
长. 解
b sin (2k1源自 1) 12b sin
(2k2
1) 2
2
k1 3, k2 2, 2 600 nm
1
2k2 2k1
1 1
2
5 600 7
nm
428 .6 nm
14 – 6 单缝衍射 例2 如图所示，一雷达位于路边 15 m 处，它的
x1 f
b
f
第一暗纹的衍射角
1
arcsin
b
RL
b
P
x
O
f
14 – 6 单缝衍射
第一暗纹的衍射角
一定 b增大，1减小
b
减小，
增大
1
bb10a,,rc11sin bπ02
光直线传播 衍射最大
b 一定，越大，1越大，衍射效应越明显.
（2）中央明纹 （ k 1的两暗纹间）
角范围 sin 线范围 f x f
b
b
b
b
中央明纹的宽度
l0
2x1
2
b
f
14 – 6 单缝衍射 单缝宽度变化，中央明纹宽度如何变化？
14 – 6 单缝衍射 单缝实验（缝宽度变化对条纹的影响）
14 – 6 单缝衍射 入射波长变化，衍射效应如何变化 ?
14 – 6 单缝衍射
一 半波带法
A
b
B
缝长
R
A
L
A1
C
P Q
O
bsin 2k / 2
B /2
b
A
R
L
A
P Q
B
A1
bsin (2k 1) / 2 A2 C
O
k 1,2,3,
B /2
14 – 6 单缝衍射
R
L
A
A1
A2 C
B /2
P
BC bsin
Q
k
O
2
（ k 个半波带）
bsin 0
中央明纹中心
bsin 2k k 干涉相消（暗纹）2k个半波带
b sin
b sin
k (22k2（介1)于2明干暗涉之加间强）（明(k纹）1,个22,k半3波,1带)
14 – 6 单缝衍射
二 光强分布
mm的单缝上，缝后有焦距为40 cm的凸透镜，求透镜焦
平面上出现的衍射中央明纹的宽度。
解： bsin
sin
b
L 2x 2D tan
2D 2 D
D
b
25.460107 0.40 0.437 103
m
1.0103 m
2
d 15 m
b 0.10 m
根据暗纹条件 b sin , arcsin 10.37
b
s2 s s1 d(cot2 cot1)
d[cot(15 ) cot(15 )] 153 m
14 – 6 单缝衍射
例3 波长为546 nm的平行光垂直照射在 b = 0.437
越大，
越大，衍射效应越明显.
1
14 – 6 单缝衍射
（3）条纹宽度（相邻条纹间距）
bsin 2k k 干涉相消（暗纹）
b sin
(2k
2 1)
干涉加强（明纹）
2
l
k1 f
k
f
f
b
除了中央明纹外的其 他明纹、暗纹的宽度
问：单缝上下微小移动时，衍射图有否变化？