铁电体及其相变完
第21讲7-3铁电相变与晶体结构变化

图7.21 几种势阱形状 (a)抛物线势阱;(b)非谐势阱; (c)双平衡位置势阱
从以上讨论中可见,自发极化不可能出现在 抛物线型势阱中,考虑自发极化时,必须要 考虑到力常数的非线性特征。
离子在平衡位置附近的振动以格波的形式在 晶体中传播。显然,考察晶体的自发极化不 能只考虑离子在单个势阱中的振动,应该把 晶体作为一个整个来考虑。
钛酸钡晶体在居里点以下还发生多次铁电铁电相变在0℃±5℃时,晶体结构转变为 正交晶系,mm2点群。自发极化方向由原 立方晶体的[001]方向转为[011]方向。
晶体同样也在自发极化方向上伸长,这相 当于原顺电相的立方晶胞在两个轴向上同 时产生了自发极化,因而晶胞沿着面对角 线方向伸长,形成单斜格子。
为了解释晶格振动模的软化与铁电性的关系, 可以考察晶格振动的一个简化模型。 假定质量为m,有效电荷为q的离子在非谐势阱 中振动。 等效力常数 离子的振动方程
K K0 K ' T K ' ' T 2
离子在晶格平衡位置附近的振动可以看成在 势阱底部的运动 当离子偏离平衡位置时将受到恢复力f的作用
f K1 x K 2 x
3
其中K1、K2为力常数。因此离子所在势阱的 势函数u为
u
x 0
1 1 2 fdx K1 x K 2 x 4 2 4
形成自发极化的条件是
qEe f 0
当温度较低时,钛离子的平均热运动能量下降, 那些由热涨落所形成的势运动能量特别低的钛 离子,就不足以克服钛离子位移后因钛氧离子 间的相互作用所形成的内电场,因此就向着某 一个氧离子,产生自发位移,从而使这个晶胞 出现电矩。这种自发位移便能波及到周围晶胞 中的所有钛离子,使它们同时都沿着同一方向 发生位移,因而形成一个自发极化的小区域, 这就是电畴。与此同时晶胞的形状发生了畸变, 晶胞沿着钛离子移动的方向伸长,在其他两个 垂直方向上缩短,从而转变成四方晶系结构。
铁电性(材料物理性能)
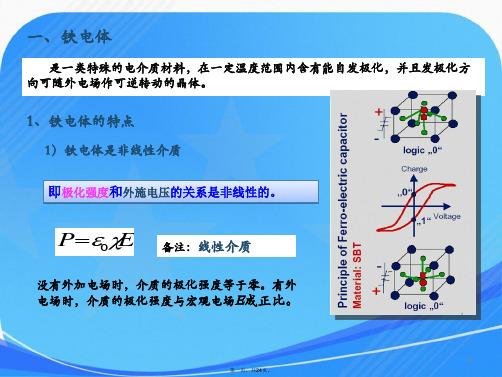
BaTiO3单晶电畴结构的差异,导致两
者之间在铁电性质方面的微小差别。
2211
第二十一页,共24页。
3)电滞回线的意义
A.判定铁电体的依据
铁电材料在外加交变电场作用下都能形成电滞回线,不同材料和不同工艺条件对 电滞回线的形状都有很大的影响。
B.由于有剩余极化强度,因而铁电体可用来作信息存储、图象显示。
AO
铁电体微观结构的特点决定了它有许多特殊
E
的宏观性质,从而区别于普通电介质。
铁电电滞回线(Ps为自发极化强度,Ec为矫顽力)
1144
第十四页,共24页。
A.施加电场
➢沿电场方向的电畴扩展,变大;而
P
Ps B
C
与电场反平行方向的电畴则变小。极 化强度随外电场增加而增加,如图中
oA段曲线。
Pr Ps Pr
压峰效应
如在BaTiO3中加入Bi2/3SnO3 ,其居里点几乎完 全消失,显示出直线性的温度特性可认为其机理是 加入非铁电体后,破坏了原来的内电场,使自发极 化减弱,即铁电性减小。
压峰的目的 为了降低居里点处的介电常数的蜂值,即降低ε-T非线性,也使工
作状态相应于ε-T平缓区。
2244
第二十四页,共24页。
顺电性晶体与铁电性晶体的转变温度称为铁电居里点t时铁电相转变为顺电相电滞回线消失这时p与e一般有线性关系p二铁电体的居里外斯定律居里点附近居里外斯定律为忽略12指铁电体的微观结构性质以及因此而可能显示出来的宏观性质指铁电体的微观结构性质以及因此而可能显示出来的宏观性质电滞回线电畴结构自发极化以及相应的晶胞形变自发应变居里点居里外斯定律等
+
铁电体及其相变

应力诱导相变 是指在应力作 用下,铁电体 晶体结构发生 可逆变化的现
象。
铁电体相变的应用
铁电存储器:利用铁电体的相变特性,实现数据的存储和读取 铁电场效应晶体管:利用铁电体的相变特性,实现晶体管的开关功能 铁电传感器:利用铁电体的相变特性,实现对物理量的检测和测量 铁电显示技术:利用铁电体的相变特性,实现图像的显示和更新
铁电晶体管:利用铁电体的电 场效应,实现晶体管的开关功 能
铁电光子学:利用铁电体的电 场效应,实现光子器件的调制 和控制
铁电材料在生物医学领域的 应用:利用铁电材料的生物 相容性,实现生物医学器件 的制备和应用
铁电体的相变
铁电体的相变类型
顺电相变:铁电体从顺电相变为铁电相 的过程
反电相变:铁电体从铁电相变为反电相 的过程
目的:提高铁电体的性能
效果:提高铁电体的电学性能、热 稳定性等
添加标题
添加标题
添加标题
添加标题
方法:通过表面处理,如涂层、掺 杂等
应用:在电子、能源等领域有广泛 应用
复合改性
复合材料:铁 电体与其他材 料复合,提高
性能
ቤተ መጻሕፍቲ ባይዱ
改性方法:添 加其他元素或 改变结构,提 高铁电体性能
应用领域:电 子、能源、生 物医学等领域
气相沉积法:在高温下,将 铁电体原料蒸发成气体,然 后在基底上沉积形成铁电体 薄膜
铁电体的性能优化
掺杂改性
掺杂元素:如稀土元素、过渡金属元素等 掺杂方式:固溶体、非晶态、纳米颗粒等 掺杂效果:提高铁电体的电学性能、热稳定性、机械强度等 掺杂机理:通过改变铁电体的晶体结构、电子结构等来优化性能
表面改性
添加标题 添加标题
铁电体的热释电性是指其晶体结构中存在电偶极矩,且电偶极矩的大小可以随温度变化而改变。 铁电体的电致伸缩性是指其晶体结构中存在电偶极矩,且电偶极矩的大小可以随外加电场而改变。
03第三章 铁电相变的宏观理论3

3.1.2 弹性吉布斯自由能展开
• 为研究铁电相变,首先考虑独立变量选择。 在实验过程中,应力和温度便于控制,故 X和T应选为独立变量; • 由于铁电相变必须用极化来表征,相变的 发生取决于极化对特征函数影响,而极化P 与电位移的关系为D=ε 0E+P,所以选D为 独立变量是适当的,则有相应特征函数G1
dU TdS X i dxi EmdDm .
其它特征函数的全微分形式
dA SdT X i dxi Em dDm , dH TdS xi dX i Dm dEm , dH1 TdS xi dX i Em dDm , dH 2 TdS X i dxi Dm dEm , dG SdT xi dX i Dm dEm , dG1 SdT xi dX i Em dDm , dG2 SdT X i dxi Dm dEm .
E 2G1 2 4 a ( T T ) 3 D 5 D . 0 0 2 D D
• 因为讨论的是电场很弱时的介电性,所以上式 右边取E=0时值。在顺电相无自发极化,上式 成为居里-外斯定律;在铁电相,D等于Ps,得
4a0 (T T0 ) 2r 1{1 [1 4a0r 2 (T T0 )]1/ 2}.
第三章 铁电相变的宏观理论
• 铁电体热力学理论始于1940年代,最早的工作是 Mü iler对罗息盐研究。基本思想是将自由能展开为 极化的各次幂之和,并建立展开式中各系数与宏观 可测量之间关系。它的优点是只用少数几个参量即 可预言各种宏观可测量及它们对温度的依赖性,便 于进行实验检验。 • 自BaTiO3出现后,Ginzburg和Devonshire等人开展 一系列研究工作来完善铁电体热力学理论,Kittel 将其推广到反铁电体。现在,普遍采用的形式基本 上与Devonshire相同,所以有时简称为Devonshire 理论。在铁电体各种著作中,热力学理论占有相当 大篇幅,特别是Grindley专门对铁电体热力学理论 作出全面系统论述。
铁电体的基本特征

铁电体的基本特征铁电体的基本特征铁电体是一种具有特殊电性质的材料,其具有两个极性状态,可以在外加电场作用下发生极化反转,这种特殊的性质使得铁电体在电子学、光学、声学等领域有着广泛的应用。
本文将从晶体结构、热力学性质、电学性质和磁学性质四个方面介绍铁电体的基本特征。
一、晶体结构铁电体的晶体结构通常是非中心对称晶体结构,其具有空间反演对称性破缺。
这种非中心对称结构使得铁电体具有了极化现象。
常见的铁电材料包括钛酸锆(ZrTiO4)、钛酸镧(LaTiO3)、钛酸钡(BaTiO3)等。
二、热力学性质1.相变温度铁电材料具有相变温度,即在一定温度范围内由无序相向有序相转变。
这种相变通常伴随着极化反转现象。
例如,BaTiO3在120℃左右发生相变,同时极化方向也发生了反转。
2.比热和热容铁电材料的比热和热容通常具有峰值,在相变温度附近出现。
这是因为相变时铁电材料吸收或释放大量的热量。
三、电学性质1.极化铁电体具有两个稳定的极化状态,即正向极化和负向极化。
在外加电场作用下,铁电体可以发生极化反转,即从一个稳定状态转变为另一个稳定状态。
这种极化反转现象是铁电材料应用于存储器、传感器等领域的基础。
2.介电常数铁电体的介电常数随着温度和频率的变化而变化。
在相变温度附近,介电常数会发生突变,这是因为相变时极化方向发生了反转。
四、磁学性质1.自旋玻璃态一些铁电材料具有自旋玻璃态,即在低温下呈现出玻璃态,并且具有自旋玻璃特征。
例如,BiFeO3就是一种具有自旋玻璃态的铁电材料。
2.多铁性一些铁电材料同时具有铁磁性和铁电性,这种材料被称为多铁材料。
多铁材料具有更加丰富的物理性质和应用前景。
例如,BiFeO3就是一种典型的多铁材料。
总结铁电体具有非中心对称晶体结构、相变温度、比热和热容、极化、介电常数、自旋玻璃态和多铁性等特征。
这些特征使得铁电体在存储器、传感器、光学器件等领域有着广泛的应用前景。
铁电体及其相变完共38页文档

G 11 20(T T 0)D 21 4D 41 6D 6
介电方程:
E 0 (T T 0 )D D 3D 5
G1(D)的极值位置可由下列方程确定:
G D 1 [0(T T 0) D 2 D 4]D 0
1):T T1时, D=0, 顺电相
2)T T0时, D=Ds, 铁电相
Dm D s
3):T0TT1时 ,
a.在T=TC处,发生一级相变,特征为顺电相和铁电相可以共存。
b.存在热滞现象。 E 0 (T T 0 )D D 3D 5
升温时,铁电相可滞后到T=T1时发生转变为顺电相。 降温时,顺电相可滞后到T=T0时发生转变为铁电相。
c. 在零场下,自发极化强度:
Ps
Ps Ds , 及Pc Dc. (T Tc ) Ps 0 , (T Tc )
Tc
G1(D)有五个极值,D0,Ds 都是一级相变铁电体在各个温度下的态函数G1
极小值,表明铁电相和顺电相可
以共存。
其中G1(Ds), G1(0)中最小者为稳 定相,另一相为亚稳态相。
Ds
T0 T T1
哪一个为稳定相与热过程有关。
一级相变临界行为
Tc
T0
3 2 160
和
D
2 c
3 4
T0 Tc T1
晶态转变——固态到液态 磁相变——顺磁到铁磁,顺磁到反铁磁态
铁电相变——顺电态到铁电态 超导相变…….
2.相变的描述
Landau相变理论:对称性破缺和序参量
当宏观物理环境(如:温度或压力)变化时物质结构的 对称性发生变化或消失,称这种现象为对称破缺。 相变发生时,粒子内不同种类的相互作用通过对称破 缺导致不同的有序相。
Tc
铁电体及其相变完

2.组分调控相变问题
准同型相界:(MPB) 铁电性、压电性、热释 电等效应显著
FT 铁电四方相 FR 铁电三方相 PC 顺电立方相
PbZrO3
Mole % PbTiO3
PbTiO3
PZT材料的相图
PbZr1-xTixO3是制备铁电存储器的一类重要材料, 具备优良的铁电、压电和光学特性受到人们的青睐。
铁电相变的实质是出现自发极化,在一个相中为零,而 在令一个相中不为零。 选取自发极化为序参量。
铁电相变属于相变问题,可用热力学方法分析。
一、相变
相变现象丰富多彩,如大海里的万顷碧波,初秋 早晨湖面上的袅袅青烟和高山上的缕缕薄雾,夏天黄 昏时万里云空中的朵朵彩云及冬日雪后琳琅满目的雪 花和冰晶便是水的各种相变。由此可见自然界中相变 的千姿百态之一斑。千姿百态的水。
E 0, D 2E D2 0
T TC T T2, D 0.
T1 T T2 TC T T1
得到:T2
T0
9 2 200
对比:T1
T0
2 40
存在一个小的温区,电场诱导顺电相到铁电相的转变。
小结
二级相变临界行为
Ps
Ps 0,T Tc
当宏观物理环境(如:温度或压力)变化时物质结构的 对称性发生变化或消失,称这种现象为对称破缺。 相变发生时,粒子内不同种类的相互作用通过对称破 缺导致不同的有序相。
为描述相变中系统对称性的变化,为描述其对称元素 的变化,引入一个物理量η ,叫序参量。
η用来标记相变温度以下的有序相。 系统的对称性在η为非零时发生,是突变的;序参量的 变化则有两种。
e
铁电材料的铁电相变行为研究

铁电材料的铁电相变行为研究近年来,铁电材料的研究备受关注。
铁电材料是一类能在外电场作用下发生电极化的晶体材料,其具有独特的铁电相变行为。
研究铁电材料的铁电相变行为对于理解材料的性质以及应用于传感器、存储器等领域具有重要意义。
首先,我们来介绍一下铁电材料的基本概念。
铁电材料是一类具有正负电荷分离的晶体材料,其内部由偏离中心的阳离子和偏离中心的阴离子构成。
在没有外电场作用下,这些离子呈现出对称的排列。
然而,当外电场作用于铁电材料时,正负电荷分离的离子会产生移动,导致晶体整体呈现出非对称的电极化状态。
这种电极化是可逆的,即当外电场撤离时,晶体会恢复到无电场作用下的对称状态。
铁电材料的铁电相变行为是指在一定的温度和电场条件下,晶体从一种铁电相变为另一种铁电的现象。
这种相变过程具有快速和可控性的特点,因此在研究铁电相变行为的基础上,可以开发出各种铁电器件和功能材料。
目前,研究者们已经发现了多种不同类型的铁电相变,如铁电-铁电相变、铁电-非铁电相变等。
这些相变行为的研究有助于深入了解铁电材料的性质和机制。
铁电相变行为的研究可以从多个角度入手。
例如,从理论上研究铁电相变的驱动力和机制,可以通过分析能量和熵的变化来解释铁电相变的原理。
同时,通过实验手段可以研究铁电材料的结构、形貌和性能等方面的变化。
例如,可以利用X 射线衍射和透射电子显微镜等技术手段来观察铁电相变的晶体结构和微观形貌的变化。
铁电相变行为的研究不仅限于基础理论,还涉及到材料性能的改进和新材料的开发。
通过调控电场和温度等参数,可以实现铁电相变的控制和调节。
这种可调控性使得铁电材料在传感器、存储器以及电子器件等领域应用广泛。
例如,在存储器领域,铁电材料可用于制作非挥发性存储器,具有高速度和较大存储容量的特点。
在传感器领域,铁电材料可用于制作压力传感器和温度传感器等,具有高灵敏度和稳定性的特点。
然而,铁电相变行为的研究仍面临着一些挑战。
首先,铁电相变的机制和动力学过程仍不完全清楚,需要进一步的实验和理论研究。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
——场致相变
e td 2d d
3
5
临界温度T2确定: 存在拐点,有
E 0, D 2E 0 2 D
T TC
T T2 , D 0.
T1 T T2 TC T T1
9 2 得到:T2 T0 200
2 对比:T1 T0 4 0
在居里点附近系数γ,δ不随温度变化,但系数
具有温度特性,在居里温度以上为正;居里温度以下为负。
0 (T Tc )
铁电性的一般热力学方程
G1 E D D3 D5 D 1
1 1 1 2 4 G1 D D D 6 2 4 6
XT
自发极化:
0 P (Tc T ), T Tc
2 s
T
Tc
居里-外斯定律:
XT
C/2 , T Tc Tc T
C , T Tc T Tc
T
Tc
2.一级铁电相变
0
相变为一级相变; 令
Tc
一级相变铁电体在各个温度下的态函数G1
0 (T T0 )
则,自由能函数
介电方程:
1 1 1 2 D 4 D 6 G1 0 (T T0 ) D 2 4 6
E 0 (T T0 ) D D3 D5
G1(D)的极值位置可由下列方程确定:
G1 [ 0 (T T0 ) D 2 D 4 ]D 0 D
dG1 Si dX i E dD dT
0
0
当系统不受外力,恒温条件下,自发极化沿某一方向
1 1 1 2 4 G1 D D D 6 2 4 6
E=0时的自由能
0 保证D增加时,G1出现自由能极小值 正、负关系到相变的类型
0 相变为二级相变; 0 相变为一级相变;
晶态转变——固态到液态 磁相变——顺磁到铁磁,顺磁到反铁磁态
铁电相变——顺电态到铁电态
超导相变…….
2.相变的描述
Landau相变理论:对称性破缺和序参量 当宏观物理环境(如:温度或压力)变化时物质结构的 对称性发生变化或消失,称这种现象为对称破缺。 相变发生时,粒子内不同种类的相互作用通过对称破 缺导致不同的有序相。
《铁电体物理学》 钟维烈
注意:晶体取向对铁电性产生影响
1500
1500
(b)
Intensity (arb.units)(Leabharlann ) (111) orientation
(100) orientation
Intensity (arb.units)
1200
1200 900 600 300
Py (110) (100)
T0 T T1
Ds
哪一个为稳定相与热过程有关。
一级相变临界行为
3 2 3 2 Tc T0 和 Dc T0 Tc T1 16 0 4 a.在T=TC处,发生一级相变,特征为顺电相和铁电相可以共存。
b.存在热滞现象。 E 0 (T T0 ) D D3 D5 升温时,铁电相可滞后到T=T1时发生转变为顺电相。 降温时,顺电相可滞后到T=T0时发生转变为铁电相。 c. 在零场下,自发极化强度:
第四章
电介质物理
§1 电介质的介电极化机制 §2 电介质的介电驰豫 §3 铁电体的晶体结构及分类 §4 几种典型的铁电有序相 §5 铁电相变的热力学理论
§4.5 铁电相变的热力学理论
铁电体在某一温度发生从非铁电相到铁电相的转变, 或者从铁电相到另一个铁电相的转变,伴随结构的转 变。晶体从一种结构转变为另外一种结构,热力学称 成为相变。
T Tc T Tc T Tc
T Tc 时,D总为单值函数 T Tc 时,D总为单值函数 T Tc 时,D程多值函数,表现出电滞回线行为 T Tc 时,D始终为单值函数,不表现出电滞回线行为。
E
当处于顺电态时,外加电场不能诱导铁电相。
电场对一级相变影响
据压电方程:
D
T TC
Intensity (arb.units)
600 300 0
Py (110)
20
30
(111)
2θ /(o)
40
(200)
900
(100)
1200
50
60
2
-6
-4
-2
0
2
4
6
8
Applied voltage /(V)
PZT薄膜(100)取向的薄膜与(111)取向的薄膜相比, 随(100)取向的增强,薄膜铁电性减弱
Ps Pc
Ps Ds , 及Pc Dc . (T Tc ) Ps 0, (T Tc )
一级铁电相变,自发极化强度在转 变点Tc上发生间断。
T
O
Tc T1
d.在弱电场下,介电性能:
在顺电相,
XT
2
E 0 (T T0 ) D D3 D5
居里-外斯常数的倒数
当T<TC时,G1取极小值,得出自发极化为:
1 1 1 2 4 G1 D D D 6 2 4 6
2 D [1
2
4 0
2
(Tc T )]1 2 , T Tc
TC低温附近时,当TC-T不太大时,近似为:
0 D (Tc T ), T Tc
2000 1500 1000 500 0 60 20
(d) 650 C(30s)
30
40
50
30
40
50
60
2θ
-4 -2 0 2 4 applied voltage (V) 6 8
2θ
随晶粒尺寸减小,铁电性 减弱,当小于临界尺寸时, 铁电性消失
18 16 14 12 10 8 6 4 2 0
Polarization /(μ m/cm
2
150nm
experimental date theoritical curve
38 40 42 44 46 48 50 52 54 56 58 60 grain size /(nm)
临界尺寸小于40nm,铁 电性消失 铁电临界尺寸也可由Tc=0 的尺寸确定,根据计算结果 BaTiO3:44nm; PbTiO3:4.2nm
3.电场对铁电相变的影响
居里温度的确定
极化强度随温度的关系 ——极化强度消失温度
400
介电常数随温度的关系
——出现峰值温度
TC
350
300
TC
250
100
200
300
400
500
T ( C)
o
电场对二级相变影响
据压电方程:
P
E 0 (T Tc ) D D 3 D 5
2.组分调控相变问题
2
Tc T1
T
O
T0 Tc
3.存在场致相变行为
二、铁电相变的其它问题
Intensity (arb.units)
2000 (a) 560 C(60s) 1500 1000 500 0
o
2000 (b) 590 C(30s) 1500 1000 500 0 2500
O O o
当
0
时二级相变,
1 1 1 2 4 G1 D D D 6 2 4 6
0 时,G1只有一个极小值,
D=0对应顺电相。
G1
0 0
0 时,D=0对应G1极大值,
顺电相不稳定;稳定态的电位 移不等于零,对应铁电相。 Devonshire假设:
二级相变自由能
D0
3 2 0 (T Tc ) , T Tc 16 1
在铁电相,E=0时,D=±Ds,
T
O
T0 Tc
3 2 8 0 (Tc ) T , T Tc 32 0 结论: XT 1
在居里点上系统的
发生间断,
居里点两侧, XT 曲线斜率之比为-8。
一级相变临界行为
1.自发极化
Ps Ds , (T Tc ) Ps 0,
(T Tc )
Ps Pc
热滞
T
2.介电常数
1
2
O
XT
3 0 (T Tc ) , T Tc 16 1 3 2 8 0 (Tc ) T , T Tc 32 0
2
a)外场E=0时,上式为:
0 P (Tc T ), T Tc , E 0
2 s
b)外场
E 0时,得到:
0 (T Tc )
XT 3 D2 5 D4
1
XT
XT
2 0 (T Tc ), T Tc
可得到如下结论:
Ps
Ps 0, T Tc
600 300 0 20 30 40 50 60
(111)
900
0 20
50
Polarization(μ C/cm )
1500
30
40
(200)
50
60
40
(c) mixed orientation
30 20 10 0 -10 -20 -30 -40 -50 -8
(111) orientation (100) orientation mixed orientation
1) :T T1时, D=0, 顺电相 2)T T0时,
D=Ds, 铁电相
