2014年全国高中数学联赛真题(A卷)参考答案解析
2002~2014年全国高中数学联赛(安徽赛区)预赛试题及解答
4.
设 P1 , P2 是平面上两点, P2 k +1 是 P2 k 关于 P1 的对称点, P2 k + 2 是 P2 k +1 关于 P2 的对称点,
k ∈ N * .若 P1 P2 = 1 ,则 P2013 P2014 =
. .
5.
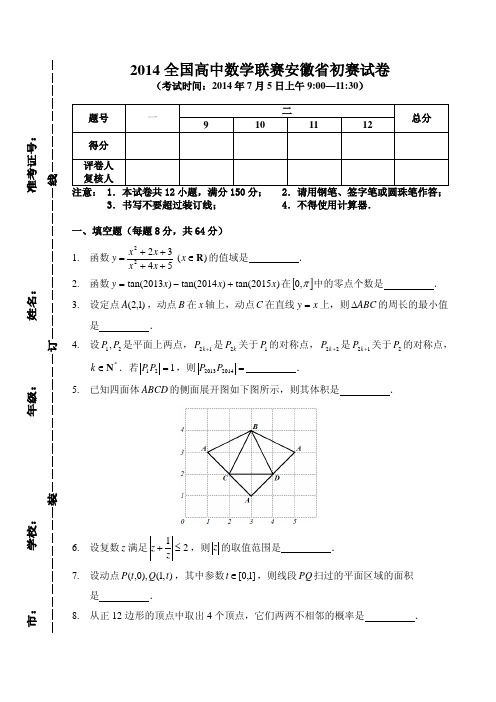
已知四面体 ABCD 的侧面展开图如下图所示,则其体积是
6. 7.
ABCD 一定是菱形,否则如图所示,可固定两对角
点(不妨设是 B, D ) ,过 A,C 分别做 BD 的平行线, 调整另外两点 A, C 的位置,使它们分别位于两平行 线上,则 ∆ABD 和 ∆CBD 的面积都不变,但 L 变大.从而 AB=AD, BC=CD.类似地, AB=BC, CD=DA. 即 ABCD 是菱形-----12 分
2 (3) aω + bω + c = 0 .将第(4)式乘 a 减去第(3)式乘 b 得 2 + ( + ) + = 0 ( 4 ) b a c a ω ω
1 1 12. (1)设 f ( x) = x 3 − x − 1 ,则 f ′( x) = 3 x 2 − 1 . f ( x) 在 − ∞, − 单调增,在 x = − 3 3 处取得极大值 2 1 1 1 处取得极小值 , − 1 < 0 ,在 − 单调减,在 x = 3 3 3 3 3 2
P2 k + 2 = 2k ( P2 − P1 ) + P2 P2 k +1 = 2 P1 − P2 k 4. . ⇒ P2 k + 2 = 2( P2 − P1 ) + P2 k ⇒ P2 k +1 = 2k ( P1 − P2 ) + P2 P2 k + 2 = 2 P2 − P2 k +1 从而, P2 k +1 P2 k + 2 = 4k P1 P2 .特别, P2013 P2014 = 4024 .
2014年湖南省高中数学竞赛真题及答案解析(A卷)word

2014年湖南高中数学竞赛试卷一、选择题(本大题共6小题,每小题5分,共30分)1.设22{|,,}M a a x y x y Z ==-∈,则 ( )A .9,10M M ∈∈B .9,10M M ∉∈C .9,10M M ∈∉D . 9,10M M ∉∉2. 设条件p :实数,m n 满足24,03;m n mn <+<⎧⎨<<⎩条件q :实数,m n 满足01,2 3.m n <<⎧⎨<<⎩则 ( ) A .p 是q 的充分不必要条件 B .p 是q 的必要不充分条件C .p 是q 的充要条件D .p 既不是q 的充分条件又不是q 的必要条件3. 若{}n a 是等差数列,若120132014201320140,0,0a a a a a >+>⋅<,则使前n 项和0n S >成立的最大自然数n 是 ( )A .4025B .4026C .4027D .40284. 给定平面向量(1,1)a =,平面向量131(22b -=是向量a 经过 ( ) A .顺时针旋转60所得 B .顺时针旋转120所得C .逆时针旋转60所得D .逆时针旋转120所得5. 在如图所示的三棱柱中,点A 、1BB 的中点M 及11B C 的中点N 所决定的平面把三棱柱割成体积不同的两部分,则较小部分与原三棱柱的体积之比为 ( )A .2336B .1336C .1323D .12236. 已知圆222:C x y r +=,两点*P P 、在以O 为起点的射线上,并且满足*2||||OP OP r ⋅=,则称*P P 、关于圆对称,那么双曲线221x y -=上的点(,)P x y 关于圆22:1C x y +=的对称点*P 所满足的方程是 ( )A .2244x y x y -=+B .22222()x y x y -=+C .22442()x y x y -=+D .222222()x y x y -=+二、填空题(本大题共6小题,每小题8分,共48分)7.已知22()53196|53196|f x x x x x =-++-+,则(20)(14)f f +=________________.8.已知0,sin cos ,24x x x ππ<<-=若1tan tan x x +可以表示成ca b π-的形式(,,a b c 为正整数),则a b c ++=_______________.9.不等式32||24||30x x x --+<的解集是__________________.10.已知一无穷等差数列中有3项(顺序排列单不一定相连):13,25,41.则可以判断得出2013_________(填“是”、“不是”或“不能确定”)数列中的一项.11.随机摸选一个三位数I ,则I 含有因子5的概率为_______________.12.已知实数,x y 满足05030x y x y y -≤⎧⎪+-≥⎨⎪-≤⎩.若不等式222()()a x y x y +≤+恒成立,则实数a 的最大值是_____________.三、解答题(本大题共4小题,共72分)*13.(本小题满分16分)已知O 为ABC ∆的内部一点,BAO CAO CBO ACO ∠=∠=∠=∠,试研究ABC ∆的三边满足的关系,并证明你的结论.14.(本小题满分16分)某旅游区每年各月份接待的人数近似的满足周期性规律,即第n 个月从事旅游服务工作的人数()f n 可近似地用函数()100[cos()]f n A n k ωα=++来刻画,其中正整数n 表示月份且*n N ∈.例如1n =表示1月份,A 和k 是正整数,0,(0,)2πωα>∈.统计发现,该地区每年各月份从事旅游服务工作的人数有以下规律:①每年相同的月份,该地区从事旅游服务工作的人数基本相同;②该地区从事旅游服务工作的人数最多的8月份和最少的2月份相差400人;③2月份该地区从事旅游服务工作的人数约为100人,随后逐月递增直到8月份达到最多.(1)试根据已知信息,确定一个符合条件的()f n 的表达式;(2)一般地,当该地区从事旅游服务工作的人数在400或400以上时,该地区也进入了一年中的旅游“旺季”,那么一年中的哪几个月是该地区的旅游“旺季”?请说明理由.15.(本小题满分20分)若实数0x 满足00()f x x =,则称0x x =为函数()f x 的一个不动点.已知32()3f x x ax bx =+++(其中,a b 为常数)有互异的两个极值点1x 和2x .试判断是否存在实数组(,)a b ,使得1x 和2x 皆为不动点,并证明你的结论.16.(本小题满分20分)已知数列{}n x 满足21122,2,6n n n x x x x x ++=+==,数列{}n y 满足21122,3,9n n n y y y y y ++=+==,求证:存在正整数0n ,使得对任意0n n >都有n n x y >.。
答案与评分细则(14年高中数学联赛四川试题)

2014年全国高中数学联赛(四川)参考答案及评分标准说明:1、评阅试卷时,请依据评分标准.选择题和填空题只设5分和0分两档;其它各题的评阅,请严格按照评分标准规定的评分档次给分,不要再增加其它中间档次.2、如果考生的解答题方法和本解答不同,只要思路合理,步骤正确,在评阅时可参考本评分标准适当划分档次评分,5分一个档次,不要再增加其它中间档次. 一、选择题(本大题共6个小题,每小题5分,共30分)1、D2、B3、A4、B5、C6、C 二、填空题(本大题共6个小题,每小题5分,共30分)7、326 8、14 9、80 10、0 11、5 12、28 三、解答题(本大题共4个小题,每小题20分,共80分)13、已知a 为常数,函数1()ln(1xf x ax x−=−+. (1)求函数()f x 的单调递减区间;(2)若83a =−,求()f x 的极值.解:(1)函数()f x 的定义域为(1,1)−.()ln(1)ln(1)f x x x ax =−−+−,2112()111f x a a x x x −−′=−−=−−+− (5分) 因为11x −<<,故2221x−≤−−; ① 当2a >−时,()0f x ′<恒成立,故单调递减区间为(1,1)−; ② 当2a =−时,(1,0)x ∈−时()0f x ′<;0x =时()0f x ′=; (0,1)x ∈时()0f x ′<; 故单调递减区间为(1,1)−;③ 当2a <−时,由()0f x ′<知221a x−<−,即22a x a +>1x <<或者1x −<<;故单调递减区间为,(1,−. 综上所述,当2a ≥−时,单调递减区间为(1,1)−;当2a <−时,单调递减区间为,(1,−−年全国高中数学联赛(四川)试题(2)823a =−<−,由()0f x ′=知驻点为12x =−,或12x =; 于是: 112x −<<−时'()0f x <;1122x −<<时'()0f x >;112x <<时'()0f x <. (15分) 所以,()f x 有极小值14()ln 323f −=−+,有极大值14()ln 323f =−.(20分)14、已知不等式31cos 4cos sin 3222≤++−a x a x x 对一切R x ∈恒成立,求实数a 的取值范围.解:设31cos 4cos sin 3)(222−++−=a x a x x x f ,则28cos 4cos 4)(22−++−=a x a x x f 令x t cos =,则]1,1[−∈t故当]1,1[−∈t 时,22()44280g t t at a =−++−≤恒成立 二次函数()g t 的对称轴2a t =, ①当12a≤−,即2a ≤−时,()g t 在]1,1[−∈t 上单减, 故有()g t 的最大值2(1)4320g a a −=−−≤,解得42a −≤≤−; (5分)②当112a −<<,即22a −<<时,有()g t 的最大值2(22802ag a =−≤, 解得22a −<<; (10分) ③当12a≥,即2a ≥时,()g t 在]1,1[−∈t 上单增,故有()g t 的最大值2(1)4320g a a =+−≤,解得24a ≤≤; (15分) 综上可知,所求a 的取值范围是[4,4]−. (20分)15、已知k 为给定正整数,数列{}n a 满足13a =,2*211(31)3()k n n a S n −+=−+∈N ,其中n S 是{}n a 的前n 项和.令3121log ()()n n b a a a n n =∈"*N ,记213||2kk i i T b ==−∑.若k T ∈*N ,求k 的所有可能值.解:由条件知22121212(31)333k k k a +−−=−×+=,又 2211(31)3k n n a S −+=−+,2211(31)3k n n a S −−=−+(2n ≥) 故2211(31)k n n n a a a −+−=−,即22113k n n a a −+=.于是2223221212)3(2)n k n k k n a a n +−−−−==≥,显然1n =也符合.所以,数列{}n a 的通项公式22321()n k k n a n +−−=∈*N . (5分)从而3121log ()n n b a a a n ="111(223)21ni i k n k ==⋅+−−∑1121n k −=+−.(10分) 于是1()32221n n k b k −+−=−,从而n k ≤时302n b −<;1n k ≥+时302nb −>. 所以222111333||()()22221kk kk i i i i i i k k T b b b k ===+=−=−+−=−∑∑∑. (15分) 因为k T ∈*N ,即2(21)|k k −,故2(21)|(411)k k −−+,于是(21)|1k − 故211k −=,解得1k =.所以所求k 的所有可能值为1k =. (20分)16、过椭圆22132x y +=的右焦点F 作两条垂直的弦AB 、CD ,设AB 、CD 的中点分别为M 、N .(1)求证:直线MN 必过定点,并求出这个定点;(2)若弦AB 、CD 的斜率均存在,求△FMN 的面积的最大值. 解:(1)由题意知,(1,0)F .① 当弦AB 、CD 的斜率均存在,设AB 的斜率为k ,则CD 的斜率为1k−. 设:(1)AB y k x =−,代入椭圆方程22132x y +=,得2222(32)6(36)0k x k x k +−+−=,所以223232A B M x x k x k +==+,22(1)32M M k y k x k −=−=+,故点22232(,3232k kM k k −++.因为CD ⊥AB ,所以将点M 的坐标中的k 换为1k −,即得点2232(,)2323kN k k ++.(5分)(i )当1k ≠±时,22222222332332332MNk kk k k k k k +++=−++24210(1)56633k k k k k +−==−−, 此时直线MN 的方程为222253()233323k ky xk k k −−=−+−+,则直线MN 过定点3(,0)5. (ii )当1k =±时,易得直线MN 的方程为35x =,也过点3(,0)5. ② 当弦AB 或弦CD 的斜率不存在时,易知直线MN 为x 轴,也过点3(,0)5.综上可知,直线MN 必过定点E 3(,0)5. (10分)(2)由(1)知S △FMN =1||||2M N EF y y ⋅⋅− 2212253223k kk k −=−++2222(1)(32)(23)k k k k +=++ (15分) 不妨设0k >,则6424222222222212101012(12212)(1)(32)(23)(32)(23)k k k k k k S k k k k −−++−+−−′==++++ 由0S ′=知1k =.又(0,1)k ∈时,0S ′>; (1,)k ∈+∞时,0S ′<; 故当1k =时,S 有最大值为425.所以,△FMN 的面积的最大值是425. (20分)。
2014年全国统一高考数学试卷(理科)(大纲版)(含解析版)A3

2014年全国统一高考数学试卷(理科)(大纲版)一、选择题(本大题共12小题,每小题5分)1.(5分)设z=,则z的共轭复数为()A.﹣1+3i B.﹣1﹣3i C.1+3i D.1﹣3i2.(5分)设集合M={x|x2﹣3x﹣4<0},N={x|0≤x≤5},则M∩N=()A.(0,4]B.[0,4)C.[﹣1,0)D.(﹣1,0]3.(5分)设a=sin33°,b=cos55°,c=tan35°,则()A.a>b>c B.b>c>a C.c>b>a D.c>a>b4.(5分)若向量、满足:||=1,(+)⊥,(2+)⊥,则||=()A.2B .C.1D .5.(5分)有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有()A.60种B.70种C.75种D.150种6.(5分)已知椭圆C :+=1(a>b>0)的左、右焦点为F1、F2,离心率为,过F2的直线l交C于A、B两点,若△AF1B的周长为4,则C的方程为()A .+=1B .+y2=1C .+=1D .+=17.(5分)曲线y=xe x﹣1在点(1,1)处切线的斜率等于()A.2e B.e C.2D.18.(5分)正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为()A .B.16πC.9πD .9.(5分)已知双曲线C的离心率为2,焦点为F1、F2,点A在C上,若|F1A|=2|F2A|,则cos∠AF2F1=()A .B .C .D .10.(5分)等比数列{a n}中,a4=2,a5=5,则数列{lga n}的前8项和等于()A.6B.5C.4D.311.(5分)已知二面角α﹣l﹣β为60°,AB⊂α,AB⊥l,A为垂足,CD⊂β,C∈l,∠ACD=135°,则异面直线AB与CD所成角的余弦值为()A .B .C .D .12.(5分)函数y=f(x)的图象与函数y=g(x)的图象关于直线x+y=0对称,则y=f(x)的反函数是()A.y=g(x)B.y=g(﹣x)C.y=﹣g(x)D.y=﹣g(﹣x)二、填空题(本大题共4小题,每小题5分)13.(5分)的展开式中x2y2的系数为.(用数字作答)14.(5分)设x、y 满足约束条件,则z=x+4y的最大值为.15.(5分)直线l1和l2是圆x2+y2=2的两条切线,若l1与l2的交点为(1,3),则l1与l2的夹角的正切值等于.16.(5分)若函数f(x)=cos2x+asinx 在区间(,)是减函数,则a的取值范围是.三、解答题17.(10分)△ABC的内角A、B、C的对边分别为a、b、c,已知3acosC=2ccosA,tanA=,求B.18.(12分)等差数列{a n}的前n项和为S n,已知a1=13,a2为整数,且S n≤S4.(1)求{a n}的通项公式;(2)设b n =,求数列{b n}的前n项和T n.19.(12分)如图,三棱柱ABC﹣A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.(Ⅰ)证明:AC1⊥A1B;(Ⅱ)设直线AA1与平面BCC1B1的距离为,求二面角A1﹣AB﹣C的大小.20.(12分)设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为0.6、0.5、0.5、0.4,各人是否需使用设备相互独立.(Ⅰ)求同一工作日至少3人需使用设备的概率;(Ⅱ)X表示同一工作日需使用设备的人数,求X的数学期望.21.(12分)已知抛物线C:y2=2px(p>0)的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且|QF|=|PQ|.(Ⅰ)求C的方程;(Ⅱ)过F的直线l与C相交于A、B两点,若AB的垂直平分线l′与C相交于M、N两点,且A、M、B、N四点在同一圆上,求l的方程.22.(12分)函数f(x)=ln(x+1)﹣(a>1).(Ⅰ)讨论f(x)的单调性;(Ⅱ)设a1=1,a n+1=ln(a n+1),证明:<a n ≤(n∈N*).2014年全国统一高考数学试卷(理科)(大纲版)参考答案与试题解析一、选择题(本大题共12小题,每小题5分)1.(5分)设z=,则z的共轭复数为()A.﹣1+3i B.﹣1﹣3i C.1+3i D.1﹣3i【考点】A1:虚数单位i、复数;A5:复数的运算.【专题】5N:数系的扩充和复数.【分析】直接由复数代数形式的除法运算化简,则z的共轭可求.【解答】解:∵z==,∴.故选:D.【点评】本题考查复数代数形式的除法运算,考查了复数的基本概念,是基础题.2.(5分)设集合M={x|x2﹣3x﹣4<0},N={x|0≤x≤5},则M∩N=()A.(0,4]B.[0,4)C.[﹣1,0)D.(﹣1,0]【考点】1E:交集及其运算.【专题】5J:集合.【分析】求解一元二次不等式化简集合M,然后直接利用交集运算求解.【解答】解:由x2﹣3x﹣4<0,得﹣1<x<4.∴M={x|x2﹣3x﹣4<0}={x|﹣1<x<4},又N={x|0≤x≤5},∴M∩N={x|﹣1<x<4}∩{x|0≤x≤5}=[0,4).故选:B.【点评】本题考查了交集及其运算,考查了一元二次不等式的解法,是基础题.3.(5分)设a=sin33°,b=cos55°,c=tan35°,则()A.a>b>c B.b>c>a C.c>b>a D.c>a>b【考点】HF:正切函数的单调性和周期性.【专题】56:三角函数的求值.【分析】可得b=sin35°,易得b>a,c=tan35°=>sin35°,综合可得.【解答】解:由诱导公式可得b=cos55°=cos(90°﹣35°)=sin35°,由正弦函数的单调性可知b>a,而c=tan35°=>sin35°=b,∴c>b>a故选:C.【点评】本题考查三角函数值大小的比较,涉及诱导公式和三角函数的单调性,属基础题.4.(5分)若向量、满足:||=1,(+)⊥,(2+)⊥,则||=()A.2B .C.1D .【考点】9O:平面向量数量积的性质及其运算.【专题】5A:平面向量及应用.【分析】由条件利用两个向量垂直的性质,可得(+)•=0,(2+)•=0,由此求得||.【解答】解:由题意可得,(+)•=+=1+=0,∴=﹣1;(2+)•=2+=﹣2+=0,∴b2=2,则||=,故选:B.【点评】本题主要考查两个向量垂直的性质,两个向量垂直,则它们的数量积等于零,属于基础题.5.(5分)有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有()A.60种B.70种C.75种D.150种【考点】D9:排列、组合及简单计数问题.【专题】5O:排列组合.【分析】根据题意,分2步分析,先从6名男医生中选2人,再从5名女医生中选出1人,由组合数公式依次求出每一步的情况数目,由分步计数原理计算可得答案.【解答】解:根据题意,先从6名男医生中选2人,有C62=15种选法,再从5名女医生中选出1人,有C51=5种选法,则不同的选法共有15×5=75种;故选:C.【点评】本题考查分步计数原理的应用,注意区分排列、组合的不同.6.(5分)已知椭圆C :+=1(a>b>0)的左、右焦点为F1、F2,离心率为,过F2的直线l交C于A、B两点,若△AF1B的周长为4,则C的方程为()A .+=1B .+y2=1C .+=1D .+=1【考点】K4:椭圆的性质.【专题】5D:圆锥曲线的定义、性质与方程.【分析】利用△AF1B的周长为4,求出a=,根据离心率为,可得c=1,求出b,即可得出椭圆的方程.【解答】解:∵△AF1B的周长为4,∵△AF1B的周长=|AF1|+|AF2|+|BF1|+|BF2|=2a+2a=4a,∴4a=4,∴a=,∵离心率为,∴,c=1,∴b==,∴椭圆C 的方程为+=1.故选:A.【点评】本题考查椭圆的定义与方程,考查椭圆的几何性质,考查学生的计算能力,属于基础题.7.(5分)曲线y=xe x﹣1在点(1,1)处切线的斜率等于()A.2e B.e C.2D.1【考点】62:导数及其几何意义.【专题】52:导数的概念及应用.【分析】求函数的导数,利用导数的几何意义即可求出对应的切线斜率.【解答】解:函数的导数为f′(x)=e x﹣1+xe x﹣1=(1+x)e x﹣1,当x=1时,f′(1)=2,即曲线y=xe x﹣1在点(1,1)处切线的斜率k=f′(1)=2,故选:C.【点评】本题主要考查导数的几何意义,直接求函数的导数是解决本题的关键,比较基础.8.(5分)正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为()A .B.16πC.9πD .【考点】LG:球的体积和表面积;LR:球内接多面体.【专题】11:计算题;5F:空间位置关系与距离.【分析】正四棱锥P﹣ABCD的外接球的球心在它的高PO1上,记为O,求出PO1,OO1,解出球的半径,求出球的表面积.【解答】解:设球的半径为R,则∵棱锥的高为4,底面边长为2,∴R2=(4﹣R)2+()2,∴R=,∴球的表面积为4π•()2=.故选:A.【点评】本题考查球的表面积,球的内接几何体问题,考查计算能力,是基础题.9.(5分)已知双曲线C的离心率为2,焦点为F1、F2,点A在C上,若|F1A|=2|F2A|,则cos∠AF2F1=()A .B .C .D .【考点】KC:双曲线的性质.【专题】5D:圆锥曲线的定义、性质与方程.【分析】根据双曲线的定义,以及余弦定理建立方程关系即可得到结论.【解答】解:∵双曲线C的离心率为2,∴e=,即c=2a,点A在双曲线上,则|F1A|﹣|F2A|=2a,又|F1A|=2|F2A|,∴解得|F1A|=4a,|F2A|=2a,||F1F2|=2c,则由余弦定理得cos∠AF2F1===.故选:A.【点评】本题主要考查双曲线的定义和运算,利用离心率的定义和余弦定理是解决本题的关键,考查学生的计算能力.10.(5分)等比数列{a n}中,a4=2,a5=5,则数列{lga n}的前8项和等于()A.6B.5C.4D.3【考点】89:等比数列的前n项和.【专题】54:等差数列与等比数列.【分析】利用等比数列的性质可得a1a8=a2a7=a3a6=a4a5=10.再利用对数的运算性质即可得出.【解答】解:∵数列{a n}是等比数列,a4=2,a5=5,∴a1a8=a2a7=a3a6=a4a5=10.∴lga1+lga2+…+lga8=lg(a1a2•…•a8)=4lg10=4.故选:C.【点评】本题考查了等比数列的性质、对数的运算性质,属于基础题.11.(5分)已知二面角α﹣l﹣β为60°,AB⊂α,AB⊥l,A为垂足,CD⊂β,C∈l,∠ACD=135°,则异面直线AB与CD所成角的余弦值为()A .B .C .D .【考点】LM:异面直线及其所成的角.【专题】5G:空间角.【分析】首先作出二面角的平面角,然后再构造出异面直线AB与CD所成角,利用解直角三角形和余弦定理,求出问题的答案.【解答】解:如图,过A点做AE⊥l,使BE⊥β,垂足为E,过点A做AF∥CD,过点E做EF⊥AE,连接BF,∵AE⊥l∴∠EAC=90°∵CD∥AF又∠ACD=135°∴∠FAC=45°∴∠EAF=45°在Rt△BEA中,设AE=a,则AB=2a,BE=a,在Rt△AEF中,则EF=a,AF=a,在Rt△BEF中,则BF=2a,∴异面直线AB与CD所成的角即是∠BAF,∴cos∠BAF===.故选:B.【点评】本题主要考查了二面角和异面直线所成的角,关键是构造二面角的平面角和异面直线所成的角,考查了学生的空间想象能力和作图能力,属于难题.12.(5分)函数y=f(x)的图象与函数y=g(x)的图象关于直线x+y=0对称,则y=f(x)的反函数是()A.y=g(x)B.y=g(﹣x)C.y=﹣g(x)D.y=﹣g(﹣x)【考点】4R:反函数.【专题】51:函数的性质及应用.【分析】设P(x,y)为y=f(x)的反函数图象上的任意一点,则P关于y=x的对称点P′(y,x)一点在y=f(x)的图象上,P′(y,x)关于直线x+y=0的对称点P″(﹣x,﹣y)在y=g(x)图象上,代入解析式变形可得.【解答】解:设P(x,y)为y=f(x)的反函数图象上的任意一点,则P关于y=x的对称点P′(y,x)一点在y=f(x)的图象上,又∵函数y=f(x)的图象与函数y=g(x)的图象关于直线x+y=0对称,∴P′(y,x)关于直线x+y=0的对称点P″(﹣x,﹣y)在y=g(x)图象上,∴必有﹣y=g(﹣x),即y=﹣g(﹣x)∴y=f(x)的反函数为:y=﹣g(﹣x)故选:D.【点评】本题考查反函数的性质和对称性,属中档题.二、填空题(本大题共4小题,每小题5分)13.(5分)的展开式中x2y2的系数为70.(用数字作答)【考点】DA:二项式定理.【专题】5P:二项式定理.【分析】先求出二项式展开式的通项公式,再令x、y的幂指数都等于2,求得r的值,即可求得展开式中x2y2的系数.【解答】解:的展开式的通项公式为T r+1=•(﹣1)r ••=•(﹣1)r ••,令8﹣=﹣4=2,求得r=4,故展开式中x2y2的系数为=70,故答案为:70.【点评】本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.14.(5分)设x、y 满足约束条件,则z=x+4y的最大值为5.【考点】7C:简单线性规划.【专题】31:数形结合.【分析】由约束条件作出可行域,化目标函数为直线方程的斜截式,由图得到最优解,联立方程组求出最优解的坐标,代入目标函数得答案.【解答】解:由约束条件作出可行域如图,联立,解得C(1,1).化目标函数z=x+4y 为直线方程的斜截式,得.由图可知,当直线过C点时,直线在y轴上的截距最大,z最大.此时z max=1+4×1=5.故答案为:5.【点评】本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.15.(5分)直线l1和l2是圆x2+y2=2的两条切线,若l1与l2的交点为(1,3),则l1与l2的夹角的正切值等于.【考点】IV:两直线的夹角与到角问题.【专题】5B:直线与圆.【分析】设l1与l2的夹角为2θ,由于l1与l2的交点A(1,3)在圆的外部,由直角三角形中的边角关系求得sinθ=的值,可得cosθ、tanθ 的值,再根据tan2θ=,计算求得结果.【解答】解:设l1与l2的夹角为2θ,由于l1与l2的交点A(1,3)在圆的外部,且点A与圆心O之间的距离为OA==,圆的半径为r=,∴sinθ==,∴cosθ=,tanθ==,∴tan2θ===,故答案为:.【点评】本题主要考查直线和圆相切的性质,直角三角形中的变角关系,同角三角函数的基本关系、二倍角的正切公式的应用,属于中档题.16.(5分)若函数f(x)=cos2x+asinx 在区间(,)是减函数,则a的取值范围是(﹣∞,2] .【考点】HM:复合三角函数的单调性.【专题】51:函数的性质及应用;57:三角函数的图像与性质.【分析】利用二倍角的余弦公式化为正弦,然后令t=sinx换元,根据给出的x的范围求出t的范围,结合二次函数的图象的开口方向及对称轴的位置列式求解a的范围.【解答】解:由f(x)=cos2x+asinx=﹣2sin2x+asinx+1,令t=sinx,则原函数化为y=﹣2t2+at+1.∵x ∈(,)时f(x)为减函数,则y=﹣2t2+at+1在t ∈(,1)上为减函数,∵y=﹣2t2+at+1的图象开口向下,且对称轴方程为t=.∴,解得:a≤2.∴a的取值范围是(﹣∞,2].故答案为:(﹣∞,2].【点评】本题考查复合函数的单调性,考查了换元法,关键是由换元后函数为减函数求得二次函数的对称轴的位置,是中档题.三、解答题17.(10分)△ABC的内角A、B、C的对边分别为a、b、c,已知3acosC=2ccosA,tanA=,求B.【考点】GL:三角函数中的恒等变换应用;HP:正弦定理.【专题】58:解三角形.【分析】由3acosC=2ccosA,利用正弦定理可得3sinAcosC=2sinCcosA,再利用同角的三角函数基本关系式可得tanC,利用tanB=tan[π﹣(A+C)]=﹣tan(A+C)即可得出.【解答】解:∵3acosC=2ccosA,由正弦定理可得3sinAcosC=2sinCcosA,∴3tanA=2tanC,∵tanA=,∴2tanC=3×=1,解得tanC=.∴tanB=tan[π﹣(A+C)]=﹣tan(A+C)=﹣=﹣=﹣1,∵B∈(0,π),∴B=【点评】本题考查了正弦定理、同角的三角函数基本关系式、两角和差的正切公式、诱导公式等基础知识与基本技能方法,考查了推理能力和计算能力,属于中档题.18.(12分)等差数列{a n}的前n项和为S n,已知a1=13,a2为整数,且S n≤S4.(1)求{a n}的通项公式;(2)设b n =,求数列{b n}的前n项和T n.【考点】8E:数列的求和.【专题】55:点列、递归数列与数学归纳法.【分析】(1)通过S n≤S4得a4≥0,a5≤0,利用a1=13、a2为整数可得d=﹣4,进而可得结论;(2)通过a n=13﹣3n,分离分母可得b n =(﹣),并项相加即可.【解答】解:(1)在等差数列{a n}中,由S n≤S4得:a4≥0,a5≤0,又∵a1=13,∴,解得﹣≤d ≤﹣,∵a2为整数,∴d=﹣4,∴{a n}的通项为:a n=17﹣4n;(2)∵a n=17﹣4n,∴b n ===﹣(﹣),于是T n=b1+b2+……+b n=﹣[(﹣)+(﹣)+……+(﹣)]=﹣(﹣)=.【点评】本题考查求数列的通项及求和,考查并项相加法,注意解题方法的积累,属于中档题.19.(12分)如图,三棱柱ABC﹣A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.(Ⅰ)证明:AC1⊥A1B;(Ⅱ)设直线AA1与平面BCC1B1的距离为,求二面角A1﹣AB﹣C的大小.【考点】LW:直线与平面垂直;MJ:二面角的平面角及求法.【专题】5F:空间位置关系与距离.【分析】(Ⅰ)由已知数据结合线面垂直的判定和性质可得;(Ⅱ)作辅助线可证∠A1FD为二面角A1﹣AB﹣C的平面角,解三角形由反三角函数可得.【解答】解:(Ⅰ)∵A1D⊥平面ABC,A1D⊂平面AA1C1C,∴平面AA1C1C⊥平面ABC,又BC⊥AC∴BC⊥平面AA1C1C,连结A1C,由侧面AA1C1C为菱形可得AC1⊥A1C,又AC1⊥BC,A1C∩BC=C,∴AC1⊥平面A1BC,AB1⊂平面A1BC,∴AC1⊥A1B;(Ⅱ)∵BC⊥平面AA1C1C,BC⊂平面BCC1B1,∴平面AA1C1C⊥平面BCC1B1,作A1E⊥CC1,E为垂足,可得A1E⊥平面BCC1B1,又直线AA1∥平面BCC1B1,∴A1E为直线AA1与平面BCC1B1的距离,即A1E=,∵A1C为∠ACC1的平分线,∴A1D=A1E=,作DF⊥AB,F为垂足,连结A1F,又可得AB⊥A1D,A1F∩A1D=A1,∴AB⊥平面A1DF,∵A1F⊂平面A1DF∴A1F⊥AB,∴∠A1FD为二面角A1﹣AB﹣C的平面角,由AD==1可知D为AC中点,∴DF==,∴tan∠A1FD==,∴二面角A1﹣AB﹣C的大小为arctan【点评】本题考查二面角的求解,作出并证明二面角的平面角是解决问题的关键,属中档题.20.(12分)设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为0.6、0.5、0.5、0.4,各人是否需使用设备相互独立.(Ⅰ)求同一工作日至少3人需使用设备的概率;(Ⅱ)X表示同一工作日需使用设备的人数,求X的数学期望.【考点】C8:相互独立事件和相互独立事件的概率乘法公式;CH:离散型随机变量的期望与方差.【专题】5I:概率与统计.【分析】记A i表示事件:同一工作日乙丙需要使用设备,i=0,1,2,B表示事件:甲需要设备,C 表示事件,丁需要设备,D表示事件:同一工作日至少3人需使用设备(Ⅰ)把4个人都需使用设备的概率、4个人中有3个人使用设备的概率相加,即得所求.(Ⅱ)X的可能取值为0,1,2,3,4,分别求出PX i,再利用数学期望公式计算即可.【解答】解:由题意可得“同一工作日至少3人需使用设备”的概率为0.6×0.5×0.5×0.4+(1﹣0.6)×0.5×0.5×0.4+0.6×(1﹣0.5)×0.5×0.4+0.6×0.5×(1﹣0.5)×0.4+0.6×0.5×0.5×(1﹣0.4)=0.31.(Ⅱ)X的可能取值为0,1,2,3,4P(X=0)=(1﹣0.6)×0.52×(1﹣0.4)=0.06P(X=1)=0.6×0.52×(1﹣0.4)+(1﹣0.6)×0.52×0.4+(1﹣0.6)×2×0.52×(1﹣0.4)=0.25P(X=4)=P(A2•B•C)=0.52×0.6×0.4=0.06,P(X=3)=P(D)﹣P(X=4)=0.25,P(X=2)=1﹣P(X=0)﹣P(X=1)﹣P(X=3)﹣P(X=4)=1﹣0.06﹣0.25﹣0.25﹣0.06=0.38.故数学期望EX=0×0.06+1×0.25+2×0.38+3×0.25+4×0.06=2【点评】本题主要考查了独立事件的概率和数学期望,关键是找到独立的事件,计算要有耐心,属于难题.21.(12分)已知抛物线C:y2=2px(p>0)的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且|QF|=|PQ|.(Ⅰ)求C的方程;(Ⅱ)过F的直线l与C相交于A、B两点,若AB的垂直平分线l′与C相交于M、N两点,且A、M、B、N四点在同一圆上,求l的方程.【考点】KH:直线与圆锥曲线的综合.【专题】5E:圆锥曲线中的最值与范围问题.【分析】(Ⅰ)设点Q的坐标为(x0,4),把点Q的坐标代入抛物线C的方程,求得x0=,根据|QF|=|PQ|求得p的值,可得C的方程.(Ⅱ)设l的方程为x=my+1 (m≠0),代入抛物线方程化简,利用韦达定理、中点公式、弦长公式求得弦长|AB|.把直线l′的方程代入抛物线方程化简,利用韦达定理、弦长公式求得|MN|.由于MN垂直平分线段AB,故AMBN四点共圆等价于|AE|=|BE|=|MN|,由此求得m的值,可得直线l的方程.【解答】解:(Ⅰ)设点Q的坐标为(x0,4),把点Q的坐标代入抛物线C:y2=2px(p>0),可得x0=,∵点P(0,4),∴|PQ|=.又|QF|=x0+=+,|QF|=|PQ|,∴+=×,求得p=2,或p=﹣2(舍去).故C的方程为y2=4x.(Ⅱ)由题意可得,直线l和坐标轴不垂直,y2=4x的焦点F(1,0),设l的方程为x=my+1(m≠0),代入抛物线方程可得y2﹣4my﹣4=0,显然判别式△=16m2+16>0,y1+y2=4m,y1•y2=﹣4.∴AB的中点坐标为D(2m2+1,2m),弦长|AB|=|y1﹣y2|==4(m2+1).又直线l′的斜率为﹣m,∴直线l′的方程为x=﹣y+2m2+3.过F的直线l与C相交于A、B两点,若AB的垂直平分线l′与C相交于M、N两点,把线l′的方程代入抛物线方程可得y2+y﹣4(2m2+3)=0,∴y3+y4=,y3•y4=﹣4(2m2+3).故线段MN的中点E的坐标为(+2m2+3,),∴|MN|=|y3﹣y4|=,∵MN垂直平分线段AB,故AMBN四点共圆等价于|AE|=|BE|=|MN|,∴+DE2=MN2,∴4(m2+1)2 ++=×,化简可得m2﹣1=0,∴m=±1,∴直线l的方程为x﹣y﹣1=0,或x+y﹣1=0.【点评】本题主要考查求抛物线的标准方程,直线和圆锥曲线的位置关系的应用,韦达定理、弦长公式的应用,体现了转化的数学思想,属于难题.22.(12分)函数f(x)=ln(x+1)﹣(a>1).(Ⅰ)讨论f(x)的单调性;(Ⅱ)设a1=1,a n+1=ln(a n+1),证明:<a n ≤(n∈N*).【考点】6B:利用导数研究函数的单调性;RG:数学归纳法.【专题】53:导数的综合应用.【分析】(Ⅰ)求函数的导数,通过讨论a的取值范围,即可得到f(x)的单调性;(Ⅱ)利用数学归纳法即可证明不等式.【解答】解:(Ⅰ)函数f(x)的定义域为(﹣1,+∞),f′(x)=,①当1<a<2时,若x∈(﹣1,a2﹣2a),则f′(x)>0,此时函数f(x)在(﹣1,a2﹣2a)上是增函数,若x∈(a2﹣2a,0),则f′(x)<0,此时函数f(x)在(a2﹣2a,0)上是减函数,若x∈(0,+∞),则f′(x)>0,此时函数f(x)在(0,+∞)上是增函数.②当a=2时,f′(x)≥0,此时函数f(x)在(﹣1,+∞)上是增函数,③当a>2时,若x∈(﹣1,0),则f′(x)>0,此时函数f(x)在(﹣1,0)上是增函数,若x∈(0,a2﹣2a),则f′(x)<0,此时函数f(x)在(0,a2﹣2a)上是减函数,若x∈(a2﹣2a,+∞),则f′(x)>0,此时函数f(x)在(a2﹣2a,+∞)上是增函数.(Ⅱ)由(Ⅰ)知,当a=2时,此时函数f(x)在(﹣1,+∞)上是增函数,当x∈(0,+∞)时,f(x)>f(0)=0,即ln(x+1)>,(x>0),又由(Ⅰ)知,当a=3时,f(x)在(0,3)上是减函数,当x∈(0,3)时,f(x)<f(0)=0,ln(x+1)<,下面用数学归纳法进行证明<a n ≤成立,①当n=1时,由已知,故结论成立.②假设当n=k 时结论成立,即,则当n=k+1时,a n+1=ln(a n+1)>ln (),a k+1=ln(a k+1)<ln (),即当n=k+1时,成立,综上由①②可知,对任何n∈N•结论都成立.【点评】本题主要考查函数单调性和导数之间的关系,以及利用数学归纳法证明不等式,综合性较强,难度较大.。
2014年全国高中数学联赛A卷真题word版

一试一、填空题1. 若正数b a ,满足()b a b a +=+=+632log log 3log 2,则b a 11+的值为________.2. 设集合⎭⎬⎫⎩⎨⎧≤≤≤+213b a b a 中的最大元素与最小元素分别为m M ,,则m M -的值为__________.3. 若函数()12-+=x a x x f 在[)+∞,0上单调递增,则实数a 的取值范围是__________.4. 数列{}n a 满足21=a ,()()*+∈++=N n a n n a n n 1221,则=+++2013212014a a a a Λ . 5. 正四棱锥ABCD P -中,侧面是边长为1的正三角形,N M ,分别是边BC AB ,的中点,则异面直线MN 与PC 之间的距离是__________.6. 设椭圆Γ的两个焦点是21,F F ,过点1F 的直线与Γ交于点Q P ,.若212F F PF =,且1143QF PF =,则椭圆Γ的短轴与长轴的比值为__________.7. 设等边三角形ABC 的内切圆半径为2,圆心为I .若点P 满足1=PI ,则APB ∆与APC ∆的面积之比的最大值为__________.8. 设D C B A ,,,是空间四个不共面的点,以21的概率在每对边之间连一条边,任意两对点之间是否连边是相互独立的,则B A ,可用(一条边或者若干条边组成的)空间折线连接的概率为__________.二、解答题9. 平面直角坐标系xOy 中,P 是不在x 轴上的一个动点,满足条件:过P 可作抛物线x y 42=的两条切线,两切点连线P l 与PO 垂直.设直线P l 与直线PO ,x 轴的交点分别为R Q ,.(1)证明R 是一个定点; (2)求QR PQ 的最小值. 10. 数列{}n a 满足61π=a ,()n n a a sec arctan 1=+()*∈N n .求正整数m ,使得1001sin sin sin 21=⋅⋅⋅m a a a Λ. 11. 确定所有的复数α,使得对任意复数21,z z ()2121,1,z z z z ≠<,均有 ()()222121z z z z αααα++≠++.二试一、设实数c b a ,,满足1=++c b a ,0>abc .求证:412+<++abc ca bc ab .二、如图,在锐角ABC ∆中,︒≠∠60BAC ,过点B 、C 分别作ABC ∆的外接圆⊙O 的切线BD 、EC ,且满足BC CE BD ==.直线DE 与AB 、AC 的延长线分别交于点F 、G .设CF 与BD 交于点M ,CE 与BG 交于点N .求证:AN AM =.三、设{}100,,3,2,1Λ=S .求最大的整数k ,使得S 有k 个互不相同的非空子集,具有性质:对这k 个子集中任意两个不同子集,若它们的交非空,则它们交集中的最小元素与这两个子集中的最大元素均不相同.四、设整数201421,,,x x x Λ模2014互不同余,整数201421,,,y y y Λ模2014也互不同余. 证明:可将201421,,,y y y Λ重新排列为201421,,,z z z Λ,使得201420142211,,,z x z x z x +++Λ模4028互不同余.。
2014年全国高中数学联赛试题及答案详解(A卷)

2013
解:由题设
an
2(n 1) n
an1
2(n 1) n
2n n 1 an2
2(n 1) n
2n n 1
23 2
a1
2n1 (n
1)
.
记数列{an} 的前 n 项和为 Sn ,则
Sn =
2 + 2 × 3 + 22 × 4 + + 2n−1(n +1)
2015 2013
2015
.
2013
5. 正四棱锥 P ABCD 中,侧面是边长为 1 的正三角形,M , N 分别是边 AB, BC 的中
点,则异面直线 MN 与 PC 之间的距离是
.
答案: 2 . 4
解:设底面对角线 AC, BD 交于点 O ,过点 C 作直
线 MN 的垂线,交 MN 于点 H . 由 于 PO 是 底 面 的 垂 线 , 故 PO CH , 又
解:记 f (z) (z )2 z .则
f (z1) f (z2 ) (z1 )2 z1 (z2 )2 z2
(z1 z2 2)(z1 z2 ) z1 z2 .
①
假如存在复数 z1, z2 ( z1 , z2 1, z1 ≠ z2 ) ,使得 f (z1) f (z2 ) ,则由①知,
连接的情况数.
(1) 有 AB 边:共 25 32 种情况.
(2) 无 AB 边,但有 CD 边:此时 A , B 可用折线连接当且仅当 A 与 C , D 中至少一
点相连,且 B 与 C , D 中至少一点相连,这样的情况数为 (22 1)(22 1) 9 .
2014年全国高中数学联赛江苏赛区初赛参考答案与评分细则(定稿)

2014年全国高中数学联赛江苏赛区初赛参考答案与评分细则一、填空题(本题满分70分,每小题7分)1.若x ≥2,则函数f (x )=x +1x +1的最小值是 .答案:73.2.已知函数f (x )=e x .若f (a +b )=2,则f (3a )·f (3b )的值是 . 答案:8.3.已知数列{a n }是各项均不为0的等差数列,公差为d ,S n 为其前n 项和,且满足a n 2=S 2n -1,n ∈N *,则数列{a n }的通项a n = . 答案:2n -1.4.若函数f (x )=⎩⎨⎧2x 2-3x , x ≥0,-2x 2+ax ,x <0是奇函数,则实数a 的值是_________. 答案:-3. 5.已知函数f (x )=|lg|x -103||.若关于x 的方程f 2(x )-5f (x )-6=0的实根之和为m ,则f (m )的值是 . 答案:1.6.设α、β都是锐角,且cos α=55,sin(α+β)=35,则cos β等于 . 答案:2525.说明:若学生得出255或2525,255,本题得4分.7.四面体ABCD 中,AB =3,CD =5,异面直线AB 和CD 之间的距离为4,夹角为60°,则四面体ABCD 的体积为 . 答案:53.8.若满足∠ABC =π3,AC =3,BC =m 的△ABC 恰有一解,则实数m 的取值范围是 .答案:(0,3]∪{23}.9.设集合S ={1,2,…,8},A ,B 是S 的两个非空子集,且A 中最大的数小于B 中的最小数,则这样的集合对(A ,B )的个数是 . 答案:769.10.如果正整数m 可以表示为x 2-4y 2 (x ,y ∈Z ),那么称m 为“好数”.问1,2,3,…,2014中“好数”的个数为 . 答案:881.二、解答题(本题满分80分,每小题20分)11.已知a ,b ,c 为正实数,a x =b y =c z ,1x +1y +1z=0,求abc 的值.证明:设a x =b y =c z =p >0,则a =1xp ,b =1yp ,c =1zp .…………………… 10分所以abc =1xp·1yp·1zp =111x y zp++. …………………… 15分因为1x +1y +1z=0,所以abc =0p =1. …………………… 20分12.已知F 1,F 2分别是双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的左右焦点,点B 的坐标为(0,b ),直线F 1B 与双曲线C 的两条渐近线分别交于P ,Q 两点,线段PQ 的垂直平分线与x 轴交于点M .若MF 2=12F 1F 2,求双曲线C 的离心率.解:设双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的半焦距长为c ,则点F 1,F 2的坐标分别(-c ,0),(c ,0).从而直线F 1B 的方程为x -c +y b=1,双曲线C :x 2a 2-y 2b 2=1的渐近线方程为x 2a 2-y 2b 2=0.联立⎩⎨⎧x -c +yb =1,x 2a 2-y2b 2=0,消去y 得,b 2x 2-2a 2cx -a 2c 2=0.由韦达定理得:线段PQ 中点的坐标(a 2c b 2,c 2b ). ………………………… 10分因此PQ 中垂线的方程是:y -c 2b =-c b (x -a 2cb2).在上式中,令y =0,得M (c +a 2cb 2,0). ………………………… 15分另一方面,由MF 2=12F 1F 2,则M (2c ,0),或M (0,0)(舍去),由此可得,c +a 2cb2=2c ,即a =b ,故e =2. ………………………… 20分13.如图,已知△ABC 是锐角三角形,以AB 为直径的圆交边AC 于点D ,交边AB 上的高CH于点E .以AC 为直径的半圆交BD 的延长线于点G .求证:AG =AE .证明:连结BE ,CG . 因为AB 为直径,所以∠AEB =90°,BG ⊥AC . 又EH ⊥AB ,在△AEB 中,由射影定理得 AE 2=AH ·AB . 因为AC 为直径,所以∠AGC =90°.在△AGC 中,由射影定理得AG 2=AD ·AC . …………10分因为∠BDC =∠BHC =90°, 所以B ,C ,D ,H 四点共圆,从而由割线定理知AH ·AB =AD ·AC . …………………… 15分 所以AE 2=AG 2,即AE =AG . …………………… 20分14.(1)正六边形被3条互不交叉(端点可以重合)的对角线分割成4个三角形.将每个三角形区域涂上红、蓝两种颜色之一,使得有公共边的三角形涂的颜色不同.怎样分割并涂色可以使红色三角形个数与蓝色三角形个数的差最大?(2) 凸2016边形被2013条互不交叉(端点可以重合)的对角线分割成2014个三角形.将每个三角形区域涂上红、蓝两种颜色之一,使得有公共边的三角形涂的颜色不同.在上述分割并涂色的所有情形中,红色三角形个数与蓝色三角形个数之差的最大值是多少?证明你的结论.ABCDEFABCDGE HABCDGEH解:(1)3条对角线分得4个三角形,相邻的两个涂色相异,则既有红 色三角形,又有蓝色三角形.不妨设红色三角形多于蓝色三角形.则蓝色三角形至少有1个,红色三角形最多3个,红色三角形个数与蓝色三角形个数之差不超过3-1=2.如图连接AC ,CE ,EA ,△ACE 涂蓝色,其余3个三角形涂红色,差为2. 故红色三角形个数与蓝色三角形个数之差的最大值为2. …………………… 5分 (2)2013条互不交叉(端点可以重合)的对角线分割成2014个三角形.每个三角形区域涂红、蓝两种颜色之一,使得有公共边的三角形涂的颜色不同.设红色三角形多于蓝色三角形.每个蓝色三角形三条边中至少有一条对角线,即三条边中对角线的条数只能为1、2或3.每条对角线只属于一个蓝色三角形.设边中恰含k (k =1,2,3)条对角线的蓝色三角形的个数为m k ,则对角线条数m 1+2m 2+3m 3=2013, 蓝色三角形个数m 1+m 2+m 3=3m 1+3m 2+3m 33≥m 1+2m 2+3m 33= 20133 =671,红色三角形个数≤2013-671=1343,红色三角形个数与蓝色三角形个数之差≤1343-671=672. ……………………10分 注意到凸6边形中红色三角形个数与蓝色三角形个数之差的最大值为2,此时6边形的边均为红色; 假定凸3k 边形中,红色三角形个数与蓝色三角形个 数之差的最大值为k 且凸3k 边形的边均为红色.则凸3(k +1)边形A 1A 2A 3…A 3k A 3k +1A 3k +2A 3k +3中的凸3k 边形A 1A 2A 3…A 3k 按假定涂色,红色三角形个数与蓝色三角形个数之差最大值为k 且边A 1A 3k 为红色.如图,则△A 1A 3k A 3k +2区域涂蓝色,△A 3k A 3k +1A 3k +2区域涂红色,△A 1A 3k +2A 3k +3区域涂红色,凸3(k +1)边形中红色三角形个数与蓝色三角形个数之差的值为k +2-1= k +1.即按上述方法涂色,凸2016边形中红色三角形个数与蓝色三角形个数之差为20163 = 672.所以凸2016边形中红色三角形个数与蓝色三角形个数之差的最大值为672.……………………20分ABCDEFA 1A 3k +1A 3kA 3k +2A 3k +3。
2014年全国高考数学试题及答案word版

2014年全国高考数学试题及答案word版一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一个是正确的。
1. 若函数f(x) = ax^2 + bx + c,其中a ≠ 0,且f(1) = 3,f(-1) = 1,则f(0)的值为:A. 2B. 3C. -1D. 12. 设等差数列{an}的前n项和为Sn,若a1 = 1,a4 = 4,则S5的值为:A. 15B. 10C. 5D. 33. 若复数z满足|z| = 1,且z的实部为1/2,则z的虚部为:A. √3/2B. -√3/2C. √3/2iD. -√3/2i4. 设函数f(x) = x^3 - 3x^2 + 2,若f(x)在区间(1,2)内有极值,则该极值点为:A. 1B. 2D. 1/25. 若直线l:y = kx + b与圆C:x^2 + y^2 = 1相交于两点A、B,且|AB| = √2,则k的取值范围为:A. (-∞, -1] ∪ [1, +∞)B. [-1, 1]C. (-1, 1)D. [0, 1]6. 设函数f(x) = x^2 - 4x + 3,若f(x)在区间[0,3]上单调递增,则f(x)的最大值为:A. 0B. 3C. 9D. 127. 若向量a = (1, 2),b = (2, 1),则向量a与向量b的数量积为:A. 3B. 4C. 5D. 68. 若直线l的倾斜角为45°,则直线l的斜率为:A. 1B. -1C. √2D. -√29. 设函数f(x) = x^3 - 3x^2 + 2x,若f(x)在区间(0,1)内有极值,则该极值点为:B. 1C. 2/3D. 1/210. 若复数z满足|z| = 1,且z的实部为1,则z的虚部为:A. 0B. 1C. -1D. √3/211. 设等比数列{an}的前n项和为Sn,若a1 = 2,q = 2,则S4的值为:A. 30B. 16C. 8D. 412. 若函数f(x) = x^2 - 4x + 3,若f(x)在区间[1,3]上单调递减,则f(x)的最小值为:A. 0B. 3C. -1D. 2二、填空题:本题共4小题,每小题5分,共20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2a QF1 QF2 PF1 PF2 2c 4 .
于是
QF2 PF1 PF2 QF1 2c 1 .
设 H 为 线 段 PF1 的 中点 ,则 F1 H 2, QH 5 , 且 有
F2 H PF1 .由勾股定理知,
QF2 QH F2 H F1 F2 F1 H ,
即 (2c 1) 2 52 (2c) 2 22 , 解 得 c 5 , 进 而 a 7 ,
2
2
2
2
2
b 2 6 . a 7 7. 设等边三角形 ABC 的内切圆半径为 2,圆心为 I .若点 P 满足 PI 1 ,则△APB 与 △APC 的面积之比的最大值为 .
b = 2 6 ,因此椭圆Г的短轴与长轴的比值为
1. 若正数 a, b 满足 2 log 2 a 3 log 3 b log 6 ( a b) , 则
1 1 的值为 a b
.
答案: 108 . 解:设 2 log 2 a 3 log 3 b log 6 ( a b) k ,则 a 2k 2 , b 3k 3 , a b 6k ,从而
( z1 ) 2 z1 ≠ ( z2 ) 2 z2 .
1 sin AP AB sin sin 0 6 sin 2 , 1 sin sin sin AP AC sin 0 3 3 3 6 2
其中, 0
IAP0 . 6 IP 由 AP0 I 知, sin 0 2 AI 1 sin cos 6 2 1 cos sin 2 6
1 1 ,于是 cot 15 ,所以 2r 4
3 5 . 2 解:由 PI 1 知点 P 在以 I 为圆心的单位圆 K 上.
答案:
2
设 BAP .在圆 K 上取一点 P0 ,使得 取到最大值 0 ,此时 P0 应落在 IAC 内, 且是 AP0 与圆 K 的切点.由于 0 0
,故 3
①
SAPB SAPC
tan am tan a1 tan a2 (利用①) tan a2 tan a3 tan am1
由
tan a1 1 . tan am1 3m 1
…………………20 分
1 1 ,得 m = 3333 . 3m 1 100
4
11. (本题满分 20 分) 确定所有的复数 , 使得对任意复数 z1 , z2 ( z1 , z2 1, z1 ≠ z2 ) , 均有
8. 设 A , B , C , D 是空间四个不共面的点,以 点相连,且 B 与 C , D 中至少一点相连,这样的情况数为 (22 1) (22 1) 9 .
(3) 无 AB 边,也无 CD 边:此时 AC ,CB 相连有 22 种情况, AD , DB 相连也有 22 种 情况,但其中 AC , CB , AD , DB 均相连的情况被重复计了一次,故 A , B 可用折线连 接的情况数为 22 22 1 7 . 48 3 以上三类情况数的总和为 32 9 7 48 ,故 A , B 可用折线连接的概率为 . 64 4 二、解答题:本大题共 3 小题,共 56 分.解答应写出文字说明、证明过程或
当 b 2 2 时,
PQ QR
的最小值为 2 2 .
…………………16 分
10. (本题满分 20 分)数列 {an } 满足 a1 数 m ,使得
, an1 arctan (sec an ) ( n N* ) .求正整 6
1 . 100 解:由已知条件可知,对任意正整数 n , an1 , ,且 2 2 tan an1 sec an . sin a1 sin a2 sin am
答案: [2, 0] .
a 解:在 [1, ) 上, f ( x) x 2 ax a 单调递增, 等价于 1 , 即 a 2 .在 [0, 1] 2 a 上, f ( x) x 2 ax a 单调递增,等价于 0 ,即 a 0 . 2 因此实数 a 的取值范围是 [2, 0] .
答案: 6. 设椭圆Г的两个焦点是 F1 , F2 ,过点 F1 的直线与Г交于点 P, Q .若 PF2 F1 F2 , 且 3 PF1 4 QF1 ,则椭圆Г的短轴与长轴的比值为 答案: .
2 6 . 7
解:不妨设 PF1 4, QF1 3 .记椭圆Г的长轴,短轴的长度分别为 2a , 2b ,焦距 为 2c ,则 PF2 F1 F2 2c ,且由椭圆的定义知,
4. 数列 {an } 满足 a1 2 ,an1 答案: 2015 .
2013
a2014 2(n 2) an (n N* ) ,则 n 1 a1 a2 a2013
.
解:由题设
2(n 1) 2(n 1) 2n an1 an2 n n n 1 2(n 1) 2n 23 a1 2n1 (n 1) . n n 1 2 记数列 {an } 的前 n 项和为 S n ,则 an
1 1 a b 6k k 2 k 3 22 33 108 . a b ab 2 3 3 则 M m 的值 2. 设集合 b 1 a b 2 中的最大元素与最小元素分别为 M , m , a 为 . 答案: 5 2 3 . 3 3 解:由 1 a b 2 知, b 2 5 ,当 a 1, b 2 时,得最大元素 M 5 .又 a 1 3 3 3 b a 2 a 2 3 ,当 a b 3 时,得最小元素 m 2 3 . a a a 因此, M m 5 2 3 . . 3. 若函数 f ( x) x 2 a x 1 在 [0, ) 上单调递增,则实数 a 的取值范围是
n = 2n (n + 1) − 2= 2n n .
故
a2014 22013 2015 2015 . 2013 a1 a2 a2013 2 2013 2013
5. 正四棱锥 P ABCD 中, 侧面是边长为 1 的正三角形,M , N 分别是边 AB, BC 的中 . 点,则异面直线 MN 与 PC 之间的距离是
②ห้องสมุดไป่ตู้
3 sin cot 3 15 3 3 5 2 . 2 3 cot 3 15 3 sin 2
SAPB 3 5 的最大值为 . 2 SAPC
根据①、②可知,当 P P0 时,
1 的概率在每对点之间连一条边,任 2 意两对点之间是否连边是相互独立的,则 A , B 可用(一条边或者若干条边组成的)空间 折线连接的概率为 . 3 答案: . 4 解:每对点之间是否连边有 2 种可能,共有 26 64 种情况.考虑其中 A , B 可用折线 连接的情况数. (1) 有 AB 边:共 25 32 种情况. (2) 无 AB 边,但有 CD 边:此时 A , B 可用折线连接当且仅当 A 与 C , D 中至少一
S n = 2 + 2 × 3 + 22 × 4 + + 2n −1 (n + 1) ,
所以
2 S n = 2 × 2 + 22 × 3 + 23 × 4 + + 2n (n + 1) ,
1
将上面两式相减,得
S= 2n (n + 1) − (2n −1 + 2n − 2 + + 2 + 2) n
①
.由①得, tan 2 a sec 2 a 1 tan 2 a ,故 由于 sec an 0 ,故 an1 0, n 1 n n 2 1 3n 2 , tan 2 an n 1 tan 2 a1 n 1 3 3 3n 2 . …………………10 分 即 tan an 3 因此 tan am tan a1 tan a2 sin a1 sin a2 sin am sec a1 sec a2 sec am
2 . 4 解:设底面对角线 AC , BD 交于点 O ,过点 C 作直 线 MN 的垂线,交 MN 于点 H . 由 于 PO 是 底 面 的 垂 线 , 故 PO CH , 又 AC CH ,所以 CH 与平面 POC 垂直,故 CH PC . 2 2 因此 CH 是直线 MN 与 PC 的公垂线段,又 CH ,故异面直线 MN 与 CN 2 4 2 . PC 之间的距离是 4
演算步骤.
9.(本题满分 16 分)平面直角坐标系 xOy 中, P 是不在 x 轴上的一个动点,满足条件: 过 P 可作抛物线 y 2 4 x 的两条切线,两切点连线 lP 与 PO 垂直. 设直线 lP 与直线 PO, x 轴的交点分别为 Q, R .
(1) 证明 R 是一个定点; (2) 求
2014 年全国高中数学联合竞赛一试(A 卷) 参考答案及评分标准
说明: 1. 评阅试卷时,请依据本评分标准. 填空题只设 8 分和 0 分两档;其他各题的 评阅,请严格按照本评分标准的评分档次给分,不要增加其他中间档次. 2. 如果考生的解答方法和本解答不同,只要思路合理、步骤正确,在评卷时可 参考本评分标准适当划分档次评分,解答题中第 9 小题 4 分为一个档次,第 10、 11 小题 5 分为一个档次,不要增加其他中间档次. 一、填空题:本大题共 8 小题,每小题 8 分,共 64 分.
