交通流三要素之间的关系-文档资料
合集下载
第七章交通流三参数之间的关系

参考文献
1、任福田,刘小明,荣建等.交通工程学. 北京:人民交通 出版社,2003.7
2、刘建军.交通工程学基础. 北京:人民交通出版社, 1995.7
第七章 交通流量、速度和密度之间来自关系授课内容:1、三参数之间的关系
2、速度—密度之间的关系
3、交通流量—密度之间的关系
4、交通流量—速度之间的关系
授课要求:
掌握交通流中交通流量、速度和密度各参数之间
的关系,会分析和应用三参数之间的关系。
第一节 三参数之间的关系
一、交通流的三个参数关系
描述交通流的三个参数是交通量、速度和交通密 度,它们之间的关系可以用下式表示:
Q VK
式中:Q——交通量(辆/h);
V——速度(km/h);
K——交通密度(辆/km)。
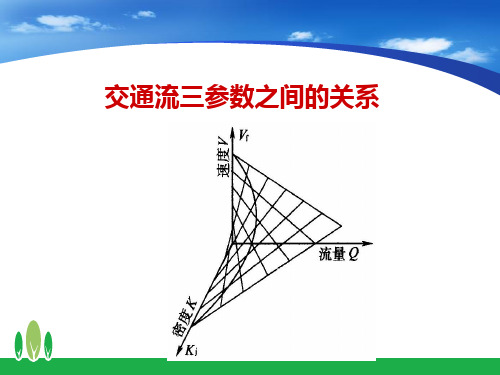
二、交通量、速度和交通密度的关系曲线 由交通量、速度和交通密度三者关系图(图 7-1 ) 可见:
图7—1交通量、速度和交通密度的关系
(1)Qm是速度-流量图上的峰值,表示最大流量。
(2)Vm是流量取最大值(Q=Qm)时的速度,称为 临界速度。
例7-1已知某公路上畅行速度Vf=80 km/h,阻塞密度Kj =105veh/km,速度一密度符合直线关系式。 求:(1)在该路段上期望得到的最大流量? (2)此时所对应的车速是多少? 解:(1)该路段上期望得到的最大流量为: Qm=1/4 KjVf=1/4*80*105= 2100(veh/h)
阻塞密度值:kj=1000/hd=1000/8.05=124辆 /km,如假定ht=1.5s,由于 ht=3600/Q
因此,最大通行能力Qm=3600/1.5=2400辆/h。 此时的速度Vm=Qm/Km=2400/62=38.7km/ h。
交通流三个参数K Q V之间关系概要

V=60-3/4*70=7.5(km/h)
Q= KV=7.5*70=525(veh/h)
Qm=1/4 KjVf=1/4*60*80=1200(veh/h)
例7-3假定车辆平均长度为6.lm,在阻塞密度时,单车 道车辆间的平均距离为1.95m,因此车头间距h= 8.05m,试说明流量与密度的关系。 解:因为hd=1000/k
第二节 速度和密度之间的关系
1934年,格林希尔兹(Greenshields)提出了 速度一密度线性模型。
K v v( ) f 1Kj
式中:Vf-一畅行速度; Kj——阻塞密度。
这一模型较为直观、实用(图7-2),且与实 测数据拟合良好。
当 K = 0 时, V 值可达理论最高速度,即畅行速度 Vf 。实际上, AE 线不与纵坐标轴相交,而是趋于该 轴因为在道路上至少有一辆车V以速度Vf行驶。这时, Vf只受道路条件限制。该图也可以表示流量,根据直 线关系,直线上任意点的纵横坐标与原点O所围成的 面积表示交通量,如运行点 C ,速度为 Vm ,密度为 Km,其交通量为 Qm=VmKm,即图上的矩形面积。
过C点作一条平行于流量坐标轴的线,将曲线分 成两部分,这条线以上的部分,为不拥挤部分,速度 随流量的增加而降低,直至达到通行能力的流量Qm 为止,速度为Vm;这条线以下部分为拥挤部分,流 量和速度都下降。
综合以上三个参数的关系可知:当道路上交通密 度小时,车辆可自由行驶,平均车速高,交通流量不 大;随着交通密度增大,交通流量也增加,但车速下 降;当交通密度增加到最佳密度时,交通流量达到最 大值,即交通流量达到了道路的通行能力,车辆的行 驶形成了车队跟随现象,车速低且均衡;当交通密度 继续增大,即超过了最佳密度,交通流量下降,车速 明显下降,直到车速接近于零,道路出现阻塞,交通 密度达到最大值,即阻塞密度,交通流量等于零。
交通流三个参数KQV之间关系解读

图7-3所示。
图7-3交通量和密度的关系
当交通密度为零时,流量为零,故曲线通过坐标 原点。当交通密度增加,流量增大,直至达到道路的 通行能力,即曲线C点的交通量达到最大值,对应的 交通密度为最佳密度Km;从C点起,交通密度增加, 速度下降,交通量 减少,直到阻塞密度Kj,速度等 于零,流量等于零;由坐标原点向曲线上任一点画矢 径。这些矢径的斜率,表示矢端的平均速度。通过A 点的矢径与曲线相切,其斜率为畅行速度Vf;对于密 度比Km小的点,表示不拥挤情况,而密度比Km大 的点,表示拥挤情况。
例7-2 在长400m的道路上行驶28辆车,速度-密度为直 线关系,V=60-3/4 K,
求:该道路的Vf ,Kj ,Q ,Qm 。 解:V=60-3/4 K=60(1- K/80)
Vf=60 km/h K=N/L=28/0.4=70(veh/km) V=60-3/4*70=7.5(km/h) Q= KV=7.5*70=525(veh/h) Qm=1/4 KjVf=1/4*60*80=1200(veh/h)
线同样是一条抛物线(图7-4)
图7—4 速度与流量的关系
当交通密度为零时,畅行交通流的车速就可能达 到最高车速,如图中曲线的最高点A,就是畅行速度 Vf,而流量等于零。当交通密度等于阻塞密度时,速 度等于零,流量也等于零,因此,曲线通过坐标原点。
过C点作一条平行于流量坐标轴的线,将曲线分 成两部分,这条线以上的部分,为不拥挤部分,速度 随流量的增加而降低,直至达到通行能力的流量Qm 为止,速度为Vm;这条线以下部分为拥挤部分,流 量和速度都下降。
对于式(7-6)若另dQ/dK=0,则可求出对应于 Qm的Km值:
km
1 2
k
j
从而
交通流量速度密度三者之间的关系.

交通流量、速度、密度三者之间的关系
交通流量、速度、密度三者之间的关系
交通流量、速度、密度是描述交通流基本特 征的三个主要参数,它们之间相互联系、相 互制约。
主要内容:
一、概述 二、流量、速度、密度三者之间的关系
一、概述
1.交通流近似看作是由交通体组成的一种粒子流体, 同其他流体一样,可以用交通流量、速度和密度三 个基本参数来描述。
谢谢!
二、流量、速度、密度三者关系
dQ 0 dV
2V 1 0 Vf
1 V V f Vm Qm 2
1 Vm V f 2 K 1 K m j 2
1 Qm V f K j 4
二、流量、速度、密度三者关系
当车流密度小于最佳车流密度时,车流处于 自由行驶状态,平均车速高。交通量没有达 到最大值,密度增大,交通量也增大;当车 流密度接近或等于最佳车流密度时,车流出 现车队跟驰现象,车速受到限制。各种车辆 接近某一车速等速行驶,交通量将要达到最 大值;当车流密度大于最佳车流密度时,车 流处于拥挤状态,由于车流密度逐渐增大, 车速和交通量同时降低,交通发生阻塞,甚
一、概述
2.密度:
密度K:单位长度车道上某一瞬间所存在的车 辆数,表示道路空间上的车辆密集程度,即
N K L
式中:N——某瞬间在长度为L的路段上行驶的 车辆数,单位:辆 L——路段长度,单位:km
二、流量、速度、密度三者关系
1. V—K 关系(Greenshields模型(线性模型) ):
假设线性关系:V = a – bK(1)
Q K V
式中:Q——流量,辆/h K——密度,辆/公里 V——区间平均速度,km/h
交通流量、速度、密度三者之间的关系
交通流量、速度、密度是描述交通流基本特 征的三个主要参数,它们之间相互联系、相 互制约。
主要内容:
一、概述 二、流量、速度、密度三者之间的关系
一、概述
1.交通流近似看作是由交通体组成的一种粒子流体, 同其他流体一样,可以用交通流量、速度和密度三 个基本参数来描述。
谢谢!
二、流量、速度、密度三者关系
dQ 0 dV
2V 1 0 Vf
1 V V f Vm Qm 2
1 Vm V f 2 K 1 K m j 2
1 Qm V f K j 4
二、流量、速度、密度三者关系
当车流密度小于最佳车流密度时,车流处于 自由行驶状态,平均车速高。交通量没有达 到最大值,密度增大,交通量也增大;当车 流密度接近或等于最佳车流密度时,车流出 现车队跟驰现象,车速受到限制。各种车辆 接近某一车速等速行驶,交通量将要达到最 大值;当车流密度大于最佳车流密度时,车 流处于拥挤状态,由于车流密度逐渐增大, 车速和交通量同时降低,交通发生阻塞,甚
一、概述
2.密度:
密度K:单位长度车道上某一瞬间所存在的车 辆数,表示道路空间上的车辆密集程度,即
N K L
式中:N——某瞬间在长度为L的路段上行驶的 车辆数,单位:辆 L——路段长度,单位:km
二、流量、速度、密度三者关系
1. V—K 关系(Greenshields模型(线性模型) ):
假设线性关系:V = a – bK(1)
Q K V
式中:Q——流量,辆/h K——密度,辆/公里 V——区间平均速度,km/h
交通工程-交通流三参数之间的关系06
❖
V=60-3/4*70=7.5(km/h)
❖
Q= KV=7.5*70=525(veh/h)
❖ Qm=1/4 KjVf=1/4*60*80=1200(veh /h)
❖ 4、假定车辆平均长度为6.lm,在阻塞密度时,
单车道车辆间的平均距离5m,试说明流量与密度的关系。
❖试计算该道路的最大流量。 ❖解:对照车速-密度的对数模型,可得: ❖Vm=40km/h;则Vf=80km/h; ❖Kj=82辆/km; ❖则Qm=1/4Vf*Kj=1640辆/h。
3、交通量三参数之间关系的应用
拥挤收费——交通需求管理策略
流量-密度关系曲线
交通量三参数之间关系的应用
拥挤收费
通过对驶入城市中心区的车辆征收额外的 通行费达到调节中心区交通流的目的,从 而使城市中心区的交通流运行在最佳状态。
❖ 1998年8月,新加坡政府将ERP扩充到整个中心 商业区、高速公路和交通拥挤的区域。新加坡拥 挤收费的目的非常单一,就是为了控制交通拥挤 现象,同时辅以高达130%的小汽车牌照税进一 步限制小汽车的保有,削弱了拥挤收费政策的负 面影响,增强了拥挤收费实施的效果。
❖ 技术手段
❖ 早期的ALS和RPS均采取出入收费区域出示纸质凭证 的方式运行。
实施效果: 收费区域交 通量减少了 22%;
交通事故降 低5~10%;
公交利用率 大幅提高, 增减了16条 公交线路和 200多辆公交 车。
3、交通量三参数之间关系的应用
拥挤收费需解 决的关键问题
拥挤区域、拥挤收费时段、拥挤收费 费率、收费方式等。
新加 坡电 子拥 挤收 费区 域入 口图
❖ 新加坡交通拥挤收费典型成功案例
❖ 收费水平和收益分析 ❖ 新加坡的电子收费系统(ERP)是一种单次分级
7交通流量、速度和密度之间的关系

=
N L
V = KV
第二节 速度- 密度的关系
现象:当道路上的车辆增多、车流密度增大时,驾驶员被迫降 低车速。当车流密度由大变小时,车速又会增加。
探求速度和密度之间的关系
车流密度适中 直线关系模型 车流密度很大 对数关系模型 车流密度很小 指数模型
广义速度-密度模型
特征变量
划分交通是否拥挤的重要特征值
数学模型
Q = KV = KV f ( 1 K K
j
)=Vf(K -
K K
2
)
j
Q Qm 斜率最大 车速最高
K增大, Q增大
K=Km Q=Qm K增大, Q减小
Km = Vm = 1 2 1 2 1 4 K
j
Vf VfK
K=0, Q=0
不拥挤 Km
拥挤 K=Kj Q=0 Kj K
Qm =
j
第四节 速度-交通流量的关系
即K=Kj,b=Vf/Kj,
直线关系模型
V = a - bK = V f Vf K
j
K =Vf(1-
K K
j
)
V = a - bK = V f -
Vf K
j
K =Vf(1-
K K
j
)
V
Vf
K=0,V=Vf
K=Kj,V=0
?状态
Vm=38.7
交通量最大 Qm=KmVm=2400
Km=62
?状态
Kj
K
第七章 交通流量、速度和密度之间的关系
第一节 三参数之间的关系
假设交通流为自由流,在长度为 L 的路段上 有连续前进的 N 辆车,其速度为V,则:
L路段上的车流密度为: K =
第六章 流量速度密度三者关系

(vf)2* 0 12.0 5 4 9 40 .6 9* 3 2 7.0 6 3 1 .1
kj
2* 0 13.6 9 5 3 41 .6 92 3 2
1* 7.0 6 (3 1 .1* 717 * 4.6 9 3 2 6.4 27
20
20
❖ 即: vf 6.4 2(7 km /h)
vf kj
一、概述 二、流量、速度、密度三者之间的关系
3
一、概述
1. 交通流——交通体组成的粒子流。如同其它流 体一样,也可以用流量、速度、密度三个参数来 描述。
Q KV
❖ 式中:Q——流量,辆/h K——密度,辆/公里 V——区间平均速度,km/h
4
一、概述
❖ 三维空间曲线投影到二维 空间:
Qm
(1) Qm是u—q图上的峰值,表示
15
二、流量、速度、密度三者关系
❖ 例6.1 在某公路一个观测断面上,用电子秒 表观测车头时距,求出每5min之内平均车头 时距,同时用雷达计速仪观测各车辆车速, 求出每5min之内的平均车速,其结果见表63,试分析该路的交通量、车速、密度三者关 系。
16
二、流量、速度、密度三者关系
❖ 车头时距:相邻两车的车头通过道路某一断
第六章 交通流量、速度、密度 三者之间的关系
1
第六章 交通流量、速度、密度三者 之间的关系
本章要求: ❖ 交通流可以看成是一种流体,可以用流量、
速度、密度三个参数来表述。要求掌握三 者之间的相互关系,明确最佳流量、最佳 速度和最佳密度的真正含义及作为划分交 通是否拥挤的重要特征值。
2
第六章 交通流量、速度、密度三者 之间的关系
n
n
xi2 xiyi 0
交通流三参数之间的关系

三个参数之间的关系式为 Q ? Vs K
适合于所有稳定的交通流
最大流量 Qm 临界速度 (critical density )vm 临界密度 (critical density )Km 阻塞密度 (jam density )Kj 自由流速度 (free-flow speed)Vf
22、、交停通车流三场参布数局之间原的则关系
交通流三参数之间的关系
2 、交通停流车三场参数布之局间原的则关系
(1) 连续流和间断流 (2) 流量-速度-密度之间的关系 (Q-V-K 关系) (3) 速度-密度之间的关系 (V-K 关系) (4) 流量-密度之间的关系 (Q-K 关系) (5) 流量-速度之间的关系 (Q-V 关系)
22、、交停通车流三场参布数局之间原的则关系
?试用格林希尔茨线性模型求该路段在密度为 30辆 /Km 时的路段平均交通量。该道路的最大交通量 为多少?对应的速度和密度值是多少?
200
400
600
800
q (pcu /h /lane )
速度—密度线性关系模型与实测结果对比
2、停车场布局原则
(3) 速(1度) -密度之间的关系 (b) Grenberg (对数)模型
V
?
Vm
ln
Kj K
适用于交通流密度很大时
2、停车场布局原则
(3) 速(1度) -密度之间的关系 (c) Underwood (指数)模型
) /h
50
m
v(k 40
30
20 0
南京市:龙蟠南路路段
)
ne
/la
2min Underwood 2min Greenberg
(pcu/h
5min Underwood
适合于所有稳定的交通流
最大流量 Qm 临界速度 (critical density )vm 临界密度 (critical density )Km 阻塞密度 (jam density )Kj 自由流速度 (free-flow speed)Vf
22、、交停通车流三场参布数局之间原的则关系
交通流三参数之间的关系
2 、交通停流车三场参数布之局间原的则关系
(1) 连续流和间断流 (2) 流量-速度-密度之间的关系 (Q-V-K 关系) (3) 速度-密度之间的关系 (V-K 关系) (4) 流量-密度之间的关系 (Q-K 关系) (5) 流量-速度之间的关系 (Q-V 关系)
22、、交停通车流三场参布数局之间原的则关系
?试用格林希尔茨线性模型求该路段在密度为 30辆 /Km 时的路段平均交通量。该道路的最大交通量 为多少?对应的速度和密度值是多少?
200
400
600
800
q (pcu /h /lane )
速度—密度线性关系模型与实测结果对比
2、停车场布局原则
(3) 速(1度) -密度之间的关系 (b) Grenberg (对数)模型
V
?
Vm
ln
Kj K
适用于交通流密度很大时
2、停车场布局原则
(3) 速(1度) -密度之间的关系 (c) Underwood (指数)模型
) /h
50
m
v(k 40
30
20 0
南京市:龙蟠南路路段
)
ne
/la
2min Underwood 2min Greenberg
(pcu/h
5min Underwood
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
V K=0,V=Vf;
K=Kj,V=0;
Vf
A(K1,V1) K1<0.5Km,
V1>0.5Vf;
Vm
交通量最大 Qm=KmVm
B(0.5Kj,0.5VK1>0.5Km,
f)
V1<0.5Vf;
C(K2,V2)
Km
Kj K
11
2、对数V-K关系模型(格林伯模型)
V
V
模型缺点:当K 0时,速度趋向于无穷大,需修正。 ➢ 故该模型适用于交通密度较大时。
➢ V-K关系:
✓ 线性模型: V=a-bK =Vf -V Kfj K=Vf(1-K Kj )
✓ 对数模型:V
Vm
ln(K j K
)
✓ 指数模型:V
-K
Vfe Km
➢ Q-✓K关广系义:模Q型:VfV(K=V-fKK(j21)- KKj)nVKfj(kK2j)2Kj4Vf
➢ Q-V关系: QKj(v-vvf2)VKfj(VV2 f)2Kj4 Vf
交通流三要素 之间的关系
教学内容及目标
掌 握
理 解
2
交通流三要素
请思考:三要素从不同的角度描述了交通流的特性, 那么他们之间是否存在着某些关系,如果存在,这些 关系能否更深入、更综合的描述交通情况?
➢ 交通流量(Q):单位时间内
度通量过车道辆路对断面交或通车设道备的的车需辆数求;
➢ 车流密度(K):单位路段长 度上存在的车辆数;
18
其图像不 是普通的 二维直线, 也不是三 维的双曲 马鞍面, 而是一条 空间曲线。
y kx
QzxKyV
6
2、三要素基本关系分析(3)
反映交通流特性的几个 重要特征量:
➢ 最大交通流量(Qm); ➢ 临界密度(Km); ➢ 临界速度(Vm); ➢ 畅行速度(Vf); ➢ 阻塞密度(Kj);
7
二、速度- 密度关系模型
现象:当道路上的车辆增多、车流密度增大时, 驾驶员被迫降低车速。当车流密度由大变小时, 车速又会增加。
探求速度和密度之间的关系
车流密度适中 直线关系模型
车流密度很大 对数关系模型
车流密度很小 指数关系模型
广义速度-密度模型
8
1、线性V-K模型(格林.希尔治模型)
交通密度适中时观察所得数据。
9
1、线性V-K模型(格林.希尔治模型)
Q KV
V
Vf(1
-
K Kj
)
QVf(K-K K2 j)V Kfj(KK 2j)2K4 jVf
Q Qm
K增大, Q增大
斜率最大 车速最高
K=Km Q=Qm
K=0,Q =0
不拥挤
拥挤
Km
K增大, Q减小
K=Kj Q=0
K Kj
1 Km = 2 K j
1 Vm = 2V f
1
Qm
=
V 4
fK
j
16
四、流量- 速度关系模型
Q KV
K
V Kj (1- Vf
)
QKj (VVf )2KjVf Vf 2 4
Q=0,V V
=Vf
Vf
K增大, Q增大, V减小
Vm
K=Kj Q=0 V=0
不拥挤 拥挤
Q=Qm V=Vm
K增大, Q减小, V减小
Q Qm
1 Km = 2 K j
1 Vm = 2V f
1
Qm
=
V 4
fK
j
17
总结
➢ Q-V-K基本关系:Q=VK;
❖ 假定 V=a-bK
当K=0时,V可达到理论最高速度(Vf),
即K=0,V=Vf,
a=Vf
当K达到最大值(Kj)时,车速为0, b=Vf/K
即K=Kj,V=0,
j
线性关系模型: Va-bKVf -VKfjKVf(1-KKj)
或
K
K
j
(1-
V Vf
)
10
1、线性V-K模型(格林.希尔治模型) V=a-bK =Vf -V Kfj K=Vf(1-K Kj )
Vf
安德伍德模型
的适用范围
A(K1,V1)
B(0.5Kj,0. 5Vf)
格林伯模型 的适用范围
C(K2,V2)
Kj K 14
4、广义模型(派普斯模型)
V
Vf(1 -
K )n Kj
n是大于零的实数,当n=1时,为线性关系 式
➢ 是一组V-K模型通用的线族。 ➢ n=1是其中一个特例。
15
三、流量- 密度关系模型
12
3、指数V-K关系模型(安德伍德模型)
V
-K
V Vfe Km
K
➢ 模型缺点:当K Kj时,V≠0,需修正。 ➢ 故该模型适用于交通密度较小时。
13
3、指数V-K关系模型(安德伍德模型)
注意:不同的模型适用范围不同!
车流密度适中:希尔治的线性模型;
车辆密度很小:安德伍德的指数模型;
V
车流密度很大:格林伯的对数模型;
t
整理:
NNN
Q= t
=
L
=
V=KV L
V
4
2、三要素基本关系分析(1)
➢Q-V-K基本关系式: Q=KV
Q:平均流量(辆/h); V:空间平均车速(km/h); K:平均密度(辆/km)。
Q、V、K均是平均值;
这个关系式是一个流体力 学公式,式中的三个参数 中只有两个独立变量;
5
2、三要素基本关系分析(2) Q=KV的图像是怎么样的?
反映车辆能获取的服务质量
➢ 车辆速度(V):单位时间内 车辆移动的距离;
3
一、交通流三要素基本关系
1、三要素基本关系式推导
假设交通流为自由流,在长度为 L 的路段 上有连续前进的 N 辆车,其速度为V,则:
L路段上的车流密度为: K = N L
A
N辆车通过A断面所用的时间为: t = L V
N辆车通过A断面的交通流量为:Q = N
