浮点数范围
32位字长的浮点数

32位字长的浮点数
32位字长的浮点数是一种基于32位二进制(即32个0或1)编码表示的数据类型,用于表示带有小数部分的数值。
浮点数被分为三个部分:符号位、指数位和尾数位。
其中,符号位决定了浮点数的正负性,0表示正数,1表示负数。
指数位用来表示浮点数的数量级,通过移动小数点的位置来表示不同数量级的数值。
尾数位用于存储浮点数的精度和小数部分的数值。
由于32位的二进制编码空间有限,所以浮点数的表示范围和精度是有限的。
一般情况下,32位浮点数的范围约为-10^38到10^38之间,并且具有大约7位的有效数字。
具体的表示方式和精度取决于浮点数的规范和编码方式。
总之,32位字长的浮点数是一种用32位二进制编码表示的数据类型,用于表示带有小数部分的数值,具有一定的范围和精度。
c语言float范围值的大小

c语言float范围值的大小
C语言中的float类型是一种浮点数类型,它可以表示一定范围的实数值,并且可以进行各种数学运算。
float类型在C语言中是非常常用的数据类型,在进行科学、工程和金融等领域的编程时非常重要。
float类型的大小不是固定的,它取决于编译器的实现和目标平台的架构。
但是,根据IEEE 754标准,float类型的范围大约是从
1.17549435E-38到3.40282347E+38。
这个范围非常广泛,可以表示很多不同的实数值。
具体来说,float类型的取值范围可以分为正数、负数、零和特殊值四种情况。
正数的范围是从1.17549435E-38到3.40282347E+38,负数的范围是从-1.17549435E-38到-3.40282347E+38,零的范围是0.0,特殊值包括正无穷大、负无穷大和NaN(不是一个数字)等。
需要注意的是,float类型只有6-7个有效数字,所以在进行高精度计算时需要特别注意数值的精度。
如果需要更高的精度,可以使用double类型或long double类型,它们的范围和精度比float类型更高。
总之,float类型是C语言中非常重要的数据类型,它可以表示一定范
围内的实数值,并且可以进行各种数学运算。
了解float类型的范围和特性,对于C语言编程的学习和应用都非常重要。
计算32位浮点数表示范围
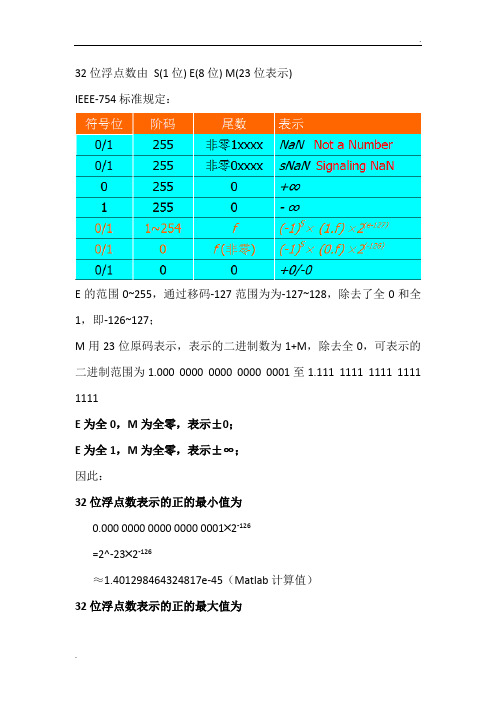
32位浮点数由S(1位) E(8位) M(23位表示)
IEEE-754标准规定:
E的范围0~255,通过移码-127范围为为-127~128,除去了全0和全1,即-126~127;
M用23位原码表示,表示的二进制数为1+M,除去全0,可表示的二进制范围为1.000 0000 0000 0000 0001至1.111 1111 1111 1111 1111
E为全0,M为全零,表示±0;
E为全1,M为全零,表示±∞;
因此:
32位浮点数表示的正的最小值为
0.000 0000 0000 0000 0001╳2-126
=2^-23╳2-126
≈1.401298464324817e-45(Matlab计算值)
32位浮点数表示的正的最大值为
1.111 1111 1111 1111 1111╳2-126
=(2-2-23)╳2127
≈3.40282346638529e+38(Matlab计算值)
负数部分与正数部分对称,因此表示的十进制范围为
[-3.40282346638529e+38, -1.401298464324817e-45]
U[1.401298464324817e-45, 3.40282346638529e+38]
因为10^6<2^23<10^7,所以32位浮点型数据的表达的有效数字最少为6位,23位浮点数表示的数字最大误差为1/2^23,约等于1.19209289550781e-07,误差最大影响到小数点后第七位,因此整数位1和小数位前6位都是有效数字。
二进制和十进制整数可以无差转换;
二进制小数转十进制小数可以无差转换,十进制转二进制会产生误差,如2.2,会是一个无限循环的二进制小数。
c++浮点数的规则

c++浮点数的规则
C++浮点数的规则是指在C++中使用浮点数进行运算或者比较时需要注意的一些规则,包括浮点数的表示范围、精度、舍入误差等。
首先,C++中使用双精度浮点数(double)表示的范围是
-1.79769e+308到1.79769e+308,单精度浮点数(float)的表示范围是-3.40282e+38到3.40282e+38。
对于超出这个范围的数,会出现溢出现象。
其次,浮点数的精度是有限的,因为计算机只能使用有限的位数来表示浮点数。
在C++中,双精度浮点数的精度一般是15位有效数字,而单精度浮点数的精度则是7位有效数字。
因此,在进行浮点数比较时,需要注意舍入误差的影响。
最后,需要注意浮点数的舍入误差。
由于浮点数在计算机中的表示是有限的,因此进行浮点数运算可能会产生舍入误差。
例如,对于0.1这个数,在计算机中无法精确表示,因此进行多次浮点数运算后,可能会出现精度损失的情况。
综上所述,C++浮点数的规则包括了浮点数的表示范围、精度和舍入误差等方面,需要在编程中注意这些规则,以避免因为浮点数计算产生的错误影响程序的正确性和性能。
- 1 -。
4字节浮点数表示范围

4字节浮点数,也称为单精度浮点数,通常使用IEEE 754标准来表示。
它使用32个比特(也就是4个字节)来表示一个浮点数,其中1位表示符号,8位表示指数,23位表示尾数。
在这种表示方法中,一个4字节浮点数可以表示的数值范围是非常大的,具体如下:
-最小正数:1.1022197 E-38
-最大值:3.4028235 E+38
-最小负数:-1.1897314 E-38
-最大负数:-3.4028235 E+38
因此,4字节浮点数可以表示的数值范围是非常大的,可以精确地表示大多数科学计算中的数值。
但是,由于浮点数的表示方法存在舍入误差,所以在某些情况下可能会出现精度损失的情况。
16位浮点数范围

16位浮点数范围
16位浮点数是一种表示实数的数据类型,它可以表示的范围和精度都有限制。
在IEEE标准中,16位浮点数被称为“半精度浮点数”,它使用1个符号位、5个指数位和10个小数位来表示一个实数。
其表示范围为正负0到正负65504之间的实数,其中0和65504是特殊值,分别表示正负无穷大和NaN(非数值)。
在这个范围内,16位浮点数可以表示的实数有约65500万个,分布在整个实数轴上。
因为16位浮点数的精度有限,所以在进行高精度计算时需要注意舍入误差的问题。
同时,在进行科学计算、图像处理等领域时,也需要考虑数据类型的选择和转换,以保证计算正确和效率。
- 1 -。
整数和浮点数的区别

回复:浮点数的表示方法浮点数的表示方法浮点数,是指小数点在数据中的位置可以左右移动的数据。
它通常被表示成:N = M* RE这里的M(Mantissa)被称为浮点数的尾数,R(Radix)被称为阶码的基数,E(Exponent)被称为阶的阶码。
计算机中一般规定R为2、8或16、是一个确定的常数,不需要在浮点数中明确表示出来。
因此,要表示浮点数,一是要给出尾数M的值,通常用定点小数形式表示,它决定了浮点数的表示精度,即可以给出的有效数字的位数。
二是要给出阶码,通常用整数形式表示,它指出的是小数点在数据中的位置,决定了浮点数的表示范围。
浮点数也要有符号位。
在计算机中,浮点数通常被表示成如下格式:Ms是尾数的符号位,即浮点数的符号位,安排在最高一位;E 是阶码,紧跟在符号位之后,占用m位,含阶码的一位符号;M 是尾数,在低位部分,占用n位。
合理地选择m和n的值是十分重要的,以便在总长度为1+m+n个二进制表示的浮点数中,既保证有足够大的数值范围,又保证有所要求的数值精度。
例如,在PDP-11/70计算机中,用32位表示的一个浮点数,符号位占一位,阶码用8位,尾数用23位,数的表示范围约为±1.7*10±38 ,精度约为10进制的7位有效数字。
若不对浮点数的表示格式作出明确规定,同一个浮点数的表示就不是唯一的。
例如0.5也可以表示为0.05×101 , 50×10-2 等。
为了提高数据的表示精度,也为了便于浮点数之间的运算与比较,规定计算机内浮点数的尾数部分用纯小数形式给出,而且当尾数的值不为0时,其绝对值应大于或等于0.5,这被称为浮点数的规格化表示。
对不符合这一规定的浮点数,要通过修改阶码并同时左右移尾数的办法使其变成满足这一要求的表示形式,这种操作被称为的规格化处理,对浮点数的运算结果就经常需要进行规格化处理。
当一个浮点数的尾数为0,不论其阶码为何值,该浮点数的值都为0。
number的取值范围

number的取值范围
摘要:
一、引言
二、整数和浮点数
三、整数的取值范围
1.正整数
2.负整数
3.零
四、浮点数的取值范围
1.正浮点数
2.负浮点数
3.零
五、特殊数字和无穷大
六、总结
正文:
一、引言
在数学中,数字是我们用来表达数值的工具。
在计算机科学中,数字的取值范围是一个重要概念,了解这个范围有助于我们更好地理解和运用数字。
二、整数和浮点数
在计算机科学中,数字主要分为整数和浮点数两种。
整数是没有小数部分的数字,而浮点数则有小数部分。
三、整数的取值范围
1.正整数:大于零的整数,如1、2、3 等。
2.负整数:小于零的整数,如-1、-2、-3 等。
3.零:数值为零的整数。
四、浮点数的取值范围
1.正浮点数:大于零的浮点数,如1.0、
2.5 等。
2.负浮点数:小于零的浮点数,如-1.0、-2.5 等。
3.零:数值为零的浮点数。
五、特殊数字和无穷大
在数学中,还有一些特殊的数字,如无穷大和无穷小。
无穷大表示一个数无限大,而无穷小表示一个数无限小。
这些特殊数字在计算机科学中也有应用。
六、总结
数字的取值范围是一个广泛的概念,包括正整数、负整数、零、正浮点数、负浮点数等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
任意精度的浮点数的二进制码的构成如下:
符号位|阶码|尾数
任意精度浮点数的二进制码转换成十进制数的计算公式:
()()12-符号值偏移阶码值浮点数=尾数值
其中:
1、符号位只占一位,只有“0”或“1”两个符号值,“0”表示浮点数为非负值,“1” 表
示浮点数为负值,所以有:
1)、当符号值为“0”时:
()
()111-=-=符号值0
2)、当符号值为“1”时: ()()1111-=-=-符号值
2、“阶码”的位数随浮点数精度不同而不同,其作用是决定“尾数”小数点的最终位置:
1)、“阶码数字段”的值即为“阶码值”;
2)、2的“阶码位数减1”次方减1即为“阶码偏移量”:
()1-阶码数阶码偏移量=2位-1
3)、“阶码值”减去“阶码偏移量”即为“偏移阶码值”:
()
1+阶码数偏移阶码值=阶码值-2位-1
3、“尾数”的位数随浮点数精度不同而不同,其主要作用是表示浮点数的有效数:
1)、“尾数字段”直接表示的“整型值”称为“尾码值”;
2)、机器默认浮点数的“尾数字段”前面带有省略的数符“1”和“.”(注:小数点),
小数字段“1.尾数”的值即为“尾数值”:
()()2尾数位数尾数位数尾数值=尾码值+2
-综上所述,可得: ()()()112⎡⎤+⎢⎥⎣⎦-阶码数阶码值尾数位数-2符号值尾数位数浮点数=尾码值+2-1-位
单精度浮点数:
单精度浮点数的二进制码构成如下:
符号位1位|阶码8位|尾数23位
()()()()()()
71-15012183886082+--⇒阶码值23-2符号值23符号值阶码值单精度浮点数=尾码值+2单精度浮点数=尾码值+- 1、(十进制:0.0)等效于(十六进制:00000000)
等效于(二进制:00000000000000000000000000000000)
2、(十进制:1.0)等效于(十六进制:3F800000)
等效于(二进制:00111111100000000000000000000000)
3、最大值为(十进制:3.402823E+038)等效于(十六进制:7F7FFFFF)
等效于(二进制:01111111011111111111111111111111)
4、最小值为(十进制:-3.402823E+038)等效于(十六进制:FF7FFFFF
等效于(二进制:11111111011111111111111111111111)
双精度浮点数:
双精度浮点数的二进制码构成如下:
符号位1位|阶码11位|尾数52位
()()()()()()
101--107512145035996273704962+--⇒阶码值52-2符号值52符号值阶码值单精度浮点数=尾码值+2单精度浮点数=尾码值+- 1、(十进制:0.0)等效于(十六进制:0000000000000000)
等效于(二进制:
0000000000000000000000000000000000000000000000000000000000000000)
2、(十进制:1.0)等效于(十六进制:3FF0000000000000)
等效于(二进制:
0011111111110000000000000000000000000000000000000000000000000000)
3、最大值为(十进制:1.797693E+308)等效于(十六进制:7FEFFFFFFFFFFFFF) 等效于(二进制:
0111111111101111111111111111111111111111111111111111111111111111)
4、最小值为(十进制:-1.797693E+308)等效于(十六进制:FFEFFFFFFFFFFFFF) 等效于(二进制:
1111111111101111111111111111111111111111111111111111111111111111)。
