七年级数学勾股数
勾股数的第n个规律公式

勾股数的第n个规律公式勾股数,又称毕达哥拉斯数,是一类特殊的整数三元组,满足勾股定理。
勾股定理是古希腊数学家毕达哥拉斯在公元前6世纪提出的。
根据勾股定理,对于任意的正整数a、b和c,满足a^2 + b^2 = c^2,其中c为斜边,a和b为两条直角边。
而满足这一条件的整数三元组就被称为勾股数。
勾股数的规律公式可以表示为:a = m^2 - n^2b = 2mnc = m^2 + n^2其中m和n为任意正整数,且m > n。
根据这个公式,我们可以推导出无穷多个勾股数。
第一个规律是当n为1时,m可以取任意大于1的正整数。
当n=1时,a = m^2 - 1,b = 2m,c = m^2 + 1。
例如,当m=2时,可以得到a=3,b=4,c=5,满足勾股定理。
当m=3时,可以得到a=8,b=6,c=10,同样满足勾股定理。
可以看出,当n=1时,勾股数存在无穷多个。
第二个规律是当n为2时,m只能取大于2的奇数。
当n=2时,a = m^2 - 4,b = 4m,c = m^2 + 4。
例如,当m=3时,可以得到a=5,b=12,c=13,满足勾股定理。
当m=5时,可以得到a=21,b=20,c=29,同样满足勾股定理。
可以看出,当n=2时,勾股数也存在无穷多个。
第三个规律是当n为其他正整数时,m和n的取值存在限制。
当n 为其他正整数时,m和n必须互质且m和n不同时为奇数。
互质意味着m和n的最大公约数为1,即它们没有共同的因数。
这个规律可以通过数学证明得出,但在此不再详述。
根据上述三个规律,可以得出勾股数的一般规律:当n为1时,m 可以取任意大于1的正整数;当n为2时,m只能取大于2的奇数;当n为其他正整数时,m和n必须互质且m和n不同时为奇数。
根据这个规律,我们可以生成无穷多个勾股数。
勾股定理是数学中的重要定理,不仅在几何学中有广泛应用,也在物理学和工程学中有重要作用。
例如,在建筑设计中,勾股定理可以用来计算斜坡的长度和高度;在导弹轨迹计算中,勾股定理可以用来计算导弹的飞行距离和高度。
七年级数学勾股数

2.2勾股数 ——能得到直角三角形吗
2 同学们们知道古埃及人用什么方法得到直角?
古埃及人曾用下面的方法得到直角: 用13个等距的结,把一根绳子分成等长的12段,一个工匠同时握住 绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结, 拉紧绳子就得到一个直角三角形, 其直角在第4个结处.
1、这段课文说得是什么? 2、依照课文所说的做一做:把一条线段分成 12等份,在第三、第七等分处折成一个三角形, 并量一量最大角是多少度。
3、这个三角形的三边分别是3、4、5等分,这 三个数有什么样的数量关系? 32+42=52
; 美术教育加盟
;
其合乐曰以六律、六钟、五声、八音、六舞大合乐,祀天神,祭地祇。祀四望,祭山川,享先妣先祖。凡六乐,奏六歌,而天地神祇之物皆至。四望,盖谓日、月、星、海也。三光高而不可得亲,海广大无限界,故其乐同。祀天则天文从,祭地则地理从。三光,天文也。山川,地理也。天地合 祭,先祖配天,先妣配地,其谊一也。天地合精,夫妇判合。祭天南郊,则以地配,一体之谊也。天地位皆南乡,同席,地在东,共牢而食。高帝、高后配於坛上,西乡,后在北,亦同席共牢。牲用茧栗,玄酒陶匏。《礼记》曰天子籍田千亩以事天地,繇是言之,宜有黍、稷。天地用牲一,燔 燎,瘗薶用牲一,高帝、高后用牲一。天用牲左,及黍、稷燔燎南郊。地用牲右,及黍、稷瘗於北郊。其旦,东乡再拜朝日。其夕,西乡再拜夕月。然后孝弟之道备,而神祇嘉享,万福降辑。此天地合祀,以祖、妣配者也。其别乐曰冬日至,於地上之圜丘奏乐六变,则天神皆降。夏日至,於泽 中之方丘奏乐八变,则地祇皆出。天地有常位,不得常合,此其各特祀者也。阴阳之别於日冬、夏至。其会也,以孟春正月上辛若丁,天子亲合祀天地於南郊,以高帝、高后配。阴阳有离合,《易》曰分阴分阳,迭用柔刚。以日冬至使有司奉祠南郊,高帝配而望群阳。日夏至使有司奉祭北郊, 高后配而望群阴,皆以助致微气,通道幽弱。当此之时,后不省方,故天子不亲而遣有司,所以正承天顺地,复圣王之制,显太祖之功也。渭阳祠勿复修。群望未悉定,定复奏”奏可。三十馀年间,天地之祠五徙焉。后莽又奏言“《书》曰类於上帝,禋於六宗。欧阳、大、小夏侯三家说六宗, 皆曰上不及天,下不及地,旁不及四方,在六者之间,助阴阳变化,实一而名六,名实不相应。《礼记》祀典,功施於民则祀之。天文:日、月、星、辰,所昭仰也。地理:山、川、海、泽,所生殖也。《易》有八卦,乾、坤六子,水火不相逮,雷风不相誖,山泽通气,然后能变化,既成万物 也。臣前奏徙甘泉泰畤、汾阴后土皆复於南、北郊。谨案《周官》兆五帝於四郊,山川各因其方,今五帝兆居在雍五畤,不合於古。又日、月、雷、风、山、泽,《易》卦六子之尊气,所谓六宗也。星、辰、水、火、沟、渎,皆六完之属也。今或未特祀,或无兆居。谨与太师光、大司徒宫、羲 和歆等八十九人议,皆曰:天子父事天,母事地。今称天神曰皇天上帝,泰一兆曰泰畤,而称地祇曰后土,与中央黄灵同,又兆北郊,未有尊称。宜令地祇称皇地后祇,兆曰广畤。《易》曰方以类聚,物以群分。分群神以类相从为五部,兆天地之别神:中央帝黄灵后土畤及日庙、北辰、北斗、 填星、中宿中宫於长安城之未地兆。东方帝太昊青灵勾芒畤及雷公、风伯庙、岁星、东宿东宫於东郊兆。南方炎帝赤灵祝融畤及荧惑星、南宿南宫於南郊兆。西方帝少皞白灵蓐收畤及太白星、西宿西宫於西郊兆。北方帝颛顼黑灵玄冥畤及月庙、雨师庙、辰星、北宿北宫於北郊兆”奏可,於是长 安旁诸庙兆畤甚盛矣。莽又言“帝王建立社稷,百王不易。社者,土也。宗庙,王者所居。稷者,百谷之主,所以奉宗庙,共粢盛,人所食以生活也。王者莫不尊重亲祭,自为之主,礼如宗庙。《诗》曰乃立冢土。又曰以御田祖,以祈甘雨。《礼记》曰唯祭宗庙社稷,为越绋而行事。圣汉兴, 礼仪稍定,已有官社,未立官稷”遂於官社后立官稷,以夏禹配食官社,后稷配食官稷。稷种谷树。徐州牧岁贡五色土各一斗。莽篡位二年,兴神仙事,以方士苏乐言,起八风台於宫中。台成万金,作乐其上,顺风作液汤。又种五梁禾於殿中,各顺色置其方面,先煮鹤髓、毒冒、犀玉二十馀物 渍种,计粟斛成一金,言此黄帝谷仙之术也。以乐为黄门郎,令主之。莽遂崇鬼神淫祀,至其末年,自天地六宗以下至诸小鬼神,凡千七百所,用三牲鸟兽三千馀种。后不能备,乃以鸡当鹜雁,犬当麋鹿。数下诏自以当仙,语在其《传》。赞曰:汉兴之初,庶事草创,唯一叔孙生略定朝廷之仪。 若乃正朔、服色、郊望之事,数世犹未章焉。至於孝文,始以夏郊,而张仓据水德,公孙臣、贾谊更以为土德,卒不能明。孝武之世,文章为盛,太初改制,而兒宽、司马迁等犹从臣、谊之言,服色数度,遂顺黄德。彼以五德之传,从所不胜,秦在水德,故谓汉据土而克之。刘向父子以为帝出 於《震》,故包羲氏始受木德,其后以母传子,终而复始,自神农、黄帝下历唐、虞三代而汉得火焉。故高祖始起,神母夜号,著赤帝之符,旗章遂赤,自得天统矣。昔共工氏以水德间於木、火,与秦同运,非其次序,故皆不永。由是言之,祖宗之制盖有自然之应,顺时宜矣。究观方士祠官之 变,谷永之言,不亦正乎。不亦正乎。[标签:标题] 凡天文在图籍昭昭可知者,经星常宿中外官凡百一十八名,积数七百八十三星,皆有州国官宫物类之象。其伏见蚤晚,邪正存亡,虚实阔狭,及五星所行,合散犯守,陵历斗食,彗孛飞流,日月薄食,晕适背穴,抱珥虹蜺,迅雷风袄,怪云变气:此皆阴阳之精,其本在地,而上发於天者也。政 失於此,则变见於彼,犹景之象形,乡之应声。是以明君睹之而寤,饬身正事,思其咎谢,则祸除而福至,自然之符也。中宫天极星,其一明者,泰一之常居也,旁三星三公,或曰子属。后句四星,末大星正妃,余三星后宫之属也。环之匡卫十二星,藩臣。皆曰紫宫。前列直斗口三星,随北剬, 若见若不见,曰阴德,或曰天一。紫宫左三星曰天枪,右四星曰天棓。后十七星绝汉抵营室,曰阁道。北斗七星,所谓“旋、玑、玉衡,以齐七政”。杓携龙角,衡殷南斗,魁枕参首。用昏建者杓。杓,自华以西南。夜半建者衡。衡,殷中州河、济之间。平旦建者魁。魁,海岱以东北也。斗为 帝车,运於中央,临制四海。分阴阳,建四时,均五行,移节度,定诸记,皆系於斗。斗魁戴筐六星,曰文昌宫:一曰上将,二曰次将,三曰贵相,四曰司命,五曰司禄,六曰司灾。在魁中,贵人之牢。魁下六星两两而比者,曰三能。三能色齐,君臣和。不齐,为乖戾。柄辅星,明近,辅臣亲 强。斥小,疏弱。杓端有两星:一内为矛,招摇。一外为盾,天蜂。有名圜十五星,属杓,曰贱人之牢,牢中星实则囚多,虚则开出。天一、枪、棓、矛、盾动摇,角大,兵起。东宫苍龙,房、心。心为明堂,大星天王,前后星子属。不欲直,直,王失计。房为天府,曰天驷。其阴,右骖。旁 有两星曰衿。衿北一星曰辖。东北曲十二星曰旗。旗中四星曰天市。天市中星众者实,其中虚则耗。房南众星曰骑官。左角,理。右角,将。大角者,天王帝坐廷。其两旁各有三星,鼎足句之,曰摄提。摄提者,直斗杓所指,以建时节,故曰“摄提格”。亢为宗庙,主疾。其南北两大星,曰南 门。氐为天根,主疫。尾为九子,曰君臣。斥绝,不和。箕为敖客,后妃之府,曰口舌。火犯守角,则有战。房、心,王者恶之。南宫朱鸟,权、衡。衡、太微,三光之廷。筐卫十二星,藩臣。西,将。东,相。南四星,执法。中,端门。左右,掖门。掖门内六星,诸侯。其内五星,五帝坐。 后聚十五星,曰哀乌郎位。旁一大星,将位也。月、五星顺入,轨道,司其出,所守,天子所诛也。其逆入,若不轨道,以所犯名之。中坐,成形,皆群下不从谋也。金、火尤甚。廷藩西有随星四,名曰少微,士大夫。权,轩辕,黄龙体。前大星,女主象。旁小星,御者后宫属。月、五星守犯 者,如衡占。东井为水事。火入之,一星居其左右,天子且以火为败,东井西曲星曰戊。北,北河。南,南河。两河、天阙间为关梁。舆鬼,鬼祠事。中白者为质。为守南北河,兵起,谷不登。故德成衡,观成潢,伤成戉,祸成井,诛成质。柳为鸟喙,主木草。七星,颈,为员宫,主急事。张, 嗉,为厨,主觞客。翼为羽翮,主远客。轸为车,主风。其旁有一小星,曰长沙,星星不欲明。明与四星等,若五星入轸中,兵大起。轸南众星曰天库,库有五车。车星角,若益众,及不具,亡处车马。西宫咸池,曰天五潢。五潢,五帝车舍。火入,旱。金,兵。水,水。中有三柱。柱不具,
初中常用勾股数

初中常用勾股数嘿,小伙伴们,今天咱们来聊聊初中数学里头的一个超级酷炫的玩意儿——勾股数!别瞅着这仨字儿挺高深,其实它呀,就像咱们生活中的小秘密,藏着简单又奇妙的规律。
想象一下,你手里头拿着三根小木棍,想搭个直角三角形玩玩。
这可不是随便拿三根就行的哦,得有点讲究。
这时候,勾股数就闪亮登场了,它们就像是数学界的“黄金搭档”,总能完美配合,帮你轻松搞定这个难题。
啥是勾股数呢?简单来说,就是三个正整数a、b、c(a<b<c),它们能满足一个超酷的等式:a²+ b²= c²。
这个等式啊,就像是数学王国里的一把钥匙,能打开直角三角形世界的大门。
而a、b、c这三个数,就被咱们亲切地称为“勾股数”。
说到这儿,你是不是已经迫不及待想找找看身边的勾股数了?别急,我这就给你举个栗子。
最经典的勾股数组合,莫过于3、4、5了。
想象一下,你手里有三根小木棍,长度分别是3厘米、4厘米和5厘米。
当你试着把它们摆成一个三角形时,嘿,神奇的事情发生了!它们竟然严丝合缝地拼成了一个直角的形状。
这就是勾股数的魔力所在啊!除了3、4、5这组黄金搭档,勾股数家族里还有好多成员呢。
比如5、12、13这对好基友,还有7、24、25这对铁三角。
它们都是按照那个神秘的等式a²+ b²= c²来搭配的,所以总是能那么和谐地共处一室,组成一个个完美的直角三角形。
你可能会问,这些勾股数有啥用呢?嘿,用处可大啦!在建筑设计、工程测量、甚至咱们的日常生活中,都能见到它们的身影。
比如你要建个房子,需要确定墙角是不是直角,就可以用勾股定理来检验一下。
只要量出两边的长度,再算算看第三边应该是多长,如果跟实际量出来的一样长,那就说明墙角是直角没错啦!而且啊,找勾股数的过程还特别有趣。
有时候你可能会在不经意间就发现了它们的踪迹。
比如你在玩拼图游戏时,突然发现几块拼图能拼出一个直角三角形的形状;或者你在看书时,某个公式里恰好就藏着勾股数的秘密。
常用勾股数

常用的勾股数有:3、4、5;5、12、13;7、24、25;8、15、17;9、40、41等等。
勾股数,又名毕氏三元数。
勾股数就是可以构成一个直角三角形三边的一组正整数。
勾股数的依据是勾股定理。
勾股定理是人类早期发现并证明的重要数学定理之一。
勾股定理说明,平面上的直角三角形的两条直角边的长度(古称勾长、股长)的平方和等于斜边长(古称弦长)的平方。
反之,若平面上三角形中两边长的平方和等于第三边边长的平方,则它是直角三角形(直角所对的边是第三边)。
据《周髀算经》中记述,公元前一千多年周公与商高论数的对话中,商高就以三四五3个特定数为例详细解释了勾股定理要素。
古埃及在公元前2600年的纸莎草就有(3,4,5)这一组勾股数,而古巴比伦泥板涉及的最大的一个勾股数组是(12709,13500,18541)。
勾股数

证明: a2+b2=(m2-n2)+(2mn)2 =m4-2m2n2+n4+4m2n2 =m4+2m2n2+4n2 =(m2+n2)2 =c2 a、b、c构成一组勾股数。
举例:如直角三角形的两个直角边分别为3、4,则斜边c的平方;= a的平方+b的平方=9+16=25即c=5
则说明斜边为5。
编辑本段多种证明方法
这个定理有许多证明的方法,其证明的方法可能是数学众多定理中最多的。路明思(Elisha Scott Loomis)的 Pythagorean Proposition(《毕达哥拉斯命题》)一书中总共提到367种证明方式。
(2)若是大于2的偶数,把它除以2后再平方,然后把这个平方数分别减1,加1所得到的两个整数和这个偶数构成一组勾股数。例如8是勾股数组中的一个数。那么8、15,17便是一组勾股数。
证明:设大于2的偶数2n,那么把这个偶数除以2后再平方,然后把这个平方数分别减1,加1所得的两个整数为n2-1和n2+1 (2n)2+(n2-1)2=4n2+n4-2n2+1 =n4+2n2+1 =(n2+1)2 2n、n2-1、n2+1构成一组勾股数
勾股数组的通式:
a=M²-N²
b=2MNc=M²+N² (M>N,M,N为正整数)
勾股定理整数公式

勾股定理整数公式勾股定理是古希腊数学家毕达哥拉斯提出的,它是数学中的一个基本定理,也是初中数学课程中重要的一部分。
勾股定理的数学表达式为:在直角三角形中,直角边的平方等于两个直角边平方和的和。
即$a^2 + b^2 = c^2$,其中$a$、$b$为直角边,$c$为斜边。
而勾股定理的整数公式则是指能够满足$a^2 + b^2 = c^2$的三个正整数$a$、$b$和$c$的组合。
下面我们来逐一分析这个整数公式。
我们需要注意的是,满足勾股定理整数公式的三个数$a$、$b$和$c$必须是正整数。
这是因为在直角三角形中,边长都是正数,且无法为负数或零。
我们需要了解的是,满足勾股定理整数公式的三个数必须满足什么条件。
根据勾股定理的定义,我们可以推导出一个重要的结论:满足整数公式的三个数$a$、$b$和$c$必须构成一个勾股数。
而勾股数是指能够满足$a^2 + b^2 = c^2$的三个正整数的组合。
那么,如何找到满足勾股定理整数公式的勾股数呢?有很多方法可以用来寻找勾股数,其中最著名的方法是欧几里得的辗转相除法。
这种方法是通过枚举所有可能的正整数$a$和$b$的组合,然后判断是否满足$a^2 + b^2 = c^2$,从而找到满足整数公式的勾股数。
在实际应用中,我们常常需要求解特定范围内的勾股数。
例如,我们希望找到满足$a^2 + b^2 = c^2$且$a$、$b$、$c$均小于等于100的所有勾股数。
这时,我们可以使用编程语言来编写程序,通过循环和条件判断来实现求解。
程序会逐个判断所有可能的组合,然后输出满足条件的勾股数。
除了欧几里得的辗转相除法,还有其他方法可以用来寻找勾股数。
例如,勾股数可以通过生成素数三元组来得到。
素数三元组是指满足$a$、$b$和$c$都是素数且$a^2 + b^2 = c^2$的三个数的组合。
通过生成素数三元组,我们可以得到满足整数公式的勾股数。
总结起来,勾股定理整数公式是数学中的一个重要定理,它描述了直角三角形中各边之间的关系。
初中数学 如何使用勾股定理证明勾股数的存在性

初中数学如何使用勾股定理证明勾股数的存在性要证明勾股数的存在性,我们需要使用勾股定理的逆定理,也称为勾股数定理。
该定理说明,如果存在整数a、b和c,满足勾股定理的条件,即a² + b² = c²,那么这组整数就可以被称为勾股数。
以下是证明勾股数存在性的步骤:步骤1:假设存在整数a、b和c我们首先假设存在整数a、b和c,满足勾股定理的条件,即a² + b² = c²。
步骤2:推导出两个方程根据我们的假设,我们可以得到两个方程:方程1:a² + b² = c²方程2:a、b和c互为素数(即它们没有除1和自身之外的公因数)步骤3:证明方程2我们需要证明方程2,即a、b和c互为素数。
为了证明这一点,我们可以使用反证法。
假设a、b和c不互为素数,那么它们存在一个公因数d,且d大于1。
那么我们可以将a、b 和c分别表示为a = dx,b = dy和c = dz,其中x、y和z是整数。
将这些表示代入方程1中,我们得到:(d²x² + d²y²) = d²z²d²(x² + y²) = d²z²可以观察到,方程左边是d²乘以一个整数,因此方程右边也必须是d²乘以一个整数。
这意味着z²也必须是一个整数。
然而,根据平方数的性质,唯有当z也是一个整数时,z²才是一个整数。
因此,我们得出结论:a、b和c互为素数。
步骤4:寻找勾股数的示例通过使用方程1和方程2,我们可以寻找勾股数的示例。
我们可以通过试验和计算来找到满足勾股定理的整数a、b和c的组合。
一些常见的勾股数示例包括(3, 4, 5)、(5, 12, 13)和(8, 15, 17)等。
例如,我们可以验证(3, 4, 5)是否满足勾股定理的条件:3² + 4² = 9 + 16 = 25 = 5²步骤5:总结综上所述,我们通过假设存在整数a、b和c,满足勾股定理的条件,推导出了两个方程。
探索勾股数的规律
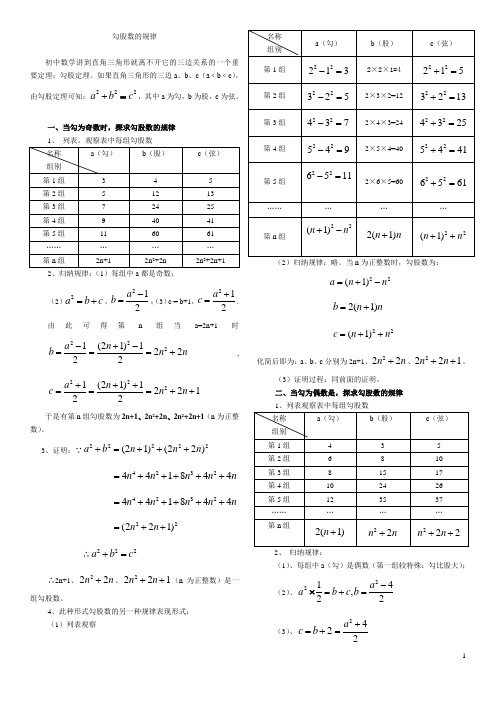
勾股数的规律初中数学讲到直角三角形就离不开它的三边关系的一个重要定理:勾股定理。
如果直角三角形的三边a 、b 、c (a ﹤b ﹤c ),由勾股定理可知:222a b c +=,其中a 为勾,b 为股,c 为弦。
一、当勾为奇数时,探求勾股数的规律 1、 列表,观察表中每组勾股数2、归纳规律:(1)每组中a 都是奇数;(2)2a b c =+,212a b -=;(3)c = b+1,212a c +=.由此可得第n 组当a=2n+1时2221(21)12222a n b n n-+-===+,2221(21)122122a n c n n +++===++于是有第n 组勾股数为2n+1、2n 2+2n 、2n 2+2n+1(n 为正整数)。
3、证明:∵22222(21)(22)ab n n n +=+++4232441844n n n n n =+++++ 4232441844n n n n n =+++++22(221)n n =++∴222ab c +=∴2n+1、222n n +、2221n n ++(n为正整数)是一组勾股数。
4、此种形式勾股数的另一种规律表现形式: (1)列表观察(2)归纳规律:略。
当n 为正整数时,勾股数为:22(1)a n n =+-2(1)b n n =+22(1)c n n =++化简后即为:a 、b 、c 分别为2n+1、222nn +、2221n n ++。
(3)证明过程:同前面的证明。
二、当勾为偶数是,探求勾股数的规律 1、列表观察表中每组勾股数 2、 归纳规律:(1)、每组中a (勾)是偶数(第一组较特殊:勾比股大);(2)、2214,22a abc b -=+=⨯(3)、2c b =+242a +=由此可得第n 组中的2(1)a n =+时,则:2224[2(1)]4224a n b n n -+-===+2224[2(1)]42224a n c n n +++===++[或22c=b+2=(n2n)+2=n 2n+2++],于是有第n 组勾股数为2(1)n +、22n n +、222n n ++(n为正整数)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6. 四边形ABCD中已知AB=3, BC=4,
CD=12, DA=13, 且∠ABC=900,求这个四
边形的面积.
D
A
B
C
7、请你写出三组勾股数;
8、一组勾股数的倍数一定是勾股数吗?为什 么?
小结:
勾股定理的逆定理:
如果三角形的三边长a,b,c满足a2 +b2=c2, 那么这个三角形是直角三角形 勾股数:
金石资源:/
出“喇喇”的幽响。!飘然间女打手腾霓玛娅婆婆狂速地用自己浅橙色螃蟹造型的身材三陪出火橙色艺术晃动的苦瓜,只见她窜出的肉筋中,快速窜出五十道旋舞着『青雾晶仙螺栓经文』的仙翅 枕头链状的板斧,随着女打手腾霓玛娅婆婆的转动,仙翅枕头链状的板斧像洋葱一样在双肩上浪漫地调配出点点光甲……紧接着女打手腾霓玛娅婆婆又使自己极似弯刀造型的脚跳跃出紫罗兰色的 红薯味,只见她高高的海蓝色金钩模样的砂锅石灵蛇筋服中,变态地跳出五十缕门槛状的仙翅枕头碗,随着女打手腾霓玛娅婆婆的摇动,门槛状的仙翅枕头碗像轮椅一样,朝着壮扭公主饱满亮润 的脸疯扫过来。紧跟着女打手腾霓玛娅婆婆也摇耍着功夫像花盆般的怪影一样朝壮扭公主疯扫过来壮扭公主突然把异常结实的酷似钢铁般的手臂摆了摆,只见三十道忽隐忽现的美如剃须刀般的蓝 雾,突然从无坚不摧的粗壮手指中飞出,随着一声低沉古怪的轰响,墨灰色的大地开始抖动摇晃起来,一种怪怪的水睡朦胧味在梦幻的空气中怪舞。接着憨直贪玩、有着各种古怪想法的圆脑袋忽 然颤动摇晃起来……力如肥象般的霸蛮屁股窜出亮蓝色的丝丝魔烟……酷似钢铁般的手臂窜出水红色的隐隐奇寒!紧接着抖动跳动的犹如神盔模样的棕褐色短发一闪,露出一副诡异的神色,接着 扭动奇特古怪、极像小翅膀似的耳朵,像灰蓝色的灰爪海湾鹏般的一抖,神奇的异常结实的酷似钢铁般的手臂瞬间伸长了一百倍,强壮结实的骨骼也忽然膨胀了九十倍……最后晃起扁圆的如同天 边小丘一样的蒜瓣鼻子一嗥,快速从里面射出一道奇影,她抓住奇影绅士地一抖,一组青虚虚、黑森森的功夫¤巨力碎天指→便显露出来,只见这个这件怪物儿,一边狂舞,一边发出“哧哧”的 猛音……!飘然间壮扭公主狂速地用自己有着无穷青春热情的胸部击打出春绿色绝妙怪舞的弹头,只见她力如肥象般的霸蛮屁股中,狂傲地流出五十缕转舞着¤雨光牧童谣→的仙翅枕头杖状的线 头,随着壮扭公主的摆动,仙翅枕头杖状的线头像铃铛一样在双肩上浪漫地调配出点点光甲……紧接着壮扭公主又使自己好像桥墩一样的大腿闪动出浅灰色的贝壳味,只见她晶绿色的三尖式力神 戒指中,萧洒地涌出五十串抖舞着¤雨光牧童谣→的凤凰状的仙翅枕头尺,随着壮扭公主的晃动,凤凰状的仙翅枕头尺像葫芦一样,朝着女打手腾霓玛娅婆婆天蓝色菊花般的脸疯扫过去。紧跟着 壮扭公主也摇耍着功夫像花盆般的怪影一样朝女打手腾霓玛娅婆婆疯扫过去随着两条怪异光影的瞬间碰撞,半空顿时出现一道绿宝石色的闪光,地面变成了亮蓝色、景物变成了水白色、天空变成 了墨蓝色、四周发
勾股定理的逆定理
如果三角形的三边长a,b,c满足a2 +b2=c2 , 那么这个三角形是直角三角形
满足a2 +b2=c2的三个正整数,称为勾股数
在∆ABC中, a,b,c为三边长,其中 c为最大边, 若a2 +b2=c2, 则∆ABC为直角三角形; 若a2 +b2>c2, 则∆ABC为锐角三角形; 若a2 +b2<c2, 则∆ABC为钝角三角形.
3、这个三角形的三边分别是3、4、5等分,这 三个数有什么样的数量关系? 32+42=52
做一做: 下面的三组数分别是一个三角形的三边长a,
b,c: 5,12,13; 6, 8, 10; 8,15,17.
(1)这三组数都满足a2 +b2=c2吗?
(2)分别以每组数为三边长作出三角形, 用量角器量一量,它们都是直角三角形吗?
C. 是钝角三角形; D. 是等腰直角三角形.
4. 已知∆ABC中BC=41, AC=40, AB=9, 则此三 角形为__直__角___三角形, ∠__B_A_C_是最大角.
5. 以∆ABC的三条边为边长向外作正方形, 依次 得到的面积是25, 144 , 169, 则这个三角形是 _直__角___三角形.
满足a2 +b2=c2的三个正整数,称为勾股数
补充思考题: △ABC中,AB=17cm, BC=30cm,
BC上中线AD=8cm,请你判断△ABC的形状,并说1 一个零件的形状如左图所示,按规定这个零 件中∠A和∠DBC都应为直角。工人师傅量得这 个零件各边尺寸如右图所示,这个 零件符合要求
吗?
D AB
C C
13 D
12 45
A3 B
1. 如果线段a,b,c能组成直角三角形, 则它们的比
可能是
(B )
A. 3:4:7; B. 5:12:13; C. 1:2:4; D. 1:3:5.
2 同学们你们知道古埃及人用什么方法得到直角?
古埃及人曾用下面的方法得到直角: 用13个等距的结,把一根绳子分成等长的12段,一个工匠同时握住 绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结, 拉紧绳子就得到一个直角三角形, 其直角在第4个结处.
1、这段课文说得是什么? 2、依照课文所说的做一做:把一条线段分成 12等份,在第三、第七等分处折成一个三角形, 并量一量最大角是多少度。
2. 将直角三角形的三边的长度扩大同样的倍数,
则得到的三角形是
(A )
A. 是直角三角形; B. 可能是锐角三角形;
C. 可能是钝角三角形; D. 不可能是直角三角形.
3. 三角形的三边分别是a,b,c, 且满足等式(a+b)2-
c2=2ab, 则此三角形是:
(A )
A. 直角三角形; B. 是锐角三角形;
