七年级数学平行线几何模型之M型解题方法专题练习

合集下载

第7章平面图形的认识(二)-平行线中的常见模型苏科版七年级数学下册专题练习(含答案)

七年级下册平面图形的认识（二）：专题：平行线中的常见四大模型专题：平行线中的常见模型模型一：“猪蹄”模型（也称“M”模型）模型一“猪蹄”模型（M模型）点P在EF左侧，在AB、 CD内部“猪蹄”模型结论1：若AB∥CD，则∠P=∠AEP+∠CFP；结论2：若∠P=∠AEP+∠CFP，则AB∥CD.典型例题例1：如图，已知AB∥DE，∠1＝30°，∠2＝35°，则∠BCE的度数为（）A．70° B．65° C．35° D．5°例2：如图，AD∥CE，∠ABC＝95°，则∠2﹣∠1的度数是（）A．105°B．95°C．85°D．75°例3：如图，直线a∥b，射线DF与直线a相交于点C，过点D作DE⊥b于点E，已知∠1＝25°，求∠2的度数．例4：如图，AB∥CD，∠E＝35°，∠F＝∠G＝30°，则∠A+∠C的度数为　．例5：如图，AB∥CD，∠E＝120°，∠F＝90°，∠A+∠C的度数是（）A．30°B．35°C．40°D．45°例6：如图，AB∥CD，∠E+∠G＝∠H，则∠A+∠B+∠C+∠D+∠F的度数为．例7：如图，直线l1∥l2，点∠α、∠β夹在两平行线之间．（1）若∠α＝∠β，∠1＝40°，求∠2的度数；（2）直接写出∠1、∠2、∠α、∠β之间的数量关系，不用说明理由．例8：（1）如图1，已知AB∥CD，若∠EAF=∠EAB，∠ECF=∠ECD，求证：∠AFC=∠AEC；（2）如图2，若AB∥CD，∠EAF=∠EAB，∠ECF=∠ECD，求证：∠AFC=∠AEC；（3）若AB∥CD，∠EAF=∠EAB，∠ECF∠ECD，则∠AFC与∠AEC的数量关系是（用含有n的代数式表示，不证明）．例9：如图①，已知AB∥CD，CE、BE的交点为E，现作如下操作：第1次操作，分别作∠ABE和∠DCE的平分线，交点为E1，第2次操作，分别作∠ABE1和∠DCE1的平分线，交点为E2，第3次操作，分别作∠ABE2和∠DCE2的平分线，交点为E3，…，第n次操作，分别作∠ABE n﹣1和∠DCE n﹣1的平分线，交点为E n．（1）如图①，求证：∠BEC＝∠ABE+∠DCE；（2）如图②，求证：∠BE1C＝∠BEC；（3）从图①开始进行上述的n次操作，若∠BE n C＝α°，求∠BEC的大小（直接写出结论）．模型二：“铅笔”模型（也称“U”型模型）模型二：“铅笔”模型（“U”型）点P在EF右侧，在AB、 CD内部“铅笔”模型结论1：若AB∥CD，则∠P+∠AEP+∠PFC=360°；结论2：若∠P+∠AEP+∠PFC= 360°，则AB∥CD.典型例题例1：一大门栏杆的平面示意图如图所示，BA垂直地面AE于点A，CD平行于地面AE，若∠BCD＝135°，则∠ABC＝度．例2：如图，直线l1∥l2，若∠1＝35°，则∠2+∠3＝．例3：如图，已知AB∥CD，E为AB，CD之间一点，连接BE，DE．（1）猜想∠BED时，∠B，∠D的数量关系，并证明；（2）作∠ABE，∠CDE的角平分线BF，DF交于点F．①依题意补全图形；②直接用等式表示∠BFD与∠BED的数量关系．例4：如图，已知AB∥CD，∠ABE与∠CDE的平分线相交于点F．（1）如图1，若∠E＝70°，求∠BFD的度数；（2）如图2，若∠ABM＝∠ABF，∠CDM＝∠CDF，写出∠M和∠E之间的数量关系，并证明你的结论．例5：实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等．如图，一束光线m射到平面镜a上，被a反射到平面镜b上，又被b反射的光线为n．（1）当m∥n时，若∠1＝50°，则∠2＝，∠3＝；（2）当m∥n时，若∠1＝x°（0＜x＜90），则∠3＝；（3）根据（1）（2）结果，反过来猜想：当两平面镜a，b的夹角∠3为多少度时，m∥n．请说明理由（可以在图中添加适当的角度标记进行说明）例6：如图，AB∥CD，点E为两直线之间的一点．（1）如图1，若∠BAE＝35°，∠DCE＝20°，则∠AEC＝；（2）如图2，试说明，∠BAE+∠AEC+∠ECD＝360°；（3）①如图3，若∠BAE的平分线与∠DCE的平分线相交于点F，判断∠AEC与∠AFC 的数量关系，并说明理由；②如图4，若设∠E＝m，∠BAF＝∠FAE，∠DCF＝∠FCE，请直接用含m、n的代数式表示∠F的度数．模型三：“抬头”模型（也称“靴子”或称“臭脚”模型）模型三“抬头”模型（“靴子”模型）点P在EF右侧，在AB、 CD外部“靴子”模型结论1：若AB∥CD，则∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP；结论2：若∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP，则AB∥CD.典型例题例1：如图，AB//CD，∠P=40°，∠D=100°，则∠ABP的度数是 .例2：已知，AB∥CD.(1)如图1，求证:∠A-∠C=∠E;(2)如图2，EF平分∠AEC，CF平分∠ECD，∠F=105°，求∠A的度数.例3：已知直线∥，点A，B在直线上(B在A左侧)，点C在直线b上，E点在直线b下方，连接 AE 交直线b于点D.(1)如图1，若∠BAD=110°，∠DCE=45°，求∠DEC的度数;(2)如图2，∠BAD 的邻补角的角平分线与∠DEC 的角平分线所在的直线交于点M，试探究∠AME与∠ECD之间的数量关系，并说明理由.例4：已知AB∥CD．（1）如图1，求证：∠EAB＝∠C+∠E；（2）如图2，点F在∠AEC内且在AB、CD之间，EF平分∠AEC，CF平分∠ECD，请猜想∠F与∠EAB的数量关系并证明；（3）如图3，点M在AB上，点N在CD上，点E是AB上方一点，点G在AB、CD之间，连接EM、EN，GM的延长线MF平分∠AME，NE平分∠CNG，若2∠MEN+∠MGN＝105°，求∠AME的度数．:模型四：“骨折”模型（也称“X射线”模型）模型四“骨折”模型点P在EF左侧，在AB、 CD外部“骨折”模型结论1：若AB∥CD，则∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP；结论2：若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP，则AB∥CD.例1：如图，AB∥CD，∠E＝40°，∠A＝110°，则∠C的度数为．例2：如图，AB∥CD，∠ABE＝125°，∠C＝30°，则∠α＝（）A．70°B．75°C．80°D．85°例3：已知：如图，AB∥CD．（1）若∠1＝∠2，试判断∠E与∠F的大小关系，并说明你的理由．（2）猜想∠1、∠2、∠E、∠F之间存在怎样的数量关系？并说明理由．例4：（1）（问题）如图1，若AB∥CD，∠AEP＝40°，∠PFD＝130°．求∠EPF的度数；（2）（问题迁移）如图2，AB∥CD，点P在AB的上方，问∠PEA，∠PFC，∠EPF之间有何数量关系？请说明理由；（3）（联想拓展）如图3所示，在（2）的条件下，已知∠EPF＝α，∠PEA的平分线和∠PFC的平分线交于点G，用含有α的式子表示∠G的度数．例5：已知AB∥MN．（1）如图1，求证：∠N+∠E＝∠B；（2）若F为直线MN、AB之间的一点，∠E＝∠EFB，BG平分∠ABF交MN于点G，EF 交MN于点C．①如图2，若∠N＝57°，且BG∥EN，求∠E的度数；②如图3，若点K在射线BG上，且满足∠KNM＝∠ENM，若∠NKB＝∠EFB，∠E＝∠FBD，直接写出∠E的度数．参考答案专题四：平行线中的常见模型模型一：“猪蹄”模型（也称“M”模型）模型一“猪蹄”模型（M模型）点P在EF左侧，在AB、 CD内部“猪蹄”模型结论1：若AB∥CD，则∠P=∠AEP+∠CFP；结论2：若∠P=∠AEP+∠CFP，则AB∥CD.典型例题例1：如图，已知AB∥DE，∠1＝30°，∠2＝35°，则∠BCE的度数为（B）A．70° B．65° C．35° D．5°解析：作CF∥AB，∵AB∥DE，∴CF∥DE，∴AB∥DE∥CF，∴∠1＝∠BCF，∠FCE＝∠2，∵∠1＝30°，∠2＝35°，∴∠BCF＝30°，∠FCE＝35°，∴∠BCE＝65°，故选：B．例2：如图，AD∥CE，∠ABC＝95°，则∠2﹣∠1的度数是（C）A．105°B．95°C．85°D．75°解析：如图，作BF∥AD，∵AD∥CE，∴AD∥BF∥EC，∴∠1＝∠3，∠4+∠2＝180°，∠3+∠4＝95°，∴∠1+∠4＝95°，∠2+∠4＝180°，∴∠2﹣∠1＝85°．故选：C．例3：如图，直线a∥b，射线DF与直线a相交于点C，过点D作DE⊥b于点E，已知∠1＝25°，求∠2的度数．解析：过点D作DG∥b，∵a∥b，且DE⊥b，∴DG∥a，∴∠1＝∠CDG＝25°，∠GDE＝∠3＝90°∴∠2＝∠CDG+∠GDE＝25°+90°＝115°．☆模型拓展：M叠M型例4：如图，AB∥CD，∠E＝35°，∠F＝∠G＝30°，则∠A+∠C的度数为35°．解析：如图所示，延长AE，CG，交于点H，过H作HP∥AB，∵AB∥CD，∴PH∥CD，∴∠A＝∠AHP，∠C＝∠CHP，∴∠A+∠C＝∠AHC，∵∠F＝∠CGF＝30°，∴EF∥CH，∴∠AHC＝∠AEF＝35°，∴∠A+∠C＝35°，故答案为：35°．例5：如图，AB∥CD，∠E＝120°，∠F＝90°，∠A+∠C的度数是（）A．30°B．35°C．40°D．45°解析：分别过E，F作GE∥AB，FH∥AB，∵AB∥CD，∴AB∥GE∥FH∥CD，∴∠1＝∠A，∠2＝∠C，∠GEF+∠HFE＝180°，∵∠E＝120°，∠F＝90°，∴∠1+∠GEF+∠HFE+∠2＝210°，∴∠1+∠2＝210°﹣180°＝30°，即∠A+∠C＝30°，故选：A．例6：如图，AB∥CD，∠E+∠G＝∠H，则∠A+∠B+∠C+∠D+∠F的度数为360°．解析：如图所示，延长AE，DG交于点Q，由题可得，∠A+∠D＝∠Q，∠B+∠H+∠C＝360°，又∵∠Q＝∠AEF+∠DGF﹣∠F，∴∠A+∠D＝∠AEF+∠DGF﹣∠F，即∠F＝∠AEF+∠DGF﹣（∠A+∠D），又∵∠AEF+∠DGF＝∠H，∴∠A+∠B+∠C+∠D+∠F＝∠A+∠B+∠C+∠D+∠AEF+∠DGF﹣（∠A+∠D）＝∠B+∠C+∠H＝360°，故答案为：360°．例7：如图，直线l1∥l2，点∠α、∠β夹在两平行线之间．（1）若∠α＝∠β，∠1＝40°，求∠2的度数；（2）直接写出∠1、∠2、∠α、∠β之间的数量关系，不用说明理由．解析：（1）如图，延长AE交直线l2于点E，∵l1∥l2，∴∠3＝∠1＝40°，∵∠α＝∠β，∴AB∥CD，∴∠2+∠3＝180°，∴∠2＝180°﹣∠3＝180°﹣40°＝140°．（2）∠1+∠2+∠β﹣○α＝180°．理由：∵l1∥l2，∴∠3＝∠1．∵∠BED＝180°﹣∠α，∴∠3+∠2+∠β+180°﹣α＝360°，即∠1+∠2+∠β﹣∠α＝180°．☆模型拓展：M套M型例8：（1）如图1，已知AB∥CD，若∠EAF=∠EAB，∠ECF=∠ECD，求证：∠AFC=∠AEC；（2）如图2，若AB∥CD，∠EAF=∠EAB，∠ECF=∠ECD，求证：∠AFC=∠AEC；（3）若AB∥CD，∠EAF=∠EAB，∠ECF=∠ECD，则∠AFC与∠AEC的数量关系是（用含有n的代数式表示，不证明）．解：（1）如图1，连接AC，设∠EAF＝x°，∠ECF＝y°，∠EAB＝2x°，∠ECD＝2y°，∵AB∥CD，∴∠BAC+∠ACD＝180°，∴∠CAE+2x°+∠ACE+2y°＝180°，∴∠CAE+∠ACE＝180°﹣（2x°+2y°），∠FAC+∠FCA＝180°﹣（x°+y°），∴∠AEC＝180°﹣（∠CAE+∠ACE）＝180°﹣[180°﹣（2x°+2y°）]＝2x°+2y°，＝2（x°+y°），∠AFC＝180°﹣（∠FAC+∠FCA）＝180°﹣[180°﹣（x°+y°）]＝x°+y°，∴∠AFC=∠AEC；（2）如图2，连接AC，设∠EAF＝x°，∠ECF＝y°，∠EAB＝3x°，∠ECD＝3y°，∵AB∥CD，∴∠BAC+∠ACD＝180°，∴∠CAE+3x°+∠ACE+3y°＝180°，∴∠CAE+∠ACE＝180°﹣（3x°+3y°），∠FAC+∠FCA＝180°﹣（2x°+2y°），∴∠AEC＝180°﹣（∠CAE+∠ACE）＝180°﹣[180°﹣（3x°+3y°）]＝3x°+3y°＝3（x°+y°），∠AFC＝180°﹣（∠FAC+∠FCA）＝180°﹣[180°﹣（2x°+2y°）]＝2x°+2y°＝2（x°+y°），∴∠AFC=∠AEC；（3）若∠AFC=∠EAB，∠ECF=∠ECD，则∠AFC与∠AEC的数量关系是：∠AFC=∠AEC．故答案为：∠AFC=∠AEC．例9：如图①，已知AB∥CD，CE、BE的交点为E，现作如下操作：第1次操作，分别作∠ABE和∠DCE的平分线，交点为E1，第2次操作，分别作∠ABE1和∠DCE1的平分线，交点为E2，第3次操作，分别作∠ABE2和∠DCE2的平分线，交点为E3，…，第n次操作，分别作∠ABE n﹣1和∠DCE n﹣1的平分线，交点为E n．（1）如图①，求证：∠BEC＝∠ABE+∠DCE；（2）如图②，求证：∠BE1C＝∠BEC；（3）从图①开始进行上述的n次操作，若∠BE n C＝α°，求∠BEC的大小（直接写出结论）．【解答】解：（1）如图①，过E作EF∥AB．∵AB∥CD，∴AB∥EF∥CD，∴∠B＝∠1，∠C＝∠2．∵∠BEC＝∠1+∠2，∴∠BEC＝∠ABE+∠DCE；（2）如图2．∵∠ABE和∠DCE的平分线交点为E1，∴由（1）可得，∠CE1B＝∠ABE1+∠DCE1＝∠ABE+∠DCE＝∠BEC；（3）如图2．∵∠ABE2和∠DCE2的平分线，交点为E3，∴∠BE3C＝∠ABE3+∠DCE3＝∠ABE2+∠DCE2＝∠CE2B＝∠BEC；…以此类推，∠E n＝∠BEC，∴当∠E n＝α度时，∠BEC＝2nα°模型二：“铅笔”模型（也称“U”型模型）模型二：“铅笔”模型（“U”型）点P在EF右侧，在AB、 CD内部“铅笔”模型结论1：若AB∥CD，则∠P+∠AEP+∠PFC=360°；结论2：若∠P+∠AEP+∠PFC= 360°，则AB∥CD.典型例题例1：一大门栏杆的平面示意图如图所示，BA垂直地面AE于点A，CD平行于地面AE，若∠BCD＝135°，则∠ABC＝135度．【解析】解：如图，过点B作BF∥CD，∵CD∥AE，∴CD∥BF∥AE，∴∠1+∠BCD＝180°，∠2+∠BAE＝180°，∵∠BCD＝135°，∠BAE＝90°，∴∠1＝45°，∠2＝90°，∴∠ABC＝∠1+∠2＝135°．故答案为：135．例2：如图，直线l1∥l2，若∠1＝35°，则∠2+∠3＝215°．【解析】解：过点E作EF∥11，∵11∥12，EF∥11，∴EF∥11∥12，∴∠1＝∠AEF＝35°，∠FEC+∠3＝180°，∴∠2+∠3＝∠AEF+∠FEC+∠3＝35°+180°＝215°．故答案为：215°．例3：如图，已知AB∥CD，E为AB，CD之间一点，连接BE，DE．（1）猜想∠BED时，∠B，∠D的数量关系，并证明；（2）作∠ABE，∠CDE的角平分线BF，DF交于点F．①依题意补全图形；②直接用等式表示∠BFD与∠BED的数量关系．【解析】（1）∠B+∠BED+∠D＝360°．证明：过点E作EG∥AB．∴∠B+∠BEG＝180°．∵AB∥CD，EG∥AB，∴EG∥CD，∴∠DEG+∠D＝180°，∴∠B+∠BEG+∠DEG+∠D＝180°+180°．即∠B+∠BED+∠D＝360°；（2）解：①如图所示：②由（1）得∠ABC+∠BED+∠CDE＝360°，∵∠ABE，∠CDE的角平分线BF，DF交于点F，∴∠ABC＝2∠FBE，∠CDE＝2∠FDE，∴2∠FBE+∠BED+2∠CDE＝360°，即∠FBE+∠BED+∠CDE＝180°，∵∠BFD+∠FBE+∠BED+∠CDE＝360°，∴∠BFD=180°－∠BED例4：如图，已知AB∥CD，∠ABE与∠CDE的平分线相交于点F．（1）如图1，若∠E＝70°，求∠BFD的度数；（2）如图2，若∠ABM＝∠ABF，∠CDM＝∠CDF，写出∠M和∠E之间的数量关系，并证明你的结论．【解析】解：（1）如图1，过点E作EN∥AB，∵EN∥AB，∴∠ABE+∠BEN＝180°，∵AB∥CD，AB∥NE，∴NE∥CD，∴∠CDE+∠NED＝180°，∴∠ABE+∠E+∠CDE＝360°，∵∠E＝70°，∴∠ABE+∠CDE＝290°，∵∠ABE与∠CDE的平分线相交于点F，∴∠ABF+∠CDF＝（∠ABE+∠CDE）＝145°，过点F作FG∥AB，∵FG∥AB，∴∠ABF＝∠BFG，∵AB∥CD，FG∥AB，∴FG∥CD，∴∠CDF＝∠GFD，∴∠BFD＝∠ABF+∠CDF＝145°；（2）结论：∠E+6∠M＝360°，证明：∵设∠ABM＝x，∠CDM＝y，则∠FBM＝2x，∠EBF＝3x，∠FDM＝2y，∠EDF＝3y，由（1）得：∠ABE+∠E+∠CDE＝360°，∴6x+6y+∠E＝360°，∵∠M+∠EBM+∠E+∠EDM＝360°，∴6x+6y+∠E＝∠M+5x+5y+∠E，∴∠M＝x+y，∴∠E+6∠M＝360°．例5：实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等．如图，一束光线m射到平面镜a上，被a反射到平面镜b上，又被b反射的光线为n．（1）当m∥n时，若∠1＝50°，则∠2＝100°，∠3＝　90°；（2）当m∥n时，若∠1＝x°（0＜x＜90），则∠3＝　90°；（3）根据（1）（2）结果，反过来猜想：当两平面镜a，b的夹角∠3为多少度时，m∥n．请说明理由（可以在图中添加适当的角度标记进行说明）【解析】解：（1）∵m∥n，∴∠4+∠2＝180°，∵∠5＝∠1＝50°，∴∠4＝80°，∴∠2＝100°，∴∠6＝∠7＝40°，∴∠3＝180°﹣∠5﹣∠6＝90°，故答案为：100°；90°；（2）∵m∥n，∴∠4+∠2＝180°，∵∠5＝∠1＝x°，∴∠4＝180°﹣2x°，∴∠2＝2x°，∴∠6＝∠7＝90°﹣x°，∴∠3＝180°﹣∠5﹣∠6＝180°﹣x°﹣90°+x°＝90°，故答案为：90°；（3）根据（1）、（2）猜想：当两平面镜a、b的夹角∠3是90°时，总有m∥n，证明：∵∠3＝90°，∴∠5+∠6＝90°，∴∠1+∠7＝90°，∴∠1+∠5+∠6+∠7＝180°，又∵∠1+∠4+∠5+∠2+∠6+∠7＝360°，∴∠4+∠2＝180°，∴m∥n．例6：如图，AB∥CD，点E为两直线之间的一点．（1）如图1，若∠BAE＝35°，∠DCE＝20°，则∠AEC＝55°；（2）如图2，试说明，∠BAE+∠AEC+∠ECD＝360°；（3）①如图3，若∠BAE的平分线与∠DCE的平分线相交于点F，判断∠AEC与∠AFC 的数量关系，并说明理由；②如图4，若设∠E＝m，∠BAF＝∠FAE，∠DCF＝∠FCE，请直接用含m、n的代数式表示∠F的度数．【解析】解：如图所示，过点E作EF∥AB，∵AB∥CD∴AB∥CD∥EF，∴∠BAE＝∠1，∠ECD＝∠2，∴∠AEC＝∠1+∠2＝∠BAE+∠ECD＝35°+20°＝55°，故答案为55°．（2）如图所示，过点E作EG∥AB，∵AB∥CD∴AB∥CD∥EG，∴∠A+∠1＝180°，∠C+∠2＝180°，∴∠A+∠1+∠2+∠C＝360°，即∠BAE+∠AEC+∠ECD＝360°．（3）①2∠AFC+∠AEC＝360°，理由如下：由（1）可得，∠AFC＝∠BAF+∠DCF，∵AF平分∠BAE，CF平分∠DCE，∴∠BAE＝2∠BAF，∠DCE＝2∠DCF，∴∠BAE+∠DCE＝2∠AFC，由（2）可知，∠BAE+∠AEC+∠DCE＝360°，∴2∠AFC+∠AEC＝360°．②由①知∠F+∠FAE+∠E+∠FCE＝360°，∵∠BAF＝∠FAE，∠DCF＝∠FCE，∠BAF+∠DCF＝∠F，∴∠F＝（∠FAE+∠FCE），∴∠FAE+∠FCE＝n∠F，∴∠F+∠E+n∠F＝360°，∴（n+1）∠F＝360°﹣∠E＝360°﹣m，∴∠F＝．模型三：“抬头”模型（也称“靴子”或称“臭脚”模型）模型三“抬头”模型（“靴子”模型）点P在EF右侧，在AB、 CD外部“靴子”模型结论1：若AB∥CD，则∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP；结论2：若∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP，则AB∥CD.典型例题例1：如图，AB//CD，∠P=40°，∠D=100°，则∠ABP的度数是140°.【解析】过点P作PM∥AB，∵AB∥CD，∴PM∥AB∥CD，∴∠MPB=∠ABP，∠D=∠DPM=100°，∴∠MPB=∠BPD+∠DPM=40°+100°=140°，∴∠ABP=∠MPB=140°.例2：已知，AB∥CD.(1)如图1，求证:∠A-∠C=∠E;(2)如图2，EF平分∠AEC，CF平分∠ECD，∠F=105°，求∠A的度数.【解析】（1）证明: 过点E作EF∥AB，∵AB∥CD，∴EF∥AB∥CD，∴∠FEA=∠EAB，∠FEC=∠C，∴∠AEC=∠FEA-∠FEC=∠EAB-∠C，即∠A-∠C=∠E.（2）解:过点E作EG∥FC，∵EF平分∠AEC，CF平分∠ECD，设∠AEF=∠CEF=，∠ECF=∠FCD=，∵EG∥FC，∴∠CEG=∠ECF=，∠FEG+∠F=180°.∵∠F=105°，∴∠FEG=180°-∠F=75°，∴∠CEG+∠CEF=75°，即+=75°,∴2x+2y=150°.由(1)知，∠A=∠AEC+∠ECD=2x+2y=150°.例3：已知直线∥，点A，B在直线上(B在A左侧)，点C在直线b上，E点在直线b下方，连接 AE 交直线b于点D.(1)如图1，若∠BAD=110°，∠DCE=45°，求∠DEC的度数;(2)如图2，∠BAD 的邻补角的角平分线与∠DEC 的角平分线所在的直线交于点M，试探究∠AME与∠ECD之间的数量关系，并说明理由.例4：已知AB∥CD．（1）如图1，求证：∠EAB＝∠C+∠E；（2）如图2，点F在∠AEC内且在AB、CD之间，EF平分∠AEC，CF平分∠ECD，请猜想∠F与∠EAB的数量关系并证明；（3）如图3，点M在AB上，点N在CD上，点E是AB上方一点，点G在AB、CD之间，连接EM、EN，GM的延长线MF平分∠AME，NE平分∠CNG，若2∠MEN+∠MGN＝105°，求∠AME的度数．:【解析】（1）过点E作EF∥DC，∵BA∥DC，∴EF∥DC∥AB，∴∠AEF=∠BAE=110°，∠CEF=∠DCE=45°.∴∠DEC=∠AEF-∠CEF=110°-45°=65°.（2）过点M作MF∥BA，过点E作EG∥CD，设∠BAE=，∠ECD=，∵BA∥CD，∴MF∥AB∥CD∥EG.∴∠BAE=∠AEG=，∠DCE=∠CEG=，∴∠DEC=-.∵EM平分∠DEC，AM平分∠BAD的邻补角，∴∠MEC=，∠1==，∵MF∥AB，∴∠AMF=∠1=，∠MEG=∠CEG+∠MEC=，∵MF∥EG，∴∠FME=∠MEG=，∴∠AME=∠AMF+∠FME=，∴∠AME=.模型四：“骨折”模型（也称“X射线”模型）模型四“骨折”模型点P在EF左侧，在AB、 CD外部“骨折”模型结论1：若AB∥CD，则∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP；结论2：若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP，则AB∥CD.例1：如图，AB∥CD，∠E＝40°，∠A＝110°，则∠C的度数为70°．解析：∵AB∥CD，∴∠A+∠AFD＝180°，∵∠A＝110°，∴∠AFD＝70°，∴∠CFE＝∠AFD＝70°，∵∠E＝40°，∠C+∠E+∠CFE＝180°，∴∠C＝180°﹣∠E﹣∠CFE＝180°﹣40°﹣70°＝70°，故答案为：70°．例2：如图，AB∥CD，∠ABE＝125°，∠C＝30°，则∠α＝（D）A．70°B．75°C．80°D．85°【解析】解：如图，作EF∥AB，∵AB∥EF，AB∥CD，∴EF∥CD，∴∠B+∠BEF＝180°，∠C＝∠CEF，∵∠ABE＝125°，∠C＝30°，∴∠BEF＝55°，∠CEF＝30°，∴∠BEC＝55°+30°＝85°．故选：D．例3：已知：如图，AB∥CD．（1）若∠1＝∠2，试判断∠E与∠F的大小关系，并说明你的理由．（2）猜想∠1、∠2、∠E、∠F之间存在怎样的数量关系？并说明理由．【解答】解：（1）∠E＝∠F，理由如下：∵AB∥CD，∴∠ABC＝∠BCD，∵∠1＝∠2，∴∠EBC＝∠FCB，∴BE∥CF，∴∠E＝∠F；（2）∠1+∠F＝∠BEF+∠2，理由如下：如图，延长BE交DC的延长线于点M，在四边形EMCF中，∠FEM+∠EMC+∠MCF+∠F＝360°，∵∠FEM＝180°﹣∠BEF，∠MCF＝180°﹣∠2，∴∠180°﹣∠BEF+∠EMC+180°﹣∠2+∠F＝360°，∵AB∥CD，∴∠1＝∠EMC，∴∠180°﹣∠BEF+∠1+180°﹣∠2+∠F＝360°，∴∠1+∠F＝∠BEF+∠2例4：（1）（问题）如图1，若AB∥CD，∠AEP＝40°，∠PFD＝130°．求∠EPF的度数；（2）（问题迁移）如图2，AB∥CD，点P在AB的上方，问∠PEA，∠PFC，∠EPF之间有何数量关系？请说明理由；（3）（联想拓展）如图3所示，在（2）的条件下，已知∠EPF＝α，∠PEA的平分线和∠PFC的平分线交于点G，用含有α的式子表示∠G的度数．【解答】解：（1）如图1，过点P作PM∥AB，∴∠1＝∠AEP＝40°．（两直线平行，内错角相等）∵AB∥CD，（已知）∴PM∥CD，（平行于同一条直线的两直线平行）∴∠2+∠PFD＝180°．（两直线平行，同旁内角互补）∵∠PFD＝130°，∴∠2＝180°﹣130°＝50°．∴∠1+∠2＝40°+50°＝90°．即∠EPF＝90°．（2）∠PFC＝∠PEA+∠P．理由：如图2，过P点作PN∥AB，则PN∥CD，∴∠PEA＝∠NPE，∵∠FPN＝∠NPE+∠FPE，∴∠FPN＝∠PEA+∠FPE，∵PN∥CD，∴∠FPN＝∠PFC，∴∠PFC＝∠PEA+∠FPE，即∠PFC＝∠PEA+∠P；（3）如图，过点G作AB的平行线GH．∵GH∥AB，AB∥CD，∴GH∥AB∥CD，∴∠HGE＝∠AEG，∠HGF＝∠CFG，又∵∠PEA的平分线和∠PFC的平分线交于点G，∴∠HGE＝∠AEG＝，∠HGF＝∠CFG＝，由（1）可知，∠CFP＝∠P+∠AEP，∴∠HGF＝（∠P+∠AEP）＝（α+∠AEP），∴∠EGF＝∠HGF﹣∠HGE＝（α+∠AEP）＝+∠AEP﹣∠HGE＝例5：已知AB∥MN．（1）如图1，求证：∠N+∠E＝∠B；（2）若F为直线MN、AB之间的一点，∠E＝∠EFB，BG平分∠ABF交MN于点G，EF 交MN于点C．①如图2，若∠N＝57°，且BG∥EN，求∠E的度数；②如图3，若点K在射线BG上，且满足∠KNM＝∠ENM，若∠NKB＝∠EFB，∠E＝∠FBD，直接写出∠E的度数．【解答】解：（1）如图，过E作EH∥MN，∴∠N＝∠HEN，又∵MN∥AB，∴EH∥AB∥MN，∴∠B＝∠HEB，即∠B＝∠HEN+∠NEB＝∠N+∠BEN；（2）①如图，过F作FP∥EN，交MN于H点，则BG∥EN∥FP，∵∠N＝57°，∴∠CHF＝∠CGB＝∠ABG＝57°，∵BG平分∠ABF，∴∠ABF＝2∠ABG＝114°，∵EN∥PF，∴∠E＝∠EFP，∵∠E＝∠EFB，∴114°+∠E＝4∠E，∴∠E＝38°；②如图，过点F作FP∥AD，设∠E＝a＝∠FBD，则∠PFB＝α，∠EFP＝3α，∴∠ENM＝2a，∠KNM＝，当K在BG上，∠NKB＝∠EFB＝4a，∴∠NGB＝＝∠ABG＝∠GBF，∴，∴a＝22.5°；当K在BG延长线上时，∠NGB＝，∠ABG＝，∴，∴a＝18°，综上所述，∠E＝22.5°或18°．。

七年级数学上册-专题强化：平行线常考模型归纳解析版

专题强化：平行线常考模型归纳【题型归纳】题型一：M 型（含锯齿型）A．30︒B．【答案】B 【分析】作c b ∥，根据平行线的判定和性质可得【详解】解：如图，作c ∵a b ∥，∴a c b ∥∥，∴41∠=∠，52∠=∠，∴451270∠+∠=∠+∠=∵1210︒∠-∠=，∴2180∠=︒，∴140∠=︒，故选：B．【点睛】本题考查了平行线的判定和性质，求出2．（2021下·重庆北碚·七年级西南大学附中校考期末）如图，侧），点G 在直线CD 上，的角平分线交与点Q ，且点②∠AEF +2∠PQG ＝270°；③若∠A．4B．3C．2D．1【答案】A【分析】①过点F作FH∥AB，利用平行线的性质以及已知即可证明；②利用角平分线的性质以及平行线的性质得到∠3=2∠2，∠CGF+2∠1+∠3=180°，结合①的结论即可证明；③由已知得到∠MGC＝3∠CGF，结合①的结论即可证明；④由已知得到∠MGC＝(n+1)∠CGF，结合①的结论即可证明．【详解】解：①过点F作FH∥AB，如图：∵AB∥CD，∴AB∥FH∥CD，∴∠AEF=∠EFH，∠CGF=∠GFH，∵EF⊥FG，即∠EFG=∠EFH+∠GFH=90°，∴∠AEF+∠CGF=90°，故①正确；②∵AB∥CD，PQ平分∠APG，GQ平分∠FGP，∴∠APQ=∠2，∠FGQ=∠1，④∵∠MGF＝n∠CGF，故选：A．【点睛】本题主要考查了平行线的性质，角平分线的定义等知识点，作辅助线求得∠AEF +∠CGF =90°，是解此题的关键．3．（2023下·山东聊城·七年级校考阶段练习）如图，已知直线12l l ∥，3l 、4l 和1l 、2l 分别交于点A 、B 、C 、D ，点P 在直线3l 或4l 上且不与点A 、B 、C 、D 重合．记1AEP ∠=∠，2PFB ∠=∠，3E P F ∠=∠．(1)若点P 在图（1）位置时，求证：312Ð=Ð+Ð；(2)若点P 在图（2）位置时，写出1∠、2∠、3∠之间的关系并给予证明．【答案】(1)证明见解析(2)312360∠∠∠++=︒，证明见解析【分析】此题两个小题的解题思路是一致的，过P 作直线1l 、2l 的平行线，利用平行线的性质得到和1∠、2∠相等的角，然后结合这些等角和3∠的位置关系，来得出1∠、2∠、3∠的数量关系．【详解】（1）过P 作1PQ l ∥，∵12l l ∥，∴12PQ l l ∥∥，由两直线平行，内错角相等，可得：1QPE ∠=∠、2QPF ∠=∠；∵3QPE QPF ∠=∠+∠，∴312Ð=Ð+Ð．（2）关系：312360∠∠∠++=︒．过P 作1PQ l ∥，∵12l l ∥，∴12PQ l l ∥∥，同（1）可证得：3CEP DFP ∠=∠+∠；∵11802180CEP DFP ∠+∠=︒∠+∠=︒，，∴12360CEP DFP ∠+∠+∠+∠=︒，即312360∠∠∠++=︒．【点睛】本题主要考查平行线的性质，能够正确多出辅助线是解题关键．A．110︒B．115︒【答案】A 【分析】过N 点作NH AB ∥，则BEN ENG GNM MNF ∠+∠+∠+∠【详解】解：过N 点作NH AB ∥，则AB NH CD ∥∥，如图所示：180BEN ENH HNF NFG ∴∠+∠=∠+∠=︒，360BEN ENG GNM MNF NFG ∴∠+∠+∠+∠+=︒，160BEN ∠=︒ ，200ENG GNM MNF NFG ∴∠+∠+∠+∠=︒，NG 平分ENM ∠，ENG GNM ∴∠=∠，200GNM GNM MNF NFG ∴∠+∠+∠+∠=︒，NF NG ⊥ ，90GNM MNF GNF ∴∠+∠∠︒＝＝，90200GNM NFG ∴∠+︒+∠︒＝，110MNG NFG ∴∠+∠︒＝．故选：A．【点睛】此题考查了平行线的性质、平行公理的应用、角平分线的性质，解题的关键是正确作出辅助线．5．（2021下·湖南株洲·七年级统考期末）①如图1，AB ∥CD ，则360A E C ∠+∠+∠=︒；②如图2，AB ∥CD ，则P A C ∠=∠-∠；③如图3，AB ∥CD ，则1E A ∠=∠+∠；④如图4，直线AB ∥CD ∥EF ，点O 在直线EF 上，则180αβγ∠-∠+∠=︒．以上结论正确的个数是（）A．1个B．2个C．3个D．4个【答案】C 【分析】①过点E 作直线EF ∥AB ，由平行线的性质：两直线平行，同旁内角互补，即可得出结论；②如图2，先根据三角形外角的性质得出∠1＝∠C +∠P ，再根据两直线平行，内错角相等即可作出判断；③如图3，过点E作直线EF∥AB，由平行线的性质可得出∠A+∠AEC﹣∠1＝180°，即得∠AEC＝180°+∠1﹣∠A；④如图4，根据平行线的性质得出∠α＝∠BOF，∠γ+∠COF＝180°，再利用角的关系解答即可．【详解】解：①如图1，过点E作直线EF∥AB，∵AB∥CD，∴AB∥CD∥EF，∴∠A+∠1＝180°，∠2+∠C＝180°，∴∠A+∠1+∠2+∠C＝360°，∴∠A+∠AEC+∠C=360°，故①正确；②如图2，∵∠1是△CEP的外角，∴∠1＝∠C+∠P，∵AB∥CD，∴∠A＝∠1，即∠P＝∠A﹣∠C，故②正确；③如图3，过点E作直线EF∥AB，∵AB∥CD，∴AB∥CD∥EF，∴∠A+∠3＝180°，∠1＝∠2，∴∠A+∠AEC﹣∠1＝180°，即∠AEC＝180°+∠1﹣∠A，故③错误；④如图4，∵AB∥EF，∴∠α＝∠BOF ，∵CD ∥EF ，∴∠γ+∠COF ＝180°，∵∠BOF ＝∠COF +∠β，∴∠COF ＝∠α﹣∠β，∴∠γ+∠α﹣∠β＝180°，故④正确；综上结论正确的个数为3，故选：C．【点睛】本题考查的是平行线的性质及三角形外角的性质，熟练掌握平行线的性质，根据题意作出辅助线是解答此题的关键．6．（2021下·广东东莞·七年级东莞市光明中学校考期中）（1）如图（1）AB CD ，猜想BPD ∠与B D ∠∠、的关系，说出理由．（2）观察图（2），已知AB CD ，猜想图中的BPD ∠与B D ∠∠、的关系，并说明理由．（3）观察图（3）和（4），已知AB CD ，猜想图中的BPD ∠与B D ∠∠、的关系，不需要说明理由．【答案】（1）360B BPD D ∠+∠+∠=︒，理由见解析；（2）BPD B D ∠=∠+∠，理由见解析；（3）图（3）BPD D B ∠=∠-∠，图（4）BPD B D∠=∠-∠【分析】（1）过点P 作EF AB ∥，得到180B BPE ∠+∠=︒，由AB CD ，EF AB ∥，得到EF CD ，得到180EPD D ∠+∠=︒，由此得到360B BPD D ∠+∠+∠=︒；（2）过点P 作PE AB ，由PE AB CD ∥∥，得到12B D ∠=∠∠=∠，，从而得到结论12BPD B D ∠=∠+∠=∠+∠；（3）由AB CD ，根据两直线平行，内错角相等与三角形外角的性质，即可求得BPD ∠与B D ∠∠、的关系．【详解】（1）解：猜想360B BPD D ∠+∠+∠=︒．理由：过点P 作EF AB ∥，∴180B BPE ∠+∠=︒，∵AB CD ，EF AB ∥，∴EF CD ，∴180EPD D ∠+∠=︒，∴360B BPE EPD D ∠+∠+∠+∠=︒，∴360B BPD D ∠+∠+∠=︒；（2）BPD B D ∠=∠+∠．理由：如图，过点P 作PE AB ，∵AB CD ，∴PE AB CD ∥∥，∴12B D ∠=∠∠=∠，，∴12BPD B D ∠=∠+∠=∠+∠；（3）如图（3）：BPD D B ∠=∠-∠．理由：∵AB CD ，∴1D ∠=∠，∵1B P ∠=∠+∠，∴D B P ∠=∠+∠，即BPD D B ∠=∠-∠；如图（4）：BPD B D ∠=∠-∠．理由：∵AB CD ，∠=∠，∵1D P∠=∠+∠，∴B D P∠=∠+∠，即BPD B D∠=∠-∠．【点睛】此题考查了平行线的性质，平行公理的推论，三角形的外角的性质定理，熟记平行线的性质是解题的关键．题型三：鸡翅型【答案】【感知探究】证明见解析；【类比迁移】F BMF DNF∠=∠-∠；【结论应用】20【分析】本题主要考查平行线的判定和性质，作辅助线是解题的关键．（1）过点E作EF AB∥，根据平行线的性质可求解；（2）如图②，过F作FH AB∥，根据平行线的性质即可得到结论；（3）如图③，过C作CG AB∥，根据平行线的性质即可得到结论．【详解】（1）证明：如图①，过点E作EF AB∥，∠=∠，又∵AB CD∥，∴EF CD∥，NEF DNE∴∠=∠，∴∠=∠+∠，MEN MEF NEF即MEN BME DNE∠=∠+∠；（2）解：BMF MFN FND∠=∠+∠．∥，证明：如图②，过F作FK ABBMF MFK，∵AB CD∴FK CD∥，FND KFN∴∠=∠，∴∠=∠-∠=∠-∠，MFN MFK KFN BMF FND 即：BMF MFN FND∠=∠+∠．故答案为：BMF MFN FND∠=∠+∠；（3）如图③，过C作CG AB∥，∴∠=︒-∠=︒，GCA BAC18060∵AB DE∥，∴CG DE∥，∴∠=∠=︒，80GCD CDE∴∠=︒，ACD20故答案为：20．8．（2021下·广东河源·七年级河源市第二中学校考期中）已知直线12l l ∥，A 是l1上的一点，B 是l2上的一点，直线l3和直线l1，l2交于C 和D ，直线CD 上有一点P ．(1)如果P 点在C ，D 之间运动时，问PAC ∠，APB ∠，PBD ∠有怎样的数量关系？请说明理由．(2)若点P 在C ，D 两点的外侧运动时（P 点与C ，D 不重合），试探索PAC ∠，APB ∠，PBD ∠之间的关系又是如何？（请直接写出答案，不需要证明）【答案】(1)PAC PBD APB∠+∠=∠(2)当点P 在直线1l 上方时，∠-∠=∠PBD PAC APB ；当点P 在直线2l 下方时，∠-∠=∠PAC PBD APB ．【分析】（1）过点P 作1PE l ∥，由“平行于同一条直线的两直线平行”可得出12PE l l ∥∥，再由“两直线平行，内错角相等”得出PAC APE ∠=∠、PBD BPE ∠=∠，再根据角与角的关系即可得出结论；（2）按点P 的两种情况分类讨论：①当点P 在直线1l 上方时；②当点P 在直线2l 下方时，同理（1）可得PAC APE ∠=∠、PBD BPE ∠=∠，再根据角与角的关系即可得出结论．【详解】（1）解：PAC PBD APB ∠+∠=∠．过点P 作1PE l ∥，如图1所示．1PE l ∥，12l l ∥，∴12PE l l ∥∥，PAC APE ∴∠=∠，PBD BPE ∠=∠，APB APE BPE ∠=∠+∠ ，PAC PBD APB ∴∠+∠=∠．（2）解：结论：当点P 在直线1l 上方时，∠-∠=∠PBD PAC APB ；当点P 在直线2l 下方时，∠-∠=∠PAC PBD APB ．①当点P 在直线1l 上方时，如图2所示．过点P 作1PE l ∥．1PE l ∥，12l l ∥，∴12PE l l ∥∥，PAC APE ∴∠=∠，PBD BPE ∠=∠，APB BPE APE ∠=∠-∠ ，PBD PAC APB ∴∠-∠=∠．②当点P 在直线2l 下方时，如图3所示．过点P 作1PE l ∥．1PE l ∥，12l l ∥，∴12PE l l ∥∥，PAC APE ∴∠=∠，PBD BPE ∠=∠，APB APE BPE ∠=∠-∠ ，PAC PBD APB ∴∠-∠=∠．两直线平行，内错角相等(1)求证：180B C A ∠+∠-∠=︒：(2)如图②，AQ BQ 、分别为DAC EBC ∠∠、的平分线所在直线，试探究(3)如图③，在（2）的前提下，且有AC QB ∥，直线AQ BC 、=DAC ACB CBE ∠∠∠：：．【答案】(1)见解析(2)2=180AQB C ∠+∠︒，理由见解析(3)122：：【分析】（1）过点C 作CF AD ∥，则CF BE ∥，根据平行线的性质可得出据此可得；（2）过点Q 作QM AD ∥，则QM BE ∥，根据平行线的性质、角平分线的定义可得出1()2AQB CBE CAD ∠=∠-∠，结合（1）的结论可得出2AQB ∠（3）由（2）的结论可得出12CAD CBE ∠=∠①，由QP PB ⊥求出CAD CBE ∠∠、的度数，再结合（1）的结论可得出ACB ∠可求出结论．【详解】（1）在图①中，过点C 作CF AD ∥，则CF BE ∥．∵CF AD BE ∥∥，∴ACF A BCF ∠=∠∠，∴ACB B A ∠+∠-∠=∠（2）在图2中，过点Q ∵QM AD QM BE ∥，∥∴AQM NAD BQM ∠=∠∠，∵AQ 平分CAD ∠，BQ ∴1,2NAD CAD EBQ ∠=∠∠∴AQB BQM AQM ∠=∠-∠∵180(C CBE ︒∠=-∠∴2180AQB C ∠+∠=（3）∵AC QB ∥，∴12AQB CAP ∠=∠=∴180ACB ACP ∠=︒-∠∵2180AQB ACB ∠+∠=∴1.2CAD CBE ∠=∠．又∵QP PB ⊥，∴90CAP ACP ∠+∠=︒，即180CAD CBE ∠+∠=︒，∴60120CAD CBE ∠=︒∠=︒，，∴180120()ACB CBE CAD ∠=︒-∠-∠=︒，∴60120120122DAC ACB CBE ∠∠∠=︒︒︒=：：：：：：，故答案为：122：：．【点睛】本题主要考查平行线的的判定与性质，解题的关键是熟练掌握平行线的性质、添加辅助线构建平行线．题型四：骨折型【答案】40︒/40度【分析】本题主要考查了平行线的判定和性质．过点即可得到结论．【详解】解：如图，过点C 80ABC ∠=︒ ，80BCF ABC ∴∠=∠=︒，又AB DE ∥ ，DE CF ∴∥，180DCF CDE ∴∠+∠=︒，40DCF ∴∠=︒，80BCD BCF DCF ∴∠=∠-∠=︒-(1)如图1，已知50A ∠=︒，150D ∠=︒，求APD ∠的度数；(2)如图2，判断∠PAB 、CDP ∠、APD ∠之间的数量关系，请写出证明过程．(3)如图3，在（2）的条件下，AP PD ⊥，DN 平分PDC ∠，若12PAN PAB APD ∠+∠=∠，求【答案】(1)80︒(2)180CDP PAB APD ∠+∠-∠=︒，证明见解析(3)45︒【分析】（1）过点P 作EF AB ∥，根据平行线的性质可得50APE A ∠=∠=︒，180EPD ∠=︒-可求出APD ∠的度数；（2）过点P 作EF AB ∥，则AB EF CD ∥∥，根据平行线的性质可得CDP DPF ∠=∠，FPA ∠又FPA DPF APD ∠=∠-∠，即可得出180CDP PAB APD ∠+∠-∠=︒；（3）PD 交AN 于点O ，由AP PD ⊥，得出90APO ∠=︒，由12PAN PAB APD ∠+∠=∠得出1902PAN PAB ∠+∠=︒，由90POA PAN ∠+∠=︒，得出12POA PAB ∠=∠，由对顶角相等得出∠由角平分线的性质得出12ODN PDC ∠=∠，即1180()2AND PAB PDC ∠=︒-∠+∠，由（2）得：CDP DPF ∴∠=∠，FPA ∠+∠FPA DPF APD ∠=∠-∠ ，180DPF APD PAB ∴∠-∠+∠=180CDP PAB APD ∴∠+∠-∠=︒，故答案为：CDP PAB ∠+∠-∠（3）如图3，PD 交AN 于点AP PD ⊥ ，90APO ∴∠=︒，12PAN PAB APD ∠+∠=∠ ，【答案】（1）证明见解析；（2）证明见解析；（3）120°．【分析】（1）过点A作AD∥MN，根据两直线平行，内错角相等得到∠MCA＝∠DAC，∠PBA＝∠DAB，根据角的和差等量代换即可得解；（2）由两直线平行，同旁内角互补得到∴、∠CAB+∠ACD＝180°，由邻补角定义得到∠ECM+∠ECN＝180°，再等量代换即可得解；（3）由平行线的性质得到，∠FAB＝120°﹣∠GCA，再由角平分线的定义及平行线的性质得到∠GCA﹣∠ABF＝60°，最后根据三角形的内角和是180°即可求解．【详解】解：（1）证明：如图1，过点A作AD∥MN，∵MN∥PQ，AD∥MN，∴AD∥MN∥PQ，∴∠MCA＝∠DAC，∠PBA＝∠DAB，∴∠CAB＝∠DAC+∠DAB＝∠MCA+∠PBA，即：∠CAB＝∠MCA+∠PBA；（2）如图2，∵CD∥AB，∴∠CAB+∠ACD＝180°，∵∠ECM+∠ECN＝180°，∵∠ECN＝∠CAB∴∠ECM＝∠ACD，即∠MCA+∠ACE＝∠DCE+∠ACE，∴∠MCA＝∠DCE；（3）∵AF∥CG，∴∠GCA+∠FAC＝180°，∵∠CAB＝60°即∠GCA+∠CAB+∠FAB＝180°，∴∠FAB＝180°﹣60°﹣∠GCA＝120°﹣∠GCA，由（1）可知，∠CAB＝∠MCA+∠ABP，∵BF平分∠ABP，CG平分∠ACN，∴∠ACN＝2∠GCA，∠ABP＝2∠ABF，又∵∠MCA＝180°﹣∠ACN，∴∠CAB＝180°﹣2∠GCA+2∠ABF＝60°，∴∠GCA﹣∠ABF＝60°，∵∠AFB+∠ABF+∠FAB＝180°，∴∠AFB＝180°﹣∠FAB﹣∠FBA＝180°﹣（120°﹣∠GCA）﹣∠ABF＝180°﹣120°+∠GCA﹣∠ABF＝120°．【点睛】本题主要考查了平行线的性质，线段、角、相交线与平行线，准确的推导是解决本题的关键．【专题强化】（5）（6）当点E 在CD 的下方时，同理可得∠AEC =α-β或β-α．综上所述，∠AEC 的度数可能为β-α，α+β，α-β，360°-α-β，即①②③④．故选：D ．【点睛】本题主要考查平行线的性质的运用，解题时注意两直线平行，同位角相等；两直线平行，内错角相等以及分类讨论．14．（2016上·甘肃张掖·八年级统考期末）如图，直线12l l ∥，125A ∠=︒，85B ∠=︒，则12∠+∠=（）A．30︒B．35︒C．36︒D．40︒【答案】A 【分析】作直线32l l ∥，42l l ∥，根据平行线的性质可得13∠=∠，26∠=∠，45180∠+∠=︒，进而即可求得12∠+∠．【详解】解：如图，作直线32l l ∥，42l l ∥，∵12l l ∥，∴1234l l l l ∥∥∥，∴13∠=∠，26∠=∠，45180∠+∠=︒，∵125A ∠=︒，85B ∠=︒，∴345612585210∠+∠+∠+∠=︒+︒=︒，∴3621018030∠+∠=︒-︒=︒，∴123630∠+∠=∠+∠=︒，故选：A．【点睛】本题考查了平行线的判定和性质，掌握平行线的性质是解题的关键．15．（2021·江苏南通·南通田家炳中学校考二模）如图，已知//AB CD ，140A ∠=︒，120E ∠=︒，则C ∠的度数是（）A．80°B．120°C．100°D．140°【答案】C 【分析】过E 作直线MN //AB ，根据两直线平行，同旁内角互补即可求出∠1，进而可求出∠2，然后根据平行于同一条直线的两直线平行可得MN //CD ，根据平行线性质从而求出∠C ．【详解】解：过E 作直线MN //AB ，如下图所示，∵MN //AB ，∴∠A +∠1＝180°（两直线平行，同旁内角互补），∴∠1＝180°﹣∠A ＝180°﹣140°＝40°，∵12120AEC ∠=∠+∠=︒，∴211204080AEC ∠=∠-∠=︒-︒=︒∵MN //AB ，AB //CD ，∴MN //CD ，∴∠C +∠2＝180°（两直线平行，同旁内角互补），∴∠C ＝180°﹣∠2＝180°﹣80°＝100°，故选：C．【点睛】此题考查的是平行线的判定及性质，掌握构造平行线的方法是解决此题的关键．16．（2021上·山东青岛·八年级统考期末）如图，//AB CD ，点E 在AC 上，110A ∠=︒，15D ∠=︒，则下列结论正确的个数是（）（1）AE EC =；（2）85AED ∠=︒；（3）A CED D ∠=∠+∠；（4）45BED ∠=︒A．1个B．2个C．3个D．4个【答案】B 【分析】利用平行线的性质和三角形的性质依次判断即可求解．【详解】解：∵AB ∥CD ，∴∠A +∠C ＝180°，又∵∠A ＝110°，∴∠C ＝70°，∴∠AED ＝∠C +∠D ＝85°，故（2）正确，∵∠C +∠D +∠CED ＝180°，∴∠D +∠CED ＝110°，∴∠A ＝∠CED +∠D ，故（3）正确，∵点E 在AC 上的任意一点，∴AE 无法判断等于CE ，∠BED 无法判断等于45°，故（1）、（4）错误，故选：B ．【点睛】本题考查了平行线的性质，三角形的外角的性质，掌握平行线的性质是本题的关键．17．（2020下·重庆·七年级重庆南开中学校考期末）如图，直线//m n ，在Rt ABC 中，90B Ð=°，点A 落在直线m 上，BC 与直线n 交于点D ，若2130∠=︒，则1∠的度数为（）.A．30°B．40°C．50°D．65°【答案】B【分析】由题意过点B 作直线//l m ，利用平行线的判定定理和性质定理进行分析即可得出答案．【详解】解：如图，过点B 作直线//l m ，∵直线m//n，//l m ，∴//l n ，∴∠2+∠3=180°，∵∠2=130°，∴∠3=50°，∵∠B=90°，∴∠4=90°-50°=40°，∵//l m ，∴∠1=∠4=40°．故选：B．【点睛】本题主要考查平行线的性质定理和判定定理，熟练掌握两直线平行，平面内其外一条直线平行于其中一条直线则平行于另一条直线是解答此题的关键．18．（2020下·重庆南岸·七年级统考期末）如图,AB //EF,∠D=90°,则α,β,γ的大小关系是（）A．βαγ=+B．90βαγ=+-︒C．90βγα=+︒-D．90βαγ=+︒-【答案】D 【分析】通过作辅助线,过点C 和点D 作CG //AB,DH //AB,可得CG //DH //AB,根据AB //EF,可得AB //EF //CG //DH,再根据平行线的性质即可得γ+β-α=90°,进而可得结论．【详解】解：如图,过点C 和点D 作CG //AB,DH //AB,∵CG //AB,DH //AB,∴CG //DH //AB,∵AB //EF,∴AB //EF //CG //DH,∵CG //AB,∴∠BCG=α,∴∠GCD=∠BCD-∠BCG=β-α,∵CG //DH,∴∠CDH=∠GCD=β-α,∵HD //EF,∴∠HDE=γ,∵∠EDC=∠HDE+∠CDH=90°,∴γ+β-α=90°,∴β=α+90°-γ．故选：D．【点睛】本题考查了平行线的性质,解决本题的关键是掌握平行线的性质．19．（2020下·浙江绍兴·七年级统考期末）如图，已知AB//CD，则α∠，∠β，γ∠之间的等量关系为（）A．180αβγ∠+∠-∠=︒B．180βγα︒∠+∠-∠=C．360αβγ︒∠+∠+∠=D．180αβγ∠+∠+∠=︒【答案】C 【分析】过点E 作EF∥AB，则EF∥CD，然后通过平行线的性质求解即可．【详解】解：过点E 作EF∥AB，则EF∥CD，如图，∵AB∥EF∥CD，∴∠γ+∠FED=180°，∵∠ABE+∠FEB=180°，∠ABE=∠α，∠FED+∠FEB=∠β，∴∠γ+∠FED+∠ABE+∠FEB=360°，∴∠α+∠β+∠γ=360°，故选：C．【点睛】本题主要考查了平行线的性质，正确作出辅助线是解答此题的关键．20．（2019·山东泰安·统考中考真题）如图，直线12l l ，130∠=︒，则23∠+∠=（）A．150°B．180°C．210°D．240°【答案】C 【分析】根据题意作直线l 平行于直线l 1和l 2，再根据平行线的性质求解即可.【详解】解：作直线l 平行于直线l 1和l 2．12////l l l ，143035180︒︒∴∠=∠=∠+∠=，．245∠=∠+∠ ，2+3=4+5+3=30180210︒︒︒∴∠∠∠∠∠+=．故选C．【点睛】本题主要考查平行线的性质，掌握两直线平行同旁内角互补，两直线平行内错角相等是解题关键．21．（2016·浙江杭州·七年级期中）如图所示，若AB∥EF，用含α、β、γ的式子表示x ，应为（）A．αβγ++B．βγα+-C．180αγβ︒--+D．180αβγ︒++-【答案】C 【分析】过C 作CD∥AB，过M 作MN∥EF，推出AB∥CD∥MN∥EF，根据平行线的性质得出α+∠BCD=180°，∠DCM=∠CMN，∠NMF=γ，求出∠BCD=180°-α，∠DCM=∠CMN=β-γ，即可得出答案．【详解】过C 作CD∥AB，过M 作MN∥EF，∵AB∥EF，∴AB∥CD∥MN∥EF，∴α+∠BCD=180°，∠DCM=∠CMN，∠NMF=γ，∴∠BCD=180°-α，∠DCM=∠CMN=β-γ，∴x =∠BCD+∠DCM=180αγβ︒--+，故选：C．【点睛】本题考查了平行线的性质的应用，主要考查了学生的推理能力．二、填空题【答案】80︒/80度【分析】过点F作FM CD∥，所以∥，因为AB CDÐ，再根据平行线的性质即可求得∠，进而可求出EFAEFM【详解】解：如图，过点F作FM CD∥，∵AB CD∥，∴AB CD FM∥∥，∴180∠DEF EFM∠+∠=︒，MFA【答案】60︒【分析】过点B 作BD EF ∥进而可得12∠+∠ABD =∠【详解】解：如图，过点 Rt ABC △中，30A ∠=︒，∴9060ABC A ∠=︒-∠=︒．BD EF ∥，∴1ABD ∠=∠．BD EF ∥，MN EF ∥，∴MN BD ∥，∴2CBD ∠=∠，∴12∠+∠ABD CBD =∠+∠=故按为：60︒．【点睛】本题主要考查平行线性质，平行公理的推论，三角板中的角度计算等知识点，解题的关键是正确【答案】1402n ︒+︒，再根据两直线平行，内错角相等，∥ AB CD ，∴BCD ABC n ∠=∠=︒，BAD ADC ∠=∠又∵BE 平分ABC ∠，DE 平分ADC ∠，∴1122ABE ABC n ∠=∠=︒，11804022EDC ADC ∠=∠=⨯︒=︒，∵AB EF CD ∥∥，∴12BEF ABE n ∠=∠=︒，40FED EDC ∠=∠=︒，∴1402BED FED BEF n ∠=∠+∠=︒+︒，故答案为：1402n ︒+︒．l l∥，直线12∵AB ∥CD ，AB ∥PM∵AB ∥PM ∥CD ，∴∠1+∠APM =180°，∠MPC +∠3=180°，∴∠1+∠APC +∠3=360°；（2）如图，过点P 、Q 作PM 、QN 平行于AB ，∵AB ∥CD ，∵AB ∥PM ∥QN ∥CD ，∴∠1+∠APM =180°，∠MPQ +∠PQN =180°，∠NQC +∠4=180°；∴∠1+∠APQ +∠PQC +∠4=540°；根据上述规律，显然作（n -2）条辅助线，运用（n -1）次两条直线平行，同旁内角互补．即可得到∠1+∠2+∠3+…+∠n =180°（n -1）．故答案为：()1801n -︒【点睛】此题考查了平行线的性质．注意掌握辅助线的作法是解此题的关键．三、解答题27．（2022上·黑龙江哈尔滨·七年级统考期末）已知，DE 平分ADB ∠交射线BC 于点E ，BDE BED ∠=∠．(1)如图1，求证：AD BC ∥；(2)如图2，点F 是射线DA 上一点，过点F 作FG BD ∥交射线BC 于点G ，点N 是FG 上一点，连接NE ，求证：DEN ADE ENG ∠=∠+∠；(3)如图3，在（2）的条件下，连接DN ，点P 为BD 延长线上一点，DM 平分BDE ∠交BE 于点M ，若DN 平分PDM ∠，DE EN ⊥，DBC DNE FDN ∠-∠=∠，求EDN ∠的度数．【答案】(1)见解析(2)见解析(3)45︒【分析】（1）利用角平分线的定义可得ADE BDE =∠∠，然后再利用等量代换可得ADE BED ∠=∠，从而利用平行线的判定，即可解答；（2）过点E 作EH BD ∥，可知EH FG ∥，利用平行线的性质可得=DEH BDE ∠∠，HEN ENG ∠=∠，由BDE ADE =∠∠，可知=ADE DEH ∠∠，由=DEN DEH HEN ∠∠+∠，可证得结论；（3）设=2BDM x ∠，利用角平分线的定义可得==2BDM MDE x ∠∠，从而可得==2=4ADE BDE BDM x ∠∠∠，进而可得=2=8ADB BDE x ∠∠，然后利用平行线的性质可得=1808B x ∠︒-，再根据垂直定义可得90DEN ∠=︒，最后利用（2）的结论可得=904ENG x ∠︒-，再利用角平分线的定义可得=90MDN x ∠︒-，从而可得=903EDN x ∠︒-，进而可得=3DNE x ∠，790FDN x ∠=-︒，再根据已知790FDN x ∠=-︒，列出关于x 的方程，进行计算即可解答．【详解】（1）证明：∵DE 平分ADB ∠，∴ADE BDE =∠∠，∵BDE BED ∠=∠，∴ADE BED ∠=∠，∴AD BE ；（2）证明：过点E 作EH BD ∥，∴=DEH BDE ∠∠，∵BDE ADE =∠∠，∴=ADE DEH ∠∠，∵BD FG ，∴EH FG ∥，∴HEN ENG ∠=∠，∵=DEN DEH HEN ∠∠+∠，∴DEN ADE ENG ∠=∠+∠；（3）解：设=2BDM x ∠，∵DM 平分BDE ∠，∴==2BDM MDE x ∠∠，∴==2=4ADE BDE BDM x ∠∠∠∴=2=8ADB BDE x ∠∠，∵AD BC ∥，∴=180=1808B ADB x ∠︒-∠︒-，∵DE EN ⊥，∴90DEN ∠=︒，由（2）得：DEN ADE ENG ∠=∠+∠∴==90ENG DEN ADE ∠∠-∠︒-∵DN 平分PDM ∠，∴(11==180MDN PDM ∠∠︒-∠∴18083=790x x x ︒---︒，解得：15x =︒，∴=903=45EDN x ∠︒-︒，∴EDN ∠的度数为45︒．【点睛】本题考查了平行线的判定与性质及角平分线的定义，垂直定义，熟练掌握平行线的判定及性质是解题的关键．28．（2023下·江苏·七年级泰州市姜堰区第四中学校考周测）如图，AB CD ∥，12110∠+∠=︒，求G ∠的度数．【答案】110︒【分析】过点G 作GM AB ∥，根据AB CD ，GM AB CD ∥∥，进而根据平行线的性质即可求EGF ∠的度数．【详解】解：过点G 作GM AB ∥，∵AB CD ，∴GM AB CD ∥∥，∴1EGM ∠∠=，2FGM ∠∠=，∴12110EGF EGM FGM ∠∠∠∠∠=+=+=︒，【点睛】本题考查了平行线的判定与性质，解决本题的关键是作辅助线及灵活应用平行线的判定与性质解决问题．29．（2023下·江苏·七年级专题练习）已知AB CD ∥，连接A ，C 两点．(1)如图1，CAB ∠与ACD ∠的平分线交于点E ，则AEC ∠等于(2)如图2，点M 在射线AB 反向延长线上，点N 在射线CD 4570AMN ACN ∠=︒∠=︒，，求MEC ∠的度数；(3)如图3，图4，M ，N 分别为射线AB ，射线CD 上的点，()AMN ACN αβαβ∠=∠=≠，，请直接写出图中MEC ∠的度数（用含α，β的式子表示）【答案】(1)90(2)57.5︒(3)1118022αβ︒-+或1118022βα︒-+【分析】（1）根据平行线的性质得到180BAC ACD ∠+∠=︒，即可求出答案；（2）过点E 作EF AB ∥，得到EF CD ∥，根据平行线的性质得到平分线的定义求出1122.522BME BMN ECD ACD ∠=∠=︒∠=∠，（3）由平行线的性质：两直线平行同旁内角互补，两直线平行内错角相等，即可求解．【详解】（1）解：如图1，∵AB CD ∥，∴180BAC ACD ∠+∠=︒，∵,AE CE 分别平分BAC ACD ∠∠，，∴1122CAE BAC ACE ACD ∠=∠∠=∠，，∵AB CD ∥，∴EF CD ∥，∴BME MEF FEC ∠=∠∠，∵,ME CE 分别平分BMN ∠，∴122.52BME BMN ∠=∠=︒∴MEC MEF CEF ∠=∠+∠（3）①如图3，过点E 作EF ∵AB CD ∥，∴EF CD ∥，∴180AME MEF ∠+∠=︒，∵1122AME AMN α∠=∠=，∴11802MEF α∠=︒-，∵1122ECD ACD β∠=∠=，∴12FEC ECD β∠=∠=，∵AB CD ∥，∴EF CD ∥，∴1122AME MEF α∠=∠=，∠∵1122ECD ACD β∠=∠=，∴11802FEC β∠=︒-，∴180MEC MEF CEF ∠=∠+∠=【点睛】此题考查了平行线的性质及角平分线的定义，解题的关键是正确掌握平行线的性质：两直线平行同旁内角互补，两直线平行内错角相等．30．（2022上·河南平顶山·八年级统考期末）出BED ∠的度数．（2）如图2，AB CD ，点E F ∠之间的关系并说明理由．（3）如图3，AB 与CD 相交于点95BFD ∠=︒，直接写出BED ∠【答案】（1）66︒；（2）2BED F ∠=∠，理由见解析；（3）130︒【分析】（1）过点E 作EM AB ∥，可得ABE MEB ∠=∠，CDE MED ∠=∠，可求解；（2）过点E 作EG AB ∥，可求出2(23)2(14)BED ∠=∠+∠=∠+∠，过点F 作FH AB ∥，可求出14BFD ∠=∠+∠，由此即可求解；（3）延长DE 交BF 于点P ，可得BED EBP BPD EBP BFD PDF ∠=∠+∠=∠+∠+∠，BED EBG BPD EDG BGD EBG ∠=∠+∠=∠+∠+∠，BF 平分ABE ∠，DF 平分CDE ∠，可得22BED EBP PDF BGD ∠=∠+∠+∠，由此即可求解．【详解】解：（1）如图，过点E 作EM AB ∥，∵AB CD ，∴EM AB CD ∥∥，∴ABE MEB ∠=∠，CDE MED ∠=∠，∵=45ABE ∠︒，21CDE ∠=︒，∴45MEB ∠=︒，21MED ∠=︒，∴452166BED MEB MED ∠=∠+∠=︒+︒=︒．（2）2BED F ∠=∠，理由如下：过点E 作EG AB ∥，∵AB CD ，∴EG AB CD ∥∥，∴512∠=∠+∠，634∠=∠+∠，∵BF 平分ABE ∠，DF 平分CDE ∠，∴12∠=∠，3=4∠∠，∴2(23)2(14)BED ∠=∠+∠=∠+∠，同理，过点F 作FH AB ∥，∴FH AB CD ∥∥，∴1BFH ∠=∠，4DFH ∠=∠，∵BFD BFH DFH ∠=∠+∠，∴14BFD ∠=∠+∠，∴22(14)BFD ∠=∠+∠，∴2BED BFD ∠=∠，即2BED F ∠=∠．（3）如图，延长DE 交BF 于点P ，∴BED EBP BPD EBP BFD PDF ∠=∠+∠=∠+∠+∠，BED EBG BPD EDG BGD EBG ∠=∠+∠=∠+∠+∠，∵BF 平分ABE ∠，DF 平分CDE ∠，∴2EBG EBP ∠=∠，2EDG PDF ∠=∠，∴22BED EBP PDF BGD ∠=∠+∠+∠，∴22EBP BFD PDF EBP PDF BGD ∠+∠+∠=∠+∠+∠，∴952()60EBP PDF EBP PDF ∠+∠+︒=∠+∠+︒，∴35EBP PDF ∠+∠=︒，∴953595130BED EBP PDF ∠=∠+∠+︒=︒+︒=︒．【点睛】本题主要考查平行线的性质，理解平行线的性质，三角形外角的性质是解题的关键．31．（2022下·广东东莞·七年级东莞市光明中学校考期中）阅读下面内容，并解答问题．已知：如图1，AB CD ∥，直线EF 分别交AB ，CD 于点E ，F ．BEF ∠的平分线与DFE ∠的平分线交于点G ．(1)求证：EG FG⊥；(2)填空，并从下列①、②两题中任选一题说明理由．我选择题．①在图1的基础上，分别作BEG∠的平分线与DFG∠的平分线交于点M 为．②如图3，AB CD∥，直线EF分别交AB，CD于点E，F．点O在直线 ,AB CD//∴∠+∠=︒BEF DFE180平分BEFEG∠，FG(1)如图1，连接GM ，HM ．求证：∠M ＝∠AGM (2)如图2，在∠GHC 的角平分线上取两点M 、Q ，使得∠关系，并说明理由．【答案】(1)证明见详解(2)180GQH M ∠=︒-∠；理由见详解【分析】（1）过点M 作MN AB ∥，由AB CD ∥，可知MN AB CD ∥∥．由此可知：AGM GMN ∠=∠，CHM HMN ∠=∠，故=AGM CHM GMN HMN M ∠+∠=∠+∠∠；（2）由（1）可知=AGM CHM M ∠+∠∠．再由CHM GHM ∠=∠，∠AGM ＝∠HGQ ，可知：M HGQ GHM ∠=∠+∠，利用三角形内角和是180°，可得180GQH M ∠=︒-∠．【详解】（1）解：如图：过点M 作MN AB ∥，∴MN AB CD ∥∥，∴AGM GMN ∠=∠，CHM HMN ∠=∠，∵M GMN HMN ∠=∠+∠，∴=M AGM CHM ∠∠+∠．（2）解：180GQH M ∠=︒-∠，理由如下：如图：过点M 作MN AB ∥，由（1）知=M AGM CHM ∠∠+∠，∵HM 平分GHC ∠，∴CHM GHM ∠=∠，∵∠AGM ＝∠HGQ ，∴M HGQ GHM ∠=∠+∠，∵180HGQ GHM GQH ∠+∠+∠=︒，∴180GQH M ∠=︒-∠．【点睛】本题考查了利用平行线的性质求角之间的数量关系，正确的作出辅助线是解决本题的关键，同时这也是比较常见的几何模型“猪蹄模型”的应用．33．（2022下·江苏常州·七年级统考期中）问题情境：如图①，直线AB CD∥，点E，F分别在直线AB，CD上．(1)猜想：若1130∠=︒，2150∠=︒，试猜想P∠=______°；(2)探究：在图①中探究1∠，2∠之间的数量关系，并证明你的结论；∠，P(3)拓展：将图①变为图②，若12325∠=︒，求PGF∠+∠=︒，75EPG∠的度数．【答案】(1)80︒(2)36012∠=︒-∠-∠；证明见详解P(3)140︒【分析】（1）过点P作MN AB∥，利用平行的性质就可以求角度，解决此问；（2）利用平行线的性质求位置角的数量关系，就可以解决此问；（3）分别过点P、点G作MN AB∥，然后利用平行线的性质求位置角的数量关系即可．∥、KR AB【详解】（1）解：如图过点P作MN AB∥，∵AB CD∥，∴AB MN CD∥∥．∴1180∠+∠=︒，EPN∠+∠=︒．FPN2180∵1130∠=︒，2150∠=︒，∴12360∠+∠+∠+∠=︒EPN FPN∴36013015080∠+=︒-︒-︒=︒．EPN FPN∵P EPN FPN∠=∠+∠，∴∠P=80°．故答案为：80︒；（2）解：36012∠=︒-∠-∠，理由如下：P如图过点P作MN AB∥，∵AB CD∥，∴AB MN CD∥∥．∴1180EPN∠+∠=︒，∠+∠=︒．FPN2180∴12360∠+∠+∠+∠=︒EPN FPN∵EPN FPN P∠+∠=∠，∠=︒-∠-∠．36012P（3）如图分别过点P、点G作MN AB∥∥、KR AB∵AB CD∥，∴AB MN KR CD∥∥∥．∴1180∠+∠=︒，EPNNPG PGR∠+∠=︒，180∠+∠=︒．RGF2180∴12540∠+∠+∠+∠++∠=︒EPN NPG PGR RGF∵75∠=∠+∠=︒，EPG EPN NPG∠+∠=∠，PGR RGF PGF∠+∠=︒，12325思路点拨：小明的思路是：如图2，过P 作PE AB ，通过平行线性质，可分别求出APE ∠、CPE ∠的度数，从而可求出APC ∠的度数；小丽的思路是：如图3，连接AC ，通过平行线性质以及三角形内角和的知识可求出APC ∠小芳的思路是：如图4，延长AP 交DC 的延长线于E ，通过平行线性质以及三角形外角的相关知识可求出APC ∠的度数．问题解决：请从小明、小丽、小芳的思路中任选一种思路进行推理计算，你求得的APC ∠的度数为问题迁移：（1）如图5，AD BC ∥，点P 在射线OM 上运动，当点P 在A 、B 两点之间运动时，ADP ∠BCP β∠=∠．CPD ∠、α∠、∠β之间有何数量关系？请说明理由；（2）在（1）的条件下，如果点P 在A 、B 两点外侧运动时（点P 与点A 、B 、O 三点不重合）写出CPD ∠、α∠、∠β间的数量关系．【答案】110；（1）CPD αβ∠=∠+∠，理由见解析；（2）CPD βα∠=∠-∠或CPD a ∠=∠解析【分析】小明的思路是：过P 作PE AB ，构造同旁内角，利用平行线性质，可得APC ∠=（1）过P 作PE AD ∥交CD 于E ，推出AD PE BC ∥∥，根据平行线的性质得出a DPE ∠=∠即可得出答案；（2）画出图形（分两种情况：①点P 在BA 的延长线上，②点P 在AB 的延长线上），根据平行线的性质得出DPE α∠=∠，CPE β∠=∠，即可得出答案．【详解】解：小明的思路：如图2，过P 作PE AB ，∵AB CD ∥，∴PE AB CD ∥∥，∴18050APE A ︒∠=-∠=︒，18060CPE C ︒∠=-∠=︒，∴5060110APC ∠=︒+︒=︒，故答案为：110；（1）CPD αβ∠=∠+∠，理由如下：如图5，过P 作PE AD ∥交CD 于E ，∵AD BC ∥，∴AD PE BC ∥∥，∴a DPE ∠=∠，CPE β∠=∠，∴CPD DPE CPE a β∠=∠+∠=∠+∠；（2）当P 在BA 延长线时，CPD βα∠=∠-∠；理由：如图6，过P 作PE AD ∥交CD 于E ，∵AD BC ∥，∴AD PE BC ∥∥，∴DPE α∠=∠，CPE β∠=∠，∴CPD CPE DPE βα∠=∠-∠=∠-∠；当P 在BO 之间时，CPD a ∠=∠-∠理由：如图7，过P 作PE AD ∥交∵AD BC ∥，∴AD PE BC ∥∥，∴DPE α∠=∠，CPE β∠=∠，∴CPD DPE CPE α∠=∠-∠=∠-∠【点睛】本题考查了三角形的内角和定理，平行线的判定和性质，主要考查学生的推理能力，解决问题的关键是作辅助线构造内错角以及同旁内角．。

人教版数学七年级下册：第五章相交线与平行线——专题练习(附答案)

小专题（一）平行线中的“拐点”问题模型1 M型【例1】如图，已知AB∥CD，则∠B，∠BED，∠D之间有何数量关系？请说明理由．【思路点拨】由已知条件知，AB∥CD，但图形中没有截这两条平行线的第三条直线，因而不能直接用平行线的性质解决．为此可构造第三条直线，即过点E 作EF∥AB，于是BE，DE就可以作为第三条直线了．变式当点E运动到平行线的外侧1．已知AB∥CD，点E为AB，CD之外任意一点．(1)如图1，探究∠BED与∠B，∠D的数量关系，并说明理由；(2)如图2，探究∠CDE与∠B，∠BED的数量关系，并说明理由．2．(1)如图1中，AB∥CD，则∠E＋∠G与∠B＋∠F＋∠D有何关系？(2)在图2中，若AB∥CD，又能得到什么结论？如果出现多个拐点时，可以作多条平行线，从而将多拐点问题转化为一个拐点问题来处理．M型最终的结论为：朝左的角之和等于朝右的角之和．模型2 铅笔型【例2】如图，直线AB∥CD，∠B，∠BED，∠D之间有什么关系呢？为什么？3．(1)①如图1，MA1∥NA2，则∠A1＋∠A2＝度；②如图2，MA1∥NA3，则∠A1＋∠A2＋∠A3＝度；③如图3，MA1∥NA4，则∠A1＋∠A2＋∠A3＋∠A4＝度；④图4，MA1∥NA5，则∠A1＋∠A2＋∠A3＋∠A4＋∠A5＝度；从上述结论中你发现了什么规律？(2)如图5，MA1∥NAn，则∠A1＋∠A2＋∠A3＋…＋∠An＝度．小专题(二) 利用平行线的性质求角的度数类型1 直接利用平行线的性质与判定求角度1．如图，OC是∠AOB的平分线，l∥OB.若∠1＝52°，则∠2的度数为( ) A．52° B．54° C．64° D．69°2．如图，CD∥AB，点O在AB上，OE平分∠BOD，OF⊥OE，∠D＝110°，则∠AOF 的度数是( )A．20° B．25° C．30° D．35°3．如图，AB∥CD，CB∥DE，∠B＝50°，则∠D＝．4．如图，已知EF∥AD，∠1＝∠2，∠BAC＝80°，求∠AGD的度数．类型2 借助学具的特征求角度5．如图，将直尺与30°角的三角尺叠放在一起．若∠1＝40°，则∠2的大小是( )A．40° B．60° C．70° D．80°6．如图，一块直角三角板的两锐角的顶点刚好落在平行线l1，l2上，已知∠C是直角，则∠1＋∠2的度数等于( )A．75° B．90° C．105° D．120°类型3 折叠问题中求角度7．将一个长方形纸片折叠成如图所示的图形．若∠ABC＝26°，则∠ACD＝．8．如图，一个四边形纸片ABCD，∠B＝∠D＝90°，∠C＝130°.把纸片按如图所示折叠，使点B落在AD边上的B′点，AE是折痕，则∠AEB的度数是．类型4 抽象出平行线模型求角度(建模思想)9．如图，∠AOB的一边OA为平面镜，∠AOB＝38°，一束光线(与水平线OB平行)从点C射入经平面镜反射后，反射光线落在OB上的点E处，已知∠ADC＝∠ODE.则∠DEB的度数是度．10．如图1是我们常用的折叠式小刀，图2中刀柄外形是一个梯形挖去一个小半圆，其中刀片的两条边缘线可看成两条平行的线段，转动刀片时会形成如图2所示的∠1与∠2，则∠1与∠2的度数和是．小专题(三) 平行线的性质与判定的综合运用——教材P37T13的变式与应用教材母题(教材P37T13)：完成下面的证明．(1)如图1，点D，E，F分别是三角形ABC的边BC，CA，AB上的点，DE∥BA，DF ∥CA.求证：∠FDE＝∠A.证明：∵DE∥BA，∴∠FDE＝．∵DF∥CA，∴∠A＝．∴∠FDE＝∠A.(2)如图2，AB和CD相交于点O，∠C＝∠COA，∠D＝∠BOD.求证AC∥BD.证明：∵∠C＝∠COA，∠D＝∠BOD，又∠COA＝∠BOD( )，∴∠C＝．∴AC∥BD(内错角相等，两直线平行)．(1)判定两直线平行的方法有五种：①平行线的定义；②平行公理的推论；③同位角相等，两直线平行；④内错角相等，两直线平行；⑤同旁内角互补，两直线平行．(2)判定两直线平行时，定义一般不常用，其他四种方法要灵活运用，推理时要注意书写格式．(3)由两条直线平行得到同位角相等、内错角相等或同旁内角互补，解题时应结合图形先确认所成的角是不是两平行线被第三条直线所截得的同位角或内错角或同旁内角，同时要学会简单的几何说理，做到每一步有理有据．1．如图，已知AD⊥BC，EF⊥BC，垂足分别为D，F，∠2＋∠3＝180°.试说明：∠GDC＝∠B.下面是不完整的说理过程，请你将横线上的过程和括号里的理由补充完整．解：因为AD⊥BC，EF⊥BC(已知)，①所以∠ADB＝∠EFB＝ (垂直的定义)．②所以 (同位角相等，两直线平行)．③所以∠1＋∠2＝ (两直线平行，同旁内角互补)．④又因为∠2＋∠3＝180°( )，⑤所以∠1＝∠3( )．⑥所以AB∥DG( )．⑦所以∠GDC＝∠B( )．2．如图，点G在射线BC上，射线DE与AB，AG分别交于点H，M.若DF∥AB，∠B＝75°，∠D＝105°，求证：∠AME＝∠AGC.3．如图，AB∥CD，AE平分∠BAD，CD与AE相交于点F，∠CFE＝∠E.求证：AD ∥BC.4．如图，∠E＝∠1，∠3＋∠ABC＝180°，BE是∠ABC的平分线．你能判断DF 与AB的位置关系吗？请说明理由．5．如图，AB⊥BD于点B，点E是BD上的点，AE平分∠BAC，CE平分∠ACD，且∠1＋∠2＝90°.求证：CD⊥BD.6．如图，把一张长方形ABCD的纸片沿EF折叠后，ED与BC的交点为G，点D，C分别落在D′，C′的位置上．若∠EFG＝55°，求∠1，∠2的度数．7．如图，已知BC∥GE，∠AFG＝∠1＝50°.(1)求证：AF∥DE；(2)若AQ平分∠FAC，交BC于点Q，且∠Q＝15°，求∠ACQ的度数．参考答案：小专题（一）平行线中的“拐点”问题模型1 M型【例1】如图，已知AB∥CD，则∠B，∠BED，∠D之间有何数量关系？请说明理由．【思路点拨】由已知条件知，AB∥CD，但图形中没有截这两条平行线的第三条直线，因而不能直接用平行线的性质解决．为此可构造第三条直线，即过点E 作EF∥AB，于是BE，DE就可以作为第三条直线了．【解答】∠BED＝∠B＋∠D.理由：过点E作EF∥AB，则EF∥CD.∴∠B＝∠BEF，∠D＝∠DEF.∴∠BED＝∠BEF＋∠DEF＝∠B＋∠D.变式当点E运动到平行线的外侧1．已知AB∥CD，点E为AB，CD之外任意一点．(1)如图1，探究∠BED与∠B，∠D的数量关系，并说明理由；(2)如图2，探究∠CDE与∠B，∠BED的数量关系，并说明理由．解：(1)∠B＝∠BED＋∠D.理由如下：过点E作EF∥AB，则AB∥CD∥EF.∴∠BEF＝∠B，∠D＝∠DEF.∵∠BEF＝∠BED＋∠DEF，∴∠B＝∠BED＋∠D.(2)∠CDE＝∠B＋∠BED.理由如下：过点E作EF∥AB，则AB∥CD∥EF.∴∠B＋∠BEF＝180°，∠CDE＋∠DEF＝180°.又∵∠DEF＝∠BEF－∠BED，∴∠CDE＋∠BEF－∠BED＝∠B＋∠BEF，即∠CDE＝∠B＋∠BED.拓展平行线间有多个拐点2．(1)如图1中，AB∥CD，则∠E＋∠G与∠B＋∠F＋∠D有何关系？(2)在图2中，若AB∥CD，又能得到什么结论？解：(1)∠BEF＋∠FGD＝∠B＋∠EFG＋∠D.理由：过点E，F，G分别作EM∥AB，FN∥AB，GH∥AB，由AB∥CD，得AB∥EM∥FN∥GH∥CD.∴∠BEM＝∠B，∠MEF＝∠EFN，∠NFG＝∠FGH，∠HGD＝∠D.∴∠BEF＋∠FGD＝∠BEM＋∠MEF＋∠FGH＋∠HGD＝∠B＋∠EFN＋∠NFG＋∠D＝∠B＋∠EFG＋∠D.(2)在图2中，有∠E1＋∠E2＋∠E3＋…＋∠En＝∠B＋∠F1＋∠F2＋…＋∠Fn－1＋∠D.如果出现多个拐点时，可以作多条平行线，从而将多拐点问题转化为一个拐点问题来处理．M型最终的结论为：朝左的角之和等于朝右的角之和．模型2 铅笔型【例2】如图，直线AB∥CD，∠B，∠BED，∠D之间有什么关系呢？为什么？【解答】∠B＋∠BED＋∠D＝360°.理由：过点E作EF∥AB.∵AB∥CD，∴AB∥CD∥EF.∴∠B＋∠BEF＝180°，∠D＋∠DEF＝180°. ∴∠B＋∠BEF＋∠D＋∠DEF＝360°，即∠B＋∠BED＋∠D＝360°.拓展平行线间有多个拐点3．(1)①如图1，MA1∥NA2，则∠A1＋∠A2＝180度；②如图2，MA1∥NA3，则∠A1＋∠A2＋∠A3＝360度；③如图3，MA1∥NA4，则∠A1＋∠A2＋∠A3＋∠A4＝540度；④图4，MA1∥NA5，则∠A1＋∠A2＋∠A3＋∠A4＋∠A5＝720度；从上述结论中你发现了什么规律？(2)如图5，MA1∥NAn，则∠A1＋∠A2＋∠A3＋…＋∠An＝180(n－1)度．解：每增加一个角，度数增加180°.小专题(二) 利用平行线的性质求角的度数类型1 直接利用平行线的性质与判定求角度1．如图，OC是∠AOB的平分线，l∥OB.若∠1＝52°，则∠2的度数为( C ) A．52° B．54° C．64° D．69°2．如图，CD∥AB，点O在AB上，OE平分∠BOD，OF⊥OE，∠D＝110°，则∠AOF 的度数是( D )A．20° B．25° C．30°D．35°3．如图，AB∥CD，CB∥DE，∠B＝50°，则∠D＝130°．4．如图，已知EF∥AD，∠1＝∠2，∠BAC＝80°，求∠AGD的度数．解：∵EF∥AD，∴∠2＝∠3(两直线平行，同位角相等)．∵∠1＝∠2，∴∠1＝∠3(等量代换)．∴AB∥DG(内错角相等，两直线平行)．∴∠BAC＋∠AGD＝180°(两直线平行，同旁内角互补)．∵∠BAC＝80°，∴∠AGD＝100°.类型2 借助学具的特征求角度5．如图，将直尺与30°角的三角尺叠放在一起．若∠1＝40°，则∠2的大小是( D )A．40° B．60° C．70° D．80°6．如图，一块直角三角板的两锐角的顶点刚好落在平行线l1，l2上，已知∠C是直角，则∠1＋∠2的度数等于( B )A．75° B．90° C．105° D．120°类型3 折叠问题中求角度7．将一个长方形纸片折叠成如图所示的图形．若∠ABC＝26°，则∠ACD＝128°．8．如图，一个四边形纸片ABCD，∠B＝∠D＝90°，∠C＝130°.把纸片按如图所示折叠，使点B落在AD边上的B′点，AE是折痕，则∠AEB的度数是65°．类型4 抽象出平行线模型求角度(建模思想)9．如图，∠AOB的一边OA为平面镜，∠AOB＝38°，一束光线(与水平线OB平行)从点C射入经平面镜反射后，反射光线落在OB上的点E处，已知∠ADC＝∠ODE.则∠DEB的度数是76度．10．如图1是我们常用的折叠式小刀，图2中刀柄外形是一个梯形挖去一个小半圆，其中刀片的两条边缘线可看成两条平行的线段，转动刀片时会形成如图2所示的∠1与∠2，则∠1与∠2的度数和是90°．小专题(三) 平行线的性质与判定的综合运用——教材P37T13的变式与应用教材母题(教材P37T13)：完成下面的证明．(1)如图1，点D，E，F分别是三角形ABC的边BC，CA，AB上的点，DE∥BA，DF ∥CA.求证：∠FDE＝∠A.证明：∵DE∥BA，∴∠FDE＝∠BFD(两直线平行，内错角相等)．∵DF∥CA，∴∠A＝∠BFD(两直线平行，同位角相等)．∴∠FDE＝∠A.(2)如图2，AB和CD相交于点O，∠C＝∠COA，∠D＝∠BOD.求证AC∥BD.证明：∵∠C＝∠COA，∠D＝∠BOD，又∠COA＝∠BOD(对顶角相等)，∴∠C＝∠D．∴AC∥BD(内错角相等，两直线平行)．(1)判定两直线平行的方法有五种：①平行线的定义；②平行公理的推论；③同位角相等，两直线平行；④内错角相等，两直线平行；⑤同旁内角互补，两直线平行．(2)判定两直线平行时，定义一般不常用，其他四种方法要灵活运用，推理时要注意书写格式．(3)由两条直线平行得到同位角相等、内错角相等或同旁内角互补，解题时应结合图形先确认所成的角是不是两平行线被第三条直线所截得的同位角或内错角或同旁内角，同时要学会简单的几何说理，做到每一步有理有据．1．如图，已知AD⊥BC，EF⊥BC，垂足分别为D，F，∠2＋∠3＝180°.试说明：∠GDC＝∠B.下面是不完整的说理过程，请你将横线上的过程和括号里的理由补充完整．解：因为AD⊥BC，EF⊥BC(已知)，①所以∠ADB＝∠EFB＝90°(垂直的定义)．②所以AD∥EF(同位角相等，两直线平行)．③所以∠1＋∠2＝180°(两直线平行，同旁内角互补)．④又因为∠2＋∠3＝180°(已知)，⑤所以∠1＝∠3(同角的补角相等)．⑥所以AB∥DG(内错角相等，两直线平行)．⑦所以∠GDC＝∠B(两直线平行，同位角相等)．2．如图，点G在射线BC上，射线DE与AB，AG分别交于点H，M.若DF∥AB，∠B＝75°，∠D＝105°，求证：∠AME＝∠AGC.证明：∵DF∥AB(已知)，∴∠D＝∠BHM(两直线平行，同位角相等)．又∵∠B＝75°，∠D＝105°(已知)，∴∠B＋∠BHM＝75°＋105°＝180°.∴DE∥BC(同旁内角互补，两直线平行)．∴∠AME＝∠AGC(两直线平行，同位角相等)．3．如图，AB∥CD，AE平分∠BAD，CD与AE相交于点F，∠CFE＝∠E.求证：AD ∥BC.证明：∵AE平分∠BAD(已知)，∴∠1＝∠2(角平分线的定义)．∵AB∥CD(已知)，∴∠1＝∠CFE(两直线平行，同位角相等)．又∵∠1＝∠2(已证)，∠CFE＝∠E(已知)，∴∠2＝∠E(等量代换)．∴AD∥BC(内错角相等，两直线平行)．4．如图，∠E＝∠1，∠3＋∠ABC＝180°，BE是∠ABC的平分线．你能判断DF 与AB的位置关系吗？请说明理由．解：DF∥AB.理由：∵BE是∠ABC的平分线，∴∠1＝∠2(角平分线的定义)．∵∠E＝∠1(已知)，∴∠E＝∠2(等量代换)．∴AE∥BC(内错角相等，两直线平行)．∴∠A＋∠ABC＝180°(两直线平行，同旁内角互补)．∵∠3＋∠ABC＝180°(已知)，∴∠A＝∠3(等量代换)．∴DF∥AB(同位角相等，两直线平行)．5．如图，AB⊥BD于点B，点E是BD上的点，AE平分∠BAC，CE平分∠ACD，且∠1＋∠2＝90°.求证：CD⊥BD.证明：∵AE平分∠BAC，CE平分∠ACD(已知)，∴∠BAC＝2∠1，∠ACD＝2∠2(角平分线的性质)．∴∠BAC＋∠ACD＝2∠1＋2∠2＝2(∠1＋∠2)．∵∠1＋∠2＝90°(已知)，∴∠BAC＋∠ACD＝180°.∴AB∥CD(同旁内角互补，两直线平行)．∴∠B＋∠D＝180°(两直线平行，同旁内角互补)．∴∠D＝180°－∠B(等式的性质)．∵AB⊥BD(已知)，∴∠B＝90°(垂直的定义)．∴∠D＝90°，即CD⊥BD.6．如图，把一张长方形ABCD的纸片沿EF折叠后，ED与BC的交点为G，点D，C分别落在D′，C′的位置上．若∠EFG＝55°，求∠1，∠2的度数．解：∵AD∥BC，∠EFG＝55°，∴∠2＝∠GED，∠DEF＝∠EFG＝55°(两直线平行，内错角相等)．由折叠，知∠GEF＝∠DEF＝55°.∴∠GED＝110°.∴∠2＝110°.∴∠1＝180°－∠2＝70°(两直线平行，同旁内角互补)．7．如图，已知BC∥GE，∠AFG＝∠1＝50°.(1)求证：AF∥DE；(2)若AQ平分∠FAC，交BC于点Q，且∠Q＝15°，求∠ACQ的度数．解：(1)证明：∵BC∥GE，∴∠E＝∠1＝50°.∵∠AFG＝∠1＝50°，∴∠E＝∠AFG＝50°.∴AF∥DE.(2)过点A作AP∥GE，∵BC∥GE，∴AP∥GE∥BC.∴∠FAP＝∠AFG＝50°，∠PAQ＝∠Q＝15°.∴∠FAQ＝∠FAP＋∠PAQ＝65°.∵AQ平分∠FAC，∴∠CAQ＝∠FAQ＝65°.∴∠CAP＝80°.∴∠ACQ＝180°－∠CAP＝100°.。

专题1.11 《平行线》几何模型1(知识讲解)七年级数学下册基础知识专项讲练(浙教版)

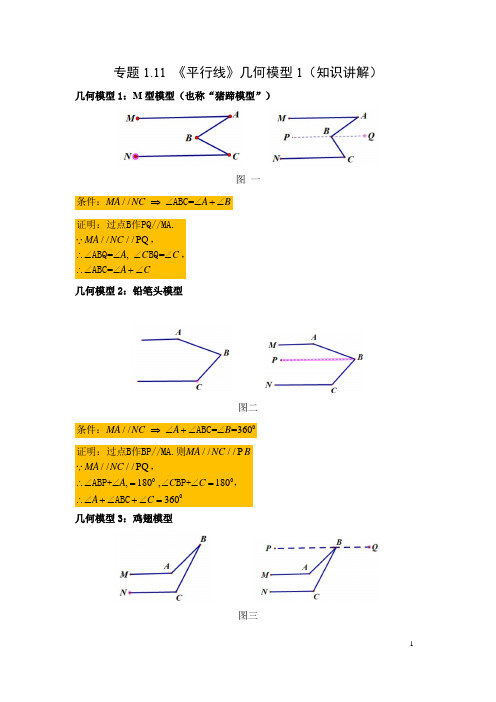
专题1.11 《平行线》几何模型1（知识讲解）几何模型1：M 型模型（也称“猪蹄模型”）图一//=MA NC A B ⇒∠∠+∠条件：ABC ////PQ =,==MA NC A C C A C∴∠∠∠∠∴∠∠+∠证明：过点B 作PQ//MA.，ABQ BQ ，ABC几何模型2：铅笔头模型图二0//==360MA NC A B ⇒∠+∠∠条件：ABC000////P ////PQ ,180,180360MA NC BMA NC A C C A C∴∠∠=∠∠=∴∠+∠+∠=证明：过点B 作BP//MA.则，ABP+BP+，ABC几何模型3：鸡翅模型图三//-=MA NC A B ⇒∠∠∠条件：C////PQ ////PQ ,,,MA NC MA NC A C C B CBQ A C B∴∠∠∠∠∴∠=∠∠∴∠-∠=∠证明：过点B 作PQ//MA.则，ABQ=BQ=，ABQ-几何模型4：折鸡翅模型图四//MA NC A B ⇒∠=∠+∠条件：C ////PQ ////PQ ,,,MA NC MA NC A C C ABC CBQ A ACB C∴∠∠∠∠∴∠=∠∠∴∠==∠+∠证明：过点B 作PQ//MA.则，ABQ=BQ=，ABQ-几何模型5：多个M 型模型12121//......n n MA NB P PPAQ Q Q B -⇒∠+∠++∠=∠+∠+∠++∠条件：证明思路参考几何模型1几何模型6：多个铅笔头模型12121//......n n MA NB P P P A Q Q Q B -⇒∠+∠++∠=∠+∠+∠++∠条件：证明思路参考几何模型2类型一、M 型模型1（2020·宁波市惠贞书院七年级期中）如图，//AB EF ，设90C ∠=︒，那么x ，y ，z 的关系式______．【答案】90x y z +-=︒【分析】过C 作//CN AB ，过D 作//DM AB ，根据平行线的性质可知//////AB CN DM EF ，然后根据平行线的性质即可求解；解：如图，过C 作//CN AB ，过D 作//DM AB ，∴//////AB CN DM EF ，∴1x =∠，23∠∠=，4z ∠=，∴90BCD ∠=︒，∴1290∠+∠=︒，∴390x +∠=︒，∴3490x z +∠+∠=︒+，∴90x y z +=︒+，∴90x y z +-=︒．故答案为：90x y z +-=︒．【点拨】本题考查了平行线的性质，两直线平行同位角相等，两直线平行内错角相等，正确理解平行线的性质是解题的关键；举一反三：【变式1】（2020·四川成都市·天府四中七年级期中）如图，//,,3527'EE MN CA CB EAC ⊥∠=︒，则MBC ∠=____________________．【答案】5433'【分析】过C 点做EF 的平行线，利用平行线的性质，即可证明．解：过C 点做EF 的平行线,GH//,EF MN////,EF GH MN ∴3527'EAC ACH ∴∠=∠=，又,CA CB ⊥90,ACB ∴∠=︒5433',HCB ACB ACH ∴∠=∠-∠=︒又//,GH MN5433'HCB CBM ∴∠=∠=.故答案为：5433'．【点拨】本题考查了通过平行线的性质求解角度问题，解题关键在于过中间的点作已知直线的平行线．【变式2】（2019·辽宁大连市·七年级期末）阅读材料：如图1，点A 是直线MN 上一点，MN 上方的四边形ABCD 中，140ABC ∠=︒，延长BC ，2DCE MAD ADC ∠=∠+∠，探究DCE ∠与MAB ∠的数量关系，并证明.小白的想法是：“作ECF ECD ∠=∠（如图2），通过推理可以得到CF MN ，从而得出结论”.请按照小白的想法．．．．．完成解答：拓展延伸：保留原题条件不变，CG 平分ECD ∠，反向延长CG ，交MAB ∠的平分线于点H （如图3），设MAB α∠=，请直接写出H ∠的度数（用含α的式子表示）.【答案】阅读材料：40∠=︒+∠ECD MAB ，见解析；拓展延伸：120CHA α=∠︒-. 【分析】（1）作ECF ECD ∠=∠，DG MN ，BH MN ，由平行线性质可得180MAD ADG ∠+∠=︒，结合已知2DCE MAD ADC ∠=∠+∠，可证180CDG DCF ∠+∠=︒，进而得到DG CF ，从而CF BH ，140BCF MAB ABC ∠+∠=∠=︒，将180180BCF ECF ECD ∠=︒-∠=︒-∠代入可得40∠=︒+∠ECD MAB .（2）过H 点作HP∴MN ，可得∴CHA=∴PHA+∴PHC ，结合（1）的结论和CG 平分∴ECD 可得∴PHC =∴FCH =120°-3MAB 2∠，即可得120CHA α=∠︒-.解：【阅读材料】作ECF ECD ∠=∠，DG MN ，BH MN （如图1）.∵DG MN ，∴180MAD ADG ∠+∠=︒.∴()180CDG MAD ADC ∠+∠+∠=︒.∵2DCE MAD ADC ∠=∠+∠，∴2180CDG DCE ∠+∠=︒.∴180CDG DCF ∠+∠=︒.∴DG CF .∵DG MN ，∴MN CF .∵BH MN ，∴CF BH .∴BCF CBH ∠=∠，MAB ABH ∠=∠.∴140BCF MAB ABC ∠+∠=∠=︒.∵180180BCF ECF ECD ∠=︒-∠=︒-∠，∴40∠=︒+∠ECD MAB .【拓展延伸】结论：120CHA α=∠︒-.理由：如图，作ECF ECD ∠=∠，过H 点作HP∴MN ，∴∴PHA=∴MAH=1BAM 2∠，由（1）得FC∴MN ，∴FC∴HP ，∴∴PHC=∴FCH ，∴40∠=︒+∠ECD MAB ,CG 平分∴ECD ， ∴∴ECG=20°+1MAB 2∠，∴∴FCH=180ECG ECF ︒-∠-∠=180°-(40MAB ︒+∠)-(20°+1MAB 2∠)=120°-3MAB 2∠ ∴∴CHA=∴PHA+∴PHC=1MAB 2∠∠+（120°-3MAB 2∠）=120°-MAB ∠即：120CHA α=∠︒-.【点评】本题主要考查了平行线的性质的运用，解决问题的关键是作平行线构造内错角，运用等角的余角（补角）相等进行推导．余角和补角计算的应用，常常与等式的性质、等量代换相关联．解题时注意方程思想的运用．类型二、铅笔头型模型2 （2020·山东聊城市·七年级期末）直线AB 、CD 被直线EF 所截，AB∴CD ，点P 是平面内一动点．（1）若点P 在直线CD 上，如图∴，∴α＝50°，则∴2＝ °．（2）若点P 在直线AB 、CD 之间，如图∴，试猜想∴α、∴1、∴2之间的等量关系并给出证明；（3）若点P在直线CD的下方，如图∴，（2）中∴α、∴1、∴2之间的关系还成立吗？请作出判断并说明理由．【答案】（1）50；（2）∴α＝∴1+∴2，证明见解析；（3）不成立．理由见解析．【分析】（1）由题意直接根据平行线的性质可直接求解；（2）由题意过P作PG∴AB，则PG∴AB∴CD，利用平行线的性质即可求解；（3）根据题意过P作PH∴AB，则PH∴AB∴CD，利用平行线的性质进行分析即可求解．解：（1）∵AB∥CD，∠α＝50°∴∠2＝∠α＝50°，故答案为：50；（2）∠α＝∠1+∠2．证明：过P作PG∥AB，∵AB∥CD，∴PG∥AB∥CD，∴∠2＝∠EPG，∠1＝∠FPG，∵∠α＝∠EPF＝∠EPG+∠FPG，∴∠α＝∠1+∠2；（3）不成立．理由：过P 作PH ∥AB ，∵AB ∥CD ，∴PH ∥AB ∥CD ，∴∠2＝∠EPH ，∠1＝∠FPH ，∵∠α＝∠EPF ＝∠EPH ﹣∠FPH ，∴∠α＝∠2﹣∠1，故不成立．【点拨】本题主要考查平行线的性质，注意掌握并灵活运用平行线的性质是解题的关键．举一反三：【变式1】（2020·河北邢台市·八年级月考）如图1，四边形MNBD 为一张长方形纸片．（1）如图2，将长方形纸片剪两刀，剪出三个角（BAE AEC ECD ∠∠∠、、），则BAE AEC ECD ∠+∠+∠=__________°．（2）如图3，将长方形纸片剪三刀，剪出四个角（BAE AEF EFC FCD ∠∠∠∠、、、），则BAE AEF EFC FCD ∠+∠+∠+∠=__________°．（3）如图4，将长方形纸片剪四刀，剪出五个角（BAE AEF EFG FGC GCD ∠∠∠∠∠、、、、），则BAE AEF EFG FGC GCD ∠+∠+∠+∠+∠=___________°．（4）根据前面探索出的规律，将本题按照上述剪法剪n 刀，剪出()1n +个角，那么这()1n +个角的和是____________°．【答案】（1）360；（2）540；（3）720；（4）180n．【分析】（1）过点E作EH∴AB，再根据两直线平行，同旁内角互补即可得到三个角的和等于180°的2倍；（2）分别过E、F分别作AB的平行线，根据两直线平行，同旁内角互补即可得到四个角的和等于180°的三倍；（3）分别过E、F、G分别作AB的平行线，根据两直线平行，同旁内角互补即可得到四个角的和等于180°的三倍；（4）根据前三问个的剪法，剪n刀，剪出n+1个角，那么这n+1个角的和是180n度．证明：（1）过E作EH∥AB（如图②）．∵原四边形是长方形，∴AB∥CD，又∵EH∥AB，∴CD∥EH（平行于同一条直线的两条直线互相平行）．∵EH∥AB，∴∠A+∠1=180°（两直线平行，同旁内角互补）．∵CD∥EH，∴∠2+∠C=180°（两直线平行，同旁内角互补）．∴∠A+∠1+∠2+∠C=360°，又∵∠1+∠2=∠AEC，∴∠BAE+∠AEC+∠ECD=360°；（2）分别过E、F分别作AB的平行线，如图③所示，用上面的方法可得∠BAE+∠AEF+∠EFC+∠FCD=540°；（3）分别过E 、F 、G 分别作AB 的平行线，如图④所示，用上面的方法可得∠BAE+∠AEF+∠EFG+∠FGC+∠GCD=720°；（4）由此可得一般规律：剪n 刀，剪出n+1个角，那么这n+1个角的和是180n 度．故答案为：（1）360；（2）540；（3）720；（4）180n ．【点拨】题主要考查了多边形的内角和，作平行线并利用两直线平行，同旁内角互补是解本题的关键，总结规律求解是本题的难点．举一反三：【变式2】（2020·湖北随州市·七年级期末）已知12l l //，点A ，C 分别在直线1l ，2l 上，点B 在直线1l 与2l 之间，90BCN BAM ∠<∠≤︒．（1）如图1，求证：ABC BAM BCN ∠=∠+∠．阅读并补齐下列推理过程过点B 作//BG NC ，因为12l l //，所以//AM _____（______________）所以ABG BAM ∠=∠，CBG BCN ∠=∠（_______________________）所以ABC ABG CBG BAM BCN ∠=∠+∠=∠+∠．解题反思：从上面的推理过程中，我们发现平行线具有“等角转化”的功能，在学习中要注意体会．（2）如图2，点D ，E 在直线1l 上，DBC BAM ∠=∠，BE 平分ABC ∠，求证：DBE DEB ∠=∠．（3）在（2）的条件下，过点B 作BF 平分CBE ∠，请直接写出使//BF AM 时，BAM ∠与BCN ∠之间应具备的关系．【答案】（1）BG ，平行于同一条直线的两条直线平行，两条直线平行内错角相等；（2）见解析；（3）3BAM BCN ∠=∠【分析】（1）添加平行线，根据平行于同一条直线的两条直线平行，再利用平行线的性质进行角的等量代换；（2）与（1）同理，通过添加平行线，根据平行于同一条直线的两条直线平行，再利用平行线的性质、角平分线的定义进行角的等量代换；（3）在（2）的条件下，根据已有的数量关系，加上平行线得到的内错角相等进行等量代换即可．解：（1）BG ，平行于同一条直线的两条直线平行，两条直线平行内错角相等；（2）过点B 作BG //NC ，12//l l ，AM //BG ∴DEB EBG ∴∠=∠，CBG BCN ∠=∠，由（1）知，ABC BAM BCN ∠=∠+∠，又DBC BAM ∠=∠，ABC DBC BCN ∴∠=∠+∠，ABC ABD DBC ∠=∠+∠，ABD BCN ∴∠=∠，∴ABD CBG ∠=∠， BE 平分ABC ∠，ABE CBE ∴∠=∠，DBE EBG ∴∠=∠，DEB DBE ∴∠=∠（3）BAM 3BCN ∠=∠，理由如下：∴DBC ＝∴DBE ＋∴EBF ＋∴FBC ，∴BF∴AM ，∴∴EBF ＝∴DEB ，∴BF 平分∴CBE ，∴∴CBF ＝∴EFB ，而由（2）知：∴DBE ＝∴DEB ，∴∴DBC ＝3∴FBC ，∴CN∴AM ，∴CN∴BF ，∴∴FBC＝∴BCN，∴DBC＝3∴BCN，而∴BAM＝∴DBC，∴∴BAM＝3∴BCN【点拨】本题考查平行线的推论和性质，熟练掌握平行线的性质，并灵活进行等量代换是关键．。

平行线几何模型(M模型)(知识讲解)-2022-2023学年七年级数学下册基础知识专项讲练(人教版)

专题5.22平行线几何模型（M模型）（知识讲解）几何模型1：M型模型（也称“猪蹄模型”）图一//=MA NC A B⇒∠∠+∠条件：ABC////PQ=,==MA NCA C CA C∴∠∠∠∠∴∠∠+∠证明：过点B作PQ//MA.，ABQ BQ，ABC几何模型2：鸡翅模型图三//-=MA NC A B⇒∠∠∠条件：C////PQ////PQ,,,MA NCMA NCA C CB CBQA C B∴∠∠∠∠∴∠=∠∠∴∠-∠=∠证明：过点B作PQ//MA.则，ABQ=BQ=，ABQ-几何模型3：折鸡翅模型图四//MA NC A B⇒∠=∠+∠条件：C ////PQ////PQ ,,,MA NC MA NC A C C ABC CBQ A ACB C∴∠∠∠∠∴∠=∠∠∴∠==∠+∠ 证明：过点B作PQ//MA.则，ABQ=BQ =，ABQ-几何模型4：多个M 型模型12121//......n n MA NB P P P A Q Q Q B-⇒∠+∠++∠=∠+∠+∠++∠条件：【典型例题】类型一、平行线几何模型➽➼猪蹄模型➻➸求解✬✬证明1．请阅读小明同学在学习平行线这章知识点时的一段笔记，然后解决问题．小明：老师说在解决有关平行线的问题时，如果无法直接得到角的关系，就需要借助辅助线来帮助解答，今天老师介绍了一个“美味”的模型“猪蹄模型”．即已知：如图1，AB CD ∥，E 为AB 、CD 之间一点，连接AE ，CE 得到AEC ∠．求证：AEC A C∠=∠+∠小明笔记上写出的证明过程如下:证明：过点E 作EF AB∥∵1A∠=∠∵AB CD ∥，EF AB∥∴EF CD∥∴2C∠=∠∴12AEC ∠=∠+∠∴AEC A C∠=∠+∠请你利用“猪蹄模型”得到的结论或解题方法，完成下面的两个问题．(1)如图，若AB CD ∥，60E ∠=o ，求B C F ∠+∠+∠；(2)如图，AB CD ∥，BE 平分ABG ∠，CF 平分DCG ∠，27G H ∠=∠+ ，求H ∠．【答案】(1)240 ；(2)51【分析】（1）作EM AB ∥，FN CD ∥，如图，根据平行线的性质得EM AB FN CD ∥∥∥，所以1B ∠=∠，23∠∠=，4180C ∠+∠= ，然后利用等量代换计算240B F C ∠+∠+∠= ；（2）分别过G 、H 作AB 的平行线MN 和RS ，根据平行线的性质和角平分线的性质可用ABG ∠和DCG ∠分别表示出H ∠和G ∠，从而可找到H ∠和G ∠的关系，结合条件可求得51H ∠= ．解：（1）作EM AB ∥，FN CD ∥，如图，且AB CD ∥180∴180227BHC BHC -∠=∠+ ，∴51BHC ∠= ．【点拨】本题考查了平行线的性质和判定的应用，能运用平行线的性质和判定进行推理是解此题的关键，注意：①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补，反之亦然．举一反三：【变式】阅读下面内容，并解答问题．已知：如图1，AB CD ，直线EF 分别交AB ，CD 于点E ，F ．BEF ∠的平分线与DFE ∠的平分线交于点G ．(1)求证：EG FG ⊥；(2)填空，并从下列①、②两题中任选一题说明理由．我选择题．①在图1的基础上，分别作BEG ∠的平分线与DFG ∠的平分线交于点M ，得到图2，则EMF ∠的度数为．②如图3，AB CD ，直线EF 分别交AB ，CD 于点E ，F ．点O 在直线AB ，CD 之间，且在直线EF 右侧，BEO ∠的平分线与DFO ∠的平分线交于点P ，则EOF ∠与EPF ∠满足的数量关系为．【答案】(1)见解析；(2)①45︒；②结论：2EOF EPF ∠=∠【分析】（1）利用平行线的性质解决问题即可；（2）①利用基本结论EMF BEM MFD ∠=∠+∠求解即可；②利用基本结论EOF BEO DFO ∠=∠+∠，EPF BEP DFP ∠=∠+∠，求解即可．（1）证明：如图，过G 作GH AB ，AB CD ，AB GH CD ∴ ，BEG EGH DFG FGH ∠∠∠∠∴==，，180BEF DFE ∴∠+∠=EG 平分BEF ∠，FG 12GEB BEF ∴∠=∠，12GEB GFD ∴∠+∠=∠在EFG ∆中，GEF ∠+∠EGF GEB GFD ∴∠=∠+∠EG FG ∴⊥；）解：①如图2中，由题意，EM 平分BEG ∠，MF 1(2BEM MFD ∴∠+∠=∠EMF BEM MFD ∴∠=∠+∠故答案为：45︒；结论：2EOF EPF ∠=∠理由：如图3中，由题意，PE 平分BEO ∠，PF 2BEO BEP ∴∠=∠，DFO ∠类型二、平行线几何模型➽➼鸡翅模型➻➸求解✬✬证明2．已知直线12l l ∥，3l 和1l ，2l 分别交于C ，D 点，点A ，B 分别在线1l ，2l 上，且位于3l 的左侧，点P 在直线3l 上，且不和点C ，D 重合．(1)如图1，有一动点P 在线段CD 之间运动时，求证：12APB ∠=∠+∠；(2)如图2，当动点P 在C 点之上运动时，猜想APB ∠、1∠、2∠有何数量关系，并说明理由．【答案】(1)证明见解析；(2)21APB ∠=∠+∠，理由见解析．【分析】()1过点P 作1//PE l ，根据12l l //可知2//PE l ，故可得出1APE ∠=∠，2.BPE ∠=∠再由APB APE BPE ∠=∠+∠即可得出结论；()2过P 作//PE AC ，依据12l l //，可得//PE BD ，进而得到2BPE ∠=∠，1APE ∠=∠，再根据BPE APE APB ∠=∠+∠，即可得出21APB ∠=∠+∠．（1）证明：如图1，过点P 作1//PE l ，12//l l ，2//PE l ∴，1APE ∴∠=∠，2BPE ∠=∠．又APB APE BPE ∠=∠+∠ ，12APB ∴∠=∠+∠；（2）解：21APB ∠=∠+∠．理由如下：如图2，过P 作//PE AC ，12//l l ，//PE BD ∴，2BPE ∴∠=∠，1APE ∠=∠，BPE APE APB ∠=∠+∠ ，21APB ∴∠=∠+∠．【点拨】本题考查的是平行线的性质，根据题意作出辅助线，构造出平行线是解答此题的关键．举一反三：【变式】【原题】已知直线AB ∥CD ，点P 为平行线AB ，CD 之间的一点，如图1，若∠ABP =50°，∠CDP =60°，BE 平分∠ABP ，DE 平分∠CDP ．(1)则∠P =______，∠E =______．(2)【探究】如图2，当点P 在直线AB 的上方时，若∠ABP =α，∠CDP =β，∠ABP 和∠CDP 的平分线交于点1E ，∠ABE 1与1CDE ∠的角平分线交于点2E ，∠ABE 2与∠CDE 2的角平分线交于点3E ，…以此类推，求∠E 2的度数，并猜想∠E n 的度数．(3)【变式】如图3，∠ABP 的角平分线的反向延长线和∠CDP 的补角的角平分线交于点E ，试直接写出∠P 与∠E 的数量关系．类型三、平行线几何模型➽➼多个M型模型➻➸求解✬✬证明3．探究：(1)如图①，已知AB CD，图中∠1，∠2，∠3之间有什么关系？(2)如图②，已知AB CD，图中∠1，∠2，∠3，∠4之间有什么关系？(3)如图③，已知AB CD，请直接写出图中∠1，∠2，∠3，∠4，∠5之间的关系；【答案】(1)∠1＋∠3＝∠2；(2)∠1＋∠3＝∠2＋∠4；(3)∠1＋∠3＋∠5＝∠2＋∠4．【分析】（1）过点E作EM∥AB，根据平行线的性质及角的和差求解即可；（2）过点F作NF∥AB，结合（1）并根据平行线的性质及角的和差求解即可；（3）过点G作GM∥AB，结合（2）并根据平行线的性质及角的和差求解即可．（1）解：如图①，过点E作EM∥AB，∵AB∥CD，∴AB∥CD∥EM，∴∠1＝∠NEM，∠3＝∠MEF，∴∠1＋∠3＝∠NEM＋∠MEF，即∠1＋∠3＝∠2；（2）如图②，过点F作NF∥AB，∵AB∥CD，∴AB ∥CD ∥FN ，∴∠4＝∠NFH ，由（1）知，∠1＋∠EFN ＝∠2，∴∠1＋∠EFN ＋∠NFH ＝∠2＋∠4，即∠1＋∠3＝∠2＋∠4；（3）如图③，过点G 作GM ∥AB ，∵AB ∥CD ，∴AB ∥CD ∥GM ，∴∠5＝∠MGN ，由（2）得，∠1＋∠3＝∠2＋∠FGM ，∴∠1＋∠3＋∠5＝∠2＋∠FGM ＋∠MGN ，即∠1＋∠3＋∠5＝∠2＋∠4．【点拨】此题考查了平行线的性质，熟记两直线平行，内错角相等是解题的关键．举一反三：【变式】【发现】如图，已知AB ∥CD ，直线AB ，CD 被EF 所截．若EM ，FN 分别平分∠AEF 和∠DFE ，判断EM 与FN 之间的位置关系，并证明你的结论；【变式】如图，已知180AEF EFC ∠+∠=︒，∠M ＝∠N ，求证∠1＝∠2；【拓展】如图，AB ∥CD ，∠1＝∠2，求证∠M ＝∠N ．∵AB∥CD，∴∠1＝∠EPD．∵∠1＝∠2，【点拨】本题考查平行线的性质和判定，熟练掌握平行线的性质和判定是解题的关键．类型四、平行线几何模型➽➼综合模型➻➸求解✬✬证明4．根据下列叙述填依据．(1)已知如图1，AB CD ∥，求∠B +∠BFD +∠D 的度数．解：过点F 作FE AB∥所以∠B +∠BFE =180°（）因为AB CD ∥、FE AB ∥（已知）所以（）所以∠D +∠DFE =180°（）所以∠B +∠BFE +∠D =∠B +∠BFE +∠EFD +∠D =360°(2)根据以上解答进行探索．如图（2）（3）AB EF 、∠D 与∠B 、∠F 有何数量关系（请选其中一个简要证明）备用图：(3)如图（4）AB EF ，∠C =90°，∠α与∠β、∠γ有何数量关系（直接写出结果，不需要说明理由）【答案】(1)两直线平行，同旁内角互补；FE CD ∥，平行于同一直线的两直线平行；两直线平行，同旁内角互补；(2)见解析；(3)90αβγ∠+∠-∠=︒【分析】（1）过点F 作FE AB ∥，得到∠B +∠BFE =180°，再根据AB CD 、FE AB ∥得到FE CD ∥，∠D +∠DFE =180°，最后利用角度的和差即可得出答案；（2）类比问题（1）的解题方法即可得解；（3）类比问题（1）的解题方法即可得解．（1）解：过点F 作FE AB ∥，如图，∴∠B +∠BFE =180°（两直线平行，同旁内角相等），∵AB CD ∥、FE AB ∥（已知）∴FE CD ∥（平行于同一直线的两直线平行），∴∠D +∠DFE =180°（两直线平行，同旁内角互补），∴∠B +∠BFE +∠D =∠B +∠BFE +∠EFD +∠D =360°；故答案为：两直线平行，同旁内角互补；FE CD ∥，平行于同一直线的两直线平行；两直线平行，同旁内角互补；（2）解：选图（2），∠D 与∠B 、∠F 的数量关系为：∠BDF +∠B =∠F ；理由如下：过点D 作DC//AB ，∴∠B =∠BDC ，∵AB EF ∥，DC AB ∥，∴DC EF ∥，∴∠CDF =∠F ，∴∠BDF +∠BDC =∠F ，即∠BDF +∠B =∠F ；选图（3），∠D 与∠B 、∠F 的数量关系：∠BDF +∠B =∠F过点D 作DC AB ∥，∴∠B =∠BDC ，∵AB EF ∥，DC AB ∥，∴DC EF ∥，∴∠CDF =∠F ，∴∠BDF +∠BDC =∠F ，即∠BDF +∠B =∠F∠BDF +∠B =∠F ；（3）解：90αβγ∠+∠-∠=︒如图（4）所示，过点C 作MC AB ∥，过D 作DN EF ∥，∴BCM α∠=∠，NDE g Ð=Ð，∵AB CM ∥，EF AB ∥，DN EF∥∴AB EF CM DN ∥∥∥，∴CDN MCD Ð=Ð，∵90MCD BCM Ð+Ð=°，CDN NDE b Ð=Ð+Ð，∴90αβγ∠+∠-∠=︒．【点拨】本题考查根据平行线的性质探究角的关系和平行线公理推论的运用，熟练掌握平行线的性质和平行线公理推论的运用是解题的关键．举一反三：【变式】已知：AB ∥EF ，在平面内任意选取一点C ．利用平行线的性质，探究∠B 、∠F、∠C满足的数量关系．(1)将探究∠B、∠C、∠F之间的数量关系填写下表：(2)请选择其中一个图形进行说明理由．图（2）∠F-∠B=∠C图（3）∠B-∠F=∠C图（4）∠B+∠F+∠C=360°图（5）∠B-∠F=∠C图（6）∠F-∠B=∠C（2）解：图（1）∠C与∠B、∠F之间的数量关系是：∠B+∠F=∠C．理由：过点C作CG∥AB，∴∠BCG=∠B，∵AB∥EF，∴CG∥EF，∴∠GCF=∠F，∴∠BCG+∠GCF=∠B+∠F，∴∠B+∠F=∠BCF；图（2）∠C与∠B、∠F之间的数量关系是：∠F-∠B=∠C．理由：过点C作CG∥AB，∴∠BCG=∠B，∵AB∥EF，∴CG∥EF，∴∠GCF=∠F，∴∠GCF-∠BCG=∠F-∠B，∴∠F-∠B=∠BCF；图（3）∠C与∠B、∠F之间的数量关系是：∠B-∠F=∠C．理由：过点C作CG∥AB，∴∠BCG=∠B，∵AB∥EF，∴CG∥EF，∴∠GCF=∠F，∴∠BCG-∠GCF=∠B-∠F，∴∠B-∠F=∠BCF；图（4）∠C与∠B、∠F之间的数量关系是：∠B+∠F+∠C=360°．理由：过点C作CG∥AB，∴∠BCG+∠B=180°，∵AB∥EF，∴CG∥EF，∴∠GCF+∠F=180°，∴∠BCG+∠B+∠GCF+∠F=180°+180°，∴∠B+∠F+∠BCF=360°；图（5）∠C与∠B、∠F之间的数量关系是：∠B-∠F=∠C．理由：过点C作CG∥AB，∴∠BCG=∠B，∵AB∥EF，∴CG∥EF，∴∠GCF=∠F，∴∠BCG-∠GCF=∠B-∠F，∴∠B-∠F=∠BCF；图（6）∠C与∠B、∠F之间的数量关系是：∠F-∠B=∠C．理由：过点C作CG∥AB，∴∠BCG=∠B，∵AB∥EF，∴CG∥EF，∴∠GCF=∠F，∴∠GCF-∠BCG=∠F-∠B，∴∠F-∠B=∠BCF；【点拨】本题考查平行线的判定和性质，解题的关键是学会添加常用辅助线，构造平行线解决问题．。

人教版七年级数学下册练习第3讲平行线的构造模型及综合(含答案)

人教版七年级数学下册练习第3讲平行线的构造模型及综合命题：例：如图，有下列三个条件：①DE∥BC:②∠1=∠2；③∠B=∠C.(1)若从这三个条件中任选两个作为题设，另一个作为结论，组成一个命题，一共能组成几个命题，请你都写出来；(2)请你就其中的一个真命题给出推理过程。

平移：1.小明和小华在手工制作课上用铁丝制作楼梯模型如图1 所示,那么他们用的铁丝( )A、一样多B、小明的多C、小华的多D、不能确定2.如图，第1个图案是由黑白两种颜色的正六边形地面砖组成，第2个，第3个图案可以看作是第1个图案经过平移而得，那么第4个图案中有白色六边形地面砖______块，第n个图案中有白色地面砖__________ 块．3.如图，将Rt△ABC沿AB方向平移得到Rt△DEF，已知BE=6，EF=8，CG=3，求阴影部分的面积。

探究：夹在平行线间的折线问题，平行线的构造：“铅笔”型，“M”型，过拐点作已知直线的平行线。

例1．已知：如图，AC∥BD，折线AMB夹在两条平行线间．判断∠M，∠A，∠B的关系；(1)(2)例2.如图所示,已知AB∥CD,分别探讨下面的四个图形中∠APC与∠PAB﹑∠PCD的关系,请你从所得关系中任意选取一个加以说明。

(1) (2)练习：1.如图1所示，将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上，若∠1=35°，则∠2的度数为．2.如图2所示是汽车灯的剖面图,从位于O 点灯发出光照射到凹面镜上反射出的光线BA,CD 都是水平线,若∠ABO=α,∠DCO=60∘,则∠BOC 的度数为（）A.180∘−αB. 120∘−αC. 60°+αD. 60∘−α3.如图3，AB ∥CD ，∠B=115°，∠C=45°，则∠BEC 的度数为__________°．图1 图2 图3例3：如图3-1，已知：AB ∥CD ，点E ，F 分别在AB ，CD 上，且OE ⊥OF ．（1）求证：∠1＋∠2＝90°；（2）如图3-2，分别在OE ，CD 上取点G ，H ，使FO 平分∠CFG ，EO 平分∠AEH ，求证：FG ∥EH ．例4：如图4，a ∥b ，∠2＝∠3，∠1＝40°，则∠4的度数是度．EDCBA 4321ba图4H GABCDOE F 12图3-2图3-121F E ODC BA例5：如图，已知∠B=25°，∠BCD=45°，∠CDE=30°，∠E=10°，求证：AB∥EF:练习：1.如图AB∥CD，∠B=∠C，求证：BE∥CF。

七年级数学下册平行线四大模型专项训练(40道)(举一反三)(人教版)

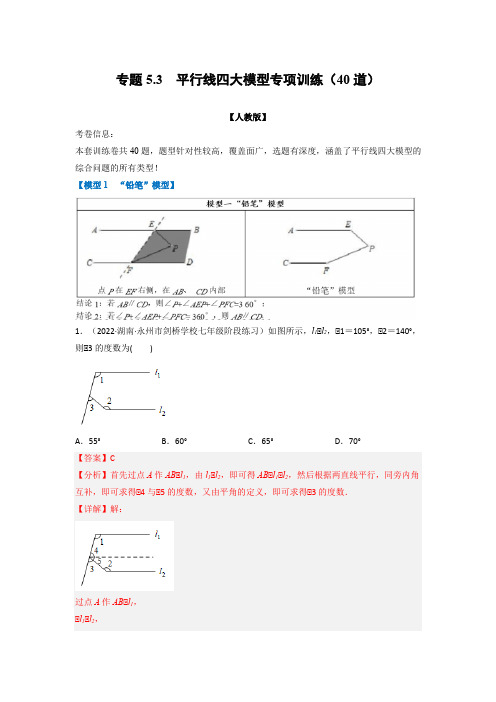
专题5.3 平行线四大模型专项训练（40道）【人教版】考卷信息：本套训练卷共40题，题型针对性较高，覆盖面广，选题有深度，涵盖了平行线四大模型的综合问题的所有类型！【模型1 “铅笔”模型】1．（2022·湖南·永州市剑桥学校七年级阶段练习）如图所示，l1∥l2，∥1＝105°，∥2＝140°，则∥3的度数为()A．55°B．60°C．65°D．70°【答案】C【分析】首先过点A作AB∥l1，由l1∥l2，即可得AB∥l1∥l2，然后根据两直线平行，同旁内角互补，即可求得∥4与∥5的度数，又由平角的定义，即可求得∥3的度数．【详解】解：过点A作AB∥l1，∥l1∥l2，∥AB∥l1∥l2，∥∥1+∥4=180°,∥2+∥5=180°，∥∥1=105°,∥2=140 °，∥∥4=75°,∥5=40°，∥∥4+∥5+∥3=180°，∥∥3=65°.故选：C.【点睛】本题考查的知识点是平行线的性质，解题的关键是熟练的掌握平行线的性质. 2．（2022·贵州六盘水·七年级期中）如图所示，若AB∥EF，用含α、β、γ的式子表示x，应为（）A．α+β+γB．β+γ−αC．180°−α−γ+βD．180°+α+β−γ【点睛】本题考查了平行线的性质的应用，主要考查了学生的推理能力．3．（2022·甘肃·北京师范大学庆阳实验学校七年级期中）如图，如果AB∥CD，那么∥B＋∥F ＋∥E＋∥D＝___°．【答案】540∥AB∥CD，EM∥CD，FN∥CD，F，∠E=80°，求∠BFD的度数.【答案】∠BFD=140°.【分析】先设∠ABE=2x，∠CDE=2y，由题意的∠ABF=∠FBE=x，∠EDF=∠CDF=y，题意得到x+y=140°；由侧M图ABFDC知，∠BFD=∠ABF+∠CDF=x+y=140°.【详解】设∠ABE=2x，∠CDE=2y，∵∠ABE与∠CDE的角平分线相交于点F，∴∠ABF=∠FBE=x，∠EDF=∠CDF=y，由笔尖图ABEDC知，∠ABE+∠E+∠CDE=360°，即2x+80°+2y=360°，x+y=140°，由侧M图ABFDC知，∠BFD=∠ABF+∠CDF=x+y=140°.【点睛】本题考查平行线的性质和角平分线，解题的关键是设∠ABE=2x，∠CDE=2y，并由题意得到x，y的关系式.5．（2022·全国·七年级专题练习）已知如图所示，AB//CD，∠ABE=3∠DCE，∠DCE=28°，求∠E的度数.【答案】56°.【分析】由平行线的性质可知∠ABF=∠DFE，由三角形邻补角可得∠E=∠ABE−∠DCE，带入题干信息即可得出答案.【详解】由平行线的性质可知∠ABF=∠DFE，由三角形邻补角以及鸟嘴图DCEFBA知∠E=∠ABE−∠DCE=3×28°−28°=56°.【点睛】本题考查平行线的性质，知道同位角相等时解题的关键.6．（2022·全国·七年级）(1)问题情景：如图1，AB//CD，∥P AB=130°，∥PCD=120°，求∥APC 的度数．小明想到一种方法，但是没有解答完：如图2，过P作PE//AB，∥∥APE+∥P AB=180°，∥∥APE=180°-∥P AB=180°-130°=50°∥AB//CD，∥PE//CD．……请你帮助小明完成剩余的解答．(2)问题迁移：请你依据小明的解题思路，解答下面的问题：如图3，AD//BC，当点P在A、B两点之间时，∥ADP=∥α，∥BCP=∥β，则∥CPD，∥α，∥β之间有何数量关系？请说明理由．∥AD∥BC∥∥CPD=∥DPE+∥CPE=∥α+∥β.【点睛】本题考查了平行线的性质和判定的应用，主要考察学生的推理能力，解决问题的关键是作辅助线构造内错角以及同旁内角.7．（2022·全国·七年级专题练习）如图1，四边形MNBD为一张长方形纸片．（1）如图2，将长方形纸片剪两刀，剪出三个角（∠BAE、∠AEC、∠ECD），则∠BAE+∠AEC+∠ECD=__________°．（2）如图3，将长方形纸片剪三刀，剪出四个角（∠BAE、∠AEF、∠EFC、∠FCD），则∠BAE+∠AEF+∠EFC+∠FCD=__________°．（3）如图4，将长方形纸片剪四刀，剪出五个角（∠BAE、∠AEF、∠EFG、∠FGC、∠GCD），则∠BAE+∠AEF+∠EFG+∠FGC+∠GCD=___________°．（4）根据前面探索出的规律，将本题按照上述剪法剪n刀，剪出(n+1)个角，那么这(n+1)个角的和是____________°．【答案】（1）360；（2）540；（3）720；（4）180n．【分析】（1）过点E作EH∥AB，再根据两直线平行，同旁内角互补即可得到三个角的和等于180°的2倍；（2）分别过E、F分别作AB的平行线，根据两直线平行，同旁内角互补即可得到四个角的和等于180°的三倍；（3）分别过E、F、G分别作AB的平行线，根据两直线平行，同旁内角互补即可得到四个角的和等于180°的三倍；（4）根据前三问个的剪法，剪n刀，剪出n+1个角，那么这n+1个角的和是180n度．【详解】（1）过E作EH∥AB（如图②）．∥原四边形是长方形，∥AB∥CD，又∥EH∥AB，∥CD∥EH（平行于同一条直线的两条直线互相平行）．∥EH∥AB，∥∥A+∥1=180°（两直线平行，同旁内角互补）．∥CD∥EH，∥∥2+∥C=180°（两直线平行，同旁内角互补）．又∥∥1+∥2=∥AEC，∥∥BAE+∥AEC+∥ECD=360°；（2）分别过E、F分别作AB的平行线，如图③所示，用上面的方法可得∥BAE+∥AEF+∥EFC+∥FCD=540°；（3）分别过E、F、G分别作AB的平行线，如图④所示，用上面的方法可得∥BAE+∥AEF+∥EFG+∥FGC+∥GCD=720°；（4）由此可得一般规律：剪n刀，剪出n+1个角，那么这n+1个角的和是180n度．故答案为：（1）360；（2）540；（3）720；（4）180n．【点睛】本题主要考查了多边形的内角和，作平行线并利用两直线平行，同旁内角互补是解本题的关键，总结规律求解是本题的难点．8．（2022·安徽合肥·七年级期末）问题情景：如图1，AB∥CD，∥P AB＝140°，∥PCD＝135°，求∥APC的度数．（1）丽丽同学看过图形后立即口答出：∥APC＝85°，请补全她的推理依据．如图2，过点P作PE∥AB，因为AB∥CD，所以PE∥CD．（）所以∥A+∥APE＝180°，∥C+∥CPE＝180°．（）因为∥P AB＝140°，∥PCD＝135°，所以∥APE＝40°，∥CPE＝45°，∥APC＝∥APE+∥CPE＝85°．问题迁移：（2）如图3，AD∥BC，当点P在A、B两点之间运动时，∥ADP＝∥α，∥BCP＝∥β，求∥CPD与∥α、∥β之间有什么数量关系？请说明理由．（3）在（2）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请直接写出∥CPD与∥α、∥β之间的数量关系．【答案】（1）平行于同一条直线的两条直线平行（或平行公理推论），两直线平行，同旁内角互补；（2）∠CPD=∠α+∠β，理由见解析；（3）∠CPD=∠β−∠α或∠CPD=∠α−∠β【分析】（1）根据平行线的判定与性质填写即可；（2）过P作PE∥AD交CD于E，推出AD∥PE∥BC，根据平行线的性质得出∥α=∥DPE，∥β=∥CPE，即可得出答案；（3）画出图形（分两种情况①点P在BA的延长线上，②点P在AB的延长线上），根据平行线的性质得出∥α=∥DPE，∥β=∥CPE，即可得出答案．【详解】解：（1）如图2，过点P作PE∥AB，因为AB∥CD，所以PE∥CD．（平行于同一条直线的两条直线平行）所以∥A+∥APE＝180°，∥C+∥CPE＝180°．（两直线平行同旁内角互补）因为∥P AB＝140°，∥PCD＝135°，所以∥APE＝40°，∥CPE＝45°，∥APC＝∥APE+∥CPE＝85°．故答案为：平行于同一条直线的两条直线平行；两直线平行，同旁内角互补；（2）∥CPD=∥α+∥β，理由如下：如图3所示，过P作PE∥AD交CD于E，∥AD∥BC，∥AD∥PE∥BC，∥∥α=∥DPE，∥β=∥CPE，∥∥CPD=∥DPE+∥CPE=∥α+∥β；（3）当P在BA延长线时，如图4所示：过P作PE∥AD交CD于E，同（2）可知：∥α=∥DPE，∥β=∥CPE，∥∥CPD=∥β-∥α；当P在AB延长线时，如图5所示：同（2）可知：∥α=∥DPE，∥β=∥CPE，∥∥CPD=∥α-∥β．综上所述，∥CPD与∥α、∥β之间的数量关系为：∥CPD=∥β-∥α或∥CPD=∥α-∥β．【点睛】本题考查了平行线的性质和判定定理，正确作出辅助线是解答此题的关键．【模型2 “猪蹄”模型】9．（2022·全国·七年级）如图所示，直角三角板的60°角压在一组平行线上，AB∥CD，∠ABE= 40°，则∠EDC=______度．【答案】20【分析】如图（见详解），过点E作EF∥AB，先证明AB∥EF∥CD，再由平行线的性质定理得到∠ABE=∠BEF=40°，∠EDC=∠DEF，结合已知条件∠BED=60°即可得到．【详解】解：由题意可得：∠BED=60°．如图，过点E作EF∥AB，又∥AB∥CD，∥AB∥EF∥CD，∥∠ABE=∠BEF=40°，∠EDC=∠DEF，∥∠BED=60°，∥∠DEF+∠BEF=60°，∥∠DEF=20°，即：∠EDC=20°．故答案为：20．【点睛】本题重点考查了平行线的性质定理的运用．从“基本图形”的角度看，本题可以看作是“M”型的简单运用．解法不唯一，也可延长B E交CD于点G，结合三角形的外角定理来解决；或连结BD，结合三角形内角和定理来解决．10．（2022·河南平顶山·八年级期末）如图：(1)如图1，AB∥CD，∠ABE=45°，∠CDE=21°，直接写出∠BED的度数．(2)如图2，AB∥CD，点E为直线AB，CD间的一点，BF平分∠ABE，DF平分∠CDE，写出∠BED 与∠F之间的关系并说明理由．(3)如图3，AB与CD相交于点G，点E为∠BGD内一点，BF平分∠ABE，DF平分∠CDE，若∠BGD= 60°，∠BFD=95°，直接写出∠BED的度数．【答案】(1)∥BED=66°；(2)∥BED=2∥F，见解析；(3)∥BED的度数为130°．【分析】（1）首先作EF∥AB，根据直线AB∥CD，可得EF∥CD，所以∥ABE=∥1=45°，∥CDE=∥2=21°，据此推得∥BED=∥1+∥2=66°；（2）首先作EG∥AB，延长DE交BF于点H，利用三角形的外角性质以及角平分线的定义即可得到∥BED=2∥F；（3）延长DF交AB于点H，延长GE到I，利用三角形的外角性质以及角平分线的定义即可得到∥BED的度数为130°．（1）解：（1）如图，作EF∥AB，，∥直线AB∥CD，∥EF∥CD，∥∥ABE=∥1=45°，∥CDE=∥2=21°，∥∥BED=∥1+∥2=66°；（2）解：∥BED=2∥F，理由是：过点E作EG∥AB，延长DE交BF于点H，∥AB∥CD，∥AB∥CD∥EG，∥∥5=∥1+∥2，∥6=∥3+∥4，又∥BF平分∥ABE，DF平分∥CDE，∥∥2=∥1，∥3=∥4，则∥5=2∥2，∥6=2∥3，∥∥BED=2(∥2+∥3)，又∥F+∥3=∥BHD，∥BHD+∥2=∥BED，∥∥3+∥2+∥F=∥BED，综上∥BED=∥F+12∥BED，即∥BED=2∥F；（3）解：延长DF交AB于点H，延长GE到I，∥∥BGD=60°，∥∥3=∥1+∥BGD=∥1+60°，∥BFD=∥2+∥3=∥2+∥1+60°=95°，∥∥2+∥1=35°，即2(∥2+∥1) =70°，∥BF平分∥ABE，DF平分∥CDE，∥∥ABE=2∥2，∥CDE=2∥1，∥∥BEI=∥ABE +∥BGE=2∥2+∥BGE，∥DEI=∥CDE+∥DGE=2∥1+∥DGE，∥∥BED=∥BEI+∥DEI=2(∥2+∥1)+( ∥BGE+∥DGE)=70°+60°=130°，∥∥BED的度数为130°．【点睛】本题考查了平行线的判定和性质，三角形的外角性质等知识，掌握平行线的判定和性质，正确添加辅助线是解题关键．11．（2022·江苏常州·七年级期中）问题情境：如图①，直线AB∥CD，点E，F分别在直线AB，CD上．(1)猜想：若∠1=130°，∠2=150°，试猜想∠P=______°；(2)探究：在图①中探究∠1，∠2，∠P之间的数量关系，并证明你的结论；(3)拓展：将图①变为图②，若∠1+∠2=325°，∠EPG=75°，求∠PGF的度数．∥AB∥CD，∥AB∥MN∥CD．∥∠1+∠EPN=180°，∠2+∠FPN=180°．∥∠1=130°，∠2=150°，∥∠1+∠2+∠EPN+∠FPN=360°∥∠EPN+FPN=360°−130°−150°=80°．∥∠P=∠EPN+∠FPN，∥∥P=80°．故答案为：80°；（2）解：∠P=360°−∠1−∠2，理由如下：如图过点P作MN∥AB，∥AB∥CD，∥AB∥MN∥CD．∥∠1+∠EPN=180°，∠2+∠FPN=180°．∥∠1+∠2+∠EPN+∠FPN=360°∥∠EPN+∠FPN=∠P，∠P=360°−∠1−∠2．（3）如图分别过点P、点G作MN∥AB、KR∥AB∥AB∥CD，∥AB∥MN∥KR∥CD．∥∠1+∠EPN=180°，∠NPG+∠PGR=180°，∠RGF+∠2=180°．∥∠1+∠EPN+∠NPG+∠PGR+RGF+∠2=540°∥∠EPG=∠EPN+∠NPG=75°，∠PGR+∠RGF=∠PGF，∠1+∠2=325°，∥∠PGF+∠1+∠2+∠EPG=540°∥∠PGF=540°−325°−75°=140°故答案为：140°．【点睛】本题考查了平行线的性质定理，准确的作出辅助线和正确的计算是解决本题的关键．12．（2022·山东聊城·七年级阶段练习）已知直线AB//CD，EF是截线，点M在直线AB、CD之间．(1)如图1，连接GM，HM．求证：∥M＝∥AGM＋∥CHM；(2)如图2，在∥GHC的角平分线上取两点M、Q，使得∥AGM＝∥HGQ．试判断∥M与∥GQH 之间的数量关系，并说明理由．解：如图：过点M作MN∥AB，∥MN∥AB∥CD，∥∠AGM=∠GMN，∠CHM=∠HMN，∥∠M=∠GMN+∠HMN，∥∠M=∠AGM+∠CHM．（2）解：∠GQH=180°−∠M，理由如下：如图：过点M作MN∥AB，由（1）知∠M=∠AGM+∠CHM，∥HM平分∠GHC，∥∠CHM=∠GHM，∥∥AGM＝∥HGQ，∥∠M=∠HGQ+∠GHM，∥∠HGQ+∠GHM+∠GQH=180°，∥∠GQH=180°−∠M．【点睛】本题考查了利用平行线的性质求角之间的数量关系，正确的作出辅助线是解决本题的关键，同时这也是比较常见的几何模型“猪蹄模型”的应用．13．（2022·广东韶关·七年级期中）如图1，点A、B分别在直线GH、MN上，∠GAC=∠NBD，∠C=∠D.（1）求证：GH//MN；（提示：可延长AC交MN于点P进行证明）（2）如图2，AE平分∠GAC，DE平分∠BDC，若∠AED=∠GAC，求∠GAC与∠ACD之间的数量关系；∠GAC，若（3）在（2）的条件下，如图3，BF平分∠DBM，点K在射线BF上，∠KAG=13∠AKB=∠ACD，直接写出∠GAC的度数．【答案】（1）见解析；（2）∠ACD =3∠GAC ，见解析；（3）(54019)°或(54023)°．【分析】（1）根据平行线的判定与性质求证即可；（2）根据三角形的内角和为180°和平角定义得到∠AQD =∠E +∠EAQ ，结合平行线的性质得到∠BDQ =∠E +∠EAQ ，再根据角平分线的定义证得∠CDB =2∠E +∠GAC ，结合已知即可得出结论；（3）分当K 在直线GH 下方和当K 在直线GH 上方两种情况，根据平行线性质、三角形外角性质、角平分线定义求解即可．【详解】解：（1）如图1，延长AC 交MN 于点P ，∥∠ACD =∠C ，∥AP//BD ，∥∠NBD =∠NPA ，∥∠GAC =∠NBD ，∥∠GAC =∠NPA ，∥GH//MN ；（2）延长AC 交MN 于点P ，交DE 于点Q ，∥∠E +∠EAQ +∠AQE =180°，∠AQE +∠AQD =180°，∥∠AQD =∠E +∠EAQ ，∥AP//BD ，∥∠AQD =∠BDQ ，∥∠BDQ =∠E +∠EAQ ，∥AE 平分∠GAC ，DE 平分∠BDC ，∥∠GAC =2∠EAQ ，∠CDB =2∠BDQ ，∥∠CDB =2∠E +∠GAC ，∥∠AED =∠GAC ，∠ACD =∠CDB ，∥GH//MN，540°540°14．（2022·全国·九年级专题练习）如图所示，已知AB//CD，BE平分∠ABC，DE平分∠ADC，(∠A+∠C)求证：∠E=12∥AB∥CD，（1）如图1，E为AB，CD之间一点，连接BE，DE，得到∥BED．求证：∥BED＝∥B+∥D；（2）如图，连接AD，BC，BF平分∥ABC，DF平分∥ADC，且BF，DF所在的直线交于点F．①如图2，当点B在点A的左侧时，若∥ABC＝50°，∥ADC＝60°，求∥BFD的度数．②如图3，当点B在点A的右侧时，设∥ABC＝α，∥ADC＝β，请你求出∥BFD的度数．（用含有α，β的式子表示）【答案】（1）见解析；（2）55°；（3）180°−12α+12β【分析】（1）根据平行线的判定定理与性质定理解答即可；（2）①如图2，过点F作FE//AB，当点B在点A的左侧时，根据∠ABC=50°，∠ADC=60°，根据平行线的性质及角平分线的定义即可求∠BFD的度数；②如图3，过点F作EF//AB，当点B在点A的右侧时，∠ABC=α，∠ADC=β，根据平行线的性质及角平分线的定义即可求出∠BFD的度数．【详解】解：（1）如图1，过点E作EF//AB，则有∠BEF=∠B，∵AB//CD，∴EF//CD，∴∠FED=∠D，∴∠BED=∠BEF+∠FED=∠B+∠D；（2）①如图2，过点F作FE//AB，有∠BFE=∠FBA．∵AB//CD，∴EF//CD．∴∠EFD=∠FDC．∴∠BFE+∠EFD=∠FBA+∠FDC．即∠BFD=∠FBA+∠FDC，有∠BFE+∠FBA=180°．(1)判定∥BAE，∥CDE与∥AED之间的数量关系，并证明你的结论；(2)如图2，若∥BAE，∥CDE的角平分线交于点F，直接写出∥AFD与∥AED之间的数量关系；(3)将图2中的射线DC沿DE翻折交AF于点G得图3，若∥AGD的余角等于2∥E的补角，求∥BAE的大小．【答案】(1)∠BAE+∠CDE=∠AED；【点睛】本题考查了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．17．（2022·广东·高州市第一中学附属实验中学七年级阶段练习）如图1，已知AB∥CD，∥B ＝30°，∥D＝120°；(1)若∥E＝60°，则∥F＝；(2)请探索∥E与∥F之间满足的数量关系？说明理由；(3)如图2，已知EP平分∥BEF，FG平分∥EFD，反向延长FG交EP于点P，求∥P的度数．【答案】(1)90°(2)∠F=∠E+30°，理由见解析(3)15°【分析】（1）如图1，分别过点E，F作EM//AB，FN//AB，根据平行线的性质得到∠B=∠BEM=30°，∠MEF=∠EFN，∠D+∠DFN=180°，代入数据即可得到结论；（2）如图1，根据平行线的性质得到∠B=∠BEM=30°，∠MEF=∠EFN，由AB//CD，AB//FN，得到CD//FN，根据平行线的性质得到∠D+∠DFN=180°，于是得到结论；（3）如图2，过点F作FH//EP，设∠BEF=2x°，则∠EFD=(2x+30)°，根据角平分线的定义得到∠PEF=12∠BEF=x°，∠EFG=12∠EFD=(x+15)°，根据平行线的性质得到∠PEF=∠EFH=x°，∠P=∠HFG，于是得到结论．（1）解：如图1，分别过点E，F作EM//AB，FN//AB，∴EM//AB//FN，∴∠B=∠BEM=30°，∠MEF=∠EFN，又∵AB//CD，AB//FN，∴CD//FN，∴∠D+∠DFN=180°，又∵∠D=120°，∴∠DFN=60°，∴∠BEF=∠MEF+30°，∠EFD=∠EFN+60°，∴∠EFD=∠MEF+60°∴∠EFD=∠BEF+30°=90°；故答案为：90°；（2）解：如图1，分别过点E，F作EM//AB，FN//AB，∴EM//AB//FN，∴∠B=∠BEM=30°，∠MEF=∠EFN，又∵AB//CD，AB//FN，∴CD//FN，∴∠D+∠DFN=180°，又∵∠D=120°，∴∠DFN=60°，∴∠BEF=∠MEF+30°，∠EFD=∠EFN+60°，∴∠EFD=∠MEF+60°，∴∠EFD=∠BEF+30°；（3）解：如图2，过点F作FH//EP，由（2）知，∠EFD=∠BEF+30°，设∠BEF=2x°，则∠EFD=(2x+30)°，∵EP平分∠BEF，GF平分∠EFD，∴∠PEF=12∠BEF=x°，∠EFG=12∠EFD=(x+15)°，∵FH//EP，∴∠PEF=∠EFH=x°，∠P=∠HFG，∵∠HFG=∠EFG−∠EFH=15°，∴∠P=15°．【点睛】本题考查了平行线的性质，角平分线的定义，熟练掌握平行线的性质定理是解题的关键．18．（2022·河南·商丘市第十六中学七年级期中）已知AB∥CD，线段EF分别与AB，CD相交于点E，F．（1）请在横线上填上合适的内容，完成下面的解答：如图1，当点P在线段EF上时，已知∥A＝35°，∥C＝62°，求∥APC的度数；解：过点P作直线PH∥AB，所以∥A＝∥APH，依据是；因为AB∥CD，PH∥AB，所以PH∥CD，依据是；所以∥C＝（），所以∥APC＝（）+（）＝∥A+∥C＝97°．（2）当点P，Q在线段EF上移动时（不包括E，F两点）：①如图2，∥APQ+∥PQC＝∥A+∥C+180°成立吗？请说明理由；②如图3，∥APM＝2∥MPQ，∥CQM＝2∥MQP，∥M+∥MPQ+∥PQM＝180°，请直接写出∥M，∥A与∥C的数量关系．【答案】（1）两直线平行，内错角相等；平行于同一条直线的两条直线平行；∥CPH；∥APH，∥CPH；（2）①∥APQ+∥PQC＝∥A+∥C+180°成立，理由见解答过程；②3∥PMQ+∥A+∥C＝360°．【分析】（1）根据平行线的判定与性质即可完成填空；（2）结合（1）的辅助线方法即可完成证明；（3）结合（1）（2）的方法，根据∥APM＝2∥MPQ，∥CQM＝2∥MQP，∥PMQ+∥MPQ+∥PQM ＝180°，即可证明∥PMQ，∥A与∥C的数量关系．【详解】解：过点P作直线PH∥AB，所以∥A＝∥APH，依据是两直线平行，内错角相等；因为AB∥CD，PH∥AB，所以PH∥CD，依据是平行于同一条直线的两条直线平行；所以∥C＝（∥CPH），所以∥APC＝（∥APH）+（∥CPH）＝∥A+∥C＝97°．故答案为：两直线平行，内错角相等；平行于同一条直线的两条直线平行；∥CPH；∥APH，∥CPH；（2）①如图2，∥APQ+∥PQC＝∥A+∥C+180°成立，理由如下：过点P作直线PH∥AB，QG∥AB，∥AB∥CD，∥AB∥CD∥PH∥QG，∥∥A＝∥APH，∥C＝∥CQG，∥HPQ+∥GQP＝180°，∥∥APQ+∥PQC＝∥APH+∥HPQ+∥GQP+∥CQG＝∥A+∥C+180°．∥∥APQ+∥PQC＝∥A+∥C+180°成立；②如图3，过点P作直线PH∥AB，QG∥AB，MN∥AB，∥AB∥CD，∥AB∥CD∥PH∥QG∥MN，∥∥A＝∥APH，∥C＝∥CQG，∥HPQ+∥GQP＝180°，∥HPM＝∥PMN，∥GQM＝∥QMN，∥∥PMQ＝∥HPM+∥GQM，∥∥APM＝2∥MPQ，∥CQM＝2∥MQP，∥PMQ+∥MPQ+∥PQM＝180°，∥∥APM+∥CQM＝∥A+∥C+∥PMQ＝2∥MPQ+2∥MQP＝2（180°﹣∥PMQ），∥3∥PMQ+∥A+∥C＝360°．【点睛】考核知识点：平行线的判定和性质．熟练运用平行线性质和判定，添加适当辅助线是关键．19．（2022·湖北武汉·七年级期末）如图1，点A在直线MN上，点B在直线ST上，点C在MN，ST之间，且满足∠MAC+∠ACB+∠SBC=360°．（1）证明：MN//ST；（2）如图2，若∠ACB=60°，AD//CB，点E在线段BC上，连接AE，且∠DAE=2∠CBT，试判断∠CAE与∠CAN的数量关系，并说明理由；（3）如图3，若∠ACB=180°（n为大于等于2的整数），点E在线段BC上，连接AE，若∠MAE=nn∠CBT，则∠CAE:∠CAN=______．【答案】（1）见解析；（2）见解析；（3）n-1【分析】（1）连接AB，根据已知证明∥MAB+∥SBA=180°，即可得证；（2）作CF∥ST，设∥CBT=α，表示出∥CAN，∥ACF，∥BCF，根据AD∥BC，得到∥DAC=120°，求出∥CAE即可得到结论；（3）作CF∥ST，设∥CBT=β，得到∥CBT=∥BCF=β，分别表示出∥CAN和∥CAE，即可得到比值．【详解】解：（1）如图，连接AB，，∵∠MAC+∠ACB+∠SBC=360°，∠ACB+∠ABC+∠BAC=180°，∴∠MAB+∠SBA=180°，∴MN//ST（2）∠CAE=2∠CAN，理由：作CF//ST，则MN//CF//ST,如图，设∠CBT=α，则∠DAE=2α．∠BCF=∠CBT=α，∠CAN=∠ACF=60°−α，∵AD//BC，∠DAC=180°−∠ACB=120°，∴∠CAE=120°−∠DAE=120°−2α=2(60°−α)=2∠CAN．即∠CAE=2∠CAN．（3）作CF//ST，则MN//CF//ST,如图，设∠CBT=β，则∠MAE=nβ．∵CF//ST，∴∠CBT=∠BCF=β，∠ACF=∠CAN=180°n −β=180°−nβn，∠CAE=180°−∠MAE−∠CAN=180°−nβ−180°n +β=n−1n(180°−nβ)，∠CAE:∠CAN=n−1n :1n=n−1，故答案为n−1．【点睛】本题主要考查平行线的性质和判定，解题关键是角度的灵活转换，构建数量关系式．20．（2022·重庆江北·七年级期末）如图1，AB//CD，点E、F分别在AB、CD上，点O在直线AB、CD之间，且∠EOF=100°．（1）求∠BEO+∠OFD的值；（2）如图2，直线MN分别交∠BEO、∠OFC的角平分线于点M、N，直接写出∠EMN−∠FNM 的值；（3）如图3，EG在∠AEO内，∠AEG=m∠OEG；FH在∠DFO内，∠DFH=m∠OFH，直线MN 分别交EG、FH分别于点M、N，且∠FMN−∠ENM=50°，直接写出m的值．∥AB∥CD，∥EM平分∥BEO，FN平分∥CFO，设∠BEM=∠OEM=x，∠CFN=∠OFN=y，∥∠BEO+∠DFO=260°∥∠BEO+∠DFO=2x+180°−2y=260°，∥x-y=40°，∥MK∥AB，NH∥CD，AB∥CD，∥AB∥MK∥NH∥CD，∥∠EMK=∠BEM=x，∠HNF=∠CFN=y，∠KMN=∠HNM，∥∠EMN+∠FNM=∠EMK+∠KMN−（∠HNM+∠HNF）=x+∠KMN−∠HNM−y=x-y=40°，故∠EMN−∠FNM的值为40°；（3）如图，设直线FK与EG交于点H，FK与AB交于点K，∥AB∥CD，∥∠AKF=∠KFD，∥∠AKF=∠EHK+∠HEK=∠EHK+∠AEG，∥∠KFD=∠EHK+∠AEG，∥∠EHK=∠NMF−∠ENM=50°，∥∠KFD=50°+∠AEG，即∠KFD−∠AEG=50°，∥∠AEG=n∠OEG，FK在∥DFO内，∠DFK=n∠OFK．∥∠CFO=180°−∠DFK−∠OFK=180°−∠KFD−1n∠KFD，∠AEO=∠AEG+∠OEG=∠AEG+1n∠AEG，∥∠BEO+∠DFO=260°，∥∠AEO+∠CFO=100°，∥∠AEG+1n ∠AEG+180°−∠KFD−1n∠KFD=100°，即(1+1n)(∠KFD−∠AEG)＝80°，∥(1+1n)×50°＝80°，解得n=53．经检验，符合题意，故答案为：53．【点睛】本题主要考查平行线的性质，角平分线的定义，灵活运用平行线的性质是解题的关键．21．（2022·黑龙江哈尔滨·七年级期末）已知，AB∥CD，点E在CD上，点G，F在AB上，点H在AB，CD之间，连接FE，EH，HG，∥AGH＝∥FED，FE∥HE，垂足为E．（1）如图1，求证：HG∥HE；（2）如图2，GM平分∥HGB，EM平分∥HED，GM，EM交于点M，求证：∥GHE＝2∥GME；（3）如图3，在（2）的条件下，FK平分∥AFE交CD于点K，若∥KFE：∥MGH＝13：5，求∥HED的度数．【答案】（1）见解析；（2）见解析；（3）40°【分析】（1）根据平行线的性质和判定解答即可；（2）过点H作HP∥AB，根据平行线的性质解答即可；（3）过点H作HP∥AB，根据平行线的性质解答即可．【详解】证明：（1）∥AB∥CD，∥∥AFE＝∥FED，∥∥AGH＝∥FED，∥∥AFE＝∥AGH，∥EF∥GH，∥∥FEH+∥H＝180°，∥FE∥HE，∥∥FEH＝90°，∥∥H＝180°﹣∥FEH＝90°，∥HG∥HE；（2）过点M作MQ∥AB，∥AB∥CD，∥MQ∥CD，过点H作HP∥AB，∥AB∥CD，∥HP∥CD，∥GM平分∥HGB，∥∥BGM＝∥HGM＝1∥BGH，2∥EM平分∥HED，∥∥HEM＝∥DEM＝1∥HED，2∥MQ∥AB，∥∥BGM＝∥GMQ，∥MQ∥CD，∥∥QME＝∥MED，∥∥GME＝∥GMQ+∥QME＝∥BGM+∥MED，∥HP∥AB，∥∥BGH＝∥GHP＝2∥BGM，∥HP∥CD，∥∥PHE＝∥HED＝2∥MED，∥∥GHE＝∥GHP+∥PHE＝2∥BGM+2∥MED＝2（∥BGM+∥MED），∥∥GHE＝∥2GME；（3）过点M作MQ∥AB，过点H作HP∥AB，由∥KFE：∥MGH＝13：5，设∥KFE＝13x，∥MGH＝5x，由（2）可知：∥BGH＝2∥MGH＝10x，∥∥AFE+∥BFE＝180°，∥∥AFE＝180°﹣10x，∥FK平分∥AFE，∥AFE，∥∥AFK＝∥KFE＝12(180°−10x)=13x，即12解得：x＝5°，∥∥BGH＝10x＝50°，∥HP∥AB，HP∥CD，∥∥BGH＝∥GHP＝50°，∥PHE＝∥HED，∥∥GHE＝90°，∥∥PHE＝∥GHE﹣∥GHP＝90°﹣50°＝40°，∥∥HED＝40°．【点睛】本题考查了平行线的判定与性质，熟练掌握平行线的判定与性质定理以及灵活构造平行线是解题的关键．22.（2022·广西柳州·七年级期中）已知直线a∥b，直线EF分别与直线a，b相交于点E，F，点A，B分别在直线a，b上，且在直线EF的左侧，点P是直线EF上一动点（不与点E，F 重合），设∥P AE＝∥1，∥APB＝∥2，∥PBF＝∥3．(1)如图1，当点P在线段EF上运动时，试说明∥1＋∥3＝∥2；(2)当点P在线段EF外运动时有两种情况．①如图2写出∥1，∥2，∥3之间的关系并给出证明；②如图3所示，猜想∥1，∥2，∥3之间的关系（不要求证明）．【答案】(1)证明见详解(2)①∠3=∠1+∠2；证明见详解；②∠1=∠2+∠3；证明见详解【分析】（1）如图4过点P作PC∥a，利用平行线的传递性可知PC∥a∥b，根据平行线的性质可知∠1=∠APC，∠3=∠BPC，根据等量代换就可以得出∠2=∠1+∠3；（2）①如图5过点P作PC∥a，利用平行线的传递性可知PC∥a∥b，根据平行线的性质可知∠3=∠BPC，∠1=∠APC，根据等量代换就可以得出∠3=∠1+∠2；②如图6过点P作PC∥a，利用平行线的传递性可知PC∥a∥b，根据平行线的性质可知∠1=∠APC，∠3=∠BPC，根据等量代换就可以得出∠1=∠2+∠3．（1）解：如图4所示：过点P作PC∥a，∥a∥b∥PC∥a∥b∥∠1=∠APC，∠3=∠BPC，∥∠2=∠APC+∠BPC，∥∠2=∠1+∠3；（2）解：①如图5过点P作PC∥a，∥a∥b∥PC∥a∥b∥∠3=∠BPC，∠1=∠APC，∥∠BPC=∠2+∠APC，∥∠3=∠1+∠2；②如图6过点P作PC∥a，∥a∥b∥PC∥a∥b∥∠1=∠APC，∠3=∠BPC，∥∠APC=∠2+∠BPC，∥∠1=∠2+∠3．【点睛】本题利用“猪蹄模型”及其变式考查了利用平行线的性质求角之间的数量关系，准确的作出辅助线和找到对应的内错角是解决本题的关键．【模型3 “臭脚”模型】23．（2022·全国·八年级课时练习）（1）已知：如图（a），直线DE∥AB．求证：∠ABC+∠CDE=∠BCD；（2）如图（b），如果点C在AB与ED之外，其他条件不变，那么会有什么结果？你还能就本题作出什么新的猜想？【答案】（1）见解析；（2）当点C在AB与ED之外时，∠ABC−∠CDE=∠BCD，见解析【分析】（1）由题意首先过点C作CF∥AB，由直线AB∥ED，可得AB∥CF∥DE，然后由两直线平行，内错角相等，即可证得∥ABC+∥CDE=∥BCD；（2）根据题意首先由两直线平行，内错角相等，可得∥ABC=∥BFD，然后根据三角形外角的性质即可证得∥ABC-∥CDE=∥BCD．【详解】解：（1）证明：过点C作CF∥AB，∥AB∥ED，∥AB∥ED∥CF，∥∥BCF=∥ABC，∥DCF=∥EDC，∥∥ABC+∥CDE=∥BCD；（2）结论：∥ABC-∥CDE=∥BCD，证明：如图：∥AB∥ED，∥∥ABC=∥BFD，在∥DFC中，∥BFD=∥BCD+∥CDE，∥∥ABC=∥BCD+∥CDE，∥∥ABC-∥CDE=∥BCD．若点C在直线AB与DE之间，猜想∠ABC+∠BCD+∠CDE=360°,∥AB∥ED∥CF，∥∠ABC+∠BCF=180°,∠CDE+∠DCF=180°,∥∠ABC+∠BCD+∠CDE=∠ABC+∠BCF+∠DCF+∠CDE=360°.【点睛】本题考查的是平行线的性质及三角形外角的性质，熟练掌握平行线的性质是解答本题的关键，注意掌握辅助线的作法．24．（2022·全国·七年级）已知，AE//BD，∠A=∠D．（1）如图1，求证：AB//CD；（2）如图2，作∠BAE的平分线交CD于点F，点G为AB上一点，连接FG，若∠CFG的平分线交线段AG于点H，连接AC，若∠ACE=∠BAC+∠BGM，过点H作HM⊥FH交FG的延长线于点M，且3∠E−5∠AFH=18°，求∠EAF+∠GMH的度数．【答案】（1）见解析；（2）72°【分析】（1）根据平行线的性质得出∠A+∠B=180°，再根据等量代换可得∠B+∠D=180°，最后根据平行线的判定即可得证；（2）过点E作EP//CD，延长DC至Q，过点M作MN//AB，根据平行线的性质及等量代换可得出∠ECQ=∠BGM=∠DFG，再根据平角的含义得出∠ECF=∠CFG，然后根据平行线的性质及角平分线的定义可推出∠BHF=∠CFH,∠CFA=∠FAB；设∠FAB=α,∠CFH=β，根据角的和差可得出∠AEC=2∠AFH，结合已知条件3∠AEC−5∠AFH=180°可求得∠AFH=18°，最后根据垂线的含义及平行线的性质，即可得出答案．【详解】（1）证明：∵AE//BD∴∠A+∠B=180°∵∠A=∠D∴∠B+∠D=180°∴AB//CD；（2）过点E作EP//CD，延长DC至Q，过点M作MN//AB∵AB//CD∴∠QCA=∠CAB，∠BGM=∠DFG，∠CFH=∠BHF，∠CFA=FAG∵∠ACE=∠BAC+∠BGM∴∠ECQ+∠QCA=∠BAC+∠BGM∴∠ECQ=∠BGM=∠DFG∵∠ECQ+ECD=180°,∠DFG+CFG=180°∴∠ECF=∠CFG∵AB//CD∴AB//EP∴∠PEA=∠EAB,∠PEC=∠ECF∵∠AEC=∠PEC−∠PEA∴∠AEC=∠ECF−∠EAB∴∠ECF=∠AEC+∠EAB∵AF平分∠BAE∴∠EAF=∠FAB=12∠EAB∵FH平分∠CFG∴∠CFH=∠HFG=12∠CFG∵CD//AB∴∠BHF=∠CFH,∠CFA=∠FAB设∠FAB=α,∠CFH=β∵∠AFH=∠CFH−∠CFA=∠CFH−∠FAB∴∠AFH=β−α，∠BHF=∠CFH=β∴∠ECF+2∠AFH=∠AEC+∠EAB+2∠AFH=∠AEC+2β∴∠ECF+2∠AFH=∠E+2∠BHF∴∠AEC=2∠AFH∵3∠AEC−5∠AFH=180°∴∠AFH=18°∵FH⊥HM∴∠FHM=90°∴∠GHM=90°−β∵∠CFM+∠NMF=180°∴∠HMB=∠HMN=90°−β∵∠EAF=∠FAB∴∠EAF=∠CFA=∠CFH−∠AFH=β−18°∴∠EAF+∠GMH=β−18°+90°−β=72°∴∠EAF+∠GMH=72°．【点睛】本题考查了平行线的判定及性质，角平分线的定义，能灵活根据平行线的性质和判定进行推理是解此题的关键．25．（2022·广东·东莞市光明中学七年级期中）（1）如图（1）AB∥CD，猜想∥BPD与∥B、∥D 的关系，说出理由．（2）观察图（2），已知AB∥CD，猜想图中的∥BPD与∥B、∥D的关系，并说明理由．（3）观察图（3）和（4），已知AB∥CD，猜想图中的∥BPD与∥B、∥D的关系，不需要说明理由．【答案】（1）∥B+∥BPD+∥D=360°，理由见解析；（2）∥BPD=∥B+∥D，理由见解析；（3）∥BPD=∥D-∥B或∥BPD=∥B-∥D，理由见解析【分析】（1）过点P作EF∥AB，根据两直线平行，同旁内角互补即可求解；（2）首先过点P作PE∥AB，由AB∥CD，可得PE∥AB∥CD，根据两直线平行，内错角相等，即可得∥1=∥B，∥2=∥D，则可求得∥BPD=∥B+∥D．（3）由AB∥CD，根据两直线平行，内错角相等与三角形外角的性质，即可求得∥BPD与∥B、∥D的关系．【详解】解：（1）如图（1）过点P作EF∥AB，∥∥B+∥BPE=180°，∥AB∥CD，EF∥AB，∥EF∥CD，∥∥EPD+∥D=180°，∥∥B+∥BPE+∥EPD+∥D=360°，∥∥B+∥BPD+∥D=360°．（2）∥BPD=∥B+∥D．理由：如图2，过点P作PE∥AB，∥AB∥CD，∥PE∥AB∥CD，∥∥1=∥B，∥2=∥D，∥∥BPD=∥1+∥2=∥B+∥D．（3）如图（3），∥BPD=∥D-∥B．理由：∥AB∥CD，∥∥1=∥D，∥∥1=∥B+∥BPD，∥∥D=∥B+∥BPD，即∥BPD=∥D-∥B；如图（4），∥BPD=∥B-∥D．理由：∥AB∥CD，∥∥1=∥B，∥∥1=∥D+∥BPD，∥∥B=∥D+∥BPD，即∥BPD=∥B-∥D．【点睛】此题考查了平行线的性质与三角形外角的性质．此题难度不大，解题的关键是注意掌握平行线的性质，注意辅助线的作法．26．（2022·浙江台州·七年级期末）如图，已知AD⊥AB于点A，AE∥CD交BC于点E，且EF⊥AB 于点F．求证：∠C=∠1+∠2．证明：∥AD⊥AB于点A，EF⊥AB于点F，（已知）∥∠DAB=∠EFB=90°．（垂直的定义）∥AD∥EF，（）∥__________=∠1（）∥AE∥CD，（已知）∥∠C=________．（两直线平行，同位角相等）∥∠AEB=∠AEF+∠2，∥∠C=∠1+∠2．（等量代换）【答案】见解析【分析】首先根据同位角相等，两直线平行AD//EF，再根两直线平行，内错角相等得到∠AEF=∠1．最后根据两直线平行，同位角相等得到∠C=∠AEB，再进行等量代换即可．【详解】证明：∥AD⊥AB于点A，EF⊥AB于点F，∥∠DAB=∠EFB=90°．∥AD//EF，（同位角相等，两直线平行）∥∠AEF=∠1．（两直线平行，内错角相等）∥AE//CD，∥∠C=∠AEB．∥∠AEB=∠AEF+∠2，∥∠C=∠1+∠2．【点睛】本题考查了平行线的判定和性质的综合应用，掌握相关知识是解题的关键．27．（2022·广东珠海·七年级期中）已知AM//CN，点B为平面内一点，AB⊥BC于B．（1）如图1，点B在两条平行线外，则∠A与∠C之间的数量关系为______；（2）点B在两条平行线之间，过点B作BD⊥AM于点D．①如图2，说明∠ABD=∠C成立的理由；②如图3，BF平分∠DBC交DM于点F,BE平分∠ABD交DM于点E．若∠FCB+∠NCF= 180°,∠BFC=3∠DBE，求∠EBC的度数．【答案】（1）∥A+∥C=90°；（2）①见解析；②105°【分析】（1）根据平行线的性质以及直角三角形的性质进行证明即可；（2）①过点B作BG∥DM，根据平行线找角的联系即可求解；②先过点B作BG∥DM，根据角平分线的定义，得出∥ABF=∥GBF，再设∥DBE=α，∥ABF=β，根据∥CBF+∥BFC+∥BCF=180°，可得2α+β+3α+3α+β=180°，根据AB∥BC，可得β+β+2α=90°，最后解方程组即可得到∥ABE=15°，进而得出∥EBC=∥ABE+∥ABC=15°+90°=105°．【详解】解：（1）如图1，AM与BC的交点记作点O，∥AM∥CN，∥∥C=∥AOB，∥AB∥BC，∥∥A+∥AOB=90°，（2）①如图2，过点B作BG∥DM，∥BD∥AM，∥DB∥BG，∥∥DBG=90°，∥∥ABD+∥ABG=90°，∥AB∥BC，∥∥CBG+∥ABG=90°，∥∥ABD=∥CBG，∥AM∥CN，BG∥DM，∴BG//CN,∥∥C=∥CBG，∥ABD=∥C；②如图3，过点B作BG∥DM，∥BF平分∥DBC，BE平分∥ABD，∥∥DBF=∥CBF，∥DBE=∥ABE，由（2）知∥ABD=∥CBG，设∥DBE=α，∥ABF=β，则∥ABE=α，∥ABD=2α=∥CBG，∥GBF=∥AFB=β，∥BFC=3∥DBE=3α，∥∥AFC=3α+β，∥∥AFC+∥NCF=180°，∥FCB+∥NCF=180°，∥∥FCB=∥AFC=3α+β，∥BCF中，由∥CBF+∥BFC+∥BCF=180°得：2α+β+3α+3α+β=180°，∥AB∥BC，∥β+β+2α=90°，∥α=15°，∥∥ABE=15°，∥∥EBC=∥ABE+∥ABC=15°+90°=105°．【点睛】本题主要考查了平行线的性质的运用，解决问题的关键是作平行线构造内错角，运用等角的余角（补角）相等进行推导．余角和补角计算的应用，常常与等式的性质、等量代换相关联．解题时注意方程思想的运用．28．（2022·湖南·新田县云梯学校七年级阶段练习）①如图1，AB∥CD，则∠A+∠E+∠C= 360°；②如图2，AB∥CD，则∠P=∠A−∠C；③如图3，AB∥CD，则∠E=∠A+∠1；④如图4，直线AB∥CD∥EF，点O在直线EF上，则∠α−∠β+∠γ=180°．以上结论正确的个数是（）A．1个B．2个C．3个D．4个【答案】B【分析】①过点E作直线EF∥AB，由平行线的性质：两直线平行，同旁内角互补，即可得出结论；②如图2，先根据三角形外角的性质得出∥1＝∥C+∥P，再根据两直线平行，内错角相等即可作出判断；③如图3，过点E作直线EF∥AB，由平行线的性质可得出∥A+∥AEC﹣∥1＝180°，即得∥AEC＝180°+∥1﹣∥A；④如图4，根据平行线的性质得出∥α＝∥BOF，∥γ+∥COF＝180°，再利用角的关系解答即可．【详解】解：①如图1，过点E作直线EF∥AB，∥AB∥CD，∥AB∥CD∥EF，∥∥A+∥1＝180°，∥2+∥C＝180°，∥∥A+∥B+∥AEC＝360°，故①错误；②如图2，∥∥1是∥CEP的外角，∥∥1＝∥C+∥P，∥AB∥CD，∥∥A＝∥1，即∥P＝∥A﹣∥C，故②正确；③如图3，过点E作直线EF∥AB，∥AB∥CD，∥AB∥CD∥EF，∥∥A+∥3＝180°，∥1＝∥2，∥∥A+∥AEC﹣∥1＝180°，即∥AEC＝180°+∥1﹣∥A，故③错误；④如图4，∥AB∥EF，∥∥α＝∥BOF，∥CD∥EF，∥∥γ+∥COF＝180°，∥∥BOF＝∥COF+∥β，∥∥COF＝∥α﹣∥β，∥∥γ+∥α﹣∥β＝180°，故④正确；综上结论正确的个数为2，故选：B．【点睛】本题考查的是平行线的性质及三角形外角的性质，熟练掌握平行线的性质，根据题意作出辅助线是解答此题的关键．【模型4 “铅笔”模型】29．（2022·福建·浦城县教师进修学校八年级期中）如图，直线MA∥NB，∥A=70°，∥B=40°，则∥P=___________度．【答案】30【答案】180°【分析】延长EA交CD于点F，则有∥2+∥EFC=∥3，然后根据AB//CD可得∥1=∥EFD，最后根据领补角及等量代换可求解．【详解】解：延长EA交CD于点F，如图所示：∵AB//CD，∴∥1=∥EFD，∵∥2+∥EFC=∥3，∴∠EFC=∠3−∠2，∵∠EFC+∠EFD=180°，∴∠1+∠3−∠2=180°；故答案为180°．【点睛】本题主要考查三角形外角的性质及平行线的性质，熟练掌握三角形外角的性质及平行线的性质是解题的关键．31．（2022·湖北·浠水县兰溪镇兰溪初级中学七年级期中）如图，已知AB//DE，∥ABC=80°，∥CDE=140°，则∥BCD=_____．【答案】40°【分析】延长ED交BC于M，根据两直线平行，内错角相等证明∥BMD=∥ABC，再求解∠CMD，再利用三角形的外角的性质可得答案．【详解】解：延长ED交BC于M，∥AB//DE，∥∥BMD=∥ABC=80°，∥∠CMD=180°−∠BMD=100°；又∥∥CDE=∥CMD+∥C，∥∠BCD=∠CDE−∠CMD=140°−100°=40°．。

七年级(下)数学重难点专题训练：平行线中拐点问题模型汇总(40道经典题)

七年级下数学重难点专题训练：平行线拐点问题模型汇总模型一：“Ｍ”型（猪蹄模型）例：1．（1）如图1，已知AB∥CD，求证：∠BED＝∠1+∠2．（2）如图2，已知AB∥CD，写出∠1、∠EGH与∠2、∠BEG之间数量关系，并加以证明．（3）如图3，已知AB∥CD，直接写出∠1、∠3、∠5、与∠2、∠4、∠6之间的关系．【分析】（1）过点E作EF∥AB，依据平行线的性质，即可得到∠3+∠4＝∠1+∠2，进而得出∠BED＝∠1+∠2；（2）分别过点E、G作EF∥AB，GH∥AB，依据平行线的性质，即可得到∠1+∠5+∠6＝∠3+∠4+∠2，进而得到∠1+∠EGH＝∠2+∠BEG；（3）分别过平行线间的折点作AB的平行线，依据平行线的性质，即可得到∠1、∠3、∠5与∠2、∠4、∠6之间的关系．【解答】解：（1）证明：如图，过点E作EF∥AB，∵AB∥CD，∴AB∥CD∥EF，∴∠3＝∠1，∠4＝∠2，∴∠3+∠4＝∠1+∠2，即∠BED＝∠1+∠2；（2）∠1+∠EGH＝∠2+∠BEG，理由如下：如图，分别过点E、G作EF∥AB，GH∥AB，∵AB∥CD，∴AB∥EF∥GH∥CD，∴∠1＝∠3，∠4＝∠5，∠6＝∠2，∴∠1+∠5+∠6＝∠3+∠4+∠2，即∠1+∠EGH＝∠2+∠BEG；（3）由题可得，向左的角度数之和与向右的角度数之和相等，∴∠1、∠3、∠5与∠2、∠4、∠6之间的关系为：∠1+∠3+∠5＝∠2+∠4+∠6．通关训练：2．如图，已知AB∥CD，∠B＝30°，∠D＝120°．（1）若∠E＝60°，则∠F＝．（2）请探索∠E与∠F之间满足何数量关系？并说明理由；（3）如图2，已知EP平分∠BEF，FG平分∠EFD，反向延长FG交EP于点P，求∠P 的度数．3．如图，AB∥CD，点A，E，B，C不在同一条直线上．（1）如图1，求证：∠E+∠C﹣∠A＝180°（2）如图2．直线F A，CP交于点P，且∠BAF＝∠BAE，∠DCP＝∠DCE．①试探究∠E与∠P的数量关系：②如图3，延长CE交P A于点Q，若AE∥PC，∠BAQ＝α（0°＜α＜22.5°），则∠PQC的度数为（用含α的式子表示）4．如图，已知AB∥CD，现将直角三角形PMN放入图中，其中∠P＝90°，PM交AB于点E，PN交CD于点F．（1）当直角三角形PMN所放位置如图①所示时，∠PFD与∠AEM存在怎样的数量关系？请说明理由．（2）当直角三角形PMN所放位置如图②所示时，请直接写出∠PFD与∠AEM之间存在的数量关系．（3）在（2）的条件下，若MN与CD交于点O，且∠AEM＝40°，∠DON＝20°，则∠N的度数为．5．已知，AB∥CD．点M在AB上，点N在CD上．（1）如图1中，∠BME、∠E、∠END的数量关系为：；（不需要证明）如图2中，∠BMF、∠F、∠FND的数量关系为：；（不需要证明）（2）如图3中，NE平分∠FND，MB平分∠FME，且2∠E+∠F＝180°，求∠FME的度数；（3）如图4中，∠BME＝60°，EF平分∠MEN，NP平分∠END，且EQ∥NP，则∠FEQ 的大小是否发生变化，若变化，请说明理由，若不变化，求出∠FEQ的度数．6．请阅读小明同学在学习平行线这章知识点时的一段笔记，然后解决问题．小明：老师说在解决有关平行线的问题时，如果无法直接得到角的关系，就需要借助辅助线来帮助解答，今天老师介绍了一个“美味”的模型﹣﹣﹣“猪蹄模型”．即已知：如图1，AB∥CD，E为AB、CD之间一点，连接AE，CE得到∠AEC．求证：∠AEC＝∠A+∠C．小明笔记上写出的证明过程如下：证明：过点E作EF∥AB，∴∠1＝∠A．∵AB∥CD，EF∥AB，∴EF∥CD．∴∠2＝∠C．∵∠AEC＝∠1+∠2，∴∠AEC＝∠A+∠C．请你利用“猪蹄模型”得到的结论或解题方法，完成下面的两个问题．（1）如图2，若AB∥CD，∠E＝60°，则∠B+∠C+∠F＝．（2）如图3，AB∥CD，BE平分∠ABG，CF平分∠DCG，∠G＝∠H+27°，E、B、H 共线，F、C、H共线，则∠H＝．7．如图1，已知AB∥CD，BP、DP分别平分∠ABD、∠BDC．（1）∠BPD＝°；（2）如图2，将BD改为折线BED，BP、DP分别平分∠ABE、∠EDC，其余条件不变，若∠BED＝140°，求∠BPD的度数；（3）如图3，若∠BEF＝152°，∠EFD＝136°，BP、DP分别平分∠ABE、∠CDF，其余条件不变，那么∠BPD＝°．8．已知AB∥CD，点E在AB与CD之间．（1）图1中，试说明：∠BED＝∠ABE+∠CDE；（2）图2中，∠ABE的平分线与∠CDE的平分线相交于点F，请利用（1）的结论说明：∠BED＝2∠BFD．（3）图3中，∠ABE的平分线与∠CDE的平分线相交于点F，请直接写出∠BED与∠BFD之间的数量关系．9．已知：点E、点G分别在直线AB、直线CD上，点F在两直线外，连接EF、FG （1）如图1，AB∥CD，求证：∠AEF+∠FGC＝∠EFG；（2）若直线AB与直线CD不平行，连接EG，且EG同时平分∠BEF和∠FGD如图2，请探索∠AEF、∠FGC、∠EFG之间的数量关系？并说明理由．10．如图，已知AB∥CD．（1）发现问题：若∠ABF＝∠ABE，∠CDF＝∠CDE，则∠F与∠E的等量关系为．（2）探究问题：若∠ABF＝∠ABE，∠CDF＝∠CDE．猜想：∠F与∠E的等量关系，并证明你的结论．（3）归纳问题：若∠ABF＝∠ABE，∠CDF＝∠CDE．直接写出∠F与∠E的等量关系．11．【引入】如图1，已知∠ABC+∠ECB＝180°，∠P＝∠Q，求证：∠1＝∠2．【变式】如图2，AB∥CD，∠1＝∠2，求证：∠F＝∠Ｍ模型二：铅笔模型例：12．模型与应用．【模型】（1）如图①，已知AB∥CD，求证∠1+∠MEN+∠2＝360°．【应用】（2）如图②，已知AB∥CD，则∠1+∠2+∠3+∠4+∠5+∠6的度数为．如图③，已知AB∥CD，则∠1+∠2+∠3+∠4+∠5+∠6+…+∠n的度数为．（3）如图④，已知AB∥CD，∠AM1M2的角平分线M1O与∠CM n M n﹣1的角平分线M n O 交于点O，若∠M1OM n＝m°．在（2）的基础上，求∠2+∠3+∠4+∠5+∠6+……+∠n ﹣1的度数．（用含m、n的代数式表示）【分析】（1）过点E作EF∥CD，根据平行线的判定得出EF∥AB，根据平行线的性质得出即可；（2）过E作EQ∥CD，过F作FW∥CD，过G作GR∥CD，过H作HY∥CD，根据平行线的判定得出EQ∥FW∥GR∥HY∥AB∥CD，根据平行线的性质得出即可；（3）过点O作SR∥AB，根据平行线的性质得出即可；【解答】（1）证明：过点E作EF∥CD，∵AB∥CD，∴EF∥AB，∴∠1+∠MEF＝180°，同理∠2+∠NEF＝180°，∴∠1+∠2+∠MEN＝360°；【应用】（2）过E作EQ∥CD，过F作FW∥CD，过G作GR∥CD，过H作HY∥CD，∵CD∥AB，∴EQ∥FW∥GR∥HY∥AB∥CD，∴∠1+∠MEQ＝180°，∠QEF+∠EFW＝180°，∠WFG+∠FGR＝180°，∠RGH+∠GHY＝180°，∠YHN+∠6＝180°，∴∠1+∠2+∠3+∠4+∠5+∠6＝5×180°＝900°，同理∠1+∠2+∠3+∠4+∠5+∠6+…+∠n＝180°（n﹣1），故答案为：900°，180°（n﹣1）；（3）解：过点O作SR∥AB，∵AB∥CD，∴SR∥CD，∴∠AM1O＝∠M1OR同理∠C M n O＝∠M n OR∴∠A M1O+∠CM n O＝∠M1OR+∠M n OR，∴∠A M1O+∠CM n O＝∠M1OM n＝m°，∵M1O平分∠AM1M2，∴∠AM1M2＝2∠A M1O，同理∠CM n M n﹣1＝2∠CM n O，∴∠AM1M2+∠CM n M n﹣1＝2∠AM1O+2∠CM n O＝2∠M1OM n＝2m°，又∵∠A M1M2+∠2+∠3+∠4+∠5+∠6+……+∠n﹣1+∠CM n M n﹣1＝180°（n﹣1），∠2+∠3+∠4+∠5+∠6+…+∠n﹣1＝（180n﹣180﹣2m）°．通关训练：13．如图1，MA1∥NA2，则∠A1+∠A2＝度．如图2，MA1∥NA3，则∠A1+∠A2+∠A3＝度．如图3，MA1∥NA4，则∠A1+∠A2+∠A3+∠A4＝度．如图4，MA1∥NA5，则∠A1+∠A2+∠A3+∠A4+∠A5＝度．从上述结论中你发现了什么规律？如图5，MA1∥NA n，则∠A1+∠A2+∠A3+…+∠A n＝度．14．如图，AB∥CD，点F在CE上，∠EAF＝∠BAF，若∠AEC＝105°，∠DCE＝115°，求∠AFC的度数．15．直线AB∥CD，E为直线AB、CD之间的一点，完成以下问题：（1）如图1，若∠B＝15°，∠BED＝90°，则∠D＝；（2）如图2，若∠B＝α，∠D＝β，求出∠BED的度数（用a、β表示）；（3）如图3，若∠B＝α，∠C＝β，则a、β与∠BEC之间有什么等量关系？请猜想证明．16．问题情境：如图1，AB∥CD，∠P AB＝135°，∠PCD＝125°．求∠APC度数．小明的思路是：如图2，过P作PE∥AB，通过平行线性质，可求得∠APC的度数．请写出具体求解过程．问题迁移：（1）如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP＝∠α，∠BCP＝∠β．∠CPD、∠α、∠β之间有何数量关系？请说明理由；（2）在（1）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出∠CPD、∠α、∠β间的数量关系．17．如图，BN∥CD，点A是直线BN上一点，P是直线AB与直线CD之间一点，连接AP，PC．（1）求证：∠BAP+∠C＝∠P；（2）过点C作CM平分∠PCD，过点C作CE⊥CM交∠NAP的角平分线于点E，过点P作PF∥AE交CM于点F，探索∠CFP和∠APC的数量关系，并说明理由；（3）在（2）的条件下，若2∠AEC﹣∠CPF＝240°，Q是直线CD上一点，请直接写出∠PFQ和∠FQD的数量关系．模型三：钩型（臭脚模型和骨折模型）例：18．（1）如图1，AB∥CD，CF平分∠DCE，若∠DCF＝30°，∠E＝20°，求∠ABE 的度数；（2）如图2，已知AB∥CD，∠EBF＝2∠ABF，CF平分∠DCE，若∠F的2倍与∠E的补角的和为190°，求∠ABE的度数；（3）如图3，若P是（2）中的射线BE上一点，G是CD上任一点，PQ平分∠BPG，PQ∥GN，GM平分∠DGP，若∠B＝30°，求∠MGN的度数．【分析】根据平行线的判定与性质，三角形的内角和定理，三角形的一个外角等于与它不相邻的两个内角的和的性质，角平分线的定义解答即可．【解答】解：（1）过E作EM∥AB∵AB∥CD∴CD∥EM∥AB∴∠ABE＝∠BEM∠DCE＝∠CEM∵CF平分∠DCE∴∠DCE＝2∠DCF∵∠DCF＝30°∴∠DCE＝60°∴∠CEM＝60°又∵∠CEB＝20°∴∠BEM＝∠CEM﹣∠CEB＝40°∴∠ABE＝40°，（2）过E作EM∥AB，过F作FN∥AB∵∠EBF＝2∠ABF∴设∠ABF＝x，∠EBF＝2x，则∠ABE＝3x ∵CF平分∠DCE∴设∠DCF＝∠ECF＝y，则∠DCE＝2y∵AB∥CD∴EM∥AB∥CD∴∠DCE＝∠CEM＝2y∠BEM＝∠ABE＝3x∴∠CEB＝∠CEM﹣∠BEM＝2y﹣3x同理∠CFB＝y﹣x∵2∠CFB+（180°﹣∠CEB）＝190°∴2（y﹣x）+180°﹣（2y﹣3x）＝190°∴x＝10°∴∠ABE＝3x＝30°，（3）过P作PL∥AB∵GM平分∠DGP∴设∠DGM＝∠PGM＝y，则∠DGP＝2y ∵PQ平分∠BPG∴设∠BPQ＝∠GPQ＝x，则∠BPG＝2x∵PQ∥QN∴∠PGN＝∠GPQ＝x∵AB∥CD∴PL∥AB∥CD∴∠GPL＝∠DGP＝2y∠BPL＝∠ABP＝30°∵∠BPL＝∠GPL﹣∠BPG∴30°＝2y﹣2x∴y﹣x＝15°∵∠MGN＝∠PGM﹣∠PGN＝y﹣x∴∠MGN＝15°．通关训练：19．已知AM∥CN，点B为平面内一点，AB⊥BC于B．（1）如图1，直接写出∠A和∠C之间的数量关系；（2）如图2，过点B作BD⊥AM于点D，求证：∠ABD＝∠C；（3）如图3，在（2）问的条件下，点E、F在DM上，连接BE、BF、CF，BF平分∠DBC，BE平分∠ABD，若∠FCB+∠NCF＝180°，∠BFC＝3∠DBE，求∠EBC的度数．20．为增强学生体质，感受中国的传统文化，学校将国家级非物质文化遗产“抖空竹”引入阳光特色大课间．如图是某同学“抖空竹”时的一个瞬间，王聪把它抽象成如图的数学问题：已知AB∥CD，∠EAB＝80°，∠ECD＝110°，求∠E的度数．21．如图，BE∥CF，∠A＝30°，∠C＝80°，求∠B的度数．22．（1）（问题）如图1，若AB∥CD，∠AEP＝40°，∠PFD＝130°．求∠EPF的度数；（2）（问题迁移）如图2，AB∥CD，点P在AB的上方，问∠PEA，∠PFC，∠EPF之间有何数量关系？请说明理由；（3）（联想拓展）如图3所示，在（2）的条件下，已知∠EPF＝α，∠PEA的平分线和∠PFC的平分线交于点G，用含有α的式子表示∠G的度数．23．已知AB∥CD，点E在AB上，点G在CD上，点F在直线AB、CD之间，分别连接EF、FG，∠BEF+∠DGF＝2∠EFG．（1）如图1，求∠EFG的度数；（2）如图2，若∠BEF的角平分线与FG的延长线交于点M，求证：∠AEF﹣2∠FME ＝60°；（3）如图3，已知点P在FG的延长线上，点K在CD上，点N在∠PGC内，分别连接NG，NK．若NK∥EF，∠PGN＝2∠NGC，请直接写出∠AEF﹣∠GNK的值．24．同一平面内的两条直线有相交和平行两种位置关系．（1）如图1，若AB∥CD，点P在AB、CD内部，请写出∠BPD、∠B、∠D之间的数量关系（不必说明理由）；（2）如图2，将直线AB绕点B逆时针方向转一定角度交直线CD于点Q，利用（1）中的结论求∠BPD、∠B、∠D、∠BQD之间有何数量关系？并证明你的结论；（3）如图3，设BF交AC于点M，AE交DF于点N．已知∠AMB＝140°，∠ANF＝105°，利用（2）中的结论直接写出∠B+∠E+∠F的度数和∠A比∠F大多少度．25．综合探究：已知，AB∥CD，点M、N分别是AB、CD上两点，点G在AB、CD之间，连接MG、NG．（1）如图1，若GM⊥GN，求∠AMG+∠CNG的度数；（2）如图2，若点P是CD下方一点，MG平分∠BMP，ND平分∠GNP，已知∠BMG ＝40°，求∠MGN+∠MPN的度数．26．已知直线AB∥CD．（1）如图1，请直接写出∠BME、∠E、∠END的数量关系为；（2）如图2，∠ABM＝∠MBE，∠CDN＝∠NDE，直线MB、ND交于点F，若∠F ＝10°，求∠E的度数；（3）如图3，∠BME的角平分线所在的直线与∠CNE的角平分线相交于点P，试探究∠P与∠E之间的数量关系，并证明你的结论．27．如图，已知直线AB∥CD．（1）在图1中，点M在直线AB上，点N在直线CD上，∠BME、∠E、∠END的数量关系是；（不需证明）（2）如图2，若GN平分∠CNE，FE平分∠AMG，且∠G+∠E＝60°，求∠AMG的度数；（3）如图3，直线BM平分∠ABE，直线DN平分∠CDE相交于点F，求∠F：∠E的值；（4）若∠ABM＝∠MBE，∠CDN＝∠NDE，则＝．（用含有n的代数式表示）28．如图1所示，AB∥CD，E为直线CD下方一点，BF平分∠ABE．（1）求证：∠ABE+∠C﹣∠E＝180°．（2）如图2，EG平分∠BEC，过点B作BH∥GE，求∠FBH与∠C之间的数量关系．（3）如图3，CN平分∠ECD，若BF的反向延长线和CN的反向延长线交于点M，且∠E+∠M＝130°，请直接写出∠E的度数．29．如图，平面内的直线有相交和平行两种位置关系（1）如图①，已知AB∥CD，求证：∠BPD＝∠B+∠D；（提示；可过点P作PO∥AB）（2）如图②，已知AB∥CD，求证：∠B＝∠P+∠D．30．如图，AB∥CD，分别探讨下面四个图形中∠APC与∠A，∠C的关系，请你从所得的关系中任意选取一个加以说明．图（1）结论：；图（2）结论：；图（3）结论：；图（4）结论：．你准备证明的是图，请在下面写出证明过程．31．如图1，将两根笔直的细木条MN，EF用图钉固定并平行摆放，将一根橡皮筋拉直后用图钉分别周定在MN，EF上，橡皮筋的两端点分别记为点A，点B．（1）图1中，点P在AB上，若∠1＝110°，则∠2＝°；（2）P为橡皮筋上一点，用皮筋的弹性拉动橡皮筋，使A，B，P三点不在同一直线，后用图固定点P．①如图2，若点P在两根细木条所在直线之间，且∠1+∠2＝90°，试判断线段AP与BP所在直线的位置关系，并说明理由；②如图3，若点P在两根细木条所在直线的同侧，且∠1+∠2＝90°，∠1＝31°，试求∠APB的度数；（3）如图4，P1，P2两点在两根细木条所在直线之间，拉动橡皮筋并固定，若∠1+∠2＝90°，则∠AP1P2+∠BP1P2＝°．32．阅读下面材料：小明遇到这样一个问题：如图1，AC∥BD，点E为直线AC上方一点，连接CE、DE，猜想∠C、∠D、∠E的数量关系，并证明．小明发现，可以过点E作MN∥AC来解决问题，如图2，请你完成解答；用学过的知识或参考小明的方法，解决下面的问题：如图3，AB∥CD，P是平面内一点，连接AP、CP，使AP∥BD，∠APC＝100°，BM、CM分别平分∠ABD、∠DCP交于点M，求∠M的度数．33．如图，已知直线MB∥ND，A、C分别为MB、ND上的点，E为直线MB、ND外的一点，连接AE、EC．（1）E在直线MB的上方（如图1），求证：∠AEC+∠ECD＝∠EAB；（2）若∠MAE与∠NCE两角的角平分线交于F点，请在图2中将图形补充完整，并直接写出∠AEC与∠AFC之间的数量关系；（3）若∠EAB的角平分线的反向延长线与∠NCE的角平分线交于G点（如图3），且∠AGC比∠AEC的倍多50°，求∠AEC的度数．34．已知直线AB∥CD，E为直线AB、CD外的一点，连接AE、EC．（1）E在直线AB的上方（如图1），求证：∠AEC+∠EAB＝∠ECD；（2）∠BAF＝2∠EAF，∠DCF＝2∠ECF（如图2），求证：∠AEC＝∠AFC；（3）若E在直线AB、CD之间，在（2）条件下（如图3），且∠AFC比∠AEC的倍少40°，则∠AEC的度数为（不用写出解答过程）．35．如图：已知AB∥DE，若∠ABC＝60°，∠CDE＝140°，求∠BCD的度数．36．如图，已知AB∥CD，点E在直线AB，CD之间．（1）求证：∠AEC＝∠BAE+∠ECD；（2）若AH平分∠BAE，将线段CE沿CD平移至FG．①如图2，若∠AEC＝90°，HF平分∠DFG，求∠AHF的度数；②如图3，若HF平分∠CFG，试判断∠AHF与∠AEC的数量关系并说明理由．37．如图，平面内有两条直线同AB、CD，且AB∥CD，P为一动点．（1）当点P移动到如图（1）的位置时，这时∠APC与∠A，∠C有怎样的关系？并说明理由；（2）当点P移动到如图（2）的位置时，这时∠APC与∠A，∠C又有怎样的关系？说明你的理由；（3）当点P移动到如图（3）的位置时，直接写出∠APC与∠A，∠C的关系式；（4）当点P移动到如图（4）的位置时，直接写出∠APC与∠A，∠C的关系式．38．如图所示，已知AB∥CD，分别探讨下面四个图形中，∠APC，∠P AB与∠PCD的关系．39．已知AB∥CD，点P为平面内一点，连接AP、CP．（1）探究：如图（1）∠P AB＝145°，∠PCD＝135°，则∠APC的度数是；如图（2）∠P AB＝45°，∠PCD＝60°，则∠APC的度数是．（2）在图2中试探究∠APC，∠P AB，∠PCD之间的数量关系，并说明理由．（3）拓展探究：当点P在直线AB，CD外，如图（3）、（4）所示的位置时，请分别直接写出∠APC，∠P AB，∠PCD之间的数量关系．40．探究：（1）如图a，若AB∥CD，则∠B+∠D＝∠E，你能说明为什么吗？（2）反之，若∠B+∠D＝∠E，直线AB与CD有什么位置关系？请证明；（3）若将点E移至图b所示位置，此时∠B、∠D、∠E之间有什么关系？请证明；（4）若将E点移至图c所示位置，情况又如何？（5）在图d中，AB∥CD，∠E+∠G与∠B+∠F+∠D又有何关系？（6）在图e中，若AB∥CD，又得到什么结论？七年级下数学重难点专题训练：平行线拐点问题模型汇总1．（1）如图1，已知AB∥CD，求证：∠BED＝∠1+∠2．（2）如图2，已知AB∥CD，写出∠1、∠EGH与∠2、∠BEG之间数量关系，并加以证明．（3）如图3，已知AB∥CD，直接写出∠1、∠3、∠5、与∠2、∠4、∠6之间的关系．【分析】（1）过点E作EF∥AB，依据平行线的性质，即可得到∠3+∠4＝∠1+∠2，进而得出∠BED＝∠1+∠2；（2）分别过点E、G作EF∥AB，GH∥AB，依据平行线的性质，即可得到∠1+∠5+∠6＝∠3+∠4+∠2，进而得到∠1+∠EGH＝∠2+∠BEG；（3）分别过平行线间的折点作AB的平行线，依据平行线的性质，即可得到∠1、∠3、∠5与∠2、∠4、∠6之间的关系．【解答】解：（1）证明：如图，过点E作EF∥AB，∵AB∥CD，∴AB∥CD∥EF，∴∠3＝∠1，∠4＝∠2，∴∠3+∠4＝∠1+∠2，即∠BED＝∠1+∠2；（2）∠1+∠EGH＝∠2+∠BEG，理由如下：如图，分别过点E、G作EF∥AB，GH∥AB，∵AB∥CD，∴AB∥EF∥GH∥CD，∴∠1＝∠3，∠4＝∠5，∠6＝∠2，∴∠1+∠5+∠6＝∠3+∠4+∠2，即∠1+∠EGH＝∠2+∠BEG；（3）由题可得，向左的角度数之和与向右的角度数之和相等，∴∠1、∠3、∠5与∠2、∠4、∠6之间的关系为：∠1+∠3+∠5＝∠2+∠4+∠6．2．如图，已知AB∥CD，∠B＝30°，∠D＝120°．（1）若∠E＝60°，则∠F＝90°．（2）请探索∠E与∠F之间满足何数量关系？并说明理由；（3）如图2，已知EP平分∠BEF，FG平分∠EFD，反向延长FG交EP于点P，求∠P 的度数．【分析】（1）分别过点E，F作EM∥AB，FN∥AB，根据平行线的性质得到∠B＝∠BEM ＝30°，∠MEF＝∠EFN，∠D+∠DFN＝180°，代入数据即可得到结论；（2）根据平行线的性质得到∠B＝∠BEM＝30°，∠MEF＝∠EFN，由AB∥CD，AB∥FN，得到CD∥FN，根据平行线的性质得到∠D+∠DFN＝180°，于是得到结论；（3）过点F作FH∥EP，设∠BEF＝2x°，则∠EFD＝（2x+30）°，根据角平分线的定义得到∠PEF＝∠BEF＝x°，∠EFG＝∠EFD＝（x+15）°，根据平行线的性质得到∠PEF＝∠EFH＝x°，∠P＝∠HFG，于是得到结论．【解答】解：（1）如图1，分别过点E，F作EM∥AB，FN∥AB，∴EM∥AB∥FN，∴∠B＝∠BEM＝30°，∠MEF＝∠EFN，又∵AB∥CD，AB∥FN，∴CD∥FN，∴∠D+∠DFN＝180°，又∵∠D＝120°，∴∠DFN＝60°，∴∠BEF＝∠MEF+30°，∠EFD＝∠EFN+60°，∴∠EFD＝∠MEF+60°∴∠EFD＝∠BEF+30°＝90°；故答案为：90°；（2）如图1，分别过点E，F作EM∥AB，FN∥AB，∴EM∥AB∥FN，∴∠B＝∠BEM＝30°，∠MEF＝∠EFN，又∵AB∥CD，AB∥FN，∴CD∥FN，∴∠D+∠DFN＝180°，又∵∠D＝120°，∴∠DFN＝60°，∴∠BEF＝∠MEF+30°，∠EFD＝∠EFN+60°，∴∠EFD＝∠MEF+60°，∴∠EFD＝∠BEF+30°；（3）如图2，过点F作FH∥EP，由（2）知，∠EFD＝∠BEF+30°，设∠BEF＝2x°，则∠EFD＝（2x+30）°，∵EP平分∠BEF，GF平分∠EFD，∴∠PEF＝∠BEF＝x°，∠EFG＝∠EFD＝（x+15）°，∵FH∥EP，∴∠PEF＝∠EFH＝x°，∠P＝∠HFG，∵∠HFG＝∠EFG﹣∠EFH＝15°，∴∠P＝15°．3．如图，AB∥CD，点A，E，B，C不在同一条直线上．（1）如图1，求证：∠E+∠C﹣∠A＝180°（2）如图2．直线F A，CP交于点P，且∠BAF＝∠BAE，∠DCP＝∠DCE．①试探究∠E与∠P的数量关系：②如图3，延长CE交P A于点Q，若AE∥PC，∠BAQ＝α（0°＜α＜22.5°），则∠PQC的度数为180°﹣8α（用含α的式子表示）【分析】（1）如图1，过E作EF∥AB，根据平行线的性质即可得到结论；（2）①设∠BAF＝x，∠BAE＝3x，∠DCP＝y，∠DCE＝3y，由（1）知，∠E＝180°﹣∠C+∠A＝180°﹣3（y﹣x），如图2，过P作PG∥CD，根据平行线的性质即可得到结论；②如图3，过P作PG∥CD，根据平行线的性质即可得到结论．【解答】解：（1）如图1，过E作EF∥AB，∵AB∥CD，∴AB∥EF∥CD，∴∠AEF＝∠A，∠C+∠FEC＝180°，∴∠E＝∠AEF+∠FEC＝∠A+180°﹣∠C，即∠E+∠C﹣∠A＝180°；（2）①∵∠BAF＝∠BAE，∠DCP＝∠DCE，∴设∠BAF＝x，∠BAE＝3x，∠DCP＝y，∠DCE＝3y，由（1）知，∠E＝180°﹣∠C+∠A＝180°﹣3（y﹣x），如图2，过P作PG∥CD，∵AB∥CD，∴AB∥PG，∴∠GP A＝∠BAF＝x，∠GPC＝∠PCD＝y，∴∠APC＝y﹣x，即∠E＝180°﹣3∠P；②如图3，过P作PG∥CD，∵∠BAQ＝α，∴∠QAE＝2α，∵AE∥PC，∴∠QAE＝∠APC＝2α，由①知，∠AEC＝180°﹣3∠APC＝180°﹣6α，∴∠PQC＝∠AEC﹣∠QAE＝180°﹣6α﹣2α＝180°﹣8α，故答案为：180°﹣8α．4．如图，已知AB∥CD，现将直角三角形PMN放入图中，其中∠P＝90°，PM交AB于点E，PN交CD于点F．（1）当直角三角形PMN所放位置如图①所示时，∠PFD与∠AEM存在怎样的数量关系？请说明理由．（2）当直角三角形PMN所放位置如图②所示时，请直接写出∠PFD与∠AEM之间存在的数量关系．（3）在（2）的条件下，若MN与CD交于点O，且∠AEM＝40°，∠DON＝20°，则∠N的度数为30°．【分析】（1）作PH∥AB，根据平行线的性质得到∠AEM＝∠HPM，∠PFD＝∠HPN，根据∠MPN＝90°解答；（2）根据平行线的性质得到∠PFD+∠BHN＝180°，根据∠P＝90°解答；（3）根据对顶角相等，直角三角形的性质，平行线的性质以及三角形外角的性质计算即可求解．【解答】解：（1）如图①，作PH∥AB，则∠AEM＝∠HPM，∵AB∥CD，PH∥AB，∴PH∥CD，∴∠PFD＝∠HPN，∵∠MPN＝90°，∴∠PFD+∠AEM＝90°，故答案为：∠PFD+∠AEM＝90°；（2）猜想：∠PFD﹣∠AEM＝90°；理由如下：∵AB∥CD，∴∠PFD+∠BHN＝180°，∵∠BHN＝∠PHE，∴∠PFD+∠PHE＝180°，∵∠P＝90°，∴∠PHE+∠PEB＝90°，∵∠PEB＝∠AEM，∴∠PHE+∠AEM＝90°，∴∠PFD﹣∠AEM＝90°；（3）∵∠P＝90°，∠PEB＝∠AEM＝40°，∴∠PHE＝90°﹣∠PEB＝90°﹣40°＝50°，∵AB∥CD，∴∠HFO＝∠PHE＝50°，∵∠DON＝20°，∴∠N＝∠HFO﹣∠DON＝30°．故答案为：30°．5．已知，AB∥CD．点M在AB上，点N在CD上．（1）如图1中，∠BME、∠E、∠END的数量关系为：∠BME＝∠MEN﹣∠END；（不需要证明）如图2中，∠BMF、∠F、∠FND的数量关系为：∠BMF＝∠MFN+∠FND；（不需要证明）（2）如图3中，NE平分∠FND，MB平分∠FME，且2∠E+∠F＝180°，求∠FME的度数；（3）如图4中，∠BME＝60°，EF平分∠MEN，NP平分∠END，且EQ∥NP，则∠FEQ 的大小是否发生变化，若变化，请说明理由，若不变化，求出∠FEQ的度数．【分析】（1）过E作EH∥AB，易得EH∥AB∥CD，根据平行线的性质可求解；过F作FH∥AB，易得FH∥AB∥CD，根据平行线的性质可求解；（2）根据（1）的结论及角平分线的定义可得2（∠BME+∠END）+∠BMF﹣∠FND＝180°，可求解∠BMF＝60°，进而可求解；（3）根据培训心得性质及角平分线的定义可推知∠FEQ＝∠BME，进而可求解．【解答】解：（1）过E作EH∥AB，如图1，∴∠BME＝∠MEH，∵AB∥CD，∴HE∥CD，∴∠END＝∠HEN，∴∠MEN＝∠MEH+∠HEN＝∠BME+∠END，即∠BME＝∠MEN﹣∠END．如图2，过F作FH∥AB，∴∠BMF＝∠MFK，∵AB∥CD，∴FH∥CD，∴∠FND＝∠KFN，∴∠MFN＝∠MFK﹣∠KFN＝∠BMF﹣∠FND，即：∠BMF＝∠MFN+∠FND．故答案为∠BME＝∠MEN﹣∠END；∠BMF＝∠MFN+∠FND．（2）由（1）得∠BME＝∠MEN﹣∠END；∠BMF＝∠MFN+∠FND．∵NE平分∠FND，MB平分∠FME，∴∠FME＝∠BME+∠BMF，∠FND＝∠FNE+∠END，∵2∠MEN+∠MFN＝180°，∴2（∠BME+∠END）+∠BMF﹣∠FND＝180°，∴2∠BME+2∠END+∠BMF﹣∠FND＝180°，即2∠BMF+∠FND+∠BMF﹣∠FND＝180°，解得∠BMF＝60°，∴∠FME＝2∠BMF＝120°；（3）∠FEQ的大小没发生变化，∠FEQ＝30°．由（1）知：∠MEN＝∠BME+∠END，∵EF平分∠MEN，NP平分∠END，∴∠FEN＝∠MEN＝（∠BME+∠END），∠ENP＝∠END，∵EQ∥NP，∴∠NEQ＝∠ENP，∴∠FEQ＝∠FEN﹣∠NEQ＝（∠BME+∠END）﹣∠END＝∠BME，∵∠BME＝60°，∴∠FEQ＝×60°＝30°．6．请阅读小明同学在学习平行线这章知识点时的一段笔记，然后解决问题．小明：老师说在解决有关平行线的问题时，如果无法直接得到角的关系，就需要借助辅助线来帮助解答，今天老师介绍了一个“美味”的模型﹣﹣﹣“猪蹄模型”．即已知：如图1，AB∥CD，E为AB、CD之间一点，连接AE，CE得到∠AEC．求证：∠AEC＝∠A+∠C．小明笔记上写出的证明过程如下：证明：过点E作EF∥AB，∴∠1＝∠A．∵AB∥CD，EF∥AB，∴EF∥CD．∴∠2＝∠C．∵∠AEC＝∠1+∠2，∴∠AEC＝∠A+∠C．请你利用“猪蹄模型”得到的结论或解题方法，完成下面的两个问题．（1）如图2，若AB∥CD，∠E＝60°，则∠B+∠C+∠F＝240°．（2）如图3，AB∥CD，BE平分∠ABG，CF平分∠DCG，∠G＝∠H+27°，E、B、H 共线，F、C、H共线，则∠H＝51°．【分析】（1）由EM∥AB，FN∥EM，FN∥CD分别得∠1＝∠B，∠2＝∠3，∠4+∠C＝180°，由角的和差计算∠B+∠C+∠F的度数为240°；（2）由角平分线得∴∠ABG＝2∠1，∠DCG＝2∠4，根据直线EF∥AB，EF∥CD得2∠1+∠7＝180°，2∠4+∠8＝180°，等式的性质得2（∠1+∠4）＝∠BGC+180°；直线MN∥AB，MN∥CD得∠1＝∠5，∠4＝∠6，等量代换2（∠5+∠6）＝∠BGC+180°，又因∠BGC＝∠BHC+27°求得∠BHC的度数为51°．【解答】解：（1）过点E、F分别作EM∥AB，FN∥AB，如图2所示：∵EM∥AB，∴∠1＝∠B，又∵FN∥AB，∴FN∥EM，∴∠2＝∠3，又∵AB∥CD，∴FN∥CD，∴∠4+∠C＝180°，又∵∠BEF＝∠1+∠2，∠EFC＝∠3+∠4，∠BEF＝60°∴∠B+∠EFC+∠C＝∠1+∠3+∠4+∠C＝（∠1+∠2）+（∠4+∠C）＝60°+180°＝240°；（2）过点G、H作EF∥AB，MN∥AB，如图3所示：∵BE平分∠ABG，CF平分∠DCG，∴∠ABG＝2∠1，∠DCG＝2∠4，又∵EF∥AB，∴2∠1+∠7＝180°，又∵AB∥CD，∴EF∥CD，∴2∠4+∠8＝180°，∴∠7+∠8＝360°﹣2（∠1+∠4），又∵∠7+∠8+∠BGC＝180°，∴2（∠1+∠4）＝∠BGC+180°，又∵MN∥AB，∴∠1＝∠5，又∵AB∥CD，∴MN∥CD，∴∠4＝∠6，∴2（∠5+∠6）＝∠BGC+180°，又∵∠5+∠6+∠BHC＝180°，∴∠BGC+2∠BHC＝180°，又∠BGC＝∠BHC+27°，∴3∠BHC+27°＝180°，∴∠BHC＝51°；故答案为：240°，51°．7．如图1，已知AB∥CD，BP、DP分别平分∠ABD、∠BDC．（1）∠BPD＝90°°；（2）如图2，将BD改为折线BED，BP、DP分别平分∠ABE、∠EDC，其余条件不变，若∠BED＝140°，求∠BPD的度数；（3）如图3，若∠BEF＝152°，∠EFD＝136°，BP、DP分别平分∠ABE、∠CDF，其余条件不变，那么∠BPD＝54°．【分析】（1）先根据平行线的性质得出∠ABD+∠BDC＝∠180°，再根据角平分线的定义得出∠PBD+∠PDB的度数，由三角形内角和定理即可得出结论；（2）连接BD，先求出∠EBD+∠EDB的度数，再由平行线的性质得出∠ABD+∠CDB的度数，由角平分线的性质得出∠PBE+∠PDE的度数，根据∠BPD＝180°﹣∠PBE﹣PDE﹣∠EBD﹣∠EDB即可得出结论．（3）连接BD，先求出∠EBD+∠FDB的度数，再求出∠PBE+∠PDF的度数，再利用三角形内角和定理即可解决．【解答】解：（1）∵AB∥CD，∴∠ABD+∠BDC＝∠180°，∵BP、DP分别平分∠ABD、∠BDC，∴∠PBD+∠PDB＝90°，∴∠BPD＝180°﹣90°＝90°．（2）连接BD，∵∠BED＝140°，∴∠EBD+∠EDB＝40°，∵AB∥CD，∴∠ABD+∠CDB＝180°，∵BP、DP分别平分∠ABE、∠EDC，∴∠PBE＝∠ABE，∠PDE＝∠CDE，∴∠PBE+∠PDE＝×（180°﹣40°）＝70°，∴∠BPD＝180°﹣∠PBE﹣PDE﹣∠EBD﹣∠EDB＝70°．（3）连接BD，∵∠BEF＝152°，∠EFD＝136°，∴∠EBD+∠FDB＝360°﹣（152°+136°）＝72°，∵BP、DP分别平分∠ABE、∠FDC，∴∠PBE＝∠ABE，∠PDF＝∠CDF，∴∠PBE+∠PDF＝×（180°﹣72°）＝54°，∴∠BPD＝180°﹣（∠EBD+∠FDB）﹣（∠PBE+∠PDF）＝54°．故答案为：90；54°．8．已知AB∥CD，点E在AB与CD之间．（1）图1中，试说明：∠BED＝∠ABE+∠CDE；（2）图2中，∠ABE的平分线与∠CDE的平分线相交于点F，请利用（1）的结论说明：∠BED＝2∠BFD．（3）图3中，∠ABE的平分线与∠CDE的平分线相交于点F，请直接写出∠BED与∠BFD之间的数量关系．【分析】（1）图1中，过点E作EG∥AB，则∠BEG＝∠ABE，根据AB∥CD，EG∥AB，所以CD∥EG，所以∠DEG＝∠CDE，进而可得∠BED＝∠ABE+∠CDE；（2）图2中，根据∠ABE的平分线与∠CDE的平分线相交于点F，结合（1）的结论即可说明：∠BED＝2∠BFD；（3）图3中，根据∠ABE的平分线与∠CDE的平分线相交于点F，过点E作EG∥AB，则∠BEG+∠ABE＝180°，因为AB∥CD，EG∥AB，所以CD∥EG，所以∠DEG+∠CDE ＝180°，再结合（1）的结论即可说明∠BED与∠BFD之间的数量关系．【解答】解：（1）如图1中，过点E作EG∥AB，则∠BEG＝∠ABE，因为AB∥CD，EG∥AB，所以CD∥EG，所以∠DEG＝∠CDE，所以∠BEG+∠DEG＝∠ABE+∠CDE，即∠BED＝∠ABE+∠CDE；（2）图2中，因为BF平分∠ABE，所以∠ABE＝2∠ABF，因为DF平分∠CDE，所以∠CDE＝2∠CDF，所以∠ABE+∠CDE＝2∠ABF+2∠CDF＝2（∠ABF+∠CDF），由（1）得：因为AB∥CD，所以∠BED＝∠ABE+∠CDE，∠BFD＝∠ABF+∠CDF，所以∠BED＝2∠BFD．（3）∠BED＝360°﹣2∠BFD．图3中，过点E作EG∥AB，则∠BEG+∠ABE＝180°，因为AB∥CD，EG∥AB，所以CD∥EG，所以∠DEG+∠CDE＝180°，所以∠BEG+∠DEG＝360°﹣（∠ABE+∠CDE），即∠BED＝360°﹣（∠ABE+∠CDE），因为BF平分∠ABE，所以∠ABE＝2∠ABF，因为DF平分∠CDE，所以∠CDE＝2∠CDF，∠BED＝360°﹣2（∠ABF+∠CDF），由（1）得：因为AB∥CD，所以∠BFD＝∠ABF+∠CDF，所以∠BED＝360°﹣2∠BFD．9．已知：点E、点G分别在直线AB、直线CD上，点F在两直线外，连接EF、FG （1）如图1，AB∥CD，求证：∠AEF+∠FGC＝∠EFG；（2）若直线AB与直线CD不平行，连接EG，且EG同时平分∠BEF和∠FGD如图2，请探索∠AEF、∠FGC、∠EFG之间的数量关系？并说明理由．【分析】（1）过F作FQ∥AB，利用平行线的性质，即可得到∠AEF+∠FGC＝∠EFQ+∠GFQ＝∠EFG；（2）延长AB，CD，交于点P，依据∠FEP＝180°﹣∠AEF，∠FGP＝180°﹣∠FGC，即可得到∠FEP+∠FGP＝360°﹣（∠AEF+∠FGC），再根据四边形内角和，即可得到四边形EFGP中，∠F+∠P＝360°﹣（∠FEP+∠FGP）＝∠AEF+∠FGC，进而得出结论．【解答】解：（1）如图1，过F作FQ∥AB，∵AB∥CD，∴FQ∥CD，∴∠AEF＝∠QFE，∠FGC＝∠GFQ，∴∠AEF+∠FGC＝∠EFQ+∠GFQ＝∠EFG；（2）如图2，延长AB，CD，交于点P，∵EG同时平分∠BEF和∠FGD，∴∠FEG＝∠PEG，∠FGE＝∠PGE，∴∠F＝∠P，∵∠FEP＝180°﹣∠AEF，∠FGP＝180°﹣∠FGC，∴∠FEP+∠FGP＝360°﹣（∠AEF+∠FGC），∵四边形EFGP中，∠F+∠P＝360°﹣（∠FEP+∠FGP）＝360°﹣[360°﹣（∠AEF+∠FGC）]＝∠AEF+∠FGC，即2∠EFG＝∠AEF+∠FGC．10．如图，已知AB∥CD．（1）发现问题：若∠ABF＝∠ABE，∠CDF＝∠CDE，则∠F与∠E的等量关系为∠BED＝2∠BFD．（2）探究问题：若∠ABF＝∠ABE，∠CDF＝∠CDE．猜想：∠F与∠E的等量关系，并证明你的结论．（3）归纳问题：若∠ABF＝∠ABE，∠CDF＝∠CDE．直接写出∠F与∠E的等量关系．【分析】（1）首先连接FE并延长，易得∠BED＝∠BFD+∠EBF+∠EDF，又由BF、DF 分别平分∠ABE、∠CDE，以及（1）的结论，易证得∠BED＝2∠BFD；（2）过点E、F分别作AB的平行线EG、FH，由平行线的传递性可得AB∥EG∥FH∥CD，根据平行线的性质得到∠ABF＝∠BFH，∠CDF＝∠DFH，根据已知条件即可得到结论．（3）由（1）（2）即可得出∠F与∠E的等量关系．【解答】解：（1）∠BED＝2∠BFD．证明：连接FE并延长，∵∠BEG＝∠BFE+∠EBF，∠DEG＝∠DFE+∠EDF，∴∠BED＝∠BFD+∠EBF+∠EDF，∵BF、DF分别平分∠ABE、∠CDE，∴∠ABE+∠CDE＝2（∠EBF+∠EDF），∵∠BED＝∠ABE+∠CDE，∴∠EBF+∠EDF＝∠BED，∴∠BED＝∠BFD+∠BED，∴∠BED＝2∠BFD；（2）过点E、F分别作AB的平行线EG、FH，由平行线的传递性可得AB∥EG∥FH∥CD，∵AB∥FH，∴∠ABF＝∠BFH，∵FH∥CD，∴∠CDF＝∠DFH，∴∠BFD＝∠DFH+∠BFH＝∠CDF+∠ABF；同理可得∠BED＝∠DEG+∠BEG＝∠ABE+∠CDE；∵∠BFD＝∠DFH+∠BFH＝∠CDF+∠ABF＝（∠ABE+∠CDE）＝∠BED，∴∠BED＝3∠BFD．（3）由（1）（2）可得∠BED＝n∠BFD．11．【引入】如图1，已知∠ABC+∠ECB＝180°，∠P＝∠Q，求证：∠1＝∠2．【变式】如图2，AB∥CD，∠1＝∠2，求证：∠F＝∠Ｍ【分析】【引入】先判定AB∥DE，则∠ABC＝∠BCD，再由∠P＝∠Q，则∠PBC＝∠QCB，从而得出∠1＝∠2．【变式】延长EF交CD于G，利用平行线的性质得出∠1＝∠EGD，进而得出∠EGD＝∠2，再利用平行线的判定方法得出答案．【解答】【引入】证明：∵∠ABC+∠ECB＝180°，∴AB∥DE，∴∠ABC＝∠BCD，∵∠P＝∠Q，∴PB∥CQ，∴∠PBC＝∠BCQ，∵∠1＝∠ABC﹣∠PBC，∠2＝∠BCD﹣∠BCQ，∴∠1＝∠2．【变式】证明：延长EF交CD于G，如图：∵AB∥CD，∴∠1＝∠EGD∵∠1＝∠2，∴∠EGD＝∠2∴EF∥MN，∴∠EFM＝∠M．12．模型与应用．【模型】（1）如图①，已知AB∥CD，求证∠1+∠MEN+∠2＝360°．【应用】（2）如图②，已知AB∥CD，则∠1+∠2+∠3+∠4+∠5+∠6的度数为900°．如图③，已知AB∥CD，则∠1+∠2+∠3+∠4+∠5+∠6+…+∠n的度数为180°（n﹣1）．（3）如图④，已知AB∥CD，∠AM1M2的角平分线M1O与∠CM n M n﹣1的角平分线M n O 交于点O，若∠M1OM n＝m°．在（2）的基础上，求∠2+∠3+∠4+∠5+∠6+……+∠n ﹣1的度数．（用含m、n的代数式表示）【分析】（1）过点E作EF∥CD，根据平行线的判定得出EF∥AB，根据平行线的性质得出即可；（2）过E作EQ∥CD，过F作FW∥CD，过G作GR∥CD，过H作HY∥CD，根据平行线的判定得出EQ∥FW∥GR∥HY∥AB∥CD，根据平行线的性质得出即可；（3）过点O作SR∥AB，根据平行线的性质得出即可；【解答】（1）证明：过点E作EF∥CD，∵AB∥CD，∴EF∥AB，∴∠1+∠MEF＝180°，同理∠2+∠NEF＝180°，∴∠1+∠2+∠MEN＝360°；【应用】（2）过E作EQ∥CD，过F作FW∥CD，过G作GR∥CD，过H作HY∥CD，∵CD∥AB，∴EQ∥FW∥GR∥HY∥AB∥CD，∴∠1+∠MEQ＝180°，∠QEF+∠EFW＝180°，∠WFG+∠FGR＝180°，∠RGH+∠GHY＝180°，∠YHN+∠6＝180°，∴∠1+∠2+∠3+∠4+∠5+∠6＝5×180°＝900°，同理∠1+∠2+∠3+∠4+∠5+∠6+…+∠n＝180°（n﹣1），故答案为：900°，180°（n﹣1）；（3）解：过点O作SR∥AB，∵AB∥CD，∴SR∥CD，∴∠AM1O＝∠M1OR同理∠C M n O＝∠M n OR∴∠A M1O+∠CM n O＝∠M1OR+∠M n OR，∴∠A M1O+∠CM n O＝∠M1OM n＝m°，∵M1O平分∠AM1M2，∴∠AM1M2＝2∠A M1O，同理∠CM n M n﹣1＝2∠CM n O，∴∠AM1M2+∠CM n M n﹣1＝2∠AM1O+2∠CM n O＝2∠M1OM n＝2m°，又∵∠A M1M2+∠2+∠3+∠4+∠5+∠6+……+∠n﹣1+∠CM n M n﹣1＝180°（n﹣1），∠2+∠3+∠4+∠5+∠6+…+∠n﹣1＝（180n﹣180﹣2m）°．13．如图1，MA1∥NA2，则∠A1+∠A2＝180度．如图2，MA1∥NA3，则∠A1+∠A2+∠A3＝360度．如图3，MA1∥NA4，则∠A1+∠A2+∠A3+∠A4＝540度．如图4，MA1∥NA5，则∠A1+∠A2+∠A3+∠A4+∠A5＝720度．从上述结论中你发现了什么规律？如图5，MA1∥NA n，则∠A1+∠A2+∠A3+…+∠A n＝180（n﹣1）度．【分析】首先过各点作MA1的平行线，由MA1∥NA2，可得各线平行，根据两直线平行，同旁内角互补，即可求得答案，注意找到规律：MA1∥NA n，则∠A1+∠A2+∠A3+…+∠A n＝180（n﹣1）度是关键．【解答】解：如图1，∵MA1∥NA2，∴∠A1+∠A2＝180°．如图2，过点A2作A2C1∥A1M，∵MA1∥NA3，∴A2C1∥A1M∥NA3，∴∠A1+∠A1A2C1＝180°，∠C1A2A3+∠A3＝180°，∴∠A1+∠A2+∠A3＝360°．如图3，过点A2作A2C1∥A1M，过点A3作A3C2∥A1M，∵MA1∥NA3，∴A2C1∥A3C2∥A1M∥NA3，∴∠A1+∠A1A2C1＝180°，∠C1A2A3+∠A2A3C2＝180°，∠C2A3A4+∠A4＝180°，∴∠A1+∠A2+∠A3+∠A4＝540°．如图4，过点A2作A2C1∥A1M，过点A3作A3C2∥A1M，过点A4作A4C3∥A1M，∵MA1∥NA5，∴A2C1∥A3C2∥A4C3∥NA5，∴∠A1+∠A1A2C1＝180°，∠C1A2A3+∠A2A3C2＝180°，∠C2A3A4+∠A3A4C3＝180°∠C3A4A5+∠A5＝180°，∴∠A1+∠A2+∠A3+∠A4+∠A5＝720°．从上述结论中你发现了规律：如图5，MA1∥NA n，则∠A1+∠A2+∠A3+…+∠A n＝180（n ﹣1）度．故答案为：180，360，540，720，180（n﹣1）．14．如图，AB∥CD，点F在CE上，∠EAF＝∠BAF，若∠AEC＝105°，∠DCE＝115°，求∠AFC的度数．【分析】过点E作EM∥AB，由平行线的性质得到∠MEC＝65°，从而得到∠AEM＝40°，再根据平行线的性质得到∠EAB＝180°﹣∠AEM＝140°，进而得到∠EAF＝35°，最后根据三角形的外角定理即可求解．【解答】解：如图，过点E作EM∥AB，∵AB∥CD，∴EM∥CD，∴∠MEC+∠DCE＝180°，∵∠DCE＝115°，∴∠MEC＝180°﹣115°＝65°，∵∠AEC＝∠MEC+∠AEM，∠AEC＝105°，∴∠AEM＝40°，∵EM∥AB，∴∠AEM+∠EAB＝180°，∴∠EAB＝180°﹣∠AEM＝140°，∵∠EAB＝∠EAF+∠BAF，∠EAF＝∠BAF，∴∠EAF+3∠EAF＝140°，∴∠EAF＝35°，∴∠AFC＝∠EAF+∠AEC＝35°+105°＝140°．15．直线AB∥CD，E为直线AB、CD之间的一点，完成以下问题：（1）如图1，若∠B＝15°，∠BED＝90°，则∠D＝75°；（2）如图2，若∠B＝α，∠D＝β，求出∠BED的度数（用a、β表示）；（3）如图3，若∠B＝α，∠C＝β，则a、β与∠BEC之间有什么等量关系？请猜想证明．【分析】（1）过E作EF∥AB，根据两直线平行，内错角相等进行计算；（2）过E作EF∥AB，根据两直线平行，同旁内角互补进行计算；（3）过点E作EF∥AB，根据两直线平行，内错角相等，以及两直线平行，同旁内角互补进行计算．【解答】解：（1）过E作EF∥AB，∵AB∥CD，∴EF∥CD，∵∠B＝15°，∴∠BEF＝15°，又∵∠BED＝90°，∴∠DEF＝75°，∵EF∥CD，∴∠D＝75°，故答案为：75°；（2）过E作EF∥AB，∵AB∥CD，∴EF∥CD，∴∠B+∠BEF+∠DEF+∠D＝360°，又∵∠B＝α，∠D＝β，∴∠BED＝∠BEF+∠DEF＝360°﹣α﹣β，故答案为：∠BED＝360°﹣α﹣β；（3）猜想：∠BEC＝180°﹣α+β．证明：过点E作EF∥AB，则∠BEF＝180°﹣∠B＝180°﹣α，∵AB∥EF，AB∥CD，∴EF∥CD，∴∠CEF＝∠C＝β，∴∠BEC＝∠BEF+∠CEF＝180°﹣α+β．16．问题情境：如图1，AB∥CD，∠P AB＝135°，∠PCD＝125°．求∠APC度数．小明的思路是：如图2，过P作PE∥AB，通过平行线性质，可求得∠APC的度数．请写出具体求解过程．问题迁移：（1）如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP＝∠α，∠BCP＝∠β．∠CPD、∠α、∠β之间有何数量关系？请说明理由；（2）在（1）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出∠CPD、∠α、∠β间的数量关系．【分析】过P作PE∥AB，构造同旁内角，通过平行线性质，可得∠APC＝45°+55°＝100°．（1）过P作PE∥AD交CD于E，推出AD∥PE∥BC，根据平行线的性质得出∠α＝∠DPE，∠β＝∠CPE，即可得出答案；（2）分两种情况：①点P在A、M两点之间，②点P在B、O两点之间，分别画出图形，根据平行线的性质得出∠α＝∠DPE，∠β＝∠CPE，即可得出结论．【解答】解：过P作PE∥AB，∵AB∥CD，∴PE∥AB∥CD，∴∠APE＝180°﹣∠A＝45°，∠CPE＝180°﹣∠C＝55°，∴∠APC＝45°+55°＝100°；（1）∠CPD＝∠α+∠β，理由如下：。

七年级数学下册《平行线的经典模型》

七年级数学下册《平行线的经典模型》平行线的经典模型题型一、平行加拐点——“M”模型例1：如图，AB∥CD，求∠BAP、∠APC、∠PCD的关系式，并加以证明。

解：根据平行线的性质，得到PE∥AB，因此∠1＝∠BAP。

又因为AB∥CD，PE∥AB，所以PE∥CD，因此∠2＝∠PCD。

所以∠1＋∠2＝∠BAP＋∠PCD，即∠APC＝∠BAP＋∠PCD。

练一练】1、如图，BA∥DE，∠B＝30°，∠D＝40°，则∠C的度数是（）。

A、10°B、35°C、70°D、80°2、如图，AB∥DE，则∠1、∠2、∠3关系是（）。

A、∠3＞∠1＋∠2B、∠2＝∠3－∠1C、∠3＝∠1＋∠2D、无法确定3、如图，AB∥CD，∠BED＝90°，则∠1与∠2之间的数量关系是（）。

A、∠2＝2∠1B、∠2－∠1＝90°C、∠1＋∠2＝180°D、无法确定4、如图，已知AB∥CD∥EF，GC⊥CF，∠B＝60°，∠EFC＝45°，求∠BCG的度数。

5、如图，一个含有30°角的直角三角板的两个顶点放在一个矩形的对边上，如果∠1＝25°，那么∠2的度数是（）。

A、130°B、105°C、115°D、125°6、将一个直角三角板和一把直尺按如图所示放置，若∠α＝43°，则∠β＝？例2：已知如图，AB∥CD∥EF，点M、N、P分别在AB、CD、EF上，NQ平分∠___。

1）若∠AMN＝50°，∠EPN＝70°，求∠MNP，∠DNQ的度数；2）若∠AMN＝x度，∠EPN＝y度，请直接写出∠DNQ的度数（用含x，y的代数式表示）；3）试探究：∠___与∠___，∠___之间的数量关系，并说明理由。

练一练】如图，已知AB∥MP∥CD，MN平分∠AMD，∠A＝40°，∠D＝50°，求∠NMP的度数。

专题01 平行线模型-“猪蹄”模型(M模型)(原卷版)

专题01 平行线模型-“猪蹄”模型（M 模型）几何学有形象化的好处，几何会给人以数学直觉，不能把几何学等同于逻辑推理，只会推理，缺乏数学直觉，是不会有创造的。

现在初一的学生刚刚开始接触几何的证明，普遍会出现证明步骤不规范，在书写的时候也会出现无从下手的情况，做题速度也普遍变慢，只有少数学生能够在规定时间内正确作答。

所以，只要学生能够学会利用平行线的性质和判定的几个基本模型去解决实际问题，会起到事半功倍的效果。

本次课主要学习平行线模型-“猪蹄”模型（M 模型），为以后的学习打好一个坚实的基础。

【模型刨析】模型一“猪蹄”模型（M 模型）点P 在EF 左侧，在AB 、 CD 内部“猪蹄”模型结论1：若AB ∥CD ，则∠P =∠AEP +∠CFP ；结论2：若∠P =∠AEP +∠CFP ，则AB ∥CD .【典例分析】【典例1】（2022春•上虞区期末）如图1，已知点E ，F 分别是直线AB ，CD 上的点，点M 在AB 与CD 之间，且AB ∥CD ．（1）若∠EMF ＝80°，则∠AEM +∠CFM ＝．（2）如图2，在图1的基础上，作射线EN ，FN 交于点N ，使∠AEN ＝∠AEM ，∠CFN ＝∠CFM ，设∠EMF ＝α，猜想∠ENF 的度数（用α表示），并说明理由．（3）如图3，在图1的基础上，分别作射线EP，FP交于点P，作射线EQ，FQ 交于点Q，若∠AEP＝∠AEM，∠CFP＝∠CFM，∠BEQ＝∠BEM，∠DFQ＝∠DFM，请直接写出∠P与∠Q间的数量关系．【变式1-1】（2021秋•兴城市期末）如图是A，B，C三岛的平面图，C岛在A 岛的北偏东52°方向，C岛在B岛的北偏西43°方向，求从C岛看A，B两岛的视角∠ACB的度数．【变式1-2】（2022春•朝阳县期末）学习完平行线的性质与判定之后，我们发现借助构造平行线的方法可以帮我们解决许多问题．（1）小明遇到了下面的问题：如图1，l1∥l2，点P在l1，l2内部，探究∠A，∠APB，∠B的关系，小明过点P作l1的平行线，可得∠APB，∠A，∠B之间的数量关系是：∠APB＝　．（2）如图2，若AC∥BD，点P在AC，BD外部，∠A，∠B，∠APB的数量关系是否发生变化？请写出证明过程．【变式1-3】（2021秋•长春期末）小明同学遇到这样一个问题：如图①，已知：AB∥CD，E为AB、CD之间一点，连接BE，ED，得到∠BED．求证：∠BED＝∠B+∠D．小亮帮助小明给出了该问的证明．证明：过点E作EF∥AB，则有∠BEF＝∠B．∵AB∥CD，∴EF∥CD，∴∠FED＝∠D，∴∠BED＝∠BEF+∠FED＝∠B+∠D．请你参考小亮的思考问题的方法，解决问题：直线l1∥l2，直线EF和直线l1、l2分别交于C、D两点，点A、B分别在直线l1、l2上，猜想：如图②，若点P在线段CD上，∠PAC＝15°，∠PBD＝40°，求∠APB的度数．拓展：如图③，若点P在直线EF上，连接PA、PB（BD＜AC），直接写出∠PAC、∠APB、∠PBD之间的数量关系．【夯实基础】1．（2022春•内乡县期末）如图，AB∥CD，∠1＝45°，∠2＝30°，则∠3的度数为（）A．55°B．75°C．80°D．105°2．（2022春•安新县期末）如图所示是汽车灯的剖面图，从位于O点灯发出光照射到凹面镜上反射出的光线BA，CD都是水平线，若∠ABO＝α，∠DCO＝60°，则∠BOC的度数为（）A．180°﹣αB．120°﹣αC．60°+αD．60°﹣α3．（2020•韶关模拟）如图，C岛在A岛的北偏东45°方向，C岛在B岛的北偏西25°方向，则从C岛看A、B两岛的视角∠ACB的度数是（）A．70°B．20°C．35°D．110°4．（2019•淮安区校级二模）如图，AB∥CD，∠1＝45°，∠3＝75°，则∠2的度数为（）A．30°B．35°C．40°D．45°5．（2019•青岛模拟）如图，AB∥CD，点E在线段BC上，若∠1＝40°，∠2＝30°，则∠3的度数是（）A．50°B．55°C．60°D．70°6．（2022•朝阳区校级模拟）已知l1∥l2，一个含有30°角的三角尺按照如图所示的位置摆放，若∠1＝65°，则∠2＝度．7．（2022春•诸暨市期末）从汽车灯的点O处发出的一束光线经灯的反光罩反射后沿CO方向平行射出，已知入射光线OA的反射光线为AB，∠OAB＝∠COA＝72°．在如图中所示的截面内，若入射光线OD经反光罩反射后沿DE射出，且∠ODE＝27°．则∠AOD的度数是．8．（2022春•文登区期末）将一副三角板如图摆放，使两个直角顶点重合，斜边平行，则∠1＝．9．（2021秋•九江期末）如图．BA∥DE，∠B＝30°，∠D＝40°，求∠C的度数．10．（2021春•海淀区校级期末）如图，AB∥CD，∠B＝26°，∠D＝39°，求∠BED的度数．11．（2021春•拱墅区期中）小明同学在完成七年级下册数学第1章的线上学习后，遇到了一些问题，请你帮他解决一下．（1）如图1，已知AB∥CD，则∠AEC＝∠BAE+∠DCE成立吗？请说明理由．（2）如图2，已知AB∥CD，BE平分∠ABC，DE平分∠ADC，BE、DE所在直线交于点E，若∠FAD＝50°，∠ABC＝40°，求∠BED的度数．12．（2021春•云梦县期中）如图，BE平分∠ABD，DE平分∠BDC．（1）若∠1+∠2＝90°，求证：AB∥CD；（2）若AB∥CD，求∠BED的度数．【能力提升】13．（2021春•沧县期中）引入在解决有关平行线的问题时，如果无法直接得到角的关系，就需要借助辅助线来帮助解答，如图是一个“美味”的模型﹣﹣“猪蹄模型”．如图所示，AB ∥CD，点E在直线AB与CD之间，连接AE、CE，求证：∠AEC＝∠BAE+∠DCE．嘉琪想到了下面的思路，请根据思路继续完成求证：证明：如图，过点E作EF∥AB．思考当点E在如图所示的位置时，其他条件不变，写出∠BAE，∠AEC，∠DCE 三者之间的数量关系并说明理由．应用如图，延长线段AE交直线CD于点M，已知∠BAE＝132°，∠DCE＝118°，求∠MEC的度数．提升点E、F、G在直线AB与CD之间，连接AE、EF、FG和CG，其他条件不变，如图．若∠EFG＝m°，直接写出∠BAE+∠AEF+∠FGC+∠DCG的总度数．14．（2022春•阳江期末）如图1，AB∥CD，EOF是直线AB、CD间的一条折线．（1）试证明：∠O＝∠BEO+∠DFO．（2）如果将折一次改为折二次，如图2，则∠BEO、∠O、∠P、∠PFC之间会满足怎样的数量关系，证明你的结论．15．（2022春•来宾期末）如图，直线PQ∥MN，直角三角尺ABC的∠BAC＝30°，∠ACB＝90°．（1）若把三角尺按图甲方式放置，则∠MAC+∠PBC＝ °；（2）若把三角尺按图乙方式放置，点D，E，F是三角尺的边与平行线的交点，若∠AEN＝∠A，求∠BDF的值；（3）如图丙，三角尺的直角顶点C始终在两条平行线之间，点G在线段CD 上，连接EG，适当转动三角尺，使得CE恰好平分∠MEG，求的值．。

专题01平行线的四大模型(原卷版)-2023-2024学年七年级数学下册压轴题(人教版)

专题01 平行线的四大模型平行线的性质和判定是证明角相等、研究角的关系的重要依据，是研究几何图形位置关系与数量关系的基础，是平面几何的一个重要内容和学习简单的逻辑推理的素材。

它不但为三角形的内角和定理的证明提供了转化的方法，而且也是今后学习三角形、四边形知识的基础.本节课重点学习平行线的基础模型的应用迁移.模型一“铅笔”模型点P在EF右侧，在AB、CD内部“铅笔”模型结论1：若AB∥CD，则∠P+∠AEP+∠PFC=3 60°；结论2：若∠P+∠AEP+∠PFC= 360°，则AB∥CD.专题分析模型分类模型分析【典例1】（2023秋•南岗区校级期中）已知，射线FG分别交射线AB、DC于点F、G，点E为射线FG上一点．（1）如图1，若∠A+∠D＝∠AED，求证：AB∥CD．（2）如图2，若AB∥CD，求证：∠A﹣∠D＝∠AED．（3）如图3，在（2）的条件下，DI交AI于点Ⅰ，交AE于点K，∠EDI＝∠CDE，∠BAI＝∠EAI，∠I＝∠AED＝25°，求∠EKD的度数．【变式11】（2023•渝中区校级模拟）如图，已知直线a∥b，∠BAC＝90°，∠1＝40°，则∠2的度数为（）A．40°B．50°C．130°D．140°典例分析【变式12】（2023•金安区一模）如图，已知a∥b，∠1＝45°，∠2＝125°，则∠ABC的度数为（）A．100°B．105°C．115°D．125°【变式13】（2022春•肇州县期末）如图，AB∥CD，∠C＝110°，∠B＝120°，则∠BEC ＝（）A．110°B．120°C．130°D．150°【变式14】（2023春•巴南区月考）已知直线MN∥PQ，点C、B分别在直线MN、PQ上，点A在直线MN和PO之间．（1）如图1，求证：∠CAB﹣∠MCA＝∠PBA；（2）如图2，CD∥AB，点E在直线PQ上，且∠MCA＝∠DCE，求证：∠ECN＝∠CAB；（3）如图3，BF平分∠PBA，CG平分∠ACN，且AF∥CG．若∠CAB＝50°，直接写出∠AFB的度数．【变式15】（2023春•遂宁期末）如图，直线PQ∥MN，两个三角形如图①放置，其中∠ABC ＝∠CDE＝90°，∠ACB＝30°，∠BAC＝60°，∠DCE＝∠DEC＝45°，点E在直线PQ上，点B，C均在直线MN上，且CE平分∠ACN．（1）求∠DEQ的度数；（2）如图②，若将△ABC绕B点以每秒3°的速度按逆时针方向旋转（A，C的对应点分别为F，G）．设旋转时间为t秒，当t＝10时，边BG与CD有何位置关系？请说明理由．模型分析模型二“猪蹄”模型（模型）点P在EF左侧，在AB、CD内部“猪蹄”模型结论1：若AB∥CD，则∠P=∠AEP+∠CFP；结论2：若∠P=∠AEP+∠CFP，则AB∥CD.典例分析【典例2】（2023春•邵阳县期末）如图，直线AB∥CD，连接EF，直线AB，CD及线段EF 把平面分成①②③④四个部分，规定：线上各点不属于任何部分．当动点G落在某个部分时，连接GE，GF，构成∠EGF，∠GEB，∠GFD三个角．（1）当动点G落在第③部分时，如图一，试说明：∠EGF，∠GEB，∠GFD三者的关系；（2）当动点G落在第②部分时，如图二，思考（1）中三者关系是否仍然成立若不成立，说明理由．【变式21】（2023•盘锦）如图，直线AB∥CD，将一个含60°角的直角三角尺EGF按图中方式放置，点E在AB上，边GF，EF分别交CD于点H，K，若∠BEF＝64°，则∠GHC 等于（）A．44°B．34°C．24°D．14°【变式22】（2023•盘锦）如图，直线AB∥CD，将一个含60°角的直角三角尺EGF按图中方式放置，点E在AB上，边GF，EF分别交CD于点H，K，若∠BEF＝64°，则∠GHC 等于（）A．44°B．34°C．24°D．14°【变式23】（2023•海南模拟）如图，已知AB∥DE，∠B＝20°，∠D＝130°，那么∠BCD 等于（）A．60°B．70°C．80°D．90°【变式24】（2023春•覃塘区期末）如图，AB∥CD，将一副直角三角板作如下摆放，∠GEF ＝60°，∠MNP＝45°．下列结论：①GE∥MP；②∠EFN＝150°；③∠BEF＝65°；④∠AEG＝35°，其中正确的个数是（）A．1B．2C．3D．4【变式25】（2023春•赣县区期末）【问题背景】：同学们，观察小猪的猪蹄，你会发现一个熟悉的几何图形，我们就把这个图形的形象称为“猪蹄模型”，猪蹄模型中蕴含着角的数量关系．【问题探究】：（1）如图1，AB∥CD，E为AB、CD之间一点，连接BE、DE，得到∠BED 与∠B、∠D之间的数量关系，并说明理由；【类比迁移】：（2）请你利用上述“猪蹄模型”得到的结论或解题方法，完成下面的问题：如图2，直线AB∥CD，若∠B＝23°，∠G＝35°，∠D＝25°，求∠BEG+∠GFD的度数；【灵活应用】：（3）如图3，直线AB∥CD，若∠E＝∠B＝60°，∠F＝85°，则∠D＝25度．【变式26】（2023春•邵阳期末）如图1，直线AB∥CD，P是截线MN上的一点．（1）若∠MNB＝45°，∠MDP＝20°，求∠MPD；（2）如图1，当点P在线段MN上运动时，∠CDP与∠ABP的平分线交于Q，问是否为定值，若是定值，请求出；若不是定值，请说明理由；（3）如图2，若T是直线MN上且位于M点的上方的一点，如图所示，当点P在射线MT上运动时，∠CDP与∠ABP的平分线交于Q，问的值是否和（2）问中的情况一样呢？请你写出探究过程，说明理由．【变式27】（2023春•防城港期末）阅读下面材料：（1）小亮同学遇到这样一个问题：已知：如图甲，AB∥CD，E为直线AB，CD之间一点，连接BE、DE得到∠BED．求证：∠BED＝∠B+∠D．下面是小亮写出了该问题的证明，请你帮他把证明过程补充完整．证明：过点E作EF∥AB，则有∠BEF＝∠B，∵AB∥CD，∴CD∥EF，∴∠FED＝∠D，∴∠BED＝∠BEF+∠FED＝∠B+∠D．（2）请你参考小亮思考问题的方法，解决问题：如图乙，直线a∥b，BE平分∠ABC，DE平分∠ADC，若∠ABC＝50°，∠ADC＝60°，求∠BED的度数，（过点E作EF∥AB）模型分析模型三“臭脚”模型点P在EF右侧，在AB、CD外部“臭脚”模型结论1：若AB∥CD，则∠P=∠AEP∠CFP或∠P=∠CFP∠AEP；结论2：若∠P=∠AEP∠CFP或∠P=∠CFP∠AEP，则AB∥CD.典例分析【典例3】（2023春•中山区期末）如图，∠ABE+∠BED＝∠CDE．（1）如图1，求证AB∥CD；（2）如图2，点P在AB上，∠CDP＝∠EDP，BF平分∠ABE，交PD于点F，探究∠BFP，∠BED的数量关系，并证明你的结论；（3）在（2）的条件下，如图3，PQ交ED延长线于点Q，∠DPQ＝2∠APQ，∠PQD ＝80°，求∠CDE的度数．【变式31】已知AB ∥CD ．（1）如图1，求证：∠ABE +∠DCE ﹣∠BEC ＝180°；（2）如图2，∠DCE 的平分线CG 的反向延长线交∠ABE 的平分线BF 于F ．若BF ∥CE ，∠BEC ＝26°，求∠BFC ．结论1：若AB ∥CD ，则∠P =∠CFP ∠AEP 或∠P =∠AEP ∠CFP ；结论2：若∠P =∠CFP ∠AEP 或∠P =∠AEP ∠CFP ，则AB ∥CD .模型四“骨折”模型点P 在EF 左侧，在AB 、 CD 外部·“骨折”模型模型分析典例分析【典例4】（2022秋•朝阳区校级期末）已知AB∥CD，点E在AB上，点F在DC上，点G 为射线EF上一点．（1）【基础问题】如图1，试说明：∠AGD＝∠A+∠D．（完成图中的填空部分）证明：过点G作直线MN∥AB，又∵AB∥CD，∴∥CD∵MN∥AB，∴∠＝∠MGA．∵MN∥CD，∴∠D＝（）∴∠AGD＝∠AGM+∠DGM＝∠A+∠D．（2）【类比探究】如图2，当点G在线段EF延长线上时，请写出∠AGD、∠A、∠D三者之间的数量关系，并说明理由．（3）【应用拓展】如图3，AH平分∠GAE，DH交AH于点H，且∠GDH＝2∠HDF，∠HDF＝22°，∠H＝32°，直接写出∠DGA的度数为°．【变式41】（2022秋•肃州区校级期末）如图（1），AB∥CD，∠AEP＝40°，∠PFD＝130°，求∠EPF的度数．小明想到了以下方法：解：如图（1），过点P作PM∥AB，∴∠1＝∠AEP＝40°（两直线平行，内错角相等）∵AB∥CD（已知）∴PM∥CD（平行于同一条直线的两直线平行）∴∠2+∠PFD＝180°（两直线平行，同旁内角互补）∵∠PFD＝130°（已知）∴∠2＝180°﹣130°＝50°∴∠EPF＝∠1+∠2＝40°+50°＝90°即∠EPF＝90°【探究】如图（2），AB∥CD，∠AEP＝50°，∠PFC＝120°，求∠EPF的度数．【应用】如图（3），在【探究】的条件下，∠PEA的平分线和∠PFC的平分线交于点G，求∠G的度数．【变式42】（2022春•朝阳县期末）学习完平行线的性质与判定之后，我们发现借助构造平行线的方法可以帮我们解决许多问题．（1）小明遇到了下面的问题：如图1，l1∥l2，点P在l1，l2内部，探究∠A，∠APB，∠B的关系，小明过点P作l1的平行线，可得∠APB，∠A，∠B之间的数量关系是：∠APB＝．（2）如图2，若AC∥BD，点P在AC，BD外部，∠A，∠B，∠APB的数量关系是否发生变化？请写出证明过程．【变式43】（2020春•乳山市期中）【信息阅读】材料信息：如图①，AB∥DE，点C是直线AB，DE外任意一点，连接BC，DC．方法信息：如图②，在“材料信息”的条件下，∠B＝55°，∠D＝35°，求∠BCD的度数．解：过点C作CF∥AB．∴∠BCF＝∠B＝55°．∵AB∥DE，∴CF∥DE．∴∠DCF＝∠D＝35°．∴∠BCD＝55°﹣35°＝20°．【问题解决】（1）通过【信息阅读】，猜想：∠B，∠D，∠BCD之间有怎样的等量关系？请直接写出结论：；（2）如图③，在“材料信息”的条件下，改变点C的位置，∠B，∠D，∠BCD之间的等量关系是否改变？若不改变，请写出理由；若改变，请写出新的等量关系及理由．1.（2023春•建昌县期末）如图，将一个含30°角的直角三角板的直角顶点C放在直尺的两边MN，PQ之间，则下列结论中：①∠1＝∠3；②∠2＝∠3；③∠1+∠3＝90°；④若∠3＝60°，则AB⊥PQ，其中正确结论的个数是（）A．1个B．2个C．3个D．4个2．（2023春•芜湖期末）如图所示是汽车灯的剖面图，从位于O点灯发出光照射到凹面镜上反射出的光线BA，CD都是水平线，若∠ABO＝α，∠DCO＝60°，则∠BOC的度数为（）A．180°﹣αB．120°﹣αC．60°+αD．60°﹣α3．（2022•恩施州）已知直线l1∥l2，将含30°角的直角三角板按如图所示摆放．若∠1＝120°，则∠2＝（）A．120°B．130°C．140°D．150°4．（2022•博山区一模）如图，直线a∥b，点M、N分别在直线a、b上，P为两平行线间一点，那么∠1+∠2+∠3等于（）A．360°B．300°C．270°D．180°5．（2021春•椒江区校级月考）如图，已知AB∥CD，∠BAD和∠BCD的平分线交于点E，∠FBC＝n°，∠BAD＝m°，则∠AEC等于（）度．A．90﹣+m B．90﹣﹣C．90﹣D．90﹣+ 6．（2023春•赫山区期末）【问题情景】（1）如图1，AB∥CD，∠P AB＝135°，∠PCD＝115°，求∠APC的度数；【问题迁移】（2）如图2，已知∠MON，AD∥BC，点P在射线OM上运动，当点P在A，B两点之间运动时，连接PD，PC，∠ADP＝∠α，∠BCP＝∠β，求∠CPD与∠α，∠β之间的数量关系，并说明理由；【知识拓展】（3）在（2）的条件下，若将“点P在A，B两点之间运动”改为“点P在A，B两点外侧运动（点P与点A，B，O三点不重合）”其他条件不变，请直接写出∠CPD 与∠α，∠β之间的数量关系．7．（2022春•良庆区校级期中）已知AM∥CN，点B为平面内一点，AB⊥BC于B．（1）如图1，直接写出∠A和∠C之间的数量关系；（2）如图2，过点B作BD⊥AM于点D，求证：∠ABD＝∠C；（3）如图3，在（2）问的条件下，点E、F在DM上，连接BE、BF、CF，BF平分∠DBC，BE平分∠ABD，若∠FCB＝∠CFD，∠BFC＝3∠DBE，求∠EBC的度数．8．（2021秋•平昌县期末）如图，AD∥BC，∠BAD的平分线交BC于点G，∠BCD＝90°．（1）试说明：∠BAG＝∠BGA；（2）如图1，点F在AG的反向延长线上，连接CF交AD于点E，若∠BAG﹣∠F＝45°，求证：CF平分∠BCD．（3）如图2，线段AG上有点P，满足∠ABP＝3∠PBG，过点C作CH∥AG．若在直线AG上取一点M，使∠PBM＝∠DCH，求的值．9．（2023春•黑山县期中）问题情境我们知道，“两条平行线被第三条直线所截，同位角相等，内错角相等，同旁内角互补”，所以在某些探究性问题中通过“构造平行线”可以起到转化的作用．已知三角板ABC中，∠BAC＝60°，∠B＝30°，∠C＝90°，长方形DEFG中，DE∥GF．问题初探（1）如图（1），若将三角板ABC的顶点A放在长方形的边GF上，BC与DE相交于点M，AB⊥DE于点N，求∠EMC的度数．分析：过点C作CH∥GF．则有CH∥DE，从而得∠CAF＝∠HCA，∠EMC＝∠MCH，从而可以求得∠EMC的度数．由分析得，请你直接写出：∠CAF的度数为，∠EMC的度数为．类比再探（2）若将三角板ABC按图（2）所示方式摆放（AB与DE不垂直），请你猜想写∠CAF 与∠EMC的数量关系，并说明理由．（3）请你总结（1），（2）解决问题的思路，在图（3）中探究∠BAG与∠BMD的数量关系？并说明理由．10．（2022春•龙亭区校级期末）如图，已知AB∥CD，E、F分别在AB、CD上，点G在AB、CD之间，连接GE、GF．（1）当∠BEG＝40°，EP平分∠BEG，FP平分∠DFG时：①如图1，若EG⊥FG，则∠P的度数为；②如图2，在CD的下方有一点Q，EG平分∠BEQ，FD平分∠GFQ，求∠Q+2∠P的度数；（2）如图3，在AB的上方有一点O，若FO平分∠GFC．线段GE的延长线平分∠OEA，则当∠EOF+∠EGF＝100°时，请直接写出∠OEA与∠OFC的数量关系．11．（2023春•孝义市期末）综合与探究数学活动课上，老师以“一个含45°的直角三角板和两条平行线”为背景展开探究活动，如图1，已知直线m∥n，直角三角板ABC中，∠ACB＝90°，∠BAC＝∠ABC＝45°．（1）如图1，若∠2＝65°，则∠1＝；（直接写出答案）（2）“启航”小组在图1的基础上继续展开探究：如图2，调整三角板的位置，当三角板ABC的直角顶点C在直线n上，直线m与AB，AC相交时，他们得出的结论是：∠1﹣∠2＝135°，你认为启航小组的结论是否正确，请说明理由；（3）如图3，受到“启航”小组的启发，“睿智”小组提出的问题是：在图2的基础上，继续调整三角板的位置，当点C不在直线n上，直线m与AC，BC相交时，∠1与∠2有怎样的数量关系？请你用平行线的知识说明理由．12．（2023春•安化县期末）在课后学习中，小红探究平行线中的线段与角的数量关系，如图，直线AB∥CD，点N在直线CD上，点P在直线AB上，点M为平面上任意一点，连接MP，MN，PN．（1）如图1，点M在直线CD上，PM平分∠APN，试说明∠PMN＝∠MPN；（2）如图2，点M在直线AB，CD之间，∠PMN＝70°，∠MNC＝30°，求∠APM的度数；（3）如图3，∠APM和∠MNC的平分线交于点Q，∠PQN与∠PMN有何数量关系？并说明理由．12．（2023春•甘井子区期末）如图1，点M在射线BA，CD之间，0°＜∠ABM＜30°，连接BM，过点M作ME⊥BM交射线CD于点E，且∠MED﹣∠B＝90°．（1）求证：AB∥CD；（2）过点C作∠ECN＝∠B，交直线ME于点N，先按要求画图，再解决下列问题．①当CN在CD上方，满足∠CNE＝5∠B时，在图2中画图，求∠B的度数；②作∠BME的角平分线交射线CD于点K，交∠ECN的角平分线于点F，请直接写出∠MKC与∠MFC之间的数量关系．。

七年级数学下册-专题01平行线(四种模型)专项训练(解析版)

专题01平行线（四种模型）专项训练题型一：M 模型（锯齿形）题型二：笔尖型题型三：“鸡翅”型题型四：“骨折”型模型一：M 模型如图，若AB //CD，你能确定∠B、∠D 与∠BED 的大小关系吗？解：∠B＋∠D＝∠DEB ．理由如下：过点E 作EF //AB又∵AB//CD．∴EF//CD．∴∠D =∠DEF．∠B=∠BEF．∴∠B＋∠D＝∠BEF＋∠DEF＝∠DEB即∠B＋∠D＝∠DEB ．一．选择题（共3小题）1．（2023春•临淄区期末）如图，//AB EF ，90C ∠=︒，则α、β和γ的关系是()A ．βαγ=+B ．180αβγ++=︒C ．90αβγ+-=︒D ．180βγα+-=︒【分析】此题可以构造辅助线，利用三角形的外角的性质以及平行线的性质建立角之间的关系．【解答】解：延长DC 交AB 与G ，延长CD 交EF 于H ．在直角BGC ∆中，190α∠=︒-；EHD ∆中，2βγ∠=-，//AB EF ，12∴∠=∠，90αβγ∴︒-=-，即90αβγ+-=︒．故选：C ．【点评】本题考查的是平行线的性质，根据题意作出辅助线是解答此题的关键．2．（2023春•天宁区校级期中）如图，//AB CD ，EMNF 是直线AB 、CD 间的一条折线．若140∠=︒，260∠=︒，370∠=︒，则4∠的度数为()A ．55︒B ．50︒C ．40︒D ．30︒【分析】过M 作//OM AB ，//PN AB ，根据平行线的性质得到1EMO ∠=∠，4PNF ∠=∠，OMN PNM ∠=∠，由角的和差得到(1)(4)14EMN MNF MNP MNP ∠-∠=∠+∠-∠+∠=∠-∠，代入数据即可得到结论．【解答】解：如图2，过M 作//OM AB ，//PN AB ，//AB CD ，//////AB OM PN CD ∴，1EMO ∴∠=∠，4PNF ∠=∠，OMN PNM ∠=∠，(1)(4)14EMN MNF MNP MNP ∴∠-∠=∠+∠-∠+∠=∠-∠，6070404∴︒-︒=︒-∠，450∴∠=︒．故选：B ．【点评】本题考查的是平行线的性质，根据题意作出辅助线，构造出平行线是解答此题的关键．3．（2022春•海安市校级月考）如图，//AB EF ，90C ∠=︒，则α、β、γ的关系为()A ．βαγ=+B ．90αβγ+-=︒C ．180αβγ++=︒D ．90βγα+-=︒【分析】此题可以构造辅助线，利用三角形的外角的性质以及平行线的性质建立角之间的关系．【解答】解：延长DC 交AB 于G ，延长CD 交EF 于H ．直角BGC ∆中，190α∠=︒-；EHD ∆中，2βγ∠=-，//AB EF ，12∴∠=∠，90αβγ∴︒-=-，即90αβγ+-=︒．故选：B ．【点评】此题主要考查了三角形的外角的性质以及平行线的性质，解题的关键是通过作辅助线，构造了三角形以及由平行线构成的内错角．二．解答题（共6小题）4．（2023春•仪征市期末）如图1，已知线段AB 、线段CD 被直线l 所截于点A 、点C ，150∠=︒，2∠的度数是1∠的3倍少20︒．（1）求证：//AB CD ；（2）如图2，连接BD ，AB 沿BD 方向平移得到EF ，点F 在BD 上，点G 是BD 上的一点，连接AG 、EG ，30BAG ∠=︒，20FEG ∠=︒，求AGE ∠的度数；（3）如图3，点M 是线段BD 上一点，点N 是射线CD 上一点，CAM ∠度数为k ，AMN ∠度数为m ，MND ∠度数为n ，请直接写出k 、m 、n 之间的数量关系．（本题的角均小于180)︒【分析】（1）根据已知先求得1∠的邻补角BAC ∠的度数，得到2BAC ∠=∠即可得结论；（2）过G 作//GQ AB ，利用平行线的性质定理和平行公理的推论即可；（3）利用平行线的性质定理和平行公理的推论即可．【解答】证明：（1）150∠=︒ ，2∠的度数是1∠的3倍少20︒，23120130∴∠=∠-︒=︒，180250ACD ∴∠=︒-∠=︒，12∴∠=∠，//AB CD ∴；（2）过G 作//GQ AB ，30AGQ BAG ∴∠=∠=︒，//AB EF ，//GQ EF ∴，20GEF EGQ ∴∠=∠=︒，50AGE AGQ EGQ ∴∠=∠+∠=︒；（3）//AB CD ，与（2）同理可得：AMN MAB MND ∠=∠+∠，AMN m ∠= ，MND n ∠=，m n MAB ∴=+∠，150∠=︒ ，CAM k ∠=，180118050BAM CAM k ∴∠=︒-∠-∠=︒-︒-，130m n k ∴=+︒-，即130m n k -+=︒．【点评】本题考查了平行线的性质定理及平行公理的推论，理解题意是解决问题的关键．5．（2022春•赣榆区期末）已知：如图，//AB CD ，BFE FEC ∠=∠．求证：ABF DCE ∠=∠．（1）下面是小明同学的推理过程，请按先后顺序填写空格：解：连接BC ．BFE FEC ∠=∠ （已知），∴BF //（内错角相等，两直线平行）．(FBC ECB ∴∠=∠)，//AB CD （已知），ABC DCB ∴∠=∠（两直线平行，内错角相等）ABC FBC DCB ∴∠-∠=∠-()，即ABF DCE ∠=∠．（2）试用其他方法进行推理，并书写证明过程．【分析】（1）连接BC ，根据已知，得出//BF CE ，根据平行线的性质得到FBC ECB ∠=∠，再根据//AB CD 得出ABC DCB ∠=∠，进而得出ABC FBC DCB ECB ∠-∠=∠-∠即可得出答案；（2）延长BF 交DC 的延长线于H ，根据平行线的性质可得ABF H ∠=∠，再利用等量代换可得H DCE ∠=∠，进而可判定//BH CE ，然后可得BFE FEC ∠=∠．【解答】（1）解：连接BC ．BFE FEC ∠=∠ （已知），//BF CE ∴（内错角相等，两直线平行）．(FBC ECB ∴∠=∠两直线平行，内错角相等），//AB CD （已知），ABC DCB ∴∠=∠（两直线平行，内错角相等）(ABC FBC DCB ECB ∴∠-∠=∠-∠等式的基本性质），即ABF DCE ∠=∠．故答案为：BF ，CE ；两直线平行，内错角相等；ECB ∠；等式的基本性质．（2）证明：延长BF 交DC 的延长线于H ，//AB CD ，ABF H ∴∠=∠，ABF DCE ∠=∠ ．H DCE ∴∠=∠，//BH CE ∴，BFE FEC ∴∠=∠．【点评】本题考查了平行线的判定和性质，熟练应用判定定理和性质定理是解题的关键，平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．平行线的判定是由角的数量关系判断两直线的位置关系．平行线的性质是由平行关系来寻找角的数量关系．应用平行线的判定和性质定理时，一定要弄清题设和结论，切莫混淆．6．（2023春•天宁区校级期中）已知：如图，180ABE CEB ∠+∠=︒，12∠=∠，求证：M N ∠=∠．【分析】首先证明//AB CD ，再根据平行线的性质得出ABE DEB ∠=∠，然后结合已知条件可得到MBE NEB ∠=∠，进而可判定//BM EN ，据此可得出结论．【解答】证明：180ABE CEB ∠+∠=︒ ，//AB CD ∴，ABE DEB ∴∠=∠，即：12MBE NEB ∠+∠=∠+∠，又12∠=∠ ，MBE NEB ∴∠=∠，//BM EN ∴，M N ∴∠=∠．【点评】此题主要考查了平行线的判定和性质，解答此题的关键是准确识图，熟练掌握平行线的判定及性质：两直线平行⇔同位角相等，两直线平行⇔内错角相等，两直线平行⇔同旁内角互补．7．（2023春•崇川区期中）如图1，已知直线EF 与直线AB 交于点E ，与直线CD 交于点F ，EM 平分AEF ∠交直线CD 于点M ，且FEM FME ∠=∠．（1）试判断直线AB 与CD 的位置关系，并说明理由；（2）点G 是射线MD 上的一个动点（不与点M ，F 重合），EH 平分FEG ∠交直线CD 于点H ，过点H 作//HN EM 交直线AB 于点N ．设EHN α∠=，EGF β∠=．①如图2，当点G 在点F 的右侧，且50α=︒时，求β的值；②当点G 在运动过程中，α和β之间有怎样的数量关系？请写出你的猜想，并加以证明．【分析】（1）由EM 平分AEF ∠，得到AEM FEM ∠=∠，又FEM FME ∠=∠，所以AEM FME ∠=∠，证得//AB CD ．（2）①由EH 平分FEG ∠，EM 平分AFE ∠，得到12HEM HEF FEM AEG ∠=∠+∠=∠，由//HN EM ，//AB CD 可得，HEM EHN α∠=∠=，GEB EGF β=∠=，即可得到结果．②当点G 在点F 的左侧时，由EM 平分AEF ∠，EH 平分FEH ∠，得到12HEM HEF FEM AEG ∠=∠+∠=∠，由//AB CD ，//HN EM ，得到AEG β∠=，HEM α∠=，从而得到结果．【解答】解（1）如图1，//AB CD ，理由如下：EM 平分AEF ∠，AEM FEM ∴∠=∠，FEM FME ∠=∠ ，AEM FME ∴∠=∠，//AB CD ∴．（2）①如图2，EH 平分FEG ∠，12HEF FEG ∴∠=∠，EM 平分AFE ∠，12FEM AEF ∴∠=∠，12HEM HEF FEM AEG ∴∠=∠+∠=∠，//HN EM ，HEM EHN α∴∠=∠=，//AB CD ，GEB EGF β∴∠=∠=，1(180)2αβ∴=︒-，180218025080βα∴=︒-=︒-⨯︒=︒．②α和β之间的数量关系为2βα=或1802βα=︒-．理由如下：当点G 在点F 的右侧时，由①得1802βα=︒-，当点G 在点F 的左侧时，如图3，EM 平分AEF ∠，2AEF FEM ∴∠=∠，EH 平分FEH ∠，2GEF HEF ∴∠=∠，222AEG AEF GEF FEM HEF HEM ∴∠=∠-∠=∠-∠=∠，//AB CD ，AEG β∴∠=，//HN EM ，HEM α∴∠=，2βα∴=，综上得，α和β之间的数量关系为2βα=或1802βα=︒-．【点评】本题主要考查了平行线的判定与性质，角平分线的定义，熟练运用平行线的判定与性质是解题关键．8．（2023春•海安市期末）如图，在ABC ∆中，ACB BAC ∠=∠．过点A 作//MN BC ．（1）判断AC 是否平分BAN ∠，并说明理由；（2）如图2，点D 是射线CB 上一动点（不与点B ，C 重合），AE 平分BAD ∠交射线BC 于E ，过点E 作EF AC ⊥于F ．①当点D 在点B 左侧时，若20AEF ∠=︒，求ADB ∠的度数；②点D 在运动过程中，AEF ∠和ADB ∠之间有怎样的数量关系？请写出你的猜想，并说明理由．【分析】（1）根据//MN BC 得ACB CAN ∠=∠，结合已知条件得证；（2）①在直角三角形AFE 中，20AEF ∠=︒，则9070EAF EAF ∠=︒-∠=︒，根据19020702EAF BAC BAE DAE CAN DAN ∠=∠+∠=︒-︒=︒=∠+∠=∠，从而求出140DAN ∠=︒，即可求出ADB ∠；②分两种情况进行讨论，当点D 在点B 左侧时和点D 在点B 右侧时，数形结合即可解答．【解答】解：（1）AC 平分BAN ∠，//MN BC ，ACB CAN ∴∠=∠，ACB BAC ∠=∠ ．BAC CAN ∴∠=∠，AC ∴平分BAN ∠，（2）EF AC ⊥ ，9070EAF EAF ∴∠=︒-∠=︒，AC 、AE 是角平分线，DAE BAE ∴∠=∠，BAC CAN ∠=∠，19020702EAF BAC BAE DAE CAN DAN ∴∠=∠+∠=︒-︒=︒=∠+∠=∠，140DAN ∴∠=︒，40ADB ∴∠=︒．②设AEF α∠=，EF AC ⊥ ，90EAF α∴∠=︒-，如图2，当点D 在点B 左侧时，由（1）知12NAC BAC BAN ∠=∠=∠，AE 平分BAD ∠交射线BC 于E ，12DAE BAE BAD ∴∠=∠=∠，又1111()902222EAF BAE BAC BAD BAN BAD BAN DAN α∠=∠+∠=∠+∠=∠+∠=∠=︒- ，1802DAN α∴∠=︒-，//MN BC ，180ADB DAN ∴∠+∠=︒，180180(1802)2ADB DAN αα∴∠=︒-∠=︒-︒-=，2ADB AEF ∴∠=∠；当点D 在点B 右侧时，如图：AC 、AE 是角平分线，12DAE BAE BAD ∴∠=∠=∠，12BAC CAN BAN ∠=∠=∠，1111()902222EAF BAC BAE BAN BAD BAN BAD DAN α∠=∠-∠=∠-∠=∠-∠=∠=︒- ，1802DAN α∴∠=︒-，//MN BC ，1802ADB DAN α∴∠=∠=︒-，1802ADB AEF ∴∠=︒-∠．综上，2ADB AEF ∠=∠或1802AEF ︒-∠．【点评】本题主要考查了平行线的性质与判定，角平分线的定义的运用，解决问题的关键是掌握两直线平行内错角相等，两直线平行同旁内角，利用角的和差关系进行推理论证．9．（2023春•姜堰区期末）已知12//l l ，李想同学将ABC ∆放置在这两条平行线上展开探究，其中ABC ∆三边与两条平行线分别交于点D 、E 、F 、G ．（1）【特例探究】如图1，90C ∠=︒．①CED CGF ∠+∠=270度；②若CED ∠与CGF ∠的角平分线相交于点P ，则EPG ∠=度；（2）【一般探索】如图2，C α∠=，EPG β∠=．①若13DEP CED ∠=∠，13FGP CGF ∠=∠，求α与β的关系；②若1DEP CED n ∠=∠，1(2FGP CGF n n ∠=∠ 且n 为整数），直接写出α与β的关系；（3）【拓展应用】如图3，CED ∠与CGF ∠的角平分线相交于点1P ，1PED ∠与1PGF ∠的角平分线相交于点2P ，2P ED ∠与2P GF ∠的角平分线相交于点3P ；⋯，以此类推，则2023360C EP G︒-∠∠的值是多少？（直接写出结果）【分析】（1）①作1//CM l 根据平行线的性质可得180CED ECM ∠+∠=︒，_180CGF GCM ∠+∠=︒两式相加即可得360CED CGF C ∠+∠=︒-∠；②由①知：360CED CGF C ∠+∠=︒-∠，再根据平行线的性质以及角平分线的定义即可得：1()2EPG CED CGF ∠=∠+∠化简整理即可；（2）①13DEP CED ∠=∠，13FGP CGF ∠=∠时，结合（1）中的结论和平行线的性质，可得α与β之间的关系；②类似于前面的证明，结合平行线的性质和角平分线的定义即可得结论；（3）根据角平分线的定义和平行线的性质找到规律即可得结论．【解答】解：（1）①作1//CM l ，180CED ECM ∴∠+∠=︒，2l //1l ，2//CM l ∴，_180CGF GCM ∴∠+∠=︒，360CED ECM CGF GCM ∴∠+∠+∠+∠=︒，90ECG ECM CGF ∠=∠+∠=︒ ，_90360CED CGF ∴∠+∠+︒=︒，270CED CGF ∴∠+∠=︒，故答案为270︒；②CED ∠ 与CGF ∠的角平分线相交于点P ，2CED CEP ∴∠=∠，2CGF CGP ∠=∠，由①知：270CED CGF ∠+∠=︒，22270CEP CGP ∴∠+∠=︒，135CEP CGP ∴∠+∠=︒，360CEP CGP EPG ECG ∠+∠+∠+∠=︒ ，135EPF ∴∠=︒；（2）21//l l ，ECG α∠=，由（1）①知360CED CGF ECF ∠+∠+∠=︒，360360CED CGF ECG α∴∠+∠=︒-∠=︒-，由（1）②知若13DEP CED ∠=∠，13FGP CGF ∠=∠，∴23CED CEP ∠=∠，23CGF CGP ∠=∠，2222()(360)3333CEP CGP CED CGF CED CGF α∴∠+∠=∠+∠=∠+∠=︒-，360CEP CGP EPG ECG ∠+∠+∠+∠=︒ ，∴2(360)3603αβα︒-++=︒，整理得：3360αβ+=︒；②若1DEP CED n ∠=∠，1(2FGP CGF n n∠=∠ 且n 为整数）时，由①同理可得α与β的关系：360n αβ+=︒；（3）通过前面的证明易得360360CED CGF C α∠+∠=︒-∠=︒-，当CED ∠与CGF ∠的角平分线相交于点1P ，1PED ∠与1PGF ∠的角平分线相交于点2P ，2P ED ∠与2P GF ∠的角平分线相交于点3P ；⋯，以此类推，则111111()()(360)222EPG CED CGF CED CGF α∠=∠+∠∠+∠=︒-，222111()())(360)422EP G CED CGF CED CGF α∠=∠+∠=∠+∠==︒-，333111()())(360)822EP G CED CGF CED CGF α∠=∠+∠=∠+∠=︒-，444111()())(360)1622EP G CED CGF CED CGF α∠=∠+∠=∠+∠=︒-，551(360)2EP G α∠=︒-，.....．1(360)2n nEP G α∠=︒-，当2023n =时，202320231(360)2EP G α∠=︒-，∴20232023202336036021(360)2C EP G αα︒-∠︒-==∠︒-，【点评】本题考查了平行线的性质，以及角平分线的定理，灵活运用所学知识找到规律是解决问题的关键．模型二、笔尖型如图，AB //CD，探索∠B、∠D 与∠DEB 的大小关系？解：∠B＋∠D＋∠DEB＝360°．理由如下：过点E作EF//AB．又∵AB//CD．∴EF//CD．∴∠B+∠BEF＝180°．∠D+∠DEF＝180°．∴∠B＋∠D+∠DEB＝∠B＋∠D+∠BEF＋∠DEF＝360°．即∠B＋∠D＋∠DEB＝360°．一．选择题（共3小题）1．（2022春•海陵区期末）如图//∠+∠+∠=a b，M、N分别在a、b上，P为两平行线间一点，那么123( )A．180︒B．270︒C．360︒D．540︒【分析】首先过点P作//PA a，构造三条平行线，然后利用两直线平行，同旁内角互补进行做题．【解答】解：过点P作//a b PA，PA a，则////∠+∠=︒，1180NPA∴∠+∠=︒，3180MPA∴∠+∠+∠=︒．123360故选：C．【点评】两直线平行时，应该想到它们的性质，由两直线平行的关系得到角之间的数量关系，从而达到解决问题的目的．2．（2023春•沭阳县期末）如图，把一块含有30︒角的直角三角板的两个顶点放在直尺的对边上．如果137∠=︒，那么2∠的度数是()A．30︒B．25︒C．23︒D．37︒【分析】根据平行线的性质，两直线平行，内错角相等，进而可以得出答案．【解答】解：如图，直尺的两条边平行，137∠=︒，∴∠=∠=︒，1337直角三角板的一个角为30︒，∴∠+∠=︒，2360∴∠=︒-︒=︒，2603723故选：C．【点评】本题主要考查了平行线的性质，注意隐含条件，直尺的两条对边平行和直角三角板的一个锐角是30︒是解题的关键．3．（2023春•东台市月考）某小区车库门口的“曲臂直杆道闸”（如图）可抽象为如图所示模型．已知AB垂直于水平地面AE．当车牌被自动识别后，曲臂直杆道闸的BC段将绕点B缓慢向上抬高，CD段则一直保持水平状态上升（即CD与AE始终平行），在该运动过程中ABC BCD∠+∠的度数始终等于()度A．360B．180C．250D．270【分析】过点B作//∠+∠=︒，从而可C CBGBG AE，利用平行线的性质可得180BAE ABG∠+∠=︒，180得360BAE∠=︒，最后进行计算即可解答．∠+∠+∠=︒，然后根据垂直定义可得90BAE ABC BCD【解答】解：过点B作//BG AE，BAE ABG∴∠+∠=︒，180AE CD，//∴，BG CD//∴∠+∠=︒，180C CBG∴∠+∠+∠+∠=︒，BAE ABG CBG C360BAE ABC BCD∴∠+∠+∠=︒，360⊥，BA AE∴∠=︒，90BAE∴∠+∠=︒-∠=︒，ABC BCD BAE360270故选：D．【点评】本题考查了平行线的性质，熟练掌握铅笔模型是解题的关键．二．填空题（共3小题）4．（2022春•崇川区校级月考）如图，直线//∠=︒，则3∠=78度，345∠+∠+∠=∠=︒，250a b，128度．【分析】过3∠的顶点作已知直线的平行线，充分运用平行线的性质，不难发现：312∠=∠+∠，∠+∠+∠=︒345360【解答】解：如图所示：过3∠的顶点作//c a，a b，//∴，a b c////∠=∠，16∴∠=∠，72又367∠=∠+∠，∴∠=∠+∠=︒；31278又4675180∠+∠=∠+∠=︒∴∠+∠+∠=︒．345360【点评】注意此类题中常见的辅助线：构造已知直线的平行线．根据平行线的性质发现并证明：312∠=∠+∠；∠+∠+∠=︒．3453605．（2022春•淮安期末）如图，//∠∠和CFGAB CD，E、F分别是AB、CD上的点，EH、FH分别是AEG的角平分线．若110∠=125︒．∠=︒，则HG【分析】过点G作//CD GM，∠+∠=︒，再结合已知可得// GM AB，根据平行线的性质可得180AEG EGM然后利用平行线的性质可得180∠+∠=︒，再利用角平分线的定AEG CFG∠+∠=︒，从而可得250CFG MGF义可得125∠+∠=︒，最后利用四边形的内角和定理进行计算即可解答．HEG GFH【解答】解：过点G作//GM AB，∴∠+∠=︒，AEG EGM180，//AB CD//CD GM ∴，180CFG MGF ∴∠+∠=︒，360AEG EGM CFG MGF ∴∠+∠+∠+∠=︒，110EGF EGM MGF ∠=∠+∠=︒ ，360250AEG CFG EGF ∴∠+∠=︒-∠=︒，EH 、FH 分别是AEG ∠和CFG ∠的角平分线，12HEG AEG ∴∠=∠，12GFH CFG ∠=∠，1112522HEG GFH AEG CFG ∴∠+∠=∠+∠=︒，360125H HEG HFG EGF ∴∠=︒-∠-∠-∠=︒，故答案为：125．【点评】本题考查了平行线的性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．6．（2023春•邗江区期中）将一副三角板如图1所示摆放，30BAC ∠=︒，45E ∠=︒，直线//GH MN ，现将三角板ABC 绕点A 以每秒1︒的速度顺时针旋转，同时三角板DEF 绕点D 以每秒3︒的速度顺时针旋转，如图2，设时间为t 秒，当0120t时，若边BC 与三角板DEF 的一条直角边（边DE ，)DF 平行，则所有满足条件的t 的值为15或105或60．【分析】先根据题意画出旋转后的图形，由已知条件，利用平行线的旋转，求出旋转角之间的关系，列出方程解答即可．【解答】解：由题意得：30HAC BAH BAC t ∠=∠+∠=︒+︒，3FDM t ∠=︒，（1）当//BC DE 时，如图所示：延长AC 交MN 于点P ，①DE 在MN 上方，//DE BC ，DE DF ⊥，AC BC ⊥，//AP DF ∴，FDM MPA ∴∠=∠，//MN GH ，MPA HAC ∴∠=∠，FDM HAC ∴∠=∠，即330t t =+，15t =；②1DE 在MN 下方时，1(3180)F DP t ∠=-︒，1//DE BC ，11DE DF ⊥，AC BC ⊥，1//AP DF ∴，1F DM MPA ∴∠=∠，//MN GH ，MPA HAC ∴∠=∠，1F DM HAC ∴∠=∠，即318030t t -=+，解之得：105t =；如图：当//BC DF 时，延长AC 交MN 于点I ，①DF 在MN 上方，(1803)FDN t ∠=-度，//DF BC ，AC BC ⊥，//AI DE ∴，90FDN MIA ∴∠+∠=︒，//MN GH ，MIA HAC ∴∠=∠，90FDN HAC ∴∠+∠=︒，即18033090t t -++=，解之得：60t =；②DF 在MN 下方，2(1803)F DN t ∠=-度，2//DF BC ，AC BC ⊥，22ED DF ⊥，2//AC DE ∴，2AIM MDE ∴∠=∠，//MN GH ，MIA HAC ∴∠=∠，2E DM HAC ∴∠=∠，即318030t t -=+，解之得：105t =，综上可知：所有满足条件的t 的值为：15或105或60，故答案为：15或105或60．【点评】本题主要考查了平行线的性质，解题关键是根据题意，画出旋转后的图形．三．解答题（共3小题）7．（2022春•海州区校级期中）如图，在ABC ∆中，点D 、E 分别在AB 、BC 上，且//DE AC ，12∠=∠．求证：//AF BC ．【分析】根据平行线的性质得出1C ∠=∠，求出2C ∠=∠，根据平行线的判定得出即可．【解答】证明：//DE AC ，1C ∴∠=∠，12∠=∠ ，2C ∴∠=∠，//AF BC ∴．【点评】本题考查了平行线的判定和性质，熟练应用判定定理和性质定理是解题的关键，平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．平行线的判定是由角的数量关系判断两直线的位置关系．平行线的性质是由平行关系来寻找角的数量关系．应用平行线的判定和性质定理时，一定要弄清题设和结论，切莫混淆．8．（2023春•盐都区期中）如图，在ABC ∆中，点D 、E 分别在AB 、BC 上，//AF BC ，12∠=∠，求证：//DE AC ．【分析】由两直线平行内错角相等得到1C ∠=∠，再根据同位角相等两直线平行可解题．【解答】证明：//AF BC ，1C ∴∠=∠，12∠=∠ ，2C ∴∠=∠，//DE AC ∴．【点评】本题考查平行线的判定与性质，是重要考点，掌握相关知识是解题关键．9．（2022春•亭湖区校级月考）如图，已知1BDC ∠=∠，23180∠+∠=︒．（1）AD 与EC 平行吗？试说明理由．（2）若DA 平分BDC ∠，DA FA ⊥于点A ，182∠=︒，试求FAB ∠的度数．【分析】（1）直接利用平行线的判定与性质得出//AB CD ，进而得出3180ADC ∠+∠=︒，即可得出答案；（2）利用角平分线的定义结合平行线的性质得出2∠，即可得出答案．【解答】（1）解：AD 与EC 平行，理由如下：1BDC ∠=∠ ，//AB CD ∴（同位角相等，两直线平行），2ADC ∴∠=∠（两直线平行，内错角相等），23180∠+∠=︒ ，3180ADC ∴∠+∠=︒（等量代换），//AD CE ∴（同旁内角互补，两直线平行）；（2）解：1BDC ∠=∠ ，182∠=︒，82BDC ∴∠=︒，DA 平分BDC ∠，1412ADC BDC ∴∠=∠=︒（角平分线定义），241ADC ∴∠=∠=︒（已证），又DA FA ⊥ ，90FAD ∴∠=︒（垂直定义），2904149FAB FAD ∴∠=∠-∠=︒-︒=︒．【点评】此题主要考查了平行线的判定与性质，正确得出90AEC FAD ∠=∠=︒是解题关键．模型三、“鸡翅”型如图，已知AB//CD，试猜想∠A、∠E、∠C 的关系，并说明理由．解：∠AEC=∠A-∠C,理由如下：过点E 作EF //AB又∵AB//CD．∴EF//CD．∴∠A+∠FEA=180°，∠C+∠FEC=180°∴∠AEC＝∠FEC-∠FEA=180°-∠C –(180°-∠A)=∠A-∠C即：∠AEC=∠A-∠C 一、单选题1．（2021下·湖南株洲·七年级统考期末）①如图1，AB ∥CD ，则360A E C ∠+∠+∠=︒；②如图2，AB ∥CD ，则P A C ∠=∠-∠；③如图3，AB ∥CD ，则1E A ∠=∠+∠；④如图4，直线AB ∥CD ∥EF ，点O 在直线EF 上，则180αβγ∠-∠+∠=︒．以上结论正确的个数是（）A．1个B．2个C．3个D．4个【答案】C【分析】①过点E作直线EF∥AB，由平行线的性质：两直线平行，同旁内角互补，即可得出结论；②如图2，先根据三角形外角的性质得出∠1＝∠C+∠P，再根据两直线平行，内错角相等即可作出判断；③如图3，过点E作直线EF∥AB，由平行线的性质可得出∠A+∠AEC﹣∠1＝180°，即得∠AEC＝180°+∠1﹣∠A；④如图4，根据平行线的性质得出∠α＝∠BOF，∠γ+∠COF＝180°，再利用角的关系解答即可．【详解】解：①如图1，过点E作直线EF∥AB，∵AB∥CD，∴AB∥CD∥EF，∴∠A+∠1＝180°，∠2+∠C＝180°，∴∠A+∠1+∠2+∠C＝360°，∴∠A+∠AEC+∠C=360°，故①正确；②如图2，∵∠1是△CEP的外角，∴∠1＝∠C+∠P，∵AB∥CD，∴∠A＝∠1，即∠P＝∠A﹣∠C，故②正确；③如图3，过点E作直线EF∥AB，∵AB∥CD，∴AB∥CD∥EF，∴∠A +∠3＝180°，∠1＝∠2，∴∠A +∠AEC ﹣∠1＝180°，即∠AEC ＝180°+∠1﹣∠A ，故③错误；④如图4，∵AB ∥EF ，∴∠α＝∠BOF ，∵CD ∥EF ，∴∠γ+∠COF ＝180°，∵∠BOF ＝∠COF +∠β，∴∠COF ＝∠α﹣∠β，∴∠γ+∠α﹣∠β＝180°，故④正确；综上结论正确的个数为3，故选：C ．【点睛】本题考查的是平行线的性质及三角形外角的性质，熟练掌握平行线的性质，根据题意作出辅助线是解答此题的关键．二、解答题2．（2021下·浙江台州·七年级统考期末）如图，已知AD AB ⊥于点A ，AE ∥CD 交BC 于点E ，且EF AB ⊥于点F ．求证：12C ∠=∠+∠．证明：∵AD AB ⊥于点A ，EF AB ⊥于点F ，（已知）∴90DAB EFB ∠=∠=︒．（垂直的定义）∴AD ∥EF ，（）∴__________1=∠（）∵AE ∥CD ，（已知）∴C ∠=________．（两直线平行，同位角相等）∵2AEB AEF ∠=∠+∠，∴12C ∠=∠+∠．（等量代换）【答案】见解析1PE l ∥，12l l ∥，∴12PE l l ∥∥，PAC APE ∴∠=∠，PBD BPE ∠=∠，APB APE BPE ∠=∠+∠ ，PAC PBD APB ∴∠+∠=∠．（2）解：结论：当点P 在直线1l 上方时，∠-∠=∠PBD PAC APB ；当点P 在直线2l 下方时，∠-∠=∠PAC PBD APB ．①当点P 在直线1l 上方时，如图2所示．过点P 作1PE l ∥．1PE l ∥，12l l ∥，∴12PE l l ∥∥，PAC APE ∴∠=∠，PBD BPE ∠=∠，APB BPE APE ∠=∠-∠ ，PBD PAC APB ∴∠-∠=∠．②当点P 在直线2l 下方时，如图3所示．过点P 作1PE l ∥．1PE l ∥，12l l ∥，∴12PE l l ∥∥，PAC APE ∴∠=∠，PBD BPE ∠=∠，APB APE BPE ∠=∠-∠ ，PAC PBD APB ∴∠-∠=∠．【点睛】本题考查了平行线的性质以及角的计算，解题的关键是根据“两直线平行，内错角相等”找到相等的角．本题属于基础题，难度不大，解决该题型题目时，根据平行线的性质得出相等（或互补）的角是关键．4．（2021下·广东东莞·七年级东莞市光明中学校考期中）（1）如图（1）AB CD ，猜想BPD ∠与B D ∠∠、的关系，说出理由．（2）观察图（2），已知AB CD ，猜想图中的BPD ∠与B D ∠∠、的关系，并说明理由．（3）观察图（3）和（4），已知AB CD ，猜想图中的BPD ∠与B D ∠∠、的关系，不需要说明理由．【答案】（1）360B BPD D ∠+∠+∠=︒，理由见解析；（2）BPD B D ∠=∠+∠，理由见解析；（3）图（3）BPD D B ∠=∠-∠，图（4）BPD B D∠=∠-∠【分析】（1）过点P 作EF AB ∥，得到180B BPE ∠+∠=︒，由AB CD ，EF AB ∥，得到EF CD ，得到180EPD D ∠+∠=︒，由此得到360B BPD D ∠+∠+∠=︒；（2）过点P 作PE AB ，由PE AB CD ∥∥，得到12B D ∠=∠∠=∠，，从而得到结论12BPD B D ∠=∠+∠=∠+∠；（3）由AB CD ，根据两直线平行，内错角相等与三角形外角的性质，即可求得BPD ∠与B D ∠∠、的关系．【详解】（1）解：猜想360B BPD D ∠+∠+∠=︒．理由：过点P 作EF AB ∥，∴180B BPE ∠+∠=︒，∵AB CD ，EF AB ∥，∴EF CD ，∴180EPD D ∠+∠=︒，∴360B BPE EPD D ∠+∠+∠+∠=︒，∴360B BPD D ∠+∠+∠=︒；（2）BPD B D ∠=∠+∠．理由：如图，过点P 作PE AB ，∵AB CD ，∴PE AB CD ∥∥，∴12B D ∠=∠∠=∠，，∴12BPD B D ∠=∠+∠=∠+∠；（3）如图（3）：BPD D B ∠=∠-∠．理由：∵AB CD ，∴1D ∠=∠，∵1B P ∠=∠+∠，∴D B P ∠=∠+∠，即BPD D B ∠=∠-∠；如图（4）：BPD B D ∠=∠-∠．理由：∵AB CD ，∴1B ∠=∠，∵1D P ∠=∠+∠，∴B D P ∠=∠+∠，即BPD B D ∠=∠-∠．【点睛】此题考查了平行线的性质，平行公理的推论，三角形的外角的性质定理，熟记平行线的性质是解题的关键．5．（2021下·浙江·七年级期末）已知//AM CN ，点B 为平面内一点，AB BC ⊥于B ．（1）如图1，点B 在两条平行线外，则A ∠与C ∠之间的数量关系为______；（2）点B 在两条平行线之间，过点B 作BD AM ⊥于点D ．①如图2，说明ABD C ∠=∠成立的理由；②如图3，BF 平分DBC ∠交DM 于点,F BE 平分ABD ∠交DM 于点E ．若180,3FCB NCF BFC DBE ∠∠∠∠+=︒=，求EBC ∠的度数．【答案】（1）∠A +∠C =90°；（2）①见解析；②105°【分析】（1）根据平行线的性质以及直角三角形的性质进行证明即可；（2）①过点B 作BG ∥DM ，根据平行线找角的联系即可求解；②先过点B 作BG ∥DM ，根据角平分线的定义，得出∠ABF =∠GBF ，再设∠DBE =α，∠ABF =β，根据∠CBF +∠BFC +∠BCF =180°，可得2α+β+3α+3α+β=180°，根据AB ⊥BC ，可得β+β+2α=90°，最后解方程组即可得到∠ABE =15°，进而得出∠EBC =∠ABE +∠ABC =15°+90°=105°．【详解】解：（1）如图1，AM 与BC 的交点记作点O ，∵AM ∥CN ，∴∠C =∠AOB ，∵AB ⊥BC ，∴∠A +∠AOB =90°，∴∠A +∠C =90°；（2）①如图2，过点B 作BG ∥DM ，∵BD⊥AM，∴DB⊥BG，∴∠DBG=90°，∴∠ABD+∠ABG=90°，∵AB⊥BC，∴∠CBG+∠ABG=90°，∴∠ABD=∠CBG，∵AM∥CN，BG∥DM，BG CN//,∴∠C=∠CBG，∠ABD=∠C；②如图3，过点B作BG∥DM，∵BF平分∠DBC，BE平分∠ABD，∴∠DBF=∠CBF，∠DBE=∠ABE，由（2）知∠ABD=∠CBG，∴∠ABF=∠GBF，设∠DBE=α，∠ABF=β，则∠ABE=α，∠ABD=2α=∠CBG，∠GBF=∠AFB=β，∠BFC=3∠DBE=3α，∴∠AFC =3α+β，∵∠AFC +∠NCF =180°，∠FCB +∠NCF =180°，∴∠FCB =∠AFC =3α+β，△BCF 中，由∠CBF +∠BFC +∠BCF =180°得：2α+β+3α+3α+β=180°，∵AB ⊥BC ，∴β+β+2α=90°，∴α=15°，∴∠ABE =15°，∴∠EBC =∠ABE +∠ABC =15°+90°=105°．【点睛】本题主要考查了平行线的性质的运用，解决问题的关键是作平行线构造内错角，运用等角的余角（补角）相等进行推导．余角和补角计算的应用，常常与等式的性质、等量代换相关联．解题时注意方程思想的运用．6．（2021下·福建厦门·七年级厦门市第十一中学校考期中）已知，//AE BD ，A D ∠=∠．（1）如图1，求证：//AB CD ；（2）如图2，作BAE ∠的平分线交CD 于点F ，点G 为AB 上一点，连接FG ，若CFG ∠的平分线交线段AG 于点H ，连接AC ，若ACE BAC BGM ∠=∠+∠，过点H 作HM FH ⊥交FG 的延长线于点M ，且3518E AFH ∠-∠=︒，求EAF GMH ∠+∠的度数．【答案】（1）见解析；（2）72︒【分析】（1）根据平行线的性质得出180A B ∠+∠=︒，再根据等量代换可得180B D ∠+∠=︒，最后根据平行线的判定即可得证；（2）过点E 作//EP CD ，延长DC 至Q ，过点M 作//MN AB ，根据平行线的性质及等量代换可得出ECQ BGM DFG ∠=∠=∠，再根据平角的含义得出ECF CFG ∠=∠，然后根据平行线的性质及角平分线的定义可推出,BHF CFH CFA FAB ∠=∠∠=∠；设,FAB CFH αβ∠=∠=，根据角的和差可得出2AEC AFH ∠=∠，结合已知条件35180AEC AFH ∠-∠=︒可求得18AFH ∠=︒，最后根据垂线的含义及平行线的性质，即可得出答案．AFH CFH CFA CFH FAB∠=∠-∠=∠-∠∴∠=-，BHF CFHβAFHβα∠=∠=ECF AFH AEC EAB AFH AECβ∴∠+∠=∠+∠+∠=∠+222∴∠+∠=∠+∠ECF AFH E BHF22∴∠=∠2AEC AFH∠-∠=︒AEC AFH35180AFH∴∠=︒18⊥FH HM∴∠=︒90FHM∴∠=︒-GHMβ90∠+∠=︒CFM NMF180∴∠=∠=︒-HMB HMNβ90∠=∠EAF FABEAF CFA CFH AFHβ∴∠=∠=∠-∠=-︒18∴∠+∠=-︒+︒-=︒EAF GMHββ189072EAF GMH∴∠+∠=︒．72【点睛】本题考查了平行线的判定及性质，角平分线的定义，能灵活根据平行线的性质和判定进行推理是解此题的关键．模型四、“骨折模型”如图，已知BC//DE，试猜想∠A、∠B、∠D的关系，并说明理由．解：∠BAD=∠D-∠B,理由如下：过点A作AG//BC又∵CB//DE．∴AG//DE∴∠GAB+∠B=180°，∠GAD+∠D=180°∴∠BAD＝∠GAB-∠GAD=180°-∠B–(180°-∠D)=∠D-∠B即：∠BAD=∠D-∠B注：平行线四大模型大题不可直接使用，必须证明后再用，选择填空满足条件即可直接用！【答案】60︒【分析】过点B作BD EF∥=∠进而可得12∠+∠ABD【详解】解：如图，过点Rt ABC△中，30∠=︒，A∴9060∠=︒-∠=︒．ABC ABD EF∥，∠=∠．∴1ABD【答案】40︒/40度∥【分析】过C作CF AB∠=︒即可得到答案；CDE140CF【点睛】本题考查平行线的判定与性质，解题的关键是作出辅助线，根据平行线性质得到角度关系．二、解答题4．（2021·全国·九年级专题练习）已知AB//CD，求证：∠B＝∠E＋∠D【答案】见解析【分析】过点E作EF∥CD，根据平行线的性质即可得出∠B=∠BOD，根据平行线的性质即可得出∠BOD=∠BEF、∠D=∠DEF，结合角之间的关系即可得出结论．【详解】证明：过点E作EF∥CD，如图∵AB∥CD，∴∠B=∠BOD，∵EF∥CD（辅助线），∴∠BOD=∠BEF（两直线平行，同位角相等）；∠D=∠DEF（两直线平行，内错角相等）；∴∠BEF=∠BED+∠DEF=∠BED+∠D（等量代换），∴∠BOD=∠E+∠D（等量代换），即∠B=∠E+∠D．【点睛】本题考查了平行线的性质以及角的计算，解题的关键是根据平行线的性质找出相等或互补的角．5．（2021下·山西晋中·七年级统考期中）综合与探究【问题情境】王老师组织同学们开展了探究三角之间数量关系的数学活动（1）如图1，//∠、EF MN，点A、B分别为直线EF、MN上的一点，点P为平行线间一点，请直接写出PAF ∠之间的数量关系；PBN∠和APB【问题迁移】（2）如图2，射线OM 与射线ON 交于点O ，直线//m n ，直线m 分别交OM 、ON 于点A 、D ，直线n 分别交OM 、ON 于点B 、C ，点P 在射线OM 上运动，①当点P 在A 、B （不与A 、B 重合）两点之间运动时，设ADP α∠=∠，BCP β∠=∠．则CPD ∠，α∠，∠β之间有何数量关系？请说明理由．②若点P 不在线段AB 上运动时（点P 与点A 、B 、O 三点都不重合），请你画出满足条件的所有图形并直接写出CPD ∠，α∠，∠β之间的数量关系．【答案】（1）360PAF PBN APB ∠+∠+∠=°；（2）①CPD αβ∠=∠+∠，理由见解析；②图见解析，CPD βα∠=∠-∠或CPD αβ∠=∠-∠【分析】（1）作PQ ∥EF ，由平行线的性质，即可得到答案；（2）①过P 作//PE AD 交CD 于E ，由平行线的性质，得到DPE α∠=∠，CPE β∠=∠，即可得到答案；②根据题意，可对点P 进行分类讨论：当点P 在BA 延长线时；当P 在BO 之间时；与①同理，利用平行线的性质，即可求出答案．【详解】解：（1）作PQ ∥EF ，如图：∵//EF MN ，∴////EF MN PQ ，∴180PAF APQ ∠+∠=°，180PBN BPQ ∠+∠=°，∵APB APQ BPQ∠=∠+∠∴360PAF PBN APB ∠+∠+∠=°；（2）①CPD αβ∠=∠+∠；理由如下：如图，过P 作//PE AD 交CD 于E ，∵//AD BC ，∴////AD PE BC ，∴DPE α∠=∠，CPE β∠=∠，∴CPD DPE CPE αβ∠=∠+∠=∠+∠；②当点P 在BA 延长线时，如备用图1：∵PE ∥AD ∥BC ，∴∠EPC=β，∠EPD =α，∴CPD βα∠=∠-∠；当P 在BO 之间时，如备用图2：∵PE ∥AD ∥BC ，∴∠EPD =α，∠CPE =β，∴CPD αβ∠=∠-∠．【点睛】本题考查了平行线的性质，解题的关键是熟练掌握两直线平行同旁内角互补，两直线平行内错角相等，从而得到角的关系．6．（2021下·新疆克拉玛依·七年级统考期末）（1）如图1，l1∥l2，求∠A1+∠A2+∠A3＝______．（直接写出结果）（2）如图2，l1∥l2，求∠A1+∠A2+∠A3+∠A4＝_____．（直接写出结果）（3）如图3，l1∥l2，求∠A1+∠A2+∠A3+∠A4+∠A5＝_______．（直接写出结果）（4）如图4，l1∥l2，求∠A1+∠A2+…+∠A n＝_______．（直接写出结果）【答案】（1）360°；（2）540°；（3）720°；（4）（n-1）180°【分析】（1）过点A2作A2B∥l1，根据平行线的性质，即可求解；（2）过点A2作A2B∥l1，过点A3作A3C∥l1，根据平行线的性质，即可求解；（3）根据平行线的性质，即可求解；（4）根据平行线的性质，即可求解．【详解】解：（1）过点A2作A2B∥l1，∵l1∥l2，∴A2B∥l1∥l2，∴∠A1+∠A1A2B=180°，∠A3+∠A3A2B=180°，∴∠A1+∠A1A2A3+∠A3＝∠A1+∠A1A2B+∠A3+∠A3A2B=180°+180°=360°，故答案是：360°；（2）过点A2作A2B∥l1，过点A3作A3C∥l1，∵l1∥l2，【答案】（1）∠APD=80°；（2）∠PAB+∠CDP-∠APD=180°；（3）∠AND=45°【分析】（1）首先过点P作PQ∥AB，则易得AB∥PQ∥CD，然后由两直线平行，同旁内角互补以及内错∴∠A=∠APQ=50°，∵AB∥CD，∴PQ∥CD，∴∠D+∠DPQ=180°，则∠DPQ=180°-150°=30°，∴∠APD=∠APQ+∠DPQ=50°+30°=80°；（2）∠PAB+∠CDP-∠APD=180°，如图，作PQ∥AB，∴∠PAB=∠APQ，∵AB∥CD，∴PQ∥CD，∴∠CDP+∠DPQ=180°，即∠DPQ=180°-∠CDP，∵∠APD=∠APQ-∠DPQ，∴∠APD=∠PAB-(180°-∠CDP)=∠PAB+∠CDP-180°；∴∠PAB+∠CDP-∠APD=180°；(3)设PD交AN于O，如图，∵AP⊥PD，∴∠APO=90°，（1）如图2，小明将折线调节成50,75,25B C D ∠=︒∠=︒∠=︒，判别（2）如图3，若25C D ∠=∠=︒，调整线段AB 、BC 使得//AB CD 并写出计算过程．（3）若85,25,//C D AB DE ∠=︒∠=︒，求出此时B ∠的度数，要求画出图形，直接写出度数，不要求计算【分析】（1）过点C作CF∥AB，利用平行线的判定和性质解答即可；（2）分别画图3和图4，根据平行线的性质可计算∠B的度数；（3）分别画图，根据平行线的性质计算出∠B的度数．【详解】解：（1）AB∥DE，理由是：如下图，过点C作CF∥AB，∴∠B=∠BCF=50°，∵∠BCD=75°，∴∠DCF=25°，∵∠D=25°，∴∠D=∠DCF=25°，∴CF∥DE，∴AB∥DE；（2）如下图，∵AB∥CD，∴∠B=∠BCD=25°；如图4：∵AB∥CD，∴∠B+∠BCD=180°，∴∠ABC=180°-25°=155°；（3）由（1）得：∠B=85°-25°=60°；如图5，过C作CF∥AB，则AB∥CF∥CD，∴∠FCD=∠D=25°，∵∠BCD=85°，∴∠BCF=85°-25°=60°，∵AB∥CF，∴∠B+∠BCF=180°，∴∠B=120°；如图6，∵∠C=85°，∠D=25°，∴∠CFD=180°-85°-25°=70°，∵AB∥DE，∴∠B=∠CFD=70°，如图7，同理得：∠B=25°+85°=110°，综上所述，∠B的度数为60°或120°或70°或110°．【点睛】本题主要考查了平行线的性质和三角形内角和的运用，解决问题的关键是作辅助线构造同位角以及内错角，依据平行线的性质及三角形外角性质进行推导计算．9．（2021下·湖北武汉·七年级统考期中）如图1，MN∥PQ，点C、B分别在直线MN、PQ上，点A在直线MN、PQ之间．（1）求证：∠CAB＝∠MCA+∠PBA；（2）如图2，CD∥AB，点E在PQ上，∠ECN＝∠CAB，求证：∠MCA＝∠DCE；（3）如图3，BF平分∠ABP，CG平分∠ACN，AF∥CG．若∠CAB＝60°，求∠AFB的度数．【答案】（1）证明见解析；（2）证明见解析；（3）120°．【分析】（1）过点A作AD∥MN，根据两直线平行，内错角相等得到∠MCA＝∠DAC，∠PBA＝∠DAB，根据角的和差等量代换即可得解；（2）由两直线平行，同旁内角互补得到∴、∠CAB+∠ACD＝180°，由邻补角定义得到∠ECM+∠ECN＝180°，再等量代换即可得解；（3）由平行线的性质得到，∠FAB＝120°﹣∠GCA，再由角平分线的定义及平行线的性质得到∠GCA﹣∠ABF ＝60°，最后根据三角形的内角和是180°即可求解．【详解】解：（1）证明：如图1，过点A作AD∥MN，∵MN∥PQ，AD∥MN，∴AD∥MN∥PQ，∴∠MCA＝∠DAC，∠PBA＝∠DAB，∴∠CAB＝∠DAC+∠DAB＝∠MCA+∠PBA，即：∠CAB＝∠MCA+∠PBA；（2）如图2，∵CD∥AB，∴∠CAB+∠ACD＝180°，∵∠ECM+∠ECN＝180°，∵∠ECN＝∠CAB∴∠ECM＝∠ACD，即∠MCA+∠ACE＝∠DCE+∠ACE，∴∠MCA＝∠DCE；（3）∵AF∥CG，∴∠GCA+∠FAC＝180°，∵∠CAB＝60°。

平行线必考几何题型专训(6大题型)—2023-2024学年七年级数学下册(浙教版)(解析版)

平行线必考几何题型专训（6大题型+10道拓展培优）【题型目录】题型一根据平行线的判定与性质求解题型二根据平行线的性质探究角的关系题型三平行线的性质在生活中的实际应用题型四平行线中的旋转问题题型五平行线中的折叠问题题型六平行线中的平移问题【经典例题一根据平行线的判定与性质求解】【例1】（2023下·江苏南通·七年级校联考阶段练习）如图，AB BC ⊥于点B ，DC BC ⊥于点C ，DE 平分ADC ∠交BC 于点E ，点F 为线段CD 延长线上一点，BAF EDF ∠=∠．(1)求证：DE AF ∥；(2)若=40F ︒∠，求DAF ∠的度数．【答案】(1)证明见解析(2)40DAF ∠=︒【分析】（1）根据AB BC ⊥，DC BC ⊥得出AB CF ，根据平行线的性质可得180BAF F ∠+∠=︒，进而得出180EDF F ∠+∠=︒，根据平行线判定定理即可得结论；（2）根据平行线的性质得出ADE DAE ∠=∠，EDC F ∠=∠，根据角平分线的定义即可得答案．【详解】（1）证明：∵AB BC ⊥于点B ，DC BC ⊥于点C ，∴90B C ∠=∠=︒，∴180B C ∠+∠=︒，∴AB CF ，∴180BAF F ∠+∠=︒，∵BAF EDE ∠=∠，∴180EDE F ∠+∠=︒，∴DE AF ∥．（2）解：∵DE AF ∥，∴ADE DAE ∠=∠，EDC F ∠=∠，∵DE 平分ADC ∠，∴ADE CDE ∠=∠，∴40DAF F ∠=∠=︒．【点睛】本题考查平行线的判定与性质，同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行；熟练掌握平行线的判定定理是解题关键．【变式训练】 1．（2024下·全国·七年级假期作业）如图，已知直线,AB CD 被直线EF 所截，EG 平分AEF ∠，FG 平分EFC ∠，1290∠+∠=︒，AB CD 吗？为什么？因为EG 平分AEF ∠，FG 平分EFC ∠（已知），所以2AEF ∠∠=___________，2EFC ∠∠=___________，所以AEF EFC ∠∠+=___________（），因为1290∠+∠=︒（），所以AEF EFC ∠∠+=___________︒，所以AB CD （）．【答案】平行，见解析【分析】本题考查了角平分线的定义、平行线的判定，熟练掌握平行线的判定是解题关键．先根据角平分线的定义可得21AEF ∠=∠，22EFC ∠=∠，从而可得180AEF EFC ∠+∠=︒，再根据平行线的判定即可得．【详解】解：因为EG 平分AEF ∠，FG 平分EFC ∠（已知），所以21AEF ∠=∠，22EFC ∠=∠，所以()212AEF EFC ∠+∠=∠+∠（等量代换），因为1290∠+∠=︒（已知），所以180AEF EFC ∠+∠=︒，所以AB CD （同旁内角互补，两直线平行）． 2．（2023下·陕西西安·七年级校考阶段练习）如图，直线AB 和CD 被直线MN 所截．(1)如图1，EG 平分BEF ∠，FH 平分DFE ∠（平分的是一对同旁内角），则1∠与2∠满足______时， AB CD ∥，并说明平行的理由；(2)如图2，EG 平分MEB ∠，FH 平分DFE ∠（平分的是一对同位角），则1∠与2∠满足______时，AB CD ∥，并说明平行的理由；(3)如图3，EG 平分AEF ∠，FH 平分DFE ∠（平分的是一对内错角），则1∠与2∠满足______时，AB CD ∥，并说明平行的理由．【答案】(1)1290∠+∠=︒，见解析(2)12∠=∠，见解析(3)12∠=∠，见解析【分析】（1）根据角平分线的定义可得21BEF ∠=∠，22EFD ∠=∠，故1∠与2∠满足1290∠+∠=︒，即可得出()212180BEF EFD ∠+∠=∠+∠=︒，即可判断AB CD ∥；（2）根据角平分线的定义可得21BEM ∠=∠，22EFD ∠=∠，故1∠与2∠满足12∠=∠，即可得BEM DFE ∠=∠，即可判断AB CD ∥；（3）同（2）的分析即得结论．【详解】（1）当1∠与2∠满足1290∠+∠=︒时， AB CD ∥，理由如下：∵EG 平分BEF ∠，FH 平分DFE ∠，∴21BEF ∠=∠，22EFD ∠=∠，∵1290∠+∠=︒，∴()212180BEF EFD ∠+∠=∠+∠=︒，∴AB CD ∥；（2）当1∠与2∠满足12∠=∠时，AB CD ∥，理由如下：∵EG 平分MEB ∠，FH 平分DFE ∠，∴21BEM ∠=∠，22EFD ∠=∠，∵12∠=∠，∴BEM DFE ∠=∠，∴AB CD ∥；（3）当1∠与2∠满足12∠=∠时，AB CD ∥，理由如下：∵EG 平分AEF ∠，FH 平分DFE ∠，∴21AEF ∠=∠，22EFD ∠=∠，∵12∠=∠，∴AEF DFE ∠=∠，∴AB CD ∥．【点睛】本题考查了角平分线的定义和平行线的判定，熟练掌握平行线的判定方法是解题的关键，常见的判定两直线平行的方法有：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行． 3．（2023下·河北石家庄·七年级石家庄市第二十一中学校考期中）如图，直线EF 与直线AB ，CD 分别相交于点M ，O ，OP ，OQ 分别平分COE ∠和DOE ∠，与AB 交于点P ，Q ，已知90OPQ DOQ ∠+∠=︒．(1)若:2:5DOQ DOF ∠∠=，求FOQ ∠的度数；(2)对AB CD ∥说明理由．【答案】(1)140FOQ =︒∠(2)见解析【分析】（1）根据角平分线的定义得出EOQ DOQ =∠∠，设2DOQ EOQ x ==∠∠，则5DOF x =∠，根据题意得出225180x x x ++=︒，求出x 的值，即可得出答案；（2）根据OP ，OQ 分别平分COE ∠和DOE ∠，得出119022COP DOQ COE EOD ∠+∠=+=︒∠∠，根据90OPQ DOQ ∠+∠=︒，得出COP OPQ =∠∠，根据平行线的判断即可得出结论．【详解】（1）解：∵OQ 平分DOE ∠，∴EOQ DOQ =∠∠，∵:2:5DOQ DOF ∠∠=，∴设2DOQ EOQ x ==∠∠，则5DOF x =∠，∴225180x x x ++=︒，解得：20x =︒，∴527140FOQ DOF DOQ x x x =+=+==︒∠∠∠；（2）证明：∵OP ，OQ 分别平分COE ∠和DOE ∠，∴12COP EOP COE ==∠∠∠，12EOQ DOQ EOD ==∠∠∠，∴119022COP DOQ COE EOD ∠+∠=+=︒∠∠，∵90OPQ DOQ ∠+∠=︒，∴COP OPQ =∠∠，∴AB CD ∥．【点睛】本题主要考查了平行线的判定，角平分线的定义，余角的性质，解题的关键是熟练掌握平行线的判断方法． 4．（2022下·河北保定·七年级统考期中）如图，点E 在直线DC 上，射线EF 、EB 分别平分AED ∠、AEC ∠．(1)试判断EF 、EB 的位置关系，并说明理由；(2)若5A ∠=∠，且4590∠+∠=︒，求证：AB EF ∥．【答案】(1)EB EF ⊥，理由见解析(2)见解析【分析】（1）根据角平分线定义以及平角的定义即可求证；（2）由等角的余角相等可证得25∠=∠，进而可得2A ∠=∠，再由内错角相等两直线平行即可证得．【详解】（1）解：EB EF ⊥，理由如下：∵EB 平分AEC ∠，EF 平分AED ∠，∴1342AEC ∠=∠=∠，1122AED ∠=∠=∠，180AED AEC ∠+∠=︒，∴111123()180902222BEF AED AEC AED AEC ∠=∠+∠=∠+∠=∠+∠=⨯︒=︒，∴EB EF ⊥；（2）证明：∵2390∠+∠=︒（已证），4590∠+∠=︒（已知），又∵3=4∠∠，∴25∠=∠，∵5A ∠=∠，∴2A ∠=∠，∴AB EF ∥．【点睛】本题考查了角平分线定义，平角定义，平行线的判定，等角的余角相等，综合掌握以上知识并熟练应用是解题的关键． 5．（2021下·山西大同·七年级校考期中）已知：三角形ABC 和三角形DEF 位于直线MN 的两侧中，直线MN 经过点C ，且BC MN ⊥，其中A ABC CB =∠∠，DEF DFE ∠=∠，90∠+∠=︒ABC DFE ，点E 、F 均落在直线MN 上．（1）如图1，当点C 与点E 重合时，求证：//DF AB ；聪明的小丽过点C 作//CG DF ，并利用这条辅助线解决了问题．请你根据小丽的思考，写出解决这一问题的过程．（2）将三角形DEF 沿着NM 的方向平移，如图2，求证：//DE AC ；（3）将三角形DEF 沿着NM 的方向平移，使得点E 移动到点E '，画出平移后的三角形DEF ，并回答问题，若DFE α∠=，则CAB ∠=________．（用含α的代数式表示）【答案】（1）见解析；（2）见解析；（3）见解析；2α．【分析】（1）过点C 作//CG DF ，得到DFE FCG ∠=∠，再根据90BCF ∠=︒，90∠+∠=︒ABC DFE ，得到ABC BCG ∠=∠，进而得到//CG AB ，最后证明//DF AB ；（2）先证明90ACB DEF ∠+∠=︒，再证明90ACB ACE ∠+∠=︒，得到DEF ACE ∠=∠，问题得证；（3）根据题意得到DFE DEF α∠=∠=，根据（２）结论得到∠DEF=∠ECA=α，进而得到=90BC AC A B α=∠︒−∠，根据三角形内角和即可求解．【详解】解：（1）过点C 作//CG DF ，DFE FCG ∴∠=∠，BC MN ⊥，90BCF ∴∠=︒，90BCG FCG ∴∠+∠=︒，90BCG DFE ∴∠+∠=︒，90ABC DFE ∠+∠=︒，ABC BCG ∴∠=∠，//CG AB ∴，//DF AB ∴；（2）解：ABC ACB ∠=∠，DEF DFE ∠=∠，又90ABC DFE ∠+∠=︒，90ACB DEF ∴∠+∠=︒，BC MN ⊥，90BCM ∴∠=︒，90ACB ACE ∴∠+∠=︒，DEF ACE ∴∠=∠，//DE AC ∴；（3）如图三角形DEF 即为所求作三角形．∵DFE α∠=，∴DFE DEF α∠=∠=，由（2）得，DE ∥AC ，∴∠DEF=∠ECA=α，∵90ACB ACE ∠+∠=︒，∴∠ACB=90α︒−，∴ =90BC AC A B α=∠︒−∠，∴∠A=180°-A ABC CB −∠∠=2α．故答案为为：2α．【点睛】本题考查了平行线的判定，三角形的内角和等知识，综合性较强，熟练掌握相关知识，根据题意画出图形是解题关键．【经典例题二根据平行线的性质探究角的关系】【例2】（2023下·江苏·七年级专题练习）如图，已知AB DE ABC CED ∠∠∥，、的平分线交于点F ．探究BFE ∠与BCE ∠之间的数量关系，并证明你的结论．【答案】2BCE BFE ∠=∠，见解析【分析】本题主要考查了平行线的判定与性质，过点C 作直线MN AB ∥，然后证明MN DE ∥，根据平行线的性质可得=DEC ECN ∠∠，=ABC BCN ∠∠，进而可得BCE ABC DEC ∠=∠+∠，同理可得BFE ABF DEF ∠=∠+∠，再根据角平分线的性质可得2ABC ABF ∠=∠，2DEC DEF ∠=∠，等量代换可得答案．【详解】解：过点C 作直线MN AB ∥，∵AB DE MN AB ∥，∥，∴MN DE ∥，∴DEC ECN =∠∠，AB MN ，∴ABC BCN ∠=∠，∴BCE ABC DEC ∠=∠+∠，同理BFE ABF DEF ∠=∠+∠，∵ABC CED ∠∠、的平分线交于点F ，∴22ABC ABF DEC DEF ∠=∠∠=∠，，∴222BCE ABF DEF BFE ∠=∠+∠=∠．【变式训练】 1．（2024上·山西晋城·七年级统考期末）综合与探究如图，已知直线a b c ∥∥，点A ，B 在直线a 上，点C ，D 在直线c 上，P 是直线b 上的一个动点．(1)当点P 移动到如图1所示的位置时，,,PAB PCD APC ∠∠∠之间的数量关系为________(2)当点P 移动到如图2所示的位置时，（1）中的结论是否仍然成立？若成立，请说明理由；若不成立，请写出新的结论并说明理由．(3)如图3，已知20,50,45,15B BCD CDE E ∠=︒∠=︒∠=︒∠=︒．试判断AB 与EF 是否平行，并说明理由：【答案】(1)360PAB PCD APC ∠+∠+∠=︒(2)（1）中结论不成立，APC PAB PCD ∠=∠+∠．理由见解析(3)平行．理由见解析【分析】本题考查的是平行线的判定与性质，熟记平行线的性质与判定方法并灵活应用是解本题的关键．（1）利用平行线的性质证明12180∠+∠=︒，34180∠+∠=︒，从而可得结论；（2）利用平行线的性质证明1PAB ∠=∠，2PCD ∠=∠，从而可得结论；（3）如图，过点C 作CM EF ∥．由（2），得CDE DCM E ∠=∠+∠．求解20BCM ∠=︒．结合20B ∠=︒，进一步可得结论．【详解】（1）解：如图，∵a b c ∥∥，∴12180∠+∠=︒，34180∠+∠=︒，∴1234360∠+∠+∠+∠=︒，∴360PAB PCD APC ∠+∠+∠=︒．（2）（1）中结论不成立，APC PAB PCD ∠=∠+∠．理由：如图，∵a b ∥，1PAB ∴∠=∠．∵b c ∥，2PCD ∴∠=∠．12APC ∠=∠+∠，APC PAB PCD ∴∠=∠+∠．（3）平行．理由如下：如图，过点C 作CM EF ∥．由（2），得CDE DCM E ∠=∠+∠．45,15CDE E ︒∠︒∠==Q ，30DCM CDE E ∴∠=∠−∠=︒．50BCD ∠=︒，20BCM BCD DCM ∴∠=∠−∠=︒．又20B ︒∠=，BCM B ∴∠=∠．C AB M ∴∥．CM EF Q ∥，∴AB EF ∥．2．（2021下·湖北武汉·七年级校考阶段练习）已知，如图，AB 与CD 交于点O ．(1)如图1，若AC BD ∥，请直接写出A C ∠+∠与B D ∠+∠的数量关系为_________．(2)如图2，若AC 不平行BD ，（1）中的结论是否仍然成立？请判断并证明你的结论．（注：不能用三角形内角和定理）【答案】(1)A C B D ∠+∠=∠+∠，证明见解析(2)（1）中结论成立，证明见解析【分析】（1）先证明A B ∠=∠，C D ∠=∠，可得A C B D ∠+∠=∠+∠；（2），过A 作AH BD ∥交CD 于N ，结合（1）可得：B D BAN AND ∠+∠=∠+∠，过C 作CG AH ∥，ACN CAN ACN ACG GCN ∠+∠=∠+=∠，证明OAC ACO OAN CAN ACN OAN GCN BAN AND ∠+∠=∠+∠+=∠+∠=∠+∠，从而可得结论成立．【详解】（1）解：A C B D ∠+∠=∠+∠，理由如下：∵AC BD ∥，∴A B ∠=∠，C D ∠=∠，∴A C B D ∠+∠=∠+∠；（2）（1）中结论成立，理由如下：如图，过A 作AH BD ∥交CD 于N ，结合（1）可得：B D BAN AND ∠+∠=∠+∠，过C 作CG AH ∥，∴AND GCD ∠=∠，ACG CAN ∠=∠，∴ACN CAN ACN ACG GCN ∠+∠=∠+=∠，∴OAC ACO OAN CAN ACN OAN GCN BAN AND ∠+∠=∠+∠+=∠+∠=∠+∠，∴B D OAC ACO ∠+∠=∠+∠；【点睛】本题考查的是平行线的性质，熟记平行线的性质并作出合适的辅助线是解本题的关键． 3．（2023上·河北石家庄·八年级统考阶段练习）如图，我们生活中经常接触的小刀刀柄外形是一个直角梯形（下底挖去一小半圆），刀片上、下是平行的．把处于闭合状态的刀片打开，使刀背与直角腰的夹角为1∠，刀片转动的角为2∠．(1)若155∠=︒，求2∠的度数．(2)刀片在打开过程中，若2∠为钝角，求证：2901∠=︒+∠．【答案】(1)145︒(2)见解析【分析】（1）根据平行线的性质得到155BCE ∠=∠=︒，DCE CDF ∠=∠，由互余得到9035DCE BCE ∠=︒−∠=︒，则35CDF DCE ∠=∠=︒，根据邻补角即可得到2∠的度数；（2）由（1）可知，AB DF CE ∥∥，则1BCE ∠=∠，DCE CDF ∠=∠，由90BCE DCE ∠+∠=︒得到90901DCE BCE ∠=︒−∠=︒−∠，则901CDF DCE ∠=∠=︒−∠，根据邻补角即可得到结论．【详解】（1）解：如图，过点C 作CE DF ∥，由题意可知，AB DF ∥，∴AB DF CE ∥∥，∴155BCE ∠=∠=︒，DCE CDF ∠=∠，∵90BCE DCE ∠+∠=︒，∴90905535DCE BCE ∠=︒−∠=︒−︒=︒，∴35CDF DCE ∠=∠=︒，∴218018035145CDF ∠=︒−∠=︒−︒=︒；（2）由（1）可知，AB DF CE ∥∥，∴1BCE ∠=∠，DCE CDF ∠=∠，∵90BCE DCE ∠+∠=︒，∴90901DCE BCE ∠=︒−∠=︒−∠，∴901CDF DCE ∠=∠=︒−∠，∴()2180180901901CDF ∠=︒−∠=︒−︒−∠=︒+∠；即2901∠=︒+∠．【点睛】此题主要考查平行线的性质、邻补角等知识，熟练掌握平行线的性质是解题的关键． 4．（2023下·贵州毕节·七年级校联考期中）在综合与实践课上，老师让同学们以“两条平行线,AB CD 和一块含60︒角的直角三角尺(90,60)EFG EFG EGF ∠=︒∠=︒”为主题开展数学活动． (1)如图1，三角尺的60︒角的顶点G 在CD 上．240∠=︒，则1∠的度数为________．(2)如图2，小颖把三角尺的两个锐角的顶点,E G 分别放在AB 和CD 上，请你探索AEF ∠与FGC ∠之间的数量关系是_______．(3)如图3，小亮把三角尺的直角顶点F 放在CD 上，30︒角的顶点E 在AB 上．若AEG α∠=，DFG β∠=，请直接写出AEG ∠与DFG ∠的数量关系（用含,αβ的式子表示）．【答案】(1)80︒(2)90AEF FGC ∠+∠=︒(3)120αβ−=︒【分析】（1）根据平行线的性质可知1EGD ∠=∠，依据2180FGE EGD ∠+∠+∠=︒，可求出1∠的度数；（2）过点F 作∥FP AB ，得到FP AB CD ∥∥，通过平行线的性质把AEF ∠和FGC ∠转化到EFG ∠上即可；（3）依据AB CD ∥，可知180AEF CFE ∠+∠=︒，再根据18090CFE DFG ∠=︒−∠−︒，30AEF AEG ∠=∠−︒，代入180AEF CFE ∠+∠=︒，即可求出120AEG DFG ∠−∠=︒．【详解】（1）解：AB CD ∥，1EGD ∴∠=∠，2180FGE EGD ∠+∠+∠=︒，260180EGD ∴∠+︒+∠=︒，80EGD ∴∠=︒，180∴∠=︒；故答案为：80︒；（2）90AEF FGC ∠+∠=︒，理由如下：如图，过点F 作∥FP AB ，CD A B ∥，FP AB CD ∴∥∥，AEF EFP ∴∠=∠，FGC GFP ∠=∠，AEF FGC EFP GFP EFG ∴∠+∠=∠+∠=∠，90EFG ∠=︒，90AEF FGC ∴∠+∠=︒；故答案为：90AEF FGC ∠+∠=︒；（3）120αβ−=︒，理由如下：AB CD ∥，180AEF CFE ∠+∠=︒∴，18090CFE DFG ∠=︒−∠−︒，30AEF AEG ∠=∠−︒，3018090180AEG DFG ∴∠−︒+︒−∠−︒=︒，120AEG DFG ∴∠−∠=︒，120αβ∴−=︒．【点睛】本题考查了平行线的性质，正确作出辅助线是解决问题的关键．5．（2023下·浙江杭州·七年级统考期末）已知AB CD ∥，点E 在AB 上，点F 在CD 上，点Q 为射线EF 上一点．(1)如图1，若22A ∠=︒，35C ∠=︒，则AQC ∠= ．(2)如图2，当点Q 在线段EF 的延长线上时，请写出A ∠、C ∠和AQC ∠三者之间的数量关系，并说明理由．(3)如图3，AH 平分QAB ∠，CH 交AH 于点H ．①若CH 平分QCD ∠，求AQC ∠和AHC ∠的数量关系．②若:1:3QCH DCH ∠∠=，33HCD ∠=︒，25AHC ∠=︒，直接写出AQC ∠的度数为．【答案】(1)57︒(2)数量关系：A C AQC ∠−∠=∠，理由见解析(3)① AHC ∠=12AQC ∠，②72AQC ∠=︒【分析】（1）过点Q 作QH ∥AB ，进而利用两直线平行，内错角相等解答即可；（2）过点Q 作MN ∥CD ，进而利用两直线平行，内错角相等解答即可；（3）①过点H 作PH ∥CD ，根据平行线的性质和角平分线的定义解答即可；②根据①的结论，利用角的关系解答即可．【详解】（1）解：过点Q 作QH ∥AB ，AB ∥CD ，QH ∴∥AB ∥CD ，35C CQH ∴∠=∠=︒，22A HQA ∠=∠=︒，352257AQC CQH HQA ∴∠=∠+∠=︒+︒=︒，故答案为：57︒；（2）数量关系：A C AQC ∠−∠=∠，证明：过点Q 作MN ∥CD ，AB ∥CD ，AB ∴∥MN ，NQC C ∴∠=∠，180MQA A ∠=︒−∠，180AQC NQC MQA A C ∴∠=︒−∠−∠=∠−∠．（3）①过点H 作PG ∥CD ，AB ∥CD ，AB ∴∥PH ，PHC HCD ∴∠=∠，180GHA HAB ∠=︒−∠，AHC HAB HCD ∴∠=∠−∠．又AH 平分CAB ∠，CH 平分QCD ∠，HAB ∴∠=12QAB ∠，HCD ∠=12QCD ∠ AHC ∴∠=12 ()QAB QCD ∠−∠由（2）可得AHC ∠=12.AQC ∠②72AQC ∠=︒，理由如下：QCH ∠：1:3DCH ∠=，33HCD ∠=︒，25AHC ∠=︒，11QCH ∴∠=︒，33DCH ∠=︒，332558HAB ∴∠=︒+︒=︒，5824472AQC ∴∠=︒⨯−︒=︒，故答案为：72︒．【点睛】本题考查平行线的判定和性质，关键是添加辅助线，根据两直线平行，内错角相等解答．【经典例题三平行线的性质在生活中的实际应用】【例3】（2023下·江苏泰州·七年级统考期末）如图1是一盏可折叠台灯．图2、图3是其平面示意图，支架AB 、BC 为固定支撑杆，支架OC 可绕点C 旋转调节．已知灯体顶角52DOE ∠=︒，顶角平分线OP 始终与OC 垂直．(1)如图2，当支架OC 旋转至水平位置时，OD 恰好与BC 平行，求支架BC 与水平方向的夹角θ∠的度数；(2)若将图2中的OC 绕点C 顺时针旋转15︒到如图3的位置，求此时OD 与水平方向的夹角OQM ∠的度数．【答案】(1)64︒(2)49︒【分析】（1）利用角平分线定义可得1262DOP DOE ∠=∠=︒，由垂直定义可得90COP ∠=︒，得出116COD COP DOP ∠=∠+∠=︒，再运用平行线性质即可得出答案；（2）过点C 作CG MN ∥，过点O 作OF CG ∥，根据平行线的性质求解即可．【详解】（1）解：如图2，52DOE ∠=︒，OP 平分DOE ∠，1262DOP DOE ∴∠=∠=︒，OP OC ⊥，90COP ∴∠=︒，9026116COD COP DOP ∴∠=∠+∠=︒+︒=︒，OD BC ∥，180********C COD ∴∠=︒−∠=︒−︒=︒，OC BF ∥，64COF C ∴∠=∠=︒，即64θ∠=︒；（2）如图3，过点C 作CG MN ∥，过点O 作OF CG ∥，则15COF OCG ∠=∠=︒，116COD ∠=︒，11615131FOQ COD COF ∴∠=∠+∠=︒+︒=︒，CG MN ∥，OF CG ∥，OF MN ∴∥，180OQM FOQ ∴∠+∠=︒，180********OQM FOQ ∴∠=︒−∠=︒−︒=︒．【点睛】本题考查了平行线性质等，适当添加辅助线，构造平行关系是解题关键．【变式训练】 1．（2023下·江苏·七年级期中）如图1，某段道路AB CD ，两旁安装了两个探照灯M 和N ．灯M 光束从MB 开始旋转至180︒便立即回转，灯N 光束从NC 开始旋转至180︒便立即回转．灯M 转动的速度是每秒1度，灯N 转动的速度是每秒2度，灯M 转动的时间为t 秒． (1)如图2，灯M 光束先转动30秒后，灯N 光束才开始转动．①直接写出灯M 光束和灯N 光束，灯先回转；(填M 或N )②在灯M 光束回转之前，当两灯的光束平行时，求t 的值；(2)如图3，两灯同时转动，且均不回转．连接MN ，且2BMN MND ∠=∠，若两灯光束交于点E ，在转动过程中，请探究BME ∠与MEF ∠的数量关系是否发生变化？并说明理由．【答案】(1)①N ；②当t 的值为60或140时，两灯的光束互相平行(2)不变，BME MEF ∠=∠．理由见解析【分析】（1）①分别计算M 、N 回转时间，然后比较即可；②根据M 、N 均未回转即30120t <<和N 回转后即120180t <<两种情况，进行求解即可；（2）由AB CD ，可得180BMN MND ∠+∠=︒，则12060BMN MND ∠=︒∠=︒，，由2BME t CNF t ∠=︒∠=︒，，得1202120NME t MNF t ∠=︒−︒∠=︒−︒，，求得180MEN t ∠=︒−︒，则MEF t ∠=︒，进而可得BME MEF ∠=∠．【详解】（1）①解：光束M 回转时间为1801180t =÷=（秒）；光束N 回转时间180230120t =÷+=（秒）；∵120180<，∴光束N 先回转，故答案为：N ；②解：当30120t <<时，如图1，∵AB CD ，∴BMM MM C ''∠=∠， ∵MM NN ''∥，∴N NC MM C ''∠=∠， ∴BMM N NC ''∠=∠，∴()230t t =−，解得60t =；当120180t <<时，如图2，∵AB CD ，∴180BMM MM D ''∠+∠=︒， ∵MM NN ''∥，∴N ND MM D ''∠=∠， ∴180BMM N ND ''∠+∠=︒，∴()230180180t t +−−=⎡⎤⎣⎦，解得140t =，综上所述，当t 的值为60或140时，两灯的光束互相平行；（2）解：不变，BME MEF ∠=∠．理由如下：∵AB CD ，∴180BMN MND ∠+∠=︒，∵2BMN MND ∠=∠，∴12060BMN MND ∠=︒∠=︒，，∵2BME t CNF t ∠=︒∠=︒，，∴1202120NME t MNF t ∠=︒−︒∠=︒−︒，，∴()()1801202120180MEN t t t ∠=︒−︒−︒−︒−︒=︒−︒，∴MEF t ∠=︒，∠=∠．∴BME MEF【点睛】本题考查了平行线的性质的应用，一元一次方程的应用．解题的关键在于明确角度之间的数量关系．2．（2022下·江苏泰州·七年级校考阶段练习）光线照射到镜面会产生反射现象，由光学知识，入射光线与镜面的夹角与反射光线与镜面的夹角相等，例如：在图1中，有∠1＝∠2．(1)如图2，已知镜子MO与镜子ON的夹角∠MON＝90°，请判断入射光线AB与反射光线CD的位置关系，并说明理由；(2)如图3，有一口井，已知入射光线AO与水平线OC的夹角为50°，当平面镜MN与水平线OC的夹角为°，能使反射光线OB正好垂直照射到井底；(3)如图4，直线EF上有两点A、C，分别引两条射线AB、CD．∠BAF＝120°，∠DCF＝40°，射线AB、CD 分别绕A点、C点以3度/秒和1度/秒的速度同时逆时针转动，设时间为t秒，在射线AB转动一周的时间内，是否存在某时刻，使得CD与AB平行？若存在，求出所有满足条件的时间t．【答案】(1)AB∥CD，理由见解析(2)70(3)在射线AB转动一周的时间内，存在时间t，使得CD与AB平行，其t=10s或100s．【分析】（1）计算∠ABC+∠BCD的值便可得出结论；（2）先计算出∠AOB，进而得∠AOM+∠BON的值，再根据入射光线与镜面的夹角与反射光线与镜面的夹角相等，得出结果；（3）分四种情况讨论：当0s≤t≤20s时，当20s＜t≤40s时，当40s＜t≤80s时，当80s＜t≤120s时，根据角度大小变化关系锁确AB∥CD时的t值．【详解】（1）解：AB∥CD．理由如下：∵∠1=∠2，∠3=∠4，∴∠ABC=180°-∠1-∠2=180°-2∠2，∠BCD=180°-∠3-∠4=180°-2∠3，∴∠ABC+∠BCD=360°-2（∠2+∠3），∵∠BOC=90°，∴∠2+∠3=90°，∴∠ABC+∠BCD=180°，∴AB∥CD；（2）解：∵∠AOC=50°，∠BOC=90°，∴∠AOM+∠BON=180°-90°-50°=40°，∵∠AOM=∠BON，∴∠AOM=∠BON=20°，∴∠COM=20°+50°=70°，∠CON=20°+90°=110°，∴当平面镜MN与水平线OC的夹角为70°时，能使反射光线OB正好垂直照射到井底，故答案为：70；（3）解：①当0s≤t≤20s时，如下图，若AB∥CD，则∠BAC=∠ACD，即120+3t=140+t，解得t=10，∴当t=10s时AB∥CD；②当20s＜t≤40s时，如下图，有∠BAE ＜90°＜∠ACD ，则AB 与CD 不平行；③当40s ＜t≤80s 时，如下图，有∠BAC ＜∠ACD ，AB 与CD 不平行；④当80s ＜t≤120s 时，如下图，若AB ∥CD ，则∠BAC=∠DCF ，即3t -240=t -40，解得t=100，∴当t=100s 时，AB ∥CD ；综上可知，在射线AB 转动一周的时间内，存在时间t ，使得CD 与AB 平行，其t=10s 或100s ．【点睛】本题主要考查了平行线的性质与判定，关键是应用分类讨论思想解决问题． 3．（2023下·吉林松原·七年级统考期末）如图，PQ MN ∥，A 、B 分别为直线MN 、PQ 上两点，且45BAN ∠=︒，若射线AM 绕点A 顺时针旋转至AN 后立即回转，射线BQ 绕点B 逆时针旋转至BP 后立即回转，两射线分别绕点A 、点B 不停地旋转，若射线AM 转动的速度是/a ︒秒，射线BQ 转动的速度是/b ︒秒，且a 、b 满足2|6|(1)0a b −+−=．（友情提醒：钟表指针走动的方向为顺时针方向）(1)=a ，b = ；(2)若射线AM 、射线BQ 同时旋转，问至少旋转多少秒时，射线AM 、射线BQ 互相垂直．(3)若射线AM 绕点A 顺时针先转动18秒，射线BQ 才开始绕点B 逆时针旋转，在射线BQ 到达BA 之前，问射线AM 再转动多少秒时，射线AM 、射线BQ 互相平行？【答案】(1)6，1(2)907t =s(3)射线AM 再转动907秒或18秒时，射线AM 、射线BQ 互相平行【分析】（1）依据()2610a b −+−=，即可得到a ，b 的值；（2）依据90ABO BAO ∠+∠=︒，180ABQ BAM ∠+∠=︒，即可得到射线AM 、射线BQ 第一次互相垂直的时间；（3）分两种情况讨论，依据ABQ BAM '''∠=∠时，BQ AM '''，列出方程即可得到射线AM 、射线BQ 互相平行时的时间．【详解】（1）2|6|(1)0a b −+−=， 60a ∴−=，10b −=，6a ∴=，1b =，故答案为：6，1；（2）设至少旋转t 秒时，射线AM 、射线BQ 互相垂直．如图，设旋转后的射线AM 、射线BQ 交于点O ，则BO AO ⊥，90ABO BAO ∴∠+∠=︒，PQ MN ∥，180ABQ BAM ∴∠+∠=︒，90OBQ OAM ∴∠+∠=︒，又OBQ t ∠=︒，6OAM t ∠=︒，690t t ∴︒+︒=︒，90()7t s ∴=；（3）设射线AM 再转动t 秒时，射线AM 、射线BQ 互相平行．如图，射线AM 绕点A 顺时针先转动18秒后，AM 转动至AM '的位置，186108MAM '∠=⨯=︒，分两种情况：①当918t <<时，QBQ t '∠=︒，6M AM t '''∠=︒，45BAN ABQ ∠=︒=∠，45ABQ t '∴∠=︒−︒，645BAM M AM M AB t ''''''∠=∠−∠=−︒，当ABQ BAM '''∠=∠时，BQ AM '''，此时，45645t t ︒−︒=−︒，解得907t =；②当1827t <<时，QBQ t '∠=︒，690NAM t ''∠=︒−︒，45BAN ABQ ∠=︒=∠，45ABQ t '∴∠=︒−︒，45(690)1356BAM t t ''∠=︒−︒−︒=︒−︒，当ABQ BAM '''∠=∠时，BQ AM '''，此时，451356t t ︒−︒=︒−，解得18t =；综上所述，射线AM 再转动907秒或18秒时，射线AM 、射线BQ 互相平行．【点睛】本题主要考查了平行线的性质，非负数的性质以及角的和差关系的运用，解决问题的关键是运用分类思想进行求解，解题时注意：若两个非负数的和为0，则这两个非负数均等于0．【经典例题四平行线中的旋转问题】【例4】（2023上·吉林长春·七年级校考期末）将一副直角三角板按如图①方式摆放在直线MN 上（直角三角板ABC 和直角三角板EDC ，90EDC ∠=︒，60DEC ∠=︒，30DCE ∠=︒，90ABC ∠=︒，45BAC BCA ∠=∠=︒），保持三角板EDC 不动，将三角板ABC 绕点C 以每秒5︒的速度顺时针旋转，旋转时间为t 秒，当AC 与射线CN 重合时停止旋转．(1)如图②，当AC 为DCE ∠的平分线时，t =____________；(2)当18t =时，求BCD ∠的度数；(3)在旋转过程中，当三角板ABC 的AB 边平行于三角板EDC 的某一边时（不包含重合的情形），直接写出t 的值．【答案】(1)3(2)15︒(3)t 的值为15或27或35【分析】本题考查旋转的性质、角平分线的性质、平行线的性质，关键在于数形结合，分类讨论．（1）根据角平分线的定义求出1152ACE DCE ∠=∠=︒，然后求出t 的值即可；（2）当18t =时，旋转角为90︒，可求出ACE ∠，即可求出BCD ∠；（3）分三种情况进行讨论，分别画出图形，求出t 的值即可．【详解】（1）解：如图2，∵90EDC ∠=︒，60DEC ∠=︒，∴30DCE ∠=︒，∵AC 平分DCE ∠， ∴1152ACE DCE ∠=∠=︒， ∴1535t ==，（2）当18t =秒时，CA 的旋转角度为185=90⨯︒︒，即90ACE ∠=︒，如图，∴=BCD ACE ACB DCE ∠∠−∠−∠=904530︒−︒−︒15=︒；（3）①当AB DE ∥时，如图，此时BC 与CD 重合，旋转角度为75BCA ECD ∠+∠=︒，∴()3045515t =+÷=；②当AB CE ∥时，如图，∵AB CE ∥，∴90BCE B ∠=∠=︒，∴9045135ACE ∠=︒+︒=︒，∴135527t =÷=；③当AB CD ∥时，如图，∵AB CD ∥，∴90BCD D ∠=∠=︒，∴309045175ACE ∠=︒+︒+︒=︒，∴175535t =÷=．【变式训练】 1．（2023下·江苏连云港·七年级校考阶段练习）为了美化夜景，在某段道路两旁安置了两座可旋转激光灯．如图，灯A 射线自AM 开始顺时针旋转至AN 便立即回转，灯B 射线自BP 顺时针旋转至BQ 便立即回转，两灯不停交叉照射巡视．若灯A 转动的速度是a ︒/秒，灯B 转动的速度是b ︒/秒，且a 、b 满足()2340a a b −++−=．假定主道路是平行的，即PQ MN ∥，且:1:3BAN ABP ∠∠=．(1)填空：=a _______，b =_______，BAN ∠=_______︒；(2)若灯B 射线先转动30秒，灯A 射线才开始转动，在灯B 射线到达BQ 之前，灯A 射线转动几秒，两灯的光束互相平行？(3)如图，两灯同时转动，在灯A 射线到达AN 之前，若射出的光束交于点C ，过C 作CD AC ⊥交PQ 于点D ，则在转动过程中，BAC ∠与BCD ∠的数量关系是否发生变化？若不变，请求出其数量关系；若改变，请求出其取值范围．【答案】(1)3 1 45(2)15秒或82.5秒(3)不发生改变32BAC BCD ∠=∠【分析】（1）根据绝对值与平方数的非负性即可求解；根据同旁内角互补并结合已知条件可求得BAN ∠的度数．（2）根据题意，当两灯的光束互相平行时，内错角相等即可列出方程求解．（3）设灯B 射线转动的角度PBC x ∠=，则灯A 射线转动的角度3MAC x ∠=设法把BAC ∠与BCD ∠用含x 的代数式表示出来即可获得两角的关系式．【详解】（1）∵()2340a a b −++−=，∴30,40a a b −=+−=∴3,1a b ==．∵PQ MN ∥，∴180BAN ABP ∠+∠=︒．由:1:3BAN ABP ∠∠=得3ABP BAN ∠=∠∴4180BAN ∠=︒，∴45BAN ∠=︒．（2）如图．设在灯B 射线赶到达BQ 之前，灯A 射线转动t 秒，两灯的光束平行，①在灯射线到达AN 之前，由题意得，303t t +=，解得：15t =（秒）②在灯A 射线到达AN 之后，由题意得：()()318030180t t −︒++︒=︒（同旁内角互补，两直线平行）解得：82.5t =（秒）∴灯转动15秒或82.5秒时，两灯的光束互相平行．（3）BAC ∠与BCD ∠的数量关系不发生变化．理由如下：如图．由⑴知45BAN ∠=︒，∴18045135ABP MAB ∠=∠=︒−︒=︒．设灯B 射线转动的角度PBC x ∠=，则灯A 射线转动的角度3MAC x ∠=∴3x 135BAC MAC MAB ∠=∠−∠=−︒，①135ABC ABP PBC x ∠=∠−∠=︒−，∴()()18018031351351802BCA BAC ABC x x x ∠=︒−∠−∠=︒−−︒−︒−=︒−∵CD AC ⊥，∴()90901802290BCD BCA x x =︒−=︒−︒−=−︒∠∠②由①②得，23BAC BCD ∠=∠ ∴32BAC BCD ∠=∠【点睛】本题考查了绝对值与平方数的非负性、平行线的判定、三角形内角和、用含字母的代数式表示角度等知识点，熟练掌握平行线的性质是解题的关键． 2．（2023下·河南新乡·七年级统考期末）综合与实践数学社团的同学以“两条平行线AB ，CD 和一块含45︒角的直角三角尺()90EFG EFG ∠=︒”为主题开展数学活动，已知点E ，F 不可能同时落在直线AB 和CD 之间．探究：（1）如图1，把三角尺的45︒角的顶点E ，G 分别放在AB ，CD 上，若150BEG ∠=︒，求FGC ∠的度数；类比：（2）如图2，把三角尺的锐角顶点G 放在CD 上，且保持不动，若点E 恰好落在AB 和CD 之间，且AB 与EF 所夹锐角为25︒，求FGC ∠的度数；迁移：（3）把三角尺的锐角顶点G 放在CD 上，且保持不动，旋转三角尺，若存在()545FGC DGE DGE ∠=∠∠<︒，直接写出射线GF 与AB 所夹锐角的度数．【答案】（1）105︒（2）115︒（3）67.5︒或11.25°【分析】（1）根据平行线的性质得出180BEG EGD +=︒∠∠，得出30EGD ∠=︒，即可求解．（2）设AB 交EF 于点M ，则25BME ∠=︒，过点E 作EN CD ∥，推出EN AB ∥．根据平行线的性质得出则25NEM BME ∠=∠=︒．求出NEG ∠，即可求解；（3）根据题意，进行分类讨论：①当点E 在CD 上方时，②当点E 在CD 下方时，正确画出图形，根据平行线的性质求解即可.【详解】解：（1）∵AB CD ∥，180BEG EGD ∴∠+∠=︒．又150BEG ∠=︒，30EGD ∴∠=︒，1803045105FGC ∴∠=︒−︒−︒=︒．（2）如图1，设AB 交EF 于点M ，则25BME ∠=︒，过点E 作EN CD ∥，∵AB CD ∥，EN CD ∥EN AB ∴∥．25NEM BME ∴∠=∠=︒．452520NEG ∴∠=︒−︒=︒．又EN CD ∥，20DGE NEG ∴∠=∠=︒，1802045115FGC ∴∠=︒−︒−︒=︒．（3）67.5︒或11.25°．如图2，AB 交GF 于点H ，当点E 在CD 上方时，设EGD x ∠=，则5FGC x ∠=，∴545180x x +︒+=︒，解得22.5x =︒．∴4522.567.5AHG HGD ∠=∠=︒+︒=︒；如图3，延长GF 交AB 于点H ，当点E 在CD 下方时，设EGD y ∠=，则5FGC y ∠=，∴()545180y y +︒−=︒，解得33.75y =︒，∴4533.7511.25AHG HGD ∠=∠=︒−︒=︒．综上所述，AHG ∠的度数为67.5︒或11.25°．【点睛】本题主要考查了平行线的性质，解题的关键是掌握平行线的性质：两直线平行，同位角相等，内错角相等，同旁内角互补． 3．（2022上·陕西延安·七年级统考阶段练习）如图1，已知PQ MN ∥，点A ，B 分别在MN ，PQ 上，且45BAN ∠=︒，射线AM 绕点A 顺时针旋转至AN 便立即逆时针回转（速度是a ︒/秒），射线BP 绕点B 顺时针旋转至BQ 便立即逆时针回转（速度是b ︒/秒）、且a 、b 满足()2310a b −+−=．(1)如图2，两条射线同时旋转，设旋转时间为t 秒()60t <，两条旋转射线交于点C ，过C 作CD AC ⊥交PQ 于点D ，求BAC ∠与BCD ∠的数量关系；(2)若射线BP 先旋转20秒，射线AM 才开始旋转，设射线AM 旋转时间为t 秒()160t <，若旋转中AM BP ∥，求t 的值．【答案】(1)23BAC BCD ∠=∠；(2)若旋转中AM BP ∥，t 的值为10或85．【分析】（1）根据非负数的性质即可得到a ，b 的值，由题意可得3135BAC t ∠=−︒，再根据PQ MN ∥即可得到ACB CBD CAN ∠=+∠，从而可得1802BCA t ∠=︒−，再根据=90ACD ∠︒，可得290BCD t ∠=−︒，从而可得32BAC BCD ∠∠=：：，即可得出结论；（2）分三种情况讨论，列出方程即可得到射线AM 、射线BP 互相平行时的时间．【详解】（1）解：∵a 、b 满足()2310a b −+−=．∴3010a b −=−=，，∴31a b ==，，由题意得3CAM t CBD t ∠=∠=，，∵180345CAN t BAN ∠=︒−∠=︒，， ∴4518033135BAC t t ∠=︒−︒−=−︒（），过点C 作CE PQ ∥，∴CBD BCE t ∠=∠=，∵PQ MN ∥，∴PQ CE MN ∥∥，∴1803CAN ACE t ∠=∠=︒−，∵ACE BCE ACB ∠+∠=∠，∴18031802ACB CBD CAN t t t ∠=+∠=+︒−=︒−，∵CD AC ⊥，∴=90ACD ∠︒，∴()90901802290BCD ACB t t ∠=︒−∠=︒−︒−=−︒，∴32BAC BCD ∠∠=：：，即23BAC BCD ∠=∠；（2）解：∵160t <，∴()2011803480t t +⨯<<，，即射线BP 旋转的角度小于180︒，①当3180t <，即060t <<时，()3201t t =+⨯，解得：10t =；②当1803270t <<且()20190t +⨯>，即7090t <<时， ()3180201180t t −++⨯=，解得：85t =；③当()360348020190t t <<+⨯>且，即120160t <<时， ()3360201t t −=+⨯，解得：190t =（不合题意，舍去）；∴若旋转中AM BP ∥，t 的值为10或85．【点睛】本题主要考查了平行线的性质，非负数的性质，旋转的性质以及角的和差关系的运用，解决问题的关键是运用分类思想进行求解，解题时注意：若两个非负数的和为0，则这两个非负数均等于0． 4．（2023上·广西贵港·七年级校考期末）如图，直线AB CD ∥，MN AB ⊥分别交AB ，CD 于点M 、N ，射线MP 、MQ 分别从MA 、MN 同时开始绕点M 顺时针旋转，分别与直线CD 交于点E 、F ，射线MP 每秒转10︒，射线MQ 每秒转5︒，ER ，FR 分别平分PED ∠，QFC ∠，设旋转时间为t 秒()018t <<．(1)用含t 的代数式表示：AMP ∠=________︒，QMB ∠=________︒；(2)当4t =时，REF ∠=________︒．(3)当130MEN MFN ∠+∠=︒时，求出t 的值．【答案】(1)10t ，()905t −(2)70(3)8t =或283t =.【分析】（1）由题意不难得出10AMP t ∠=︒，5NMF t ∠=︒，继而得到()905QMB t ∠=−︒；（2）由平行线的性质可得10MEF AMP t ∠=∠=︒，再结合ER 是PED ∠的平分线，即可求解；（3）由平行线的性质可得10MEN AMP t ∠=∠=︒，再由MN AB ⊥得到MN CD ⊥，从而求得905MFN t ∠=︒−︒，分两种情况讨论：当点E 在N 左侧时和当点E 在N 右侧时，结合已知条件，即可求解；【详解】（1）解：由题意得：10AMP t ∠=︒，5NMF t ∠=︒，AB CD ∥，MN AB ⊥，()90905905QMB NMF t t ∴︒∠=︒−∠=︒−︒=−；故答案为：10t ，()905t −；（2）AB CD ∥，10MEF AMP t ∴∠=∠=︒，ER Q 是PED ∠的平分线，()()111801801090522REF MEF t t ∴∠=︒−∠=︒−︒=︒−︒，∴当4t =时，905470REF ∠=︒−⨯︒=︒；故答案为：70；（3）①当点E 在N 左侧时，AB CD ∥，10MEN AMP t ∴∠=∠=︒，MN AB ⊥，MN CD ∴⊥，5NMF t ∠=︒，905MFN t ∴∠=︒−︒，130MEN MFN ∠+∠=︒，10905130t t ∴︒+︒−︒=︒，解得：8t =；②当点E 在N 右侧时，如图，AB CD ∥，10AMP t ∠=︒，180MEN AMP ∴∠+∠=︒，18010MEN t ∴∠=︒−︒，MN AB ⊥，MN CD ∴⊥，5NMF t ∠=︒，905MFN t ∴∠=︒−︒，130MEN MFN ∠+∠=︒，180********t t ∴︒−︒+︒−︒=︒，解得：283t =；【点睛】本题主要考查平行线的性质，解题的关键是对这些知识点的掌握和熟练应用． 5．（2022下·天津南开·七年级校联考期中）将一副三角板中的两个直角顶点C 按如图方式叠放在一起．(1)若45DCE ∠=︒，则ACB ∠的度数为________；若140ACB ∠=︒，则DCE ∠的度数为________；(2)猜想ACB ∠与DCE ∠的大小关系，并说明理由；(3)若将三角板BCE ∠绕点C 按顺时针方向继续旋转，当90ACE ∠<︒时，这两块三角尺是否存在一组边互相平行？请画出图形，并直接写出ACE ∠的大小．【答案】(1)135︒；40︒(2)180ACB DCE ∠+∠=︒，见解析(3)存在，见解析，当AC EB ∥时45ACE ∠=︒，当AD BC ∥时，30ACE ∠=︒【分析】（1）根据角度之间的和、差计算即可；（2）根据角度之间的和、差计算即可；（3）分两种情况讨论：AC EB ∥和AD BC ∥，根据图形，利用平行线的性质和角度之间的和、差关系求解即可．【详解】（1）解：若45DCE ∠=︒，90ACD BCE ∠=∠=︒，904545ACE ACD DCE ∴∠=∠−∠=︒−︒=︒，4590135ACB ACE DCE ∴∠=∠+∠=︒+︒=︒；若140ACB ∠=︒，90ACD BCE ∠=∠=︒，1409050ACE ACB BCE ∴∠=∠−∠=︒−︒=︒，905040DCE ACD ACE ∴∠=∠−∠=︒−︒=︒；故答案为：135︒；40︒；（2）证明：90ACB DCB ∠=︒+∠，90DCE DCB ∠=︒−∠，9090180ACB DCE DCB DCB ∴∠+∠=︒+∠+︒−∠=︒；（3）解：如图所示，当AC EB ∥时，45CEB ∠=︒，∴45ACE CEB ∠=∠=︒；。

专题5 平行线中的模型——初中几何与代数必考模型+例题+变式

【详解】解：①如图：过点E作，
， ,
，
，
；
②如图，过E点作，过F点作
过G点作，
，
，
，
，
即 ;
③如图：
，
根据以上规律可得：
．
【点睛】本题主要考查了平行线的性质，根据题意将复杂的图形转化为基本图形是解题的关键．
变式1
4.把一副三角板放在水平桌面上，摆放成如图所示的形状，使两个直角顶点重合，两条斜边平行，则∠1的度数是（）
变式2
5.如图，已知AB∥DE，∠1＝30°，∠2＝35°，则∠BCE的度数为（）
A. 70°B. 65°C. 35°D. 5°
【答案】B
【解析】
【分析】作CF∥AB，根据平行线的性质可以得到∠1＝∠BCF，∠FCE＝∠2，从而可得∠BCE的度数，本题得以解决．
【详解】作CF∥AB，
∵AB∥DE，
平行线中的模型
模型一M型
1、M型基础
例题1
1.如图，若，则，你能说明为什么吗？
【答案】见解析
【解析】
【分析】过作，利用两直线平行，内错角相等来证明．
【详解】解：过作，
则，
，
，
，
．
【点睛】本题考查了平行线的性质与判定，关键是过点作的平行线，利用平行线的性质来证明．
例题2
2.在图中，，与又有何关系？
【点睛】本题主要考查平行线的性质，熟练掌握平行线的性质是解答的关键.
培优
变式6
9.（1）如图1已知：∠B=25°，∠BED=80°，∠D=55°．探究AB与CD有怎样的位置关系.
（2）如图2已知AB∥EF，试猜想∠B，∠F，∠BCF之间的关系，写出这种关系，并加以证明.

初中七年级数学平行线四大模型题

七下专题：平行线四大模型知识导航一、平行线的定义1、定义：在同一平面内，不相交的两条直线叫做平行线，直线a与直线b互相平行，记作a∥b．2、在同一平面内，两条直线的位置关系只有两种：(1)相交；(2)平行．这里，我们把重合的两直线看成一条直线．【注】初中不涉及到重合．二、平行公理及推论平行公理：经过直线外一点，有且只有一条直这条直线平行．推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行．三、行线的判定判定1：同位角相等，两直线平行．判定2：内错角相等，两直线平行．判定3：同旁内角互补，两直线平行．四、平行线的性质性质1：两直线平行，同位角相等．性质2：两直线平行，内错角相等．性质3：两直线平行，同旁内角互补．五、两条平行线间的距离同时垂直于两条平行线，并且夹在这两条平行线间的线段的长度叫做这两条平行线的距离，平行线间的距离处处相等．如图2，EF的长度就是AB和CD这两条平行线的距离题型一基础巩固例1（1）（二中广雅）如图，已知AB∥CD，CB平分∠ACD，且∠A:∠ACD＝3:1，则∠B的度数为．（2）（武昌七校七下期中）如图，已知AB平行CD，能判断BE平行CF的条件是（）A．∠1＝∠3B．∠2＝∠4C．∠1＝∠4D．∠1＝∠2（3）如图AF∥CD，BC平分∠ACD，交AF于点B，点E在CD上，BD平分∠EBF，交CE的延长线于点D，且BD⊥BC，下列结论：①BC平分∠ABE；②AC∥BE；③∠BCD＋∠CDB＝90°；④∠DBF＝2＝S△ABD．∠ABC；⑤S△BCEA．2个B．3个C．4个D．5个练1（1）两条直线被第三条直线所截，那么内错角之间的大小关系是（）A．相等B．互补C．不相等D．无法确定（2）（二中广雅七下期中）如图，∠1＝∠2，且∠3＝105°，则∠4的度数为（）A．75°B．62°C．82°D．108°(3)(武昌七校七下期中)完成下面的推理填空：如图，已知AD⊥BC，EF⊥BC，垂足分别为D、F，∠2＋∠3＝180°，求证：∠GDC＝∠B．证明:∵AD⊥BC，EF⊥BC(已知)，∴∠ADB＝＝90°(垂直的定义)，∴AD∥EF()∴（），又∠2＋∠3＝180°(已知)，∵∠1＝∠3(同角的补角相等)，∴∥（），∴∠GDC＝∠B()．模块二四大模型之“铅笔”“猪蹄”模型知识导航四大模型之模型一：“铅笔”模型点P在EF右侧，在AB、CD内部“铅笔”模型结论1：若AB∥CD，则∠P＋∠AEP＋∠PFC＝360°；结论2：若∠P＋∠AEP＋∠PFC＝360°，则AB∥CD．四大模型之模型二：“猪蹄”模型点P在EF左侧，在AB、CD内部“猪蹄”模型结论1：若AB∥CD，则∠P＝∠AEP＋∠PFC；结论2：若∠P＝∠AEP＋∠PFC，则AB∥CD．题型一“铅笔”与“猪蹄”的证明例2（1）若AE∥CF，求证：∠P＋∠AEP＋∠PFC＝360°．（2）若AE∥CF，求证：∠P＝∠AEP＋∠PFC．（2）若∠P＝∠AEP＋∠PFC，求证：AE∥CF．题型二“铅笔”“猪蹄”基础应用例3（1）（七一月考）已知EF∥MN，一直角三角板如图放置，∠ACB＝90°．①如图1，若∠1＝60°，则∠2＝度；②如图2，若∠1＝∠B－20°，则∠2＝度．练2（1）若∠P＋∠AEP＋∠PFC＝360°，求证：AE∥CF；．练3（1）如图，已知直线a∥b，∠1＝40°，∠2＝60°，则∠3等于（）A．100°B．60°C．40°D．20°（2）如图，a∥b，M、N分别在a，b上，P为两平行线间一点，那么∠1＋∠2＋∠3＝．巅峰突破已知：如图，AF∥CD，求证：∠A＋∠C＋∠E＝∠B＋∠D＋∠F．（2）（武昌区七下期中）如图，已知a∥b，∠1＝100°，∠2＝140°，则∠3＝模块三四大模型之“臭脚”“骨折”模型知识导航四大模型之模型三：“臭脚”模型点P在EF右侧，在AB、CD外部“臭脚”模型结论1：若AB∥CD，则∠P＝∠AEP－∠CFP或∠P＝∠CFP－∠AEP；结论2：若∠P＝∠AEP－∠CFP或∠P＝∠CFP－∠AEP，则AB∥CD．四大模型之模型三：“骨折”模型点P在EF左侧，在AB、CD外部“骨折”模型结论1：若AB∥CD，则∠P＝∠CFP－∠AEP或∠P＝∠AEP－∠CFP；结论2：若∠P＝∠CFP－∠AEP或∠P＝∠AEP－∠CFP，则AB∥CD．题型一“臭脚”与“骨折”的证明例4（1）若AE∥CF，求证：∠P＝∠AEP－∠CFP．（2）若AE∥CF，求证：∠P＝∠CFP－∠AEP．练4（1）若∠P＝∠AEP－∠CFP，则AE∥CF．（2）若∠P＝∠CFP－∠AEP，求证：AE∥CF．题型二“臭脚”“骨折”基础应用例5（梅苑中学七下期中）已知直线AB∥CD，E是直线AB的上方一点，连接AE、EC ①如图1，求证：∠AEC＋∠EAB＝∠ECD；②如图2，AF平分∠BAE，CF平分∠DCE，且∠AFC比∠AEC的32倍少40°，直接写出∠AEC的度数．练5（1）如图，已知直线AB∥CD，∠C＝115°，∠A＝25°，则∠E＝（）A．70°B．80°C．90°D．100°（2）如图，已知a∥b，∠3＝50°，则∠1＋∠2＝．例6★★如图，AC∥DE，∠EFG＝∠A＋∠E，试判断AB和FG的位置关系，井说明你的理由．练6如图，AB∥EF，∠B＝50°，∠C＝20°，∠E＝130°，求证：BC∥DE．总结归纳所有的四大模型解决方法都是：转折角处画平行线（拐点＋平行）“铅笔”模型“猪蹄”模型“骨折”模型“臭脚”模型典题示例已知∠B＝25°，∠BCD＝45°，∠CDE＝30°，∠E＝10°，求证：AB∥EF．【考点】“铅笔”“猪蹄”模型结合配套作业平行线四大模型（一）1．如图，∠1＝∠2，且∠3＝108°，则∠4的度数为（）A．72°B．62°C．82°D．80°2．下列说法中，正确的有（）①两点之间，线段最短；②在同一平面内，过一点有且只有一条直线与已知直线平行；③平行于同一直线的两条直线互相平行A．0个B．1个C．2个D．3个3．如图，l1∥l2，∠1＝120°，∠2＝100°，则∠3＝．4．如图，射线AC∥BD，∠A＝70°，∠B＝40°，则∠P＝．第4题图第5题图5．（武珞路七下期中）如图，直线AB、CD、EF被直线GF所截，∠1＝70°，∠2＝110°，∠3＝70°，求证：AB∥CD证明：∵∠1＝70°，∠3＝70°（已知）∴∠1＝∠3（）∴∥（）∵∠2＝110°，∠3＝70°（已知）∴＋＝180°（等式性质）∴∥（）∴AB∥CD．；请证明．②在图2中，∠BMF 、∠F 、∠FND 的数量关系为；请证明．7.如图，已知180EFC BDC ︒∠+∠=，DEF B ∠=∠．（1）试判断DE 与BC 的位置关系，并说明理由．（2）若DE 平分ADC ∠，3BDC B ∠=∠，求EFC ∠的度数．6．（武昌区七下期末）如图，直线AB ∥CD ，①在图1中，∠BME 、∠E 、∠END 的数量关系为9.如图（1）所示是一根木尺折断后的情形，你可能注意过，木尺折断后的断口一般是参差不齐的，那么请你深入考虑一下其中所包含的一类数学问题，我们不妨取名叫“木尺断口问题”．（1）如图（2）所示，已知//AB CD ，请问B Ð，D ∠，E ∠有何关系并说明理由；（2）如图（3）所示，已知//AB CD ，请问B Ð，E ∠，D ∠又有何关系并说明理由；（3）如图（4）所示，已知//AB CD ，请问E G +∠∠与B F D ++∠∠∠有何关系并说明理由8.如图1，AB ∥CD ，∠PAB =130°，∠PCD =120°，求∠APC 的度数．小明的思路是：过P 作PE ∥AB ，通过平行线性质来求∠APC ．（1）按小明的思路，求∠APC 的度数；（2）如图2，AB ∥CD ，点P 在射线OM 上运动，记∠PAB =α，∠PCD =β当点P 在B 、D 两点之间运动时，问∠APC 与α、β之间有何数量关系？请说明理由；（3）在（2）的条件下，如果点P 在B 、D 两点外侧运动时（点P 与点O 、B 、D 三点不重合），请直接写出∠APC 与α、β之间的数量关系．（2）如图，当点G 在AB 上方时，且90EGF ︒∠=，求证：90︒∠-∠=BEG DFG；（3）如图，在（2）的条件下，过点E 作直线HK 交直线CD 于K ，FT 平分DFG ∠交HK 于点T ，延长GE 、FT 交于点R ，若ERT TEB ∠=∠，请你判断FR 与HK 的位置关系，并证明．（不可以直接用三角形内角和180°）10、已知AB //CD ，点E 、F 分别在AB 、CD 上，点G 为平面内一点，连接EG 、FG ．（1）如图，当点G 在AB 、CD 之间时，请直接写出∠AEG 、∠CFG 与∠G 之间的数量关系__________．。

专题5.24 平行线几何模型(M模型)(巩固培优篇)(专项练习)七年级数学下册基础知识专项讲练

专题5.24平行线几何模型（M 模型）（巩固培优篇）（专项练习）1．已知直线AB //CD ，EF 是截线，点M 在直线AB 、CD 之间．(1)如图1，连接GM ，HM ．求证：∠M ＝∠AGM ＋∠CHM ；(2)如图2，在∠GHC 的角平分线上取两点M 、Q ，使得∠AGM ＝∠HGQ ．试判断∠M 与∠GQH 之间的数量关系，并说明理由．2．阅读下面内容，并解答问题．已知：如图1，AB CD ，直线EF 分别交AB ，CD 于点E ，F ．BEF ∠的平分线与DFE ∠的平分线交于点G ．(1)求证：EG FG ⊥；(2)填空，并从下列①、②两题中任选一题说明理由．我选择题．①在图1的基础上，分别作BEG ∠的平分线与DFG ∠的平分线交于点M ，得到图2，则EMF ∠的度数为．②如图3，AB CD ，直线EF 分别交AB ，CD 于点E ，F ．点O 在直线AB ，CD 之间，且在直线EF 右侧，BEO ∠的平分线与DFO ∠的平分线交于点P ，则EOF ∠与EPF ∠满足的数量关系为．3．已知直线a b ∥，直线EF 分别与直线a ，b 相交于点E ，F ，点A ，B 分别在直线a ，b 上，且在直线EF 的左侧，点P 是直线EF 上一动点（不与点E ，F 重合），设∠PAE ＝∠1，∠APB ＝∠2，∠PBF ＝∠3．(1)如图1，当点P 在线段EF 上运动时，试说明∠1＋∠3＝∠2；(2)当点P 在线段EF 外运动时有两种情况．①如图2写出∠1，∠2，∠3之间的关系并给出证明；②如图3所示，猜想∠1，∠2，∠3之间的关系（不要求证明）．4．问题情境：如图①，直线AB CD ∥，点E ，F 分别在直线AB ，CD 上．(1)猜想：若1130∠=︒，2150∠=︒，试猜想P ∠=______°；(2)探究：在图①中探究1∠，2∠，P ∠之间的数量关系，并证明你的结论；(3)拓展：将图①变为图②，若12325∠+∠=︒，75EPG ∠=︒，求PGF ∠的度数．5．如图：(1)如图1，AB CD ∥，=45ABE ∠︒，21CDE ∠=︒，直接写出BED ∠的度数．(2)如图2，AB CD ∥，点E 为直线AB ，CD 间的一点，BF 平分ABE ∠，DF 平分CDE ∠，写出BED ∠与F ∠之间的关系并说明理由．(3)如图3，AB 与CD 相交于点G ，点E 为BGD ∠内一点，BF 平分ABE ∠，DF 平分CDE ∠，若60BGD ∠=︒，95BFD ∠=︒，直接写出BED ∠的度数．6．（1）已知：如图（a ），直线DE AB ∥．求证：ABC CDE BCD ∠+∠=∠；（2）如图（b ），如果点C 在AB 与ED 之外，其他条件不变，那么会有什么结果？你还能就本题作出什么新的猜想？7．如图，//AB CD ，点E 在直线AB ，CD 内部，且AE CE ⊥．（1）如图1，连接AC ，若AE 平分BAC ∠，求证：CE 平分ACD ∠；（2）如图2，点M 在线段AE 上，①若MCE ECD ∠=∠，当直角顶点E 移动时，BAE ∠与MCD ∠是否存在确定的数量关系?并说明理由；②若1MCE ECD n∠=∠（n 为正整数），当直角顶点E 移动时，BAE ∠与MCD ∠是否存在确定的数量关系?并说明理由．8．已知直线l 1//l 2，A 是l 1上的一点，B 是l 2上的一点，直线l 3和直线l 1，l 2交于C 和D ，直线CD 上有一点P ．（1）如果P 点在C ，D 之间运动时，问∠PAC ，∠APB ，∠PBD 有怎样的数量关系？请说明理由．（2）若点P 在C ，D 两点的外侧运动时（P 点与C ，D 不重合），试探索∠PAC ，∠APB ，∠PBD 之间的关系又是如何？（请直接写出答案，不需要证明）9．（1）如图，AB //CD ，CF 平分∠DCE ，若∠DCF =30°，∠E =20°，求∠ABE 的度数；（2）如图，AB//CD，∠EBF=2∠ABF，CF平分∠DCE，若∠F的2倍与∠E的补角的和为190°，求∠ABE的度数．（3）如图，P为（2）中射线BE上一点，G是CD上任一点，PQ平分∠BPG，GN//PQ，GM平分∠DGP，若∠B＝30°，求∠MGN的度数．10．如图1，已知AB∥CD，∠B＝30°，∠D＝120°；(1)若∠E＝60°，则∠F＝；(2)请探索∠E与∠F之间满足的数量关系？说明理由；(3)如图2，已知EP平分∠BEF，FG平分∠EFD，反向延长FG交EP于点P，求∠P 的度数．11．如图1，AB//CD，E是AB，CD之间的一点．(1)判定∠BAE，∠CDE与∠AED之间的数量关系，并证明你的结论；(2)如图2，若∠BAE，∠CDE的角平分线交于点F，直接写出∠AFD与∠AED之间的数量关系；(3)将图2中的射线DC沿DE翻折交AF于点G得图3，若∠AGD的余角等于2∠E 的补角，求∠BAE的大小．12．已知AB//CD．（1）如图1，E为AB，CD之间一点，连接BE，DE，得到∠BED．求证：∠BED＝∠B+∠D；（2）如图，连接AD，BC，BF平分∠ABC，DF平分∠ADC，且BF，DF所在的直线交于点F．①如图2，当点B在点A的左侧时，若∠ABC＝50°，∠ADC＝60°，求∠BFD的度数．②如图3，当点B在点A的右侧时，设∠ABC＝α，∠ADC＝β，请你求出∠BFD的度数．（用含有α，β的式子表示）13．已知，AB∥CD．点M在AB上，点N在CD上．（1）如图1中，∠BME、∠E、∠END的数量关系为：；（不需要证明）如图2中，∠BMF 、∠F 、∠FND 的数量关系为：；（不需要证明）（2）如图3中，NE 平分∠FND ，MB 平分∠FME ，且2∠E ＋∠F ＝180°，求∠FME 的度数；（3）如图4中，∠BME ＝60°，EF 平分∠MEN ，NP 平分∠END ，且EQ ∥NP ，则∠FEQ 的大小是否发生变化，若变化，请说明理由，若不变化，求出∠FEQ 的度数．14．如图1，点A 、B 分别在直线GH 、MN 上，GAC NBD ∠=∠，C D ∠=∠.（1）求证：//GH MN ；（提示：可延长AC 交MN 于点P 进行证明）（2）如图2，AE 平分GAC ∠，DE 平分BDC ∠，若AED GAC ∠=∠，求GAC ∠与ACD ∠之间的数量关系；（3）在（2）的条件下，如图3，BF 平分DBM ∠，点K 在射线BF 上，13KAG GAC ∠=∠，若AKB ACD ∠=∠，直接写出GAC ∠的度数．15．已知AB ∥CD ，∠ABE 的角分线与∠CDE 的角分线相交于点F ．（1）如图1，若BM 、DM 分别是∠ABF 和∠CDF 的角平分线，且∠BED ＝100°，求∠M的度数；（2）如图2，若∠ABM＝13∠ABF，∠CDM＝13∠CDF，∠BED＝α°，求∠M的度数；（3）若∠ABM＝1n∠ABF，∠CDM＝1n∠CDF，请直接写出∠M与∠BED之间的数量关系．16．已知直线AM、CN和点B在同一平面内，且AM∥CN，AB⊥BC．（1）如图1，求∠A和∠C之间的数量关系；（2）如图2，若BD⊥AM，垂足为D，求证：∠ABD＝∠C；（3）如图3，已知点D、E、F都在直线AM上，且∠ABD＝∠NCB，BF平分∠DBC，BE平分∠ABD．若∠FCB+∠NCF＝180°，∠BFC＝3∠DBE，请直接写出∠EBC的度数．17．如图1，点A在直线MN上，点B在直线ST上，点C在MN，ST之间，且满足MAC ACB SBC∠+∠+∠360=︒．（1）证明：//MN ST；（2）如图2，若60ACB ∠=︒，//AD CB ，点E 在线段BC 上，连接AE ，且2DAE CBT ∠=∠，试判断CAE ∠与CAN ∠的数量关系，并说明理由；（3）如图3，若180ACB n︒∠=（n 为大于等于2的整数），点E 在线段BC 上，连接AE ，若MAE n CBT ∠=∠，则:CAE CAN ∠∠=______．18．如图1，直线AB //CD ，点P 在两平行线之间，点E 在AB 上，点F 在CD 上，连接PE ，PF ．（1）若∠PEB =60°，∠PFD =50°，请求出∠EPF ．（请写出必要的步骤，并说明理由）（2）如图2，若点P ，Q 在直线AB 与CD 之间时，∠1=30°，∠2=40°，∠3=70°，请求出∠4=．（不需说明理由，请直接写出答案）（3）如图3，在图1的基础上，作P 1E 平分∠PEB ，P 1F 平分∠PFD ，若设∠PEB ＝x °，∠PFD ＝y °，则∠P 1=（用含x ，y 的式子表示）．若P 2E 平分∠P 1EB ，P 2F 平分∠P 1FD ，可得∠P 2；P 3E 平分∠P 2EB ，P 3F 平分∠P 2FD ，可得∠P 3…，依次平分下去，则∠Pn ＝．（用含x ，y 的式子表示）19．已知//AM CN ，点B 为平面内一点，AB BC ⊥于B ．（1）如图1，点B 在两条平行线外，则A ∠与C ∠之间的数量关系为______；（2）点B 在两条平行线之间，过点B 作BD AM ⊥于点D ．①如图2，说明ABD C ∠=∠成立的理由；②如图3，BF 平分DBC ∠交DM 于点,F BE 平分ABD ∠交DM 于点E ．若180,3FCB NCF BFC DBE ∠∠∠∠+=︒=，求EBC ∠的度数．20．如图1，MN ∥PQ ，点C 、B 分别在直线MN 、PQ 上，点A 在直线MN 、PQ 之间．（1）求证：∠CAB ＝∠MCA +∠PBA ；（2）如图2，CD ∥AB ，点E 在PQ 上，∠ECN ＝∠CAB ，求证：∠MCA ＝∠DCE ；（3）如图3，BF 平分∠ABP ，CG 平分∠ACN ，AF ∥CG ．若∠CAB ＝60°，求∠AFB 的度数．21．如图，//MN GH ，点A 、B 分别在直线MN 、GH 上，点O 在直线MN 、GH 之间，若116NAO ∠=︒，144OBH ∠=︒．（1）AOB ∠=︒；（2）如图2，点C 、D 是NAO ∠、GBO ∠角平分线上的两点，且35CDB ∠=︒，求ACD ∠的度数；（3）如图3，点F 是平面上的一点，连结FA 、FB ，E 是射线FA 上的一点，若MAE ∠=n OAE ∠，HBF n OBF ∠=∠，且60AFB ∠=︒，求n 的值．22．如图1，AB //CD ，点E 、F 分别在AB 、CD 上，点O 在直线AB 、CD 之间，且100EOF ∠=︒．（1）求BEO OFD ∠+∠的值；（2）如图2，直线MN 分别交BEO ∠、OFC ∠的角平分线于点M 、N ，直接写出EMN FNM ∠-∠的值；（3）如图3，EG 在AEO ∠内，AEG m OEG ∠=∠；FH 在DFO ∠内，DFH m OFH ∠=∠，直线MN 分别交EG 、FH 分别于点M 、N ，且50FMN ENM ∠-∠=︒，直接写出m 的值．23．已知//AB CD ，定点E ，F 分别在直线AB ，CD 上，在平行线AB ，CD 之间有一动点P ．（1）如图1所示时，试问AEP ∠，EPF ∠，PFC ∠满足怎样的数量关系?并说明理由．（2）除了（1）的结论外，试问AEP ∠，EPF ∠，PFC ∠还可能满足怎样的数量关系?请画图并证明（3）当EPF ∠满足0180EPF ︒<∠<︒，且QE ，QF 分别平分PEB ∠和PFD ∠，①若60EPF ∠=︒，则EQF ∠=__________°．②猜想EPF ∠与EQF ∠的数量关系．（直接写出结论）24．如图1，由线段,,,AB AM CM CD 组成的图形像英文字母M ，称为“M 形BAMCD ”．（1）如图1，M 形BAMCD 中，若//,50AB CD A C ∠+∠=︒，则M ∠=______；（2）如图2，连接M 形BAMCD 中,B D 两点，若150,B D AMC α∠+∠=︒∠=，试探求A ∠与C ∠的数量关系，并说明理由；（3）如图3，在（2）的条件下，且AC 的延长线与BD 的延长线有交点，当点M 在线段BD 的延长线上从左向右移动的过程中，直接写出A ∠与C ∠所有可能的数量关系．参考答案1．(1)证明见详解(2)180GQH M ∠=︒-∠；理由见详解【分析】（1）过点M 作MN AB ∥，由AB CD ∥，可知MN AB CD ∥∥．由此可知：AGM GMN ∠=∠，CHM HMN ∠=∠，故=AGM CHM GMN HMN M ∠+∠=∠+∠∠；（2）由（1）可知=AGM CHM M ∠+∠∠．再由CHM GHM ∠=∠，∠AGM ＝∠HGQ ，可知：M HGQ GHM ∠=∠+∠，利用三角形内角和是180°，可得180GQH M ∠=︒-∠．（1）解：如图：过点M 作MN AB ∥，∴MN AB CD ∥∥，∴AGM GMN ∠=∠，CHM HMN ∠=∠，∵M GMN HMN ∠=∠+∠，∴=M AGM CHM ∠∠+∠．（2）解：180GQH M ∠=︒-∠，理由如下：如图：过点M 作MN AB ∥，由（1）知=M AGM CHM ∠∠+∠，∵HM 平分GHC ∠，∴CHM GHM ∠=∠，∵∠AGM ＝∠HGQ ，∴M HGQ GHM ∠=∠+∠，∵180HGQ GHM GQH ∠+∠+∠=︒，∴180GQH M ∠=︒-∠．【点拨】本题考查了利用平行线的性质求角之间的数量关系，正确的作出辅助线是解决本题的关键，同时这也是比较常见的几何模型“猪蹄模型”的应用．2．(1)见分析(2)①45︒；②结论：2EOF EPF∠=∠【分析】（1）利用平行线的性质解决问题即可；（2）①利用基本结论EMF BEM MFD ∠=∠+∠求解即可；②利用基本结论EOF BEO DFO ∠=∠+∠，EPF BEP DFP ∠=∠+∠，求解即可．解：（1）证明：如图，过G 作GH AB ，AB CD ，AB GH CD ∴ ，BEG EGH DFG FGH ∠∠∠∠∴==，，180BEF DFE ∴∠+∠=︒，EG 平分BEF ∠，FG 平分DFE ∠，12GEB BEF ∴∠=∠，12GFD DFE ∠=∠，111()90222GEB GFD BEF DFE BEF DFE ∴∠+∠=∠+∠=∠+∠=︒，在EFG ∆中，180GEF GFE G ∠+∠+∠=︒，90EGF GEB GFD ∴∠=∠+∠=︒，EG FG ∴⊥；（2）解：①如图2中，由题意，90BEG DFG ∠+∠=︒，EM 平分BEG ∠，MF 平分DFG ∠，1()452BEM MFD BEG DFG ∴∠+∠=∠+∠=︒，45EMF BEM MFD ∴∠=∠+∠=︒，故答案为：45︒；②结论：2EOF EPF ∠=∠．理由：如图3中，由题意，EOF BEO DFO ∠=∠+∠，EPF BEP DFP ∠=∠+∠，PE 平分BEO ∠，PF 平分DFO ∠，2BEO BEP ∴∠=∠，2DFO DFP ∠=∠，2EOF EPF ∴∠=∠，故答案为：2EOF EPF ∠=∠．【点拨】本题考查平行线的性质和判定，角平分线的性质，垂直的定义，解题的关键是熟练掌握相关的性质．3．(1)证明见详解(2)①312Ð=Ð+Ð；证明见详解；②123∠=∠+∠；证明见详解【分析】（1）如图4过点P 作PC a ∥，利用平行线的传递性可知PC a b ∥∥，根据平行线的性质可知1APC ∠=∠，3BPC ∠=∠，根据等量代换就可以得出213∠=∠+∠；（2）①如图5过点P 作PC a ∥，利用平行线的传递性可知PC a b ∥∥，根据平行线的性质可知3BPC ∠=∠，1APC ∠=∠，根据等量代换就可以得出312Ð=Ð+Ð；②如图6过点P 作PC a ∥，利用平行线的传递性可知PC a b ∥∥，根据平行线的性质可知1APC ∠=∠，3BPC ∠=∠，根据等量代换就可以得出123∠=∠+∠．（1）解：如图4所示：过点P 作PC a ∥，∵a b∥∴PC a b∥∥∴1APC ∠=∠，3BPC ∠=∠，∵2APC BPC ∠=∠+∠，∴213∠=∠+∠；（2）解：①如图5过点P 作PC a ∥，∵a b∥∴PC a b∥∥∴3BPC ∠=∠，1APC ∠=∠，∵2BPC APC ∠=∠+∠，∴312Ð=Ð+Ð；②如图6过点P 作PC a ∥，∵a b∥∴PC a b∥∥∴1APC ∠=∠，3BPC ∠=∠，∵2APC BPC ∠=∠+∠，∴123∠=∠+∠．【点拨】本题利用“猪蹄模型”及其变式考查了利用平行线的性质求角之间的数量关系，准确的作出辅助线和找到对应的内错角是解决本题的关键．4．(1)80︒(2)36012P ∠=︒-∠-∠；证明见详解(3)140︒【分析】（1）过点P 作MN AB ∥，利用平行的性质就可以求角度，解决此问；（2）利用平行线的性质求位置角的数量关系，就可以解决此问；（3）分别过点P 、点G 作MN AB ∥、KR AB ∥，然后利用平行线的性质求位置角的数量关系即可．（1）解：如图过点P 作MN AB ∥，∵AB CD ∥，∴AB MN CD ∥∥．∴1180EPN ∠+∠=︒，2180FPN ∠+∠=︒．∵1130∠=︒，2150∠=︒，∴12360EPN FPN ∠+∠+∠+∠=︒∴36013015080EPN FPN ∠+=︒-︒-︒=︒．∵P EPN FPN ∠=∠+∠，∴∠P =80°．故答案为：80︒；（2）解：36012P ∠=︒-∠-∠，理由如下：如图过点P 作MN AB ∥，∵AB CD ∥，∴AB MN CD ∥∥．∴1180EPN ∠+∠=︒，2180FPN ∠+∠=︒．∴12360EPN FPN ∠+∠+∠+∠=︒∵EPN FPN P ∠+∠=∠，36012P ∠=︒-∠-∠．（3）如图分别过点P 、点G 作MN AB ∥、KR AB ∥∵AB CD ∥，∴AB MN KR CD ∥∥∥．∴1180EPN ∠+∠=︒，180NPG PGR ∠+∠=︒，2180RGF ∠+∠=︒．∴12540EPN NPG PGR RGF ∠+∠+∠+∠++∠=︒∵75EPG EPN NPG ∠=∠+∠=︒，PGR RGF PGF ∠+∠=∠，12325∠+∠=︒，∴12540PGF EPG ∠+∠+∠+∠=︒∴54032575140PGF ∠=︒-︒-︒=︒故答案为：140︒．【点拨】本题考查了平行线的性质定理，准确的作出辅助线和正确的计算是解决本题的关键．5．(1)∠BED =66°；(2)∠BED =2∠F ，见分析；(3)∠BED 的度数为130°．【分析】（1）首先作EF ∥AB ，根据直线AB ∥CD ，可得EF ∥CD ，所以∠ABE =∠1=45°，∠CDE =∠2=21°，据此推得∠BED =∠1+∠2=66°；（2）首先作EG ∥AB ，延长DE 交BF 于点H ，利用三角形的外角性质以及角平分线的定义即可得到∠BED =2∠F ；（3）延长DF 交AB 于点H ，延长GE 到I ，利用三角形的外角性质以及角平分线的定义即可得到∠BED的度数为130°．解：（1）如图，作EF∥AB，，∵直线AB∥CD，∴EF∥CD，∴∠ABE=∠1=45°，∠CDE=∠2=21°，∴∠BED=∠1+∠2=66°；（2）解：∠BED=2∠F，理由是：过点E作EG∥AB，延长DE交BF于点H，∵AB∥CD，∴AB∥CD∥EG，∴∠5=∠1+∠2，∠6=∠3+∠4，又∵BF平分∠ABE，DF平分∠CDE，∴∠2=∠1，∠3=∠4，则∠5=2∠2，∠6=2∠3，∴∠BED=2(∠2+∠3)，又∠F+∠3=∠BHD，∠BHD+∠2=∠BED，∴∠3+∠2+∠F=∠BED，综上∠BED=∠F+12∠BED，即∠BED=2∠F；（3）解：延长DF交AB于点H，延长GE到I，∵∠BGD=60°，∴∠3=∠1+∠BGD=∠1+60°，∠BFD=∠2+∠3=∠2+∠1+60°=95°，∴∠2+∠1=35°，即2(∠2+∠1)=70°，∵BF平分∠ABE，DF平分∠CDE，∴∠ABE=2∠2，∠CDE=2∠1，∴∠BEI=∠ABE+∠BGE=2∠2+∠BGE，∠DEI=∠CDE+∠DGE=2∠1+∠DGE，∴∠BED=∠BEI+∠DEI=2(∠2+∠1)+(∠BGE+∠DGE)=70°+60°=130°，∴∠BED的度数为130°．【点拨】本题考查了平行线的判定和性质，三角形的外角性质等知识，掌握平行线的判定和性质，正确添加辅助线是解题关键．∠-∠=∠，见分析6．（1）见分析；（2）当点C在AB与ED之外时，ABC CDE BCD【分析】（1）由题意首先过点C作CF∥AB，由直线AB∥ED，可得AB∥CF∥DE，然后由两直线平行，内错角相等，即可证得∠ABC+∠CDE=∠BCD；（2）根据题意首先由两直线平行，内错角相等，可得∠ABC=∠BFD，然后根据三角形外角的性质即可证得∠ABC-∠CDE=∠BCD．解：（1）证明：过点C作CF∥AB，∵AB∥ED，∴AB∥ED∥CF，∴∠BCF=∠ABC，∠DCF=∠EDC，∴∠ABC +∠CDE =∠BCD ；（2）结论：∠ABC -∠CDE =∠BCD ，证明：如图：∵AB ∥ED ，∴∠ABC =∠BFD ，在△DFC 中，∠BFD =∠BCD +∠CDE ，∴∠ABC =∠BCD +∠CDE ，∴∠ABC -∠CDE =∠BCD ．若点C 在直线AB 与DE 之间，猜想360ABC BCD CDE ︒∠+∠+∠=,∵AB ∥ED ∥CF ，∴180,180,ABC BCF CDE DCF ︒︒∠+∠=∠+∠=∴360ABC BCD CDE ABC BCF DCF CDE ︒∠+∠+∠=∠+∠+∠+∠=.【点拨】本题考查的是平行线的性质及三角形外角的性质，熟练掌握平行线的性质是解答本题的关键，注意掌握辅助线的作法．7．（1）见分析；（2）①∠BAE +12∠MCD =90°，理由见分析；②∠BAE +1n n +∠MCD =90°，理由见分析.【分析】（1）根据平行的性质可得∠BAC +∠DCA =180°，再根据AE CE ⊥可得∠EAC +∠ECA =90°，根据AE 平分∠BAC 可得∠BAE =∠EAC ,等量代换可得∠ECD +∠EAC =90°，继而求得∠DCE =∠ECA ；（2）①过E作EF∥AB，先利用平行线的传递性得出EF∥AB∥CD，再利用平行线的性质及已知条件可推得答案；②过E作EF∥AB，先利用平行线的传递性得出EF∥AB∥CD，再利用平行线的性质及已知条件可推得答案.（1）解：因为//AB CD，所以∠BAC+∠DCA=180°，因为AE CE，所以∠EAC+∠ECA=90°，因为AE平分∠BAC，所以∠BAE=∠EAC，所以∠BAE+∠DCE=90°，所以∠EAC+∠DCE=90°，所以∠DCE=∠ECA，所以CE平分∠ACD；（2）①∠BAE与∠MCD存在确定的数量关系：∠BAE+12∠MCD=90°，理由如下：过E作EF∥AB，∵AB∥CD，∴EF∥AB∥CD，∴∠BAE=∠AEF，∠FEC=∠DCE，∵∠E=90°，∴∠BAE+∠ECD=90°，∵∠MCE=∠ECD，∴∠BAE+12∠MCD=90°；②∠BAE 与∠MCD 存在确定的数量关系：∠BAE +1n n +∠MCD =90°，理由如下：过E 作EF ∥AB ，∵AB ∥CD ，∴EF ∥AB ∥CD ，∴∠BAE =∠AEF ，∠FEC =∠DCE ，∵∠E =90°，∴∠BAE +∠ECD =90°，∵∠MCE =1n ∠ECD ，∴∠BAE +1n n +∠MCD =90°.【点拨】本题主要考查平行线的性质和角平分线的定义，解决本题的关键是要添加辅助线利用平行性质.8．（1）PAC PBD APB ∠+∠=∠；（2）当点P 在直线1l 上方时，∠-∠=∠PBD PAC APB ；当点P 在直线2l 下方时，∠-∠=∠PAC PBD APB ．【分析】（1）过点P 作1//PE l ，由“平行于同一条直线的两直线平行”可得出12////PE l l ，再由“两直线平行，内错角相等”得出PAC APE ∠=∠、PBD BPE ∠=∠，再根据角与角的关系即可得出结论；（2）按点P 的两种情况分类讨论：①当点P 在直线1l 上方时；②当点P 在直线2l 下方时，同理（1）可得PAC APE ∠=∠、PBD BPE ∠=∠，再根据角与角的关系即可得出结论．解：（1）PAC PBD APB ∠+∠=∠．过点P 作1//PE l ，如图1所示．1//PE l ，12l l //，12////PE l l ∴，PAC APE ∴∠=∠，PBD BPE ∠=∠，APB APE BPE ∠=∠+∠ ，PAC PBD APB ∴∠+∠=∠．（2）结论：当点P 在直线1l 上方时，∠-∠=∠PBD PAC APB ；当点P 在直线2l 下方时，∠-∠=∠PAC PBD APB ．①当点P 在直线1l 上方时，如图2所示．过点P 作1//PE l ．1//PE l ，12l l //，12////PE l l ∴，PAC APE ∴∠=∠，PBD BPE ∠=∠，APB BPE APE ∠=∠-∠ ，PBD PAC APB ∴∠-∠=∠．②当点P 在直线2l 下方时，如图3所示．过点P 作1//PE l ．1//PE l ，12l l //，12////PE l l ∴，PAC APE ∴∠=∠，PBD BPE ∠=∠，APB APE BPE ∠=∠-∠ ，PAC PBD APB ∴∠-∠=∠．【点拨】本题考查了平行线的性质以及角的计算，解题的关键是根据“两直线平行，内错角相等”找到相等的角．本题属于基础题，难度不大，解决该题型题目时，根据平行线的性质得出相等（或互补）的角是关键．9．（1）∠ABE =40°；（2）∠ABE =30°；（3）∠MGN =15°．【分析】（1）过E 作EM ∥AB ，根据平行线的判定与性质和角平分线的定义解答即可；（2）过E 作EM ∥AB ，过F 作FN ∥AB ，根据平行线的判定与性质，角平分线的定义以及解一元一次方程解答即可；（3）过P 作PL ∥AB ，根据平行线的判定与性质，三角形的内角和定理，三角形的一个外角等于与它不相邻的两个内角的和的性质，角平分线的定义解答即可．解：（1）过E 作EM ∥AB ，∵AB ∥CD ，∴CD ∥EM ∥AB ，∴∠ABE ＝∠BEM ，∠DCE ＝∠CEM ，∵CF 平分∠DCE ，∴∠DCE＝2∠DCF，∵∠DCF＝30°，∴∠DCE＝60°，∴∠CEM＝60°，又∵∠CEB＝20°，∴∠BEM＝∠CEM﹣∠CEB＝40°，∴∠ABE＝40°；（2）过E作EM∥AB，过F作FN∥AB，∵∠EBF＝2∠ABF，∴设∠ABF＝x，∠EBF＝2x，则∠ABE＝3x，∵CF平分∠DCE，∴设∠DCF＝∠ECF＝y，则∠DCE＝2y，∵AB∥CD，∴EM∥AB∥CD，∴∠DCE＝∠CEM＝2y，∠BEM＝∠ABE＝3x，∴∠CEB＝∠CEM﹣∠BEM＝2y﹣3x，同理∠CFB＝y﹣x，∵2∠CFB+（180°﹣∠CEB）＝190°，∴2（y﹣x）+180°﹣（2y﹣3x）＝190°，∴x＝10°，∴∠ABE＝3x＝30°；（3）过P作PL∥AB，∵GM 平分∠DGP ，∴设∠DGM ＝∠PGM ＝y ，则∠DGP ＝2y ，∵PQ 平分∠BPG ，∴设∠BPQ ＝∠GPQ ＝x ，则∠BPG ＝2x ，∵PQ ∥GN ，∴∠PGN ＝∠GPQ ＝x ，∵AB ∥CD ，∴PL ∥AB ∥CD ，∴∠GPL ＝∠DGP ＝2y ，∠BPL ＝∠ABP ＝30°，∵∠BPL ＝∠GPL ﹣∠BPG ，∴30°＝2y ﹣2x ，∴y ﹣x ＝15°，∵∠MGN ＝∠PGM ﹣∠PGN ＝y ﹣x ，∴∠MGN ＝15°．【点拨】此题考查平行线的判定与性质，角平分线的定义，三角形的内角和定理，解题关键在于作辅助线和掌握判定定理．10．(1)90︒(2)30F E ∠=∠+︒，理由见分析(3)15︒【分析】（1）如图1，分别过点E ，F 作//EM AB ，//FN AB ，根据平行线的性质得到30B BEM ∠=∠=︒，MEF EFN ∠=∠，180D DFN ∠+∠=︒，代入数据即可得到结论；（2）如图1，根据平行线的性质得到30B BEM ∠=∠=︒，MEF EFN ∠=∠，由//AB CD ，//AB FN ，得到//CD FN ，根据平行线的性质得到180D DFN ∠+∠=︒，于是得到结论；（3）如图2，过点F 作//FH EP ，设2BEF x ∠=︒，则(230)EFD x ∠=+︒，根据角平分线的定义得到12PEF BEF x ∠=∠=︒，1(15)2EFG EFD x ∠=∠=+︒，根据平行线的性质得到PEF EFH x ∠=∠=︒，P HFG ∠=∠，于是得到结论．（1）解：如图1，分别过点E ，F 作//EM AB ，//FN AB ，////EM AB FN ∴，30B BEM ∴∠=∠=︒，MEF EFN ∠=∠，又//AB CD ，//AB FN ，//CD FN ∴，180D DFN ∴∠+∠=︒，又120D ∠=︒ ，60DFN ∴∠=︒，30BEF MEF ∴∠=∠+︒，60EFD EFN ∠=∠+︒，60EFD MEF ∴∠=∠+︒3090EFD BEF ∴∠=∠+︒=︒；故答案为：90︒；（2）解：如图1，分别过点E ，F 作//EM AB ，//FN AB ，////EM AB FN ∴，30B BEM ∴∠=∠=︒，MEF EFN ∠=∠，又//AB CD ，//AB FN ，//CD FN ∴，180D DFN ∴∠+∠=︒，又120D ∠=︒ ，60DFN ∴∠=︒，30BEF MEF ∴∠=∠+︒，60EFD EFN ∠=∠+︒，60EFD MEF ∴∠=∠+︒，30EFD BEF ∴∠=∠+︒；（3）解：如图2，过点F 作//FH EP ，由（2）知，30EFD BEF ∠=∠+︒，设2BEF x ∠=︒，则(230)EFD x ∠=+︒，EP 平分BEF ∠，GF 平分EFD ∠，12PEF BEF x ∴∠=∠=︒，1(15)2EFG EFD x ∠=∠=+︒，//FH EP ，PEF EFH x ∴∠=∠=︒，P HFG ∠=∠，15HFG EFG EFH ∠=∠-∠=︒ ，15P ∴∠=︒．【点拨】本题考查了平行线的性质，角平分线的定义，熟练掌握平行线的性质定理是解题的关键．11．(1)BAE CDE AED ∠+∠=∠；(2)12AFD AED ∠=∠；(3)60=︒∠BAE 【分析】（1）作EF ∥AB ，如图1，则EF ∥CD ，利用平行线的性质得∠1=∠EAE ，∠2=∠CDE ，从而得到∠BAE +∠CDE =∠AED（2）如图2，由（1）的结论得∠AFD =12∠BAE ，∠CDF =12∠CDE ，则∠AFD =12（∠BAE +∠CDE ），加上（1）的结论得到∠AFD =12∠AED ；（3）由（1）的结论得∠AGD =∠BAF +∠CDG ，利用折叠性质得∠CDG =4∠CDF ，再利用等量代换得到∠AGD =2∠AED -32∠BAE ，加上90°-∠AGD =180°-2∠AED ，从而计算出∠BAE 的度数．解：(1)∠BAE +∠CDE =∠AED理由如下：作EF ∥AB ，如图1∵AB ∥CD∴EF ∥CD∴∠1=∠BAE ，∠2=∠CDE∴∠BAE +∠CDE =∠AED(2)如图2，由（1）的结论得∠AFD =∠BAF +∠CDF∵∠BAE 、∠CDE 的两条平分线交于点F∴∠BAF =12∠BAE ，∠CDF =12∠CDE∴∠AFE =12（∠BAE +∠CDE ）∵∠BAE +∠CDE =∠AED∴∠AFD =12∠AED(3)由（1）的结论得∠AGD =∠BAF +∠CDG而射线DC 沿DE 翻折交AF 于点G∴∠CDG =4∠CDF∴∠AGD =∠BAF +4∠CDF =12∠BAE +2∠CDE =12∠BAE +2（∠AED -∠BAE ）=2∠AED -32∠BAE ∵90°-∠AGD =180°-2∠AED∴90°-2∠AED +32∠BAE =180°-2∠AED ∴∠BAE =60°【点拨】本题考查了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．12．（1）见分析；（2）55°；（3）1118022αβ︒-+【分析】（1）根据平行线的判定定理与性质定理解答即可；（2）①如图2，过点F 作//FE AB ，当点B 在点A 的左侧时，根据50ABC ∠=︒，60ADC ∠=︒，根据平行线的性质及角平分线的定义即可求BFD ∠的度数；②如图3，过点F 作//EF AB ，当点B 在点A 的右侧时，ABC α∠=，ADC β∠=，根据平行线的性质及角平分线的定义即可求出BFD ∠的度数．解：（1）如图1，过点E 作//EF AB ，则有BEF B ∠=∠，//AB CD ，//EF CD ∴，FED D ∴∠=∠，BED BEF FED B D ∴∠=∠+∠=∠+∠；（2）①如图2，过点F 作//FE AB ，有BFE FBA ∠=∠．//AB CD ，//EF CD ∴．EFD FDC ∴∠=∠．BFE EFD FBA FDC ∴∠+∠=∠+∠．即BFD FBA FDC ∠=∠+∠，BF 平分ABC ∠，DF 平分ADC ∠，1252FBA ABC ∴∠=∠=︒，1302FDC ADC ∠=∠=︒，55BFD FBA FDC ∴∠=∠+∠=︒．答：BFD ∠的度数为55︒；②如图3，过点F 作//FE AB ，有180BFE FBA ∠+∠=︒．180BFE FBA ∴∠=︒-∠，//AB CD ，//EF CD ∴．EFD FDC ∴∠=∠．180BFE EFD FBA FDC ∴∠+∠=︒-∠+∠．即180BFD FBA FDC ∠=︒-∠+∠，BF 平分ABC ∠，DF 平分ADC ∠，1122FBA ABC α∴∠=∠=，1122FDC ADC β∠=∠=，1118018022BFD FBA FDC αβ∴∠=︒-∠+∠=︒-+．答：BFD ∠的度数为1118022αβ︒-+．【点拨】本题考查了平行线的判定与性质，解决本题的关键是熟练掌握平行线的判定与性质．13．（1）∠BME ＝∠MEN ﹣∠END ；∠BMF ＝∠MFN ＋∠FND ；（2）120°；（3）不变，30°【分析】（1）过E 作EH ∥AB ，易得EH ∥AB ∥CD ，根据平行线的性质可求解；过F 作FH ∥AB ，易得FH ∥AB ∥CD ，根据平行线的性质可求解；（2）根据（1）的结论及角平分线的定义可得2（∠BME +∠END ）+∠BMF -∠FND =180°，可求解∠BMF =60°，进而可求解；（3）根据平行线的性质及角平分线的定义可推知∠FEQ =12∠BME ，进而可求解．解：（1）过E 作EH ∥AB ，如图1，∴∠BME ＝∠MEH ，∵AB ∥CD ，∴HE ∥CD ，∴∠END ＝∠HEN ，∴∠MEN ＝∠MEH ＋∠HEN ＝∠BME ＋∠END ，即∠BME ＝∠MEN ﹣∠END ．如图2，过F 作FH ∥AB ，∴∠BMF ＝∠MFK ，∵AB ∥CD ，∴FH∥CD，∴∠FND＝∠KFN，∴∠MFN＝∠MFK﹣∠KFN＝∠BMF﹣∠FND，即：∠BMF＝∠MFN＋∠FND．故答案为∠BME＝∠MEN﹣∠END；∠BMF＝∠MFN＋∠FND．（2）由（1）得∠BME＝∠MEN﹣∠END；∠BMF＝∠MFN＋∠FND．∵NE平分∠FND，MB平分∠FME，∴∠FME＝∠BME＋∠BMF，∠FND＝∠FNE＋∠END，∵2∠MEN＋∠MFN＝180°，∴2（∠BME＋∠END）＋∠BMF﹣∠FND＝180°，∴2∠BME＋2∠END＋∠BMF﹣∠FND＝180°，即2∠BMF＋∠FND＋∠BMF﹣∠FND＝180°，解得∠BMF＝60°，∴∠FME＝2∠BMF＝120°；（3）∠FEQ的大小没发生变化，∠FEQ＝30°．由（1）知：∠MEN＝∠BME＋∠END，∵EF平分∠MEN，NP平分∠END，∴∠FEN＝12∠MEN＝12（∠BME＋∠END），∠ENP＝12∠END，∵EQ∥NP，∴∠NEQ＝∠ENP，∴∠FEQ＝∠FEN﹣∠NEQ＝12（∠BME＋∠END）﹣12∠END＝12∠BME，∵∠BME＝60°，∴∠FEQ＝12×60°＝30°．【点拨】本题主要考查平行线的性质及角平分线的定义，作平行线的辅助线是解题的关键．14．（1）见分析；（2）3ACD GAC ∠=∠，见分析；（3）54019⎛⎫ ⎪⎝⎭°或54023︒⎛⎫ ⎪⎝⎭．【分析】（1）根据平行线的判定与性质求证即可；（2）根据三角形的内角和为180°和平角定义得到AQD E EAQ ∠=∠+∠，结合平行线的性质得到BDQ E EAQ ∠=∠+∠，再根据角平分线的定义证得2CDB E GAC ∠=∠+∠，结合已知即可得出结论；（3）分当K 在直线GH 下方和当K 在直线GH 上方两种情况，根据平行线性质、三角形外角性质、角平分线定义求解即可．解：（1）如图1，延长AC 交MN 于点P ，∵ACD C ∠=∠，∴//AP BD ，∴NBD NPA ∠=∠，∵GAC NBD ∠=∠，∴GAC NPA ∠=∠，∴//GH MN ；（2）延长AC 交MN 于点P ，交DE 于点Q ，∵180E EAQ AQE ∠+∠+∠=°，180AQE AQD ∠+∠=°，∴AQD E EAQ ∠=∠+∠，∵//AP BD ，∴AQD BDQ ∠=∠，∴BDQ E EAQ ∠=∠+∠，∵AE 平分GAC ∠，DE 平分BDC ∠，∴2GAC EAQ ∠=∠，2CDB BDQ ∠=∠，∴2CDB E GAC ∠=∠+∠，∵AED GAC ∠=∠，ACD CDB ∠=∠，∴23ACD GAC GAC GAC ∠=∠+∠=∠；（3）当K 在直线GH 下方时，如图，设射线BF 交GH 于I ，∵//GH MN ，∴AIB FBM ∠=∠，∵BF 平分MBD ∠，∴1(180)2DBF FBM DBN ∠=∠=-∠°，∴AIB DBF ∠=∠，∵AIB KAG AKB ∠+∠=∠，AKB ACD ∠=∠，∴ACD DBF KAG ∠=∠+∠，∵13KAG GAC ∠=∠，GAC NBD ∠=∠，∴11(180)332GAC DBN ACD GAC ∠+-∠=∠=∠°，即1190332GAC GAC GAC ∠+-∠=∠°，解得：54019GAC ⎛⎫∠= ⎪⎝⎭ ．当K 在直线GH 上方时，如图，同理可证得1(180)2AIB DBN AKB KAG ∠=-∠=∠+∠°，则有113(180)32GAC GAC GAC ∠+∠=-∠ ，解得：54023GAC ⎛⎫∠= ⎪⎝⎭ ．综上，故答案为54019⎛⎫ ⎪⎝⎭°或54023︒⎛⎫ ⎪⎝⎭．【点拨】本题考查平行线的判定与性质、角平分线的定义、三角形的外角性质、三角形的内角和定理、平角定义、角度的运算，熟练掌握相关知识的联系与运用是解答的关键．15．（1）65°（2）3606α︒-︒（3）2n ∠M +∠BED =360°【分析】（1）首先作EG ∥AB ，FH ∥AB ，利用平行线的性质可得∠ABE +∠CDE =260°，再利用角平分线的定义得到∠ABF +∠CDF =130°，从而得到∠BFD 的度数，再根据角平分线的定义可求∠M 的度数；（2）先由已知得到∠ABE =6∠ABM ，∠CDE =6∠CDM ，由（1）得∠ABE +∠CDE =360°-∠BED ，∠M =∠ABM +∠CDM ，等量代换即可求解；（3）先由已知得到ABF n ABM ∠=∠，CDF n CDM ∠=∠，由（2）的方法可得到2n ∠M +∠BED =360°．解：（1）如图1，作//EG AB ，//FH AB ，∵AB CD ∥，∴EG AB FH CD ∥∥∥，∴ABF BFH ∠=∠，CDF DFH ∠=∠，180ABE BEG ∠+∠=︒，180GED CDE ∠+∠=︒，∴360ABE BEG GED CDE ∠+∠+∠+∠=︒，∵100BED BEG DEG ∠=∠+∠=︒，∴260ABE CDE ∠+∠=︒，∵ABE ∠的角平分线和CDE ∠的角平分线相交于F ，∴130ABF CDF ∠+∠=︒，∴130BFD BFH DFH ∠=∠+∠=︒，∵BM 、DM 分别是ABF ∠和CDF ∠的角平分线，∴12MBF ABF ∠=∠，12MDF CDF ∠=∠，∴65MBF MDF ∠+∠=︒，∴1306565BMD ∠=︒-︒=︒；（2）如图2，∵13ABM ABF ∠=∠，13CDM CDF ∠=∠，∴3ABF ABM ∠=∠，3CDF CDM ∠=∠，∵ABE ∠与CDE ∠两个角的角平分线相交于点F ，∴6ABE ABM ∠=∠，6CDE CDM ∠=∠，∴66360ABM CDM BED ∠+∠+∠=︒，∵BMD ABM CDM ∠=∠+∠，∴6360BMD BED ∠+∠=︒，∴3606BMD α︒-︒∠=；（3）∵∠ABM ＝1n ∠ABF ，∠CDM ＝1n∠CDF ，∴ABF n ABM ∠=∠，CDF n CDM ∠=∠，∵ABE ∠与CDE ∠两个角的角平分线相交于点F ，∴2ABE n ABM ∠=∠，2CDE n CDM ∠=∠，∴22360n ABM n CDM BED ∠+∠+∠=︒，∵M ABM CDM ∠=∠+∠，∴2360n M BED ∠+∠=︒．【点拨】本题主要考查了平行线的性质和角平分线的计算，关键在于掌握两直线平行同位角相等，内错角相等，同旁内角互补的性质．16．（1）∠A +∠C =90°；（2）见分析；（3）∠EBC =105°．【分析】（1）通过平行线性质和直角三角形内角关系求解．（2）画辅助平行线找角的联系．（3）利用（2）的结论，结合角平分线性质求解．解：（1）如图1，∵AM∥CN，∴∠C=∠AOB，∵AB⊥BC，∴∠ABC=90°，∴∠A+∠AOB=90°，∠A+∠C=90°，故答案为：∠A+∠C=90°；（2）如图2，过点B作BG∥DM，∵BD⊥AM，∴DB⊥BG，∴∠DBG=90°，∴∠ABD+∠ABG=90°，∵AB⊥BC，∴∠CBG+∠ABG=90°，∴∠ABD=∠CBG，∵AM∥CN，∴∠C=∠CBG，∴∠ABD=∠C；（3）如图3，过点B作BG∥DM，∵AM∥CN，∴CN∥BG，∴∠CBG=∠BCN，∵BF平分∠DBC，BE平分∠ABD，∴∠DBF=∠CBF，∠DBE=∠ABE，∵∠ABD=∠NCB，∴∠ABD=∠CBG，∴∠ABF=∠GBF，设∠DBE=α，∠ABF=β，则∠ABE=α，∠ABD=2α=∠CBG，∠GBF=∠AFB=β，∠BFC=3∠DBE=3α，∵BG∥DM，∴∠DFB=∠GBF=β，∴∠AFC=∠BFC+∠DFB=3α+β，∵∠AFC+∠NCF=180°，∠FCB+∠NCF=180°，∴∠FCB=∠AFC=3α+β，△BCF中，由∠CBF+∠BFC+∠BCF=180°得：2α+β+3α+3α+β=180°，∵AB⊥BC，∴β+β+2α=90°，∴α=15°，∴∠ABE=15°，∴∠EBC =∠ABE +∠ABC =15°+90°=105°．【点拨】本题考查平行线性质，三角形内角和定理，角平分线的定义，画辅助线，找到角的关系是求解本题的关键．17．（1）见分析；（2）见分析；（3）n -1【分析】（1）连接AB ，根据已知证明∠MAB +∠SBA =180°，即可得证；（2）作CF ∥ST ，设∠CBT =α，表示出∠CAN ，∠ACF ，∠BCF ，根据AD ∥BC ，得到∠DAC =120°，求出∠CAE 即可得到结论；（3）作CF ∥ST ，设∠CBT =β，得到∠CBT =∠BCF =β，分别表示出∠CAN 和∠CAE ，即可得到比值．解：（1）如图，连接AB ，，360MAC ACB SBC ∠+∠+∠=︒ ，180ACB ABC BAC ∠+∠+∠=︒，180MAB SBA ∴∠+∠=︒，//MN ST∴（2）2CAE CAN ∠=∠，理由：作//CF ST ，则////,MN CF ST 如图，设CBT α∠=，则2DAE α∠=．BCF CBT α∠=∠=，60CAN ACF α∠=∠=︒-，AD //BC ，180120DAC ACB ∠=︒-∠=︒，12012022(60)2CAE DAE CAN αα∴∠=︒-∠=︒-=︒-=∠．即2CAE CAN ∠=∠．（3）作//CF ST ，则////,MN CF ST 如图，设CBT β∠=，则MAE n β∠=．//CF ST ，CBT BCF β∴∠=∠=，180180n ACF CAN n nββ︒︒-∠=∠==，1801180180(180)n CAE MAE CAN n n n n βββ︒-∠=︒-∠-∠=︒--+=︒-，11::1n CAE CAN n n n-∠∠==-，故答案为n 1-．【点拨】本题主要考查平行线的性质和判定，解题关键是角度的灵活转换，构建数量关系式．18．（1）110°；（2）80°；（3）()()11,22nx y x y ⎛⎫+︒+︒ ⎪⎝⎭【分析】（1）过点P 作PH ∥AB ∥CD ，根据平行线的性质：两直线平行，内错角相等即可证得；（2）同理依据两直线平行，内错角相等即可证得∠1+∠4=∠2+∠3，求得∠4=80°；（3）利用（1）的结论和角平分线的性质即可写出结论．解：（1）如图1，过点P 作PH ∥AB ∥CD ，∴∠1=∠EPH ，∠2=∠FPH ，而∠EPF =∠EPH +∠FPH ，∴∠EPF =∠1+∠2=110°；（2）过点P 作//PM AB ,//QN AB ，//PM AB ，1EPM ∴∠=∠，//,//,//QN AB PM AB AB CD ，//P //QN//AB M DC ∴，MPQ NQP ∴∠=∠，2NQF ∠=∠，3EPM MPQ ∠=∠+∠ ，4PQN NQF ∠=∠+∠，∴∠1+∠4=∠2+∠3，∵∠1=30°，∠2=40°，∠3=70°，∴∠4=80°，故答案为：80°；（3）过点P 作////PH AB CD ，1PE 平分PEB ∠，11PEB PEP ∴∠=∠，同理11DFP PFP ∠=∠，∴111EPF PEB PFP ∠=∠+∠1122PFD BEP =+()12PFD BEP =+()12x y =+︒，同理1()()2n n y P x ∠=+︒，故答案为：11()2P x y ∠=+︒，1(()2n n y P x ∠=+︒．【点拨】本题考查了平行线性质的应用，解题的关键是学会添加常用辅助线，构造平行线解决问题，学会探究规律，利用规律解决问题．19．（1）∠A +∠C =90°；（2）①见分析；②105°【分析】（1）根据平行线的性质以及直角三角形的性质进行证明即可；（2）①过点B 作BG ∥DM ，根据平行线找角的联系即可求解；②先过点B 作BG ∥DM ，根据角平分线的定义，得出∠ABF =∠GBF ，再设∠DBE =α，∠ABF =β，根据∠CBF +∠BFC +∠BCF =180°，可得2α+β+3α+3α+β=180°，根据AB ⊥BC ，可得β+β+2α=90°，最后解方程组即可得到∠ABE =15°，进而得出∠EBC =∠ABE +∠ABC =15°+90°=105°．解：（1）如图1，AM 与BC 的交点记作点O ，∵AM ∥CN ，∴∠C =∠AOB ，∵AB ⊥BC ，∴∠A +∠AOB =90°，∴∠A +∠C =90°；（2）①如图2，过点B 作BG ∥DM ，∵BD⊥AM，∴DB⊥BG，∴∠DBG=90°，∴∠ABD+∠ABG=90°，∵AB⊥BC，∴∠CBG+∠ABG=90°，∴∠ABD=∠CBG，∵AM∥CN，BG∥DM，BG CN//,∴∠C=∠CBG，∠ABD=∠C；②如图3，过点B作BG∥DM，∵BF平分∠DBC，BE平分∠ABD，∴∠DBF=∠CBF，∠DBE=∠ABE，由（2）知∠ABD=∠CBG，∴∠ABF=∠GBF，设∠DBE=α，∠ABF=β，则∠ABE=α，∠ABD=2α=∠CBG，∠GBF=∠AFB=β，∠BFC=3∠DBE=3α，∴∠AFC=3α+β，∵∠AFC+∠NCF=180°，∠FCB+∠NCF=180°，∴∠FCB=∠AFC=3α+β，△BCF中，由∠CBF+∠BFC+∠BCF=180°得：2α+β+3α+3α+β=180°，∵AB⊥BC，∴β+β+2α=90°，∴α=15°，∴∠ABE=15°，∴∠EBC=∠ABE+∠ABC=15°+90°=105°．【点拨】本题主要考查了平行线的性质的运用，解决问题的关键是作平行线构造内错角，运用等角的余角（补角）相等进行推导．余角和补角计算的应用，常常与等式的性质、等量代换相关联．解题时注意方程思想的运用．20．（1）证明见分析；（2）证明见分析；（3）120°．【分析】（1）过点A作AD∥MN，根据两直线平行，内错角相等得到∠MCA＝∠DAC，∠PBA＝∠DAB，根据角的和差等量代换即可得解；（2）由两直线平行，同旁内角互补得到∴、∠CAB+∠ACD＝180°，由邻补角定义得到∠ECM+∠ECN＝180°，再等量代换即可得解；（3）由平行线的性质得到，∠FAB＝120°﹣∠GCA，再由角平分线的定义及平行线的性质得到∠GCA﹣∠ABF＝60°，最后根据三角形的内角和是180°即可求解．解：（1）证明：如图1，过点A作AD∥MN，∵MN∥PQ，AD∥MN，∴AD∥MN∥PQ，∴∠MCA＝∠DAC，∠PBA＝∠DAB，∴∠CAB＝∠DAC+∠DAB＝∠MCA+∠PBA，即：∠CAB＝∠MCA+∠PBA；（2）如图2，∵CD∥AB，∴∠CAB+∠ACD＝180°，∵∠ECM+∠ECN＝180°，∵∠ECN＝∠CAB∴∠ECM＝∠ACD，即∠MCA+∠ACE＝∠DCE+∠ACE，∴∠MCA＝∠DCE；（3）∵AF∥CG，∴∠GCA+∠FAC＝180°，∵∠CAB＝60°即∠GCA+∠CAB+∠FAB＝180°，∴∠FAB＝180°﹣60°﹣∠GCA＝120°﹣∠GCA，由（1）可知，∠CAB＝∠MCA+∠ABP，∵BF平分∠ABP，CG平分∠ACN，∴∠ACN＝2∠GCA，∠ABP＝2∠ABF，又∵∠MCA＝180°﹣∠ACN，∴∠CAB＝180°﹣2∠GCA+2∠ABF＝60°，∴∠GCA﹣∠ABF＝60°，∵∠AFB+∠ABF+∠FAB＝180°，∴∠AFB＝180°﹣∠FAB﹣∠FBA＝180°﹣（120°﹣∠GCA）﹣∠ABF＝180°﹣120°+∠GCA﹣∠ABF＝120°．【点拨】本题主要考查了平行线的性质，线段、角、相交线与平行线，准确的推导是解决本题的关键．21．（1）100；（2）75°；（3）n=3．【分析】（1）如图：过O作OP//MN，由MN//OP//GH得∠NAO+∠POA=180°，∠POB +∠OBH =180°，即∠NAO +∠AOB +∠OBH =360°，即可求出∠AOB ；（2）如图：分别延长AC 、CD 交GH 于点E 、F ，先根据角平分线求得58NAC ∠=︒，再根据平行线的性质得到58CEF ∠=︒；进一步求得18DBF ∠=︒，17DFB ∠=︒，然后根据三角形外角的性质解答即可；（3）设BF 交MN 于K ，由∠NAO =116°，得∠MAO =64°，故∠MAE =641n n ︒⨯+，同理∠OBH =144°，∠HBF =n ∠OBF ，得∠FBH =1441n n ︒⨯+，从而=n BKA FBH n ∠∠=⨯︒+1441，又∠FKN =∠F +∠FAK ，得144606411n n n n ︒︒︒⨯=+⨯++，即可求n ．解：（1）如图：过O 作OP //MN ，∵MN //GHl∴MN //OP //GH∴∠NAO +∠POA =180°，∠POB +∠OBH =180°∴∠NAO +∠AOB +∠OBH =360°∵∠NAO =116°，∠OBH =144°∴∠AOB =360°-116°-144°=100°；（2）分别延长AC 、CD 交GH 于点E 、F ，∵AC 平分NAO ∠且116NAO ∠=︒，∴58NAC ∠=︒，又∵MN //GH ，∴58CEF ∠=︒；∵144OBH ∠=︒，36OBG ∠=︒∵BD 平分OBG ∠，∴18DBF ∠=︒，又∵,CDB ∠=︒35∴351817DFB CDB DBF ∠=∠-∠=-=︒；∴175875ACD DFB AEF ∠=∠+∠=︒+︒=︒；（3）设FB 交MN 于K ，∵116NAO ∠=︒，则MAO ∠=︒64；∴641n MAE n ∠=⨯︒+∵144OBH ∠=︒，∴+1n FBH n ∠=⨯︒144，=n BKA FBH n ∠∠=⨯︒+1441，在△FAK 中，64601n BKA FKA F n ∠=∠+∠=⨯︒+︒+,∴144646011n n n n ⨯︒=⨯︒+︒++，∴3n =．经检验：3n =是原方程的根，且符合题意.【点拨】本题主要考查平行线的性质及应用，正确作出辅助线、构造平行线、再利用平行线性质进行求解是解答本题的关键．22．（1）260BEO DFO ∠+∠=︒；（2）EMN FNM ∠-∠的值为40°；（3）53．【分析】（1）过点O 作OG ∥AB ，可得AB ∥OG ∥CD ，利用平行线的性质可求解；（2）过点M 作MK ∥A B ，过点N 作NH ∥CD ，由角平分线的定义可设∠BEM =∠OEM =x ，∠CFN =∠OFN =y ，由∠BEO +∠DFO =260°可求x -y =40°，进而求解；（3）设直线FK 与EG 交于点H ，FK 与AB 交于点K ，根据平行线的性质即三角形外角的性质及50FMN ENM ∠-∠=︒，可得50KFD AEG ∠-∠=︒，结合260AEG n OEG DFK n OFK BEO DFO ∠=∠=∠∠+∠=︒，，，可得11180100AEG AEG KFD KFD n n∠+∠+︒-∠-∠=︒，即可得关于n 的方程，计算可求解n 值．。

专题5.23 平行线几何模型(M模型)(基础篇)(专项练习)七年级数学下册基础知识专项讲练

专题5.23平行线几何模型（M模型）（基础篇）（专项练习）一、单选题1．如图，已知AB∥DE，∠1＝30°，∠2＝35°，则∠BCE的度数为（）A．70°B．65°C．35°D．5°2．把一副三角板放在水平桌面上，摆放成如图所示的形状，使两个直角顶点重合，两条斜边平行，则∠1的度数是（）A．90°B．105°C．120°D．135°3．如图，已知AB∥DE，∠1＝30°，∠2＝35°，则∠BCE的度数为（）A．70°B．65°C．35°D．50°4．如图，已知//a b，将直角三角形如图放置，若∠2=40°，则∠1为（）A．120°B．130°C．140°D．150°5．如图，∠BCD＝90°，AB∥DE，则α与β一定满足的等式是（）A ．α+β＝180°B ．α+β＝90°C ．β＝3αD ．α﹣β＝90°6．如图，//AB CD ，点E 在AC 上，110A ∠=︒，15D ∠=︒，则下列结论正确的个数是（）（1）AE EC =；（2）85AED ∠=︒；（3）A CED D ∠=∠+∠；（4）45BED ∠=︒A ．1个B ．2个C ．3个D ．4个7．如图，∠BCD ＝70°，AB ∥DE ，则∠α与∠β满足（）A ．∠α+∠β＝110°B ．∠α+∠β＝70°C ．∠β﹣∠α＝70°D ．∠α+∠β＝90°8．如图所示，如果AB ∥CD ，则∠α、∠β、∠γ之间的关系为（）A ．∠α+∠β+∠γ＝180°B ．∠α－∠β+∠γ＝180°C ．∠α+∠β－∠γ＝180°D ．∠α－∠β－∠γ＝180°[9．如图,AB //EF,∠D=90°,则α,β,γ的大小关系是（）A ．βαγ=+B ．90βαγ=+-︒C ．90βγα=+︒-D ．90βαγ=+︒-10．如图，直线a//b ，一块含60°角的直角三角板ABC （∠A=60°）按如图所示放置．若∠1=43°，则∠2的度数为（）A ．101°B ．103°C ．105°D ．107°11．如图，AB ∥CD ，∠BED=61°，∠ABE 的平分线与∠CDE 的平分线交于点F ，则∠DFB=（）A ．149°B ．149.5°C ．150°D ．150.5°12．如图，玲玲在美术课上用丝线绣成了一个“2”，AB ∥DE ，∠A =30°，∠ACE =110°，则∠E 的度数为（）A ．30°B ．150°C ．120°D ．100°13．如图，已知直线a ∥b ，∠1=40°，∠2=60°．则∠3等于（）A ．100°B ．60°C ．40°D ．20°14．①如图1，AB ∥CD ，则360A E C ∠+∠+∠=︒；②如图2，AB ∥CD ，则P A C ∠=∠-∠；③如图3，AB ∥CD ，则1E A ∠=∠+∠；④如图4，直线AB ∥CD ∥EF ，点O 在直线EF 上，则180αβγ∠-∠+∠=︒．以上结论正确的个数是（）A ．1个B ．2个C ．3个D ．4个15．如图，已知直线AB 、CD 被直线AC 所截，//AB CD ，E 是平面内任意一点（点E 不在直线AB 、CD 、AC 上），设BAE α∠=，DCE β∠=．下列各式：①αβ+，②αβ-，③a β-，④360αβ︒--，AEC ∠的度数可能是（）A ．②③B ．①④C ．①③④D ．①②③④16．如图，AB ∥CD ，点E ，P 在直线AB 上（P 在E 的右侧），点G 在直线CD 上，EF ⊥FG ，垂足为F ，M 为线段EF 上的一动点，连接GP ，GM ，∠FGP 与∠APG 的角平分线交与点Q ，且点Q 在直线AB ，CD 之间的区域，下列结论：①∠AEF +∠CGF ＝90°；②∠AEF +2∠PQG ＝270°；③若∠MGF ＝2∠CGF ，则3∠AEF +∠MGC ＝270°；④若∠MGF ＝n ∠CGF ，则∠AEF 11n ++∠MGC ＝90°．正确的个数是（）A ．4B ．3C ．2D ．1二、填空题17．如图所示，直角三角板的60°角压在一组平行线上，AB CD ∥，40ABE ∠=︒，则EDC ∠=______度．18．如图，在ABC 中，24AC =，25AB =，7BC =．在AB 上取一点E ，AC 上取一点F ，连接EF ，若125EFC ∠=︒，过点B 作//BD EF ，且点D 在AB 的右侧，则CBD ∠的度数为__________．19．如图，//,,3527'EE MN CA CB EAC ⊥∠=︒，则MBC ∠=____________________．20．已知直线a ∥b ，将一块含30°角的直角三角板ABC 按如图所示方式放置（∠BAC ＝30°），并且顶点A ，C 分别落在直线a ，b 上，若∠1＝22°，则∠2的度数是_____．21．如图，AB ∥EF ，设∠C ＝90°，那么x ，y ，z 的关系式为______．22．如图，直线AB //CD ，点M 、N 分别在直线AB 、CD 上，点E 为直线AB 与CD 之间的一点，连接ME 、NE ，且∠MEN =80°，∠AME 的角平分线与∠CNE 的角平分线交于点F ，则∠MFN 的度数为______________．23．如图，已知AB //CD ，易得∠1+∠2+∠3=360°，∠1+∠2+∠3+∠4=540°，根据以上的规律求∠1+∠2+∠3+…+∠n =__________°．24．如图，AB CD ∥，EF 平分BED ∠，66DEF D ︒∠+∠=，28B D ∠-∠=︒，则BED ∠=__________．25．如图，已知AB//CD ，120AFC ∠=︒，13EAF EAB ∠=∠，13ECF ECD ∠=∠，则AEC ∠=____度．26．如图，已知：AB ∥CD ，∠1=50°，∠2=113°，则∠3=___度．三、解答题27．在数学课本中，有这样一道题：已知：如图1，B C BEC ∠+∠=∠．求证：//AB CD请补充下面证明过程：证明：过点E ，作//EF AB ，如图2∴B ∠=∠______（_________________）∵B C BEC ∠+∠=∠，BEF ∠+∠_______=BEC ∠（已知）∴B C BEF FEC ∠+∠=∠+∠（___________）∴∠______=∠_______∴//EF _____（________________）∵//EF AB∴//AB CD28．如图所示，已知//AB CD ，BE 平分ABC ∠，DE 平分ADC ∠，求证：1()2E A C ∠=∠+∠29．如图，AB //CD ，点E 为两平行线间的一点．请证明两个结论．（1）12BED ∠=∠+∠；（2）360EBM EDN BED ∠+∠+∠= ．30．如图所示，//HD GE ，CB 平分GCF ∠，AF 平分HAB ∠，F ∠的余角等于2B ∠的补角，求BAH ∠的度数.参考答案1．B【分析】作CF∥AB，根据平行线的性质可以得到∠1＝∠BCF，∠FCE＝∠2，从而可得∠BCE的度数，本题得以解决．解：作CF∥AB，∵AB∥DE，∴CF∥DE，∴AB∥DE∥DE，∴∠1＝∠BCF，∠FCE＝∠2，∵∠1＝30°，∠2＝35°，∴∠BCF＝30°，∠FCE＝35°，∴∠BCE＝65°，故选：B．【点拨】本题考查平行线的性质，解答本题的关键是明确题意，利用平行线的性质解答．2．B【分析】先作直线OE平行于直角三角板的斜边，根据平行线的性质即可得到答案.解：作直线OE平行于直角三角板的斜边．可得：∠A＝∠AOE＝60°，∠C＝∠EOC＝45°，故∠1的度数是：60°+45°＝105°．故选B．【点拨】本题考查平行线的性质，解题的关键是掌握平行线的性质.3．B【分析】根据平行线的性质和∠1=30°，∠2=35°，可以得到∠BCE的度数，本题得以解决．解：作CF∥AB，∵AB∥DE，∴CF∥DE，∴AB∥DE∥CF，∴∠1=∠BCF，∠FCE=∠2，∵∠1=30°，∠2=35°，∴∠BCF=30°，∠FCE=35°，∴∠BCE=65°，故选：B．【点拨】本题考查平行线的性质，解答本题的关键是明确题意，利用平行线的性质解答．4．B【分析】过A作AB∥a，即可得到a∥b∥AB，依据平行线的性质，即可得到∠5的度数，进而得出1的度数．解：标注字母，如图所示，过A作AB∥a，∵a∥b，∴a∥b∥AB，∴∠2=∠3=40°，∠4=∠5，又∵∠CAD=90°，∴∠4=50°，∴∠5=50°，∴∠1=180°-50°=130°，故选：B．【点拨】本题考查了平行线的性质，平行公理，熟记性质并作出辅助线是解题的关键．5．D【分析】过C 作CF ∥AB ，根据平行于同一条直线的两条直线平行得到AB ∥DE ∥CF ，根据平行线的性质得到11802βα∠=∠∠=︒-∠，，作差即可．解：详：过C 作CF ∥AB ，∵AB ∥DE ，∴AB ∥DE ∥CF ，∴11802βα∠=∠∠=︒-∠，，∴1802118090BCD αβ∠-∠=︒-∠-∠=︒-∠=︒，故选：D ．【点拨】考查平行公理已经平行线的性质，解题的关键是注意辅助线的作法，作出辅助线．6．B【分析】利用平行线的性质和三角形的性质依次判断即可求解．解：∵AB ∥CD ，∴∠A +∠C ＝180°，又∵∠A ＝110°，∴∠C ＝70°，∴∠AED ＝∠C +∠D ＝85°，故（2）正确，∵∠C +∠D +∠CED ＝180°，∴∠D +∠CED ＝110°，∴∠A ＝∠CED +∠D ，故（3）正确，∵点E 在AC 上的任意一点，∴AE 无法判断等于CE ，∠BED 无法判断等于45°，故（1）、（4）错误，故选：B ．【点拨】本题考查了平行线的性质，三角形的外角的性质，掌握平行线的性质是本题的关键．7．B【分析】过点C作CF∥AB，根据平行线的性质得到∠BCF＝∠α，∠DCF＝∠β，由此即可解答．解：如图，过点C作CF∥AB，∵AB∥DE，∴AB∥CF∥DE，∴∠BCF＝∠α，∠DCF＝∠β，∵∠BCD＝70°，∴∠BCD=∠BCF+∠DCF＝∠α+∠β＝70°，∴∠α+∠β＝70°．故选B．【点拨】本题考查了平行线的性质，正确作出辅助线，熟练掌握平行线的性质进行推理证明是解决本题的关键.8．C【分析】过E作EF∥AB，由平行线的质可得EF∥CD，∠α+∠AEF=180°，∠FED=∠γ，由∠β=∠AEF+∠FED即可得∠α、∠β、∠γ之间的关系．解：过点E作EF∥AB，∴∠α+∠AEF=180°（两直线平行，同旁内角互补），∵AB∥CD，∴EF∥CD，∴∠FED=∠EDC（两直线平行，内错角相等），∵∠β=∠AEF+∠FED，又∵∠γ=∠EDC，∴∠α+∠β-∠γ=180°，故选：C．【点拨】本题主要考查了平行线的性质，正确作出辅助线是解答此题的关键．9．D【分析】通过作辅助线,过点C和点D作CG//AB,DH//AB,可得CG//DH//AB,根据AB//EF,可得AB//EF//CG//DH,再根据平行线的性质即可得γ+β-α=90°,进而可得结论．解：如图,过点C和点D作CG//AB,DH//AB,∵CG//AB,DH//AB,∴CG//DH//AB,∵AB//EF,∴AB//EF//CG//DH,∵CG//AB,∴∠BCG=α,∴∠GCD=∠BCD-∠BCG=β-α,∵CG//DH,∴∠CDH=∠GCD=β-α,∵HD//EF,∴∠HDE=γ,∵∠EDC=∠HDE+∠CDH=90°,∴γ+β-α=90°,∴β=α+90°-γ．故选：D．【点拨】本题考查了平行线的性质,解决本题的关键是掌握平行线的性质．10．B【分析】如图，首先证明∠AMO=∠2；然后运用对顶角的性质求出∠ANM=43°，借助三角形外角的性质求出∠AMO即可解决问题．解：如图，∵直线a∥b，∴∠AMO=∠2；∵∠ANM=∠1，∠1=43°，∴∠ANM=43°，∴∠AMO=∠A+∠ANM=60°+43°=103°，∴∠2=∠AMO=103°．故选：B．【点拨】该题主要考查了平行线的性质、对顶角的性质、三角形的外角性质等几何知识点及其应用问题；牢固掌握平行线的性质、对顶角的性质等几何知识点是灵活运用、解题的基础．11．B【分析】过点E作EG∥AB，根据平行线的性质可得“∠ABE+∠BEG=180°，∠GED+∠EDC=180°”，根据角的计算以及角平分线的定义可得“∠FBE+∠EDF=1∠ABE+∠CDE）”，再依据四边形内角和为360°结合角的计算即可得出2结论．解：如图，过点E作EG∥AB，∵AB∥CD，∴AB∥CD∥GE，∴∠ABE+∠BEG=180°，∠GED+∠EDC=180°，∴∠ABE+∠CDE+∠BED=360°；又∵∠BED=61°，∴∠ABE+∠CDE=299°．∵∠ABE和∠CDE的平分线相交于F，∴∠FBE+∠EDF=12（∠ABE+∠CDE）=149.5°，∵四边形的BFDE的内角和为360°，∴∠BFD=360°-149.5°-61°=149.5°．故选B．【点拨】本题考查了平行线的性质、三角形内角和定理以及四边形内角和为360°，解决该题型题目时，根据平行线的性质得出相等（或互补）的角是关键．12．D解：过C作CQ∥AB，∵AB∥DE，∴AB∥DE∥CQ，∵∠A=30°，∴∠A=∠QCA=30°，∠E+∠ECQ=180°，∵∠ACE=110°，∴∠ECQ=110°−30°=80°，∴∠E=180°−80°=100°，故选D.13．A解：过点C作CD∥a，∵a∥b，∴CD∥a∥b，∴∠ACD=∠1=40°，∠BCD=∠2=60°，∴∠3=∠ACD+∠BCD=100°．故选A．【点拨】本题考查平行线的判定与性质．14．B【分析】①过点E作直线EF∥AB，由平行线的性质：两直线平行，同旁内角互补，即可得出结论；②如图2，先根据三角形外角的性质得出∠1＝∠C+∠P，再根据两直线平行，内错角相等即可作出判断；③如图3，过点E作直线EF∥AB，由平行线的性质可得出∠A+∠AEC﹣∠1＝180°，即得∠AEC＝180°+∠1﹣∠A；④如图4，根据平行线的性质得出∠α＝∠BOF，∠γ+∠COF＝180°，再利用角的关系解答即可．解：①如图1，过点E作直线EF∥AB，∵AB∥CD，∴AB∥CD∥EF，∴∠A+∠1＝180°，∠2+∠C＝180°，∴∠A+∠B+∠AEC＝360°，故①错误；②如图2，∵∠1是△CEP的外角，∴∠1＝∠C+∠P，∵AB∥CD，∴∠A＝∠1，即∠P＝∠A﹣∠C，故②正确；③如图3，过点E作直线EF∥AB，∵AB∥CD，∴AB∥CD∥EF，∴∠A+∠3＝180°，∠1＝∠2，∴∠A+∠AEC﹣∠1＝180°，即∠AEC＝180°+∠1﹣∠A，故③错误；④如图4，∵AB∥EF，∴∠α＝∠BOF，∵CD∥EF，∴∠γ+∠COF＝180°，∵∠BOF＝∠COF+∠β，∴∠COF＝∠α﹣∠β，∴∠γ+∠α﹣∠β＝180°，故④正确；综上结论正确的个数为2，故选：B．【点拨】本题考查的是平行线的性质及三角形外角的性质，熟练掌握平行线的性质，根据题意作出辅助线是解答此题的关键．15．D【分析】由题意根据点E有6种可能位置，分情况进行讨论，依据平行线的性质以及三角形外角性质进行计算求解即可．解：（1）如图1，由AB∥CD，可得∠AOC=∠DCE1=β，∵∠AOC=∠BAE1+∠AE1C，∴∠AE1C=β-α．（2）如图2，过E2作AB平行线，则由AB∥CD，可得∠1=∠BAE2=α，∠2=∠DCE2=β，∴∠AE2C=α+β．（3）如图3，由AB∥CD，可得∠BOE3=∠DCE3=β，∵∠BAE3=∠BOE3+∠AE3C，∴∠AE3C=α-β．（4）如图4，由AB∥CD，可得∠BAE4+∠AE4C+∠DCE4=360°，∴∠AE4C=360°-α-β．（5）（6）当点E在CD的下方时，同理可得∠AEC=α-β或β-α．综上所述，∠AEC的度数可能为β-α，α+β，α-β，360°-α-β，即①②③④．故选：D．【点拨】本题主要考查平行线的性质的运用，解题时注意两直线平行，同位角相等；两直线平行，内错角相等以及分类讨论．16．A【分析】①过点F作FH∥AB，利用平行线的性质以及已知即可证明；②利用角平分线的性质以及平行线的性质得到∠3=2∠2，∠CGF+2∠1+∠3=180°，结合①的结论即可证明；③由已知得到∠MGC＝3∠CGF，结合①的结论即可证明；④由已知得到∠MGC＝(n+1)∠CGF，结合①的结论即可证明．解：①过点F作FH∥AB，如图：∵AB∥CD，∴AB∥FH∥CD，∴∠AEF=∠EFH，∠CGF=∠GFH，∵EF⊥FG，即∠EFG=∠EFH+∠GFH=90°，∴∠AEF+∠CGF=90°，故①正确；②∵AB∥CD，PQ平分∠APG，GQ平分∠FGP，∴∠APQ=∠2，∠FGQ=∠1，∴∠3=∠APQ+∠2=2∠2，∠CGF+∠FGQ+∠1+∠3=∠CGF+2∠1+∠3=180°，即2∠1=180°-2∠2-∠CGF ，∴2∠2+2∠1=180°-∠CGF ，∵∠PQG =180°-(∠2+∠1)，∴2∠PQG =360°-2(∠2+∠1)=360°-(180°-∠CGF )=180°+∠CGF ，∴∠AEF +2∠PQG =∠AEF +180°+∠CGF =180°+90°=270°，故②正确；③∵∠MGF ＝2∠CGF ，∴∠MGC ＝3∠CGF ，∴3∠AEF +∠MGC ＝3∠AEF +3∠CGF ＝3(∠AEF +∠CGF )=3⨯90°＝270°；3∠AEF +∠MGC ＝270°，故③正确；④∵∠MGF ＝n ∠CGF ，∴∠MGC ＝(n+1)∠CGF ，即∠CGF =11n +∠MGC ，∵∠AEF +∠CGF =90°，∴∠AEF 11n ++∠MGC ＝90°，故④正确．综上，①②③④都正确，共4个，故选：A ．【点拨】本题主要考查了平行线的性质，角平分线的定义等知识点，作辅助线求得∠AEF +∠CGF =90°，是解此题的关键．17．20【分析】如图（见详解），过点E 作EF AB ∥，先证明AB EF CD ∥∥，再由平行线的性质定理得到40ABE BEF ∠=∠=︒，EDC DEF ∠=∠，结合已知条件60BED ∠=︒即可得到．解：由题意可得：60BED ∠=︒．如图，过点E 作EF AB ∥，又∵AB CD ∥，∴AB EF CD ∥∥，∴40ABE BEF ∠=∠=︒，EDC DEF ∠=∠，∵60BED ∠=︒，∴60DEF BEF ∠+∠=︒，∴20DEF ∠=︒，即：20EDC ∠=︒．故答案为：20．【点拨】本题重点考查了平行线的性质定理的运用．从“基本图形”的角度看，本题可以看作是“M ”型的简单运用．解法不唯一，也可延长B E 交CD 于点G ，结合三角形的外角定理来解决；或连结BD ，结合三角形内角和定理来解决．18．35︒【分析】在ABC 中，由三边的长度可得出222AC BC AB +=，进而可得出ABC 为直角三角形且90ACB ∠=︒，由于平行线之间有拐点，所以过点C 作//CM EF 交AB 于点M ，则//BD CM ，利用平行的性质可得出MCF ∠的度数，结合BCM ACB MCF ∠=∠-∠可求出BCM ∠的度数，再利用“两直线平行，内错角相等”即可求出CBD ∠的度数．解：在ABC 中，24AC =，25AB =，7BC =，∵22224762525+==，即222AC BC AB +=，∴ABC 为直角三角形且90ACB ∠=︒．过点C 作//CM EF 交AB 于点M ，则//BD CM ，如下图所示，∵//CM EF ，125EFC ∠=︒，∴18055MCF EFC ∠=︒-∠=︒，∴35BCM ACB MCF ∠=∠-∠=︒．又∵//BD CM ，∴35CBD BCM ∠=∠=︒．故答案为：35︒．【点拨】本题考查了勾股定理的逆定理以及平行线的性质，利用勾股定理的逆定理，找出90ACB ∠=︒并知道过拐点作已知直线的平行线是解题的关键．19．5433'【分析】过C 点作EF 的平行线，利用平行线的性质，即可证明．解：过C 点作EF 的平行线,GH //,EF MN ////,EF GH MN ∴3527'EAC ACH ∴∠=∠=︒，又,CA CB ⊥ 90,ACB ∴∠=︒5433',HCB ACB ACH ∴∠=∠-∠=︒又//,GH MN 5433'HCB CBM ︒∴∠=∠=.故答案为：5433'︒．【点拨】本题考查了通过平行线的性质求解角度问题，解题关键在于过中间的点作已知直线的平行线．20．38°【分析】过点B 作BD ∥a ，可得∠ABD=∠1=22°，a ∥b ，可得BD ∥b ，进而可求∠2的度数．解：如图，过点B 作BD ∥a ，∴∠ABD=∠1=22°，∵a∥b，∴BD∥b，∴∠2=∠DBC=∠ABC-∠ABD=60°-22°=38°．故答案为：38°．【点拨】本题考查了平行线的性质，解决本题的关键是掌握平行线的性质．21．y=90°-x+z．【分析】作CG//AB，DH//EF，由AB//EF，可得AB//CG//HD//EF，根据平行线性质可得∠x=∠1，∠CDH=∠2，∠HDE=∠z，由∠C＝90°，可得∠1+∠2=90°，由∠y=∠z+∠2，可证∠y=∠z+90°-∠x即可．解：作CG//AB，DH//EF，∵AB//EF，∴AB//CG//HD//EF，∴∠x=∠1，∠CDH=∠2，∠HDE=∠z∵∠BCD＝90°∴∠1+∠2=90°，∠y=∠CDH+∠HDE=∠z+∠2，∵∠2=90°-∠1=90°-∠x，∴∠y=∠z+90°-∠x．即y=90°-x+z．【点拨】本题考查平行线的性质，掌握平行线的性质，利用辅助线画出准确图形是解题关键．22．40°或140°【分析】分两种情况画图讨论：分别过点E和点F作EG∥AB，FH∥AB，可得EG∥FH∥AB，根据AB∥CD，可得EG∥FH∥AB∥CD，情况一根据平行线的性质可得∠MFN=∠MFH+∠NFH=∠AMF+∠CNF=40°；情况二根据平行线的性质可得∠MFN=∠MFH+∠NFH=∠AMF+∠CNF=140°．进而得到结论．解：分两种情况画图讨论：分别过点E和点F作EG∥AB，FH∥AB，∴EG∥FH∥AB，∵AB∥CD，∴EG∥FH∥AB∥CD，如图，∵EG∥AB∥CD，∴∠AME=∠MEG，∠CNE=∠NEG，∴∠AME+∠CNE=∠MEG+∠NEG=∠MEN=80°，∵∠AME的角平分线与∠CNE的角平分线交于点F，∴∠AMF=12∠AME，∠CNF=12∠CNE，∴∠AMF+∠CNF=12（∠AME+∠CNE）=40°，∵FH∥AB∥CD，∴∠MFH=∠AMF，∠NFH=∠CNF，∴∠MFN=∠MFH+∠NFH=∠AMF+∠CNF=40°，如图，∵EG∥AB∥CD，∴∠BME=∠MEG，∠DNE=∠NEG，∴∠BME +∠DNE =∠MEG +∠NEG =∠MEN =80°，∴∠AME +∠CNE =360°-（∠BME +∠DNE ）=280°∵∠AME 的角平分线与∠CNE 的角平分线交于点F ，∴∠AMF =12∠AME ，∠CNF =12∠CNE ，∴∠AMF +∠CNF =12（∠AME +∠CNE ）=140°，∵FH ∥AB ∥CD ，∴∠MFH=∠AMF ，∠NFH =∠CNF ，∴∠MFN =∠MFH+∠NFH =∠AMF +∠CNF =140°．综上所述：∠MFN 的度数为40°或140°．故答案为：40°或140°．【点评】本题主要考查了平行线的性质，解决本题的关键是掌握平行线的性质．23．()1801n -【分析】过点P 作平行于AB 的直线，运用两次两条直线平行，同旁内角互补即可得到三个角的和；分别过点P ，Q 作AB 的平行线，运用三次平行线的性质，即可得到四个角的和；同样作辅助线，运用（n -1）次平行线的性质，则n 个角的和是()1801n -︒．解：（1）如图，过点P 作一条直线PM 平行于AB ，∵AB ∥CD ，AB ∥PM∵AB ∥PM ∥CD ，∴∠1+∠APM =180°，∠MPC +∠3=180°，∴∠1+∠APC +∠3=360°；（2）如图，过点P 、Q 作PM 、QN 平行于AB ，∵AB ∥CD ，∵AB ∥PM ∥QN ∥CD ，∴∠1+∠APM =180°，∠MPQ +∠PQN =180°，∠NQC +∠4=180°；∴∠1+∠APQ +∠PQC +∠4=540°；根据上述规律，显然作（n -2）条辅助线，运用（n -1）次两条直线平行，同旁内角互补．即可得到∠1+∠2+∠3+…+∠n =180°（n -1）．故答案为：()1801n -︒【点拨】此题考查了平行线的性质．注意掌握辅助线的作法是解此题的关键．24．80︒【分析】过E 点作EM ∥AB ，根据平行线的性质可得∠BED =∠B +∠D ，利用角平分线的定义可求得∠B +3∠D =132°，结合∠B -∠D =28°即可求解．解：过E 点作EM ∥AB ，∴∠B =∠BEM ，∵AB ∥CD ，∴EM ∥CD ，∴∠MED =∠D ，∴∠BED =∠B +∠D ，∵EF 平分∠BED ，∴∠DEF =12∠BED ，∵∠DEF +∠D =66°，∴12∠BED +∠D =66°，∴∠BED +2∠D =132°，即∠B +3∠D =132°，∵∠B -∠D =28°，∴∠B =54°，∠D =26°，∴∠BED =80°．故答案为：80°．【点拨】本题主要考查平行线的性质，角平分线的定义，作出辅助线证出∠BED =∠B +∠D 是解题的关键．25．90解：如图，过点E 作EH ∥AB ，过点F 作FG ∥AB ，∵AB ∥CD ，∴AB ∥FG ∥CD ，AB ∥EH ∥CD ，∴AFG FAB Ð=Ð，GFC FCD Ð=Ð，AFG FAB Ð=Ð，GFC FCD Ð=Ð，又∵13EAF EAB ∠=∠，13ECF ECD ∠=∠，∴3EAB EAF Ð=Ð，3ECD ECF Ð=Ð，∴4FAB EAF Ð=Ð，4ECD ECF Ð=Ð，∴44120AFC AFG GFC FAB ECD EAF ECF Ð=Ð+Ð=Ð+Ð=Ð+Ð=°，即：30EAF ECF Ð+Ð=°，∴()33390AEC EAB ECD EAF ECF EAF ECF Ð=Ð+Ð=Ð+Ð=Ð+Ð=o ．故答案为：90．【点拨】本题考查了平行线的性质，平行公理，作辅助线构造内错角是解题的关键．26．63【分析】如图，易知∠3＝∠2－∠1，计算即可.解：如图所示，根据平行线的性质易知∠3＝∠2－∠1＝113°－50°＝63°.【点拨】本题主要考查平行线的性质，熟练掌握平行线的性质是解答的关键.27．BEF；两直线平行内错角相等；FEC；等量代换；C；FEC；DC；内错角相等两直线平行【分析】根据平行线的判定与性质即可完成证明过程．解：过点E，作//EF AB，如图2，B BEF∴∠=∠（两直线平行内错角相等），B C BEC∠+∠=∠，BEF FEC BEC∠+∠=∠（已知），B C BEF FEC∴∠+∠=∠+∠（等量代换），C FEC∴∠=∠，//EF DC∴（内错角相等两直线平行），//EF AB，//AB CD∴．故答案为：BEF，两直线平行内错角相等，FEC，等量代换，C，FEC，DC，内错角相等两直线平行．【点拨】本题考查了平行线的判定与性质，解决本题的关键是准确区分平行线的判定与性质，并熟练运用．28．见分析【分析】先根据平行线的性质得出∠A＝∠ADC，∠C＝∠ABC，再由BE平分∠ABC，DE平分∠ADC可知∠1＝12∠ADC，∠2＝12∠ABC，根据三角形外角的性质即可得出结论．解：如图：∵AB∥CD，∴∠A＝∠ADC，∠C＝∠ABC．∵BE 平分∠ABC ，DE 平分∠ADC ，∴∠1＝12∠ADC ，∠2＝12∠ABC ．∵∠3是三角形的外角，∴∠3＝∠E ＋∠2＝∠C ＋∠1，1122E ABC C ADC ∴∠+∠=∠+∠，即∠E ＋12∠C ＝∠C ＋12∠A ，∴∠E ＝12（∠A ＋∠C ）．【点拨】本题考查的是平行线的性质，三角形的外角，以及角平分线等知识点，熟知以上知识点是解题的关键．29．（1）见分析；（2）见分析．【分析】（1）过点E 作//EF AB ，根据平行线的性质求证即可；（2）根据平行线的性质即可得证；解：（1）过点E 作//EF AB ，∵AB ∥CD ，∴AB ∥EF ∥CD ，1BEF ∴∠=∠，2DEF ∠=∠，12BED ∴∠=∠+∠．（2）//AM EF180MBE BEF ∴∠+∠= ，//CD EF180NDE DEF ∴∠+∠= ，又∵∠BED =∠BEF +∠DEF ，360EBM EDN BED ∴∠+∠+∠= ．【点拨】本题考查了平行线的性质和平行公理的推论，熟练掌握平行线的性质是解题的关键．30．60BAH ∠=︒.【分析】先设HAF FAB x ∠=∠=，BCG BCF y ∠=∠=.由题意的2B HAB BCG x y ∠=∠+∠=+，2F HAF FCG y x ∠=∠+∠=+，又因为F ∠的余角等于2B ∠的补角，所以()()90218022y x x y ︒-+=︒-+，最终求得BAH ∠.解：设HAF FAB x ∠=∠=，BCG BCF y ∠=∠=.由基本图形HABCG 知2B HAB BCG x y ∠=∠+∠=+，由基本图形HAFCG 知2F HAF FCG y x ∠=∠+∠=+，因为F ∠的余角等于2B ∠的补角，所以()()90218022y x x y ︒-+=︒-+，解得30x =︒，所以260BAH x ∠==︒【点拨】本题考查平行线的性质、角平分线、余角和补角，解题的关键是设HAF FAB x ∠=∠=，BCG BCF y ∠=∠=，由题意得到有关x ，y 有关的等式.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

平行线几何模型之M 型解题方法专题练习
一、解答题
1．在数学课本中，有这样一道题：已知：如图1，B C BEC ∠+∠=∠．求证：//AB CD 请补充下面证明过程：
证明：过点E ，作//EF AB ，如图2 ∴B ∠=∠______（_________________）
∵B C BEC ∠+∠=∠，BEF ∠+∠_______=BEC ∠（已知） ∴B C BEF FEC ∠+∠=∠+∠（___________） ∴∠______=∠_______
∴//EF _____（________________） ∵//EF AB ∴//AB CD
2．（2021·山东禹城·七年级期中）（1）如图1，//AB CD ，33A ∠=︒，40C ∠=︒，则APC ∠= ︒；
（2）如图2，//AB DC ，点P 在射线OM 上运动，当点P 在B 、D 两点之间运动时，BAP α∠=∠，
DCP β∠=∠，求CPA ∠与α∠、β∠之间的数量关系，并说明理由；
（3）在（2）的条件下，如果点P 在B 、D 两点外侧运动时（点P 与点B 、D 、O 三点不重合），请你直接写出CPA ∠与α∠、β之间的数量关系．
3．（2021·北京西城·七年级期末）如图，AB//CD，点E为两平行线间的一点．请证明两个结论．（1）12
∠=∠+∠；
BED
（2）360
∠+∠+∠=．
EBM EDN BED
4．如图所示，已知//AB CD ，BE 平分ABC ∠，DE 平分ADC ∠，求证：1
()2
E A C ∠=∠+∠
5．直线AB 、CD 被直线EF 所截，AB ∥CD ，点P 是平面内一动点．
（1）若点P 在直线CD 上，如图①，∠α＝50°，则∠2＝ °．
（2）若点P 在直线AB 、CD 之间，如图②，试猜想∠α、∠1、∠2之间的等量关系并给出证明；（3）若点P 在直线CD 的下方，如图③，（2）中∠α、∠1、∠2之间的关系还成立吗？请作出判断并说明理由．
6．
（2021·河北·曲阳县教育和体育局教研室七年级期中）已知：如图1，12180︒∠+∠=，∠=∠AEF HLN ．
（1）判断图中平行的直线，并给予证明；
（2）如图2，2∠=∠PMQ QMB ，2∠=∠PNQ QND ，请判断P ∠与Q ∠的数量关系，并证明．
7．（1）如图1，已知//AB CD ，ABF DCE ∠=∠，求证：BFE FEC ∠=∠
（2）如图2，已知//AB CD ，14
EAF EAB ∠=∠，14ECF ECD ∠=∠，求证：3
4AFC AEC ∠=∠
8．如图，若//AB CD ，则B D E ∠+∠=∠，你能说明为什么吗？
AB CD，又得到什么结论？
9．在图中，若//
AB CD，E是AB、CD之间的一点．10．（2021·湖北硚口·七年级月考）如图1，//
（1）判定BAE ∠，CDE ∠与AED ∠之间的数量关系，并证明你的结论；
（2）如图2，若BAE ∠、CDE ∠的两条平分线交于点F ．直接写出AFD ∠与AED ∠之间的数量关系；（3）将图2中的射线DC 沿DE 翻折交AF 于点G 得图3，若AGD ∠的余角等于2E ∠的补角，求BAE ∠的大小．
11．（2021·
黑龙江道里·七年级期末）已知，AB ∥CD ，点E 在CD 上，点G ，F 在AB 上，点H 在AB ，CD 之间，连接FE ，EH ，HG ，∠AGH ＝∠FED ，FE ⊥HE ，垂足为E ．（1）如图1，求证：HG ⊥HE ；
（2）如图2，GM 平分∠HGB ，EM 平分∠HED ，GM ，EM 交于点M ，求证：∠GHE ＝2∠GME ；
（3）如图3，在（2）的条件下，FK 平分∠AFE 交CD 于点K ，若∠KFE ：∠MGH ＝13：5，求∠HED 的度数．
12．
（2021·重庆江北·七年级期末）如图1，AB //CD ，点E 、F 分别在AB 、CD 上，点O 在直线AB 、CD 之间，且100EOF ∠=︒．
（1）求BEO OFD ∠+∠的值；
（2）如图2，直线MN 分别交BEO ∠、OFC ∠的角平分线于点M 、N ，直接写出EMN FNM ∠-∠的值；（3）如图3，EG 在AEO ∠内，AEG m OEG ∠=∠；FH 在DFO ∠内，DFH m OFH ∠=∠，直线MN 分别交EG 、FH 分别于点M 、N ，且50FMN ENM ∠-∠=︒，直接写出m 的值．
13．
（2021·湖北武昌·七年级期末）如图1，点A 在直线MN 上，点B 在直线ST 上，点C 在MN ，ST 之间，且满足MAC ACB SBC ∠+∠+∠360=︒．（1）证明：//MN ST ；
（2）如图2，若60ACB ∠=︒，//AD CB ，点E 在线段BC 上，连接AE ，且2DAE CBT ∠=∠，试判断CAE ∠与CAN ∠的数量关系，并说明理由；（3）如图3，若180ACB n
︒
∠=
（n 为大于等于2的整数），点E 在线段BC 上，连接AE ，若MAE n CBT ∠=∠，则:CAE CAN ∠∠=______．
14．（2021·
湖北梁子湖·七年级期中）如图1，直线AB //CD ，点P 在两平行线之间，点E 在AB 上，点F 在CD 上，连接PE ，PF ．
（1）若∠PEB =60°，∠PFD =50°，请求出∠EPF ．（请写出必要的步骤，并说明理由）
（2）如图2，若点P ，Q 在直线AB 与CD 之间时，∠1=30°，∠2=40°，∠3=70°，请求出∠4= ．（不需说明理由，请直接写出答案）
（3）如图3，在图1的基础上，作P 1E 平分∠PEB ，P 1F 平分∠PFD ，若设∠PEB ＝x °，∠PFD ＝y °，则∠P 1= （用含x ，y 的式子表示）．若P 2E 平分∠P 1EB ，P 2F 平分∠P 1FD ，可得∠P 2；P 3E 平分∠P 2EB ，P 3F 平分∠P 2FD ，可得∠P 3…，依次平分下去，则∠P n ＝．（用含x ，y 的式子表示）
15．
（2021·广东新丰·七年级期中）如图1，点A 、B 分别在直线GH 、MN 上，GAC NBD ∠=∠，C D ∠=∠.
（1）求证：//GH MN ；（提示：可延长AC 交MN 于点P 进行证明）
（2）如图2，AE 平分GAC ∠，DE 平分BDC ∠，若AED GAC ∠=∠，求GAC ∠与ACD ∠之间的数量关系；（3）在（2）的条件下，如图3，BF 平分DBM ∠，点K 在射线BF 上，1
3
KAG GAC ∠=∠，若AKB ACD ∠=∠，
直接写出GAC ∠的度数．。