平行线有关模型汇总
初中数学 中考复习 第01讲—平行线的五大拐点模型
模型一：铅笔头模型基础（1）如图，若CD AB //，此时，E D B ∠∠∠,,之间有什么关系？请证明解答：如图，过点E 作AB l //得证360=∠+∠+∠E D B（2）反之，如图，若360=∠+∠+∠E D B ，直线AB 与CD 有什么位置关系？请证明解答：如图，过点E 作AB l //得证CD l //则CD AB //总结：①辅助线：过拐点作平行线②若CD AB //，则360=∠+∠+∠E D B③若360=∠+∠+∠E D B ，则CD AB //模型一：铅笔头模型进阶如图，两直线CD AB ,平行，则=∠+∠+∠+∠+∠+∠654321解答：如图，过F 作AB l //1，过G 作12//l l ，过H 作23//l l ，过I 作34//l l 得证900654321=∠+∠+∠+∠+∠+∠总结：①辅助线：过拐点作平行线，且有多少个拐点就作多少条平行线②)1(180121-=∠+∠+⋅⋅⋅+∠+∠-n A A A A n n【2-n 个拐点】模型二：锯齿模型基础（1）如图，若CD AB //，则E D B ∠=∠+∠，你能说明为什么吗？解答：如图，过点E 作AB l //得证E D B ∠=∠+∠（2）在图中，CD AB //，G E ∠+∠与D F B ∠+∠+∠又有何关系？解答：如图，过点E 作AB l //1，过点F 作AB l //2，过点G 作AB l //3得证G E ∠+∠=D F B ∠+∠+∠（3）在图中，若CD AB //，又得到什么结论？解答：同理可得n n E E E D F F F B ∠++∠+∠=∠+∠++∠+∠+∠- 21121总结：①辅助线：过拐点作平行线，且有多少个拐点就作多少条平行线 ②所有朝左的角之和等于所有朝右的角之和模型二：锯齿模型进阶【例1】如图所示，已知CD AB //，BE 平分ABC ∠，DE 平分ADC ∠，求证：)(21C A E ∠+∠=∠解答：①方法一：锯齿模型【锯齿ABEDC 】如图，过点E 作AB EF //+转化思想得证 ②方法二：8字模型（详解见第2讲）总结：①辅助线：过拐点作平行线，且有多少个拐点就作多少条平行线 ②所有朝左的角之和等于所有朝右的角之和 ③转化思想【例2】如图，已知CD AB //，EAB EAF ∠=∠41，ECD ECF ∠=∠41，求证： AEC AFC ∠=∠43解答：锯齿BAECD+锯齿BAFCD ；过点E 作AB GE //，过点F 作CD HF //+方程思想【βα,表示角度】得证总结：①辅助线：过拐点作平行线，且有多少个拐点就作多少条平行线 ②所有朝左的角之和等于所有朝右的角之和 ③方程思想【例3】如图，CD AB //，61=∠BED ，ABE ∠的平分线与CDE ∠的平分线交于点F ，则=∠DFB （ ） A.149B.5.149C.150D.5.150解答：锯齿CDFBA+铅笔头CDEBA ；得证B总结：①辅助线：过拐点作平行线，且有多少个拐点就作多少条平行线 ②铅笔头模型：角之和=180×（拐点个数+1）③锯齿模型：所有朝左的角之和等于所有朝右的角之和【例4】如图，已知点P 是矩形ABCD 内一点（不含边界），设21,θθ=∠=∠PBA PAD ，43,θθ=∠=∠PDC PCB ，若 50,80=∠=∠CPD APB ，则（ ）A. 30)()(3241=+-+θθθθB.40)()(3142=+-+θθθθC.70)()(4321=+-+θθθθ D.180)()(4321=+++θθθθ解答：锯齿ADPCB+锯齿DAPBC ；得证A总结：①辅助线：过拐点作平行线，且有多少个拐点就作多少条平行线 ②所有朝左的角之和等于所有朝右的角之和模型三：臭脚模型基础如图，若CD AB //，E D B ∠∠∠,,之间有什么关系？请证明解答：如图，过点E 作AB l //得证B E D ∠=∠+∠臭脚模型基础（汇总）总结：①辅助线：过拐点作平行线，且有多少个拐点就作多少平行线模型三：臭脚模型进阶如图，直线CD AB //，50,30,90,30=∠=∠=∠=∠CNP HMN FGH EFA ，则GHM ∠的大小是解答：①方法一：如图，过点H 作AB QH //则有铅笔头AFGHQ+臭脚QHMNC 得证 40=∠GHM ②方法二：锯齿BFGHMND 得证40=∠GHM 总结：①辅助线：过拐点作平行线，且有多少个拐点就作多少平行线模型四：蛇型基础如图，若D C B CD AB ∠∠∠,,,//之间有什么关系？请证明解答：过点C 作AB l //得证180=∠-∠+∠D C B 总结：①辅助线：过拐点作平行线，且有多少个拐点就作多少平行线模型五：蜗牛模型基础如图，若D C B DE AB ∠∠∠,,,//之间有什么关系？请证明解答：过点C 作AB l //得证180=∠+∠+∠D C B 总结：①辅助线：过拐点作平行线，且有多少个拐点就作多少平行线。
平行线四种常见模型解题技巧(解析版)--2024年新八年级数学
平行线四种常见模型解题技巧题型聚焦题型一：“猪蹄”模型题型二：“铅笔”模型题型三：“鸡翅”模型题型四：“骨折”模型难题突破模型一：“猪蹄”模型如图，若AB⎳CD，你能确定∠B、∠D与∠BED的大小关系吗？解：∠B+∠D=∠DEB．理由如下：过点E 作 EF⎳AB又 ∵AB⎳CD．∴EF⎳CD．∴∠D=∠DEF．∠B=∠BEF．∴∠B+∠D=∠BEF+∠DEF=∠DEB即∠B+∠D=∠DEB．猪蹄模型的基本特征：一组平行线，中间有一个点，分别与平行线上的点构成“猪蹄”。
如图，已知AB∥CD，求∠E、∠B、∠D之间的数量关系．思路1：过拐点作平行线过点E作EF∥AB，∴∠B=∠BEF，又∵AB∥CD，∴EF∥CD，∴∠D=∠DEF，∴∠E=∠BEF+∠DEF=∠B+∠D．∴∠E=∠B+∠D．思路2：延长BE交CD于点F∵AB∥CD，∴∠B=∠BFD，∴∠D+∠BFD=∠BED，∴∠B+∠D=∠E．小结证明的方法还有很多，同学们可以多多尝试。
重点在于构造平行线的三线八角，就可以得到经典结论：猪蹄模型顶点在同一侧的角之和等于顶点在另一侧的角之和。
猪蹄模型(又名燕尾模型、M字模型)结论：∠B+∠D=∠E步骤总结步骤一：过猪蹄(拐点)作平行线步骤二：借助平行线的性质找相等或互补的角步骤三：推导出角的数量关系模型二、“铅笔”模型如图，AB⎳CD，探索∠B、∠D与∠DEB的大小关系？解：∠B+∠D+∠DEB=360°．理由如下：过点E 作 EF⎳AB．又 ∵AB⎳CD．∴EF⎳CD．∴∠B+∠BEF=180°．∠D+∠DEF=180°．∴∠B+∠D+∠DEB=∠B+∠D+∠BEF+∠DEF=360°．即∠B+∠D+∠DEB=360°．从猪蹄模型可以看出，点E是凹进去了，如果点E是凸出来，如下图：那么，像这样的模型，我们就称为铅笔头模型。
模型结论：∠B+∠E+∠D=360°二、模型证明如图，若AB⎳CD，求证：∠B+∠E+∠D=360°证明一：如图，过点E作FG⎳AB∵ AB⎳FG，AB⎳CD∴ FG⎳CD∵ AB⎳FG∴∠BEF+∠B=180°(两直线平行，同旁内角互补)∵FG⎳CD∴ ∠D+∠DEF=180°(两直线平行，同旁内角互补)∴ ∠BEF+∠B+∠D+∠DEF=360°∴∠B+∠D+∠BED=360°证明二：如图，连接BD，∵AB⎳CD∴∠ABD+∠BDC=180°在△BDE中，∠DBE+∠E+∠EDB=180°∴ ∠DBE+∠E+∠EDB+∠ABD+∠BDC=360°∴ ∠ABD+∠DBE+∠E+∠EDB+∠BDC=360°∴∠ABE+∠E+∠CDE=360°证明该模型结论的还有其他方法，这里就没有全部写出来，可以自行证明。
平行线知识点四大模型
平行线四大模型平行线的判定与性质l、平行线的判定根据平行线的定义，如果平面内的两条直线不相交，就可以判断这两条直线平行，但是，由于直线无限延伸，检验它们是否相交有困难，所以难以直接根据定义来判断两条直线是否平行，这就需要更简单易行的判定方法来判定两直线平行．判定方法l：两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行．简称：同位角相等，两直线平行．判定方法2：两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行．简称：内错角相等，两直线平行，判定方法3：两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行．简称：同旁内角互补，两直线平行，如上图：若已知∠1=∠2，则AB∥CD（同位角相等，两直线平行）；若已知∠1=∠3，则AB∥CD（内错角相等，两直线平行）；若已知∠1+ ∠4= 180°，则AB∥CD（同旁内角互补，两直线平行）．平行公理推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行．2、平行线的性质利用同位角相等，或者内错角相等，或者同旁内角互补，可以判定两条直线平行．反过来，如果已知两条直线平行，当它们被第三条直线所截，得到的同位角、内错角、同旁内角也有相应的数量关系，这就是平行线的性质．性质1：两条平行线被第三条直线所截，同位角相等．简称：两直线平行，同位角相等性质2：两条平行线被第三条直线所截，内错角相等.简称：两直线平行，内错角相等性质3：两条平行线被第三条直线所截，同旁内角互补．简称：两直线平行，同旁内角互补本讲进阶平行线四大模型点P在EF右侧，在AB、CD内部“铅笔”模型结论1：若AB∥CD，则∠P+∠AEP+∠PFC=3 60°；结论2：若∠P+∠AEP+∠PFC= 360°，则AB∥CD.模型二“猪蹄”模型（M模型）点P在EF左侧，在AB、CD内部“猪蹄”模型结论1：若AB∥CD，则∠P=∠AEP+∠CFP；结论2：若∠P=∠AEP+∠CFP，则AB∥CD.模型三“臭脚”模型点P在EF右侧，在AB、CD外部“臭脚”模型结论1：若AB∥CD，则∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP；结论2：若∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP，则AB∥CD.模型四“骨折”模型·点P在EF左侧，在AB、CD外部“骨折”模型结论1：若AB∥CD，则∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP；结论2：若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP，则AB∥CD.巩固练习平行线四大模型证明（1）已知AE // CF ,求证∠P +∠AEP +∠PFC = 360°. （2）已知∠P=∠AEP+∠CFP，求证AE∥CF．（3）已知AE∥CF，求证∠P=∠AEP-∠CFP.（4）已知∠P= ∠CFP -∠AEP ,求证AE //CF .模块一平行线四大模型应用例1（1）如图，a∥b,M、N分别在a、b上，P为两平行线间一点，那么∠l+∠2+∠3= ．(2)如图，AB∥CD，且∠A=25°，∠C=45°，则∠E的度数是．(3)如图，已知AB∥DE，∠ABC=80°，∠CDE =140°，则∠BCD= .(4) 如图，射线AC∥BD，∠A= 70°，∠B= 40°，则∠P= ．.练(1)如图所示，AB∥CD，∠E=37°，∠C= 20°，则∠EAB的度数为．(2) 如图，AB∥CD，∠B=30°，∠O=∠C．则∠C= ..例2如图，已知AB∥DE，BF、DF分别平分∠ABC、∠CDE，求∠C、∠F的关系.练如图，已知AB ∥DE ，∠FBC =n 1∠ABF ，∠FDC =n1∠FDE . (1)若n =2,直接写出∠C 、∠F 的关系 ； (2)若n =3，试探宄∠C 、∠F 的关系；(3)直接写出∠C 、∠F 的关系 （用含n 的等式表示）.例3如图，已知AB∥CD，BE平分∠ABC，DE平分∠ADC．求证：∠E= 2 (∠A+∠C) .练如图，己知AB∥DE，BF、DF分别平分∠ABC、∠CDE，求∠C、∠F的关系.例4如图，∠3==∠1+∠2，求证：∠A+∠B+∠C+∠D= 180°．练（武昌七校2015-2016 七下期中）如图，AB⊥BC，AE平分∠BAD交BC于E，AE⊥DE，∠l+∠2= 90°，M、N分别是BA、CD的延长线上的点，∠EAM和∠EDN的平分线相交于点F则∠F的度数为（）．A. 120°B. 135°C. 145°D. 150°模块二平行线四大模型构造例5如图，直线AB∥CD，∠EFA= 30°，∠FGH= 90°，∠HMN=30°，∠CNP= 50°，则∠GHM= .练如图，直线AB∥CD，∠EFG =100°，∠FGH =140°，则∠AEF+ ∠CHG= .例6 已知∠B =25°，∠BCD=45°，∠CDE =30°，∠E=l0°，求证：AB∥EF．练已知AB∥EF，求∠l-∠2+∠3+∠4的度数.(1)如图(l)，已知MA1∥NA n，探索∠A1、∠A2、…、∠A n，∠B1、∠B2…∠B n-1之间的关系．(2)如图(2)，己知MA1∥NA4，探索∠A1、∠A2、∠A3、∠A4，∠B1、∠B2之间的关系．(3)如图(3)，已知MA1∥NA n，探索∠A1、∠A2、…、∠A n之间的关系．如图所示，两直线AB∥CD平行，求∠1+∠2+∠3+∠4+∠5+∠6．。
平行线的判定模型
平行线的判定模型
1.同位角判定法：如果两条直线被一条横线（称为横截线）所截，且同位角相等，则这两条直线是平行的。
2.内错角判定法：如果两条直线被一条横线所截，且内错角互补（和为180度），则这两条直线是平行的。
3.副交角判定法：如果两条直线被一对平行线所截，副交角相等，则这两条直线是平行的。
4.斜率判定法：如果两条直线的斜率相等，则这两条直线是平行的。
注意，这个判定法只适用于不垂直的直线，对于垂直的直线则斜率不存在。
其中，同位角判定法和内错角判定法基于直线与横截线的相交关系，而副交角判定法基于直线与平行线的相交关系。
这些判定模型是基于几何性质和角度的推理，可以用于判断平行关系的成立或者非成立。
需要注意的是，这些判定模型只适用于二维空间中的直线和平行线判定，而对于三维空间中的直线和平行线，还需要借助向量的概念和性质进行判断。
同时，这些判定模型是根据平行线的定义和性质推导出来的，可以作为判断平行关系的依据，但并非绝对准确，必须根据具体问题和情境进行判断和验证。
平行线四大模型(归纳总结)
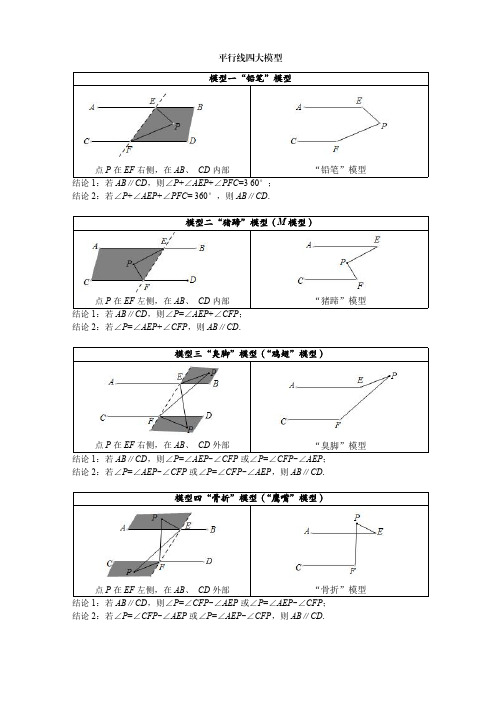
点 P 在 EF 左侧，在 AB、 CD 外部
“骨折”模型
结论 1：若 AB∥CD，则∠P=∠CFP-∠AEP 或∠P=∠AEP-∠CFP；
结论 2：若∠P=∠CFP-∠AEP 或∠P=∠AEP-∠CFP，则 AB∥CD.
【发散思维】
图 1： 180
图 2： 180
图 3： 180
“猪蹄”模型
模型三“臭脚”模型（“鸡翅”模型）
点 P 在 EF 右侧，在 AB、 CD 外部
“臭脚”模型
结论 1：若 AB∥CD，则∠P=∠AEP-∠CFP 或∠P=∠CFP-∠AEP；
结论 2：若∠P=∠AEP-∠CFP 或∠P=∠CFP-∠AEP，则 AB∥CD.
模型四“骨折”模型（“鹰嘴”模型）
图 4： 180
图 5： 180 图 6： 180
【探索发现】
思考 1：
1 +2 ++ n 与 1+2 ++ n1 的关系?
思考 2：
1+2 ++ n =
.
平行线四大模型 模、 CD 内部 结论 1：若 AB∥CD，则∠P+∠AEP+∠PFC=3 60°； 结论 2：若∠P+∠AEP+∠PFC= 360°，则 AB∥CD.
“铅笔”模型
模型二“猪蹄”模型（M 模型）
点 P 在 EF 左侧，在 AB、 CD 内部 结论 1：若 AB∥CD，则∠P=∠AEP+∠CFP； 结论 2：若∠P=∠AEP+∠CFP，则 AB∥CD.
平行线四大模型
平行线四大模型1、平行线的判定根据平行线的定义，如果平面内的两条直线不相交，就可以判断这两条直线平行，但是，由于直线无限延伸，检验它们是否相交有困难，所以难以直接根据定义来判断两条直线是否平行，这就需要更简单易行的判定方法来判定两直线平行．判定方法1：两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行．简称：同位角相等，两直线平行．判定方法2：两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行．简称：内错角相等，两直线平行，判定方法3：两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行．简称：同旁内角互补，两直线平行，如上图：若已知∠1=∠2，则AB∥CD（同位角相等，两直线平行）；若已知∠1=∠3，则AB∥CD（内错角相等，两直线平行）；若已知∠1+∠4=180°，则AB∥CD（同旁内角互补，两直线平行）．另有平行公理推论也能证明两直线平行：平行公理推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行．2、平行线的性质利用同位角相等，或者内错角相等，或者同旁内角互补，可以判定两条直线平行．反过来，如果已知两条直线平行，当它们被第三条直线所截，得到的同位角、内错角、同旁内角也有相应的数量关系，这就是平行线的性质．性质1：两条平行线被第三条直线所截，同位角相等．简称：两直线平行，同位角相等性质2：两条平行线被第三条直线所截，内错角相等.简称：两直线平行，内错角相等性质3：两条平行线被第三条直线所截，同旁内角互补．简称：两直线平行，同旁内角互补平移3.平移是指在平面内，将一个图形沿着某个方向移动一定的距离，这样的图形运动叫做图形的平移（translation），简称平移。
4.平移的性质经过平移，对应线段平行（或共线）且相等，对应角相等，对应点所连接的线段平行且相等；平移变换不改变图形的形状、大小和方向(平移前后的两个图形是全等形)。
（1）图形平移前后的形状和大小没有变化，只是位置发生变化;（2）图形平移后，对应点连成的线段平行且相等（或在同一直线上）（3）多次平移相当于一次平移。
平行线中的核心模型
平行线中核心模型【知识要点】模型一“铅笔”模型点P在EF右侧，在AB、CD内部“铅笔”模型结论1：若AB∥CD，则∠P+∠AEP+∠PFC=3 60°；模型二“猪蹄”模型（M模型）点P在EF左侧，在AB、CD内部“猪蹄”模型结论1：若AB∥CD，则∠P=∠AEP+∠CFP；模型三“臭脚”模型点P在EF右侧，在AB、CD外部“臭脚”模型结论1：若AB∥CD，则∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP；结论2：若∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP，则AB∥CD.点P在EF左侧，在AB、CD外部“骨折”模型结论1：若AB∥CD，则∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP；结论2：若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP，则AB∥CD.【典例精析】（一）平行线四大模型证明（1）已知AE // CF ,求证∠P +∠AEP +∠PFC = 360°.（2）已知∠P=∠AEP+∠CFP，求证AE∥CF．（3）已知AE∥CF，求证∠P=∠AEP-∠CFP.（4）已知∠P= ∠CFP -∠AEP ,求证AE //CF .（二）平行线四大模型应用例1：（1）如图，a∥b,M、N分别在a、b上，P为两平行线间一点，那么∠l+∠2+∠3= ．(2)如图，AB∥CD，且∠A=25°，∠C=45°，则∠E的度数是．(3)如图，已知AB ∥DE ，∠ABC =80°，∠CDE =140°，则∠BCD = .(4) 如图，射线AC ∥BD ，∠A = 70°，∠B = 40°，则∠P = ．练习：(1)如图所示，AB ∥CD ，∠E =37°，∠C = 20°，则∠EAB 的度数为 ．(2) 如图，AB ∥CD ，∠B =30°，∠O =∠C ．则∠C = .例2：如图，已知AB ∥DE ，BF 、 DF 分别平分∠ABC 、∠CDE ，求∠C 、 ∠F 的关系.练习：如图，已知AB ∥DE ，∠FBC =n 1∠ABF ，∠FDC =n1∠FDE . (1)若n =2,直接写出∠C 、∠F 的关系 ； (2)若n =3，试探宄∠C 、∠F 的关系；(3)直接写出∠C 、∠F 的关系 （用含n 的等式表示）.例3：如图，已知AB∥CD，BE平分∠ABC，DE平分∠ADC．求证：∠E= 2 (∠A+∠C) .练习：如图，己知AB∥DE，BF、DF分别平分∠ABC、∠CDE，求∠C、∠F的关系.例4：如图，∠3==∠1+∠2，求证：∠A+∠B+∠C+∠D= 180°．练习：如图，AB⊥BC，AE平分∠BAD交BC于E，AE⊥DE，∠l+∠2= 90°，M、N分别是BA、CD的延长线上的点，∠EAM和∠EDN的平分线相交于点F则∠F的度数为（）．A. 120°B. 135°C. 145°D. 150°（三）平行线四大模型构造例5：如图，直线AB∥CD，∠EFA= 30°，∠FGH= 90°，∠HMN=30°，∠CNP= 50°，则∠GHM= .练习：如图，直线AB∥CD，∠EFG =100°，∠FGH =140°，则∠AEF+ ∠CHG= .例6：已知∠B =25°，∠BCD=45°，∠CDE =30°，∠E=l0°，求证：AB∥EF．练习：(1)已知AB∥EF，求∠l-∠2+∠3+∠4的度数.(2)如图(1)，已知MA1∥NA n，探索∠A1、∠A2、…、∠A n，∠B1、∠B2…∠B n-1之间的关系．如图(2)，己知MA1∥NA4，探索∠A1、∠A2、∠A3、∠A4，∠B1、∠B2之间的关系．如图(3)，已知MA1∥NA n，探索∠A1、∠A2、…、∠A n之间的关系．(3)如图所示，两直线AB∥CD平行，求∠1+∠2+∠3+∠4+∠5+∠6．课后作业1.如图，AB // CD // EF , EH ⊥CD 于H ,则∠BAC +∠ACE +∠CEH 等于( ).A . 180°B . 270°C . 360°D . 450° 2．（武昌七校2015-2016七下期中） 若AB ∥CD ，∠CDF =32∠CDE ，∠ABF =32∠ABE ，则∠E ：∠F =( )．A ．2:1B ．3:1C ．4:3D ．3:23.如图3，己知AE ∥BD ，∠1=130°，∠2=30°，则∠C = .4.如图，已知直线AB ∥CD ，∠C =115°，∠A = 25°，则∠E = ．5．如阁所示，AB ∥CD ，∠l =l l 0°，∠2=120°，则∠α= .6．如图所示，AB ∥DF ，∠D =116°，∠DCB =93°，则∠B = .7．如图，将三角尺的直角顶点放在直线a上，a∥b.∠1=50°，∠2 =60°，则∠3的度数为 .8．如图，AB∥CD，EP⊥FP, 已知∠1=30°，∠2=20°．则∠F的度数为．9.如图，若AB∥CD，∠BEF=70°，求∠B+∠F+∠C的度数.10．已知，直线AB∥CD．(1)如图l，∠A、∠C、∠AEC之间有什么关系？请说明理由；（2）如图2，∠AEF、∠EFC、∠FCD之间有什么关系？请说明理由；(3)如图3，∠A 、∠E 、∠F 、∠G 、∠H 、∠O 、∠C 之间的关是 .挑战压轴题如图1，直线AB ∥CD ，P 是截线MN 上的一点，MN 与CD 、AB 分别交于E 、F ． (1) 若∠EFB =55°，∠EDP = 30°，求∠MPD 的度数；(2) 当点P 在线段EF 上运动时，∠CPD 与∠ABP 的平分线交于Q ,问：DPBQ∠∠是否为定值？若是定值，请求出定值；若不是，说明其范围；(3) 当点P 在线段EF 的延长线上运动时，∠CDP 与∠ABP 的平分线交于Q ，问DPBQ∠∠的值足否定值，请在图2中将图形补充完整并说明理由．。
平行线有关模型汇总
直线平行的条件和性质1. 猪蹄模型已知：如图，AB ∥CD ，求证：∠B+∠D=∠BED 。
2. 铅笔模型如图,已知: CD AB ∥,求证: ∠+B ∠D +∠=BED 360°. (至少用三种方法)3. 其他4. 角平分线如图1，在ABC ∆中,BE 平分,ABC CE ∠平分ACB ∠.若80A ∠=︒，则BEC ∠= ;若A n ∠=︒，求BEC ∠用含n 的代数式表示)如图3，在ABC ∆中，BO 平分外角,CBD CO ∠平分外角BCE ∠.若A n ∠=︒，求BOC ∠.如图5，在ABC ∆中，BE 平分ABC ∠, CE 平分外角ACM ∠.若A n ∠=︒，求BEC ∠.5. “8”字形 如图b 所示的“”字型，其也存在着一个等式：1+2=3+4∠∠∠∠，请证明；6. “A ”字型如图a 所示的“”字型，我们可称其为“A 字型”或“塔形”，其存在一个等式：1+2=3+4∠∠∠∠，请证明；7. 燕尾形如图c所示，其也存在着如下等式：D A B C∠=∠+∠+∠，请证明一．考点：平行线的性质，角度的计算与证明．二．重难点：常见的几种两条直线平行的结论1．两条平行线被第三条直线所截，一组同位角的角平分线平行；2．两条平行线被第三条直线所截，一组内错角的角平分线平行；3．两条平行线被第三条直线所截，一组同旁内角的角平分线垂直．三．易错点：1．性质是由图形的“位置关系”决定“数量关系”；2．两条平行线之间的距离其实可看成点到直线的距离．题型一：猪蹄模型例1. 如图，直线a∥b，直角三角形ABC的顶点B在直线a上，∠C=90°，∠β=55°，则∠α的度数为（）A． 15° B． 25° C． 35° D． 55°题型二：铅笔模型∠+∠+∠+∠=（）例2. 如图，AB∥CD，A E F CA ． 180°B ． 360°C ． 540°D ． 720°题型三：铅笔、猪蹄模型综合压轴例3. 某学习小组发现一个结论：已知直线a ∥b ，若直线c ∥a ，则c ∥b ．他们发现这个结论运用很广，请你利用这个结论解决以下问题：已知直线AB ∥CD ，点E 在AB 、CD 之间，点P 、Q 分别在直线AB 、CD 上，连接PE 、EQ ． （1）如图1，运用上述结论，探究∠PEQ 与∠APE +∠CQE 之间的数量关系，并说明理由； （2）如图2，PF 平分∠BPE ，QF 平分∠EQD ，当∠PEQ ＝140°时，求出∠PFQ 的度数； （3）如图3，若点E 在CD 的下方，PF 平分∠BPE ，QH 平分∠EQD ，QH 的反向延长线交PF 于点F ．当∠PEQ ＝70°时，请求出∠PFQ 的度数．题型三：其他例4. （周练）如图，已知AB ∥CD ，则∠A 、∠C 、∠P 的关系为.FE DCBA练习1. 如图，若AB∥CD，则α、β、γ之间的关系为．题型四：翻折例5. 如图所示，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置，若∠EFB=65°，则∠AED′等于______例6. 如图，将四边形纸片ABCD沿MN折叠，点A、D分别落在点A1、D1处．若∠1＋∠2＝140°，则∠B＋∠C＝°．题型五：角平分线例7. 如图，在△ABC中，∠ABC与∠ACB的平分线交于点O．（1）如图1，已知∠ABC＝40°，∠ACB＝60°，求∠BOC的度数．（2）如图2，已知∠A＝90°，求∠BOC的度数．（3）如图1，设∠A＝m°，求∠BOC的度数．例8. 如图13, 1BA 和1CA 分别是ABC ∆的内角平分线和外角平分线，2BA 是1A BD ∠的角平分线，2CA 是1A CD ∠的角平分线，3BA 是2A BD ∠的角平分线，3CA 是2A CD ∠的角平分线，若A α∠=，则2018A ∠为 .1. 如图，∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F 的度数为（ ）A ．180°B ．360°C ．540°D ．720°2. 如图，将ABC ∆纸片沿DE 折叠，使点A 落在点'A 处，且'A B 平分ABC ∠，'A C 平分ACB ∠，若'110BA C ∠=︒，则12∠+∠的度数为（ ） A. 80° B. 90° C. 100° D. 110°3. 如图，将矩形纸带ABCD ，沿EF 折叠后，C 、D 两点分别落在C ′、D ′的位置，经测量得∠EFB=65°，则∠AED ′的度数是（ ）A ． 65°B ． 55°C ． 50°D ． 25°4. 如图，已知30B ∠=︒，55BCD ∠=︒，45CDE ∠=︒，20E ∠=︒，求证：AB ∥CD ．AFBC ED3.5. 如图，已知AB ∥DE ，BF ，EF 分别平分∠ABC 与∠CED ，若140BCE ∠=︒，求BFE ∠的度数．1. 如图，ABCDE 是封闭折线，则∠A 十∠B ＋∠C ＋∠D ＋∠E 为_______度．2. 如图，△ABE 和△ACD 是△ABC 分别沿着AB ，AC 边翻折180°形成的，若∠BAC ＝150°，则∠θ的度数是_______．3. 如图，在△ABC 中，∠C ＝90°．若BD ∥AE ，∠DBC ＝20°，则∠CAE 的度数是A ．40°B ．60°C ．70°D ．80° 4. 如图，把矩形沿对折后使两部分重合，若，则=（ ）A ．110°B ．115°C ．120°D ．130°A BCD E1.如图所示，将△ABC沿着DE翻折，若∠1+∠2=80°，则∠B=____度．2. 如图，若AB∥CD，BF平分∠ABE，DF平分∠CDE，∠BED=70o，则∠BFD=________．3. 将一张长方形纸片如图所示折叠后，再展开．如果∠1=55o，那么∠2等于( )A．55o B．60o C．65o D．70o4. 问题情境：如图1，AB∥CD，∠PAB＝130°，∠PCD＝120°．求∠APC度数．小明的思路是：如图2，过P作PE∥AB，通过平行线性质，可得∠APC＝50°+60°＝110°．问题迁移：（1）如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP ＝∠α，∠BCP＝∠β．∠CPD、∠α、∠β之间有何数量关系？请说明理由；（2）在（1）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出∠CPD、∠α、∠β间的数量关系．5. 在△ABC中，∠A＝40°（1）如图1，若两内角∠ABC、∠ACB的角平分线交于点P，则∠P＝，∠A与∠P 之间的数量关系是．为什么有这样的关系？请证明它；（2）如图2，若内角∠ABC、外角∠ACE的角平分线交于点P，则∠P＝，∠A与∠P 之间的数量关系是；（3）如图3，若两外角∠EBC、∠FCB的角平分线交于点P，则∠P＝，∠A与∠P 之间的数量关系是．6. 【探究发现】如图1，在△ABC中，点P是内角∠ABC和外角∠ACD的角平分线的交点，试猜想∠P与∠A 之间的数量关系，并证明你的猜想．【迁移拓展】如图2，在△ABC中，点P是内角∠ABC和外角∠ACD的n等分线的交点，即∠PBC＝∠ABC，∠PCD＝∠ACD，试猜想∠P与∠A之间的数量关系，并证明你的猜想．【应用创新】已知，如图3，AD、BE相交于点C，∠ABC、∠CDE、∠ACE的角平分线交于点P，∠A＝35°，∠E＝25°，则∠BPD＝．。
七年级数学下册专题01 平行线的四大模型(原卷版)-7年级数学下册压轴题攻略(人教版)
专题01 平行线的四大模型平行线的性质和判定是证明角相等、研究角的关系的重要依据，是研究几何图形位置关系与数量关系的基础，是平面几何的一个重要内容和学习简单的逻辑推理的素材。
它不但为三角形的内角和定理的证明提供了转化的方法，而且也是今后学习三角形、四边形知识的基础.本节课重点学习平行线的基础模型的应用迁移.模型一“铅笔”模型点P在EF右侧，在AB、CD内部“铅笔”模型结论1：若AB∥CD，则∠P+∠AEP+∠PFC=3 60°；结论2：若∠P+∠AEP+∠PFC= 360°，则AB∥CD.专题分析模型分类模型分析【典例1】（2023秋•南岗区校级期中）已知，射线FG分别交射线AB、DC于点F、G，点E为射线FG上一点．（1）如图1，若∠A+∠D＝∠AED，求证：AB∥CD．（2）如图2，若AB∥CD，求证：∠A﹣∠D＝∠AED．（3）如图3，在（2）的条件下，DI交AI于点Ⅰ，交AE于点K，∠EDI＝∠CDE，∠BAI＝∠EAI，∠I＝∠AED＝25°，求∠EKD的度数．【变式1-1】（2023•渝中区校级模拟）如图，已知直线a∥b，∠BAC＝90°，∠1＝40°，则∠2的度数为（）A．40°B．50°C．130°D．140°典例分析【变式1-2】（2023•金安区一模）如图，已知a∥b，∠1＝45°，∠2＝125°，则∠ABC的度数为（）A．100°B．105°C．115°D．125°【变式1-3】（2022春•肇州县期末）如图，AB∥CD，∠C＝110°，∠B＝120°，则∠BEC ＝（）A．110°B．120°C．130°D．150°【变式1-4】（2023春•巴南区月考）已知直线MN∥PQ，点C、B分别在直线MN、PQ上，点A在直线MN和PO之间．（1）如图1，求证：∠CAB﹣∠MCA＝∠PBA；（2）如图2，CD∥AB，点E在直线PQ上，且∠MCA＝∠DCE，求证：∠ECN＝∠CAB；（3）如图3，BF平分∠PBA，CG平分∠ACN，且AF∥CG．若∠CAB＝50°，直接写出∠AFB的度数．【变式1-5】（2023春•遂宁期末）如图，直线PQ∥MN，两个三角形如图①放置，其中∠ABC ＝∠CDE＝90°，∠ACB＝30°，∠BAC＝60°，∠DCE＝∠DEC＝45°，点E在直线PQ上，点B，C均在直线MN上，且CE平分∠ACN．（1）求∠DEQ的度数；（2）如图②，若将△ABC绕B点以每秒3°的速度按逆时针方向旋转（A，C的对应点分别为F，G）．设旋转时间为t秒，当t＝10时，边BG与CD有何位置关系？请说明理由．模型分析模型二“猪蹄”模型（模型）点P在EF左侧，在AB、CD内部“猪蹄”模型结论1：若AB∥CD，则∠P=∠AEP+∠CFP；结论2：若∠P=∠AEP+∠CFP，则AB∥CD.典例分析【典例2】（2023春•邵阳县期末）如图，直线AB∥CD，连接EF，直线AB，CD及线段EF 把平面分成①②③④四个部分，规定：线上各点不属于任何部分．当动点G落在某个部分时，连接GE，GF，构成∠EGF，∠GEB，∠GFD三个角．（1）当动点G落在第③部分时，如图一，试说明：∠EGF，∠GEB，∠GFD三者的关系；（2）当动点G落在第②部分时，如图二，思考（1）中三者关系是否仍然成立若不成立，说明理由．【变式2-1】（2023•盘锦）如图，直线AB∥CD，将一个含60°角的直角三角尺EGF按图中方式放置，点E在AB上，边GF，EF分别交CD于点H，K，若∠BEF＝64°，则∠GHC等于（）A．44°B．34°C．24°D．14°【变式2-2】（2023•盘锦）如图，直线AB∥CD，将一个含60°角的直角三角尺EGF按图中方式放置，点E在AB上，边GF，EF分别交CD于点H，K，若∠BEF＝64°，则∠GHC等于（）A．44°B．34°C．24°D．14°【变式2-3】（2023•海南模拟）如图，已知AB∥DE，∠B＝20°，∠D＝130°，那么∠BCD 等于（）A．60°B．70°C．80°D．90°【变式2-4】（2023春•覃塘区期末）如图，AB∥CD，将一副直角三角板作如下摆放，∠GEF ＝60°，∠MNP＝45°．下列结论：①GE∥MP；②∠EFN＝150°；③∠BEF＝65°；④∠AEG＝35°，其中正确的个数是（）A．1B．2C．3D．4【变式2-5】（2023春•赣县区期末）【问题背景】：同学们，观察小猪的猪蹄，你会发现一个熟悉的几何图形，我们就把这个图形的形象称为“猪蹄模型”，猪蹄模型中蕴含着角的数量关系．【问题探究】：（1）如图1，AB∥CD，E为AB、CD之间一点，连接BE、DE，得到∠BED 与∠B、∠D之间的数量关系，并说明理由；【类比迁移】：（2）请你利用上述“猪蹄模型”得到的结论或解题方法，完成下面的问题：如图2，直线AB∥CD，若∠B＝23°，∠G＝35°，∠D＝25°，求∠BEG+∠GFD的度数；【灵活应用】：（3）如图3，直线AB∥CD，若∠E＝∠B＝60°，∠F＝85°，则∠D＝25度．【变式2-6】（2023春•邵阳期末）如图1，直线AB∥CD，P是截线MN上的一点．（1）若∠MNB＝45°，∠MDP＝20°，求∠MPD；（2）如图1，当点P在线段MN上运动时，∠CDP与∠ABP的平分线交于Q，问是否为定值，若是定值，请求出；若不是定值，请说明理由；（3）如图2，若T是直线MN上且位于M点的上方的一点，如图所示，当点P在射线MT上运动时，∠CDP与∠ABP的平分线交于Q，问的值是否和（2）问中的情况一样呢？请你写出探究过程，说明理由．【变式2-7】（2023春•防城港期末）阅读下面材料：（1）小亮同学遇到这样一个问题：已知：如图甲，AB∥CD，E为直线AB，CD之间一点，连接BE、DE得到∠BED．求证：∠BED＝∠B+∠D．下面是小亮写出了该问题的证明，请你帮他把证明过程补充完整．证明：过点E作EF∥AB，则有∠BEF＝∠B，∵AB∥CD，∴CD∥EF，∴∠FED＝∠D，∴∠BED＝∠BEF+∠FED＝∠B+∠D．（2）请你参考小亮思考问题的方法，解决问题：如图乙，直线a∥b，BE平分∠ABC，DE平分∠ADC，若∠ABC＝50°，∠ADC＝60°，求∠BED的度数，（温馨提示：过点E作EF∥AB）模型分析模型三“臭脚”模型“臭脚”模型结论1：若AB∥CD，则∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP；结论2：若∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP，则AB∥CD.典例分析【典例3】（2023春•中山区期末）如图，∠ABE+∠BED＝∠CDE．（1）如图1，求证AB∥CD；（2）如图2，点P在AB上，∠CDP＝∠EDP，BF平分∠ABE，交PD于点F，探究∠BFP，∠BED的数量关系，并证明你的结论；（3）在（2）的条件下，如图3，PQ交ED延长线于点Q，∠DPQ＝2∠APQ，∠PQD ＝80°，求∠CDE的度数．【变式3-1】已知AB∥CD．（1）如图1，求证：∠ABE+∠DCE﹣∠BEC＝180°；（2）如图2，∠DCE的平分线CG的反向延长线交∠ABE的平分线BF于F．若BF∥CE，∠BEC＝26°，求∠BFC．模型分析结论1：若AB∥CD，则∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP；结论2：若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP，则AB∥CD.典例分析【典例4】（2022秋•朝阳区校级期末）已知AB∥CD，点E在AB上，点F在DC上，点G 为射线EF上一点．（1）【基础问题】如图1，试说明：∠AGD＝∠A+∠D．（完成图中的填空部分）证明：过点G作直线MN∥AB，又∵AB∥CD，∴∥CD∵MN∥AB，∴∠＝∠MGA．∵MN∥CD，∴∠D＝（）∴∠AGD＝∠AGM+∠DGM＝∠A+∠D．（2）【类比探究】如图2，当点G在线段EF延长线上时，请写出∠AGD、∠A、∠D三者之间的数量关系，并说明理由．（3）【应用拓展】如图3，AH平分∠GAE，DH交AH于点H，且∠GDH＝2∠HDF，∠HDF＝22°，∠H＝32°，直接写出∠DGA的度数为°．【变式4-1】（2022秋•肃州区校级期末）如图（1），AB∥CD，∠AEP＝40°，∠PFD＝130°，求∠EPF的度数．小明想到了以下方法：解：如图（1），过点P作PM∥AB，∴∠1＝∠AEP＝40°（两直线平行，内错角相等）∵AB∥CD（已知）∴PM∥CD（平行于同一条直线的两直线平行）∴∠2+∠PFD＝180°（两直线平行，同旁内角互补）∵∠PFD＝130°（已知）∴∠2＝180°﹣130°＝50°∴∠EPF＝∠1+∠2＝40°+50°＝90°即∠EPF＝90°【探究】如图（2），AB∥CD，∠AEP＝50°，∠PFC＝120°，求∠EPF的度数．【应用】如图（3），在【探究】的条件下，∠PEA的平分线和∠PFC的平分线交于点G，求∠G的度数．【变式4-2】（2022春•朝阳县期末）学习完平行线的性质与判定之后，我们发现借助构造平行线的方法可以帮我们解决许多问题．（1）小明遇到了下面的问题：如图1，l1∥l2，点P在l1，l2内部，探究∠A，∠APB，∠B的关系，小明过点P作l1的平行线，可得∠APB，∠A，∠B之间的数量关系是：∠APB＝．（2）如图2，若AC∥BD，点P在AC，BD外部，∠A，∠B，∠APB的数量关系是否发生变化？请写出证明过程．【变式4-3】（2020春•乳山市期中）【信息阅读】材料信息：如图①，AB∥DE，点C是直线AB，DE外任意一点，连接BC，DC．方法信息：如图②，在“材料信息”的条件下，∠B＝55°，∠D＝35°，求∠BCD的度数．解：过点C作CF∥AB．∴∠BCF＝∠B＝55°．∵AB∥DE，∴CF∥DE．∴∠DCF＝∠D＝35°．∴∠BCD＝55°﹣35°＝20°．【问题解决】（1）通过【信息阅读】，猜想：∠B，∠D，∠BCD之间有怎样的等量关系？请直接写出结论：；（2）如图③，在“材料信息”的条件下，改变点C的位置，∠B，∠D，∠BCD之间的等量关系是否改变？若不改变，请写出理由；若改变，请写出新的等量关系及理由．1.（2023春•建昌县期末）如图，将一个含30°角的直角三角板的直角顶点C放在直尺的两边MN，PQ之间，则下列结论中：①∠1＝∠3；②∠2＝∠3；③∠1+∠3＝90°；④若∠3＝60°，则AB⊥PQ，其中正确结论的个数是（）A．1个B．2个C．3个D．4个2．（2023春•芜湖期末）如图所示是汽车灯的剖面图，从位于O点灯发出光照射到凹面镜上反射出的光线BA，CD都是水平线，若∠ABO＝α，∠DCO＝60°，则∠BOC的度数为（）A．180°﹣αB．120°﹣αC．60°+αD．60°﹣α3．（2022•恩施州）已知直线l1∥l2，将含30°角的直角三角板按如图所示摆放．若∠1＝120°，则∠2＝（）A．120°B．130°C．140°D．150°4．（2022•博山区一模）如图，直线a∥b，点M、N分别在直线a、b上，P为两平行线间一点，那么∠1+∠2+∠3等于（）A．360°B．300°C．270°D．180°5．（2021春•椒江区校级月考）如图，已知AB∥CD，∠BAD和∠BCD的平分线交于点E，∠FBC＝n°，∠BAD＝m°，则∠AEC等于（）度．A．90﹣+m B．90﹣﹣C．90﹣D．90﹣+ 6．（2023春•赫山区期末）【问题情景】（1）如图1，AB∥CD，∠P AB＝135°，∠PCD＝115°，求∠APC的度数；【问题迁移】（2）如图2，已知∠MON，AD∥BC，点P在射线OM上运动，当点P在A，B两点之间运动时，连接PD，PC，∠ADP＝∠α，∠BCP＝∠β，求∠CPD与∠α，∠β之间的数量关系，并说明理由；【知识拓展】（3）在（2）的条件下，若将“点P在A，B两点之间运动”改为“点P在A，B两点外侧运动（点P与点A，B，O三点不重合）”其他条件不变，请直接写出∠CPD 与∠α，∠β之间的数量关系．7．（2022春•良庆区校级期中）已知AM∥CN，点B为平面内一点，AB⊥BC于B．（1）如图1，直接写出∠A和∠C之间的数量关系；（2）如图2，过点B作BD⊥AM于点D，求证：∠ABD＝∠C；（3）如图3，在（2）问的条件下，点E、F在DM上，连接BE、BF、CF，BF平分∠DBC，BE平分∠ABD，若∠FCB＝∠CFD，∠BFC＝3∠DBE，求∠EBC的度数．8．（2021秋•平昌县期末）如图，AD∥BC，∠BAD的平分线交BC于点G，∠BCD＝90°．（1）试说明：∠BAG＝∠BGA；（2）如图1，点F在AG的反向延长线上，连接CF交AD于点E，若∠BAG﹣∠F＝45°，求证：CF平分∠BCD．（3）如图2，线段AG上有点P，满足∠ABP＝3∠PBG，过点C作CH∥AG．若在直线AG上取一点M，使∠PBM＝∠DCH，求的值．9．（2023春•黑山县期中）问题情境我们知道，“两条平行线被第三条直线所截，同位角相等，内错角相等，同旁内角互补”，所以在某些探究性问题中通过“构造平行线”可以起到转化的作用．已知三角板ABC中，∠BAC＝60°，∠B＝30°，∠C＝90°，长方形DEFG中，DE∥GF．问题初探（1）如图（1），若将三角板ABC的顶点A放在长方形的边GF上，BC与DE相交于点M，AB⊥DE于点N，求∠EMC的度数．分析：过点C作CH∥GF．则有CH∥DE，从而得∠CAF＝∠HCA，∠EMC＝∠MCH，从而可以求得∠EMC的度数．由分析得，请你直接写出：∠CAF的度数为，∠EMC的度数为．类比再探（2）若将三角板ABC按图（2）所示方式摆放（AB与DE不垂直），请你猜想写∠CAF 与∠EMC的数量关系，并说明理由．（3）请你总结（1），（2）解决问题的思路，在图（3）中探究∠BAG与∠BMD的数量关系？并说明理由．10．（2022春•龙亭区校级期末）如图，已知AB∥CD，E、F分别在AB、CD上，点G在AB、CD之间，连接GE、GF．（1）当∠BEG＝40°，EP平分∠BEG，FP平分∠DFG时：①如图1，若EG⊥FG，则∠P的度数为；②如图2，在CD的下方有一点Q，EG平分∠BEQ，FD平分∠GFQ，求∠Q+2∠P的度数；（2）如图3，在AB的上方有一点O，若FO平分∠GFC．线段GE的延长线平分∠OEA，则当∠EOF+∠EGF＝100°时，请直接写出∠OEA与∠OFC的数量关系．11．（2023春•孝义市期末）综合与探究数学活动课上，老师以“一个含45°的直角三角板和两条平行线”为背景展开探究活动，如图1，已知直线m∥n，直角三角板ABC中，∠ACB＝90°，∠BAC＝∠ABC＝45°．（1）如图1，若∠2＝65°，则∠1＝；（直接写出答案）（2）“启航”小组在图1的基础上继续展开探究：如图2，调整三角板的位置，当三角板ABC的直角顶点C在直线n上，直线m与AB，AC相交时，他们得出的结论是：∠1﹣∠2＝135°，你认为启航小组的结论是否正确，请说明理由；（3）如图3，受到“启航”小组的启发，“睿智”小组提出的问题是：在图2的基础上，继续调整三角板的位置，当点C不在直线n上，直线m与AC，BC相交时，∠1与∠2有怎样的数量关系？请你用平行线的知识说明理由．12．（2023春•安化县期末）在课后学习中，小红探究平行线中的线段与角的数量关系，如图，直线AB∥CD，点N在直线CD上，点P在直线AB上，点M为平面上任意一点，连接MP，MN，PN．（1）如图1，点M在直线CD上，PM平分∠APN，试说明∠PMN＝∠MPN；（2）如图2，点M在直线AB，CD之间，∠PMN＝70°，∠MNC＝30°，求∠APM的度数；（3）如图3，∠APM和∠MNC的平分线交于点Q，∠PQN与∠PMN有何数量关系？并说明理由．12．（2023春•甘井子区期末）如图1，点M在射线BA，CD之间，0°＜∠ABM＜30°，连接BM，过点M作ME⊥BM交射线CD于点E，且∠MED﹣∠B＝90°．（1）求证：AB∥CD；（2）过点C作∠ECN＝∠B，交直线ME于点N，先按要求画图，再解决下列问题．①当CN在CD上方，满足∠CNE＝5∠B时，在图2中画图，求∠B的度数；②作∠BME的角平分线交射线CD于点K，交∠ECN的角平分线于点F，请直接写出∠MKC与∠MFC之间的数量关系．。
平行线中的四大经典模型(浙教版)(解析版)
平行线中的四大经典模型【浙教版】【模型1 “猪蹄”型（含锯齿型）】1．（2020下·湖北武汉·七年级统考期末）如图，AB∥CD，EF平分∠BED，∠DEF+∠D=66°，∠B−∠D=28°，则∠BED=．【答案】80°【分析】过E点作EM∥AB，根据平行线的性质可得∠BED=∠B+∠D，利用角平分线的定义可求得∠B+3∠D=132°，结合∠B-∠D=28°即可求解．【详解】解：过E点作EM∥AB，∴∠B=∠BEM，∵AB∥CD，∴EM∥CD，∴∠MED=∠D，∴∠BED=∠B+∠D，∵EF平分∠BED，∴∠DEF=1∠BED，2∵∠DEF+∠D=66°，∠BED+∠D=66°，∴12∴∠BED+2∠D=132°，即∠B+3∠D=132°，∵∠B-∠D=28°，∴∠B=54°，∠D=26°，∴∠BED=80°．故答案为：80°．【点睛】本题主要考查平行线的性质，角平分线的定义，作出辅助线证出∠BED=∠B+∠D是解题的关键．2．（2023上·辽宁鞍山·七年级统考期中）如图，已知AB∥CD，BE平分∠ABC，DE平分∠ADC，∠BAD=80°，∠BCD=n°，则∠BED的度数为．（用含n的式子表示）n°【答案】40°+12【分析】首先过点E作EF∥AB，由平行线的传递性得AB∥CD∥EF，再根据两直线平行，内错角相等，得n°，∠EDC=40°，再由出∠BCD=∠ABC=n°，∠BAD=∠ADC=80°，由角平分线的定义得出∠ABE=12两直线平行，内错角相等得出∠BEF=∠ABE=1n°∠FED=∠EDC=40°，由∠BED=∠BEF+∠FED即可2得出答案．【详解】解：如图，过点E作EF∥AB，则AB∥CD∥EF，∵AB∥CD，∴∠BCD=∠ABC=n°，∠BAD=∠ADC=80°，又∵BE平分∠ABC，DE平分∠ADC，∴∠ABE=12∠ABC=12n°，∠EDC=12∠ADC=12×80°=40°，∵AB∥EF∥CD，∴∠BEF=∠ABE=12n°，∠FED=∠EDC=40°，∴∠BED=∠FED+∠BEF=40°+12n°，故答案为：40°+12n°．【点睛】本题考查平行线的性质，角平分线的定义，解题关键是作出正确的辅助线，掌握平行线的性质和角平分线的定义．3．（2023下·广东河源·七年级河源市第二中学校考期中）已知直线l1∥l2，A是l1上的一点，B是l2上的一点，直线l3和直线l1，l2交于C和D，直线CD上有一点P．(1)如果P点在C，D之间运动时，问∠PAC，∠APB，∠PBD有怎样的数量关系？请说明理由．(2)若点P在C，D两点的外侧运动时（P点与C，D不重合），试探索∠PAC，∠APB，∠PBD之间的关系又是如何？（请直接写出答案，不需要证明）【答案】(1)∠PAC+∠PBD=∠APB(2)当点P在直线l1上方时，∠PBD−∠PAC=∠APB；当点P在直线l2下方时，∠PAC−∠PBD=∠APB．【分析】（1）过点P作PE∥l1，由“平行于同一条直线的两直线平行”可得出PE∥l1∥l2，再由“两直线平行，内错角相等”得出∠PAC=∠APE、∠PBD=∠BPE，再根据角与角的关系即可得出结论；（2）按点P的两种情况分类讨论：①当点P在直线l1上方时；②当点P在直线l2下方时，同理（1）可得∠PAC=∠APE、∠PBD=∠BPE，再根据角与角的关系即可得出结论．【详解】（1）解：∠PAC+∠PBD=∠APB．过点P作PE∥l1，如图1所示．∵PE∥l1，l1∥l2，∴PE∥l1∥l2，∴∠PAC=∠APE，∠PBD=∠BPE，∵∠APB=∠APE+∠BPE，∴∠PAC+∠PBD=∠APB．（2）解：结论：当点P在直线l1上方时，∠PBD−∠PAC=∠APB；当点P在直线l2下方时，∠PAC−∠PBD=∠APB．①当点P在直线l1上方时，如图2所示．过点P作PE∥l1．∵PE∥l1，l1∥l2，∴PE∥l1∥l2，∴∠PAC=∠APE，∠PBD=∠BPE，∵∠APB=∠BPE−∠APE，∴∠PBD−∠PAC=∠APB．②当点P在直线l2下方时，如图3所示．过点P作PE∥l1．∵PE∥l1，l1∥l2，∴PE∥l1∥l2，∴∠PAC=∠APE，∠PBD=∠BPE，∵∠APB=∠APE−∠BPE，∴∠PAC−∠PBD=∠APB．【点睛】本题考查了平行线的性质以及角的计算，解题的关键是根据“两直线平行，内错角相等”找到相等的角．本题属于基础题，难度不大，解决该题型题目时，根据平行线的性质得出相等（或互补）的角是关键．4．（2023下·山东聊城·七年级统考阶段练习）已知直线AB//CD，EF是截线，点M在直线AB、CD之间．(1)如图1，连接GM，HM．求证：∠M＝∠AGM＋∠CHM；(2)如图2，在∠GHC的角平分线上取两点M、Q，使得∠AGM＝∠HGQ．试判断∠M与∠GQH之间的数量关系，并说明理由．【答案】(1)证明见详解(2)∠GQH=180°−∠M；理由见详解【分析】（1）过点M作MN∥AB，由AB∥CD，可知MN∥AB∥CD．由此可知：∠AGM=∠GMN，∠CHM=∠HMN，故∠AGM+∠CHM=∠GMN+∠HMN=∠M；（2）由（1）可知∠AGM+∠CHM=∠M．再由∠CHM=∠GHM，∠AGM＝∠HGQ，可知：∠M=∠HGQ+∠GHM，利用三角形内角和是180°，可得∠GQH=180°−∠M．【详解】（1）解：如图：过点M作MN∥AB，∴MN∥AB∥CD，∴∠AGM=∠GMN，∠CHM=∠HMN，∵∠M=∠GMN+∠HMN，∴∠M=∠AGM+∠CHM．（2）解：∠GQH=180°−∠M，理由如下：如图：过点M作MN∥AB，由（1）知∠M=∠AGM+∠CHM，∵HM平分∠GHC，∴∠CHM=∠GHM，∵∠AGM＝∠HGQ，∴∠M=∠HGQ+∠GHM，∵∠HGQ+∠GHM+∠GQH=180°，∴∠GQH=180°−∠M．【点睛】本题考查了利用平行线的性质求角之间的数量关系，正确的作出辅助线是解决本题的关键，同时这也是比较常见的几何模型“猪蹄模型”的应用．5．（2023下·福建莆田·七年级莆田第二十五中学校考阶段练习）如图，AB//CD，点E在直线AB，CD内部，且AE⊥CE．（1）如图1，连接AC，若AE平分∠BAC，求证：CE平分∠ACD；（2）如图2，点M在线段AE上，①若∠MCE=∠ECD，当直角顶点E移动时，∠BAE与∠MCD是否存在确定的数量关系?并说明理由；∠ECD（n为正整数），当直角顶点E移动时，∠BAE与∠MCD是否存在确定的数量关系?并②若∠MCE=1n说明理由．【答案】（1）见解析；（2）①∠BAE +12∠MCD =90°，理由见解析；②∠BAE +n n+1∠MCD =90°，理由见解析.【分析】（1）根据平行的性质可得∠BAC +∠DCA =180°，再根据AE ⊥CE 可得∠EAC +∠ECA =90°，根据AE 平分∠BAC 可得∠BAE =∠EAC ,等量代换可得∠ECD +∠EAC =90°，继而求得∠DCE =∠ECA ；（2）①过E 作EF ∥AB ，先利用平行线的传递性得出EF ∥AB ∥CD ，再利用平行线的性质及已知条件可推得答案；②过E 作EF ∥AB ，先利用平行线的传递性得出EF ∥AB ∥CD ，再利用平行线的性质及已知条件可推得答案.【详解】（1）解：因为AB//CD ，所以∠BAC +∠DCA =180°，因为AE ⊥CE ，所以∠EAC +∠ECA =90°，因为AE 平分∠BAC ，所以∠BAE =∠EAC ，所以∠BAE +∠DCE =90°，所以∠EAC +∠DCE =90°，所以∠DCE =∠ECA ，所以CE 平分∠ACD ；（2）①∠BAE 与∠MCD 存在确定的数量关系：∠BAE +12∠MCD =90°， 理由如下： 过E 作EF ∥AB ，∵AB∥CD，∴EF∥AB∥CD，∴∠BAE=∠AEF，∠FEC=∠DCE，∵∠E=90°，∴∠BAE+∠ECD=90°，∵∠MCE=∠ECD，∴∠BAE+12∠MCD=90°；②∠BAE与∠MCD存在确定的数量关系：∠BAE+nn+1∠MCD=90°，理由如下：过E作EF∥AB，∵AB∥CD，∴EF∥AB∥CD，∴∠BAE=∠AEF，∠FEC=∠DCE，∵∠E=90°，∴∠BAE+∠ECD=90°，∵∠MCE=1n∠ECD，∴∠BAE+nn+1∠MCD=90°.【点睛】本题主要考查平行线的性质和角平分线的定义，解决本题的关键是要添加辅助线利用平行性质. 6．（2023·全国·七年级专题练习）（1）如图1，已知AB//CD，∠ABF=∠DCE，求证：∠BFE=∠FEC（2）如图2，已知AB//CD，∠EAF=14∠EAB，∠ECF=14∠ECD，求证：∠AFC=34∠AEC【答案】（1）见解析；（2）见解析【分析】（1）如图：延长BF、DC相较于E，由AB//CD可得∠ABF=∠E，再结合∠ABF=∠DCE可得∠DCE=∠E，即可得当BE//DE，最后运用两直线平行、内错角相等即可证明结论；（2）如图2：连接AC，设∠EAF=x，∠ECF=y，∠EAB=4x，∠ECD=4y，根据平行线性质得出∠BAC+∠ACD=180°，求出∠CAE+∠ACE=180°-（4x+4y），再求出∠AEC和∠AFC，最后比较即可得到结论．【详解】（1）证明：如图：延长BF、DC相较于G∵AB//CD∴∠ABF=∠G∵∠ABF=∠DCE∴∠DCE=∠G∴BG//CE∴∠BFE=∠FEC；（2）如图2：连接AC，设∠EAF=x，∠ECF=y，∠EAB=4x，∠ECD=4y，∵AB//CD，∴∠BAC+∠ACD=180°∴∠CAE+4x+∠ACE+4y=180°∴∠CAE+∠ACE=180°-（4x+4y），∠F AC+∠FCA=180°-（3x+3y），∴∠AEC=180°-（∠CAE+∠ACE）=180°-[80°-（4x+4y）]=4x+4y=4（x+y）∠AFC=180°-（∠F AC+∠FCA）=180°-[180°-（3x+3y））]=3x+3y=3（x+y），∴∠AFC=34∠AEC．【点睛】本题主要考查了平行线的判定与性质、三角形内角和定理的应用等知识点，灵活应用平行线的判定与性质以及三角形内角和定理正确的表示角成为解答本题的关键．7．（2017下·湖北武汉·七年级统考期中）如图1，已知AB∥CD，∠B＝30°，∠D＝120°；(1)若∠E＝60°，则∠F＝；(2)请探索∠E与∠F之间满足的数量关系？说明理由；(3)如图2，已知EP平分∠BEF，FG平分∠EFD，反向延长FG交EP于点P，求∠P的度数．【答案】(1)90°(2)∠F=∠E+30°，理由见解析(3)15°【分析】（1）如图1，分别过点E，F作EM//AB，FN//AB，根据平行线的性质得到∠B=∠BEM=30°，∠MEF=∠EFN，∠D+∠DFN=180°，代入数据即可得到结论；（2）如图1，根据平行线的性质得到∠B=∠BEM=30°，∠MEF=∠EFN，由AB//CD，AB//FN，得到CD//FN，根据平行线的性质得到∠D+∠DFN=180°，于是得到结论；（3）如图2，过点F作FH//EP，设∠BEF=2x°，则∠EFD=(2x+30)°，根据角平分线的定义得到∠PEF=1 2∠BEF=x°，∠EFG=12∠EFD=(x+15)°，根据平行线的性质得到∠PEF=∠EFH=x°，∠P=∠HFG，于是得到结论．【详解】（1）解：如图1，分别过点E，F作EM//AB，FN//AB，∴EM//AB//FN，∴∠B=∠BEM=30°，∠MEF=∠EFN，又∵AB//CD，AB//FN，∴CD//FN，∴∠D+∠DFN=180°，又∵∠D=120°，∴∠DFN=60°，∴∠BEF=∠MEF+30°，∠EFD=∠EFN+60°，∴∠EFD=∠MEF+60°∴∠EFD=∠BEF+30°=90°；故答案为：90°；（2）解：如图1，分别过点E，F作EM//AB，FN//AB，∴EM//AB//FN，∴∠B=∠BEM=30°，∠MEF=∠EFN，又∵AB//CD，AB//FN，∴CD//FN，∴∠D+∠DFN=180°，又∵∠D=120°，∴∠DFN=60°，∴∠BEF=∠MEF+30°，∠EFD=∠EFN+60°，∴∠EFD=∠MEF+60°，∴∠EFD=∠BEF+30°；（3）解：如图2，过点F作FH//EP，由（2）知，∠EFD=∠BEF+30°，设∠BEF=2x°，则∠EFD=(2x+30)°，∵EP平分∠BEF，GF平分∠EFD，∴∠PEF=12∠BEF=x°，∠EFG=12∠EFD=(x+15)°，∵FH//EP，∴∠PEF=∠EFH=x°，∠P=∠HFG，∵∠HFG=∠EFG−∠EFH=15°，∴∠P=15°．【点睛】本题考查了平行线的性质，角平分线的定义，熟练掌握平行线的性质定理是解题的关键．8．（2020下·浙江绍兴·七年级统考期末）问题情境：如图1，已知AB∥CD，∠APC=108°．求∠PAB+∠PCD 的度数．经过思考，小敏的思路是：如图2，过P作PE∥AB，根据平行线有关性质，可得∠PAB+∠PCD=360°−∠APC=252°．问题迁移：如图3，AD∥BC，点P在射线OM上运动，∠ADP=∠α，∠BCP=∠β．(1)当点P在A、B两点之间运动时，∠CPD、∠α、∠β之间有何数量关系？请说明理由．(2)如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出∠CPD、∠α、∠β之间的数量关系．(3)问题拓展：如图4，MA1∥NA n，A1−B1−A2−⋯−B n−1−A n是一条折线段，依据此图所含信息，把你所发现的结论，用简洁的数学式子表达为．【答案】(1)∠CPD=∠α+∠β，理由见解析(2)∠CPD=∠β-∠α或∠CPD=∠α-∠β(3)∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠B n−1【分析】（1）过P作PE∥AD，根据平行线的判定可得PE∥AD∥BC，再根据平行线的性质即可求解；（2）过P作PE∥AD，根据平行线的判定可得PE∥AD∥BC，再根据平行线的性质即可求解；（3）问题拓展：分别过A2，A3…，An-1作直线∥A1M，过B1，B2，…，Bn-1作直线∥A1M，根据平行线的判定和性质即可求解．【详解】（1）∠CPD=∠α+∠β，理由如下：如图，过P作PE∥AD交CD于E，∵AD∥BC，∴AD∥PE∥BC，∴∠α=∠DPE，∠β=∠CPE，∴∠CPD=∠DPE+∠CPE=∠α+∠β；（2）当P在BA延长线时，∠CPD=∠β-∠α；理由：如图，过P作PE∥AD交CD于E，∵AD∥BC，∴AD∥PE∥BC，∴∠α=∠DPE，∠β=∠CPE，∴∠CPD=∠CPE-∠DPE=∠β-∠α；当P在BO之间时，∠CPD=∠α-∠β．理由：如图，过P作PE∥AD交CD于E，∵AD∥BC，∴AD∥PE∥BC，∴∠α=∠DPE，∠β=∠CPE，∴∠CPD=∠DPE-∠CPE=∠α-∠β．（3）问题拓展：分别过A2，A3…，An-1作直线∥A1M，过B1，B2，…，Bn-1作直线∥A1M，由平行线的性质和角的和差关系得∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠B n−1．故答案为：∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠B n−1．【点睛】本题主要考查了平行线的判定和性质的应用，主要考查学生的推理能力，第（2）问在解题时注意分类思想的运用．9．（2020下·重庆九龙坡·七年级统考期末）已知，AB∥CD．点M在AB上，点N在CD上．（1）如图1中，∠BME、∠E、∠END的数量关系为：；（不需要证明）如图2中，∠BMF、∠F、∠FND的数量关系为：；（不需要证明）（2）如图3中，NE平分∠FND，MB平分∠FME，且2∠E＋∠F＝180°，求∠FME的度数；（3）如图4中，∠BME＝60°，EF平分∠MEN，NP平分∠END，且EQ∥NP，则∠FEQ的大小是否发生变化，若变化，请说明理由，若不变化，求出∠FEQ的度数．【答案】（1）∠BME＝∠MEN﹣∠END；∠BMF＝∠MFN＋∠FND；（2）120°；（3）不变，30°【分析】（1）过E作EH∥AB，易得EH∥AB∥CD，根据平行线的性质可求解；过F作FH∥AB，易得FH∥AB∥CD，根据平行线的性质可求解；（2）根据（1）的结论及角平分线的定义可得2（∠BME+∠END）+∠BMF-∠FND=180°，可求解∠BMF=60°，进而可求解；（3）根据平行线的性质及角平分线的定义可推知∠FEQ=1∠BME，进而可求解．2【详解】解：（1）过E作EH∥AB，如图1，∴∠BME＝∠MEH，∵AB∥CD，∴HE∥CD，∴∠END＝∠HEN，∴∠MEN＝∠MEH＋∠HEN＝∠BME＋∠END，即∠BME＝∠MEN﹣∠END．如图2，过F作FH∥AB，∴∠BMF＝∠MFK，∵AB∥CD，∴FH∥CD，∴∠FND＝∠KFN，∴∠MFN＝∠MFK﹣∠KFN＝∠BMF﹣∠FND，即：∠BMF＝∠MFN＋∠FND．故答案为∠BME＝∠MEN﹣∠END；∠BMF＝∠MFN＋∠FND．（2）由（1）得∠BME＝∠MEN﹣∠END；∠BMF＝∠MFN＋∠FND．∵NE平分∠FND，MB平分∠FME，∴∠FME＝∠BME＋∠BMF，∠FND＝∠FNE＋∠END，∵2∠MEN ＋∠MFN ＝180°，∴2（∠BME ＋∠END ）＋∠BMF ﹣∠FND ＝180°，∴2∠BME ＋2∠END ＋∠BMF ﹣∠FND ＝180°，即2∠BMF ＋∠FND ＋∠BMF ﹣∠FND ＝180°，解得∠BMF ＝60°，∴∠FME ＝2∠BMF ＝120°；（3）∠FEQ 的大小没发生变化，∠FEQ ＝30°．由（1）知：∠MEN ＝∠BME ＋∠END ，∵EF 平分∠MEN ，NP 平分∠END ，∴∠FEN ＝12∠MEN ＝12（∠BME ＋∠END ），∠ENP ＝12∠END ，∵EQ ∥NP ，∴∠NEQ ＝∠ENP ，∴∠FEQ ＝∠FEN ﹣∠NEQ ＝12（∠BME ＋∠END ）﹣12∠END ＝12∠BME ，∵∠BME ＝60°，∴∠FEQ ＝12×60°＝30°．【点睛】本题主要考查平行线的性质及角平分线的定义，作平行线的辅助线是解题的关键．10．（2023下·辽宁大连·如图，AB//CD ，点O 在直线CD 上，点P 在直线AB 和CD 之间，∠ABP =∠PDQ =α，PD 平分∠BPQ ．（1）求∠BPD 的度数（用含α的式子表示）；（2）过点D 作DE//PQ 交PB 的延长线于点E ，作∠DEP 的平分线EF 交PD 于点F ，请在备用图中补全图形，猜想EF 与PD 的位置关系，并证明；（3）将（2）中的“作∠DEP的平分线EF交PD于点F”改为“作射线EF将∠DEP分为1:3两个部分，交PD于点F”，其余条件不变，连接EQ，若EQ恰好平分∠PQD，请直接写出∠FEQ=__________（用含α的式子表示）．【答案】（1）∠BPD=2α；（2）画图见解析，EF⊥PD，证明见解析；（3）45°−α2或45°−32α【分析】（1）根据平行线的传递性推出PG//AB//CD，再利用平行线的性质进行求解；（2）猜测EF⊥PD，根据PD平分∠BPQ,∠BPD=2α，推导出∠BPD=∠DPQ=2α，再根据DE//PQ、EF平分∠DEP，通过等量代换求解；（3）分两种情况进行讨论，即当∠PEF:∠DEF=1:3与∠DEF:∠PEF=1:3，充分利用平行线的性质、角平分线的性质、等量代换的思想进行求解．【详解】（1）过点P作PG//AB，∵AB//CD,PG//AB，∴PG//AB//CD，∴∠BPG=∠ABP=α,∠DPG=∠PDQ=α，∴∠BPD=∠BPG+∠DPG=2α．（2）根据题意，补全图形如下：猜测EF⊥PD，由（1）可知：∠BPD=2α，∵PD平分∠BPQ,∠BPD=2α，∴∠BPD=∠DPQ=2α，∵DE//PQ，∴∠EDP=∠DPQ=2α，∴∠DEP=180°−∠BPD−∠EDP=180°−4α，又EF平分∠DEP，∠PEF=12∠DEP=90°−2α，∴∠EFD=180°−∠PEF−∠BPD=90°，∴EF⊥PD．（3）①如图1，∠PEF:∠DEF=1:3，由（2）可知：∠EPD=∠DPQ=∠EDP=2α,∠DEP=180°−4α，∵∠PEF:∠DEF=1:3，∴∠PEF=14∠DEP=45°−α，∠DEF=34∠DEP=135°−3α，∵DE//PQ，∴∠DEQ=∠PQE，∠EDQ+∠PQD=180°，∵∠EDP=2α,∠PDQ=α，∴∠EDQ=∠EDP+∠PDQ=3α，∠PQD=180°−∠EDQ=180°−3α，又EQ平分∠PQD，∴∠PQE=∠DQE=∠DEQ=12∠PQD=90°−32α，∴∠FEQ=∠DEF−∠DEQ=135°−3α−(90°−32α)=45°−32α；②如图2，∠DEP=180°−4α，∠PQD=180°−3α（同①）；若∠DEF:∠PEF=1:3，则有∠DEF=14∠DEP=14×(180°−4α)=45°−α，又∠PQE=∠DQE=12∠PQD=12×(180°−3α)=90°−32α，∵DE//PQ，∴∠DEQ=∠PQE=90°−32α，∴∠FEQ=∠DEQ−∠DEF=45°−12α，综上所述：∠FEQ=45°−32α或45°α2，故答案是：45°−α2或45°−32α．【点睛】本题考查了平行线的性质、角平分线、三角形内角和定理、垂直等相关知识点，解题的关键是掌握相关知识点，作出适当的辅助线，通过分类讨论及等量代换进行求解．【模型2 “铅笔”型】1．（2012下·广东茂名·七年级统考期中）如图，AB∥ED，∠B+∠C+∠D=（）A．180°B．360°C．540°D．270°【答案】B【分析】过C点作直线CF∥AB，根据平行线的性质可得∠B+∠BCF=180°，∠FCD+∠D=180°，然后再计算∠B+∠C+∠D即可.【详解】如图，过C点作直线CF∥AB，∵AB∥ED，∴CF∥ED，∴∠B+∠BCF=180°，∠FCD+∠D=180°，∴∠B+∠BCF+∠FCD+∠D=360°，即∠B+∠BCD+∠D=360°.故选：B【点睛】本题主要考查了平行线的性质，熟练掌握平行线的性质是解题的关键.2．（2012·江苏常州·七年级统考期中）一大门的栏杆如图所示，BA垂直地面AE于点A，CD平行于地面AE，则∠ABC＋∠BCD＝．【答案】270°【分析】过B作BF∥AE，则CD∥BF∥AE．根据平行线的性质即可求解．【详解】过B作BF∥AE，∵CD∥AE，则CD∥BF∥AE，∴∠BCD+∠1=180°，又∵AB⊥AE，∴AB⊥BF，∴∠ABF=90°，∴∠ABC+∠BCD=90°+180°=270°．故答案为：270．【点睛】本题主要考查了平行线的性质，两直线平行，同旁内角互补．正确作出辅助线是解题的关键．3．（2023下·陕西西安·七年级西安市第八十三中学校联考期中）如图1所示的是一个由齿轮、轴承、托架2所示的是手动变速箱托架工作时某一时刻的示意图，已知AB∥CD，CG∥EF，∠BAG=150°，∠DEF=130°，则∠AGC的度数是．【答案】80°【分析】过点F作FM∥CD，因为AB∥CD，所以AB∥CD∥FM，再根据平行线的性质可以求出∠MFA，∠EFM，进而可求出∠EFA，再根据平行线的性质即可求得∠AGC．【详解】解：如图，过点F作FM∥CD，∵AB∥CD，∴AB∥CD∥FM，∴∠DEF+∠EFM=180°，∠MFA+∠BAG=180°，∵∠BAG=150°，∠DEF=130°，∴∠MFA=30°，∠EFM=50°，∴∠EFA=∠EFM+∠AFM=80°，∵CG∥EF，∴∠AGC=∠EFA=80°．故答案为80°．【点睛】本题考查平行线的性质，解题关键是结合图形利用平行线的性质进行角的转化和计算．4．（2023下·广东东莞·七年级东莞市长安实验中学校考期中）如图，已知AB∥CD．（1）如图1所示，∠1+∠2＝；（2）如图2所示，∠1+∠2+∠3＝；并写出求解过程．（3）如图3所示，∠1+∠2+∠3+∠4＝；（4）如图4所示，试探究∠1+∠2+∠3+∠4+⋯+∠n＝．【答案】（1）180°；（2）360°；（3）540°；（4）（n-1）×180°【分析】（1）由两直线平行，同旁内角互补，可得答案；（2）过点E作AB的平行线，转化成两个图1，同理可得答案；（3）过点E，点F分别作AB的平行线，转化成3个图1，可得答案；（4）由（2）（3）类比可得答案．【详解】解：（1）如图1，∵AB∥CD，∴∠1+∠2=180°（两直线平行，同旁内角互补）．故答案为：180°；（2）如图2，过点E作AB的平行线EF，∵AB∥CD，∴AB∥EF，CD∥EF，∴∠1+∠AEF=180°，∠FEC+∠3=180°，∴∠1+∠2+∠3=360°；（3）如图3，过点E，点F分别作AB的平行线，类比（2）可知∠1+∠2+∠3+∠4=180°×3=540°，故答案为：540°；（4）如图4由（2）和（3）的解法可知∠1+∠2+∠3+∠4+…+∠n=（n-1）×180°，故答案为：（n-1）×180°．【点睛】此题考查了平行线的性质．注意掌握辅助线的作法是解此题的关键．5．（2020下·江苏淮安·七年级统考期末）问题情境：如图1，AB∥CD，∠PAB=130°，∠PCD=120°，求∠APC 的度数．思路点拨：小明的思路是：如图2，过P作PE∥AB，通过平行线性质，可分别求出∠APE、∠CPE的度数，从而可求出∠APC的度数；小丽的思路是：如图3，连接AC，通过平行线性质以及三角形内角和的知识可求出∠APC的度数；小芳的思路是：如图4，延长AP交DC的延长线于E，通过平行线性质以及三角形外角的相关知识可求出∠APC 的度数．问题解决：请从小明、小丽、小芳的思路中任选一种思路进行推理计算，你求得的∠APC的度数为°；问题迁移：（1）如图5，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP=∠α，∠BCP=∠β．∠CPD、∠α、∠β之间有何数量关系？请说明理由；（2）在（1）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出∠CPD、∠α、∠β间的数量关系．【答案】110；（1）∠CPD=∠α+∠β，理由见解析；（2）∠CPD=∠β−∠α或∠CPD=∠a−∠β，理由见解析【分析】小明的思路是：过P作PE∥AB，构造同旁内角，利用平行线性质，可得∠APC=110°．（1）过P作PE∥AD交CD于E，推出AD∥PE∥BC，根据平行线的性质得出∠a=∠DPE，∠β=∠CPE，即可得出答案；（2）画出图形（分两种情况：①点P在BA的延长线上，②点P在AB的延长线上），根据平行线的性质得出∠α=∠DPE，∠β=∠CPE，即可得出答案．【详解】解：小明的思路：如图2，过P作PE∥AB，∵AB∥CD，∴PE∥AB∥CD，∴∠APE=180°−∠A=50°，∠CPE=180°−∠C=60°，∴∠APC=50°+60°=110°，故答案为：110；（1）∠CPD=∠α+∠β，理由如下：如图5，过P作PE∥AD交CD于E，∵AD∥BC，∴AD∥PE∥BC，∴∠a=∠DPE，∠β=∠CPE，∴∠CPD=∠DPE+∠CPE=∠a+∠β；（2）当P在BA延长线时，∠CPD=∠β−∠α；理由：如图6，过P作PE∥AD交CD于E，∵AD∥BC，∴AD∥PE∥BC，∴∠α=∠DPE，∠β=∠CPE，∴∠CPD=∠CPE−∠DPE=∠β−∠α；当P在BO之间时，∠CPD=∠a−∠β．理由：如图7，过P作PE∥AD交CD于E，∵AD∥BC，∴AD∥PE∥BC，∴∠α=∠DPE，∠β=∠CPE，∴∠CPD=∠DPE−∠CPE=∠α−∠β．【点睛】本题考查了三角形的内角和定理，平行线的判定和性质，主要考查学生的推理能力，解决问题的关键是作辅助线构造内错角以及同旁内角．6．（2020下·内蒙古·七年级校考期中）综合与探究：（1）问题情境：如图1，AB∥CD,∠PAB=130°,∠PCD=120°．求∠APC的度数．小明想到一种方法，但是没有解答完：如图2，过P作PE∥AB，∴∠APE+∠PAB=180°．∴∠APE=180°−∠PAB=180°−130°=50°．∵AB∥CD．∴PE∥CD．…………请你帮助小明完成剩余的解答．（2）问题探究：请你依据小明的思路，解答下面的问题：如图3，AD∥BC，点P在射线OM上运动，∠ADP=∠α,∠BCP=∠β．当点P在A，B两点之间时，∠CPD,∠α,∠β之间有何数量关系？请说明理由．【答案】（1）110°；（2）∠CPD=∠α+∠β，理由见解析【分析】（1）过P作PE//AB，构造同旁内角，通过平行线性质，可得∠APC=50°+60°=110°．（2）过P作PE//AD交CD于E，推出AD//PE//BC，根据平行线的性质得出∠α=∠DPE，∠β=∠CPE，即可得出答案．【详解】解：（1）过P作PE∥AB，∴∠APE+∠PAB=180°，∴∠APE=180°−∠PAB=180°−130°=50°．∵AB∥CD，∴PE∥CD．∴∠CPE+∠PCD=180°，∴∠CPE=180°−120°=60°，∴∠APC=50°+60°=110°．（2）∠CPD=∠α+∠β，如图3，过P作PE//AD交CD于E，∵AD//BC，∴AD//PE//BC，∴∠α=∠DPE，∠β=∠CPE，∴∠CPD=∠DPE+∠CPE=∠α+∠β；【点睛】本题考查了平行线的性质和判定的应用，主要考查学生的推理能力，解决问题的关键是作辅助线构造内错角以及同旁内角．7．（2020下·天津滨海新·七年级统考期末）如图1，四边形MNBD为一张长方形纸片．（1）如图2，将长方形纸片剪两刀，剪出三个角（∠BAE、∠AEC、∠ECD），则∠BAE+∠AEC+∠ECD=__________°．（2）如图3，将长方形纸片剪三刀，剪出四个角（∠BAE、∠AEF、∠EFC、∠FCD），则∠BAE+∠AEF+∠EFC+∠FCD=__________°．（3）如图4，将长方形纸片剪四刀，剪出五个角（∠BAE、∠AEF、∠EFG、∠FGC、∠GCD），则∠BAE+∠AEF+∠EFG+∠FGC+∠GCD=___________°．（4）根据前面探索出的规律，将本题按照上述剪法剪n刀，剪出(n+1)个角，那么这(n+1)个角的和是____________°．【答案】（1）360；（2）540；（3）720；（4）180n．【分析】（1）过点E作EH∥AB，再根据两直线平行，同旁内角互补即可得到三个角的和等于180°的2倍；（2）分别过E、F分别作AB的平行线，根据两直线平行，同旁内角互补即可得到四个角的和等于180°的三倍；（3）分别过E、F、G分别作AB180°的三倍；（4）根据前三问个的剪法，剪n刀，剪出n+1个角，那么这n+1个角的和是180n度．【详解】（1）过E作EH∥AB（如图②）．∵原四边形是长方形，∴AB∥CD，又∵EH∥AB，∴CD∥EH（平行于同一条直线的两条直线互相平行）．∵EH∥AB，∴∠A+∠1=180°（两直线平行，同旁内角互补）．∵CD∥EH，∴∠2+∠C=180°（两直线平行，同旁内角互补）．∴∠A+∠1+∠2+∠C=360°，又∵∠1+∠2=∠AEC，∴∠BAE+∠AEC+∠ECD=360°；（2）分别过E、F分别作AB的平行线，如图③所示，用上面的方法可得∠BAE+∠AEF+∠EFC+∠FCD=540°；（3）分别过E、F、G分别作AB的平行线，如图④所示，用上面的方法可得∠BAE+∠AEF+∠EFG+∠FGC+∠GCD=720°；（4）由此可得一般规律：剪n刀，剪出n+1个角，那么这n+1个角的和是180n度．故答案为：（1）360；（2）540；（3）720；（4）180n．【点睛】本题主要考查了多边形的内角和，作平行线并利用两直线平行，同旁内角互补是解本题的关键，总结规律求解是本题的难点．8．（2023下·浙江·七年级期末）已知AB//CD，定点E，F分别在直线AB，CD上，在平行线AB，CD之间有一动点P．（1）如图1所示时，试问∠AEP，∠EPF，∠PFC满足怎样的数量关系?并说明理由．（2）除了（1）的结论外，试问∠AEP，∠EPF，∠PFC还可能满足怎样的数量关系?请画图并证明（3）当∠EPF满足0°<∠EPF<180°，且QE，QF分别平分∠PEB和∠PFD，①若∠EPF=60°，则∠EQF=__________°．②猜想∠EPF与∠EQF的数量关系．（直接写出结论）【答案】（1）∠AEP+∠PFC=∠EPF）∠AEP+∠EPF+∠PFC=360°；（3）①150°或30；②∠EPF+2∠EQF=360°或∠EPF=2∠EQF【分析】（1）由于点P是平行线AB，CD之间有一动点，因此需要对点P的位置进行分类讨论：如图1，当P点在EF的左侧时，∠AEP，∠EPF，∠PFC满足数量关系为：∠EPF=∠AEP+∠PFC；（2）当P点在EF的右侧时，∠AEP，∠EPF，∠PFC满足数量关系为：∠AEP+∠EPF+∠PFC=360°；（3）①若当P点在EF的左侧时，∠EQF=∠BEQ+∠QFD=150°；当P点在EF的右侧时，可求得∠BEQ+∠QFD=30°；②结合①可得∠EPF=180°−2∠BEQ+180°−2∠DFQ=360°−2(∠BEQ+∠PFD)，由∠EQF=∠BEQ+∠DFQ，得出∠EPF+2∠EQF=360°；可得EPF=∠BEP+∠PFD，由∠BEQ+∠DFQ=∠EQF，得出∠EPF= 2∠EQF．【详解】解：（1）如图1，过点P作PG//AB，∵PG//AB，∴∠EPG=∠AEP，∵AB//CD，∴PG//CD，∴∠FPG=∠PFC，∴∠AEP+∠PFC=∠EPF；（2）如图2，当P点在EF的右侧时，∠AEP，∠EPF，∠PFC满足数量关系为：∠AEP+∠EPF+∠PFC=360°；过点P作PG//AB，∵PG//AB，∴∠EPG+∠AEP=180°，∵AB//CD，∴PG//CD，∴∠FPG+∠PFC=180°，∴∠AEP+∠EPF+∠PFC=360°；（3）①如图3，若当P点在EF的左侧时，∵∠EPF=60°，∴∠PEB+∠PFD=360°−60°=300°，∵EQ，FQ分别平分∠PEB和∠PFD，∴∠BEQ=12∠PEB，∠QFD=12∠PFD，∴∠EQF=∠BEQ+∠QFD=12(∠PEB+∠PFD)=12×300°=150°；如图4，当P点在EF的右侧时，∵∠EPF=60°，∴∠PEB+∠PFD=60°，∴∠BEQ+∠QFD=12(∠PEB+∠PFD)=12×60°=30°；故答案为：150°或30；②由①可知：∠EQF=∠BEQ+∠QFD=12(∠PEB+∠PFD)=12(360°−∠EPF)，∴∠EPF+2∠EQF=360°；∠EQF=∠BEQ+∠QFD=12(∠PEB∠PFD)=12∠EPF，∴∠EPF=2∠EQF．综合以上可得∠EPF与∠EQF的数量关系为：∠EPF+2∠EQF=360°或∠EPF=2∠EQF．【点睛】本题主要考查了平行线的性质，平行公理和及推论等知识点，作辅助线后能求出各个角的度数，是解此题的关键．9．（2023下·浙江宁波·七年级统考期中）如图，AB//CD，定点E，F分别在直线AB，CD上，在平行线AB，CD之间有一个动点P，满足0°<∠EPF<180°．（1）试问：∠AEP，∠EPF，∠PFC满足怎样的数量关系？解：由于点P是平行线AB，CD之间一动点，因此需对点P的位置进行分类讨论．如图1，当点P在EF的左侧时，易得∠AEP，∠EPF，∠PFC满足的数量关系为∠AEP+∠PFC=∠EPF；如图2，当点P在EF的右侧时，写出∠AEP，∠EPF，∠PFC满足的数量关系_________．（2）如图3，QE，QF分别平分∠PEB和∠PFD，且点P在EF左侧．①若∠EPF=100°，则∠EQF的度数为______；②猜想∠EPF与∠EQF的数量关系，并说明理由；③如图4，若∠BEQ与∠DFQ的角平分线交于点Q1，∠BEQ1与∠DFQ1的角平分线交于点Q2，∠BEQ2与∠DFQ2的角平分线交于点Q3，以此类推，则∠EPF与∠EQ2020F满足怎样的数量关系？（直接写出结果）【答案】（1）∠AEP+∠EPF+∠PFC=360°；（2）①130°；②∠EPF+2∠EQF=360°，见解析；③∠EPF+22021∠EQ2020F＝360°【分析】（1）过点P作PH//AB，利用平行线的性质即可求解；（2）根据（1）的结论结合角平分线的定义，平角的定义，运用整体思想即可求解．【详解】解：（1）如图2，当点P在EF的右侧时，过点P作PM//AB，则PM//CD，∴∠AEP+∠EPM＝180°，∠PFC+∠MPF＝180°，∴∠AEP+∠EPM+∠PFC+∠MPF＝360°，即：∠AEP+∠EPF+∠PFC＝360°；故答案为：∠AEP+∠EPF+∠PFC＝360°；（2）①由（1）得：∠DFQ+∠BEQ＝∠EQF，∠PEA+∠PFC＝∠EPF，∵∠EPF＝100°，∴∠PEA+∠PFC＝100°，∵QE，QF分别平分∠PEB和∠PFD，∴∠DFP＝2∠DFQ，∠BEP＝2∠BEQ，∵∠PFC+∠DFP＝180°，∠PEA+∠BEP＝180°，∴∠PFC+2∠DFQ＝180°，∠PEA+2∠BEQ＝180°，∴∠PFC+2∠DFQ＋∠PEA+2∠BEQ＝360°，∴100°+2∠DFQ＋2∠BEQ＝360°，∴∠DFQ+∠BEQ＝130°，∴∠EQF＝∠DFQ+∠BEQ＝130°，故答案为：130°；②∠EPF+2∠EQF＝360°，理由如下：∵QE，QF分别平分∠PEB和∠PFD，∴∠DFP＝2∠DFQ，∠BEP＝2∠BEQ，∵∠PFC+∠DFP＝180°，∠PEA+∠BEP＝180°，∴∠PFC+2∠DFQ＝180°，∠PEA+2∠BEQ＝180°，∴∠PFC+2∠DFQ＋∠PEA+2∠BEQ＝360°，∴∠PFC＋∠PEA +2(∠DFQ +∠BEQ)＝360°，∵由（1）得：∠DFQ+∠BEQ＝∠EQF，∠PEA+∠PFC＝∠EPF，∴∠EPF +2∠EQF＝360°；③∵Q1E，Q1F分别平分∠QEB和∠QFD，∴∠DFP＝2∠DFQ＝22∠DFQ1，∠BEP＝2∠BEQ＝22∠BEQ1，∵∠PFC+∠DFP＝180°，∠PEA+∠BEP＝180°，∴∠PFC+22∠DFQ1＝180°，∠PEA+22∠BEQ1＝180°，∴∠PFC+22∠DFQ1＋∠PEA+22∠BEQ1＝360°，∴∠PFC＋∠PEA +22(∠DFQ1 +∠BEQ1)＝360°，∵由（1）得：∠DFQ1+∠BEQ1＝∠EQ1F，∠PEA+∠PFC＝∠EPF，∴∠EPF +22∠EQ1F＝360°；同理可得：∠EPF +23∠EQ2F＝360°，∠EPF +24∠EQ3F＝360°，……∴∠EPF+22021∠EQ2020F＝360°．【点睛】本题主要考查了平行线的性质，平行公理及推论，角平分线的定义等知识点，作辅助线后能求出各个角的度数，利用整体思想解决第（2）问是解此题的关键．10．（2020下·辽宁大连·七年级统考期末）阅读下面材料，完成（1)～（3）题．数学课上，老师出示了这样—道题：如图1，已知AB//CD,点E,F分别在AB,CD上，EP⊥FP,∠1=60°．求∠2的度数．同学们经过思考后，小明、小伟、小华三位同学用不同的方法添加辅助线，交流了自己的想法：小明：“如图2，通过作平行线，发现∠1=∠3,∠2=∠4，由已知EP⊥FP,可以求出∠2的度数．”小伟：“如图3这样作平行线，经过推理，得∠2=∠3=∠4,也能求出∠2的度数．”小华：∵如图4，也能求出∠2的度数．”(1)请你根据小明同学所画的图形(图2)，描述小明同学辅助线的做法，辅助线：______；(2)请你根据以上同学所画的图形，直接写出∠2的度数为_________°；老师：“这三位同学解法的共同点，都是过一点作平行线来解决问题，这个方法可以推广．”请大家参考这三位同学的方法，使用与他们类似的方法，解决下面的问题：(3)如图，AB//CD，点E,F分别在AB，CD上，FP平分∠EFD,∠PEF=∠PDF,若∠EPD=a,请探究∠CFE与∠PEF 的数量关系（(用含α的式子表示)，并验证你的结论．【答案】（1）过点Р作PQ//AC；（2）30；（3）∠CFE−2∠PEF=180∘−a．【分析】（1）根据图中所画虚线的位置解答即可；（2）过点Р作PQ//AC，根据平行线的性质可得∠1=∠3，∠2=∠4，由EP⊥FP可得∠3+∠4=90°，即可得出∠1+∠2=90°，进而可得答案；（3）设∠CFE=x,∠PEF=∠PDF=y，过点P作PQ//AB，根据平行线的性质可得∠BEP+∠EPQ= 180°,∠CFE=∠FEB=x，∠PDF=∠DPQ，进而根据角的和差关系即可得答案．【详解】（1）由图中虚线可知PQ//AC，∴小明同学辅助线的做法为过点Р作PQ//AC，故答案为：过点Р作PQ//AC（2）如图2，过点Р作PQ//AC，∵AB//CD，∴PQ//AB//CD，∴∠1=∠3，∠2=∠4，∵EP⊥FP，∴∠EPF=∠3+∠4=90°，∴∠1+∠2=90°，∵∠1=60°，∴∠2=30°，故答案为：30（3）如图，设∠CFE=x,∠PEF=∠PDF=y，过点P作PQ//AB，∴∠BEP+∠EPQ=180°,∠CFE=∠FEB=x∵AB//CD,∴PQ//CD,∴∠PDF=∠DPQ∴∠DPQ=∠EHF=∠PDF=y∵∠CFE=∠FEB=x=∠FEP+∠BEP∴x=y+(180−a+y)∴x−2y=180−α，即∠CFE−2∠PEF=180∘−a．【点睛】本题考查平行线的性质，两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；正确作出辅助线，熟练掌握平行线的性质是解题关键．【模型3 “鸡翅”型】1．（2023下·湖南株洲·七年级统考期末）①如图1，AB∥CD，则∠A+∠E+∠C=360°；②如图2，AB ∥CD，则∠P=∠A−∠C；③如图3，AB∥CD，则∠E=∠A+∠1；④如图4，直线AB∥CD∥EF，点O在直线EF上，则∠α−∠β+∠γ=180°．以上结论正确的个数是（）A．1个B．2个C．3个D．4个【答案】C【分析】①过点E作直线EF∥AB，由平行线的性质：两直线平行，同旁内角互补，即可得出结论；②如图2，先根据三角形外角的性质得出∠1＝∠C+∠P，再根据两直线平行，内错角相等即可作出判断；③如图3，过点E作直线EF∥AB，由平行线的性质可得出∠A+∠AEC﹣∠1＝180°，即得∠AEC＝180°+∠1﹣∠A；④如图4，根据平行线的性质得出∠α＝∠BOF，∠γ+∠COF＝180°，再利用角的关系解答即可．【详解】解：①如图1，过点E作直线EF∥AB，∵AB∥CD，∴AB∥CD∥EF，∴∠A+∠1＝180°，∠2+∠C＝180°，∴∠A+∠1+∠2+∠C＝360°，∴∠A+∠AEC+∠C=360°，故①正确；②如图2，∵∠1是△CEP的外角，∴∠1＝∠C+∠P，∵AB∥CD，∴∠A＝∠1，即∠P＝∠A﹣∠C，故②正确；③如图3，过点E作直线EF∥AB，∵AB∥CD，∴AB∥CD∥EF，∴∠A+∠3＝180°，∠1＝∠2，∴∠A+∠AEC﹣∠1＝180°，即∠AEC＝180°+∠1﹣∠A，故③错误；④如图4，∵AB∥EF，∴∠α＝∠BOF，∵CD∥EF，∴∠γ+∠COF＝180°，∵∠BOF＝∠COF+∠β，∴∠COF＝∠α﹣∠β，∴∠γ+∠α﹣∠β＝180°，故④正确；综上结论正确的个数为3，故选：C．【点睛】本题考查的是平行线的性质及三角形外角的性质，熟练掌握平行线的性质，根据题意作出辅助线是解答此题的关键．2．（2023上·七年级课时练习）（1）已知：如图（a），直线DE∥AB．求证：∠ABC+∠CDE=∠BCD；（2）如图（b），如果点C在AB与ED之外，其他条件不变，那么会有什么结果？你还能就本题作出什么新的猜想？【答案】（1）见解析；（2）当点C在AB与ED之外时，∠ABC−∠CDE=∠BCD，见解析【分析】（1）由题意首先过点C作CF∥AB，由直线AB∥ED，可得AB∥CF∥DE，然后由两直线平行，内错角相等，即可证得∠ABC+∠CDE=∠BCD；（2）根据题意首先由两直线平行，内错角相等，可得∠ABC=∠BFD，然后根据三角形外角的性质即可证得∠ABC-∠CDE=∠BCD．【详解】解：（1）证明：过点C作CF∥AB，∵AB∥ED，∴AB∥ED∥CF，∴∠BCF=∠ABC，∠DCF=∠EDC，∴∠ABC+∠CDE=∠BCD；（2）结论：∠ABC-∠CDE=∠BCD，证明：如图：∵AB∥ED，∴∠ABC=∠BFD，在△DFC中，∠BFD=∠BCD+∠CDE，∴∠ABC=∠BCD+∠CDE，∴∠ABC-∠CDE=∠BCD．若点C在直线AB与DE之间，猜想∠ABC+∠BCD+∠CDE=360°,。
相交线与平行线常见的四大类6种模型
相交线与平行线的概念还可以与其他数学分支如代数、数论等相结合，产生新的交叉应 用和研究领域。
THANKS
感谢观看
相交线与平行线常见的四大类6种模 型
目录
• 引言 • 相交线模型 • 平行线模型 • 角的性质与判定 • 距离与长度的计算 • 模型的应用与拓展
01
引言
目的和背景
理解和掌握相交线与 平行线的基本概念和 性质
培养空间观念和推理 能力，为进一步学习 几何知识打下基础
分析和解决与相交线 与平行线相关的实际 问题
性质
平行线间距离相等；平行线同位角 相等，内错角相等。
判定
同位角相等，两直线平行；内错角 相等，两直线平行；同旁内角互补， 两直线平行。
直线与平面平行
定义
一条直线与一个平面没有交点， 则称这条直线与该平面平行。
性质
直线与平面平行，则该直线上任 意一点到平面的距离相等；直线 与平面平行，过该直线的平面与 已知平面的交线与该直线平行。
面积法
通过构造三角形或平行四边形等图形，利用面积公式间接求出点 到直线的距离。
向量法
在平面直角坐标系中，利用向量的数积和模长公式计算点到直 线的距离。
平行线间的距离
垂线段法
在两条平行线间作垂线段，该垂线段的长度即为平行线间的距离。
斜率截距法
已知平行线的斜率和截距，通过公式直接计算平行线间的距离。
四大类6种模型概述
斜交线
两条直线在同一平面内，但不平行 也不垂直，它们的交角不等于90度。
垂直线
两条直线在同一平面内，它们之间 的交角等于90度。
四大类6种模型概述
同位角相等
两条平行线被一条横截线所截，同位 角相等。
(完整版)平行线知识点+四大模型
平行线四大模型平行线的判定与性质l、平行线的判定根据平行线的定义，如果平面内的两条直线不相交，就可以判断这两条直线平行，但是，由于直线无限延伸，检验它们是否相交有困难，所以难以直接根据定义来判断两条直线是否平行，这就需要更简单易行的判定方法来判定两直线平行．判定方法l：两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行．简称：同位角相等，两直线平行．判定方法2：两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行．简称：内错角相等，两直线平行，判定方法3：两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行．简称：同旁内角互补，两直线平行，如上图：若已知∠1=∠2，则AB∥CD（同位角相等，两直线平行）；若已知∠1=∠3，则AB∥CD（内错角相等，两直线平行）；若已知∠1+ ∠4= 180°，则AB∥CD（同旁内角互补，两直线平行）．另有平行公理推论也能证明两直线平行：平行公理推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行．2、平行线的性质利用同位角相等，或者内错角相等，或者同旁内角互补，可以判定两条直线平行．反过来，如果已知两条直线平行，当它们被第三条直线所截，得到的同位角、内错角、同旁内角也有相应的数量关系，这就是平行线的性质．性质1：两条平行线被第三条直线所截，同位角相等．简称：两直线平行，同位角相等性质2：两条平行线被第三条直线所截，内错角相等.简称：两直线平行，内错角相等性质3：两条平行线被第三条直线所截，同旁内角互补．简称：两直线平行，同旁内角互补本讲进阶平行线四大模型模型一“铅笔”模型点P在EF右侧，在AB、CD内部“铅笔”模型结论1：若AB∥CD，则∠P+∠AEP+∠PFC=3 60°；结论2：若∠P+∠AEP+∠PFC= 360°，则AB∥CD.模型二“猪蹄”模型（M模型）点P在EF左侧，在AB、CD内部“猪蹄”模型结论1：若AB∥CD，则∠P=∠AEP+∠CFP；结论2：若∠P=∠AEP+∠CFP，则AB∥CD.模型三“臭脚”模型点P在EF右侧，在AB、CD外部“臭脚”模型结论1：若AB∥CD，则∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP；结论2：若∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP，则AB∥CD.模型四“骨折”模型·点P在EF左侧，在AB、CD外部“骨折”模型结论结论2：若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP，则AB∥CD.巩固练习平行线四大模型证明（1）已知AE // CF ,求证∠P +∠AEP +∠PFC = 360°. （2）已知∠P=∠AEP+∠CFP，求证AE∥CF．（3）已知AE∥CF，求证∠P=∠AEP-∠CFP.（4）已知∠P= ∠CFP -∠AEP,求证AE //CF.模块一平行线四大模型应用例1（1）如图，a∥b,M、N分别在a、b上，P为两平行线间一点，那么∠l+∠2+∠3= ．(2)如图，AB∥CD，且∠A=25°，∠C=45°，则∠E的度数是．(3)如图，已知AB∥DE，∠ABC=80°，∠CDE =140°，则∠BCD= .(4) 如图，射线AC∥BD，∠A= 70°，∠B= 40°，则∠P= ．练(1)如图所示，AB∥CD，∠E=37°，∠C= 20°，则∠EAB的度数为．(2) 如图，AB∥CD，∠B=30°，∠O=∠C．则∠C= .例2如图，已知AB ∥DE ，BF 、 DF 分别平分∠ABC 、∠CDE ，求∠C 、 ∠F 的关系.练如图，已知AB ∥DE ，∠FBC =n 1∠ABF ，∠FDC =n1∠FDE . (1)若n =2,直接写出∠C 、∠F 的关系 ； (2)若n =3，试探宄∠C 、∠F 的关系；(3)直接写出∠C 、∠F 的关系 （用含n 的等式表示）.例3如图，已知AB∥CD，BE平分∠ABC，DE平分∠ADC．求证：∠E= 2 (∠A+∠C) .练如图，己知AB∥DE，BF、DF分别平分∠ABC、∠CDE，求∠C、∠F的关系.例4如图，∠3==∠1+∠2，求证：∠A+∠B+∠C+∠D= 180°．练（武昌七校2015-2016 七下期中）如图，AB⊥BC，AE平分∠BAD交BC于E，AE⊥DE，∠l+∠2= 90°，M、N分别是BA、CD的延长线上的点，∠EAM和∠EDN的平分线相交于点F则∠F的度数为（）．A. 120°B. 135°C. 145°D. 150°模块二平行线四大模型构造例5如图，直线AB∥CD，∠EF A= 30°，∠FGH= 90°，∠HMN=30°，∠CNP= 50°，则∠GHM= .练如图，直线AB∥CD，∠EFG=100°，∠FGH=140°，则∠AEF+ ∠CHG= .例6 已知∠B =25°，∠BCD=45°，∠CDE =30°，∠E=l0°，求证：AB∥EF．练已知AB∥EF，求∠l-∠2+∠3+∠4的度数.(1)如图(l)，已知MA1∥NA n，探索∠A1、∠A2、…、∠A n，∠B1、∠B2…∠B n-1之间的关系．(2)如图(2)，己知MA1∥NA4，探索∠A1、∠A2、∠A3、∠A4，∠B1、∠B2之间的关系．(3)如图(3)，已知MA1∥NA n，探索∠A1、∠A2、…、∠A n之间的关系．如图所示，两直线AB∥CD平行，求∠1+∠2+∠3+∠4+∠5+∠6．。
初中数学：平行线中的几何模型
初中数学：平行线中的几何模型若∥a b ，则∠=∠+∠213a b //，∠=∠+∠MON NOQ 2若∥a b ，则∠+∠+∠=︒123360a b //，∠=∠+∠MON NOQ 2若∥a b ，则∠=∠+∠123a b //，∠=∠∠NOQ MON +2若∥a b ，则∠=∠+∠312 a b //，∠∠∠MON NOQ =+2=∠+∠++∠+∠∠+∠+∠++∠+∠--B B B B M A A A N n n n 121121如图所示，分别过点、-A A A n 121作直线的平行线、-l l l n 121，且、-l l l n 121、∠∠∠-A A A n 121分别分为、，、，、∠∠∠∠∠∠--αβαβαβn n 112211-a l l l b n ////////121 a l //1，l l //12，-l b n //1=∠+∠++∠+∠∠+∠+∠++∠+∠--B B B B M A A A N n n n 121121，则∠+∠+∠++∠+∠=︒-M A A A N n n 180121如图所示，分别过点、-A A A n 121作直线a 的平行线、-l l l n 121，且、-l l l n 121、∠∠∠-A A A n 121分别分为、，、，、∠∠∠∠∠∠--αβαβαβn n 112211-a l l l b n ////////121 a l //1，l l //12，-l b n //1∠+∠+∠++∠+∠=︒-M A A A N n n 180121三角形中的几何模型结论：①∠+∠=∠+∠A B CAD BC AB CD②+>+D A B C结论：①∠=∠+∠+∠AB AC BD CD②+>+、BP CP 分别是BP 是∠ABC 的角平分线，CP 是ACB 的外角平分线，则：1BP 平分、CP 分别是∠ABC 和∠ACB 的外角平分线，则：∠=︒-∠P A 2901BP 平分=AC，=AD AE，∠=BAC ≌∆ABD ACE ∠=∠BAC DAE条件：∆ABC和∆ADE是等边三角形∆ABC≌∆∆ABD ACE ∠=∠BHA CHO≌∆∆ABD ACE=∆SABD21∴=AM AN∴AO平分条件：∆ABC和∆ADE是等边三角形，且B、A、E三线共线结论：①≌∆∆ABD ACE②∠=∠=∠=BOC BAC DAE60≌∆∆ABD ACE∆ABC和∠=︒= BOC OP OC60,常见应用图形等腰直角三角形条件：∆ABC 和∆ADE 是等腰直角三角形 结论：①≌∆∆ABD ACE②=BD CE 且⊥BD CE③连接AO ，AO 平分∠COD证明：证法同等边三角形.正方形条件：正方形ABCD 和正方形AEFG 结论：①≌∆∆ADE ABG②=BG DE 且⊥BG DE ③连接AO ，AO 平分∠BOE证明：证法同等边三角形.顶角相等的等腰三角形条件：∆ABC 和∆ADE 是等腰三角形 且∠=∠=αBAC DAE 结论：①≌∆∆ABD ACE ②∠=αBOC③连接AO ，AO 平分∠BOE证明：证法同等边三角形.60°含30°ABC 是等边三角形，、E 是边BC 上两点，且∠DAE ∆ABC 是等边三角形，≌∆∆ACF ABD在条件：=AB AC ，∠=︒BAC 120，条件：等腰∆ABCBAC90，Rt中，∠=︒D、E是边BC上两点，且∠DAE常见应用图形90°含45°条件： E 、F 是正方形ABCD 的边BC 、CD上的点，且∠=︒EAF 45 结论：①=+EF BE DF②∆CEF 的周长等于正方形边长的2倍③若⊥AH EF ,则=AH AB ④=+∆∆∆S S S AEF ABE ADF证明：如图所示，延长EB 至点M ，使BM =DF ，连接AM四边形ABCD 是正方形 ∴AB =AD ，∠D =∠ABC =90° ∴∠ABM =90° BM =DF≌∴∆∆ABM ADF (SAS)∴=AM AF ,∠=∠BAM DAF ∴=AM AF，∠=︒∠=︒BAD EAF 9045 ∴∠+∠=︒BAE DAF 45∴∠+∠=︒BAE BAM 45,即∠=︒MAE 45 ≌∴∆∆MAE FAE (SAS) =+==+++=++∴==+∆BC CD BCCE BE DF CF C CE EF CF EF EM BE DFCEF 2==∆∆S S ME EF AEM AEF ,∴=AB AH 又=∆∆S S ABM DAF ∴=+∆∆∆S S S AEF ABE ADF90°含45°条件： E 、F 是正方形ABCD 的边CB 、DC延长线上的点，且∠=︒EAF 45 结论：①=-EF DF BE②∆CEF 的周长等于DF 的2倍 ③若⊥AH EF ,则=AH AB ④=-∆∆∆S S S AEF ADF ABE证明： 证法同上.条件：⊥AB BD ,⊥DE BD ,⊥AC =AC CE⊥AB BD ,⊥DE BD ,⊥AC ⊥AB BE ,⊥DE BD ,⊥AC BD 且=AB BEA∠=αDCE∠=αA B∠=∠ABC E AFD=∠=∠=α结论：①≌∆ABCDE CE=ABE ACD EDF=∠=∠BEABC BED;②≌∆ABC 和△ADE 是等腰直角三角形，连接BE 、CD ，⊥AH BE ,延长交CD 于点M ===AQ HE AP BH MQ MP ,,≌∆∆CPM DQM 条件：已知正方形ABCD 和AEFG ，连接BG 、DE 是DE 中点，延长BG 于点H①⊥AH BG ；②AM BG 2=1；=AD AB =，∠+∠=︒∠∠DAN BAH DAN ABH 90条件：已知AB=AC，AD=AE，连接BG DE，∠+∠=︒BAC DAE180，M DE中点中，点D 是BC 的中点AD 到E ，使DE =AD ABD ≌△ECD ；②AB //ABC 中，点D 是BC 的中点，AC 边上任意一点 ED 到F ，使DF =DE BDF ≌△CDE ；②BF //CE条件：如图，l l //12，点D 是BC AD 交l 2于点E ABD ≌△ECD l l //12∠=∠ADB EDC条件：已知∠=∠12，D是OAOE OD，连接OB上取=条件：已知∠=∠DC OC12，⊥方法：延长DC交OB于点EOCD OCE≌∆//CD OB12∠=∠原理说明：两点之间，线段最短原理说明：①轴对称的性质②两点之间，线段最短①轴对称的性质②两点之间，线段最短①轴对称的性质②两点之间，线段最短原理说明：①轴对称的性质②垂线段最短原理说明：①平移的性质②两点之间，线段最短原理说明：①平移的性质；②轴对称的性质；③两点之间，线段最短三角形两边之差小于第三边问题描述：如图，在l上找一点P，使①轴对称的性质②三角形两边之差小于第三边①绝对值的非负性线段垂直平分线上的点到线段两端点【总结】轴对称辅助线作法——作点关于线的对称点，连接另一点.。
平行线模型
平行线模型一、猪蹄型（在拐点作平行线，利用内错角倒角）已知：AB//CD，求证：∠B+∠D=∠E.证明：过点E作MN//AB.∠MN//AB（辅助线）.∠∠B=∠1（两直线平行，内错角相等）.∠MN//AB（辅助线），AB//CD（已知）∠MN//CD（平行于同一直线的两直线互相平行）∠∠2=∠D（两直线平行，内错角相等）∠∠1+∠2=∠BED（等式性质）∠∠B+∠D=∠BED（等量代换）结论：朝左的角之和=朝右的角之和二、铅笔型（在拐点作平行线，利用同旁内角倒角）解：（1）∵AB∥CD（已知）∴∠1+∠2=180°（两直线平行，同旁内角互补）（2）过点E作一条直线EF平行于AB，∵AB∥EF，AB∥CD（已知）∴CD∥EF（平行于同一条直线的两条直线平行）∴∠1+∠AEF=180°，∠FEC+∠3=180°（两直线平行，同旁内角互补）∵∠AEF+∠FEC=∠AEC，∠1+∠AEF+∠FEC+∠3=360°（等式性质）∴∠1+∠2+∠3=360°（等量代换）（3）过点E、F作EG、FH平行于AB，∵AB∥CD（已知）∴AB∥EG∥FH∥CD（平行于同一条直线的两条直线平行）∴∠1+∠AEG=180°，∠GEF+∠EFH=180°，∠HFC+∠4=180°（两直线平行，同旁内角互补）∵∠AEG+∠GEF=∠AEF，∠EFH+∠HFC=∠EFC，∠1+∠AEG+∠GEF+∠EFH+∠HFC+∠4=540°（等式性质）∴∠1+∠2+∠3+∠4=540°（等量代换）（4）根据上述规律，显然作（n-2）条辅助线，运用（n-1）次两条直线平行，同旁内角互补．即可得到n组同旁内角，n个角的和是180（n-1）°．三、前扬角型（在拐点作平行线，利用内错角倒角）∠B=∠E+∠C过点E作GF//AB∵AB∥CD（已知）∴GF∥CD（平行于同一条直线的两条直线平行）∴∠B=∠BEF，∠C=∠CEF（两直线平行，内错角相等）.∵∠BEF=∠BEC+∠CEF（等式性质）∴∠B=∠BEC+∠C（等量代换）四、后翻角型（在拐点作平行线，利用内错角倒角）∠C=∠E+∠B过点E作GF//AB∵AB∥CD（已知）∴GF∥CD（平行于同一条直线的两条直线平行）∴∠B=∠BEF，∠C=∠CEF（两直线平行，内错角相等）.∵∠CEF=∠BEF+∠CEB（等式性质）∴∠C=∠B+∠CEB（等量代换）五、综合型（在拐点作平行线，利用平行性质倒角）∠B+∠E-∠D=180°CD//EF，AB//GF→∠1+∠2=∠ABC。
平行线四大模型
E
A
B
C
D
FA
B
C
D
典例练习
（1）如图，a∥b,M、N 分别在 a、b 上，P 为两平行线间一点，那么∠l+∠2+∠3=
．
典例练习
如图，AB∥CD，且∠A=25°，∠C=45°，则∠E的度数是
．
典例练习
如图，已知AB∥DE，∠ABC=80°，∠CDE =140°，则∠BCD=
典例练习
如图，射线AC∥BD，∠A= 70°，∠B= 40°，则∠P=
剖析三 猪脚模型与铅笔模型的变形
【例 4】如图，已知 AB∥DE，∠ABC＝50°，∠CDE＝150°，则∠BCD 的值为( )
A
B
D
E
A．20° 【答案】A
B．50°
C．40°
C D．30°
041
“骨折”模型
剖析四 臭脚模型
条件：点P在EF左侧，在AB、 CD外部
结论1：若AB∥CD， ∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP；
A
B
F MC
P
D
E
021
“铅笔”模型
剖析二 铅笔模型
条件：点P在EF右侧，在AB、 CD内部
结论1：若AB∥CD， 则∠P+∠AEP+∠PFC=360°
结论2：若∠P+∠AEP+∠PFC= 360° 则AB∥CD.
A
E
A
B
A
E1
P E2
C
F
图1
C
D
图2
C 图3
B
A
E1 E2
E3
D
C 图4
B E1 E2 E3
专题5.4 平行线中的四大经典模型(人教版)(解析版)
∵ PE ∥ l1，l1∥l2， ∴ PE ∥ l1∥l2， ∴ ∠PAC = ∠APE，∠PBD = ∠BPE， ∵ ∠APB = ∠APE − ∠BPE， ∴ ∠PAC − ∠PBD = ∠APB． 【点睛】本题考查了平行线的性质以及角的计算，解题的关键是根据“两直线平行，内错角相等”找到相等的 角．本题属于基础题，难度不大，解决该题型题目时，根据平行线的性质得出相等（或互补）的角是关键． 4．（2023 下·山东聊城·七年级统考阶段练习）已知直线 AB//CD，EF 是截线，点 M 在直线 AB、CD 之间．
专题 5.4 平行线中的四大经典模型
【模型 1 “猪蹄”型（含锯齿型）】
【人教版】
1．（2020 下·湖北武汉·七年级统考期末）如图，퐴 ∥ 퐶 ，퐸 平分∠ 퐸 ，∠ 퐸 + ∠ = 66°，∠ −
∠ = 28°，则∠ 퐸 =
．
【答案】80° 【分析】过 E 点作 EM∥AB，根据平行线的性质可得∠BED=∠B+∠D，利用角平分线的定义可求得 ∠B+3∠D=132°，结合∠B-∠D=28°即可求解． 【详解】解：过 E 点作 EM∥AB，
AE 平分∠BAC 可得∠BAE=∠EAC,等量代换可得∠ECD+∠EAC=90°，继而求得∠DCE=∠ECA； （2）①过 E 作 EF∥AB，先利用平行线的传递性得出 EF∥AB∥CD，再利用平行线的性质及已知条件可推得
答案； ②过 E 作 EF∥AB，先利用平行线的传递性得出 EF∥AB∥CD，再利用平行线的性质及已知条件可推得答案. 【详解】（1）解：因为퐴 //퐶 ， 所以∠BAC+∠DCA=180°， 因为퐴퐸 ⊥ 퐶퐸， 所以∠EAC+∠ECA=90°， 因为 AE 平分∠BAC， 所以∠BAE=∠EAC， 所以∠BAE+∠DCE=90°， 所以∠EAC+∠DCE=90°， 所以∠DCE=∠ECA， 所以 CE 平分∠ACD； （2）①∠BAE 与∠MCD 存在确定的数量关系：∠BAE+12∠MCD=90°， 理由如下： 过 E 作 EF∥AB，
《平行线四大模型》专题
A
B
F
C
D
E
E
F
A
B
C
D
四、典例分析--“钩子型”
【典例1】如图，已知 BC//DE，试猜想∠A、∠B、∠D 的关系，并说明理由．
解：∠D=∠A+∠B , 理由如下：
∵∠AFB+∠A+∠B=180° 又∵∠AFB+∠AFC=180° ∴∠A+∠B=∠AFC ∵BC//DE，∴∠AFC=∠D ∴∠D=∠A+∠B
解：∠B＋∠D＝∠DEB．理由如下：
过点E 作 EF // AB． ∵ EF // AB ， ∴∠B=∠BEF． 又 ∵ AB//CD． ∴ EF//CD． ∴ ∠D =∠DEF． ∴∠B＋∠D＝∠BEF＋∠DEF＝∠DEB． 即∠B＋∠D＝∠DEB．
A E
C
B F
D
典例拓展1：
A1 A2 A3 B1 B2
平行线“拐点”专题
温故知新
平行线的判定与性质
线的关系
两直线平行
平行线的性质
同旁内角互补
平行线经典四大模型
1.猪蹄型
A
B
E
C
D
4.钩子型
2.铅笔型
A
B
E
C
D
A
B
F
C
D
E
3.靴子型
E
A
B
C
D
一、典例分析--“猪蹄型”（M模型）
【典例1】如图，若 AB // CD，你能确定∠B、∠D与∠BED 的大小关系吗？
∴ ∠D +∠DEF＝180°．
C
∴ ∠B＋∠D+∠DEB
＝∠B＋∠D+∠BEF＋∠DEF ＝360°．
平行线中的核心模型
平行线中核心模型知识要点】模型二“猪蹄”模型（M模型）结论1：若AB〃CD,则ZP二ZAEP+ZCFP；结论1：若AB〃CD,则ZP二ZCFP-ZAEP或ZP二ZAEP-ZCFP；结论2：若ZP=ZCFP-ZAEP或ZP二ZAEP-ZCFP,则AB〃CD.典例精析】EACF一)平行线四大模型证明(1)已知AE//CF ，求证ZP+ZAEP+ZPFC 二360°(2)已知ZP=ZAEP+ZCFP,求证AE 〃CF.已知AE 〃CF,求证ZP=ZAEP-ZCFP.3) 已知ZP=ZCFP-ZAEP,求证AE//CF.4) (二)平行线四大模型应用例1：(1)如图，a 〃b,M 、N 分别在a 、b 上，P 为两平行线间一点，那么Zl+Z2+Z3=⑵如图，AB 〃CD ，且ZA=25°,ZC=45°，则ZE 的度数是.⑶如图，已知AB 〃DE,ZABC=80°,Z CDE =140°，则ZBCD=⑷如图，射线AC 〃BD,ZA 二70°,ZB=40°，则ZP 二练习：⑴如图所示，AB 〃CD ，ZE=37°，ZC=20°，^IJZEAB 的度数为⑵如图，AB#CD ，ZB=30°，ZQ=ZC.则ZC 二例2：如图，已知AB 〃DE ，BF 、DF 分别平分ZABC.ZCDE ，求ZC 、ZF 的关系.练习：如图，已知AB 〃DE ，ZFBC=丄ZABF ，ZFDC=1ZFDE.nn(1)若n=2,直接写出ZC 、ZF 的关系；A-B练习：如图，AB丄BC,AE平分ZBAD交BC于E,AE丄DE,ZI+Z2二90°,上的点，ZEAM和ZEDN的平分线相交于点F则ZF的度数为（）.A.120°B.135°C.145°D.150 M例3：如图，已知AB〃CD,BE平分ZABC,DE平分ZADC.求证：ZE二2（ZA+ZC）练习：如图，己知AB〃DE,BF、DF分别平分ZABC、ZCDE,求ZC、ZF的关系.例4：如图，Z3二二Z1+Z2,求证：ZA+ZB+ZC+ZD二180（三）平行线四大模型构造例5：如图，直线AB〃CD,ZEFA二30°,ZFGH二gOo’ZHMN^Oo’ZCNP二50°，则ZGHM二.3DLi 练习：如图，直线AB〃CD,ZEFG=100°,ZFGH=140°，则ZAEF+ZCHG二练习：⑴已知AB〃EF,求ZI-Z2+Z3+Z4的度数.⑵如图⑴，已知MA〃NA，探索ZA、ZA、…、ZA,1n12n关系．今…也!之间的6Li课后作业1如图，AB//CD//EF,EH丄CD于H，则ZBAC+ZACE+ZCEH等于（）.A.180°B.270°C.360°D.450°2．（武昌七校2015-2016七下期中）若AB〃CD,ZCDF二2ZCDE,ZABF=-ZABE,则ZE：ZF=（）.33A．2:1B．3:1 C．4:3 D．3:2BED7.如图，将三角尺的直角顶点放在直线a上，a〃b.Z1=50°,Z2=60°,则Z3的度数为8.如图，AB〃CD,EP丄FP,已知Z1=30°,Z2=20°.则ZF的度数为9•如图，若AB〃CD,ZBEF=70。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
直线平行的条件和性质
1. 猪蹄模型
已知：如图，AB ∥CD ，求证：∠B+∠D=∠BED 。
2. 铅笔模型
如图,已知: CD AB ∥,求证: ∠+B ∠D +∠=BED 360°. (至少用三种方法)
3. 其他
4. 角平分线
如图1，在ABC ∆中,BE 平分,ABC CE ∠平分ACB ∠.若80A ∠=︒，则BEC ∠= ;若A n ∠=︒，求BEC ∠用含n 的代数式表示)
如图3，在ABC ∆中，BO 平分外角,CBD CO ∠平分外角BCE ∠.若A n ∠=︒，求BOC ∠.
如图5，在ABC ∆中，BE 平分ABC ∠, CE 平分外角ACM ∠.若A n ∠=︒，求BEC ∠.
5. “8”字形 如图b 所示的“
”字型，其也存在着一个等式：1+2=3+4∠∠∠∠，请证明；
6. “A ”字型
如图a 所示的“”字型，我们可称其为“A 字型”或“塔形”，其存在一个等式：
1+2=3+4∠∠∠∠，请证明；
7. 燕尾形
如图c所示，其也存在着如下等式：D A B C
∠=∠+∠+∠，请证明
一．考点：平行线的性质，角度的计算与证明．
二．重难点：常见的几种两条直线平行的结论
1．两条平行线被第三条直线所截，一组同位角的角平分线平行；
2．两条平行线被第三条直线所截，一组内错角的角平分线平行；
3．两条平行线被第三条直线所截，一组同旁内角的角平分线垂直．
三．易错点：
1．性质是由图形的“位置关系”决定“数量关系”；
2．两条平行线之间的距离其实可看成点到直线的距离．
题型一：猪蹄模型
例1. 如图，直线a∥b，直角三角形ABC的顶点B在直线a上，∠C=90°，∠β=55°，则∠α的度数为（）
A． 15° B． 25° C． 35° D． 55°
题型二：铅笔模型
∠+∠+∠+∠=（）
例2. 如图，AB∥CD，A E F C
A ． 180°
B ． 360°
C ． 540°
D ． 720°
题型三：铅笔、猪蹄模型综合压轴
例3. 某学习小组发现一个结论：已知直线a ∥b ，若直线c ∥a ，则c ∥b ．他们发现这个结论运用很广，请你利用这个结论解决以下问题：
已知直线AB ∥CD ，点E 在AB 、CD 之间，点P 、Q 分别在直线AB 、CD 上，连接PE 、EQ ． （1）如图1，运用上述结论，探究∠PEQ 与∠APE +∠CQE 之间的数量关系，并说明理由； （2）如图2，PF 平分∠BPE ，QF 平分∠EQD ，当∠PEQ ＝140°时，求出∠PFQ 的度数； （3）如图3，若点E 在CD 的下方，PF 平分∠BPE ，QH 平分∠EQD ，QH 的反向延长线交PF 于点F ．当∠PEQ ＝70°时，请求出∠PFQ 的度数．
题型三：其他
例4. （周练）如图，已知AB ∥CD ，则∠A 、∠C 、∠P 的关系为.
F
E D
C
B
A
练习1. 如图，若AB∥CD，则α、β、γ之间的关系为．
题型四：翻折
例5. 如图所示，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置，若∠EFB=65°，则∠AED′等于______
例6. 如图，将四边形纸片ABCD沿MN折叠，点A、D分别落在点A1、D1处．若∠1＋∠2＝140°，则∠B＋∠C＝°．
题型五：角平分线
例7. 如图，在△ABC中，∠ABC与∠ACB的平分线交于点O．
（1）如图1，已知∠ABC＝40°，∠ACB＝60°，求∠BOC的度数．
（2）如图2，已知∠A＝90°，求∠BOC的度数．
（3）如图1，设∠A＝m°，求∠BOC的度数．
例8. 如图13, 1BA 和1CA 分别是ABC ∆的内角平分线和外角平分线，2BA 是1A BD ∠的角平分线，2CA 是1A CD ∠的角平分线，3BA 是2A BD ∠的角平分线，3CA 是2A CD ∠的角平分线，若A α∠=，则2018A ∠
为 .
1. 如图，∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F 的度数为（ ）
A ．180°
B ．360°
C ．540°
D ．720°
2. 如图，将ABC ∆纸片沿DE 折叠，使点A 落在点'A 处，且'A B 平分ABC ∠，'A C 平分
ACB ∠，若'110BA C ∠=︒，则12∠+∠的度数为（ ） A. 80° B. 90° C. 100° D. 110°
3. 如图，将矩形纸带ABCD ，沿EF 折叠后，C 、D 两点分别落在C ′、D ′的位置，经测量得∠EFB=65°，则∠AED ′的度数是（ ）
A ． 65°
B ． 55°
C ． 50°
D ． 25°
4. 如图，已知30B ∠=︒，55BCD ∠=︒，45CDE ∠=︒，20E ∠=︒，求证：AB ∥CD ．
A
F
B
C E
D
3.
5. 如图，已知AB ∥DE ，BF ，EF 分别平分∠ABC 与∠CED ，若140BCE ∠=︒，求BFE ∠的度数．
1. 如图，ABCDE 是封闭折线，则∠A 十∠B ＋∠C ＋∠D ＋∠E 为_______度．
2. 如图，△ABE 和△ACD 是△ABC 分别沿着AB ，AC 边翻折180°形成的，若∠BAC ＝150°，则∠θ的度数是_______．
3. 如图，在△ABC 中，∠C ＝90°．若BD ∥AE ，∠DBC ＝20°，则∠CAE 的度数是
A ．40°
B ．60°
C ．70°
D ．80° 4. 如图，把矩形
沿
对折后使两部分重合，若
，则
=（ ）
A ．110°
B ．115°
C ．120°
D ．130°
A B
C
D E
1.如图所示，将△ABC沿着DE翻折，若∠1+∠2=80°，则∠B=____度．
2. 如图，若AB∥CD，BF平分∠ABE，DF平分∠CDE，∠BED=70o，则∠BFD=________．
3. 将一张长方形纸片如图所示折叠后，再展开．如果∠1=55o，那么∠2等于( )
A．55o B．60o C．65o D．70o
4. 问题情境：如图1，AB∥CD，∠PAB＝130°，∠PCD＝120°．求∠APC度数．
小明的思路是：如图2，过P作PE∥AB，通过平行线性质，可得∠APC＝50°+60°＝110°．问题迁移：
（1）如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP ＝∠α，∠BCP＝∠β．∠CPD、∠α、∠β之间有何数量关系？请说明理由；
（2）在（1）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出∠CPD、∠α、∠β间的数量关系．
5. 在△ABC中，∠A＝40°
（1）如图1，若两内角∠ABC、∠ACB的角平分线交于点P，则∠P＝，∠A与∠P 之间的数量关系是．为什么有这样的关系？请证明它；
（2）如图2，若内角∠ABC、外角∠ACE的角平分线交于点P，则∠P＝，∠A与∠P 之间的数量关系是；
（3）如图3，若两外角∠EBC、∠FCB的角平分线交于点P，则∠P＝，∠A与∠P 之间的数量关系是．
6. 【探究发现】
如图1，在△ABC中，点P是内角∠ABC和外角∠ACD的角平分线的交点，试猜想∠P与∠A 之间的数量关系，并证明你的猜想．
【迁移拓展】
如图2，在△ABC中，点P是内角∠ABC和外角∠ACD的n等分线的交点，即∠PBC＝∠ABC，∠PCD＝∠ACD，
试猜想∠P与∠A之间的数量关系，并证明你的猜想．
【应用创新】
已知，如图3，AD、BE相交于点C，∠ABC、∠CDE、∠ACE的角平分线交于点P，∠A＝35°，∠E＝25°，则∠BPD＝．。