流体力学第十章答案
《流体力学》所有做过的习题答案
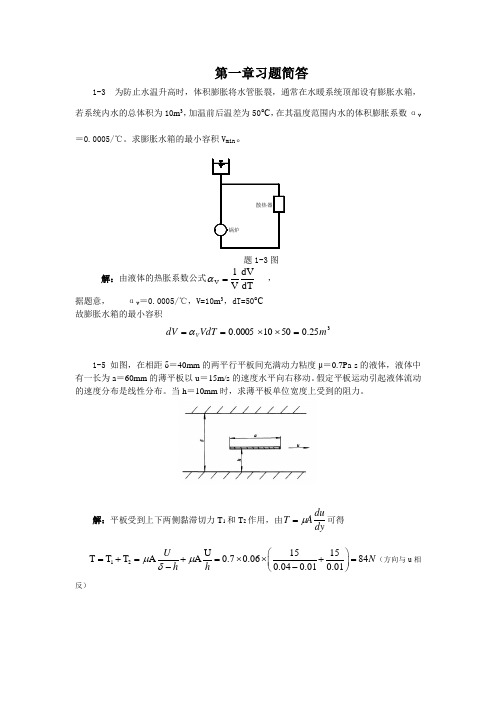
第一章习题简答1-3 为防止水温升高时,体积膨胀将水管胀裂,通常在水暖系统顶部设有膨胀水箱,若系统内水的总体积为10m 3,加温前后温差为50°С,在其温度范围内水的体积膨胀系数αv=0.0005/℃。
求膨胀水箱的最小容积V min 。
题1-3图解:由液体的热胀系数公式dTdVV 1V =α , 据题意, αv =0.0005/℃,V=10m 3,dT=50°С 故膨胀水箱的最小容积325.050100005.0m VdT dV V =⨯⨯==α1-5 如图,在相距δ=40mm 的两平行平板间充满动力粘度μ=0.7Pa·s 的液体,液体中有一长为a =60mm 的薄平板以u =15m/s 的速度水平向右移动。
假定平板运动引起液体流动的速度分布是线性分布。
当h =10mm 时,求薄平板单位宽度上受到的阻力。
解:平板受到上下两侧黏滞切力T 1和T 2作用,由dyduAT μ=可得 12U 1515T T T AA 0.70.06840.040.010.01U N h h μμδ⎛⎫=+=+=⨯⨯+= ⎪--⎝⎭(方向与u 相反)1-7 温度为20°С的空气,在直径为2.5cm 的管中流动,距管壁上1mm 处的空气速度为3cm/s 。
求作用于单位长度管壁上的黏滞切力为多少?解:温度为20°С的空气的黏度为18.3×10-6 Pa·s 如图建立坐标系,且设u=ay 2+c 由题意可得方程组⎪⎩⎪⎨⎧+-=+=ca ca 22)001.00125.0(03.00125.00 解得a = -1250,c =0.195 则 u=-1250y 2+0.195则y dy y d dy du 2500)195.01250(2-=+-= Pa dyduAT 561048.4)0125.02500(1025.0103.18--⨯-=⨯-⨯⨯⨯⨯⨯==∴πμ (与课本后的答案不一样。
流体力学张兆顺课后答案

流体力学张兆顺课后答案【篇一:流体力学知识点大全】书籍:《全美经典-流体动力学》《流体力学》张兆顺、崔桂香《流体力学》吴望一《一维不定常流》《流体力学》课件清华大学王亮主讲目录:第一章绪论第二章流体静力学第三章流体运动的数学模型第四章量纲分析和相似性第五章粘性流体和边界层流动第六章不可压缩势流第七章一维可压缩流动第八章二维可压缩流动气体动力学第九章不可压缩湍流流动第十章高超声速边界层流动第十一章磁流体动力学第十二章非牛顿流体第十三章波动和稳定性第一章绪论1、牛顿流体:剪应力和速度梯度之间的关系式称为牛顿关系式,遵守牛顿关系式的流体是牛顿流体。
2没有内摩擦,也就没有内耗散和损失。
层流:纯粘性流体,流体分层,流速比较小;湍流:随着流速增加,流线摆动,称过渡流,流速再增加,出现漩涡,混合。
因为流速增加导致层流出现不稳定性。
定常流:在空间的任何点,流动中的速度分量和热力学参量都不随时间改变,3、欧拉描述:空间点的坐标;拉格朗日:质点的坐标;4、流体的粘性引起剪切力,进而导致耗散。
5、无黏流体—无摩擦—流动不分离—无尾迹。
6、流体的特性:连续性、易流动性、压缩性不可压缩流体:d??0dtconst是针对流体中的同一质点在不同时刻保持不变,即不可压缩流体的密度在任何时刻都保持不变。
是一个过程方程。
7、流体的几种线流线:是速度场的向量线,是指在欧拉速度场的描述;同一时刻、不同质点连接起来的速度场向量线;dr?u?x,tdr?u?0迹线:流体质点的运动轨迹,是流体质点运动的几何描述;同一质点在不同时刻的位移曲线;涡线:涡量场的向量线,u,dr???x,t??dr???0涡线的切线和当地的涡量或准刚体角速度重合,所以,涡线是流体微团准刚体转动方向的连线,形象的说:涡线像一根柔性轴把微团穿在一起。
第二章流体静力学1、压强:p?lim?fdf??a?0?ada静止流场中一点的应力状态只有压力。
2、流体的平衡状态:1)、流体的每个质点都处于静止状态,==整个系统无加速度;2)、质点相互之间都没有相对运动,==整个系统都可以有加速度;由于流体质点之间都没有相对运动,导致剪应力处处为零,故只有:体积力(重力、磁场力)和表面力(压强和剪切力)存在。
流体力学第8、10、11章课后习题

第八章 边界层理论基础一、主要内容(一)边界层的基本概念与特征1、基本概念:绕物体流动时物体壁面附近存在一个薄层,其内部存在着很大的速度梯度和漩涡,粘性影响不能忽略,我们把这一薄层称为边界层。
2、基本特征:(1)与物体的长度相比,边界层的厚度很小;(2)边界层内沿边界层厚度方向的速度变化非常急剧,即速度梯度很大; (3)边界层沿着流体流动的方向逐渐增厚;(4)由于边界层很薄,因而可以近似地认为边界层中各截面上压强等于同一截面上边界层外边界上的压强;(5)在边界层内粘性力和惯性力是同一数量级;(6)边界层内流体的流动与管内流动一样,也可以有层流和紊流2种状态。
(二)层流边界层的微分方程(普朗特边界层方程)22100y x x x y y x v pv v v v x y x y py v v x y νρ⎧∂∂∂∂+=-+⎪∂∂∂∂⎪⎪∂⎪=⎨∂⎪⎪∂∂⎪+=∂∂⎪⎩其边界条件为:在0y =处,0x y v v == 在δ=y 处,()x v v x = (三)边界层的厚度从平板表面沿外法线到流速为主流99%的距离,称为边界层的厚度,以δ表示。
边界层的厚度δ顺流逐渐加厚,因为边界的影响是随着边界的长度逐渐向流区内延伸的。
图8-1 平板边界层的厚度1、位移厚度或排挤厚度1δδδδ=-=-⎰⎰1001()(1)x x v v v dy dy v v2、动量损失厚度2δδρρ∞∞=-=-⎰⎰221()(1)x x x x v vv v v dy dy v v v(四)边界层的动量积分关系式δδρρδτ∂∂∂-=--∂∂∂⎰⎰200x x w Pv dy v v dy dx x x x对于平板上的层流边界层,在整个边界层内每一点的压强都是相同的,即P =常数。
这样,边界层的动量积分关系式变为δδτρ∞-=-⎰⎰200w x x d d v dy v v dy dx dx 二、本章难点(一)平板层流边界层的近似计算 根据三个关系式:(1)平板层流边界层的动量积分关系式;(2)层流边界层内的速度分布关系式;(3)切向应力关系式。
《流体力学》课后习题答案.pdf

得:T1 = t1 + 273 = 50 + 273 = 323K ,T2 = t2 + 273 = 78 + 273 = 351K
根据
p
=
mRT V
,有:
p1
=
mRT1 V1
,
p2
=
mRT2 V2
得: V2 V1
=
p1 p2
T2 T1
=
9.8067 104 5.8840 105
351 323
=
0.18
设管段长度 l,管段表面积: A = dl
单位长度管壁上粘滞力: = A u = dl u − 0 = 3.14 0.025 0.03
l y l
0.001
1-8 解: A = 0.8 0.2 = 0.16m2 ,u=1m/s, = 10mm , = 1.15Pa s
T = A u = A u − 0 = 1.15 0.16 1 = 18.4N
1
=
T1 b
=
A b
u
−0 −h
=
0.7 0.06b b
15 − 0 0.04 − 0.01
=
21N
/m,方向水平向左
下表面单位宽度受到的内摩擦力:
2
=
T2 b
=
Au−0 b h−0
=
0.7 0.06b 15 − 0
b
0.01− 0
= 63N
/m,方向水平向左
平板单位宽度上受到的阻力:
= 1 + 2 = 21+ 63 = 84N ,方向水平向左。
h1 = 5.6m
2.4 解:如图 1-2 是等压面,3-4 是等压面,5-6 段充的是空气,因此 p6 = p5 ,6-7 是等压面,
华中科技大学流体力学习题参考答案(1)

严新华主编《水力学(修订本)》教材(科技文献出版社2001年版)部分习题参考答案第一章 习题答案1-1 水的运动粘性系数s m /10006.126-⨯=ν;空气的动力粘性系数s Pa ⋅⨯=-51081.1μ。
1-2 活塞移动速度s m V /49.0=。
1-3 动力粘性系数s Pa ⋅=151.0μ。
1-4 2/5.11m N =τ。
1-5 阻力矩m N M ⋅=6.39。
第二章 习题答案2-1(a )图中2/6.68m KN p A =;绝对压强2/93.169m KN p A='。
(b )图中22/4.29,0,/6.19m KN p p m KN p A B C -===;绝对压强222/93.71,/33.101,/93.120m KN p m KN p m KN p AB C ='='='。
2-2 20/4900m N p -=;液面真空值20/4900m N p V =。
2-3(1)2/54.115m KN p A =';2/47.17m KN p A =。
(2)压力表读数m h m KN p M 213.1,/63.92==。
2-4 A 点表压强2/8.9m KN p A -=;液面空气真空度2/6.19m KN p V =。
2-5 m H 40.0=。
2-6 cm h 1284=。
2-7 O H 84.172mmh V =。
2-8 ①2/22.185m KN p p B A =-;②2/42.175m KN p p B A =-。
2-9 ⑴21/86.1m KN p p B A -=-为油时:ρ;⑵21/784.0m KN p p B A -=-为空气时:ρ。
2-10 ⎪⎭⎫⎝⎛-='b a 1ρρ;gH b a p p BA ρ=-。
2-11 241/1084.118m N p ⨯=。
2-12 )/3.101(/84.37822m KN p m KN p a =='取:。
[工程流体力学(水力学)]第二版--禹华谦1-10章习题解答
![[工程流体力学(水力学)]第二版--禹华谦1-10章习题解答](https://img.taocdn.com/s3/m/e3696bd46294dd88d0d26bff.png)
第一章 绪论1-1.20℃的水2.5m 3,当温度升至80℃时,其体积增加多少?[解] 温度变化前后质量守恒,即2211V V ρρ= 又20℃时,水的密度31/23.998m kg =ρ 80℃时,水的密度32/83.971m kg =ρ321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆ 1-2.当空气温度从0℃增加至20℃时,运动粘度ν增加15%,重度γ减少10%,问此时动力粘度μ增加多少(百分数)?[解] 原原ρννρμ)1.01()15.01(-+==原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμ此时动力粘度μ增加了3.5%1-3.有一矩形断面的宽渠道,其水流速度分布为μρ/)5.0(002.02y hy g u -=,式中ρ、μ分别为水的密度和动力粘度,h 为水深。
试求m h 5.0=时渠底(y =0)处的切应力。
[解] μρ/)(002.0y h g dydu-=)(002.0y h g dydu-==∴ρμτ 当h =0.5m ,y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4.一底面积为45×50cm 2,高为1cm 的木块,质量为5kg ,沿涂有润滑油的斜面向下作等速运动,木块运动速度u=1m/s ,油层厚1cm ,斜坡角22.620 (见图示),求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时,等速下滑yu AT mg d d sin μθ== 001.0145.04.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg s Pa 1047.0⋅=μ1-5.已知液体中流速沿y 方向分布如图示三种情况,试根据牛顿内摩擦定律yud d μτ=,定性绘出切应力沿y 方向的分布图。
[解]第二章 流体静力学2-1.一密闭盛水容器如图所示,U 形测压计液面高于容器内液面h=1.5m ,求容器液面的相对压强。
流体力学第十章 相似原理和因次分析

例如: 粘滞力相似:由 Re m Re p 得
vmlm
m
v pl p
m p
p
vm l p 1 v p lm l
重力相似:由 Frm Frp 得
vm g m lm vp g pl p
gm g p
lp vm 1 vp lm l
由此可以看出,有时要想做到完全相似是不可能 的,只能考虑主要因素做近似模型实验。
Fm mVm vm tm 3 1 2 2 l v t l v Fp pVp v p t p
也可写成:
F 1 2 2 l v
令:
F
l v
2 2
Ne
Ne称为牛顿数, 它是作用力与 惯性力的比值。
Ne称为牛顿数,它是某种作用力与惯性 力的比值,是无量纲数。由此可知,模型 与原型的流场动力相似,它们的牛顿数必 相等。
qv g H f
f const 2 时, 2
当重力加速度 g 不变时,三角堰流量与堰
顶水头 H 的关系为:
qv CH ~ H
5 2 5 2
其中 c 只能用实验方法或其他方法确定。
【例】 不可压缩粘性流体在粗糙管内定常流动时,沿管道 的压强降 p 与管道长度 L ,内径 d ,绝对粗糙度 ,流体的平均 流速 v ,密度 和动力粘度 有关。试用瑞利法导出压强降的表 达式。 【解】 按照瑞利法可以写出压强降 p kLa d a a v a a a (b)
第三节
动力相似的准则(模型率)
一.相似准则的提出
相似原理说明两个流动系统相似必须在几何相似、 运动相似和动力相似三个方面都得到满足。 但实际应用中,并不能用定义来检验流动是否相 似,因为通常原型的流动是未知的。这就产生一个问
流体力学课后作业答案

v1
2
2g
h2
v2
2
2g
1
v1 2.572m/s, v2 =4.287m/s
F P P Q( 2v2 1v1 ) 1 2
1 2
列动量方程
P ghC1 A1 1 1 2
2
gh1 B 13.23kN P2 ghC 2 A2
gh2 B 4.763kN
26
4-20 环形断面管道中水温10℃,流量Q=400L/min, 流 当量粗糙高度K=0.15mm,d=75mm,D=100mm。求 体 在管长l=300m管段上的沿程水头损失。 力 Q 4Q 查水温得 解: v 1.94m/s 学 2 2 A (D d ) 6 2 1.308 10 m /s 2 2
流 2-7 测压管中水银柱差Δh=100mm,在水深h=2.5m处安 体 装测压表M,求其读数,并图示测压管水头线的位置。 力 学
测压管水头线 p0 h’ h M
解: p p0 w gh
Hg g h w gh (13.6 0.1 1 2.5) 9.8 37.83kPa
P Px Pz 121.85kN
2 2
=arctg
Pz Px
78.4
P指向圆柱中心
50
作图题1. 画出图中AB 面上的静压强分布图 形。 pa
ρgh1 ρgh2 ρgh3 pa+ρgh2 ρgh ρgh1 ρg(h-h2) ρgh pa+ρgh1
流 体 力 学
ρg(h-h2)
ρg(h+R)
/ 25 10
3
0.006
2 lg
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
流体力学第十章答案【篇一:流体力学讲义第十章堰流】明渠缓流由于流动边界急剧变化而引起的明渠急变流现象。
本章主要介绍各类堰流的水力特征、基本公式、应用特点及水力计算方法。
概述一、堰和堰流堰:在明渠缓流中设置障壁,它既能壅高渠中的水位,又能自然溢流,这障壁就称为堰。
堰流(weir flow):缓流越过阻水的堰墙溢出流动的局部水流现象称为堰流。
选择:堰流特定的局部现象是:a.缓流通过障壁;b.缓流溢过障壁;c.急流通过障壁;d.急流溢过障壁。
研究堰流的主要目的:探讨流经堰的流量q及与堰流有关的特征量之间的关系。
堰流的基本特征量(图10-1)1.堰顶水头h;2.堰宽b;3.上游堰高p、下游堰高p1;图10-15.上、下水位差z;二、堰的分类1.根据堰壁厚度d与水头h的关系,如图10-2:图10-2图10-32.根据上游渠道宽度b与堰宽b的关系,图10-4:3.根据堰与水流方向的交角:图10-44.按下游水位是否影响堰流性质:5.按堰口的形状:堰可分为矩形堰、梯形堰、三角堰。
三、堰流及孔流的界限1.堰流:当闸门启出水面,不影响闸坝泄流量时。
孔流:当闸门未启出水面,以致影响闸坝泄流量时。
2.堰流和孔流的判别式(1)宽顶堰式闸坝堰流:e/h ≥0.65 孔流: e/h 0.65(2)实用堰式闸坝(闸门位于堰顶最高点时)堰流:e/h ≥0.75 孔流: e/h 0.75式中: e——闸门开启高度;h——堰孔水头。
判断:从能量角度看,堰流和闸孔出流的过程都是一种势能转化为动能的过程。
对第一节堰流的基本公式一、堰流基本公式推导(图10-7)由大孔口的流量公式及,并考虑上游行近流速的影响,令图10-6得堰流的基本公式:(10-1)式中:m——堰流流量系数,m=。
二、堰流公式图10-7若考虑到侧收缩影响及淹没影响,则堰流公式为:(10-2)——淹没系数,≤1.0;(10-3)式中:——侧收缩系数,≤1.0 。
m0——计及行近流速的流量系数第二节薄壁堰薄壁堰(如图10-8)主要用途:用作量水设备。
薄壁堰口的横断面形状不同,相应的流量系数也不同。
图10-8一、矩形薄壁堰1. 基本公式(10-4)2.无侧收缩、自由式、水舌下通风的矩形正堰:采用巴赞公式计算:(10-5)公式适用范围:b=0.2~2.0m,p=0.24~0.75m,h=0.05~1.24m,式中h、p均以m计。
初步设计时,取,则:(10-6)3. 有侧收缩、自由式、水舌下通风的矩形正堰:4.矩形薄壁堰的淹没判别条件(图10-9)1)堰下游水位高出堰顶标高,即zh;——必要条件2)在堰下游发生淹没式水跃衔接,即hthc ——充分条件(10-7)(10-8)淹没溢流时,不仅堰的过水能力降低,而且下游水面波动较大,溢流不稳定。
所以用于测量流量用的薄壁堰,不宜在淹没条件下工作。
图10-9二、三角形堰(图10-10)堰通常用于实验室作小流量测量。
当堰为直角三角堰时:适用条件:(10-9)。
图10-10三、梯形薄壁堰当时的自由出流时的梯形薄壁堰公式为:说明:当(10-10)时,侧收缩梯形堰倾斜部分所增加的流量,正好的梯形抵消矩形堰侧收缩影响所减小的流量。
即有侧收缩的堰作自由出流时的流量等于没有侧收缩的自由出流矩形堰的流量。
注:以上三类薄壁堰的流量计算公式均是指自由出流。
图10-11问题1:当用矩形薄壁堰来测量流量时,,下,水流最稳定,测量精度最高。
a.有侧收缩自由出流;b.有侧收缩淹没出流;c.无侧收缩自由出流;d.无侧收缩淹没出流。
问题2:为保证薄壁堰为自由出流,应满足:a.堰上水头尽量小,水舌下游空间应与大气相通;b.堰上水头不宜过小,水舌下游空间应与大气相通;c.堰上水头尽量小,水舌下游空间不应与大气相通;d.堰上水头不宜过小,水舌下游空间不应与大气相通。
第三节实用堰实用堰的主要用途:用作蓄水建筑物——坝,或净水建筑物的溢流设备,如图10-12。
图10-12一、曲线型实用堰(图10-13)1.真空实用堰、非真空实用堰非真空实用堰(non-vacuum weir):若堰面的剖面曲线基本上与堰的水舌下缘外形相符,水流作用于堰面上的压强仍近似为大气压强,这种堰称为非真空实用堰。
真空实用堰(vacuum weir):若堰面的剖面曲线低于堰的水舌下缘,溢流水舌脱离堰面,脱离处的空气被水流带走而形成真空区,这种堰称为真空实用堰。
选择:当曲线型实用堰的实际作用水头大于设计水头时,则过堰流量会: a.减小; b.增加;c.【篇二:10第十章明渠流和闸孔出流及堰流】txt>10—1某梯形断面粉质粘土渠道中的均匀流动,如图所示。
已知渠底宽度b=2.0m,水深h0=1.2m,边坡系数m=1.0,渠道底坡度i=0.0008,粗糙系数n=0.025,试求渠中流量q和断面平均流速v,并校核渠道是否会被冲刷或淤积. 解:a=bh0?mh02?(2?1.2?1?1.22)m2?3.84m2??b?2h?(2?2?m?5.39m1q?1i2n5a3?5?23?23?0.000820.025qa??3.843?5.39m/s?3.46m/s33v=3.463.84m/s?0.90m/s校核:由表10-3查得粉质粘土最大允许流速为1m/s,因h0=1.2m1.0m,需乘以系数k=1.25,所以vmax=1?1.25 m/s=1.25m/s,最小允许流速vmin=0.4m/s,满足vmaxvvmin条件。
10—2 设有半正方形和半圆形两种过流断面形状的渠道,具有相同的n=0.02,a=1.0m,i=0.001,试比较它们在均匀流时的流量q的大小。
解:设正方形渠道流量为q1,半圆形渠道流量为q2,12q1=a1c?i12n115a13?1353?2?2q2?a2c?i22n2a2?23q1q2?(其中 i1?i2,n1?n2,a1?a2?a,2由于 a?2h1,h1??2?12)3,?1?4h1??2?又a?2,r2?1??0.89 , q1?(0.89)3q2?0.93q21523q1?q2?i1n12a13?3??0.00120.0235?13??23m/s?0.8m/s330.80.93m/s?0.86m/s10—3 某梯形断面渠道中的均匀流动,流量q=20m3/s,渠道底宽b=5.0m,水深h0=2.5m,边坡系数m=1.0,粗糙系数n=0.025,试求渠道底坡i。
1解:由q?i2n5a3??23知i?(qn5a?3?23)107 2a?bh0?mh0?(5?2.5?1?2.5)m?18.75m2222??b?2h?(5?2??12.07mi?(20?0.02553?23)?0.0004218.75?12.070.0003?i?0.01可保证正常的排水条件,且不必人工加固。
10—4为测定某梯形断面渠道的粗糙系数n值,选取l=1500m长的均匀流段进行测量。
已知渠底宽度b=10m,边坡系数m=1.5,水深h0=3.0m。
两断面的水面高差?z=0.3m,流量q=50m3/s,试计算n 值。
解:z1?z2??z?hf,i?j?jf?1hfl?0.31500?0.0002由均匀流基本方程可得n=i2q5ac3-23,式中a=(10?3.01.5?3.0)m2243.5m2??(10?2?3.0??20.82m1?0.025010—5 某梯形断面渠道底坡i=0.004,底宽b=5.0m,边坡系数m=1.0,粗糙系数n=0.02,n??43.53?20.8230.000225?2求流量q=10m3/s时的正常水深h0及断面平均流速v0。
1解:q?i2n5a?3?23?1?h(b?mh)?3?i2n251(b?23222将已知值代入,由试算法可得 h0=0.76ma?bh0?mh0?(5?0.76?1?0.76)m?4.38m2v0?qa?104.38m/s?2.28m/s310—6 某梯形断面渠道中的均匀流,流量q=3.46m/s,渠底坡度i=0.0009,边坡系数m=1.5,粗糙系数n=0.02,正常水深h0=1.25m,试设计渠底宽度b。
解:q?ac??h0(b?mh0)?3?i2251n(b?2h03将已知值代入,由试算法可得b=0.80m。
10—7 设有一块石砌体矩形陡槽,陡槽中为均匀流。
已知流量q=2.0m/s,底坡i?0.09,粗糙系数n?0.020,断面宽深比?h?3bh0?2.0,试求陡槽的断面尺寸h0及b。
解:?h?bh0?2.0,b?2h0,a?2h0,??4h0,52?232代入均匀流基本方程得 (2h0)3(4h0)?qn10.86mi2将已知值代入,解得:h0=0.43m,b=2?0.43m108 10—8 试拟定某梯形断面均匀流渠道的水力最优断面尺寸。
已知边坡系数m?1.5,粗糙系数n?0.025,底坡i?0.002,流量q=3.0m3/s。
解:由水力最佳条件知?h?bh0?m)?1.5)?0.6122b?0.61h0,a?bh0?mh0?2.11h0??b?2h?4.22h0将已知值代入均匀流基本方程得3.0?0.02515?(2.11h0)(4.22h0)23?230.0022解得:h0?1.09m,b?0.61?1.09m?0.66m10—9 需在粉质粘土地段上设计一条梯形断面渠道。
已知均匀流流量q=3.5m3/s,渠底坡度i=0.005,边坡系数m=1.5,粗糙系数n=0.025,试分别按(1)不冲允许流速vmax及(2)水力最优条件设计渠道断面尺寸,并确定采用哪种方案设计的断面尺寸和分析是否需要加固。
解:(1)由表10-3查得粉质粘土vmax=1.0m/sa=qvmax=3.51.0222=3.5m=bh0+mh0=bh0+1.5h0 (1)1由vmax==1n1223iac-23,1.0=0.00520.0253.5c3-23,c=16.66mb=2m=2(2)bh=h02))a=bh0+mh0=0.61h0+1.5h0=2.11h0222,c=b+2h0=0.61h0+3.61h0=4.22h0q=1n1253iac-23,3.5=23810.025122530.005(2.11h)(4.22h0)230.59m100.931467=h032,h03=0.93,h0=0.97m,b=0.61?0.97m 2a=2.11h0=1.99mqa=3.51.99m/s=1.76m/svmax=1.0m/s。
按不冲允许流速计算结果水深太浅,故按水力最优条件设计断面尺寸,需加固,可采用干砌块石(vmax=2.0m/s)。
10—10 某圆形污水管道,如图所示。
已知管径d=1000mm,粗糙系数n=0.016,底坡i=0.01,试求最大设计充满度时的均匀流流量q及断面平均流速v。
