三阶系统的综合分析与设计
实验四三阶系统的瞬态响应及稳定性分析
实验四三阶系统的瞬态响应及稳定性分析引言：实际工程中经常遇到三阶系统，对三阶系统的瞬态响应及稳定性进行分析能够帮助我们更好地设计和优化控制系统。
本实验旨在通过实验，研究三阶系统的瞬态响应及稳定性，并加深对其理论知识的理解和掌握。
实验一：三阶系统的瞬态响应1.实验目的：通过三阶系统的瞬态响应实验，观察系统的输出响应情况，了解系统的动态特性。
2.实验仪器：示波器、波形发生器、三阶系统实验箱3.实验原理：三阶系统的瞬态响应是指系统在初始状态发生突变时，输出的响应情况。
三阶系统的瞬态响应主要涉及到系统阶跃响应、系统脉冲响应。
4.实验步骤：a.将波形发生器的正弦波信号输入三阶系统实验箱。
b.设置示波器的观测通道，将示波器的探头连接到三阶系统实验箱的输出端口。
c.调节波形发生器的频率和幅度，观察示波器上得到的输出响应波形。
5.数据处理：a.根据示波器上输出的响应波形，可以观察到系统的超调量、调整时间等指标，根据公式可以计算得到这些指标的具体数值。
b.将实验得到的数据记录下来，进行分析和比较。
1.实验目的：通过三阶系统的稳定性分析实验，了解系统的稳定性及稳定性判据。
2.实验仪器：示波器、三阶系统实验箱3.实验原理：三阶系统的稳定性是指系统在初始状态发生突变或受到外部扰动时，系统是否能够回到稳定状态。
常见的稳定性分析方法包括极点判据、频率响应法等。
4.实验步骤：a.将示波器的探头连接到三阶系统实验箱的输出端口。
b.调节系统的输入信号，观察示波器上得到的系统输出响应波形。
c.根据观察到的输出波形，分析系统的稳定性。
5.数据处理：a.根据实验得到的数据和观察到的波形，可以从输入输出关系中提取出系统的稳定性信息，比如振荡频率、稳定的输出值等。
b.根据提取出的信息，判断系统的稳定性。
实验三：实验结果和分析1.通过实验一，我们可以观察到三阶系统的瞬态响应，并根据输出波形，计算得到系统的超调量、调整时间等指标。
通过对比不同输入频率和幅度下的响应波形，可以分析系统的动态特性。
三阶系统综合分析与设计
目录摘要 (1)1 设计内容 (2)1.1 设计题目 (2)1.2 设计任务 (2)２绘制三阶系统的根轨迹 (3)2.1 常规方法绘制根轨迹 (3)2.2用MATLAB绘制根轨迹 (4)3 不同条件下K的取值 (5)3.1 当-8为闭环系统的一个极点时，K的取值 (5)3.2 主导极点阻尼比为0.7时的k值 (6)4 求系统的稳态误差 (6)4.1 位置误差系数 (7)4.2 速度误差系数 (7)4.3 加速度误差系数 (8)4.4 输入信号为25.2)(1)(tttt r++=时的稳态误差 (8)5 绘制单位阶跃响应曲线 (8)6 频域特性分析 (9)6.1绘制Bode图和Nyquist曲线 (9)6.2相角裕度和幅值裕度 (12)7 加入非线性环节判断稳定性 (13)7.1 求死区特性环节的描述函数 (13)7.2 根据负倒描述函数和Nyquist图判断系统的稳定性 (14)8 设计体会 (15)参考文献 (17)摘要三阶系统是以三级微分方程为运动方程的控制系统。
在控制工程中，三阶系统非常普遍，其动态性能指标的确定是比较复杂。
在工程上常采用闭环主导极点的概念对三阶系统进行近似分析，或直接用MATLAB软件进行高阶系统分析。
在课程设计中，要掌握用MATLAB绘制闭环系统根轨迹和系统响应曲线，用系统的闭环主导极点来估算三系统的动态性能，以及在比较点及开环传递函数之间加一个非线性环节判断其稳定性。
1 设计内容1.1 设计题目三阶系统的综合分析和设计初始条件：某单位反馈系统结构图如图1-1所示：图1-1 图1-2 1.2 设计任务要求完成的主要任务: （包括课程设计工作量及其技术要求，以及说明书撰写等具体要求）1、试绘制随根轨迹2、当-8为闭环系统的一个极点时，K=?3、求取主导极点阻尼比为0.7时的K 值（以下K 取这个值）4、分别求取位置误差系数、速度误差系数、加速度误差系数及输入信号为25.2)(1)(t t t t r ++=单位阶跃信号、斜坡信号及单位加速度信号时的稳态误差5、用Matlab 绘制单位阶跃相应曲线6、绘制Bode 图和Nyquist 曲线，求取幅值裕度和相角裕度7、如在比较点及开环传递函数之间加1个死区非线性环节，如图1-2所示，其中2,10==k e ，试求取非线性环节的描述函数，并根据负倒描述函数和Nyquist 图判断系统的稳定性8、认真撰写课程设计报告。
实验三-三阶系统的阶跃响应及稳定性分析实验
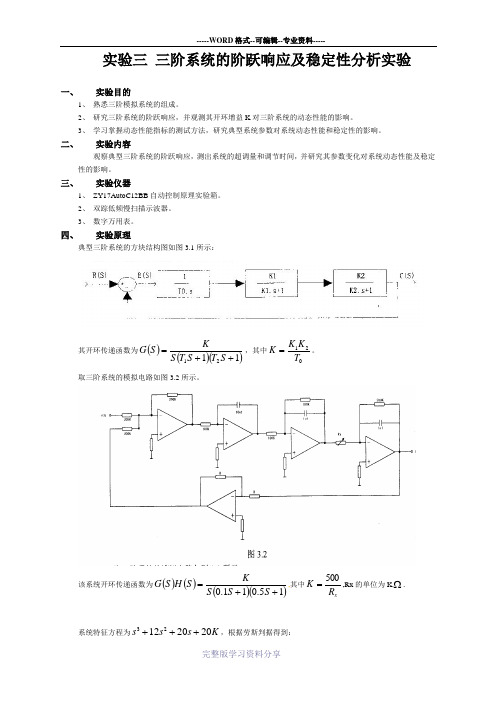
实验三 三阶系统的阶跃响应及稳定性分析实验一、 实验目的1、 熟悉三阶模拟系统的组成。
2、 研究三阶系统的阶跃响应，并观测其开环增益K 对三阶系统的动态性能的影响。
3、 学习掌握动态性能指标的测试方法，研究典型系统参数对系统动态性能和稳定性的影响。
二、 实验内容观察典型三阶系统的阶跃响应，测出系统的超调量和调节时间，并研究其参数变化对系统动态性能及稳定性的影响。
三、 实验仪器1、 ZY17AutoC12BB 自动控制原理实验箱。
2、 双踪低频慢扫描示波器。
3、 数字万用表。
四、 实验原理典型三阶系统的方块结构图如图3.1所示：其开环传递函数为()()()1121++=S T S T S K S G ，其中021T K K K =。
取三阶系统的模拟电路如图3.2所示。
该系统开环传递函数为()()()()15.011.0++=S S S K S H S G,其中x R K 500=,Rx 的单位为K Ω.系统特征方程为K s s s 20201223+++，根据劳斯判据得到：系统稳定0<K<12系统临时稳定K=12系统不稳定K>12根据K可求取Rx，改变Rx即可实现三种典型的实验。
该系统的阶跃响应图如所示，图3.3.1，图3.3.2和图3.3.3分别对应于系统处于稳定，临界稳定和不稳定的三种情况。
五、实验步骤1、利用实验仪器，按照实验原理设计并连接由一个积分环节和两个惯性环节组成的三阶闭环系统的模拟电路。
此实验可使用运放单元（一）、（二）、（三）、（五）、（六）及元器件单元中的电容和可调电阻。
（1）同时按下电源单元中的按键开关S001,S002,再按下S003，调节可调电位器W001,使T006（-12V-----+12V）输出电压为+1V，形成单位阶跃信号电路，然后将S001,S002再次按下关闭电源。
（2）按照图3.2连接好电路，按下电路中所用到的运放单元的按键开关。
（3）用导线将连接好的模拟电路的输入端与T006相连接，电路的输出端与示波器相连接。
三阶系统综合分析与设计解析
三阶系统是以三级微分方程为运动方程的控制系统。在控制工程中，三阶系统非常普遍，其动态性能指标的确定是比较复杂。在工程上常采用闭环主导极点的概念对三阶系统进行近似分析，或直接用MATLAB软件进行高阶系统分析。在课程设计中，要掌握用MATLAB绘制闭环系统根轨迹和系统响应曲线，用系统的闭环主导极点来估算三系统的动态性能，以及在比较点与开环传递函数之间加一个非线性环节判断其稳定性。
8、认真撰写课程设计报告。
２ 绘制三阶系统
图2系统结构图
由图1可得，三阶系统的开环传递函数为：
G（s）=ห้องสมุดไป่ตู้
2.1
根据绘制根轨迹的规则，可知该系统的根轨迹绘制步骤如下：
（1）根轨迹的起点和终点。根轨迹起于开环极点，终于开环零点。
开环极点分别为0、-3、-6，无开环零点。
（2）根轨迹的分支数。n=3，m=0，所以分支数为3 。且它们是连续的并且对称于实轴。
1 设计内容
1.1 设计题目
三阶系统的综合分析和设计
初始条件：某单位反馈系统结构图如图1-1所示：
图1-1 图1-2
1.2 设计任务
要求完成的主要任务:（包括课程设计工作量及其技术要求，以及说明书撰写等具体要求）
1、试绘制随根轨迹
2、当-8为闭环系统的一个极点时，K=?
3、求取主导极点阻尼比为0.7时的K值（以下K取这个值）
于是分离点方程为：
因此可以求得分离点d=-1.3,d=-4.7（不合题意，舍去）
(6)根轨迹与虚轴的交点。
闭环特征方程式为
对上式应用劳斯判据，有：
1 18
9 k
k
令劳斯表中 行的首项为零，得k= 162,根据 行的系数，得辅助方程
9 +k=0
三阶系统的分析与校正
课程设计报告( 2013—2014年度第一学期)名称：自动控制理论题目：三阶系统的分析与校正院系：控计学院班级：自动化1105学号：学生姓名：指导教师：袁桂丽设计周数：1周成绩：日期：2014年1月9目录一、《自动控制理论A》课程设计任务书 (1)二、《自动控制理论A》课程设计 (3)三、设计正文 (4)五课程设计心得 (21)六参考文献 (22)一、《自动控制理论A 》课程设计任务书1. 目的与要求本次课程设计是在学完自动控制理论课程后进行的。
详细介绍MATLAB 的控制系统工具箱的用法以及SIMULINK 仿真软件，使学生能够应用MATLAB 对自动控制理论课程所学的内容进行深层次的分析和研究，能用MATLAB 解决复杂的自动控制系统的分析和设计题目；能用MATLAB 设计控制系统以满足具体的性能指标； 能灵活应用MATLAB 的CONTROL SYSTEM 工具箱和SIMULINK 仿真软件，分析系统的性能，进行控制系统设计。
2. 主要内容简要介绍控制系统理论的基本概念和基本方法，并介绍MATLAB 软件的基本知识。
包括MATLAB 的基本操作命令、数据结构、矩阵运算、编程算法等; 简要介绍MATLAB 的控制系统工具箱的用法。
包括控制系统的模型及相互转换、时域分析方法、频域分析方法等应用MATLAB 工具箱进行分析研究，增强理解;简要介绍SIMULINK 仿真软件，介绍SIMULINK 的应用方法及各种强大功能，应用SIMULINK 对系统进行仿真研究;简要介绍控制系统分析与设计所必须的工具箱函数，包括模型建立、模型变换、模型简化、模型实现、模型特性、方程求解、时域响应、频域响应、根轨迹等各个方面。
1. 在掌握控制系统基本理论和控制系统工具箱函数的基础上，利用MATLAB 及其工具箱函数来解决所给控制系统的分析与设计问题,并上机实验;撰写课程设计报告。
2. 设计任务2.1 自选单位负反馈系统，开环传递函数)s (G 0[一个三阶或以上系统]。
自动控制原理课程设计--三阶系统分析与校正
自动控制原理课程设计--三阶系统分析与校正
随着工业化日益发展，自动控制相关的技术日趋重要，三阶系统分析与校正也变得更加重要了。
三阶系统是一种外增调控系统，具有以下特征：它具有反馈回路，并以反应延迟为组件。
在有效的调节过程中，三阶系统的表现更佳，能够更有效地进行调节，满足较高的精度要求。
因此，三阶系统分析与校正一直是自动控制原理书中重要的课程，也是许多工业相关专业常安排的课程。
三阶系统分析与校正课程的任务非常重要，主要包括三阶系统的建模、解析与数值分析，以及信号处理中系统的校正。
首先，要了解三阶系统的定性模型，以及系统的动态特性，掌握三阶系统的时延与振荡的影响原则。
其次，要掌握解析法及数值法，能够敏锐地指出未知系统的动态特性，分析系统的调节误差。
最后，要理解三阶系统的校正原理，掌握系统校正过程中的参数估计方法与滤波技术。
在实际应用中，能够用校正方法有效地改善系统的性能。
此外，三阶系统分析与校正还为许多智能技术与机器学习提供了坚实的把柄，比如自动机器人与机器视觉、智能控制与自主导航等先进技术。
在应用广泛的同时，三阶系统分析与校正课程也一直是重要的技术训练课程，对不同领域的工程师都有着十分重要作用。
通过学习三阶系统分析与校正课程，学生们将掌握分析、计算以及改善三阶系统性能的基础技术，更深入地认识自动控制的相关原理，并能灵活运用，能够更好地应用到实际工程中。
学习课程的重点，是培养学生的独立解决工程问题的分析、解决能力，帮助学生将自动控制原理技术付诸实施，最终让这些技术能够更好地服务于工业发展中。
I型三阶系统典型分析及综合设计
I型三阶系统典型分析及综合设计I型三阶系统是指具有三个自由度的积分器的系统，即系统具有三个积分器。
它是一种常见的控制系统结构，常用于系统对静态误差有较高要求的控制应用中。
典型分析：1. 零极点分析：对于I型三阶系统，由于具有三个积分器，系统的开环传递函数的分母可以表示为s^3，即系统有一个零点在无穷远处。
同时，根据系统的需求，可以根据实际情况设计系统的零点和极点位置。
2. 频率响应分析：通过对系统的频率响应进行分析，可以了解系统对不同频率信号的响应情况。
对于I型三阶系统，频率响应主要关注系统的增益和相位特性。
可以通过绘制系统的幅频曲线和相频曲线来进行频率响应分析。
3. 稳定性分析：稳定性是控制系统设计中的重要指标之一。
对于I型三阶系统，可以通过分析系统的极点位置来判断系统的稳定性。
如果系统的极点都在左半平面，即实部为负，那么系统是稳定的。
综合设计：在进行I型三阶系统综合设计时，可以根据系统的要求和性能指标，设计合适的控制器结构来实现系统的控制目标。
常用的设计方法包括PID控制器设计和状态反馈控制器设计。
具体的设计步骤包括：1. 确定系统的需求和性能指标，如静态误差要求、响应速度要求等。
2. 根据系统的需求和性能指标，选择合适的控制器结构，如PID控制器、状态反馈控制器等。
3. 设计控制器的参数，通常可以通过经验法则、频率响应设计法或优化方法来确定控制器的参数。
4. 进行控制系统的仿真和实验验证，根据实际效果对控制器进行调整和优化，确保系统满足设计要求。
综合设计中还需要考虑到系统的稳定性、鲁棒性、控制器结构的实现难度等因素。
根据不同的应用场景，可以进行在线自适应控制和模型预测控制等高级控制方法的设计和实现。
I型三阶系统的典型分析与综合设计要点
I型三阶系统的典型分析与综合设计要点一、系统建模在进行系统的分析与设计之前，首先需要确定系统的数学模型。
对于I型三阶系统，可以通过系统的状态空间表达式或传递函数表达式进行建模。
传递函数表达式为：G(s)=K/[(s+a)(s+b)(s+c)]其中，s为复数变量，K为系统增益，a、b、c为三个振荡极点。
二、系统分析1. 频率响应分析：可以通过绘制系统的Bode图来分析系统的频率响应特性，包括增益和相位特性。
根据振荡极点的位置和增益的选择，可以确定系统的带宽、截止频率、相位裕度等参数。
2. 时域响应分析：可以通过求解系统的微分方程，利用Laplace变换或其他方法，得到系统的时域响应。
可以分析系统的超调量、上升时间、峰值时间、稳态误差等指标，评估系统的动态性能。
3. 稳定性分析：可以利用Routh-Hurwitz或Nyquist等方法，判断系统在闭环条件下的稳定性。
通过分析系统的特征方程的根的位置，可以确定系统的稳定性，并提出改进措施。
三、系统综合设计1.振荡极点的选取：根据系统的要求和性能指标的要求，选择合适的振荡极点。
振荡极点的位置会直接影响系统的频率响应和动态性能。
2.增益的选择：根据系统的要求和稳定性的要求，选择合适的系统增益。
增益的选择会影响系统的稳定性、超调量和动态特性。
3.控制器设计：根据系统的频率响应和时域响应的要求，设计合适的控制器。
可以采用比例控制器、积分控制器、微分控制器或其组合形式，通过调整控制器的参数来实现系统的性能改进。
4.稳定性分析与优化：通过稳定性分析方法，评估系统的稳定性，并提出优化措施。
可以利用壳牌准则，确定系统的稳定域，并在稳定域内进行控制器参数的调整和优化。
总结：I型三阶系统的典型分析与综合设计要点主要包括系统建模、系统分析和系统综合设计三个方面。
通过系统建模，可以得到系统的传递函数表达式，作为分析和设计的基础。
在系统分析中，可以通过频率响应分析、时域响应分析和稳定性分析，评估系统的性能指标和稳定性。
三阶系统的分析与校正
三阶系统的分析与校正引言：在控制系统中，三阶系统是一种常见且重要的系统。
它具有更高的阶数，因此对于控制系统的性能和稳定性有着更高的要求。
因此，对于三阶系统的分析和校正具有一定的复杂性。
本文将围绕三阶系统的分析和校正展开讨论，并介绍常见的校正方法。
一、三阶系统的基本特点和模型表示三阶系统是一个具有三个自由度的系统，可以用如下的传递函数表示：G(s)=K/(s^3+a*s^2+b*s+c)其中，K为传递函数的增益，a、b、c分别为系统的阻尼、震荡频率和系统自然频率。
二、三阶系统的稳定性分析稳定性是控制系统设计和校正的基本要求。
对于三阶系统的稳定性分析可以采用Bode图和Nyquist图等方法。
1. Bode图分析通过绘制传递函数的幅频响应和相频响应曲线，可以得到系统的幅度余弦曲线和相位余弦曲线。
根据Bode图的特点，可以确定系统的稳定性。
2. Nyquist图分析Nyquist图是对传递函数的极坐标表示。
通过绘制传递函数的Nyquist图，可以分析系统的稳定性。
以上两种方法都可以用来评估系统的稳定性。
如果系统的Bode图和Nyquist图图像均在单位圆内，则系统是稳定的。
三、三阶系统的校正方法校正是为了使控制系统具有所需的性能指标，通过调整系统中的参数和控制器等手段实现。
1.PID控制器的设计PID控制器是最常用的控制器之一，具有简单、稳定、易于实现等特点。
PID控制器由比例控制、积分控制和微分控制三部分组成。
通过调整PID控制器中的三个参数，可以实现对三阶系统的控制。
2.根轨迹法根轨迹法是一种经典的校正方法，通过分析系统的根轨迹来设计合适的校正器。
根轨迹是描述系统根位置随参数变化而变化的曲线。
通过调整参数，可以使根轨迹满足设计要求，进而实现对系统的校正。
3.频率响应方法频率响应方法基于传递函数的幅频响应和相频响应特性进行校正。
根据系统的特性，通过调整增益和相位等参数，可以实现对系统的校正。
以上是常见的三阶系统的校正方法，可以根据实际需求选择合适的方法进行校正。
I型三阶系统的典型分析与综合设计要点
成绩 ______自动控制原理课程设计报告题目：Ｉ型三阶系统的典型分析与综合设计系别专业名称班级学号姓名指导教师重庆邮电大学移通学院自动化系制2013 年 12 月摘要：在科学技术高速发展的今天，自动控制技术已经广泛的运用与制造业，农业，交通，航空航天等众多部门，极大地提高了社会劳动生产率，改善了人们的劳动环境，丰富和提高了人民的生活水平。
在今天的社会中，自动化装置已经无所不在，为人类文明进步做出了重要的贡献。
自动控制原理的课程设计是检验我们学过只是扎实程度的好机会，也让我们的知识体系更加系统，更加完善。
在不断学习新知识的基础上得到动手能力的训练，启发创新思维及独立解决实际问题的能力，提高设计，装配，调试能力。
In the rapid development of science and technology, automatic control technology has been widely used with many sectors such as manufacturing, agriculture, transportation, aerospace, and greatly improve the social labor productivity, and improve people's working environment, enrich and improve the people'sstandard of living. In today's society, the automation device has been everywhere, and made important contributions to the progress of human civilization. Curriculum design of automatic control theory to test we learned just a solid degree of good opportunities, but also to our body of knowledge more systematically, more perfect. Constantly learning new knowledge based on training ability, and inspire innovative thinking and the ability to solve practical problems independently, and to improve the design, assembly, commissioning and capacity.关键字：系统分析性能指标系统校验设计系统Keywords: System Performance Analysis System Design System Calibration目录一、系统说明（概述）5二、系统分析6三、系统综合8四、系统物理模拟图10总结13参考文献14重庆邮电大学移通学院《自动控制原理》课程设计（简明）任务书一、 设计题目：Ｉ型三阶系统的典型分析与综合设计 二、 系统说明：设单位反馈系统开环传递函数为0()(10.1)(10.02)kG S s s s =++，试设计串联校正装置，使系统满足70,1,%40%V s K t σ≥≤≤三、 基本要求：a) 利用频率法分析系统：（1） 作原系统的Bode 图；（2）分析原系统的性能，当原系统的性能不满足设计要求时，则进行系统校正。
三阶系统综合分析及设计
三阶系统综合分析及设计三阶系统是指系统的传递函数中包含三个一阶导数的系统。
它是一种常见的动态系统模型，广泛应用于控制系统分析与设计中。
系统分析与设计是指对一个系统进行调查、研究和设计的过程。
对于三阶系统的分析与设计，可以从以下几个方面进行综合分析与设计。
首先，需要对三阶系统进行数学建模。
数学模型是对实际系统进行描述的形式化表示。
对于三阶系统，可以通过从实际物理模型出发，通过系统边界的确定、基本假设的制定、动态方程的建立等步骤，得到系统的数学模型。
例如，对于一个机械振动系统，可以根据牛顿第二定律和阻尼定律，建立系统的运动方程。
其次，需要对三阶系统进行分析。
系统分析是对系统行为和性能的研究。
对于三阶系统，可以通过传递函数的频率响应、稳定性、阶跃响应、频率响应等进行分析。
例如，可以通过求解传递函数的极点和零点，判断系统的稳定性；通过求解传递函数的阶跃响应，了解系统的过渡过程特性。
然后，可以进行三阶系统的控制器设计。
控制器设计是为了实现对系统的特定要求或目标，通过调整控制器参数来改变系统的行为。
对于三阶系统，可以根据控制需求，设计合适的控制器类型（比如PID控制器、模糊控制器、自适应控制器等），并进行参数调整。
例如，可以通过根轨迹设计法或频率域指标设计法，调整PID控制器的参数。
此外，还可以进行三阶系统的性能评估。
性能评估是对系统性能进行定量评价的过程。
对于三阶系统，可以使用多种指标来评估其性能，如稳态误差、一致性、灵敏度等。
例如，可以计算系统的稳态误差，评估系统对于输入信号的跟踪性能；可以通过灵敏度函数，评估系统对于参数扰动和测量噪声的敏感性。
最后，需要对三阶系统进行仿真与实验验证。
仿真与实验验证是对系统理论设计进行实际验证的过程。
可以利用计算机软件（如MATLAB、Simulink）进行仿真，通过输入特定信号，观察系统的响应；也可以通过实验装置，在实际系统中搭建相应的电路、控制算法等进行验证。
通过仿真与实验验证，可以验证系统设计的有效性，同时根据实际情况对系统进行调整与优化。
三阶系统综合分析与设计
目录1 绘制随根轨迹 (2)1.1 根轨迹绘制步骤 .................................................................................................................... 2 1.2 用MA TLAB 绘制随根轨迹 . (2)2 不同条件下K 值的求取 (3)2.1 -6为闭环系统的一个极点时 ................................................................................................ 3 2.2取主导极点阻尼比为0.7 . (4)3 线性系统的稳态误差计算及原理 (5)3.1 稳态误差的计算 .................................................................................................................... 5 3.2 输入信号为22)(1)(t t t t r ++=时的稳态误差 (7)4 用Matlab 绘制单位阶跃相应曲线..................................... 7 5 绘制Bode 图和Nyquist 曲线.. (7)5.1 BODE 图的绘制 ..................................................................................................................... 7 5.2 Nyquist 曲线的绘制 (8)6 幅值裕度和相角裕度................................................ 9 7 系统加入非线性环节的稳定性分析 (9)7.1 非线性环节的描述函数的求取 ............................................................................................ 9 7.2 负倒描述函数的求取 .......................................................................................................... 11 7.3 系统稳定性的判据及原理 .................................................................................................. 12 7.4 系统稳定性判据的应用 (13)小结与体会......................................................... 14 参考文献.. (15)三阶系统综合分析与设计1 绘制随根轨迹某单位反馈系统结构图如图1-1所示：)4)(2(++s s s K)(s R )(s C -图1-1 单位反馈系统结构图系统传递函数=)(s G )4)(2(++s s s k1.1 根轨迹绘制步骤由图1-1知1）确定实轴上的根轨迹。
三阶系统综合分析与设计
引言在控制工程中，三阶系统非常普遍，但是三阶系统属于高阶系统, 其动态性能指标的确定是比较复杂，不能像二阶系统那样可以用特定的公式计算。
因此，我们可以借助于MATLAB软件对高阶系统进行分析。
在课程设计中，我们不仅要掌握用MATLAB绘制闭环系统根轨迹和和系统响应曲线，还要掌握BODE图和Nyquist 曲线的绘制。
以及在比较点与开环传递函数之间加一个非线性环节后用负倒描述函数和Nyquist 曲线判断系统的稳定性。
1设计内容1.1设计题目：三阶系统综合分析与设计初始条件：某单位反馈系统结构图如图1所示:图1-1 图1-21.2设计任务要求完成的主要任务：1、试绘制随根轨迹2、当-8为闭环系统的一个极点时，K=?3、求取主导极点阻尼比为0.7时的K值(以下K取这个值)4、分别求取位置误差系数、速度误差系数、加速度误差系数及输入信号为r(t) 1(t)2.5t t2单位阶跃信号、斜坡信号及单位加速度信号时的稳态误差5、用Matlab绘制单位阶跃相应曲线6、绘制Bode图和Nyquist曲线，求取幅值裕度和相角裕度7、如在比较点与开环传递函数之间加1个非线性环节，如图2所示,其中e。
1,k 2，试求取非线性环节的描述函数，并根据负倒描述函数和Nyquist图判断系统的稳定性&认真撰写课程设计报告。
2方案设计2.1 MATLAB绘制根轨迹绘制轨迹利用的函数是rlocus函数：1、首先根轨迹绘制需要明确的是根轨迹起于开环极点(包括无限极点) ，终于开环零点(包括无限零点) 。
根据系统开环传递函数k可知：系统s(s 3)( s 6)根轨迹有3条分支，开环零点无限远，有三个开环极点，分别是0, -3，-6。
2、实轴上的根轨迹是那些在其右侧开环实数零点和开环实数极点总数和为奇数的区间，所以该系统根轨迹在实轴上的区间为(-% ,-6］、［-3,0］。
3、该系统根轨迹有3条渐近线，求渐近线与实轴交点，得［-3.0j］, 而渐近线与实轴正方向的夹角为m 1，既有-，，5。
三阶系统的分析与校正
三阶系统的分析与校正引言三阶系统是一种常见的动态系统模型，广泛应用于控制系统、电路和信号处理等领域。
在三阶系统的分析和校正过程中，我们需要了解系统的特性、稳定性和动态响应，并结合校正方法进行系统优化。
一、三阶系统特性分析三阶系统由三个一阶子系统相连而成，其传递函数一般表示为：G(s)=(K*(s+z1)*(s+z2))/((s+p1)*(s+p2)*(s+p3))1. 特性根（Characteristic Roots）：三阶系统共有三个特性根，分别对应传递函数中的(s + p1)、(s + p2)和(s + p3)项。
特性根的位置和实部决定了系统的稳定性和动态响应，虚部决定了系统的振荡频率。
2. 分布根（Distribution Roots）：分布根是系统传递函数分子项(s + z1)和(s + z2)的根，它们决定了系统的增益和阻尼比。
增益越大，系统对输入的变化越敏感；阻尼比越小，系统越容易产生振荡。
3. 极点（Poles）和零点（Zeros）：系统传递函数的极点和零点是系统特性的重要指标，极点的位置和数量决定了系统的阻尼性能和稳定性，零点的位置和数量决定了系统的频率响应和相位特性。
二、三阶系统的稳定性分析判断三阶系统的稳定性可以通过判别系统的特性根的实部是否小于零，即特性根是否在左半平面。
1.极点分布：特性根的位置通过求解传递函数分母的特征方程来确定。
将特征方程中的系数代入矩阵当中，可以使用特征值计算软件来求解特征方程，得到特性根的位置和数量。
如果所有特性根的实部小于零，则系统是稳定的。
2.极点分布与稳定性的关系：三阶系统特性根的位置与稳定性之间存在一一对应的关系，通过特性根的位置可以判断系统的稳定性。
具体关系如下：-全部特性根的实部小于零：系统是稳定的。
-有一个特性根的实部大于零：系统是不稳定的。
-有两个特性根的实部大于零：系统是振荡的。
-有两个特性根的实部小于零，另一个特性根的实部等于零：系统是边界稳定的。
自动控制原理课程设计三阶系统分析与校正
自动控制原理课程设计--三阶系统分析与校正课程实习报告课程名称：自动控制原理及专业软件课程实习题目名称：三阶系统分析与校正年级专业及班级：建电1001姓名： *******学号： ***************指导教师： ***********评定成绩：教师评语：指导老师签名：年月日扬州大学自控原理课程设计任务书1课程设计目的与任务自动控制原理课程设计是综合性与实践性较强的教学环节。
本课程设计的任务是使学生初步掌握控制系统数字仿真的基本方法，同时学会利用MATLAB语言进行控制方针和辅助设计的基本技能。
2课程设计的设计课题题目：三阶系统的校正与分析设单位负反馈的开环传递函数为：G（s）=K/S(S+1)(S+5),设计校正装置，使系统在阶跃输入下的超调量小于等于30%，调节时间小于等于5s，而单位斜坡输入时的稳态误差小于等于15%。
要求：（1）确定采用何种校正装置。
仿真校正前系统的开环对数频率特性图以及系统的根轨迹图。
（2）将校正前性能指标与期望指标进行比较，确定串联校正网络Gc(s)的传递函数，仿真出校正网络的开环频率特性曲线图。
仿真校正后猪呢哥哥系统的开环对数频率特性图以及根轨迹仿真图。
（3）当输入r(t)=1时，仿真出校正前系统的的单位阶跃响应曲线h(t)。
分析校正前后的单位阶跃响应曲线，得出结果分析结论。
3课程设计的基本要求（1）学习掌握MATLAB语言的基本命令，基本操作和程序设计；掌握MATLAB语言在自动控制原理中的应用；掌握SIMULINK的基本操作，使用其工具建立系统模型进行仿真。
（2）应用MATLAB/SIMULINK进行控制系统分析、设计。
通过建立数学模型，在MATLAB环境下对模型进行仿真，使理论与实际得到最优结合。
（3）撰写自控原理课程设计报告。
目录1.前言 (3)2.未校正系统分析 (4)2.1复域分析 (4)2.2时域分析 (5)2.3频域分析 (6)2.4用SIMULINK进行仿真 (8)3.选定合适的校正方案 (9)3.1分析确定校正装 (9)3.2设计串联超前校正网络的步骤 (9)3.3参数计算 (9)3.4校正系统伯德图 (10)4.校正后系统分析 (11)4.1复域分析.... (11)4.2时域分析 (12)4.3频域分析 (13)4.4用SIMULINK进行仿真 (14)4.5校正后的实验电路图 (15)5.致谢 (16)6.参考文献 (17)1.前言所谓自动控制，是指没有人直接参与的情况下，利用外加的设备或装置（称控制装置或控制器），使机器、设备或生产过程（统称被控量）的某个工作状态或参数（即被控量）自动地按照预定的规律运行。
实验13 三阶系统的模拟与研究
实验十三 三阶系统的模拟与研究一、实验原理三阶系统的方框图如下：)(3s G图13-1 三阶系统方框图)(1s G )(2s G)1)(1)(1()(321+++=s T s T s T K s G 系统开环传递函数为：Ks T s T s T K s ++++=)1)(1)(1()(321φ 闭环传递函数为：0)1)(1)(1(321=++++K s T s T s T闭环特征方程为：当某惯性环节中的时间常数非常大时，就相当于积分环节，成为1型或2型系统。
求解特征方程可以得到闭环特征根；而根据特征根的性质（实数根或复数根、根具有正或负实部；复数根的阻尼比等）可以得知系统的阶跃响应和稳定性。
根据系统的类型和开环增益还可以分析系统的稳态误差。
一般说来，通过求根方式来获得系统的稳定性信息是非常麻烦而且困难的。
通常的分析法是借助于Routh 判据——线性方程的根与系数的关系，来判断系统的稳定性。
根据系统的结构、参数的不同，高阶系统与二阶系统类似，可以为过阻尼的、欠阻尼的和无阻尼的，也可以是不稳定的。
若图13－1中的部分惯性环节改为积分环节，就形成了1型或2型等系统，消除误差的比例增强，但由Routh 判据，相应的稳定性会减弱。
高阶系统也可以用运放电路模拟。
改变运放电路中的各参数，就可以改变系统的放大系数，或类型。
通过实验观察研究系统参数变化对高阶系统的动态及稳态性能的影响，对防止系统因参数或结构变化导致特性变坏甚至不稳定、采取措施改善系统性能，具有非常重要的意义。
图13-2 三阶系统的三种状态下的单位阶跃响应曲线a. 不稳定b. 临界稳定c. 稳定改变控制系统的模拟电路中的参数（如电阻、电容值）或结构，就可以使系统运行在稳定、临界稳定和不稳定三种不同的状态。
图13-2中a、b、c所示的曲线分别描述了系统为不稳定、临界稳定和稳定这三种情况。
三阶系统的稳态性能分析，与实验三类似。
二、实验目的1.通过实验进一步了解高阶系统动态及稳态性能与系统结构参数的关系，为下一步学习掌握控制系统的设计和校正打下基础。
matlab课程设计-- 三阶系统综合分析与介绍
matlab课程设计-- 三阶系统综合分析与介绍设计说明书设计题目三阶系统综合分析与介绍完成日期2013 年9 月 6 日专业班级设计者指导教师课程设计成绩评定目录前言 (2)第一章设计要求 (3)第二章 k值讨论 (3)第三章系统稳态误差讨论 (4)3.1 位置误差系数 (5)3.2 速度误差系数 (5)3.3 加速度误差系数 (6)3.4 稳态误差系数 (6)第四章利用MATLAB绘制曲线 (7)4.1 根轨迹讨论 (6)4.2 绘制根轨迹曲线 (8)4.3 绘制阶跃响应曲线 (9)4.4 频域特性分析 (10)4.5 相裕角度及幅值角度 (12)第五章稳定性分析 (12)5.1 死区特性环节的描述函数 (13)5.2 负倒函数及奈氏图判断稳定性.. 14总结与体会 (16)参考文献 (17)前言MATLAB软件提供了丰富的矩阵处理功能，使用简单，很快收到控制界研究者的普遍重视，并陆续开发了各种工具箱，如控制系统工具箱，系统辨识工具箱及仿真环境simulink等。
该软件是由美国Mathwork公司于二十世纪八十年代推向市场，其名称全称源自于Matrix Laboratory,。
MATLAB将高性能的数值计算和可视化集成在一起，并提供了大量的内置函数，从而被广泛的应用于科学计算、控制系统和信息处理等领域的分析、仿真和设计工作。
MATLAB软件包括五大通用功能，数值计算功能（Nemeric）、符号运算功能（Symbolic）、数据可视化功能（Graphic）、数字图形文字统一处理功能（Notebook）和建模仿真可视化功能（Simulink）。
其中，符号运算功能的实现是通过请求MAPLE内核计算并将结果返回到MATLAB命令窗口。
该软件有三大特点，一是功能强大；二是界面友善、语言自然；三是开放性强。
目前，Mathworks公司已推出30多个应用工具箱。
MATLAB在线性代数、矩阵分析、数值及优化、数值统计和随机信号分析、电路与系统、系统动力学、次那好和图像处理、控制理论分析和系统设计、过程控制、建模和仿真、通信系统以及财政金融等众多领域的理论研究和工程设计中得到了广泛应用。
三阶段评价体系打造评价多棱镜提升学生的多元能力
三阶段评价体系打造评价多棱镜提升学生的多元能力三阶段立体评价体系主要由即时性评价、阶段性评价和总结性评价三部分组成。
第一阶段：即时性评价即时性评价主要针对课堂中学生的学习过程及其结果的当堂评价，并通过评价来影响学生的学习过程。
它是建立在事实判断基础上的评价，因而它具有评价的差异性、针对性和即时性，它能及时地给学生提出改进的建议和发展方向。
即时性评价主要采用配套策略（见评价策略），主要作用是激发学生的学习兴趣。
第二阶段：阶段性评价阶段性评价以单元为阶段进行测评。
主要结合预设的数学活动进行评价。
测评内容：丰富多彩不拘泥于课本形式，例如：《想办法求出旗杆的高度》1、活动要求：⑴运用学过的比例的知识，选择合适的工具；⑵写出实验步骤、测量的数据及计算的结果；⑶展示时要边演示边讲解。
2、活动分析：解决此题学生需要选择1根可测量的杆子和1根米尺，在阳光明媚的日子里利用同时同地杆高和影长成正比例的知识，测量出旗杆的影长后，运用正比例知识计算出旗杆的高度。
3、活动目的：⑴通过把实际问题转化成数学问题，可以发展和评价学生的数学化能力；（2）在活动过程中需要进行工具选择、模型建构、数据测量等操作，可以发展和评价学生的数学操作能力；（3）活动结束后，学生（小组）需要汇报活动的过程和结果，可以发展和评价学生的数学表达和交流的能力。
测评形式：多种多样，富有趣味性。
可以用书面方式评价也可以用实践活动评价。
测评结果：每次单元评价或综合评价活动实施之后，根据《小学生数学多元能力评价标准》对学生各元能力水平做出评定。
第三阶段：总结性评价总结性评价更像是对学生的发展趋势的综合展现，主要包括各单元八元能力的记录及发展趋势，并根据发展形势每生一份总结性诊断报告。
纵向比较：学生的能力并不是稳定发展的，表现为有时向好、有时向差。
通过总结性评价统计表能及时发现学生能力在时间维度上发展变化的情况，对于教师来说，就可以及时调整因材施教的策略；对于学生本人来说，则可以总结学习中的成功经验或反思学习中存在的问题，从而提高学生学习的主动性，最终使学生学会学习。
三阶系统综合分析与设计
三阶系统综合分析与设计引⾔在控制⼯程中，三阶系统⾮常普遍，但是三阶系统属于⾼阶系统,其动态性能指标的确定是⽐较复杂，不能像⼆阶系统那样可以⽤特定的公式计算。
因此，我们可以借助于MATLAB软件对⾼阶系统进⾏分析。
在课程设计中，我们不仅要掌握⽤MATLAB绘制闭环系统根轨迹和和系统响应曲线，还要掌握BODE图和Nyquist曲线的绘制。
以及在⽐较点与开环传递函数之间加⼀个⾮线性环节后⽤负倒描述函数和Nyquist曲线判断系统的稳定性。
1 设计内容1.1 设计题⽬:三阶系统综合分析与设计初始条件：某单位反馈系统结构图如图1所⽰：图1-1 图1-2 1.2 设计任务要求完成的主要任务:1、试绘制随根轨迹2、当-8为闭环系统的⼀个极点时，K=?3、求取主导极点阻尼⽐为0.7时的K 值（以下K 取这个值）4、分别求取位置误差系数、速度误差系数、加速度误差系数及输⼊信号为25.2)(1)(t t t t r ++=单位阶跃信号、斜坡信号及单位加速度信号时的稳态误差5、⽤Matlab 绘制单位阶跃相应曲线6、绘制Bode 图和Nyquist 曲线，求取幅值裕度和相⾓裕度7、如在⽐较点与开环传递函数之间加1个⾮线性环节，如图2所⽰，其中2,10==k e ，试求取⾮线性环节的描述函数，并根据负倒描述函数和Nyquist 图判断系统的稳定性 8、认真撰写课程设计报告。
2 ⽅案设计2.1 MATLAB 绘制根轨迹绘制轨迹利⽤的函数是rlocus 函数：1、⾸先根轨迹绘制需要明确的是根轨迹起于开环极点（包括⽆限极点），终于开环零点（包括⽆限零点）。
根据系统开环传递函数)6)(3(++s s s k可知：系统根轨迹有3条分⽀，开环零点⽆限远，有三个开环极点，分别是0，-3，-6。
2、实轴上的根轨迹是那些在其右侧开环实数零点和开环实数极点总数和为奇数的区间，所以该系统根轨迹在实轴上的区间为(-∞,-6]、[-3,0]。
3、该系统根轨迹有3条渐近线，求渐近线与实轴交点,得[-3.0j],⽽渐近线与实轴正⽅向的夹⾓为πθ312+=l ，既有35,,3πππ。
浅谈学生分析与设计能力的培养--以三阶控制系统的稳定性分析为例
浅谈学生分析与设计能力的培养--以三阶控制系统的稳定性分析为例宋燕【摘要】本文以三阶系统的稳定性分析为例，讲述了自动控制原理实验课程由验证性实验教学为主向分析与设计性为主进行教学改革的必要性。
倡导该课程应加强学生综合分析与设计能力的培养，让实验课程真正成为理论课程的延展和补充，从而加强学生对理论知识的理解。
%By analyzing the stability of three order system, we present the necessity of the education reform on the course of the experiment of automatic control theory from verification teaching to analysis and design teaching.In this paper,we insist that the curriculum should strengthen the cultivation of analysis ability and design ability of the students.In this way,the experiment course could become the extension and complementary of the theoretic course,thus enhance the understanding for the students on theoretic knowledge.【期刊名称】《电子测试》【年(卷),期】2014(000)013【总页数】3页(P113-114,112)【关键词】三阶系统的稳定性;自动控制原理实验;教学改革;分析与设计【作者】宋燕【作者单位】上海市现代光学系统重点实验室，教育部光学仪器与系统工程研究中心，上海理工大学光电信息与计算机工程学院200093【正文语种】中文自动控制原理课程不仅是自动化专业的基础课，而且在机械、电气、测控、仪器仪表、电子信息等工科专业课程也具有很重要的作用。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
三阶系统的综合分析与设计摘要：真对三阶系统综合分析与设计问题，试绘制根轨迹，通过分离点的求解，理论分析单位阶跃响应，2tt=单位阶跃信号、斜坡信号及单位加速度信号时的稳态误差，tr++3(t))(1并求取当-6为闭环系统的一个极点时的K值，求取主导极点阻尼比为0.7时的K值，绘制Bode图和Nyquist曲线，求取幅值裕度和相角裕度，并验证了其正确性和有效性。
主题词：三阶系统，根轨迹，单位阶跃响应，传递函数关键词 Third-order system's generalized analysis Abstract：Analyzes and designs the question really to the third-order systems synthesis. Draw root locus.Through solving separation point. Theoretical analysis unit order step response2tt=. Unit Laplace domain signals. Ramp+r+t3)(1)(tsignals and unit of the steady-state error acceleration signal. And when calculating the 6 - for the closed-loop system when a pole of K value. Calculating the dominant pole damping ratio is 0.7 of K value. Draw Bode diagram and the Nyquist curve. Calculating the amplitude margins, and phase Angle tolerance. And to verify its validity and availability. And to verify its validity and availability.Key words：Third-order system.Root locus.Unit order step-response.Transfer function0引言：在控制工程中，三阶系统非常普遍，但是三阶系统属于高阶系统,其动态性能指标的确定是比较复杂，不能像二阶系统那样可以用特定的公式计算。
因此，我们可以借助于MATLAB 软件对高阶系统进行分析。
要掌握用MATLAB绘制闭环系统根轨迹和和系统响应曲线，还要掌握BODE图和Nyquist曲线的绘制。
以及在比较点与开环传递函数之间加一个非线性环节后用负倒描述函数和Nyquist曲线判断系统的稳定性。
1．理论基础1.1根轨迹：根轨迹是开环系统某一参数从零变化到无穷大时，闭环系统特征根在s平面上变化的轨迹。
根轨迹由180度、0度和参量根轨迹。
1.2闭环系统：输出量直接或间接地反馈到输入端，形成闭环参与控制的系统成为闭环控制系统。
也叫反馈控制系统。
为了实现闭环控制，必须对输出量进行测量，并将测量的结果反馈到输入端与输入量进行相减得到偏差，再由偏差产生直接控制作用去消除偏差。
整个系统形成一个闭环。
对于自动控制系统而言，闭环系统，在方框图中，任何一个环节的输入都可以受到输出的反馈作用。
控制装置的输入受到输出的反馈作用时，该系统就称为全闭环系统，或简称为闭环系统。
1.3MATLAB 绘制根轨迹 1.4单位阶跃响应 1.5绘制BODE 图 2．方法提出初始条件：某单位反馈系统结构图如图1、2所示：)图1 图2要求绘制根轨迹，k 值的求取，稳态误差，单位阶跃响应，BODE 图和Nyquist 曲线判断稳定性。
3．实验验证3.1理论绘制根轨迹根据绘制根轨迹的规则，可知该系统的根轨迹绘制步骤如下： 开环传递函数为：7.13()(2)(5)G s s s s =++3.3.1根轨迹的起点、终点和根轨迹条数根轨迹起于开环极点（包括无限极点），终于开环零点（包括开环零点）。
系统有三个极点（n=3）,没有零点（m=0）,即有三条根轨迹分支，它们的起始点为开环极点(0，-2，-5)；因为没有开环零点，所以三条根轨迹分支均沿着渐近线趋向无限远处。
3.1.2实轴上的根轨迹根轨迹在实轴上的分布，实轴上的某一区域，若是右边开环实数零、极点个数之和为奇数，则该区域必是根轨迹可知,实轴上的[-∞,-5] 和 [-2, 0]区域为根轨迹。
3.1.3根轨迹的确定本系统根轨迹的渐近线有三条，据其与实轴的夹角公式:(21)180,0,1,2,a k k n mφ+=︒=- 把n=3,m=0代入求得：(21)(21)18060,180,300(0,1,2)3a k k k n m φ︒︒︒++=︒===- 渐近线与实轴的交点为：0257303n m jijip zn mασ---===---∑∑3.1.4分离点的求解系统中没有有限零点，由法则五得：111025d d d ++=++ 解得：72d =-和76d =-由于根轨迹区域为[-2, 0]，所以取76d =- 3.1.5根轨迹与虚轴的交点 闭环特征方程式为327100s s s k +++= 对上式应用劳斯判据，有：3s1 102s 7 k1s7*107k- 0s k令劳斯表中1s 行的首项为零，得k= 70,根据2s 行的系数，得辅助方程： 72s +k=0将k=70代入上式并令s j ω=,解得交点坐标 3.16/rad s ω=图2-1 闭环根轨迹图理论上绘制的根轨迹应如图3-1所示。
所以，理论分析验证MATLAB 绘制的根轨迹正确。
3.2理论分析单位阶跃响应开环传递函数为：7.13()(2)(5)G s s s s =++当输入信号为单位阶跃函数()1()r t t =时，输出稳态误差为11ess kp =+，0lim ()p s k G s →=→∞，所以稳态误差ess =0。
由图3-1可以看出单位阶跃响应的的稳定值为1，与输入()1()r t t =相等，所以稳态误差为零。
上面的理论分析稳态误差ess =0。
与用MATLAB 绘制的曲线的趋势相符，所以MATLAB 绘制的图形正确。
图3-2 单位阶跃响应3.3理论分析BODE 图开环传递函数为7.13()(2)(5)G s s s s =++=0.713(1)(1)25s s s ++，交接频率为12/rad s ω=，25/rad s ω=。
2/rad s ω<时，斜率为：20/dB dec -；当2/5/rad s rad s ω<<时，斜率为：40/dB dec -；当5/rad s ω>时，斜率为：60/dB dec -。
所以MATLAB 绘制的BODE 图（如图3-2所示）正确。
图3-3 BODE 图分析相角裕度和幅值裕度：()1c A ω==（c ω为截止频率）求得c ω=0.67/rad s相角裕度18090arctan arctan25ccωωγ=---=63.85deg.()90arctanarctan(21)25xxx k ωωϕωπ=---=+ k 取0,1,2…（x ω为穿越频率）求得x ω=3.16/rad s .幅值裕度：h =-20log ︱()x A ω︱=19.83dB.将相角裕度和幅值裕度与图3-2中的实际值相比，几乎没有误差。
所以说，用MATLAB绘制的BODE 图和求出的相角裕度和幅值裕度均正确，恰好与理论相符。
3.4分析Nyquist 曲线绘制Nyquist 曲线有三点重要因素：1.开环幅相曲线的起点（ω=0）和终点（ω→∞）开环传递函数为7.13()(2)(5)G s s s s =++，所以222222249.917.13(10)()(10)49[(10)49]jG j ωωωωωωω-=---+-+，令实部P=22249.91(10)49ωω--+，虚部Q=22227.13(10)[(10)49]jωωωω---+，当0ω→时，P=-0.04991，Q →-∞；当ω→∞时，P=0，Q=0。
这是一个I 型系统，根据绘制原则，开环幅相曲线起于-90的无穷远处。
2.开环幅相曲线与实轴的交点：令Q=0，得到3.16/rad s ω==，此时，P=-0.1。
所以开环幅相曲线经过点（-0.1，0）。
3.开环幅相曲线的变化范围：上面的计算中可以看到开环幅相曲线经过负实轴，最终回到零，所以可以推测出曲线经过第三和第四象限。
绘制出的Nyquist 曲线如图3-4所示：根据分析当 3.16/rad s ω<时，Q>0,但是由于Q 值很小,所以开环幅相曲线看起来几乎是和实轴重合的,但实际上是Q>0的。
图3-4 Nyquist 曲线图2-4和图2-6中绘制的Nyquist 曲线都包含了ω从0--∞→和0+→∞的部分，所以图形是关于实轴对称的，而图3-4绘制出ω从0+→∞的部分。
理论分析的Nyquist 曲线和用MATLAB 绘制的曲线是相符的。
4．结论MATLAB 它有着强大的数据处理能力，处理速度快，精度高，它不仅可以用来绘制曲线，而且可以用来帮助解方程，以及做仿真处理，帮助验证理论分析的真确性。
这次我做的是一个三阶系统的综合分析和设计，主要完成的任务是绘制根轨迹﹑绘制单位阶跃响应﹑求稳态误差﹑绘制BODE 图和Nyquist 曲线﹑求幅值裕度和相角裕度以及加入非线性死区利用负倒描述函数和Nyquist 曲线来判断系统的稳定性。
并解决了加入非线性死区利用负倒描述函数和Nyquist 曲线来判断系统的稳定性。
<参考文献>[1]胡寿松.自动控制原理（第四版）[M].科学出版社，2001.9[2]刘慧英.自动控制原理 导教·导学·导教（第四版）[M].西北工业大学出版社，2003.11 [3]袁冬莉.自动控制原理（解题题典）[M].西北工业大学出版社，2003.3 [4]张 静.MATLAB 在控制系统中的应用[M].电子工业出版社，2007。