高中数学回归课本(直线与圆的方程)
回归教材变式专题八直线与圆.doc

回归教材变式专题八、直线与圆1.己知点A(1,V3),B(-1,3V3),求直线AB的斜率.变式1:已知点A(l,73),5(-1,373),则直线A3的倾斜角是()7t ° 7t八 2〃n 5勿A. —B, — C. — D.—3 6 3 6变式2:已知点4(1, -1), 5(5, 2),直线/的倾斜角是直线A8的倾斜角的一半,求直线/的斜率.2.求过点P(2, 3),并且在两轴上的截距相等的直线方程.变式1:直线2尤一3),一6 = 0在x轴上的截距为。
,在y轴上的截距为人,则()A. Q = 3,b = 2B. a = 3,b = —2C. a = —3,b = 2D. o = —3,b = —2变式2:过点P(2,3),且在两坐标轴上的截距互为相反数的直线方程是.变式3:直线/经过点户(2, 3),且与两坐标轴围成一个等腰直角三角形,求直线/的方程.3.求直线2x-5y-10 = 0与坐标轴围成的三角形的面积.变式1:过点(-5, -4)且与两坐标轴围成的三角形面积为5的直线方程是.变式2:已知直线/过点F(2,l),且与工轴、y轴的正半轴分别交于A、B两点,。
为坐标原点,则左OAB而积的最小值为.4.求过点A(l-4),且与直线2工+ 3),+ 5 = 0平行的直线的方程.变式1:已知过点A(-29m)和B(m,4)的直线与直线2x + y -1 = 0平行,则m的值为()A. 0B. -8C. 2D. 10变式2:与直线2x + 3y + 5 = 0平行,且距离等于而的直线方程是.变式3:已知三条直线2x + 3y + 5 = 0, 4x — 3y +1 = 0, mx - ,y = 0不能构成三角形,求实数m 的取值集合.5.若直线ox + 2> + 6 = 0和直线工+。
(。
+ 1)),+(6p —1) = 0垂直,求。
的值.变式1:若直线«:ox + 2y + 6 = 0与直线匕:尤+仔―l)y + (/—1) = 0平行但不重合,则。
高三数学回归教材:第9章 直线与圆

第九章 直线与圆一、知识梳理(一)直线与方程 1、倾斜角和斜率(1)倾斜角概念、范围;(2)斜率概念、公式、范围、增减变化; 2、直线方程形式①点斜式;②斜截式;③两点式;④截距式;⑤一般式;⑥参数方程; 3、两直线位置关系(1)平行:斜率关系、截距关系; (2)垂直:斜率关系; 4、两直线交点及距离(1)两点间距离:12PP =(2)点到直线距离:d(3)两平行线距离:d =;5、直线系方程(1)定点直线系:00()y y k x x -=-或00()()0A x x B y y -+-=; (2)共点直线系:111222()0A x B y C A x B y C λ+++++=;(3)平行直线系:与直线0Ax By C ++=平行的直线系0Ax By m ++=; (4)垂直直线系:与直线0Ax By C ++=垂直的直线系0Bx Ay n -+=; (二)圆与方程 1、圆的方程(1)标准方程、一般方程、参数方程; (2)点与圆位置关系;(3)圆的直径式方程:1212()()()()0x x x x y y y y --+--=;(4)一般方程的特点:二次项系数相同且不为0、无xy 项、系数满足特定关系、圆心和半径的待定; (5)圆的方程求法:几何性质法、待定系数法;几何法、代数法; 2、圆与圆位置关系(1)关系类型:相交、外切、内切、相离;(2)①相交121212||r r O O r r ⇔-<<+;②外切1212O O r r ⇔=+;③内切1212||O O r r ⇔=-;④相离1212O O r r ⇔>+;3、圆系方程(1)过点11(,)A x y 、22(,)B x y 的圆系方程:1212112112()()()()[()()()()]0x x x x y y y y x x y y y y x x λ--+--+-----=1212()()()()()0x x x x y y y y ax by c λ⇔--+--+++=,0ax by c ++=是直线AB 的方程,λ是待定系数; (2)过直线l :0Ax By C ++=与圆C :220x y Dx Ey F ++++=的交点的圆系方程:22()0x y Dx Ey F Ax By C λ+++++++=,λ是待定系数;(3)过圆:221110x y D x E y F ++++=与圆:222220x y D x E y F ++++=的交点的圆系方程:1C 2C2222111222()0x y D x E y F x y D x E y F λ+++++++++=,λ是待定系数;4、圆的切线方程(1)已知圆220x y Dx Ey F ++++=①若已知切点00(,)x y 在圆上,则切线只有一条,其方程是0000()()022D x xE y y x x y yF ++++++=;当00(,)x y 圆外时,0000()()022D x xE y y x x y yF ++++++=表示过两个切点的切点弦方程;②过圆外一点的切线方程可设为00()y y k x x -=-,再利用相切条件求k ,这时必有两条切线,注意不 要漏掉平行于y 轴的切线;③斜率为k 的切线方程可设为y kx b =+,再利用相切条件求b ,必有两条切线; (2)已知圆222x y r +=①过圆上的000(,)P x y 点的切线方程为200x x y y r +=;②斜率为k的圆的切线方程为y kx =±5、圆的相交弦方程;6、阿波罗尼斯圆:设AB a =,PAPBλ=,APB ∠的内角分线、外角平分线与AB 交点分别为C 、D ,则点P 轨迹为圆,圆心为CD 中点,半径为CD 的一半;(三)直线与圆1、直线与圆位置关系(1)关系类型:相交、相切、相离;(2)判定方法:①几何法:比较 d 与r ;②代数法:比较△与0; (3)弦长求法:①几何法:AB =AB = (4)切线方程;(5)切点弦直线方程; 2、对称问题(1)点关于直线轴对称:利用“垂直”、“平分”列方程组求出对顶点的坐标.特别:00(,)P x y 关于x a =的对称点为00(2,)P a x y '-;00(,)P x y 关于y b =的对称点为00(,2)P x b y '-; (2)曲线关于点、直线中心对称或轴对称:转化为点的中心对称或轴对称(可选特殊点,也可选任意点);①曲线(,)0f x y =关于点(,)a b 的对称曲线方程是(2,2)0f a x b y --=; ②曲线(,)0f x y =关于直线y kx b =+的对称曲线求法:设(,)0f x y =上任意一点00(,)P x y ,P 关于y kx b =+的对称点为(,)P x y ',则00122y y k x x y y x x k b-⎧⋅=-⎪-⎪⎨++⎪=⋅+⎪⎩,解出0x 、0y 代入(,)0f x y =,即可求出(,)0f x y =关于y kx b =+的对称曲线方程;(3)常见的对称结论:①点(,)x y 关于x 轴的对称点为(,)x y -; ②点(,)x y 关于y 轴的对称点为(,)x y -; ③点(,)x y 关于(0,0)的对称点为(,)x y --; ④点(,)x y 关于点(,)a b 的对称点为(2,2)a x b y --; ⑤点(,)x y 关于直线0x y -=的对称点为(,)y x ;⑥点(,)x y 关于直线0x y +=的对称点为(,)y x --;⑦点(,)x y 关于直线(1)y kx m k =+=±的对称点为,x y 值互换,只适用于1k =±);⑨设00(,)M x y 关于直线22:0(0)l Ax ByC A B ++=+≠的对称点为11(,)N x y ,则 22001222200122()22()22B A x ABy AC x A B A B x ABy BC y A B ⎧---=⎪⎪+⎨---⎪=⎪⎩+,1010x x y y ⎧=-⎪⎪⎨⎪=⎪⎩,记d '=,则|d '|表示00(,)M x y 到直线l 的距离,从而:101022x x d y y d ⎧=-'⎪⎪⎨⎪=-'⎪⎩,即有00(,2)2x d y d N ''.二、学习误区1.设直线方程时要分斜率是否存在;2.设直线方程为斜截式时,注意参数的具体含义,a 、b 、m 、n 灵活处理; 3.y kx b =+与x my n =+;。
高中数学第七章 直线与圆的方程课件

解:设所求圆的方程为:
(x-1)2+(y-3)2=r2
因为圆C和直线3x-4y-7=0相切 所以圆心C到这条直线的距离等于半径r 根据点到直线的距离公式,得
r= | 3×1— 4×3 — 7 | 32+(-4)2 因此,所求圆的方程是 = 16 O
C M
x
5
256 = 25
(x-1)2+(y-3)2
y
P(x , y )
M ( x0 , y0 )
x02 + y02
=
r2
x0x +y0 y = r2
O
x
结束 返回 下一页
知识点拨:
已知圆的方程是
的切线的方程:
x 2 y 2 r 2, 经过圆上一点 M ( x0 , y0 )
x0x +y0 y = r2
过圆(x-a)2+(y-b)2=r2上一点M(x0,y0) 的切线方程为:
P(x , y )
M ( x0 , y0 )
x
x0x +y0 y = r2
结束 返回 下一页
圆的标准方程
2 x 2 y 2 r,求经过圆上一点 例2 已知圆的方程是
M ( x0 , y0 ) 的切线的方程。
( x1 , y1 ) ( x2 , y2 ) x1 x2 y1 y2
解法三(利用平面向量知识): OM MP OM MP= 0
所以切线方程为:y = x± 2
(2)在y轴上截距是 2 的切线方程。 y = ± x+ 2
结束 返回 下一页
圆的标准方程
(1) 圆心为C(a,b),半径为r 的圆的标准方程为 (x-a) 2 + (y-b) 2 = r2
高中数学 第二章 直线和圆的方程一般式方程课件 新人教A版选择性必修第一册

ab
a
b a
2,
ab
8
,即
b 2a ab 8
,解得
a b
2 4
或
a b
2 4
.
a 0,a 2,b 4 ,a b 6 .
14
5. 已知在 ABC 中, A(1,2) ,B(3,4) ,C(2,5) .求: (1) BC 边所在直线的一般式方程; (2) BC 边上的高 AH 所在直线的一般式方程.
0 0
,
∴
x
y
2 1
,
∴直线 l : mx y 1 2m 0,a 恒过一定点 (2 ,1) .故选 A.
13
4. 若直线的截距式 x y 1 化为斜截式为 y 2x b ,化为一般式为 ab
bx ay 8 0 ,且 a 0 ,则 a b __________.
解析:由 x y 1 ,得 y b x b ,一般式为 bx ay ab 0 ,
方程.
解:经过点 A(6 , 4) ,斜率为 4 的直线的点斜式方程是 y 4 4 (x 6) ,
3
3
化为一般式,得 4x 3y 12 0 .
9
例 2 把直线 l 的一般式方程 x 2y 6 0 化为斜截式,求出直线 l 的斜率以及 它在 x 轴与 y 轴上的截距,并画出图形.
12
3. 无论 m 取何实数,直线 l : mx y 1 2m 0 恒过一定点,则该定点坐标为( )
A. (2 ,1)
B. (2 ,1)
C. (2 ,1)
D. (2 ,1)
解析:直线 l : mx y 1 2m 0 可化为 m(x 2) ( y 1) 0 ,
由题意,可得
x
y
2020高中数学三轮复习回归知识点15直线与圆
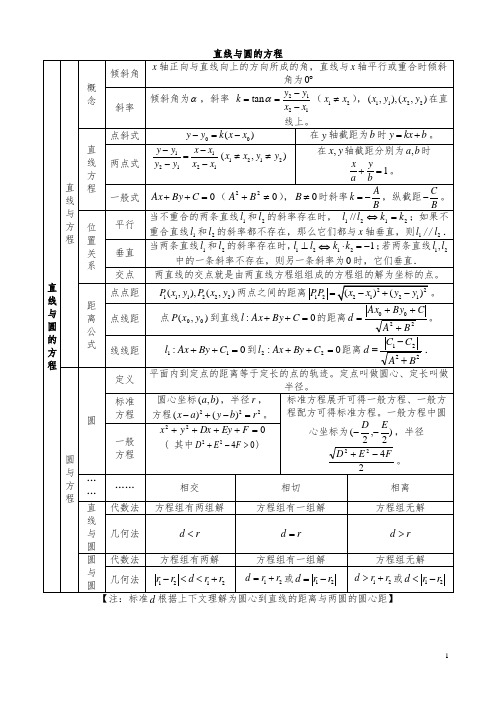
Ax0 By0 C 。 A2 B2
式 线线距
l1 : Ax By C1 0 到 l2 : Ax By C2 0 距离 d
C1 C2 . A2 B2
定义
平面内到定点的距离等于定长的点的轨迹。定点叫做圆心、定长叫做 半径。
标准 圆心坐标 (a,b) ,半径 r , 标准方程展开可得一般方程、一般方
圆
方程
方程 (x a)2 ( y b)2 r2 。 程配方可得标准方程。一般方程中圆
x2 y 2 Dx Ey F 0
心坐标为 ( D , E ) ,半径
一般
( 其中 D2 E2 4F 0)
22
方程
D2 E2 4F 。
2
… …
……
相交
相切
相离
1
系
中的一条斜率不存在,则另一条斜率为 0 时,它们垂直.
交点 两直线的交点就是由两直线方程组组成的方程组的解为坐标的点。
点点距 距 离 点线距 公
P1(x1, y1), P2 (x2, y2 ) 两点之间的距离 P1P2 (x2 x1)2 ( y2 y1)2 。
点 P(x0 , y0 ) 到直线 l : Ax By C 0的距离 d
B
B
位 置 关
平行 垂直
当不重合的两条直线 l1 和 l2 的斜率存在时, l1 // l2 k1 k2 ;如果不 重合直线 l1 和 l2 的斜率都不存在,那么它们都与 x 轴垂直,则 l1 // l2 . 当两条直线 l1 和 l2 的斜率存在时,l1 l2 k1 k2 1;若两条直线 l1, l2
点斜式
y y0 k(x x0 )
人教版高中数学第四章——直线与圆方程的应用(共16张PPT)教育课件

自
己
弄
五
分
钟
就
弄
完
所
以
最
后
通
常
变
成
我
自
己
弄
。
但
这
样
做
有
一
个
不
好
的
后
果
就
是
当
Hale Waihona Puke 你真的■
电
:
“
色
情
男
女
是
你
和
尔
东
口
罗
其
实
不
是
■电你是否有这样经历,当 你在做某一项工作 和学习的时候,脑 子里经常会蹦出各 种不同的需求。比 如你想安 心下来看2小时的书,大脑会 蹦出口渴想喝水, 然后喝水的时候自 然的打开电视。。 。。。。,一个小 时过去 了,可能书还没看2页。很多 时候甚至你自己都 没有意思到,你的 大脑不停地超控你 的注意力,你就这 么轻易 的被你的大脑所左右。你已 经不知不觉地变成 了大脑的奴隶。尽 管你在用它思考, 但是你要明白你不 应该隶属 于你的大脑,而应该是你拥 有你的大脑,并且 应该是你可以控制 你的大脑才对。一 切从你意识到你可 以控制你 的大脑的时候,会改变你的 很多东西。比如控 制你的情绪,无论 身处何种境地,都 要明白自己所
港口
台风
轮船
思考1:解决这个问题的本质是什么?
思考2:你有什么办法判断轮船航线 是否经过台风圆域?
思考3:如图所示建立直角坐标系, 取10km为长度单位,那么轮船航线 所在直线和台风圆域边界所在圆的 方程分别是什么?
y
港 口
x
台o
轮
新教材人教A版高中数学选择性必修第一册-第二章-直线和圆的方程-精品教学课件(共270页)可修改全文

探究二
素养形成
当堂检测
方法总结光的反射问题中,反射角等于入射角,但反射光线的斜率
并不等于入射光线的斜率.当镜面水平放置时,它们之间是互为相
反数的关系.另外,在光的反射问题中也经常使用对称的方法求解.
探究一
探究二
素养形成
当堂检测
变式训练一束光线从点A(-2,3)射入,经x轴上点P反射后,通过点
B(5,7),求点P的坐标.
作用 (2)确定平面直角坐标系中一条直线位置的几何要素是:直线
上的一个定点以及它的倾斜角,二者缺一不可
点析倾斜角还可以这样定义:在平面直角坐标系中,对于一条与x轴
相交的直线,把x轴所在的直线绕着交点按逆时针方向旋转到和直
线重合时所转过的最小正角称为这条直线的倾斜角.并规定:与x轴
平行或重合的直线的倾斜角为0°.
>0,解得
+1-2
1<m<2.
探究一
探究二
素养形成
当堂检测
延伸探究2若将本例中的“N(2m,1)”改为“N(3m,2m)”,其他条件不变,
结果如何?
-1-2
=1,解得
+1-3
解:(1)由题意知
m=2.
1
(2)由题意知 m+1=3m,解得 m=2.
探究一
探究二
素养形成
当堂检测
一题多解——利用斜率解决反射问题
A.2
B.1
1
C.
2
D.不存在
答案:A
)
探究一
探究二
素养形成
当堂检测
直线的倾斜角
例1已知直线l过原点,l绕原点按顺时针方向转动角α(0°<α<180°)后,
2025版新教材高中数学第2章直线和圆的方程2

2.5.1 直线与圆的位置关系学习任务1.驾驭直线与圆的三种位置关系:相交、相切、相离.(重点) 2.会用代数法和几何法来推断直线与圆的三种位置关系.(难点) 3.能用直线与圆的方程解决一些简洁的数学问题.(难点) 核心素养通过探讨直线与圆的位置关系,提升逻辑推理、数学运算、直观想象的数学素养.直线Ax +By +C =0与圆(x -a )2+(y -b )2=r 2的位置关系及推断位置关系 相交 相切 相离 公共点个数_2__个_1__个_0__个推断方法几何法: 设圆心到直线的距离为d = |Aa +Bb +C |A 2+B 2_d <r __ _d =r __ _d >r __代数法:由⎩⎪⎨⎪⎧Ax +By +C =0,x -a 2+y -b 2=r 2,消元得到一元二次方程,可得方程的判别式Δ_Δ>0__ _Δ=0__ _Δ<0__提示:“几何法”侧重于图形的几何性质,步骤较简洁;“代数法”则侧重于“坐标”与“方程”,推断直线与圆的位置关系,一般用几何法.做一做:1.直线3x +4y =5与圆x 2+y 2=16的位置关系是( A ) A .相交 B .相切 C .相离D .相切或相交[解析] 圆心到直线的距离d =532+42=1<4,所以直线与圆相交.2. 已知直线l :y =k (x +3)和圆C :x 2+(y -1)2=1,若直线l 与圆C 相切,则k = 0或 3 .[解析] 直线l 的一般式方程为kx -y +3k =0,圆C 的圆心为(0,1),半径为1,由直线l 与圆C 相切得||-1+3k k 2+1=1,解得k =0或 3.解决实际问题的一般程序细致读题(审题)→建立数学模型→解答数学模型→检验,给出实际问题的答案.用坐标法解决平面几何问题的“三步曲”第一步:建立适当的平面直角坐标系,用坐标和方程表示问题中的几何元素,如点、直线,将平面几何问题转化为代数问题.其次步:通过代数运算,解决代数问题.第三步:把代数运算结果“翻译”成几何结论.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
回归课本(七)直线与圆的参数方程一.考试内容:直线的倾斜角和斜率.直线方程的点斜式和两点式.直线方程的一般式. 两条直线平行与垂直的条件.两条直线的交角.点到直线的距离. 用二元一次不等式表示平面区域.简单的线性规划问题. 曲线与方程的概念.由已知条件列出曲线方程.圆的标准方程和一般方程.了解参数方程的概念.圆的参数方程.二.考试要求:(1)理解直线的倾斜角和斜率的概念,掌握过两点的直线的斜率公式.掌握直线方程的点斜式、两点式、一般式,并能根据条件熟练地求出直线方程. (2)掌握两条直线平行与垂直的条件,两条直线所成的角和点到直线的距离公式.能够根据直线的方程判断两条直线的位置关系. (3)了解二元一次不等式表示平面区域.(4)了解线性规划的意义,并会简单的应用. (5)了解解析几何的基本思想,了解坐标法.(6)掌握圆的标准方程和一般方程,了解参数方程的概念,理解圆的参数方程.【注意】本部分内容在高考中主要考查两个类型的问题:①基本概念和求直线方程;②直线与圆的位置关系等综合性试题. 求解有时还要用到平几的基本知......识和向量的基本方法.........三.基础知识:1.直线的五种方程(1)点斜式 11()y y k x x -=- (直线l 过点111(,)P x y ,且斜率为k ). (2)斜截式 y kx b =+(b 为直线l 在y 轴上的截距).(3)两点式112121y y x x y y x x --=--(12y y ≠)(111(,)P x y 、222(,)P x y (12x x ≠)). (4)截距式 1x ya b+=(a b 、分别为直线的横、纵截距,0a b ≠、)(5)一般式 0Ax By C ++=(其中A 、B 不同时为0).2..两条直线的平行和垂直(1)若111:l y k x b =+,222:l y k x b =+①121212||,l l k k b b ⇔=≠;②12121l l k k ⊥⇔=-.(2)若1111:0l A x B y C ++=,2222:0l A x B y C ++=,且A 1、A 2、B 1、B 2都不为零,①11112222||A B C l l A B C ⇔=≠;②1212120l l A A B B ⊥⇔+=; 3.夹角公式(1)2121tan ||1k k k k α-=+.(111:l y k x b =+,222:l y k x b =+,121k k ≠-)(2)12211212tan ||A B A B A A B B α-=+. (1111:0l A x B y C ++=,2222:0l A x B y C ++=,12120A A B B +≠).直线12l l ⊥时,直线l 1与l 2的夹角是2π. 4. 1l 到2l 的角公式 (1)2121tan 1k k k k α-=+.(111:l y k x b =+,222:l y k x b =+,121k k ≠-)(2)12211212tan A B A B A A B B α-=+.(1111:0l A x B y C ++=,2222:0l A x B y C ++=,12120A A B B +≠).直线12l l ⊥时,直线l 1到l 2的角是2π. 5.四种常用直线系方程(1)定点直线系方程:经过定点000(,)P x y 的直线系方程为00()y y k x x -=-(除直线0x x =),其中k 是待定的系数; 经过定点000(,)P x y 的直线系方程为00()()0A x x B y y -+-=,其中,A B 是待定的系数. (2)共点直线系方程:经过两直线1111:0l A x B y C ++=,2222:0l A x B y C ++=的交点的直线系方程为111222()()0A x B y C A x B y C λ+++++=(除2l ),其中λ是待定的系数.(3)平行直线系方程:直线y kx b =+中当斜率k 一定而b 变动时,表示平行直线系方程.与直线0Ax By C ++=平行的直线系方程是0Ax By λ++=(0λ≠),λ是参变量.(4)垂直直线系方程:与直线0Ax By C ++= (A ≠0,B ≠0)垂直的直线系方程是0Bx Ay λ-+=,λ是参变量.6.点到直线的距离d =(点00(,)P x y ,直线l :0Ax By C ++=).7. 0Ax By C ++>或0<所表示的平面区域设直线:0l Ax By C ++=,则0Ax By C ++>或0<所表示的平面区域是:若0B ≠,当B 与Ax By C ++同号时,表示直线l 的上方的区域;当B 与Ax By C ++异号时,表示直线l 的下方的区域.简言之,同号在上,异号在下.若0B =,当A 与Ax By C ++同号时,表示直线l 的右方的区域;当A 与Ax By C ++异号时,表示直线l 的左方的区域. 简言之,同号在右,异号在左. 8. 111222()()0A x B y C A x B y C ++++>或0<所表示的平面区域设曲线111222:()()0C A x B y C A x B y C ++++=(12120A A B B ≠),则111222()()0A x B y C A x B y C ++++>或0<所表示的平面区域是: 111222()()0A x B y C A x B y C ++++>所表示的平面区域上下两部分; 111222()()0A x B y C A x B y C ++++<所表示的平面区域上下两部分.9. 圆的四种方程(1)圆的标准方程 222()()x a y b r -+-=.(2)圆的一般方程 220x y Dx Ey F ++++=(224D E F +->0).(3)圆的参数方程 cos sin x a r y b r θθ=+⎧⎨=+⎩.(4)圆的直径式方程 1212()()()()0x x x x y y y y --+--=(圆的直径的端点是11(,)A x y 、22(,)B x y ).10. 圆系方程(1)过点11(,)A x y ,22(,)B x y 的圆系方程是1212112112()()()()[()()()()]0x x x x y y y y x x y y y y x x λ--+--+-----=1212()()()()()0x x x x y y y y ax by c λ⇔--+--+++=,其中 0ax by c ++=是直线AB 的方程,λ是待定的系数.(2)过直线l :0Ax By C ++=与圆C :220x y Dx Ey F ++++=的交点的圆系方程是22()0x y Dx Ey F Ax By C λ+++++++=,λ是待定的系数.(3) 过圆1C :221110x y D x E y F ++++=与圆2C :222220x y D x E y F ++++=的交点的圆系方程是2222111222()0x y D x E y F x y D x E y F λ+++++++++=,λ是待定的系数.11.点与圆的位置关系点00(,)P x y 与圆222)()(r b y a x =-+-的位置关系有三种若d =d r >⇔点P 在圆外;d r =⇔点P 在圆上;d r <⇔点P 在圆内.13.直线与圆的位置关系直线0=++C By Ax 与圆222)()(r b y a x =-+-的位置关系有三种:0<∆⇔⇔>相离r d ;0=∆⇔⇔=相切r d ; 0>∆⇔⇔<相交r d .其中22BA C Bb Aa d +++=.14.两圆位置关系的判定方法设两圆圆心分别为O 1,O 2,半径分别为r 1,r 2,d O O =21条公切线外离421⇔⇔+>r r d ; 条公切线外切321⇔⇔+=r r d ;条公切线相交22121⇔⇔+<<-r r d r r ; 条公切线内切121⇔⇔-=r r d ; 无公切线内含⇔⇔-<<210r r d .15.圆的切线方程(1)已知圆220x y Dx Ey F ++++=.①若已知切点00(,)x y 在圆上,则切线只有一条,其方程是当00(,)x y 圆外时, 0000()()022D x xE y y x x y yF ++++++=表示过两个切点的切点弦方程.②过圆外一点的切线方程可设为00()y y k x x -=-,再利用相切条件求k ,这时必有两条切线,注意不要漏掉平行于y 轴的切线.③斜率为k 的切线方程可设为y kx b =+,再利用相切条件求b ,必有两条切线.(2)已知圆222x y r +=.①过圆上的000(,)P x y 点的切线方程为200x x y y r +=;②斜率为k的圆的切线方程为y kx =±.四.基本方法和数学思想1.设三角形的三个顶点是A (x 1,y 1)、B(x 2,y 2)、C (x 3,y 3),则⊿ABC 的重心G 为(3,3321321y y y x x x ++++);2.直线l 1:A 1x+B 1y+C 1=0与l 2: A 2x+B 2y+C 2=0垂直的充要条件是A 1A 2+B 1B 2=0;3.两条平行线Ax+By+C 1=0与 Ax+By+C 2=0的距离是2221BA C C d +-=;4.Ax 2+Bxy+Cy 2+Dx+Ey+F=0表示圆的充要条件 :A=C ≠0且B=0且D 2+E 2-4AF>0;5.过圆x 2+y 2=r 2上的点M(x 0,y 0)的切线方程为:x 0x+y 0y=r 2;6.以A(x 1,y 2)、B(x 2,y 2)为直径的圆的方程是(x -x 1)(x -x 2)+(y -y 1)(y -y 2)=0;7.求解线性规划问题的步骤是:(1)根据实际问题的约束条件列出不等式;(2)作出可行域,写出目标函数;(3)确定目标函数的最优位置,从而获得最优解;8.圆的性质的应用.初中知识回顾:五.高考题回顾一、相切问题: 1.(04年辽宁卷.13)若经过点(1,0)P -的直线与圆224230x y x y ++-+=相切,则此直线在y 轴上的截距是 .2. 北京卷)从原点向圆 x 2+y 2-12y +27=0作两条切线,则该圆夹在两条切线间的劣弧长为( )(A )π (B )2π (C )4π (D )6π3. (天津卷)将直线2x -y +λ=0,沿x 轴向左平移1个单位,所得直线与圆x 2+y 2+2x -4y=0相切,则实数λ的值为 A .-3或7 B .-2或8 C .0或10 D .1或11 二、公共点问题:4.(04年北京卷.理12)曲线C :{cos 1sin x y θθ==-+(为参数)的普通方程是________,如果曲线C 与直线0x y a ++=有公共点,那么实数a 的取值范围是_______. 5.(全国卷I)已知直线l 过点),(02-,当直线l 与圆x y x 222=+有两个交点时,其斜率k 的取值范围是( )(A )),(2222- (B )),(22- (C )),(4242-(D )),(8181- 6(04年福建卷.文理13)直线20x y +=被曲线2262150x y x y +---=所截得的弦长等于 . 三、方程问题:6.(04年上海卷.文理8)圆心在直线270x y --=上的圆C 与y 轴交于两点(0,4),(0,2)A B --, 则圆C 的方程为 .7. (湖南卷)设直线0132=++y x 和圆03222=--+x y x 相交于点A 、B ,则弦AB 的垂直平分线方程是 .四、对称问题: 8.(04年全国卷二.文理4)已知圆C 与圆22(1)1x y -+=关于直线y x =-对称,则圆C 的方程为( ).A.22(1)1x y ++=B.221x y +=C.22(1)1x y ++=D.22(1)1x y +-=9.(上海)直线y=21x 关于直线x =1对称的直线方程是x+2y-2=0 .五、最值问题:10.(04年全国卷三. 文16)设P 为圆221x y +=上的动点,则点P 到直线34100x y --=的距离的最小值为 .六、线性规划问题:11. (全国卷Ⅰ)在坐标平面上,不等式组⎩⎨⎧+-≤-≥131x y x y 所表示的平面区域的面积为(C ) (A )2(B )23(C )223(D )212. (湖北卷)某实验室需购某种化工原料106千克,现在市场上该原料有两种包装,一种是每袋35千克,价格为140元;另一种是每袋24千克,价格为120元. 在满足需要的条件下,最少要花费 元.13. (江西卷)设实数x , y 满足的最大值是则x y y y x y x ,03204202⎪⎩⎪⎨⎧≤->-+≤-- .七.与向量相结合14.(湖南卷)已知直线ax +by +c =0与圆O :x 2+y 2=1相交于A 、B 两点,且|AB|=3,则OB OA ⋅ = .六.课本中习题归纳 一、 直线的方程及其位置关系 1(1)直线的倾斜角α的取值范围是 。
