匀变速直线运动位移及时间-位移及速度关系
匀变速直线运动的位移与时间、速度的关系

匀变速直线运动的位移与时间、速度的关系【知识点归纳】1、匀变速直线运动位移与时间的关系的公式表达:2021at t v s += s 为t 时间内的位移。
当a=0时,t v s 0= 当v 0=0时,221at s =当a<0时,2021at t v s -= 可见2021at t v s +=是匀变速直线运动位移公式的一般表示形式,只要知道运动物体的初速度v 0和加速度a ,就可以计算出任意一段时间内的位移,从而确定任意时刻物体所在的位置。
位移公式也可以用速度——时间图像求出面积得位移而推出。
2、匀变速直线运动的位移和速度的关系as v v t 2202=-这个关系式是匀变速直线运动规律的一个重要的推论。
关系式中不含时间t ,在一些不涉及到时间的问题中,应用这个关系是较方便的。
3、匀变速直线运动的两个推论1.匀变速直线运动的物体在连续相等的时间(T)内的位移之差为一恒量。
公式:S 2-S 1=S 3-S 2=S 4-S 3=…=S n -S n-1=△S=aT2 2.某段时间中间时刻的瞬时速度等于这段时间的平均速度,即: v v t =2【案例分析】例1.某物体作变速直线运动,关于此运动下列论述正确的是( )A .速度较小,其加速度一定较小B .运动的加速度减小,其速度变化一定减慢C .运动的加速度较小,其速度变化一定较小D .运动的速度减小,其位移一定减小例2.火车从车站由静止开出做匀加速直线运动,最初一分钟行驶540米,则它在最初l0秒行驶的距离是( )A .90米B .45米C .30米D .15米例3一物体由静止沿光滑斜面匀加速下滑距离为L 时,速度为V ,当它的速度是v /2时,它沿全面下滑的距离是A .L /2 B.2L/2 C .L /4 D .3L /4例4:一物体以初速度v 1做匀变速直线运动,经时间t 速度变为v 2求:(1)物体在时间t 内的位移. (2)(3)比较vt/2和v s/2例5:一辆沿平直路面行驶的汽车,速度为36km/h .刹车后获得加速度的大小是4m/s 2,求:(1)刹车后3s 末的速度;(2)从开始刹车至停止,滑行一半距离时的速度.例6、一个质点作初速为零的匀加速运动,试求它在1s ,2s ,3s ,…内的位移s 1,s 2,s 3,…之比和在第1s ,第2s ,第3s ,…内的位移S Ⅰ,S Ⅱ,S Ⅲ,…之比各为多少?【一试身手】1.下列说法正确的是A .加速度增大,速度一定增大B .速度变化量Δv 越大,加速度就越大C .物体有加速度,速度就增加D .物体速度很大,加速度可能为零2. 关于速度和加速度的关系A .物体的速度为零时,加速度一定为零B .物体的加速度为零时,速度一定为零C .物体的速度改变时,加速度不一定改变D .物体的加速度方向改变时,速度方向不一定改变3.如图所示,Ⅰ、Ⅱ两条直线分别描述P 、Q 两个物体的s —t 图象,下列说法正确的是A .两物体均做匀速直线运动B .M 点表示两物体在时间t 内有相同的位移C .t 时间内P 的位移较小D .0~t ,P 比Q 的速度大,t 以后P 比Q 的速度小 4.某质点做匀变速直线运动,加速度的大小为2m/s 2,则在任意1s 内A .质点的末速度一定是初速度的2倍B .质点的末速度一定比初速度大2m/sC .质点的初速度可能比末速度大2m/sD .质点的速度大小一定改变了2m/s 5.做匀变速直线运动的质点,它在通过某一段位移中点位置的速度为v ,通过这段位移所用时间的中间时刻的速度为u ,则该质点A .做匀加速运动时,v <uB .做匀减速运动时,v <uC .做匀加速运动时,v >uD .做匀减速运动时,v >u6.一个质点做方向不变的直线运动,加速度的方向始终与速度的方向相同,但加速度的大小逐渐减小为零,在此过程中( )A .速度逐渐减小,当加速度减小到零时,速度达到最小值B .速度逐渐增大,当加速度减小到零时,速度达到最大值C .位移逐渐增大,当加速度减小到零时,位移将不再增大D .位移逐渐减小,当加速度减小到零时,位移达到最小值7.关于匀变速直线运动,下列说法中正确的是A 、加速度越大,物体的速度一定越大B 、加速度越小,物体的位移一定越小C 、物体在运动过程中的加速度保持不变D 、匀减速直线运动中,位移随时间的增加而减小8.质点做直线运动,当时间t = t 0时,位移S > 0,速度v > 0,加速度a > 0,此后加速度a 逐渐减小,则它的 ( )A .速度的变化越来越慢B .速度逐渐减小C .位移继续增大D .位移、速度始终为正值t st o M Ⅰ Ⅱ9.甲、乙、丙和丁是以时间为横轴的匀变速直线运动的图象,下面说法正确的是( )A .图甲是加速度—时间图象B .图乙是加速度—时间图象C .图丙是位移—时间图象D .图丁是速度—时间图象10.滑块以某一初速度冲上斜面做匀减速直线运动,到达斜面顶端时的速度为零.已知滑块通过斜面中点时的速度为v ,则滑块在前一半路程中的平均速度大小为A 、212 vB 、(2+1)vC 、2vD 、21v 11.一匀变速运动物体的位移随时间变化的函数关系是S=4t+t 2(m), 则它运动的初速度、加速度及2s末的速度分别是( )A . 0、 4m/s 2 、4m/sB . 4m/s 、 2m/s 2 、8m/sC . 4m/s 、1m/s 2 、8m/sD . 4m/s 、 2m/s 2 、6m/s12.一个物体做初速度为零的匀加速运动,该物体通过前一半位移和通过后一半位移所用的时间之比是( )A .2∶1B .2∶ 1C .(2+1)∶1D .(2-1)∶1二、填空题1.汽车以2m/s 2的加速度由静止开始启动,则第5s 末汽车的速度是_______m/s ,第5s 内汽车的平均速度是________m/s, 第5s 内汽车的位移是___________m 。
匀变速直线运动的位移与时间的关系

新知讲解
得-v =xt=v0t+t12at2=v0+12at=2v0+ 2 at= v0+v20+at=v0+2 v即有-v =v0+2 v=v
故在匀变速直线运动中,某一段时间内的平均速度等于该 段时间内中间时刻的瞬时速度,又等于这段时间内初速度和末 速度的算术平均值。
新知讲解
拓展学习:匀变速直线运动位移公式的推导
拓展提高
2、一质点沿一直线运动,t=0时,位于坐标原点,下图为质点做
直线运动的速度时间图象.由图可知:
(1)该质点的位移随时间变化的关系式是:x=_-__4_t_+__0_.2_t_2__。
(2)在时刻t=_1_0__s时,质点距坐标原点最远。 (3)从t=0到t=20 s内质点的位移是__0_m___;
新知讲解
分析 两个问题都是已知匀变速直线运动的时间来计算 位移。
第(1)问需要用匀变速直线运动的位移与时间的关系 式计算。
第(2)问中,飞机着舰做匀减速直线运动的加速度需 要根据速度与时间的关系式计算。匀减速运动各矢量的方向 较为复杂,因此需要建立一维坐标系来确定它们的正负。
新知讲解
解:(1)根据匀变速直线运动的位移与时间的关系式,有
与v0同向,则a取正值;若a与v0反向,则a取负值;
(3)如果初速度为
0,
x
1 2
at2
(4)解题时先用字母代表物理量,再代入数值进行计算,代入数
据时,各物理量的单位要统一。
知识拓展
x
1 2
at2
匀变速直线的位移-时间图像
因为位移公式是关于t的 一元二次函数,故x-t图象是 一条抛物线(一部分)。
新知讲解
分析:由于把动车进站过程视为匀减速直线运动,因此 可以应用匀变速直线运动的速度与位移关系式计算动车的加 速度。本题加速度方向跟速度方向相反,因此需要建立一维 坐标系来处理相关物理量的正负号。
匀变速直线运动中位移与时间的关系

匀变速直线运动中位移与时间的关系一、匀速直线运动的位移时间关系1、匀速直线运动的速度始终保持不变,所以 vt x =2、从v-t 图像看位移匀变速直线运动的速度时间图像是一条平行于时间轴的直线即 v观察v-t 图像发现面积刚好就是 0v 位移,其中0v 是高,t 是底。
o t t 面积 位移二、匀变速直线运动的位移时间关系问题:匀速直线运动中位移大小可以用v-t 图像与坐标轴位的面积表示。
这个结论能否用于匀变速直线运动呢?1、我们知道对于变速运动的描述,最初使用的是平均速度即tx v ∆∆= ① 我们由①式出发稍微做一个变形就可以得到t v x ∆=∆ ② 2、我们来看一下匀变速直线运动的v-t 图像v0vo t我们观察图形会发现是一个梯形,所以我们不能用底乘以高即0v t 表示示其面积,那为什么就不行呢?因为这个图像中我们可以看出来从0到t 时刻存在一个很大的速度变化量即v ∆。
若从梯形中间做一条线,将其一分为二,我们在观察,还是不想矩形,但是会发现看其中一半是v ∆变小了,如果我们一直这样分下去会发现对一个细长的小梯形来说v ∆ 0,也就是说这个细长的梯形就可以看做一个矩形了,那么我们就可以用他的面积来表示位移的大小了。
于是我们就将梯形划分成许多细长的小梯形,所有小梯形的面积之和就是这段时间内物体的位移大小,也是整个梯形的面积。
故我们可以用梯形的面积来代表晕变速直线运动的位移大小。
所以我们求位移就可以通过求解梯形的面积。
解梯形的面积高下底上底⨯+==2s x t v v x t ⨯+=20––––––③高中位线⨯==s xt v x t ⨯=2––––––④ 因为at v v t +=0,所以我们将③式做一个简单的变形会得到2021at t v x += 这就是匀变速直线运动中位移与时间的关系,即位移公式3.对比将 ④三式进行对比会发现202t tv v v v +== 即中间时刻的速度等于平均速度等于初末速度之和的一半例:汽车刹车前的速度0v =5m/s ,a=-0.42s m ,求(1)开始刹车后20s 内滑行的距离?(2)汽车从刹车开始,位移x=30m 所用的时间?(3)在静止前2.5s 内滑行的距离?解:(1)错解:由2021at t v x +=可知x =5⨯202204.021⨯⨯-=20m 正解:法1:由a v at v v t 0t 0-v t =+=可知刹车制停的时间 又已知s m v /50= 2/4.0s m a -= 0=t v故t=12.5s 由于12.5<20,所以在t=12.5s 以后车就静止不动了。
匀变速直线运动的位移与时间的关系公式

匀变速直线运动的位移与时间的关系公式
匀变速直线运动的位移与时间的关系公式可以由运动学公式推导得到,具体分为两种情况:
1. 匀速直线运动的位移与时间的关系公式:
位移 = 速度 ×时间
其中,位移表示物体在运动过程中从起点到终点的距离,速度表示物体的运动速度,时间表示运动的时间长度。
2. 变速直线运动的位移与时间的关系公式:
位移 = 初速度 ×时间 + 0.5 ×加速度 ×时间²
其中,初速度表示运动开始时的速度,加速度表示运动过程中的加速度。
这个公式描述了的位移与时间的关系可以用来计算变速直线运动下物体在不同时间点的位置。
注意,这个公式的适用条件是运动过程中加速度是一个常量。
另外还有一种特殊情况,匀变速直线运动中,如果物体的位移与时间的关系符合二次函数的形式,可以使用二次函数公式来描述位移与时间的关系。
例如:位移 = a ×时间² + b ×时间 + c,其中a、b和c是常数。
匀变速直线运动的位移与时间 位移与速度的关系

三.匀变速直线运动的位移与时间的关系四.匀变速直线运动的速度与位移的关系[要点导学]1.位移公式物体做匀速直线运动的v-t图线如图2-3-1所示,在时间t内物体的位移对应v-t图象中矩形OCAB的面积,对应匀速直线运动物体的位移公式:x=vt;物体做匀变速直线运动的v-t,图线如图2-3-2所示,同理可知,在时间t内物体的位移对应v-t图象中梯形ODEF的面积,因此,匀变速度直线运动物体的位移公式为_____________________。
此位移公式是采用“微元法”把匀变速直线运动转化为匀速直线运动推导出来的,同学们应结合教材内容,深入理解这一研究方法及位移公式的推导过程,并加以应用。
2.对匀变速直线运动位移公式:的理解(1)式中共有四个物理量,仅就该公式而言,知三求一;(2)式中x、v0、a是矢量,在取初速度v0方向为正方向的前提下,匀加速直线运动a取正值,匀减速直线运动a取______,计算的结果x>0,说明位移的方向与初速度方向______,x<0,说明位移的方向与初速度方向________。
(3)对于初速度为零的匀加速直线运动,位移公式为:x=at2/23.匀变速直线运动速度与位移的关系由速度公式vt =v+at和位移公式联立消去时间t,可得速度与位移的关系式:vt2-v2=2ax此式是匀变速直线运动规律的一个重要推论,如果问题的已知量和未知量都不涉及时间,应用此式求解比较方便,对于初速度为零的匀变速直线运动,此式可简化为_______。
4.匀变速直线运动的平均速度由和可得,应用此式时请注意:(1)此式只适用于匀变速直线运动,不论是匀加速直线运动还是匀减速直线运动都适用,但对非匀变速直线运动的平均速度只能用平均速度的定义式来计算。
(2)式中的“v0+vt”是矢量和,不是代数和。
对匀变速直线运动来说,v和vt在一条直线上,可以通过规定正方向,把矢量运算转化为代数运算。
(3)由和速度公式vt=v0+at得=vt/2,即时间t内的平均速度等于中间时刻的瞬时速度。
匀变速直线运动的位移公式推导过程

匀变速直线运动的位移公式推导过程首先,我们来定义一些关键的物理量。
设物体在时间t的位置为x(t),位移为Δx,起始位置为x₀,起始时间为t₀,末尾时间为t₁,起始速度为v₀,末尾速度为v₁,加速度为a。
根据物体在匀变速直线运动中的定义,我们可以得到以下三个基本物理关系:1. 速度-时间关系:v(t) = v₀ + at2.位移-时间关系:Δx=x₁-x₀3.位移-速度关系:Δx=½(v₀+v₁)(t₁-t₀)现在我们来具体推导出位移公式。
首先,我们可以通过速度-时间关系求得末尾速度v₁:v₁ = v₀ + at₁将v₁代入位移-速度关系中,可以得到:Δx = ½(v₀ + (v₀ + at₁))(t₁ - t₀)通过整理,我们可以得到:Δx = (v₀ + v₀ + at₁)(t₁ - t₀)/2Δx = (2v₀ + at₁)(t₁ - t₀)/2 ------------式(1)接下来,我们需要消除t₁和t₀,即将式(1)中的时间表示用位移表示。
根据位移-时间关系,可以得到:Δx=x₁-x₀将x₁和x₀通过速度-时间关系和位移-时间关系表示,有:x₁ = x₀ + v₀(t₁ - t₀) + ½ at₁²将上式代入Δx=x₁-x₀中,可以得到:Δx = v₀(t₁ - t₀) + ½ at₁²根据速度-时间关系t₁-t₀=(v₁-v₀)/a将t₁ - t₀代入Δx = v₀(t₁ - t₀) + ½ at₁²中,可以得到:Δx=v₀((v₁-v₀)/a)+½a((v₁-v₀)/a)²Δx=(v₀v₁-v₀²)/a+(v₁-v₀)²/(2a)通过整理,我们可以得到:Δx=(v₀v₁-v₀²)/a+(v₀²-2v₀v₁+v₁²)/(2a)Δx=(v₀v₁-v₀²+v₀²-2v₀v₁+v₁²)/(2a)Δx=(v₁²-v₀²)/(2a)------------式(2)最后,我们通过比较式(1)和式(2)可以发现它们是相等的,因此我们得到了匀变速直线运动的位移公式:Δx=(v₀+v₁)(t₁-t₀)/2=(v₁²-v₀²)/(2a)这就是匀变速直线运动的位移公式的推导过程。
匀变速直线运动的位移与时间的关系
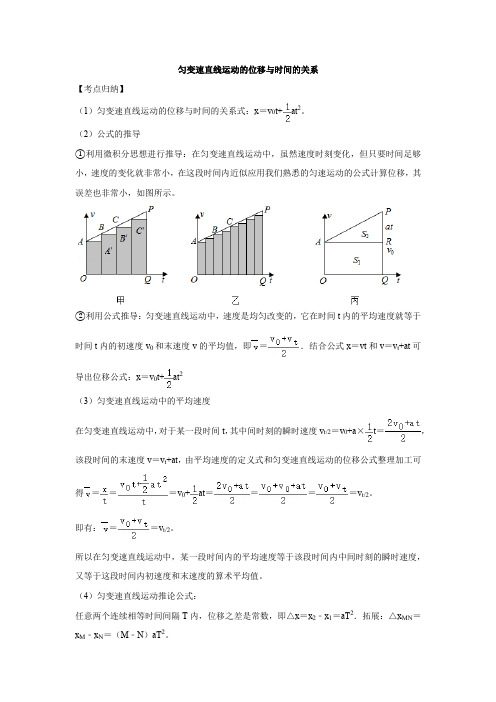
匀变速直线运动的位移与时间的关系【考点归纳】(1)匀变速直线运动的位移与时间的关系式:x=v0t+at2。
(2)公式的推导①利用微积分思想进行推导:在匀变速直线运动中,虽然速度时刻变化,但只要时间足够小,速度的变化就非常小,在这段时间内近似应用我们熟悉的匀速运动的公式计算位移,其误差也非常小,如图所示。
②利用公式推导:匀变速直线运动中,速度是均匀改变的,它在时间t内的平均速度就等于时间t内的初速度v0和末速度v的平均值,即=.结合公式x=vt和v=v t+at可导出位移公式:x=v0t+at2(3)匀变速直线运动中的平均速度在匀变速直线运动中,对于某一段时间t,其中间时刻的瞬时速度v t/2=v0+a×t=,该段时间的末速度v=v t+at,由平均速度的定义式和匀变速直线运动的位移公式整理加工可得===v0+at====v t/2。
即有:==v t/2。
所以在匀变速直线运动中,某一段时间内的平均速度等于该段时间内中间时刻的瞬时速度,又等于这段时间内初速度和末速度的算术平均值。
(4)匀变速直线运动推论公式:任意两个连续相等时间间隔T内,位移之差是常数,即△x=x2﹣x1=aT2.拓展:△x MN=x M﹣x N=(M﹣N)aT2。
推导:如图所示,x1、x2为连续相等的时间T内的位移,加速度为a。
【命题方向】例1:对基本公式的理解汽车在平直的公路上以30m/s的速度行驶,当汽车遇到交通事故时就以7.5m/s2的加速度刹车,刹车2s内和6s内的位移之比()A.1:1B.5:9C.5:8D.3:4分析:求出汽车刹车到停止所需的时间,汽车刹车停止后不再运动,然后根据位移时间公式求出2s内和6s内的位移。
解:汽车刹车到停止所需的时间>2s所以刹车2s内的位移=45m。
t0<6s,所以刹车在6s内的位移等于在4s内的位移。
=60m。
所以刹车2s内和6s内的位移之比为3:4.故D正确,A、B、C错误。
匀变速直线运动的四个基本公式

第二章 匀变速直线运动的研究 一、四个基本公式1、 匀变速直线运动速度随时间变化规律公式:at v v +=02、匀变速直线运动位移随时间变化规律公式:2021at t v x += 【例1】以10 m/s 的速度匀速行驶的汽车,刹车后做匀减速直线运动。
若汽车刹车后第2 s 内的位移为6.25 m(刹车时间超过2 s),则刹车后6 s 内汽车的位移是多大?3、匀变速直线运动位移与速度的关系:ax v v 2202=-【例2】身高为2 m 的宇航员,用背越式跳高,在地球上能跳2 m ,在另一星球上能跳5 m ,若只考虑重力因素影响,地球表面重力加速度为g ,则该星球表面重力加速度约为( ) A.52g B.25g C.15g D.14g 【例7】一辆车由静止开始作匀变速直线运动,在第8 s 末开始刹车,经4 s 停下来,汽车刹车过程也是匀变速直线运动,那么前后两段加速度的大小之比和位移之比x 1 ׃ x 2分别是( )A 、=1:4 ,x 1 ׃ x 2=1:4B 、=1:2,x 1 ׃ x 2=1:4C 、=1:2 ,x 1 ׃ x 2=2:1 C 、=4:1 ,x 1 ׃ x 2=2:1【例6】一只小球自屋檐自由下落,在Δt =0.25 s 内通过高度为Δh =2 m 的 窗口,求窗口的顶端距屋檐多高?(取g =10 m/s2)4、匀变速直线运动平均速度公式:(v0+v1)/2 通过图像关系证明二、 匀变速直线运动的三个推论1、 某段时间内中间时刻的瞬时速度等于这段时间内的平均速度:试证明此结论:2、某段位移内中间位置的瞬时速度2x v 与这段位移的初、末速度0v 与t v 的关系为:()220221t x v v v +=试证明此结论:【例3】一列从车站开出的火车,在平直轨道上做匀加速直线运动,已知这列火车的长度为l , 火车头经过某路标时的速度为v 1,而车尾经过这个路标时的速度为v 2,求: (1)火车的加速度a ;(2)火车中点经过此路标时的速度v ; (3)整列火车通过此路标所用的时间t 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例
与 • 一质点由静止以加速度大小a1先匀加速t1时间,再 练 以加速度大小a2匀减速减速至0,需时t2,则( )
• A 、质点位移为
1 2
a1t1(t1
t2
)
•
B 、质点位移为
1 2 a2t2(t1 t2)
ABC
• C 、平均速度为
在数值上等于图线与坐标轴所围的
0
tt
面积。(其中横轴上方的面积代表位移
为正方向,横轴下方的面积代表位移为负
方向。)
匀变速直线运动的规律:
小 结
速 平位度 均移公 速公式 度式公式xvt vv0 vt 0120 aatt2
2
vt
2
位移—速度公式 v 2 – v02 = 2 a x
纸带数据处理公式 S2-s1=s3-s2=s4-s3=…..=at2
度a和该时刻物体的速度v0的大小。
(a=1.67m/s2 v0 =1.67m/s)
小
结 一、匀速直线运动的位移公式: x = v t
二、匀变速直线运动的位移公式:
x = v0 t + 2—1 a t 2
三、匀变速直线运动的平均速度公式
v 0 t
v v0
2
2
v0
四、在 v-t 图象中,物体的位移 x
综合应用,可以解决所有的匀变速直线运动。
推 做一做:
论 1、写出初速度为0的匀变速直线运动的位
一 移时间关系式。 x = 2—1 a t 2
• 2、你能自己推导得出匀变速直线运动的平
均速度公式吗?试一试
? v 0 2
0
1 2
at
t
2
匀 匀变速直线运动的位移与速度的关系
变
速 直 线 运 动 的
第二章 匀变速直线运动的研究
3、匀变速直线运动的位移与时间的关系 4、匀变速直线运动的位移与速度的关系
复
V
习
匀速直线运动 v = v0
V0
0
t
匀变速直线运动 v = v0 + a t
思 考
能否通过v-t 图象进一步
知道物体位移与时间的关系?
匀 匀速直线运动的位移公式: x = v t
速
V
V
直 线V
1 4
(a1t1
a2t2
)
• D、a1:a2=t1:t2
例
与 • 例1、做匀加速直线运动的质点,通过某一
练 段位移x的时间为t1,通过下一段同样长的位移
x的时间为t2,求质点的加速度。
解法一:作质点运动示意图如图所示:
a
VA
t1
VB
t2
VC
解法二:作v-t图如图所示
v vC vB
A
X
B
X
C
设质点运动方向为正方向,由运动学 公式得:
列方程: v = v 0+at
x = v0 t + 2—1 a t 2
v 2 – v02 = 2 a x
a 2 02
2x
注意:1、优点:不需计算时间t 。
位
2、公式中四个矢量 v、v0、a、x
移 与
要规定统一的正方向。
速
3、若v0 = 0 ,则v = ?
v a x 度 初速度为0的匀变速直线运动: 2 = 2
as6s5s4 9 t2s3s2s1
五个公式的选用方法
• 1、如果题中无位移s,也不让求位移,一般选用速 度公式;
• 2、如果题中无末速度v,也不求,一般选用位移 公式;
• 3、如果题中无运动时间t,也不用求,一般选用 位移-速度公式;
• 4、如果题中无加速度a,也不用求,一般选用平 均速度公式;
A B过程:x=vAt1+at12/2
①
B C过程: x=vBt2+at22/2
v
速
直
线
v0
运
动v
的 v0
位
移 v0
0
v02—1t a t 2 △v
公
式0
t
tt
2—1 a t 2 △v
v0 t
v0
t
tt
说 明
1.公式 x = v0 t + 2—1 a t 2 中的 x 、v0 、
a 均为矢量,应用时必须选取统一方向为正方
向。
2.利用 x = v0 t + 2—1 a t 2 和v = v0 + a t
t
0
tt
运V
V
动 的
0
t
t t -V
位 结论:在匀速直线运动的 v-t 图象中,物体 移 的位移 x 在数值上等于图线与坐标轴所围的
矩形面积。
(其中横轴上方的面积代表位移为正方向, 横轴下方的面积代表位移为负方向)
思
考
与
讨
论
对于匀变速直线运动,它的位移与
: 它的 v-t 图象,是不是也有类似的关系
A S = 2—1述直时( 结线间OC论运的+找动关A出的系B匀位式) 变移呢×速与?OA
运0
动 的 位
t t x = 2—1 ( v0 + v ) t v = v0 + a t
移 匀变速直线运动位
移与时间的关系式 (简称位移公式)
x = v0 t + 2—1 a t 2
匀 变
x = v0 t + 2—1 a t 2
呢?
阅读课本P37-38,思考并发表你的意见
匀
变
V
速
V4 V3
直
V2
线
V1 V0
运
动
0 t1 t2 t3 t4 t t
的
位 结论:在匀变速直线运动的 v-t 图象中,物体的位移
移 x 在数值上等于图线与坐标轴所围的面积。
(横轴上方的面积与横轴下方的面积有什么分别?)
匀 变
v
V
B
思考:能否利用上
速 直 V0 线C
C 4m/s,-4m/s2
D 4m/s, 4m/s2
2、某物体做直线运动,物体的速度-时间图象如
图所示,若初速度的大小为v0,末速度的大小为v,则在
时间t1内物体的平均速度(C )
v
A 等于 v 0
2
B 小于 v 0
C 大于
v
2 0
2
D条件不足,无法比较
v v0
o
t1
t
例 与 练
• 一个物体做匀变速直线运动,从某时刻 起,通过20m的位移用时4s,紧接着通过 下一段20m位移用时为2s,求物体的加速
as6s5s9 4T 2s3s2s1
课 本 例 题
规范: 一般应先用字母代表物理量进行运算, 得出用已知量表达未知量的关系式,然后再把数 值代入式中,求出未知量的值,这样做能够清楚 地看出未知量与已知量的关系,计算也比较简便。
课 本 例 题
课 本 例 题
例 1、物体的位移随时间变化的函数关系为x=(4t与 2t2)m,则它运动的初速度、加速度分别为( C ) 练 A 4m/s,-2m/s2 B 4m/s, 2m/s2
的 关 系
4、若v = 0 ,则v 0= ? 匀减速至速度为0的匀变速直线运动:–
v02
=
2
a
x
推 自主探究:
论
s1 s2
二
纸带数据处理公式
s3Βιβλιοθήκη s4oT2T
3T
4T
在匀变速直线运动中,相邻相等时间 内的位移差为一定值aT2
s2-s1=s3-s2=s4-s3=…..=aT2 应用:纸带处理求加速度a:——逐差法
