2.3 匀变速直线运动的位移与时间的关系
2.3.1匀变速直线运动的位移与时间的关系

【知识拓展】
1 2
x at
2
因为位移公式是关于t的一元
二次函数,故x-t图象是一条抛物
线(一部分)。
注意:x-t图象不是物体运动的
轨迹,而是位移随时间变化的规律。
匀变速直线的位移-时间图像
【例3】有些汽车刹车后,停止转动的轮胎在地面上发生滑动,可以明
7 89
12t13t14
t
V
V
如果把整个运动过程分割得非常
非常细,很多很多小矩形的面积之和
就能非常精确地代表物体的位移了。
V0
0
t
t
这是物理上常用的微元法。
匀变速直线运动的位移仍可用图线与坐标轴所围的面积表示。
科学
方法
∆t 内是简单的匀速直线运动---- 化简
分割许多很小的时间间隔∆t---- 微分
站的加速度是多少?它还要行驶多远才能停下来?
解: 沿动车运动方向为正方向建立一维坐标系。把动车通过3000m
的运动称为前一过程,之后到停下来称为后一过程。
设在前一过程中的末位置为 M 点。初速度 v0 =126 km/h=35 m/s,
末速度vM=54 km/h=15 m/s,位移 x1 = 3000m。
匀速直线运动的位移就是v – t 图线
与坐标轴所夹的矩形“面积”
图象法
v/(m∙s-1)
v
v
x=v(t2-t1)/s
t1-t2时间内的位移
01. 匀速直线运动的位移
x1=12m
x2= -12m
v/m·s-1
x/m
10
匀速直线运动的v-t 图象中,图线与时间轴围
8
【学霸笔记】物理必修一2.3匀变速直线运动位移与时间的关系

第三节匀变速直线运动的位移与时间的关系一、位移时间公式1、推导:①图像法:(由v-t图像求位移)---微元的思想结论:做匀变速直线运动的物体的位移对应着v-t图象中的图线与对应的时间轴所包围的面积.即:位移与时间关系式:x=v0t+12at2.②解析法:(由平均速度求得)⎪⎪⎩⎪⎪⎨⎧+=+==atvvvvvt vxtt2得:x=v0t+12at2.2、物理意义:在匀变速直线运动中位移随时间变化的规律。
3、注意:①适用范围:匀变速直线运动。
②决定关系:位移的决定式,即匀变速直线运动中位移是由初速度、加速度、时间共同决定。
③比例关系:二次关系,也叫非线性关系。
④同一性:x、a、v0、vt具有同一性。
⑤合理性:已知位移反求时间,可能有两个值,要合理取舍。
二、速度--时间公式应用1、使用方法:①判断:运动性质(a为定值)。
②确定:研究对象和研究过程。
③设定:正方向(一般初速度的方向为正方向,无初速度则选择加速度为正方向)。
④公式应用:x=v0t+12at2;(此式子为矢量式,应将方向带入求解)⑤结果:结果如何为矢量,大小方向都需要求解。
2、例子:已知一个物体以向西的初速度4m/s做匀变速直线运动,其加速度大小为2m/s2,求1s末、2s末、4s末、8s末的速度和位移和路程,如果该物体是汽车,则结果又将如何?.三、推论1、逐差相等原理:在匀变速直线运动中,相邻相等的时间间隔位移之差是一个定值。
表达式:△x=aT 2.推导:⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=212022019213421221T a T v x T a T v x aT T v x ⎪⎪⎩⎪⎪⎨⎧+=-+=-20232012521321T a T v x x T a T v x x 2aT x =∆ 2、比例关系:初速度为零的匀加速直线运动中①在前T ,前2T ,前3T 的位移之比1:4:9……n2②在第T ,第2T ,第3T 的位移之比1:3:4……(2n-1) 3、逆向思维法:末速度为零的匀减速直线运动可以看做反向的初速度为零的匀加速直线运动。
2.3_匀变速直线运动的位移与时间的关系(笔记上传)

特别提醒(非常实用):末速度为零的 匀减速直线运动可看成初速度为零,加速度 同原来相同的反方向匀加速直线运动。
A
v0
a
0
B
v0
A
a
0
B
又v=v0+at
1 2 得: x v 0 t at 2
1 2 2.对位移公式 x v 0 t at 的理解: 2
⑴反映了位移随时间的变化规律。
⑵因为υ 0、a、x均为矢量,使用公式时应先规定正
方向。(一般以υ 0的方向为正方向,若物体做匀加速 运动,a取正值,若物体做匀减速运动,则a取负值)。 (3)特别提醒:t是指物体运动的实际时间,要将位 移与发生这段位移的时间对应起来。
示
思考: 1、这个过程体现了什么科学思想方法?
答:把过程先微分后再累加(积分)的思想。 (无限分割,逐渐逼近)
2、是否是任何运动的位移仍都可以用V-t图中图
线与坐标轴所围的面积表示呢? 答:是的
1.由图可知:梯形OABC的面积S=(OC+AB)×OA/2
1 代入各物理量得: x (v0 v)t 2
位置X0出发。
d为匀加速直线运动的x-t图像。想想这 是数学上的哪种函数呢?那么匀减速直
线运动呢?
二次函数,抛物线。
交点M所代表的物理意义是什么?
X0
a、b、c、d三个物体在t1时刻相遇 0
t1
t
【问题思考】
如果一位同学问:“我们研究的是直线运动,为
什么画出来的匀变速直线运动的x-t图像不是直线?”
三、用图像表示位移(拓展)
复习:你还能画出静止的x-t图像吗?那么匀速直线运动呢?匀变速直线 运动呢?试试试看。 a为静止物体的x-t图像:平行于时间轴的直线。 b为匀速直线运动的x-t图像:一条倾斜的直线。 c也为匀速直线运动的x-t图像:只不过 在0时刻时不在0位置出发,而是在某一
必修一 2.3匀变速直线运动的位移与时间的关系

二、匀变速直线运动的位移
1、从v-t图象中探究匀变速直线运动的位移
vቤተ መጻሕፍቲ ባይዱ
v – t 图线与t轴所夹
v
v0
面
积
的梯形“面积”是否匀变
t
t
速直线运动的位移呢?
位移
数值
梯形面积
V/m/s
V
将△t 取小,匀变速直线运动在△t时间
内可等效为匀速直线运动,各匀速直线运
动位移之和,就近似等于匀变速直线运动
的位移,在v-t图像中,即各小矩形面积之
间的关系式和速度与时间的关系式,那么速度与
位移有什么关系,你能推导吗?
位移与时间的关系式:x = v0t +
2
at
速度与时间的关系式:v = v0 + at
v2 - v0 2 = 2ax
这就是匀变速直线运动的速度与位移的关系
式。如果在所研究的问题中,已知量和未知量都
不涉及时间,利用这个公式求解,往往会更简便。
和近似等于匀变速直线运动的位移,显然
梯形的面积就代表做匀变速直线运动物体
V0
0
在0~t这段时间的位移。
t/s
t
v
v
v0
v0
0
0
t
t
t
结论:物体的位移对应着v-t图象与t
轴围成的的“面积”。
t
1 2
匀变速直线运动的位移公式: x v0t 2 at
(1)t是指物体运动的实际时间(刹车问题)
(2)使用公式时应先规定正方向
前进,2.4 s后离舰升空。飞机匀加速滑行的距离是多少?
(2)飞机在航母上降落时,需用阻拦索使飞机迅速停下来。若某
匀变速直线运动的位移与时间的关系+同步课件-2022-2023学年高一上学期物理人教版必修第一册

面积之和可
以更精确地
表示物体在
整个过程中
的位移.
③把整个过程分得非常非常细,如图所示,小矩形合在一起成了一
个梯形,梯形面积就代表物体在相应时间间隔内的位移.
v/m·s-1
极限思想
5
0
v0
2
4
t/s
5
前4s内位移、路程各是多
少?
下图,为一物体做匀变速直线
运动的v-t图像,加速度为a
0 +
为“初态”来反向研究问题的方法,如物体做加速运动
看成反向的减速运动,物体做减速运动看成反向的加速
运动。该方法一般用在末状态已知的情况。采用逆向思
维方法,往往能收到事半功倍的效果。
物体做匀加速直线运动,相继经
过两段距离为16 m的路程,第一
段用时4 s,第二段用时2 s,则物
体的加速度是?
一辆汽车刹车后做匀减速直线
A.质点一直向x轴正方向运动
B.质点做匀变速直线运动
C.质点在第2s内的平均速度的大小为3m/s
D.质点在前2s内的位移为零
v-t图像(0-v-0模
型): 1 V t
2
m
x=v̅t=
Vm=a1t1
Vm=a2t2
Vm
a1t1
a2 t 2
V
2
2
2
X5
X4
X2
X3
X1
S1
S2
S3
S4
S5
1 2
2.3匀变速直线运动位移与时间的关系
1.匀速直线运动:v-t图像所围面积就是位移,即x=vt
2.匀变速直线运动:v-t图像求位移
①把物体的运动
2.3匀变速直线运动位移与时间的关系

得:0
8:0.0384m,与真实值的差距更小了。
在第一节探究小车速度与时间变化的规律,我们得到的纸带:
0.0416m
012 3 4 5
6
7
8
9
取每四个计时点为一个计数点: 0.0288m
0
4
8
取每两个计时点为一个计数点: 0.0352m
02
4
6
8
以原始计时点作为计数点:
0.0384m
01 2 3 4 5
0 0.02 0.04 0.06 0.08 0.10 0.12 0.14 0.16
如果把运动无限分割,每小段运动持续的时间趋于零,无数个非常小的 矩形面积之和(无数段匀速运动的位移之和)刚好是梯形的面积。
由此可得: 匀变速直线运动的位移=无数段匀速运动的位移之和
=无数个非常小的矩形面积之和=梯形的面积 即:匀变速直 线运动的位移大小等于速度图线与坐标轴所围成 的面积大小
02
4
6
8
0 4 得:0
2:0.10 0.04=0.004m 2 6:0.26 0.04=0.0104m 6
4:0.18 0.04=0.0072m 8:0.34 0.04=0.0136m
8:0.0352m,与真实值的差距减小了一点。
在第一节探究小车速度与时间变化的规律,我们得到的纸带:
0.0416m
6
7
8
方法总结:可以把匀加速直线运动分成几段运动,把各 段运动看成匀速直线运动(以各段运动的初速度)。我们 可以看出, 把整个运动分的段数越多,每段运动持续的 时间越短,位移的计算结果就越接近真实值。我们再从 图象来看。
对上述过程分别用图像表达:
v(m/s)
2-3匀变速直线运动的位移与时间的关系(考点解读)-2023-2024学年高中(002)
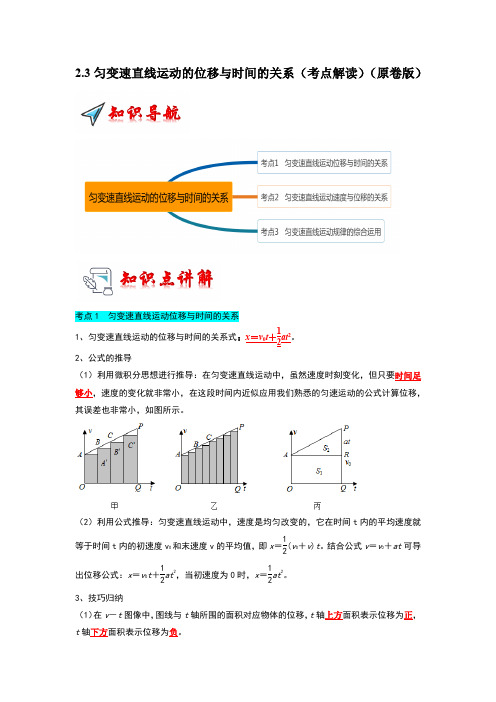
2.3匀变速直线运动的位移与时间的关系(考点解读)(原卷版)考点1 匀变速直线运动位移与时间的关系1、匀变速直线运动的位移与时间的关系式:x =v 0t +12at 2。
2、公式的推导(1)利用微积分思想进行推导:在匀变速直线运动中,虽然速度时刻变化,但只要时间足够小,速度的变化就非常小,在这段时间内近似应用我们熟悉的匀速运动的公式计算位移,其误差也非常小,如图所示。
(2)利用公式推导:匀变速直线运动中,速度是均匀改变的,它在时间t 内的平均速度就等于时间t 内的初速度v 0和末速度v 的平均值,即x =12(v 0+v )t 。
结合公式v =v 0+at 可导出位移公式:x =v 0t +12at 2,当初速度为0时,x =12at 2。
3、技巧归纳(1)在v -t 图像中,图线与t 轴所围的面积对应物体的位移,t 轴上方面积表示位移为正,t 轴下方面积表示位移为负。
(2)位移公式x =v 0t +12at 2只适用于匀变速直线运动。
(3)公式中x 、v 0、a 都是矢量,应用时必须选取正方向;一般选v 0的方向为正方向.当物体做匀减速直线运动时,a 取负值,计算结果中,位移x 的正负表示其方向。
(4)当v 0=0时,x =12at 2,即由静止开始的匀加速直线运动的位移公式,位移x 与t 2成正比。
4、匀变速直线运动中的平均速度该段时间的末速度v=v t +at ,由平均速度的定义式和匀变速直线运动的位移公式整理加工可所以在匀变速直线运动中,某一段时间内的平均速度等于该段时间内中间时刻的瞬时速度,又等于这段时间内初速度和末速度的算术平均值。
5、匀变速直线运动推论公式:任意两个连续相等时间间隔T 内,位移之差是常数,即△x=x 2-x 1=aT 2.拓展:△x MN =x M -x N =(M-N )aT 2。
推导:如图所示,x 1、x 2为连续相等的时间T 内的位移,加速度为a 。
考点2 匀变速直线运动速度与位移的关系 1、匀变速直线运动位移与速度的关系。
2.3匀变速直线运动的位移与时间的关系

第二种计算方法较简单。
12
课前学习
核心探究
核心素养
学习小结
[探究归纳] 1.公式的适用条件:适用于匀变速直线运动。 2.公式的意义:公式 v2-v20=2ax 反映了初速度 v0、末速度 v、加速度 a、位移 x 之
间的关系,当其中三个物理量已知时,可求另一个未知量。 3.公式的矢量性:公式中 v0、v、a、x 都是矢量,应用时必须选取统一的正方向,
核心探究
核心素养
学习小结
t2=3 s内的位移:x2=9 m, 解得小球沿斜面上滑在第1 s内的位移为
x=x2-x1=5 m。 答案 5 m
25
课前学习
核心探究
核心素养
学习小结
[针对训练2] 一辆汽车正在平直的公路上以72 km/h的速度行驶,司机看见红色信 号灯便立即踩下制动器,此后,汽车开始做匀减速直线运动。设汽车减速过程的 加速度大小为5 m/s2,求:
x1=v0t1+12at21=(20×2-12×5×22) m=30 m。 (2)因为 t2=5 s>t,所以汽车 5 s 末已停止运动,可应用逆向思维法,把它看 成逆向的初速度为零的匀加速直线运动,则有 x2=12at2=12×5×42 m=40 m。 答案 (1)30 m (2)40 m
27
课前学习
17
课前学习
核心探究
核心素养
学习小结
解析 (1)根据公式 v2-v20=2ax,v0= v2-2ax= 502-2×5.0×160 m/s=30 m/s。 (2)不装弹射系统时,v2=2aL,L=2va2=2×5052.0 m=250 m。 答案 (1)30 m/s (2)250 m
18
课前学习
核心探究
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.3 匀变速直线运动的位移与时间的关系
1.关于匀加速直线运动,下面说法正确的是( )
①位移与时间的平方成正比 ②位移总是随时间增加而增加 ③加速度、速度、位移三者方向一致 ④加速度、速度、位移的方向并不是都相同
A .①②
B .②③
C .③④
D .②④
2.做匀减速直线运动的物体经过4 s 后停止,若在第1 s 内的位移是14 m ,则最后1 s 的位移是( )
A .3.5 m
B .2 m
C .1 m
D .0
3.一辆汽车从静止开始由甲地出发,沿平直公路开往乙地,汽车先做匀加速运动,接着做匀减速运动,开到乙地刚好停止,其速度图象如图8所示,那么在0~t 0和t 0~3t 0两段时间内的( )
A .加速度大小之比为1∶3
B .加速度大小之比为3∶1
C .位移大小之比为2∶1
D .位移大小之比为1∶2
4.如图9所示为在同一直线上运动的甲、乙两物体的v -t 图象,则由图象可知( )
A .它们速度方向相同,加速度方向相反
B .它们速度方向、加速度方向均相反
C .在t 1时刻它们相遇
D .在0~t 2时间内它们的位移相同
5.一玩具汽车由静止开始以恒定的加速度a 向东运动t s 后,加速度变为向西,大小不变,再经过t s 时,物体的运动情况是( )
A .小汽车位于出发点以东,速度为零
B .小汽车位于出发点以东,继续向东运动
C .小汽车回到出发点,速度为零
D .小汽车回到出发点,运动方向向西
图9
图
8
6.做匀减速直线运动的物体,它的加速度大小为a ,初速度大小是v 0,经过时间t 速度减小到零,则它在这段时间内的位移大小表达错误的是( )
A .v 0t +12at 2 B.v 0t -12
at 2 C.v 02t D.12
at 2 7.物体从静止开始做匀加速直线运动,已知第2 s 内的位移为x ,则物体运动的加速度大小为( )
A.2x
B.x 2
C.23x
D.32
x
8.做直线运动的物体速度v 与时间t 的函数关系为v =3-2t ,此函数式中选定__________(物理量)的方向为正方向,物体刚开始做________运动.若此函数关系表示汽车刹车全过程,则汽车的初速度是______ m/s ,加速度是____ m/s 2.该汽车刹车1 s 冲出的距离是____ m ,刹车2 s 的位移______ m.
9.汽车紧急刹车时,加速度大小为6 m/s 2,且必须在2 s 内停下来.
(1)汽车允许的最大行驶速度是多少?
(2)刹车过程汽车的位移是多少?
参考答案
课后巩固提升
1.B 2.B
3.D [由a =Δv Δt 得:a 1=v 0t 0,a 2=-v 02t 0
,a 1∶a 2=2∶1,A 、B 错;0~t 0和t 0~3t 0两时间段的平均速度v 1=v 2=v 0
2
,故位移大小之比x 1∶x 2=(v 1t 0)∶(v 2· 2t 0)=1∶2(也可由面积之比直接得出位移之比),故选项C 错,D 对.]
4.AD
5.A [设小汽车向东运动为正方向,则汽车在2t s 内的速度-时间图象如右图所示.由图线容易看出,汽车在2t s 内的位移为正,即在2t s 末汽车在出发点以东,在2t s 末汽车的速度为零.]
6.A [根据位移公式可知B 正确,A 错.末速度v =0,故由x =v 0+v 2
t 可知C 正确.若将该运动按时间顺序反过来看作是初速度为零的匀加速直线运动,则D 正确.]
7.C [x 2-x 1=12at 22-12at 21=12a ×22-12a ×12=2a -12a =32a 则32a =x ,所以a =2x 3
] 8.v 0 匀减速直线运动 3 -2 2 2.25
解析 将v =3-2t 与v t =v 0+at 对比,可得出:v 0=3 m/s ,a =-2 m/s 2.
9.(1)12 m/s (2)12 m
解析 解法1:以汽车的行驶方向为正方向,由题意知:a =-6 m/s 2,v =0,t =2 s.
(1)由公式v =v 0+at 可得v 0=v -at =0-(-6)×2 m/s=12 m/s.
(2)由公式x =v 0t +1
2at 2得:x =12×2 m +12×(-6)×22 m =12 m.
解法2:将汽车的匀减速运动看作反向的匀加速运动,则a =6 m/s 2,
(1)v 0=at =6×2 m/s=12 m/s
(2)x =12at 2=12
×6×22 m =12 m。
