匀变速直线运动的位移与时间的关系1
匀变速直线运动的位移与时间、速度的关系
匀变速直线运动的位移与时间、速度的关系【知识点归纳】1、匀变速直线运动位移与时间的关系的公式表达：2021at t v s += s 为t 时间内的位移。
当a=0时，t v s 0= 当v 0=0时，221at s =当a<0时，2021at t v s -= 可见2021at t v s +=是匀变速直线运动位移公式的一般表示形式，只要知道运动物体的初速度v 0和加速度a ，就可以计算出任意一段时间内的位移，从而确定任意时刻物体所在的位置。
位移公式也可以用速度——时间图像求出面积得位移而推出。
2、匀变速直线运动的位移和速度的关系as v v t 2202=-这个关系式是匀变速直线运动规律的一个重要的推论。
关系式中不含时间t ，在一些不涉及到时间的问题中，应用这个关系是较方便的。
3、匀变速直线运动的两个推论1．匀变速直线运动的物体在连续相等的时间(T)内的位移之差为一恒量。
公式：S 2-S 1=S 3-S 2=S 4-S 3=…=S n -S n-1=△S=aT2 2．某段时间中间时刻的瞬时速度等于这段时间的平均速度，即： v v t =2【案例分析】例1．某物体作变速直线运动，关于此运动下列论述正确的是( )A ．速度较小，其加速度一定较小B ．运动的加速度减小，其速度变化一定减慢C ．运动的加速度较小，其速度变化一定较小D ．运动的速度减小，其位移一定减小例2．火车从车站由静止开出做匀加速直线运动，最初一分钟行驶540米，则它在最初l0秒行驶的距离是( )A ．90米B ．45米C ．30米D ．15米例3一物体由静止沿光滑斜面匀加速下滑距离为L 时，速度为V ，当它的速度是v ／2时，它沿全面下滑的距离是A ．L ／2 B.2L/2 C ．L ／4 D ．3L ／4例4：一物体以初速度v １做匀变速直线运动，经时间t 速度变为v ２求：(1)物体在时间t 内的位移. (2)(3)比较vt/2和v s/2例5：一辆沿平直路面行驶的汽车，速度为36km/h ．刹车后获得加速度的大小是4m/s 2，求：(1)刹车后3s 末的速度；(2)从开始刹车至停止，滑行一半距离时的速度．例6、一个质点作初速为零的匀加速运动，试求它在1s ，2s ，3s ，…内的位移s 1，s 2，s 3，…之比和在第1s ，第2s ，第3s ，…内的位移S Ⅰ，S Ⅱ，S Ⅲ，…之比各为多少？【一试身手】1．下列说法正确的是A ．加速度增大，速度一定增大B ．速度变化量Δv 越大，加速度就越大C ．物体有加速度，速度就增加D ．物体速度很大，加速度可能为零2. 关于速度和加速度的关系A ．物体的速度为零时，加速度一定为零B ．物体的加速度为零时，速度一定为零C ．物体的速度改变时，加速度不一定改变D ．物体的加速度方向改变时，速度方向不一定改变3．如图所示，Ⅰ、Ⅱ两条直线分别描述P 、Q 两个物体的s —t 图象，下列说法正确的是A ．两物体均做匀速直线运动B ．M 点表示两物体在时间t 内有相同的位移C ．t 时间内P 的位移较小D ．0～t ，P 比Q 的速度大，t 以后P 比Q 的速度小 4．某质点做匀变速直线运动，加速度的大小为2m/s 2，则在任意1s 内A ．质点的末速度一定是初速度的2倍B ．质点的末速度一定比初速度大2m/sC ．质点的初速度可能比末速度大2m/sD ．质点的速度大小一定改变了2m/s 5．做匀变速直线运动的质点，它在通过某一段位移中点位置的速度为v ，通过这段位移所用时间的中间时刻的速度为u ，则该质点A ．做匀加速运动时，v ＜uB ．做匀减速运动时，v ＜uC ．做匀加速运动时，v ＞uD ．做匀减速运动时，v ＞u6．一个质点做方向不变的直线运动，加速度的方向始终与速度的方向相同，但加速度的大小逐渐减小为零，在此过程中（ ）A ．速度逐渐减小，当加速度减小到零时，速度达到最小值B ．速度逐渐增大，当加速度减小到零时，速度达到最大值C ．位移逐渐增大，当加速度减小到零时，位移将不再增大D ．位移逐渐减小，当加速度减小到零时，位移达到最小值7．关于匀变速直线运动，下列说法中正确的是A 、加速度越大，物体的速度一定越大B 、加速度越小，物体的位移一定越小C 、物体在运动过程中的加速度保持不变D 、匀减速直线运动中，位移随时间的增加而减小8．质点做直线运动，当时间t = t 0时，位移S > 0，速度v > 0，加速度a > 0，此后加速度a 逐渐减小，则它的 （ ）A ．速度的变化越来越慢B ．速度逐渐减小C ．位移继续增大D ．位移、速度始终为正值t st o M Ⅰ Ⅱ9．甲、乙、丙和丁是以时间为横轴的匀变速直线运动的图象，下面说法正确的是（ ）A ．图甲是加速度—时间图象B ．图乙是加速度—时间图象C ．图丙是位移—时间图象D ．图丁是速度—时间图象10．滑块以某一初速度冲上斜面做匀减速直线运动，到达斜面顶端时的速度为零.已知滑块通过斜面中点时的速度为v ，则滑块在前一半路程中的平均速度大小为A 、212 vB 、（2+1）vC 、2vD 、21v 11．一匀变速运动物体的位移随时间变化的函数关系是S=4t+t 2(m), 则它运动的初速度、加速度及２ｓ末的速度分别是( )A ． 0、 4m/s 2 、4m/sB ． 4m/s 、 2m/s 2 、８m/sC ． 4m/s 、1m/s 2 、８m/sD ． 4m/s 、 ２m/s 2 、６m/s12．一个物体做初速度为零的匀加速运动，该物体通过前一半位移和通过后一半位移所用的时间之比是（ ）A ．2∶1B ．2∶ 1C ．(2+1)∶1D ．(2-1)∶1二、填空题1．汽车以2m/s 2的加速度由静止开始启动，则第5s 末汽车的速度是_______m/s ，第5s 内汽车的平均速度是________m/s, 第5s 内汽车的位移是___________m 。
匀变速直线运动中位移与时间的关系
匀变速直线运动中位移与时间的关系一、匀速直线运动的位移时间关系1、匀速直线运动的速度始终保持不变，所以 vt x =2、从v-t 图像看位移匀变速直线运动的速度时间图像是一条平行于时间轴的直线即 v观察v-t 图像发现面积刚好就是 0v 位移，其中0v 是高，t 是底。
o t t 面积 位移二、匀变速直线运动的位移时间关系问题：匀速直线运动中位移大小可以用v-t 图像与坐标轴位的面积表示。
这个结论能否用于匀变速直线运动呢？1、我们知道对于变速运动的描述，最初使用的是平均速度即tx v ∆∆= ① 我们由①式出发稍微做一个变形就可以得到t v x ∆=∆ ② 2、我们来看一下匀变速直线运动的v-t 图像v0vo t我们观察图形会发现是一个梯形，所以我们不能用底乘以高即0v t 表示示其面积，那为什么就不行呢？因为这个图像中我们可以看出来从0到t 时刻存在一个很大的速度变化量即v ∆。
若从梯形中间做一条线，将其一分为二，我们在观察，还是不想矩形，但是会发现看其中一半是v ∆变小了，如果我们一直这样分下去会发现对一个细长的小梯形来说v ∆ 0，也就是说这个细长的梯形就可以看做一个矩形了，那么我们就可以用他的面积来表示位移的大小了。
于是我们就将梯形划分成许多细长的小梯形，所有小梯形的面积之和就是这段时间内物体的位移大小，也是整个梯形的面积。
故我们可以用梯形的面积来代表晕变速直线运动的位移大小。
所以我们求位移就可以通过求解梯形的面积。
解梯形的面积高下底上底⨯+==2s x t v v x t ⨯+=20––––––③高中位线⨯==s xt v x t ⨯=2––––––④ 因为at v v t +=0，所以我们将③式做一个简单的变形会得到2021at t v x += 这就是匀变速直线运动中位移与时间的关系，即位移公式3.对比将 ④三式进行对比会发现202t tv v v v +== 即中间时刻的速度等于平均速度等于初末速度之和的一半例：汽车刹车前的速度0v =5m/s ，a=-0.42s m ,求（1）开始刹车后20s 内滑行的距离？（2）汽车从刹车开始，位移x=30m 所用的时间？（3）在静止前2.5s 内滑行的距离？解：（1）错解：由2021at t v x +=可知x =5⨯202204.021⨯⨯-=20m 正解：法1：由a v at v v t 0t 0-v t =+=可知刹车制停的时间 又已知s m v /50= 2/4.0s m a -= 0=t v故t=12.5s 由于12.5<20，所以在t=12.5s 以后车就静止不动了。
匀变速直线运动的位移与时间的关系公式
匀变速直线运动的位移与时间的关系公式
匀变速直线运动的位移与时间的关系公式可以由运动学公式推导得到，具体分为两种情况：
1. 匀速直线运动的位移与时间的关系公式：
位移 = 速度 ×时间
其中，位移表示物体在运动过程中从起点到终点的距离，速度表示物体的运动速度，时间表示运动的时间长度。
2. 变速直线运动的位移与时间的关系公式：
位移 = 初速度 ×时间 + 0.5 ×加速度 ×时间²
其中，初速度表示运动开始时的速度，加速度表示运动过程中的加速度。
这个公式描述了的位移与时间的关系可以用来计算变速直线运动下物体在不同时间点的位置。
注意，这个公式的适用条件是运动过程中加速度是一个常量。
另外还有一种特殊情况，匀变速直线运动中，如果物体的位移与时间的关系符合二次函数的形式，可以使用二次函数公式来描述位移与时间的关系。
例如：位移 = a ×时间² + b ×时间 + c，其中a、b和c是常数。
1.2.3 匀变速直线运动的位移与时间的关系1
小 结
一、匀速直线运动的位移公式：
x=vt
二、匀变速直线运动的位移公式：
1a t2 x = v0 t + — 2 三、在 v-t 图象中，物体的位移 x 在数值上
等于图线与坐标轴所围的面积。 （其中横轴上方的面积代表位移为正方向， 横轴下方的面积代表位移为负方向。）
分 割 逼 近 法
V
割圆术
0
t
V
B
V0
C
0
思考：能否推导出 匀变速直线运动的 1 ( OC + AB ) ×OA S= — 2位移与时间的关系 式呢？ A
t t
1 v0 + v ) x= 2 v = v0 + a t
—(
t
匀变速直线运动位 移与时间的关系式 （简称位移公式）
1a t2 x = v0 t + — 2
1a t2 x = v0 t + 2
动，走了12s时，发现还有乘客没上来，于
是立即做匀减速运动至停车。汽车从开出 到停止总共历时20s，行进了50 m。求汽车 的最大速度。
作业
• 作业本：P16 T1-5 T7-10 • 选作T6 、11 、12
分割和逼近的方法在物理学研究中有着广泛的 应用。早在公元263年，魏晋时的数学家刘徽首创 了“割圆术”——圆内正多边形的边数越多，其周 长和面积就越接近圆的周长和面积。
科学思想方法：先把过 程无限分割,以“不变” 近似代替“变”,然后再 进行累加的思想 。
提高练习
• 从车站开出的汽车，做匀加速直线运
第二章
匀变速直线运动的研究
第三节、匀变速直线运动的位移与时间的关系
复 习
运动情况
1 匀速直线运动 2 初速度为v0的匀加速直线运动 3 初速度为0的匀加速直线运动 4 初速度为v0的匀减速直线运动 5 初速度为0的匀加速直线运动 6 初速度为-v0的匀减速直线运动
匀变速直线运动的位移与时间的关系
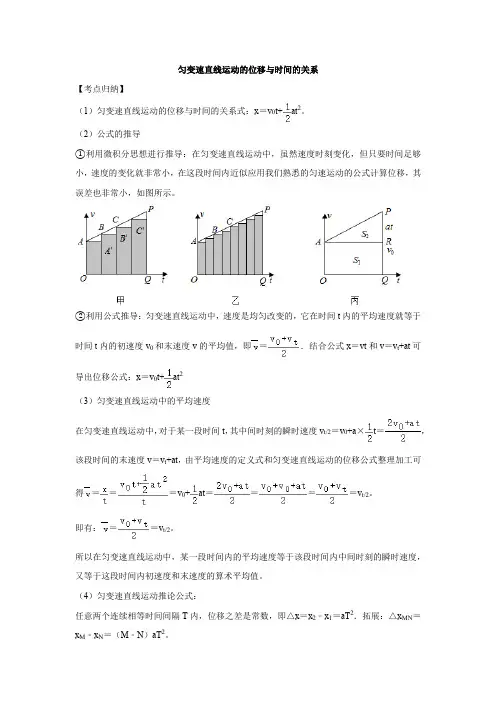
匀变速直线运动的位移与时间的关系【考点归纳】（1）匀变速直线运动的位移与时间的关系式：x＝v0t+at2。
（2）公式的推导①利用微积分思想进行推导：在匀变速直线运动中，虽然速度时刻变化，但只要时间足够小，速度的变化就非常小，在这段时间内近似应用我们熟悉的匀速运动的公式计算位移，其误差也非常小，如图所示。
②利用公式推导：匀变速直线运动中，速度是均匀改变的，它在时间t内的平均速度就等于时间t内的初速度v0和末速度v的平均值，即＝．结合公式x＝vt和v＝v t+at可导出位移公式：x＝v0t+at2（3）匀变速直线运动中的平均速度在匀变速直线运动中，对于某一段时间t，其中间时刻的瞬时速度v t/2＝v0+a×t＝，该段时间的末速度v＝v t+at，由平均速度的定义式和匀变速直线运动的位移公式整理加工可得＝＝＝v0+at＝＝＝＝v t/2。
即有：＝＝v t/2。
所以在匀变速直线运动中，某一段时间内的平均速度等于该段时间内中间时刻的瞬时速度，又等于这段时间内初速度和末速度的算术平均值。
（4）匀变速直线运动推论公式：任意两个连续相等时间间隔T内，位移之差是常数，即△x＝x2﹣x1＝aT2．拓展：△x MN＝x M﹣x N＝（M﹣N）aT2。
推导：如图所示，x1、x2为连续相等的时间T内的位移，加速度为a。
【命题方向】例1：对基本公式的理解汽车在平直的公路上以30m/s的速度行驶，当汽车遇到交通事故时就以7.5m/s2的加速度刹车，刹车2s内和6s内的位移之比（）A.1：1B.5：9C.5：8D.3：4分析：求出汽车刹车到停止所需的时间，汽车刹车停止后不再运动，然后根据位移时间公式求出2s内和6s内的位移。
解：汽车刹车到停止所需的时间＞2s所以刹车2s内的位移＝45m。
t0＜6s，所以刹车在6s内的位移等于在4s内的位移。
＝60m。
所以刹车2s内和6s内的位移之比为3：4．故D正确，A、B、C错误。
高中物理必修一-匀变速直线运动位移与时间的关系
匀变速直线运动位移与时间的关系知识集结知识元匀变速直线运动的位移与时间的关系知识讲解匀变速直线运动的位移与时间的关系式：x=v0t+at2．公式的推导①利用微积分思想进行推导：在匀变速直线运动中，虽然速度时刻变化，但只要时间足够小，速度的变化就非常小，在这段时间内近似应用我们熟悉的匀速运动的公式计算位移，其误差也非常小，如图所示．②利用公式推导：匀变速直线运动中，速度是均匀改变的，它在时间t内的平均速度就等于时间t内的初速度v0和末速度v的平均值，即．结合公式x=vt和v=v0+at可导出位移公式：x=v0t+ at2例题精讲匀变速直线运动的位移与时间的关系例1.一个物体由静止开始做匀加速直线运动，第1s内的位移是1m，物体在第3s内的位移是（）A．2m B．3m C．5m D．8m例2.为了测定某轿车在平直路上启动阶段的加速度（轿车启动时的运动可近似看成是匀加速直线运动），某人拍摄一张在同一底片上多次曝光的照片，如图所示，如果拍摄时每隔2s曝光一次，轿车车身总长为4.5m，那么这辆轿车的加速度为（）A．1m/s2B．2.25m/s2C．3m/s2D．4.25m/s2例3.2015年9月2日，“抗战专列”在武汉地铁4号线亮相，引得乘车市民纷纷点赞．若该地铁列车先从甲站开始做初速度为零、加速度大小为a的匀加速直线运动，通过位移L后，立即做加速度大小也为a的匀减速直线运动，恰好到乙站停下．则列车从甲站到乙站所用时间为（）A．B．2C．2D．4当堂练习单选题练习1.一个物体在水平直线上做匀加速直线运动，初速度为3m/s，经过4s它的位移为24m，则这个物体运动的加速度等于（）A．1.5m/s2B．2m/s2C．4m/s2D．0.75m/s2练习2.小球以某一较大初速度冲上一足够长光滑斜面，加速度大小为5m/s2则小球在沿斜面上滑过程中最后一秒的位移是（）A．2.0m B．2.5m C．3.0m D．3.5m练习3.“蛟龙号”是我国首台自主研制的作业型深海载人潜水器，它是目前世界上下潜能力最强的潜水器．假设某次海试活动中，“蛟龙号”完成海底任务后竖直上浮，从上浮速度为v时开始计时，此后“蛟龙号”匀减速上浮，经过时间t上浮到海面，速度恰好减为零，则“蛟龙号”在t0（t0<t）时刻距离海平面的深度为（）A．B．C．D．练习4.一个物体由静止开始做匀加速直线运动，第1s内的位移是1m，物体在第3s内的位移是（）A．2m B．3m C．5m D．8m练习5.为了测定某轿车在平直路上启动阶段的加速度（轿车启动时的运动可近似看成是匀加速直线运动），某人拍摄一张在同一底片上多次曝光的照片，如图所示，如果拍摄时每隔2s曝光一次，轿车车身总长为4.5m，那么这辆轿车的加速度为（）A．1m/s2B．2.25m/s2C．3m/s2D．4.25m/s2练习6.2015年9月2日，“抗战专列”在武汉地铁4号线亮相，引得乘车市民纷纷点赞．若该地铁列车先从甲站开始做初速度为零、加速度大小为a的匀加速直线运动，通过位移L后，立即做加速度大小也为a的匀减速直线运动，恰好到乙站停下．则列车从甲站到乙站所用时间为A．B．2C．2D．4。
匀变速直线运动的位移与时间的关系
新知导入
对于运动问题，人们不仅 关注物体运动的速度随时 间变化的规律，而且还希 望知道物体运动的位移随 时间变化的规律。 今天，我们就来重点探究匀变速直线运动的位 移与时间有怎样的关系？
新知讲解
一、匀速直线运动的位移 1、匀速直线运动的位移与时间的关系：x=vt，它 的v-t图象是平行于t轴的一条直线。
新知讲解
对后一过程，末速度 v＝0，初速度 vM ＝ 15 m/s。
由 v2 ＝ vM2 ＋ 2ax2 ，有
动车进站的加速度大小为 0.167 m/s2 ，方向 与动车运动方向相反；还要行驶 674 m才能停下 来。
知识拓展
匀变速直线运动的重要推论
1．平均速度 在匀变速直线运动中，对于某一段时间t，其 中间时刻的瞬时速度vt＝v0＋a× t＝v0＋ at， 该段时间的末速度v＝v0＋at，由平均速度的 定义式和匀变速直线运动的位移公式整理加 工可得。
新知讲解
分析：由于把动车进站过程视为匀减速 直线运动，因此可以应用匀变速直线运动的 速度与位移关系式计算动车的加速度。本题 加速度方向跟速度方向相反，因此需要建立 一维坐标系来处理相关物理量的正负号。
新知讲解
解： 沿动车运动方向为正方向建立一维坐标系。把 动车通过3000m 的运动称为前一过程，之后到停下 来称为后一过程。 设在前一过程中的末位置为 M 点。初速度 v0 ＝126 km/h＝35 m/s，末速度vM＝54 km/h＝15 m/s，位移 x1 ＝ 3000m。 对前一过程，根据匀变速直线运动的速度与位移的 关系式，有
V0 0
由图可知梯形的面积：S梯形=（V0+V
即位移：x
1 2
(v0
第二章第3节匀变速直线运动的位移与时间的关系1
40
t=700
2
积)表示汽车这段时间内通过的位移,由三角形面积 S=
得 t=35 s。
m,解
答案:35 s
点评:分析匀变速直线运动问题的方法较多,但公式法与图象法
是两种最主要的方法,应用图象法解题时,可巧妙利用图象的斜率与
面积等,快捷而简便。
(1)公式中的 x、v 0、a 均是矢量,应用公式时,应先确定正方
向。
1
2
(2)当 v0=0 时,x= at2,表示初速度为零的匀加速直线运动的位移
与时间的关系。
(3)当 a=0 时,x=v0t,表示匀速直线运动的位移与时间的关系。
预习交流
如图所示,v-t 图象中图线与时间轴所围的矩形的面积有时在时
形面积之和趋近于 v-t 图线下面的面积。可以想象,如果把整个运
动过程划分得非常非常细,很多很多小矩形的面积之和就能准确代
表物体的位移了,位移的大小等于图丙中梯形的面积。
当时间间隔分割得足够小时,折线趋近于直线 AP,设想的运动
就代表了真实的运动,由此可以求出匀变速运动在时间 t 内的位移,
它在数值上等于直线 AP 下方的梯形 OAPQ 的面积(图丙)。这个面
简答:打开阻力伞是为了增大减速的加速度;可以用 v-t 图象求
1
出跑道长度,也可以用位移公式求出,由 x=v0t+ at2 及 0=v0+at 解得
2
x=1 250 m。
预习导引
1.匀速直线运动的位移
(1)做匀速直线运动的物体在时间 t 内的位移 x=vt。
(2)做匀速直线运动的物体,如图所示,其 v-t 图象是一条平行于
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、匀速直线运动的位移
匀速直线运动，物体的位移对应着 图 匀速直线运动，物体的位移对应着v-t图 像中的一块矩形的面积。 像中的一块矩形的面积。
二、匀变速直线运动的位移
1、 匀变速直线运动，物体的位移对 匀变速直线运动， 应着v-t图像中图线与时间轴之间包围 应着 图像中图线与时间轴之间包围 梯形面积。 的梯形面积。 2、公式 、
v＝（ 0＋v）/2 ＝（v ） ＝（
[课堂探究] 课堂探究]
• 一质点以一定初速度沿竖直方向抛出，得到它 一质点以一定初速度沿竖直方向抛出， 的速度一时间图象如图所示．试求出它在前2 的速度一时间图象如图所示．试求出它在前 s 内的位移，后2 s内的位移，前4s内的位移． 内的位移， 内的位移， 内的位移． 内的位移 内的位移
[课堂探究] 课堂探究]
一质点沿一直线运动， ＝ 时 • 一质点沿一直线运动，t＝0时， 位于坐标原点， 位于坐标原点，图为质点做直 线运动的速度一时间图象． 线运动的速度一时间图象．由 图可知： 图可知： • (1)该质点的位移随时间变化的 该质点的位移随时间变化的 关系式是:x＝ . 关系式是:x＝ • (2)在时刻 在时刻t= s时，质点距 在时刻 时 坐标原点最远． 坐标原点最远． • (3)从t＝0到t＝20 s内质点的位 从＝ 到＝ 内质点的位 移是 ；通过的路程是 ； • 参考答案：(1)一4t+0.2t2 (2)10 参考答案： 一 (3)0 40 m
三、匀变速直线运动的位移与 速度的关系
v2 － v02 = 2 a s
匀变速直线运动公式
1、速度公式 v = v0 + at 、 2、位移公式 S = v0 t+1/2 at2 、 3、推论 、
v2 － v02 = 2 a s
4、平均速度公式 v＝（ 0＋v）/ 2 、 ＝（v ＝（ ）
课堂训练
3、以10m/s的速度匀速行驶的汽车刹车后 、 的速度匀速行驶的汽车刹车后 做匀减速运动。若汽车刹车后第2s内的 做匀减速运动。若汽车刹车后第 内的 位移为6.25m（刹车时间超过 ），则 ），则 位移为 （刹车时间超过2s）， 刹车后6s内汽车的位移是多大 内汽车的位移是多大？ 刹车后 内汽车的位移是多大？ a=-2.5m/s2 20m 4、以10m/s的速度行驶的汽车关闭油门后 、 的速度行驶的汽车关闭油门后 后做匀减速运动，经过6s停下来 停下来， 后做匀减速运动，经过 停下来，求汽 车刹车后的位移大小。 车刹车后的位移大小。 30m
1、射击时，火药在枪筒里燃烧。燃气膨胀， 推动弹头加速运动。我们把子弹在枪筒里 的运动看做是匀加速直线运动，假设子弹 的加速度是a＝5×105m/s，枪筒长 x＝ 0.64m，我们计算子弹射出枪口时的速度。 800m/s
2、一辆载满乘客的客机由于某种原 、 因紧急着陆， 因紧急着陆，着陆时的加速度大小 着陆前的速度为60m/s， 为6m/s2，着陆前的速度为 ， 问飞机着陆后12s内滑行的距离为多 问飞机着陆后 内滑行的距离为多 大？ 300m
[课堂探究] 课堂探究]
• 如图所示，初速度为负值的匀减速直线运动，位移由 如图所示，初速度为负值的匀减速直线运动， 两部分组成:t1时刻之前位移 为负值； 时刻之后位 时刻之前位移x1为负值 两部分组成 时刻之前位移 为负值；t2时刻之后位 为正值； 时间内总位移x＝｜ 移x2为正值；故在 ～t2时间内总位移 ＝｜ ｜一｜ 为正值 故在0～ 时间内总位移 ＝｜x2｜ x1｜ ｜
3、一辆沿平直公路行驶的汽车，经过路口 、一辆沿平直公路行驶的汽车， 其速度为36km/h，经过路口后以 时，其速度为 ， 2m/s2的加速度加速行驶，求： 的加速度加速行驶， （1）加速 后的速度和距路口的位移 ）加速3s后的速度和距路口的位移 （2）从开始加速到达该路所限制的最高时 ） 速72km/h时，距路口的位移。 时 距路口的位移。 （1）16m/s ） （2）75m ） 39m
小结
一、匀速直线运动的位移 匀速直线运动的位移 1、匀速直线运动，物体的位移对应着 图像中 匀速直线运动， 匀速直线运动 物体的位移对应着v-t图像中 的一块矩形的面积。 的一块矩形的面积。 2、公式：S ＝ v t 、公式： 二、匀变速直线运动的位移与时间的关系 1、 匀变速直线运动，物体的位移对应着 t图 、 匀变速直线运动，物体的位移对应着v- 图 中图线与时间轴之间包围的梯形面积。 像 中图线与时间轴之间包围的梯形面积。 2、公式 、 3、平均速度公式 、
• X=一4t+0.2t2 一 • 请你根据本式求出 v0和a；并描绘出 ；并描绘出x-t 图像
课堂训练
1、射击时，火药在枪筒里燃烧。燃气膨胀， 、射击时，火药在枪筒里燃烧。燃气膨胀， 推动弹头加速运动。 推动弹头加速运动。我们把子弹在枪筒里 的运动看做是匀加速直线运动， 的运动看做是匀加速直线运动，假设子弹 的加速度是a＝ × 的加速度是 ＝5×105m/s，枪筒长 x＝ ， ＝ 0.64m，我们计算子弹射出枪口时的速度。 ，我们计算子弹射出枪口时的速度。 800m/s
3、匀变速直线运动的平均速度公式 、 v＝（ 0＋v）/2 ＝（v ＝（ ）
课堂训练
1、一辆汽车以1m/s2的加速度加速行驶了 、一辆汽车以 12s，驶过了 ，驶过了180m，求汽车开始加速时的 ， 速度是多少？ 速度是多少？ 9m/s 2、骑自行车的人以 、骑自行车的人以5m/s的初速度匀减速上 的初速度匀减速上 一个斜坡，加速度的大小为0.4m/s2，斜坡 一个斜坡，加速度的大小为 长30m，骑自行车的人通过斜坡需要多少 ， 时间？ 时间？ 10s