河北科技大学大学物理答案11章分解

合集下载

大学物理2精讲精练答案

第十一章静电场例题答案：11-1 （B ） 11-2（B ）11-3（B ）11-4．；从O 点指向()30220824R qdd R R qd εεπ≈-ππ缺口中心点11-5.；；沿矢径OP0/ελd ()2204dR d-πελ11-6(D)11-7.向右 ;向右2εσ023εσ11-8(1)，r <R;(2)o2r 4r k E ε=，r >R 。

204r r 4RkE ε=[解](1)作与球体同心、而半径r <R 的球面S 1。

球体内电荷密度ρ随r 变化，因此，球面S 1内包含的电荷。

根据高斯定理和已知的电荷体密度ρ(r )，()dr r r 4Q ro21⎰ρπ=可求得球体内任意点的场强。

即，得：()⎰⎰ρπε=⋅=Φr2s o r dr r r 41s d E 1 ，r <R 。

o2r 4r k E ε=(2)作与球体同心、半径r >R 的球面S 2，因R 外电荷为零，故S 2内的电荷Q 2=Q 1，根据高斯定理得：Φ==4πr 2E r =，∴()⎰⎰ρπε=⋅R 02s 0r dr r r 41s d E 2⎰πεR3dr kr 41，r >R 。

204r r 4R kE ε=11-9(D) 11-10(C) 11-11.单位正电荷在d 0L⋅=⎰A E l 静电场中沿任意闭合路径绕行一周，电场力作功等于零有势（或保守力）11-12. 45 V —15 V 11-13. -2000V 11-14. (B) 11-15.，０，，。

20R4QπεR 4Q 0πε20r 4Qπε11-16()()a b b c R R R R /ln /ln 21=λλ[解]：设B 上带正电荷，内表面上电荷线密度为λ1，外表面上电荷线密度为λ2，而A 、C 上相应地感应等量负电荷，如图所示．则A 、B 间场强分布为 E 1=λ1 / 2πε0r ，方向由B 指向A B 、C 间场强分布为 E 2=λ2 / 2πε0r ，方向由B 指向CB 、A 间电势差11100ln 22E r d d a ab bR R b BA R R aR r r R λλεε=⋅=-=ππ⎰⎰UB 、C 间电势差22200ln 22E r d d ccb b R Rc BC R R bR r U r R λλεε=⋅=-=ππ⎰⎰因U BA ＝U BC ,得到()()a b b c R R R R /ln /ln 21=λλ练习详解：11-1.（1）E 0=0；（2）E 0=0；（3）=k ；（4）0E 2aq 4i= k 0E 2aq 2i[解](1)如图(a )所示，各点电荷在点o 处产生的场强两两对应相消，所以，点o 处场强E 0=0(2)取图中(b )所示坐标。

(完整版)大学物理课后习题答案详解

第一章质点运动学1、(习题1.1)：一质点在xOy 平面内运动，运动函数为2x =2t,y =4t 8-。

（1）求质点的轨道方程；（2）求t =1 s t =2 s 和时质点的位置、速度和加速度。

解：（1）由x=2t 得，y=4t 2-8 可得： y=x 2-8 即轨道曲线（2）质点的位置： 22(48)r ti t j =+- 由d /d v r t =则速度： 28v i tj =+ 由d /d a v t =则加速度： 8a j =则当t=1s 时，有 24,28,8r i j v i j a j =-=+= 当t=2s 时，有 48,216,8ri j v i j a j =+=+=2、（习题1.2）：质点沿x 在轴正向运动，加速度kv a -=，k 为常数．设从原点出发时速度为0v ，求运动方程)(t x x =.解：kv dt dv-= ⎰⎰-=t vv kdt dv v 001 tk e v v -=0t k e v dtdx-=0 dt ev dx tk tx-⎰⎰=000)1(0t k e kv x --=3、一质点沿x 轴运动，其加速度为a = 4t (SI)，已知t = 0时，质点位于x 0=10 m 处，初速度v 0 = 0．试求其位置和时间的关系式．解： =a d v /d t 4=t d v 4=t d t ⎰⎰=vv 0d 4d tt t v 2=t 2v d =x /d t 2=t 2t t x txx d 2d 020⎰⎰= x 2= t 3 /3+10 (SI)4、一质量为m 的小球在高度h 处以初速度0v 水平抛出，求：（1）小球的运动方程；（2）小球在落地之前的轨迹方程；（3）落地前瞬时小球的d d r t ，d d v t ，tv d d . 解：（1） t v x 0= 式（1）2gt 21h y -= 式（2） 201()(h -)2r t v t i gt j =+（2）联立式（1）、式（2）得 22v 2gx h y -=（3）0d -gt d rv i j t = 而落地所用时间 gh2t = 所以 0d -2gh d r v i j t =d d v g j t=- 2202y 2x )gt (v v v v -+=+= 2120212202)2(2])([gh v gh g gt v t g dt dv +=+=5、已知质点位矢随时间变化的函数形式为22r t i tj =+，式中r 的单位为m ，t 的单位为s .求：（1）任一时刻的速度和加速度；（2）任一时刻的切向加速度和法向加速度。

大学物理课后习题答案详解

第一章质点运动学1、(习题1.1)：一质点在xOy 平面内运动，运动函数为2x =2t,y =4t 8-。

（1）求质点的轨道方程；（2）求t =1 s t =2 s 和时质点的位置、速度和加速度。

解：（1）由x=2t 得，y=4t 2-8 可得： y=x 2-8 即轨道曲线（2）质点的位置： 22(48)r ti t j =+- 由d /d v r t =则速度： 28v i tj =+ 由d /d a v t =则加速度： 8a j =则当t=1s 时，有 24,28,8r i j v i j a j =-=+= 当t=2s 时，有48,216,8r i j v i j a j =+=+=2、（习题1.2）：质点沿x 在轴正向运动，加速度kv a -=，k 为常数．设从原点出发时速度为0v ，求运动方程)(t x x =.解： kv dt dv-= ⎰⎰-=t vv kdt dv v 001 tk e v v -=0t k e v dtdx-=0 dt e v dx t k tx-⎰⎰=000)1(0t k e kv x --=3、一质点沿x 轴运动，其加速度为 a t (SI)，已知t 0时，质点位于x处，初速度v ．试求其位置和时间的关系式．解：=a d v /d t 4=t d v 4=t d t⎰⎰=vv 0d 4d tt t v 2=t 2v d =x /d t 2=t 2t t x txx d 2d 020⎰⎰= x 2= t 3 /3+10 (SI)4、一质量为m 的小球在高度h 处以初速度0v 水平抛出，求：（1）小球的运动方程；（2）小球在落地之前的轨迹方程；（3）落地前瞬时小球的d d r t ，d d v t ，tv d d . 解：（1） t v x 0= 式（1）2gt 21h y -= 式（2） 201()(h -)2r t v t i gt j =+（2）联立式（1）、式（2）得 22v 2gx h y -=（3）0d -gt d rv i j t = 而落地所用时间 gh2t = 所以0d -2g h d r v i j t =d d v g j t =- 2202y 2x )gt (v v v v -+=+= 2120212202)2(2])([gh v gh g gt v t g dt dv +=+= 5、已知质点位矢随时间变化的函数形式为22r t i tj =+，式中r 的单位为m ，t 的单位为s .求：（1）任一时刻的速度和加速度；（2）任一时刻的切向加速度和法向加速度。

大学物理2,11第十一章思考题

1、一根长为l 、质量为m 的均匀细棒悬于通过其一端的光滑水平固定轴上，构成一个复摆。

该摆作微小摆动时的周期等于多少？【答案：gl 32π2】详解：如图所示，均匀细棒所受的重力矩为θsin 2l mg M -=2lmg -≈式中负号表示重力矩阻碍细棒向正角位移方向摆动。

细棒对悬点O 的转动惯量为231ml J =由刚体定轴转动定律得222d d 312tml l mg θθ=- 或023d d 22=+θθlgt 令lg232=ω，则该复摆作微小摆动的周期为 ωπ2=T gl 32π2= 2、两个质点各自作简谐振动，它们的振幅相同、周期相同。

第一个质点的振动方程为x 1 = A cos(ωt + ϕ)。

当第一个质点从相对于其平衡位置的正位移处回到平衡位置时，第二个质点正在最大正位移处。

求第二个质点的振动方程。

【答案：)π21cos(2-+=ϕωt A x 】详解：设第二个质点的初相为，由题意得2π=-βϕ 即2π-=ϕβ 图4-22因此第二个质点的振动方程为)π21cos(2-+=ϕωt A x3、一根轻弹簧上端固定，下端系一个质量为m 1的物体，稳定后在m 1下边又系一个质量为m 2的物体，于是弹簧又伸长了∆x 。

如果将m 2移去，并令m 1振动，其振动周期为多少？【答案：gm xm 21π2∆】详解：设弹簧下端只系质量为m 1的物体时，弹簧伸长x 1，其平衡方程为11kx g m =弹簧下端系质量为m 1和m 2的两个物体时，弹簧伸长x 2，这时的平衡方程为221)(kx g m m =+将以上两个平衡方程相减得)(122x x k g m -=x k ∆=由此解得弹簧的劲度系数为xgm k ∆=2 当移去m 2，并令m 1振动时，其振动周期为k m T 1π2=gm x m 21π2∆= 4、一个质点作简谐振动，其运动速度与时间的关系曲线如图11-11所示。

如果质点的振动规律用余弦函数描述，则其初相等于多少？【答案：π65-或π67】详解：质点作简谐振动的运动速度与时间的关系为0.5图11-11-mO图11-15m)sin(ϕωωυ+-=t A )π21cos(++=ϕωωt A因此质点的运动速度也作简谐振动，其初相为π21+=ϕϕυ由-t 关系曲线得运动速度初始时的旋转矢量图如图所示。

大学物理课答案11章

习题1111-1．测量星体表面温度的方法之一是将其看作黑体，测量它的峰值波长m λ，利用维恩定律便可求出T 。

已知太阳、北极星和天狼星的m λ分别为60.5010m -⨯，60.4310m -⨯和60.2910m -⨯，试计算它们的表面温度。

解：由维恩定律：m T b λ=，其中：310898.2-⨯=b ，那么：太阳：362.8981057960.510m bT K λ--⨯===⨯；北极星：362.8981067400.4310m bT K λ--⨯===⨯；天狼星：362.8981099930.2910m bT K λ--⨯===⨯。

11-2．宇宙大爆炸遗留在宇宙空间的均匀背景辐射相当于温度为K 3的黑体辐射，试计算：（1）此辐射的单色辐出度的峰值波长；（2）地球表面接收到此辐射的功率。

解：（1）由m T b λ=，有342.898109.66103m b m T λ--⨯===⨯；（2）由4M T σ=，有：424P T R σπ=⨯地，那么：328494(637010) 5.67103 2.3410P W π-=⨯⨯⨯⨯⨯=⨯。

11-3．在加热黑体过程中，其单色辐出度对应的峰值波长由0.69μm 变化到0.50μm ，求总辐出度改变为原来的多少倍？解：由 b T m =λ 和 4T M σ=可得，63.3)5.069.0()()(440400====m m T T M M λλ11-4．已知000K 2时钨的辐出度与黑体的辐出度之比为259.0。

设灯泡的钨丝面积为2cm 10，其他能量损失不计，求维持灯丝温度所消耗的电功率。

解：∵4P T S σ=⋅黑体，消耗的功率等于钨丝的幅出度，所以，44840.2591010 5.67102000235P S T W ησ--==⨯⨯⨯⨯⨯=。

11-5．天文学中常用热辐射定律估算恒星的半径。

现观测到某恒星热辐射的峰值波长为m λ；辐射到地面上单位面积的功率为W 。

大学物理(普通物理学第六版)111第十一章(二)

一. 选择题[ B ]自测4. 一个动量为p 的电子，沿图示方向入射并能穿过一个宽度为D 、磁感强度为B(方向垂直纸面向外)的均匀磁场区域，则该电子出射方向和入射方向间的夹角为(A) p eBD 1cos -=α． (B) peBD 1sin -=α．(C) ep BD 1sin-=α． (D) epBD 1cos -=α．提示：[ D ]2. A 、B 两个电子都垂直于磁场方向射入一均匀磁场而作圆周运动．A 电子的速率是B 电子速率的两倍．设R A ，R B 分别为A 电子与B 电子的轨道半径；T A ，T B 分别为它们各自的周期．则 (A) R A ∶R B =2，T A ∶T B =2． (B) R A ∶R B 21=，T A ∶T B =1． (C) R A ∶R B =1，T A ∶T B 21=． (D) R A ∶R B =2，T A ∶T B =1．提示：[ C ]3. 如图所示，在磁感强度为B 的均匀磁场中，有一圆形载流导线，a 、b 、c是其上三个长度相等的电流元，则它们所受安培力大小的关系为 (A) F a > F b > F c ． (B) F a < F b < F c ． (C) F b > F c > F a ． (D) F a > F c > F b ．提示：[A ]4. 如图，无限长直载流导线与正三角形载流线圈在同一平面内，若长直导线固定不动，则载流三角形线圈将 (A) 向着长直导线平移． (B) 离开长直导线平移． (C) 转动． (D) 不动．提示：[ D ]基础6. 两个同心圆线圈，大圆半径为R ，通有电流I 1；小圆半径为r ，通有电流I 2，方向如图．若r << R (大线圈在小线圈处产生的磁场近似为均匀磁场)，当它们处在同一平面内时小线圈所受磁力矩的大小为 (A)Rr I I 22210πμ． (B)Rr I I 22210μ．(C)rR I I 22210πμ． (D) 0．提示：二. 填空题自测10. 如图所示，一半径为R ，通有电流为I 的圆形回路，位于Oxy 平面内，圆心为O ．一带正电荷为q 的粒子，以速度v沿z 轴向上运动，当带正电荷的粒子恰好通过O 点时，作用于圆形回路上的力为_0_，作用在带电粒子上的力为_0_．基础14. 如图，在粗糙斜面上放有一长为l 的木制圆柱，已知圆柱质量为m ，其上绕有N 匝导线，圆柱体的轴线位于导线回路平面内，整个装置处于磁感强度大小为B 、方向竖直向上的均匀磁场中．如果绕组的平面与斜面平行，则当通过回路的电流I =()NlB mg 2/时，圆柱体可以稳定在斜面上不滚动．提示：自测12. 磁场中某点处的磁感强度为)SI (20.040.0j i B-=，一电子以速度j i 66100.11050.0⨯+⨯=v (SI)通过该点，则作用于该电子上的磁场力F 为)(10814N k-⨯．(基本电荷e =1.6×10-19C)提示：基础19. 如图，一个均匀磁场B 只存在于垂直于图面的P 平面右侧，B的方向垂直于图面向里．一质量为m 、电荷为q 的粒子以速度v 射入磁场．v在图面内与界面P 成某一角度．那么粒子在从磁场中射出前是做半径为qBm v的圆周运动．如果q > 0时，粒子在磁场中的路径与边界围成的平面区域的面积为S ，那么q < 0时，其路径与边界围成的平面区域的面积是S qB mv -⎪⎪⎭⎫⎝⎛2π．5. 如图所示，在真空中有一半径为a 的3/4圆弧形的导线，其中通以稳恒电流I ，导线置于均匀外磁场B 中，且B与导线所在平面垂直．则该载流导线bc 所受的磁力大小为aIB 2．6．氢原子中电子质量m ，电荷e ，它沿某一圆轨道绕原子核运动，其等效圆电流的磁矩大小p m 与电子轨道运动的动量矩大小L 之比=Lp m m e 2. 提示：三. 计算题自测18. 如图所示线框，铜线横截面积S = 2.0 mm 2，其中OA 和DO ＇两段保持水平不动，ABCD 段是边长为a 的正方形的三边，它可绕OO ＇轴无摩擦转动．整个导线放在匀强磁场B 中，B的方向竖直向上．已知铜的密度ρ = 8.9×103 kg/m 3，当铜线中的电流I =10 A时，导线处于平衡状态，AB 段和CD 段与竖直方向的夹角α =15°．求磁感强度B的大小．解：线圈的电流如图所示，才能保持平衡。

大学物理第十一章课后答案

第十一章电流与磁场11-1 电源中的非静电力与静电力有什么不同？答：在电路中，电源中非静电力的作用是，迫使正电荷经过电源内部由低电位的电源负极移动到高电位的电源正极，使两极间维持一电位差。

而静电场的作用是在外电路中把正电荷由高电位的地方移动到低电位的地方，起到推动电流的作用；在电源内部正好相反，静电场起的是抵制电流的作用。

电源中存在的电场有两种：1、非静电起源的场；2、稳恒场。

把这两种场与静电场比较，静电场由静止电荷所激发，它不随时间的变化而变化。

非静电场不由静止电荷产生，它的大小决定于单位正电荷所受的非静电力，q非F E =。

当然电源种类不同，非F 的起因也不同。

11-2静电场与恒定电场相同处和不同处？为什么恒定电场中仍可应用电势概念？答：稳恒电场与静电场有相同之处，即是它们都不随时间的变化而变化，基本规律相同，并且都是位场。

但稳恒电场由分布不随时间变化的电荷产生，电荷本身却在移动。

正因为建立稳恒电场的电荷分布不随时间变化，因此静电场的两条基本定理，即高斯定理和环路定理仍然适用，所以仍可引入电势的概念。

11-3一根铜导线表面涂以银层，当两端加上电压后，在铜线和银层中，电场强度是否相同？电流密度是否相同？电流强度是否相同？为什么？答：此题涉及知识点：电流强度d sI =⋅⎰j s ，电流密度概念，电场强度概念，欧姆定律的微分形式j E σ=。

设铜线材料横截面均匀，银层的材料和厚度也均匀。

由于加在两者上的电压相同，两者的长度又相等，故铜线和银层的场强E相同。

由于铜线和银层的电导率σ不同，根据j E σ=知，它们中的电流密度j 不相同。

电流强度d sI =⋅⎰j s ，铜线和银层的j 不同但相差不太大，而它们的横截面积一般相差较大，所以通过两者的电流强度，一般说来是不相同的。

11-4一束质子发生侧向偏转，造成这个偏转的原因可否是：（1）电场？（2）磁场？（3）若是电场和磁场在起作用，如何判断是哪一种场？答：造成这个偏转的原因可以是电场或磁场。

大学物理下册11-15章答案(修改过,红色为修正地方还有以下解释)

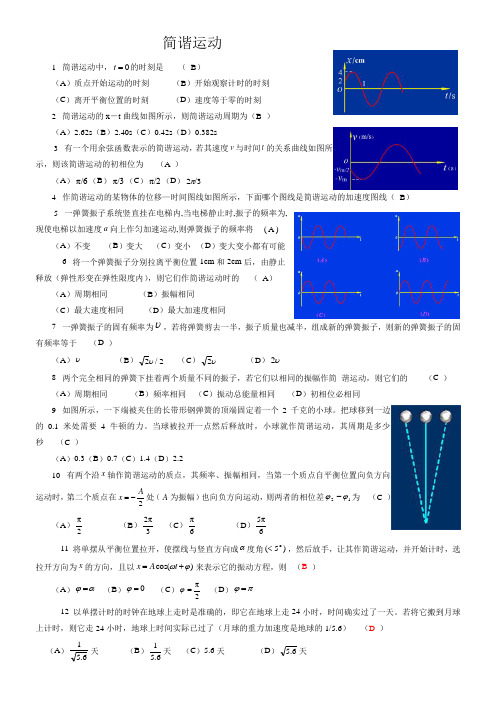
简谐运动1 简谐运动中，0=t 的时刻是（ B ）（A ）质点开始运动的时刻（B ）开始观察计时的时刻（C ）离开平衡位置的时刻（D ）速度等于零的时刻2 简谐运动的x －t 曲线如图所示，则简谐运动周期为（B ）（A ）2.62s （B ）2.40s （C ）0.42s （D ）0.382s3 有一个用余弦函数表示的简谐运动，若其速度v 与时间t 的关系曲线如图所示，则该简谐运动的初相位为（A ）（A ）π/6（B ）π/3（C ）π/2（D ）/32π4 作简谐运动的某物体的位移—时间图线如图所示，下面哪个图线是简谐运动的加速度图线（ B ）5 一弹簧振子系统竖直挂在电梯内,当电梯静止时,振子的频率为,现使电梯以加速度a 向上作匀加速运动,则弹簧振子的频率将 ( A )（A ）不变（B ）变大（C ）变小（D ）变大变小都有可能6 将一个弹簧振子分别拉离平衡位置1cm 和2cm 后，由静止释放（弹性形变在弹性限度内），则它们作简谐运动时的（ A ）（A ）周期相同（B ）振幅相同（C ）最大速度相同（D ）最大加速度相同7 一弹簧振子的固有频率为υ，若将弹簧剪去一半，振子质量也减半，组成新的弹簧振子，则新的弹簧振子的固有频率等于（D ）（A ）υ （B ）2/2υ （C ）υ2 （D ）υ28 两个完全相同的弹簧下挂着两个质量不同的振子，若它们以相同的振幅作简谐运动，则它们的（C ）（A ）周期相同（B ）频率相同（C ）振动总能量相同（D ）初相位必相同9 如图所示，一下端被夹住的长带形钢弹簧的顶端固定着一个2千克的小球。

把球移到一边的0.1米处需要4牛顿的力。

当球被拉开一点然后释放时，小球就作简谐运动，其周期是多少秒（C ）（A ）0.3（B ）0.7（C ）1.4（D ）2.210 有两个沿x 轴作简谐运动的质点，其频率、振幅相同，当第一个质点自平衡位置向负方向运动时，第二个质点在2A x -=处（A 为振幅）也向负方向运动，则两者的相位差12ϕϕ-为（C ）（A ）2π （B ）3π2 （C ）6π （D ）6π5 11 将单摆从平衡位置拉开，使摆线与竖直方向成α度角)5(o <，然后放手，让其作简谐运动，并开始计时，选拉开方向为x 的方向，且以)cos(ϕω+=t A x 来表示它的振动方程，则（B ）（A ）αϕ= （B ）0=ϕ （C ）2π=ϕ （D ）πϕ= 12 以单摆计时的时钟在地球上走时是准确的，即它在地球上走24小时，时间确实过了一天。

大学物理第11章重点小结

b
f
R L

P
f
第一暗纹的衍射角
bห้องสมุดไป่ตู้
o
x
1 arcsin

b
第十一章光学
49
物理学
第五版
第一暗纹的衍射角 1 arcsin b b增大， 1减小 0, 1 0 b 一定光直线传播 π b减小， 1增大 b , 1 2

衍射最大
b一定，越大， 1越大，衍射效应越明显.
第十一章光学
42
物理学
第五版
已知解
l 10.0 cm
λ 546 nm
Δ1 Δ2 2(n 1)l 107.2
107.2 107.2 546107 cm n 1 1 2l 2 10.0 cm
1.000 29
第十一章光学
43
物理学
第五版
例用折射率 n =1.58 的很薄的云母片覆盖在双缝实验中的一条缝上，这时屏上的第七级亮条纹移到原来的零级亮条纹的位置上。如果入射光波长为 550 nm 求此云母片的厚度是多少？ • 解设云母片厚度为 d 。无云母片时，零级亮纹在屏上 P 点，则到达 P 点的两束光的光程差为零。加上云母片后，到达P 点的两光束的光程差为
物理学
第五版
第十一章
光
学
第十一章光学
物理学
第五版
11-0
教学基本要求
光的干涉
一理解相干光的条件及获得相干光的方法.
二掌握光程的概念以及光程差和相位差的关系，理解在什么情况下的反射光有相位跃变.
第十一章光学
2
物理学

大学物理下(毛峰版)课后习题答案ch11+热力学基础+习题及答案

第11章热力学基础习题及答案1、内能和热量的概念有何不同？下面两种说法是否正确？（1）物体的温度越高，则热量越多；（2）物体的温度越高，则内能越大。

答：内能是组成物体的所有分子的动能与势能的总和。

热量是热传递过程中所传递的能量的量度。

内能是状态量，只与状态有关而与过程无关，热量是过程量，与一定过程相对应。

（1）错。

热量是过程量，单一状态的热量无意义。

（2）对。

物体的内能与温度有关。

2、V p -图上封闭曲线所包围的面积表示什么?如果该面积越大，是否效率越高? 答：封闭曲线所包围的面积表示循环过程中所做的净功．由于1Q A 净=η，净A 面积越大，效率不一定高，因为η还与吸热1Q 有关． 3、评论下述说法正确与否?(1)功可以完全变成热，但热不能完全变成功；(2)热量只能从高温物体传到低温物体，不能从低温物体传到高温物体．(3)可逆过程就是能沿反方向进行的过程，不可逆过程就是不能沿反方向进行的过程．答：(1)不正确．有外界的帮助热能够完全变成功；功可以完全变成热，但热不能自动地完全变成功； (2)不正确．热量能自动从高温物体传到低温物体，不能自动地由低温物体传到高温物体．但在外界的帮助下，热量能从低温物体传到高温物体．(3)不正确．一个系统由某一状态出发，经历某一过程达另一状态，如果存在另一过程，它能消除原过程对外界的一切影响而使系统和外界同时都能回到原来的状态，这样的过程就是可逆过程．用任何方法都不能使系统和外界同时恢复原状态的过程是不可逆过程．有些过程虽能沿反方向进行，系统能回到原来的状态，但外界没有同时恢复原状态，还是不可逆过程． 4、用热力学第一定律和第二定律分别证明，在V p -图上一绝热线与一等温线不能有两个交点．题4图解：（1）由热力学第一定律有 A E Q +∆= 若有两个交点a 和b ，则经等温b a →过程有 0111=-=∆A Q E 经绝热b a →过程 012=+∆A E 012<-=∆A E从上得出21E E ∆≠∆，这与a ,b 两点的内能变化应该相同矛盾．（2）若两条曲线有两个交点，则组成闭合曲线而构成了一循环过程，这循环过程只有吸热，无放热，且对外做正功，热机效率为%100，违背了热力学第二定律． 5、一循环过程如图所示，试指出： (1)ca bc ab ,,各是什么过程； (2)画出对应的V p -图； (3)该循环是否是正循环?(4)该循环作的功是否等于直角三角形面积?(5)用图中的热量ac bc ab Q Q Q ,,表述其热机效率或致冷系数．题5图题6图解：(1) a b 是等体过程bc 过程：从图知有KT V =，K 为斜率由vRT pV = 得 KvRp =故bc 过程为等压过程ca 是等温过程(2)V p -图如图(3)该循环是逆循环(4)该循环作的功不等于直角三角形面积，因为直角三角形不是V p -图中的图形．(5) abca bc abQ Q Q Q e -+=6、两个卡诺循环如图所示，它们的循环面积相等，试问： (1)它们吸热和放热的差值是否相同； (2)对外作的净功是否相等； (3)效率是否相同?答：由于卡诺循环曲线所包围的面积相等，系统对外所作的净功相等，也就是吸热和放热的差值相等．但吸热和放热的多少不一定相等，效率也就不相同．7、4.8kg 的氧气在27.0℃时占有1000m³的体积，分别求在等温、等压情况下，将其体积压缩到原来的1/2所需做的功、所吸收的热量以及内能的变化。

大学物理课后答案第十一章

第十一章机械振动一、基本要求1．掌握简谐振动的基本特征，学会由牛顿定律建立一维简谐振动的微分方程，并判断其是否谐振动。

2. 掌握描述简谐运动的运动方程，理解振动位移，振)cos(0ϕω+=t A x 幅，初位相，位相，圆频率，频率，周期的物理意义。

能根据给出的初始条件求振幅和初位相。

3. 掌握旋转矢量法。

4. 理解同方向、同频率两个简谐振动的合成规律，以及合振动振幅极大和极小的条件。

二、基本内容1. 振动物体在某一平衡位置附近的往复运动叫做机械振动。

如果物体振动的位置满足，则该物体的运动称为周期性运动。

否则称为非周)()(T t x t x +=期运动。

但是一切复杂的非周期性的运动，都可以分解成许多不同频率的简谐振动（周期性运动）的叠加。

振动不仅限于机械运动中的振动过程，分子热运动，电磁运动，晶体中原子的运动等虽属不同运动形式，各自遵循不同的运动规律，但是就其中的振动过程讲，都具有共同的物理特征。

一个物理量，例如电量、电流、电压等围绕平衡值随时间作周期性（或准周期性）的变化，也是一种振动。

2. 简谐振动简谐振动是一种周期性的振动过程。

它可以是机械振动中的位移、速度、加速度，也可以是电流、电量、电压等其它物理量。

简谐振动是最简单，最基本的周期性运动，它是组成复杂运动的基本要素，所以简谐运动的研究是本章一个重点。

（1）简谐振动表达式反映了作简谐振动的物体位移随时间)cos(0ϕω+=t A x 的变化遵循余弦规律，这也是简谐振动的定义，即判断一个物体是否作简谐振动的运动学根据。

但是简谐振动表达式更多地用来揭示描述一个简谐运动必须涉及到的物理量、、（或称描述简谐运动的三个参量），显然三个参量A ω0ϕ确定后，任一时刻作简谐振动的物体的位移、速度、加速度都可以由对应地t 得到。

2cos()sin(00πϕωωϕωω++=+-=t A t A v )cos()cos(0202πϕωωϕωω±+=+-=t A t A a （2）简谐运动的动力学特征为：物体受到的力的大小总是与物体对其平衡位置的位移成正比、而方向相反，即，它是判定一个系统的运动过程kx F -=是否作简谐运动的动力学根据，只要受力分析满足动力学特征的，毫无疑问地系统的运动是简谐运动。

河北科技大学大学物理答案解析11章

习题11-1 面积很大的导体平板A 与均匀带电平面B 平行放置，如习题11-1图所示。

已知A 与B 相距d ，两者相对的部分的面积为S 。

(1)设B 面带电量为q ，A 板的面电荷密度为1s 及2s ，求A 板与B 面之电势差。

(2)若A 板带电量为Q ，求1s 及2s 。

(1)d S q U 0212/εσσ-+=；（2）S q Q 21+=σ，SqQ 22-=σ习题11-1图习题11-2图习题11-3图11-2 如习题11-2图所示，有三块互相平行的导体板，外面的两块用导线连接，原来不带电。

中间一块上所带总面电荷密度为521310.C m --醋。

求每块板的两个表面的面电荷密度各是多少？（忽略边缘效应。

）解：从上到下6个面一次为面1、2、3、4、5、6.261σσσ==，8323σσσ=-=，8554σσσ=-= 11-3 如习题11-3图所示，半径为1R 的导体球带有电荷q ，球外有一个内、外半径为2R 、3R 的同心导体球壳，壳上带有电荷Q 。

求：(1)两球的电势1j 及2j ；(2)两球的电势差j D ；(3)用导线把球和壳连接在一起后，1j ，2j 及j D 分别为多少？ (4)在情形(1)、(2)中，若外球接地，1j ，2j 和j D 为多少？(5)设外球离地面很远，若内球接地，情况如何？解：（1）3024R Q q πεϕ+=，2010301444R qR q R Q q πεπεπεϕ-++=；(2)两球的电势差201044R q R q U πεπε-=；(3) 30214R Qq πεϕϕ+==，0=U ；(4) 02=ϕ，2010144R q R q πεπεϕ-=(5)内球带电量为3213111/R R R R Q q +--='，01=ϕ，1020244R q R q πεπεϕ'-'=11-4 如习题11-4图所示，一半径为a 的非导体球，放于内半径为b ，外半径为c 的导体球壳的中心。

大学物理第11章习题答案.

第11章电磁感应11.１基本要求１２别感应电动势的方向。

３。

４５６７８11.２基本概念１ε：把单位正电荷从负极通过电源内部移到正极时，非静电力所作的功，即W qε=２３k E ：变化的磁场在其周围所激发的电场。

与静电场不同，感生电场的电场线是闭合的，所以感生电场也称有旋电场。

４５：有使回路保持原有电流不变的性质，是回路本身的“电磁惯性”的量度。

自感系数L ：//m L I N I =ψ=Φ ６L ε：当通过回路的电流发生变化时，在自身回路中所产生的感应电动势。

７M ：211212M I I ψψ== ８12ε：当线圈２的电流2I 发生变化时，在线圈１中所产生的感应电动势。

９m W ：贮存在磁场中的能量。

自感贮存磁能：212m W LI =磁能密度m w ：单位体积中贮存的磁场能量22111222m B w μH HB μ===１０D d d I dt Φ=s d t∂=∂⎰DS ，位移电流并不表示有真实的电荷在空间移动。

但是，位移电流的量纲和在激发磁场方面的作用与传导电流是一致的。

１１d t∂=∂D j 11.３基本规律１定律：描述电磁感应现象的基本规律有两条。

（１）楞次定律：感生电流的磁场所产生的磁通量总是反抗回路中原磁通量的改变。

楞次定律是判断感应电流方向的普适定则。

（２）法拉第电磁感应定律：不论什么原因使通过回路的磁通量（或磁链）发生变化，回路中均有感应电动势产生，其大小与通过该回路的磁通量（或磁链）随时间的变化成正比，即mi d dtεΦ=-２()BBK AAi εd d ==⨯⎰⎰E l v B l ，若0i ε>,则表示电动势方向由A B →;若0i ε<,则表示电动势方向B A →３m K ls i d Φd εd d dtdt =⋅=-=-⎰⎰BE l S （对于导体回路）BK Ai εd =⎰E l （对于一段导体）４L dIεL dt=- ５12212d ΨdIεM dt dt=-=- ６sd ⋅⎰D S =0VdV q ρ=⎰l d ⋅⎰E l = - s d t∂⋅∂⎰BS =0sd ⋅⎰B Sc l sd d t ∂⎛⎫⋅=+⋅ ⎪∂⎝⎭⎰⎰D H l j S11.４学习指导学习法拉第电磁感应定律要注意，公式中的电动势是整个回路的电动势，式中负号是楞次定律的要求，用以判断电动势的方向。

科技大学大学物理下册第六版答案

第九章振动习题：P37〜39 1 , 2, 3, 4, 5, 6, 7, 8, 16.49-1 一个质点作简谐运动，振幅为忙在起始时刻质点的位移为-今，且向尤轴正方向运动，代表此简谐运动的旋转矢童为（）分析与解由振动曲线可知，初始时刻质点的位移为-冲/2.且向震轴负方向运动•图（町是其相应的錠转矢最图.山旋转矢童法可知初相位为2TT /3•振动曲线上给出质点从-A/2处运动到十M 处所需时间为I 矢由对应旋转矢量图可知相应的相位差A 甲=4ir/3，则角频率孙二、中£Z = （4ir/3） 6_ \故选（D ）»本题也可根分析与解（巧图中旋转矢量的矢端往耳轴上投影点的位移为-片/2,且投影点的运动方向指向0龙轴正向，即其速度的耳分量大于零*故满足题意因而正确答案为少-2已知某简谐运动的振动曲线如图心）所朋■则此简谐运动的运动方程为（（A ）（C ） X = 2 COS J -yTTi - -^-71 “2叫CTD )cm(R)工 h 2<X»s( ； TTi + -j-7T (D) x =+ y I ( cm )cm )据振动曲线所给信息，逐一代入方程来找出正确答案.9*3 两个同周期简i皆运动曲线如图（"所示*，的相位比勺的相位（）5）落后牙（R）超前壬（C）落后仃（D）超前7T分析与解由振动曲线图作出相应的旋转久量图（b）即可得到答案为（叭9-4 一质点做简谐运动，周期为T,当它由平衡位置向X轴正方向运动时,从1/2最大位移处到最大位移处这段路程所需的时间（）A、T/12B、T/8C、T/6D、T/4分析（C）,通过相位差和时间差的关系计算。

可设位移函数y=A*sin（w t）,其中w =2n /T ;当y=A/2, w t1= n /6 ;当y=A, w t2= n /2 ;△t=t2 -t1=［n /（2 w ）］-［n /（6 w ）］= n /（3 w ）=T/69 -目当质点以频率¥作简谐运动时，它的动能的变化频率为（）（A 】寺「B）P（（J）2胖（D） 4卩分析与解质点作简谐运动的动能表武为- （a +护），可见其周期为简谐运动周期的一半［则频率为简谐运动频率卩的两倍+因而止确答案为（C）.9- E ］图（町巾所啣的是两个简谐运动的曲线，若这两个简谐运动可叠加+ 则合成的余弦振动的初相位为（）31（A ）亍力（B ）（｛；） TT（D ） 0分析与解由振动曲线可以知道，这是两个同振动方向、同频率简谐运动, 它们的相位差是“（即反相位）+运动方程分别为口 = A cos a ）t 和x 2 = -^-cos （（ot+£灯）》它们的振幅不同•对于这样两个简谐运动，叮用旋转矢量法，如图（b ）很方便求得合运动方程为^=ycos 族.因而正确答案为（D ）.9-0有一个弹簧振子，振幅/ =2.0x107叫周期°趴初相炉二 3ir/4.试写出它的运动方程，并作出火"图卩“图和a"图.解因3=2IT /T\则运动方程根据题中给出的数据得x - 2. 0 x 10 _2€08（ 2衣 + 0. 75TT ）（in ）振子的速度和加速度分别为v = dx/dt 石x 10'2ftin(27TZ +0* 75ir) ( m • s'1)(i = d 2x/di 3 - - 8TT 2 x 10 2CDS (21TZ + 0* 75TF ) (m ・ s 1)尤- — f 及＜i 7图如图所示*X = /lcos( (dt + 少)=4cos/ 2打『9-0 若简谐运动方程为x=o. 10 ws(20m+0. 257T)(m)r求：(1)振幅、频率.角频率、周期和初相；(2) t=2合时的位移、速度和加速度.解(1 )将x =0, lOcos (20ir^ + 0. 25ir) ( ni)与女二A€os(t^(十炉)比较后可得;振幅4二①【0 m,角频率w = 20^-\初柑申 Z 25□则周期T = = 0. I筑频率卩=1/『二10 Hz.(2) t^2s时的位移、速度、加速度分别为x =0. 10CO9(40TT +O.25TT) =7J)7 xlO*2mv = dx/d/ =「27T5in(40ir +0. 25TT)=- 4.44 m - s« - d^/di1= -40ir2cos(407r +0. 25ir) = -2. 79 x 10L m ・少-凹某振动质点的工-丄曲线如图(町所示，试求：(1)运动方程；(2)点戶对应的相位；(3)到达点尸相应位置所需的时间.解（1）质点振动振幅=0. W m 而由振动曲线可画出q =0和=4 8 时旋转矢量，如图（b ）所示.由IS 可见初相気二亠忻/3（或純=5ir/3） t 而由-和)=ir/2 + TT /3得曲=5^/24 & ' +则运动方程为文=0.］仇0彳 - TT /3)( m)（2）图（町中点F 的位置是质点从A/2处运动到正向的端点处.对应的旋转矢量图如图（町所示.当初相取列=7用时’点P 的相位为和十。

大学物理第三版第11章部分习题解答

2 r 25 10 m处的电势; (1) r1 1510 m, 2
2
(2) 如果用导线把AB两球连接起来再求以上两点的电势
第11章部分习题解答
解: (1)
q E 2 4 0 r 1
R1 r R2
r R2
R2
q
R1
U1 q
R2
q 4 0 r
第11章部分习题解答
第11章部分习题解答
P408题11.3.4 如图所示,两个无限大带电平板,电荷面密度分别为 ,设P为两板间任意一点.(1)求A板上的电荷在P点产生的场强 E A ; (2)求B板上的电荷在P点产生的场强 E B ;(3)求A、B两板上的电荷在P点产生的场强;(4)如果把B板拿走，A板上的电荷如何分布?求它在P点产生的场强.
1 Q2 We 2 QU 球壳、 2 8 0 R3
Q 1 1 1 We We1 We 2 ( ) 8 0 R1 R2 R3
2
第11章部分习题解答
(2)
1 Q2 We ' QU 球壳、 2 8 0 R3
2010.5.25
第11章部分习题解答
解：因为A、B都是无限大带电平板,所以 (1) (2)
EA 2 0
方向向右
EB 2 0
EP E A EB 0
方向向右
(3)
方向向右
第11章部分习题解答
(4) 如果将B板拿走,A上的电荷将均匀分布在左右两个面上,每一个面上的电荷面密度为 / 2 ,它们在P点产生的场强大小都是 2 E'A 方向向右 2 0 4 0
第11章部分习题解答
证明: 该电容器是由两个电容分别为 C1 和 C2 的电容器并联而成的

大学物理答案第11章

第十一章恒定磁场11－1两根长度相同的细导线分别多层密绕在半径为R 和r 的两个长直圆筒上形成两个螺线管，两个螺线管的长度相同，R ＝2r ，螺线管通过的电流相同为I ，螺线管中的磁感强度大小r R B B 、满足（）（A ）r R B B 2=（B ）r R B B = （C ）r R B B =2（D ）r R B B 4=分析与解在两根通过电流相同的螺线管中，磁感强度大小与螺线管线圈单位长度的匝数成正比．根据题意，用两根长度相同的细导线绕成的线圈单位长度的匝数之比21==R r n n r R 因而正确答案为（C ）.11－2一个半径为r 的半球面如图放在均匀磁场中，通过半球面的磁通量为（）（A ）B r 2π2 （B ）B r 2π （C ）αB r cos π22（D ）αB r cos π2题 11-2 图分析与解作半径为r 的圆S ′与半球面构成一闭合曲面，根据磁场的高斯定理，磁感线是闭合曲线，闭合曲面的磁通量为零，即穿进半球面S 的磁通量等于穿出圆面S ′的磁通量；S B ⋅=m Φ．因而正确答案为（D ）．11－3下列说法正确的是（）（A ）闭合回路上各点磁感强度都为零时，回路内一定没有电流穿过（B ）闭合回路上各点磁感强度都为零时，回路内穿过电流的代数和必定为零（C ）磁感强度沿闭合回路的积分为零时，回路上各点的磁感强度必定为零（D ）磁感强度沿闭合回路的积分不为零时，回路上任意一点的磁感强度都不可能为零分析与解由磁场中的安培环路定律，磁感强度沿闭合回路的积分为零时，回路上各点的磁感强度不一定为零；闭合回路上各点磁感强度为零时，穿过回路的电流代数和必定为零.因而正确答案为（B ）．11－4在图（ａ）和（ｂ）中各有一半径相同的圆形回路L1、L2，圆周内有电流I1、I2，其分布相同，且均在真空中，但在（ｂ）图中L2回路外有电流I3，P 1、P 2为两圆形回路上的对应点，则（）（A ）⎰⎰⋅=⋅21L L d d l B l B ，21P P B B =（B ）⎰⎰⋅≠⋅21L L d d l B l B ，21P P B B =（C ）⎰⎰⋅=⋅21L L d d l B l B ，21P P B B ≠（D ）⎰⎰⋅≠⋅21L L d d l B l B ，21P P B B ≠题 11-4 图分析与解由磁场中的安培环路定律，积分回路外的电流不会影响磁感强度沿回路的积分；但同样会改变回路上各点的磁场分布．因而正确答案为（C ）．11－5半径为R 的圆柱形无限长载流直导体置于均匀无限大磁介质之中，若导体中流过的恒定电流为I ，磁介质的相对磁导率为μｒ（μｒ＜1），则磁介质内的磁化强度为（）（A ）()r I μr π2/1--（B ）()r I μr π2/1- （C ）r I μr π2/-（D ）r μI r π2/分析与解利用安培环路定理可先求出磁介质中的磁场强度，再由M ＝（μｒ－1）H 求得磁介质内的磁化强度，因而正确答案为（B ）．11－6北京正负电子对撞机的储存环是周长为240m 的近似圆形轨道，当环中电子流强度为8mA 时，在整个环中有多少电子在运行？已知电子的速率接近光速.分析一个电子绕存储环近似以光速运动时，对电流的贡献为c I e I /Δ=，因而由lNec I =，可解出环中的电子数.解通过分析结果可得环中的电子数10104⨯==ecIlN 11－7已知铜的摩尔质量M ＝63.75ｇ·mol －1，密度ρ＝8.9g · cm－3，在铜导线里，假设每一个铜原子贡献出一个自由电子，（1）为了技术上的安全，铜线内最大电流密度26.0A mm m j -=⋅，求此时铜线内电子的漂移速率v d ；（2）在室温下电子热运动的平均速率是电子漂移速率v d 的多少倍？分析一个铜原子的质量A N M m /=,其中N A 为阿伏伽德罗常数，由铜的密度ρ可以推算出铜的原子数密度m ρn /=根据假设，每个铜原子贡献出一个自由电子，其电荷为e ，电流密度d m ne j v =．从而可解得电子的漂移速率v d ．将电子气视为理想气体，根据气体动理论，电子热运动的平均速率em kTπ8=v 其中k 为玻耳兹曼常量，m e 为电子质量．从而可解得电子的平均速率与漂移速率的关系．解（1）铜导线单位体积的原子数为M ρN n A /=电流密度为j m 时铜线内电子的漂移速率14A s m 1046.4--⋅⨯===eN M j ne j m m d ρv （2）室温下（T ＝300Ｋ）电子热运动的平均速率与电子漂移速率之比为81042.2π81⨯≈=ed d m kTv v v 室温下电子热运动的平均速率远大于电子在恒定电场中的定向漂移速率．电子实际的运动是无规热运动和沿电场相反方向的漂移运动的叠加．考虑到电子的漂移速率很小，电信号的信息载体显然不会是定向漂移的电子．实验证明电信号是通过电磁波以光速传递的．11－8有两个同轴导体圆柱面，它们的长度均为20m，内圆柱面的半径为3.0mm，外圆柱面的半径为9.0mm.若两圆柱面之间有10μA电流沿径向流过，求通过半径为6.0mm的圆柱面上的电流密度．题11-8 图分析如图所示是同轴柱面的横截面，电流密度j对中心轴对称分布．根据恒定电流的连续性，在两个同轴导体之间的任意一个半径为r的同轴圆柱面上流过的电流I 都相等，因此可得rlIjπ2=解由分析可知，在半径r＝6.0mm的圆柱面上的电流密度2mAμ3.13π2-⋅==rlIj11－9如图所示，已知地球北极地磁场磁感强度B的大小为6.0×10－5T．如设想此地磁场是由地球赤道上一圆电流所激发的，此电流有多大？流向如何？解设赤道电流为I，则由教材第11－4节例2知，圆电流轴线上北极点的磁感强度()RIRRIRB2422/3222μμ=+=因此赤道上的等效圆电流为A1073.1249⨯==μRBI由于在地球地磁场的Ｎ极在地理南极，根据右手螺旋法则可判断赤道圆电流应该是由东向西流，与地球自转方向相反．题 11-9 图11－10如图所示，有两根导线沿半径方向接触铁环的a 、b 两点，并与很远处的电源相接.求环心O 的磁感强度．题 11-10 图分析根据叠加原理，点O 的磁感强度可视作由ef 、b e 、fa 三段直线以及ac b 、a d b 两段圆弧电流共同激发．由于电源距环较远，0=ef B ．而b e 、fa 两段直线的延长线通过点O ，由于0Idl r ⨯=，由毕奥－萨伐尔定律知0be fa ==B B ．流过圆弧的电流I 1、I 2的方向如图所示，两圆弧在点O 激发的磁场分别为21101π4r l I μB =,22202π4rl I μB = 其中l 1、l 2分别是圆弧ac b 、a d b 的弧长，由于导线电阻R 与弧长l 成正比，而圆弧ac b 、a d b 又构成并联电路，故有2211l I l I =将21B B 、叠加可得点O 的磁感强度B ．解由上述分析可知，点O 的合磁感强度0π4π42220211021=-=-=r l I μr l I μB B B 11－11如图所示，几种载流导线在平面内分布，电流均为I ，它们在点O 的磁感强度各为多少？题 11-11 图分析应用磁场叠加原理求解．将不同形状的载流导线分解成长直部分和圆弧部分，它们各自在点O 处所激发的磁感强度较容易求得，则总的磁感强度∑=iB B 0.解（ａ）长直电流对点O 而言，有0d =⨯r l I ，因此它在点O 产生的磁场为零，则点O 处总的磁感强度为1/4圆弧电流所激发，故有RIμB 800=B 0的方向垂直纸面向外．（ｂ）将载流导线看作圆电流和长直电流，由叠加原理可得RIμR I μB π22000-=B 0的方向垂直纸面向里．（c ）将载流导线看作1/2圆电流和两段半无限长直电流，由叠加原理可得RIμR I μR I μR I μR I μB 4π24π4π4000000+=++=B 0的方向垂直纸面向外．11－12载流导线形状如图所示（图中直线部分导线延伸到无穷远），求点O 的磁感强度B ．题 11-12 图分析由教材11－4节例题2的结果不难导出，圆弧载流导线在圆心激发的磁感强度RαI μB π40=，其中α为圆弧载流导线所张的圆心角，磁感强度的方向依照右手定则确定；半无限长载流导线在圆心点O 激发的磁感强度R IμB π40=，磁感强度的方向依照右手定则确定.点O 的磁感强度O B 可以视为由圆弧载流导线、半无限长载流导线等激发的磁场在空间点O 的叠加. 解根据磁场的叠加在图（ａ）中，k i k k i B RI μR I μR I μR I μR I μπ24π4π44000000--=---= 在图（ｂ）中，k i k i i B RI μR I μR I μR I μR I μπ41π14π44π4000000-⎪⎭⎫ ⎝⎛+-=---= 在图（c ）中，k j i B RIμR I μR I μπ4π4830000---= 11－13如图(a)所示，载流长直导线的电流为I ，试求通过矩形面积的磁通量．题 11-13 图分析由于矩形平面上各点的磁感强度不同，故磁通量Φ≠BS ．为此，可在矩形平面上取一矩形面元d S ＝l d x ，如图（ｂ）所示，载流长直导线的磁场穿过该面元的磁通量为x l xId π2d d 0μ=⋅=ΦS B矩形平面的总磁通量ΦΦ⎰=d解由上述分析可得矩形平面的总磁通量⎰==Φ211200lnπ2d π2d dd d Ilx l xIμμ 11－14已知10mm 2裸铜线允许通过50A 电流而不会使导线过热．电流在导线横截面上均匀分布．求导线内、外磁感强度的分布.题 11-14 图分析可将导线视作长直圆柱体，电流沿轴向均匀流过导体，故其磁场必然呈轴对称分布，即在与导线同轴的圆柱面上的各点，B 大小相等、方向与电流成右手螺旋关系．为此，可利用安培环路定理，求出导线表面的磁感强度．解围绕轴线取同心圆为环路L ，取其绕向与电流成右手螺旋关系，根据安培环路定理，有∑⎰=⋅=⋅I μB 0πr 2d l B在导线内r ＜R ，2222ππRIr r R I I ==∑，因而 202πRIrμB =在导线外r ＞R ，I I =∑，因而rIμB 2π0=磁感强度分布曲线如图所示．11－15有一同轴电缆，其尺寸如图（ａ）所示．两导体中的电流均为I ，但电流的流向相反，导体的磁性可不考虑．试计算以下各处的磁感强度：（1）r ＜R 1；（2）R 1＜r ＜R 2；（3）R 2＜r ＜R 3；（4）r ＞R 3．画出B －r 图线．题 11-15 图分析同轴电缆导体内的电流均匀分布，其磁场呈轴对称，取半径为r 的同心圆为积分路径，πr 2d ⋅=⋅⎰B l B ，利用安培环路定理∑⎰=⋅I μ0d l B ，可解得各区域的磁感强度．解由上述分析得 r ＜R 12211ππ12πr R μr B =⋅ 21012πR IrμB =R 1＜r ＜R 2I μr B 022π=⋅rIμB 2π02=R 2＜r ＜R 3()()⎥⎦⎤⎢⎣⎡---=⋅I R R R r I μr B 22232203ππ2π 2223223032πR R r R r I μB --= r ＞R 3()02π04=-=⋅I I μr B04=B磁感强度B （r ）的分布曲线如图（ｂ）．11－16如图所示，N 匝线圈均匀密绕在截面为长方形的中空骨架上．求通入电流I 后，环内外磁场的分布．题 11-16 图分析根据右手螺旋法则，螺线管内磁感强度的方向与螺线管中心轴线构成同心圆，若取半径为r 的圆周为积分环路，由于磁感强度在每一环路上为常量，因而πr 2d ⋅=⋅⎰B l B依照安培环路定理∑⎰=⋅I μ0d l B ，可以解得螺线管内磁感强度的分布．解依照上述分析，有∑=⋅I μr B 02πr ＜R 102π1=⋅r B 01=BR 2＞r ＞R 1NI μr B 022π=⋅rNIμB 2π02=r ＞R 202π3=⋅r B 03=B在螺线管内磁感强度B 沿圆周，与电流成右手螺旋．若112R R R <<-和R 2，则环内的磁场可以近似视作均匀分布，设螺线环的平均半径()1221R R R +=，则环内的磁感强度近似为 RNIμB 2π0≈11－17电流I 均匀地流过半径为R 的圆形长直导线，试计算单位长度导线内的磁场通过图中所示剖面的磁通量．题 11-17 图分析由题11－14可得导线内部距轴线为r 处的磁感强度()202πR Irμr B =在剖面上磁感强度分布不均匀，因此，需从磁通量的定义()S B d ⎰=r Φ来求解．沿轴线方向在剖面上取面元ｄS ＝l ｄr ，考虑到面元上各点B 相同，故穿过面元的磁通量ｄΦ＝B ｄS ，通过积分，可得单位长度导线内的磁通量⎰=Sr B Φd解由分析可得单位长度导线内的磁通量4πd 2π0020Iμr R Ir μΦR==⎰11－18已知地面上空某处地磁场的磁感强度40.410T B -=⨯，方向向北．若宇宙射线中有一速率715.010m s -=⨯v 的质子，垂直地通过该处．求：（1）洛伦兹力的方向；（2）洛伦兹力的大小，并与该质子受到的万有引力相比较．题 11-18 图解（1）依照B F ⋅=v q L 可知洛伦兹力L F 的方向为B ⊥v 的方向，如图所示．（2）因B ⊥v ，质子所受的洛伦兹力N 102.316-⨯==B F v q L在地球表面质子所受的万有引力N 1064.126p -⨯==g m G因而，有101095.1/⨯=G F L ，即质子所受的洛伦兹力远大于重力． 11－19霍尔效应可用来测量血流的速度，其原理如图所示．在动脉血管两侧分别安装电极并加以磁场．设血管直径为d ＝2.0mm ，磁场为B ＝0.080T ，毫伏表测出血管上下两端的电压为U H ＝0.10mV ，血流的流速为多大？题 11-19 图分析血流稳定时，有H qE B q =v由上式可以解得血流的速度．解依照分析m/s 63.0===dBU B E HH v 11－20带电粒子在过饱和液体中运动，会留下一串气泡显示出粒子运动的径迹．设在气泡室有一质子垂直于磁场飞过，留下一个半径为3.5cm 的圆弧径迹，测得磁感强度为0.20Ｔ，求此质子的动量和动能．解根据带电粒子回转半径与粒子运动速率的关系有m /s kg 1012.121⋅⨯===-ReB m p vkeV 35.222==mp E k11－21从太阳射来的速度为0.80×108m /ｓ的电子进入地球赤道上空高层范艾伦辐射带中，该处磁场为4.0×10－7Ｔ，此电子回转轨道半径为多大？若电子沿地球磁场的磁感线旋进到地磁北极附近，地磁北极附近磁场为2.0×10－5Ｔ，其轨道半径又为多少？解由带电粒子在磁场中运动的回转半径高层范艾伦辐射带中的回转半径m 101.1311⨯==eB m R v地磁北极附近的回转半径m 2322==eB m R v11－22如图（ａ）所示，一根长直导线载有电流I 1＝30A ，矩形回路载有电流I 2＝20A ．试计算作用在回路上的合力．已知d ＝1.0cm ， b ＝8.0cm ，l ＝0.12m ．题 11-22图分析矩形上、下两段导线受安培力F 1和F 2的大小相等，方向相反，对不变形的矩形回路来说，两力的矢量和为零．而矩形的左右两段导线，由于载流导线所在处磁感强度不等，所受安培力F 3和F 4大小不同，且方向相反，因此线框所受的力为这两个力的合力．解由分析可知，线框所受总的安培力F 为左、右两边安培力F 3和F 4之矢量和，如图（ｂ）所示，它们的大小分别为dlI I μF π22103=()b d lI I μF +=π22104故合力的大小为()N 1028.1π2π2321021043-⨯=+-=-=b d lI I μd l I I μF F F 合力的方向朝左，指向直导线．11－23一直流变电站将电压为500k V 的直流电，通过两条截面不计的平行输电线输向远方．已知两输电导线间单位长度的电容为3.0×10－11F·m －1，若导线间的静电力与安培力正好抵消．求：（1）通过输电线的电流；（2）输送的功率．分析当平行输电线中的电流相反时，它们之间存在相互排斥的安培力，其大小可由安培定律确定．若两导线间距离为d ，一导线在另一导线位置激发的磁感强度dIμB π20=,导线单位长度所受安培力的大小BI F B =．将这两条导线看作带等量异号电荷的导体，因两导线间单位长度电容C 和电压U 已知，则单位长度导线所带电荷λ＝CU ，一导线在另一导线位置所激发的电场强度dελE 0π2=，两导线间单位长度所受的静电吸引力λE F E =．依照题意，导线间的静电力和安培力正好抵消，即0=+E B F F从中可解得输电线中的电流．解（1）由分析知单位长度导线所受的安培力和静电力分别为dI μBI F B π220==dεU C λE F E 022π2== 由0=+E BF F 可得dεU C d I μ02220π2π2=解得A 105.4300⨯==μεCUI （2）输出功率W 1025.29⨯==IU N11－24在氢原子中，设电子以轨道角动量π2/h L =绕质子作圆周运动，其半径为m 1029.5110-⨯=a ．求质子所在处的磁感强度．h 为普朗克常量，其值为s J 1063.634⋅⨯-分析根据电子绕核运动的角动量π20h a m L ==v可求得电子绕核运动的速率v ．如认为电子绕核作圆周运动，其等效圆电流v/π20a e T e i ==在圆心处，即质子所在处的磁感强度为02a i μB =解由分析可得，电子绕核运动的速率π2ma h=v其等效圆电流2020π4/π2ma hev a e i ==该圆电流在圆心处产生的磁感强度T 5.12π82202000===ma heμa i μB 11－25如图[a]所示，一根长直同轴电缆，内、外导体之间充满磁介质，磁介质的相对磁导率为μr （μr ＜1），导体的磁化可以忽略不计．沿轴向有恒定电流I 通过电缆，内、外导体上电流的方向相反．求：（1）空间各区域内的磁感强度和磁化强度；*（2）磁介质表面的磁化电流．题 11-25 图分析电流分布呈轴对称，依照右手定则，磁感线是以电缆对称轴线为中心的一组同心圆．选取任一同心圆为积分路径，应有⎰⋅=⋅r H d π2l H ，利用安培环路定理⎰∑=⋅fId l H求出环路内的传导电流，并由H μB =，()H μM r 1-=，可求出磁感强度和磁化强度．再由磁化电流的电流面密度与磁化强度的关系求出磁化电流．解（1）取与电缆轴同心的圆为积分路径，根据磁介质中的安培环路定理，有∑=fπ2I r H对r ＜R 1221f ππr R I I =∑ 得2112πR IrH =忽略导体的磁化（即导体相对磁导率μr =1），有01=M ，21012πR IrμB =对R 2＞r ＞R 1I I=∑f得rI H 2π2=填充的磁介质相对磁导率为μr ，有()r I μM r 2π12-=，rI μμB r 2π02= 对R 3＞r ＞R 2()()2223223ππR r R R I I I f -⋅--=∑ 得()()222322332πR R r r R I H --= 同样忽略导体的磁化，有03=M ，()()2223223032πR R r r R I μB --= 对r ＞R 30=-=∑I I If得04=H ，04=M ，04=B（2）由r M I s 2π⋅=，磁介质内、外表面磁化电流的大小为()()I μR R M I r si 12π112-=⋅= ()()I μR R M I r se 12π222-=⋅=对抗磁质（1r μ<），在磁介质内表面（r ＝R 1），磁化电流与内导体传导电流方向相反；在磁介质外表面（r ＝R 2），磁化电流与外导体传导电流方向相反．顺磁质的情况与抗磁质相反．H （r ）和B （r ）分布曲线分别如图（ｂ）和（c ）所示．。

大学物理11-22章例题习题答案

第十一章静电场例题答案：11-1 （B ） 11-2（B ） 11-3（B ）11-4． ()30220824Rqdd R R qd εεπ≈-ππ；从O 点指向缺口中心点 11-5. 0/ελd ；()2204d R d-πελ ；沿矢径OP 11-6(D) 11-7.02εσ 向右 ; 023εσ向右 11-8 (1)o 2r 4r k E ε=，r <R ; (2) 204r r4R k E ε=，r >R 。

[解](1)作与球体同心、而半径r <R 的球面S 1。

球体内电荷密度ρ随r 变化，因此，球面S 1内包含的电荷()dr r r 4Q ro 21⎰ρπ=。

根据高斯定理和已知的电荷体密度ρ(r )，可求得球体内任意点的场强。

即()⎰⎰ρπε=⋅=Φr 02s o r dr r r 41s d E 1 ，得：o2r 4r k E ε=，r <R 。

(2)作与球体同心、半径r >R 的球面S 2，因R 外电荷为零，故S 2内的电荷Q 2=Q 1，根据高斯定理得：Φ=()⎰⎰ρπε=⋅R 02s 0r dr r r 41s d E 2 =4πr 2E r =⎰πεR30dr kr 41，∴204r r 4R kE ε=，r >R 。

11-9(D) 11-10(C) 11-11.d 0L⋅=⎰ E l 单位正电荷在静电场中沿任意闭合路径绕行一周，电场力作功等于零有势（或保守力）11-12. 45 V —15 V 11-13. -2000V 11-14. (B) 11-15.20R 4Q πε，０，R4Q 0πε，20r 4Qπε。

11-16()()a b b c R R R R /ln /ln 21=λλ [解]：设B 上带正电荷，内表面上电荷线密度为λ1，外表面上电荷线密度为λ2，而A 、C 上相应地感应等量负电荷，如图所示．则A 、B 间场强分布为E 1=λ1 / 2πε0r ，方向由B 指向AB 、C 间场强分布为 E 2=λ2 / 2πε0r ，方向由B 指向CB 、A 间电势差11100ln 22E r d d a a bbR R b BA R R aR r r R λλεε=⋅=-=ππ⎰⎰U B 、C 间电势差 22200ln 22E r d d c c bbR R c BC R R bR r U r R λλεε=⋅=-=ππ⎰⎰因U BA ＝U BC ,得到 ()()a b b c R R R R /ln /ln 21=λλ 练习详解：11-1. （1）E 0=0；（2）E 0=0；（3）0E=k2a q 4i ；（4）0E = k 2aq 2i[解](1)如图(a )所示，各点电荷在点o 处产生的场强两两对应相消，所以，点o 处场强E 0=0(2)取图中(b )所示坐标。