六年级奥数图形问题精选
六年级图形奥数练习题

六年级图形奥数练习题考题一:1. 在平面直角坐标系中,顶点为O(0,0),A(2,0),B(2,1),C(0,1)的四边形OABC是一个矩形。
请计算矩形OABC的周长和面积。
解答:首先,根据顶点坐标可以得知矩形OABC的边长,OA和OC的长度都为2,OB和OD的长度都为1.那么,矩形的周长为:2 + 1 + 2 + 1 = 6矩形的面积为:2 * 1 = 2考题二:2. 如图所示,矩形ABCD的长为3cm,宽为2cm,以BC为底边,以BC为轴将矩形顺时针旋转90度(即旋转一个直角),得到矩形BCDE。
求矩形BCDE的周长和面积。
(图略)解答:根据题意,矩形BCDE是由矩形ABCD顺时针旋转90度得到的,那么矩形BCDE的长就等于矩形ABCD的宽,宽就等于矩形ABCD的长。
所以,矩形BCDE的长为2cm,宽为3cm.矩形BCDE的周长为:2 + 3 + 2 + 3 = 10矩形BCDE的面积为:2 * 3 = 6考题三:3. 在平面直角坐标系中,有一个直角三角形,顶点为A(0,0),B(3,0),C(0,4)。
请问直角三角形ABC的斜边长度是多少?解答:根据题意,直角三角形ABC的斜边就是BC的长度。
根据两点间的距离公式,可以计算出BC的长度。
BC的长度= √((x2 - x1)^2 + (y2 - y1)^2)代入坐标值,BC的长度= √((3 - 0)^2 + (0 - 4)^2) = √(9 + 16) = √25 = 5考题四:4. 一个正方形内接在一个半径为r的圆中,且边与圆的切点分别是正方形的四个顶点,请计算正方形的面积。
解答:设正方形的边长为a,正方形的对角线长度为d。
根据题意,正方形的对角线d等于圆的直径,即2r。
而对角线d等于正方形的边长a乘以√2。
所以,a * √2 = 2r,得到a = 2r / √2 = r * √2正方形的面积等于边长的平方,即a^2 = (r * √2)^2 = 2r^2考题五:5. 如图所示,一个边长为10cm的正方形中内接着一个半径为r的圆。
六年级图形问题综合(奥数)含答案

六年级图形问题综合(奥数)含答案例3. AKF 与三角形ADG 面积之和等于5平方厘米,DC=CE=3厘米。
求三角形BEK 的面积。
D例4. 如图,三角形ABC 的AB 和AC 两条边分别被分成5等分。
三角形ABC 面积是500,求图中阴影部分的面积?例5. 如图,设正方形ABCD 的面积为120,E 、F 分别为边AB 、AD 的中点,FC=3GC ,则阴影部分的面积是多少?A B C DF EG例6. 在如图所示的三角形AGH 中,三角形ABC ,BCD ,CDE ,DEF,EFG ,FGH 的面积分别是1,2,3,4,5,6平方厘米,那么三角形EFH 的面积是多少平方厘米?A B DEF G H例7. 如图,在平行四边形ABCD 中,AC 为对角线,EF 平行于AC ,如果三角形AED 的面积为12平方厘米,,求三角形DCF 的面积。
D CA B E F练习:1. 已知正方形ABCD 的边长是5cm ,又EF=FG ,FD=DG ,求三角形ECG 的面积。
E B CGDAF2. 正三角形ABC 的边长为12厘米,BD ,DE ,EF ,FG 四条线段把它的面积5等分,求AF ,FD ,DC ,AG ,GE ,EB 的长。
A B G E CDF3. 如图所示是某个六边形公园ABCDEF ,M 为AB 中点,N 为CD 中点,,P 为DE 中点,Q 为FA 中点,其中游览区APEQ 与BNDM 的面积之和为900平方米。
中间的湖泊面积为361平方米,其余的部分是草地,问草地面积共有多少平方米?A B C DEFQPN M4. 如图,AE=EC ,BD=2DC ,AF=3BF ,若三角形ABC 的面积为270平方厘米,求图中阴影部分的面积。
5. 如下图,正方形ABCD 的边长为12, P 是边AB 上的任意一点,M 、N 、I 、H 分别是边BC 、AD 上的三等分点,E 、F 、G 是边CD 上的四等分点,图中阴影部分的面积是______.6. 如图正方形ABCD 的边长是4厘米,CG 是3厘米,长方形DEFG 的长DG 是5厘米,那么它的宽DE 是______厘米.7. 如图,CE=4EA , BD=3CD ,AF=5BF 。
六年级奥数题:图形提高(三(B)
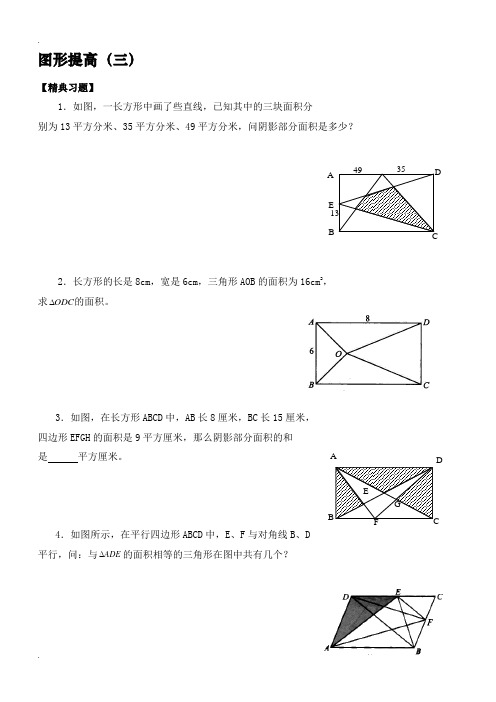
图形提高(三)【精典习题】1.如图,一长方形中画了些直线,已知其中的三块面积分别为13平方分米、35平方分米、49平方分米,问阴影部分面积是多少?2.长方形的长是8cm,宽是6cm,三角形AOB的面积为16cm2,求ODC∆的面积。
3.如图,在长方形ABCD中,AB长8厘米,BC长15厘米,四边形EFGH的面积是9平方厘米,那么阴影部分面积的和是平方厘米。
4.如图所示,在平行四边形ABCD中,E、F与对角线B、D 平行,问:与ADE∆的面积相等的三角形在图中共有几个?AB CDEGFAEB CD49 35135.如图所示,平行四边形ABCD中,ADG∆面积是5平方厘米,∆的面积是3平方厘米,问DHC∆面积是6.2平方厘米,PHF∆的面积是多少平方厘米?PEG6.如图所示,O是平行四边形ABCD内的一点,AD=3DE。
已知三个空白三角形面积分别是19,20,35平方厘米,三角形BOC的面积是多少平方厘米?7.如下图,ABCD是个长方形,DEFG是个平行四边形,E点在BC边上,FG过A点,已知,三角形AKF与三角形ADG面积之和等于5平方厘米。
DC=CE=5厘米。
求BEK∆的面积。
7.如图,ABCD是长方形,图中的数字是各部分的面积数,则图中阴影部分的面积为______。
8.如图,正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四边各分成两段,其中长的一段是 短的2倍。
这个长方形的面积是多少?9.有红、黄、绿三块大小一样的正方形纸片,放在一个正方 形盒内,它们之间互相叠合(如右图),已知露在外面的部分中,红色面积是24,黄色面积是14,绿色面积是10,那么正方形盒 子的面积是多少?10.如图,下面△AOB 和△ DOC 的面积分别为20平方厘米 和24平方厘米,长方形AODE 的面积为30平方厘米,求△BOC 的面积为多少平方厘米?10.这是一块正方形的地板砖示意图。
其中AA 1=AA 2=BB 1=BB 2=CC 1=CC 2=DD 1=DD 2。
(完整版)六年级奥数图形问题精选
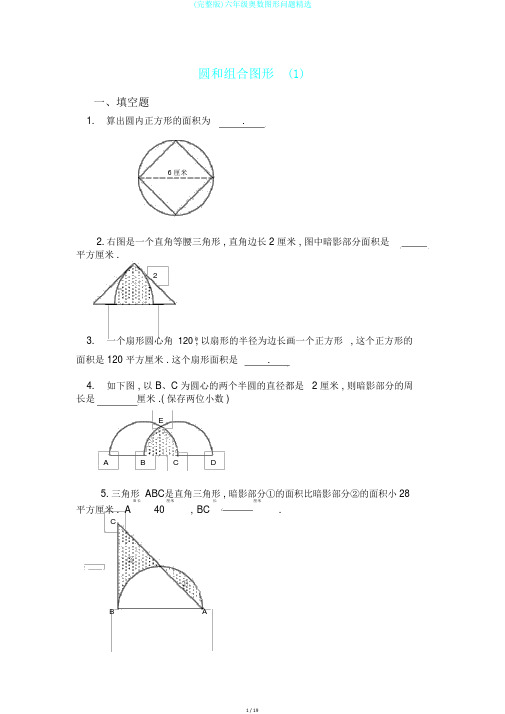
圆和组合图形 (1)一、填空题1. 算出圆内正方形的面积为 .6 厘米2. 右图是一个直角等腰三角形 , 直角边长 2 厘米 , 图中暗影部分面积是平方厘米 .23. 一个扇形圆心角 120 , 以扇形的半径为边长画一个正方形 , 这个正方形的 面积是 120 平方厘米 . 这个扇形面积是.4. 如下图 , 以 B 、C 为圆心的两个半圆的直径都是 2 厘米 , 则暗影部分的周 长是 厘米 .( 保存两位小数 )EA B C D5. 三角形 ABC 是直角三角形 , 暗影部分①的面积比暗影部分②的面积小28B 长40 厘米 , BC 长 厘米.平方厘米 . AC②①B A6.如右图 , 暗影部分的面积为 2 平方厘米 , 等腰直角三角形的面积为.7.扇形的面积是 31.4 平方厘米 , 它所在圆的面积是 157 平方厘米 , 这个扇形的圆心角是度.8. 图中扇形的半径OA=OB=6 厘米 .AOB 45 ,AC 垂直 OB 于 C, 那么图中暗影部分的面积是平方厘米 . ( 3.14 )A645O C B9. 右图中正方形周长是20 厘米 . 图形的总面积是平方厘米.10. 在右图中 ( 单位 : 厘米 ), 两个暗影部分面积的和是平方厘米.151220二、解答题11.ABC 是等腰直角三角形 . D 是半圆周的中点 , BC 是半圆的直径 , 已知 :AB=BC=10, 那么暗影部分的面积是多少?( 圆周率 3.14 )A10 BDC12.如图 , 半圆 S1的面积是 14.13 平方厘米 , 圆 S2的面积是 19.625 平方厘米 . 那么长方形 ( 暗影部分的面积 ) 是多少平方厘米 ?S2S113. 如图 , 已知圆心是 O, 半径 r=9 厘米 ,1 2 15 ,那么暗影部分的面积是多少平方厘米 ?( 3.14 )A12B C14.右图中 4 个圆的圆心是正方形的 4 个极点 , 它们的公共点是该正方形的中心 . 假如每个圆的半径都是1 厘米 , 那么暗影部分的总面积是多少平方厘米 ?———————————————答 案——————————————————————1. 18 平方厘米 .由图示可知 , 正方形两条对角线的长都是 6 厘米 , 正方形由两个面积相等的三角形组成 . 三角形底为 6 厘米 , 高为 3 厘米 , 故正方形面积为 6 3 12 18 ( 平2方厘米 ).2.1.14 平方厘米 .由图示可知 , 图中暗影部分面积为两个圆心角为 45 的扇形面积减去直角三角形的面积 . 即3.14 2 245 1 平方厘米).2 2 22 (3603.125.6 平方厘米 .由已知条件可知圆的半径的平方为 120 平方厘米 . 故扇形面积为120120 125.6 ( 平方厘米 ).4.3.09 厘米 .边结 BE 、 CE, 则 BE=CE=BC= 1( 厘米 ), 故三角形 BCE 为等边三角形 . 于是EBC BCE ⌒ ⌒60 厘米 ). 于是暗影部分周长60 . BE=CE= 3.14 2 1.045( 为 2 1 3.09 ( 厘米 ). 3605.32.8 厘米 .从图中能够看出暗影部分①加上空白部分的面积是半圆的面积 , 暗影部分②加上空白部分的面积是三角形 ABC 的面积 . 又已知①的面积比②的面积小 28 平方厘米 , 故半圆面积比三角形 ABC 的面积小 28 平方厘米 .40 21628( 平方厘米 ), 三角形 ABC 的面积为半圆面积为2 2628+28=656( 平方厘米 ). BC 的长为 656 2 40 32.8( 厘米 ).6.37 9平方厘米 . 13将等腰直角三角形补成一个正方形 , 设正方形边长为 x 厘米 , 则圆的半径为x厘米 . 图中暗影部分面积是正方形与圆的面积之差的1, 于是有281 x 23200x 28 2 , 解得 x 2 . 故等腰直角三角形的面积为2133200137 9( 平方厘米 ). 13 2137. 72 .扇形面积是圆面积的 31.4 1571, 故扇形圆心角为 360 的 1即 72 .5 58.5.13.三角形 ACO 是一个等腰直角三角形 , 将 AO 看作底边 , AO 边上的高为AO 2 6 23 ( 厘米 ), 故三角形 ACO 的面积为16 3 9( 平方厘米 ). 而扇6 245 2形面积为14.13( 平方厘米 ), 从而暗影部分面积为 36014.13- 9=5.13( 平方厘米 ). 9.142.75.由正方形周长是 20 厘米 , 可得正方形边长也就是圆的半径为 20 4 5 ( 厘米 ). 图形总面积为两个 3圆面积加上正方形的面积 , 即 43.14 5232 52 142.75( 平方厘米 ).410.90 平方厘米 .图中暗影部分的面积是从两个以直角三角形直角边为直径的半圆及一个直 角三角的面积和中减去一个以直角三角形斜边为直径的半圆的面积即12 2 21 (16 2)2 1 12 15 1 (20 2)2 1 ( 平方厘米 ). 22 2210BA11. 如图作出协助线 , 则暗影部分的面积为三角形AED 的面积减去正方形 BEDO 的面积再加上圆面积的 1.O4三角形 AED 的面积是 (10 10 2) (10 2)1; 正方形面 C积是 (10 2)2 , 圆面积的 1 是 12 3.14 (10 2) 2 , 故暗影部分面积为 :4 4 1 1(10 10 2) (10 2) (10 2)2 (10 2) 22 425 (平方厘米) .12. 由已知半圆 S 1 的面积是 14.13 平方厘米得半径的平方为9 ( 平方厘米 ), 故半径为 3 厘米 , 直径为 6 厘米 . 又因圆 S 2 的面积为平方厘米 , 所以 2 半径的平方为S6.25( 平方厘米 ), 于是它的半径为 2.5 厘米 , 直径为 5 厘米 .90ED暗影部分面积为 (6 5) 5 5( 平方厘米 ).13.因 OA=OB , 故三角形 OAB 为等腰三角形 , 即OBA 1 15 , AOB 180 15 2 150 , 同理 AOC 150 , 于是BOC 360 150 2 60 .扇形面积为 : 60 92 42.39 ( 平方厘米 ).36014.正方形能够切割成两个底为 2, 高为 1 的三角形 , 其面积为12 1 2 2 ( 平方厘米 ).2正方形内空白部分面积为 4 个1圆即一个圆的面积与正方形面积之差, 即4122 2 (平方厘米),所有空白部分面积为2(2) 平方厘米. 故暗影部分面积为四个圆面积之和与两个空白面积之和的差, 即为12 4 2 2(2)8 (平方厘米).十二、圆和组合图形(2)一、填空题1. 如图 , 暗影部分的面积是.21 22.大圆的半径比小圆的半径长 6 厘米 , 且大圆半径是小圆半径的 4 倍. 大圆的面积比小圆的面积大平方厘米 .3.在一个半径是4.5 厘米的圆中挖去两个直径都是 2 厘米的圆 . 剩下的图形的面积是平方厘米 .(取 3.14,结果精准到1平方厘米)4.右图中三角形是等腰直角三角形 , 暗影部分的面积是(平方厘米).5.如图所求 , 圆的周长是 16.4 厘米 , 圆的面积与长方形的面积正好相等 . 图中暗影部分的周长是厘米 . (3.14 )6. 如图 , 1 15 的圆的周长为62.8 厘米 , 平行四边形的面积为100 平方厘米 . 暗影部分的面积是.7. 有八个半径为 1 厘米的小圆 , 用它们的圆周的一部分连成一个花瓣图形 ( 如图 ). 图中黑点是这些圆的圆心 . 假如圆周率 3.1416 , 那么花瓣图形的面积 是 平方厘米 .D 是正方形 , ED=DA=AF=2 厘米 暗影部分的面积是.8. 已知 : ABC ,CB GED A F9. 图中 , 扇形 BAC 的面积是半圆 ADB 的面积的 11倍, 那么 , CAB 是度.3C DA O B10. 右图中的正方形的边长是 2 厘米 , 以圆弧为分界限的甲、 乙两部分的面积 差 ( 大减小 ) 是 平方厘米 .( 取 3.14)甲乙2二、解答题11. 如图 : 暗影部分的面积是多少?四分之一大圆的半径为r .( 计算时圆周率取22) 712.已知右图中大正方形边长是 6 厘米 , 中间小正方形边长是 4 厘米 . 求暗影部分的面积 .13.有三个面积都是 S 的圆放在桌上 , 桌面被圆覆盖的面积是 2S+2, 而且重合的两块是等面积的 , 直线 a 过两个圆心 A、B, 假如直线 a 下方被圆覆盖的面积是 9, 求圆面积 S 的值 .A B aC14.如下图 , 一块半径为 2 厘米的圆板 , 从平面上 1 的地点沿线段 AB、BC、 CD 滚到 2 的地点 , 假如 AB、BC、CD 的长都是 20 厘米 , 那么圆板的正面滚过的面积是多少平方厘米 ?12BDA120C———————————————答案——————————————————————1. 6.两个扇形面积相等 , 故暗影部分面积等于一个长为 3, 宽为 2 的长方形面积 , 为 6 个平方单位 .2. 188.4.小圆的半径为 6 (4 1) 2 ( 厘米 ), 大圆的半径为 2 4 8 ( 厘米 ). 大圆的面积比小圆的面积大 (82 2 2 )188.4 ( 平方厘米 ).3.57.2(2 2) 22 57.305 ( 平方厘米 ) ≈57( 平方厘米 ).4.10.26.从圆中能够看出 , 暗影部分的面积是两个半圆的面积与三角形面积之差, 即3.14 (6 2)2162 10.26 ( 平方厘米 ).25.20.5.设圆的半径为 r, 则圆面积即长方形面积为 r 2 , 故长方形的长为 DC r .暗影部分周长DC BCBA⌒r( r r 1 2 r5 2 rAD r)45416.4 20.5 ( 厘米 ).46.48 5( 平方厘米 ).6A如图 , 连接 OA 、AC, 过 A 点作 CD 的垂线交 CD 于BE. 三角形 ACD 的面积为 100 250 ( 平方厘米 ).C E1 DO又圆半径为 6.28 (3.14 2) 10 ( 厘米 ), 由于 1 15 ,又 OA=OD , 故 AOC 15 2 30 , 扇形 AOC 的面积为30 3.14 102 26 1 ( 平方厘米 ). 三角形 AOC 的面积为 502 25 ( 平方厘米 ).3606方形面积为 26 125 11 ( 平方厘米 ), 从而暗影部分的面积为 501148 5( 平6 6 6 6方厘米 ).7. 19.1416.花瓣图形的构造是正方形的面积 , 加上四个 3圆面积后 , 再割去四个半圆的4面积 . 圆的半径为 1 厘米 , 正方形边长为 4 厘米 . 故花瓣图形的面积是4 212 3 41214 1619.1416 ( 平方厘米 ).428.2.43 平方厘米 .CB①②G如图 , 将①移到②得 : 暗影部分面积等于梯形 CEFB 的面积减去三角形 CED 、三角形 CDA 、扇形 AFG 的面积 , 即 DAF21212 212245E (2 2 3)22.43 ( 平方厘222360米 ).9. 60.设扇形 ABC 圆心角的度数是 x, 半圆的半径 OA=r , 有x(2r )2 1 1 1 r 2 ,3603 2解得 x=60.10. 0.14.扇形面积为 3.14 221 3.14 ( 平方厘米 ), 甲部分面积为2 214 13.14 2 0.43 ( 平方厘米 ), 乙部分面积为 3.14 2 2 2 0.57 ( 平方 24厘米 ), 甲乙两部分面积差为 0.57 0.43 0.14 ( 平方厘米 ).11.如图 , 小正方形的边长为 r, 则①的面积为 :2②2r 21 22 r rr ,4 7 2227①③②的面积为12222 rr 1 r 2 , ①和②的面积和为2 7 2 7 41 22 r 2 1 r 222r 2. 即暗影部分面积为 2r 2 .4 7 47712.将暗影部分旋转后 , 能够看出所求暗影部分面积为大正方形面积的一半减去小正形的一半 , 即暗影部分面积等于 62 2 4 2 2 10 ( 平方厘米 ).13. 设一个暗影部分的面积为 x, 则有 : 3S 2x 2S2 , 于是 S 2x 2 (1)又 2S 3 9 , 于是有 x 4S 18x 2 , 解得 S=6.23 12BDA14.圆板的正面滚过的部分如右图暗影部分所求 ,它的面积为 :1 22 (20 2) 4 1 42 ( 20 4)21 61 234 (20 2) 4 ( 42 22 ) 22 204 228.07 ( 平方厘米 ).4 2 3面积计算(三)专题简析:关于一些比较复杂的组合图形,有时直接分解有必定的困难,这时,能够经过把此中的部分图形进行平移、翻折或旋转,化难为易。
六年级奥数几何图形汇总

几何部分题型大汇总1.2.3.如下图,两个相同的直角三角形重叠在一起,求阴影部分的面积是多少?4.四个相同的长方形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是144,小正方形的面积是4,若用x、y表示长方形的长和宽,则小长方形的长为______,宽为______。
第4题图第5题5.三角形EDF的面积比三角形ABE的面积大6平方厘米,已知长方形ABCD的长和宽分别为6、4厘米,DF长多少厘米?6.如图中三角形ABC被分成了甲(阴影部分)、乙两部分,BD=DC= 4,BE=2,EA=4,那么甲部分的面积是乙部分面积的几倍?7.如图,正方形ABCD的面积为3平方厘米,M是AD边上的中点,求阴影部分面积?8.有红黄蓝三块大小一样的正方形纸片,放在一个底面为正方形的盒,它们之间互相叠合.已知露在外面的部分中,红色面积是20.黄色面积是14,绿色面积为10,求正方形盒底的面积。
9.如图,梯形ABCD的上底AD长为3厘米,下底BC长为9厘米.三角形ABO的面积为12平方厘米,则梯形ABCD的面积为多少?10.已知如图大正方形的边长是5厘米,小正方形的边长是3厘米,求阴影部分的面积?11.如图,三角形ABC的面积为1,BD:DC=2:1,E是AC的中点,AD与BE相交于点P,那么四边形PDCE的面积为多少?12.如图,一块长方形的布料ABCD,被剪成大小相等的甲、乙、丙、丁四块,其中甲块布料的长与宽的比为a:b=3:2,那么丁块布料的长与宽的比是______.13.如图一块长方形铁皮,利用图中的阴影部分刚好能做成一个圆柱形油桶(接头处忽略不计).求油桶的容积?14.直角三角形ABC的三条边分别是5cm, 3cm和4cm,将它的直角边AC对折到斜边AB上,使AC 与AD重合,如下图,则图中阴影部分(未重叠部分)的面积是多少平方厘米?15.如图,已知直角三角形的面积是12平方厘米,求阴影部分面积.16.半径20厘米圆的外面和里面各有一个正方形,外面正方形的面积是多少,里面正方形的面积是多少?第16题第18题18.19.如下图,三角形ABC是等腰直角三角形,一直角边长为4厘米,求阴影部分的面积?20.已知下图平行四边形的面积是36平方厘米,求图中阴影部分面积.要求写出计算过。
六年级奥数--几何问题
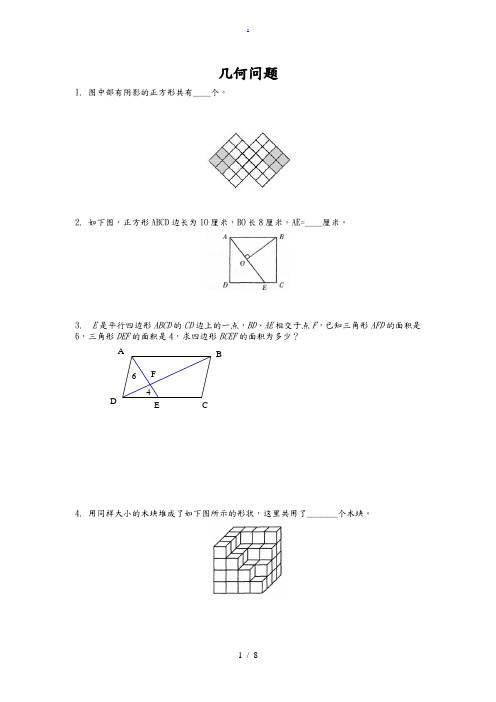
几何问题1. 图中部有阴影的正方形共有____个。
2. 如下图,正方形ABCD边长为lO厘米,BO长8厘米。
AE=____厘米。
3. E是平行四边形ABCD的CD边上的一点,BD、AE相交于点F,已知三角形AFD的面积是6,三角形DEF的面积是4,求四边形BCEF的面积为多少?46FED CBA4. 用同样大小的木块堆成了如下图所示的形状,这里共用了_______个木块。
面积问题1. 一个长方体的表面积是400平方厘米,其中有一个顶点处两条棱长分别是5cm和10cm,求此处的另一条棱长。
2. 如下图,有一个边长是6cm的立方体,如果它的左上方截去一个边分别是6,4,2cm的长方体,那么它的表面积现在是多少?3. 用棱长是1厘米的立方块拼成如下图所示的立体图形,问该图形的表面积是多少平方厘米?4. 把19个棱长为1厘米的正方体重叠在一起,按下图中的方式拼成一个立体图形.,求这个立体图形的表面积.5. 有三个大小一样的正方体,将接触的面用胶粘接在一起成图示的形状,表面积比原来减少了16平方厘米.求所成形体的表面积。
6. 在一个棱长为50厘米的正方体木块,在它的八个角上各挖去一个棱长为5厘米的小正方体,问剩下的立体图形的表面积是多少?7. 一个正方体木块,棱长是1米,沿着水平方向将它锯成2片,每片又锯成3长条,每条又锯成4小块,共得到大大小小的长方体24块,那么这24块长方体的表面积之和是多少?8. 21个棱长为1厘米的小正方体组成一个立体如右图.它的表面积是平方厘米.9. 如下图所示,由三个正方体木块粘合而成的模型,它们的棱长分别为1米、2米、4米,要在表面涂刷油漆,如果大正方体的下面不涂油漆,则模型涂刷油漆的面积是多少平方米?10. 一个长方体的宽和高相等,并且都等于长的一半(如图).将这个长方体切成12个小长方体,这些小长方体的表面之和为600平方分米.求这个大长方体原来的表面积.11. 如右图,以OA为斜边的直角三角形的面积是24 平方厘米,斜边长10 厘米,将它以O点为中心旋转90°,问:三角形扫过的面积是________?( π取3)A. 90B. 93C. 96D. 99答案:1. 面积为1 的正方形有8 个,面积为4 的正方形有8 个,面积为9 的正方形有8 个,面积为16 的正方形有2 个,共计26 个.2. 解:△AOB与△EDA相似,对应边成比例。
六年级奥数复习系列练习四(平面图形的面积)
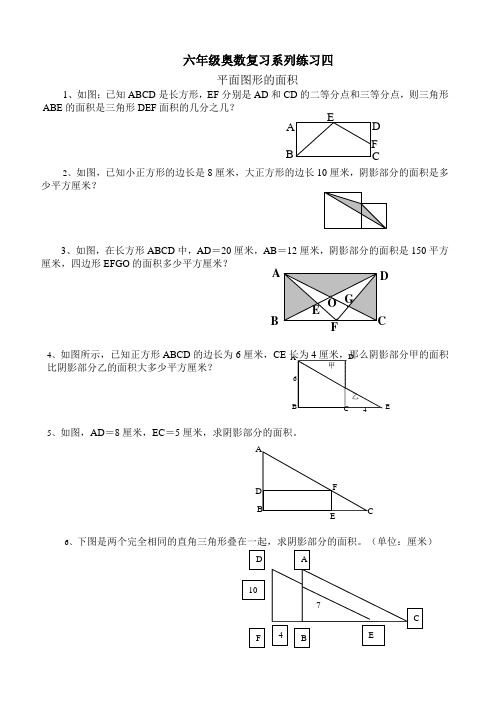
平面图形的面积
1、如图:已知ABCD是长方形,EF分别是AD和CD的二等分点和三等分点,则三角形ABቤተ መጻሕፍቲ ባይዱ的面积是三角形DEF面积的几分之几?
2、如图,已知小正方形的边长是8厘米,大正方形的边长10厘米,阴影部分的面积是多少平方厘米?
3、如图,在长方形ABCD中,AD=20厘米,AB=12厘米,阴影部分的面积是150平方厘米,四边形EFGO的面积多少平方厘米?
4、如图所示,已知正方形ABCD的边长为6厘米,CE长为4厘米,那么阴影部分甲的面积比阴影部分乙的面积大多少平方厘米?
5、如图,AD=8厘米,EC=5厘米,求阴影部分的面积。
6、下图是两个完全相同的直角三角形叠在一起,求阴影部分的面积。(单位:厘米)
六年级图形问题综合(奥数)含答案

平面图形计算(一) 经典图形:1 3 13 11.任意三角形 ABC 中,CD=-AC , EC= —BC ,则三角形CDE 的面积占总面积的=—(为什么?)343 4 42. 任意平行四边形中任意一点,分别连接四个顶点,构成的四个三角形中,上下两个三角形面积之和4.正方形的面积等于边长的平方,或者等于对角线的平方2,或者等于斜边的平方4.(为什么?)例题:例1 .如右图,三角形 ABC 的面积是10, BE=2AB , CD=3BC ,求三角形BDE 的面积。
例2.如图,已知三角形 ABC 的面积是1,延长AB 至D ,使BD=AB ,延长BC 至E ,使CE=2BC ,延 长CA 至F ,使AF=3AC ,求三角形 DEF 的面积。
FA B :C' DE等于左右两个三角形面积之和。
(为什么?) 3.任意梯形,连接对角线,构成四个三角形。
面积之积等于左右两个三角形面积之积。
(1)腰上的两个三角形面积相等; (2)上下两个三角形 (为什么?)2•等腰直角三角形面积等于直角边的平方例3.如图,三角形ABC的面积是180平方厘米,D是BC的中点,AE=ED , EF=2BF,求AEF的面积。
AKF与三角形ADG面积之和等于5平方厘米,DC=CE=3厘米。
求三角形BEK的面积。
例5.如图,三角形ABC的AB和AC两条边分别被分成5等分。
三角形ABC面积是500,求图中阴影部分的面积?4I%TTnnJkrn&^C例6.如图,设正方形ABCD的面积为120, E、F分别为边AB、AD的中点,FC=3GC,则阴影部分的面积是多少?例7.在如图所示的三角形AGH中,三角形ABC BCD CDE DEF,EFG FGH的面积分别是1 , 2, 3, 4, 5, 6平方厘米,那么三角形EFH的面积是多少平方厘米?例8.如图,在平行四边形ABCD中,AC为对角线,EF平行于AC如果三角形AED的面积为12平方厘米,,求三角形DCF的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆和组合图形(1)一、填空题1.算出圆内正方形的面积为 .2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是 平方厘米.120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .4.如图所示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是 厘米.(保留两位小数)5.三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28长 厘米.6.如右图,阴影部分的面积为2平方厘米,等腰直角三角形的面积7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC 垂直OB 于C ,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是 平方厘米.10.在右图中(单位:厘米),两个阴影部分面积的和是 平方厘米.45二、解答题11. ABC 是等腰直角三角形. D 是半圆周的中点, BC 是半圆的直径,已知: AB =BC =10,那么阴影部分的面积是多少?(圆周率14.3=π)12.如图,半圆S 1的面积是14.13平方厘米,圆S 2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O ,半径r =9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米?)14.3(≈π14.右图中4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?———————————————答 案——————————————————————1. 18平方厘米.由图示可知,正方形两条对角线的长都是6厘米,正方形由两个面积相等的三角形构成.三角形底为6厘米,高为3厘米,故正方形面积为1822136=⨯⨯⨯(平方厘米).2. 1.14平方厘米.由图示可知,图中阴影部分面积为两个圆心角为45的扇形面积减去直角三角形的面积.即14.12122236045214.32=⨯⨯-⨯⨯⨯(平方厘米).3. 125.6平方厘米.由已知条件可知圆的半径的平方为120平方厘米.故扇形面积为6.12536012012014.3=⨯⨯(平方厘米).4. 3.09厘米.边结BE 、CE ,则BE=CE=BC=1(厘米),故三角形BCE 为等边三角形.于是60=∠=∠BCE EBC .BE=CE=045.136060214.3=⨯⨯(厘米).于是阴影部分周长为09.312045.1=+⨯(厘米).5. 32.8厘米.从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②加上空白部分的面积是三角形ABC 的面积.又已知①的面积比②的面积小28平方厘米,故半圆面积比三角形ABC 的面积小28平方厘米.半圆面积为6282124014.32=⨯⎪⎭⎫ ⎝⎛⨯(平方厘米),三角形ABC 的面积为628+28=656(平方厘米).BC 的长为8.32402656=÷⨯(厘米).6. 13937平方厘米.将等腰直角三角形补成一个正方形,设正方形边长为x 厘米,则圆的半径为2x 厘米.图中阴影部分面积是正方形与圆的面积之差的81,于是有282114.322⨯=⎪⎭⎫⎝⎛⨯-x x ,解得1332002=x .故等腰直角三角形的面积为1393721133200=⨯(平方厘米). ⌒⌒7. 72.扇形面积是圆面积的511574.31=÷,故扇形圆心角为360的51即72.8. 5.13.三角形ACO 是一个等腰直角三角形,将AO 看作底边,AO 边上的高为3262=÷=÷AO (厘米),故三角形ACO 的面积为93621=⨯⨯(平方厘米).而扇形面积为13.1436045614.32=⨯⨯(平方厘米),从而阴影部分面积为14.13-9=5.13(平方厘米).9. 142.75.由正方形周长是20厘米,可得正方形边长也就是圆的半径为5420=÷(厘米).图形总面积为两个43圆面积加上正方形的面积,即75.1425243514.322=+⨯⨯⨯(平方厘米).10. 90平方厘米.图中阴影部分的面积是从两个以直角三角形直角边为直径的半圆及一个直角三角的面积和中减去一个以直角三角形斜边为直径的半圆的面积即()902114.3)220(2115122114.3)216(2114.3212222=⨯⨯÷-⨯⨯+⨯⨯÷+⨯⨯÷(平方厘米).11. 如图作出辅助线,则阴影部分的面积为三角形AED 的面积减去正方形BEDO 三角形AED 的面积是21)210()21010(⨯÷⨯÷+;积是2)210(÷,圆面积的41是2)210(14.341÷⨯⨯,故阴影部分面积为:22)210(14.341)210(21)210()21010(÷⨯⨯+÷-⨯÷⨯÷+125.32625.19255.37=+-=(平方厘米).12. 由已知半圆S 1的面积是14.13平方厘米得半径的平方为914.3213.14=÷⨯(平方厘米),故半径为3厘米,直径为6厘米. 又因圆S 2的面积为19.625平方厘米,所以S 2半径的平方为25.614.3625.19=÷(平方厘米),于是它的半径为2.5厘米,直径为5厘米. 阴影部分面积为55)56(=⨯-(平方厘米).13. 因OA=OB ,故三角形OAB 为等腰三角形,即 150215180,151=⨯-=∠=∠=∠AOB OBA , 同理150=∠AOC ,于是602150360=⨯-=∠BOC . 扇形面积为:39.42914.3360602=⨯⨯(平方厘米).14. 正方形可以分割成两个底为2,高为1的三角形,其面积为221221=⨯⨯⨯(平方厘米).正方形内空白部分面积为4个41圆即一个圆的面积与正方形面积之差,即2212-=-⨯ππ(平方厘米),所有空白部分面积为)2(2-π平方厘米. 故阴影部分面积为四个圆面积之和与两个空白面积之和的差,即为 8)2(22412=-⨯-⨯⨯ππ(平方厘米).十二、圆和组合图形(2)一、填空题1.如图,阴影部分的面积是 .2.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大 平方厘米.3.在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.(π取3.14,结果精确到1平方厘米)4.右图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).5.如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π6.如图,151=∠的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面积是 .2 1 27.有八个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形(如图).图中黑点是这些圆的圆心.如果圆周率1416.3=π,那么花瓣图形的面积是 平方厘米.8.已知:ABC D 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .9.图中,扇形BAC 的面积是半圆ADB 的面积的311倍,那么,CAB ∠是 度.10.右图中的正方形的边长是2厘米,以圆弧为分界线的甲、乙两部分的面积差(大减小)是 平方厘米.(π取3.14)2二、解答题11.如图:阴影部分的面积是多少?四分之一大圆的半径为r .(计算时圆周率22)取12.已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积.13.有三个面积都是S 的圆放在桌上,桌面被圆覆盖的面积是2S +2,并且重合的两块是等面积的,直线a 过两个圆心A 、B , 如果直线a 下方被圆覆盖的面积是9,求圆面积S 的值.14.如图所示,1的位置沿线段AB 、BC 、CD 滚到2的位置,如果AB 、BC 、C D 的长都是20厘米,那么圆板的正面滚过的面积是多少平方厘米?———————————————答 案——————————————————————1. 6.两个扇形面积相等,故阴影部分面积等于一个长为3,宽为2的长方形面积,为6个平方单位.2. 188.4.小圆的半径为2)14(6=-÷(厘米),大圆的半径为842=⨯(厘米).大圆的面积比小圆的面积大4.18814.3)28(22=⨯-(平方厘米).3. 57.305.57214.3)22(14.35.422=⨯⨯÷-⨯(平方厘米)≈57(平方厘米).4. 10.26.从圆中可以看出,阴影部分的面积是两个半圆的面积与三角形面积之差,即26.10621)26(14.322=⨯-÷⨯(平方厘米).5. 20.5.设圆的半径为r ,则圆面积即长方形面积为2r π,故长方形的长为r DC π=.阴影部分周长r r r r r r AD BA BC DC ππππ245241)(⨯=⨯+-++=+++=5.204.1645=⨯=(厘米).6. 6548(平方厘米).如图,连结OA 、AC ,过A 点作CD 的垂线交CD 于E .三角形ACD 的面积为502100=÷(平方厘米).又圆半径为10)214.3(28.6=⨯÷(厘米),因为1=∠又OA=OD ,故30215=⨯=∠AOC ,扇形AOC 的面积为61261014.3360302=⨯⨯(平方厘米).三角形AOC 的面积为25250=÷(平方厘米).方形面积为611256126=-(平方厘米),从而阴影部分的面积为654861150=-(平⌒方厘米).7. 19.1416.花瓣图形的结构是正方形的面积,加上四个43圆面积后,再割去四个半圆的面积.圆的半径为1厘米,正方形边长为4厘米.故花瓣图形的面积是1416.1916421144314222=+=⨯⨯⨯-⨯⨯⨯+πππ(平方厘米). 8. 2.43平方厘米. 如图,将①移到②得:阴影部分面积等于梯形CEFB 的面积减去三角形CED 、三角形CDA 、扇形AFG 的面积,即 43.236045214.32122122212)322(22=⨯⨯-⨯-⨯⨯-⨯⨯⨯+(平方厘米).9. 60.设扇形ABC 圆心角的度数是x ,半圆的半径OA=r ,有2221311)2(360r r x ⨯⨯⨯=⨯⨯ππ, 解得x=60.10. 0.14.扇形面积为14.341214.32=⨯⨯(平方厘米),甲部分面积为43.0214.32122=÷-⨯(平方厘米),乙部分面积为57.04122214.3=⨯⨯-÷(平方厘米),甲乙两部分面积差为14.043.057.0=-(平方厘米11. 如图,小正方形的边长为2r ,则①的面积为: 72227224122r r r r =⨯-⎪⎭⎫ ⎝⎛⨯⨯, ②的面积为222417272221r r r =-⎪⎭⎫ ⎝⎛⨯⨯,2227224172241r r r =⨯⨯-⨯⨯.即阴影部分面积为272r .12. 将阴影部分旋转后,可以看出所求阴影部分面积为大正方形面积的一半减去小正形的一半,即阴影部分面积等于10242622=÷-÷(平方厘米).13. 设一个阴影部分的面积为x ,则有:2223+=-S x S ,于是22+=x S (1) 又9232=-x S ,于是有23184+-=S x ,解得S=6.14. 圆板的正面滚过的部分如右图阴影部分所求,它的面积为: )420(4614)220(22122-+⨯⨯+⨯-+⨯⨯ππ 07.228323204221)24(414)220(4222≈+=⨯⨯+⨯-⨯-⨯-+⨯πππ(平方厘米).D面积计算(三)专题简析:对于一些比较复杂的组合图形,有时直接分解有一定的困难,这时,可以通过把其中的部分图形进行平移、翻折或旋转,化难为易。
