01第一章参考答案
第1章的参考答案.doc

1.什么是计算机语言?答:计算机语言是人机交流的语言,也称为程序设计语言。
人们通过给计算机一系列命令,让计算机按给定的命令一步步地工作来实现计算机控制。
2.机器语言、汇编语言和高级语言分别有什么特点?答:(1)机器语言是最底层的计算机语言。
在用机器语言编写的程序中,每一条机器指令都是二进制形式的代码,即由一连串的二进制数符。
和1组合起来的编码。
程序中的每一条指令规定了计算机要完成的一个操作。
在指令代码中,一般包括操作码和地址码,其中操作码告诉计算机做何种操作,即“干什么”,地址码则指出被操作的对象存放在什么位置。
用机器语言编写的程序,计算机硬件可以直接识别。
由于机器语言程序是由二进制数符0和1组成的系列,所以用它编写的程序直接针对计算机硬件,执行效率高,能充分发挥计算机的速度和性能,这也是机器语言的优点。
但是由于二进制数序列“难学、难记、难写、难检查、难调试”,编写起来非常繁琐,而且用机器语言编写的程序完全依赖于机器,程序的可移植性差,所以一般不用机器语言编写程序。
(2)汇编语言:人们用一些容易记忆和辨别的有意义的符号来表示机器指令,如用指令助记符表示机器语言指令代码中的操作码,用地址符号表示地址码。
这样用一些符号表示机器指令的语言就是汇编语言,也称为符号语言。
汇编语言与机器语言一一对应,依赖于机器硬件,移植性不好,但执行效率比较高。
针对计算机特定硬件而编制的汇编语言程序,能准确发挥计•算机硬件的功能和特长,程序精练而质量高,所以至今仍是一种常用而强有力的软件开发工具。
(3)高级语言高级语言是一种更接近于自然语言的计算机语言,包括Fortran. Basic、Pascak Cobol 及C 语言等。
高级语言源程序主要由语句(statements)构成,语句是要计算机完成指定任务的命令。
高级语言有各自的语法,独立于具体机器,移植性好。
为了使高级语言编写的程序能够在不同的计算机系统上运行,首先必须将程序翻译成运行程序的计算机特有的机器语言。
柴诚敬化工原理课后答案(01)第一章 流体流动

第一章 流体流动流体的重要性质1.某气柜的容积为6 000 m 3,若气柜内的表压力为5.5 kPa ,温度为40 ℃。
已知各组分气体的体积分数为:H 2 40%、 N 2 20%、CO 32%、CO 2 7%、C H 4 1%,大气压力为 101.3 kPa ,试计算气柜满载时各组分的质量。
解:气柜满载时各气体的总摩尔数()mol 4.246245mol 313314.860000.10005.53.101t =⨯⨯⨯+==RT pV n 各组分的质量:kg 197kg 24.246245%40%4022H t H =⨯⨯=⨯=M n m kg 97.1378kg 284.246245%20%2022N t N =⨯⨯=⨯=M n mkg 36.2206kg 284.246245%32%32CO t CO =⨯⨯=⨯=M n m kg 44.758kg 444.246245%7%722CO t CO =⨯⨯=⨯=M n m kg 4.39kg 164.246245%1%144CH t CH =⨯⨯=⨯=M n m2.若将密度为830 kg/ m 3的油与密度为710 kg/ m 3的油各60 kg 混在一起,试求混合油的密度。
设混合油为理想溶液。
解: ()kg 120kg 606021t =+=+=m m m331221121t m 157.0m 7106083060=⎪⎪⎭⎫ ⎝⎛+=+=+=ρρm m V V V 33t t m m kg 33.764m kg 157.0120===V m ρ 流体静力学3.已知甲地区的平均大气压力为85.3 kPa ,乙地区的平均大气压力为101.33 kPa ,在甲地区的某真空设备上装有一个真空表,其读数为20 kPa 。
若改在乙地区操作,真空表的读数为多少才能维持该设备的的绝对压力与甲地区操作时相同? 解:(1)设备内绝对压力绝压=大气压-真空度= ()kPa 3.65Pa 1020103.8533=⨯-⨯(2)真空表读数真空度=大气压-绝压=()kPa 03.36Pa 103.651033.10133=⨯-⨯4.某储油罐中盛有密度为960 kg/m 3的重油(如附图所示),油面最高时离罐底9.5 m ,油面上方与大气相通。
新课程标准数学必修1第一章课后习题解答[唐金制]
![新课程标准数学必修1第一章课后习题解答[唐金制]](https://img.taocdn.com/s3/m/2fe1ab2c647d27284b735174.png)
新课程标准数学必修1第一章课后习题解答第一章 集合与函数概念1.1集合练习(P5)1.(1)中国∈A ,美国∉A ,印度∈A ,英国∉A.(2)∵A={x |x 2=x }={0,1},∴-1∉A. (3)∵B={x |x 2+x -6=0}={-3,2},∴3∉A.(4)∵C={x ∈N|1≤x ≤10}={1,2,3,4,5,6,7,8,9,10},∴8∈C ,9.1∉C.2.(1){x |x 2=9}或{-3,3}; (2){2,3,5,7};(3){(x ,y )|⎩⎨⎧+=+=6-2x y 3x y }或{(1,4)};(4){x ∈R |4x -5<3}或{x |x <2}. 练习(P7)1.∅,{a },{b },{c },{a ,b },{a ,c },{b ,c },{a ,b ,c }.2.(1)a ∈{a ,b ,c }. (2)∵x 2=0,∴x =0.∴{x |x 2=0}={0}.∴0∈{0}.(3)∵x 2+1=0,∴x 2=-1.又∵x ∈R ,∴方程x 2=-1无解.∴{x ∈R |x 2+1=0}=∅.∴∅=∅. (4). (5)∵x 2=x ,∴x =0或x =1.∴{x |x 2=x }={0,1}.∴{0}{0,1}.(6)∵x 2-3x +2=0,∴x =1或x =2.∴{x |x 2-3x +2=0}={1,2}.∴{2,1}={1,2}.3.(1)由于1是任何正整数的公约数,任何正整数都是自身的公约数,所以8的公约数是1,2,4,8,即B={1,2,4,8}.∴AB.(2)显然B ⊆A ,又∵3∈A ,且3∉B ,∴B A. (3)4与10的最小公倍数是20,4与10的公倍数应是20的倍数,显然A=B.练习(P11)1.A∩B={5,8},A ∪B={3,5,6,7,8}.2.∵x 2-4x -5=0,∴x =-1或x =5.∴A={x |x 2-4x -5=0}={-1,5},同理,B={-1,1}.∴A ∪B={-1,5}∪{-1,1}={-1,1,5},A∩B={-1,5}∩{-1,1}={-1}.3.A∩B={x |x 是等腰直角三角形},A ∪B={x |x 是等腰三角形或直角三角形}.4.∵B={2,4,6},A={1,3,6,7},∴A∩(B)={2,4,5}∩{2,4,6}={2,4}, (A)∩(B)={1,3,6,7}∩{2,4,6}={6}.习题1.1 A 组(P11)1.(1)∈ (2)∈ (3)∉ (4)∈ (5)∈ (6)∈2.(1)∈ (2)∉ (3)∈3.(1){2,3,4,5}; (2){-2,1};(3){0,1,2}.(3)∵-3<2x -1≤3,∴-2<2x ≤4.∴-1<x ≤2.又∵x ∈Z ,∴x =0,1,2.∴B={x ∈Z |-3<2x -1≤3}={0,1,2}.4.(1){y |y ≥-4}; (2){x |x ≠0}; (3){x |x ≥54}. 5.(1)∵A={x |2x -3<3x }={x |x >-3},B={x |x ≥2},∴-4∉B ,-3∉A ,{2}B ,B A.(2)∵A={x |x 2-1=0}={-1,1},∴1∈A ,{-1}A ,∅A ,{1,-1}=A. (3);. 6.∵B={x |3x -7≥8-2x }={x |x ≥3},∴A ∪B={x |2≤x <4}∪{x |x ≥3}={x |x ≥2},A∩B={x |2≤x <4}∩{x |x ≥3}={x |3≤x <4}.7.依题意,可知A={1,2,3,4,5,6,7,8},所以A∩B={1,2,3,4,5,6,7,8}∩{1,2,3}={1,2,3}=B ,A∩C={1,2,3,4,5,6,7,8}∩{3,4,5,6}={3,4,5,6}=C.又∵B ∪C={1,2,3}∪{3,4,5,6}={1,2,3,4,5,6}.∴A∩(B ∪C)={1,2,3,4,5,6,7,8}∩{1,2,3,4,5,6}={1,2,3,4,5,6}.又∵B∩C={1,2,3}∩{3,4,5,6}={3},∴A ∪(B∩C)={1,2,3,4,5,6,7,8}∪{3}={1,2,3,4,5,6,7,8}=A.8.(1)A ∪B={x |x 是参加一百米跑的同学或参加二百米跑的同学}.(2)A∩C={x |x 是既参加一百米跑又参加四百米跑的同学}.9.B∩C={x |x 是正方形}, B={x |x 是邻边不相等的平行四边形},A={x |x 是梯形}.10.∵A ∪B={x |3≤x <7}∪{x |2<x <10}={x |2<x <10},∴(A ∪B)={x |x ≤2或x ≥10}.又∵A∩B={x |3≤x <7}∩{x |2<x <10}={x |3≤x <7},∴(A∩B)={x |x <3或x ≥7}. (A)∩B={x |x <3或x ≥7}∩{x |2<x <10}={x |2<x <3或7≤x <10},A ∪(B)={x |3≤x <7}∪{x |x ≤2或x ≥10}={x |x ≤2或3≤x <7或x ≥10}.习题1.2 A 组(P24)1.∵A={1,2},A ∪B={1,2},∴B ⊆A ,∴B=∅,{1},{2},{1,2}.2.集合D={(x ,y )|2x -y =1}∩{(x ,y )|x +4y =5}表示直线2x -y =1与直线x +4y =5的交点坐标;由于D={(x ,y )|⎩⎨⎧=+=54y x 1y -2x }={(1,1)},所以点(1,1)在直线y =x 上,即D C. 3.B={1,4},当a =3时,A={3},则A ∪B={1,3,4},A∩B=∅;当a ≠3时,A={3,a },若a =1,则A ∪B={1,3,4},A∩B={1};若a =4,则A ∪B={1,3,4},A∩B={4};若a ≠1且a ≠4,则A ∪B={1,a ,3,4},A∩B=∅.综上所得,当a =3时,A ∪B={1,3,4},A∩B=∅;当a =1,则A ∪B={1,3,4},A∩B={1};当a =4,则A ∪B={1,3,4},A∩B={4};当a ≠3且a ≠1且a ≠4时,A ∪B={1,a ,3,4},A∩B=∅.4.作出韦恩图,如图1-1-3-16所示,图1-1-3-16由U=A ∪B={x ∈N|0≤x ≤10},A∩(B)={1,3,5,7},可知B={0,2,4,6,8,9,10}.1.2函数及其表示练习(P19)1.(1)要使分式741+x 有意义,需4x+7≠0,即x≠47-. 所以这个函数的定义域是(-∞,47-)∪(47-,+∞); (2)要使根式有意义,需1-x≥0,且x+3≥0,即-3≤x≤1.所以这个函数的定义域是[-3,1].2.(1)f(2)=28,f(-2)=-28,f(2)+f(-2)=0;(2)f(a)=3a 3+2a ,f(-a)=-3a 3-2a ,f(a)+f(-a)=0.3.(1)两个函数的对应法则相同,而表示导弹飞行高度与时间关系的函数y=500x-5x 2是有实际背景的,这里x≥0;函数y=500x-5x 2,x ∈R ,这两个函数的定义域不同,故这两个函数不相等.(2)函数g(x)=x 0=1(x≠0)与函数f(x)=1,x ∈R 的对应法则相同,但定义域不同,所以不是相等的函数.已知函数解析式求函数值及不同变量的函数值的关系.练习(P23)1.设矩形一边长为xcm ,则另一边长为22x -50=22500x -.由题意,得y=x 22500x -,x ∈(0,50).2.图(A)与事件(2).图(B)与事件(3).图(D)与事件(1)吻合得最好.图(C)可叙述为:我出发后,为了赶时间,加速行驶,走了一段后,发现时间还早,于是放慢了速度.3.解析:由绝对值的知识,有f(x)=⎩⎨⎧<+-≥-.2,2,2,2x x x x 所以,f(x)=|x-2|的图象如下图所示.图1-2-2-234.与A 中元素60°对应的B 中的元素是23;与B 中元素22相对应的A 中的元素是45°. 习题1.2 A 组(P24)1.(1)(-∞,4)∪(4,+∞). (2)R .(3)要使分式有意义,只需x 2-3x+2≠0,即x≠1,且x≠2,所以这个函数的定义域是(-∞,1)∪(1,2)∪(2,+∞).(4)要使函数有意义,只需⎩⎨⎧≠≤⇒⎩⎨⎧≠-≥-,1,40104x x x x 即x≤4,且x≠1. 所以这个函数的定义域是(-∞,1)∪(1,4]. 2.(1)g(x)=xx 2-1=x-1,x≠0,该函数虽然与f(x)的对应关系相同,但是定义域不同, 所以f(x)与g(x)不相等. (2)g(x)=(x )4=x 2,x≥0,该函数虽然与f(x)的对应关系相同,但是定义域不同,所以f(x)与g(x)不相等. (3)g(x)=36x =x 2,x ∈R ,该函数与f(x)的对应关系相同,定义域相同,所以f(x)与g(x)相等.3. (1) (2)x ∈R ,y ∈R . x ∈(-∞,0)∪(0,+∞),y ∈(-∞,0)∪(0,+∞).图1-2-2-24 图1-2-2-25(3) (4)x ∈R ,y ∈R . x ∈R ,y ∈[-2,+∞).图1-2-2-26 图1-2-2-27 4.f(2-)=8+52,f(-a)=3a 2+5a+2,f(a+3)=3a 2+13a+14; f(a)+f(3)=3a 2-5a+16.5.(1)点(3,14)不在f(x)的图象上;(2)f(4)=-3;(3)x=14.6.解析:由韦达定理知1+3=-b ,1×3=c ,∴b=-4,c=3.∴f(x)=x 2-4x+3.∴f(-1)=(-1)2-4×(-1)+3=8. 答案:f(-1)=8.7. (1) (2)图1-2-2-28 图1-2-2-29 8.y=x 10 x ∈(0,+∞),y=21l-x x ∈(0,21l), y=22x d - x ∈(0,d),l=2x+x 20(x>0),l=2202+d . 9.由题意,可知容器内溶液高度为x 的体积等于注入的溶液的体积,即π(2d )2·x=vt ,整理得x=24d v π·t. 当容器注满时有π(2d )2h=vt ,得t=vh d 42π. 所以该函数的定义域是t ∈[0,v h d 42π],值域是x ∈[0,h ]. 10.共8个映射.图1-2-2-30B 组1.(1)[-5,0]∪[2,6);(2)[0,+∞);(3)[0,2)∪(5,+∞).2.图1-2-2-31(1)点(x ,0)和(5,y),即纵坐标为0或横坐标为5的点不能在图象上. (2)略.3.略.4.(1)t=512342x x -++,x ∈[0,12];(2)t=58320+≈3小时. 1.3 函数的基本性质练习(P32)1.从生产效率与生产线上工人数量的关系看,在生产劳动力较少的情况下,随人数的增加效率随着增大,但是到了一定数量后,人数再增多效率反而降低了.这说明劳动力可能过剩,出现了怠工等现象.2.图象如图1-3-2-2所示,图1-3-2-2函数的单调增区间为[8,12),[13,18);函数的单调减区间为[12,13),[18,20].3.函数的单调区间是[-1,0),[0,2),[2,4),[4,5].在区间[-1,0),[2,4)上是减函数;在区间[0,2),[4,5]上是增函数.4.证明:设x 1、x 2∈R ,且x 1<x 2,则f (x 1)-f (x 2)=(-2x 1+1)-(-2x 2+1)=2(x 2-x 1).∵x 1<x 2,∴x 2-x 1>0.∴f (x 1)>f (x 2).∴函数f (x )=-2x +1在R 上是减函数.5.如图1-3-2-3所示,图1-3-2-3从图象上可以发现f (-2)是函数的一个最小值.练习(P36)1.(1)对于函数f (x )=2x 4+3x 2,其定义域为(-∞,+∞).因为对定义域内的每一个x ,都有f (-x )=2(-x )4+3(-x )2=2x 4+3x 2=f (x ),所以函数f (x )=2x 4+3x 2为偶函数.(2)对于函数f (x )=x 3-2x ,其定义域为(-∞,+∞).因为对定义域内的每一个x ,都有f (-x )=(-x )3-2(-x )=-x 3+2x =-(x 3-2x )=-f (x ),所以函数f (x )=x 3-2x 为奇函数.(3)对于函数f (x )=xx 12+,其定义域为(-∞,0)∪(0,+∞). 因为对定义域内的每一个x ,都有f (-x )=x x -+-1)(2=xx 12+-=-f (x ), 所以函数f (x )=xx 12+-为奇函数. (4)对于函数f (x )=x 2+1,其定义域为(-∞,+∞).因为对定义域内的每一个x ,都有f (-x )=(-x )2+1=x 2+1=f (x ),所以函数f (x )=x 2+1为偶函数.2.f (x )的图象如图1-3-2-4所示,g (x )的图象如图1-3-2-5所示.图1-3-2-4 图1-3-2-5习题1.2 A 组(P39)1.(1)函数的单调区间是(-∞,25],(25,+∞). 函数y =f (x )在区间(-∞,25]上是减函数,在区间(25,+∞)上是增函数. (2)函数的单调区间是(-∞,0],(0,+∞).函数y =f (x )在区间(0,+∞)上是减函数,在区间(-∞,0]上是增函数. 图略.2.(1)设0<x 1<x 2,则有f (x 1)-f (x 2)=(x 12+1)-(x 22+1)=x 12-x 22=(x 1-x 2)(x 1+x 2).∵0<x 1<x 2,∴x 1-x 2<0,x 1+x 2<0. ∴f (x 1)>f (x 2). ∴函数f (x )在(-∞,0)上是减函数.(2)设0<x 1<x 2,则有f (x 1)-f (x 2)=(111x -)-(121x -)=21x 11x -=2121x x x x -. ∵0<x 1<x 2,∴x 1-x 2<0,x 1x 2>0. ∴f (x 1)<f (x 2). ∴函数f (x )在(-∞,0)上是增函数.3.设x 1、x 2是(-∞,+∞)上任意两个实数,且x 1<x 2.则y 1-y 2=(mx 1+b )-(mx 2+b )=m (x 1-x 2).∵x 1<x 2,∴x 1-x 2<0.当m <0时,∴y 1-y 2>0,即y 1>y 2.∴此时一次函数y =mx +b (m <0)在(-∞,+∞)上是减函数.同理可证一次函数y =mx +b (m >0)在(-∞,+∞)上是增函数.综上所得,当m <0时,一次函数y =mx +b 是减函数;当m >0时,一次函数y =mx +b 是增函数.4.心率关于时间的一个可能的图象,如图1-3-2-6所示,图1-3-2-65.y =502x -+162x -2100=501-(x 2-8100x )-2100=501-(x -4050)2+307 050. 由二次函数的知识,可得当月租金为4 050元时,租赁公司的月收入最大,最大收益为307 050元.6.图略,函数f (x )的解析式为⎩⎨⎧<-≥+.0),1(,0),1(x x x x x x B 组1.(1)函数f (x )在(-∞,1)上为减函数,在[1,+∞)上为增函数;函数g (x )在[2,4]上为增函数.(2)函数f (x )的最小值为-1,函数g (x )的最小值为0.2.设矩形熊猫居室的宽为x m ,面积为y m 2,则长为2330x -m , 那么y =x 2330x -=21(30x -3x 2)=23-(x -5)2+275.所以当x =5时,y 有最大值275, 即宽x 为5 m 时才能使所建造的每间熊猫居室面积最大,最大面积是275m 2. 3.函数f (x )在(-∞,0)上是增函数.证明:设x 1<x 2<0,则-x 1>-x 2>0.∵函数f (x )在(0,+∞)上是减函数,∴f (-x 1)<f (-x 2).∵函数f (x )是偶函数,∴f (-x )=f (x ).∴f (x 1)<f (x 2).∴函数f (x )在(-∞,0)上是增函数.第一章 复习参考题A 组(P44)1.(1)A={-3,3};(2)B={1,2};(3)C={1,2}.2.(1)线段AB 的垂直平分线;(2)以定点O 为原心,以3 cm 为半径的圆.3.属于集合的点是△ABC 的外接圆圆心.4.A={-1,1},(1)若a =0,则B=∅,满足B ⊆A ;(2)若a =-1,则B={-1},满足B ⊆A ;(3)若a =1,则B={1},满足B ⊆A.综上所述,实数a 的值为0,-1,1.5.A∩B={(x ,y )|⎩⎨⎧=+=0y 3x 0y -2x }={(x ,y )|⎩⎨⎧==0y 0x }={(0,0)}; A∩C={(x ,y )|⎩⎨⎧==3y -2x 0y -2x }=∅; B∩C={(x ,y )|⎩⎨⎧==+3y -2x 0y 3x }={(x ,y )|⎪⎪⎩⎪⎪⎨⎧-==5953y x }={(53,59-)}; (A∩B )∪(B∩C )={(0,0),(53,59-)}. 6.(1)要使函数有意义,必须|x |-2≥0,即x ≤-2或x ≥2,所以函数的定义域为{x |x ≤-2或x ≥2};(2)要使函数有意义,必须⎩⎨⎧≥+≥-,05,02x x 即⎩⎨⎧-≥≥,5,2x x 得x ≥2.所以函数的定义域为{x |x ≥2};(3)要使函数有意义,必须⎩⎨⎧≠-≥-,05||,04x x 即x ≥4,且x ≠5. 所以函数的定义域为{x |x ≥4,且x ≠5}.7.(1)f (a )+1=111++-a a =12+a ; (2)f (a +1)=)1(1)1(1+++-a a =a a +-2. 8.(1)∵f (-x )=22)(1)(1x x ---+=2211xx -+,∴f (-x )=f (x ). (2)∵f (x 1)=22)1(1)1(1x x -+=221111x x -+=222211x x x x -+=1122-+x x =2211x x -+-,∴f (x 1)=-f (x ). 9.二次函数f (x )的对称轴是直线x =8k ,则有8k ≤5或8k ≥20.解得k ≤40或k ≥160,即实数k 的取值范围是(-∞,40]∪[160,+∞).10.(1)函数y =x -2是偶函数; (2)它的图象关于y 轴对称;(3)函数在(0,+∞)上是减函数;(4)函数在(-∞,0)上是增函数.B 组 1.同时参加田径和球类比赛的有3人,只参加游泳一项比赛的有9人.提示:由题意知有15人参加游泳比赛,有8人参加田径比赛,有14人参加球类比赛,所以15+8+14=37,知共有37人次参加比赛.由已知共有28名同学参赛,且没有人同时参加三项,而37-28=9,知共有9名同学参加两项比赛.已知同时参加游泳和田径的有3人,同时参加游泳和球类的有3人,因此同时参加田径和球类的有3人;又已知有15人参加游泳比赛,因此只参加游泳一项的有9人.2.实数a 的取值范围为{a |a ≥0}.3.∵(A ∪B )=(A )∩(B )={1,3},A∩(B )={2,4},∴B={1,2,3,4}.∴B={5,6,7,8,9}.4.f (1)=1×(1+4)=5; f (-3)=-3×(-3-4)=21; f (a +1)=⎩⎨⎧-<++-≥++.1),3)(1(,1),5)(1(a a a a a a 5.证明:(1)f )2(21x x +=a ·221x x ++b =22221b ab b ax x +++=21(ax 1+b )+21(ax 2+b )=21[f (x 1)+f (x 2)], ∴f (221x x +)=21[f (x 1)+f (x 2)]. (2)g (221x x +)=(221x x +)2+a ·221x x ++b =21(21x +ax 1+b )+21(22x +ax 2+b )-41(x 1-x 2)2 =21[g (x 1)+g (x 2)]-41(x 1-x 2)2, ∵-41(x 1-x 2)2≤0, ∴g (221x x +)≤21[g (x 1)+g (x 2)]. 6.(1)奇函数f (x )在[-b ,-a ]上是减函数;(2)偶函数g (x )在[-b ,-a ]上是减函数.7.若全月纳税所得额为500元,则应交纳税款为500×5%=25(元).此时月工资为800+500=1 300(元);若全月纳税所得额为2000元,则应交纳税款为500×5%+1500×10%=175(元).此时月工资为800+500+1500=2800(元).由于此人交纳税款为26.78元,则此人的工资在区间(1300,2800)内,所以他当月的工资、薪金所得是800+500+1.02578.26-≈1317.8(元).奇、偶函数的性质(1)奇偶函数的定义域关于原点对称;奇函数的图象关于原点对称,偶函数的图象关于y 轴对称.(2)奇偶性是函数的整体性质,对定义域内任意一个x 都必须成立.(3)f (-x )=f (x )⇔f (x )是偶函数,f (-x )=-f (x )⇔f (x )是奇函数.(4)f (-x )=f (x )⇔f (x )-f (-x )=0,f (-x )=-f (x )⇔f (x )+f (-x )=0.(5)两个奇函数的和(差)仍是奇函数,两个偶函数的和(差)仍是偶函数.奇偶性相同的两个函数的积(商、分母不为零)为偶函数,奇偶性相反的两个函数的积(商、分母不为零)为奇函数;如果函数y =f (x )和y =g (x )的奇偶性相同,那么复合函数y =f [g (x )]是偶函数,如果函数y =f (x )和y =g (x )的奇偶性相反,那么复合函数y =f [g (x )]是奇函数,简称为“同偶异奇”.(6)如果函数y =f (x )是奇函数,那么f (x )在区间(a ,b )和(-b ,-a )上具有相同的单调性;如果函数y =f (x )是偶函数,那么f (x )在区间(a ,b )和(-b ,-a )上具有相反的单调性.(7)定义域关于原点对称的任意函数f (x )可以表示成一个奇函数与一个偶函数的和,即f (x )=2)()(2)()(x f x f x f x f -++--.(8)若f (x )是(-a ,a )(a >0)上的奇函数,则f (0)=0;若函数f (x )是偶函数,则f (x )=f (-x )=f (|x |)=f (-|x |).若函数y =f (x )既是奇函数又是偶函数,则有f (x )=0。
01第一章流体流动输送习题
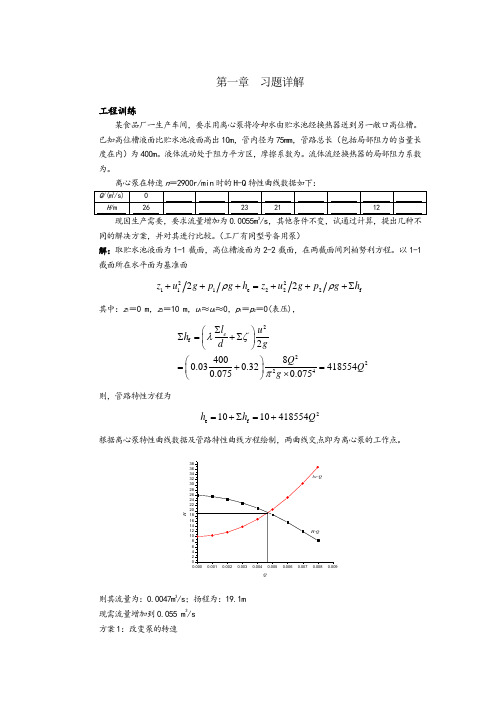
pB p2 H2O g h2 R2 Hg gR2 p3 H2O g R1 h2 h1 H2O g h2 R2 Hg gR2
则
pAB pA pB Hg gR1 H2O gh1 H2O g R1 h2 h1 H2O g h2 R2 Hg gR2 Hg g R1 R2 H2O g h1 R1 h2 h1 h2 R2
习题1-14 附图
耗的轴功率,泵的效率取为65%。
解:在敞口贮槽液面与管道设备入口处截面间列柏努利方程,以贮槽液面所在水平面为基准
水平面
gz1 u12 2 p1 we gz2 u22 2 p2 wf
其中:z1=0 m,z2=10 m,u1≈u2≈0,p1=0(表压),p2=×106 Pa(表压),
管路所需功率为: Ne gheVs 9.8115.1 98515 3600 608 W
阀门全开时管路所需压头为: he 7 1.93u1.75 14.2 m 管路所需功率为: Ne gheVs 9.8114.2 98515 3600 572 W
1-14 用离心泵将敞口贮槽中的大豆油(密度为940
Q/(m3/s)Biblioteka 0H/m26
23
21
12
现因生产需要,要求流量增加为 0.0055m3/s,其他条件不变,试通过计算,提出几种不
同的解决方案,并对其进行比较。(工厂有同型号备用泵)
解:取贮水池液面为 1-1 截面,高位槽液面为 2-2 截面,在两截面间列柏努利方程。以 1-1
截面所在水平面为基准面
z1 u12 2g p1 g he z2 u22 2g p2 g hf
9
2
u2 9.81
新版化工原理习题答案(01)第一章 流体流动

第一章 流体流动流体的重要性质1.某气柜的容积为6 000 m 3,若气柜内的表压力为 kPa ,温度为40 ℃。
已知各组分气体的体积分数为:H 2 40%、 N 2 20%、CO 32%、CO 2 7%、CH 4 1%,大气压力为 kPa ,试计算气柜满载时各组分的质量。
解:气柜满载时各气体的总摩尔数()mol 4.246245mol 313314.860000.10005.53.101t =⨯⨯⨯+==RT pV n 各组分的质量:kg 197kg 24.246245%40%4022H t H =⨯⨯=⨯=M n m kg 97.1378kg 284.246245%20%2022N t N =⨯⨯=⨯=M n mkg 36.2206kg 284.246245%32%32CO t CO =⨯⨯=⨯=M n m kg 44.758kg 444.246245%7%722CO t CO =⨯⨯=⨯=M n m kg 4.39kg 164.246245%1%144CH t CH =⨯⨯=⨯=M n m2.若将密度为830 kg/ m 3的油与密度为710 kg/ m 3的油各60 kg 混在一起,试求混合油的密度。
设混合油为理想溶液。
解: ()kg 120kg 606021t =+=+=m m m331221121t m 157.0m 7106083060=⎪⎪⎭⎫ ⎝⎛+=+=+=ρρm m V V V 33t t m m kg 33.764m kg 157.0120===V m ρ 流体静力学3.已知甲地区的平均大气压力为 kPa ,乙地区的平均大气压力为 kPa ,在甲地区的某真空设备上装有一个真空表,其读数为20 kPa 。
若改在乙地区操作,真空表的读数为多少才能维持该设备的的绝对压力与甲地区操作时相同 解:(1)设备内绝对压力绝压=大气压-真空度= ()kPa 3.65Pa 1020103.8533=⨯-⨯ (2)真空表读数真空度=大气压-绝压=()kPa 03.36Pa 103.651033.10133=⨯-⨯4.某储油罐中盛有密度为960 kg/m 3的重油(如附图所示),油面最高时离罐底9.5 m ,油面上方与大气相通。
01第一章 带传动答案

第一章带传动一、选择题1、在一般机械传动中,应用最广的带传动是( B )。
A.平带传动B.普通V带传动C.同步带传动2、普通V带的横截面为( C )。
A.矩形B.圆形C.等腰梯形3、按国家标准,普通V带有( B )种型号。
A.六B.七C.八4、在相同条件下,普通V带横截尺寸( C ),其传递的功率也()。
A.越小越大B.越大越小C.越大越大5、普通V带的楔角α为( C )。
A.36.B.38C.406、(A)结构用于基准直径较小的带轮。
A.实心式B.孔板式C.轮辐式7、V带带轮的轮槽角( A )V带的楔角。
A.小于B.大于C.等于8、在V带传动中,张紧轮应置于()内侧且靠近( C )处。
A.松边小带轮B.紧边大带轮C.松边大带轮9、V带安装好后,要检查带的松紧程度是否合适,一般以大拇指按下带( B )mm左右为宜。
A.5 B.15 C.2010、在V带传动中,带的根数是由所传递的(B )大小确定的。
A.速度B.功率C.转速11、V带速度在轮槽中的正确位置是( C )。
A.B.C.12、考虑带的使用寿命,要求小带轮基准d d1( A )国家标准规定的最小值。
A.不小于B.不大于C.等于13、( B )是带传动的特点之一。
A.传动比准确B.在过载时会产生打滑现象C.应用在传动准确的场合14、( C )传动具有传动比准确的特点。
A.普通V带B.窄V带C.同步带15、窄V带的相对高度值与普通V带的相对高度值相比,其数值( A )。
A.大B.小C.相同16、窄V带已广泛用于( B )且结构要求紧凑的机械传动中。
A.高速、小功率B.高速、大功率C.低速、小功率二、判断题1、(√)V带传动常用于机械传动的高速端。
2、(√)绳芯结构的V带柔韧性好,适用于转速较高的场合。
3、(√)一般情况下,小带轮的轮槽角要小些,大带轮的轮槽角要大些。
4、(×)普通V带传动的传动比i一般都应大于7。
5、(√)为了延长传动带的使用寿命,通常尽可能地带轮基准直径选得大些。
涉税服务实务-第一章导论01答案

涉税服务实务-第一章导论01答案01、【多选题】下列各项中属于涉税专业服务特点的有()。
A.公正性B.自愿性C.有偿性D.独立性E.专一性【答案】ABCD【解析】涉税专业服务有五个特点:公正性、自愿性、有偿性、独立性、专业性。
02、【多选题】(2020年)下列关于涉税专业服务的特点的表述,正确的有()。
A.涉税专业服务行业是沟通税务机关与纳税人的中介,与征纳双方存在利益冲突B.税务师执业的独立性是指税务师在其接受涉税专业服务委托的权限内,独立行使涉税专业服务权,不受其他机关、社会团体和个人的干预C.公正性是涉税专业服务行业执业的基本要求,离开公正性,涉税专业服务行业的存在就失去了意义D.涉税专业服务在注重社会效益的同时,获取合理报酬,并为委托人提供优质的服务E.涉税专业服务行业是一种知识密集型的专业服务行业【答案】BCDE【解析】选项A,涉税专业服务行业是沟通税务机关与纳税人的中介,与征纳双方没有任何利益冲突。
03、【多选题】(2020年)下列关于涉税专业服务的表述,正确的有()。
A.税务师不能以任何方式强迫纳税人,扣缴义务人委托其开展涉税专业服务,涉税专业服务对象也不得违背涉税服务人员的意志B.税务师是独立行使自己职责的行为主体,其从事的涉税专业服务活动不受税务机关控制,更不受纳税人、扣缴义务人左右C.税务师从事的业务属于涉税专业服务范畴,必须依照民法有关服务活动的基本原则,坚持自愿委托,这种服务关系的建立要符合服务双方的共同意愿D.涉税专业服务关系的建立可以转移征纳关系,即转移纳税人、扣缴义务人的法律责任E.在涉税专业服务对象向其寻求涉税专业服务时,税务师不得拒绝服务【答案】ABC【解析】选项D,在涉税专业服务过程中产生的税收法律责任,无论出自纳税人、扣缴义务人的原因,还是由于税务师的原因,其承担者均应为纳税人或扣缴义务人,而不能因为建立了涉税专业服务关系而转移征纳关系,即转移纳税人、扣缴义务人的法律责任;选项E,税务师具有选择服务对象的自由,在涉税专业服务对象向其寻求涉税专业服务时,税务师拥有接受委托或拒绝服务的选择权。
工程热力学01章习题提示与答案

习题提示与答案 第一章 基本概念及定义1-1 试确定表压力为0.1 kPa 时U 形管压力计中的液柱高度差。
(1)液体为水,其密度为1 000 kg/m 3;(2)液体为酒精,其密度为789 kg/m 3。
提示:表压力数值等于U 形管压力计显示的液柱高度的底截面处液体单位面积上的力,g h p ρ∆=e 。
答案:(1) mm 10.19=∆水h (2) mm 12.92=∆酒精h 。
1-2 测量锅炉烟道中真空度时常用斜管压力计。
如图1-17所示,若α=30°,液柱长度l =200 mm ,且压力计中所用液体为煤油,其密度为800 kg/m 3 ,试求烟道中烟气的真空度为多少mmH 2O(4 ℃)。
提示:参照习题1-1的提示。
真空度正比于液柱的“高度”。
答案:()C 4O mmH 802v =p 。
1-3 在某高山实验室中,温度为20 ℃,重力加速度为976 cm/s 2,设某U 形管压力计中汞柱高度差为30 cm ,试求实际压差为多少mmHg(0 ℃)。
提示:描述压差的“汞柱高度”是规定状态温度t =0℃及重力加速度g =980.665cm/s 2下的汞柱高度。
答案:Δp =297.5 mmHg(0℃)。
1-4 某水塔高30 m ,该高度处大气压力为0.098 6 MPa ,若水的密度为1 000 kg/m 3 ,求地面上水管中水的压力为多少MPa 。
提示:地面处水管中水的压力为水塔上部大气压力和水塔中水的压力之和。
答案:Mpa 8 0.392=p 。
1-5 设地面附近空气的温度均相同,且空气为理想气体,试求空气压力随离地高度变化的关系。
又若地面大气压力为0.1 MPa ,温度为20 ℃,求30 m 高处大气压力为多少MPa 。
提示: h g p p ρ-=0 →TR hg p p g d d -=,0p 为地面压力。
答案:MPa 65099.0=p 。
1-6 某烟囱高30 m ,其中烟气的平均密度为0.735 kg/m 3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章证券投资概述一、名词解释证券证券是商品经济和社会化大生产发展的产物,其含义非常广泛。
从法律意义上说,证券是指各类记载并代表一定权利的法律凭证的统称,用以证明持券人有权依其所持证券记载的内容而取得应有的权益。
从一般意义上来说,证券是指用以证明或设定权利所做成的书面凭证,它表明证券持有人或第三者有权取得该证券拥有的特定权益,或证明其曾经发生过的行为。
有价证券有价证券(valuable papers)是指标有票面金额,证明持券人有按期取得一定收入并可自由转让和买卖的所有权或债权凭证,这类证券本身没有价值,但由于它代表着一定量的财产权利,持有者可凭以直接取得一定量的商品、货币,或是取得利息、股息等收入,因而可以在证券市场上买卖和流通,客观上具有了交易价格。
商品证券商品证券是证明持券人有商品所有权或使用权的凭证,取得这种证券就等于取得这种商品的所有权,持券者对这种证券所代表的商品所有权受法律保护。
属于商品证券的有提货单、运货单、仓库栈单等货币证券货币证券是指本身能使持券人或第三者取得货币索取权的有价证券,货币证券主要包括两大类:一类是商业证券,主要包括商业汇票和商业本票;另一类是银行证券,主要包括银行汇票、银行本票和支票。
资本证券资本证券是指由金融投资或与金融投资有直接联系的活动而产生的证券。
持券人对发行人有一定的收入请求权,它包括股票、债券及其衍生品种如认股权证、可转换证券等。
证券市场证券市场是证券发行和交易的场所。
证券市场可分为证券发行市场和证券流通市场。
证券发行市场是新证券首次向社会公众发行的市场,又称一级市场或初级市场。
证券流通市场是转手买卖已发行证券的市场,又称二级市场或次级市场。
证券市场的两个构成部分既有联系,又有区别,相互依存,相互制约,是一个不可分割的整体。
投资所谓投资,就是经济主体为获得预期经济利益而在当前进行资金投入,用以购买金融资产或实物资产达到增值的行为和过程,投资过程包括资金投入、资产增值、收回资金3个阶段。
金融投资金融投资就是投资主体为获取预期收益,预先垫付货币以形成金融资产,并借以获取收益的经济行为。
金融投资包括股票投资、债券投资、期货投资等有价证券投资和个人在银行的储蓄行为。
个人把钱送存银行,也能使投资者获得一定的未来收益,因而也是一种金融投资。
证券投资所谓证券投资,是指个人或法人对有价值证券的购买行为,这种行为会使投资者在证券持有期内获得与其所承担的风险相对称的收益。
直接金融投资投资者以购买股票、债券、商业票据等形式进行金融投资,称为直接金融投资。
间接金融投资投资者将资金存入银行或其他机构,以储蓄存款或企业存款、机构存款的形式存在,称为间接金融投资。
二、多项选择题1、ABCDE2、ABC3、ABDE4、ABCDE三、简答题1.什么是投资?如何正确理解投资的含义?所谓投资,就是经济主体为获得预期经济利益而在当前进行资金投入,用以购买金融资产或实物资产达到增值的行为和过程,投资过程包括资金投入、资产增值、收回资金3个阶段。
对任何经济社会和经济人而言,持续不断地进行投资是保持经济利益持续增长必不可少的前提条件,可以从以下几个方面来认识投资:(1)投资是现在支出一定价值的经济活动。
从当前来看,投资现在就要支付一定的资金;从长远来看,投资就是为了获取未来的报酬而现在采取的付出资金的经济行为。
(2)投资具有时间性。
也就是说,现在付出的价值只能到未来的时间才能收回,而且未来的时间越长,未来收益的不确定性就越大,从而风险就越大。
(3)投资具有一定的风险性。
风险就是指未来收益的不确定性。
当前投入的价值是确定的,但是,未来可能获取的收益却是不确定的,这种未来收益的不确定性就是风险。
2.什么是证券投资?它与实物投资有何异同?证券投资是以有价证券的存在和流通为前提条件的,是一种金融投资,它和实物投资之间既有密切联系,又存在一定的区别。
实物投资是对现实的物质资产的投资,它的投资会形成社会资本存量和生产能力的直接增加,并可直接增加社会物质财富或提供社会所需要的服务,它被称为直接投资。
证券投资所形成的资金运动是建立在金融资产的基础上的,投资于证券的资金通过金融工具的发行转移到企业部门,它被称为间接投资。
证券投资和实物投资并不是竞争性的,而是互补的。
实物投资在其无法满足巨额资本的需求时,往往要借助于证券投资。
证券投资的资金来源于社会储蓄,这部分社会储蓄虽然没有直接投资于生产经营活动,而是通过证券市场间接投资于实物投资,但由于证券市场自身机制的作用,不但使资金在盈余单位和不足单位之间重新配置,解决了资金不足的矛盾,而且还会促使社会资金流向经济效益好的部门和企业,提高资金利用效率和社会生产力水平。
高度发达的证券投资使实物投资更为便捷,通过金融投资可使实物投资筹建到所需资本。
尽管证券投资在发达商品经济条件下占有重要的地位,但是还应看到,实物资产是金融资产存在和发展的基础。
金融资产的收益也最终来源于实物资产在社会在生产过程中的创造。
因而证券投资的资金运动是以实物投资的资金运动为根据的,实物投资对证券投资有重大影响;同时,企业生产能力的变化会影响到投资者对该企业证券的前景预算,从而使金融投资的水平发生变化。
3.证券投资一般要经过哪些步骤?证券投资是一项复杂的投资活动,要求投资者必须十分熟悉投资的程序,了解投资过程的每一个环节并严格遵循。
证券投资程序大致可以分为准备阶段、了解阶段、分析阶段和决策阶段等四个过程。
(1)准备阶段投资的前提是需要预先筹集一笔资金。
在投资之前,必须确定能否筹集到一定数量的资金,然后才能考虑如何投资、投在何处等问题。
就个人投资者来说,其资金来源主要是自身的积蓄,也包括继承的遗产、亲友的馈赠、产业的变卖、保险的赔偿金等其他资金来源。
投资者须先根据个人收入及家庭支出,编制家庭预算,然后计算能有多少节余,制定出投资计划。
机构投资者的资金来源因性质不同而异。
例如商业银行的资金主要来源于客户的存款、自有资金和盈利收入;保险机构的资金主要来自部分保险费收入;社会团体机构的资金主要来自可支配的资金等。
(2)了解阶段一旦投资者将投资所需要款项筹措好,就必须深入了解投资的各个方面。
首先应熟悉投资中的收益与风险。
投资的主要目的是获得收益,当然希望收益越多越好,但在取得盈利的同时,连带有损失本金的危险,风险是收益的必然代价。
正视风险与收益的关系,树立正确的风险意识,要求投资者先衡量自身具有多大的风险承受能力,然后决定拟投入多少资金,以及选择何种投资对象。
其次,应广泛了解投资对象的收益与风险情况。
投资对象的种类繁多,就有价证券而言,就有债券、股票等形式,各种证券因其性质、时间长短、有无担保等的不同,收益与风险的大小都有差异,而且收益的支付方式,风险所包含的内容是互不相同。
因此,必须熟悉各种情况,才能进行投资对象的选择。
再次,由于证券交易大都通过经纪商在证券市场上进行,所以必须进一步了解证券市场的组织和机制、经纪商的职能和作用、买卖证券的程序和手续、管理证券交易的法律法规、证券的交割和清算、买卖证券的佣金费用等。
否则就无从进行证券买卖,甚至蒙受不应有的损失。
(3)分析阶段投资者对于各种证券的性质及其收益与风险,市场上经营方式等各种情况大致有了一般的认识和了解以后,在决定选择哪种证券之前,必须围绕该证券进行全面的宏观与微观经济分析。
首先需要判断当时的经济形势的变动趋势,需要对此经济趋势下各种行业的发展前途作出判断;其次,需要根据发行证券的公司的财务力量、销售状况、产品结构和适宜的生产设备等预测公司未来的收益和风险程度;最后,还需根据证券市场行情,对证券的真实价值、上市价格和价格涨落的趋势进行认真的分析,因为证券的质量决定于其真实价值,价值的市场反映便是市场价格,市场价格受到多种因素的影响,经常发生变动。
这里牵扯到种类繁多的因素和错综复杂的相互关系,如不进行深入细致的研究分析,就无从获悉其真相。
这会造成投资者盲目选购,导致买进收益低、风险大的证券,或者没有选择买卖时机,在价高时买进,价跌时抛出,带来巨大损失。
(4)决策阶段通过以上各个阶段和步骤,投资者有了条件按照自己拟定的投资目标,针对个人对收益和风险的衡量,考虑到今后对资金的需要和用途并预计未来经济环境及本身财务状况的变化后,作出妥当、合理的决策,决定将资金投入到何种具体的证券上去。
操作过程开始后,需要了解和严格遵守证券交易中的委托、成交、清算和交割的一系列程序,确保顺利地完成证券投资过程。
5.你认为在人生的青年、中年、老年等不同生命周期阶段,会各自偏重4种投资目标中的哪一种?请说明理由。
人在不同的年龄,拥有不同的人格气质。
在青年,人往往拥有较大的闯劲,喜欢冒险,因此在青年阶段会偏重于资本增值的目标;而在中年人趋于变的保守,这时人们进行投资的目标往往侧重于资本保全和总收益。
而在老年人的承受风险能力有所下降,因此此时会侧重于避险目标。
.5.试说明直接金融投资与间接金融投资的主要区别和相互关系。
直接投资是指投资主体将资金直接投入社会再生产过程,从事创造和实现商品价值的活动。
如开办企业、公司,购买房地产等,从直接生产经营活动中获取经济利益。
间接投资是指投资者置身于生产经营活动之外,将资金委托给他人使用,投资者坐收其利并到期收回本金。
购买证券即属于间接投资。
区别主要从种类、特征、优缺点上进行比较;相互关系互相补充、都是投资的形式,目的相同等等。
