初中数学《直角三角形》公开课ppt北师大版3
合集下载
北师大版数学八年级上册《直角三角形—逆命题、逆定理》课件
条件：一个三角形是等边三角形. 结论：它的每个角都等于60°. 逆命题：如果 一个三角形的每个角都等于60°，
那么 这个三角形是等边三角形.
练习：
指出下列命题的条件和结论，说出其的逆命题.
（3）全等三角形的对应角相等. 条件：两个三角形是全等三角形. 结论：它们的对应角相等.
逆命题：如果两个三角形的对应角相等，
⑵同位角相等，两直线平行 同位角相等 两直线平行
⑶如果a＝b，那么a2＝b2。
a＝b
a2＝b2
⑷如果a2＝b2，那么a＝b。
a2＝b2
a＝b
观察表中的命题，命题⑴与命题⑵有什么关系？ 命题⑶与命题⑷呢？
命题
条件
结论
⑴两直线平行，同位角相等 两直线平行 同位角相等
⑵同位角相等，两直线平行 同位角相等 两直线平行
练习一下
1.如图，正方形ABCD，AB=4，AE=2，DF=1， 图中有几个直角三角形？
易知:△ABE，△DEF，△FCB
A 2E2 D
均为Rt△
1 另外：△BEF也是Rt△
4
F 由勾股定理知
3
BE2=22+42=20，
EF2=22+12=5，
B
4
C
BF2=32+42=25
∴BE2+EF2=BF2
∴ △BEF是Rt△
2.琳琳想知道学校旗杆的高，他发现旗杆顶端的绳 子垂到地面还多1米，当他把绳子的下端拉开5米 后，发现下端刚好接触地面，你能帮他算出来旗 杆的高度吗？
A
x米 (x+1)米
5米
C
B
2.如图，长方形ABCD中，BC=8，CD=4，
将其沿BD折叠，点A落在A′处， 求 CF
那么 这个三角形是等边三角形.
练习：
指出下列命题的条件和结论，说出其的逆命题.
（3）全等三角形的对应角相等. 条件：两个三角形是全等三角形. 结论：它们的对应角相等.
逆命题：如果两个三角形的对应角相等，
⑵同位角相等，两直线平行 同位角相等 两直线平行
⑶如果a＝b，那么a2＝b2。
a＝b
a2＝b2
⑷如果a2＝b2，那么a＝b。
a2＝b2
a＝b
观察表中的命题，命题⑴与命题⑵有什么关系？ 命题⑶与命题⑷呢？
命题
条件
结论
⑴两直线平行，同位角相等 两直线平行 同位角相等
⑵同位角相等，两直线平行 同位角相等 两直线平行
练习一下
1.如图，正方形ABCD，AB=4，AE=2，DF=1， 图中有几个直角三角形？
易知:△ABE，△DEF，△FCB
A 2E2 D
均为Rt△
1 另外：△BEF也是Rt△
4
F 由勾股定理知
3
BE2=22+42=20，
EF2=22+12=5，
B
4
C
BF2=32+42=25
∴BE2+EF2=BF2
∴ △BEF是Rt△
2.琳琳想知道学校旗杆的高，他发现旗杆顶端的绳 子垂到地面还多1米，当他把绳子的下端拉开5米 后，发现下端刚好接触地面，你能帮他算出来旗 杆的高度吗？
A
x米 (x+1)米
5米
C
B
2.如图，长方形ABCD中，BC=8，CD=4，
将其沿BD折叠，点A落在A′处， 求 CF
最新北师大版八年级数学下册《直角三角形》精品教学课件
∴∠ABP＝∠ACP＝90°
∵PB＝PC，AP＝AP
∴Rt△ABP≌Rt△ACP(HL)
∴∠APB＝∠APC
PB＝PC，
在△PBD和△PCD中，
∠DPB＝∠DPC， DP＝DP，
∴△PBD≌△PCD(SAS)
∴∠BDP＝∠CDP
课堂小结，整体感知
1.课堂小结：请同学们回顾本节课所学的内容，有哪些收获？
实践探究，交流新知
猜想： 斜边和一条直角边分别相等的两个直角三角形全等.
1．分析命题： 条件：两个直角三角形的斜边和一条直角边分别相等； 结论：这两个直角三角形全等．
2．数学语言： 已知：如图，在△ABC和△A′B′C′中，∠C＝∠C′＝90°，AC＝A′C′，AB＝A′B′； 求证：△ABC≌△A′B′C′.
开放训练，体现应用
例2 如图，∠BAC＝90°，AD是∠BAC内部一条射线，若AB＝AC，BE⊥AD于点E
，CF⊥AD于点F.求证：AF＝BE.
证明：∵∠BAC＝90°
∴∠BAE＋∠FAC＝90°
∵BE⊥AD，CF⊥AD
∴∠BEA＝∠AFC＝90°
∴∠BAE＋∠EBA＝90°
∴∠EBA＝∠FAC.
∴∠BFD＝∠CED＝90°
DF＝DE，
在△BDF和△CDE中 ∠BFD＝∠CED，
BF＝CE，
∴△BDF≌△CDE(SAS)
∴∠B＝∠C
开放训练，体现应用
变式训练2 如图，在四边形ABCD中，∠ABC＝∠ADC＝90°，
BE⊥AC于点E，DF⊥AC于点F，CF＝AE，BC＝DA.
求证：Rt△ABE≌Rt△CDF.
开放训练，体现应用
例1 如图，有两个长度相同的滑梯，左边滑梯的高度AC与右边滑梯水平方 向的长度DF相等，两个滑梯的倾斜角∠ABCБайду номын сангаас∠EFD的大小有什么关系？
北师大版数学七年级下册第四章：1、认识三角形 课件(共65张PPT)
1.三角形内角和定理:三角形三个内角的和等于180°.
2.三角形内角和定理的应用:①在三角形中,已知任意两个内角的度数可以 求出第三个内角的度数;②已知三角形三个内角的关系,可以求出各个内角 的度数;③求一个三角形中各角之间的关系.
3.三角形按角分类:
直角三角形:有一个角是直角的三角形 锐角三角形:三个角都是锐角的三角形 钝角三角形:有一个角是钝角的三角形
∠A、∠C的公共边是
.
,∠A的对边是
栏目索引
,
图4-1-3 答案 ∠B;BC;AC 解析 △ABC中,AB与BC的夹角是∠B,∠A的对边是BC,∠A、∠C的公共 边是AC.
1 认识三角形
知识点二 三角形三个内角之间的关系
栏目索引
4.(2017广西南宁中考)如图4-1-4,△ABC中,∠A=60°,∠B=40°,则∠C等于
其所在直 直角三角形
线)的交
点位置 钝角三角形
交点在三角形内 交点在直角顶点处 交点在三角形外
三条中线交于三 角形内一点(这一 点称为三角形的 重心)
交点在三角形内
共同点
每个三角形都有三条高、三条中线、三条角平分线,它们(或它们所在的直线) 都分别交于一个点,它们都是线段
1 认识三角形
栏目索引
知识拓展
(1)得到线段垂直;(2)得到角相等 (1)得到线段相等; (2)得到面积相等
得到角相等
1 认识三角形
栏目索引
线段 的位置
锐角三角形 直角三角形
钝角三角形
三条高全在三角形内
三条中线全在三
角形内 一条高在三角形内,另外两条
与两直角边重合
三条角平分线全 在三角形内
三角形内一条,三角形外两条
新北师大版九年级数学下册《三角函数的计算》优质ppt教学课件
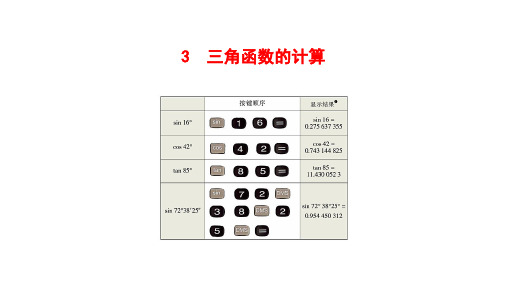
上表的显示结果是以“度”为单位的，再按 ˚ ′ ″ 键即可显示 以“度、分、秒”为单位的结果.
根据上述方法你能求出问题1中∠A的大小吗？
sin A = 1 = 0.25. 按键顺序和显示结果为
4
SHIFT sin 0 · 2 5 = 14.477 512 19°
再按 ° ′ ″ 键可显示14˚28′39″，所以∠A=14˚28′39″.
正弦值随着角度的增大（或减小）而增大（或减小）； 余弦值随着角度的增大（或减小）而减小（或增大）； 正切值随着角度的增大（或减小）而增大（或减小）.
知识点1 利用计算器求锐角三角函数值
1.如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器 求边AC的长,则下列按键顺序正确的是( D )
D 39°
E
45°
C
A
【解析】（1）由题意，AC＝AB＝610 米.
（2）DE＝AC＝610米，
在Rt△BDE中，tan∠BDE＝ BE ，
DE
故BE＝DEtan39°． 因为CD＝AE，
所以CD＝AB－DE·tan 39°
＝610－610×tan 39°≈116（米）. 答：大楼的高度CD约为116 米．
B．sin65°54′-sin35°54′=sin30°
C．2sin15°30′=sin31°
D．sin72°18′-sin12°18′=sin47°42′
•2. 已知sin α＝1 ，求α，若用科学计算器计算且结果以“度、分、秒
2
”为单位，最后按键(D )
•A．AC/ON
B. SHIFT
C．MODE
(4)sin18°＋cos55°－tan59°≈－0.7817.
北师大版九年级数学下册《三角函数的应用》精品课件PPT
都来当个小专家！
A
B 咋 办
2 如图,水库大坝的截面是梯形
ABCD,坝顶AD=6m,坡长CD=8m.坡底
D
BC=30m,∠ADC=1350. (1)求坡角∠ABC的大小;
(2)如果坝长100m,那么修建这个 C 大坝共需多少土石方(结果精确到
0.01m3 ).
先构造直 角三角形!
2020年北师大版九年级数学下册1.5《 三角函 数的应 用》课 件（共 16张pp t）
1 如图，有一斜坡AB长40m，坡顶离地面的
高度为20m,求此斜坡的倾斜角. 2.有一建筑物,在地面上A点测得其顶点 A
C的仰角为300,向建筑物前进50m至B处,又 A
测得C的仰角为450,求该建筑物的高度(结
果精确到0.1m).
B
3. 如图,燕尾槽的横断面是一个等腰梯 形,其中燕尾角∠B=550,外口宽AD=180mm, 燕尾槽的尝试是70mm,求它的里口宽BC(结 果精确到1mm).
北师大版九年级数学下册 2020年北师大版九年级数学下册1.5《三角函数的应用》课件（共16张ppt）
2020年北师大版九年级数学下册1.5《 三角函 数的应 用》课 件（共 16张pp t）
2020年北师大版九年级数学下册1.5《 三角函 数的应 用》课 件（共 16张pp t）
直角三角形的边角关系
看我露一手
解:要知道货轮继续向东航行途中有无触礁的危险,只
要过点A作AD⊥BC的延长线于点D,如果AD>10海里,则无
触礁的危险.根据题意可知,∠BAD=550,∠CAD=250,BC=
20海里.设AD=x,则
北
A
tan 550 BD , tan 250 CD ,
七年级数学北师大版下册4.三角形的三边关系课件
(1)a＝________， b＝________， c＝________，
(2)a＝________， b＝________， c＝________，
(3)a＝________， b＝________， c＝________，
计算每个三角形的任意两边之差，并与第三边比较，
你能得到什么结论? 再画一些三角形试一试.
14．已知：如图，四边形 ABCD 是任意四边形，AC 与 BD 交于 点 O. 试说明：AC＋BD＞12(AB＋BC＋CD＋DA)． 解：在△OAB 中，有 OA＋OB＞AB； 在△OAD 中，有__O__A_＋__O_D__＞__A_D_____； 在△ODC 中，有__O__D_＋__O__C_＞__C_D_____； 在△__O_B__C___中，有___O_B_＋__O__C_＞__B__C____，
2.等腰三角形的一边长为3cm，另一边长为4cm，则 它的周长是___1_0_c_m__或__1_1_c_m_； 3.等腰三角形的一边长为3cm，另一边长为8cm，则 它的周长是____1_9_c_m___.
巩固新知
1 如图，在△ABC中，BC＝BA，点D在AB上，且 AC＝CD＝DB，则图中的等腰三角形有( C )
*11.(2020·毕节)已知等腰三角形两边的长分别为 3 和 7, 则此等
腰三角形的周长为( )
A．13
B．17
C．13 或 17 D．13 或 10
【点拨】分两种情况讨论：若底边长为 3，腰长为 7，则此等腰 三角形的周长为 3＋7＋7＝17； 若底边长为 7，腰长为 3，因为 3＋3＜7，不符合三角形的三边 关系，所以此等腰三角形不存在．
【中考·贺州】一个等腰三角形的两边长分别为4，8，
北师大版数学八年级下册1.2《直角三角形》说课稿
北师大版数学八年级下册1.2《直角三角形》说课稿一. 教材分析《直角三角形》是北师大版数学八年级下册第1章第2节的内容。
本节课主要介绍直角三角形的性质，包括直角三角形的定义、直角三角形的边角关系、直角三角形的应用等。
通过学习本节课，学生能够理解直角三角形的概念，掌握直角三角形的性质，并能运用直角三角形的性质解决实际问题。
二. 学情分析学生在学习本节课之前，已经学习了三角形的基本概念和性质，对三角形有一定的认识。
但是，学生可能对直角三角形的性质和应用还不够了解。
因此，在教学过程中，教师需要通过引导学生观察、思考、讨论等方式，帮助学生理解和掌握直角三角形的性质。
三. 说教学目标1.知识与技能目标：学生能够理解直角三角形的概念，掌握直角三角形的性质，并能运用直角三角形的性质解决实际问题。
2.过程与方法目标：学生能够通过观察、思考、讨论等方式，培养自己的观察能力和思维能力。
3.情感态度与价值观目标：学生能够积极参与课堂活动，增强对数学学科的兴趣和自信心。
四. 说教学重难点1.教学重点：直角三角形的性质及其应用。
2.教学难点：直角三角形的边角关系。
五. 说教学方法与手段1.教学方法：采用问题驱动法、合作学习法、探究学习法等。
2.教学手段：利用多媒体课件、几何画板等辅助教学。
六. 说教学过程1.导入：通过复习三角形的基本概念和性质，引出直角三角形的定义。
2.探究直角三角形的性质：引导学生观察、思考直角三角形的性质，并通过几何画板软件进行演示。
3.小组讨论：学生分组讨论直角三角形的应用，分享自己的解题心得。
4.总结直角三角形的性质：引导学生总结直角三角形的性质，并进行解释。
5.练习与拓展：布置一些有关直角三角形的练习题，帮助学生巩固所学知识，并拓展学生的思维。
七. 说板书设计板书设计如下：1.定义：有一个角是直角的三角形a.两个锐角的和为90度b.直角对边最长c.直角三角形的一条直角边等于另一条直角边的平方根乘以斜边d.计算直角三角形的边长e.证明几何命题八. 说教学评价教学评价主要通过学生的课堂表现、练习题的完成情况和课后作业的完成情况进行评估。
北师大版九年级下册数学《解直角三角形》直角三角形的边角关系研讨说课复习课件
能求出其他的元素?
知道一个元素行不行？
知道两个角行不行？
A
c
b
C
a
B
合作探究
1.在图中的Rt△ABC中，根据∠A＝75°，斜边AB＝6，你能求出这个直角三角形
的其他元素吗？
能
B
6
BC
sin A
BC AB sin A 6 sin 75
AB
cos A
AC
AC AB cos A 6 cos 75
）
(2)R t△A B C 中,
因为 A B =
6米
AC
= 4 3 米,
sin 60
所以 A D - A B = 12- 4 3 ≈5.1 米.
所以改善后的滑梯会加长 5.1 m .
D
300
600
B
C
拓展探究
如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形
为“好玩三角形”,在Rt△ABC中,∠C=90°,若Rt△ABC是“好玩三角
解直角三角形
九年级下册
课件
学习目标
1
理解解直角三角形的含义。
掌握运用直角三角形的两锐角互余、勾股定
2
3
理及锐角三角函数求直角三角形的未知元素.
通过利用三角函数解决实际问题的过程，进一步提高学
生的逻辑思维能力和分析问题解决问题的能力.
自主学习
直角三角形共6个元素：三条边三个角，那么之间有哪些关系：
25°
∵∠B=25°，∴∠A=65°
b
b
30
71
又∵sinB=
，∴c=
0
sin B sin 25
c
知道一个元素行不行？
知道两个角行不行？
A
c
b
C
a
B
合作探究
1.在图中的Rt△ABC中，根据∠A＝75°，斜边AB＝6，你能求出这个直角三角形
的其他元素吗？
能
B
6
BC
sin A
BC AB sin A 6 sin 75
AB
cos A
AC
AC AB cos A 6 cos 75
）
(2)R t△A B C 中,
因为 A B =
6米
AC
= 4 3 米,
sin 60
所以 A D - A B = 12- 4 3 ≈5.1 米.
所以改善后的滑梯会加长 5.1 m .
D
300
600
B
C
拓展探究
如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形
为“好玩三角形”,在Rt△ABC中,∠C=90°,若Rt△ABC是“好玩三角
解直角三角形
九年级下册
课件
学习目标
1
理解解直角三角形的含义。
掌握运用直角三角形的两锐角互余、勾股定
2
3
理及锐角三角函数求直角三角形的未知元素.
通过利用三角函数解决实际问题的过程，进一步提高学
生的逻辑思维能力和分析问题解决问题的能力.
自主学习
直角三角形共6个元素：三条边三个角，那么之间有哪些关系：
25°
∵∠B=25°，∴∠A=65°
b
b
30
71
又∵sinB=
，∴c=
0
sin B sin 25
c
《解直角三角形》直角三角形的边角关系PPT-北师大版九年级数学下册
知2－讲
例5 在Rt△ABC中, ∠C＝90°, ∠A, ∠B, ∠C的对边分 别为a, b, c, 且c＝100, ∠A＝26°44′．求这个三角形 的其他元素.(长度精确到0．01)
导引: 已知∠A, 可根据∠B＝90°－∠A得到∠B的大小.而
解: 已知斜边, 必然要用到正弦或余弦函数.
∵∠A＝26°44′, ∠C＝90°,
例6 如图,
在△ABC中,
AB＝1,
AC＝
2，sin
B＝
2 4
，
求BC的长.
导引:要求的BC边不在直角
三角形中, 已知条件中
有∠B的正弦值, 作BC边上的高,
将∠B置于直角三角形 中, 利用解直角三角形就可
解决问题.
知3－讲
解: 如图, 过点A作AD⊥BC于点D．
2，
∵AB＝1, sin B＝ 4 2
2.
4
4
∴AD＝AB·sin B＝1×
AB2 AD2
＝
12
2 2 4
14 ,
4
∴BD＝ AC 2 AD2
2 2 2
30
2
4
. 4
CD＝ CD BD
30 4
14 4
30 14 .
4（来自《点拨》）
总结
知3－讲
通过作垂线(高), 将斜三角形分割成两个直角三角 形, 然后利用解直角三角形来解决边或角的问题, 这 种 “化斜为直”的思想很常见.在作垂线时, 要结合已知 条件, 充分利用已知条件, 如本题若过（B来点自作《A点C拨的》垂） 线,
（角度精确到1° )：
(1) 已知 a = 4， b =8；
解: 在Rt△ABC中, 由勾股定理得c＝ 42 82
北师大版八年级数学下册《直角三角形》三角形的证明PPT(第1课时)
获取新知
知识点二：直角三角形的边的关系
B
勾股定理 直角三角形两条直角边的平方
和等于斜边的平方.
A
C
关于勾股定理的证明，可以欣赏“16页的读一读”， 并可以上网搜索，诸如美国第二十任总统的证法、赵 爽弦图法等
勾股定理反过来，怎么叙述呢？
如果一个三角形两边的平方和等于第三边的平方,那 么这个三角形是直角三角形．
一项指标.现测得AB=4 cm,BC=3 cm,AD=13 cm,CD=12 cm, ∠ABC=90°,根据这些条件,能否得出∠ACD等于90°?请说明理由.
解:能.理由:在Rt△ABC中,
∵AB=4 cm,BC=3 cm,∠ABC=90°,
∴AC=
=5(cm).
在△ACD中,∵AD=13 cm,CD=12 cm,AC=5 cm,
你来给出完整的 证明过程吧，试 一试
例题讲解 例1 如图，在△ABC中，∠C＝70°，∠B＝30°，AD⊥BC 于点D，AE为∠BAC的平分线，求∠DAE的度数． 解：由题意可知， ∠BAC＝180°－∠B－∠C＝80°. ∵AE为∠BAC的平分线， ∴∠CAE＝∠BAE＝ ∠BAC＝40°. ∵AD⊥BC，∴∠ADC＝90°. ∴∠CAD＝90°－∠C＝90°－70°＝20°. ∴∠DAE＝∠CAE－∠CAD＝40°－20°＝20°.
原命题都存在逆命题 ，
但是互逆命题的真假 无法保证
如果一个定理的逆命题也是定理，那么这两个定理叫 做互逆定理，其中的一个定理叫做另一个定理的逆定理.
注意1：逆命题、互逆命题不一定是真命题， 但逆定理、互逆定理，一定是真命题.
注意2：不是所有的定理都有逆定理.
定理
“两直线平行，内错角相等”
北师大版九年级下册数学《30°、45°、60°角的三角函数值》直角三角形的边角关系说课教学课件复习
2
45°
2
2
60°
3
2
cosα tanα
3
3
2
3
2
1
2
1 2
3
想一想:
如果已知某一锐角的某种三 角函数值,你能求出这一锐 角吗?比如tanA＝1,锐角A 是多少度?
例题示范
[例1]计算： (1)sin30°+cos45°；
(2)sin260°+cos260°.
(3) 2 sin 600 3 cos 450
例题示范 例题2
(1)
3cos 600 5sin 300
1
(2)2sin30°＋cos230°－tan45°.
33 tan2 300 3 sin 600 2 cos2 450.
知识巩固
(1) sin 30 cos2 45
(2)2cos2 45 sin 300 1
知识巩固
3 2 sin 450 sin 600 2 cos 450.
tan30°=
CD CD AD a
则CD=a·tan30° 你能求出30°角的三个三角函数值吗?
探索30°角的三角函数值
①观察一副三角尺，其中有几个锐角?它们分别等于
多少度? 300
② sin30°等于多少呢?你是怎样得到
的?与同伴交流.
450
③cos30°等于多少?tan30°呢?
450 ┌ 600 ┌
2．我们求出了30°角的三个三角函数值，还有 两个特殊角——45°、60°，它们的三角函数 值分别是多少?你是如何得到的?
三角函数
锐角α
正弦sinα
300
1
2
450
2
2
北师大版七年级下册数学《认识三角形》三角形教学说课复习课件
议一议
C
A
B
在A点的小狗，为了尽快吃到B点的香肠，它选
择A—B路线，而不选择A—C—B路线，难道小狗也懂
数学？
任意两边之和大于第三边。
A
c
b
你知道 为什么
吗？
B
a
两点之间线段最短！
C
任意两边之差小于第三边。
A
a
b
Bc
C
任意两边之和大于第三边。
任意两边之差小于第三边。
A
a
b
Bc
C
第三边大于两边之差,小于两边之和。
课后作业
习题4.2 第2、3题
北师版 七年级 下册
第四章 三角形
1 认识三角形（第1课时）
课件
情景导入
讲授新课
探究点一 三角形的概念、表示方法及分类
1、三角形的定义： 由不在同一直线上的三条线段首尾顺次相接所组
成的图形叫做三角形。
注意：1、不在同一直线上； 2、首尾顺次相接。 2、三角形的表示：
三角形用符号“△”表示，如右图的三角形，记 A
三角形三边关系
三角形任意两边之和大于第三边 三角形任意两边之差小于第三边
议一议
A B
(1) 元宵节的晚上，房梁上亮起了彩 灯，装有黄色彩灯的电线与装有红色 彩灯的电线哪根长呢？说明你的理由。
利用你发现的规律填空
AB+AC
BC
c
AB+BC
AC
AC+BC
AB
(2)在一个三角形中,任意两边之和与第三边的长度有怎样 的关系?
等腰三角形
在等腰三角形中，两条相等的边叫腰，另一边叫底边。
在等腰三角形中，腰与底边的夹角叫
北师大版八年级数学下册第一章《直角三角形》精品课件
w斜边及一个锐角对应相等的两个直角三角形全等;真
w两直角边对应相等的两个直角三角形全等; 真
w一条直角边和另一条直角边上的中线对应相等的
两个直角三角形全等. 真
A
E
C
D
BG
H
F
2、如图，两根长度为12m的绳子，一端系 在旗杆上，另一端分别固定在地面的两个木 桩上，两个木桩离旗杆底部的距离相等吗？ 说明理由。 解：相等。
用HL可证Rt△ACD≌Rt△AED； 证明Rt△ACD≌Rt△AED
（3）不能
•
你们得到的三角形全等吗？你能得到什么样的结论呢？
斜边和一条直角边对应相等的两个直角三角形全等 简述为：“斜边、直角边”或“HL”
你能证明它吗？
合作探究
w已知:如图,在△ABC和△A′B′C′中, ∠C=∠C′=900
BC=B′C ′, AB=A′B′
w求证:△ABC≌△A′B′C′.
B
B′
C
A C′
测试评价 l1、已知：如图，D是△ABC的BC边的中点，
DE⊥AC，DF⊥AB，垂足分别是E.F，且DE=DF， 求证：△ABC是等腰三角形
l证明：∵ D是△ABC的BC边的中点
l∴BD=CD
l∵ DE⊥AC，DF⊥AB
l∴∠1=∠2=90° l∵BD=CD,DE=DF
1
2
l∴Rt△BDF≌Rt△CDE (HL)
A′
已知：在Rt△ABC和Rt△A′B′C′中，∠C=∠C′=90°，
AB=A′B′B′
C
A C′
A′
证明： ∵在Rt△ABC中，AC2=AB2－BC2(勾股定理)． 又∵在Rt△ A' B' C'中，A' C' 2=A'B'2－B'C'2 (勾股定理) ∵ AB=A'B'，BC=B'C'，∴AC=A'C'． ∴Rt△ABC≌Rt△A'B'C' (SSS)．
北师大版九年级下册数学《三角函数的应用》直角三角形的边角关系教学说课复习课件
你认为货轮继续向东航行途中会有触礁的危险吗？你是怎 样想的？与同伴进行交流.
问题1：货轮要向正东方向继续行驶，有 没有触礁的危险，由谁来决定？
北
A
东
B
CD
分析：根据题意，小岛四周10 n mile内有暗礁，那么货轮
继续向东航行的方向如果到A的最短距离大于10 n mile，则无触
礁的危险；如果小于或者等于10 n mile，则有触礁的危险. A到
当堂练习
解析：如图，过点A作AD⊥OB于D．
在Rt△AOD中，∵∠ADO=90°，∠AOD=30°，OA=4km，
∴AD=
1 2
OA=2km．
在Rt△ABD中，∵∠ADB=90°，∠B=∠CAB－∠AOB
=75°－30°=45°，
∴BD=AD=2km，
∴AB= 2AD= 2 2 km．
即该船航行的距离为2 2 km．
160 3 277.1
C
答：这栋楼高约为277.1m.
讲授新课
练一练
建筑物BC上有一旗杆AB，由距BC40m的D处观察旗杆顶部
A的仰角为54°，观察底部B的仰角为45°，
A
B
求旗杆的高度（精确到0.1m）.
解：在等腰三角形BCD中∠ACD=90°，
BC=DC=40m.
在Rt△ACD中， tan
∴BC = AB = 1000 = 1000 3 (m).
tan C tan 30
解此类问题，首先要找到合适的直角三角形，然后根据已知 条件解直角三角形．
练习2：如图，一架飞机从A地飞往B地，两地相距600km.飞
行员为了避开某一区域的雷雨云层，从机场起飞以后，就沿
与原来的飞行方向成30°角的方向飞行，飞行到中途，再沿
问题1：货轮要向正东方向继续行驶，有 没有触礁的危险，由谁来决定？
北
A
东
B
CD
分析：根据题意，小岛四周10 n mile内有暗礁，那么货轮
继续向东航行的方向如果到A的最短距离大于10 n mile，则无触
礁的危险；如果小于或者等于10 n mile，则有触礁的危险. A到
当堂练习
解析：如图，过点A作AD⊥OB于D．
在Rt△AOD中，∵∠ADO=90°，∠AOD=30°，OA=4km，
∴AD=
1 2
OA=2km．
在Rt△ABD中，∵∠ADB=90°，∠B=∠CAB－∠AOB
=75°－30°=45°，
∴BD=AD=2km，
∴AB= 2AD= 2 2 km．
即该船航行的距离为2 2 km．
160 3 277.1
C
答：这栋楼高约为277.1m.
讲授新课
练一练
建筑物BC上有一旗杆AB，由距BC40m的D处观察旗杆顶部
A的仰角为54°，观察底部B的仰角为45°，
A
B
求旗杆的高度（精确到0.1m）.
解：在等腰三角形BCD中∠ACD=90°，
BC=DC=40m.
在Rt△ACD中， tan
∴BC = AB = 1000 = 1000 3 (m).
tan C tan 30
解此类问题，首先要找到合适的直角三角形，然后根据已知 条件解直角三角形．
练习2：如图，一架飞机从A地飞往B地，两地相距600km.飞
行员为了避开某一区域的雷雨云层，从机场起飞以后，就沿
与原来的飞行方向成30°角的方向飞行，飞行到中途，再沿
北师大版九年级下册数学《利用三角函数测高》直角三角形的边角关系说课教学课件
• 如图，要测量物体MN的高度，可按下列步骤进行：
M
1、在测点A处安置测倾器，测
得此时M的仰角∠MCE=α；
2、在测点A与物体之间B处安置
测倾器，测得此时M的仰角
∠MDE=β；
C
α
D
A
B
ME
ME
b, MN ME a
tan tan
β
E
N
3、量出测倾器的高度
AC=BD=a，以及测点A,B之间
CH
∴AB＝DH＝1.5，BD＝AH＝6，在 Rt△ACH 中，tan∠CAH＝
，∴CH＝AH·
tan∠CAH＝
AH
6tan30°＝6×
3
＝2 3(米)，∵DH＝1.5，∴CD＝2 3＋1.5，在 Rt△CDE 中，∵∠CED＝60°，
3
2 3＋1.5
CD
CD
sin∠CED＝
，∴CE＝
＝
＝(4＋ 3)≈5.7(米)，答：拉线 CE 的长约为 5.7
本课小结
(1)侧倾器的使用
(2)误差的解决办法---用平均值
（3）到目前为止，你有那些测量物体高度的方法？
测量底部可以到达的
物体的高度，如左图
测量底部不可以直接到达
的物体的高度，如右图
随堂检测
1．如图，山顶有一座电视塔，在地面上一点 A 处测得塔顶 B 处的仰角 α＝60°，在塔
底 C 处测得 A 点俯角 β＝45°，已知塔高 60 米，则山高 CD 等于( A )
CN
3
x＋6
的高 EF 为 10.3 m
课堂探究
一、如何测量倾斜角
•测量倾斜角可以用测倾器。
----简单的侧倾器由度盘、铅锤和支杆组成
M
1、在测点A处安置测倾器，测
得此时M的仰角∠MCE=α；
2、在测点A与物体之间B处安置
测倾器，测得此时M的仰角
∠MDE=β；
C
α
D
A
B
ME
ME
b, MN ME a
tan tan
β
E
N
3、量出测倾器的高度
AC=BD=a，以及测点A,B之间
CH
∴AB＝DH＝1.5，BD＝AH＝6，在 Rt△ACH 中，tan∠CAH＝
，∴CH＝AH·
tan∠CAH＝
AH
6tan30°＝6×
3
＝2 3(米)，∵DH＝1.5，∴CD＝2 3＋1.5，在 Rt△CDE 中，∵∠CED＝60°，
3
2 3＋1.5
CD
CD
sin∠CED＝
，∴CE＝
＝
＝(4＋ 3)≈5.7(米)，答：拉线 CE 的长约为 5.7
本课小结
(1)侧倾器的使用
(2)误差的解决办法---用平均值
（3）到目前为止，你有那些测量物体高度的方法？
测量底部可以到达的
物体的高度，如左图
测量底部不可以直接到达
的物体的高度，如右图
随堂检测
1．如图，山顶有一座电视塔，在地面上一点 A 处测得塔顶 B 处的仰角 α＝60°，在塔
底 C 处测得 A 点俯角 β＝45°，已知塔高 60 米，则山高 CD 等于( A )
CN
3
x＋6
的高 EF 为 10.3 m
课堂探究
一、如何测量倾斜角
•测量倾斜角可以用测倾器。
----简单的侧倾器由度盘、铅锤和支杆组成
北师大版九年级数学下册《直角三角形的边角关系——锐角三角函数》教学PPT课件(4篇)
同理， cos
A=
AC ，cos AB
A1
=
A1C A1 B1
.
B1 B
∵AB=A1B1，
AC AB
>
A1C ，即cos A1 B1
A > cos
A1，
A A1
C
∴梯子的倾斜程度与cos A也有关系， cos A的值越 小，梯子越陡.
如图：在Rt △ABC中，∠C＝90°，
sin
A
A的对边 斜边
B1 B2 B3
A
C3 C2
C1
Rt△AB1C1∽Rt△AB2C2
新课学习
直角三角形的边与角的关系：
（2）BA1CC11
和B2C2
AC2
有什么关系？
B1
B2 B3
A
C3 C2
C1
B1C1 = B2C2 AC1 AC2
新课学习
直角三角形的边与角的关系： （3）如果改变B2在梯子上的位置（如B3）呢？
B2
斜边的比值、邻边与斜边的比值将怎
样变化？
C1 C2
A1
这是一个变化的过程.对边与斜边的比值、邻边与
斜边的比值都随着倾斜角的改变而改变.同时，如果给
定一个倾斜角的值，它的对边与斜边的比值、邻边与
斜边的比值是唯一确定的.
讲授新课
斜边
B ∠A的对边
A
C
∠A的邻边
定义：在Rt△ABC中，如果锐角A确定，那
∴ B1C1∥ B2C2，
C1 C2
A1
∴Rt△B1A1C1 ∽ Rt△B2A1C2.
讲授新课
想一想：如图.
（2）BA11CA11 和
A1C2 B2 A1
北师大版九年级下册数学《30°、45°、60°角的三角函数值》直角三角形的边角关系4精品PPT教学课
第一章 直角三角形的边角关系 30°,45°,60°角的三角函数值
2020/11/24
1
复习
在Rt△ABC中,如果锐角A确定,那么∠A
的对边与斜边的比、邻边与斜边比、
对边与邻边的比也随之确定,分别叫做
∠A的正弦、余弦、正切.
sinA＝ac cosA＝bc
A
B
c
a
b ┌C
tanA＝ba
2020/11/24
2020/11/24
16
感谢你的阅览
Thank you for reading
温馨提示：本文内容皆为可修改式文档，下载后，可根据读者的需求 作修改、删除以及打印，感谢各位小主的阅览和下载
日期：
演讲者：蒝味的薇笑巨蟹
2020/11/24
17
2a
60°
a
a
sin30°＝
B A
BC＝2aa＝21A
30°
3a ┌ C
cos30°＝
AABC＝ 23aa＝
3 2
tan30°＝
AB CC＝
a
3a＝
3 3
2020/1ቤተ መጻሕፍቲ ባይዱ/24
7
做一做
• ⑴60°角的三角函数值分别是多少? 你是怎样得到的?
• ⑵45°角的三角函数值分别是多少? 你是怎样得到的?
• ⑶完成下表:
2020/11/24
8
sin60°＝
B A
BC＝
3a 2a
＝
3 2
AC a 1
cos60°＝ AB＝2a ＝2 A
tan60°＝
B A
C
C＝
a3a＝
3
B
30°
2
2020/11/24
1
复习
在Rt△ABC中,如果锐角A确定,那么∠A
的对边与斜边的比、邻边与斜边比、
对边与邻边的比也随之确定,分别叫做
∠A的正弦、余弦、正切.
sinA＝ac cosA＝bc
A
B
c
a
b ┌C
tanA＝ba
2020/11/24
2020/11/24
16
感谢你的阅览
Thank you for reading
温馨提示：本文内容皆为可修改式文档，下载后，可根据读者的需求 作修改、删除以及打印，感谢各位小主的阅览和下载
日期：
演讲者：蒝味的薇笑巨蟹
2020/11/24
17
2a
60°
a
a
sin30°＝
B A
BC＝2aa＝21A
30°
3a ┌ C
cos30°＝
AABC＝ 23aa＝
3 2
tan30°＝
AB CC＝
a
3a＝
3 3
2020/1ቤተ መጻሕፍቲ ባይዱ/24
7
做一做
• ⑴60°角的三角函数值分别是多少? 你是怎样得到的?
• ⑵45°角的三角函数值分别是多少? 你是怎样得到的?
• ⑶完成下表:
2020/11/24
8
sin60°＝
B A
BC＝
3a 2a
＝
3 2
AC a 1
cos60°＝ AB＝2a ＝2 A
tan60°＝
B A
C
C＝
a3a＝
3
B
30°
2
4-1 认识三角形(第三课时)-2022-2023学年七年级数学下册同步精品课件(北师大版)
三角形高的特点：
1）一端是顶点
2）与底边垂直
3）是一条线段
A
画锐角三角形三边的高?
F
1）这三条高之间有怎样的位置关系？
O
在三角形内相交于一点。
2）剪一个锐角三角形，你能通过其他
B
方法做出三角形的高吗？
对折。作法：使折痕过顶点，且所过顶点的对边边缘重合
E
C
D
A
在纸上画出一个直角三角形.
1)你能画出这个三角形的三条高吗?
三角形的分类：
1）按 角 分：分为 锐角 三角形、 钝角 三角形、 直角 三角形。
2）按 边 分：分为 三边都不相等 三角形、 等腰 三角形。
注意：等边三角形是特殊的等腰三角形。
三角形三边之间的关系：
大于 第三边，
1）两边之和
2）两边之差
小于
第三边 。
学习目标
1）通过画图与观察的实践过程，认识三角形的中线、角平分线、高。
）
①BG是△EBF的高；②CD是△BGC的高；③DG是△AGC的高；④AD是△ABG的高．
A．1个
B．2个
C．3个
D．4个
【详解】
解：∵BD是△ABC的高，
∴BD⊥AC，
∴∠BDC=∠BDA=90º，
∴DG是△AGC的高，CD是△BGC的高，AD是△ABG的高；
∵EF∥AC，
∴BG⊥EF，
∴BG是△EBF的高，
试求：（3）△ACE和△ABE的周长的差；
（3）∵AE为BC边上的中线，
∴BE=CE，
∴△ACE的周长-△ABE的周长=AC+AE+CE-（AB+BE+AE）
=AC-AB=8-6=2（cm），
1）一端是顶点
2）与底边垂直
3）是一条线段
A
画锐角三角形三边的高?
F
1）这三条高之间有怎样的位置关系？
O
在三角形内相交于一点。
2）剪一个锐角三角形，你能通过其他
B
方法做出三角形的高吗？
对折。作法：使折痕过顶点，且所过顶点的对边边缘重合
E
C
D
A
在纸上画出一个直角三角形.
1)你能画出这个三角形的三条高吗?
三角形的分类：
1）按 角 分：分为 锐角 三角形、 钝角 三角形、 直角 三角形。
2）按 边 分：分为 三边都不相等 三角形、 等腰 三角形。
注意：等边三角形是特殊的等腰三角形。
三角形三边之间的关系：
大于 第三边，
1）两边之和
2）两边之差
小于
第三边 。
学习目标
1）通过画图与观察的实践过程，认识三角形的中线、角平分线、高。
）
①BG是△EBF的高；②CD是△BGC的高；③DG是△AGC的高；④AD是△ABG的高．
A．1个
B．2个
C．3个
D．4个
【详解】
解：∵BD是△ABC的高，
∴BD⊥AC，
∴∠BDC=∠BDA=90º，
∴DG是△AGC的高，CD是△BGC的高，AD是△ABG的高；
∵EF∥AC，
∴BG⊥EF，
∴BG是△EBF的高，
试求：（3）△ACE和△ABE的周长的差；
（3）∵AE为BC边上的中线，
∴BE=CE，
∴△ACE的周长-△ABE的周长=AC+AE+CE-（AB+BE+AE）
=AC-AB=8-6=2（cm），
初中数学《直角三角形》优秀课件北师大版3
❖
7.阅历之所以会对读书所得产生深浅 有别的 影响， 原因在 于阅读 并非是 对作品 的简单 再现， 而是一 个积极 主动的 再创造 过程， 人生的 经历与 生活的 经验都 会参与 进来。
❖
8.少年时阅历不够丰富，洞察力、理 解力有 所欠缺 ，所以 在读书 时往往 容易只 看其中 一点或 几点， 对书中 蕴含的 丰富意 义难以 全面把 握。
∠A,∠B,∠C的对边.∠B=45°a=6cm ，解这个直
角三角形
A
B 45°
C
随堂检测 收获喜悦
检测二：在Rt△ABC中,∠C=90°,a,b,c分别
∠A,∠B,∠C的对边. sinB=0.5，c=6. 解这
个直角三角形.
Ｂ
C=6 a
Ａ
bＣ
分层作业，巩固所学：
1、课本习题1.5 A组 ：1、2题 B、C组：1、2选一、3题
❖
2.它由一系列展示人物性格,反映人物 与人物 、人物 与环境 之间相 互关系 的具体 事件构 成。
❖
3.把握好故事情节,是欣赏小说的基础,也是整 体感知 小说的 起点。 命题者 在为小 说命题 时,也必 定以情 节为出 发点,从整体 上设置 理解小 说内容 的试题 。通常 从情节 梳理、 情节作 用两方 面设题 考查。
❖
4.根据结构来梳理。按照情节的开端 、发展 、高潮 和结局 来划分 文章层 次,进而 梳理情 节。
❖
5.根据场景来梳理。一般一个场景可 以梳理 为一个 情节。 小说中 的场景 就是不 同时间 人物活 动的场 所。
❖
6.根据线索来梳理。抓住线索是把握 小说故 事发展 的关键 。线索 有单线 和双线 两种。 双线一 般分明 线和暗 线。高 考考查 的小说 往往较 简单,线 索也一 般是单 线式。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
6. 如图，在△ ABC 中，∠ACB=90°，D 为 AB 边上的一点，∠BCD=∠A=30°，BC=4 cm， 求 AD 的长.
解：∵在△ABC 中, ∠ACB＝90°， ∠A＝30°，BC＝4 cm， ∴AB＝2BC＝8（cm），∠B＝60°.
∵∠BCD＝∠A＝30°， ∴∠B+∠BCD＝60°+30°＝90°. ∴∠CDB＝90°. ∴BD＝12BC＝2（cm）. ∴AD＝AB-BD＝8-2＝6（cm）．
的长为 4
.
12. 如图，在△ ABC 中，∠ACB=90°，BC 的垂
直平分线交 AB 于点 D，垂足为 E，当 AB=10，
∠B=30°时，△ ACD 的周长是 15
.
二级能力提升练
13. 如图，在△ ABC 中，∠C=90°，∠B=30°，AD
平分∠CAB，交 BC 于点 D，若 CD=1，求
（2）如图，过 C 作 CP⊥AB 交 AN 于 P，则线段 CP 即为小船与灯塔 C 的最短距离. ∵∠NBC＝60°，∠BPC＝90°， ∴∠PCB＝30°. ∴PB＝1BC＝15（海里）.
2
∴15÷15＝1（时）.∴10+1=11（时） ∴上午 11 时小船与灯塔 C 的距离最短.
谢谢！
●
●
7.阅历之所以会对读书所得产生深浅 有别的 影响， 原因在 于阅读 并非是 对作品 的简单 再现， 而是一 个积极 主动的 再创造 过程， 人生的 经历与 生活的 经验都 会参与 进来。
●
8.少年时阅历不够丰富，洞察力、理 解力有 所欠缺 ，所以 在读书 时往往 容易只 看其中 一点或 几点， 对书中 蕴含的 丰富意 义难以 全面把 握。
●
4.根据结构来梳理。按照情节的开端 、发展 、高潮 和结局 来划分 文章层 次,进而 梳理情 节。
●
5.根据场景来梳理。一般一个场景可 以梳理 为一个 情节。 小说中 的场景 就是不 同时间 人物活 动的场 所。
●
6.根据线索来梳理。抓住线索是把握 小说故 事发展 的关键 。线索 有单线 和双线 两种。 双线一 般分明 线和暗 线。高 考考查 的小说 往往较 简单,线 索也一 般是单 线式。
16. 上午 8 时，一条船从海岛 A 出发，以 15 海 里/时的速度向正北方向航行，上午 10 时到 达海岛 B 处，从 A，B 望灯塔 C，测得∠NAC =30°，∠NBC=60°.
（1）求从海岛 B 到灯塔 C 的距离； （2）这条船继续向正北方向航行，
问在上午或下午的什么时间小船 与灯塔 C 的距离最短？
第十三章 轴对称
第11课 有一个角为30°的直角三角形
新课学习
知识点.含30°角的直角三角形的性质
1. 在直角三角形中，如果一个锐角等于 30°，
那么它所对的直角边等于斜边的 一半 .
几何语言：
∵ AC⊥BC，∠A＝30° ，
∴
BC=1AB
2
.
2. 已知在 Rt△ ABC 中，∠B=90°，
（1）∠A=30°，BC=3，AC= 6
4. 如图，在△ ABC 中，∠C=90°，∠B=30°，AD 平分∠CAB，交 BC 于点 D.若 CD=6，求 BD 的长.
解：∵∠C＝90°，∠B＝30°， ∴∠CAB＝60°. ∵AD平分∠CAB， ∴∠CAD=∠BAD＝30°=∠B. ∴BD＝AD＝2CD＝12.
5. （例 2）如图，在△ ABC 中，∠ACB=90°，
15. 如图，在△ ABC 中，AD⊥BC 于点 D，BE
⊥AC 于点 E，AD 与 BE 相交于点 F，且
AF=DF，∠EAD=30°，求证：BF=4EF.
证明：∵BE⊥AC于点E，∴∠AEF＝90°. ∵∠EAD＝30°，∴AF＝2EF，∠AFE=60°. ∵AF＝DF，∴DF＝2EF. ∵AD⊥BC于点D，∴∠BDF＝90°. ∵∠AFE＝∠BFD=60°， ∴∠FBD＝30°. ∴BF＝2FD＝4EF.
重难易错 7. （例 3）如图，在 Rt△ ABC 中，∠C=90°，
∠B=15°，DE 垂直平分 AB 交 BC 于点 E， BE=4，求 AC 的长. 解:∵DE 垂直平分 AB， ∴AE＝BE＝4. ∴∠BAE＝∠B＝15°. ∴∠AEC＝∠BAE+∠B＝15°+15°＝30°. ∵∠C＝90°，∴AC＝12AE＝12×4＝2．
BD 的长.
解：在△ABC中，∠C＝90°，∠B＝30°， ∴∠BAC＝60°. ∵AD平分∠CAB， ∴∠DAC＝∠DAB=30°. ∵CD＝1，∴AD＝2， ∵∠DAB=∠B，∴BD =AD=2．
14. 如图，在△ ABC 中，∠C=90°，AC=BC，点
D 在 BC 上，且∠BAD=15°.
●
9.自信让我们充满激情。有了自信， 我们才 能怀着 坚定的 信心和 希望， 开始伟 大而光 荣的事 业。自 信的人 有勇气 交往与 表达， 有信心 尝试与 坚持， 能够展 现优势 与才华 ，激发 潜能与 活力， 获得更 多的实 践机会 与创造 可能。
感谢观看，欢迎指导！
；
（2）∠C=60°，AC=8，BC= 4
.
3.（例 1）如图，在△ ABC 中，AB=AC，∠C=30°，
AB⊥AD，AD=4 cm，求 BC 的长.
解：∵AB＝AC，∠C＝30°， ∴∠B＝30°. ∵AB⊥AD，AD＝4 cm， ∴BD＝8 cm. ∵∠ADB＝90°-∠B=60°，∠C＝30°, ∴∠DAC＝∠C＝30°. ∴CD＝AD＝4 cm. ∴BC＝BD+CD＝8+4＝12（cm）．
1.情节是叙事性文学作品内容构成的 要素之 一,是叙 事作品 中表现 人物之 间相互 关系的 一系列 生活事 件的发 展过程 。
●
2.它由一系列展示人物性格,反映人物 与人物 、人物 与环境 之间相 互关系 的具体 事件构 成。
●
3.把握好故事情节,是欣赏小说的基础,也是整 体感知 小说的 起点。 命题者 在为小 说命题 时,也必 定以情 节为出 发点,从整体 上设置 理解小 说内容 的试题 。通常 从情节 梳理、 情节作 用两方 面设题 考查。
.
10. 如图，在△ ABC 中，AB=AC，∠BAC=120°， AD⊥AC 交 BC 于点 D，AD=3，则 BC= 9 .
11. 如图，在△ ABC 中，AB=AC=8，∠BAC=120°，
AD 是△ ABC 的中线，AE 是∠BAD 的角平分
线，DF∥AB 交 AE 的延长线于点 F，则 DF
8. 如图，在△ ABC 中，AB=AC，∠BAC=120°， AB 的垂直平分线 DE 交 BC 于点 D，垂足为 点 E. （1）求∠BAD 的度数； （2）若 BD=2，试求 CD 的长度.
解：（1）∵AB＝AC，∠BAC＝120°， ∴∠B＝∠C＝30°. ∵DE是AB的垂直平分线， ∴∠BAD＝∠B＝30°.
（1）求从海岛 B 到灯塔 C 的距离；
解：（1）∵∠NBC＝60，∠NAC＝30°, ∴∠ACB＝30°. ∴AB＝BC. ∵AB＝15×（10-8）＝30（海里）， ∴AB=BC=30 海里. ∴从海岛 B 到灯塔 C 的距离为 30 海里.
（2）这条船继续向正北方向航行，问在上午或 下午的什么时间小船与灯塔 C 的距离最短？
（2）若 BD=2，试求 CD 的长度.
（2）∵DE是AB的垂直平分线， ∴AD=BD=2. ∵∠BAC＝120°，∠BAD＝30°， ∴∠CAD＝90°. 又∠C＝30°， ∴CD＝2AD＝4．
三级检测练
一级基础巩固练
9. 如图，在△ ABC 中，∠B=90°，∠A=30°，
AC=5，则 BC= 2.5
过点 C 作 CD⊥AB 于 D，∠A=30°，BD=1，
求 AB 的长.
解：在△ABC中，∠ACB＝90°，∠A＝30°， ∴∠B＝60°. ∵CD⊥AB，∴∠BCD＝30°. 在Rt△BCD中，∠BCD＝30°，BD＝1， ∴BC＝2BD＝2. 在Rt△ABC中，∠A＝30°，BC＝2， ∴AB＝2BC＝4．
（1）求∠CABC中，∠C＝90°，AC＝BC， ∴∠CAB＝∠CBA＝45°. 又∠BAD＝15°，∠CAD+∠BAD＝∠CAB， ∴∠CAD＝30°. （2）在Rt△ACD中，CD＝2，∠CAD＝30°， 则AD＝2CD＝4.
三级拓展延伸练