空间思维训练 数一数立体积木20张 学前教育早教幼教(高清可编辑打印)
乐高数学一起搭
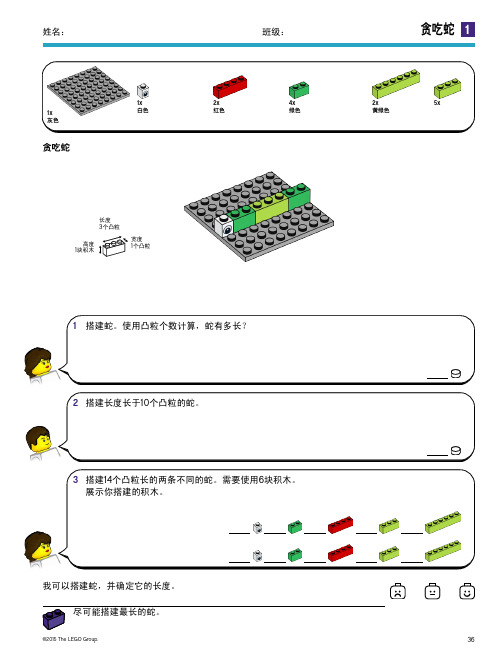
我可以搭建蛇,并确定它的长度。
贪吃蛇1x灰色1x2x红色4x2x5x 1块积木长度3个凸粒宽度1个凸粒我们聆听每位同学的解释。
母鸡鸡蛋2x 灰色1x6x 2x 4x 1x 2x 20x4x 1x在向老师寻求帮助之前,我们可以互相帮助。
2x 灰色1x6x 2x 4x 1x 2x 20x4x 1x母鸡鸡蛋我们可以解决加法问题。
2x 灰色1x 紫色1x6x 3x 4x 1x 3x 20x4x 母鸡鸡蛋通过将较小数相加得到较大数。
组数2x 灰色1x 1x 1x 1x4x 5x 绿色4x 红色10x贪吃蛇1 + 1 + 1 =我可以搭建不同长度和形状的蛇。
贪吃蛇1x灰色1x5x5x2x5x我可以确定长、宽和高。
2x 灰色2x 2x 黄绿色4x 3x4x 5x3x 5x绿色毛毛虫1块积木长度 3个凸粒宽度 1个凸粒我可以使用柱状图显示每种积木我使用了多少块。
2x 灰色2x 4x 红色4x 5x 绿色10x 10x 10x 柱状图蝴蝶我可以搭建蝴蝶翅膀图案。
蝴蝶2x 灰色2x 8x 5x 4x 10x 8x8x 紫色ABC D我们可以来进行平均分。
6x以下食物分为两等份。
每一份能分到多少?轮流搭建并解释。
4x 2x 2x10x 2x 2x 2x4x 1x 4x每天所需食物A A天天D D天母狮子公狮子=====我们可以搭建各种形状,并将其拼得更长,更宽和更高。
2x 灰色6x 6x 6x8x 8x 2x岩石灌木草原A B C草原和岩石灌木高 1块积木长3个凸粒宽1个凸粒AB我们可以将图形分为两等份。
2x 灰色12x 6x 4x12x 6x12x 6x 4x岩石水灌木草原草原和水岩石和灌木高 1块积木长3个凸粒宽1个凸粒=====我可以搭建并将十位和十位、个位和个位进行相加。
花朵2x灰色2x10x红色15x2x橙色2x绿色15x10x花束花朵BA=我可以搭建花束和单朵花来表示准确的数位。
A B C D花束花朵2x 灰色2x 10x 红色10x2x 橙色2x 绿色10x 10x花朵=我可以使用花束和单朵花计算加减法。
《搭积木》(教案)2023-2024学年数学一年级上册

教案:《搭积木》2023-2024学年数学一年级上册一、教学目标1. 让学生通过观察、操作、比较,认识立体图形和平面图形,能够正确地识别和命名。
2. 培养学生的空间观念和观察能力,提高学生的动手操作能力和创新能力。
3. 培养学生合作交流的意识,让学生在合作中学会倾听、表达和交流。
二、教学内容1. 认识立体图形:长方体、正方体、圆柱、球。
2. 认识平面图形:长方形、正方形、圆、三角形。
3. 搭建简单的立体图形和平面图形。
三、教学重点与难点1. 教学重点:认识立体图形和平面图形,能够正确地识别和命名。
2. 教学难点:搭建简单的立体图形和平面图形,培养学生的空间观念和观察能力。
四、教具与学具准备1. 教具:多媒体课件、实物模型、图片等。
2. 学具:积木、彩纸、剪刀、胶水等。
五、教学过程1. 导入:利用多媒体课件展示一些生活中的立体图形和平面图形,引导学生观察和讨论,激发学生的学习兴趣。
2. 新课:讲解立体图形和平面图形的定义、特征和命名,展示实物模型和图片,让学生直观地认识和理解。
3. 操练:让学生分组合作,利用积木搭建简单的立体图形和平面图形,培养学生的动手操作能力和合作交流意识。
4. 应用:布置一些练习题,让学生独立完成,巩固所学知识,提高学生的解决问题的能力。
5. 总结:对所学知识进行总结和归纳,强调重点和难点,让学生明确学习目标。
六、板书设计1. 《搭积木》2. 目录:教学目标、教学内容、教学重点与难点、教具与学具准备、教学过程、板书设计、作业设计、课后反思3. 正文:根据教学过程进行板书设计,突出重点和难点,简洁明了。
七、作业设计1. 填空题:让学生填写一些立体图形和平面图形的名称和特征。
2. 作图题:让学生利用彩纸、剪刀、胶水等材料,制作一些简单的立体图形和平面图形。
3. 应用题:让学生解决一些实际问题,运用所学知识进行计算和推理。
八、课后反思1. 教学内容是否充实,是否符合学生的认知水平。
学前教育 早教幼教 空间思维训练 数一数立体积木20张(高清可编辑打印)

个
个
个
个
个
个
个
个
个
有多少木块?
个
个
个
个
个
个
个
个
个
有多少木块?
个
个
个
个
个
个
个
个
个
有多少木块?
个
个
个
个
个
个
个
个
个
有多少木块?
个
个
个
个
个
个
个
个
个
Hale Waihona Puke 有多少木块?个个
个
个
个
个
个
个
个
有多少木块?
个
个
个
个
个
个
个
个
个
有多少木块?
个
个
个
个
个
个
个
个
个
有多少木块?
个
个
个
个
个
个
个
个
个
有多少木块?
个
个
个
个
个
个
个
个
个
有多少木块?
个
个
个
个
个
个
个
个
个
有多少木块?
个
个
个
个
个
个
个
个
个
有多少木块?
个
个
个
个
个
个
个
个
个
有多少木块?
个
个
个
个
个
个
个
个
个
有多少木块?
二年级 数积木块

总个数: 12+12+12+12=48(个)
拓展练习 第一层有( 第一层有(
3
)个 )个 )个 )个 )个
第二层有( 第二层有( 3 第三层有( 第三层有( 9 第四层有( 4 第四层有( 第五层有(#43;9+4+4=23(个)
把下面的积木块图按上下层分开, 上层和下层各是哪幅图?
方法二:我从前往后数, 可以分为三排。
第一排有(16 )个;第二排有( 16 ( )个。
)个:第三排有 16
16+16+16=48(个)
总个数:
方法三:我从右往左数, 方法三:我从右往左数, 可以分为四列。 可以分为四列。 第一列有(12 12 第三列有( 12 )个;第二列有( 12 )个;第四列有( )个; )个。
同学们, 同学们,有谁知道 这个椅子由几个小正方体 积木拼成的? 积木拼成的?
第三讲
数积木块
数一数,下面的图形中一共有 多少个小方块?
拆解法
方法一:我从上往下数, 分为四层。
12 第一层有(12 )个;第二层有( 个; 12 12 第三层有( )个;第四层有( 48( 12+12+12+12= 48(个) 个。
图中共有线条: 3+2+1=6(条)
探究升级(一)
同学们, 同学们, 今天的知识你掌握了吗? 今天的知识你掌握了吗?
基础演练分析(四)
动手摆一摆, 动手摆一摆,用8个方块,看谁摆得图形多。 个方块,看谁摆得图形多。
( A)
( B)
( C)
( D)
基础演练分析(一)
基础演练分析(二)
基础演练分析(三)
2021幼小衔接数学---立体图形的拼搭与个数(含答案)
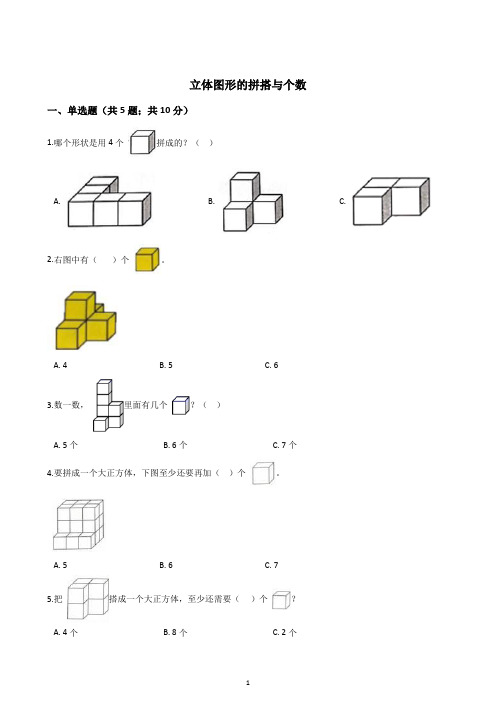
立体图形的拼搭与个数一、单选题(共5题;共10分)1.哪个形状是用4个拼成的?()A. B. C.2.右图中有()个。
A. 4B. 5C. 63.数一数,里面有几个?()A. 5个B. 6个C. 7个4.要拼成一个大正方体,下图至少还要再加()个。
A. 5B. 6C. 75.把搭成一个大正方体,至少还需要()个?A. 4个B. 8个C. 2个二、填空题(共15题;共49分)6.________个________个7.________块________块________块8.数一数,下面每幅图中各由几个小正方体拼成的。
________个________个9.有________个。
有________个。
10.________个________个________个________个11.数一数、填一填。
________个________个________个12.长方体有________个。
正方体有________个。
球有________个。
圆柱有________个。
13.________个________个________个________个14.数一数,下图中各有几个小正方体?________个________个________个15.数一数下列物体各由几个正方体摆成。
________________________________16.要搭成一个大正方体,你知道下面的积木中至少还少几个小方块吗?________个________个________个________个17.数出的个数。
________个________个________个18.数一数,选一选。
(选正确的编号填在括号里)。
个数最多的是________;由6个搭成的是________;和④的个数同样多的是________。
19.机器人。
有________个。
有________个。
有________个。
有________个。
20.数一数,填一填________________________________三、解答题(共9题;共63分)21.最多的画“○”,最少的画“√”。
《数字积木》教案(精选4篇)

《数字积木》教案(精选4篇)《数字积木》教案篇1活动目标:1.感知立体图形在空间的存在形式,正确点数立方体。
2.体验数形关系,有肯定的空间概念。
3.让幼儿在活动中感受到胜利的喜悦。
4.了解多与少的相对性。
5.喜爱数学活动,愿意参加各种操作嬉戏,培育思维的逆反性。
活动预备:多媒体、30个立方体、若干积木、笔、调查表以及操作纸。
活动过程:1.复习几何形体。
老师出示正方体、长方体让幼儿进行辨认,并能说出它们的特征。
(告知幼儿这些图形有一个统一的名字叫“立方体”。
)2.学习数立方体。
1)看图数立方体要求幼儿看清图形,正确点数正方体。
(小伴侣之间进行校对;通过多媒体来进行校对。
)2)幼儿操作活动把幼儿分成三组,用立体图形进行拼搭,要求幼儿说出“我用了几个立体图形拼搭了什么?”3)运用多媒体让幼儿正确点数立方体,学会将隐蔽部分给找出来。
通过此活动来提高小伴侣学习的爱好。
3.延长活动:数高楼运用调查表的形式让幼儿对小区内的高层楼房进行层次的统计,从中了解到我们的楼房也是通过一个个的立体图形而组成的。
教学反思畅想我们可以理解为在美术活动中的想象,既然活动的名字叫“蓝色畅想”,那幼儿的想象是很重要的,在活动中应当重点体现出来,老师为幼儿创设了大海、星空、海底世界三个情境,让幼儿在这三个情境中进行充分的畅想,说出自己的畅想,再将想的东西表现出来,拓展幼儿的思维,进展幼儿的想象力,是我们美术活动的重点。
《数字积木》教案篇2一、教材分析积木是幼儿常见的玩具,幼儿园的`孩子特殊喜爱搭积木,他们搭出的建筑各式各样。
《纲要》中指出,引导幼儿对四周环境中的数、量、形等现象产生爱好,建构初步的数概念,并学习用简洁的数学方法解决生活和嬉戏中的问题。
大班的孩子们已经有肯定的空间概念,因此我设计了《数正方体》这一数学活动,旨在进展幼儿感知立体图形的力量,建立起图形和数量的关系。
二、活动目标:1、学习有序地观看,正确点数正方体的数量,体验数形关系。
学前儿童数学教育课本

第一章学前儿童数学教育的意义及任务第一节学前儿童数学教育的意义一、数学是现代科学技术的基础和工具数学是研究现实世界的空间形式和数量关系的科学。
它产生于生产实践,与人类文明同时开始,又随着生产实践、科学技术的发展而发展,应用极为广泛。
人的全部生活实践(衣、食、住、行)几乎都离不开数学。
最简单的事例,像小朋友有几只手,班上有多少位小朋友等,均要用数量来表示。
数学还广泛地运用于音乐、科学技术、工业生产等各个方面,甚至自然界的一切生物,像花朵、蜗牛等也可用几何图形的组合予以表示。
所以伽利略曾说过:“数学是上帝用来书写宇宙的文字”。
人们还赞誉数学“是打开未来世界大门的钥匙”。
近几十年来,随着现代科学技术的发展,特别是信息论、控制论、电子计算机的产生和广泛应用,促使数学日益渗透到各学科领域中去,促进了各学科的改造和发展。
像生物数学的形成,它涉及到数量遗传学、数量生态学、数量分子生物学、数量分类学等。
反之,生物的“数学化”也为数学的发展提供了肥沃的土壤,像生物统计学、生物概率论、生物运筹学、生物信息论、生物控制论等新学科也相继产生.社会科学也不例外,数学现在已被广泛地运用于经济学、语言学、史学、心理学、教育学和管理、通讯等各个领域中,从而提高了这些学科的科学性程度。
二、数学是普通教育中的一门重要基础课程,是每个人应具备的文化素养之一由于数学在自然及社会科学中的地位和作用,因而数学历来是小学和中学的一门主要基础课程,也是一门工具课程。
数学是学生学习其它文化科学知识,从事各种实践活动的必要基础知识和工具。
从近二三十年世界范围的教育改革动态,也可说明数学教育的重要性。
像本世纪50年代前苏联第一颗人造卫星上天的冲击波震动了全世界以后,欧美国家纷纷探讨、争论他们国家为什么落后了,找到的原因中很重要的一条是在人才培养上,尤其是中小学的数学教育方面比前苏联落后。
例如1981年美国华盛顿邮报曾报导,在过去20年中,日本、德国和前苏联政府的教育计划提高了对数学的要求,而美国的中学和大学的数学课程却降低了。
幼升小学前数学思维训练(共计14讲,含答案解析)

第1讲单数双数在数学上,1、3、5有时候也叫做单数,2、4、6、8、10……叫做偶数,有时候也叫双数。
用数群的概念来解释的话,把东西两个两个地数,最后正好数完,这样的数就是双数,如果两个两个地数,还多1,这样的数就是单数。
在5~7岁这个阶段,孩子已经能够掌握10以内的双数和单数,并能够逐步地利用双数和单数的基本性质解决一些实际的问题,如开灯问题,往来问题等。
如果更深入一点,单双数的掌握,是进制的萌芽,可以启发孩子掌握进制的相关知识,很多利用单双数解决的问题,实际上就是二进制问题。
在遇到单双数问题时,经常用到下面的几个规律:◎ 单数+单数=双数◎ 单数+双数=单数◎ 双数+双数=双数◎ 单数−单数=双数◎ 单数−双数=单数◎ 双数−双数=双数◎ 双数−单数=单数典型例题典型例题 1 有一筐梨,2个2个地拿,最后还剩1个,你知道这筐梨的个数是单数还是双数?解题策略2是双数,也就是说每一次拿的都是双数,由于“双数+双数=双数”,那么拿走的梨的个数是双数,剩下的梨是1,最后是“双数+单数”,所以梨原来的数量是单数。
典型例题 2 晚上,莫妮卡在做作业的时候,停电了,莫妮卡去拉了4下开关,妈妈回来了,妈妈又去拉了5下开关。
如果来电了,灯泡是亮着的还是不亮的?解题策略我们使用表格来解决这个问题:从上面的表格可以看出,莫妮卡拉了4下灯,妈妈拉了5下灯,一共拉了9下灯,来电的时候,灯泡是不亮的。
从上面的题可以看出,灯泡的亮与否,与灯泡的起始状态和拉灯的次数有关系,但次数为双数时,灯泡的状态与起始状态一致,当次数为单数时,灯泡的状态与起始状态相反。
典型例题 3 渡船在河的两岸之间来回地接送乘客,把渡船从河的一岸划到另一岸叫渡一次。
如果原来渡船在河的北岸,渡了7次之后,船在河的北岸还是南岸?解题策略使用习题2总结的规律来解题,船的原始状态在河的北岸,渡了7次,由于7是单数,所以船目前的状态和原始状态相反,船在河的南岸。
