(完整版)样本及抽样分布.doc
抽样分布和七种理论分布

抽样分布与理论分布一、抽样分布总体分布:总体中所有个体关于某个变量的取值所形成的分布。
样本分布:样本中所有个体关于某个变量大的取值所形成的分布。
抽样分布:样品统计量的概率分布,由样本统计量的所有可能取值和相应的概率组成。
即从容量为N 的总体中抽取容量为n 的样本最多可抽取m 个样本,m 个样本统计值形成的频率分布,即为抽样分布。
样本平均数的抽样分布:设变量X 是一个研究总体,具有平均数μ和方差σ2。
那么可以从中抽取样本而得到样本平均数x ,样本平均数是一个随机变量,其概率分布叫做样本平均数的抽样分布。
由样本平均数x 所构成的总体称为样本平均数的抽样总体。
它具有参数μx 和σ2x ,其中μx 为样本平均数抽样总体的平均数,σ2x 为样本平均数抽样总体的方差,σx 为样本平均数的标准差,简称标准误。
统计学上可以证明x 总体的两个参数 μx 和σ2x 与X 总体的两个参数μ和σ2有如下关系:μx = μ σ2x = σ2 /n由中心极限定理可以证明,无论总体是什么分布,如果总体的平均值μ和σ2都存在,当样本足够大时(n>30),样本平均值x 分布总是趋近于N (μ,n2)分布。
但在实际工作中,总体标准差σ往往是未知的,此时可用样本标准差S 估计σ。
于是,以nS估计σx ,记为X S ,称为样本标准误或均数标准误。
样本平均数差数的抽样分布:二、正态分布2.1 正态分布的定义:若连续型随机变量X 的概率密度函数是⎪⎭⎫ ⎝⎛--=σμπσx ex f 22121)( (-∞<x <+∞)则称随机变量X 服从平均数为μ、方差为σ2的正态分布,记作X~N (μ,σ2)。
相应的随机变量X 概率分布函数为 F (x )=⎰∞-x dx x f )(它反映了随机变量X 取值落在区间(-∞,x )的概率。
2.2 标准正态分布当正态分布的参数μ=0,σ2=1时,称随机变量X 服从标准正态分布,记作X~N (0,1)。
第六章 样本及抽样分布1精品PPT课件

二.样本
1.抽样: 从总体中抽取若干个体的过程。
2.样本: 从总体中抽取若干个体, 观察得随机变量的一组试验 数据(观测值), 样本中所含个体的数量称为样本容量。
从总体中抽取样本, 一般假设满足下述条件: (1) 随机性: 使总体中的每一个个体有同等机会被抽取到; (2) 独立性: 每次抽样的结果既不影响其他各次抽样的结果,
1
f
xn
b
1n
0
a xi b 其他
测试题B答案:
一.填空题。
1. 1)满足X1, X2 , … X n独立且同分布
2. 21) 2 n
n
2.
Xi p i1
n
1 p
n Xi
i1
,
E X p,
p 1 p DX
n
3. 5/8
二.计算题。
解: 因为X1, X2 , … X n来自均匀分布总体 N , 2 ,则X1, X2 , …
3. 简单随机样也本不:受由其随他机各的次, 独结立果的的抽影样响方;法得到的样本, 这 种随机的, 独立的抽样方法称为简单随机抽样。
注: 今后凡是提到抽样与样本, 都是简单随机抽样与简单随 机样本。
由于从总体中抽取容量为n的样本, 即是对代表总体的随 机变量X随机的,独立的进行n次试验, 每次试验结果可以看作 一个随机变量, n 次试验结果就是n个随机变量 X1, X2 , … X n , 它们相互独立且与总体X同分布。
则的联合概率密度为 。
二. 计算题。
1. 设X1, X2 , … X n是来自均匀分布总体U (a , b)的样本, 求样本 (X1, X2 , … X n)的联合概率密度。
样本均值的抽样分布(详细资料)
抽样分布根据样本统计量去估计总体参数,必须知道样本统计量分布。
定义6.2 某个样本统计量的抽样分布,从理论上说就是在重复选取容量为n 的样本时,由每一个样本算出的该统计量数值的相对数频数分布或概率分布。
由于现实中我们不可能将所有的样本都抽出来,因此,统计的抽样分布实际上是一种理论分布。
(一)样本均值的抽样分布从单位数为N 的总体中抽取样本容量为n 的随机样本,在重复抽样的条件下共有n N 个可能的样本,在不重复抽样条件下,共有!!()!nNN C n N n =-个可能样本。
对于每一个样本,我们都可以计算出样本的均值2()x s 或或p ,因此,样本均值是一个随机变量。
所有的样本均值形成的分布就是样本均值的抽样分布。
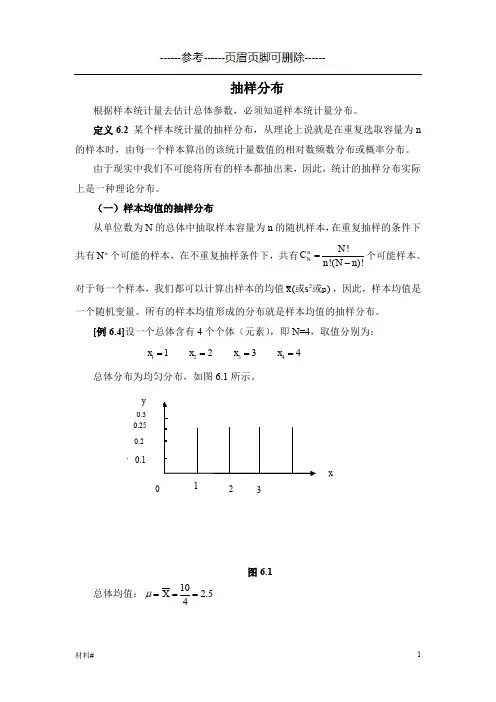
[例6.4]设一个总体含有4个个体(元素),即N=4,取值分别为:12341234x x x x ====总体分布为均匀分布,如图6.1所示。
图6.1总体均值:102.54X μ=== x总体方差:22() 1.25x x nσ-==∑若重复抽样,n=2 则共有2416=个可能样本。
具体列示如表5.1.1。
表6.1 可能的样本及其均值每个样本被抽中的概率相同,均值为116样本均值的抽样分布如表5.1.2和图5.1.2所示。
样本均值x 抽样分布的形状与原有总体的分布有关,如果原有总体是正态分布,样本均值也服从正态分布。
如果总体分布是非正态分布,当x 为大样本(30n ≥)时,样本均值的分布趋于服从正态分布;当x 为小样本时,其分布不是正态分布。
下面再让我们来看看样本均值x 抽样分布的特征:数学期望和方差。
设总体共有N 个元素,其均值为μ,方差为2σ,从中抽取容量为n 的样本。
E()x x X μ=== (6.1)22xnσσ=(重复抽样) (6.2)22()1xN nn N σσ-=-(不重复抽样) (6.3)对于无限总体,样本均值的方差,不重复抽样也可按重复抽样来处理;对于有限总体,当N 很大,而/n N 又很小,修正系数1N nN --会趋于1,不重复抽样也可按重复抽样来处理。
第五讲样本及抽样分布

第五讲 样本及抽样分布一 基本概念总体 含义1:研究对象的全体,例如一批灯泡。
含义2:研究对象的某数量指标(例如灯泡的寿命,随机变量)X 的取值全体,总体的分布是指随机变量X 的分布。
个体 组成总体的某个基本单元,例如一个个的灯泡,也指基本单元的数量指标。
样本 从总体中抽取的n 个个体,n 又称样本容量。
简单随机样本 样本中的n 个个体n X X X ,,,21 相互独立,且与总体同分布的样本,简称样本。
样本n X X X ,,,21 的实验结果n x x x ,,,21 称为样本观测值。
样本空间 样本n X X X ,,,21 的所能可能结果。
统计量 样本的不含任何参数的函数。
二 重要统计量样本均值 ,11∑==n i i X n X (而∑==ni i x n x 11称为样本均值的观测值)样本方差 ∑=-=ni i X X S 1212)( 注:212111,1σμn DX n X D EX n X E n k k n i k ====∑∑== ∑∑==--=--=n i i n i iX X D n X X E n ES 1122)(11)(11 ⎪⎭⎫ ⎝⎛---+---=∑=n X X n n n X D n n i n i 11111 212)1(2)1(211σσσ=⎥⎦⎤⎢⎣⎡+-=∑=--n i n n n n n三、抽样分布统计量的分布:大多数情况下,针对正态分布样本而言,以下不说明均指正态分布。
1、-2x 分布: 如果r.v X 的密度函数为 []12/2/12/)2/(2,0,)(---=>=n c x ecxx f n x n Γ则称X 服从参数为n 的-2x 分布,记作n n x X ),(~2又称自由度,指独立变量的个数。
如果)1,0(..,,,21N d i i X X X n ,则)(~212n x X nk k ∑=。
定理5.1 如果),(..,,,221σμdN i i X X X n ,则 ),(~2nN X σμ与∑=--=-nk k n x X X S n 12222)1(~/)()1(σ独立。
样本及抽样分布

Fn 1
(4) Fn x 在每个观测值 x i 处是右连续的,点 x i F 是 Fn x 的跳跃间断点, n x 在该点的跃度就等于 频率 f i 样本分布函数 Fn x 的图意的实数 x 总体分布函数F x 是事件 X x 的概率;样本分布函数 Fn x 是事件 X x 的频 率。根据伯努利大数定理可知, 当n 时,对于任意的正数 ,有 lim P Fn x F x 1
a, t1 , t1 , t 2 ,
,
ti1 , ti ,
,
tl 1 , b
第 i 个子区间的长度为 t i t i t i 1 i 1,2,, l
各子区间的长度可以相等,也可以不等;若使各 ba 子区间的长度相等,则有 t i
l
子区间的个数一般取为8至15个,太多则由于频率 的随机摆动而使分布显得杂乱,太少则难于显示 分布的特征。 此外,为了方便起见,分点t i 应比样本观测值 x多 i 取一位小数。 3 把所有样本观测值逐个分到各子区间内,并计算 样本观测值落在各子区间内的频数 ni及频率
我们把被研究的对象的全体称为总体(或母体), 而把组成总体的各个元素称为个体。 在上面的例子中,该厂生产的所有显像管的寿命就 是总体,而每一个显像管的寿命就是个体。 代表总体的指标(如显像管的寿命)是一个随机变 量, 所以总体就是指某个随机变量可能取的值的全体。
从总体中抽取一个个体,就是对代表总体的随机变 量进行一次试验(或观测),得到的一个试验数据 (或观测值)。 从总体中抽取一部分个体,就是对随机变量进行若干 次试验(观测)。 从总体中抽取若干个个体的过程称为抽样。 抽样结果得到的一组试验数据(观测值),称为样本 (或子样); 样本中所含个体的数量称为样本容量。
样本均值的抽样分布(详细资料)

抽样分布根据样本统计量去估计总体参数,必须知道样本统计量分布。
定义6.2 某个样本统计量的抽样分布,从理论上说就是在重复选取容量为n 的样本时,由每一个样本算出的该统计量数值的相对数频数分布或概率分布。
由于现实中我们不可能将所有的样本都抽出来,因此,统计的抽样分布实际上是一种理论分布。
(一)样本均值的抽样分布从单位数为N 的总体中抽取样本容量为n 的随机样本,在重复抽样的条件下共有n N 个可能的样本,在不重复抽样条件下,共有!!()!nNN C n N n =-个可能样本。
对于每一个样本,我们都可以计算出样本的均值2()x s 或或p ,因此,样本均值是一个随机变量。
所有的样本均值形成的分布就是样本均值的抽样分布。
[例6.4]设一个总体含有4个个体(元素),即N=4,取值分别为:12341234x x x x ====总体分布为均匀分布,如图6.1所示。
图6.1总体均值:102.54X μ=== x总体方差:22() 1.25x x nσ-==∑若重复抽样,n=2 则共有2416=个可能样本。
具体列示如表5.1.1。
表6.1 可能的样本及其均值每个样本被抽中的概率相同,均值为116样本均值的抽样分布如表5.1.2和图5.1.2所示。
样本均值x 抽样分布的形状与原有总体的分布有关,如果原有总体是正态分布,样本均值也服从正态分布。
如果总体分布是非正态分布,当x 为大样本(30n ≥)时,样本均值的分布趋于服从正态分布;当x 为小样本时,其分布不是正态分布。
下面再让我们来看看样本均值x 抽样分布的特征:数学期望和方差。
设总体共有N 个元素,其均值为μ,方差为2σ,从中抽取容量为n 的样本。
E()x x X μ=== (6.1)22xnσσ=(重复抽样) (6.2)22()1xN nn N σσ-=-(不重复抽样) (6.3)对于无限总体,样本均值的方差,不重复抽样也可按重复抽样来处理;对于有限总体,当N 很大,而/n N 又很小,修正系数1N nN --会趋于1,不重复抽样也可按重复抽样来处理。
四章样本及抽样分布
E(X )
1 n
n i 1
E( X i )
D(X )
1 n2
n
2
D(Xi )
i 1
n
X ~ N(, 2 )
n
X ~ N (0, 1) / n
iid
2.若X1,,X n ~ N (, 2 ), 则 (1) X与S 2相互独立; (2) 2
(n 1)S 2
2
~
2 (n 1);
(3)T X ~ t(n 1).
第四 章 样本及抽样分布
引言 run 随机样本 抽样分布
4.1 随机样本 一、总体与样本
1. 总体:研究对象旳全体。 一般指研究对象旳某项数量指标。 构成总体旳元素称为个体。
从本质上讲,总体就是所研究旳随机变量或 随机变量旳分布。
2. 样本:来自总体旳部分个体X1, … ,Xn 假如满足: (1)同分布性: Xi, i=1,…,n与总体同分布. (2)独立性: X1,… ,Xn 相互独立; 则称为容量为n 旳简朴随
P{ 1
1
P{ 1 F
F (n2 , n1)}
} 1
F F1 (n1, n2 )
P{ 1
1 }
得证!
F F1 (n1, n2 )
4.3 正态总体旳抽样分布定理
iid
1.若X1 ,,Xn ~ N(, 2 ), 则U
X / n
~
N(0, 1)
证明:
X
1 n
n i 1
Xi
是n 个独立旳正态随 机变量旳线性组合,故 服从正态分布
i 1
称为自由度为n的 2 分布.
2.2—分布旳密度函数f(y)曲线
f
(y)
(完整版)样本及抽样分布
第六章样本及抽样分布【基本要求】1、理解总体、个体和样本的概念;2、理解样本均值、样本方差和样本矩的概念并会计算;3、理解统计量的概念,掌握几种常用统计量的分布及其结论;4、理解分位数的概念,会计算几种重要分布的分位数。
【本章重点】样本均值、样本方差和样本矩的计算;抽样分布——2 分布,t分布,F分布;分位数的理解和计算。
【本章难点】对样本、统计量及分位数概念的理解;样本矩的计算。
【学时分配】4学时【授课内容】§6.0 前言前面五章我们研究了概率论的基本内容,从中得知:概率论是研究随机现象统计规律性的一门数学分支。
它是从一个数学模型出发(比如随机变量的分布)去研究它的性质和统计规律性;而我们下面将要研究的数理统计,也是研究大量随机现象的统计规律性,并且是应用十分广泛的一门数学分支。
所不同的是数理统计是以概率论为理论基础,利用观测随机现象所得到的数据来选择、构造数学模型(即研究随机现象)。
其研究方法是归纳法(部分到整体)。
对研究对象的客观规律性做出种种合理性的估计、判断和预测,为决策者和决策行动提供理论依据和建议。
数理统计的内容很丰富,这里我们主要介绍数理统计的基本概念,重点研究参数估计和假设检验。
§6.1 随机样本一、总体与样本1.总体、个体在数理统计学中,我们把所研究的全部元素组成的集合称为总体;而把组成总体的每个元素称为个体。
例如:在研究某批灯泡的平均寿命时,该批灯泡的全体就组成了总体,而其中每个灯泡就是个体;在研究我校男大学生的身高和体重的分布情况时,该校的全体男大学生组成了总体,而每个男大学生就是个体。
但对于具体问题,由于我们关心的不是每个个体的种种具体特性,而仅仅是它的某一项或几项数量指标X(可以是向量)和该数量指标X在总体的分布情况。
在上述例子中X是表示灯泡的寿命或男大学生的身高和体重。
在试验中,抽取了若干个个体就观察到了X的这样或那样的数值,因而这个数量指标X是一个随机变量(或向量),而X的分布就完全描写了总体中我们所关心的那个数量指标的分布状况。
5.1样本均数的抽样分布与抽样误差(精)
n由固然存在的个体变异和抽样造成的样本均数与样本均数及样本均数与总体均
数之间的差异称为均数的抽样误差。
小结
1.抽样分布和抽样误差n样本统计量抽样分布误差含义及误差产生原因n
2.样本均数抽样分布和抽样误差n正态分布总体样本均数抽样分布规律非正态分布总体样本均数抽样分布规律n
n抽样分布
n由于抽样误差存在,从同一总体中随机抽取若干份样本,所得样本统计量是不
一致的,差异无法避免但其存在一定的分布规律。
2.样本均数抽样分布和抽样误差n正态分布总体样本均数抽样分布的电脑试验n
假定某年某地所有13岁女生的身高服从总体均数为155.4 cm,总
155.4,5.32)。用计算机从该总体中体标准差为5.3cm的正态分布N(
n非正态分布总体样本均数抽样分布的电脑实验n图(a)是正偏峰分布原始数据对应的直方图,用计算机随机抽取样本量分别为5, 10, 30和50的样本各1000份,计算样本均数并绘8
9
n中心极限定理表明
n 2 N m, s从正态总体()中随机抽取例数为n的多个样本,样本均数服从正态分布;即使是从偏态总体中随机抽样,当n足够大时(如n>30),样本均数也近似正态分布,且样本均数的均数等于原分布的均数。
第五章参数估计基础
一、样本均数的抽样分布与抽样误差
内容
1.抽样误差和抽样分布
2.样本均数抽样分布和抽样误差
1.抽样误差和抽样分布
n误差泛指实测值和真实值之差。按其产生原因与性质分两大类:系统误差和随
机误差。抽样误差是一种随机误差。n抽样误差
由于生物固有的个体变异,从某一总体中随机抽取一个样本,所得样本统计量与
随机抽样,每次抽取30例组成一份样本,重复抽样100次,计算每份样本的平均身高。
样本及抽样分布范文
样本及抽样分布范文样本是从总体中抽取的一部分个体或观测值。
样本是对总体的一种估计,通过对样本进行分析和统计推断,可以得出关于总体的结论。
抽样是从总体中选择样本的过程。
抽样方法应该是随机的,以避免选择偏见和结果的错误推断。
抽样方法有很多种,常用的有简单随机抽样、系统抽样、分层抽样、群组抽样等。
抽样分布是样本统计量的分布。
当我们从总体中抽取不同的样本并计算出样本统计量时,这些统计量构成了抽样分布。
常见的样本统计量有样本均值、样本方差、样本比例等。
在统计推断中,我们通常使用样本统计量来估计总体参数。
样本统计量的抽样分布是用来描述这些统计量的变异情况的。
抽样分布的性质决定了我们对总体参数的估计的置信度。
中心极限定理是关于抽样分布的重要定理之一、中心极限定理指出,当样本容量足够大时,无论总体的形态如何,样本均值的抽样分布都近似服从正态分布。
这意味着当我们拥有一个具有较大样本容量的随机样本时,我们可以使用正态分布的性质来进行统计推断。
在使用抽样分布进行统计推断时,我们通常考虑置信区间和假设检验两个方面。
置信区间是对总体参数估计的一种方法。
通过计算样本统计量的抽样分布,我们可以构造一个区间,这个区间包含了总体参数的真实值的估计范围。
置信区间的计算通常使用样本统计量、抽样分布的分位数和置信水平来确定。
假设检验是用来检验总体参数的一些特定假设是否成立的方法。
在假设检验中,我们首先建立原假设和备择假设,然后根据样本统计量的抽样分布来计算一个检验统计量,并以此来判断原假设的可信性。
假设检验通常有三种结论:接受原假设、拒绝原假设或无法做出结论。
总之,样本及抽样分布是统计学中非常重要的概念。
通过对样本进行抽样分布的分析和推断,我们可以对总体的特征和参数进行估计,并进行统计推断。
中心极限定理、置信区间和假设检验是样本及抽样分布的重要理论和方法,为我们的研究和决策提供了有力的依据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章样本及抽样分布【基本要求】 1、理解总体、个体和样本的概念;2、理解样本均值、样本方差和样本矩的概念并会计算;3、理解统计量的概念,掌握几种常用统计量的分布及其结论;4、理解分位数的概念,会计算几种重要分布的分位数。
【本章重点】样本均值、样本方差和样本矩的计算;抽样分布—— 2 分布,t分布,F分布;分位数的理解和计算。
【本章难点】对样本、统计量及分位数概念的理解;样本矩的计算。
【学时分配】 4 学时【授课内容】§6.0前言前面五章我们研究了概率论的基本内容,从中得知:概率论是研究随机现象统计规律性的一门数学分支。
它是从一个数学模型出发(比如随机变量的分布)去研究它的性质和统计规律性;而我们下面将要研究的数理统计,也是研究大量随机现象的统计规律性,并且是应用十分广泛的一门数学分支。
所不同的是数理统计是以概率论为理论基础,利用观测随机现象所得到的数据来选择、构造数学模型(即研究随机现象)。
其研究方法是归纳法(部分到整体)。
对研究对象的客观规律性做出种种合理性的估计、判断和预测,为决策者和决策行动提供理论依据和建议。
数理统计的内容很丰富,这里我们主要介绍数理统计的基本概念,重点研究参数估计和假设检验。
§ 6.1随机样本1一、总体与样本1.总体、个体在数理统计学中,我们把所研究的全部元素组成的集合称为总体;而把组成总体的每个元素称为个体。
例如:在研究某批灯泡的平均寿命时,该批灯泡的全体就组成了总体,而其中每个灯泡就是个体;在研究我校男大学生的身高和体重的分布情况时,该校的全体男大学生组成了总体,而每个男大学生就是个体。
但对于具体问题,由于我们关心的不是每个个体的种种具体特性,而仅仅是它的某一项或几项数量指标 X ( 可以是向量 ) 和该数量指标X在总体的分布情况。
在上述例子中 X 是表示灯泡的寿命或男大学生的身高和体重。
在试验中,抽取了若干个个体就观察到了X 的这样或那样的数值,因而这个数量指标X 是一个随机变量(或向量),而 X 的分布就完全描写了总体中我们所关心的那个数量指标的分布状况。
由于我们关心的正是这个数量指标,因此我们以后就把总体和数量指标 X 可能取值的全体组成的集合等同起来。
定义 1:把研究对象的全体(通常为数量指标X 可能取值的全体组成的集合)称为总体;总体中的每个元素称为个体。
我们对总体的研究,就是对相应的随机变量X 的分布的研究,所谓总体的分布也就是数量指标 X 的分布,因此, X 的分布函数和数字特征分别称为总体的分布函数和数字特征。
今后将不区分总体与相应的随机变量,笼统称为总体 X 。
根据总体中所包括个体的总数,将总体分为:有限总体和无限总体。
例 1:考察一块试验田中小麦穗的重量:X =所有小麦穗重量的全体(无限总体);个体——每个麦穗重x2对应的分布: F ( x) P{ x} 重量 x的麦穗数 1 ( t ) 2 dt ~ N ( , 2 ) 0 xx总麦穗数 2例 2:考察一位射手的射击情况:X=此射手反复地无限次射下去所有射击结果全体;每次射击结果都是一个个体(对应于靶上的一点)1射中个体数量化 x0未中1 在总体中的比例p 为命中率0 在总体中的比例1p 为非命中率总体 X 由无数个 0,1 构成,其分布为两点分布B(1, p)P{ X 1} p, P{ X 0} 1p2.样本与样本空间为了对总体的分布进行各种研究,就必需对总体进行抽样观察。
抽样——从总体中按照一定的规则抽出一部分个体的行动。
一般地,我们都是从总体中抽取一部分个体进行观察,然后根据观察所得数据来推断总体的性质。
按照一定规则从总体X 中抽取的一组个体( X1 , X 2 ,, X n ) 称为总体的一个样本,显然,样本为一随机向量。
为了能更多更好的得到总体的信息,需要进行多次重复、独立的抽样观察(一般进行n 次),若对抽样要求①代表性:每个个体被抽到的机会一样,保证了X 1 , X 2 ,, X n的分布相同,与总体一样。
②独立性: X1 , X 2 ,, X n相互独立。
那么,符合“代表性”和“独立性”要求的样本( X 1 , X2 , , X n ) 称为简单随机样本。
易知,对有限总体而言,有放回的随机样本为简单随机样本,无放回的抽样不能保证X 1 , X 2 ,, X n的独立性;但对无限总体而言,无放回随机抽样也得到简单随机样本,我们本书则主要研究简单随机样本。
3对每一次观察都得到一组数据( x1 , x2 , , x n),由于抽样是随机的,所以观察值( x1, x2 ,, x n)也是随机的。
为此,给出如下定义:定义 2: 设总体 X 的分布函数为F ( x),若X1, X2,, X n是具有同一分布函数 F ( x) 的相互独立的随机变量,则称(X 1, X 2 , , X n)为从总体X中得到的容量为n 的简单随机样本,简称样本。
把它们的观察值( x1 , x2 ,, x n)称为样本值。
定义 3: 把样本 ( X1, X2,, X n)的所有可能取值构成的集合称为样本空间,显然一个样本值( x1, x2,, x n)是样本空间的一个点。
注:样本具有双重性,在理论上是随机变量,在具体问题中是数据。
二、样本的分布:设总体 X 的分布函数为 F (x),(X1, X2,, X n)是X的一个样本,则其联合分布函数为:nF * ( x1 ,x2 , , x n ) = F (x i ) 。
i 1例 3:设总体X ~ B(1, p) , ( X1 , X 2 , X n ) 为其一个简单随机样本,则样本空间{( x1 , x2 , ,x n ) x i 0,1 ; i 1,2, ,n } ,因为P{ X x} p x(1 p)1 x,x 0,1所以样本的联合分布列为:P{ X1 x1 , X 2 x2 ,L , X n x n } P{ X1 x1} P{ X 2 x2} L P{ X n x n }p x1 (1 p)1 x1 .p x2 (1p) 1 x2 p x n (1 p)1 x n x 0,1 i 1,2, , ni4§6.2抽样分布0、引言有了总体和样本的概念,能否直接利用样本来对总体进行推断呢?一般来说是不能的,需要根据研究对象的不同,构造出样本的各种不同函数,然后利用这些函数对总体的性质进行统计推断,为此,我们首先介绍数理统计的另一重要概念——统计量。
一、统计量(随机变量)定义 1:设( X1, X2,L , X n)是来自总体 X 的一个样本,g( X1, X2,L , X n)是样本的函数,若 g 中不含任何未知参数,则称 g ( X1, X2,, X n)是一个统计量。
设 ( x1 , x2 ,L , x n ) 是对应于样本 ( X 1 , X 2 ,L , X n ) 的样本值,则称g( x1 , x2 ,L , x n )是 g( X 1 , X 2 ,L , X n ) 的观察值。
下面列出几个常用的统计量。
1、样本均值与样本方差(随机变量)定义 2 设(X1,X 2 , , X n)是来自总体X 的一个样本,称1 nX X i为样本均值。
n i 1S2 1 nX)2[ 1n22XX i X 2 ) 1n22nX 2 nX 2 ) ( X i ( X i ( X in 1 i 1 n 1 i 1 n 1 i 11 n2nX 2n( X i )] 为样本方差。
1 i 1SS2 1 n ( X i X ) 2为样本标准差。
n 1 i 1样本均值与样本方差分别刻划了样本的位置特征及样本的分散性特征。
2. 样本矩(r.v )5设总体 X 的分布函数为 F (x) ,则称 m k E( X k ) (假设它存在)为 总体 X 的 k 阶原点矩 ;称k E[( XE( X ))k ] 为总体 X 的 k 阶中心矩 。
把总体的各阶中心矩和原点矩统称为总体矩。
特别地: m 1 = E( X ) ; 2 D ( x) 是总体 X 的期望和方差。
定义 3:设 ( X 1,X 2,, X n ) 是来自总体 X 的一个样本,则称nA k1 X i k , k =1, 2, 3 ;为 样本的 k 阶原点矩 (随机变量)n i1nB k1( X iX ) k , k =1,2,3 ;为 样本值的 k 阶中心矩 (随机变量)。
n i1特别地, A 1X ,但 B 2 与 S 2 却不同,由 S 2 与 B 2 的计算式可知: B 2n 1 S 2 ,n当 n时, B 2 = S 2 ,所以常利用 B 2 来计算 S (标准差)。
设 ( x 1 , x 2 , , x n ) 为样本 ( X 1 , X 2 , , X n ) 的观测值,则样本矩对应观测值分别为:1nx i ;xn i 1s 2 = 1ns 21n1 i( x i x )2 ; s( x i x ) 2 ;n 1n 1 i 11a knnnx i k;b k1( x i x) k ; k =1, 2, 3 ;i 1n i 1在不至于混淆的情况下,这些值也分别称为样本均值、样本方差、样本标准差、样本k 阶原点矩、样本 k 阶中心矩 。
pm k( n)k1, 2,【注】: A kL ,这就是下一章要介绍的矩估计的理论根据。
统计量是我们对总体的分布函数或数字特征进行统计推断的最重要的基本概念, 所以寻求统计量的分布成为数理统计的基本问题之一。
我们把统计量的分布称为 抽样分布 。
然而要求出一个6统计量的精确分布是十分困难的。
而在实际问题中, 大多总体都服从正态分布: 而对于正态分布,我们可以求出一些重要统计量的精确分布,这就是:二、几种常用的抽样分布 :(正态分布 中的几种统计量的分布)把 2 分布, t 分布, F 分布,统称为“统计三大分布” 。
1、正态分布由正态分布的性质,可得如下结论:1)定理: 设 X 1 , X 2, , X n 相互独立 , X i ~ N ( i , i 2 ) , i1,2, , n , 是关于 X i 的任一确定的nnn线性函数 (a i X i ) ,则 也服从正态分布,且 ~ N ( a i i ,a i 2 i 2 ) 。
i 1i1i 12)结论:若( X 1 , X 2 , , X n )是来自总体 X ~ N ( ,2) 的一个样本, X 为样本均值,则2① X ~ N( , ),由上述结论可知: X 的期望与 X 的期望相同,而 X 的方差却比 X 的方差 n小的多,即 X 的取值将更向集中。
② X 与 S 2 相互独立。
2、2分布1)定义:设( X 1, X 2,, X n )是来自总体 X ~ N( 0,1) 的一个样本,则称统计量:2nX i 2 所服从的分布是自由度为 n 的 222( n ) 。
