第三章习题参考答案与提示

合集下载

高中数学必修3第三章课后习题解答

新课程标准数学必修3第三章课后习题解答第三章概率3．1随机事件的概率练习（P113）1、（1）试验可能出现的结果有3个，两个均为正面、一个正面一个反面、两个均为反面.（2）通过与其他同学的结果汇总，可以发现出现一个正面一个反面的次数最多，大约在50次左右，两个均为正面的次数和两个均为反面的次数在25次左右. 由此可以估计出现一个正面一个反面的概率为0.50，出现两个均为正面的概率和两个均为反面的概率均为0.25.2、略3、（1）例如：北京四月飞雪；某人花两元钱买福利彩票，中了特等奖；同时抛10枚硬币，10枚都正面朝上.（2）例如：在王府井大街问路时，碰到会说中文的人；去烤鸭店吃饭的顾客点烤鸭；在1～1000的自然数任选一个数，选到的数大于1.练习（P118）1、说明：例如，计算机键盘上各键盘的安排，公交线路及其各站点的安排，抽奖活动中各奖项的安排等，其中都用到了概率. 学生可能举出各种各样的例子，关键是引导他们正确分析例子中蕴涵的概率思想.2、通过掷硬币或抽签的方法，决定谁先发球，这两种方法都是公平的. 而猜拳的方法不太公平，因为出拳有时间差，个人反应也不一样.3、这种说法是错误的. 因为掷骰子一次得到2是一个随机事件，在一次试验中它可能发生也可能不发生. 掷6次骰子就是做6次试验，每次试验的结果都是随机的，可能出现2也可能不出现2，所以6次试验中有可能一次2都不出现，也可能出现1次，2次，…，6次.练习（P121）1、0.72、0.6153、0.44、D5、B习题3.1 A组（P123）1、D.2、（1）0；（2）0.2；（3）1.3、（1）430.067645≈；（2）900.140645≈；（3）7010.891645-≈.4、略5、0.136、说明：本题是想通过试验的方法，得到这种摸球游戏对先摸者和后摸者是公平的结论. 最好把全班同学的结果汇总，根据两个事件出现的频率比较近，猜测在第一种情况下摸到红球的概率为110，在第二种下也为110. 第4次摸到红球的频率与第1次摸到红球的频率应该相差不远，因为不论哪种情况，第4次和第1次摸到红球的概率都是1 10.习题3.1 B组（P124）1、D.2、略. 说明：本题是为了学生根据实际数据作出一些推断. 一般我们假定每个人的生日在12个月中哪一个月是等可能的，这个假定是否成立，引导学生通过收集的数据作出初步的推断.3．2古典概率练习（P130）1、110. 2、17. 3、16.练习（P133）1、38，38.2、（1）113；（2）1213；（3）14；（4）313；（5）0；（6）213；（7）12；（8）1.说明：模拟的方法有两种.（1）把1～52个自然数分别与每张牌对应，再用计算机做模拟试验.（2）让计算机分两次产生两个随机数，第一次产生1～4的随机数，代表4个花色；第二次产生1～13的随机数，代表牌号.3、（1）不可能事件，概率为0；（2）随机事件，概率为49；（3）必然事件，概率为1；（4）让计算机产生1～9的随机数，1～4代表白球，5～9代表黑球.4、（1）16；（2）略；（3）应该相差不大，但会有差异. 存在差异的主要原因是随机事件在每次试验中是否发生是随机的，但在200次试验中，该事件发生的次数又是有规律的，所以一般情况下所得的频率与概率相差不大.习题3.2 A组（P133）1、游戏1：取红球与取白球的概率都为12，因此规则是公平的.游戏2：取两球同色的概率为13，异色的概率为23，因此规则是不公平的.游戏3：取两球同色的概率为12，异色的概率为12，因此规则是公平的.2、第一位可以是1～9这9个数字中的一个，第二位可以是0～9这10个数字中的一个，所以（1）190；（2）18919090-=；（3）9919010-=3、（1）0.52；（2）0.18.4、（1）12；（2）16；（3）56；（4）16.5、（1）25；（2）825.6、（1）920；（2）920；（3）12.习题3.2 B组（P134）1、（1）13；（2）14.2、（1）35；（2）310；（3）910.说明：（3）先计算该事件的对立事件发生的概率会比较简单.3、具体步骤如下：①建立概率模型. 首先要模拟每个人的出生月份，可用1,2,…,11,12表示月份，用产生取整数值的随机数的办法，随机产生1～12之间的随机数. 由于模拟的对象是一个有10个人的集体，故把连续产生的10个随机数作为一组模拟结果，可模拟产生100组这样的结果.②进行模拟试验. 可用计算器或计算机进行模拟试验.如使用Excel软件，可参看教科书125页的步骤，下图是模拟的结果：其中，A,B,C,D,E,F,G,H,I,J的每一行表示对一个10人集体的模拟结果. 这样的试验一共做了100次，所以共有100行，表示随机抽取了100个集体.③统计试验的结果. K,L,M,N列表示统计结果. 例如，第一行前十列中至少有两个数相同，表示这个集体中至少有两个人的生日在同一月. 本题的难点是统计每一行前十列中至少有两个数相同的个数. 由于需要判断的条件态度，所以用K,L,M三列分三次完成统计.其中K列的公式为“=IF(OR(A1=B1，A1=C1，A1=D1，A1=E1，A1=F1，A1=G1，A1=H1，A1=I1，A1=J1，B1=C1，B1=D1，B1=E1，B1=F1，B1=G1，B1=H1，B1=I1，B1=J1，C1=D1，C1=E1，C1=F1，C1=G1，C1=H1，C1=I1，C1=J1，D1=E1，D1=F1，D1=G1，D1=H1，D1=I1，D1=J1)，1，0)”，L列的公式为“=IF(OR(E1=F1，E1=G1，E1=H1，E1=I1，E1=J1，F1=G1，F1=H1，F1=I1，F1=J1，G1=H1，G1=I1，G1=J1，H1=I1，H1=J1，I1=J1)，1，0)”，M列的公式为“=IF(OR(K1=1，L1=1)，1，0)”，M列的值为1表示该行所代表的10人集体中至少有两个人的生日在同一个月. N1表示100个10人集体中至少有两个人的生日在同一个月的个数，其公式为“=SUM(M$1：M$100)”. N1除以100所得的结果0.98，就是用模拟方法计算10人集体中至少有两个人的生日在同一个月的概率的估计值. 可以看出，这个估计值很接近1.3．3几何概率练习（P140）1、（1）1；（2）38.2、如果射到靶子上任何一点是等可能的，那么大约有100个镖落在红色区域.说明：在实际投镖中，命中率可能不同，这里既有技术方面的因素，又是随机因素的影响，所以在投掷飞镖、射击或射箭比赛中不会以一枪或一箭定输赢，而是取多次成绩的总和，这就是为了减少随机因素的影响.习题3.3 A组（P142）1、（1）49；（2）13；（3）29；（4）23；（5）59.2、（1）126；（2）12；（3）326；（4）326；（5）12；（6）313.说明：（4）是指落在6,23,9三个相邻区域的情况，而不是编号为6,7,8,9,四个区域.3、（1）25；（2）115；（3）35. 说明：本题假设在任何时间到达路口是等可能的. 习题3.3 B 组（P142） 1、设甲到达的时间为x ，乙到达的时间为y ，则0,24x y <<. 若至少一般船在停靠泊位时必须等待，则06y x <-<或06x y <-<，必须等待的概率为：22189711241616-=-=.2、D .第三章复习参考题A 组（P145）1、56，16，23. 2、（1）0.548；（2）0.186；（3）0.266.3、（1）38；（2）14.4、（1）813；（2）726；（3）665. 5、分别计算两球均为白球的概率、均为红球的概率、均为黑球的概率，然后相加，得1223311166666636⨯⨯⨯++=⨯⨯⨯. 6、56. 说明：利用对立事件计算会比较简单. 第三章复习参考题B 组（P146）1、第一步，先计算出现正面次数与反面次数相等的概率46328=. 第二步，利用对称性，即出现正面的次数多于反面次数的概率与出现反面的次数多于正面次数的概率是相等的，所以出现正面的次数多于反面次数的概率为35(1)2816-÷=. 2、（1）是；（2）否；（3）否；（4）是.3、（1）45；（2）15；（3）25；（4）25. 说明：此题属于古典概型的一类“配对问题”，由于这里的数比较小，可以用列举法.4、参考教科书140页例4.。

数字电路第三章习题答案

S 1 S 0(A B A B )
数字电路第三章习题答案
3-10
F S 1 A S 0 B A S 0 B A B S 0 A B S 1 S 0 A B F F S 1 A S 0 B A S 0 B A B S 0 A B S 1 S 0 A B
数字电路第三章习题答案
3-11
试用六个与非门设计一个水箱控制电路。图为水箱示意图。A、B、C是三个电极。当电极被水浸没时，会有信号输出。水面在A，B间为正常状态，点亮绿灯G；水面在B、 C间或在A以上为异常状态，点亮黄灯Y；水面在C以下为危险状态．点亮红灯R。
3531736半加器的设计1半加器真值表2输出函数3逻辑图输入输出被加数a加数b4逻辑符号31837ab改为用与非门实现函数表达式变换形式
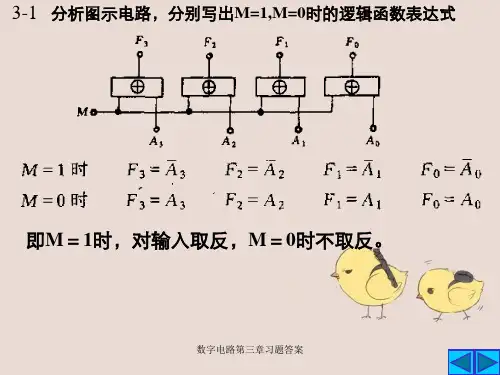
3-1 分析图示电路，分别写出M=1,M=0时的逻辑函数表达式
即M＝1时，对输入取反，M＝0时不取反。
数字电路第三章习题答案
3-2 分析图示补码电路，要求写出逻辑函数表达式，列出真值表。
3-10 试用与非门设计一个逻辑选择电路。
S1、S0为选择端，A、B为数据输入端。选择电路的功能见下表。选择电路可以有反变量输入。
数字电路第三章习题答案
3-10
F S 1 A S 0 B A S 0 B A B S 0 A B S 1 S 0 A B F F S 1 A S 0 B A S 0 B A B S 0 A B S 1 S 0 A B FS 1 S 0A B S 1 S 0(A B )S 1 S 0(A BA)B
数字电路第三章习题答案
3-5
Ai 0 0 0 0 1 1 1 1
Si Ai BiCi Ai BiCi Ai BiCi Ai BiCi

概率论~第三章习题参考答案与提示

设二维随机变量xy的概率密度为6第三章习题参考答案与提示?2121yxyxyxf?xy?其中1yx?和2yx?都是二维正态密度函数且它们对应的二维随机变量的相关系数分别为13和13它们的边缘密度函数所对应的随机变量的数学期望都是0方差都是1
第三章习题参考答案与提示
第三章随机变量的数字特征习题参考答案与提示
22．已知 X 、 Y 分别服从正态分布 N (0，32 ) 和 N (1，42 ) ，且 X 与Y 的相关系数 ρ XY = −1/ 2 ，设 Z = X / 3 + Y / 2 ，求：
（1）求数学期望 EZ ，方差 DZ ；（2）Y 与 Z 的相关系数 ρYZ ；答案与提示：本题要求熟悉数学期望、方差、协方差的性质、计算及有关正态分布的性质。
X
Y
0
1
0
0.1
0.2
1
0.3
0.4
求：（1） EX ， EY ， DX ， DY ；
（2）( X ， Y )的协方差，相关系数，协方差阵，相关阵。
答案与提示：（1） EX = 0.7 ， DX = 0.21， EY = 0.6 ， DY = 0.24 。
（2） EXY = 0.4 ； Cov ( X ,Y ) = −0.02 ， ρXY = 0.089 ；
（1） X 的概率密度；
（2）Y = 1 − 2 X 的概率密度。
答案与提示：考查服从正态分布随机变量的概率密度的一般表达形式、参数的
几何意义及正态分布随机变量的性质。
（1） f (x) = 1 e−(x−1.7)2 /6 (−∞ < x < +∞) 6π
（2） f ( y) = 1 e−( y+2.4)2 / 24 2 6π

随机数据处理方法石油大学出版社王清河课后题答案第三章

协方差阵为
⎜⎜⎝⎛
0.21 − 0.02
−00.2.042⎟⎟⎠⎞ ，
相关阵为
⎜⎜⎝⎛
−
1 0.089
− 01.089⎟⎟⎠⎞ 。
18．设随机变量（X，Y）的概率密度为
f
(x,
y)
=
⎪⎧1 ⎨8
(x
+
y)，
0
≤
x
≤
2，0 ≤
y
≤
2
⎪⎩
0，
其它
求相关系数 ρ XY 。答案与提示：欲求相关系数，需先求 DX、DY、EX、EY 、Cov ( X，Y ) 。
4
4
12．设 X、Y 的概率分布分别为
f
(x)
=
⎧2e −2 x，
⎨ ⎩
0，
x x
> ≤
0 0
求： E( X + Y ) 和 E(2X − 3Y 2 ) 。
f
( y)
=
⎧4e−4 y，
⎨ ⎩
0，
y y
> ≤
0 0
答案与提示：可利用由数学期望性质及常用分布随机变量的数学期望和方差来
计算 E( X + Y ) 和 E(2X − 3Y 2 ) ，关键是计算 EX 、 EY 、 EY 2 。
答案与提示：事件在 n 次独立重复试验中发生的次数服从参数为 n ， p 的二项分
布 B(n, p) ，当然在一次试验中发生的次数应服从 B(1, p) ，即为(0-1)分布。
可令
X
=
⎧1，事件A在试验中发生， ⎨⎩0，事件A在试验中不发生.
得 DX ≤ 1 ，即事件在一次试验中发生的次数的方差不超过 1 。

线性代数课后习题解答第三章习题解答

第三章矩阵的初等变换与线性方程组1．把下列矩阵化为行最简形矩阵：(1) ⎪⎪⎪⎭⎫ ⎝⎛--340313021201; (2) ⎪⎪⎪⎭⎫⎝⎛----174034301320; (3) ⎪⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311; (4) ⎪⎪⎪⎪⎭⎫⎝⎛------34732038234202173132.解 (1) ⎪⎪⎪⎭⎫ ⎝⎛--340313*********2)3()2(~r r r r -+-+⎪⎪⎪⎭⎫ ⎝⎛---020********* )2()1(32~-÷-÷r r ⎪⎪⎪⎭⎫ ⎝⎛--01003100120123~r r -⎪⎪⎪⎭⎫⎝⎛--300031001201 33~÷r ⎪⎪⎪⎭⎫ ⎝⎛--100031001201323~r r +⎪⎪⎪⎭⎫ ⎝⎛-1000010012013121)2(~r r r r +-+⎪⎪⎪⎭⎫ ⎝⎛100001000001(2) ⎪⎪⎪⎭⎫ ⎝⎛----1740343013201312)2()3(2~r r r r -+-+⨯⎪⎪⎪⎭⎫ ⎝⎛---31003100132021233~r r r r ++⎪⎪⎪⎭⎫ ⎝⎛000031001002021~÷r ⎪⎪⎪⎭⎫⎝⎛000031005010 (3) ⎪⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311141312323~rr r r rr ---⎪⎪⎪⎪⎭⎫ ⎝⎛--------1010500663008840034311)5()3()4(432~-÷-÷-÷r r r ⎪⎪⎪⎪⎭⎫ ⎝⎛-----22100221002210034311 2423213~r r r r r r ---⎪⎪⎪⎪⎭⎫⎝⎛---000000000022********(4) ⎪⎪⎪⎪⎭⎫⎝⎛------34732038234202173132 242321232~r r r r rr ---⎪⎪⎪⎪⎭⎫ ⎝⎛-----1187701298804202111110141312782~rr r r rr --+⎪⎪⎪⎪⎭⎫⎝⎛--410004100020201111134221)1(~r r r r r --⨯↔⎪⎪⎪⎪⎭⎫⎝⎛----0000041000111102020132~rr +⎪⎪⎪⎪⎭⎫⎝⎛--000004100030110202012.设⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛987654321100010101100001010A ，求A 。

数据与计算机通信答案(第3章)

上述两种方案由于每个原色强度过少，色彩单调，图象层次感差，对于数字电视无实际应用价值。如果可以提高三倍数据率，以每三个连续的 5 比特组分别表示一个像素，三种颜色各有 32 种强度值，共有 32768 种色彩，这对于计算机显示器而言，色彩并不算丰富，
而对于数字彩色电视机，相当不错了。如果不提高数据率，还可以通过降低分辨率或刷新速率，来换取色彩数的提高，但这也不实用的方法。
已知视频带宽 B=5MHz，所以有 5=P/105，则每行的像素数 P=5x105=525。然而，通常 CCIR-M/NTSC 制式每行只约有 450 像素，带宽 B=P/105=450/105=4.3MHz (实际技术指标 4.2Hz) 。带宽由 4.2MHz 增加到 5MHz 时，水平分辨率约增加 75 像素，增幅 16.7%。（2）计算垂直分辨率的增幅由于信号最高频率 fH=5MHz，即最短的信号周期 1/fH=0.2υs。又因为每个最短周期包含 2 个像素，则有 225 周期/行。那么，每行扫描时间为 0.2υs×225=45υs。加上水平回扫 11υs，每行往返扫描时间为 56υs ，即 56x10-6 s，假定每屏 V 行，每秒扫描 30 场（帧、屏），则每秒扫描行数为 30V。因此对于画面刷新，有 30V×56x10-6 = 1s，V = 595 行/屏。目前 NSTL 制式每行只有 525 行。垂直分辨率增加了 70 行，增幅 13.3%。
cos 2 t = cos t cos t = 1 (cos 2t + cos 0) = 1 (cos 2t + 1)
2
2
所以， f (t) = (10 cos t)2 = 100 cos 2 t = 50 + 50 cos 2t

第三章习题参考答案

第三章习题参考答案一、概念题1．注意是心理活动对一定对象的指向和集中。

2．无意注意，也叫不随意注意，是指事先没有预定目的，也不需要作意志努力的注意。

3．有意注意，也叫随意注意，是指服从于预定目的、需要作意志努力的注意。

4．有意后注意是有预定目的，但不需要付出意志努力的一种注意形式，是注意的一种特殊形式。

5．意识是指一个人对于内部和外部刺激的知觉。

6．无意识是指个体不曾觉察到的心理活动和过程。

7．前意识，也称之为"潜伏的无意识"，它是介于意识和无意识之间的一种意识水平。

8．所谓意识水平是指在某一时刻人对刺激能够觉知的程度。

9．白日梦是指只包含很低水平意识努力的意识状态。

10．人的生物节律中大约1/3是行为静止的阶段，称为睡眠。

11．注意的范围也叫做注意的广度，是指人在同一时间内所能清楚觉察到的对象的数量多少的特性。

12．注意的稳定性是指注意保持在某一对象或某一活动上的时间的久暂特性。

13．注意的分配是指在同一时间内把注意指向两种或两种以上的对象或活动。

14．注意的转移是指人有意地把注意从一个对象转移到另一个对象上，或从一种活动转移到另一种活动上。

15．注意的转移是指人有意地把注意从一个对象转移到另一个对象上，或从一种活动转移到另一种活动上。

16．所谓分心是指一个人的心理活动在必要的时间内不能充分地指向和集中，或者完全离开当前指向和集中的事物而转移到无关的事物上去的心理状态。

二、填空题1．指向性集中性2．强度紧张度3．指向的范围4．心理过程5．选择功能维持功能监督和调节6．选择功能7．时间上8．适应性的动作无关动作的停止呼吸运动的变化多余动作的产生9．觉知性10．外部事物内部刺激自身状态11．无意识水平前意识水平意识水平12．无意识13．意识状态做梦自发的14．脑电活动15．五非快速眼动睡眠快速眼动睡眠做梦16．无意注意有意注意有意后注意17．无意注意18．刺激物的强度刺激物的新异性刺激物的运动和变化19．相对强度20．绝对新异性相对新异性绝对新异刺激相对新异刺激21．目的性意志成分22．无意注意有意注意23．哈密尔顿24．一个对象同一活动分散25．无关刺激的干扰单调刺激自身的状态三、单项选择题1．④2．②3．①4．④5．②四、判断题1．—2．+ 3．+ 4．—5．+ 6．—7．—8．—9．+ 10．—五、辨析题1．（1）这种说法是不正确的。

随机数据处理方法第三版课后答案(王清河著) 中国石油大学出版社

（2） P( A3 | A) = 0.4 。 19．某专门化医院平均接待 K 型病患者 50%，L 型病患者 30%，M 型病患者 20%，而治愈率分别为 7/10、8/10、9/10。今有一患者已治愈，问此患者是 K 型病的概率是多少？
提示与答案：依题意，这是一全概率公式及贝叶斯公式的应用问的事件是互逆的。
2．如果 x 表示一个沿着数轴随机运动的质点位置，试说明下列事件的包含、
互不相容等关系：
A = {x | x ≤ 20}
B = {x | x > 3}
C = {x | x < 9}
D = {x | x < −5} E = {x | x ≥ 9}
解：（1）包含关系： D ⊂ C ⊂ A 、 E ⊂ B 。
P( AB) = P( A ∩ B ) = P( A ∪ B) = 1 − P( A ∪ B)
=1 − 1 − P(B) + P( AB) 3
从而得 2 − P(B) = 0 ，即 3 P(B) = 2 3
7．一个袋中有 5 个红球 2 个白球，从中任取一球，看过颜色后就放回袋中，然后再从袋中任取一球。求：（1）第一次和第二次都取到红球的概率；
球，也可能是黑球），并且也只有这两种可能。因此若把这两种可能看成两个事
件，这两个事件的和事件便构成了一个必然事件。
若设 A 表示：“由甲袋取出的球是白球”； B 表示：“由甲袋取出的球是黑球”； C 表示：“从乙袋取出的球是白球”。则 P(C) = 5 /12 。
18．设有一箱同类产品是由三家工厂生产的，其中 1 是第一家工厂生产的， 2
17．有两个口袋，甲袋中盛有 2 个白球 1 个黑球；乙袋中盛有 1 个白球 2 个黑球。由甲袋任取一球放入乙袋，再从乙袋中取出一球，求取到白球的概率。

物理化学第三章课后答案完整版

第三章热力学第二定律3.1 卡诺热机在的高温热源和的低温热源间工作。

求（1）热机效率；（2）当向环境作功时，系统从高温热源吸收的热及向低温热源放出的热。

解：卡诺热机的效率为根据定义3．2 卡诺热机在的高温热源和的低温热源间工作，求：（1）热机效率；（2）当从高温热源吸热时，系统对环境作的功及向低温热源放出的热解：(1) 由卡诺循环的热机效率得出（2）3．3 卡诺热机在的高温热源和的低温热源间工作，求（1）热机效率；（2）当向低温热源放热时，系统从高温热源吸热及对环境所作的功。

解：（1）(2)3．4 试说明：在高温热源和低温热源间工作的不可逆热机与卡诺机联合操作时，若令卡诺热机得到的功r W 等于不可逆热机作出的功－W 。

假设不可逆热机的热机效率大于卡诺热机效率，其结果必然是有热量从低温热源流向高温热源，而违反势热力学第二定律的克劳修斯说法。

证：（反证法）设 r ir ηη>不可逆热机从高温热源吸热，向低温热源放热，对环境作功则逆向卡诺热机从环境得功从低温热源吸热向高温热源放热则若使逆向卡诺热机向高温热源放出的热不可逆热机从高温热源吸收的热相等，即总的结果是：得自单一低温热源的热，变成了环境作功，违背了热力学第二定律的开尔文说法，同样也就违背了克劳修斯说法。

3．5 高温热源温度，低温热源温度，今有120KJ的热直接从高温热源传给低温热源，求此过程。

解：将热源看作无限大，因此，传热过程对热源来说是可逆过程3.6 不同的热机中作于的高温热源及的低温热源之间。

求下列三种情况下，当热机从高温热源吸热时，两热源的总熵变。

（1）可逆热机效率。

（2）不可逆热机效率。

（3）不可逆热机效率。

解：设热机向低温热源放热，根据热机效率的定义因此，上面三种过程的总熵变分别为。

3.7 已知水的比定压热容。

今有1 kg，10℃的水经下列三种不同过程加热成100 ℃的水，求过程的。

（1）系统与100℃的热源接触。

（2）系统先与55℃的热源接触至热平衡，再与100℃的热源接触。

大学物理第三章部分课后习题答案

大学物理第三章课后习题答案3-1 半径为R 、质量为M 的均匀薄圆盘上，挖去一个直径为R 的圆孔，孔的中心在12R 处，求所剩部分对通过原圆盘中心且与板面垂直的轴的转动惯量。

分析：用补偿法（负质量法）求解，由平行轴定理求其挖去部分的转动惯量，用原圆盘转动惯量减去挖去部分的转动惯量即得。

注意对同一轴而言。

解：没挖去前大圆对通过原圆盘中心且与板面垂直的轴的转动惯量为：2112J MR =① 由平行轴定理得被挖去部分对通过原圆盘中心且与板面垂直的轴的转动惯量为：2222213()()2424232c M R M R J J md MR =+=⨯⨯+⨯= ②由①②式得所剩部分对通过原圆盘中心且与板面垂直的轴的转动惯量为：2121332J J J MR =-=3-2 如题图3-2所示，一根均匀细铁丝，质量为M ，长度为L ，在其中点O 处弯成120θ=︒角，放在xOy 平面内，求铁丝对Ox 轴、Oy 轴、Oz 轴的转动惯量。

分析：取微元，由转动惯量的定义求积分可得解：（1）对x 轴的转动惯量为：2022201(sin 60)32Lx M J r dm l dl ML L ===⎰⎰ （2）对y 轴的转动惯量为：20222015()(sin 30)32296Ly M L M J l dl ML L =⨯⨯+=⎰（3）对Z 轴的转动惯量为：22112()32212z M L J ML =⨯⨯⨯=3-3 电风扇开启电源后经过5s 达到额定转速，此时角速度为每秒5转，关闭电源后经过16s 风扇停止转动，已知风扇转动惯量为20.5kg m ⋅，且摩擦力矩f M 和电磁力矩M 均为常量，求电机的电磁力矩M 。

分析：f M ，M 为常量，开启电源5s 内是匀加速转动，关闭电源16s 内是匀减速转动，可得相应加速度，由转动定律求得电磁力矩M 。

解：由定轴转动定律得：1f M M J β-=，即11252520.50.5 4.12516f M J M J J N m ππβββ⨯⨯=+=+=⨯+⨯=⋅ 3-4 飞轮的质量为60kg ，直径为0.5m ，转速为1000/min r ，现要求在5s 内使其制动，求制动力F ，假定闸瓦与飞轮之间的摩擦系数0.4μ=，飞轮的质量全部分布在轮的外周上，尺寸如题图3-4所示。

高鸿业第三版微观经济第三章答案详解

《微观经济学》（高鸿业第四版）第三章练习题参考答案1、已知一件衬衫的价格为80元，一份肯德鸡快餐的价格为20元，在某消费者关于这两种商品的效用最大化的均衡点上，一份肯德鸡快餐对衬衫的边际替代率MRS 是多少？解：按照两商品的边际替代率MRS 的定义公式,可以将一份肯德鸡快餐对衬衫的边际替代率写成: XYMRS XY ∆∆-=其中:X 表示肯德鸡快餐的份数;Y 表示衬衫的件数; MRS 表示在维持效用水平不变的前提下, 消费者增加一份肯德鸡快餐时所需要放弃的衬衫消费数量。

在该消费者实现关于这两件商品的效用最大化时，在均衡点上有MRS xy =P x /P y即有MRS xy =20/80=0.25它表明：在效用最大化的均衡点上，消费者关于一份肯德鸡快餐对衬衫的边际替代率MRS 为0.25。

2 假设某消费者的均衡如图1-9所示。

其中，横轴1OX 和纵轴2OX ，分别表示商品1和商品2的数量，线段AB 为消费者的预算线，曲线U 为消费者的无差异曲线，E 点为效用最大化的均衡点。

已知商品1的价格P 1=2元。

(2)求上品的价格P；2(3)写出预算线的方程；(4)求预算线的斜率；(5)求E点的MRS的值。

12解：（1）图中的横截距表示消费者的收入全部购买商品1的数量为30单位，且已知P1=2元，所以，消费者的收入M=2元×30=60。

（2）图中的纵截距表示消费者的收入全部购买商品2的数量为20单位，且由（1）已知收入M=60元，所以，商品2的价格P2斜率=－P1/P2=－2/3，得P2=M／20=3元（3）由于预算线的一般形式为：P1X1+P2X2=M所以，由（1）、（2）可将预算线方程具体写为2X1+3X2=60。

（4）将（3）中的预算线方程进一步整理为X2=-2/3 X1+20。

很清楚，预算线的斜率为－2/3。

（5）在消费者效用最大化的均衡点E上，有MRS12= = MRS12=P1/P2，即无差异曲线的斜率的绝对值即MRS等于预算线的斜率绝对值P1/P2。

3第三章弹性理论(习题及答案)

第三章弹性理论思考与练习一、选择题1．计算需求弹性的弹性系数的一般公式是( )。

A．需求量与价格之比B．需求量变动的百分比除以价格变动的百分比C．需求量变动的绝对值除以价格变动的绝对值D．价格变动的百分比除以需求量变动的百分比2．某种商品的价格变动10％，需求量变动20％。

则它的弹性系数为( )。

A．10％B．30％C．1／2D．23．如果一种商品的需求的价格弹性为2，价格由1元上升到1.02元会导致需求量( )。

A．增加4％B．增加2％C．减少4％D．减少2％4．如果一种商品的需求的价格弹性为0．5，价格由l元上升到1.04元会导致需求量( )。

A．增加4％B．增加2％C．减少4％D．减少2％5．如果需求的价格弹性为1／3，价格上升30％时，需求量将( )。

A．增加10％B．减少10％C．增加90％D．减少90％6．如果一种商品的价格上升时，需求量完全没有下降，那么该商品的需求( )。

A．完全有弹性B．完全无弹性C．富有弹性D．缺乏弹性7．如果一种商品的价格变动5％，需求量因此变动5％．那么该商品的需求( )。

A．富有弹性B．缺乏弹性C．无弹性D．单位弹性8．如果( )，我们就说一种商品的需求缺乏弹性。

A．需求量变化百分比大于价格变化百分比B．需求量变化百分比小于价格变化百分比C．需求变化大于价格变化D．价格变化大于需求变化9．如果一种商品的需求缺乏弹性，其弹性系数( )。

A．大于1B．大于0小于1C．等于1D．为010．如果一种商品的需求缺乏弹性，商品价格上升5％将使( )。

A．需求量的增加超过5％B．需求量的增加小于5％C．需求量的减少超过5％D．需求量的减少小于5％参考答案1.B；2.D；3.C；4.D；5.B；6.B；7.D；8.B；9.B；10.D二、判断题1．同一条线性需求曲线上不同点的弹性系数是不同的。

( )2．需求的价格弹性为零意味着需求曲线是一条水平线。

( )3．当某种产品的价格上升8％，而需求量减少7％时。

七年级下第三章参考答案

用表格表示的变量间关系第1课时参考答案基础性作业(必做题)1. A； 2. A； 3. A； 4. C；5.(1)公交车每月的乘车人数，公交车每月利润；(2)2000；(3)3000；(4)根据表格可知当每月乘车人数为2000人时，每月利润为0,随后每月乘车人数每增力口500人，其利润就增加1000元，A (5000-0) 4-1000=5,即假设5月份获得利润5000元时,需要增加5个500人，，5月份乘客量需达2000+5X500=4500 (人)，故答案为：4500.6.(1)行驶的路程；油箱剩余油量；(2)50, 38；(3)350.二.拓展性作业(选做题).解：240.1.(1)提出概念所用的时间和对概念接受能力)两个变量；(2)当时间是5分钟时，学生的接受能力是53.5；(3)当提出概念13分钟时，学生的接受能力最强59.9；(4)当2WxW13时，y值逐渐增大，学生的接受能力逐步增强；当13WxW20时，y值逐渐减小，学生的接受能力逐步降低.2. (1)所需资金为自变量.年利润为因变量；(2)可以投资一个7亿元的工程.也可以投资一个2亿元，再投资一个4亿元的工程.还可以投资一个1亿元，再投资一个6亿元的工程.(3)共三种方案：①1亿元，2亿元，7亿元，利润是1.45亿元.②2亿元，8亿元，利润是1.35亿元.③4亿元，6亿元，利润是1.25亿元.一・最大利润是L45亿兀.用关系式表示的变量间关系第1课时参考答案基础性作业(必做题)1. D； 2. D； 3. C； 4. y = 48x + 20 ； 5. y = -2x +166.(1)由图表中数据可得：当％每增加1时，y增加3；(2)由题意可得：y = 50 + 3(x — l) = 3x + 47；(3)某一排不可能有90个座位，理由：由题意可得：y = 3x + 47 = 90,解得：x =—.3故％不是整数，那么某一排不可能有90个座位.二.拓展性作业(选做题).解：(1)・・•当小正方形的边长由小到大变化时，图中阴影局部的面积也随之发生变化，・•・小正方形的边长是自变量，阴影局部的面积为因变量；(2)由题意可得：y = l22 -4x2 =144-4x2.(3)由(2)知：y = l44-4x\当小正方形的边长由1cm变化到5c加时，x增大,V也随之增大，-4/那么随着尢的增大而减小，所以y随着%的增大而减小，当x = 时，y 有最大值，y或才=144 - 4 x 了 = I40(CTH2).当x = 5c机时，y有最小值，y最小=144 - 4 x 5? = 44(cm2).当小正方形的边长由1刖变化到5c机时，阴影局部的面积由140cl变到44O%22.解：⑴该车平均每千米的耗油量为(45-30) + 150 = 0.1 (升/千米)，行驶路程x (千米)与剩余油量Q (升)的关系式为。

工程热力学第三章习题参考答案

第三章热力学第一定律习题参考答案思考题3-1门窗紧闭的房间……答：按题意，以房间（空气+冰箱）为对象，可看成绝热闭口系统，与外界无热量交换，Q=0电冰箱运转时，有电功输入，即W 为负值，按闭口系统能量方程：WU +Δ=0 或即热力学能增加，温度上升。

0>−=ΔW U 3-6 下列各式，适用于何种条件？答：答案列于下表公式适用条件w du q δδ+= 闭口系统，任何工质，任何过程，不论可逆与不可逆 pdv du q +=δ 闭口系统，任何工质，可逆过程 pdv dT c q v +=δ闭口系统，理想气体，可逆过程dh q =δ 闭口系统，定压过程；或开口系统与环境无技术功交换。

vdp dT c q v −=δ开口系统，理想气体，稳态稳流，可逆过程3-10 说明以下结论是否正确：（提示：采用推理原则，否定原则） ⑴ 气体吸热后一定膨胀，热力学能一定增加。

答：错误，如等容过程吸热后不膨胀；如不是等容过程吸热后热力学能也不一定增加，当对外净输出功量大于吸热量时，则热力学能不增加。

⑵ 气体膨胀一定对外作功。

答：错误，如气体向真空膨胀则不作功，另外气体膨胀对外作膨胀功的充要条件是：气体膨胀和要有功的传递和接受机构。

⑶ 气体压缩时，一定消耗外功。

答：错误，如处于冷却过程的简单可压缩系统，则会自发收缩（相当于被压缩），并不消耗外功。

⑷ 应设法利用烟气离开锅炉时带走的热量。

答：错误不应说设法利用烟气离开锅炉时带走的热量。

因为热量是过程量，不发生则不存在。

应该说设法利用烟气离开锅炉时带走的热能（或热焓）。

习题3-1 已知：min 202000/400===time N hkJ q 人人求：?=ΔU 解：依题意可将礼堂看作绝热系统，思路：1、如何选取系统？2、如何建立能量方程？ ⑴ 依题意，选取礼堂空气为系统，人看作环境，依热力学第一定律，建立能量方程：kJ time N q Q U W W Q U 51067.2602020004000×=××=⋅⋅==Δ∴=−=Δ人Q⑵ 如选“人+空气”作系统，依据热力学第一定律：W Q U −=Δ0,0,0=Δ∴==U Q W Q如何解释空气温度升高：该系统包括“人+空气”两个子系统，人散热给空气，热力学能降低，空气吸热，能内升高，二者热力学能代数和为零。

机械设计基础IA--第三章凸轮机构--习题与答案

第3章凸轮机构一、判断题（正确T，错误F）1.凸轮机构出现自锁是由于驱动力小造成的。

（）2.在凸轮从动件运动规律中，等速运动的加速度冲击最小。

（）3.适用于高速运动的凸轮机构从动件运动规律为余弦加速度运动。

（）4.基圆是凸轮实际廓线上到凸轮回转中心距离最小为半径的圆。

（）5.若要使凸轮机构压力角减小，应增大基圆半径。

（）6.凸轮机构的从动件按简谐运动规律运动时，不产生冲击。

（）二、单项选择题1. 设计凸轮机构，当凸轮角速度和从动件运动规律已知时，则。

A.基圆半径越大，压力角越大B.基圆半径越小，压力角越大C.滚子半径越小，压力角越小D.滚子半径越大，压力角越小2. 凸轮机构的从动件选用等加速等减速运动规律时，其从动件的运动。

A.将产生刚性冲击B.将产生柔性冲击C.没有冲击D.既有刚性冲击又有柔性冲击3. 在设计直动滚子从动件盘形凸轮机构时，若发生运动失真现象，可以。

A.增大滚子半径B.减少基圆半径C.增大基圆半径D.增加从动件长度4. 在下列凸轮机构中，从动件与凸轮的运动不在同一平面中的是。

A.直动滚子从动件盘形凸轮机构B.摆动滚子从动件盘形凸轮机构C.直动平底从动件盘形凸轮机构D.摆动从动件圆柱凸轮机构5. 与连杆机构相比，凸轮机构最大的缺点是。

A.设计较为复杂B.惯性力难以平衡C.点、线接触，易磨损D.不能实现间歇运动6. 有限值的突变引起的冲击为刚性冲击。

A.位移B.速度C.加速度D.频率7.对于转速较高的凸轮机构，为减小冲击振动，从动件运动规律宜采用运动规律。

A.等速B.等加速等减速C.正弦加速度8.若从动件的运动规律为等加速等减速运动规律、简谐运动规律或正弦加速度运动规律，当把凸轮转速提高一倍时，从动件的加速度是原来的倍。

A. 1B. 2C. 4D. 89.当凸轮基圆半径相同时，采用适当的从动件导路偏置可以凸轮机构推程的压力角。

A.减小B.增加C.保持原来10.滚子从动件盘形凸轮机构的滚子半径应凸轮理论廓线外凸部分的最小曲率半径。