交流电的瞬时值、最大值、有效值和平均值
瞬时值、最大值和有效值

瞬时值、最大值和有效值的区别
交流电每一瞬间的值称为瞬时值。
瞬时值是随着时间变化而变化的,是时间t的函数,用小写字母表示,如i(t)、v(t)、e(t) 分别表示电流、电压和电动势的瞬时值。
为了简略起见,可以表示为i、v、e。
最大的瞬时值称为最大值或幅值,用大写字母加下标m 表示,如I m、V m及E m分别表示电流、电压及电动势的最大值。
交流电的大小是不断变化的,通常采用有效值来计量交流电大小。
所谓交流电的有效值,就是在相同时间内与它热效应相等的直流值。
如图2.1.3 所示,让交流电和直流电分别通过同一个电阻,如果交流电在一个周期内产生的热量和直流电在相同时间内产生的热量相等,此直流电的值就为该交流电的有效值。
有效值用大写字母表示,I、V、E 分别表示电流、电压和电动势的有效值。
通常我们所说的正弦交流电的大小都是指有效值,如一般交流电表所测出的数值是有效值,一般灯泡、电器、仪表上所标注的交流电压、电流的数值也是有效值。
显然,有效值不随时间变化。
交流电压的有效值平均值瞬时值最大值

交流电压的有效值、平均值和瞬时值引言交流电是我们日常生活中常见的一种电力形式,它具有周期性变化的特点。
在分析交流电时,我们常常关注其有效值、平均值和瞬时值。
本文将对这三个概念进行详细解释,并探讨它们之间的关系。
交流电的特点交流电是指电流和电压随时间变化而周期性地改变方向和大小的电信号。
在交流电中,电流和电压都是随时间而变化的,且其波形通常呈正弦曲线。
有效值(RMS)有效值又称为均方根(Root Mean Square,简称RMS),是衡量交流电大小的一个重要参数。
它表示一个周期内正弦波振幅平方的平均数,并且与相同大小的直流电产生相同效果。
对于一个正弦波来说,其有效值等于其峰-峰值(peak-to-peak value)除以2倍根号2。
峰-峰值即为波形从最低点到最高点所经历的全部变化。
例如,一个正弦波的峰-峰值为10伏特,则其有效值为10 / (2 * √2) ≈ 3.54伏特。
有效值在电力系统中有着重要的应用,例如计算功率、电流负载等。
平均值平均值是指一个周期内交流电信号的平均数。
对于正弦波来说,其平均值为0,因为正弦波在一个周期内上升和下降的部分面积相等。
然而,在实际应用中,我们通常关注交流电信号的绝对值平均数。
这个平均数可以通过将正弦波进行整个周期的积分,并除以一个周期的长度来计算得到。
对于一个正弦波来说,其绝对值平均数等于其有效值乘以根号2 / π。
即:绝对值平均数 = 有效值* √2 / π。
例如,一个正弦波的有效值为3伏特,则其绝对值平均数为3 * √2 / π ≈1.35伏特。
瞬时值瞬时值是指交流电信号在某一时刻的具体数值。
由于交流电信号是随时间变化的,所以瞬时值可以看作是时间的函数。
对于正弦波来说,瞬时值可以表示为:V(t) = Vm * sin(ωt + φ)其中,V(t)表示瞬时值,Vm表示峰值,ω表示角频率,t表示时间,φ表示相位差。
三者之间的关系在一个周期内,交流电信号的瞬时值是不断变化的,而有效值和平均值则是对这些瞬时值进行综合考虑得到的。
交流电平均值、最大值、有效值
交流电的平均值、瞬时值、最大值、有效值1.从交流发电机来看这些概念的实值。
1、发电模式:N 匝线圈,其面积为S ,总电阻为r ,在一匀强磁场中(磁感应强度为B ),绕垂直于B 的轴,以角速度ω匀速转动;即构成交流电源;交流电源通过滑环和电刷引到外电路,即构成交流全电路。
2、概念的理解:A 、最大值,当线圈平面与磁场平行时,出现最大值。
最大电动势Em=NB ωS最大电流Im=rR Em +,R 两端的最大电压Um=I m ·R 。
注意:最大值与线圈的形状、以及转动轴处于线圈平面内哪个位置无关,但转轴应与磁感线垂直。
B 、瞬时值:交流全路中,其电动势、电流、电压、均随时间发生周期性变化,如从中性面开始计时,其瞬时值分别为:e=Emsin ωt i=Imsin ωt u=Umsin ωtC 、有效值:对于正弦(或余弦)交流电,有效值=2最大值 。
有效值也叫均方根值 即 E=2EmI=2ImU=2UmD 、 平均值: 对于某一段时间或某一过程,其平均感应电动势: I t NE 平均电流→∆∆∙=φ=U rR E 平均电压→+=I R ∙ 2、容易出现的错误:(1)有效值的理解:有效值=2最大值,学生容易把条件“正弦或余弦”交流电忽视,对于非正弦或余弦交流电,学生很难建立起电流热效应方程,以求解有效值。
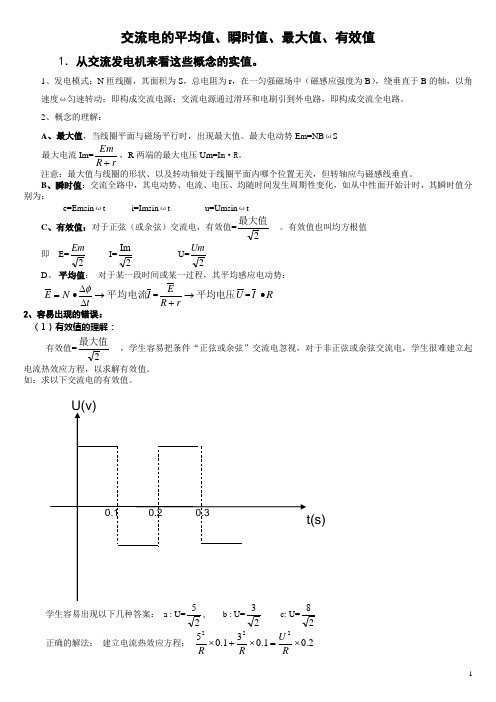
如:求以下交流电的有效值。
学生容易出现以下几种答案: a : U=2, b : U=2 c: U=2正确的解法: 建立电流热效应方程: 2.01.031.05222⨯=⨯+⨯RU R R 即: U=17 (V )注意:①各种交流用电器上所标的额定电压、电流均指有效值。
②交流电表的示数全为有效值。
③电器元件(如电容)的击穿电压(耐压值)指的是最大值,但保险丝熔断电流为有效值④一般所说交流电的值,均为有效值⑤ 求解交流电产生的热量问题时,必须用有效值,不能用平均值。
⑥中各量均为有效值。
⑦ 若计算通过电路某一截面的电量,需用电流的平均值。
高三物理交流电“四值”的理解与应用

交流电“四值”的理解与应用交变电流的大小和方向都随时间作周期性变化,所以要准确描述交变电流的产生的效果,需要用到“最大值、有效值、瞬时值、平均值”四个物理量。
交流电的“最大值、有效值、瞬时值、平均值”常称为交流电的“四值”。
这四个类似但又有区别的物理量,容易造成混乱,理解好“四值”对于学习交流电有极大的帮助。
一、准确把握概念1. 瞬时值:交流电流、电压、电动势在某一时刻所对应的值称为它们的瞬时值。
瞬时值随时间的变化而变化。
不同时刻,瞬时值的大小和方向均不同。
交流电的瞬时值取决于它的周期、幅值和初相位。
以正弦交流电为例(从中性面开始计时)。
则有:其瞬时值为:e=E m sinωt i=I m sinωt u=U m sinωt2.最大值:交变电流的最大值是指交变电流在一个周期内所能达到的最大值,它可以用来表示交变电流的强弱或电压的高低。
以正弦交流电为例。
则有:E m =nB ωS ,此时电路中的电流强度及用电器两端的电压都具有最大值,即I m =r R E m +, U m =I m R 。
3.有效值:交变电流的有效值是根据电流的热效应来定义的,让交变电流和恒定电流通过相同阻值的电阻,如果在相同的时间内产生的热量相等,我们就把这一恒定电流的数值叫做这一交变电流的有效值。
4.平均值:交变电流的平均值是指在某一段时间内产生的交变电流对时间的平均值。
对于某一段时间或某一过程,其平均感应电动势: I t N E 平均电流→∆∆∙=φ=U rR E 平均电压→+=I R ∙二、正弦交流电的“四值”之间的关系1、正弦交流电的有效值与最大值的关系: U=m mU U 707.02=,I=m mI I 707.02=注:I U 是电流、电压的有效值,I m 、U m 是电流、电压的最大值2、正弦交流电的平均值与最大值和有效值的关系:m m P I I I 637.02==π,m m P U U U 637.02==π,I I P 90.0=,U U P 90.0=注:I p 、U p 是电流、电压的平均值三、“四值”的应用例1、有一正弦式交流电源,电压有效值U=120V ,频率为f=50Hz 向一霓虹灯供电,若霓虹灯的激发电压和熄灭电压均为U 0=602V ,试估算在一个周期内,霓虹灯发光时间有多长?为什么人眼不能感到这种忽明忽暗的现象?解析:如图1所示,画出一个周期内交流电的U-t 图象,其中阴影部分对应的时间t 1表示霓虹灯不能发光的时间,根据对称性,一个周期内霓虹灯不能发光的时间为4t 1,据u=U m sinωt 求得t 1=(1/600)s 再由对称性一个周期内能发光的时间:t=T-4t 1=(1/75)s 很明显霓虹灯在工作过程中是忽明忽暗的,而熄灭的时间间隔只有(1/300)s ,(如图1中t 2时刻到t 3时刻)由于人的眼睛具有视觉暂留现象,而这个视觉暂留时间约(1/16)s 为远大于(1/300)s ,因此经过灯光刺激的人眼不会因为短暂的熄灭而有所感觉。
交流电平均值、最大值、有效值的详细区别

交流电平均值、瞬时值、最大值、有效值林永德在交流电教学中,历届学生对交流电的瞬时值、最大值、有效值、平均值的理解容易出错,有的乱用方式,有的忽视条件,如果在教学中注意以下两个方面,可以有效地防止学生所出的错误。
1.以交流发电模式为主体,揭示概念的实值。
① 发电模式:N 匝线圈,其面积为S ,总电阻为r ,在一匀强磁场中(磁感应强度为B ),绕垂直于B 的轴,以角速度ω匀速转动;即构成交流电源;交流电源通过滑环和电刷引到外电路,即构成交流全电路。
② 概念的理解:A 、最大值,当线圈平面与磁场平行时,出现最大值。
最大电动势Em=NB ωS最大电流Im=rR Em +,R 两端的最大电压Um=I m ·R 。
B 、瞬时值:交流全路中,其电动势、电流、电压、均随时间发生周期性变化,如从中性面开始计时,其瞬时值分别为:e=Emsin ωt i=Imsin ωt u=Umsin ωtC 、有效值:对于正弦(或余弦)交流电,有效值=2最大值。
即 E=2EmI=2ImU=2UmD 、 平均值: 对于某一段时间或某一过程,其平均感应电动势: I tN E 平均电流→∆∆∙=φ=U r R E 平均电压→+=I R ∙ 2、学生容易出现的错误:(1)有效值的理解:有效值=2最大值,学生容易把条件“正弦或余弦”交流电忽视,对于非正弦或余弦交流电,学生很难建立起电流热效应方程,以求解有效值。
如:求以下交流电的有效值。
学生容易出现以下几种答案: a : U=25, b : U=23c: U=28正确的解法: 建立电流热效应方程: 2.01.031.05222⨯=⨯+⨯RU R R 即: U=17 (V )(2)平均值的理解:如:交流发电模式中,从中性面开始,转过060,求此过程的平均电动势。
学生容易出现以下错误,把平均电动势理解为电动势的平均值,即E =S NB Em e e ω43260sin 02021=+=+ 正确的解法: E =N πωωπφ2326160cos 0S NB BS BS N t =∙-=∆∆ (3)求解功率或电热用交流电源给外电路供电,在求解功率或电热问题的时候,学生很容易把平均值与有效值混淆。
交变电流的瞬时值、峰值、有效值和平均值的比较

交变电流的瞬时值、峰值、有效值和平均值的比较例4如图14所示,N=50匝的矩形线圈abcd,ab边长l1=20 cm,ad边长l2=25 cm,放在磁感应强度B=0.4 T的匀强磁场中,外力使线圈绕垂直于磁感线且通过线圈中线的OO′轴以n=3 000 r/min的转速匀速转动,线圈电阻r=1 Ω,外电路电阻R=9 Ω,t=0时线圈平面与磁感线平行,ab边正转出纸外、cd边转入纸里.求:图14(1)t=0时感应电流的方向;(2)感应电动势的瞬时值表达式;(3)线圈转一圈外力做的功;(4)从图示位置转过90°的过程中流过电阻R的电荷量.t =0时线圈平面与磁感线平行,ab 边正转出纸外,cd 边转入纸里.答案 (1)感应电流方向沿adcba(2)e =314cos (100πt ) V (3)98.6 J (4)0.1 C解析 (1)根据右手定则,线圈感应电流方向为adcba . (2)线圈的角速度 ω=2πn =100π rad/s图示位置的感应电动势最大,其大小为 E m =NBl 1l 2ω代入数据得E m =314 V 感应电动势的瞬时值表达式 e =E m cos ωt =314cos (100πt ) V . (3)电动势的有效值 E =E m2线圈匀速转动的周期 T =2πω=0.02 s线圈匀速转动一圈,外力做功大小等于电功的大小,即 W =I 2(R +r )T =E 2R +r·T 代入数据得W ≈98.6 J.(4)从t =0起线圈转过90°的过程中,Δt 内流过R 的电荷量: q =N ΔΦ(R +r )Δt Δt =NB ΔS R +r =NBl 1l 2R +r 代入数据得q =0.1 C.。
交流电平均值、最大值、有效值的详细区别

交流电平均值、瞬时值、最大值、有效值林永德在交流电教学中,历届学生对交流电的瞬时值、最大值、有效值、平均值的理解容易出错,有的乱用方式,有的忽视条件,如果在教学中注意以下两个方面,可以有效地防止学生所出的错误。
1.以交流发电模式为主体,揭示概念的实值。
① 发电模式:N 匝线圈,其面积为S ,总电阻为r ,在一匀强磁场中(磁感应强度为B ),绕垂直于B 的轴,以角速度ω匀速转动;即构成交流电源;交流电源通过滑环和电刷引到外电路,即构成交流全电路。
② 概念的理解:A 、最大值,当线圈平面与磁场平行时,出现最大值。
最大电动势Em=NB ωS 最大电流Im=rR Em +,R 两端的最大电压Um=I m ·R 。
B 、瞬时值:交流全路中,其电动势、电流、电压、均随时间发生周期性变化,如从中性面开始计时,其瞬时值分别为:e=Emsin ωt i=Imsin ωt u=Umsin ωtC 、有效值:对于正弦(或余弦)交流电,有效值=2最大值。
即 E=2EmI=2ImU=2UmD 、 平均值: 对于某一段时间或某一过程,其平均感应电动势: I tN E 平均电流→∆∆•=φ=U r R E 平均电压→+=I R • 2、学生容易出现的错误:(1)有效值的理解:有效值=2最大值,学生容易把条件“正弦或余弦”交流电忽视,对于非正弦或余弦交流电,学生很难建立起电流热效应方程,以求解有效值。
如:求以下交流电的有效值。
学生容易出现以下几种答案: a : U=25, b : U=23c: U=28正确的解法: 建立电流热效应方程: 2.01.031.05222⨯=⨯+⨯RU R R 即: U=17 (V )(2)平均值的理解:如:交流发电模式中,从中性面开始,转过060,求此过程的平均电动势。
学生容易出现以下错误,把平均电动势理解为电动势的平均值,即E =S NB Em e e ω43260sin 02021=+=+ 正确的解法: E =N πωωπφ2326160cos 0S NB BS BS N t =•-=∆∆ (3)求解功率或电热用交流电源给外电路供电,在求解功率或电热问题的时候,学生很容易把平均值与有效值混淆。
交流电“四值”辩析

交流电“四值”辩析作者:姜启时来源:《数理化学习·高一二版》2013年第04期交流电的瞬时值、最大值、有效值、平均值的意义不同,只有充分理解其内涵,才能正确运用,减少失误,现例析如下:一、有效值与平均值交流电有效值是利用电流的热效应定义的,即交变电流通过某一电阻时产生的热量与直流电通过同一电阻在相同时间内产生的热量相等,则直流电的数值就是该交变电流的有效值,有效值用来计算电功率、电热等,交变电流表读数和用电器标定值均为有效值.平均值由=nΔΔt计算,而不是两时刻瞬时值的平均数,在交流电的一个周期中,Δt不同,平均值也不同,平均值常用来计算交变电流在一段时间内通过导线截面的电荷量q=t=nΔR,(=R),R为该回路的总电阻.电器元件(电容)的击穿电压为交流的最大值,但保险丝的熔断电流为有效值.图1例1如图1所示,匀强磁场的磁感应强度B =0.5 T,边长L=10 cm的正方形线圈abcd 共100匝,线圈电阻r =1 Ω,线圈绕垂直于磁感线的对称轴OO′匀速转动,角速度ω=2πrad/s,外电路电阻R=4 Ω,求:(1)转动过程中感应电动势的最大值;(2)由图示位置转过60°角时的瞬时感应电动势;(3)由图示位置转过60°角的过程中产生的平均感应电动势;(4)交变电压表的示数;(5)线圈转动一周外力所做的功;(6)由图示位置转过90°角,通过R的电荷量为多少?解析:(1)感应电动势的最大值Em=NBωS = 3.14 V.(2)转过60°时的瞬时感应电动势为e=Emcos60°=3.14×0.5 V = 1.57 V.(3)转过60°角过程中产生的平均感应电动势为=NΔΔt=NBSsin60°T/6=2.6 V.(4)电压表示数为外电路电压的有效值U=ER+r·R=Em/2R+r·R=1.78 V.(5)转动一周外力做功等于电流产生的热量 W=Q=E2R+r T=(Em/2)2R+rT=0.99 J.(6)交变电的周期T=2πω=1 s , 14周期内通过电阻R的电荷量q=·T4=R+r·T4=nBSR+r=0.1 C.点拨:求电功、电功率、焦耳热以及确定保险丝的熔断电流等物理量时,要用有效值计算.交流电压表、电流表所测的数值均是指有效值,一些交流电器铭牌上所标的额定电压(电流)值也是指有效值. 求一段时间内通过导体横截面的电荷量时要用平均值,即q=t,平均值的计算须用=nΔΔt和=R计算,切记≠E1+E22,平均值不等于有效值.二、有效值与最大值正弦交流电瞬时值随时间做周期性变化,表达式为e=Emcosωt,其电动势最大值Em=NBSω.图2 例2如图2表示一交流电随时间而变化的图象,其中电流的正值为正弦曲线的正半周,其最大值为Im;电流的负值的强度为 -Im,则该交变电流的有效值为多少?解析:在各正半周内交流电为正弦交流,相应有效值I1=Im2;各负半周为方波交流电,相应有效值即为I2 =Im ,取电阻为R ,考虑一个周期内的热效应,设该交变电流的有效值I ,根据有效值的定义有 I2RT=I21RT2+I22RT2,由此得该交变电流的有效值I=I21+I222=32Im.点拨:求交变电流有效值的方法:①I=Im2,U=Um2,E=Em2 计算,只适用于正弦式交流电;②利用有效值的定义计算(非正弦式交流电);(3)当有电能和其他形式的能转化时,利用能的转化和守恒定律来求有效值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
交流电的瞬时值、最大值、有效值和平均值
交变电流的大小和方向都随时间作周期性变化,所以要
准确描述交变电流的产生的效果,需要用到“最大值、有效
值、瞬时值、平均值”四个物理量。
交流电的“最大值、有
效值、瞬时值、平均值”常称为交流电的“四值”。
这四个
类似但又有区别的物理量,容易造成混乱,理解好“四值”
对于学习交流电有极大的帮助。
一、 准确把握概念
1. 瞬时值:交流电流、电压、电动势在某一时刻所对
应的值称为它们的瞬时值。
瞬时值随时间的变化而变化。
不
同时刻,瞬时值的大小和方向均不同。
交流电的瞬时值取决
于它的周期、幅值和初相位。
以正弦交流电为例(从中性面
开始计时)。
则有:
其瞬时值为:e=E m sinωt
i=I m sinωt u=U m sinωt
2.最大值:交变电流的最大值是指交变电流在一个周
期内所能达到的最大值,它可以用来表示交变电流的强弱或
电压的高低。
以正弦交流电为例。
则有:
E m =nB ωS ,此时电路中的电流强度及用电器两端的电压都具
有最大值,即I m =
r R E m , U m =I m R 。
3.有效值:交变电流的有效值是根据电流的热效应来定
义的,让交变电流和恒定电流通过相同阻值的电阻,如果在
相同的时间内产生的热量相等,我们就把这一恒定电流的数
值叫做这一交变电流的有效值。
交流电的有效值是根据它的热效应确定的。
交流电流i 通过电阻R在一个周期内所产生的热量和直流电流I通过同一电阻R在相同时间内所产生的热量相等, 则这个直流电流I的数值叫做交流电流i的有效值, 用大写字母表示, 如I、U 等。
一个周期内直流电通过电阻R所产生的热量为:
交流电通过同样的电阻R,在一个周期内所产生热量:根据定义,这两个电流所产生的热量应相等,即
将代入上式i=I m sinωt
4.平均值:交变电流的平均值是指在某一段时间内产生的交变电流对时间的平均值。
对于某一段时间或某一过程,其平均感应电动势:
I t
N E 平均电流→∆∆•=φ=U r R E 平均电压→+=I R •
二、正弦交流电的“四值”之间的关系
1、正弦交流电的有效值与最大值的关系: U=
m m U U 707.02=,I=m m
I I 707.02= 注:I U 是电流、电压的有效值,I m 、U m 是电流、电压的最大值
2、正弦交流电的平均值与最大值和有效值的关系:m m P I I I 637.02
==π,m m P U U U 637.02
==π,I I P 90.0=,U U P 90.0=
注:I p 、U p 是电流、电压的平均值
三、“四值”解题方法小结:
交变电流有四值,即有效值、平均值、最大值和瞬时值.各值何时应用,对照如下情况确定:
(1)在研究电容器是否被击穿时,要用峰值(最大值).因电容器上标明的电压是它在直流电源下工作时所承受的最大值.
(2)在研究交变电流的功率和产生的热量时,只能用有效值.
(3)在求解某一时刻线圈受到的磁力矩时,只能用瞬时值.
(4)在求交变电流流过导体的过程中通过导体截面积的电量时,要用平均值.。
