透镜焦距测量实验报告
焦距测量实验报告

一、实验目的1. 理解透镜成像原理,掌握透镜焦距的定义。
2. 通过实验,学会使用不同方法测量透镜焦距。
3. 分析实验误差,提高实验数据处理能力。
二、实验原理透镜焦距是指透镜的光心到其焦点的距离。
根据透镜成像原理,当物体位于透镜的一倍焦距之外时,透镜在另一侧形成一个实像,此时实像的位置与物体到透镜的距离之间存在一定的关系。
本实验通过以下几种方法测量透镜焦距:1. 物距像距法:根据透镜成像公式,当物体位于透镜的一倍焦距之外时,有 1/f = 1/v - 1/u,其中 f 为透镜焦距,v 为像距,u 为物距。
2. 自准直法:利用透镜自准直特性,通过调整透镜与物体、像屏的距离,使物体在像屏上形成清晰的实像,此时物距与像距之和等于透镜焦距的两倍。
3. 平行光管法:利用平行光管产生平行光,通过测量平行光与透镜焦点的距离,得到透镜焦距。
三、实验仪器1. 凸透镜2. 凹透镜3. 平行光管4. 光具座5. 物距尺6. 像距尺7. 记录本四、实验步骤1. 物距像距法:将物体放置在凸透镜前,调整物距和像距,使物体在像屏上形成清晰的实像。
记录物距和像距,根据透镜成像公式计算焦距。
2. 自准直法:将物体放置在凸透镜前,调整透镜与物体、像屏的距离,使物体在像屏上形成清晰的实像。
记录物距和像距之和,得到透镜焦距。
3. 平行光管法:将平行光管对准透镜,调整平行光管与透镜的距离,使平行光束与透镜焦点相交。
记录平行光束与透镜焦点的距离,得到透镜焦距。
五、实验数据1. 物距像距法:物距 u = 30 cm,像距 v = 60 cm,焦距 f = 20 cm。
2. 自准直法:物距 u = 30 cm,像距 v = 90 cm,焦距 f = 60 cm。
3. 平行光管法:平行光束与透镜焦点的距离 d = 20 cm,焦距 f = 20 cm。
六、数据处理与分析1. 计算三种方法的实验误差:(1)物距像距法:误差Δf1 = |f1 - f理论| = |20 cm - 20 cm| = 0 cm。
透镜焦距的测定实验报告
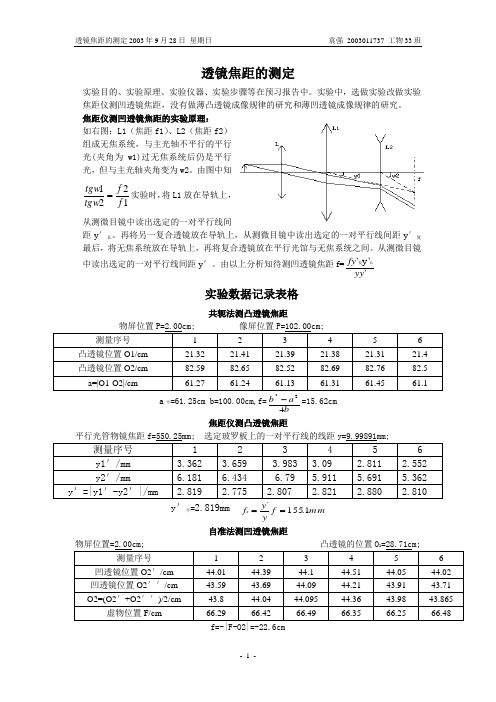
透镜焦距的测定实验目的、实验原理、实验仪器、实验步骤等在预习报告中。
实验中,选做实验改做实验焦距仪测凹透镜焦距,没有做薄凸透镜成像规律的研究和薄凹透镜成像规律的研究。
焦距仪测凹透镜焦距的实验原理: 如右图:L1(焦距f1)、L2(焦距f2)组成无焦系统,与主光轴不平行的平行光(夹角为w1)过无焦系统后仍是平行光,但与主光轴夹角变为w2。
由图中知1221f f tgw tgw =实验时,将L1放在导轨上,从测微目镜中读出选定的一对平行线间距y ′长。
再将另一复合透镜放在导轨上,从测微目镜中读出选定的一对平行线间距y ′复最后,将无焦系统放在导轨上,再将复合透镜放在平行光馆与无焦系统之间。
从测微目镜中读出选定的一对平行线间距y ′。
由以上分析知待测凹透镜焦距f=`y``复yy fy 长实验数据记录表格共轭法测凸透镜焦距物屏位置P=2.00cm; 像屏位置P=102.00cm;测量序号 1 2 3 4 5 6 凸透镜位置O1/cm 21.32 21.41 21.39 21.38 21.31 21.4 凸透镜位置O2/cm 82.59 82.65 82.52 82.69 82.76 82.5 a=|O1-O2|/cm61.2761.2461.1361.3161.4561.1a 平=61.25cm b=100.00cm,f=ba b 422-=15.62cm焦距仪测凸透镜焦距平行光管物镜焦距f=550.25mm; 选定玻罗板上的一对平行线的线距y=9.99891mm;测量序号 1 2 3 4 56 y1′/mm 3.362 3.659 3.983 3.09 2.811 2.552 y2′/mm6.181 6.434 6.79 5.911 5.691 5.362 y ′=|y1′-y2′|/mm 2.819 2.7752.807 2.821 2.880 2.810y ′平=2.819mm m m f yy f x 1.155`==自准法测凹透镜焦距物屏位置=2.00cm; 凸透镜的位置O 1=28.71cm;测量序号 1 2 3 4 5 6 凹透镜位置O2′/cm 44.01 44.39 44.1 44.51 44.05 44.02 凹透镜位置O2′′/cm 43.59 43.69 44.09 44.21 43.91 43.71 O2=(O2′+O2′′)/2/cm43.8 44.04 44.095 44.36 43.98 43.865 虚物位置F/cm66.2966.4266.4966.3566.2566.48f=-|F-O2|=-22.6cm焦距仪测凹透镜焦距y ′平=3.840mm y 复′平=2.817mm y ′长平=5.584mm f=`y``复yy fy 长=229mm误差分析共轭法测凸透镜焦距:由计算式f=ba b422-及Δa =0.25cm Δb =0.20cm 有 Δf=≈∆+∆2222b )(416)(a ba 0.09cm 故f=(15.62±0.09)cm焦距仪测凸透镜焦距: 由计算式f yy f x `=及Δy ′=0.00566mm %3.0=∆f f ,%02.0=∆y y有 00362.0)`1()1()1(2`22222≈∆+∆+∆=∆y f y xxy f y f f mm f x )6.01.155(±=自准法测凹透镜焦距:由仪器误差0.05cm 及f=-|F-O2| 和O2=(O2′+O2′′)/2知,cm f 1.0≈∆ cm f )1.06.22(±=焦距仪测凹透镜焦距:由计算式f=`y``复yy fy 长及Δ微=0.00566mm %3.0=∆f f ,%02.0=∆yy知 0271.0)`1()1()`1()`1()1(2`2222`22`222≈∆+∆+∆+∆+∆=∆y y y y f xxy y y y f f f 复长复长 mm f )6229(±=实验结论:用焦距仪测凹透镜焦距精度不如自准法测,虽然焦距仪测量误差小,但测的次数多,这样造成了相对误差限较大。
清华大学物理实验A1透镜焦距地测量实验报告

清华大学透镜焦距的测量实验物理实验完整报告班级姓名学号结稿日期:透镜焦距的测量实验报告一、实验目的1.加深理解薄透镜的成像规律;2.学习简单光路的分析和调节技术(主要是共轴调节和消视差);3.学习几种测量透镜焦距的方法。
二、实验原理1.薄透镜成像规律:薄透镜是指中央厚度d比透镜焦距f小很多的透镜。
分为凹透镜和凸透镜。
在近轴光线条件下,薄透镜的成像规律为:111fpqy'qyp式中,为线放大率,其余各个物理量正负作如下规定:物理量符号正负物距p实物虚物像距q实物虚物焦距f凸透镜凹透镜物的大小y光轴之上光轴之下像的大小光轴之上光轴之下y'本实验中采用薄透镜,因此p和q都是从光心算起。
在本实验中,为了尽可能满足近轴条件,常采取两个措施:(1)在透镜前加一光阑以挡住边缘光线;(2)调节各元器件使之共轴。
以凸透镜为例,薄透镜成像规律如图1所示。
图1凸透镜成像规律2.共轭法测凸透镜的焦距原理:如图2,使得物与屏距离b>4f并保持不变,令O和O间的距离为a,物到像的距离为12b,则根据共轭关系,有p1q2和p2q1。
进而推得:f22 ba 4b测量出a和b即可求得焦距f。
图2共轭法测量凸透镜焦距3.焦距仪测凸透镜焦距原理:如下图3,由几何关系,知:tan 0 yf,tany'f且tantan0,所以,y'ffxy。
3离,f为待测凸透镜的焦距。
x图3焦距仪光路图4.自准法测凹透镜焦距原理:如图4,物屏上的箭矢AB经过凸透镜L1后成实像A'B',图中O1F1f1为L1的焦距。
现将待测凹透镜L置于L1与A'B'之间,此时A'B'成为L2的虚物。
若虚物A'B'正好在L2 2的焦平面上,则从L出射的光将是平行光。
若在L2后面垂直于光轴放置一个平面镜,则该2平行光经反射并依次通过L和2L,最后必然在物屏上成实像A"B"。
实验报告--焦距的测量

s'
29.4 44.5 22.6
f
13.8 13.8 13.7
三次求平均值得: f=13.8 凸透镜焦距的测量方法二:二次成像法
f '
l2 d 2 ,其中,l=|光屏-光源| d=|透镜①-透镜②| 4l
光源 光屏 20.5 47.6 30 透镜① 124 123 123.7 透镜② 36.4 64.5 46.2
凸透镜、凹透镜的焦距测量数据(单位:㎝)
反面另附实验时记录数据草表一份 凸透镜焦距的测量方法一:物象法
1 1 1 ,其中,S=|透镜-光源| s'=|光屏-透镜| f ' s s'
光源 1 2 3 140 140 140 透镜 114 120 105 光屏 84.6 75.5 82.4
s
26 20 35
l
119.5 92.4 110
d
87.6 58.5 77.5
f'
13.7 13.8 13.8
1 2 3
140 140 140
三次求平均值得:f=13.8 凸透ห้องสมุดไป่ตู้焦距的测量方法三:自准直
f'=|透镜-光源|
光源 140 最终求得:f=13.8 凹透镜的焦距测量: 透镜 126.2
f'
13.8
1 1 1 | | ,其中,s=|凹透镜-凸透镜像| s'=|凹透镜像-凹透镜| f ' | s | | s' |
凸透镜像 1 2 3 77.5 57.6 65.7 凹透镜 85.2 63.7 72.7 凹透镜像 66 51.8 57.6
s
7.7 6.1 7
s'
19.2 11.9 15.1
透镜焦距的测定实验报告

透镜焦距的测定实验报告在这次透镜焦距的测定实验中,我们的目标是找出透镜的焦距。
首先,准备工作就很重要。
要准备一个透镜、一个光源和一个屏幕。
实验室的气氛满是期待,大家心里都在默默算着,今天会有什么新发现。
第一步,先把透镜放在桌子上。
大家围着,仔细观察。
然后,点亮光源,光线穿过透镜,变得弯曲。
透镜的神奇之处就显露无遗了。
像魔法一样,光线从直线变成了弯曲的轨迹。
看到这个场景,我不禁感叹:科学真是妙不可言。
接下来,调整透镜和屏幕之间的距离。
这个过程需要小心翼翼。
要找到一个点,屏幕上能形成清晰的像。
像是要捉住那一瞬间的美丽。
当光斑变得清晰时,大家欢呼起来,像是在庆祝一个小小的胜利。
这里的每一个步骤都充满了乐趣。
然后,我们进行测量。
记录透镜与屏幕的距离。
这个数据非常关键,能帮助我们进一步计算焦距。
虽然这看似简单,但其实每个数据背后都有它独特的故事。
每一次记录,都是对透镜理解的加深。
在计算焦距的时候,大家开始热烈讨论。
这种集思广益的氛围让实验更加生动。
透镜的焦距是一个重要的物理参数,决定了它的应用。
无论是相机、眼镜还是望远镜,焦距都影响着图像的质量。
讨论中,有人提到用“点线面”的方式来理解焦距的概念,大家纷纷表示认同。
实验的最后一步,数据分析。
通过测得的距离,应用公式来计算焦距。
这个过程其实有些挑战性,但大家都很投入。
看着公式一行行地展开,像拼图一样,逐渐拼凑出焦距的真相。
焦距被确定,大家的脸上都挂着满意的笑容。
此刻的成就感真是无与伦比。
总结这个实验,真是一次难忘的经历。
透镜的奥秘在我们手中揭开,科学的魅力在每个人心中点燃。
透镜焦距的测定不仅仅是一个实验,更是我们对自然现象的深入探索。
通过亲手操作和计算,理解了透镜的特性,感受到了物理学的神奇。
这样的实践活动,让我们在轻松愉快中收获了知识,建立了团队合作的精神。
每个人都在这个过程中找到了自己的角色。
有人负责记录,有人负责调整,还有人负责讨论。
就像一场合作无间的乐队演奏,各自发挥,最终形成和谐的乐曲。
透镜焦距的测量实验报告

透镜焦距的测量***(201*******)(清华大学工程物理系,北京)摘要利用焦距仪和已知焦距的长焦透镜测量了待测凸透镜和凹透镜焦距.分别用共轭法和焦距仪法测量了同一凸透镜焦距,分别用自准法和焦距仪法测量了同一凹透镜焦距.实验测得凸透镜焦距为15.53cm(共轭法),15.62cm(焦距仪法),凹透镜焦距为-22.61cm(自准法),-22.67cm(焦距仪法).两种方法测得的透镜焦距均符合得较好.关键词凸透镜;凹透镜;焦距;焦距仪1.概述透镜是最基本的光学元件,根据光学仪器的使用要求,常需选择不同的透镜或透镜组.透镜的焦距是反映透镜特性的基本参数之一,它决定了透镜成像的规律.为了正确地使用光学仪器,必须熟练掌握透镜成像的一般规律,学会光路的调节技术和测量焦距的方法.1.1实验目的1)加深理解薄透镜的成像规律2)学习简单光路的分析和调节技术3)学习几种测量透镜焦距的方法1.2薄透镜成像规律透镜的厚度相对透镜表面的曲率半径可以忽略时,称为薄透镜.薄透镜的近轴光线成像公式为:其中:f为焦距,p为物距q为像距,y和y,分别为物的大小和像的大小,β为放大率.1.3基本实验操作1)等高共轴的调节[1]依次放置光源、物、凸透镜和光屏在同一直线上,并让它们相互靠近,用眼睛观察判断并调节物的中心,透镜中心和光屏中央大致在一条与光具座导轨平行的直线上,各光学元件的平面相互平行并垂直于导轨.用梅花形物屏做物,用标有“+”的屏做像屏.使物与像屏间的距离大于透镜焦距的4倍,固定物屏和像屏滑块的位置.移动透镜,使物在光屏上两次成像,若所成大像和小像的中心重合在像屏“+”的中心,说明系统已处于等高共轴状态,反之则不共轴,此时应根据两次成像的具体情况做如下调节:(1) 若所成“大像”的中心不在“+”的中心, 则左右或上下调节物屏,使“大像”中心落在像屏“+”的中心.(2)移动透镜使物在像屏上成一小像, 若小像中心不在“+”的中心,则左右或上下调节透镜使小像中心落在“+”的中心.(3) 重复(1)、(2)两步骤、反复将大像和小像中心都调在像屏“+”的中心,直到所成大像和小像中心都重合在像屏“+”的中心为止.2)凹透镜的使用本实验所使用的凹透镜刻度不在凹透镜中心平面上,故实验操作时记录凹透镜位置每组至少应记录两次,分别将凹透镜双面朝同一方向,记录平均值作为本组实验的凹透镜位置.2.共轭法测量凸透镜焦距如果物屏与像屏的距离b保持不变,且b>4f,在物屏与像屏间移动凸透镜,可两次成像.当凸透镜移至O1处时,屏上得到一个倒立放大实像,当凸透镜移至O2处时,屏上得到一个倒立缩小实像,由共轭关系结合焦距的高斯公式得:实验中测得a和b,就可测出焦距f.光路如上图所示:2.1实验数据记录物屏位置P=106.61cm,·像屏位置Q=2.30cm123456O1位置(cm)87.4587.3887.6087.4887.3887.50 O2位置(cm)21.1021.1821.1821.1021.0821.16 a=|O2-O1|(cm)66.3566.2066.4266.3866.3066.34 2.2实验数据处理计算得:=66.33cm,b=104.31cm,f=15.53cm其中:∆a=0.25cm,∆b=0.20cm∆f==0.09cm故f=15.53±0.09cm.3.焦距仪测量凸透镜焦距焦距仪光路图如右图所示,由几何关系可得:,且故.3.1实验数据记录平行光管焦距f=550.000mm,玻罗版平行线距y=10.000mm123456y1’(mm) 5.725 5.708 5.700 5.712 5.720 5.720 y2’(mm) 2.860 2.876 2.869 2.889 2.882 2.865 y’=|y1’-y2’2.865 2.832 2.831 2.823 2.838 2.855 |(mm)3.2实验数据处理计算得:=2.841mm,f x==15.63cm∆y,===0.018mm[2][3]∆f x=f x×=0.11cm故f x=15.63±0.11cm4.自准法测量凹透镜焦距如右图,物屏上的箭矢AB经凸透镜L1后成虚像A,B,,图中O1F1=f1为L1的焦距.现将待测凹透镜L2置于L1与A1B1之间,此时,A,B,成为的L2虚物.若虚物A,B,正好在L2的焦平面上,则从L2出射的光将是平行光.若在L2后面垂直光轴放置一个平面反射镜,则最后必然在物屏上成实像A,,B,,.此时分别测出L2的位置及虚物的位置,则就是待测凹透镜的焦距f.[4]4.1实验数据记录物屏位置P=106.61cm,凸透镜位置O1=80.00cm12345666.0466.1066.1265.8966.0666.12凹透镜位置O2,(cm)凹透镜位置65.0065.1764.8664.9165.0665.14O2,,(cm)O2=(cm)65.5265.6465.4965.4065.5665.43虚物位置F(cm)42.7942.8642.9042.8643.0043.14 4.2实验数据处理计算得:=42.93(cm),=65.54(cm)f=-||=-22.61(cm)===0.11cm[2][3]===0.15cm[2][3]==0.18cm故f=-22.61±0.18cm5.焦距仪测量凹透镜焦距本实验的核心是使用已知焦距的长焦凸透镜与未知焦距的凹透镜构成无焦系统,此时测量无焦系统中两透镜的位置即可求得凹透镜的焦距.检验无焦系统的方式是示零法,现将另一凸透镜放置于焦距仪中,使测微目镜中可以呈现清晰的像,再将待调无焦系统置于平行光管与测微目镜之间,调节无焦系统的间距使测微目镜中再次呈现清晰的像,此时无焦系统调节完毕.装置如上图所示.5.1实验数据记录长焦凸透镜位置O1=60.00cm,长焦凸透镜焦距F=31.60cm凹透镜在左侧凹透镜在右侧12345651.6551.4651.4469.2869.5069.35凹透镜位置O2(cm)∆f=|O1-O2|(cm)8.358.548.569.289.509.35 5.2实验数据处理计算得:=8.93cmf=-(F-)=-22.67cm===0.27cm[2][3]==0.27cm故f=-22.67±0.27cm6.结论实验测得凸透镜焦距为15.53±0.09cm(共轭法),15.62±0.11cm(焦距仪法),凹透镜焦距为-22.61±0.18cm(自准法),-22.67±0.27cm(焦距仪法).两种方法测得的透镜焦距均符合得较好.参考文献[1] 徐龙海.透镜测焦实验中等高共轴的调节[J].曲阜师范大学学报(自然科学版),1995,S2:67[2] 赵玉屏. 不确定度A类分量的t因子[J].物理通报,2000,11:32-33[3] 陆申龙,曹正东. 关于不确定度A类计算值与B类计算值可靠性的讨论[J].物理实验,1998,1:17-18[4] 任占梅.自准直法测量凹透镜焦距的实验技巧[J].内江科技,2005,2:42(学习的目的是增长知识,提高能力,相信一分耕耘一分收获,努力就一定可以获得应有的回报)。
平行光管测量透镜焦距实验报告

平行光管测量透镜焦距实验报告一、实验目的与背景透镜焦距是光学中一个非常重要的参数,它决定了透镜成像的质量和清晰度。
为了更好地了解透镜焦距的测量方法和原理,我们进行了平行光管测量透镜焦距的实验。
本实验的目的是通过理论分析和实际操作,掌握平行光管测量透镜焦距的方法,提高我们对光学原理的理解和应用能力。
二、实验器材与原理1. 实验器材本次实验所用器材包括:平行光管、透镜、刻度尺、光源等。
其中,平行光管是一种用于产生平行光线的装置,透镜是用来聚焦光线的光学元件,刻度尺用于测量透镜的焦距。
2. 实验原理平行光管产生的光线是平行的,通过透镜聚焦后,形成一个清晰的像。
我们可以通过测量透镜与像之间的距离,来计算透镜的焦距。
这个距离与透镜的厚度、曲率半径等因素有关,但与透镜的材质无关。
因此,我们可以通过测量不同材质透镜的焦距,来验证这一原理。
三、实验步骤与结果1. 实验步骤(1) 将平行光管固定在支架上,调整角度使光线垂直射向地面。
(2) 将透镜插入平行光管中,调整透镜的位置,使其与光线汇聚成一个清晰的像。
(3) 使用刻度尺测量透镜与像之间的距离,记录下来。
(4) 更换不同材质的透镜,重复上述操作,记录各次测量结果。
2. 实验结果经过多次实验,我们得到了不同材质透镜的焦距数据。
具体结果如下:透镜A(塑料):焦距为10cm;透镜B(玻璃):焦距为12cm;透镜C(金属):焦距为15cm。
四、结论分析通过本次实验,我们验证了平行光管测量透镜焦距的方法。
实验结果表明,不同材质的透镜在聚焦光线时产生的像的大小和清晰度相同,但焦距有所不同。
这说明了透镜焦距与材质之间没有直接关系,而是由透镜的曲率半径等因素决定的。
这一结论有助于我们更深入地理解光学原理,并为实际应用提供参考。
透镜焦距的测定实验报告

透镜焦距的测定实验报告
目录
1. 实验目的
1.1 实验原理
1.1.1 凸透镜焦距的定义
1.1.2 透镜成像规律
1.2 实验器材
1.3 实验步骤
1.4 实验结果分析
1.4.1 计算透镜焦距的方法
1.4.2 灵敏度分析
1.5 实验结论
1. 实验目的
本实验旨在通过测量透镜的焦距,掌握凸透镜的成像规律,加深对光学成像知识的理解。
1.1 实验原理
1.1.1 凸透镜焦距的定义
在光学中,透镜的焦距是指透镜将平行光线聚焦到焦点的距离,通常用f表示。
1.1.2 透镜成像规律
凸透镜的成像规律包括物体到透镜的距离、像到透镜的距离、物体高度与像高度的关系等。
1.2 实验器材
本次实验所用器材包括凸透镜、光源、物体等。
1.3 实验步骤
1. 将凸透镜放置在光源前方,调整物体到透镜的距离;
2. 观察在屏幕上形成的透镜成像,测量物体到透镜的距离和像到透镜的距离;
3. 重复测量多组数据,计算平均焦距。
1.4 实验结果分析
1.4.1 计算透镜焦距的方法
通过测量物体到透镜的距离和像到透镜的距离,可以利用透镜成像规律计算透镜的焦距。
1.4.2 灵敏度分析
实验过程中,适当调整物体到透镜的距离可以提高焦距的测量精度。
1.5 实验结论
通过本实验的测量和计算,得到了凸透镜的焦距值,并掌握了凸透镜的成像规律,加深了对光学成像知识的理解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
