全等三角形SAS练习题(基础)
《用“SAS”证三角形全等》练习题

解: ∵C 是线段 AB 的中点, ∴AC=CB, ∵CD∥BE, ∴∠ACD=∠B, AC=CB, 在△ACD 和△CBE 中,∠ACD=∠B,∴△ACD≌△CBE(SAS),∴∠D= CD=BE, ∠E
6.如图,AB=AD,AC=AE,∠1=∠2,求证:
(1)△ABC≌△ADE; (2)CB=ED. 解:(1)∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠DAE, 又∵AB=AD,AC=AE,∴△ABC≌△ADE(SAS) (2)∵△ABC≌△ADE,∴CB=ED
) D
不一定 2.有两边和其中一边的对角分别相等的两个三角形_____________ 全等.
知识点1:用“SAS”判定两个三角形全等 1.下图中全等的三角形有( D ) A.图1和图2 B.图2和图3
C.图2和图4 D.图1和图3
2.(易错题) 的条件是( D
如图,AB=DB,BC=BE,欲使△ABC≌△DBE,需要增加 )
13.某大学计划为新生配备如图1所示的折叠凳.图2是折叠凳撑开后的侧 面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长相等,O是它们 的中cm,则由以上信息可推得CB的长度是多少?
解: ∵O 是 AB, CD 的中点, ∴OA=OB, OD=OC, 在△AOD 和△BOC OA=OB, 中, ∴CB=AD.∵AD=30 cm, ∠AOD=∠BOC,∴△AOD≌△BOC(SAS), OD=OC, ∴CB=30 cm
9.如图,AB=AC,AD=AE,若要得到“△ABD≌△ACE”,必须添加 一个条件,则下列所添条件不成立的是( B )
A.BD=CE B.∠ABD=∠ACE C.∠BAD=∠CAE D.∠BAC=∠DAE
八年级数学—全等三角形判定一(SSS,SAS)(基础)巩固练习【名校试题+详细解答】

【巩固练习】一、选择题1. △ABC 和△'''A B C 中,若AB =''A B ,BC =''B C ,AC =''A C .则( )A.△ABC ≌△'''A C BB. △ABC ≌△'''A B CC. △ABC ≌△'''C A BD. △ABC ≌△'''C B A2. 如图,已知AB =CD ,AD =BC ,则下列结论中错误的是( )A.AB ∥DCB.∠B =∠DC.∠A =∠CD.AB =BC3. 下列判断正确的是( )A.两个等边三角形全等B.三个对应角相等的两个三角形全等C.腰长对应相等的两个等腰三角形全等D.直角三角形与锐角三角形不全等4. 如图,AB 、CD 、EF 相交于O ,且被O 点平分,DF =CE ,BF =AE ,则图中全等三角形的对数共有( )A. 1对B. 2对C. 3对D. 4对5. 如图,将两根钢条'AA ,'BB 的中点O 连在一起,使'AA ,'BB 可以绕着点O 自由转动,就做成了一个测量工件,则''A B 的长等于内槽宽AB ,那么判定△OAB ≌△''OA B 的理由是( )A.边角边B.角边角C.边边边D.角角边6. 如图,已知AB ⊥BD 于B ,ED ⊥BD 于D ,AB =CD ,BC =ED ,以下结论不正确的是( )A.EC ⊥ACB.EC =ACC.ED +AB =DBD.DC =CB二、填空题7. 如图,AB =CD ,AC =DB ,∠ABD =25°,∠AOB =82°,则∠DCB =_________.8. 如图,在四边形ABCD中,对角线AC、BD互相平分,则图中全等三角形共有_____对.9. 如图,在△ABC和△EFD中,AD=FC,AB=FE,当添加条件_______时,就可得△ABC≌△EFD(SSS)10. 如图,AC=AD,CB=DB,∠2=30°,∠3=26°,则∠CBE=_______.11. 如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC,若∠B =20°,则∠C=_______.12. 已知,如图,AB=CD,AC=BD,则△ABC≌,△ADC≌ .三、解答题13. 已知:如图,四边形ABCD中,对角线AC、BD相交于O,∠ADC=∠BCD,AD=BC,求证:CO=DO.14. 已知:如图,AB ∥CD ,AB =CD .求证:AD ∥BC .分析:要证AD ∥BC ,只要证∠______=∠______,又需证______≌______.证明:∵ AB ∥CD ( ),∴ ∠______=∠______ ( ),在△______和△______中,⎪⎩⎪⎨⎧===),______(______),______(______),______(______ ∴ Δ______≌Δ______ ( ).∴ ∠______=∠______ ( ).∴ ______∥______( ).15. 如图,已知AB =DC ,AC =DB ,BE =CE 求证:AE =DE.【答案与解析】一.选择题1. 【答案】B ;【解析】注意对应顶点写在相应的位置.2. 【答案】D ;【解析】连接AC 或BD 证全等.3. 【答案】D ;4. 【答案】C ;【解析】△DOF ≌△COE ,△BOF ≌△AOE ,△DOB ≌△COA.5. 【答案】A ;【解析】将两根钢条'AA ,'BB 的中点O 连在一起,说明OA ='OA ,OB ='OB ,再由对顶角相等可证.6. 【答案】D ;【解析】△ABC ≌△EDC ,∠ECD +∠ACB =∠CAB +∠ACB =90°,所以EC ⊥AC ,ED +AB =BC +CD =DB.二.填空题7. 【答案】66°;【解析】可由SSS 证明△ABC ≌△DCB ,∠OBC =∠OCB =82412︒=︒, 所以∠DCB = ∠ABC =25°+41°=66°8. 【答案】4;【解析】△AOD ≌△COB ,△AOB ≌△COD ,△ABD ≌△CDB ,△ABC ≌△CDA.9. 【答案】BC =ED ;10.【答案】56°;【解析】∠CBE =26°+30°=56°.11.【答案】20°;【解析】△ABE ≌△ACD (SAS )12.【答案】△DCB ,△DAB ;【解析】注意对应顶点写在相应的位置上.三.解答题13.【解析】证明:在△ADC 与△BCD 中,,,,DC CD ADC BCD AD BC =⎧⎪∠=∠⎨⎪=⎩()...ADC BCD SAS ACD BDC OC OD ∠=∠=∴△≌△∴∴14. 【解析】3,4;ABD ,CDB ;已知;1,2;两直线平行,内错角相等;ABD ,CDB ;AB ,CD ,已知;∠1=∠2,已证;BD =DB ,公共边;ABD ,CDB ,SAS ;3,4,全等三角形对应角相等;AD ,BC ,内错角相等,两直线平行.15.【解析】证明:在△ABC 和△DCB 中D C BAAB DC AC DB BC =CB ⎧⎪⎨⎪⎩==∴△ABC ≌△DCB (SSS ) ∴∠ABC =∠DCB , 在△ABE 和△DCE 中ABC DCB AB DC BE CE =⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△DCE (SAS ) ∴AE =DE.。
三角形全等的判定(SSS、SAS) 习题
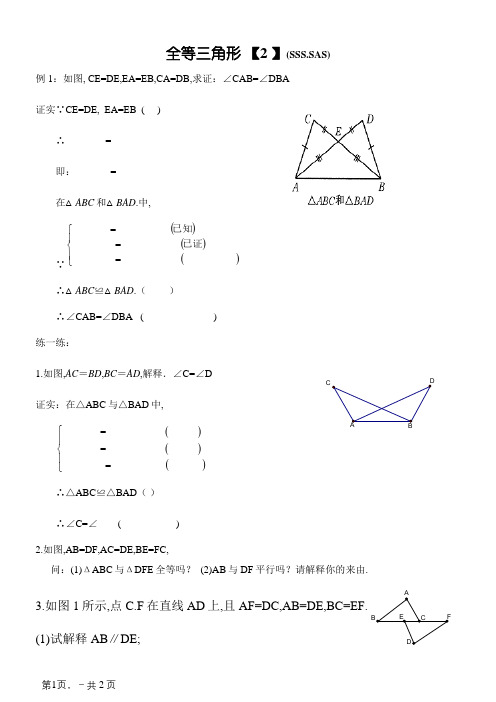
全等三角形 【2 】(SSS.SAS)例1:如图, CE=DE,EA=EB,CA=DB,求证:∠CAB=∠DBA 证实∵CE=DE, EA=EB ( )∴________=________ 即:_______=________ 在△ABC 和△BAD .中,∵()()()⎪⎩⎪⎨⎧===___________________________________________已证已知∴△ABC ≌△BAD .( ) ∴∠CAB=∠DBA ( ) 练一练:1.如图,AC =BD ,BC =AD ,解释.∠C=∠D证实:在△ABC 与△BAD 中,()()()______________________________________________= ⎧⎪= ⎨⎪=⎩ ∴△ABC ≌△BAD ( ) ∴∠C=∠___ ( ) 2.如图,AB=DF,AC=DE,BE=FC,问:(1)ΔABC 与ΔDFE 全等吗? (2)AB 与DF 平行吗?请解释你的来由.3.如图1所示,点C.F 在直线AD 上,且AF=DC,AB=DE,BC=EF.(1)试解释AB ∥DE;ABDFDCE(2)不雅察图2,图3,指出它们是如何由图1变换得到的? (3)在知足已知前提的情形下依据图2,试证实BC ∥EF .4.已知AB ⊥BD,ED ⊥BD,AB=CD,BC=DE,点B.C.D 在一条直线上,求证:AC ⊥CE.5.(多变题)已知AB=CD,AD=CB,求证:∠A=∠C一变:已知AD ∥BC,AD=CB,试证实:△ADC ≌△CBA二变:已知AD ∥BC,AD=CB,AE=CF.试证:△AFD ≌△CEB6.(现实应用)有一湖的湖岸在A.B 之间呈不规矩外形,A.B 之间的距离不能直接测量,你能用已学过的常识或办法设计测量计划并求出A.B 之间的距离吗?做一做:7.如图所示,有一块三角形的镜子,小明不当心弄决裂成1.2两块,现需配成同样 大小的一块.为了便利起见,需带上________块,其来由是__________.8.如图所示,AB ,CD 订交于O ,且AO =OB ,不雅察图形,图中已具备的另一相等 的前提是________,联想到SAS,只需补充前提________,则有△AOC ≌△_______ 9.如图,已知CA=CB,AD=BD,E,F 分离为CB,CA 的中点,求证:DE=DF10.如图,已知AB =AE,∠B =∠E,BC =ED,点F 是CD 的中点.求证:AF ⊥CD.11.已知△ABE 和三角形DEC 均为等边三角形,衔接BD,AC,求证:AC =BD图3图2图1F E D C B A E DF C B AE D CFABD EBACDCB A DCB A F E CB DAFEDCBADBAEFCF C。
全等三角形判定一(SSS,SAS)(基础)巩固练习
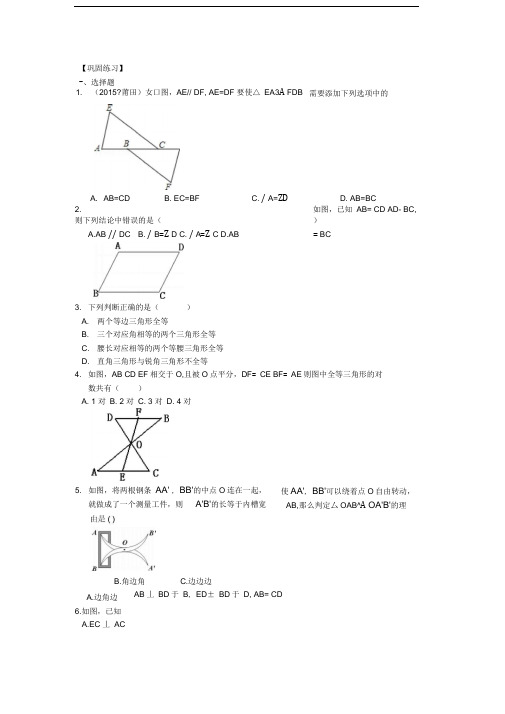
【巩固练习】-、选择题2.如图,已知AB= CD AD- BC,则下列结论中错误的是()A.AB // DCB. / B=Z DC. / A=Z CD.AB = BC3. 下列判断正确的是()A. 两个等边三角形全等B. 三个对应角相等的两个三角形全等C. 腰长对应相等的两个等腰三角形全等D. 直角三角形与锐角三角形不全等4. 如图,AB CD EF相交于O,且被O点平分,DF= CE BF= AE则图中全等三角形的对数共有()A. 1 对B. 2 对C. 3 对D. 4 对B.角边角C.边边边AB丄BD于B, ED± BD于D, AB= CD1. (2015?莆田)女口图,AE// DF, AE=DF 要使△ EA3A FDB 需要添加下列选项中的B. EC=BFC. / A=ZDD. AB=BC5. 如图,将两根钢条AA' , BB'的中点O连在一起,就做成了一个测量工件,则A'B'的长等于内槽宽使AA', BB'可以绕着点O自由转动,AB,那么判定厶OAB^A OA'B'的理A.边角边6.如图,已知A.EC 丄ACA. AB=CDB.EC = ACC.ED + AB = DBD.角角边BC= ED,以下结论不正确的是(D.DC = CB12.、填空题如图,AB= CD AC= DB,Z ABD= 25°,/ AOB= 82°,则/ DCB=点D在AB上,点E在AC上, CD与BE相交于点0,且AD= AE, AB= AC,若/ B = 贝y C= .,△ AD®7.AC BD互相平分,则图中全等三角形共有(2015?虎林市校级二模)如图,已知BD=AC,那么添加一个条件后,能得11.8.9.,/ 3= 26°,则/ CBBAC= ABC^如图,20°,12.三、解答题13. (2014春?章丘市校级期中)如图A B两点分别位于一座小山脚的两端,小明想要测量A、B两点间的距离,请你帮他设计一个测量方案,测出AB的距离.并说明其中的道理.14•已知:如图,AB // CD , AB = CD .求证:AD // BC .分析:要证AD// BC只要证/ ________ =Z __________ ,又需证______ 也_______ .证明:••• AB // CD ( ),二 / ________ =/ _________ ( ),在厶 ______ 和厶_____ 中,_____ 二____ ( ),< _____ = _____ (),、---- = -------- ()‘•••△_______ A___________ ( ).二 / ________ =/ ______ ( ).•- _____ // ______ ( ).15.如图,已知AB= DC AC= DB, BE= CE求证:AE= DE.【答案与解析】一. 选择题1. 【答案】A;【解析】解:••• AE// FD,•••/ A=Z D,•/ AB=CD•AC=BD在厶AEC和厶DFB中,f AE=DF-ZA=ZD,AC=DBk•△EAC^A FDB( SAS ,故选:A.2. 【答案】D;【解析】连接AC或BD证全等.3. 【答案】D;4. 【答案】C;【解析】△ DOF^A COE △ BOF^A AOE △ DOB^A COA.5. 【答案】A;【解析】将两根钢条AA' , BB'的中点O连在一起,说明OA= OA', OB= OB',再由对顶角相等可证•6. 【答案】D;【解析】△ ABC^^ EDC Z ECD^Z ACB=Z CA聊/ ACB= 90°,所以ECL AC, ED + AB = BC+ CD= DB.二. 填空题7. 【答案】66°;82 °【解析】可由SSS证明厶ABC^A DCB Z OBC=Z OCB= 41 , 所以Z DCB=2Z ABC= 25°+ 41 °= 66°8. 【答案】4;【解析】△ AOD^A COB △ AOB^A COD △ ABD^A CDB △ ABC^A CDA.9. 【答案】BC=AD ;【解析】解:添加BC=AD ,r AC=BD•••在△ ABC 和厶BAD 中」BC=AD ,i AB 二AB•△ ABC ◎△ BAD ( SSS),故答案为:BC=AD .10. 【答案】56°;【解析】Z CBE= 26°+ 30°= 56° .11. 【答案】20°;【解析】△ ABE^A ACD( SAS12. 【答案】△ DCB △ DAB【解析】注意对应顶点写在相应的位置上.三. 解答题13. 【解析】解:如图所示:在AB下方找一点O,连接BO并延长使BO=B O,连接AQ并延长使AO=A O,在厶AOB和厶A OB中:f AO=OA?“ ZAOB=ZA V0B y,QB 二OB'•••△AOB2A A OB ( SAS, ••• AB=A B ,量出A B'的长即可.14. 【解析】3, 4;ABD CDB已知;1, 2;两直线平行,内错角相等;ABD CDBAB, CD已知;/ 1 = 7 2,已证;BD= DB公共边;ABD CDB SAS3 , 4,全等三角形对应角相等;AD, BC内错角相等,两直线平行15. 【解析】证明:在厶ABC^n^ DCB中AB = DCAC = DBBC =CB• △ABC^A DCB(SSS•••7 ABC=7 DCB 在厶ABE和△ DCE中AB = DCABC = DCBBE =CE•••△ ABE^A DCE( SAS ••• AE= DE.。
(完整版)全等三角形的性质与判定(SSS、SAS、ASA、AAS)练习题

全等三角形的性质与判定(SSS 、SAS 、ASA 、AAS )练习题1. 如图,在△ABC 中,∠A=90°,D 、E 分别是AC 、BC 上的点,若△ADB ≌△EDB ≌△EDC ,则∠C=2. 如图,把△ABC 绕点C 顺时针旋转35°,得到△A ′B ′C ,A ′B ′交AC 于点D ,若∠A ′DC=90°,则∠A=1题图 2题图 3题图 4题图3. 如图,△AOB 中,∠B=30°,将△AOB 绕点O 顺时针旋转52°,得到△A ′OB ′,边A ′B ′与边OB 交于点C (A ′不在OB 上),则∠A ′CO=4. 如图,△ABC ≌△ADE,BC 的延长线过点E ,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,则∠DEF=5. 如图,Rt △ABC 中,∠BAC=90°,AB=AC ,分别过点B 、C 作过点A 的垂线BC 、CE ,垂足分别为D 、E ,若BD=3,CE=2,求DE 的长.6. 如图,AD 是△ABC 的角平分线,DE ⊥AB ,DF ⊥AC,垂足分别是E 、F ,连接EF,交AD 于G ,试判断AD 与EF的关系,并证明你的结论。
7. 如图所示,在△ABC 中,AD 为∠BAC 的角平分线,DE ⊥AB 于E ,DF ⊥AC 于F ,△ABC 的面积是28cm 2,AB=20cm ,AC=8cm ,求DE 的长。
8. 如图,AD=BD,AD ⊥BC 于D ,BE ⊥AC 于E ,AD 与BE 相交于点H ,则BH 与AC 相等吗?为什么?E F C D BEGB E FEF C AB A'B'BCD D B'AHE9. 已知:BD 、CE 是△ABC 的高,点F 在BD 上,BF=AC,点G 在CE 的延长线上,CG=AB,求证:AG ⊥AF10. 如图:在△ABC 中,BE 、CF 分别是AC 、AB 两边上的高,在BE 上截取BD=AC ,在CF 的延长线上截取CG=AB,连结AD 、AG.试判断AD 与AG 的关系如何?并证明之。
全等三角形判定SAS练习

用符号语言表达为:
在△ABC和△DEF中 AB=DE
B C
D
“SAቤተ መጻሕፍቲ ባይዱ”)
A
∠A=∠D AC=DF
E
F
∴△ABC≌△DEF(SAS)
知识梳理:
A
B SSA不能 判定全等
A
C A
B
D
C
B
D
1.在下列图中找出全等三角形
30º
1
2
3 Ⅲ
Ⅳ 4
5 cm
30º
6
5
30º
7
8
知识应 用
例1、如图,有一池塘,要测池塘两端A、B的距 离,可先在平地上取一个可以直接到达A和B 的点C,连结AC并延长到D, 使CD=CA.连结 BC并延长到E,使CE=CB. 连结DE,那么量出 DE的长,就是A、B的距离.为什么?
知识应 用
证明:在△ABC 和△DEC中
CA CD ACB DCE CB CE
A B
C D
∴△ABC ≌△DEC(SAS)
∴ AB=DE(全等三
E
角形的对应边相等)
例2.如图,已知AB=AC,AD=AE。
求证:∠B=∠C 证明:在△ABD和△ACE中 E AB =AC(已知) B A=A(公共角) AD=AE (已知) A ∴△ABD≌△ACE(SAS) ∴∠B=∠C(全等三角形
DE C A
D
C A
对应角相等)
B
例3 如图,AC=BD,∠CAB= ∠DBA,你 能判断BC=AD吗?说明理由。 C D 证明:在△ABC与△BAD中
AC=BD
∠CAB=∠DBA (已知) A (已知) (公共边) B
全等三角形SAS专题练习知识分享

全等三角形S A S专题练习全等三角形的判定方法SAS专题练习1.如图,AB=AC,AD=AE,欲证△ABD≌△ACE,可补充条件( )A.∠1=∠2B.∠B=∠CC.∠D=∠ED.∠BAE=∠CAD2.能判定△ABC≌△A′B′C′的条件是()A.AB=A′B′,AC=A′C′,∠C=∠C′B. AB=A′B′,∠A=∠A′,BC=B′C′C. AC=A′C′,∠A=∠A′,BC=B′CD. AC=A′C′,∠C=∠C′,BC=B′C3.如图,AB与CD交于点O,OA=OC,OD=OB,∠AOD= ,根据_________可得到△AOD≌△COB,从而可以得到AD=_________.4.如图,已知BD=CD,要根据“SAS”判定△ABD≌△ACD,则还需添加的条件是。
5.如图,AD=BC,要根据“SAS”判定△ABD≌△BAC,则还需添加的条件是6.如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程说明△ABD≌△ACD的理由.解:∵AD平分∠BAC,∴∠________=∠_________(角平分线的定义).在△ABD和△ACD中,∵∴△ABD≌△ACD()7.如图,AC与BD相交于点O,已知OA=OC,OB=OD,第1题第3题第4题第6题第5题求证:△AOB≌△COD证明:在△AOB和△COD中∵∴△AOB≌△COD( )8.已知:如图,AB=CB,∠1=∠2 △ABD 和△CBD 全等吗?9.已知:如图,AB=AC,AD=AE ,∠1 =∠2 。
试说明:△ABD ≌△ACE 。
10.已知:如图,△ABC中, AD⊥BC 于D,AD=BD, DC=DE,∠C=50°。
求∠ EBD的度数。
第7题【经典练习】1.在△ABC 和△C B A '''中,若AB=B A '',AC=C A '',还要加一个角的条件,使△ABC ≌△C B A ''',那么你加的条件是( )A .∠A=∠A ' B.∠B=∠B ' C.∠C=∠C ' D.∠A=∠B '2.下列各组条件中,能判断△ABC ≌△DEF 的是( ) A .AB=DE ,BC=EF ;CA=CD B.CA=CD ;∠C=∠F ;AC=EFC .CA=CD ;∠B=∠E D.AB=DE ;BC=EF ,两个三角形周长相等 3.已知△ABC 的6个元素,则下面甲乙丙三个三角形中,和△ABC 全等的图形是( )A.甲和乙B. 乙和丙C. 没有乙D. 没有甲4.如图工作师傅做门时,常用木条EF 固定矩形门框ABCD ,使其不变形这种做法根据是( ).A 、两点之间线段最短B 、矩形的对称性C 、矩形的四个角都是直角D 、三角形的稳定性5.如果△ABC ≌△DEF ,且△ABC 的周长95cm ,A 、B 分别与D 、E 对应并且AB=30cm ,DF=25 cm ,那么BC 的长等于( )A .40cmB .35cmC .30cmD .25cm 6.如图,AB ∥DE ,CD=BF ,若△ABC ≌△DEF ,还需要补充的条件可以是( )A .AC=EFB .AB=DEC .∠B=∠ED .不用补充 7.如图,∠CAB =∠DBA ,AC=BD ,则下列结论中,不正确的是( )A 、BC=ADB 、CO=DOC 、∠C =∠D D 、∠AOB=∠C +∠DAC B 50°50°72° a bcab c 甲D A C A D FE8.如图,AB=AC ,若AD 平分∠BAC ,则AD 与BC9.阅读理解题:如图:已知AC ,BD 相交于O,OA=OB ,OC=OD. 那么△ABC 与△BAD 全等吗?请说明理由.△ABC 与△BAD 全等吗?请说明理由.小明的解答: 21∠=∠AOD ≌△BOC而BAD=△AOD+△ADB △ABC=△BOC+△AOB所以△ABC ≌△BAD(1)你认为小明的解答有无错误;(2)如有错误给出正确解答;10.如图,点C 是AB 中点,CD ∥BE ,且CD=BE ,试探究11.如图,AE 是,BAC 的平分线∠AB=AC(1)若D 是AE 上任意一点,则△ABD ≌△ACD (2)若D 是AEBCDOA=OOD=OD12.如图,已知AB=AC ,EB=EC ,请说明BD=CD 的理由13. 如图,△ABC ,△BDF 为等腰直角三角形。
全等三角形的判定精选练习题 简单(分SSS、SAS、AAS、ASA、HL分专题)

CBA全等三角形的判定(SSS)不要写在上面,答案写在纸上1、如图1,已知AB=CD,AC=BD,求证:∠A=∠D.图1 图2 图3 图42、如图2,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.请推导下列结论:⑴∠D=∠B;⑵AE∥CF.3、已知如图3,A、E、F、C四点共线,BF=DE,AB=CD.⑴请你添加一个条件,使△DEC≌△BFA;⑵在⑴的基础上,求证:DE∥BF.4、如图4,AB=AC,BD=CD,求证:∠1=∠2.全等三角形的判定(SAS)4、如图4,AB与CD交于点O,OA=OC,OD=OB,求证AD=CB.图7 图8 图95、如图5,已知△ABC中,AB=AC,AD平分∠BAC,求证△ABD≌△ACD6、如图6,已知AB=AD,AC=AE,∠1=∠2,求证∠ADE=∠B.7、如图7,已知AB=AD,若AC平分∠BAD,求证AC平分∠BCD8、如图8,在△ABC和△DEF中,B、E、F、C,在同一直线上,①AB=DE;③∠ABC=∠DEF;④BE=CF. 证明AC=DF9、如图9,AB⊥BD,DE⊥BD,点C是BD上一点,且BC=DE,CD=AB.⑴如图1证明AC与CE垂直⑵如图2,若把△CDE沿直线BD向左平移,使△CDE的顶点C与B重合,此时第⑴问中AC与BE的位置关系还成立吗?(注意字母的变化)【典型题】1.如图1,AB∥图5图2 图32.如图2,已知:AD=AE,ABEACD∠=∠,求证:BD=CE.3.如图3,已知:ABDBACDC∠=∠∠=∠.,求证:OC=OD. 图64.如图4已知:AB=CD,AD=BC,O是BD中点,过O点的直线分别交DA和BC的延长线于E,F.求证:AE=CF.5.如图5,已知321∠=∠=∠,AB=AD.求证:BC=DE.6.如图6,已知四边形ABCD中,AB=DC,AD=BC,点F在AD上,点E在BC上,AF=CE,EF的对角线BD交于O,求证:OF=OE 7. 如图7,已知∠A=∠C,AF=CE,DE∥BF,求证:△ABF≌△CDE.8.如图8,CD⊥AB,BE⊥AC,垂足分别为D、E,BE交CD于F,且AD=DF,求证:AC= BF。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AC.=C A AB,=B A AC,A C AB,A B ,:1''⊥'⊥'如图、已知
求证:△ABC ≌△AB ’C ‘ 2、已知:如图,△ABC 中,点E 、F 分别在AB 、AC 边上,点D 是BC 边中点,且 DF ∥AB,BE=DF .求证: △BED ≌△DFC 3、已知:如图,AC=AB,AE=AD,∠1=∠2.求证:∠3=∠4
4、已知:如图 , AB=DC ,AD=BC , ∠DAB=∠BCD ,求证:△ABD ≌△CDB
5、已知:如图,AB=AC,AE 平分∠BAC.求证:∠DBE=∠DCE .
6、已知:如图,AB=CD , AE=DF , AB ∥CD .D 、E 、F 、A 在同一条直线上。
求证:△ABE ≌△DCF
第1题 第2题 第3题 第4题 第5题 第6题
7、已知:如图,∠1=∠2,BD=CD,求证:AD是∠BAC的平分线.
8、已知:如图,AD是BC上的中线,且DF=DE.求证:BE∥CF.
9、已知:如图, AC=DF,AC∥FD,AB=DE,求证:△ABC≌△DEF
10、已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.
求证:AC∥DF
11、已知:如图 , 四边形ABCD中 , AB∥CD , AD∥BC.求证:△ABD≌△CDB
12、如图,点C是AB中点,CD∥BE,且CD=BE,试探究AD与CE的关系。
第8题
第9题第10题
第11题第7题
A
C
E
第12题。
