二端口网络 习题
二端口网络2

U1b I1b U Zb I 2b 2b
U1 U1a U1b U1a U1b U U U U U 2 2a 2b 2a 2b
I1 I1a I1b I I I 2 2 a 2b
T
U1a U 2a Ta I I 1a 2a
U1b U 2b Tb I I 1b 2b U 2a U1b I 2a I1b
U 2b U1 U 2 T TaTb I I I 1 2 2b
在输入端口 U 5I U S 1 1 在输出端口
U 2 16 I 2
联立可解得
US 3.297U 2
所以
U2 1 0.3033 U S 3.297
并联
两个或两个以上二端口网络的对应端口分别 作并联连接称为二端口网络的并联,如图所示。
6 RC
在该频率下: U2 1 1 2 2 2 U1 1 5 C R 29
串联
两个或两个以上二端口网络的对应端口分别 作串联连接称为二端口网络的串联,如图所示。
串联时,二端口网络参数的计算,采用Z参数方便。
U1a I1a U Z a I 2a 2a
T TaTb
即两个二端口网络级联的等效T参数矩阵等于 各二端口网络的矩阵Ta和Tb之积。 同理,当n个二端口网络级联时,则复合后的 二端网络T参数矩阵为:
T T1 T2 T3
Tn
注意
(1) 级联时T 参数是矩阵相乘的关系,不是对应元素 相乘。
A B A B A B C D C D C D A A BC A B BD C A D C C B D D
电路第十六章(二端口网络)习题

电路第⼗六章(⼆端⼝⽹络)习题第⼗六章(⼆端⼝⽹络)习题⼀、选择题
1.图16—3(a )所⽰⼆端⼝电路的Y 参数矩阵为Y = ,图16—3(b )所⽰⼆端⼝的Z 参数矩阵为Z = 。
2.图16—4所⽰⼆端⼝⽹络的Y 参数矩阵是Y = 。
3.图16—5所⽰回转器的T 参数矩阵为。
4.图16—6所⽰的⼆端⼝⽹络中,设⼦⼆端⼝⽹络1N 的传输参数矩阵为??
D C B A ,则复
合⼆端⼝⽹络的传输参数矩阵为。
5.图16—7所⽰⼆端⼝⽹络的Y 参数矩阵为。
三、计算题
1.图16—8所⽰⼆端⼝⽹络的Z 参数是Ω=1011Z 、Ω=1512Z 、Ω=521Z ,Ω=2022Z 。
试求s U U 2。
2.求图16—11所⽰⼆端⼝⽹络的T 参数。
3.图⽰电路中,⼆端⼝⽹络N 的传输参数矩阵为 2.560.5 1.6T S
Ω??
=
,求(1)L R 等于多少时其吸收功率最⼤?
(2)若9V S U =,求L R 所吸收的最⼤功率max P ,以及此时⽹络N 吸收的功率N P
4.图⽰电路中,直流电源U S =10 V ,⽹络N 的传输参数矩阵为??
=11.0102][T ,t <0时电路处于稳态,t =0时开关S 由a 打向b 。
求t >0时的响应u (t )。
7.已知图⽰电路中,⼆端⼝⽹络N的传输参数矩阵为
1.5
2.5
0.5 1.5
T
S
Ω
=??
,t=0时闭合
开关k。
求零状态响应()
C
i t
本章作业:计算题的3、4、7、8⼩题。
二端口网络习题课

1
2
Na
2S
1
2
N
典型题(4/6)
4 解(1) 方法1
双口网络 Na 的传输参数方程为
1 I1
I2
I2 2
U1 U2 4I2
U1
Na
2S
U2
I1
3U 2
2I2
I2 I2 2U2
1
2
N
U1 U2 4I2 U2 4 I2 2U2 9U2 4I2
I1
3U 2
2I2
3 解(3)用等效电路求解。
R22 R11 9 R12 R21 6
I1 3
3 I2
18V
6
3
I1
3
18 6 //(3 3)
3A
I2
1 2
I1
1.5A
典型题(4/6)
4 图示网络中,双口网络Na 的传输参数矩阵为
1 4 Ta 3 2
求:(1)整个双口网络的传输参数;
(2)当输出端口接1电阻时,输入端口的
gr
i2 u2
i1 i2
gu2 gu1
i1 i2
0 g
g u1
0
u2
i1
g
i2
L r2C
L
u1
u2
C
1 主要内容(续)
二端口元件
(2)负阻抗变换器(NIC) 可将正阻抗变换为负阻抗
负阻抗变换器的方程
i1
i2
u1
NIC
u2
电压反向型
电流反向型
u1 i1
ku2 i2
u1 u2 i1 ki2
u1
i1
k
0
0 u2
二端口网络

二端口网络练习题1. 在图示电路中,已知 R 1=1Ω, R 2=2Ω,α=2,试计算二端口网络的开路阻抗参数矩阵Z 和短路导纳参数矩阵Y ,并说明该网络是否互易网络。
2. 求图示二端口网络的短路导纳矩阵Y 。
3. 已知线性无源二端口网络N 的传输参数矩阵⎥⎦⎤⎢⎣⎡=21.0302T ,今有一电阻R 并联于输出端(如图(a )),则输入电阻等于将R 并联于输入端(如图(b ))时的输入电阻的6倍,求该电阻R 之值。
4. 图示电路中N 为由线性电阻元件构成的二端口网络,当在a 、b 端加100V 电压时,流入网络的电流为2.5A ,同时测得c 、d 端电压u cd =60V ,若将100V 电压加于c 、d 端,则流入网络的电流为2A ,这时测得a 、b 端电压u ab =48V ,求该二端口电阻网络的传输参数。
(a)(b)R 1 ② ②/ ① ①/R 2I 题5图5.在图5所示含二端口网络N 的电路中,已知R 1=2Ω, R 2=1Ω。
开关S 断开时,测得U S =12V, U 1=6V, U 2=2V, 开关S 闭合时,测得U S =12V, U 1=4V, U 2=1V ,求网络N的传输参数矩阵T 。
6 已知如图所示二端口网络N 的短路导纳参数矩阵S ⎥⎦⎤⎢⎣⎡=1223/2Y ,求二端口网络的输入功率P 1和输出功率P 2。
7在图7所示电路中,N 为二端电阻元件构成的双口网络,已知N 的开路阻抗参数矩阵Ω⎥⎦⎤⎢⎣⎡=6/76/16/16/7Z ,试求负载电阻R f =2Ω所吸收的功率。
8. 已知图8 所示二端口网络N 的Z 参数是Z 11=10Ω,Z 1 2=15Ω,Z 21=5Ω,Z 22=20Ω。
试求转移电压比U 2 (S) / U S (S) 之值。
4Ω图7R f =2Ω图8U S 25Ω。
二端口网络 习题

1
解:方法2(按定义)
(1)端口2短路
U1 I1 1 Y11
5 I 2 I1 Y21
4I2
4
I1 U1 U
I2 U1 U
1s
2 0
2 0
1 s 5
(2)端口1短路
U 2 I1 1 Y12
解:列网孔方程
和题设Z矩阵对应,可求得:
6
练习
求图示电路的Y参数矩阵和Z参数矩阵
解:(1)按定义求解
7
解:(2)先进行三角形星形转换
8
3. 求图示二端口电路的Z参数。 解:端口施加电流源,假设频率为ω
9
4. 已知二端口的的矩阵为Z,该二端口是否含有受控源?并求
其Π型等效电路。
解: 由于 Z12 = Z21,所以,该网络不含受控源。 由于Π型电路对应于Y参数
Y12 =Y21 , Y11 =Y22
条件:仅由电阻R、L(M)、C元件构成的无源二端口网络 •对称二端口:
2
(2) Z参数方程
Z11 U1 Z11 I1 Z12 I 2 [Z ] Z 21 U 2 Z 21 I1 Z 22 I 2 Z参数又称开路阻抗参数
Z12 Z 22
Z 参数和Y参数的关系
Z Y
I1
+ U1
1
U1 Z11 I1 U2 Z 21 I1 U1 Z12 I2
I2 0
输入阻抗
I2 0
转移阻抗
I2
N
I1 0
转移阻抗 输入阻抗
+ U2
U2 Z 22 I2
第16章习题课 二端口网络

Z 21 = r + Z 3
Z 22 = Z 2 + Z 3
可见,网络内含有受控源时,Z12 ≠ Z 21。 同样的有 Y12 ≠ Y21。
传输参数 【例4】求图示二端口网络的传输参数。 】求图示二端口网络的传输参数。 解 直接建立传输参数方程
& & & U1 = (10 + 20) I1 = 30 I1 & & & & U = −3I + 20 I = 17 I
2 − 1 1 3 3 3 Yb = S ,Yc = 1 −1 2 − 3 3 6 − 1 6 S 1 3 1 − 1 2 Y = Yb + Yc = S −1 1 2
【例10】求图示二端口网络的 参数。 】求图示二端口网络的T 参数。
由以上结果求得
A = 30 = 1.765 17 C = 1 = 0.0588 S 17
参数。 【例5】求图示二端口网络的 参数。 】求图示二端口网络的H参数 解 直接建立H参数方程
& & & & & & U1 = 2 I1 + 6( I1 + I 2 ) = 8 I1 + 6 I 2 & & & & & & U = 2 I + 6( I + I ) = 6 I + 8I
参数。 【例2】求图示网络的 参数。 】求图示网络的Z参数 解 方法一 用开路法求Z参数
1
+ I & 1 & U
1
Z1 Z3
Z2
& I2 + & U2
实验21二端口网络测试

D 1和A2、B2、C2、D2,并列出它们的传输方程。
二
测量 值
端 输出端开 U11O(V) U12O(V) I11O(mA) 口 路I12=0
网
计算值 A1 B1
络 输出端短 U11S(V) I11S(mA) I12S(mA) C1 D1 I 路U12=0
二
测量 值
端 口 网
输出端开 U21O(V) 路I22=0
输出端开路I2=0
输出端短路U2=0
计算 传输参
数
U1O
I1O
R1O
U1S
IIS
RIS
(V) (mA) (KΩ) (V) (mA) (KΩ)
输入端开路I1=0
U2O
I2O
R2O
(V) (mA) (KΩ)
A=
B=
输入端短路U1=0
C=
D=
U2S
I2S
R2S
(V) (mA) (KΩ)
五、实验注意事项 1. 用电流插头插座测量电流时, 要注意判别电流表的极性及选取 适合的量程(根据所给的电路参数,估算电流表量程)。
电压和电流,即可求出A、B、C、D四个参数,此即为双端口同时测量
法。
2. 若要测量一条远距离输电线构成的二端口网络, 采用同时测量
法就很不方便。这时可采用分别测量法,即先在输入口加电压,而将输
出口开路和短路,在输入口测量电压和电流,由传输方程可得:
U1O A
R1O= ──=──(令I2=0,即输出口开路时)
实验二十一 二端口网络测试
一、实验目的 1. 加深理解二端口网络的基本理论。
2. 掌握直流二端口网络传输参数的测量技术。 二、原理说明 对于任何一个线性网络,我们所关心的往往只是输入端口和输出端 口的电压和电流之间的相互关系,并通过实验测定方法求取一个极其简 单的等值二端口电路来替代原网络,此即为“黑盒理论”的基本内容。 1. 一个二端口网络两端口的电压和电流四个变量之间的关系, 可 以用多种形式的参数方程来表示。本实验采用输出口的电压U2和电流I2 作为自变量,以输入口的电压U1和电流I1作为应变量,所得的方程称为 二端口网络的传输方程,如图21-1所示的无源线性二端口网络(又称为 四端网络)的传输方程为:U1=AU2+BI2;I1=CU2+DI2。 式中的A、B、C、D为二端口网络的传输参数,其值完全决定于网络的 拓扑结构及各支路元件的参数值。这四个参数表征了该二端口网络的基
第10章 习题解答
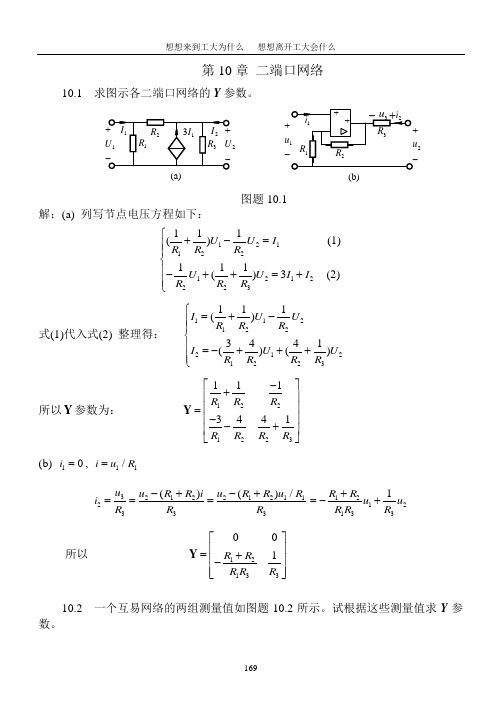
第10章 二端口网络10.1 求图示各二端口网络的Y 参数。
22u (b)图题10.1解:(a) 列写节点电压方程如下:1211221212223111() (1)111()3 (2)U U I R R R U U I I R R R ⎧+-=⎪⎪⎨⎪-++=+⎪⎩ 式(1)代入式(2) 整理得: 1121222121223111()3441()()I U U R R R I U U R R R R ⎧=+-⎪⎪⎨⎪=-+++⎪⎩所以Y 参数为:12212231113441R R R R RR R -⎡⎤+⎢⎥⎢⎥=-⎢⎥-+⎢⎥⎣⎦Y (b) 10i =, 11/i u R =3212212112333()()/u u R R i u R R u R i R R R -+-+===12121331R R u u R R R +=-+ 所以12133001R R R R R ⎡⎤⎢⎥=+⎢⎥-⎢⎥⎣⎦Y10.2 一个互易网络的两组测量值如图题10.2所示。
试根据这些测量值求Y 参数。
(a)(b)22-+U图题10.2解:图(a)中11222A,j2V 2j5j 10V j5A I U U I ===⨯==-,,由Y 参数方程得:11112221222j2j 10 (1)j5j2j 10 (2)I Y Y I Y Y ⎧==⨯+⨯⎨=-=⨯+⨯⎩ 由图(b)得 222jA 1V I Y ==⨯ (3) 对互易网络有:1221Y Y = (4)由式(3) 得: 22j 1S Y =,代入式(2) 得:2112( 2.5j5)S Y Y ==-- 再代入式(1)得:11(12.5j24)S Y =+ 所以12.5j2425j52.5j5j1.+--⎡⎤=⎢⎥--⎣⎦Y S 10.3 求图示各二端口网络的Z 参数。
(b)图题10.3解 (a):按网孔列写KVL 方程得1211221(2)2 (1)2(2)3 (2)R R I RI U RI R R I U U ++=⎧⎨++=+⎩ 将式(1)代入式(2)整理得1122123273U RI RI U RI RI =+⎧⎨=--⎩ 所以 3273RR R R ⎡⎤=⎢⎥--⎣⎦Z(b) 将∆联接的三个阻抗转换成Y 形联接,如图(c)所示,由此电路可直接写出Z 参数1j j j 0+⎡⎤=⎢⎥⎣⎦Z Ω10.4求图示各二端口网络的A 参数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
4I2
4
U&a; 20 1s
5I& 2I& 1Y21U I& & 21U & 201 5s
U & 2I& 11Y12U I& & 12U & 101s
U & 4 2 I & 1 4 I & 2 I & 2 I & 2 U & 4 2 Y 2 2 U I & & 2 2U & 1 01 4s
Y21
I2 U1
U2 0
转移导纳
+
•
U1
N
Y12
I1 U2
U1 0
转移导纳
•
I1
Y22
I2 U2
U1 0
输入导纳
N
•
I2
•
I2 +
•
U2
•互易二端口:
[Y
]
Y11 Y21
Y12
Y22
条件:仅由电阻R、L(M)、C元件构成的无源二端口网络
•对称二端口:
Y12 =Y21, Y11=Y22
2
(2) Z参数方程
其Π型等效电路。 解: 由于 Z12 = Z21,所以,该网络不含受控源。 由于Π型电路对应于Y参数 假设对应的电路如图所示: 可求得其Y参数为:
10
练习. 求图示双T型电路的Y参数。
解:根据互易性与对称性
11
U2 I2
I1 0
输入阻抗
3
二、习题 1. 求下图二端口网络的Y参数矩阵和Z参数矩阵。(作业)
1
解:方法1(列方程)
(UI& & 114I& I1&21I&U 2& )24U&2
UU&&21
5I&1 20I&2 4I&1 20I&2
4I2
4
Z
5 4
20 20
1 1
Y
Z
1
1
1
5 4
4
解:方法2(按定义) (1)端口2短路
习 题 课(二端口)
一、知识点
1. 端口条件
2. 参数方程
从一个端钮流入的电流等于从另一个端钮
流出的电流
i1
+
u1 i1
N
(1) Y参数方程
I1
Y11U1
Y12U 2
I2 Y21U1 Y22U 2
Y → 短路导纳参数
[Y
]
Y11 Y21
Y12
Y22
1
Y11
I1 U1
U2 0
输入导纳
•
I1
U1 Z11I1 Z12I2 U2 Z21I1 Z22I2
[Z
]
Z11
Z
21
Z12
Z
22
Z参数又称开路阻抗参数
Z 参数和Y参数的关系 Z Y 1
Z11
U1 I1
I2 0
Z 21
U2 I1
I2 0
Z12
U1 I2
I1 0
输入阻抗 转移阻抗 转移阻抗
•
I1
+
•
U1
•
I2
+
N
•
U2
Z 22
1 1
Y
1
1
5 4
ZY1 54
20 520
2. 如图所示电路,其Z参数方程为 解:列网孔方程
和题设Z矩阵对应,可求得:
6
练习 求图示电路的Y参数矩阵和Z参数矩阵
解:(1)按定义求解
7
解:(2)先进行三角形星形转换
8
3. 求图示二端口电路的Z参数。 解:端口施加电流源,假设频率为ω
9
4. 已知二端口的的矩阵为Z,该二端口是否含有受控源?并求
