二端口网络相关知识简介
二端口网络的特性阻抗、回转器与负阻抗变换器相关知识培训讲解

+ u2
电流反向型
ui11
u2 ki2
u1
i1
1 0
0 u2
k
i
2
T 参数矩阵
(2) 阻抗变换器关系 (以INIC为例)
I1
I2
U+
1
INIC
U+ 2
ZL
UI11
U 2 kI2
U 2 ZL I2
(1)
INIC变换器
(2)
(3)
UI11
U 2 kI2
(1) (2)
U 2 ZL I2 (3)
端口1入端阻抗为
B ZS D
AB B ZDZS C D C
A D
ZC Z0ZS
2. 传播常数
•
1 I1
•
I2 2
+
+
•
U1
N
•
U2
ZC
1'
2'
一对称二端口,端口2接特性阻抗ZC时,其端口电压、 电流关系为:
UI11
AU 2 BI2 CU 2 DI2
U 2 ZC I2
(1) ( 2) ( 3)
二端口网络的特性阻抗、回 转器与负阻抗变换器相关知
识培训讲解
二端口的特性阻抗
1. 二端口的特性阻抗
•
1 I1
•
I2 2
+
+
•
U1
N
•
U2
ZL
1'
2'
T
参数方程
UI11
AU 2 CU 2
BI2 DI2
当端口2接阻抗ZL时,U 2 Z L I2
•
二端口网络

二端口网络二端口网络是指由两个终端设备所构成的网络系统。
它是一种基于计算机网络技术的网络结构,可以实现设备间的数据传输与通信。
二端口网络常见于家庭或小型企业的局域网(LAN)环境中,用于连接电脑、打印机、路由器、交换机以及其他网络设备。
二端口网络扮演着传输信息的“管道”角色,它为设备间的信息交换提供了可靠的通道。
二端口网络的特点之一是它结构简单、易于构建。
二端口网络通常包括一个网络连接线(如网线或无线信号传输)、两个设备端口和一系列网络服务协议。
这些协议负责设备间信息交换的数据格式和协议规则。
二端口网络的结构简单明了,易操作,对于初学计算机网络的用户来说十分友好。
二端口网络的工作原理是基于分组交换技术。
在数据传输中,发送端将数据传输成一组组数据包(packet),每个数据包都有包头和数据体部分。
包头包含了目标设备的地址信息和其他控制信息;数据体则是实际要传输的数据。
数据包在传输过程中经过多个中继器(如路由器和交换机),每个中继器将数据包解析后转发至下一站,直至传输到目标设备。
在传输过程中,中继器需要参照网络服务协议解析数据包,将数据包放置在正确的端口。
通过这种方式,二端口网络实现了设备间信息的传输与通信。
二端口网络的优点是显而易见的。
首先,它支持松耦合的系统设计。
二端口网络结构简单,设备之间相对独立,可以同时支持多个设备与主机的连接。
其次,二端口网络可以在不同的操作系统平台之间实现联通。
不同设备之间可以使用标准的网络协议通信,从而实现数据传输。
此外,二端口网络还可以实现设备远程控制的功能,对于设备管理和监控来说非常有帮助。
在使用二端口网络的同时,也需要注意一些问题。
首先,网络的带宽和容量限制是不可忽视的。
网络带宽和容量可能会出现瓶颈,影响网络的传输效果。
相比于现代的多端口交换机,二端口网络的传输能力不及多端口交换机,因此在实际应用中需要注意搭建并优化网络结构。
其次,二端口网络传输的数据安全性较低,仅使用协议规则验证。
二端口网络

二端口网络
在计算机网络中,二端口网络是指由两个端口组成的网络连接系统。
这种网络
拓扑结构通常用于简单的局域网或个人网络中。
每个端口代表一个连接点,可以是物理端口或逻辑端口,用于连接设备或网络节点。
二端口网络通常用于小型网络,涉及少量设备之间的通信。
二端口网络的优点
1.简单性:由于只有两个端口,二端口网络的配置和管理相对简单,
不需要复杂的路由配置或协调。
2.高效性:通过直接连接两个设备,二端口网络在数据传输方面通常
比较高效,减少了中间节点的延迟。
3.安全性:相对于复杂的网络拓扑结构,二端口网络的安全性更高,
减少了外部攻击的可能性。
二端口网络的应用
1.个人网络:在家庭或小型办公室环境中,二端口网络常常用于连接
个人计算机、打印机或其他设备,实现简单的数据共享和通信。
2.嵌入式系统:一些嵌入式系统或物联网设备采用二端口网络,用于
设备之间的数据传输和控制。
3.虚拟网络:在虚拟化环境中,二端口网络可以用于连接虚拟机与物
理主机之间,提供基本的通信支持。
二端口网络的发展趋势
随着物联网和边缘计算的发展,二端口网络在一些特定领域仍将发挥重要作用。
同时,随着网络技术的不断进步,二端口网络也可能发展出更多应用场景和改进方面,以适应不断变化的需求。
结语
二端口网络作为一种简单而有效的网络连接系统,在特定的场景下具有独特的
优势,对于一些小型或特定需求的网络环境具有一定的适用性。
同时,二端口网络在简化配置、提高效率和增强安全性方面也有着明显的优势,可以作为一种常见的网络拓扑结构之一。
电工基础第十一章 二端口网络

式中H11、H22、H12、H21称为H参数。对于任何一个互易二端
; 口网络,H参数中只有三个是独立的, 有H12=-H21 网络对称时,
还有 H11H22-H12H21=1。
第二节 二端口网络的参数方程
2.混合(H)参数
H11
U&1 I&1
U&2 0
H 21
I&2 I&1 U&2 0
H12
由于Y参数在输入或输出端口短路时确定,故也称为短路导纳参数。
第二节 二端口网络的参数方程
3.Y 参数矩阵
导纳(Y) 参数方程可写成矩阵形式
式中
I1
I2
Y11 Y21
Y12
Y22
U1 U 2
Y
U1
U2
第一节 二端口网络的概念
二端口网络内部含有电源时称为含源二端口网络;内 部没有电源时称为无源二端口网络。根据构成网络的 元件是线性还是非线性,二端口网络又可以分为线性 和非线性两种。本章主要讨论无源线性二端口网络.
第二节 二端口网络的参数方程
一.导纳(Y)参数方程
1.导纳(Y) 参数方程
I&1
U&1 U&2
H 22
I&2 U&2
I& 1 0
I& 1 0
式中:H11为输出端口短路时输入端口的入端阻抗。
H21为输出端口短路时对输入端口的转移电流比。
H12为输入端口开路时对输出端口的转移电压比。
第十一章二端口网络解析

第二节 二端口网络的参数方程
一、导纳参数方程
1. 导纳参数方程
I1 I2
Y11U1 Y12U 2 Y21U1 Y22U 2
上式也称为Y参数方程,式中Y11、Y12、Y21、Y22
称为 Y参数,具有导纳的性质,是一组只与网络内
部结构、参数及电源频率有关而与电源大小无关的
参数。
电工基础
3. A参数矩阵
A=
A
A11 A21
A12
A22
线性无源二端口网络即互易二端口网络的A参数中只
有三个是独立的。存在
A11 A22 A12 A21 1
电工基础
第二节 二端口网络的参数方程
四、混合参数方程
1. 混合参数方程
U1 H11I1 H12U 2
I2
H 21I1
H 22U 2
•
•
•
•
图示网络P 满足端口条件 I 1 I1'
;I2
I
' 2
形成两个端口,称之为二端口网络或双口网络。
电工基础
第一节 二端口网络的概念
二端口网络内部含有电源(包括独立电源和受控电源) 时称为含源二端口网络;内部没有电源时称为无源二端口 网络。根据构成网络的元件是线性还是非线性,二端口网 络又可以分为线性和非线性两种。
第十一章 二端口网络
本章重点 二端口网络的参数方程 二端口网络的等效电路
电工基础
第十一章 二端口网络
主要内容 第一节 二端口网络的概念 第二节 二端口网络的参数方程 第三节 二端口网络的特性阻抗 第四节 二端口网络的等效电路 第五节 二端口网络的连接 第六节 理想变压器 本章小结
电工基础
第一节 二端口网络的概念
第九章二端口网络

例:Z参数←→Y参数
由Z参数方程
U U12
Z11I1 Z12I2 Z21I1 Z22I2
求解出
I1 和
I2
即:II21ZZ2ZZ221UU11ZZ1Z21Z1UU22
得到 Y参数方程。其中 Z = Z11Z22 –Z12Z21≠0
II21ZZ2ZZ221UU11ZZ1Z21Z1UU22
Y11
Y21
A Y22 Y21
B 1 CY12Y21Y11Y22 D Y11
Y 21
Y21
Y21
(2)无源线性二端口, A, B, C, D4个参数中将
只有3个是独立的。
Y 1 2 Y 2 ,1 A B D Y C 1 Y Y 2 2 2 1 1 2 Y 1 Y 2 2 Y 2 2 1 Y 1 1 Y 2 1 2 Y Y 1 2 2 1 1
各参数之间的关系 见表9-2。
【例9.5】 求示电路的Z参数,并由Z参数转换为Y参数。
解:Z参数为
Z11
U1 I1
|I202j
Z12U I21 I10j Z21
I1 2Ω +
U1
-
3Ω •
1H •
I2 +
U 2
-
Z Z11Z22 Z12Z21
Z22
U2 I2
|I103j
5j6
Z112j Z12Z21j
3.了解二端口网络等效网络的定义和条件,能够画出 Z,Y参数的等效网络,并能熟练应用。
4.深刻理解二端口网络函数的定义,并能用参数表示 转移函数;
5.了解二端口网络的连接方式及其参数计算公式,了 解典型的二端口元件模型的定义、端口伏安关系、性 质及应用。
9.1 概述
二端口网络

第五部分 二端口网络(一)基本概念和基本定理1、二端口网络的端口方程和参数 (1)端口特性方程在两个端口的四个变量1U 、2U 、1I 、2I 中任取两个为变量,另两个为函数构成的方程。
电压、电流方向如图示。
(2)描述二端口的四个参数矩阵Z 参数对于由线性R 、L (M )、C 元件组成的任意二端口无源网络都有1221Z Z =,即Z 参数矩阵是对称的。
对于对称二端口有1221ZZ =、1122Z Z =Y 参数对于由线性R 、L (M )、C 元件组成的任意二端口无源网络都有1221Y Y =,即Y 参数矩阵是对称的。
对于对称二端口有1221YY =、1122Y Y =T 参数对于由线性R 、L (M )、C 元件组成的任意二端口无源网络都有1AD BC -=,即T 参数矩阵是对称的。
对于对称二端口有A D =.H 参数2、二端口等效电路(1)T 型电路11112Z Z Z =-212Z Z =32212Z Z Z =-(2) π型电路11112Y Y Y =+2122Y Y Y =-=- 3221Y Y Y =+ (3)如果二端口不互易,则等效T 型电路含有受控电压源,如图(4)如果二端口不互易,则等效π型电路含有受控电流源,如图3、二端口的连接(1)级联(2)并联(3)串联4、回转器和复阻抗变换器(1)回转器是一种线性非互易的多端元件。
互易定理不适应回转器。
r 和g分别称为回转电阻和回转电导,简称回转常数。
(2)负阻抗变换器电流反向型:1212,UU I kI ==,电压的大小和方向均不改变;但电流1I 经传输后变为2kI ,即改变了方向;电压反向型:1212,UkU I I =-=-,电压改变了极性(方向),但电流方向不变;NIC 可把正阻抗变为负阻抗。
(二)典型例题及解题方法分析例题1:图示电路二端口网络是由线性电阻构成的,此对称二端口的传输参数A=2,B=30,若将电阻LR并联在22'-两端,输入端11'-的入端电阻为将电阻LR 并联在11'-两端的入端电阻的6倍,求LR解法1:由于二端口网络是由线性电阻构成的,所以有AD-BC=1,又是对称二端口,有A=D=2,C=(AD-1)/B=0.1对于上面左图 22L UR I =-122122U AU BI I CU DI =-⎧⎨=-⎩1212()()L L U AR B I I R C D I =-+⎧⇒⎨=-+⎩112300.12L L in L L U AR B R R I CR D R ++⇒===++ 对于上面右图 20I=11'20'//'20LL i n LL L AR U R A C R R A I C R R C⇒====++ 6'in in R R =3in R =Ω解法2由于二端口网络是由线性电阻构成的对称二端口,A=D=2,C=(AD-1)/B=0.1。
十六章 二端口网络
U 2
11
二端口网络的Y、Z参数特性:
1、对于线性R、L(M)、C元件构成的 任何无源二端口,Z12=Z21,Y12=Y21
2、对于对称的二端口,Z11=Z22,Y11=Y22 3、Z=Y-1参数
I 1 I 2
方法一:分别求Z四个 参数
+ -
+
-
U 1
第十六章 二端口网络(369)
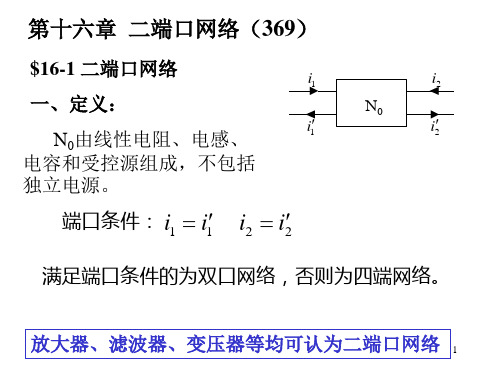
$16-1 二端口网络 一、定义: N0由线性电阻、电感、 电容和受控源组成,不包括 独立电源。 端口条件: i1
i1
i1
i2
N0
i2
i1
i2 i2
满足端口条件的为双口网络,否则为四端网络。 放大器、滤波器、变压器等均可认为二端口网络
1
二端口网络分析特性: 1、对于二端口网络,主要分析端口的电流和电压, 不涉及内部电路的工作状况。因此,本章主要讨论 端口u、i为变量的电路方程(二端口VAR约束方程) 2、二端口网络端口有四个物理量(u1、i1、u2、i2), 若其中两个为自变量,另两个为应变量,可有六组 表征网络特性的独立方程:
4
方法二:分别求出四个Y参数,从而得出Y矩阵
根据方程
1 Y1 1U 1 Y1 2U 2 I 2 Y2 1U 1 Y2 2U 2 I
0 ,U 1V,则如图 1、令 U 1 2
I Y1 2 1 U2
I 1 U 1
0 U 1
I 1
二、电流控制型二端口VAR方程
+
I 1
U 1 -
No
+
i2 ) u1 f(i1 , i2 ) u 2 f(i1 , 结构电 路 如 图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对称二端口只有两个参数是独立的。
对称二端口是指两个端口电气特性上对称。电路结 构左右对称的,端口电气特性对称;电路结构不对称的 二端口,其电气特性也可能是对称的。这样的二端口也 是对称二端口。使用时可以不分彼此。
•
I1 2
+
•
U1
5
10 10
•
•
I2
I1 2
++
U U •
•
21
2
•
I2
+ 4 •
U2 2
U 2
Y21 Δ
I1
Y11 Δ
I2
Z 21 I1
Z22 I2
其中 =Y11Y22 –Y12Y21
其矩阵形式为
U U
1 2
Z11
Z
21
Z12 Z 22
I1 I2
Z
Z11
Z
21
Z12
Z
22
称为Z参数矩阵
Z参数的实验测定
U 1 Z11I1 Z12 I2 U 2 Z21I1 Z22 I2
互易 对称
Y Y12=Y21 Y11=Y22
Z Z12=Z21 Z11=Z22
T
H
detA=1 H12= -H21 T11=T22 detH=1
5 .含有受控源的电路四个独立参数。
§3 二端口的等效电路
(1) 两个二端口网络等效: 是指对外电路而言,端口的电压、电流关系相同。
(2) 求等效电路即根据给定的参数方程画出电路。
i2
–
1 i1 3
4 i2
1-1’ 2-2’是二端口
3-3’ 4-4’不是二端口,是四端网络
i1' i1 i i1 i2' i2 i i2
不满足端口条件
2 +
u2 – 2
约定
1. 讨论范围
网络含线性 R、L、C、M与线性受控源
不含独立源
2. 参考方向
+
i1
u1 –
i1
线性RLCM 受控源
u1 nu2
1 i1 n i2
i1
+ u1
即
u1
i1
n 0
0 1 n
u2 i2
n:1
i2
+ u2
n 0
则
T
0
1
n
例2
I1 1
求T参数 + U1
I1 1
2
+
U1
2
2 2
I2
+ U2
U 1 T11U 2 T12 I2 I1 T21U 2 T22 I2
Y12U 2 Y22U 2
解一
•
I1
Yb
+
•
•
U1
Ya g U 1
•
I1
Yb
•
U1 0
•
gU1 Ya
•
I1
Yb
•
I2
+
•
+
•
U1
Ya g U 1
•
U2
•
I2
Y11
I1 U 1
U 2 0 Ya Yb
•
U
•
I2
2 +
0 Y21
I2 U 1
Y12
U 2
UI12
0
U1
Yb g 0 Yb
•
U2
U 1
21
U 2
I2
12
U 1
22
U 2
令
Y
Y11 Y21
Y12
Y22
称为Y 参数矩阵
或者由叠加原理可得:
I1 Y11U 1 Y12U 2 I2 Y21U 1 Y22U 2
I1 I2
Y11U 1 Y21U 1
Y12U 2 Y22U 2
端U1口和电U 2流共I同1和作I用2 可产视生为。
i2
+
u2 – i2
§2 二端口的参数和方程
+ i1 u1 -
i2 + u2 -
端口物理量4个 i1 i2 u1 u2
端口电压电流有六种不同的方程来表示,即可用六套 参数描述二端口网络。
•
一、 Y 参数和方程
I1
•+
设有
Z11 I1
l 个独立回路
Z12 I2 Z1l Il
U1 U1 -
Z21I1 Z22 I2 Z2l Il U 2
Y22
I2 U 2
Y U1 0
b
解二
•
I1
+
•
U1
Yb
•
Ya g U 1
•
I2
+
•
U2
I1 YaU1 Yb (U1 U 2 ) I2 Yb (U 2 U1 ) gU1
I1 (Ya Yb )U1 YbU 2
I2 ( g Yb )U1 YbU 2
Y
Ya Yb g Yb
U 2 0 Ya Yb U 2 0 Yb
•
I2
+
•
Y12
I1 U 2
U1 0 Yb
U2
Y22
I2 U 2
U 2 0 Yb Yc
互易二端口
Y
Ya Yb
Yb
若 Ya=Yc
•
Yb
Yb
Yc
+
•
U1
I1
Yb
Ya
Yc
•
I2
+
•
U2
有 Y12=Y21 ,又Y11=Y22 (电气对称),称为对称二端口。
U 1
Y22 Y21
U 2
1 Y21
I2
可得
T11
Y22 Y21
I1
Y12
Y11Y22 Y21
U 2
Y11 Y21
I2
1 T12 Y21
T21
Y12Y21 Y11Y22 Y21
T22
Y11 Y21
其矩阵形式
UI11
T11 T21
T12
T22
U 2 I2
(注意负号)
T
T11 T21
Z11 UI11 I2 0
Z 21
U 2 I1
I2 0
Z12 UI21 I1 0
Z 22
U 2 I2
I1 0
Z参数又称开路参数、阻抗参数
U 1
Y22 Δ
I1
Y12 Δ
I2
Z11 I1
Z12 I2
U 2
Y21 Δ
I1
Y11 Δ
I2
Z 21 I1
Z22 I2
互易二端口
Z12 Z21
对称二端口
2. 二端口(two-port)
当一个电路与外部电路通过两个端口连接时称 此电路为二端口网络。
+
i1
u1 –
i1
线性RLCM 受控源
i2
+
u2 – i2
3. 二端口网络与四端网络
i1
i2
i1
i2
i1
i2
二端口
i1
i2
具有公共端的二端口
i2 i1
i3 i4
四端网络
例
1 +
i1
i 3
R
4 i2
u1
i1
T 参数的实验测定
U 1 T11U 2 T12 I2 I1 T21U 2 T22 I2
T11
U 1 U 2
I2 0
T21
I1 U 2
I2 0
开路参数
T12
U 1 I2
U 2 0
T22
I1 I2
U 2 0
短路参数
例1 求所示电路的T参数
U 1 T11U 2 T12 I2 I1 T21U 2 T22 I2
I1 1
2 I2
+ U2
+ U1
2
T11
U1 U2
1 2 I2 0 2 1.5
T12
U1 I2
U2 0
I1[1 (2 // 2)] 4 Ω 0.5I1
T21
I1 U2
I2 0 0.5 S
T22
I1 I2
U2 0
I1 0.5I1
2
四、H 参数和方程 H 参数也称为混合参数
H 参数方程
(2)有些电路只存在某几种参数。
•
I1
2
•
I2
+
+
•
•
U1
U2
0.5s 0.5s
Y 0.5s
0.5s
Z参数 不存在
•
I1 +
•
U1
•
I2 +
•
2 U 2
2 Z 2
2 2
Y 参数不存在
n:1 存在T参数H参数 Z,Y 均不存在
3. 可用不同的参数表示以不同的方式连接的二端口。
4. 线性无源二端口
互易二端口网络四个参数中只有三个是独立的。
例1. 求Y 参数。
I1 Y11U 1 Y12U 2
I2
Y21U 1
Y22U 2
解:
•
I1
Yb
+
•
U1
Ya
Yc
•
I1
Yb
•
U1 0
Ya Yc
Y12 Y21 Yb
•
I1
+
•
U1
Yb
Ya
Yc
•
I2
